Формулы приведения тригонометрических функций
Формулы приведения тригонометрических функцийФормулы привидения тригонометрических функций представлены в виде таблицы. Ниже находятся некоторые формулы приведения в табличном виде. Еще ниже эти формулы приведения расписаны для некоторых тригонометрических функций в виде тригонометрических тождеств.Таблицы значений тригонометрических функций находятся на другой странице.
Формулы привидения для синуса выглядят так:
sin (π/2 + α) = cos α
sin (π + α) = — sin α
sin (3π/2 + α) = — cos α
sin (π/2 — α) = cos α
sin (π — α) = sin α
sin (3π/2 — α) = — cos α
sin (2π — α) = — sin α
Формулы приведения для тригонометрической функции синус будут следующие. Синус угла пи пополам (пи/2) плюс или минус угол альфа равняется косинусу угла альфа.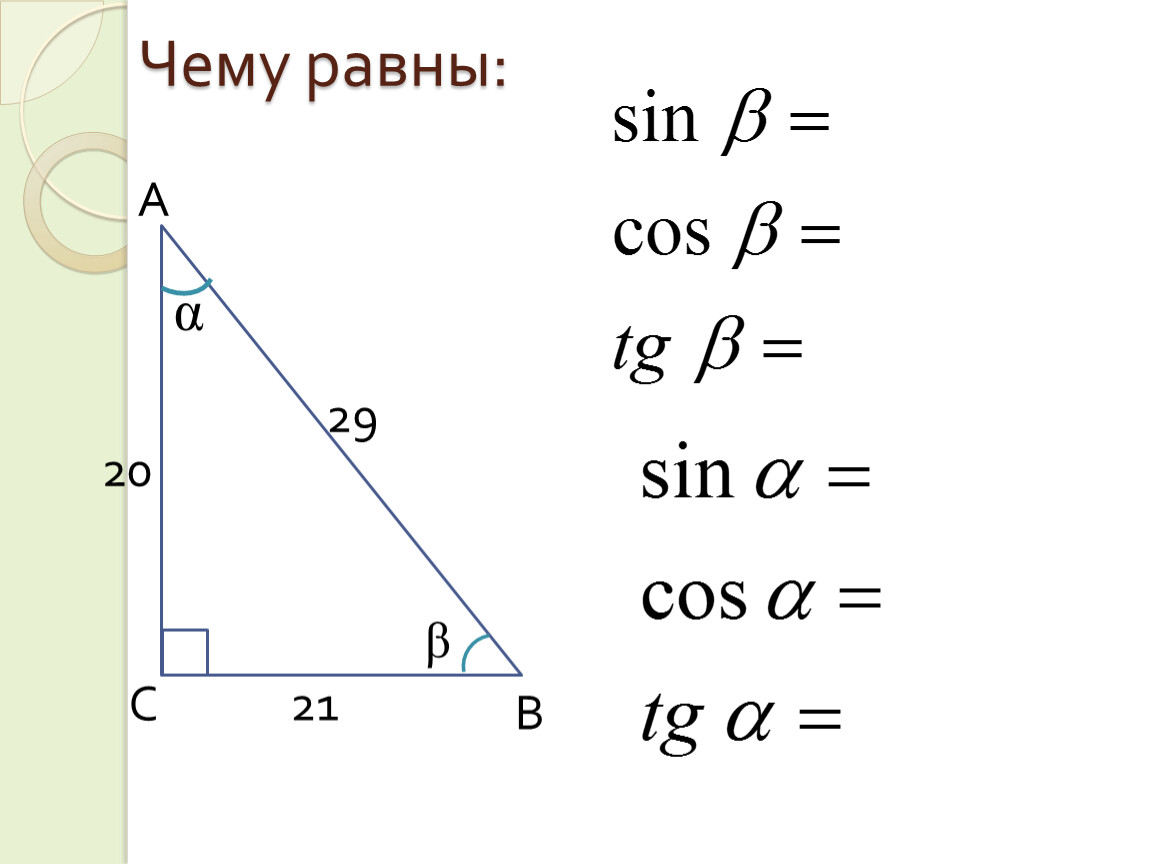
Тригонометрические формулы привидения для косинуса приобретают такой вид:
cos (π/2 + α) = — sin α
cos (π + α) = — cos α
cos (3π/2 + α) = sin α
cos (π/2 — α) = sin α
cos (π — α) = — cos α
cos (3π/2 — α) = — sin α
cos (2π — α) = cos α
Для косинуса формулы приведения имеют следующий вид. Косинус угла пи пополам (пи/2) плюс угол альфа и косинус три вторых пи минус альфа равняются минус синусу угла альфа.
Тригонометрическая функция тангенс имеет следующие формулы привидения:
tg (π/2 + α) = — ctg α
tg (π + α) = tg α
tg (3π/2 + α) = — ctg α
tg (π/2 — α) = ctg α
tg (π — α) = — tg α
tg (3π/2 — α) = ctg α
tg (2π — α) = tg α
Тригонометрические формулы приведения функции тангенс tg. Тангенс угла пи деленное на два плюс альфа и угла три вторых пи плюс альфа приравниваются минус котангенсу угла альфа. Тригонометрическая функция тангенс угла пи на два или три пи деленное на два (3/2 пи) минус альфа равна котангенсу альфа. Тангенс угла пи минус альфа равен минус тангенсу угла альфа. Формулы приведения для тангенса пи плюс альфа и тангенса два пи минус альфа равняются тангенсу угла альфа. Тригонометрические тождества. Перевод тангенса в котангенсы.
Тригонометрическая функция тангенс угла пи на два или три пи деленное на два (3/2 пи) минус альфа равна котангенсу альфа. Тангенс угла пи минус альфа равен минус тангенсу угла альфа. Формулы приведения для тангенса пи плюс альфа и тангенса два пи минус альфа равняются тангенсу угла альфа. Тригонометрические тождества. Перевод тангенса в котангенсы.
Тригонометрическая функция тангенс имеет следующие формулы привидения:
ctg (π/2 + α) = — tg α
ctg (π + α) = ctg α
ctg (3π/2 + α) = — tg α
ctg (π/2 — α) = tg α
ctg (π — α) = — ctg α
ctg (3π/2 — α) = tg α
ctg (2π — α) = ctg α
Формулы приведения функции котангенс ctg угла. Для угла 1/2 пи плюс альфа и угла 3/2 пи плюс альфа котангенс равняется минус тангенсу -tg угла альфа. Если в этих же выражениях угол альфа не прибавляется, а вычитается, тогда котангенс такого угла равняется тангенсу угла альфа. Функция котангенс пи минус альфа равна минус котангенсу угла альфа. Котангенс угла пи плюс альфа и 2 пи минус альфа будет равен котангенсу угла альфа. Тригонометрические тождества и формулы тригонометрия. Перевод котангенсов в тангенсы.
Функция котангенс пи минус альфа равна минус котангенсу угла альфа. Котангенс угла пи плюс альфа и 2 пи минус альфа будет равен котангенсу угла альфа. Тригонометрические тождества и формулы тригонометрия. Перевод котангенсов в тангенсы.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
17 января 2010 года — 1 декабря 2018 года.
© 2006 — 2021 Николай Хижняк. Все права защищены.
Формулы приведения в тригонометрии: примеры, таблицы, доказательства
Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций синус, косинус, тангенс и котангенс с углами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно. \circ \pm \alpha`):
\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
Мнемоническое правило формул приведения или как их запомнить
Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.Само привило содержит 3 этапа:
- Аргумент функции должен быть представлен в виде `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
- Для аргументов `\frac {\pi}2 \pm \alpha`, `\frac {3\pi}2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
- Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:
1. \circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac{\pi}2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac{\pi}2-\alpha)= — cos (\frac{\pi}2-\alpha)= — sin \alpha`.
Ответ: `cos(\frac {7\pi}2 — \alpha)=- sin \alpha`.
Лошадиное правило
Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?
Итак, мы имеем функции с аргументами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac {\pi}2`, `\pi`, `\frac {3\pi}2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac {\pi}2` и `\frac {3\pi}2` на вертикальной оси ординат.
Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.
То есть для аргументов с ключевыми точками, расположенными на горизонтальной оси, мы отвечаем «нет», мотая головой в стороны. А для углов с ключевыми точками, расположенными на вертикальной оси, мы отвечаем «да», кивая головой сверху вниз, как лошадь 🙂
Рекомендуем посмотреть видеоурок, в котором автор подробно объясняет, как запомнить формулы приведения без заучивания их наизусть.
Практические примеры использования формул приведения
Применение формул приведения начинается еще в 9, 10 классе. Немало задач с их использованием вынесено на ЕГЭ. Вот некоторые из задач, где придется применять эти формулы:
- задачи на решение прямоугольного треугольника;
- преобразования числовых и буквенных тригонометрических выражений, вычисление их значений;
- стереометрические задачи.
Пример 1. Вычислите при помощи формул приведения а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`. \circ=-\frac{\sqrt 3}2`.
\circ=-\frac{\sqrt 3}2`.
Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac {9\pi}8` и `cos \frac {9\pi}8`; 2) `sin \frac {\pi}8` и `cos \frac {3\pi}10`.
Решение: 1)`sin \frac {9\pi}8=sin (\pi+\frac {\pi}8)=-sin \frac {\pi}8`
`cos \frac {9\pi}8=cos (\pi+\frac {\pi}8)=-cos \frac {\pi}8=-sin \frac {3\pi}8`
`-sin \frac {\pi}8> -sin \frac {3\pi}8`
`sin \frac {9\pi}8>cos \frac {9\pi}8`.
2) `cos \frac {3\pi}10=cos (\frac {\pi}2-\frac {\pi}5)=sin \frac {\pi}5`
`sin \frac {\pi}8<sin \frac {\pi}5`
`sin \frac {\pi}8<cos \frac {3\pi}10`.
Доказательство формул приведения
Докажем сначала две формулы для синуса и косинуса аргумента `\frac {\pi}2 + \alpha`: ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha` и` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.
Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`.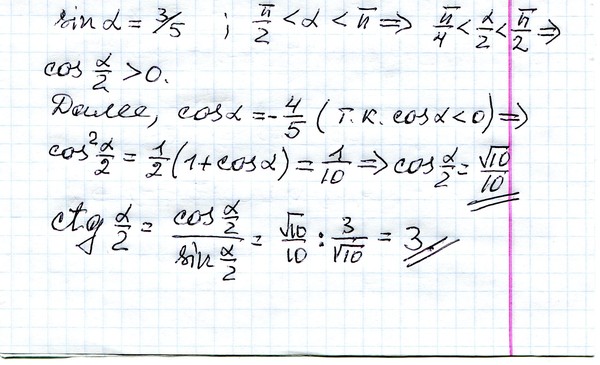 Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Выходя из определения тангенса и котангенса, получим ` tg(\frac {\pi}2 + \alpha)=\frac {sin(\frac {\pi}2 + \alpha)}{cos(\frac {\pi}2 + \alpha)}=\frac {cos \alpha}{-sin \alpha}=-ctg \alpha` и ` сtg(\frac {\pi}2 + \alpha)=\frac {cos(\frac {\pi}2 + \alpha)}{sin(\frac {\pi}2 + \alpha)}=\frac {-sin \alpha}{cos \alpha}=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac {\pi}2 + \alpha`.
Чтобы доказать формулы с аргументом `\frac {\pi}2 — \alpha`, достаточно представить его, как `\frac {\pi}2 + (-\alpha)` и проделать тот же путь, что и выше.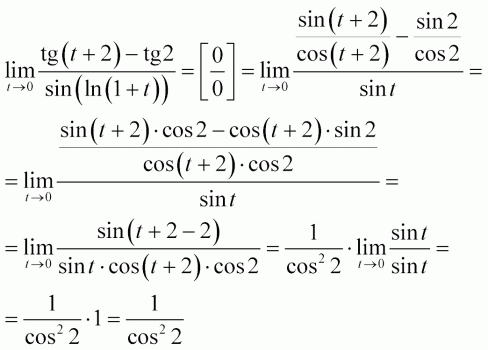 Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac {\pi}2 +(\frac {\pi}2+\alpha)` и `\frac {\pi}2 +(\frac {\pi}2-\alpha)` соответственно.
А `\frac {3\pi}2 + \alpha` и `\frac {3\pi}2 — \alpha` как `\pi +(\frac {\pi}2+\alpha)` и `\pi +(\frac {\pi}2-\alpha)`.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Формулы приведения / Блог / Справочник :: Бингоскул
Таблица формул приведения
Два правила формул приведения
- при 900 и при 2700 (в виде (π/2 ±a) или (3*π/2 ±a)) — функция меняется на кофункцию (sin на cos либо в обратную сторону, tg на ctg либо в обратную).
- при 1800 и при 3600 (в виде (π ±a) или (2*π ±a)) — функция НЕ изменяется.

2 способа запоминания формул приведения
1. «Правило лошади»:
- Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
- Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
- Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
2. Использование четности и периодичности.
нечетная функция
- sin (-α) = -sin α
- tg (-α) = -tg α
- сtg (-α) = -сtg α
четная функция
Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими:
- sin α, cos α — периодические функции с наименьшим положительным периодом 2π: sin(α+2kπ) = sin α,cos(α+2kπ) = cos α, k ∈ Z.

- tg α, ctg α — периодические функции с наименьшим положительным периодом π: tg(α+kπ) = tgα, ctg(α+kπ) = ctg α, k ∈ Z.
Формулы приведения в виде списка
sin
- sin(900 — α) = cos α
- sin (900 + α) = cos α
- sin (1800 — α) = sin α
- sin (1800 + α) = -sin α
- sin (2700 — α) = -cos α
- sin (2700 + α) = -cos α
- sin (3600 — α) = -sin α
- sin (3600 + α) = sin α
cos
- cos (900 — α) = sin α
- cos (900 + α) = -sin α
- cos (1800 — α) = -cos α
- cos (1800 + α) = -cos α
- cos (2700 — α) = -sin α
- cos (2700 + α) = sin α
- cos (3600 — α) = cos α
- cos (3600 + α) = cos α
tg
- tg(900 — α) = ctg α
- tg (900 + α) = -ctg α
- tg (1800 — α) = -tg α
- tg (1800 + α) = tg α
- tg (2700 — α) = ctg α
- tg (2700 + α) = -ctg α
- tg (3600 — α) = -tg α
- tg (3600 + α) = tg α
ctg
- ctg (900 — α) = tg α
- ctg (900 + α) = -tg α
- ctg (1800 — α) = -ctg α
- ctg (1800 + α) = ctg α
- ctg (2700 — α) = tg α
- ctg (2700 + α) = -tg α
- ctg (3600 — α) = -ctg α
- ctg (3600 + α) = ctg α
Угол альфа α находится в интервале 0 — 90°.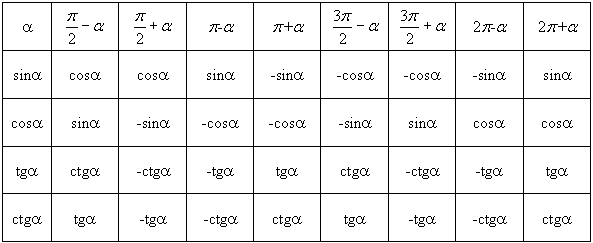 {\circ}270∘
{\circ}270∘
Эти же точки, отмеченные на тригонометрическом круге. cosα\cos \alphacosα — координата xxx, sinα\sin\alphasinα — координата yyy.
cosα\cos \alphacosα — координата xxx, sinα\sin\alphasinα — координата yyy.
Формулы приведения
Для определения значения f(x+πk2)f(x+\frac{\pi k}{2})f(x+2πk), где fff — одна из функций sin\sinsin, cos\coscos, tg\text{tg}tg или ctg\text{ctg}ctg, используются формулы приведения.
| β=\beta=β= | π2+α\frac{\pi }{2}+\alpha2π+α | π+α\pi +\alphaπ+α | 3π2+α\frac{3\pi }{2}+\alpha23π+α | π2−α\frac{\pi }{2}-\alpha2π−α | π−α\pi -\alphaπ−α | 3π2−α\frac{3\pi }{2}-\alpha23π−α |
| sinβ\sin\betasinβ | cosα\cos\alphacosα | −sinα-\sin\alpha−sinα | −cosα-\cos\alpha−cosα | cosα\cos\alphacosα | sinα\sin\alphasinα | cosα\cos\alphacosα |
| cosβ\cos\betacosβ | −sinα-\sin\alpha−sinα | −cosα-\cos\alpha−cosα | sinα\sin\alphasinα | sinα\sin\alphasinα | −cosα-\cos\alpha−cosα | −sinα-\sin\alpha−sinα |
| tgβ\text{tg}\betatgβ | −ctgα-\text{ctg}\alpha−ctgα | tgα\text{tg}\alphatgα | −ctgα-\text{ctg}\alpha−ctgα | ctgα\text{ctg}\alphactgα | −tgα-\text{tg}\alpha−tgα | ctgα\text{ctg}\alphactgα |
| ctgβ\text{ctg}\betactgβ | −tgα-\text{tg}\alpha−tgα | ctgα\text{ctg}\alphactgα | −tgα-\text{tg}\alpha−tgα | tgα\text{tg}\alphatgα | −ctgα-\text{ctg}\alpha−ctgα | tgα\text{tg}\alphatgα |
Вместо запоминания формул можно использовать .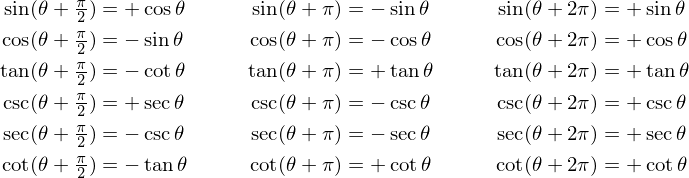 2 \frac{x}{2}=\frac{1-\cos x}{1+\cos x}tg22x=1+cosx1−cosx — тангенс половинного угла;
2 \frac{x}{2}=\frac{1-\cos x}{1+\cos x}tg22x=1+cosx1−cosx — тангенс половинного угла;
tgx2=sinx1+cosx=1−cosxsinx\text{tg} {\frac{x}{2}}=\frac{\sin x}{1+\cos x}=\frac{1-\cos x}{\sin x}tg2x=1+cosxsinx=sinx1−cosx — тангенс половинного угла.
Формулы сложения
sin(α+β)=sinαcosβ+cosαsinβ \sin (\alpha + \beta )=\sin \alpha\, \cos \beta + \cos \alpha\, \sin \betasin(α+β)=sinαcosβ+cosαsinβ
sin(α−β)=sinαcosβ−cosαsinβ \sin (\alpha — \beta )=\sin \alpha\, \cos \beta — \cos \alpha\, \sin \betasin(α−β)=sinαcosβ−cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ \cos (\alpha + \beta )=\cos \alpha \,\cos \beta — \sin \alpha\,\sin \betacos(α+β)=cosαcosβ−sinαsinβ
cos(α−β)=cosαcosβ+sinαsinβ \cos (\alpha — \beta )=\cos \alpha\, \cos \beta + \sin \alpha\, \sin \betacos(α−β)=cosαcosβ+sinαsinβ
tg(α+β)=tgα+tgβ1−tgαtgβ \text{tg} (\alpha + \beta )=\frac{\text{tg} \alpha + \text{tg} \beta }{1-\text{tg} \alpha\, \text{tg} \beta }tg(α+β)=1−tgαtgβtgα+tgβ
tg(α−β)=tgα−tgβ1+tgαtgβ \text{tg} (\alpha — \beta )=\frac{\text{tg} \alpha — \text{tg} \beta }{1+\text{tg} \alpha\, \text{tg} \beta }tg(α−β)=1+tgαtgβtgα−tgβ
(в последних двух формулах α≠π2+πn,β≠π2+πn\alpha \neq \frac{\pi }{2}+\pi n, \beta \neq \frac{\pi }{2}+\pi nα≠2π+πn,β≠2π+πn и соответственно α+β≠π2+πn,α−β≠π2+πn\alpha + \beta \neq \frac{\pi }{2} + \pi n, \alpha -\beta \neq \frac{\pi }{2}+\pi nα+β≠2π+πn,α−β≠2π+πn, nnn — целое)
ctg(α+β)=ctgαctgβ−1ctgα+ctgβ \text{ctg} (\alpha + \beta )=\frac{\text{ctg} \alpha\, \text{ctg} \beta — 1}{\text{ctg} \alpha + \text{ctg} \beta }ctg(α+β)=ctgα+ctgβctgαctgβ−1
ctg(α−β)=ctgαctgβ+1ctgα−ctgβ \text{ctg} (\alpha — \beta )=\frac{\text{ctg} \alpha\, \text{ctg} \beta + 1}{\text{ctg} \alpha — \text{ctg} \beta }ctg(α−β)=ctgα−ctgβctgαctgβ+1
(в последних двух формулах α≠πn,β≠πn\alpha \neq \pi n, \beta \neq \pi nα≠πn,β≠πn и соответственно α+β≠πn,α−β≠πn\alpha + \beta \neq \pi n, \alpha -\beta \neq \pi nα+β≠πn,α−β≠πn, nnn — целое)
2.
 4.1. Основные понятия тригонометрии
4.1. Основные понятия тригонометрии
Глава 2. Алгебраические выражения
2.4.
2.4.1.
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат. Пусть одна сторона угла α с вершиной в начале координат O идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. Из геометрии известно, что отношение длины дуги l, на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла:
Поэтому это отношение может быть выбрано характеристикой и мерой данного угла:
Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. В самом деле:
Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2πR, то всей окружности соответствует угол
радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует
градусов:
И наоборот,
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
и от радианного измерения к градусному:
Обозначение «рад» при записи часто опускают и вместо, например, 180° = π рад пишут просто 180° = π.
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
Пример 1Определите радианную меру угла, если его градусная мера равна: 1) 2°; 2) 225°.
Снова рассмотрим на координатной плоскости окружность радиуса R с центром O в начале координат. Как известно, координатные оси делят окружность на четыре дуги, которые называют четвертями.
| 1 |
| Рисунок 2.4.1.1. Окружность радиуса R |
Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора
против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом
(α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.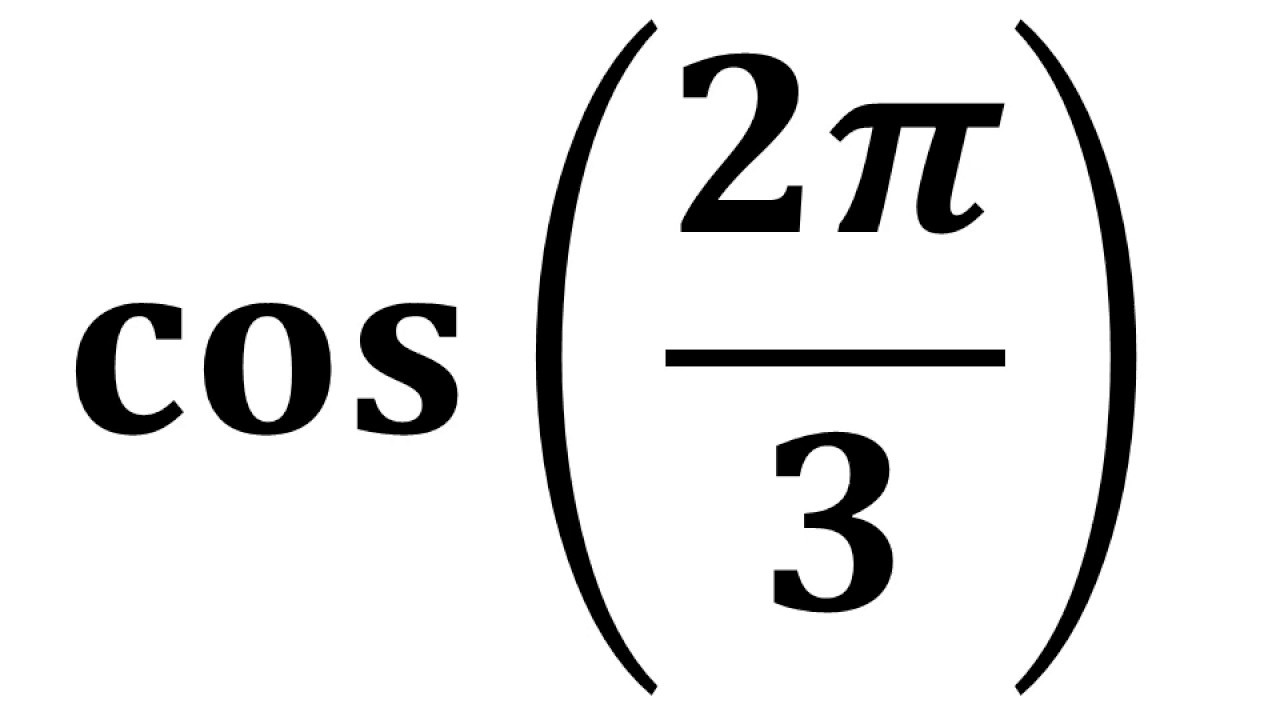
| 2 |
| Рисунок 2.4.1.2 |
Докажем, что отношения
и
не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку
такую, что
Построим окружность с центром в начале координат радиуса
Построенная окружность пересекает радиус-вектор
в точке
Так как векторы
и
коллинеарны и одинаково направлены, то
Однако равные векторы имеют равные координаты, следовательно,
Откуда следует после деления обеих частей последних равенств на R1, что
Итак, для любого угла поворота отношение координат радиус-вектора к его длине не зависит от этой длины радиус-вектора.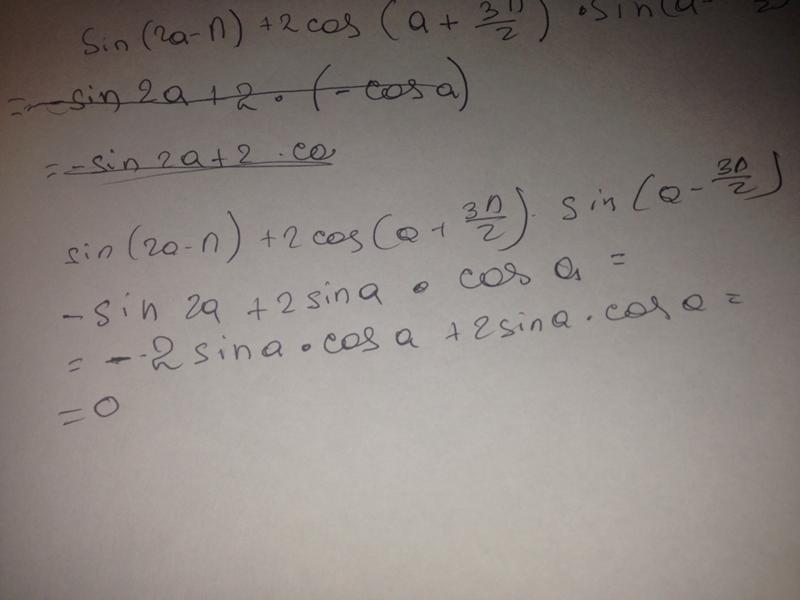 Следовательно, отношения
и
характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например, R = 1. Так мы и сделаем. Окружность единичного радиуса с центром в начале координат называется тригонометрической окружностью.
Следовательно, отношения
и
характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например, R = 1. Так мы и сделаем. Окружность единичного радиуса с центром в начале координат называется тригонометрической окружностью.
|
Модель 2.6. Координатная окружность |
Ввиду всего вышесказанного, рассмотренные отношения и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить. Введём несколько ключевых определений.
|
Модель 2.8. Функция y = cos x |
|
Модель 2. |
|
Модель 2.9. Функция y = tg x |
|
Модель 2.10. Функция y = ctg x |
Ясно, что для данного угла α функции sin α, cos α, tg α и ctg α, которые называются тригонометрическими функциями, определены однозначно (поскольку каждому углу соответствует единственная точка на тригонометрической окружности). Однако если функции sin α и cos α определены для любого угла α, то функции tg α и ctg α определены только для тех углов, для которых не равен нулю знаменатель дробей и Значит, tg α не определён для углов вида где ctg α не определён для углов вида
Поскольку синус по определению равен ординате точки на единичной окружности, а косинус − абсциссе, то знаки тригонометрических функций по четвертям будут такими:
|
|||||||||||||||||||||||||||||
Таблица 2. 4.1.2 4.1.2 |
|||||||||||||||||||||||||||||
Вычисление тригонометрических функций некоторых углов
| 3 |
| Рисунок 2.4.1.3. Вычисление углов |
Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов. Конец радиус-вектора, отвечающего углу 0°, точка A, имеет координаты (1; 0). Поэтому cos 0° = 1, sin 0° = 0, tg 0° = 0, ctg 0° не определён. Совершенно аналогично рассматриваются точки B (0; 1), C (–1; 0) и D (0; –1), что даёт:
-
sin 90° = 1, cos 90° = 0, ctg 90° = 0, tg 0° не определён.
-
sin 180° = 0, cos 180° = –1, tg 180° = 0, ctg 180° не определён.
-
sin 270° = –1, cos 270° = 0, ctg 270° = 0, tg 270° не определён.
Данные нами определения совпадают для острых углов с определениями тригонометрических функций в геометрии. В самом деле, например, синусом острого угла прямоугольного треугольника AOC (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе:
Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.
В самом деле, например, синусом острого угла прямоугольного треугольника AOC (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе:
Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.
Однако если мы поместим наш прямоугольный треугольник так, что его вершина – точка O – совпадёт с началом координат, а точка A будет лежать на единичной окружности (то есть мы выбираем тем самым гипотенузу OA = 1), то геометрическое определение синуса примет вид:
Значит, синус острого угла равен ординате точки, лежащей на тригонометрической окружности. А это как раз совпадает с нашим определением синуса. Совершенно те же самые рассуждения приводят нас к полной эквивалентности геометрического определения тригонометрических функций с тем, что дано в настоящем разделе. Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением.
Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением.
| 4 |
| Рисунок 2.4.1.4. Прямоугольный треугольник |
| 5 |
| Рисунок 2.4.1.5. Правильный треугольник |
Рассмотрим правильный треугольник ABC со стороной, равной 1. Тогда по теореме Пифагора легко найти, что длина его высоты BH равна
| 6 |
| Рисунок 2.4.1.6. Прямоугольный равнобедренный треугольник |
Значит, Рассматривая угол ABH, найдём, что Соответственно,
Рассмотрим теперь прямоугольный равнобедренный треугольник ABC с катетами, равными CA = CB = 1, CAB = 45°. Тогда по теореме Пифагора
и
Следовательно,
Тогда по теореме Пифагора
и
Следовательно,
Итак, мы вычислили значения тригонометрических функций основных углов. Составим таблицу значений тригонометрических функций, которую мы только что получили.
Пример 2Найдите значения выражений
1)
2)
|
Имеем: 1) 2) Ответ. 1) 1; 2) |
Периодические функции
Если функция f имеет период T, то она, очевидно, имеет период nT, где
Поэтому говорят о наименьшем положительном периоде (НПП) функции f. Существуют периодические функции, не имеющие НПП. Так, например, f (x) = C, где C − произвольная постоянная, является периодической, однако любое положительное число является её периодом. Очевидно, среди них нет наименьшего.
Очевидно, среди них нет наименьшего.
Доказать, что НПП функции y = sin x является 2π.
|
Из определения функции следует, что у точек x и x + 2π одинаковая ордината, следовательно, sin x = sin (x + 2π), а это означает, что 2π является периодом функции sin x. Пусть T − некоторый период функции y = sin x. Тогда для всех x должно выполняться равенство sin x = sin (x + T). При x = 0 имеем sin T = 0. Значит, T может принимать значения только πn, где Нас интересуют T < 2π. Таким периодом может быть только T = π, однако T = π не является периодом данной функции, так как равенство sin x = sin (x + π) неверно при Значит, НПП функции y = sin x является T = 2π. |
Аналогично можно показать, что функция y = cos x также имеет НПП T = 2π. А функции y = tg x и y = ctg x имеют НПП T = π.
Підсумкова контрольна робота (річна). 1-а частина
Запитання 1
Обчисліть
2sin15⁰⋅cos15⁰
варіанти відповідей
Запитання 2
Переведіть у радіани 140о
варіанти відповідей
Запитання 3
варіанти відповідей
Запитання 4
Серед наведених функцій визначіть парну функцію:
варіанти відповідей
Запитання 5
Вкажіть період функції y = 2 sinx.
варіанти відповідей
Запитання 6
Знайдіть значення кутового коефіцієнта дотичної, проведеної до графіка функції f( x) = x3-2x в точці з абсцисою х0 = 1
варіанти відповідей
Запитання 7
Знайдіть значення похідної f (х) = 4 cos x + 5 у точці х0 = π/2
варіанти відповідей
Запитання 8
Розв’яжіть рівняння cos2x=-1
варіанти відповідей
(-π ∕ 4)+πn, n-ціле
(π ∕ 4)+πn, n-ціле
Запитання 9
Скільки коренів має рівняння соs x=5
варіанти відповідей
Запитання 10
Яка з наведених нерівностей неправильна?
варіанти відповідей
Запитання 11
Спростити вираз sin 56°cos34° + cos 56°sin 34°
варіанти відповідей
Запитання 12
Знайдіть проміжки зростання функції y=4x2-16x
варіанти відповідей
Запитання 13
На малюнку зображено графік функції у = f(x). Скільки існує точок мінімуму?
Скільки існує точок мінімуму?
варіанти відповідей
Запитання 14
Знайдіть похідну функції γ=χ4 +3соsх
варіанти відповідей
Запитання 15
Значення похідної функції f(x)=3x2+6x у точці х0=1. Розв’язання завдання запишіть в зошиті.
варіанти відповідей
Запитання 16
Тіло рухається по осі абсцис за законом S(t)=10t² — 11t +6. Знайти швидкість тіла в момент часу t₀ = 1c
варіанти відповідей
Запитання 17
Знайдіть похідну функції у=2х³-4х²-х
варіанти відповідей
Запитання 18
Серед поданих функцій оберіть парну
варіанти відповідей
Запитання 19
Знайдіть область визначення функції.
варіанти відповідей
Запитання 20
варіанти відповідей
Запитання 21
варіанти відповідей
Запитання 22
Розв’яжіть рівняння
варіанти відповідей
Запитання 23
Укажіть проміжок, на якому функція, задана графіком, спадає:
варіанти відповідей
Запитання 24
Спростіть вираз sinα⋅ctgα .
варіанти відповідей
Запитання 25
Спростіть вираз ctg2 β(1− cos2 β)
варіанти відповідей
Запитання 26
Спростіть вираз cos180cos630+sin180sin630
варіанти відповідей
Запитання 27
Яке з рівнянь не має коренів?
варіанти відповідей
Запитання 28
Яка із рівностей є вірною?
1) sin2α — cos2α = 1;
2) tg α = cosα / sinα ;
3) cos2α = cosα — sinα
4) sin2α =2 sin α⋅cos α
варіанти відповідей
Запитання 29
Обчислити ∛-125 ⋅ ∜81
варіанти відповідей
Запитання 30
Точка рухається за законом S=2+20t-5t2. Знайти швидкість точки у момент t=1с. (s — вимірюється в метрах)
варіанти відповідей
Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома
Натисніть «Подобається», щоб слідкувати за оновленнями на Facebook
4} [/ текс] 3. Dana jest funkcja (w załączniku). Wskaż liczbę rozwiązań równania f (x) = -1A. 0B. 1С. 2D. 34. Funkcja f jest określona wzorem (załącznik). Оценская креветка …
dziwość podanych zdań.A. Funkcja f ma jedno miejsce zerowe.B. Funkcja f jest malejąca.C. Funkcja f jest monotoniczna.5. Narysuj wykres funkcji f (x) = ⅕x², której dziedziną jest przedział (-5; 3 & gt ;. Podaj wartość największą i wartość najmniejszą (o ile funkcja je przyjmóyjsz) (o ile funkcja je przyjmóyjsz. (załącznik) i na jego podstawie odpowiedz, dla jakich wartości m równanie f (x) = m ma trzyrozwiązania.7. Korzystając z Definicji, udowodnij, że funkcja f (x) = -xc²zestonieszniesznieszniesznieszniesznieszón) .PROSZĘ O POMOC. ROZWIĄZANIA Z OBLICZENIAMI, jeśli znasz odpowiedź na chociaż jedno pytanie to pisz
Dana jest funkcja (w załączniku). Wskaż liczbę rozwiązań równania f (x) = -1A. 0B. 1С. 2D. 34. Funkcja f jest określona wzorem (załącznik). Оценская креветка …
dziwość podanych zdań.A. Funkcja f ma jedno miejsce zerowe.B. Funkcja f jest malejąca.C. Funkcja f jest monotoniczna.5. Narysuj wykres funkcji f (x) = ⅕x², której dziedziną jest przedział (-5; 3 & gt ;. Podaj wartość największą i wartość najmniejszą (o ile funkcja je przyjmóyjsz) (o ile funkcja je przyjmóyjsz. (załącznik) i na jego podstawie odpowiedz, dla jakich wartości m równanie f (x) = m ma trzyrozwiązania.7. Korzystając z Definicji, udowodnij, że funkcja f (x) = -xc²zestonieszniesznieszniesznieszniesznieszón) .PROSZĘ O POMOC. ROZWIĄZANIA Z OBLICZENIAMI, jeśli znasz odpowiedź na chociaż jedno pytanie to pisz
1. 4} [/ текс]
4} [/ текс]
1.Датчанин są punkty a = (1; -4) i b = (2; 3) odcinek ab ma długość a.√2 b.5. c.5√2 d.252. Датчанин są punkty a = (2; -3) i b = (2; -7) odcinek ma długość a.-4 b.0 c.4 d … + znak nie skończoności
Rozwiąż równanie √2sin (x / 2-π / 4) = 1
wpisz w okienka odpowiednie liczby.матландия класа 7
Proszę potrzebuje na poniedziałek dam najjj
Proszę potrzebuje na poniedziałek dam najjj
Proszę potrzebuje na poniedziałek dam najjj
Уравнений для простого маятника Рона Куртуса
SfC Home> Физика> Механика>
Рона Куртуса (от 21 декабря 2019 г. )
)
Уравнения для простого маятника показывают, как найти частоту и период движения.
Простой маятник состоит из точечной массы, подвешенной на струне или проволоке, масса которой незначительна. Если маятник или грузик потянуть на относительно небольшой угол от вертикали и отпустить, он будет качаться назад и вперед с постоянной периодичностью и частотой. Эти требования позволяют сделать уравнения относительно простыми и называются простым гармоническим движением .
Если боб больше, у проволоки масса или угол больше, он называется физическим маятником со сложными уравнениями движения.
Хотя демпфирующие эффекты от сопротивления воздуха и трения являются факторами, они считаются незначительными для основных уравнений, касающихся частоты или периода маятника.
Вопросы, которые могут у вас возникнуть:
- Какие факторы и параметры движения маятника?
- Какие уравнения для частоты и периода?
- Каковы уравнения длины струны маятника?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Полезный инструмент: Конвертация единиц
Факторы и параметры
Основным фактором, используемым в уравнениях для расчета частоты простого маятника, является длина стержня или проволоки, при условии, что начальный угол или амплитуда качания малы. Масса или вес боба не влияет на частоту простого маятника, но ускорение свободного падения имеет значение.
Примечание : Это означает, что частота и период будут отличаться на Луне и на Земле.
Зная длину маятника, можно определить его частоту. Или, если вам нужна конкретная частота, вы можете определить необходимую длину.
Факторы и параметры простого маятника
( См. Демонстрация маятника, чтобы увидеть маятник в движении )
Уравнение периода
Период движения маятника — это время, необходимое для его качания вперед-назад, измеряется в секундах.Уравнение для периода простого маятника, начинающегося под малым углом α (альфа):
T = 2π√ (л / г)
где
- T — период в секундах
- π — греческая буква пи и приблизительно равна 3,14 .
- √ — это квадратный корень из скобок
- L — длина прутка или проволоки в метрах или футах
- g — ускорение свободного падения (9.8 м / с² или 32 фут / с² на Земле)

Таким образом, если L = 2 метра:
T = 2 * 3,14 * √ (2 / 9,8) = 6,28 * √ (0,204) = 6,28 * 0,4517
T = 2,837 секунды или немного округляем до T = 2,8 с.
Частотное уравнение
Частота маятника — это количество возвратно-поступательных колебаний в секунду, измеряемое в герцах.
Частота f является обратной величиной периода T :
f = 1 / T
f = 1 / [2π√ (л / г)]
Уравнение также можно изменить в следующем виде:
f = [√ (г / л)] / 2π
Таким образом, если L = 2 метра,
f = [√ (9.
8/2)] / 2 * 3,14
f = [√ (4,9)] / 6,28 = 2,21 / 6,28 = 0,353 Гц.
Длина провода
Вы можете найти длину стержня или проволоки для заданной частоты или периода.
Частота
Решите уравнение для L :
f = [√ (г / л)] / 2π
2πf = √ (г / л)
Возвести в квадрат обе части уравнения:
4π 2 f 2 = г / л
Решить для л :
L = г / (4π 2 f 2 )
Например, длина маятника с частотой 1 Гц (1 цикл в секунду) составляет около 0.25 метров.
Период
Аналогично, длина провода за данный период составляет:
T = 2π√ (л / г)
Квадрат с двух сторон:
T 2 = 4π 2 (л / г)
Решить для л :
L = gT 2 / 4π 2
Сводка
Если маятник простого маятника потянуть на относительно небольшой угол и отпустить, он будет качаться назад и вперед с постоянной частотой. Эти требования позволяют сделать уравнения относительно простыми и называются простым гармоническим движением .
Эти требования позволяют сделать уравнения относительно простыми и называются простым гармоническим движением .
Если демпфирующими эффектами от сопротивления воздуха и трения можно пренебречь, можно рассчитать уравнения, касающиеся частоты и периода маятника, а также длины струны.
Уравнение периода: T = 2π√ (л / г)
Частотное уравнение: f = [√ (г / л)] / 2π
Уравнения длины: L = g / (4π 2 f 2 ) и L = gT 2 / 4π 2
Делая все возможное, чтобы чувствовать себя хорошо
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Как работают маятниковые часы — From Как работают вещи
Физические ресурсы
Книги
Книги о маятниках с самым высоким рейтингом
Книги с самым высоким рейтингом по Periodic Motion
Книги по физике движения с самым высоким рейтингом
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.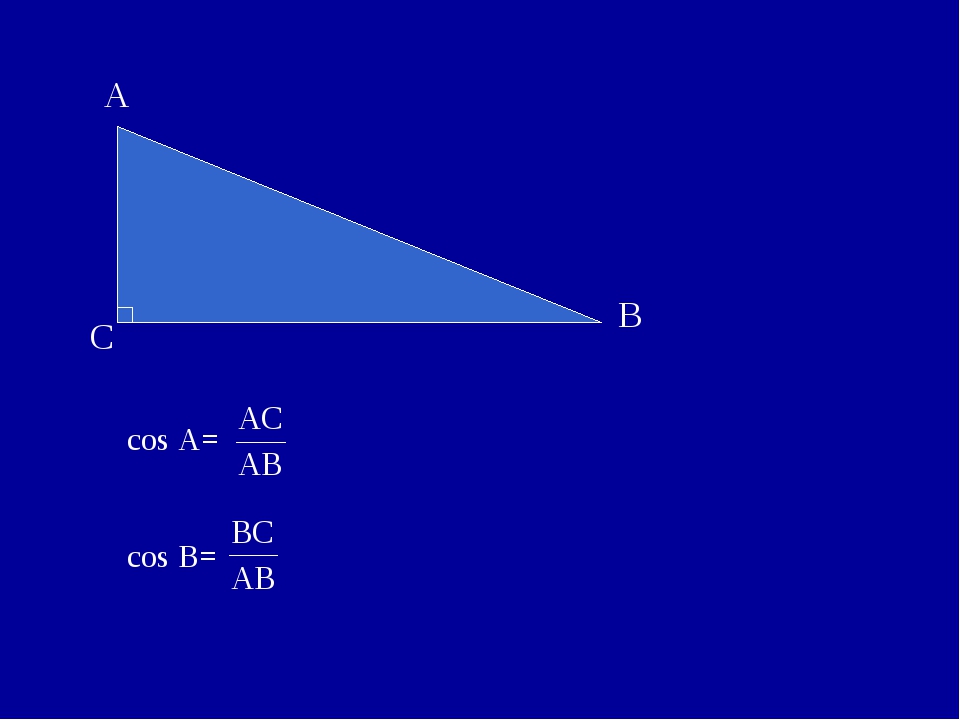 Я постараюсь вернуться к вам как можно скорее.
Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
pendulum_equations.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Физические темы
Уравнения простого маятника
Trygonometryczne wzory redukcyjne Википедии — Wolna Encyklopedia
Wzory redukcyjne — wzory pozwalające sprowadzić obliczanie wartości funkcji trygonometrycznych dowolnego ката skierowanego делают obliczenia wartości funkcji DLA ката ostrego, A dalej DLA ката о mierze г zakresu од 90 ° делать на 180 °
W poniższych wzorach używana jest miara łukowa kąta. Korzystając z miary stopniowej należy w poniższych wzorach podstawić 180 ° w miejsce π.
Korzystając z miary stopniowej należy w poniższych wzorach podstawić 180 ° w miejsce π.
Podawanie wzorów typu tg (3π2 + α) = — ctgα {\ displaystyle \ operatorname {tg} \ left ({\ frac {3 \ pi} {2}} + \ alpha \ right) = — \ operatorname {ctg} \ alpha} nie jest potrzebne, bo okresem funkcji tangens i cotangens jest π.
Wzory redukcyjne można wywieść z symetrii wykresów odpowiednich funkcji trygonometrycznych. Mianowicie, wykres funkcji sinus jest środkowo symetryczny względem dowolnego punktu osi OX o współrzędnej postaci k π i osiowo symetryczny wzglęte dowolnejódójójójDla cosinusa odpowiednie symetrie wypadają dla x = π / 2 + k π или x = k π. Dla tangensa i cotangensa mamy jedynie symetrie środkowe odpowiednio względem punktów x = k π oraz x = π / 2 + k π.
Wykresy pozwalają też na wyobrażenie sobie (i szybkie odtworzenie w pamięci lub na kartce) wzorów redukcyjnych.
1. W tym celu trzeba tylko zapamiętać jak wyglądają wykresy funkcji trygonometrycznych.Następnie przekształcamy wykres tej funkcji, którą mamy obliczyć:
2. Jeśli przed funkcją stoi minus, odbijamy wykres względem osi OX.
3. Na koniec spoglądamy na powstały wykres w miejscu, w którym przecina oś OY:
- Jeśli przecina ją w punkcie y = 1, {\ displaystyle y = 1,} to wynikiem jest cos (x) {\ displaystyle \ cos (x)}
- Jeśli przecina ją w punkcie y = −1, {\ displaystyle y = -1,} to wynikiem jest −cos (x) {\ displaystyle — \ cos (x)}
- Jeśli przecina ją w środku układu współrzędnych i rośnie, to wynikiem jest sin (x) {\ displaystyle \ sin (x)} (gdy przekształcaliśmy sinus lub cosinus) lub tg (x) {\ displaystorname { x)} (gdy przekształcaliśmy tangens lub cotangens)
- Jeśli przecina ją w środku układu współrzędnych i Maleje, to wynikiem jest −sin (x) {\ displaystyle — \ sin (x)} (gdy przekształcaliśmy sinus lub cosinus) lub −tg (x) {displaytamestyle — \ displaytamestyle — \ displaytame {tg} (x)} (gdy przekształcaliśmy tangens lub cotangens)
- Jeśli w ogóle nie przecina osi OY, a w przedziale od 0 do π {\ displaystyle \ pi} rośnie, to wynikiem jest ctg (x) {\ displaystyle \ operatorname {ctg} (x)}
- Jeśli w ogóle nie przecina osi OY, a w przedziale od 0 do π {\ displaystyle \ pi} maleje, to wynikiem jest −ctg (x) {\ displaystyle — \ operatorname {ctg} (x)}
Dla odmiany użyta zostanie miara stopniowa. {\ circ}) = {\ frac {\ sqrt {2}} {2}}}
{\ circ}) = {\ frac {\ sqrt {2}} {2}}}
W obu ostatnich przykładach pominięto okres funkcji.
2PI INTERACTIVE PRIVATE LIMITED — Компания, директора и контактные данные
2pi Interactive Private Limited — частная компания, зарегистрированная 29 августа 2011 года. Она классифицируется как негосударственная компания и зарегистрирована в Регистраторе компаний в Хайдарабаде. Его уставный акционерный капитал составляет рупий. 10,000,000, а его оплаченный капитал составляет Rs. 2 415 000. Он занимается публикацией, консультированием и поставкой программного обеспечения [публикация программного обеспечения включает производство, поставку и документацию готового (не настраиваемого) программного обеспечения, программного обеспечения операционных систем, программного обеспечения для бизнеса и других приложений, программного обеспечения для компьютерных игр для всех платформ.Консультации включают предоставление наилучшего решения в виде специального программного обеспечения после анализа потребностей и проблем пользователя.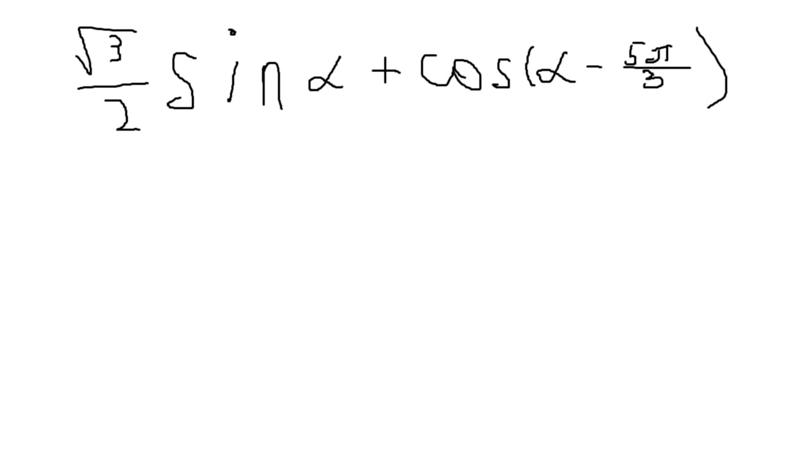 Программное обеспечение на заказ также включает программное обеспечение, изготавливаемое на заказ на основе заказов конкретных пользователей. Также включено написание программного обеспечения любого вида в соответствии с директивами пользователей; сопровождение программного обеспечения, дизайн веб-страниц]. Годовое общее собрание (AGM)
Программное обеспечение на заказ также включает программное обеспечение, изготавливаемое на заказ на основе заказов конкретных пользователей. Также включено написание программного обеспечения любого вида в соответствии с директивами пользователей; сопровождение программного обеспечения, дизайн веб-страниц]. Годовое общее собрание (AGM)2pi Interactive Private Limited в последний раз проводилось 30 сентября 2019 года, и, согласно отчетам Министерства корпоративных дел (MCA), его баланс последний раз был подан 31 марта 2019 года.
Директорами 2pi Interactive Private Limited являются Сиддхартха Бурри, Венкатарама Редди Бурри и.
Корпоративный идентификационный номер 2pi Interactive Private Limited (CIN) U72200TG2011PTC076217, регистрационный номер 76217. Его адрес электронной почты [email protected], а его зарегистрированный адрес: H. / 3/1, дорога № 11 Банджарахиллс Хайдарабад TG 500034 IN, -,.
Текущее состояние 2pi Interactive Private Limited — Активно.
Реквизиты компании
КИН | U72200TG2011PTC076217 |
Название компании | 2PI INTERACTIVE PRIVATE LIMITED |
Статус компании | Активный |
RoC | RoC-Хайдарабад |
Регистрационный номер | 76217 |
Категория компании | Компания с ограниченной ответственностью |
Подкатегория компании | Неправительственная компания |
Класс компании | Частный |
Дата регистрации | 29 августа 2011 |
Возраст компании | 9 лет, 9 мес. |
Деятельность | Публикация, консультирование и поставка программного обеспечения [Публикация программного обеспечения включает производство, поставку и документацию готового (нестандартного) программного обеспечения, программного обеспечения операционных систем, программного обеспечения для бизнеса и других приложений, программного обеспечения для компьютерных игр для всех платформ.Консультации включают предоставление наилучшего решения в виде специального программного обеспечения после анализа потребностей и проблем пользователя. Программное обеспечение на заказ также включает программное обеспечение, изготавливаемое на заказ на основе заказов конкретных пользователей. Также включено написание программного обеспечения любого вида в соответствии с директивами пользователей; сопровождение программного обеспечения, дизайн веб-страниц]. Щелкните здесь, чтобы увидеть другие компании, занимающиеся аналогичной деятельностью. |
Количество участников | – |
Предыдущие названия
Войдите, чтобы просмотреть предыдущие имена |
Предыдущий CINS
Войдите, чтобы просмотреть предыдущие cins |
Уставный капитал и количество сотрудников
Уставный капитал | ₹ 10 000 000 |
Оплаченный капитал | 2 415 000 |
Количество сотрудников | Войдите, чтобы просмотреть |
Сведения о листинге и годовом соответствии
Статус объявления | Не указано |
Дата последнего годового общего собрания | 30 сентября 2019 |
Дата последнего баланса | 31 марта 2019 |
Финансовый отчет
Бухгалтерский баланс | |
|---|---|
Оплаченный капитал | |
Запасы и излишки | |
Долгосрочные заимствования | |
Краткосрочные заимствования | |
Торговая кредиторская задолженность | |
Текущие инвестиции | |
Запасы | |
Торговая дебиторская задолженность | |
Денежная и банковская наличность | |
Прибыль и убыток | |
|---|---|
Общая выручка (оборот) | |
Итого расходы | |
Расходы на выплату вознаграждения работникам | |
Финансовые расходы | |
Амортизация | |
Прибыль до налогообложения | |
Прибыль после налогообложения | |
Разблокируйте полный отчет с историческими финансовыми данными и просмотрите все 38 документов всего за
рупий.
Графический отчет, содержащий исторические финансовые показатели.Щелкните здесь, чтобы просмотреть финансовый отчет Infosys Ltd.
Пожизненный доступ ко всем документам
Загрузите все 38 документов одним щелчком мыши
Просмотр хронологии событий — Список всех событий компании с момента создания. Щелкните здесь, чтобы просмотреть хронологию событий Infosys Ltd.
Контактная информация
Идентификатор электронной почты: [email protected]
Веб-сайт: Нажмите здесь, чтобы добавить.
Адрес:
H.№ 8-2-624 / A / B / 3/1, дорога № 11 Банджарахиллс Хайдарабад TG 500034 IN
Сведения о директоре
| DIN | Имя директора | Обозначение | Дата назначения | |||||||||
03571642 | SIDDHARTHA BURRI | Директор | 29 августа 2011 | Посмотреть другие дирекции | ||||||||
Другие компании, связанные сПредыдущие компании, связанные с
| ||||||||||||
03571639 | ВЕНКАТАРАМА РЕДДИ БУРРИ | Директор | 29 августа 2011 | Посмотреть другие дирекции | ||||||||
Другие компании, связанные сПредыдущие компании, связанные с
| ||||||||||||
Сведения о бывшем директоре
| DIN | Имя директора | Дата назначения | Дата прекращения | |
Войдите, чтобы просмотреть прошлых директоров. | ||||
Компании с похожим адресом
CIN | Имя | Адрес |
|---|---|---|
U72200TG2011PTC076217 | 2PI INTERACTIVE PRIVATE LIMITED | H.№ 8-2-624 / A / B / 3/1, дорога № 11 Банджарахиллс Хайдарабад TG 500034 IN |
AAA-2456 | SOUL BEAUTY & WELLNESS CENTER, ТОО | Блок 4-го этажа № 1 в верхней части города Банджара 8-2-270 / B / 1/1, 8-2-268 / F, 8-2-270, дорога № 3 Банджара Хиллс Хайдарабад Хайдарабад TG 500034 IN |
U45208TG2019PTC137253 | RAMANEEYA INFRA PROJECTS PRIVATE LIMITED | H NO: 8 — 2 — 624 / A / B / 3/1, ROAD NO — 11, BANJARA HILLS, HYDERABAD Хайдарабад TG 500034 IN |
U72900TG2002PTC062694 | SKYWORKS SOLUTIONS INDIA PRIVATE LIMITED | Земельный участок No. 8-2-277 / A / 3 / 1–3 / 3, 3A и 3B, IInd Floor Street No. 2, Road No. 2, Banjara Hills Хайдарабад Хайдарабад TG 500034 IN 8-2-277 / A / 3 / 1–3 / 3, 3A и 3B, IInd Floor Street No. 2, Road No. 2, Banjara Hills Хайдарабад Хайдарабад TG 500034 IN |
U01122TG2004PTC043767 | SRI SATHYA AGRI BIO-TECH PRIVATE LIMITED | F. No. C3 / B, H. No. 8-2-350 / 6 / 2,3-й этаж, Площадь Вамширамджиоти, Участок № 16, Sy. No. 360, Road № 3, Banjarahills HYDERABAD Хайдарабад TG 500034 IN |
U85191TG2010PTC069349 | AMBROSIA WELLNESS PRIVATE LIMITED | М.№ 8-2-293 / 174/4 / B / B, П. № 4,3,3 / A, 1 / A, дорога № 14 Sy № 129/82, BNReddy Colony, Banjara Hills, Хайдарабад Хайдарабад TG 500034 IN |
U33110TG2011PTC075308 | АКШАЯ АГРИБИОМЕД ЧАСТИЧНАЯ ЛИМИТЕД | УЧАСТОК № 682 (10A), H. No. 8-2-268 / A / 4 / B / 1, ШРИНИКЕТАНСКАЯ КОЛОНИЯ, Road No. 3, BANJARAHILLS HYDERABAD TG 500034 IN |
U45209TG2013PTC0 | SAICHARAN REALTORS PRIVATE LIMITED | # Костюм № 1, H № 8-2-693 / 2 / 1A / 1B / S1, Обследование первого этажа № 129/77, Дорога № 12, Банджара-Хиллз, Хайдарабад Хайдарабад TG 500034 IN |
AAN-2755 | FUTURE TRENDS TECH PARK LLP | H. № 8-2-227 / A / 3 / 1,2,3, первый этаж, блок № 2A, дорога № 2, Kingston Heights, Banjara Hi lls Hyderabad Hyderabad TG 500034 IN № 8-2-227 / A / 3 / 1,2,3, первый этаж, блок № 2A, дорога № 2, Kingston Heights, Banjara Hi lls Hyderabad Hyderabad TG 500034 IN |
Tan (pi / 9) * tan (2pi / 9) * tan (4pi / 9) — школьные Знания.com
Дано : Tan (pi / 9) * tan (2pi / 9) * tan (4pi / 9)
Найти : значение данного выражения.
Решение :
- Теперь мы дали термин tan (pi / 9) * tan (2pi / 9) * tan (4pi / 9)
tan (20) x tan (40) x tan (80)
- Теперь преобразовав его в sin и cos, мы получим:
(sin 20 / cos 20 x sin 40 / cos 40 x sin 80 / cos 80)
- Умножая на 2 в числителе и знаменателе, получаем:
2 sin (20) x sin (40) x sin (80) / 2 cos 20 x cos 40 x cos 40
2 sin x sin y = cos (xy) — cos (x + y). …………….. (i)
…………….. (i)
2 cos x cos y = cos (x + y) + cos (xy) ……… ……… (ii)
(cos (20 ° -40 °) -cos (20 ° + 40 °)) x sin80 ° / (cos (20 ° + 40 °) + cos ( 20 ° -40 °)) x cos80 °
(cos20 ° — cos60 °) x sin80 ° / (cos60 ° + cos20 °) x cos80 °
cos20 ° x sin80 ° — cos60 ° x sin80 ° / cos60 ° x cos80 ° + cos20 ° + cos80 °
(cos20 ° x sin80 ° — sin80 ° / 2) / (cos80 ° / 2 + cos20 ° + cos80 °)
- Умножая на 2 в числителе и знаменателе, получаем:
(2cos20 ° x sin80 ° — sin80 °) / (cos80 ° + 2cos20 ° + cos80 °)
2 sin x cos y = sin (x + y) — sin (xy)
2 cos x cos y = cos (x + y) + cos (xy)
(sin (20 ° + 80 °) -sin (20 ° -80 °) -sin80 °) / (cos80 ° + cos (20 ° + 80 °) + cos (20 ° -80 °))
(sin100 ° + sin60 ° -s in80 °) / (cos80 ° + cos100 ° + cos60 °)
(2cos (100 ° + 80 °) / 2sin (100 ° -80 °) / 2 + √3 / 2) / (2cos (100 + 80 ° ) / 2cos (100 ° -80 °) / 2 + 1/2)
- Теперь, упрощая это, получаем:
(2 cos90 ° sin10 ° + √3 / 2) / (2 cos90 ° cos10 ° + 1/2)
(√3 / 2) / (1/2)
√3
Ответ :
Таким образом, значение данного члена равно √3 .
Идентификаторы триггеров Идентификаторы, связанные с триггером функции перечислены ниже.
См. Синус, косинус, тангенс, косеканс, секанс, котангенс | ||||||||||
Serwis Matematyczny OMIKRON
Niech α bdzie ktem ostrym w trjkcie prostoktnym ABC.
Sinusem kta α nazywamy stosunek dugoci przyprostoktnej lecej naprzeciw kta α do dugoci przeciwprostoktnej.
Cosinusem kta α nazywamy stosunek dugoci przyprostoktnej lecej przy kcie α do dugoci przeciwprostoktnej.
Tangensem kta α nazywamy stosunek dugoci przyprostoktnej lecej naprzeciw kta α do dugoci przyprostoktnej lecej przy kcie.
Cotangensem kta α nazywamy stosunek dugoci przyprostoktnej lecej przy kcie α do dugoci przyprostoktnej lecej naprzeciw kta.
| sinα = a / c cosα = b / c tgα = a / b ctgα = b / a |
Wartoci funkcji trygonometrycznych dla wybranych ktw
Kt skierowany
Kt skierowany jst to uporzdkowana para pprostych o wsplnym wierzchoku. Jego miar okrelamy jako dodatni wtedy, gdy obrt ramienia pocztkowego w kierunku ramienia kocowego jest przeciwny do kierunku ruchu wskazwek zegara; jako ujemn, gdy obrt ramienia pocztkowego w kierunku ramienia kocowego jest zgodny z kierunkiem ruchu wskazwek zegara.
Jego miar okrelamy jako dodatni wtedy, gdy obrt ramienia pocztkowego w kierunku ramienia kocowego jest przeciwny do kierunku ruchu wskazwek zegara; jako ujemn, gdy obrt ramienia pocztkowego w kierunku ramienia kocowego jest zgodny z kierunkiem ruchu wskazwek zegara.
Miara ukowa kta
Miara ukowa kta rodkowego w okrgu okrelana jest jako stosunek dugoci uku, na ktrym ten kt jest oparty do dugoci promienia okrgu.
α — миара ukowa
α o — миара стопниова
Nieraz spotykamy si z jeszcze jedn jednostk tzw. градусами. Gradus jest to jedna setna kta prostego (czyli jedna czterysetna kta penego).
Funkcje trygonometryczne kta dowolnego
Sinusem dowolnego kta α nazywamy stosunek rzdnej dowolnego punktu lecego na kocowym ramieniu tego kta do dugoci promienia wodzcego tego punktu.
sinα = y / r
Cosinusem dowolnego kta α nazywamy stosunek odcitej dowolnego punktu lecego na kocowym ramieniu tego kta do dugoci promienia wodzcego tego punktu.
cosα = x / r
Tangensem dowolnego kta nazywamy stosunek rzdnej dowolnego punktu lecego na kocowym ramieniu tego kta do odcitej tego punktu.
tgα = y / x
Cotangensem dowolnego kta nazywamy stosunek odcitej dowolnego punktu lecego na kocowym ramieniu tego kta do rzdnej tego punktu.
ctgα = x / y
Znaki funkcji trygonometrycznych w poszczeglnych wiartkach
| wiartka | I | II | III | 3 IV | π / 2; π)(π; 3π / 2) | (3π / 2; 2π) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin α | + | + | — | — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos α + | — | — | + | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tg α | + | — | + | — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ctg α | + | — | 2 W zapamitaniu znakw (gdy s one bardzo istotne) moe pomc wierszyk: «W pierwszej wszystkie s dodatnie, w friendiej tylko sinus, w trzeciej tangens i cotangens, cosinus czwartej.  » »Wzory redukcyjne
Rozwizania rwna trygonometrycznych
|


 7.
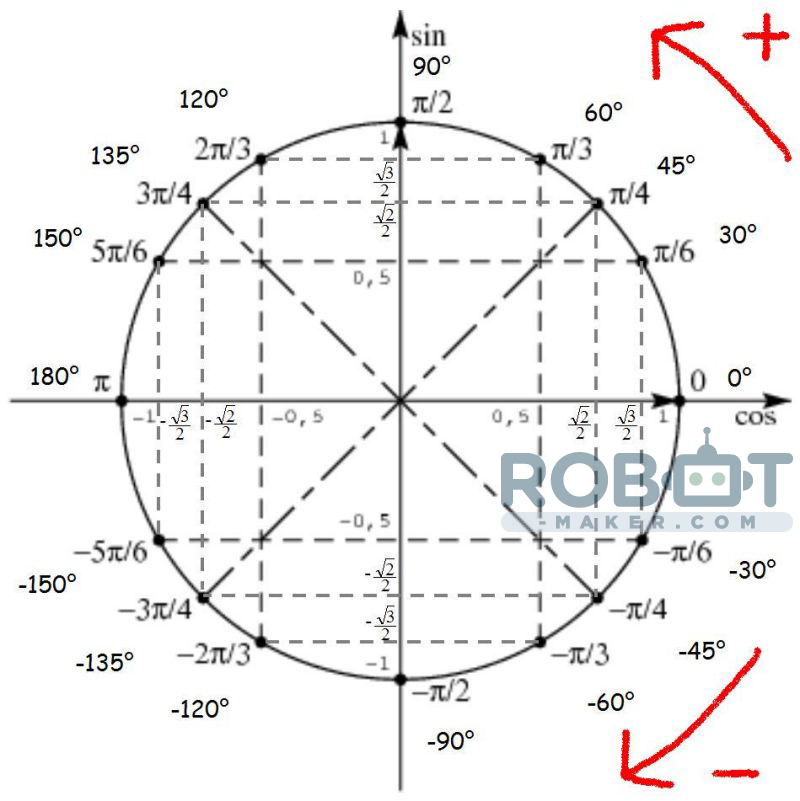
Функция y = sin x
7.
Функция y = sin x 8/2)] / 2 * 3,14
8/2)] / 2 * 3,14 , 1 дней
, 1 дней

 Также
Также  π / 2 + α czy 3 * π / 2 — α, wtedy funkcja przechodzi w cofunkcj np. sinx w cosx, ctgx w tgx, jeli jest to parzysta wielokrotno np. 2 * π / 2 + α czyli π + α для функции pozostaje niezmieniona.
π / 2 + α czy 3 * π / 2 — α, wtedy funkcja przechodzi w cofunkcj np. sinx w cosx, ctgx w tgx, jeli jest to parzysta wielokrotno np. 2 * π / 2 + α czyli π + α для функции pozostaje niezmieniona. 