Какая формула 2пир 2? – Обзоры Вики
Площадь поверхности цилиндра = 2 пи р 2 + 2 пи правая
Можно найти площадь верха (или низа). Это формула площади круга (pi r2).
Из этого следует, что 2pir такой же, как PID? 2*pi*r и pi*d — одно и то же.. Общепринято, что мы пишем первое вместо второго. Кроме того, при выводе (с использованием дифференциальных уравнений) длина окружности получается как 2*pi*r.
Что такое V пи * г 2 * Н? Формула объема цилиндра V = Bh или V = πr2h.
Дополнительно Почему окружность 2pir? Поскольку диаметр в два раза больше радиуса, длина окружности равна произведению числа пи и 2r, то есть 2 (пи) * r.
Как рассчитать площадь поверхности? Площадь поверхности — это сумма площадей всех граней (или поверхностей) трехмерной фигуры. Кубоид имеет 3 прямоугольных граней. Чтобы найти площадь поверхности прямоугольного параллелепипеда, сложите площади всех 6 граней. Мы также можем обозначить длину (l), ширину (w) и высоту (h) призмы и использовать формулу SA = 2lw + 2lh + 2hw, чтобы найти площадь поверхности.
2pir это то же самое, что Pir 2?
2 пи р – окружность, общее расстояние по внешней стороне круга. пи r в квадрате — это площадь круга. Представьте себе пиццу. Можно съесть всю площадь, но смотреть можно только на тропинку снаружи (корочка).
Пирог — настоящее число? Пи — иррациональное число, что означает, что это действительное число, которое не может быть выражено простой дробью. … Начиная с математики, ученики знакомятся с числом «пи», равным 3.14 или 3.14159. Хотя это иррациональное число, некоторые используют рациональные выражения для оценки пи, например, 22/7 из 333/106.
Что такое 1 2BH? Так как площадь этого треугольника равна половина площади параллелограмма, формула площади этого треугольника, А = 1/2ВН. … Во-первых, начнем с формулы площади треугольника, A = 1/2BH.
Как решить P 2l 2w?
Также Что означает r2h в математике? Учитывая объем цилиндр V = пи (г2)h мы просто подставляем числа.
Радиус равен половине диаметра, поэтому r = 4 см. высота h равна 12 см.
Кто открыл пи?
Пи, в математике, отношение длины окружности к ее диаметру. Символ π был изобретен Британский математик Уильям Джонс в 1706 году для представления отношения, а позже популяризировал швейцарский математик Леонард Эйлер.
Почему круг 2 пи? Первоначальный ответ: Почему в круге 2pi радиан? Поскольку длина окружности круга ровно 2 * пи, умноженного на радиус и по определению 1 радиан — это угол, образуемый частью окружности, равной по длине радиусу. 1 радиа «уходит» в общую окружность 2 * пи раз.
Как рассчитать площадь комнаты?
Стены. Чтобы рассчитать площадь стены, воспользуйтесь стандартной формулой of (Длина) x (Ширина) = Площадь.
Что такое пи * д?
Игровой автомат Длина окружности круга или сферы равен диаметру, умноженному на 3.1416. Окружность = 3.1416 ⋅ Диаметр. C = π ⋅ D. Рисунок №4. Длина окружности равна пи × диаметр.
Что такое формула площади? Для прямоугольника длиной l и шириной w формула для вычисления площади имеет следующий вид: A = lw (прямоугольник).
То есть площадь прямоугольника — это длина, умноженная на ширину. В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).
Каким образом окружность равна 2пирам? π определяется как отношение длины окружности к ее диаметру (или удвоенному радиусу). Это отношение является константой, поскольку все круги геометрически подобны, а линейные пропорции между любыми подобными геометрическими фигурами постоянны.
Кто открыл число Пи в Индии?
Математика в Индии имеет богатую историю. Индийские математики Мадхава и Арьябхата внес очень значительный вклад в нахождение точного значения π (пи).
Кто создал пи? Первое вычисление π было сделано Архимед Сиракузский (287–212 до н.э.), один из величайших математиков древнего мира.
Делает ли 1/2 BH только прямоугольные треугольники?
Формула площади треугольника: 1 / 2 × основание × высота.
Эту формулу проще записать в виде Площадь = 1 / 2 бх. Формула площади = 1 / 2 bh работает для всех треугольников, независимо от их размера и формы. Если известны высота и основание, эту формулу можно использовать для расчета площади.
Как решить Pie R 2h? 1 Ответ
- Разделим обе части на π
- Разделите обе стороны на h.
- Возьмите ± √ с обеих сторон.
- ± √Vπh = r.
- Радиус r не является отрицательным значением, поэтому оставьте положительное значение.
- г = √Vπh.
Что такое DRT решает для R?
Какая формула 2l 2w? Периметр квадратного поля определяется уравнением Р = 2л + 2в, где P представляет периметр, l представляет длину поля, а w представляет ширину поля.
Что означает 2л 2в?
Формула P=2l+2w означает, что периметр прямоугольника равен удвоенной сумме его длины и ширины.
Равномерное движение по окружности
Как известно, год, но Земле длится примерно 365 дней и соответствует периоду обращения земли вокруг Солнца. Период обращения Т — это время одного оборота. Проще всего его найти в случае равномерного кругового движения – он будет равен отношению длины окружности l=2пR к скорости, с которой движется тело:
T=(2пR)/v
Скорость V в этой формуле называется линейной. Она показывает путь, пройденный телом за единицу времени. Помимо линейной движение по окружности характеризуется также угловой скоростью w. Угловая скорость выражает не путь, а угол, на который поворачивается радиус-вектор частицы за единицу времени, и потому она определяется следующим образом: w=a/t.
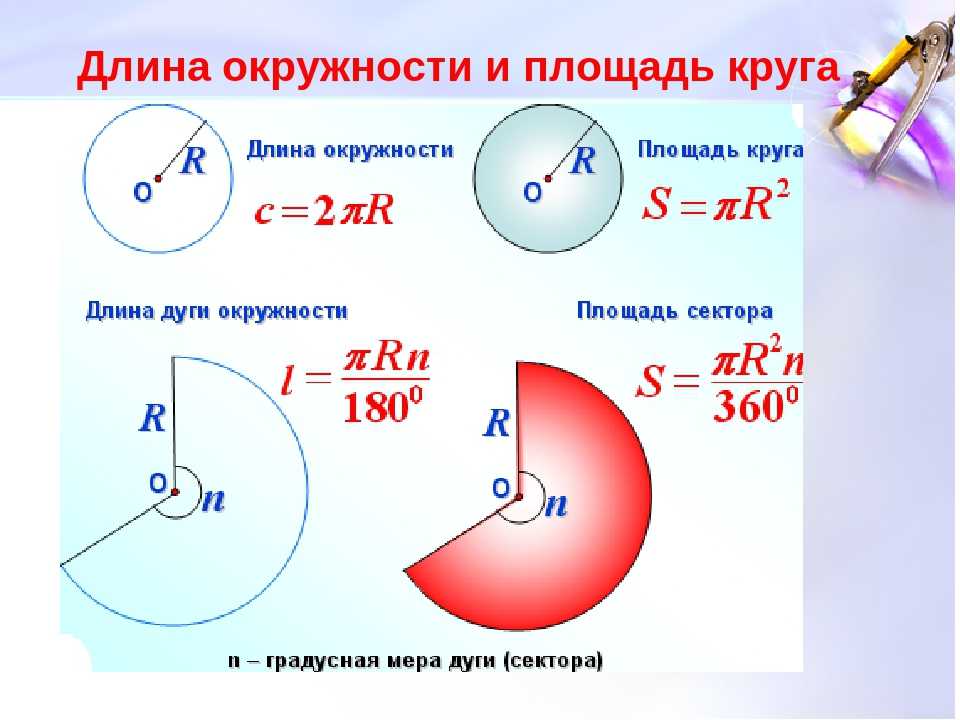Поскольку одному обороту соответствует угол a=2п радиан и время t=T, то угловую скорость можно представить в виде:
При равномерном движений по окружности неизменным остаётся лишь модуль линейной скорости, направлений её, напротив, изменяется непрерывно. Этого достаточно, чтобы ускорение было отлично от нуля. Правда, оно будет характеризовать не быстроту изменения её числового значения скорости (оно не меняется), а быстроту изменения её направления. Чтобы выяснить, от чего зависит модуль этого ускорения, заметим: чем больше скорость движения (по одной и той же окружности), тем быстрее изменяется направление вектора скорости и, следовательно, тем больше должно быть ускорение. Если же при неизменной скорости увеличивать радиус окружности, то каждый её участок (проходит за данное время) будет все более приближаться к прямой линий, а движение – всё больше походить на равномерное прямолинейное. Но про равномерное прямолинейном движении а =0.
Поэтому с ростом радиуса окружности модуль ускорения должен уменьшаться.
Таким образом, можно предположить, что при равномерном круговом движении ускорение тела прямопропорционально скорости движения и обратно пропорционально радиусу окружности, т.е. ровно отношению v/R. Однако размерность этого отношения (1/с) отличаются от размерности ускорения (м/с2). Чтобы добиться совпадения их размерностей, достаточно скорость в рассматриваемом отношений на её квадрат. Разделив (м/с)2 на (м), мы действительно получим (м/с2). Линейная скорость равна:V=wR Следовательно,
ац=v2/R=w2R=Vw
Строго говоря, в правую часть формулы нужно было бы добавить безразмерный коэффициент пропорциональности. Однако расчёты показывают, что он равен единице. Приведенная выше формула позволяет определить модуль ускорения. Поскольку ускорение – величина векторная, она характеризуется не только числовым значением, но и направлением.
149820-65-5 (DHQ)2PYR | AMERICAN ELEMENTS®
Запросить цену
| Продукт | Код продукта | Цена |
|---|---|---|
| OMXX-280159-01 | Pricing > |
Product Information
| Chemical Formula: | C 56 H 60 N 6 O 4 |
|---|---|
| Молекулярный вес: | 881. 13 |
| Синонимы: | Гидрохинин 2,5-дифенил-4,6-пиримидиндииловый диэфир; (Dhq)2Pyr гидрохинин 2,5-дифенил-4,6-пиримидиндииловый диэфир; 2,5-дифенил-4,6-бис(9-О-дигидрохининил)пиримидин; 2,5-дифенил-4,6-бис(9-О-дигидрохинил)пиримидин; 2,5-дифенил-4,6-бис(дигидрохинин)пиримидин; (Dhq)2Pyr 97%; (Dhq)2-Pyr/2,5-дифенил-4,6-бис(9-O-дигидрохинил)пиримидин |
| MDL №: | MFCD00198109 |
| EINECS / EC NO.: | N / A |
| Pubchem CID: | 11083476 |
| Имя IUPAC: | 4-[R)-[2S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S, 4S. -5-этил-1-азабицикло[2.2.2]октан-2-ил]-[6-[(R)-[(2S,4S,5R)-5-этил-1-азабицикло[2.2.2]октан -2-ил]-(6-метоксихинолин-4-ил)метокси]-2,5-дифенилпиримидин-4-ил]оксиметил]-6-метоксихинолин |
| Стандарт InchI: | InChI=1S/C56H60N6O4/c1 -5-35-33-61-27-23-39(35)29-49(61)52(43-21-25-57-47-19-17-41(63-3)31-45(43)47)65-55-51(37-13-9-7-10-14-37)56(60-54(59-55)38-15 -11-8-12-16-38)66-53(50-30-40-24-28-62(50)34-36(40)6-2)44-22-26-58-48-20 -18-42(64-4)32-46(44)48/ч7-22,25-26,31-32,35-36,39-40,49-50,52-53Х,5-6,23 -24,27-30,33-34х3,1-4х4/t35-,36-,39-,40-,49-,50-,52+,53+/м0/с1 |
| Дюймовый ключ: | SWKRDCRSJPRVNF-CVCJRGCISA-N |
| SMILES: | CCC1CN2CCC1CC2C(C3=C4C=C(C=CC4=NC=C3)OC)OC5=C(C(=NC(=N5)C6=CC=CC= C6)OC(C7CC8CCN7CC8CC)C9=C1C=C(C=CC1=NC=C9) OC) C1 = CC = CC = C1 |
| Внешний вид: | — |
| Печание пластин ): | 1,29 г/см 3 |
| Индекс преломления: | 1,69 |
Информация о безопасности
0018 h415-h419-h435Related Forms
Pyrimidines
О компании (DHQ)2PYR
(DHQ)2PYR является одним из многочисленных органических соединений, входящих в полный каталог медико-биологической продукции American Elements. American Elements поставляет материалы для медико-биологических наук в большинстве объемов, включая оптовые партии, а также может производить материалы по спецификациям заказчика. Большинство материалов можно производить в формах высокой и сверхвысокой чистоты (99 %, 99,9 %, 99,99 %, 99,999 % и выше) и ко многим стандартным классам, если применимо, включая Mil Spec (военный класс), ACS, реагентные и технические классы, фармацевтические классы, оптические, полупроводниковые и электронные классы. Пожалуйста, запросите цитату выше для получения дополнительной информации о ценах и сроках поставки.
Спецификации упаковки
Типичная оптовая упаковка включает пластиковый поддон на 5 галлонов/25 кг. ведра, волокнистые и стальные барабаны до 1-тонных супермешков в количестве полного контейнера (FCL) или загрузки грузовика (T/L). Исследования и образцы, а также гигроскопичные, окисляющие или другие чувствительные к воздуху материалы могут быть упакованы в аргоне или вакууме. Отгрузочная документация включает сертификат анализа и паспорт безопасности (SDS). Растворы упаковываются в полипропиленовые, пластиковые или стеклянные банки, вплоть до контейнеров для жидкостей на поддонах емкостью 440 галлонов и автоцистерн на 36 000 фунтов.
Сопутствующие элементы
6 C 12.010700000 Углерод
См. больше Углеродные изделия. Углерод (атомный символ: C, атомный номер: 6) является элементом блока P, группы 14, периода 2. Число электронов в каждой из оболочек углерода равно 2, 4, а его электронная конфигурация [He] 2s 2 2p 2 .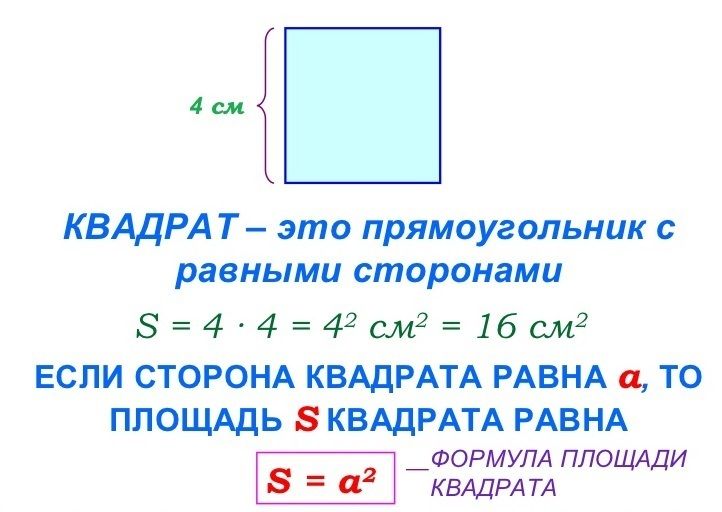
В своей элементарной форме углерод имеет номер CAS 7440-44-0. Углерод является одновременно одним из самых мягких (графит) и самых твердых (алмаз) материалов, встречающихся в природе. Это 15-й по распространенности элемент в земной коре и четвертый по распространенности элемент (по массе) во Вселенной после водорода, гелия и кислорода. Углерод был открыт египтянами и шумерами около 3750 г. до н.э. Впервые он был признан элементом Антуаном Лавуазье в 1789 году..
Вольфрамоксоалкилиденовые комплексы в качестве инициаторов стереорегулярной полимеризации 2,3-дикарбометоксинорборнадиена
Показать запись простого элемента
Оксоалкилденовые комплексы вольфрама как инициаторы стереорегулярной полимеризации 2,3-дикарбометоксинорборнадиена
дата.доступна
Мы обнаружили, что инициаторы MAP дают цис, синдиотактический поли(DCMNBD) в результате стереогенного контроля металлов. Напротив, инициаторы W(O)(CHCMe[индекс 2]Ph)(OR)[индекс 2](L) (где L = PPh[индекс 2]Me или ацетонитрил) сильно смещены в сторону образования цис, изотактических структур, в то время как инициаторы W (O) (CHCMe [индекс 2] Ph) (OR) [индекс 2] сильно смещены в сторону образования цис-синдиотактических структур. Добавление B(C[индекс 6]F[индекс 5])[индекс 3] к соединениям W(O)(CHCMe[индекс 2]Ph)(Me[индекс 2]Pyr)(OR) приводит к резкому увеличению скорость полимеризации и к увеличению цис,синдиотактичности полимера (если она уже не высокая), а добавление B(C[индекс 6]F[индекс 5])[индекс 3] к W(O)(CHCMe [subscript 2]Ph)(OR)[subscript 2] инициаторов приводит к резкому увеличению скорости полимеризации и образованию высокоцис-синдиотактических полимеров. Все данные подтверждают предположение о том, что комплексы 16e W (O) (CHCMe [индекс 2] Ph) (OR) [индекс 2] (L) могут действовать либо за счет потери L с образованием 14e W (O) (CHCMe [индекс 2] Ph)(OR) [нижний индекс 2] (которые дают в основном цис, синдиотактический поли(DCMNBD)) или путем прямой реакции с DCMNBD с образованием промежуточного соединения 18e и в основном цис, изотактического поли(DCMNBD).
source
contributor.mitauthor
Файлы в этом элементе
- Имя:
