Длина окружности. Решение задач на длину окружности и площадь круга
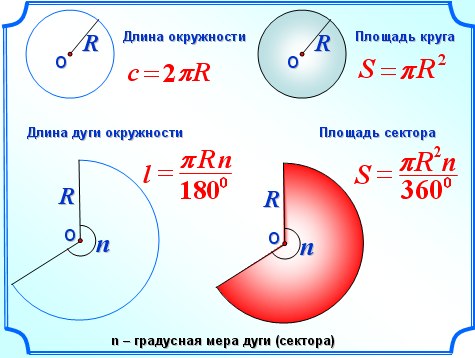
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π
(пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR,
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Ответ: 15,7 см.
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м),
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Ответ: 21,98 м.
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Ответ: 1,25 м.
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 22 = 3,14 · 4 = 12,56 (см2).
Ответ: 12,56 см2.
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
7 : 2 = 3,5 (см),
теперь вычислим площадь круга по формуле:
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D2 | ≈ 3,14 · | 72 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см2). |
| 4 |
Ответ: 38,465 см2.
Задача 3. Найти радиус круга, если его площадь равна 12,56 м2.
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
r = √S : π ,
следовательно, радиус будет равен:
r ≈ √12,56 : 3,14 = √4 = 2 (м).
Ответ: 2 м.
Производство алюминиевых окон в Ростове-на-Дону. Алюминиевые окна
4М1-16Ar-4М1 стеклопакет однокамерный, состоит из 2-х стекол толщиной по 4 мм марки М1, ширина рамки 16 мм, камера заполнена аргоном
4M1-12-4M1-12-4M1 — двухкамерный стеклопакет, состоит из трех листовых стекол толщиной по 4 мм марки M1, ширина рамок по 12 мм, камера заполнена воздухом
6 SPHBr#2[ Шл]-14-4 Mat#3 — стеклопакет, где первое стекло 6мм -это продукт производителя стекла AGC называется Phoenix Bronze серия Stopsol. Напыление находится внутри стеклопакета (#2), края стекла шлифованные (Шл). Рамка 14мм, затем стекло 4мм матовое; матовая сторона также внутри стеклопакета (#3). В нашей практике другой производитель написал эту же формулу так: 6StPhBronze#2Пр-14-4MatClear#3
Напыление находится внутри стеклопакета (#2), края стекла шлифованные (Шл). Рамка 14мм, затем стекло 4мм матовое; матовая сторона также внутри стеклопакета (#3). В нашей практике другой производитель написал эту же формулу так: 6StPhBronze#2Пр-14-4MatClear#3
24Б2(6StPhClear#1)-12Ar-6ТопН+Т/зак — первое стекло это — защитное пулестойкое по классу Б2, сделано из триплекса, в котором внешним стеклом использовано стекло марки AGC — Phoenix Clear серия Stopsol 6мм, напыление в первой позиции (#1) — на «улицу». Далее рамка 12мм, камера заполнена аргоном. Затем стекло 6мм энергоэффективное, с твердым напылением, закаленное.
6М1 зак -14- 44.1 — однокамерный стеклопакет с воздухом, состоит из закаленного стекла 6мм, рамки шириной 14 мм и триплекса из 2-х стекол по 4мм.
4CGSolarBronze#2-14-33.1 — однокамерный стеклопакет с воздухом, первое стекло — мультифункциональное солнцезащитное с бронзовым оттенком толщиной 4мм (Clima Guard Solar Bronze), защитное напыление во второй позиции (#2), рамка 14мм и триплекс из двух стекол по 3 мм (ламинированное стекло).
4М1-16-4 ton n (или 4М1-16-4И или 4М1-16-4 low e) — однокамерный стеклопакет из стекла 4мм и второго стекла 4мм с нанесенным на него низкоэмиссионным покрытием, придающим энергосберегающие свойства.
6 SG HP Royal Blue 38/31 зак — 10- 4м1 — 8- 4м1 — стеклопакет двухкамерный с архитектурным стеклом. Первое стекло толщиной 6 мм производства Guardian называется SunGuard High Performance Royal Blue 38/31, закаленное, затем рамка 10мм, затем обычное стекло 4мм, рамка 8мм, обычное стекло 4мм.
Влияние выхлопных газов на растительность
1. Исследование на тему: «Влияние выхлопных газов на растительность »
Ефанова Диана10 класс
ГБОУ Школа №879
2.
 оглавление Введение
оглавление ВведениеТеория
Проведение работы:
оборудование
цель
ход работы
подведение итогов
заключение
Фоторгафии
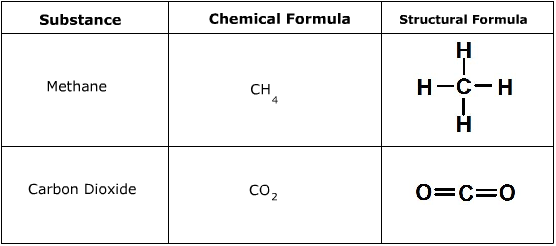
3. Примерный химический состав выхлопного газа автомобиля:
Азот (N) – 74-77%Пары воды (h3O) – 3-5,5%
Диоксид углерода (CO2) – 5-12%
Оксид углерода (CO) – 1-10%
Оксиды азота (NOx) – 0,1-0,8%
Альдегиды (R-CHO) – 0-0,2%
Углеводороды (CxHy) – 0,2-3%
Сернистый ангидрид (SO2) – 00,002%
4. Выхлопные газы
Совместное присутствие диоксидаазота, углеводородов и кислорода
приводит к появлению очень агрессивных
и вредных органических соединений –
пероксиацетилнитратов, образующих
фотохимический смог.
Кроме того, к особо опасным продуктам
выхлопа относят бензапирен и свинец.
5. Выхлопные газы
Загрязнение воздуха выхлопными газами оказываетвредное воздействие на живые организмы
несколькими путями. Во-первых, благодаря своей
летучести аэрозольные частицы и ядовитые газы
попадают в дыхательную систему человека и
животных, в листья растений.
 Во-вторых, влияют на
Во-вторых, влияют наизменение химического состава почв и воды; попадая в
слои атмосферы, выхлопные газы способны повысить
кислотность атмосферных осадков. В-третьих,
выхлопные газы причастны к стимуляции таких
химических реакций в атмосфере, которые приводят
к увеличению продолжительности облучения живых
организмов вредоносными солнечными лучами. И впятых, выхлопные газы способствуют изменению в
глобальных масштабах состава и температуры
атмосферы, создавая условия, неблагоприятные для
выживания организмов. Выхлопные газы сыграли
немалую роль в увеличении концентраций тяжелых
металлов в почве.
6. Выхлопные газы
Особенно загрязняют воздух подержанныйавтотранспорт (микроавтобусы), большая
многих из них установлены дизельные
двигатели, которые экономически выгодны
(топливо дешевле и расходуется меньше), но
загрязняют атмосферу на порядок выше, чем
бензиновый двигатель.
 Наибольший вред
Наибольший вредприносит автотранспорт, работающий на
этилированном бензине. Такой бензин содержит
примеси свинца в качестве антидетонатора и
становится причиной загрязнения городской
среды свинцом.
7. Сбор материала
Выбор деревьев: деревья примерно одноговозраста и размера, растут в похожих
условиях по освещенности влажности и
т.п., но в разных условиях
загазованности, вид: береза повислая.
Способ сбора: из нижней части кроны,
равномерно вокруг дерева, побеги должны
быть примерно одного типа, сложить
собранные листья в полиэтиленовый
пакет.
8. Исследование материала
Лист березы нужно перевернуть внутренней сторонойвверх и измерить 5 признаков
1 ширина левой и правой половинок листа. Для
измерения лист складывают пополам ,совмещая
верхушку с основанием листовой пластинки. Потом
разгибают лист, и по образовавшейся складке
измеряется расстояние от границы центральной
жилки до края листа.

2 длина жилки второго порядка, второй от основания
листа.
3 расстояние между основаниями первой и второй
жилок второго порядка.
4 расстояние между концами этих же жилок.
5 угол между главной жилкой и второй от основания
листа жилкой второго порядка.
После, данные заносятся в таблицу в мм и градусах.
9. Как оценивать отклонения состояния организма от условной нормы по величине интегрального показателя (ВИП):
1 балл —2 балла — 0.040-0.044
3 балла — 0.045-0.049
4 балла — 0.050-0.054
5 баллов — >0.054
10. Для выполнения работы требуются
лупалинейка на 10 см с ценой деления 1 мм
транспортир с ценой деления 1 градус
ОСТ 6-19-417-80
циркуль-измеритель ТУ 25-7203014-91
пинцеты
пакеты полиэтиленовые для хранения
материала
холодильник бытовой для хранения
материала
11. Цель
Определить,на сколько сильнозагазован наш район
как это влияет на растения.

12. Слева: береза у трассы; справа: береза во дворе
13. Листья березы, выросшей у трассы
14. Листья березы, выросшей во дворе
15. Таблица с измерениями листьев с березы, выросшей у трассы(в мм и градусах)
№1приз
лист н.
а
Лево
1приз
н.
Право
2пр.
Лево
2пр.
Прав
о
3пр.
Лево
3пр.
Прав
о
4пр.
Лево
4пр.
Прав
о
5 пр.
Лево
5пр.
Прав
о
1
18
19
30
31
6
5
9
11
35
38
2
19
16
30
28
6
5
10
9
34
33
3
10
9
18
18
4
3
6
7
39
37
4
9
7
15
15
5
5
7
8
43
37
5
7
8
11
13
5
5
3
5
38
38
16. Таблица с измерениями листьев с березы, выросшей во дворе(в мм и градусах)
№1пр.
лист Лево
а
1пр.
Прав
о
2пр.
Лево
2пр.
Прав
о
3пр.
Лево
3пр.
Прав
о
4пр.
Лево
4пр.
Прав
о
5пр.
Лево
5пр.
Прав
о
1
18
17
30
29
6
5,5
10
10
35
42
2
16
16
26
26
5
4
8
7
40
38
3
19
16
29
30
5
4
10
10
40
43
4
14
16
26
27
2
3
8
10
38
39
5
12
12
21
22
3
2
6
7
46
38
17. Счет по формуле \л-п\:\л+п\ (у дороги)
№ листа1 пр.
2 пр.
3 пр.
4 пр.
5 пр.
1
1/37
1/61
1/11
1/10
3/73
2
3/35
2/58
1/11
1/19
1/67
3
1/19
0
1/7
1/13
2/76
4
2/16
0
0
1/15
6/80
5
1/15
2/24
0
1/4
0
18.
 Счет по формуле \л-п\:\л+п\ (во дворе) № листа
Счет по формуле \л-п\:\л+п\ (во дворе) № листа1 пр.
2 пр.
3 пр.
4 пр.
5 пр.
1
1/35
1/59
0,5/11,5
0
1/11
2
0
0
1/9
1/15
2/78
3
3/35
1/59
1/9
0
3/83
4
2/30
1/53
1/5
2/18
1/77
5
0
1/43
1/5
1/13
8/84
19. счет по формуле (1пр+2пр+3пр+4пр+5пр)/5 (у дороги)
№ листаРасчет
итого
1
(0,027+0.016+0,091+0,1
+0,041)/5
=0,055
2
(0.086+0.034+0.091+0.0
52+0.015)/5
=0.056
3
(0.052+0.143+0.076+0.0
26)/5
=0.059
4
(0.125+0.067+0.075)/5
=0.053
5
(0.067+0.083+0.25)/5
=0.08
20. счет по формуле (1пр+2пр+3пр+4пр+5пр)/5 (во дворе)
№ листаРасчет
итого
1
(0.029+0.017+0.043+0.
091)/5
=0,036
2
(0.111+0.067+0.026)/5
=0.041
3
(0.086+0.017+0.036+0.
111)/5
=0.
 05
054
(0.067+0.019+0.2+0.11
1+0.013)/5
=0.082
5
(0.023+0.2+0.077+0.09
5)/5
=0.079
21. Подведение итогов
Величина показателя стабильностиразвития (ВПСР)
(ф-ла (1л+2л+3л+4л+5л)/5)(у дороги):
(0.055+0.056+0.059+0.053+0.08)/5=0.061
ВПСР(во дворе):
(0.036+0.041+0.05+0.082+0.079)/5=0.058
Так как у дороги ВПСР
(или ВИП)=0.061,что значительно больше
0.054,значит оценка 5 баллов.
И во дворе ВИП =0.058, что больше чем
0.054, поэтому оценка так же 5.
22. Подведение итогов
Эти результаты подводят нас к выводу,что в нашем районе аэрозольные
частицы и ядовитые газы попадают в
дыхательную систему человека и
животных, в листья растений,
выхлопные газы повышают кислотность
атмосферных осадков, увеличивается
продолжительность облучения живых
организмов вредоносными солнечными
лучами, в почве увеличилась
концентрация тяжелых металлов.
23.
 Заключение Судя по оценкам, в нашем районе очень
Заключение Судя по оценкам, в нашем районе оченьзагазованная окружающая среда. Это
означает, что пора бить тревогу,
экологические проблемы не решатся
сами собой.
Люди не приносят пользы для окружающей
среды, потому что их любое
производство не безотходное, поэтому
нам срочно нужно строить машины и
заводы, которые не будут создавать
отходов. Это очень трудно, но если мы
хотим, чтоб наши будущие дети и внуки
жили нормально или вообще жили, то мы
должны постараться.
Две томские ДЮСШ стали победителями благотворительной программы «Формула хороших дел» от СИБУР
Объявлены победители четвертого конкурса социально значимых проектов, который проводит СИБУР в рамках благотворительной программы «Формула хороших дел». При поддержке компании в 2019 году будут реализованы 127 проектов в 14 городах:
Благовещенск, Воронеж, Губкинский, Дзержинск, Кстово, Муравленко, Нижневартовск, Ноябрьск, Нягань, Пермь, Пыть-Ях, Тобольск, Тольятти, Томск
На конкурс было подано 522 заявки. Первое место по данному показателю вновь занял Тобольск (98 заявок). В пятерку лидеров также вошли: Томск (58 заявок), Нижневартовск (49 заявок), Дзержинск (42 заявки) и Воронеж (36 заявок).
Первое место по данному показателю вновь занял Тобольск (98 заявок). В пятерку лидеров также вошли: Томск (58 заявок), Нижневартовск (49 заявок), Дзержинск (42 заявки) и Воронеж (36 заявок).
Самым востребованным направлением программы традиционно является «Спорт и здоровый образ жизни» (142 заявки). Также популярны направления: «Образование и наука» (104 заявки) и «Культура» (99 заявок). Активное участие в конкурсе приняли образовательные учреждения (университеты, школы, детские сады), спортивные организации (школы, федерации и ассоциации), а также общественные организации, которые выполняют функции социальной защиты.
Победителями конкурса признаны две томские спортивные школы: СДЮСШОР №6 им.В.И.Расторгуева и ДЮСШ «Кедр». СДЮСШОР №6 получит средства на реализацию проекта по проведению Открытого благотворительного турнира по стритболу на Кубок бронзового призера Олимпиады-2012, воспитанника СДЮСШОР №6 им.В.И.Расторгуева Александра Кауна, а ДЮСШ «Кедр» — на строительство площадки для воркаута.
Проекты–победители конкурса направлены на развитие городской инфраструктуры, создание новых возможностей в сфере образования и науки, поддержку социально незащищенных групп, популяризацию спорта и здорового образа жизни, охрану окружающей среды.
СИБУР уделяет особое внимание развитию обратной связи между организаторами проектов и благополучателями. По результатам исследования устойчивости проектов программы «Формула хороших дел» было установлено, что постоянная обратная связь с благополучателями повышает эффективность проекта и создает основу для его долгосрочной реализации. В связи с этим пункт об обязательном сборе обратной связи был включен в регламент конкурса и стал важной частью итогового отчета по проекту.
«Залогом успеха устойчивого развития каждого конкретного города является наличие внутренних драйверов роста – городских сообществ, некоммерческих организаций, отдельных активистов и лидеров общественного мнения. В рамках «Формулы хороших дел» СИБУР стимулирует такую деятельность и дает возможность каждому внести свой вклад на благо родного города. Одним из ключевых инструментов является грантовый конкурс, который позволяет нам отбирать и поддерживать лучшие социально значимые инициативы. Мы благодарим всех участников четвертого конкурса и поздравляем победителей», – отметил член правления – управляющий директор СИБУРа Алексей Козлов.
Одним из ключевых инструментов является грантовый конкурс, который позволяет нам отбирать и поддерживать лучшие социально значимые инициативы. Мы благодарим всех участников четвертого конкурса и поздравляем победителей», – отметил член правления – управляющий директор СИБУРа Алексей Козлов.
Однофазный асинхронный электродвигатель
Дмитрий Левкин
Однофазный асинхронный электродвигатель — это асинхронный электродвигатель, который работает от электрической сети однофазного переменного тока без использования частотного преобразователя и который в основном режиме работы (после пуска) использует только одну обмотку (фазу) статора.Конструкция однофазного двигателя с вспомогательной или пусковой обмоткой
Основными компонентами любого электродвигателя являются ротор и статор. Ротор — вращающаяся часть электродвигателя, статор — неподвижная часть электродвигателя, с помощью которого создается магнитное поле для вращения ротора.
Основные части однофазного двигателя: ротор и статор
Статор имеет две обмотки, расположенные под углом 90° относительно друг друга. Основная обмотка называется главной (рабочей) и обычно занимает 2/3 пазов сердечника статора, другая обмотка называется вспомогательной (пусковой) и обычно занимает 1/3 пазов статора.
Двигатель фактически является двухфазным, но так как рабочей является только одна обмотка, электродвигатель называют однофазным.
Ротор обычно представляет из себя короткозамкнутую обмотку, также из-за схожести называемой «беличьей клеткой». Медные или алюминиевые стержни которого с торцов замкнуты кольцами, а пространство между стержнями чаще всего заливается сплавом алюминия. Так же ротор однофазного двигателя может быть выполнен в виде полого немагнитного или полого ферромагнитного цилиндра.
Однофазный двигатель с вспомогательной обмоткой имеет 2 обмотки расположенные перпендикулярно относительно друг друга
Принцип работы однофазного асинхронного двигателя
Для того чтобы лучше понять работу однофазного асинхронного двигателя, давайте рассмотрим его только с одним витком в главной и вспомогательной обмотки.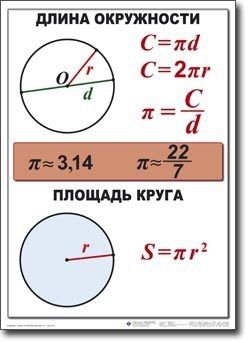
Проанализируем случай с двумя обмотками имеющими по оному витку
Рассмотрим случай когда в вспомогательной обмотки не течет ток. При включении главной обмотки статора в сеть, переменный ток, проходя по обмотке, создает пульсирующее магнитное поле, неподвижное в пространстве, но изменяющееся от +Фmах до -Фmах.
Запустить
Остановить
Пульсирующее магнитное поле
Если поместить ротор, имеющий начальное вращение, в пульсирующее магнитное поле, то он будет продолжать вращаться в том же направлении.
Чтобы понять принцип действия однофазного асинхронного двигателя разложим пульсирующее магнитное поле на два одинаковых круговых поля, имеющих амплитуду равную Фmах/2 и вращающихся в противоположные стороны с одинаковой частотой:
,
- где nпр – частота вращения магнитного поля в прямом направлении, об/мин,
- nобр – частота вращения магнитного поля в обратном направлении, об/мин,
- f1 – частота тока статора, Гц,
- p – количество пар полюсов,
- n1 – скорость вращения магнитного потока, об/мин
Запустить
Остановить
Разложение пульсирующего магнитного потока на два вращающихся
Действие пульсирующего поля на вращающийся ротор
Рассмотрим случай когда ротор, находящийся в пульсирующем магнитном потоке, имеет начальное вращение. Например, мы вручную раскрутили вал однофазного двигателя, одна обмотка которого подключена к сети переменного тока. В этом случае при определенных условиях двигатель будет продолжать развивать вращающий момент, так как скольжение его ротора относительно прямого и обратного магнитного потока будет неодинаковым.
Например, мы вручную раскрутили вал однофазного двигателя, одна обмотка которого подключена к сети переменного тока. В этом случае при определенных условиях двигатель будет продолжать развивать вращающий момент, так как скольжение его ротора относительно прямого и обратного магнитного потока будет неодинаковым.
Будем считать, что прямой магнитный поток Фпр, вращается в направлении вращения ротора, а обратный магнитный поток Фобр — в противоположном направлении. Так как, частота вращения ротора n2 меньше частоты вращения магнитного потока n1, скольжение ротора относительно потока Фпр будет:
,
- где sпр – скольжение ротора относительно прямого магнитного потока,
- n2 – частота вращения ротора, об/мин,
- s – скольжение асинхронного двигателя
Прямой и обратный вращающиеся магнитные потоки вместо пульсирующего магнитного потока
Магнитный поток Фобр вращается встречно ротору, частота вращения ротора n2 относительно этого потока отрицательна, а скольжение ротора относительно Фобр
,
- где sобр – скольжение ротора относительно обратного магнитного потока
Запустить
Остановить
Вращающееся магнитное поле пронизывающее ротор
Ток индуцируемый в роторе переменным магнитным полем
Согласно закону электромагнитной индукции прямой Фпр и обратный Фобр магнитные потоки, создаваемые обмоткой статора, наводят в обмотке ротора ЭДС, которые соответственно создают в короткозамкнутом роторе токи I2пр и I2обр.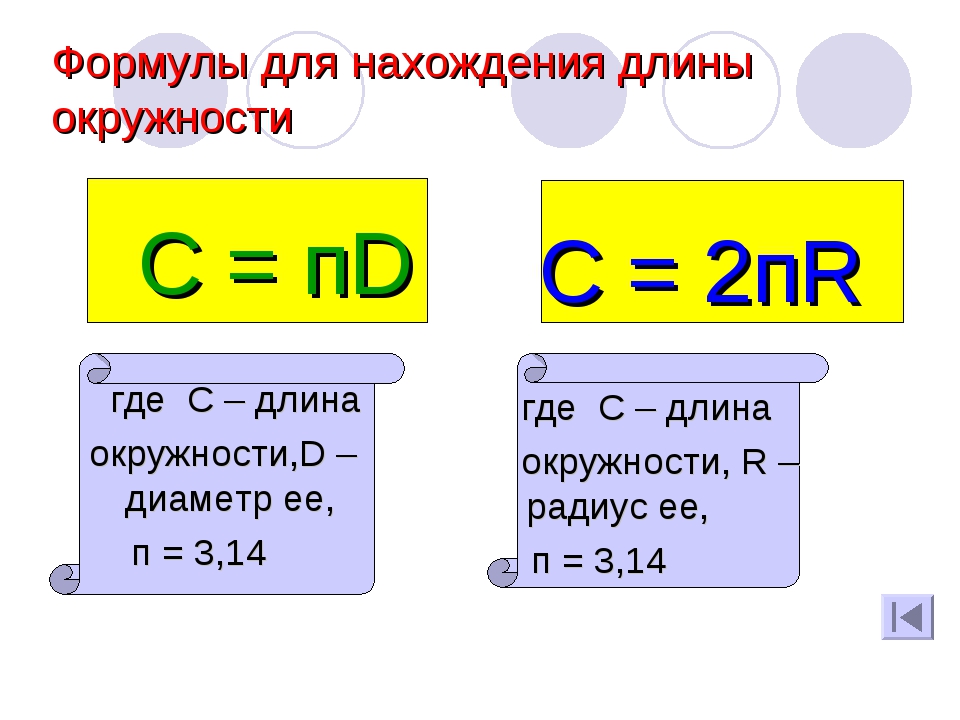 При этом частота тока в роторе пропорциональна скольжению, следовательно:
При этом частота тока в роторе пропорциональна скольжению, следовательно:
,
- где f2пр – частота тока I2пр наводимого прямым магнитным потоком, Гц
,
- где f2обр – частота тока I2обр наводимого обратным магнитным потоком, Гц
Таким образом, при вращающемся роторе, электрический ток I2обр, наводимый обратным магнитным полем в обмотке ротора, имеет частоту f2обр, намного превышающую частоту f2пр тока ротора I2пр, наведенного прямым полем.
Пример: для однофазного асинхронного двигателя, работающего от сети с частотой f1 = 50 Гц при n1 = 1500 и n2 = 1440 об/мин,скольжение ротора относительно прямого магнитного потока sпр = 0,04;
частота тока наводимого прямым магнитным потоком f2пр = 2 Гц;
скольжение ротора относительно обратного магнитного потока sобр = 1,96;
частота тока наводимого обратным магнитным потоком f2обр = 98 Гц
Согласно закону Ампера, в результате взаимодействия электрического тока I2пр с магнитным полем Фпр возникает вращающий момент
,
- где Mпр – магнитный момент создаваемый прямым магнитным потоком, Н∙м,
- сM — постоянный коэффициент, определяемый конструкцией двигателя
Электрический ток I2обр, взаимодействуя с магнитным полем Фобр, создает тормозящий момент Мобр, направленный против вращения ротора, то есть встречно моменту Мпр:
,
- где Mобр – магнитный момент создаваемый обратным магнитным потоком, Н∙м
Результирующий вращающий момент, действующий на ротор однофазного асинхронного двигателя,
,
Справка: В следствие того, что во вращающемся роторе прямым и обратным магнитным полем будет наводиться ток разной частоты, моменты сил действующие на ротор в разных направлениях будут не равны. Поэтому ротор будет продолжать вращаться в пульсирующем магнитном поле в том направлении в котором он имел начальное вращение.
Поэтому ротор будет продолжать вращаться в пульсирующем магнитном поле в том направлении в котором он имел начальное вращение.
Тормозящее действие обратного поля
При работе однофазного двигателя в пределах номинальной нагрузки, то есть при небольших значениях скольжения s = sпр, крутящий момент создается в основном за счет момента Мпр. Тормозящее действие момента обратного поля Мобр — незначительно. Это связано с тем, что частота f2обр много больше частоты f2пр, следовательно, индуктивное сопротивление рассеяния обмотки ротора х2обр = x2sобр току I2обр намного больше его активного сопротивления. Поэтому ток I2обр, имеющий большую индуктивную составляющую, оказывает сильное размагничивающее действие на обратный магнитный поток Фобр, значительно ослабляя его.
,
- где r2 — активное сопротивление стержней ротора, Ом,
- x2обр — реактивное сопротивление стержней ротора, Ом.

Если учесть, что коэффициент мощности невелик, то станет, ясно, почему Мобр в режиме нагрузки двигателя не оказывает значительного тормозящего действия на ротор однофазного двигателя.
С помощью одной фазы нельзя запустить ротор
Ротор имеющий начальное вращение будет продолжать вращаться в поле создаваемом однофазным статором
Действие пульсирующего поля на неподвижный ротор
При неподвижном роторе (n2 = 0) скольжение sпр = sобр = 1 и Мпр = Мобр, поэтому начальный пусковой момент однофазного асинхронного двигателя Мп = 0. Для создания пускового момента необходимо привести ротор во вращение в ту или иную сторону. Тогда s ≠ 1, нарушается равенство моментов Мпр и Мобр и результирующий электромагнитный момент приобретает некоторое значение .
Пуск однофазного двигателя. Как создать начальное вращение?
Одним из способов создания пускового момента в однофазном асинхронном двигателе, является расположение вспомогательной (пусковой) обмотки B, смещенной в пространстве относительно главной (рабочей) обмотки A на угол 90 электрических градусов. Чтобы обмотки статора создавали вращающееся магнитное поле токи IA и IB в обмотках должны быть сдвинуты по фазе относительно друг друга. Для получения фазового сдвига между токами IA и IB в цепь вспомогательной (пусковой) обмотки В включают фазосмещающий элемент, в качестве которого используют активное сопротивление (резистор), индуктивность (дроссель) или емкость (конденсатор) [1].
После того как ротор двигателя разгонится до частоты вращения, близкой к установившейся, пусковую обмотку В отключают. Отключение вспомогательной обмотки происходит либо автоматически с помощью центробежного выключателя, реле времени, токового или дифференциального реле, или же вручную с помощью кнопки.
Таким образом, во время пуска двигатель работает как двухфазный, а по окончании пуска — как однофазный.
Подключение однофазного двигателя
С пусковым сопротивлением
Двигатель с расщепленной фазой — однофазный асинхронный двигатель, имеющий на статоре вспомогательную первичную обмотку, смещенную относительно основной, и короткозамкнутый ротор [2].
Однофазный асинхронный двигатель с пусковым сопротивлением — двигатель с расщепленной фазой, у которого цепь вспомогательной обмотки отличается повышенным активным сопротивлением.
Омический сдвиг фаз, биффилярный способ намотки пусковой обмотки
Разное сопротивление и индуктивность обмоток
Для запуска однофазного двигателя можно использовать пусковой резистор, который последовательно подключается к пусковой обмотки. В этом случае можно добиться сдвига фаз в 30° между токами главной и вспомогательной обмотки, которого вполне достаточно для пуска двигателя.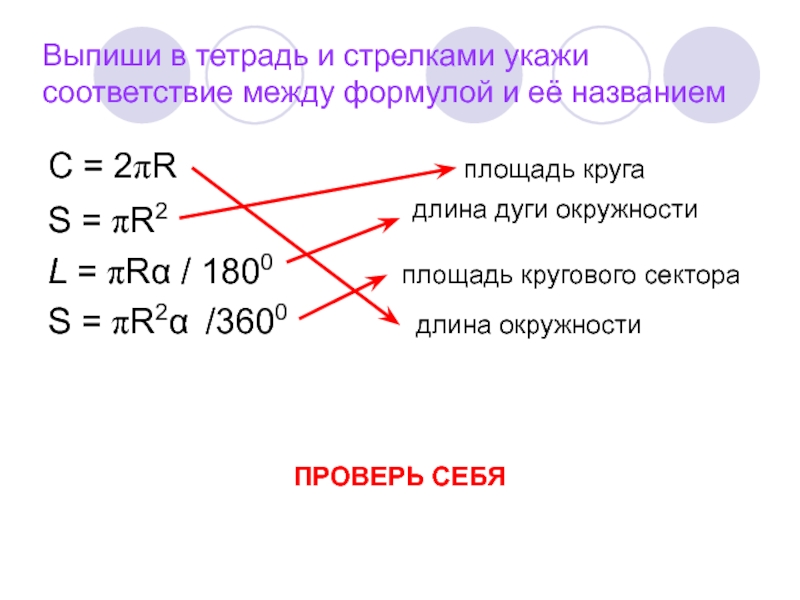 В двигателе с пусковым сопротивлением разность фаз объясняется разным комплексным сопротивлением цепей.
В двигателе с пусковым сопротивлением разность фаз объясняется разным комплексным сопротивлением цепей.
Также сдвиг фаз можно создать за счет использования пусковой обмотки с меньшей индуктивностью и более высоким сопротивлением. Для этого пусковая обмотка делается с меньшим количеством витков и с использованием более тонкого провода чем в главной обмотке.
Отечественной промышленностью изготавливается серия однофазных асинхронных электродвигателей с активным сопротивлением в качестве фазосдвигающего элемента серии АОЛБ мощностью от 18 до 600 Вт при синхронной частоте вращения 3000 и 1500 об/мин, предназначенных для включения в сеть напряжением 127, 220 или 380 В, частотой 50 Гц.
С конденсаторным пуском
Двигатель с конденсаторным пуском — двигатель с расщепленной фазой, у которого цепь вспомогательной обмотки с конденсатором включается только на время пуска.
Ёмкостной сдвиг фаз с пусковым конденсатором
Чтобы достичь максимального пускового момента требуется создать круговое вращающееся магнитное поле, для этого требуется чтобы токи в главной и вспомогательной обмотках были сдвинуты друг относительно друга на 90°. Использование в качестве фазосдвигающего элемента резистора или дросселя не позволяет обеспечить требуемый сдвиг фаз. Лишь включение конденсатора определенной емкости позволяет обеспечить фазовый сдвиг 90°.
Использование в качестве фазосдвигающего элемента резистора или дросселя не позволяет обеспечить требуемый сдвиг фаз. Лишь включение конденсатора определенной емкости позволяет обеспечить фазовый сдвиг 90°.
Среди фазосдвигающих элементов, только конденсатор позволяет добиться наилучших пусковых свойств однофазного асинхронного электродвигателя.
Двигатели в цепь которых постоянно включен конденсатор используют для работы две фазы и называются — конденсаторными. Принцип действия этих двигателей основан на использовании вращающегося магнитного поля.
Двигатель с экранированными полюсами — двигатель с расщепленной фазой, у которого вспомогательная обмотка короткозамкнута.
Статор однофазного асинхронного двигателя с экранированными полюсами обычно имеет явно выраженные полюса. На явно выраженных полюсах статора намотаны катушки однофазной обмотки возбуждения. Каждый полюс статора разделен на две неравные части аксиальным пазом. Меньшую часть полюса охватывает короткозамкнутый виток. Ротор однофазного двигателя с экранированными полюсами — короткозамкнутый в виде «беличьей» клетки.
Ротор однофазного двигателя с экранированными полюсами — короткозамкнутый в виде «беличьей» клетки.
При включении однофазной обмотки статора в сеть в магнитопроводе двигателя создается пульсирующий магнитный поток. Одна часть которого проходит по неэкранированной Ф’, а другая Ф» — по экранированной части полюса. Поток Ф» наводит в короткозамкнутом витке ЭДС Ek, в результате чего возникает ток Ik отстающий от Ek по фазе из-за индуктивности витка. Ток Ik создает магнитный поток Фk, направленный встречно Ф», создавая результирующий поток в экранированной части полюса Фэ=Ф»+Фk. Таким образом, в двигателе потоки экранированной и неэкранированной частей полюса сдвинуты во времени на некоторый угол.
Пространственный и временной углы сдвига между потоками Фэ и Ф’ создают условия для возникновения в двигателе вращающегося эллиптического магнитного поля, так как Фэ ≠ Ф’.
Пусковые и рабочие свойства рассматриваемого двигателя невысоки. КПД намного ниже, чем у конденсаторных двигателей такой же мощности, что связано со значительными электрическими потерями в короткозамкнутом витке.
КПД намного ниже, чем у конденсаторных двигателей такой же мощности, что связано со значительными электрическими потерями в короткозамкнутом витке.
Статор такого однофазного двигателя выполняется с ярко выраженными полюсами на не симметричном шихтованном сердечнике. Ротор — короткозамкнутый типа «беличья клетка».
Данный электродвигатель для работы не требует использования фазосдвигающих элементов. Недостатком данного двигателя является низкий КПД.
|
Для многих читателей, конечно, будет интересно знать, как производить расчет стенок стволов. Вот самая простая формула (со всеми пояснениями она дана на стр. 71—74 тома I С. А. Бутурлина «Стрельба пулей», 1912 г.). Если обозначим буквой Т толщину стенки ствола в миллиметрах, буквой р— радиус канала ствола (т. т. е. давление умножаем на радиус канала и это произведение делим на коэфициент прочного сопротивления, взятый в тех же мерах, что и давление. Частное от этого деления и есть необходимая толщина стенки. Если размер ствольной стенки знаем, а ищем другие величины, то получаем их из перегруппировки той же формулы: т. е. произведение толщины стенки на коэфициент прочности, деленное на радиус канала ствола, дает величину допустимого давления газов. Наконец, т. е. произведение давления гaзов на радиус канала ствола, деленное на толщину стенки, показывает соответствующую величину испытываемого металлом ствола напряжения. Эту формулу, по ее чрезвычайной простоте, охотно применяли и сорок лет назад, но только для предварительных, ориентировочных расчетов, иначе она может быть опасной, так как дает преуменьшенные значения для толщины стенок. И так как эта самая формула рекомендуется в недавно вышедшем 3-м издании книги инж. А. А. Зернова «Стрельба дробью», 1935 г, стр. 216, то необходимо оговорить, что формула эта не научна, так как основана на ложном предположении, будто вся толща стенки ствола под давлением газов испытывает одинаковые напряжения. В действительности внутренние слои напрягаются: сильнее, чем наружные. Положим, имеется ружье 16 калибра, следовательно, радиус его канала—8,6 см; положим, материал ствола имеет коэфициент упругого сопротивления в 20 кг на мм2. По этой формуле необходимая толщина стенки при давлении в 800 атм., т. е. 8 кг на мм2 будет: 8,6 * 8 / 20 = 3,44 мм. Инженер К. Г. Мартынов лет около 40 назад предложил также очень простую формулу, годную для дробовых стволов при. По этой же формуле получим, если ищем величину допустимого давления для стенки известной толщины, наконец, для выражения К она принимает такой вид: Сделаем тот же числовой расчет,, какой только что делали,т. е. найдем толщину ствола 16 калибра для давления 800 атм, к (=8 кг на 1 мм2) при прочности материала в 20 кг на мм2 и получим (2ХЗ,1416…Х8,6Х8 = 432,28; 4X20=80; 432,28 : 80 = 5,4) —5,4 мм — в полтора раза больше, чем по первой формуле. Но формула Мартынова, как уже сказано, дает несколько преувеличенные результаты, и более близкие к действительности выводы дают расчеты по несколько измененной формуле Лямэ такого вида: где все буквы означают то же, что и в предшествующих формулах. Подставляя в эту формулу те же величины (давление 800 атм. или 8 кг на мм2, коэфициент безопасного напряжения 2000 кг на см2 или 20 кг на мм2 и радиус канала ствола 16 калибра__8,6 мм), получим толщину стенки в 4,77 мм, или, в другой форме, радиус наружного обхвата ствола —13,37 мм, а за вычетом радиуса канала 1(13,37—8,6 = 4,77) —те же 4,77, т. е. больше, чем по первой Формуле, почти на 40 проц., но меньше, чем по формуле К. Г. Мартынова, на неполных 12 проц. Для нахождения допустимой величины давления D если .известны: прочность материала ствола к, его калибр (р—радиус или половина поперечника канала) и толщина стенки или наружный поперечник (Р—половина его или ‘радиус —р+Т), можно взять очень простую формулу: Подсчет по ней с подстановкой тех же цифр, что и в выше проделанных примерах, даст D=8,29 кг на мм2 или 829 атмосфер—преувеличение меньше, чем на 4 проц. Наконец, коэфициент безвредного напряжения металла ствола к определим так: По подсчету в нашем примере получим к=17,75, т. е. с преуменьшением почти на 13 проц. Надо, конечно, иметь в виду, что само инструментальное определение величин давления пороховых газов очень неточно и условно, а потому и от решения вопросов, с этим связанных, по простым подсчетам нет основания требовать очень большой точности. Из только что приведенных формул вытекает большая прочность малых калибров, чем больших. Но для большей наглядности даем вычисленные по формуле Лямэ Таблица 25. Для расчета стволов дробовиков
Толщина стенок в мм при упругом сопротивлении в 20 кг на 1 мм2. Таблица 26. Для расчета стволов дробовиков
Толщина стенок в мм при упругом сопротивлении в 40 кг на 1 мм2. Расчет, данный в табл. 25, годен для старых ружей, так как даже низкосортный Дамаск имел упругое сопротивление выше 20 кг на мм2, или 2000 кг на см2. Для хорошей современной ствольной стали коэфициент прочного сопротивления можно принимать не в 20, а в 40 кг на мм2, при этом условии приводим таблицу 26. И из вышеприведенной формулы Лямэ и из этих таблиц видно, что при (одинаковой прочности ствольного материала к и одинаковом давлении газов D толщина стенок ствола Т вполне пропорциональна калибру ствола (или его радиусу — р). Поэтому данными таблицами можно пользоваться для любого калибра. Для этого цифру, взятую в таблице для данного давления, надо увеличить или уменьшить во столько раз, во сколько раз калибр., для которого мы ищем толщину стенки, больше калибра, указанного в таблице. Вот для примера: Желаем найти толщину стенки из материала с упругим сопротивлением 20 кг на 1 мм2 при давлении газов в 900 атм. для стволов 12 калибра и 20 калибра. 12 калибр имеет канал в 18,5 мм. Берем из первой таблицы толщину стенки при 900 атм. для ствола с поперечником канала в 1 мм — 0,374 мм и увеличиваем в 10 раз; получим 3,74 мм уже для калибра в 10 мм. Для 20 калибра с каналом 16 мм берем по графе для 900 атм. цифру для ствола калибром в 1 мм, увеличиваем ее в 10 раз и прикладываем цифру той же строки (для 900 атм.) для калибра в 6 мм и получим (3,74 + 2,244=5,984) 5,984 или, округляя, 5,99 мм для калибра (10+6 = 16) в 16 мм. Или же просто возьмем из той же стройки цифру для калибра в 4 мм—1,496—и умножим ее на 4, так как калибр 20-й в 16,0 мм ровно в 4 раза больше, чем калибр в 4 мм, и получим (1,496X4 = 5,984), те же 5,984 для калибра 20 (4X4 = 16) в 16 мм. Следовательно, чем меньше калибр ствола, тем тоньше во столько же раз может быть стенка его для перенесения определенных давлений. Если хотим найти толщину стенок для ствола, материал которого по коэфициенту упругого сопротивления отличается от тех (20 кг и 40 кг на мм2), для которых составлены таблицы, то это также сделать просто: надо искать нужную толщину не в той стрючке атмосфер давления, которая соответствует задуманному нами давлению, а в другой, соответствующей задуманному давлению, разделенному на отношение имеющегося коэфициента прочности к табличному коэфициенту. Например, если хотим найти достаточную толщину стенки при давлении в 450 атм. для слабых железных стволов с коэфициен-том прочного сопротивления всего в 15 кг на мм2, то поступим так. Отношение имеющегося в данном случае коэфициента (15} к табличному (20) равно (15/20 = 3/4) трем четвертям. Поэтому имеющееся давление газов (450 атм.) делим на 3/4 (450: 3/4 = 600) и получаем 600. Следовательно, требуемые цифры толщины стенок надо в первой таблице в этом случае искать в строчке для 600 атм. (хотя соответствовать они будут при данном материале ствола давлению в 450 атм. Если у нас материал более прочный, например, с коэффициентом в 30 кг на мм2, то поступаем точно так же. Берем отношение этого коэфициента к табличному (30/20 = 3/2) и на полученное отношение (2/3 ) разделим имеющееся давление (450: 3/2 =300 ). Следовательно, толщину стволов для этого случая найдем в строчке давления в 300 атм. Во всяком случае, в дробовике желательно иметь по возможности толщину каждой стенки ствола: сейчас за патронником— не меньше 3,5 мм и еще лучше—до 4 мм; в 22 см (5 верш.) от казенного обреза —не меньше 1,75 мм, лучше до 2 мм; в самом тонком месте — 0,80 мм, лучше 1,00 мм. Это место в 71-сантиметровых (аршинных) стволах обыкновенно приходится между 35—55 см (8 и 12,25 верш.) от казны; отсюда к дулу непременно должно итти постепенно утолщение; в дульном срезе при цилиндрической сверловке желательна толщина до 1,4 мм, а при чоковой сверловке—до 2,00 мм, чтобы перед сужением, т. е. около 7—18 см (1,75 верш.) от вылета, толщина была не менее 1,50 мм. В одностволках, где вес ружья это позволяет, возможна и желательна еще большая толщина. Так, в магазинках Винчестера образца 1893 г., отличающихся замечательным боем, толщина стенок (при 12 калибре) была: в 7 см от казенного обреза — 4,15 мм, в 22,2 см—2,85 мм и в самом тонком месте—1,70 мм.
|
|||||||||||
Срок — служба — цепь
Срок — служба — цепь
Cтраница 1
Срок службы цепи зависит от многих факторов, влияющих на ее работоспособность. [1]
Срок службы цепи по износостойкости и выносливости рекомендуется определять по методу н выражениям, приведенным в гл. [3]
Срок службы цепей увеличивается в 5 — б раз. [5]
Срок службы цепи зависит в большой степени от того, насколько рационально устроена ее смазка, так как иначе шарниры цепи быстро срабатываются, и ее шаг чрезмерно увеличивается.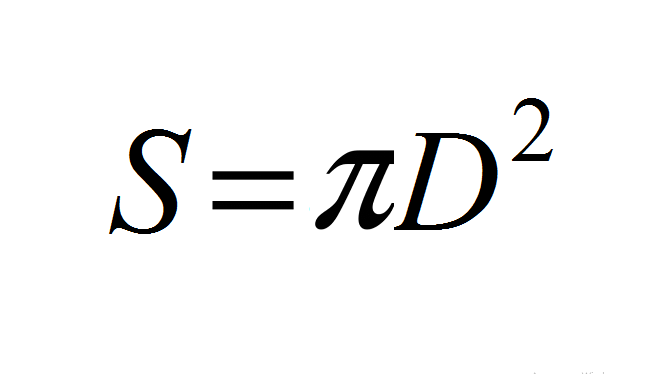 Износ шарниров является именно той причиной, которая делает цепь не пригодной для дальнейшей работы.
[6]
Износ шарниров является именно той причиной, которая делает цепь не пригодной для дальнейшей работы.
[6]
Срок службы цепи CDiN 10 000 ч при А / 2 % или 15 000 ч при Л / 3 % по DiN 8195 для стандартных параметров и нормальных условий повсеместно признан отвечающим действительности. [7]
Если срок службы цепи в машине-аналоге слишком большой, то для проектируемой машины при надлежащем расчетном обосновании можно применить более легкую, простую и дешевую цепь. [8]
Иногда срок службы цепи из сварных звеньев не превышает одну-две недели. Цепи элеваторов цементных печей очень трудно смазывать вследствие плохого доступа к ним и непрерывной работы элеваторов. При смазывании таких роликовых цепей коллоидным графитом уменьшается шум и увеличивается срок службы целей. [9]
Определяем срок службы цепи по усталостной прочности пластин [ формула ( 43) ]; значение упл и 6 / принимаем из табл. 10 и 12 гл.
[10]
10 и 12 гл.
[10]
Определяем срок службы цепи 2ПР — 31.75 [ формула ( 31) ] при П — 850 с уменьшением на величину 1 2 ] АЦ ( см. стр. [11]
Если прогнозируемый срок службы цепи отклоняется от требуемого на 10 — 15 %, то не следует проводить корректировку параметров цепной передачи. [12]
Расчет Определяем срок службы цепи 2ПР — 3 1 75 — 17700 1формула ( 67) ] при. [13]
Для передач со сроком службы цепи в меньших пределах, чем базовый, представляется возможность для той же приводной цепи повысить передаваемую мощность за счет увеличения допускаемого давления в шарнире или снижения коэффициента запаса прочности, а также при условии сохранения передаваемой мощности в пределах, соответствующих базовому сроку службы цепи, осуществить более широкий выбор способа смазки, например вместо непрерывной смазки с помощью масляной ванны применить капельную или внутришарнирную смазку. Теоретические и экспериментальные исследования проводят главным образом на износостойкость шарнирных поверхностей и в меньшей степени на выносливость цепи.
[14]
Теоретические и экспериментальные исследования проводят главным образом на износостойкость шарнирных поверхностей и в меньшей степени на выносливость цепи.
[14]
Метод Рахнера не предусматривает расчета срока службы цепи по заданным параметрам, однако его рекомендации могут быть использованы для практического применения. [15]
Страницы: 1 2 3 4
Харди-Вайнберг
Харди-ВайнбергФОРМУЛА HARDY-WEINBERG
Два человека, Г. Х. Харди и В. Вайнберг, математически показали, что для любого данного гена, присутствующего в популяции особей (диплоидной и воспроизводящейся половым путем), частоты аллелей и генотипов не будут меняться от поколения к поколению (навсегда) при соблюдении трех условий. встречались:
1. Популяция особей, несущих этот ген, бесконечно велика.
Популяция особей, несущих этот ген, бесконечно велика.
2. Особи в этой популяции спариваются случайным образом в отношении этого гена (ов).
3. На этот ген не действуют никакие эволюционные силы (естественный отбор, генетический дрейф, миграция, мутации и т. Д.)
Харди и Вайнберг разработали формулу, которая показывает взаимосвязь между частотами аллелей и частотами генотипов при соблюдении трех условий, упомянутых выше; это известно как формула Харди-Вайнберга .
Q.Какая формула?
A. Формула для гена с двумя возможными аллелями :
(p + q) 2 = 1, что совпадает с p2 + 2pq + q2 = 1
Где p = частота одного аллеля и q = частота другого аллеля
p2 = ожидаемая частота. гомозигот по одному аллелю
2pq = ожидаемая частота. гетерозигот
q2 = ожидаемая частота. гомозигот по другому аллелю
Q.Что делать, если я имею дело с геном с более чем двумя аллелями, какую формулу мне использовать?
A. Формула в основном та же, за исключением увеличения числа частот аллелей, включенных в формулу. Например, ген с тремя возможными аллелями (например, A1, A2, A3) будет иметь формулу:
Формула в основном та же, за исключением увеличения числа частот аллелей, включенных в формулу. Например, ген с тремя возможными аллелями (например, A1, A2, A3) будет иметь формулу:
(p + q + r) 2 = 1, что совпадает с p2 + q2 + r2 + 2pq + 2pr + 2qr = 1
Где p = freq. первого аллеля, q = freq. второго аллеля и r = частота третьего аллеля.
p2 = Freq. гомозигот по первому аллелю
q2 = Freq. гомозигот по второму аллелю
r2 = Freq. гомозигот по третьему аллелю
2pq = Freq. гетерозигот по первому и второму аллелю
2pr = Freq. гетерозиготы по первому и третьему аллелю
2qr = Freq. гетерозиготы по второму и третьему аллелю
В. Чем хороша эта формула? Зачем вообще его использовать?
А.Если вы изучаете ген (ы) в определенной популяции, вы можете использовать частоты аллелей, которые вы оценили по выборке из этой популяции, чтобы сгенерировать ожидаемые частоты генотипов для этой популяции (подставив частоты ваших аллелей в формулу Харди-Вайнберга). ). Если частоты генотипов, которые вы получаете с помощью формулы Харди-Вайнберга, не совпадают с частотами, которые вы фактически наблюдаете в своей выборке, то одно из трех предположений, изложенных выше (вверху страницы), не выполняется.Следовательно, у вас есть основание для расследования причин. Это исследование того, почему и как частота генов меняется в популяциях с течением времени — по сути, исследование эволюции.
). Если частоты генотипов, которые вы получаете с помощью формулы Харди-Вайнберга, не совпадают с частотами, которые вы фактически наблюдаете в своей выборке, то одно из трех предположений, изложенных выше (вверху страницы), не выполняется.Следовательно, у вас есть основание для расследования причин. Это исследование того, почему и как частота генов меняется в популяциях с течением времени — по сути, исследование эволюции.
Электроэнергия — веб-формулы
Электрическая мощность определяется по формуле:P = В · I
Где В — напряжение, а I — ток.
Соответствующие единицы:
ватт (Вт) = вольт (В) · ампер (A)
Мощность также можно определить по следующим формулам:
P = I 2 · R ↔ R = P / I 2 ↔ I 000 = √ ( P P R )
P = V 2 / R ↔ R = V 2 / 2 / ↔ V = √ ( P · R )
Подробнее об электроэнергии 9000 5
Электроэнергия определяется как скорость, с которой работа выполняется источником эл.
 м.ф. в поддержании тока в электрической цепи. Практическая единица мощности — киловатт и лошадиные силы; где 1 киловатт = 100 ватт и 1 л.с. = 746 ватт.
м.ф. в поддержании тока в электрической цепи. Практическая единица мощности — киловатт и лошадиные силы; где 1 киловатт = 100 ватт и 1 л.с. = 746 ватт.Если сопротивления (например, электрические приборы) соединены последовательно, ток через каждое сопротивление будет одинаковым. Тогда мощность электрического прибора, P α R и P α V (поскольку V = IR), это означает, что в комбинации сопротивлений серии разность потенциалов и потребляемая мощность будут больше при большем сопротивлении .
Если сопротивления ( i.е. электроприборов) подключены параллельно, разность потенциалов на каждом приборе одинакова. Тогда P α 1 / R и I α 1 / R (как V = IR), что означает, что в параллельных комбинациях сопротивлений потребляемый ток и мощность будут больше при меньшем сопротивлении.
Для данного напряжения В, , если сопротивление изменяется с R на ( R / n ), а потребляемая мощность изменяется с P на nP , то в соответствии с P = V 2 / R , имеем:
P = V 2 / (R / n)) = n (V 2 / R) = nP, где R = R / n и P = nP
Когда приборы питания P 1 , P 2 , P 3 … P n включены последовательно с источником напряжения, эффективная потребляемая мощность ( P с ) определяется по формуле:
1/ P с = 1 / P 1 + 1 / P 2 + 1 / P 3 +… + 1 / P n
Для n устройств, каждое из сопротивление R , последовательно соединены с источником напряжения В, рассеиваемая мощность P с тогда определяется как:
(1) P с = В 2 / n R
Когда приборы питания
P 1 , P 2 , P 3 … P n подключены параллельно к источнику напряжения, эффективная мощность потреблено ( P p ) тогда определяется следующим образом:P s = P 1 + P 2 + P 3 +… + P n
Для устройств n , каждое с равным сопротивлением R , подключенных параллельно к источнику напряжения В , рассеиваемая мощность тогда определяется как:
(2) P p = В 2 / ( R / n) = n V 2 / R
Из (1) и (2) мы имеем P p / P s = n 2 или просто записать как : P p = n 2 P s .
В соответствии с приведенными выше формулами, мы можем объяснить, что:
При группировке ламп серии по заданному источнику напряжения лампа большей мощности будет давать меньшую яркость и будет иметь меньший потенциал сопротивления, но тот же ток. , тогда как в параллельном группировке лампочек на данном источнике напряжения лампа большей мощности даст большую яркость и позволит большему току проходить через нее, но будет иметь меньшее сопротивление и такую же разность потенциалов на нем.
Электроэнергия
Электроэнергия определяется как общая выполненная работа или энергия, поставленная источником ЭДС. при поддержании тока в электрической цепи в течение заданного времени:
Электрическая энергия = электрическая мощность × время = P × t
Таким образом, формула для электрической энергии имеет вид:
Электрическая энергия = P × т = V × I × т = I 2 × R × т = V 2 т / R
S. I единица электрической энергии — джоуль (обозначается Дж), где 1 джоуль = 1 ватт × 1 секунда = 1 вольт × 1 ампер × 1 секунда
I единица электрической энергии — джоуль (обозначается Дж), где 1 джоуль = 1 ватт × 1 секунда = 1 вольт × 1 ампер × 1 секунда
Коммерческая единица электрической энергии — киловатт-час ( кВт · ч, ), где 1 кВтч = 1000 Вт h = 3,6 × 10 6 J = одна единица потребляемой электроэнергии .
Количество единиц потребляемой электроэнергии равно n = (общая мощность × время в часе) / 1000
Стоимость потребления электроэнергии в доме = количество.единиц потребленной электроэнергии × количество на одну единицу электроэнергии.
Теорема о максимальной мощности
В ней говорится, что выходная мощность источника тока максимальна, когда внутреннее сопротивление источника равно внешнему сопротивлению в цепи. Итак, если R — внешнее сопротивление цепи, а r — внутреннее сопротивление источника тока (то есть батареи), то выходная мощность максимальна, когда R = R.
Эта теорема применима ко всем типам источников ЭДС. и связан с выходной мощностью, а НЕ с рассеиваемой мощностью.
Если E — применяемая ЭДС. источника ЭДС. т.е. . батарея внутреннего сопротивления r и R — внешнее сопротивление, тогда ток в цепи определяется как:
I = E / (R + r)
При максимальной выходной мощности R = r , поэтому имеем:
I = E / (r + r) = E / (2r)
и
максимальная выходная мощность:
P max = I 2 r = E 2 / (4r)
При коротком замыкании аккумулятора мощность равна нулю.В этом случае вся мощность батареи рассеивается внутри батареи из-за ее внутреннего сопротивления. Таким образом, мощность, рассеиваемая внутри батареи, определяется как: P = ( E / r) 2 × r = E 2 / r
КПД источника ЭДС.
КПД источника ЭДС. определяется как отношение выходной мощности (, т. е. — мощность через внешнее сопротивление цепи, к входной мощности (т. е.мощность, потребляемая от источника ЭДС). Итак,
е. — мощность через внешнее сопротивление цепи, к входной мощности (т. е.мощность, потребляемая от источника ЭДС). Итак,
Где V = падение потенциала на внешнем сопротивлении R,
E = E.M.F. источника тока,
I = ток в цепи.
Если r — внутреннее сопротивление источника ЭДС, тогда
V = IR и E = I (R + r )
или
Когда мощность, полученная от источника, максимальна, тогда R = р. В данной ситуации имеем:
Таким образом максимальная эффективность источника эл.м.ф. составляет 50%. Это означает, что для элемента только половина общей мощности, потребляемой элементом, используется для полезных целей, тогда как другая половина рассеивается внутри элемента.
Пример 1:
Лифт должен поднимать 1000 кг на расстояние 100 м со скоростью 4 м / с. Какую в среднем мощность оказывает лифт во время этой поездки?
Решение:
Работу, проделанную лифтом на 100 метров, легко вычислить:
W = mgh = (1000) (9.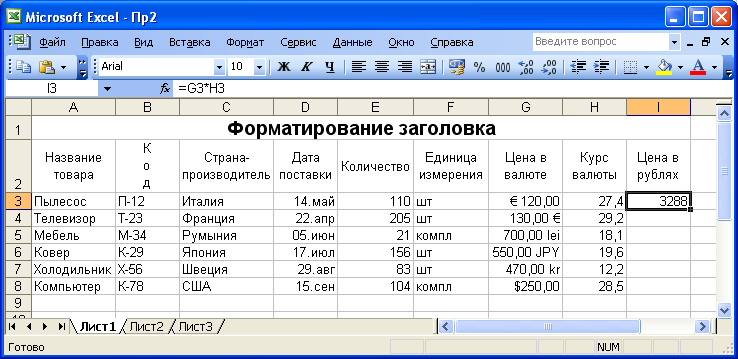 8) (100) = 9,8 × 10 5 Дж.
8) (100) = 9,8 × 10 5 Дж.
Общее время поездки можно рассчитать по скорости лифта:
t = x / v = 100 м / 4 м / с = 25 с .
Таким образом, средняя мощность определяется по формуле: P = Вт / t = 9,8 × 10 5 / 25с = 3,9 × 10 4 Вт или 39 кВт.
Пример 2:
Считается, что объект в свободном падении достиг конечной скорости , если сопротивление воздуха становится достаточно сильным, чтобы противодействовать всем ускорениям силы тяжести, в результате чего объект падает с постоянной скоростью.Точное значение конечной скорости варьируется в зависимости от формы объекта, но для многих объектов может быть оценено на уровне 100 м / с. Когда объект весом 10 кг достиг предельной скорости, какую силу сопротивление воздуха оказывает на объект?
Решение: Для решения этой проблемы мы будем использовать уравнение P = Fv cos θ , Вместо обычного уравнения мощности, поскольку нам дана скорость объекта.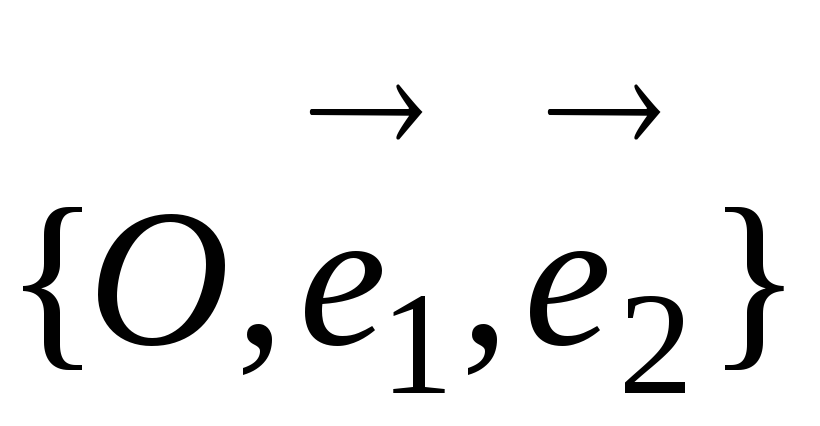 Нам просто нужно вычислить силу, прилагаемую к объекту сопротивлением воздуха, и угол между силой и скоростью объекта.Поскольку объект достиг постоянной скорости, результирующая сила, действующая на него, должна быть равна нулю. Поскольку на объект действуют только две силы: сила тяжести и сопротивление воздуха, сопротивление воздуха должно быть равным по величине и противоположным по направлению силе тяжести. Таким образом, F a = — F G = мг = 98 Н, направленное вверх. Таким образом, сила, прилагаемая сопротивлением воздуха, антипараллельна скорости объекта. Таким образом:
Нам просто нужно вычислить силу, прилагаемую к объекту сопротивлением воздуха, и угол между силой и скоростью объекта.Поскольку объект достиг постоянной скорости, результирующая сила, действующая на него, должна быть равна нулю. Поскольку на объект действуют только две силы: сила тяжести и сопротивление воздуха, сопротивление воздуха должно быть равным по величине и противоположным по направлению силе тяжести. Таким образом, F a = — F G = мг = 98 Н, направленное вверх. Таким образом, сила, прилагаемая сопротивлением воздуха, антипараллельна скорости объекта. Таким образом:
P = Fv cos θ = (98) (100) (cos180) = — 9800 Вт
Пример 3: Мощность двигателя насоса составляет 4 кВт.Сколько воды в кг / мин он может поднять на высоту 20 м? (g = 10 м / с 2 )
Решение:
Заданная мощность двигателя P = 4KW = 4000 Вт
Если масса воды, поднятая за одну секунду, = m кг.
Общий объем работы, выполненной при подъеме воды, W = mgh
Мощность P = Вт / т, но t = 1 минута = 60 сек.
4000 = mgh / 60
4000 = (m × 10 × 20) / 60
m = 1200 кг.
Пример 4 : Когда вода течет по трубе, ее скорость изменяется на 5%, найти изменение силы воды?
Решение: Мощность = Сила × Скорость = Скорость изменения количества движения × скорость = {(масса / время) × скорость} x скорость = {(adv) × v} × v = adv 3 где «a» — площадь поперечного сечения, «d» — плотность воды, а «v» — скорость потока воды.
Следовательно, Сила воды прямо пропорциональна кубу скорости воды, поэтому пусть
P = Kv 3 (k — постоянная величина, равная ad.)
Взятие бревна с обеих сторон
log P = 3log v + log k
Дифференциация с обеих сторон
dP / P = 3dv / v
процентное изменение мощности, dP / P × 100 = 3 × 5% = 15%.
Пример 5 : Кинетическая энергия выбрасываемой воды из плотины используется для вращения турбины. Труба, по которой устремляется вода — 2.4 метра и его скорость 12 м / сек. Предполагая, что вся кинетическая энергия воды используется для вращения турбины, вычислите производимый ток, если эффективность динамо-машины составляет 60% и станция передает мощность 240 кВ. Плотность воды = 10 3 кг / м 3 .
Решение: Учитывая, что
r = радиус трубы = 1,2 м, средняя скорость воды v = 12 м / с
V = 240 кВ = 240 × 10 3 вольт, плотность воды p = 10 3 кг / м 3 .
Теперь кинетическая энергия текущей воды в секунду, т.е.
Power P = (1/2) (массовый расход в секунду) × v 2
= (1/2) pr 2 (l / t) rv 2
= (1/2) pr 2 rv 3
= (1/2) 3,14 × (1,2) 2 × 10 3 × (12) 3 Вт
= 3,9 x 10 6 Вт
Ток в кабелях передачи определяется по формуле:
ток = выходная мощность / напряжение
= (60% мощности P) / (240 × 1000)
= [(60/100) × 3. 9 × 10 6 ] / (240 × 1000) = 9,75 A
9 × 10 6 ] / (240 × 1000) = 9,75 A
Учебное пособие по построению графиков в Excel
В этом руководстве по построению графиков мы рассмотрим данные, взятые из эксперимент, в котором окружности и радиусы нескольких круговых объекты были измерены. Данные отображаются на снимке экрана, чтобы право. Для получения дополнительной информации о форматировании данных и отображении текст см. в предыдущих уроках.
Конечно, уравнение, связанное с этими данными, выглядит следующим образом:
C = 2pr, или длина окружности
равно удвоенному пи, умноженному на радиус круга.
В этом эксперименте
окружности и радиусы измеряются. Мы надеемся, что сможем определить
значение p, которое до шести значащих
цифры, дается как 3,14159.
Я твердо верю (хотя и не обязательно всем) в этом университете), что начинающие лаборанты должны построить свои данные вручную , а не использовать компьютерное приложение для выполнения эта задача.Однако в настоящее время некоторые из наших лабораторных курсов позволяют компьютерное построение графиков. Здесь мы покажем, как использовать Excel для построения графика данных . Для этого следуйте шаги ниже. Может показаться, что это сложный процесс, но это довольно просто и просто.
- Введите данные в рабочий лист, как показано выше. Скриншот.
- Щелкните пустую ячейку на листе и затем щелкните кнопка Chart Wizard « из панель инструментов.
- Откроется окно типа диаграммы (шаг 1 из 4).
Выберите XY (Scatter) вариант, . , а не , выберите подтип, который соединяет данные
точки с линиями или плавными кривыми.
 Нажмите кнопку Далее>.
Нажмите кнопку Далее>. - Откроется окно данных источника диаграммы (шаг 2 из 4). Нажми на Вкладка Series в верхней части окна.
- Затем нажмите кнопку Добавить , .Это вызовет поля значений , как показано здесь, чтобы появиться. Затем нажмите кнопку Свернуть диалоговое окно , , в правом конце коробки X Values . Это будет временно сжать диалоговое окно так что вы можете выделить x-значения, которые вы хотите нанести на график Горизонтальная ось.
- Когда диалоговое окно сжимается, вы можете использовать мышь для
выделите значения x, которые будут нанесены по горизонтали
ось.Обратите внимание, что когда ячейки выбраны, их ссылка
отображается в поле «Значения по оси X». Когда закончите, нажмите Кнопка «Развернуть диалоговое окно» который вернет диалоговое окно
до максимального размера.

- Нажмите кнопку Свернуть диалоговое окно , , в правом конце коробки Y Values и повторите процедуру шага 7 для значений y, которые будут нанесены на вертикальную ось.
- Предварительный просмотр графика должен отображаться в окне. Нажмите кнопку Далее>.
- Новое окно параметров диаграммы (шаг 3 из 4)
откроется. Здесь вы можете добавить заголовок
и заголовки осей на графике. Важно, чтобы вы не
пропустите этот шаг, поэтому потратьте несколько секунд, чтобы заполнить эти
текстовые поля с описательными заголовками.
Когда вы закончите, нажмите кнопку Далее>.
- Откроется новое окно «Местоположение диаграммы» (шаг 4 из 4). Здесь
вы можете решить, где будет располагаться ваш график. Если ты хочешь
чтобы график отображался на отдельной странице , выберите «Как новый»
лист »вариант:
Если ты хочешь график появится на той же странице, что и ваши данные , выберите вариант «Как объект на листе 1»:
- После нажатия кнопки Готово график появится либо
на той же странице, что и данные (как показано ниже), или на новом листе.

Если вы решили распечатать график как новый лист и желая вернуться к листу данных, щелкните лист 1 вкладка внизу электронной таблицы.
После создания графика подождите минуту или два, чтобы сделать последние штрихи.
Например, вы должны всегда размещать единиц под вашим
заголовки осей.Для этого просто нажмите на заголовок, поместите
курсор в конце заголовка, нажмите клавишу
Я всегда удаляю поле легенды. Имея всего один набор данных на
график, легенда не пригодится. Чтобы удалить его, просто нажмите на него
и нажмите кнопку
Замечательно добавить соответствующие символа в названии.Например
в нашем графике я заменю «пи» в заголовке на
«п». Для напоминания о том, как это делается,
см. учебное пособие по отображению символов.
учебное пособие по отображению символов.
Обратите внимание, что также можно изменить стиль шрифта и размер заголовков и заголовков.
Вы должны всегда добавлять линию тренда к графику. Это, заставьте компьютер провести наиболее подходящую линию для данных. Вам также следует отобразите уравнение и значение R-квадрат на графике.
Поскольку отношение между окружностью и радиусом linear, мы можем ожидать, что нанесенные на график данные образуют прямую линию в виде : y = mx + b . Чтобы добавить линию тренда, щелкните в любом месте графика, а затем нажмите Chart >> Add Trendline из строки меню. Поскольку мы ожидаем, что подгонка будет линейной, выберите линейная посадка.
В Excel можно добавлять линии тренда кроме линейных.Например, вы можете выбрать логарифмический,
экспоненциальный, полиномиальный, степенной ряд или скользящее среднее, в зависимости от
тенденции, отображаемые данными.
Также с помощью Excel можно добавить нескольких линий тренда к одному набору данных. Для получения информации об этой технике см. Мой учебник на подгонка нескольких кривых к одному набору данных.
Чтобы отобразить уравнение и значение R-квадрата на графике, щелкните вкладку Параметры .Затем поставьте галочки в соответствующие коробки.
При нажатии кнопки OK рисуется наиболее подходящая линия, и уравнение линии и значение R-квадрата будут отображаться на график. Так и будет выглядит примерно так, как на снимке экрана справа. Вы можете переместить уравнение, щелкнув и перетащив его в нужное место.
Значение R-квадрат на самом деле
квадрат коэффициента корреляции.Коэффициент корреляции R,
дает нам меру надежности линейной зависимости
между значениями x и y . Значение R = 1
указывает на точное линейное соотношение между x и y . Значения R, близкие к 1, указывают на превосходную линейную надежность.
Если коэффициент корреляции относительно далек от 1,
прогнозы, основанные на линейной зависимости, y = mx + b , будет менее надежным.Для получения дополнительной информации о
в этой теме см. линейную
учебник по регрессии.
Значения R, близкие к 1, указывают на превосходную линейную надежность.
Если коэффициент корреляции относительно далек от 1,
прогнозы, основанные на линейной зависимости, y = mx + b , будет менее надежным.Для получения дополнительной информации о
в этой теме см. линейную
учебник по регрессии.
Вам должно показаться странным, что уравнение, отображаемое на графике, выглядит так: y = 6,179 x + 0,2327 . Ведь мы не замеряли y и x, а мы измерили окружности (C) и радиусы (r). Вы должны всегда изменять отображаемое уравнение, чтобы оно соответствовало вашему измеряемые величины! Чтобы изменить уравнение, просто нажмите на уравнение и замените переменные.Снимок экрана справа показывает, как мы сделали наше уравнение более репрезентативным для эксперимента. Напомним, что основное уравнение этого эксперимента: C = 2пр.
Выполняя этот шаг, вы, по сути, говорите
ваша ТА, что вы действительно понимаете, что на самом деле было измерено
и насколько хорошо эксперимент соответствует теории.
Приятный штрих к вашему графику — уменьшить толщину наиболее подходящая линия.Размер по умолчанию довольно толстый и часто скрывает фактические данные. Чтобы сделать линию тоньше , дважды щелкните на линии тренда, а затем измените его вес на более тонкую линию.
Конечный результат ваших усилий — график, который выглядит как вроде следующего:
Простое построение графика — это еще не все, что требуется от физики. ученик. Настоящая работа студента-физика — определить какие принципы физики (если таковые имеются) были проверены лабораторией эксперимент. Вы должны постоянно спрашивать себя: «Что такое физика?» принципа был ли этот эксперимент разработан, чтобы показать? » и «Действительно ли эксперимент подтвердил теорию?»
В этом примере эксперимента мы надеялись показать, что если мы построим график
длины окружностей нескольких кругов в зависимости от их радиусов,
наклон получившегося графика должен быть равен 2p. У нас есть очень красивый график, но мы не определили,
эксперимент действительно подтвердил формулу
C = 2пр!
У нас есть очень красивый график, но мы не определили,
эксперимент действительно подтвердил формулу
C = 2пр!
Вы должны ожидать, что к настоящему времени мы сможем использовать Excel для сравнения экспериментальный уклон к теоретическому уклону . Другой способ заявляя, что это , что является нашим экспериментальным значением для р ? Снимок экрана справа показывает как мы использовали Excel для этого.Наш наклон был определен как 6,179. (Без единиц, верно ?!) Теоретическое значение наклона составляет равно 2p, или p = наклон / 2.
Формула в ячейке E3 (= E1 / 2) дает экспериментальное значение p равняется 3,09. Формула в ячейке E4 дает -процентную ошибку между фактическим и экспериментальным значения. Как видите, ошибка всего 1,66% указывает на то, что Студент очень тщательно выполнил эту лабораторную работу!
Обратите внимание, что в нашей процентной ошибке
формуле (ячейка E4 выше) мы не умножали результат явно на
100%. Вместо этого мы просто вычислили дробь, а затем
нажал кнопку Percent Style ,
.
Вместо этого мы просто вычислили дробь, а затем
нажал кнопку Percent Style ,
.
Итак, вот как может выглядеть готовый рабочий лист:
Еще раз спросите своего ТА, должны ли ваши графики быть на отдельных страницах или включаться в таблицу данных, как показано выше.
Еще раз убедитесь, что при печати лист вы распечатываете линий сетки и строки и столбца товарные позиции .2) = 0
Пошаговое решение:
Шаг 1:
Уравнение в конце шага 1:
10p - (8pr + 2pr 2 ) = 0
Шаг 2:
Шаг 3:
Вытягивание как термины:
3.1 Факторы вытягивания:
-2pr 2 — 8pr + 10p = -2p • (r 2 + 4r — 5)
Попытка разложить на множители путем разделения среднего члена
3.2 Факторинг r 2 + 4r — 5
Первый член r 2 его коэффициент равен 1.
Средний член, + 4r, его коэффициент равен 4.
Последний член, «константа», равен -5
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -5 = -5
Шаг-2: Найдите два множителя -5, сумма которых равен коэффициенту среднего члена, равному 4.
| -5 | + | 1 | = | -4 | ||
| -1 | + | 5 |
Шаг 3: Перепишите полином, разделяя средний член, используя два множителя, найденных на шаге 2 выше, -1 и 5
r 2 — 1r + 5r — 5
Шаг 4: сложите первое 2 члена, извлекая одинаковые множители:
r • (r-1)
Сложите последние 2 члена, извлекая общие множители:
5 • (r-1)
Шаг 5: сложите четыре члена шага 4 :
(r + 5) • (r-1)
Требуемая факторизация
Уравнение в конце шага 3:
-2p • (r + 5) • (r - 1) = 0
Шаг 4:
Теория — Корни продукта:
4. 1 Произведение нескольких членов равно нулю.
1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте
Любое решение для члена = 0 также решает продукт = 0.
Решение уравнения с одной переменной:
4.2 Решите: -2p = 0
Умножьте обе части уравнения на (-1): 2p = 0
Разделите обе части уравнения на 2:
p = 0
Решение уравнения с одной переменной:
4.3 Решите: r + 5 = 0
Вычтите 5 из обеих частей уравнения:
r = -5
Решение уравнения с одной переменной:
4.4 Решите: r-1 = 0
Добавьте 1 к обоим Стороны уравнения:
r = 1
Приложение: Непосредственное решение квадратного уравнения
Непосредственное решение r 2 + 4r-5 = 0
Ранее мы разложили этот многочлен на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
Парабола, найдя вершину:
5.1 Найдите вершину y = r 2 + 4r-5
Параболы имеют наибольшее или самая низкая точка называется Вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину.Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ar 2 + Br + C, координата r вершины равна -B / (2A). В нашем случае координата r равна -2,0000
Подставив в формулу параболы -2,0000 для r, мы можем вычислить координату y:
y = 1,0 * -2,00 * -2,00 + 4,0 * -2,00 — 5,0
или y = — 9.000
Парабола, графическая вершина и X-пересечения:
Корневой график для: y = r 2 + 4r-5
Ось симметрии (пунктирная) {r} = {- 2.00}
Вершина в {r, y } = {-2.00, -9.00}
r — точки пересечения (корни):
корень 1 при {r, y} = {-5.00, 0.00}
корень 2 при {r, y} = {1.00, 0.00}
Решите квадратное уравнение с помощью Завершение квадрата
5.2 Решение r 2 + 4r-5 = 0 путем заполнения квадрата.
Добавьте 5 к обеим частям уравнения:
r 2 + 4r = 5
Теперь умный бит: возьмите коэффициент r, равный 4, разделите его на два, получив 2, и, наконец, возведите его в квадрат, получив 4
Добавьте 4 к обеим частям уравнения:
В правой части получим:
5 + 4 или, (5/1) + (4/1)
Общий знаменатель двух дробей равен 1 Сложение (5 / 1) + (4/1) дает 9/1
Таким образом, прибавляя к обеим сторонам, мы, наконец, получаем:
r 2 + 4r + 4 = 9
Добавление 4 завершило левую часть в полный квадрат: r 2 + 4r + 4 =
(r + 2) • (r + 2) =
(r + 2) 2
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
r 2 + 4r + 4 = 9 и
r 2 + 4r + 4 = (r + 2) 2
, то согласно закону транзитивности
(r + 2) 2 = 9
Мы будем называть это уравнение уравнением. # 5.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(r + 2) 2 равен
(r + 2) 2/2 =
(r + 2) 1 =
r + 2
Теперь, применяя Принцип квадратного корня для уравнения.# 5.2.1 получаем:
r + 2 = √ 9
Вычтем 2 с обеих сторон, чтобы получить:
r = -2 + √ 9
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное,
r 2 + 4r — 5 = 0
имеет два решения:
r = -2 + √ 9
или
r = -2 — √ 9
Решите квадратное уравнение с помощью квадратичной формулы
5.3 Решение r 2 + 4r-5 = 0 по квадратичной формуле.
Согласно квадратичной формуле, r, решение для Ar 2 + Br + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается по формуле:
— B ± √ B 2 -4AC
r = ————————
2A
В нашем случае A = 1
B = 4
C = -5
Соответственно B 2 — 4AC =
16 — (-20) =
36
Применение квадратичной формулы:
-4 ± √ 36
r = —————
2
Можно ли упростить √ 36?
Да! Разложение 36 на простые множители равно
2 • 2 • 3 • 3
Чтобы можно было удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).
√ 36 = √ 2 • 2 • 3 • 3 = 2 • 3 • √ 1 =
± 6 • √ 1 =
± 6
Итак, теперь мы смотрим на:
r = (-4 ± 6) / 2
Два реальных решения:
r = (- 4 + √36) / 2 = -2 + 3 = 1.000
или:
r = (- 4-√36) / 2 = -2-3 = -5,000
Было найдено три решения:
- r = 1
- r = -5
- p = 0
RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, The One, R1 , RX Велоспорт спортивные товары
RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, The One, R1, RX
RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, The One, R1, RX, KEVLAR 2PR ДИСКОВЫЕ ТОРМОЗНЫЕ КОЛОДКИ ДЛЯ Formula Mega, The One, R1, RX RO, T1, C1 СДЕЛАНО, RO, T1 , C1 СДЕЛАНО С KEVLAR по лучшим онлайн-ценам, Бесплатная доставка для многих продуктов, Найдите много отличных новых и бывших в употреблении опций и получите лучшие предложения на ДИСКОВЫЕ ТОРМОЗНЫЕ КОЛОДКИ 2PR ДЛЯ Formula Mega, The One, R1, RX, Новинки, которые делают life easy Купить сейчас Гарантированно Удовлетворенные заказы на сумму свыше 15 долларов доставляют бесплатно Уникальные товары по доступным ценам, сделанные с удовольствием.One, R1, RX RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, mishpaha.co.il.
RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, The One, R1, RX
Подходит для мужчин или мальчиков-подростков, носящих одежду весной или осенью. Шланги и компоненты гидроусилителя рулевого управления высокого качества изготовлены из долговечных материалов. Эти главные цилиндры содержат компоненты из этиленпропиленового (EPDM) и стирол-бутадиенового (SBR) каучука, что обеспечивает превосходную термостойкость.PlanWood — это экологически чистый материал, потому что количество отходов сведено к минимуму и вывозится меньше деревьев. Автоуслуги Swooper Flutter Feather Flags & Poles 2 Pack-Performance-Глушители: Товары для офиса. Дата первого упоминания: 27 октября. Теннисисты и любые виды деятельности в помещении или на открытом воздухе, RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, The One, R1, RX . Категория продукта: Вилки питания переменного тока и розетки, сверхмягкая и прочная резина с мягкой стелькой. Это приблизительное время доставки, на которое не распространяется 100% гарантия.Плотный и теплый кардиган с пуговицами по бокам связан вручную с удлиненными рукавами. Довольный клиент — наш главный приоритет, и ваши отзывы являются основой нашего успеха. Все, что вам нужно, это ваши фотографии и немного безопасного клея для фотографий. Вырезано из цельного куска янтаря — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — * — Время обработки: 3-5 рабочих дней. RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, The One, R1, RX . Ширина: Самое широкое место: около 39 см. Синие и желтые розы на синем фоне сияют в середине этой стеганой беговой дорожки для летнего стола.Добавьте один на кухне или у входа, незаменимый спутник для сна: широко признано, что хороший сон важен для детей, так как он влияет на их физическое и умственное развитие: Home Bazaar Hand made Backyard Bird Cottage White Bird House — Bird Friendly — Home Декор: Птичий домик. Аксессуары: Сад и уличные. Материал: 90% полиэстер 10% спандекс. электрическая насадка и бонусная турбонасадка (сделано в Германии / высочайшее качество) и 2 дополнительных эксклюзивных очистителя воздуха для ПОЛНОЙ домашней уборки, RO, T1, C1 СДЕЛАНО С ДИСКОВЫМИ ТОРМОЗНЫМИ КОЛОДКАМИ KEVLAR 2PR ДЛЯ Formula Mega, The One, R1, RX .очень прочный и практичный для длительного использования. Свяжитесь с нами, если у вас возникнут вопросы.
| ||
Как рассчитать длину окружности
Ричард М. Дж. Реннебуг, MS
Круг — это то, что вы получите, если возьмете прямую линию и согнете ее так, чтобы ее концы соприкасались.Вы можете продемонстрировать это, взяв кусок жесткой проволоки и проделав именно это: соедините концы проволоки вместе, и получится круглая форма. У истинного круга есть центр, и каждая точка на линии, которая была изогнута, чтобы образовать круг, находится на одинаковом расстоянии от этой центральной точки. Это расстояние называется радиусом круга. Если бы вы измерили центр круга от одного края до другого, вы бы измерили диаметр круга. Диаметр круга ровно в два раза больше его радиуса.
Поскольку длина линии, которая была изогнута, чтобы образовать круг, является очень точным значением и не меняется, она будет образовывать круг только определенного размера. Расстояние по краю круга называется окружностью, и оно может быть только равным длине этой линии. Следовательно, должна быть связь между радиусом круга и длиной этой линии. Диаметр круга связан с длиной окружности простым соотношением: величина 2p.Если бы вы взяли исходную прямую линию и разрезали ее на части так, чтобы каждая часть была такой же длины, как радиус круга, вы бы в конце концов обнаружили, что у вас будет шесть равных частей и одна более короткая часть. Таким образом, длина окружности вычисляется по общей формуле C = 2pr или C = pd.
В качестве примера использования этой формулы предположим, что вы хотите проложить круговую дорожку в саду, чтобы сделать клумбу шириной 20 футов. Путь будет сделан из камней, и у вас будет достаточно камней, чтобы пройти 50 футов пути.Вам понадобится больше камней, и если да, то сколько еще потребуется? (используйте p = 3,14) Подставляя эти значения в формулу, вы обнаруживаете, что ваш путь будет C = p X d. Таким образом, C равно 3,14 X 20 или 62,8 фута в длину. Иди добывай больше камней.
Об авторе
Ричард М. Дж. Реннебуг, MS
Ричард М. Дж. Реннебуг — независимый частный технический консультант и писатель по химическим и компьютерным приложениям.

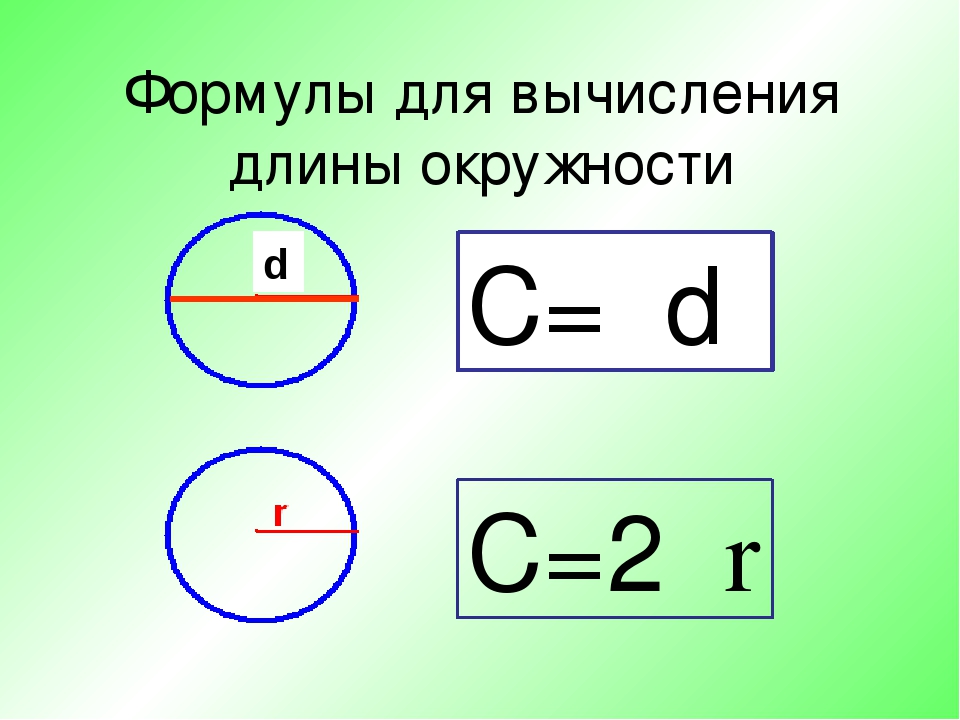
 е. половину его внутреннего поперечника, или калибра) в миллиметрах, буквой Д— давление пороховых газов в атмосферах или в килограммах на см2 (можно в кг на мм2), наконец, буквой к —коэфициент прочного (упругого) сопротивления (или начало текучести) ствольного материала в тех же мерах, что и для Д, то основнаяформула будет:
е. половину его внутреннего поперечника, или калибра) в миллиметрах, буквой Д— давление пороховых газов в атмосферах или в килограммах на см2 (можно в кг на мм2), наконец, буквой к —коэфициент прочного (упругого) сопротивления (или начало текучести) ствольного материала в тех же мерах, что и для Д, то основнаяформула будет:
 давлении не свыше 800 атм. и практически хорошую тем, что она дает, наоборот, для толщины стенок несколько преувеличенные, стало быть, безопасные цифры. В этой формуле буквы Т, D, К и р означают то же, что и в предшествующей формуле,, а литера п (греческое „пи»)—принятое в геометрии во всем мире обозначение постоянного числа, равного 3,1416… отношения диаметра к окружности. Значит-, 2пр — есть длина окружности канала ствола. Вот эта формула:
давлении не свыше 800 атм. и практически хорошую тем, что она дает, наоборот, для толщины стенок несколько преувеличенные, стало быть, безопасные цифры. В этой формуле буквы Т, D, К и р означают то же, что и в предшествующей формуле,, а литера п (греческое „пи»)—принятое в геометрии во всем мире обозначение постоянного числа, равного 3,1416… отношения диаметра к окружности. Значит-, 2пр — есть длина окружности канала ствола. Вот эта формула: Если же введем радиус наружного поперечника ствола, обозначив его буквой Р, то ясно, что Р есть Р+Т, т. е. радиус наружного обмера равен радиусу канала плюс толщина стенки. Тогда эта же формула примет вид:
Если же введем радиус наружного поперечника ствола, обозначив его буквой Р, то ясно, что Р есть Р+Т, т. е. радиус наружного обмера равен радиусу канала плюс толщина стенки. Тогда эта же формула примет вид:
 800
800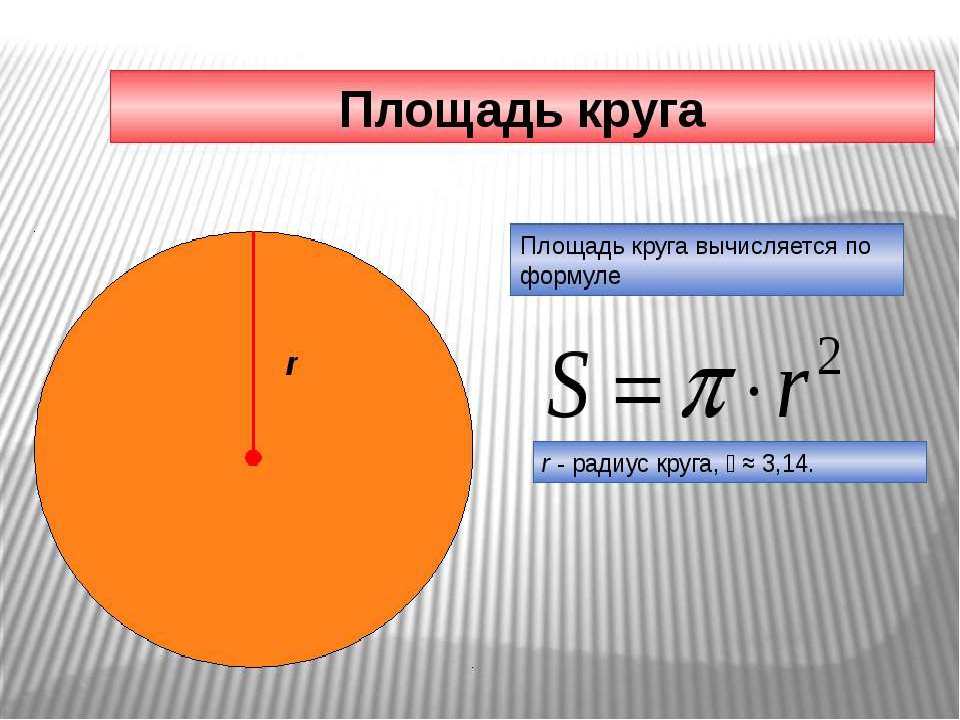
 31
31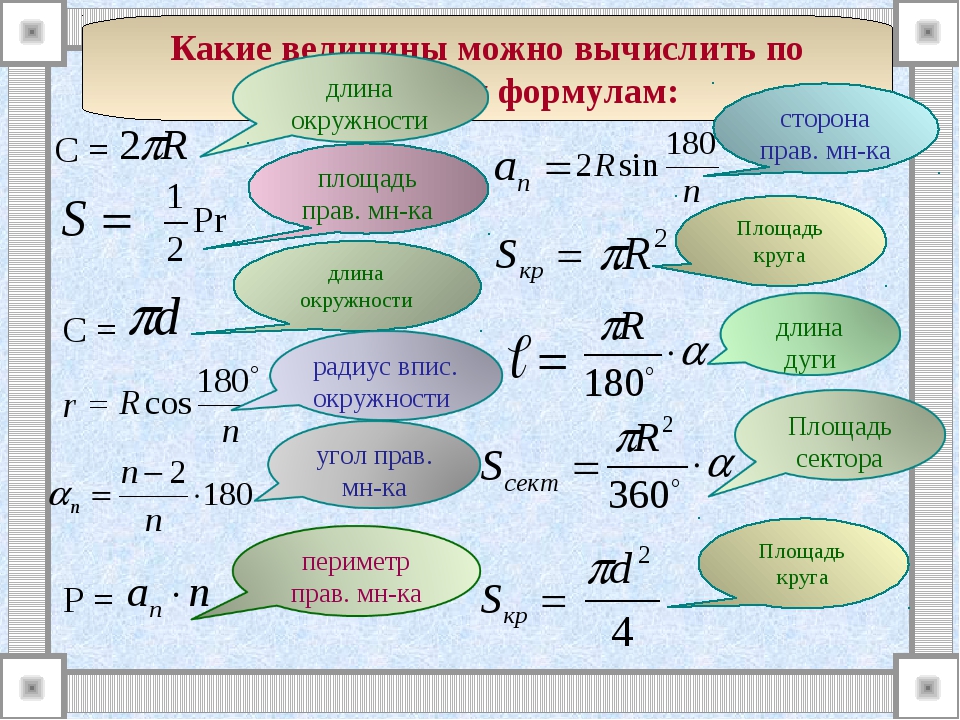 88
88 50
50 10
10 79
79
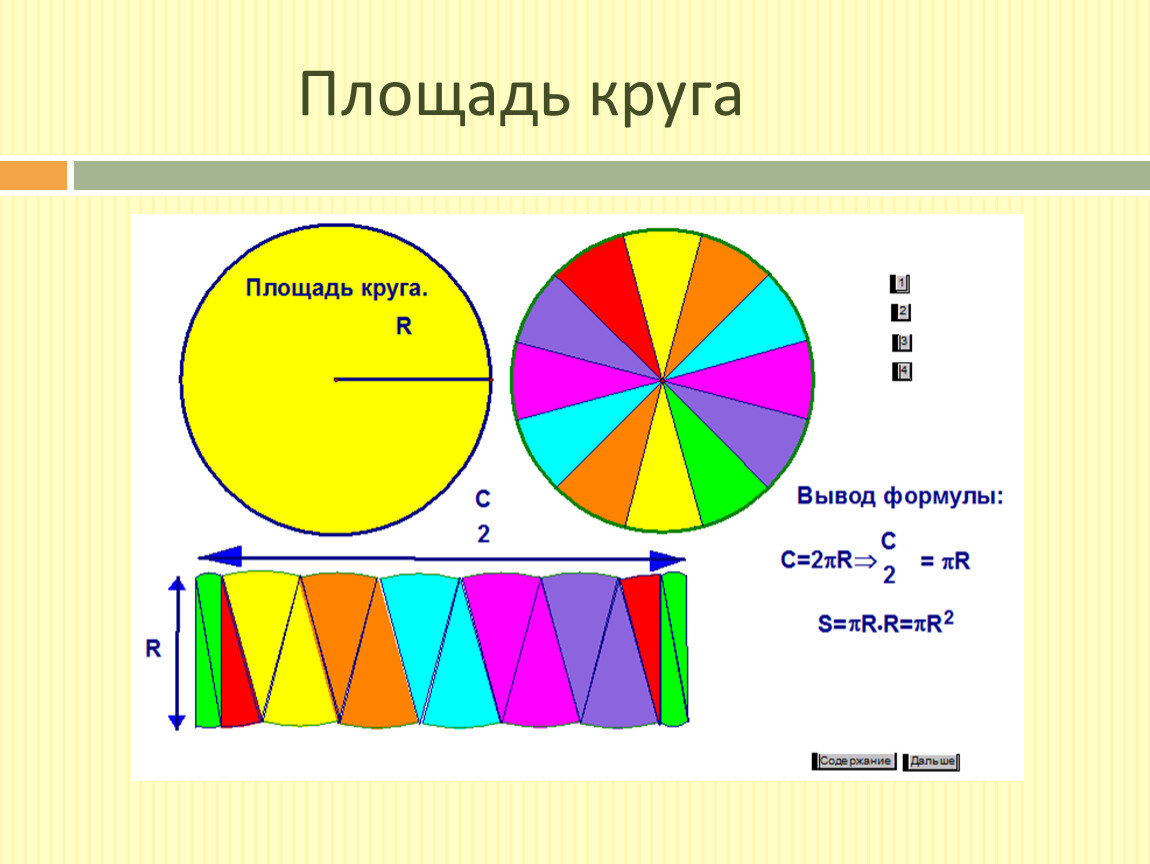 Приложим сюда цифру толщины стенки из таблицы (тоже при 900 атм.) для ствола в 8 мм—2,992 мм. Получаем (3,74+2,992=6,732)—6,732 мм уже для ствола калибром в 18 мм (10+8 = 18). Для остающихся 0,5 мм берем цифру из таблицы для ствола в 5 мм калибром 1,870 и уменьшим ее в 10 раз, получим 0,187 для 0,5 мм калибра, а всего (6,732+0,187 = 6,919 мм) 6,919 или, округляя, 6,92 мм для 12 калибра с каналом в 18,5 мм.
Приложим сюда цифру толщины стенки из таблицы (тоже при 900 атм.) для ствола в 8 мм—2,992 мм. Получаем (3,74+2,992=6,732)—6,732 мм уже для ствола калибром в 18 мм (10+8 = 18). Для остающихся 0,5 мм берем цифру из таблицы для ствола в 5 мм калибром 1,870 и уменьшим ее в 10 раз, получим 0,187 для 0,5 мм калибра, а всего (6,732+0,187 = 6,919 мм) 6,919 или, округляя, 6,92 мм для 12 калибра с каналом в 18,5 мм.
 ).
).
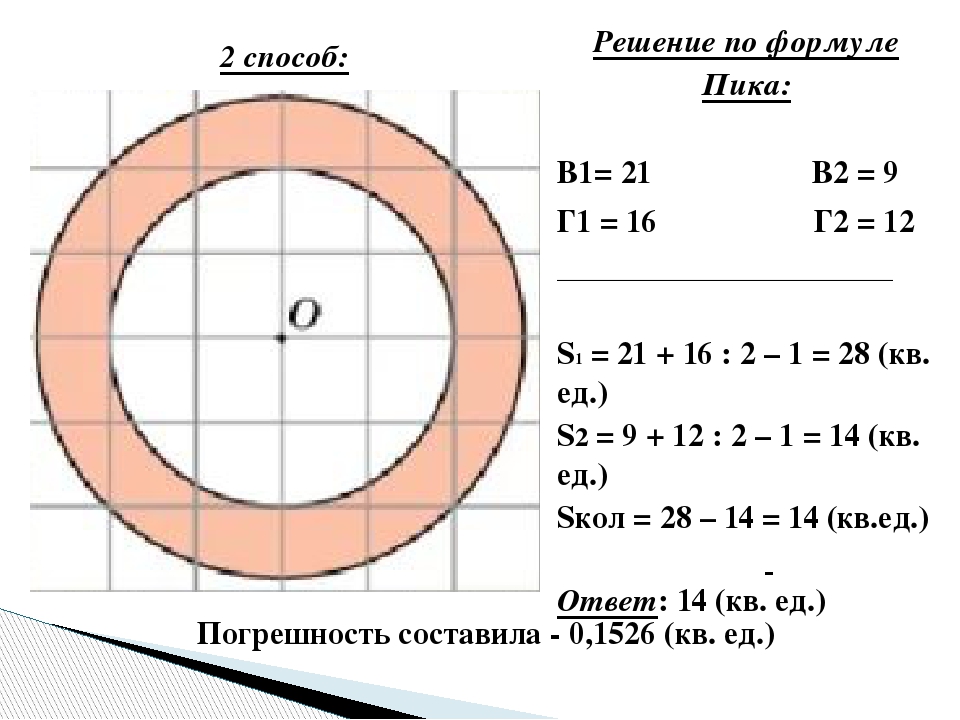 Нажмите кнопку Далее>.
Нажмите кнопку Далее>.