Учебно-методическое пособие. Сборник задач по теории множеств.
Предисловие
Профессиональное поле деятельности специалиста социальной сферы предполагает решение задач прикладного характера, обладающих теоретико-мно-жественной спецификой. Это означает, что в процессе математической подго-товки будущий выпускник вуза должен освоить содержательно-компонентный состав данной области знания, знать ее основные сущностные характеристики и процессуальную сторону их применения. Решению поставленной задачи должна способствовать разработка специальной математической литературы.
Настоящее руководство является практическим приложением к разрабо-танному автором учебному пособию «Краткий курс теории множеств» [10], которое помогает будущему выпускнику социальной сферы закрепить знаниевый аспект теории множеств и отработать методический аппарат по его применению.
Автор надеется на полезность данного учебно-методического пособия.
Пояснительная записка
Целью данного учебно-методического пособия ставились следующие за-дачи:
освоить символьно-знаковую сторону языка теории множеств;
изучить теоретико-множественные характеристики и специфику их применения;
акцентировать внимание на многоаспектность использования тео-ретико-множественного аппарата в социальной сфере;
отработать методику решения теоретико-множественных задач;
оценить качество знаний обучающихся в данной области знания.
В результате:
СТУДЕНТ ДОЛЖЕН
знать:
основы теоретико-множественного аппарата;
грамматическое построение содержательных структур теории мно-жеств;
уметь:
находить теоретико-множественный аспект в профессиональных за-дачах социальной сферы;
применять методический аппарат для решения задач по теории мно-жеств;
владеть алгоритмической составляющей теоретико-множественного анализа;
использовать теоретико-множественную терминологию для крат-кой записи социальных процессов.
Содержание данного учебно-методического пособия включает:
методические рекомендации для решения задач по теории мно-жеств;
примеры решения типовых задач по теории множеств;
задачи для самостоятельного решения;
перечень задач для контрольной работы по теории множеств;
справочный материал;
список литературы;
оглавление.
Содержание пособия
Глава 1. Методические рекомендации для решения задач по теории множеств
Для решения профессиональных задач социальной сферы, включающих теоретико-множественный аспект следует располагать следующими базовыми сведениями из данной области знания:
– Атрибутика теории множеств: множество, подмножество, элементы или точки множества;
– Сокращенная форма записи множеств;
– Виды множеств: конечные, бесконечные, пустые, универсальные, рав-номощные, счетные, несчетные;
– Используемые теоретико-множественные кванторы;
– Перечень наиболее часто встречающихся условных обозначений, ис-пользуемый в теории множеств;
– Алгебра множеств (операции объединения, пересечения, дополнения к множеству, разности, декартово произведение) и свойства алгебры множеств (Рис.1).
Базовые компоненты сведений, нужные для решения теоретико-множественных задач, находящих применение в социальной сфере
Основная атрибутика теории множеств
Для конечных и бесконечных множеств
Сокращенная форма записи множеств
С помощью характе-ристического свойства
Виды множеств
Перечень условных обозначений
Теоретико-множественные кванторы
Алгебра множеств
Свойства алгебры множеств
Рис.1. Арсенал сведений для решения профессиональных задач социальной сферы,
включающих теоретико-множественный аспект
Глава 2. Примеры решения типовых задач по теории множеств
Примеры:
Пример 1. Найти множество в данном высказывании: «Е. С. Громов и В. А. Малявко называют семь признаков креативности: оригинальность, эвристич-ность, фантазию, активность, концентрированность, четкость, чувствитель-ность» [9, с. 19].
Решение: В данном случае можно определить множество А (семь призна-ков креативности), состоящее из следующих элементов: оригинальность, эврис-тичность, фантазию, активность, концентрированность, четкость, чувствитель-ность, т.е. используя правила задания множеств можно записать:
А={оригинальность, эвристичность, фантазия, активность, концентрированность, четкость, чувствительность}.
Пример 2. Множество А – совокупность всех социальных педагогов горо-да N, до 30 лет; множество В – совокупность социальных педагогов, возраст-ной ценз которых составляет от 30–35 лет включительно; множество С – педа-гоги 36–40 лет; множество V – все социальные педагоги города N. Дайте сло-весную интерпретацию следующим записям, если а является элементом мно-жества А; b – элементом множества В; с – элементом множества С; v – эле-ментом множества V.
а)  а
а А
А  а
а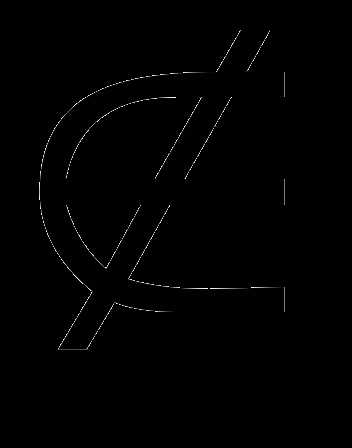
 ;
;
б)  с
с
 с
с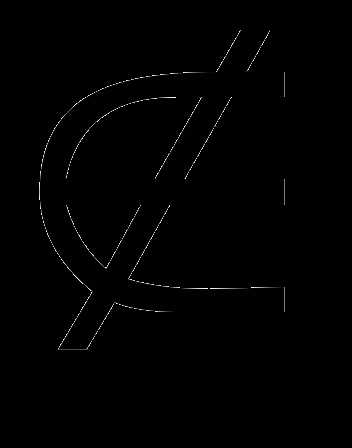
 ;
; в)  а
а А и
А и  b
b B
B  а
а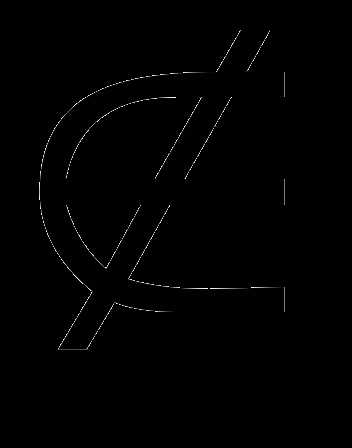
 и b
и b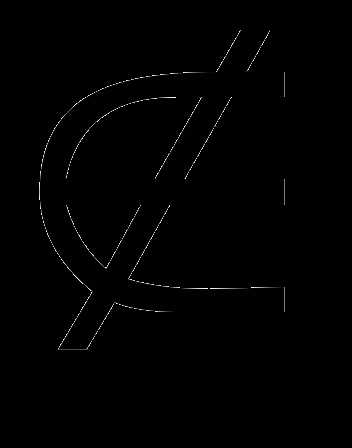
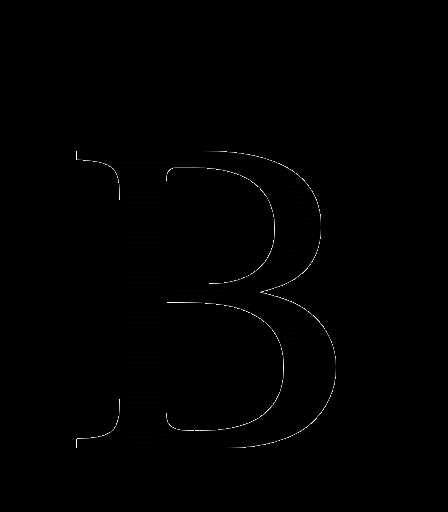 ;
; г) ( v
v V) (
V) ( v): v
v): v А.
А.
Решение: используя значение теоретико-множественных кванторов дан-ные записи можно прочитать следующим образом:
а) для любого элемента а, принадлежащего множеству А следует, что эле-мент а не принадлежит дополнению к множеству  ;
;
б) для любого элемента с, принадлежащего множеству С следует, что эле-мент с не принадлежит дополнению к множеству 
в) для любого элемента а, принадлежащего множеству А, и элемента с, принадлежащего множеству С, следует, что элемент а не принадлежит дополне-нию к множеству  и элемент с не принадлежит дополнению к множеству
и элемент с не принадлежит дополнению к множеству  ;
;
г) из всех элементов v, принадлежащих множеству V, найдется такой эле-мент v, который будет принадлежать множеству A.
Пример 3. Подобрать несколько универсальных подмножеств для следую-щих подмножеств А, В, С: подмножество А – учащиеся школы №1 города N, подмножество В – учащиеся школы №2 города N, подмножество С – учащиеся школы №3 города N.
Решение: согласно определения универсального множества для данных подмножеств А, В, С универсальными будут являться следующие множества V:
а) V – все учащиеся школ №1, №2, №3 города N;
б) V – все учащиеся городов N, M, R;
в) V – все учащиеся школ России.
Пример 4. Множество А – наиболее часто встречающиеся оценки, по-лучаемые студентами-психологами одного социального вуза, множество В – оценки студентов-экологов, множество С – оценки студентов-юристов, мно-жество D – студентов-информатиков этого вуза. Найти среди них равные мно-жества, если: А={3, 4}, B={4}, C={4, 5}, D={4, 3}.
Решение: равными считаются множества, содержащие одинаковые элементы. Тогда А=D, т.к. для этих множеств данное условие выполняется.
Пример 5. Множество А – подростки, посещающие музыкальную школу, множество В – подростки, посещающие спортивную школу. Осуществить сле-дующие операции А
 В, А\В, В\А и дать им графическую интерпрета-цию с помощью диаграмм Венна:
В, А\В, В\А и дать им графическую интерпрета-цию с помощью диаграмм Венна:а) А={Корольчук, Калашников, Пермяков}, В={Ивлев, Шишкарев};
б) А={Мохов, Новиков, Епифанов}, В={Епифанов, Солодовников}.
Решение: по определению операций объединения, пересечения и разности:
а) А В={Корольчук, Калашников, Пермяков, Ивлев, Шишкарев}, А
В={Корольчук, Калашников, Пермяков, Ивлев, Шишкарев}, А В= ={
В= ={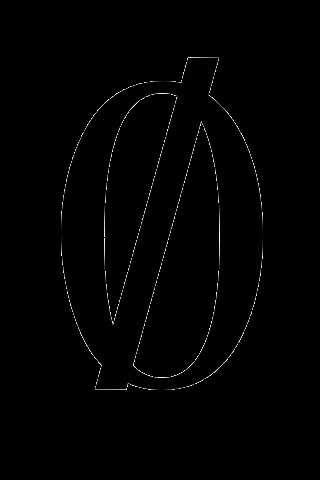 }, А\В={Корольчук, Калашников, Пермяков}, В\А={Ивлев, Шишкарев} (Рис.2).
}, А\В={Корольчук, Калашников, Пермяков}, В\А={Ивлев, Шишкарев} (Рис.2).
А В А
В А В=
В=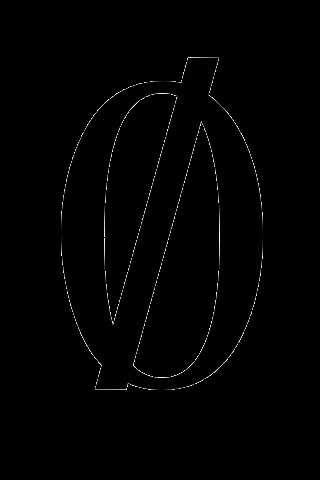 А\В В\А
А\В В\А
Рис.1. Графическая интерпретация заданных операций
б) А В={Мохов, Новиков, Епифанов, Солодовников}, А
В={Мохов, Новиков, Епифанов, Солодовников}, А В={Епифа-нов}, А\В={Мохов, Новиков}, В\А={Солодовников} (Рис.3).
В={Епифа-нов}, А\В={Мохов, Новиков}, В\А={Солодовников} (Рис.3).
А В А
В А В А\В В\А
В А\В В\А
Рис.3. Графическая интерпретация заданных операций
Пример 6. А – множество студентов, в большей степени интересующихся техническими дисциплинами, В – множество студентов, интересующихся гума-нитарными дисциплинами, в условиях одного социального вуза, V – совокуп-ность всех студентов данного вуза. Данные множества представлены с по-мощью диаграмм Венна:
V
а)
V
б)
Определить графически на данных диаграммах области  ,
, 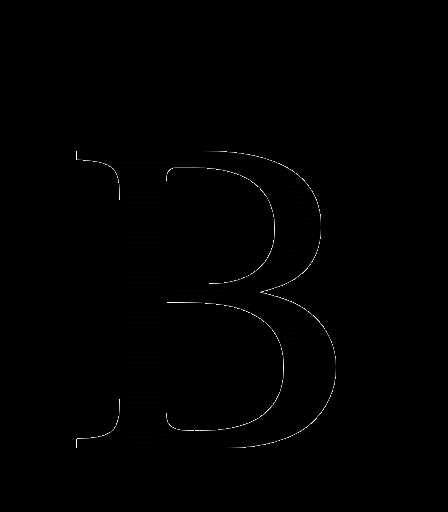 , А
, А В, А
В, А В,
В, 

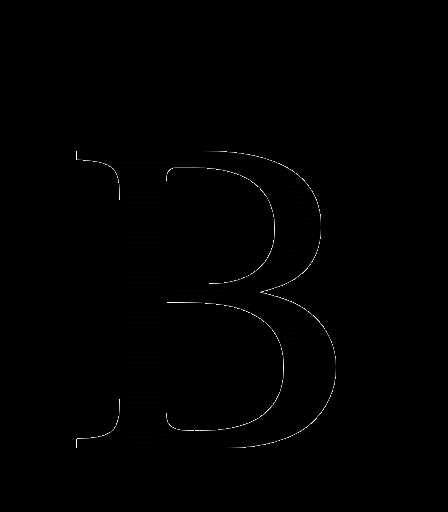 ,
, 

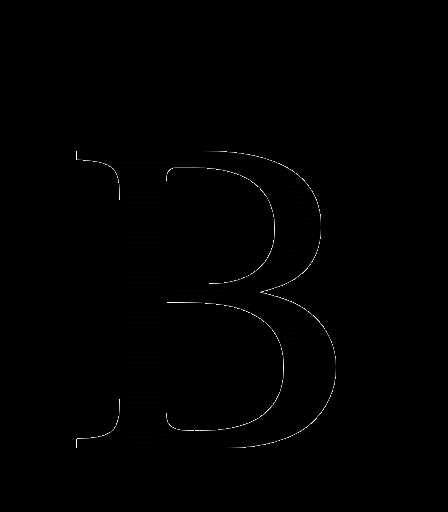 , А\В.
, А\В.
Решение: по определению операций объединения, пересечения и дополне-ния к заданному множеству получим (Рис.4):
для случая a):
V
V
V

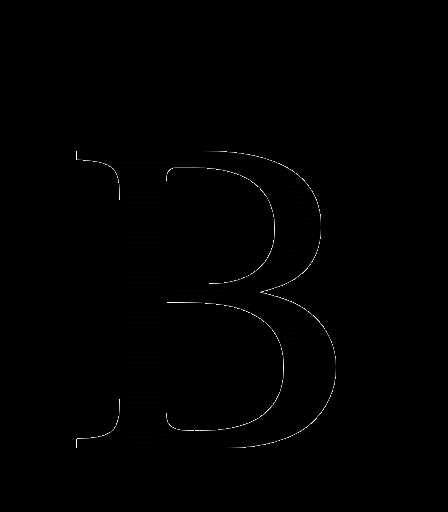 А
А В
В
V
V
V
А В=
В=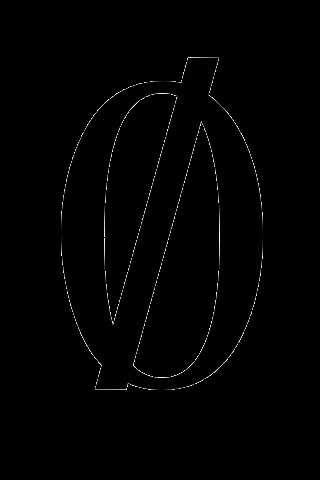

infourok.ru
Решение задач по теме «Множества и его элементы»
Множества и его элементы
УРОК 9 РЕШЕНИЕ ЗАДАЧ. Самостоятельная работа.
Цель: Систематизация знаний по теме «Множества и его элементы».
Повторение, проверка д/з:
Что обозначает слово «множество»?
Что мы называем элементом множества?
Что бывает элементами множества?
Как различают множества по числу элементов?
Какими способами можно задать множество? (перечисление элементов, характеристическое свойство)
Какое свойство называется характеристическим свойством?
Какие множества называются равными?
Какие математические «иероглифы» мы используем для сокращенной записи?
Что такое подмножество?
Что такое круги Эйлера? Зачем они? (Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления)
Что такое объединение множеств? Знак объединения.
Что такое пересечение множеств? Знак пересечения. Решить упражнение 1.
Что такое разность множеств? Знак разности. Проверить упражнения 1, 2 из д/з.
Что такое дополнение множества?
Решить упражнение 2, 3, 4.
Проверить упражнения из домашнего задания:
Найти разность множеств: К = {1; 2; 3; 7; 8; 9} и М = {0; 2; 8}. Решение: К \ М = {1; 3; 7; 9}.
Даны множества: А = {a; b; c; d}, В = {c; d;} .
Найти: а) А \ В; б) В \ А; в) (А \ В) ∪ (В \ А). Решение: а) А \ В = {a; b}; б) В \ А = ; в) (А \ В) ∪ (В \ А) = {a; b} ∪ = {a; b}.
Каждая семья, живущая в нашем доме выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают и газету, и журнал. Сколько семей живет в нашем доме?
Решение:
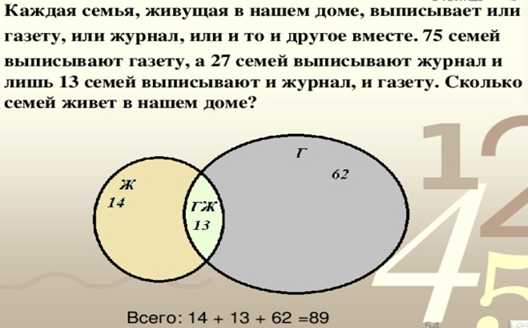
Упражнение 1: Даны два множества А = {2; 4; 6; 8; 10} и В = {3; 6; 9; 12}. Найти объединение и пересечение этих множеств.
Решение: А ∪ В = {2; 4; 6; 8; 10; 3; 6; 9; 12}, А ∩ В = {6}.
Упражнение 2: Даны два множества Х = {0; 1; 3; 5} и У = {1; 2; 3; 4}. Найти разность множеств Х и У и разность множеств У и Х. Сделайте вывод.
Решение: Х \ Y = {0, 1, 3, 5} \ {1, 2, 3, 4} = {0, 5}. Y \ X = {2; 4}.
Упражнение 3: Объяснить рисунки:
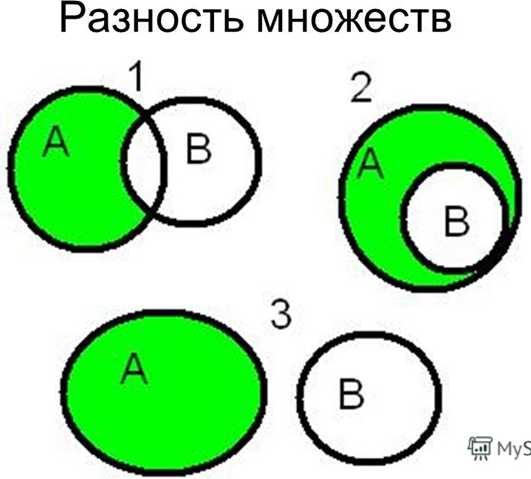
Упражнение 4: Какое число является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Решение: Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Самостоятельная работа (с последующей взаимопроверкой и проверкой)
Вариант 1
№1 Записать множество А натуральных делителей числа 12.
№2 В данном множестве В = {лев, лисица, гиена, слон, рысь} все элементы, кроме одного, обладают некоторым свойством. Запишите это характеристическое свойство и найдите элемент, не обладающий им.
№3 Даны множества: А = {1, 2, 3, 4, 5, 6} и В = {3, 4, 5, 6, 7, 8}. Найти объединение, пересечение и разность этих множеств.
Вариант 2
№1 Записать множество А натуральных делителей числа 18.
№2 В данном множестве С = {яблоко, груша, огурец, слива, абрикос} все элементы, кроме одного, обладают некоторым свойством. Запишите это характеристическое свойство и найдите элемент, не обладающий им.
№3 Даны множества: А = {3, 4, 5, 6, 7, 8} и В = {4, 5, 6, 7, 8, 9, 10}. Найти объединение, пересечение и разность этих множеств.
Взаимопроверка, проверка.
РЕШЕНИЕ:
Вариант 1:
№1 А = {1, 2, 3, 4, 6, 12}
№2 В = {х│х — хищники}, слон – лишний элемент
№3 А ∪ В = {1, 2, 3, 4, 5, 6, 7, 8}; А ∩ В = {3, 4, 5, 6}; А \ В = {1, 2}.
Вариант 2:
№1 А = {1, 2, 3, 6, 9, 18}
№2 В = {х│х — фрукты}, огурец – лишний элемент
№3 А ∪ В = {3, 4, 5, 6, 7, 8, 9, 10}; А ∩ В = {4, 5, 6, 7, 8}; А \ В = {3}
РЕШЕНИЕ ЗАДАЧ
Проверить упражнение 3 из д/з (все предложенные детьми варианты решений).
Дома вы решаете задачи №3 разными способами. Сегодня на уроке мы разберем их решение, используя круги Эйлера.
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Напомню: круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Упражнение 4: Составьте рассказ по рисунку:
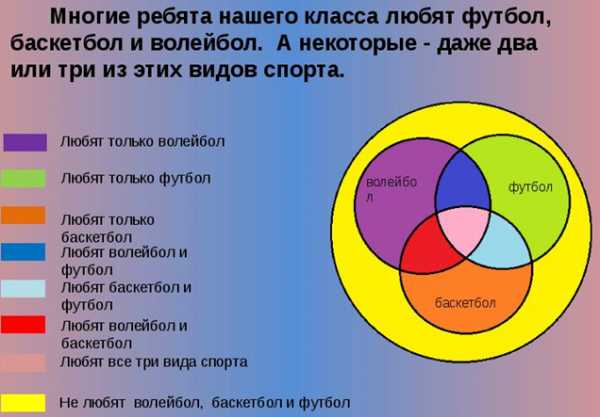
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
Решим простую задачу, применив круги Эйлера:
Задача 1: В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит только мороженое?
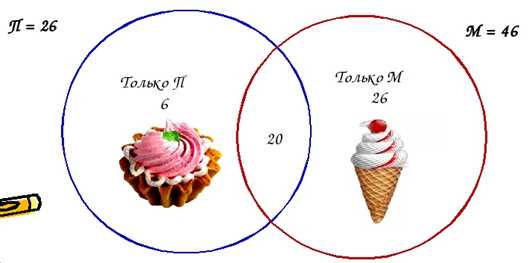
Аналогичным способом можно решить и домашнее упражнение 3. Давайте попытаемся это сделать!
Рассмотрим решение методом кругов Эйлера задач из прошлых д/з:
Задача: Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Решение:

Задача: Из 220 школьников 16 играют в баскетбол, 175 в футбол, 24 не играют в эти игры. Сколько человек одновременно играют в баскетбол и в футбол?
Решение:

И новые задачи:
Задача 2: В классе 30 учащихся. Из них 18 человек занимаются в секции легкой атлетики, 10 – плаванием, 3 человека – и тем и другим. Сколько человек не занимается ничем?
Решение:
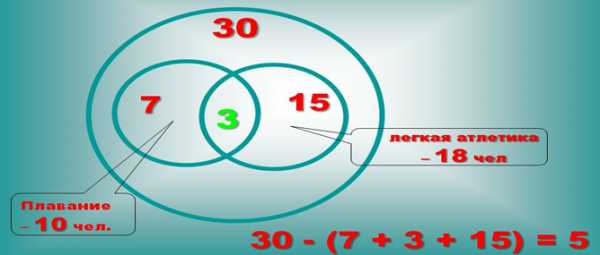
Задача 2: Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение:
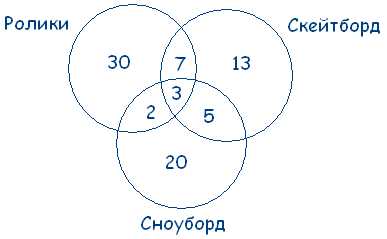
Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ: 20 человек не умеют кататься ни на одном спортивном снаряде.
Подведение итогов урока, рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.
Домашнее задание: упражнения:
Найти объединение, пересечение и разность множеств А и В, если А = {1; 2; 3; 4; 5; 6} и В = {2; 4; 6; 8; 10; 12}.
Решение: А ∪ В = {1; 3; 4; 5; 6; 8; 10; 12}, А ∩ В = {2; 4; 6}, А \ В = {1; 3; 5}.
Даны множества: А – множество всех натуральных чисел, кратных 10 и В = {1; 2; 3; … 41}. Найти: А ∩ В.
Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекабтся коллекционированием?
vseosvita.ua
Решение задач с использованием аппарата теории множеств — Студопедия.Нет
Тема программы: Соответствия между множествами. Отображения.
Цели работы:
1) Обобщить теоретические знания по теме: «Соответствия между множествами. Отображения», решить задачи.
2) Рассмотреть алгоритмы решений заданий теме «Соответствия между множествами. Отображения».
3) Формировать умение самоконтроля, рассудительность, терпение, самостоятельность.
Время выполнения: 1 час.
Теоретические основы
Одно из основных понятий современной математики — множество. Это понятие обычно принимается за первичное и поэтому не определяется через другие.
Когда в математике говорят о множестве (чисел, точек, функций и т. д.), то объединяют эти объекты в одно целое — множество, состоящее из этих объектов (чисел, точек, функций и т. д.). Основатель теории множеств, немецкий математик Георг Кантор (1845–1918) выразил эту мысль следующим образом: “Множество есть многое, мыслимое как единое, целое”.
Множество — это совокупность объектов, объединённых между собой по какому-либо признаку.
Слово “множество” в обычном смысле всегда связывается с большим числом предметов. Например, мы говорим, что в лесу множество деревьев, но если перед домом два дерева, в обычной речи не говорят, что перед домом “множество деревьев”.
Математическое же понятие множества не связывается обязательно с большим числом предметов. В математике удобно рассматривать и “множества”, содержащие 3; 2 или 1 предмет и даже “множество”, не содержащее ни одного предмета (пустое множество). Например, мы говорим о множестве решений уравнения, до того как узнаем, сколько оно имеет решений (множество вещественных решений уравнения х2+1 = 0 — пустое множество).
Произвольные множества обозначают большими латинскими буквами А, В, С, … Пустое множество, т.е. множество, которое не имеет элементов, обозначается символом .
О предметах, составляющих множество, говорят, что они принадлежат этому множеству, или являются его элементами. Элементы множества обозначают малыми латинскими буквами a, b, c, … или одной какой-нибудь буквой с индексом, например а1, а2, … ,аn.
Предложение “предмет а принадлежит множеству А”, или “предмет а — элемент множества А”, обозначают символом а А.
Способы задания множеств:
1) Множество может быть задано непосредственным перечислением всех его элементов (в произвольном порядке). В таком случае названия всех элементов множества записываются в строчку, отделяются между собой запятыми и заключаются в фигурные скобки.
Например: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}— множество цифр десятичной системы счисления,
Необходимо различать объекты, обозначаемые символами a и {a}. Символом a означается предмет, символом {a} — множество, состоящее из одного элемента а (единичное множество). Перечислением всех элементов можно задать лишь конечное множество. Такие множества, как, например, множество всех натуральных (N) или всех целых чисел (Z), нельзя задать таким способом, т.к. мы не можем перечислить все N и все Z — таких чисел бесконечное множество.
2) Имеется другой, универсальный, способ задания множества в том смысле, что этим способом может быть задано не только конечное, но и бесконечное множество. Множество может быть задано указанием характеристического свойства, т. е. такого свойства, которым обладают все элементы этого множества и не обладает ни один предмет, не являющийся его элементом.
Например: а) А = { х | sin x = 0}, б) А = {0, 1, 2, 3, 4}— множество всевозможных остатков от деления любого натурального числа на 5.
ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ
Множество В включается в множество А, если каждый элемент множества В является также элементом множества А. Множество В является подмножеством или частью множества А. Символическая запись: .
Отношение включения обозначается символом , т. е. предложение “множество В включается во множество А” записывается: В А.
Поскольку множество можно изобразить в виде геометрических фигур, логические рассуждения тоже изображаются геометрически.
Метод геометрической иллюстрации логических рассуждений был предложен великим математиком 18 века петербургским академиком Леонардом Эйлером (1707–1783) и широко применялся английским математиком Джоном Венном (1834–1923), т.е. для наглядности множества и логические рассуждения изображаются в виде кругов, которые называются кругами Эйлера или диаграммами Эйлера-Венна.
Например:
1) N Z Q R C.
2) Множество прямоугольников во множество параллелограммов множество четырёхугольников.
Частным случаем включения является равенство.
Два множества, состоящие из одних и тех же элементов называются равными (А = В).
Символическая запись:
Как показывают приведённые выше примеры, если В А, то возможны два случая:
1) Существует хотя бы один элемент множества А, не принадлежащий множеству В. В таком случае говорят, что В — собственная часть (или собственное подмножество) А, или что В строго включается в А. Отношение строгого включения обозначается : В А.
2) Не существует ни одного элемента множества А, не принадлежащего В. Этот случай равносилен отношению , т. е. равенству А = В.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Объединением А В двух множеств А и В называется множество, состоящее из общих элементов этих множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А или множеству В.
Символическая запись: .
Например:
Пересечением А В двух множеств называется множество, состоящее из всех элементов этих множеств, и не содержащее элементов других множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству А и множеству В.
Символическая запись:
Разностью А \ В двух множеств А и В называется множество, состоящее из всех элементов множества А и не содержащее элементов множества В.
Символическая запись:
Симметрической разностью А В двух множеств А и В называется множество
Пусть даны два множества А и В, В А, разность А \ В двух множеств А и В называется дополнением множества В до множества А (относительно множества А).
Сумма двух множеств является частным случаем объединения множеств.
Под парой будем всегда понимать упорядоченную пару элементов, т. е. два элемента, расположенных в определённом порядке. Элемент, занимающий первое место, называется первой координатой пары, элемент, занимающий второе место, называется второй координатой пары.
Обозначают пару элементов круглыми скобками: (a,b).
Прямым произведением двух множеств называется множество всевозможных пар (a,b), таких, что: a А, b В. Символическая запись: .
РЕШЕНИЕ ЗАДАЧ
studopedia.net
«Множества и операции над ними»
1. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
Задача 1. Представить множества , , , на диаграмме Эйлера-Венна.
Решение. Поскольку множества , и являются подмножествами множества , выберем в качестве универсального множества множество .
Диаграмма Эйлера-Венна выглядит следующим образом:
Задача 2. Записать характеристические функции множеств , и (задача 1) в виде двоичных векторов. Пронумеровать каждую область диаграммы Эйлера-Венна двоичным номером.
Решение.
Так как универсальным множеством является множество , содержащее 10 элементов, характеристические функции его подмножеств могут быть представлены десятимерными двоичными векторами. Последовательность координат таких векторов соответствуют последовательности элементов множества .На каждом подмножестве координата вектора принимает значение 1, если элемент принадлежит подмножеству, и значение 0, если не принадлежит.
Следовательно,
.
Двоичные номера областей на диаграмме Эйлера-Венна имеют 3 разряда по числу рассматриваемых множеств. Первый разряд соответствует множеству : в нем ставится 1, если область содержит элементы множества , и 0 – если не содержит. Второй разряд соответствует множеству и третий – множеству .
Задача 3. Составить булеан множества . Записать таблицу характеристических функций каждого множества.
Решение. Множество содержит четыре элемента, следовательно его булеан содержит 24=16 подмножеств.
Составим таблицу элементов булеана и их характеристических функций. При записи характеристических функций используем лексикографический метод записи последовательности двоичных векторов.
Подмножества множества (элементы булеана) | Значения характеристических функций подмножеств | |||
Элементы множества | ||||
2 | 4 | 6 | 8 | |
0 | 0 | 0 | 0 | |
0 | 0 | 0 | 1 | |
0 | 0 | 1 | 0 | |
0 | 0 | 1 | 1 | |
0 | 1 | 0 | 0 | |
0 | 1 | 0 | 1 | |
0 | 1 | 1 | 0 | |
0 | 1 | 1 | 1 | |
1 | 0 | 0 | 0 | |
1 | 0 | 0 | 1 | |
1 | 0 | 1 | 0 | |
1 | 0 | 1 | 1 | |
1 | 1 | 0 | 0 | |
1 | 1 | 0 | 1 | |
1 | 1 | 1 | 0 | |
1 | 1 | 1 | 1 | |
Задача 4. Составить диаграмму отношения включения на булеане множества и ее дерево путей. Записать все последовательности включений элементов булеана.
Решение. Диаграмма отношений включения между элементами булеана имеет 4 уровня: уровень 0 – пустое множество, характеристическая функция (0000), уровень 1 – множества, содержащие один элемент, уровень 2 – множества содержащие 2 элемента, уровень 3 – множества, содержащие 3 элемента, уровень 4 – множество , характеристическая функция (1111) (см. задачу 3).
Множества одного уровня несравнимы между собой по отношению включения, но двигаясь по любому пути диаграммы, получаем последовательную цепочку включений.
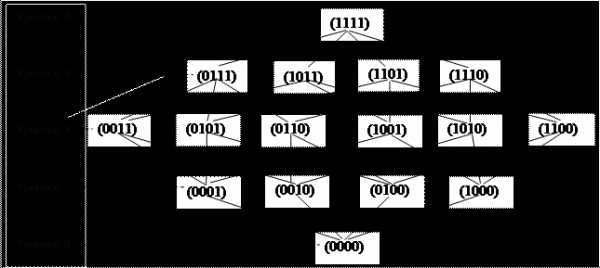
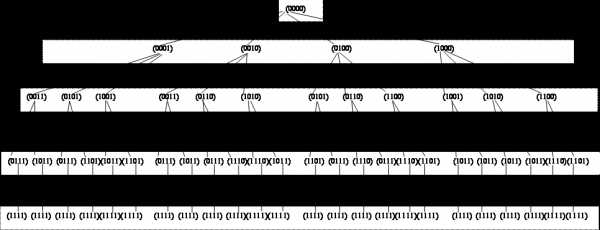
Составим дерево путей по
диаграмме включений (см. рис. стр.)
От нулевого уровня имеются четыре пути к множествам первого уровня. От каждого множества первого уровня имеется три пути к множествам второго уровня. От каждого множества второго уровня имеется два пути к множествам третьего уровня и от них по одному пути к множеству четвертого уровня.
Таким образом из 16 элементов булеана множества можно составить 24 различных последовательности множеств, упорядоченных отношением включения. Запишем эти последовательности.
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Задача 5. Доказать равенства: , , где и – подмножества какого-либо универсального множества .
Решение. Рассмотрим любой элемент универсального множества . Используя определения операций над множествами, запишем в таблицу все возможные варианты принадлежности и непринадлежности каждому из множеств. При этом принадлежность элемента множеству будем обозначать единицей, непринадлежность – нулем.
Докажем равенство .
0 | 0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 | 0 |
1 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 0 |
Как видно из таблицы элемент тогда и только тогда, когда . Следовательно, равенство справедливо для любых подмножеств множества .
Докажем равенство .
0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Как видно из таблицы элемент тогда и только тогда, когда . Следовательно, равенство справедливо для любых подмножеств множества .
Задача 6. Подмножества и множества заданы характеристическими функциями: , .
Требуется:
1) Записать списки элементов множеств и ;
2) Выполнить над множествами и операции: , , , , , , , , используя их характеристические функции.
3) Записать списки элементов всех полученных множеств.
Решение.
1) Запишем списки элементов множеств и , используя определение характеристической функции множества:
, .
2) Используя правила выполнения операций над множествами, выполним все указанные в задаче действия.
; .
; .
=; .
=; .
(см. задачу 5).
=; .
(см. задачу 5).
=; .
(см. задачу 5).
=
=
; .
, . В равенстве использовано свойство дополнения .
Задача 7. Найти множество через известные множества , , если известно, что .
Решение. Построим таблицу принадлежности произвольного элемента универсального множества каждому из множеств, записанных в системе.
0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 | 1 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 0 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 | 0 | 0 |
0 | 1 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 0 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 1 | 1 |
1 | 1 | 0 | 1 | 0 | 1 |
1 | 1 | 1 | 0 | 1 | 1 |
1 | 1 | 1 | 1 | 0 | 1 |
В таблице отмечены цветом те строки, которые соответствуют нарушению равенств системы. Выпишем строки, соответствующие системе:
| Как видно из таблицы, элемент тогда и только тогда, когда он принадлежит множеству или . Следовательно . | ||||
0 | 0 | 0 | 0 | ||
0 | 0 | 1 | 1 | , | |
1 | 0 | 1 | 1 | , | |
1 | 1 | 1 | 0 |
Задача 8. Решить уравнение .
Решение. Применим метод решения, использованный задаче 7.
Из двух последних строк таблицы очевидно, что элемент, взятый из пересечения множеств и может как принадлежать множеству , так и не принадлежать ему. Следовательно, данное уравнение не имеет решений. | |||||
0 | 0 | 0 | 0 | ||
0 | 0 | 1 | 1 | ||
0 | 1 | 0 | 0 | ||
0 | 1 | 1 | 1 | ||
1 | 0 | 0 | 1 | ||
1 | 0 | 1 | 1 | ||
1 | 1 | 0 | 1 | , | |
1 | 1 | 1 | 1 | , |
|
 |
vunivere.ru
Элементы теории множеств Лабораторная работа
Цели занятия:
Повторение приемов работы с графическими объектами и изучение возможностей их применения для графической иллюстрации решения задач.
Изучение возможностей выполнения простых вычислений в среде MS Word.
Повторение основных приемов форматирования документов средствами MS Word.
Решение задач по теме «Элементы теории множеств»
Подготовка к выполнению задания:
Повторить тему «Элементы теории множеств» по электронному конспекту, расположенному на сервере по адресу «F:\Методические материалы \ Информационные технологии \ Математика и информатика для юристов». Особое внимание обратить на примеры решения задач.
Повторить по справочной системе MS Word разделы, связанные с использованием в документе графических объектов.
Познакомиться по справочной системе MS Word с разделом «Выполнение вычислений».
Состав задания:
Используя графические объекты, изобразить приведенные ниже диаграммы Эйлера-Венна, иллюстрирующие отношения между двумя множествами. В пояснительных формулах использовать вставку символов.
A
A B = A B A B
Создать текстовый документ, содержащий пример оформления решения задачи на тему «Элементы теории множеств», приведенный ниже.
Образец решения и оформления задачи
Задача. Из 40 студентов 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого. Сколько студентов умеют плавать и играть в шахматы?
Решение.
Обозначим через C множество студентов, умеющих играть в шахматы, а через S – множество студентов, умеющих плавать. Тогда отношение между этими множествами может быть проиллюстрировано следующей диаграммой.
Студенты, обладающие хотя бы одним из перечисленных умений, принадлежат объединению этих множеств C S. Их количество согласно условию задачи m(CS)=40-5=35.
Студенты, умеющие и играть в шахматы и плавать, принадлежат пересечению тех же множеств C S.
Согласно теории m(C S)=m(C) + m(S) — m(CS). Поэтому искомое количество студентов может быть вычислено по следующей формуле m(CS)=m(C) + m(S) — m(CS) = 30 + 27 – 35 =22
Решить следующие задачи по теории множеств и оформить их аналогично рассмотренному образцу. (Для вычисления выражений использовать команду Вставка > Текст > Экспресс-блоки > Поле).
В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет, В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?
Сборная области по гимнастике завоевала на первенстве страны 4 золотых, 3 серебряных и 5 бронзовых медалей. Причем 2 лидера сборной завоевали по три медали разного достоинства, а остальные члены команды завоевали по одной медали. Сколько человек было в составе сборной?
18 мальчиков поехали на пикник. При этом 6 из них обгорели, 9 были сильно покусаны комарами, а 8 — избежали этих неприятностей и остались всем довольны. Сколько покусанных комарами мальчиков также и обгорели?
Определить число задолжников в группе, если известно, что задолженность по физкультуре имеют 5 человек, по информатике и математике — 6, Иностранному языку -7. Причем, каждый из задолжников имеет либо одну, либо три задолженности. При этом три задолженности имеют 2 человека.
В течение недели в кинотеатре демонстрировались фильмы А, В и С. Из 40 студентов, каждый из которых просмотрел либо все три фильма, либо один из трех, фильм А видели 13, фильм В — 16, фильм С — 19. Найти, сколько студентов просмотрели все три фильма.
Контрольные вопросы:
Какие способы задания множеств Вы знаете? Опишите их.
Имеются два множества А и В, причем каждый элемент множества В принадлежит множеству А. Что можно сказать об отношении между этими множествами?
Даны два числовых множества N={0,2,4,5,6,7} и M={1,3,5,7,9}. Напишите, чему равны множества A= NM, В= NM и С= N\M.
Продолжите определение: «Разностью двух множеств А и В называется множество, состоящие из тех элементов множества А…».
studfiles.net
Множества и операции над ними. Решение задач с помощью кругов Эйлера
Разделы: Математика
Современный математический язык более краток и заменяет разговорный язык специальными буквенными и символьными выражениями. Понятия и обозначения языка теории множеств составляет фундамент современного математического языка. Всякий объект, входящий во множество, называют его элементом. Например, если множество – дни недели, то понедельник элемент этого множества.
Блок 1. Множества и операции над ними.
Презентация. (Слайд 2) Вопросы к слайду 2:
- Перечислите элементы множеств:
а) арабских цифр; (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
б) натуральных чисел; (1; 2; 3; 4;…)
в) целых чисел (…-2; -1; 0; 1; 2;…). - Как называется множество цветов, стоящих в вазе? (букет).
- Перечислите элементы множества планет солнечной системы. (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун).
- Как называется множество фруктовых деревьев и кустарников растущих у дома? (сад).
- Приведите примеры множеств, элементами которого являются геометрические фигуры.
- Какие названия применяют для обозначения множеств животных? (млекопитающие, земноводные, хладнокровные и т.п.).
- Перечислите элементы множества видов спорта (футбол, теннис, волейбол и т. п.).
- Какие названия применяют для обозначения множеств кораблей? (флотилия, эскадра).
Задайте сами множество описанием.
(Слайд 3) Множества обычно обозначают большими буквами латинского алфавита: А, В, С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных разделах математики, что для них ввели специальные обозначения:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел.
(Слайд 4) Чтобы не забыть, что перечисляемые элементы объединены вместе в некоторое множество, такое перечисление производят внутри фигурных скобок {,}.
Например, цифры десятичной системы счисления задаются множеством
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Если множество состоит из чисел, то при их перечислении иногда удобнее использовать не запятую, а знак препинания “ ; ” – точку с запятой. Так как “перечислительную” запятую можно спутать с “десятичной” запятой.
Элементы множества можно перечислять в произвольном порядке. От изменения порядка перечисления элементов само множество не меняется. Например, множество гласных букв русского алфавита задается {А, Е, Ё, И, О, У, Ы, Э, Ю, Я} или {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Эти множества состоят из одних и тех же элементов, их называют равными, а для записи равенства двух множеств употребляют знак “ = ”.
{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Чтобы задать конечное множество, можно просто перечислить все его элементы.
Например, запись А = {2; 3; 5; 7; 11; 13} означает, что множество А состоит из первых шести простых чисел.
Однако задавать множество путем перечисления его элементов удобно только в том случае, когда их число невелико. Если число элементов множества достаточно велико или множество бесконечно, то явное перечисление элементов такого множества невозможно.
Способы задания, описания множеств весьма разнообразны. Например, множество всех квадратов натуральных чисел можно записать {1; 4; 9; 16; 25; …}, а множество всех чисел, которые больше 5 и меньше 12 записать {х | 5< х <12} или (5; 12). В примерах использован оборот “ … и так далее” и символ “ | ” внутри фигурных скобок заменяющий комбинацию слов “ … таких, что …”. (Множество всех х таких, что 5< х <12).
Описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один объект, отвечающий этому описанию. Предположим, о множестве С сказано, что оно состоит из чисел, делящихся на 6, но не делящихся на 3. Таких чисел просто нет. В подобных случаях множество называют пустым и обозначают символом O, в фигурные скобки его не ставят, так как никакого перечисления элементов пустого множества не происходит.
(Слайд 5) Задание 1. [3]
1) Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {– 2, – 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}; г) А = {0,1; 0,01; 0,001; 0,0001; …}; д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества: М = {5,4,6}, Р = {4,5,6}, Т = {5,6,7},
S = {4, 6}. Какое из утверждений неверно?
а) М = Р. б) Р S. в) М Т. г) Р = Т.
(Слайд 6) Словесные обороты, как “элемент х принадлежит множеству А” или “х – элемент множества А”, достаточно длинны и не всегда удобны в записи решений конкретных задач.
В математике эти выражения кратко записывают так: х А, где – знак принадлежности.
Например, 5N, лучше читать не буквально, а в “литературном переводе”, “5 – число натуральное”. Наряду со знаком принадлежит используют и его “отрицание” – знак (знак не принадлежит). Запись 0 N означает, что нуль не натуральное число.
(Слайд 7) Задание 2. [3; 1]
1. Запишите на символическом языке следующее утверждение:
а) число 10 – натуральное; б) число – 7 не является натуральным; в) число – 100 является целым; г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5 N; б) -5 Z; в) 2,(45) Q?
3. Верно ли, что:
а) 0,7 {х | х2 – 1 < 0}; б) – 7 {х | х2 + 16х ? – 64}?
(Слайд 8) Возьмем множество А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}. Каждый элемент множества А принадлежит также и множеству В. В таких случаях говорят, что множество А является подмножеством множества В, и пишут: А В.
Знак “” называют знаком включения.
Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью так называемых кругов Эйлера (Леонард Эйлер российский ученый — математик, механик, физик и астроном.). Множество изображается в виде некоторого круга, а его элементы изображаются точками этого круга (рис 1).
Рис. 1
Пустое множество считают подмножеством любого множества. А В. Будем считать, что все элементы рассматриваемых множеств взяты из некоторого одного и того же “универсального” множества К. Это множество будем изображать квадратом, а рассматриваемые множества А, В, С, … – подмножества множества К – кругами (или другими полученными из них фигурами, которые выделим штриховкой).
(Слайд 9) Задание 3. [3; 1]
1. Даны множества: А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.
Поставьте вместо … знак включения ( или ) так, чтобы получилось верное утверждение: а) А… D; б) А…В; в) С…А; г) С…В.
2. Даны три множества А = {1, 2, 3,…, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16,…,36}.
Верно ли, что: а) А В; б) В С; в) С А; г) С В?
(Слайд 10) Из данных множеств с помощью специальных операций можно образовывать новые множества:
1) Пересечением множества А и В называют множество, состоящие из всех общих 11элементов множеств А и В, т. е. из всех элементов, которые принадлежат и множеству А, и множеству В (рис. 2). Пересечение множеств А и В обозначают так: АВ. Это определение можно записать и так: АВ = {х | х А и х В}. Иными словами, пересечение двух множеств – это их общая часть. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АВ = {3; 9}. Если А = {10; 20; …90; 100} и В = {6; 12; 18;…}, то АВ = {30; 60; 90}. Можно рассматривать пересечение не только двух, но трех, четырех и т. д. множеств. Пересечение множеств В, С и D обозначают так: ВСD.
Рис. 2
(Слайд 11) Задание 4. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АВ; б) АС; в) СВ.
2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}.
Найдите АВ.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АВ) С.
(Слайд 12)
2) Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В (рис. 3). Объединение множеств А и В обозначают так: АUВ.
Рис. 3
Это определение можно записать и так: АUВ = {х | х А или х В}. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АUВ = {1; 3; 5; 7; 9; 11; 12}. Можно рассматривать объединение не только двух, но трех, четырех и т.д. множеств. Объединение множеств В, С и D обозначают так: ВUСUD.
(Слайд 13) Задание 5. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АUВ; б) АUС; в) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АUВ)UС.
3. Даны три числовых промежутка: А = (7,7; 11), В = [; ], С = (; 13].
Найдите (АUВ)UС.
Продолжение статьи
Приложение
Презентация
19.01.2011
xn--i1abbnckbmcl9fb.xn--p1ai
как решать задачи с множествами?
Первый значёк -( подковка с ножками вверх) — это ОБЪЕДИНЕНИЕ. Это значит, что нужно составить множество изо всех элементов, которые есть в обоих данных множествах. Естественно, что если каое-то число встречается и в мн-ве А и в мн-ве В, то два раза его писать не нужно. Второй значёк — (подковка с ножками вниз) — это ПЕРЕСЕЧЕНИЕ. Нужно выписать в отдельное множество те числа, которые принадлежат обоим множествам. Например -1 есть и в А и в В, значит выписываем. Косые чёрточки заменяют слово «БЕЗ». А без В — то есть всё то, что входит в А, но не выписывать то, что есть так же и в В. Например -4 есть в А, а в В нет. Годится. А число -1 есть в А, но в В тоже есть, значит не пишем. В без А — аналогично.
Как решать? 1) Прочитать внимательно определения, ЧТО означают эти значки, которые стоят между А и В. 2) Разобрать по парочке примеров на операции с множествами 3) Попытаться решить задачу самому 4) ——- 5) ПРОФИТ!!
DOC Решения задач по множествам Решения задач по теме «Множества и операции над ними» . Решения задач по теме «Множества и операции над ними» . 1. В группе из 100 туристов 70 … pi.sfedu.ru/rspu/resources/for_ling… копия еще с сайта Элементы теории множеств, логические символы, элементы … Элементы теории множеств, логические символы, элементы множества, операции над …Примеры и задачи с решениями …Примеры решения задач … pm298.ru/reshenie/elem.php копия еще с сайта Решения задач по теории множеств — Главная Автор Administrator. 29.04.2008 г. Является ли отношение, заданное на вершинах единичного куба в Rn как aRb, если в координатах вершины a не … bankzadach.ru/teoriya-mnozhestv-/in… копия еще с сайта Решения задач по теории множеств — Главная 29 апр 2008 …Автор Administrator. 29.04.2008 г. Пусть даны множества A={a,b,c,d,e,f,g,h} B= {1,2,3,4,5,6,7,8}. Тогда Image
touch.otvet.mail.ru
