Корень х 8 х 2: Решите неравенство sqrt(x+8)>x-2 (квадратный корень из (х плюс 8) больше х минус 2)

alexxlab / / Разное
2 — 4 * (-1) * (4) = 41
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)

или
$$x_{1} = — \frac{\sqrt{41}}{2} + \frac{5}{2}$$
$$x_{2} = \frac{5}{2} + \frac{\sqrt{41}}{2}$$

Т.к.
$$\sqrt{x + 8} = x — 2$$
и
$$\sqrt{x + 8} \geq 0$$
то
$$x — 2 \geq 0$$
или
$$2 \leq x$$
$$x $$x_{2} = \frac{5}{2} + \frac{\sqrt{41}}{2}$$
$$x_{1} = \frac{5}{2} + \frac{\sqrt{41}}{2}$$
$$x_{1} = \frac{5}{2} + \frac{\sqrt{41}}{2}$$
Данные корни
$$x_{1} = \frac{5}{2} + \frac{\sqrt{41}}{2}$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10} + \frac{5}{2} + \frac{\sqrt{41}}{2}$$
=
$$\frac{12}{5} + \frac{\sqrt{41}}{2}$$
подставляем в выражение
$$\sqrt{x + 8} > x — 2$$
$$\sqrt{- \frac{1}{10} + \frac{5}{2} + \frac{\sqrt{41}}{2} + 8} > -2 + — \frac{1}{10} + \frac{5}{2} + \frac{\sqrt{41}}{2}$$

     _____________         ____
    /        ____    2   \/ 41 
   /  52   \/ 41   > - + ------
  /   -- + ------    5     2   
\/    5      2

значит решение неравенства будет при:
$$x
 _____          
      \    
-------ο-------
       x1

Содержание

Уравнения / math5school.

ru

 

 

Немного теории

При решении и исследовании олимпиадных уравнений, помимо обычных школьных методов:

  • подстановки,
  • замены переменкой,
  • разложения на множители и других преобразований,

иногда используются соображения монотонности:

если функция у = f (x) – строго возрастает или строго убывает, то уравнения

f (p (x)) = f ( q (x))  и  p (x) = q (x)

равносильны.

При решении уравнений и систем уравнений иногда бывают полезны:

  • геометрическая интерпретация,
  • учёт области допустимых значений переменной или области значений функций, входящих в уравнение,
  • соображения симметрии,
  • идеи цикличности,
  • выход на линейную комбинацию между переменными  и др.

 

Задачи с решениями

1. Решить уравнение:

а) (1 + х + х2) (1 + х + х2 + . . . + х10) = (1 + х + х2 + . . . + х6)2.

б) (x2 – x + 1)4 – 10x2 (x2 – x + 1)2 + 9x4 = 0.

в) (x + 1)63 + (x + 1)62 (x – 1) + (x + 1)61 (x – 1)2 + . . . + (x – 1)63 = 0.

Решение

а) Так как х = 1 – не корень, то умножим обе части уравнения на (х – 1)2. Получим:

(х3 – 1) (х11 – 1) = (х

7 – 1)2,

х11 – 2х7 + х3 = 0,

х3 (х4 – 1)2 = 0,

х1 = 0,

х2 = –1,

х3 = +1 – посторонний корень, возникший в результате умножения на (х – 1)2.

Ответ: 0 и –1.

 

б) Пусть  y = (x2 – x + 1)2,  тогда  y2 – 10x2y + 9x4 = 0.  Решив это уравнение относительно y, получим:  

y1 = 9x2,  y2 = x2.  

Итак, данное уравнение свелось к двум следующим:

(x2 – x + 1)2 = 9x2  и  (x2 – x + 1)2 = x2,

то есть к четырём квадратным уравнениям: 

x2 – x + 1 = 3x,  x2 – x + 1 = – 3x,  x2 – x + 1 = x,  x

2 – x + 1 = – x,

решить которые не представляет труда. 

Ответ:  –1, 1,  2 – √3,  2 + √3.

 

в) Умножив обе части уравнения на

(x + 1) – (x – 1) = 2, 

получим  

(x + 1)64 – (x – 1)64 = 0. 

Отсюда  

(x + 1) = ± (x – 1), 

то есть  x = 0.

Ответ: x = 0.

 

2. Решить уравнение:

sin x = х2 + х + 1.

Решение

Если х0 не принадлежит числовому промежутку [–1; 0], то  х02 + х0 + 1 > 1 > sin х0.

Если же х0 принадлежит промежутку [–1; 0], то  х02 + х0 + 1 > 0,  а  sin х0

Значит, для любого действительного значения х0 имеет место  sin х002 + х0 + 1,  и исходное уравнение не имеет решений.

Ответ: решений нет.

 

3. Сколько корней имеет уравнение:

(7√10 + 5√11) х2 – (10√10 + 13√11) х + 4√10 + 7√11 = 0?

Решение

Рассмотрим функцию

f (x) = (7√10 + 5√11) х2 – (10√10 + 13√11) х + 4√10 + 7√11.

Это квадратичная функция, графиком которой есть парабола, направленная ветвями вверх. Так как

f (1) = √10 – √11 

то парабола пересекает ось х в двух точках, а уравнение f (x) = 0 имеет два корня.

Ответ: два корня.

 

4. Известно, что уравнение  ax5 + bx4 + c = 0  имеет три различных корня. Докажите, что и  уравнение  cx5 + bx + a = 0  также имеет три различных корня.

Решение

Число  x = 0  не может быть корнем уравнения  

ax5 + bx4 + c = 0,

так как иначе  c = 0,  и уравнение имеет не более двух различных корней, что противоречит условию.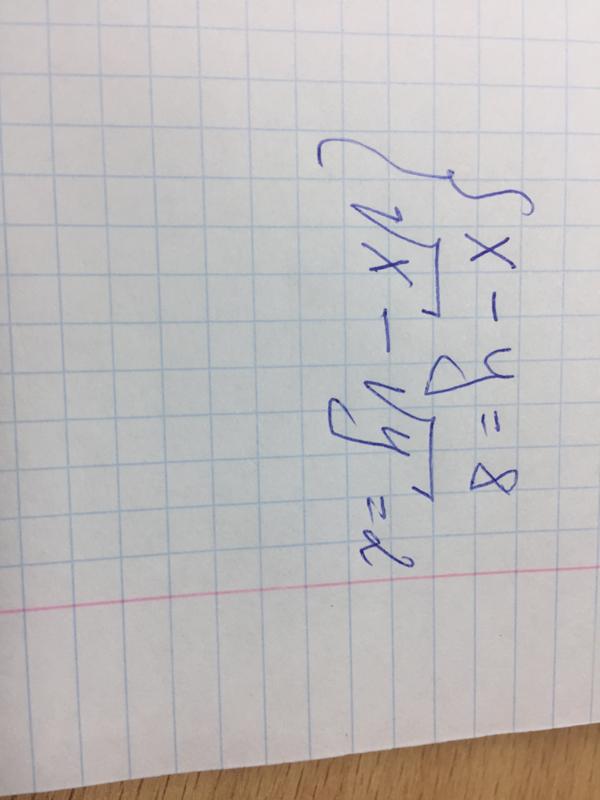

 Разделив обе части этого уравнения на x5, получаем, что

a + b/x + c/x5 = 0.

Следовательно, если x1, x2 и x3 – различные корни уравнения  ax5 + bx4 + c = 0,  то 1/x1, 1/x2 и 1/x3 – различные корни уравнения  

cx5 + bx + a = 0.

 

5. При каком положительном значении p уравнения  3x2 – 4px + 9 = 0  и  x2 – 2px + 5 = 0  имеют общий корень?

Решение

Общий корень указанных уравнений должен быть и корнем уравнения  

(3x2 – 4px + 9) – 3(x2 – 2px + 5) = 0,

равносильного уравнению

2px – 6 = 0.

Значит, х = 3/p.  Подставив это значение х, например, во второе уравнение, получим  9/p2 = 1,  откуда  p = 3.

Ответ: 3. 

 

6. Решить уравнение:

5х + 12х = 13х.

Решение

Способ 1.

Легко заметить, что, по крайней мере, одно решение это уравнение имеет, это х = 2. Докажем, что других решений нет. Запишем данное уравнение в виде:

(5/13)x + (12/13)x = 1.

Если x

(5/13)х > (5/13)2,  (12/13)х > (12/13)2

и, следовательно,

(5/13)x + (12/13)x > (5/13)2 + (12/13)2 = 1.

Аналогично, если x > 2, то

(5/13)x + (12/13)x5/13)2 + (12/13)2 = 1.

Итак, х = 2 – единственный корень.

 

Способ 2.

Записав уравнение в виде

(5/13)x + (12/13)x = 1,

видим, что имеет единственное решение х = 2. Действительно, число х = 2  удовлетворяет   уравнению. С другой стороны, функция

f (х) = (5/13)x + (12/13)x

является строго убывающей, потому что является суммой двух строго убывающих функций, и, следова­тельно, значение 1 принимает только один раз при х = 2.

 

Способ 3.

Можно ввести обозначения:

5/13 = sin α,  12/13 = cos α.

Тогда уравнение

(5/13)x + (12/13)x = 1,

равносильное исходному, примет следующий вид:

(sin α)x + (cos α)x = 1,

а это уравнение имеет единственное решение х = 2.

Ответ: 2.

 

7. Решить уравнение:

а) 8х (3х + 1) = 4.

б) 4 lg x – 32 + x lg 4 = 0.

Решение

а) Число х = 1/3 является решением данного уравнения. Докажем, что других решений нет.

При х > – 1/3 функции

у1 (х) = 8х  и  у2 (х) = 3х + 1

принимают положительные значения и возрастают, следовательно, их произведение (левая часть уравнения) также является возрастающей функцией.

Поэтому на промежутке (– 1/3; + ∞) уравнение не может иметь более одного решения.

Далее, при х – 1/3 имеем у1(х) > 0, у2(х) 0, а значит,  у1(х) · у2(х) 0.  

Поэтому на промежутке (– ∞; – 1/3] уравнение не имеет решений. Таким образом, получаем единственное решение: 1/3.

Ответ: 1/3.  

 

б) Область допустимых значений х является  х > 0  и х ≠ ±1.  Имеет место

4 lg x = x lg 4 .

Для доказательства этого равенства достаточно прологарифмировать обе части равенства по основанию 10. В таком случае

4 lg x – 32 + 4 lg x = 0,

4 lg x = 16,

4 lg x = 42,

lg x = 2,

х = 100.

Ответ: 100.

 

8. Докажите, что уравнение :

а) х10 – х7 + х2 – х + 1 = 0  не имеет действительных корней;

б) (x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0  для любых действительных значений a, b, c имеет хотя бы одно решение;

в) х4 + 5х3 + 6х2 – 4х – 16 = 0  имеет ровно два решения.

Решение

а) Рассмотрим функцию

f (х) = х10 – х7 + х2 – х + 1.

При х0 ∈ (– ∞; 0] имеем f (х0) > 0.

При х0 ∈ (0; 1) имеем f (х0) = (1 – х0) + (х02 – х07) + х010 > 0.

При х0 ∈ [1; + ∞) имеем f (х0) = (х010 – х07) + (х02 – х0) + 1 > 0.

Значит для любого действительного х0 верно, что f (х0) > 0 и, следовательно, исходное уравнение не имеет решений.

 

б) Обозначим

f (x) = (x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a).

Без ограничения общности можно считать, что а b с.

Если а = b или b = с, то  f (b) = (b – c)(b – a) = 0.

Если же а 0.

Так как функция f(x) непрерывна, то существует такое число х0 из промежутка (а; b), что

f(x0) = 0,

что и требовалось доказать.

Замечание. Это уравнение можно встретить в задаче с несколько иной формулировкой на странице Квадратный трёхчлен.

 

в) Докажем, что функция

f (x) = х4 + 5х3 + 6х2 – 4х – 16

принимает значение 0 ровно в двух точках. Для этого исследуем производную этой функции

f′(x) = 4х3 + 15х2 + 12х – 4 = (x + 2)2(4х – 1).

При х 1/4 имеет место неравенство f′(x)

при х > 1/4 – неравенство f′(x) > 0. Поэтому функция f(x) убывает па интервале (– ∞; 1/4) и возрастает на интервале (1/4; + ∞).

Поскольку

f (–10) > 0,  f (10) > 0  и  f (1/4)

то на каждом из двух указанных интервалов функция f (х) однажды принимает значение 0, а уравнение f (х) = 0 имеет ровно два решения, что и требовалось доказать.

 

9. Сколько корней на отрезке  [0, 1]  имеет уравнение  8x (1 – 2x2) (8x4 – 8x2 + 1) = 1?

Решение

Заметим, что  

8x4 – 8x2 + 1 = 2(2x2 – 1)2 – 1.  

Сделав замену  x = cos φ, исходное уравнение перепишем в виде: 

8 cos φ cos 2φ cos 4φ = – 1.

Умножая обе части на sin φ, получим 

sin 8φ = – sin φ, 

8φ = – φ + 2kπ  или  8φ = π + φ + 2kπ,

то есть

x = cos 2kπ/9   или   x = cos (π/7 + 2kπ/7). 

На отрезке  [0, 1]  лежат четыре корня уравнения:  

cos 2π/9, cos 4π/9, cos π/7  и  cos 3π/7

(корень  x = 1  – посторонний, он возник при умножении на sin φ).

Замечание: Всего указанное уравнение 7-й степени имеет 7 корней: к указанным в решении добавляются еще 

cos 2π/3 = – ½,  cos 8π/9 = – cos π/9  и  cos 5π/7 = – cos 2π/7. 

Ответ: Четыре корня.

 

10. Решить уравнение:

а) х4 + 8х3 + 18х2 + 11х + 2 = 0:

б) х4 – 4х3 – 1 = 0.

Решение

а) Разложим левую часть уравнения на множители. Для этого представим её в виде:

х4 + 8х3 + 18х2 + 11х + 2 = (х2 + ах + b) (х2 + cх + d),

где a, b, c, d подберём методом неопределённых коэффициентов. Имеем:

х4 + 8х3 + 18х2 + 11х + 2 = х4 + (a + c) x3 + (b + d + ac) x2 + (ad + bc) x + bd.

Одно из решений системы

a + c = 8,

b + d + ac = 18,

ad + bc = 11,

bd = 2;

подбираем методом подбора:

a = 5, b = 2, c = 3, d = 1,

(находить все её решения не обязательно). Значит,

х4 + 8х3 + 18х2 + 11х + 2 = (х2 + 5х + 2) (х2 + 3х + 1),

а исходное уравнение равносильно совокупности уравнений:

х2 + 5х + 2 = 0  и  х2 + 3х + 1 = 0,

решение которых элементарно.

Ответ: х1,2 = –5 ±√17/2,  х3,4 = –3 ±√5/2.

 

б) Введём новую переменную

t = x – 1,  x = t + 1,

и получим

(t + 1)4 – 4(t + 1)3 – 1 = 0,

t4 – 6t2 – 8t – 4 = 0.

Разложим левую часть уравнения на множители. Для этого представим её в виде:

t4 – 6t2 – 8t – 4 = (t2 + а)2 – (bt + c)2,

где a, b, c подберём методом неопределённых коэффициентов. Имеем:

t4 – 6t2 – 8t – 4 = t4 + (2a + b2) t2 – 2bc t + a2 – c2.

Найдём одно из решений системы

2a – b2 = –6,

bc = 4,

a2 – c2 = –4.

Решая эту систему находим:

а = –2,  b = √2,  с = 2√2 .

Значит,

t4 – 6t2 – 8t – 4 = (t2 – 2)2 – (√2t + 2√2)2 = (t2 – √2t – 2√2 – 2) (t2 + √2t + 2√2 – 2) = 0,

а уравнение

t4 – 6t2 – 8t – 4 = 0

равносильно совокупности уравнений:

t2 – √2t – 2√2 – 2 = 0  и  t2 + √2t + 2√2 – 2 = 0,

первое из которых имеет корни:

t1,2 = √2 ± √10 + 8√2/2 ,

а второе корней не имеет.

И, наконец, x1,2 = t1,2 + 1 = √2 ± √10 + 8√2/2 + 1 =  2 + √2 ± √10 + 8√2/2 .

Ответ: x1,2 = 2 + √2 ± √10 + 8√2/2.

 

Задачи без решений

1. Решить уравнение  2 sin х = 5х2 + 2х + 3.

 

2. Решить уравнение  x3 + x2 + x + 1/3 = 0.

 

3. Решить уравнение  4√1 – x + 4√1 + x = 4.

 

4. Сколько действительных корней имеет уравнение  х13 = а (1 + х14)  для каждого действительного а?

 

5. Доказать, что уравнение  x – а sin x – b = 0  при 0

 

X2 0 решение. Уравнения онлайн. Тождественные преобразования уравнений

Цели:

  1. Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
  2. Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
  3. Формирование интереса к математике через изучение новых глав математики, воспитание графической культуры через построение графиков уравнений.

Тип урока : комбинированный.

Оборудование: графопроектор.

Наглядность: таблица «Теорема Виета».

Ход урока

1. Устный счет

а) Чему равен остаток от деления многочлена р n (х) = а n х n + а n-1 х n-1 + … + а 1 х 1 + a 0 на двучлен х-а?

б) Сколько корней может иметь кубическое уравнение?

в) С помощью чего мы решаем уравнение третьей и четвертой степени?

г) Если b четное число в квадратном уравнение, то чему равен Д и х 1 ;х 2

2. Самостоятельная работа (в группах)

Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»

1 группа

Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6

Составить уравнение:

B=1 -2-3+6=2; b=-2

с=-2-3+6+6-12-18= -23; с= -23

d=6-12+36-18=12; d= -12

е=1(-2)(-3)6=36

х 4 — 2 х 3 — 23х 2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске)

Решение . Целые корни ищем среди делителей числа 36.

р = ±1;±2;±3;±4;±6…

р 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера

р 3 (x) = х 3 -х 2 -24x -36

р 3 (-2) = -8 -4 +48 -36=0, х 2 =-2

р 2 (x) = х 2 -3х -18=0

х 3 =-3, х 4 =6

Ответ: 1;-2;-3;6 сумма корней 2 (П)

2 группа

Корни: х 1 = -1; х 2 = х 3 =2; х 4 =5

Составить уравнение:

B=-1+2+2+5-8; b= -8

с=2(-1)+4+10-2-5+10=15; с=15

D=-4-10+20-10= -4; d=4

е=2(-1)2*5=-20;е=-20

8+15+4х-20=0 (это уравнение решает на доске 3 группа)

р = ±1;±2;±4;±5;±10;±20.

р 4 (1)=1-8+15+4-20=-8

р 4 (-1)=1+8+15-4-20=0

р 3 (x) = х 3 -9х 2 +24x -20

р 3 (2) = 8 -36+48 -20=0

р 2 (x) = х 2 -7х +10=0 х 1 =2; х 2 =5

Ответ: -1;2;2;5 сумма корней 8(Р)

3 группа

Корни: х 1 = -1; х 2 =1; х 3 =-2; х 4 =3

Составить уравнение:

В=-1+1-2+3=1;в=-1

с=-1+2-3-2+3-6=-7;с=-7

D=2+6-3-6=-1; d=1

е=-1*1*(-2)*3=6

х 4 — х 3 — 7х 2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)

Решение. Целые корни ищем среди делителей числа 6.

р = ±1;±2;±3;±6

р 4 (1)=1-1-7+1+6=0

р 3 (x) = х 3 — 7x -6

р 3 (-1) = -1+7-6=0

р 2 (x) = х 2 -х -6=0; х 1 =-2; х 2 =3

Ответ:-1;1;-2;3 Сумма корней 1(О)

4 группа

Корни: х 1 = -2; х 2 =-2; х 3 =-3; х 4 =-3

Составить уравнение:

B=-2-2-3+3=-4; b=4

с=4+6-6+6-6-9=-5; с=-5

D=-12+12+18+18=36; d=-36

е=-2*(-2)*(-3)*3=-36;е=-36

х 4 + 4х 3 – 5х 2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)

Решение. Целые корни ищем среди делителей числа -36

р = ±1;±2;±3…

р(1)= 1 + 4-5-36-36 = -72

р 4 (-2) = 16 -32 -20 + 72 -36 = 0

р 3 (х) = х 3 +2х 2 -9х-18 = 0

р 3 (-2)= -8 + 8 + 18-18 = 0

р 2 (х) = х 2 -9 = 0; x=±3

Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)

5 группа

Корни: х 1 = -1; х 2 =-2; х 3 =-3; х 4 =-4

Составить уравнение

х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)

Решение . Целые корни ищем среди делителей числа 24.

р = ±1;±2;±3

р 4 (-1) = 1 -10 + 35 -50 + 24 = 0

р 3 (х) = x- 3 + 9х 2 + 26x+ 24 = 0

p 3 (-2) = -8 + 36-52 + 24 = О

р 2 (х) = x 2 + 7x+ 12 = 0

Ответ:-1;-2;-3;-4 сумма-10 (И)

6 группа

Корни: х 1 = 1; х 2 = 1; х 3 = -3; х 4 = 8

Составить уравнение

B=1+1-3+8=7;b=-7

с=1 -3+8-3+8-24= -13

D=-3-24+8-24= -43; d=43

х 4 — 7х 3 — 13х 2 + 43 x — 24 = 0 (это уравнение решает потом 1 группа на доске)

Решение . Целые корни ищем среди делителей числа -24.

р 4 (1)=1-7-13+43-24=0

р 3 (1)=1-6-19+24=0

р 2 (x)= х 2 -5x — 24 = 0

х 3 =-3, х 4 =8

Ответ: 1;1;-3;8 сумма 7 (Л)

3. Решение уравнений с параметром

1. Решить уравнение х 3 + 3х 2 + mх — 15 = 0; если один из корней равен (-1)

Ответ записать в порядке возрастания

R=Р 3 (-1)=-1+3-m-15=0

х 3 + 3х 2 -13х — 15 = 0; -1+3+13-15=0

По условию х 1 = — 1; Д=1+15=16

Р 2 (х) = х 2 +2х-15 = 0

х 2 =-1-4 = -5;

х 3 =-1 + 4 = 3;

Ответ:- 1;-5; 3

В порядке возрастания: -5;-1;3. n} \)

7) a n > 1, если a > 1, n > 0

8) a n 1, n
9) a n > a m , если 0

В практике часто используются функции вида y = a x , где a — заданное положительное число, x — переменная. Такие функции называют показательными . Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \(a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \(a \neq 1\), не имеет корней, если \(b \leq 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = a x при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = a x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \(a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \(a \neq 1\) равны тогда и только тогда, когда равны их показатели. {x-2} = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \(3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

  1. Не имеют корней;
  2. Имеют ровно один корень;
  3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

  1. Если D
  2. Если D = 0, есть ровно один корень;
  3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

  1. x 2 − 8x + 12 = 0;
  2. 5x 2 + 3x + 7 = 0;
  3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

  1. x 2 − 2x − 3 = 0;
  2. 15 − 2x − x 2 = 0;
  3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

  1. x 2 + 9x = 0;
  2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

  1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
  2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

  1. x 2 − 7x = 0;
  2. 5x 2 + 30 = 0;
  3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

I. Линейные уравнения

II. Квадратные уравнения

ax 2 + bx + c = 0, a ≠ 0, иначе уравнение становится линейным

Корни квадратного уравнения можно вычислять различными способами, например:

Мы хорошо умеем решать квадратные уравнения. Многие уравнения более высоких степеней можно привести к квадратным.

III. Уравнения, приводимые к квадратным.

замена переменной: а) биквадратное уравнение ax 2n + bx n + c = 0, a ≠ 0, n ≥ 2

2) симметрическое уравнение 3 степени – уравнение вида

3) симметрическое уравнение 4 степени – уравнение вида

ax 4 + bx 3 + cx 2 + bx + a = 0, a ≠ 0, коэффициенты a b c b a или

ax 4 + bx 3 + cx 2 – bx + a = 0, a ≠ 0, коэффициенты a b c (–b) a

Т. к. x = 0 не является корнем уравнения, то возможно деление обеих частей уравнения на x 2 , тогда получаем: .

Произведя замену решаем квадратное уравнение a (t 2 – 2) + bt + c = 0

Например, решим уравнение x 4 – 2x 3 – x 2 – 2x + 1 = 0, делим обе части на x 2 ,

, после замены получаем уравнение t 2 – 2t – 3 = 0

– уравнение не имеет корней.

4) Уравнение вида (x – a )(x – b )(x – c )(x – d ) = Ax 2 , коэффициенты ab = cd

Например, (x + 2 )(x +3 )(x + 8 )(x + 12 ) = 4x 2 . Перемножив 1–4 и 2–3 скобки, получим (x 2 + 14x + 24)(x 2 +11x + 24) = 4x 2 , разделим обе части уравнения на x 2 , получим:

Имеем (t + 14)(t + 11) = 4.

5) Однородное уравнение 2 степени – уравнение вида Р(х,у) = 0, где Р(х,у) – многочлен, каждое слагаемое которого имеет степень 2.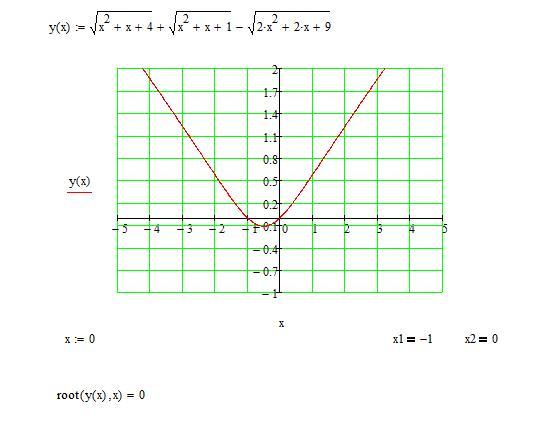

Ответ: -2; -0,5; 0

IV. Все приведенные уравнения узнаваемы и типичны, а как быть с уравнениями произвольного вида?

Пусть дан многочлен P n (x ) = a n x n + a n-1 x n-1 + …+a 1 x + a 0 , где a n ≠ 0

Рассмотрим метод понижения степени уравнения.

Известно, что, если коэффициенты a являются целыми числами и a n = 1 , то целые корни уравнения P n (x ) = 0 находятся среди делителей свободного члена a 0 . Например, x 4 + 2x 3 – 2x 2 – 6x + 5 = 0, делителями числа 5 являются числа 5; –5; 1; –1. Тогда P 4 (1) = 0, т.е. x = 1 является корнем уравнения. Понизим степень уравнения P 4 (x ) = 0 с помощью деления “уголком” многочлена на множитель х –1, получаем

P 4 (x ) = (x – 1)(x 3 + 3x 2 + x – 5).

Аналогично, P 3 (1) = 0, тогда P 4 (x ) = (x – 1)(x – 1)(x 2 + 4x +5), т. е. уравнение P 4 (x) = 0 имеет корни x 1 = x 2 = 1. Покажем более короткое решение этого уравнения (с помощью схемы Горнера).

12–2–65
1131–50
11450

значит, x 1 = 1 значит, x 2 = 1.

Итак, (x – 1) 2 (x 2 + 4x + 5) = 0

Что мы делали? Понижали степень уравнения.

V. Рассмотрим симметрические уравнения 3 и 5 степени.

а) ax 3 + bx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

б) ax 5 + bx 4 + cx 3 + cx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.

Например, покажем решение уравнения 2x 5 + 3x 4 – 5x 3 – 5x 2 + 3x + = 0

23–5–532
–121–6120
123–3–20
12520

x = –1

Получаем (x – 1) 2 (x + 1)(2x 2 + 5x + 2) = 0. Значит, корни уравнения: 1; 1; –1; –2; –0,5.

VI. Приведем список различных уравнений для решения в классе и дома.

Предлагаю читателю самому решить уравнения 1–7 и получить ответы…

для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.

Урок 6. решение уравнений графическим способом — Алгебра — 8 класс

Тема: Решение уравнений графическим способом

Содержание модуля (краткое изложение модуля):

Решим графическим способом уравнение:

x2 = −3x


Решить уравнение – значит найти такие значения x, при которых выполняется равенство x2 = −3x
Построим в одной системе координат два графика:
график функции y = x2 и график функции y = −3x.
Для каждого графика составим таблицы значений
y = x2 – на рисунке синий график



x0123−1−2−3
y0149149

y = −3x – на рисунке красный график



x0123−1−2−3
y0−3−6−9369

Заметим, что графики пересекаются в двух точках: точке с координатами (0 ; 0) и в точке с координатами (–3 ; 9). Это значит, что при x = 0 и при x = –3 функции y = x2 и y = −3x имеют одинаковые значения.
Таким образом получаем, что при x = 0 и при x = –3 выполняется равенство x2 = −3x.
Значит значения x = 0 и x = –3 являются корнями уравнения x2 = −3x.
Корни, найденные графическим способом – приближённые. Чтобы доказать точность значений корней, надо каждый из них подставить в решаемое уравнение и проверить: выполняется ли полученное равенство.
Подставим в уравнение x2 = −3x значение x = 0.

02 = −3•0


0 = 0 – верное равенство, значит x = 0 – точный корень уравнения x2 = −3x.
Подставим в уравнение x2 = −3x значение x = –3.

(−3)2 = −3•(−3)


9 = 9 – верное равенство, значит x = −3 – точный корень уравнения x2 = −3x.
Подведём итог.
Чтобы решить уравнение f1(x) = f2(x) графическим способом, необходимо:
1) Построить в одной системе координат графики функций y = f1(x) и y = f2(x). Абсциссы точек пересечения – это приближённые корни уравнения f1(x) = f2(x).
2) Необходимо подставить каждый приближённый корень в уравнение f1(x) = f2(x). Те корни, при которых получается верное равенство будут являться точными корнями уравнения f1(x) = f2(x).

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.


Как решать квадратные уравнения? Формулы и Примеры

Понятие квадратного уравнения

Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Есть три вида квадратных уравнений:

  • не имеют корней;
  • имеют один корень;
  • имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:

  • если D < 0, корней нет;
  • если D = 0, есть один корень;
  • если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие. Запишите ребенка на бесплатный вводный урок в онлайн-школе Skysmart и попробуйте сами!


Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.

Давайте-ка на примерах — вот у нас есть два уравнения:

  • x2 — 2x + 6 = 0
  • x2 — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.

  • 2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Запоминаем!

У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.

Пример 1. Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе.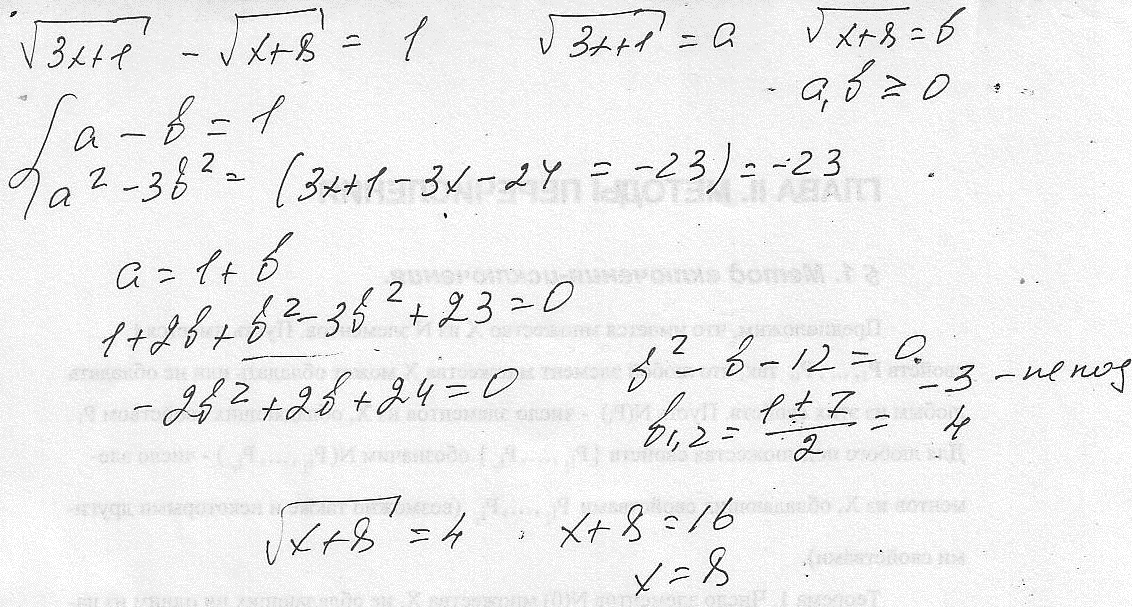 В таком случае квадратное уравнение принято назвать неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:
  • Если b = 0, то квадратное уравнение принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0.
  • Если c = 0, то квадратное уравнение выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2 + bx = 0.
  • Если b = 0 и c = 0, то квадратное уравнение выглядит так ax2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

  • ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
  • ax2 + c = 0, при b = 0;
  • ax2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax

2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.

Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x2 = 0.

Как решаем:

  1. Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
  2. По шагам решение выглядит так:

    −6x2 = 0

    x2 = 0

    x = √0

    x = 0

Ответ: 0.

Как решить уравнение ax

2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:

  • перенесем c в правую часть: ax2 = — c,
  • разделим обе части на a: x2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению ax2 + c = 0, которое:

  • не имеет корней при — c/а < 0;
  • имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8x2 + 5 = 0.

Как решать:

  1. Перенесем свободный член в правую часть:

    8x2 = — 5

  2. Разделим обе части на 8:

    x2 = — 5/8

  3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x2 + 5 = 0 не имеет корней.

Как решить уравнение ax

2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x2 + 0,125x = 0

Как решать:

  1. Вынести х за скобки

    х(0,5x + 0,125) = 0

  2. Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
  3. Решить линейное уравнение:

    0,5x = 0,125,
    х = 0,125/0,5

  4. Разделить:

    х = 0,25

  5. Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета

Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

 

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3.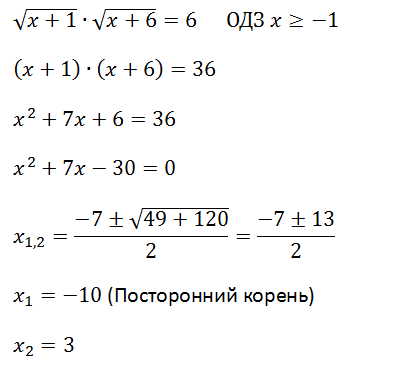 Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Пифагора: x2 − 6x + 8 = 0.

Как решаем:

  1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

  2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

    Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

    Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:

  3. Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>

     

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:

Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D.

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.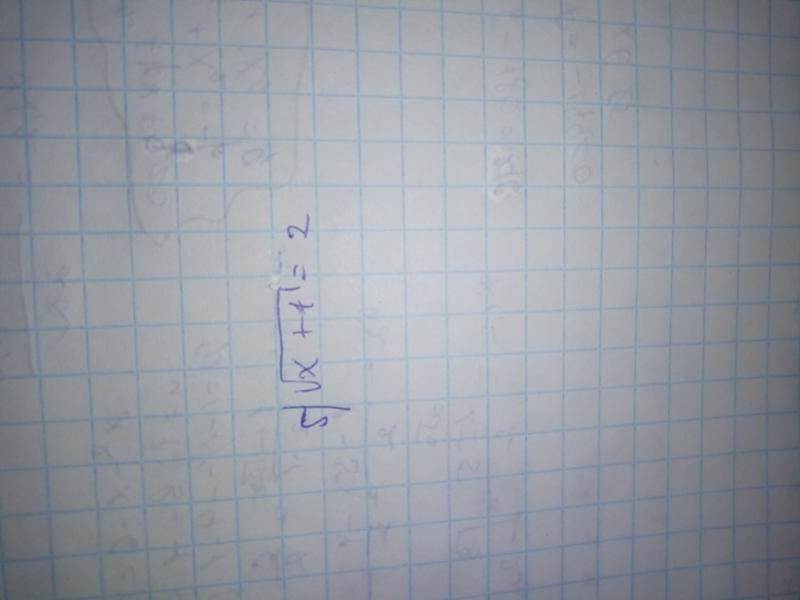

Повторим:

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

  • вычислить его значение дискриминанта по формуле D = b2−4ac;
  • если дискриминант отрицательный, зафиксировать, что действительных корней нет;
  • если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b2/2a;
  • если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.

Как решаем:

  1. Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
  2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
  3. Найдем корень

    х = — 28/2(-4)

    х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x2 = 0.

Как решаем:

  1. Произведем равносильные преобразования. Умножим обе части на −1

    54 — 6x2 = 0 | *(-1)

    6x2 — 54 = 0

  2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

    6x2 = 54

    х2 = 9

    х = ±√9

    х1 = 3, х2 = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x2— х = 0.

Как решаем:

  1. Преобразуем уравнение так, чтобы появились множители

    х(х — 1) = 0

    х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x2— 10 = 39.

Как решаем:

  1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

    x2— 10 = 39

    x2= 39 + 10

    x2= 49

    х = ±√49

    х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x2— 4x+94 = 0.

Как решаем:

  1. Найдем дискриминант по формуле

    D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112

  2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Приходите решать примеры на бытовых ситуациях, с красочными героями и в интерактивном формате.

Запишите вашего ребенка на бесплатный пробный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2— 4ac = 4n2 — 4ac = 4(n2— ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D1 = n2— ac.

Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

  • вычислить D1= n2— ac;
  • если D1< 0, значит действительных корней нет;
  • если D1= 0, значит можно вычислить единственный корень уравнения по формуле;
  • если же D1> 0, значит можно найти два действительных корня по формуле

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x2 — 4 x — 6 = 0, чем 1100x2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x2— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x2— 3x + 7 = 0 перейти к решению 2x2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

  • x₁ + x₂ = — b/a,
  • x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Уравнение. Корень уравнения | Математика

Уравнение — это равенство, которое справедливо не при любых значениях входящих в него букв, а только при некоторых. Так же можно сказать, что уравнение является равенством, содержащим неизвестные числа, обозначенные буквами.

Например, равенство  10 — x = 2  является уравнением, так как оно справедливо только при  x = 8.  Равенство  x2 = 49  — это уравнение, справедливое при двух значениях  x,  а именно, при

x = +7   и   x = -7,

так как

(+7)2 = 49   и   (-7)2 = 49.

Если вместо  x  подставить его значение, то уравнение превратится в тождество. Такие переменные, как  x,  которые только при определённых значениях обращают уравнение в тождество, называются неизвестными уравнения. Они обычно обозначаются последними буквами латинского алфавита  x,  y  и  z.

Любое уравнение имеет левую и правую части. Выражение, стоящее слева от знака  =,  называется левой частью уравнения, а стоящее справа — правой частью уравнения. Числа и алгебраические выражения, из которых состоит уравнение, называются членами уравнения:

Корни уравнения

Корень уравнения — это число, при подстановке которого в уравнение получается верное равенство. Уравнение может иметь всего один корень, может иметь несколько корней или не иметь корней вообще.

Например, корнем уравнения

10 — x = 2

является число  8,  а у уравнения

x2 = 49

два корня —  +7  и  -7.

Решить уравнение – значит, найти все его корни или доказать, что их нет.

Виды уравнений

Кроме числовых уравнений, подобных приведённым выше, где все известные величины обозначены числами, существуют ещё буквенные уравнения, в которые кроме букв, обозначающих неизвестные, входят ещё буквы, обозначающие известные (или предполагаемые известные) величины. {2} + 2 x – 8} geq 0$$
то
$$frac{x}{2} + 2 geq 0$$
или
$$-4 leq x$$
$$x $$x_{1} = 4$$
$$x_{2} = -4$$
проверяем:
$$x_{1} = 4$$
$$- sqrt{x_{1} – 2} – sqrt{x_{1} – 1} + sqrt{x_{1} + 4} = 0$$
=
$$- sqrt{-2 + 4} + – sqrt{-1 + 4} + sqrt{4 + 4} = 0$$
=

sqrt(2) – sqrt(3) = 0

– Нет
$$x_{2} = -4$$
$$- sqrt{x_{2} – 2} – sqrt{x_{2} – 1} + sqrt{x_{2} + 4} = 0$$
=
$$- sqrt{-4 – 2} + sqrt{-4 + 4} – sqrt{-4 – 1} = 0$$
=

-i*sqrt(5) – i*sqrt(6) = 0

– Нет
Тогда, окончательный ответ:
Данное ур-ние не имеет решений

x2 = 3.37850957522 – 2.26188364895e-13*i

Упрощение радикальных выражений

Мы знаем, что квадратный корень не является действительным числом, когда подкоренное выражение x отрицательно. Следовательно, мы заключаем, что область состоит из всех действительных чисел, больших или равных 0. Здесь мы выбираем 0 и некоторые положительные значения для x , вычисляем соответствующие y -значения и строим полученные упорядоченные пары.

После нанесения точек мы можем нарисовать график функции квадратного корня.

Пример 11: Для функции f (x) = x + 2 найдите f (−2), f (2) и f (6).

Решение: Замените x каждым из указанных значений.

Поскольку корень куба может быть как отрицательным, так и положительным, мы заключаем, что область состоит из всех действительных чисел. Для полноты выберите несколько положительных и отрицательных значений для x , а также 0, а затем вычислите соответствующие значения y .

Постройте точки и нарисуйте график функции кубического корня.

Пример 12: Для функции g (x) = x − 13 найдите g (−7), g (0) и g (55).

Решение: Замените x каждым из указанных значений.

Тематические упражнения

Часть A: Упрощение радикальных выражений

Упростить. ( Предположим, что все переменные представляют собой положительные числа. )

1. 36a2

2. 121b2

3. x2y2

4. 25x2y2z2

5. 180×3

6.150y3

7. 49a3b2

8. 4a4b3c

9. 45x5y3

10. 50x6y4

11. 64р2с6т5

12. 144р8с6т2

13. (x + 1) 2

14. (2x + 3) 2

15. 4 (3x − 1) 2

16. 9 (2x + 3) 2

17. 9x325y2

18. 4x59y4

19. m736n4

20.147м9н6

21. 2р2с525т4

22. 36р5с2т6

23. 27a33

24. 125b33

25. 250x4y33

26. 162a3b53

27.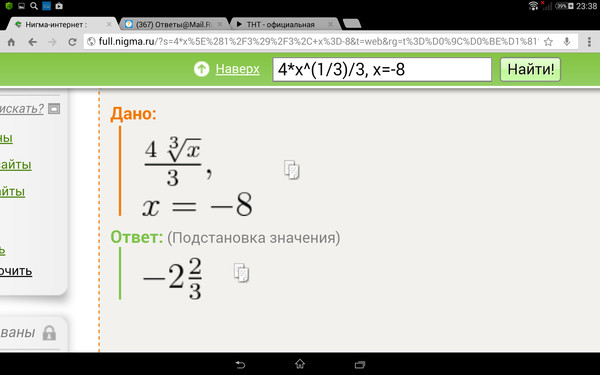 64x3y6z93

28. 216x12y33

29. 8x3y43

30. 27x5y33

31. a4b5c63

32. a7b5c33

33. 8x427y33

34.x5125y63

35. 360р5с12т133

36. 540р3с2т93

37. 81×44

38. x4y44

39. 16x4y84

40. 81x12y44

41. a4b5c64

42. 54a6c84

43. 128×64

44. 243y74

45. 32м10н55

46. 37м9н105

47. −34×2

48.79y2

49. −5x4x2y

50. −3y16x3y2

51. 12aba5b3

52. 6a2b9a7b2

53. 2x⋅8×63

54. −5×2⋅27×33

55. 2ab⋅ − 8a4b53

56. 5a2b⋅ − 27a3b33

Запишем следующее в виде радикального выражения с коэффициентом 1.

57. 52x

58. 23лет

59.2×3

60. 3y2

61. ab10a

62. 2ab2a

63. m2nmn

64. 2м2н33н

65,5 2×3

66. 3 5y3

67. 2x⋅33

68. 3 года 23

Предположим, что переменная может представлять любое действительное число, а затем упростить.

69. 4х2

70.25y2

71. 8y33

72. 125a33

73. 64×44

74. 81y44

75. 36a4

76. 100a8

77. 4a6

78. a10

79. 18a4b5

80. 48a5b3

81.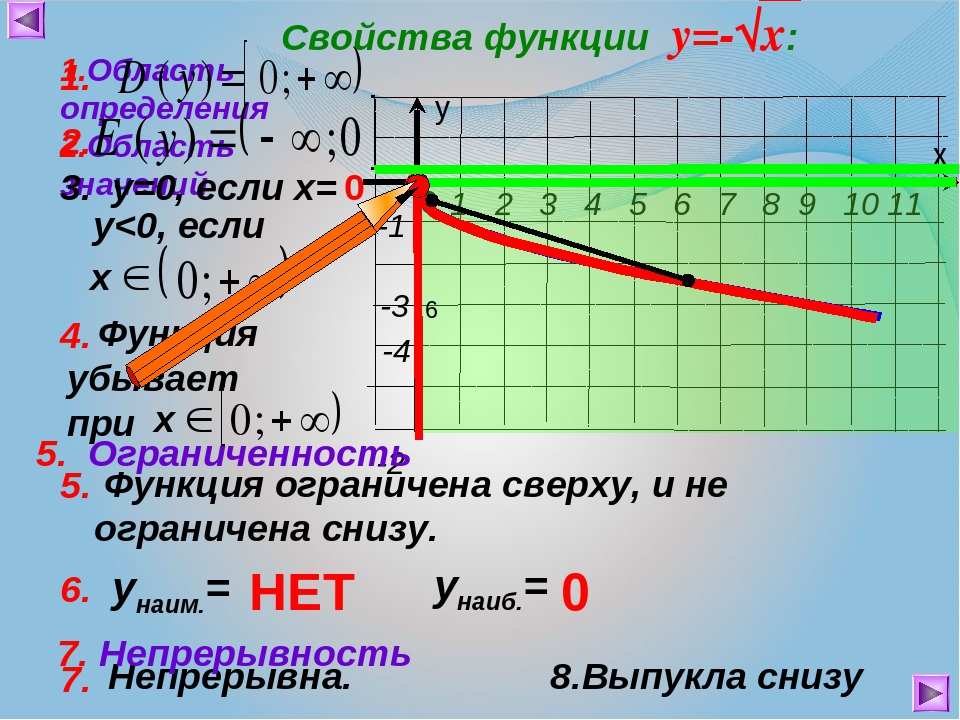 128x6y86

82. a6b7c86

Часть B: Формулы, включающие радикалы

Перехваты y для любого графика будут иметь форму (0, y ), где y — действительное число.Следовательно, чтобы найти y -перехватов, установите x = 0 и решите относительно y . Найдите интерцепторы y для следующего.

83. y = x + 4−1

84. у = х + 1−3

85. у = х − 13 + 2

86. у = х + 13−3

Используйте формулу расстояния, чтобы вычислить расстояние между заданными двумя точками.

87.(5, −7) и (3, −8)

88. (−9, 7) и (−8, 4)

89. (−3, −4) и (3, −6)

90. (−5, −2) и (1, −6)

91. (-1, 1) и (-4, 10)

92. (8, −3) и (2, −12)

Разложите на множители подкоренное выражение и затем упростите. ( Предположим, что все выражения положительны. )

93. x2−6x + 9

94. x2−10x + 25

95.4×2 + 12x + 9

96. 9×2 + 6x + 1

97. Скорость транспортного средства до того, как были задействованы тормоза, можно оценить по длине следов заноса, оставленных на дороге. На сухом асфальте скорость v в милях в час можно оценить по формуле v = 5d, где d представляет собой длину следов заноса в футах. Оцените скорость транспортного средства перед тем, как задействовать тормоза на сухом асфальте, если оставленные следы заноса составляют 36 футов.

98.Радиус сферы, r , можно рассчитать по формуле r = 6π2V32π, где V представляет собой объем сферы. Каков радиус сферы, если ее объем составляет 36π кубических сантиметров?

Период маятника T в секундах определяется формулой

Т = 2πL32

, где L — длина в футах. Рассчитайте период, учитывая следующие значения длины.Укажите точное значение и округлите приблизительное значение с точностью до десятых долей секунды.

99,8 футов

100. 32 фута

101. 1/2 фута

102. 1/8 фута

Время, t , в секундах, в течение которого объект находится в свободном падении, определяется формулой т = s4

, где с — расстояние в футах, на которое он упал.Рассчитайте время, за которое объект упадет, учитывая следующие расстояния. Укажите точное значение и округлите приблизительное значение с точностью до десятых долей секунды.

103. 48 футов

104. 80 футов

105,192 футов

106. 288 футов

Часть C: Радикальные функции

Для данной функции вычислите следующее.

107.f (x) = x − 1, найти f (1), f (2) и f (5)

108. f (x) = x + 5, найти f (−5), f (−1) и f (20)

109. f (x) = x + 3, найти f (0), f (1) и f (16)

110. f (x) = x − 5, найти f (0), f (1) и f (25)

111. g (x) = x3, найти g (−1), g (0) и g (1)

112. g (x) = x + 73, найти g (−15), g (−7) и g (20)

113. g (x) = x3−2, найти g (−1), g (0) и g (8)

114. g (x) = x − 13 + 2, найти g (0), g (2) и g (9)

Для каждой функции заполните таблицу.

115. f (x) = x + 1

116. f (x) = x − 2

117. f (x) = x3 + 1

118. f (x) = x + 23

Часть D: Обсуждение

119. Задайте для x такое значение, чтобы x2 ≠ x. Объясните, почему важно предполагать, что переменные представляют собой положительные числа.

120. Изучите и обсудите достижения Кристофа Рудольфа. За что ему приписывают?

121. Изучите и обсудите методы, используемые для вычисления квадратных корней, до того, как электронные калькуляторы начнут широко использоваться.

122. Что такое сурд и откуда взялось это слово?

Решайте уравнения с квадратными корнями — элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

  • Решите радикальные уравнения
  • Использование квадратного корня в приложениях

Прежде чем начать, пройдите тест на готовность.

  1. Упростить: ⓐ ⓑ.
    Если вы пропустили эту проблему, просмотрите (Рисунок) и (Рисунок).
  2. Решить:.
    Если вы пропустили эту проблему, просмотрите (рисунок).
  3. Решить:.
    Если вы пропустили эту проблему, просмотрите (рисунок).

Решите радикальные уравнения

В этом разделе мы будем решать уравнения, в которых переменная содержится в подкоренном выражении квадратного корня. Уравнения этого типа называются радикальными уравнениями.

Радикальное уравнение

Уравнение, в котором переменная находится в корневом выражении квадратного корня, называется радикальным уравнением.

Как обычно, при решении этих уравнений, то, что мы делаем с одной стороной уравнения, мы должны делать и с другой стороной. Поскольку возведение величины в квадрат и извлечение квадратного корня являются «противоположными» операциями, мы возведем обе стороны в квадрат, чтобы убрать знак корня и найти переменную внутри.

Но помните, что когда мы пишем, мы имеем в виду главный квадратный корень. Так всегда. Когда мы решаем радикальные уравнения, возводя обе части в квадрат, мы можем получить алгебраическое решение, которое будет отрицательным. Это алгебраическое решение не было бы решением исходного радикального уравнения; это постороннее решение . Мы видели посторонние решения и при решении рациональных уравнений.

Для уравнения:

ⓐ Есть решение? Ⓑ Есть решение?

Для уравнения:

ⓐ Есть решение? Ⓑ Есть решение?

ⓐ нет ⓑ

Для уравнения:

ⓐ Есть решение? Ⓑ Есть решение?

ⓐ нет ⓑ

Теперь посмотрим, как решить радикальное уравнение.Наша стратегия основана на соотношении извлечения квадратного корня и возведения в квадрат.

Как решать радикальные уравнения

Решить:.

Решить:.

Решить:.

Решите радикальное уравнение.

  1. Выделите радикал на одной стороне уравнения.
  2. Возведите обе части уравнения в квадрат.
  3. Решите новое уравнение.
  4. Проверьте ответ.

Решить:.

Решить:.

Решить:.

Решить:.

Решить:.

Решить:.

Когда мы используем знак корня, мы имеем в виду главный или положительный корень. Если в уравнении квадратный корень равен отрицательному числу, это уравнение не будет иметь решения.

Решить:.

Решение

Чтобы выделить радикал, вычтите 1 с обеих сторон.
Упростить.
Поскольку квадратный корень равен отрицательному числу, уравнение не имеет решения.

Решить:.

Решить:.

Если одна сторона уравнения является биномом, мы используем формулу биномиальных квадратов, когда возводим ее в квадрат.

Биномиальные квадраты

Не забывайте про средний семестр!

Решить:.

Решить:.

Решить:.

Решить:.

Решить:.

Решить:.

Когда перед радикалом стоит коэффициент, мы также должны возвести его в квадрат.

Решить:.

Решить:.

Решить:.

Решить:.

Решение

Решить:.

Решить:.

Иногда после возведения в квадрат обеих частей уравнения внутри радикала остается переменная. Когда это произойдет, мы повторяем шаги 1 и 2 нашей процедуры. Выделяем радикал и снова возводим обе части уравнения в квадрат.

Решить:.

Решение

Решить:.

Решить:.

Решить:.

Решение

Решить:.

Решить:.

Использование квадратного корня в приложениях

По мере прохождения курсов в колледже вы будете сталкиваться с формулами, включающими квадратные корни во многих дисциплинах. Мы уже использовали формулы для решения геометрических приложений.

Мы будем использовать нашу стратегию решения проблем для геометрических приложений с небольшими изменениями, чтобы дать нам план решения приложений с формулами из любой дисциплины.

Решайте приложения с помощью формул.

  1. Прочтите задачу и убедитесь, что все слова и идеи понятны. При необходимости нарисуйте фигуру и пометьте ее данной информацией.
  2. Определите то, что мы ищем.
  3. Назовите то, что мы ищем, выбрав переменную для его представления.
  4. Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
  5. Решите уравнение , используя хорошие методы алгебры.
  6. Отметьте ответ в задаче и убедитесь, что он имеет смысл.
  7. Ответьте на вопрос полным предложением.

Мы использовали формулу, чтобы найти площадь прямоугольника длиной L и шириной W . Квадрат — это прямоугольник, у которого длина и ширина равны. Если мы допустим s как длину стороны квадрата, площадь квадрата равна.

Формула дает нам площадь квадрата, если мы знаем длину стороны.Что, если мы хотим найти длину стороны для данной области? Затем нам нужно решить уравнение для s .

Мы можем использовать формулу, чтобы найти длину стороны квадрата для заданной площади.

Площадь квадрата

Мы покажем это в следующем примере.

Кэти хочет посадить квадратный газон перед своим двором. У нее достаточно дерна, чтобы покрыть площадь в 370 квадратных футов. Используйте формулу, чтобы найти длину каждой стороны ее газона.Округлите ответ до ближайшей десятой доли фута.

Серджио хочет сделать квадратную мозаику в качестве инкрустации для стола, который он строит. У него достаточно плитки, чтобы покрыть площадь в 2704 квадратных сантиметра. Используйте формулу, чтобы найти длину каждой стороны его мозаики. Округлите ответ до ближайшей десятой доли фута.

Еще одно применение квадратных корней связано с гравитацией.

Падающие предметы

На Земле, если объект падает с высоты футов, время в секундах, которое потребуется, чтобы достичь земли, определяется по формуле

Например, если объект падает с высоты 64 фута, мы можем вычислить время, необходимое для достижения земли, подставив его в формулу.

Извлеките квадратный корень из 64.
Упростим дробь.

Чтобы объект, упавший с высоты 64 фута, достиг земли, потребуется 2 секунды.

Кристи уронила свои солнцезащитные очки с моста на высоте 400 футов над рекой. Используйте формулу, чтобы определить, сколько секунд потребовалось солнцезащитным очкам, чтобы добраться до реки.

Вертолет сбросил спасательный пакет с высоты 1296 футов. Используйте формулу, чтобы определить, сколько секунд потребовалось, чтобы пакет достиг земли.

Мойщик окон сбросил ракель с платформы на высоте 196 футов над тротуаром. Используйте формулу, чтобы определить, сколько секунд прошло, чтобы ракель достиг тротуара.

Сотрудники полиции, расследующие автомобильные аварии, измеряют длину следов заноса на тротуаре.Затем они используют квадратные корни, чтобы определить скорость в милях в час, с которой машина ехала до того, как затормозила.

Следы заноса и скорость автомобиля

Если длина пятен скольжения составляет d футов, то скорость автомобиля до того, как были применены тормоза, с , можно определить по формуле

.

После автомобильной аварии следы заноса одной машины достигли 190 футов. Используйте формулу, чтобы найти скорость автомобиля до того, как были задействованы тормоза.Округлите ответ до ближайшей десятой.

Следователь ДТП измерил следы заноса автомобиля. Длина следов заноса составляла 76 футов. Используйте формулу, чтобы найти скорость автомобиля до того, как были задействованы тормоза. Округлите ответ до ближайшей десятой.

Следы заноса автомобиля, попавшего в аварию, были длиной 122 фута. Используйте формулу, чтобы найти скорость автомобиля до того, как были задействованы тормоза. Округлите ответ до ближайшей десятой.

Ключевые понятия

  • Для решения радикального уравнения:
    1. Выделите радикал на одной стороне уравнения.
    2. Возведите обе части уравнения в квадрат.
    3. Решите новое уравнение.
    4. Проверьте ответ. Некоторые полученные решения могут не работать в исходном уравнении.
  • Решение приложений с помощью формул
    1. Прочтите задачу и убедитесь, что все слова и идеи понятны.При необходимости нарисуйте фигуру и пометьте ее данной информацией.
    2. Определите то, что мы ищем.
    3. Назовите то, что мы ищем, выбрав переменную для его представления.
    4. Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
    5. Решите уравнение , используя хорошие методы алгебры.
    6. Отметьте ответ в задаче и убедитесь, что он имеет смысл.
    7. Ответьте на вопрос полным предложением.
  • Площадь квадрата
  • Падающие предметы
    • На Земле, если объект падает с высоты футов, время в секундах, которое потребуется, чтобы достичь земли, определяется по формуле.
  • Следы заноса и скорость автомобиля
    • Если длина следов заноса составляет d футов, то скорость s автомобиля до того, как были применены тормоза, может быть определена с помощью формулы.
Письменные упражнения

Объясните, почему уравнение вида не имеет решения.

  1. ⓐ Решите уравнение.
  2. ⓑ Объясните, почему одно из найденных «решений» на самом деле не было решением уравнения.
Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?

Глоссарий

радикальное уравнение
Уравнение, в котором переменная находится в подкоренном выражении квадратного корня, называется радикальным уравнением

Радикальное выражение Пошаговое решение математических задач

10.n со следующими условиями:

1. Когда n — четное число и a> 0, root (n, a)> 0, называется главным корнем.

Когда n — четное число и a <0, корень (n, a) не является действительным числом.

2. Когда n — нечетное число и a> 0, корень (n, a)> 0.

Когда n — нечетное число и a <0, root (n, a) <0

Число n в корне (n, a) (всегда натуральное число больше 1) называется индексом или порядком радикала, а a называется подкоренным выражением.4).

Радикальное выражение называется стандартным, если выполняются следующие условия:

1. Подкоренное выражение положительное.

2. Индекс корня должен быть как можно меньше.

3. Показатель степени каждого множителя подкоренного выражения является натуральным числом меньше радикального индекса.

4. В подкоренном выражении нет дробей.

5. В знаменателе дроби нет радикалов.

Под упрощением радикального выражения мы подразумеваем приведение радикального выражения в стандартную форму. {2} + b x + c = 0 \)

как уравнение вида

Этот процесс называется , завершение квадрата 4 .{2} = \ color {Cerulean} {1} \)

Чтобы завершить квадрат, добавьте \ (1 \) к обеим сторонам, завершите квадрат и затем решите, извлекая корни.

На этом этапе разделите «плюс или минус» на два уравнения и решите каждое отдельно.

Ответ :

Решения: \ (- 8 \) и \ (6 \).

Примечание

В предыдущем примере решения — целые числа. Если это так, то исходное уравнение будет учитываться.

Если уравнение множится, мы можем решить его путем факторизации.{2} — 10 х + 26 = 0 \).

Решение

Начните с вычитания \ (26 \) из обеих частей уравнения.

Здесь \ (b = -10 \), и мы определяем значение, завершающее квадрат, следующим образом:

Чтобы получить квадрат, добавьте \ (25 \) к обеим сторонам уравнения. {2} + 18 \), где \ (t \) представляет время через секунды после падения объекта.{2} + 50 \), где \ (t \) представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю? (Округлите до сотых долей секунды.)

  • Какова высота лестницы длиной \ (22 \) футов, если ее основание находится в \ (6 \) футах от здания, на которое она опирается? Округлите до ближайшей десятой доли фута.
  • Высота треугольника равна \ (\ frac {1} {2} \) длине его основания. Если площадь треугольника составляет \ (72 \) квадратных метров, найдите точную длину основания треугольника.
    • Ответ

    1. \ (\ pm 9 \)

    3. \ (\ pm \ frac {1} {3} \)

    5. \ (\ pm 2 \ sqrt {3} \)

    7. \ (\ pm \ frac {3} {4} \)

    9. \ (\ pm \ frac {\ sqrt {2}} {2} \)

    11. \ (\ pm 2 \ sqrt {10} \)

    13. \ (\ pm i \)

    15. \ (\ pm \ frac {\ sqrt {5}} {5} \)

    17. \ (\ pm \ frac {\ sqrt {2}} {4} i \)

    19.\ (\ pm 2 i \)

    21. \ (\ pm \ frac {2} {3} \)

    23. \ (\ pm 2 \ sqrt {2} \)

    25. \ (\ pm 2 i \ sqrt {2} \)

    27. \ (\ pm \ frac {\ sqrt {10}} {5} \)

    29. \ (- 9, -5 \)

    31. \ (5 \ pm 2 \ sqrt {5} \)

    33. \ (- \ frac {2} {3} \ pm \ frac {\ sqrt {6}} {3} i \)

    35. \ (\ frac {- 2 \ pm 3 \ sqrt {3}} {6} \)

    37. \ (\ frac {1} {3} \ pm \ frac {\ sqrt {6}} {6} i \)

    39.{2} = 3 (3 т + 1) \)

  • \ ((3 t + 2) (t-4) — (t-8) = 1-10 t \)
    • Ответ

    1. \ (- 15 \ pm \ sqrt {10} \)

    3. 1 \ (\ pm 2 \ sqrt {2} \)

    5. 1 \ (\ pm i \ sqrt {3} \)

    7. \ (- 15,5 \)

    9. \ (- \ frac {1} {3}, 1 \)

    11. \ (\ frac {-1 \ pm \ sqrt {5}} {2} \)

    13. \ (\ frac {-3 \ pm \ sqrt {17}} {2} \)

    15. \ (- \ frac {3} {2} \ pm \ frac {\ sqrt {11}} {2} i \)

    17.\ (\ frac {7 \ pm 3 \ sqrt {3}} {2} \)

    19. \ (\ frac {1 \ pm \ sqrt {17}} {4} \)

    21. \ (\ frac {2 \ pm \ sqrt {5}} {2} \)

    23. \ (\ frac {-3 \ pm \ sqrt {6}} {3} \)

    25. \ (\ frac {-1 \ pm \ sqrt {10}} {3} \)

    27. \ (\ frac {3 \ pm 2 \ sqrt {6}} {2} \)

    29. 1 \ (\ pm 2 i \)

    31. \ (\ frac {1 \ pm \ sqrt {17}} {4} \)

    33. \ (\ frac {-1 \ pm \ sqrt {7}} {3} \)

    35. 2 \ (\ pm 2 \ sqrt {5} \)

    37.{2} -6 (6 x + 1) = 0 \)

    Ответ

    1. \ (0.19,1.31 \)

    3. \ (- 0,45,1,12 \)

    5. \ (0,33,0,67 \)

    Упражнение \ (\ PageIndex {11} \)

    1. Создайте собственное уравнение, которое можно решить, извлекая корни. Поделитесь им и решением на доске обсуждений.
    2. Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения.{2} = q \).

      Квадратный корень — Калькулятор капитана

      Калькулятор квадратного корня

      Обратите внимание: для работы этого калькулятора требуется JavaScript.

      Определение — Что такое квадратный корень?

      Квадратный корень числа — это число, которое при умножении само на себя дает исходное число.

      Например, квадратный корень из 9 равен 3, так как 3 x 3 = 9.

      Квадратный корень из 25 равен 5, так как 5 x 5 = 25.

      Квадратный корень из 49 равен 7, так как 7 x 7 = 49.

      Квадратный корень может быть положительным или отрицательным (-3 x -3 равно 9, -5 x -5 = 25 и -7 x -7 = 49). Когда люди говорят «квадратный корень», они обычно имеют в виду положительный квадратный корень.

      Противоположность квадратному корню — это вычисление в квадрате (степень двойки).

      Для чего используется квадратный корень?

      С практической точки зрения, квадратный корень в геометрии можно использовать для определения длины стороны квадрата, когда площадь известна.

      Формула

      — Как вычислить квадратный корень из числа

      Не существует быстрой математической формулы для вычисления квадратного корня.Большинство калькуляторов используют метод очень быстрых проб и ошибок.

      Метод 1 — Метод проб и ошибок

      Метод проб и ошибок подходит для полных квадратов. Это может занять очень много времени для неидеальных квадратов, поскольку в них много десятичных знаков.

      Чтобы найти квадратный корень методом проб и ошибок:

      1. Угадайте число, которое, по вашему мнению, может быть квадратным корнем.
      2. Умножьте это число на само себя
      3. Если результат слишком низкий, попробуйте другое большее число. Если результат слишком высокий, попробуйте другое меньшее число.
      4. Продолжайте, пока не найдете квадратный корень.

      Пример. Методом проб и ошибок найти квадратный корень из 64:

      1. Попробуйте число — 5: 5 умножить на 5 = 25 (слишком мало)
      2. Попробуйте число, которое больше 6 — 10 — 10 умножить на 10 = 100 (слишком большое
      3. Попробуйте число от 6 до 10 — 8 — 8 умножить на 8 = 64 (ответ)

      Метод 2 — Быстро найти корни из точных квадратных чисел

      Этот метод позволяет быстрее найти корень из полного квадратного числа.Однако, если число не является точным корнем, этот метод не сработает.

      Метод 3. Быстрый поиск квадратного корня из любого числа

      Этот метод позволяет найти квадратный корень из любого числа (включая неполные квадраты). Это занимает немного больше времени, чем метод 2.

      Как ввести квадратный корень?

      • Вы можете скопировать символ квадратного корня -> √ <- с этой страницы и вставить его в свой документ.
      • На компьютере с Windows откройте карту символов, найдите символ квадратного корня и скопируйте его.Вставьте его там, где хотите символ.
      • На компьютере Mac нажмите option + v для символа √.

      Таблица чисел квадратного корня — полные квадраты

      • √1 = 1, как 1 x 1 = 1
      • √4 = 2, как 2 x 2 = 4
      • √9 = 3, как 3 x 3 = 9
      • √16 = 4, как 4 x 4 = 16
      • √25 = 5, поскольку 5 x 5 = 25
      • √36 = 6, поскольку 6 x 6 = 36
      • √49 = 7, поскольку 7 x 7 = 49
      • √64 = 8, как 8 x 8 = 64
      • √81 = 9, поскольку 9 x 9 = 81
      • √100 = 10, поскольку 10 x 10 = 100
      • √121 = 11, поскольку 11 x 11 = 121
      • √144 = 12, как 12 x 12 = 144
      • √225 = 15, как 15 x 15 = 225
      • √289 = 17, как 17 x 17 = 289
      • √400 = 20, как 20 x 20 = 400
      • √625 = 25, как 25 x 25 = 625
      • √900 = 30, как 30 x 30 = 900
      • √1089 = 33, так как 33 x 33 = 1,089
      • √2025 = 45, так как 45 x 45 = 2,025
      • √ 2500 = 50, поскольку 50 x 50 = 2,500
      • √3600 = 60, поскольку 60 x 60 = 3,600
      • √5625 = 75, поскольку 75 x 75 = 5,625
      • √10000 = 100, поскольку 100 x 100 = 10,000

      Таблица чисел квадратного корня — несовершенные квадраты

      Обратите внимание: для работы этой таблицы требуется JavaScript.

      Источники и другие ресурсы

      Решение проблем пропорций

      Главная | Меню ставок / пропорций | Меню алгебры

      Шаг 1: Составьте общее уравнение.
      Шаг 2: Найдите константу соразмерность.
      Шаг 3: Подставляя константу в уравнение, решите относительно неизвестная переменная.

      Давайте решим несколько задач, чтобы увидеть, как это работает, не так ли?

      Пример 1: Y прямо пропорционально x. Когда x = 5, y = 8. Чему равно y, когда x = 9?

      Сначала мы составим наше общее уравнение.Потому что y прямо пропорционально x, имеем:

      y = cx

      , где c — константа пропорциональности. Другими словами, когда x идет вверх, y идет вверх, а когда x опускается, y опускается.

      Следующее, что мы делаем, это подставляем наши значения x и y в уравнение поэтому мы можем решить для c:

      8 = (c) (5)

      Решая для c, мы получаем c = 8/5 = 1.6, и мы вставляем это в наш уравнение:

      y = 1.6x

      Теперь мы можем подставить x = 9 в уравнение чтобы узнать, что равно y:

      y = (1,6) (9)

      y = 14,4

      Итак, наш ответ: 14,4

      Пример 2: Y прямо пропорционально квадрату x. Когда x = 2, y = 32. Чему равен y, когда x = 5?

      На этот раз наше общее уравнение немного сложнее, потому что x возведен в квадрат:

      y = cx 2

      Как и раньше, мы решаем нашу константу:

      32 = (c) (2 2 )

      32 = (c) (4)

      Мы получаем c = 8:

      y = 8x 2

      Решая для y при x = 5, получаем y = (8) (5 2 ) = (8) (25) = 200

      Пример 3: Y обратно пропорционально x.Когда x = 2, y = 8. Чему равно y, когда x = 24?

      На этот раз, поскольку y обратно пропорционально x, наша общая уравнение другое:

      xy = c

      , поэтому, когда x увеличивается, y уменьшается, и наоборот. Но, кроме этого, мы решать подобные проблемы так же, как прямо пропорционально проблемы. Решая для константы, мы получаем:

      (2) (8) = c

      Итак, c = 16, и наше уравнение теперь:

      xy = 16

      Решение для y, когда x = 24 получаем y = 16/24 = 2/3

      Пример 4: Y обратно пропорционально квадратному корню из x.Когда x = 36, y = 2. Чему равен y, когда x = 64?

      Как и раньше, мы составляем наше уравнение:

      Поскольку квадратный корень из 36 равен 6, легко решить для c:

      (6) (2) = c

      Мы получаем c = 12 и теперь наше уравнение:

      Решение для y, когда x = 64 получаем 8y = 12 или y = 12/8 = 1,5, потому что квадратный корень из 64 это 8. 2 + bx + c $$.2 + 5x +6 $$. Как видите, сумма корней действительно равна $$ \ color {Red} {\ frac {-b} {a}} $$, а произведение корней составляет $$ \ color {Red} {\ frac { c} {a}} $$.

      Пример 2

      Пример ниже показывает, как эта формула применяется к квадратному уравнению x 2 — 2x — 8. И снова обе формулы — для суммы и произведения сводятся к -b / a и c / a соответственно.

      Практика Проблемы
      Задача 1

      Не решая, найти сумму и произведение корней уравнения: 2x 2 -3x -2 = 0

      Покажи ответ

      Определите коэффициенты:
      a = 2
      b = -3
      c = -2

      Теперь подставим эти значения в формулы

      Сумма корней

      $$ \ color {Красный} {\ frac {-b} {a}} = \ frac {- (- 3)} {2} = \ frac {3} {2} $$

      Продукт корней

      $$ \ color {Красный} {\ frac {c} {a}} = \ frac {-2} {2} = -1 $$

      Задача 2

      Не решая, найдите сумму и произведение корней следующего уравнения: -9x 2 -8x = 15

      Покажи ответ

      Сначала вычтите 15 с обеих сторон, чтобы уравнение имело вид 0 = ax 2 + bx + c переписать уравнение: -9x 2 -8x — 15 = 0

      Определите коэффициенты:
      a = -9
      b = -8
      c = -15

      Теперь подставьте эти значения в формулы

      Сумма корней

      $$ \ color {Красный} {\ frac {-b} {a}} = \ frac {- (- 8)} {- 9} = \ frac {-8} {9} $$

      Продукт корней

      $$ \ color {Красный} {\ frac {c} {a}} = \ frac {-15} {9} = \ frac {-5} {3} $$

      Задача 3

      Запишите квадратное уравнение с учетом следующих корней: 4 и 2

      Покажи ответ

      Есть несколько способов решить эту проблему. Вы можете создать два бинома (x-4) и (x-2) и умножить их.

      Однако, поскольку эта страница посвящена использованию наших формул, давайте воспользуемся ими, чтобы ответить на это уравнение.

      Сумма корней = 4 + 2 = 6
      Произведение корней = 4 * 2 = 8

      Мы можем использовать наши формулы, чтобы составить следующие два уравнения

      Сумма корней

      $$ \ frac {-b} {a} = 6 = \ frac {6} {1} $$

      Продукт корней

      $$ \ frac {c} {a} = 8 = \ frac {8} {1} $$

      Теперь мы знаем значения всех трех коэффициентов:
      a = 1
      b = -6
      c = 8

      Итак, наше окончательное квадратное уравнение y = 1x 2 — 6x + 8

      Вы можете дважды проверить свою работу, помешав биномам (x -4) (x-2) получить то же уравнение

      Задача 4

      Если один корень приведенного ниже уравнения равен 3, каков другой корень? x 2 -5x + k = 0

      Покажи ответ

      Запишите то, что вы знаете:
      a = 1
      b = -5
      r 1 = 3

      Теперь подставьте эти значения в формулу суммы корней

      Сумма корней

      r 1 + r 2 = -b / a 3 + г 2 = — (- 5) / 1 3 + г 2 = 5 г 2 = 2

      Следовательно, отсутствует корень 2.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *