| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных. Таблица интегралов. Таблица первообразных. Найти производную. Найти интеграл. Диффуры.
|
dpva.ru
Таблица интегралов (неопределенных и т.д.)
Интегрирование — это одна из основных операций в матанализе. Таблицы известных первообразных могут быть полезны, но сейчас они, после появления систем компьютерной алгебры, теряют свою значимость. Ниже находится список больше всего встречающихся первообразных.
Таблица основных интегралов
Другой, компактный вариант

Таблица интегралов от тригонометрических функций
От рациональных функций

От иррациональных функций

https://uchim.org/matematika/tablica-integralov — uchim.org
Интегралы от трансцендентных функций

«C» – произвольная константа интегрирования, которая определяется, если известно значение интеграла в какой-либо точке. Каждая функция имеет бесконечное число первообразных.
У большинства школьников и студентов бывают проблемы с вычислением интегралов. На этой странице собраны таблицы интегралов от тригонометрических, рациональных, иррациональных и трансцендентных функций, которые помогут в решении. Еще вам поможет таблица производных.
Видео — как находить интегралы
Если вам не совсем понятна данная тема, посмотрите видео, в котором всё подробно объясняется.Всё для учебы » Математика в школе » Таблица интегралов (неопределенных и т.д.)
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-integralov
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
uchim.org
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных. Таблица интегралов. Таблица первообразных. Найти производную. Найти интеграл. Диффуры. / / Таблица первообразных. Таблица интегралов. Таблица неопределенных интегралов. Формулы интегралов. Формулы первообразных.
| |||||||||
dpva.ru
39 Таблица основных интегралов

40 Метод непосредственного интегрирования
Определение
Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием
.Таким образом, алгоритм действий следующий:
тождественное преобразование подынтегральной функции;
применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;
использование таблицы интегралов.
41Интегрирование по частям и подставновкой
Интегрирование по частям. Если функции u ( x ) и v ( x ) имеют непрерывные первые производные и существует интеграл v ( x ) du ( x ), тосуществует и интеграл u ( x ) dv ( x ) и имеет место равенство:
u ( x ) dv ( x ) = u ( x ) • v ( x ) – v ( x ) du ( x )
или в более короткой форме:
u dv = u v – v du .
Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями (проверьте!).
Интегрирование подстановкой (замена переменной). Если функция f ( z ) определена и имеет первообразную при z Z , а функция z = g ( x )имеет непрерывную производную при x X и её область значений g ( X ) Z , то функция F ( x ) = f [ g ( x )] × g’ ( x ) имеет первообразную на Х и
F ( x ) dx = f [ g ( x )] • g’ ( x ) dx = f ( z ) dz .
42 Определен.Интеграл и его определение
Определённым интегралом от функции на отрезкеназывается предел интегральных сумм при стремлении ранга разбиения к нулю, если он существует независимо от разбиенияи выбора точек, то есть
Если существует указанный предел, то функция называется интегрируемой напо Риману.
Основные свойства определенного интеграла
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
43 Формула Ньютона — Лейбница
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.
Если непрерывна на отрезкеи— её любая первообразная на этом отрезке, то имеет место равенство |
44 Вычисление площадей с помощью интеграла.
1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :
2.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и прямыми х=а, х= b :
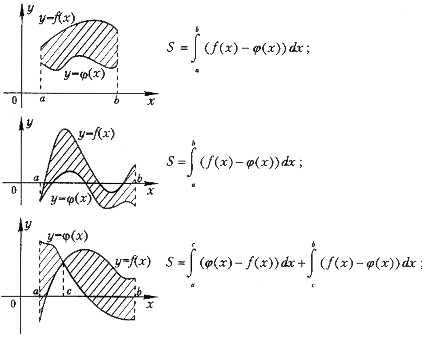
3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и :
4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и осью Ох:
studfiles.net
ТАБЛИЦА ИНТЕГРАЛОВ
ТАБЛИЦА ИНТЕГРАЛОВСписок интегралов элементарных функций
Правила интегрирования функций:
Интегралы элементарных функций:
Рациональные функции:
(первообразная от нуля есть константа, в любых пределах интегрирования интеграл от нуля равен нулю)
(«высокий логарифм»)
Логарифмы:
Экспоненциальные функции:
Иррациональные функции:
(«длинный логарифм»)
Тригонометрические функции:
Гиперболические функции:
также
также
для
для
для
для
для
для
для
для
Список интегралов от иррациональных функций
Интегралы с корнем из a2+x2:
Везде ниже: .
Интегралы с корнем из x2-a2:
Везде ниже: .
Принято , для, смотрите следующий раздел.
Заметим, что , гдепринимает только положительные значения.
где
Интегралы с корнем из a2-x2:
Везде ниже:
Интегралы с корнем из общего квадратного трёхчлена:
Здесь обозначено:
Интегралы с корнем из линейной функции:
Список интегралов от экспоненциальных функций
Неопределённые интегралы:
для
для
где erf(…) — функция ошибок
Определённые интегралы:
для , что естьлогарифмическое среднее
(интеграл Гаусса)
(!! — двойной факториал)
(модифицированнаяфункция Бесселяпервого рода)
(Дзета-функция Римана)
Список интегралов от логарифмических функций
для
для
для
для
для
для
для
,
где Ei(x) — интегральная экспонента
для
Список интегралов от тригонометрических функций
Интегралы, содержащие только синус:
Интегралы, содержащие только косинус:
Интегралы, содержащие только тангенс:
Интегралы, содержащие только секанс:
Интегралы, содержащие только косеканс:
Интегралы, содержащие только котангенс:
Интегралы, содержащие только синус и косинус:
Интегралы, содержащие только синус и тангенс:
Интегралы, содержащие только косинус и тангенс:
Интегралы, содержащие только синус и котангенс:
Интегралы, содержащие только косинус и котангенс:
Интегралы, содержащие только тангенс и котангенс:
Список интегралов от обратных тригонометрических функций
Арксинус:
Арккосинус:
Арктангенс:
studfiles.net
Таблица интегралов, правила интегрирования, интегрирование путем подведения под знак дифференциала
Основные правила интегрирования. Непосредственное интегрирование
1) Если , то
где – произвольная постоянная
2)
где – постоянная величина
3)
Пример 1.
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉
Интегрирование путем подведения под знак дифференциала
Если
Это правило значительно расширяет таблицу простейших интегралов. А именно, в силу этого правила таблица интегралов оказывается справедливой, независимо от того, является переменная интегрирования независимой переменной или дифференцируемой функцией.
Прежде чем использовать тот или иной табличный интеграл, приводим данный интеграл к виду:
Пример 2.
К оглавлению решебника по высшей математике 〉
100task.ru
|
Интеграл степенной функции. |
Интеграл степенной функции. |
|
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
|
Интеграл экспоненциальной функции. |
Интеграл экспоненты, где a-постоянное число. |
|
Интеграл сложной экспоненциальной функции. |
Интеграл экспоненциальной функции. |
|
Интеграл, равняющийся натуральному логарифму. |
Интеграл : «Длинный логарифм». |
|
|
Интеграл : «Длинный логарифм». |
|
Интеграл : «Высокий логарифм». |
Интеграл, где х в числителе заводится под знак дифференциала |
|
Интеграл : «Высокий логарифм». |
|
|
Интеграл косинуса. |
Интеграл синуса. |
|
Интеграл, равный тангенсу. |
Интеграл, равный котангенсу. |
|
Интеграл, равный как арксинусу, так и арккосинусу |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
Интеграл, равный как арксинусу, так и арккосинусу. |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
|
|
|
Интеграл равный косекансу. |
Интеграл, равный секансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арккосекансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арксекансу. |
|
Интеграл, равный гиперболическому синусу. |
Интеграл, равный гиперболическому косинусу. |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому синусу, где sinhx |
Интеграл, равный гиперболическому косинусу, где sinhx |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому секансу. |
Интеграл, равный гиперболическому косекансу. |
tehtab.ru



