2Sin2X sinx cosx 1: 2sin2x+cosx+sinx-1=0 ПОМОГИТЕ ПОЖАЛУЙСТА — Школьные Знания.com

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень 2)/2)
100	Преобразовать из градусов в радианы	88 град.

alimov-10-gdz (Алгебра — 10-11 класс

1) cos2x + cos22x = cos23x + cos24x;(cos2x – cos23x) + (cos22x – cos24x) = 0;(cosx – cos3x)(cosx + cos3x) + (cos2x – cos4x)(cos2x + cos4x) = 0;2sinxsin2x ⋅ 2cosxcos2x + 2sinxsin3x ⋅ 2cosxcos3x = 0;sin2xsin4x + sin2xsin6x = 0;sin2x(sin4x + sin6x) = 0;2sin2x ⋅ sin5xcosx = 0;sin2x = 0 или sin5x = 0 или cosx = 0;πππ2x = πk или 5x = πk или x = + πk , k ∈ Z ; x = k или x = k или225πππx = + πk (входит в первую серию корней), т. е.

x = k или x = k , k ∈ Z ;2252) sin 6 x + cos6 x = 1 ; (sin 2 x + cos 2 x)3 − 3sin 4 x cos 2 x − 3cos 4 x sin 2 x = 1 ;43 231;sin2x=±1;− sin 2 x = −1 − 3sin x cos x(sin x + cos x) =444ππ π2 x = + πk , x = + k , k ∈ Z .24 2cos2x cosxcos 2×12641. 1)+= 1;= a ; a + = 1 ; а –а+1=0; D<0 — решений нет.cosx cos2xcos xa2) sin x + 1 = sin 2 x + 1 ;sinx = a;sin xsin 2 x11a4 – a3 – a + 1 = 0;a3(a – 1) – (a – 1) = 0;a + = a2 + 2 ;aaπ(a3 – 1)(a – 1) = 0; a = 1;sinx = 1;x = + 2πk , k ∈ Z .242222642. 1) sinxsin5x = 1; т.к. |sinx| ≤ 1 и |sin5x| ≤ 1, то |sinxsin5x| ≤ 1, а;sinxsin5x = 1, только если sinx = sin5x = 1 или sinx = sin5x = – 1, т.е.176www.5balls.ruπsin x = 1  х = 2 + 2πk, k ∈ Z;;sin 5x = 1 5x = π + 2πn, n ∈ Z2 x = π + 2πk, k ∈ Zπ2; x = + 2πk , k ∈ Z или22ππ x = + n, n ∈ Z105ππsin x = −1  x = − 2 + 2πk, k ∈ Z  x = − 2 + 2πk, k ∈ Z;;;sin 5x = −1 5x = π + 2πn, n ∈ Z  x = − π + 2π n, n ∈ Z2105ππx = − + 2πk , k ∈ Z , т.е.

x = + πk , k ∈ Z ;222) sinxcos4x = – 1;возможно, лишь при sinx = 1, а cosx = – 1 или при sinx = – 1, а cos4x = 1, т. е. x = π + 2πk,k ∈ Z x = π + 2 πk, k ∈ Z2;— решений нет, или2 4x = π + 2 πn, n ∈ Z  x = π + π n,n ∈ Z4 2 x = − π + 2πk, k ∈ Zπsin x = −1  x = − + 2πk, k ∈ Z 2; ; ; x = − π + 2πk , k ∈ Z .2=cos4x12π 4x = 2πn, n ∈ Z x = n, n ∈ Z2sin x = 1;cos 4x = −15 cos x − cos 2 x = −2 sin x ;643. 1)5 cos x − cos 2 x ≥ 0:sin x ≤ 025 cos x − cos 2 x = 4 sin x5 cos x − cos 2 x ≥ 0;sin x ≤ 0225 cos x − 2 cos x − 1 − 4 + 4 cos x = 05 cos x − cos 2 x ≥ 0; решаем последнее уравнение в системе, полагаяsin x ≤ 022 cos x + 5 cos x − 5 = 0cosx = a;cos x =2a2 + 5a – 5 = 0;a1 =−5 + 65−5 − 65, т.е.,a 2 =44π−5 + 65−5 − 65  x = − 2 + 2πk, k ∈ Z; ;, или cos x −44 x = π n, n ∈ Z2Подставляем в первое неравенство системы:5cosx – 2cos2x – 1 ≥ 0 вместо cosx число65 − 5;4 65 − 5  − 2 ⋅ 90 − 10 65 − 1 = − 74 + 10 65 ≥ 0 , т.е. корни5⋅4164177www.5balls.ru5 cos x − cos 2 x ≥ 0; удовлетворяют первому неравенству системы,sin x ≤ 022 cos x + 5 cos x − 5 = 0из второго неравенстве следует, что х ∈ III, IV четверти, значит,x = − arccos2)65 − 5+ 2πk , k ∈ Z ;4cos x + cos 3x = − 2 cos x ;2 cos x cos 2 x = − 2 cos x ;2cos x(2cos x − 1) = − cos x ;a(2a 2 − 1) = −a ;cosx = a;a ≤ 02, т. е.

а=0 или a = − 1 ;a(2a − 1) ≥ 021a = 0,a = − ,a = 12π2π+ 2πk , k ∈ Z .x = + πk или x = ±23a ≤ 0a ≤ 022;;a(2a − 1) ≥ 0a(2a − 1) ≥ 022 2a(2a − 1) = aa(2a − a − 1) = 0cosx = 0 или cos x = − 1 ;2644. 1) 4|cosx| + 3 = 4sin2x;4|cosx| + 3 = 4 – 4cos2x;cosx = a;4cos2x + 4|cosx| – 1 = 0;4a2 + 4|a| – 1 = 0;a ≥ 0−4+4 2;,−4 − 4 2−4 + 4 2 a =8,a 2 =a1 =88a < 0a < 0т.е. a = − 1 + 2 или ,4−4 24+ 4 2224a 2 − 4a − 1 = 0 a =,a =88a ≥ 0; 24a + 4a − 1 = 0т.е.

a = 1 − 2 т.е. a = ± 1 − 2  ,2222 т.е. cos x = ± 1 − 2  , т.е. x = ± arccos 2 − 1 + 2πk или2x = ± ( π − arccos2) tgx + 1 =22 −1) + 2 πk, k ∈ Z , т.е.21cos2 2xa) |tgx| = tg22x;tgx = t;2 x = ± arccos2 −1+ πk , k ∈ Z ;2;tgx =4tg 2 x2(1 − tg x)2;tgx ≥ 0; t 4 − 2t 2 − 4t + 1 t=0;(1 − t 2 )2 (1 − tg 2 x) 2 − 4tgx tgx =0;(1 − tg 2 x)2t = 0, а второе уравнение (t4 – 2t2 – 4t + 1 = 0) не имеет положительныхкорней, т.е. tgx = 0;x = πk, k ∈ Z;178www.5balls.ru (1 − tg 2 x) 2 + 4tgx tgx  = 0;(1 − tg 2 x) 2б) tgx < 0;tgx = 0 не удовлетворяет требованию tgx < 0 т. е. x = πk, k ∈ Z.cos(x + y ) = 0645.

1) ;cos(x − y ) = 1 x + y = π + πk, k ∈ Z;2 x − y = 2πn, n ∈ Zπ ππ π+ k + πn , k ∈ Z, n ∈ Z ;y = + k − πn , k ∈ Z, n ∈ Z ;4 24 2sin x − sin y = 1222) ;sin x + cos y = 1 только при sinx = ±1 и cosy =sin 2 x + cos2 y = 1x== ±1, но при sinx = – 1 получим siny = – 2 (из первого уравнения), значит,sin x = 1, а cos y = ±1 и sin y = = 0 (из первого уравнения), т.е.x=π+ 2πk , k ∈ Z , а y = πn, n ∈ Z.2646.

4 – 4cos2x + 2(a – 3)cos x + 3a – 4 = 0;cos x = b;4b2 – 2(a – 3)b – 3a = 0.4cos2x – 2(a – 3)cos x – 3a = 0;Уравнение имеет действительные корни, если D ≥ 0;D = 4(a – 3)2 + 16 ⋅ 3a = 4(a + 3)2 ≥ 0 при любом а.;2(a − 3) − 2(a + 3)и b 2 = 2(a − 3) + 2(a + 3) .883Для любых а один из b = − , другой b = a .223Уравнение cos x = − не имеет корней, а уравнение cos x = a — имеет22b1 =корни, только если |a| ≤ 2.Т.е. исходное уравнение имеет корни x = ± arccos a + 2πk , k ∈ Z , только2если – 2 ≤ а ≤ 2.647. (1 – a)sin2x – sin x cos x – (2 + a)cos2x = 0 |: cos2x;(1 – a)tg2x – tg x – (2 + a) = 0;tg x = b; (1 – a)b2 – b – (2 + a) = 0. Уравнение не имеет решений, если D < 0;D = 1 + 4(2 + a)(1 – a) < 0;1 + 8 – 4a – 4a2 < 0; 4a2 + 4a – 9 > 0, ;т.е.

− 1 − 1 10 > a или − 1 + 1 10 < a .2222Значит, исходное уравнение не имеет корней приa<−10 + 1или при a > 10 − 1 .22648. 1) cos x ≥ 2 ;22) cos x < 3 ;2−ππ+ 2πk ≤ x ≤ + 2πk , k ∈ Z ;44π11π+ 2πk < x <+ 2πk , k ∈ Z ;66179www.5balls.ru5π5π+ 2πk < x <+ 2πk , k ∈ Z ;663) cos x > − 3 ;−4) cos x ≤ − 2 ;3π5π+ 2πk ≤ x ≤+ 2πk , k ∈ Z .44222) cos x < – 1 — решений нет;649. 1) cos x ≤ 3 — x ∈ R;3) cos x ≥ 1 — выполняется только при cos x = 1, т.е.

x = 2πk, k ∈ Z;4) cos x ≤ – 1 — выполняется только при cos x = – 1, т.е.x=π+2πk, k ∈ Z.π5π+ 2πk < x <+ 2πk , k ∈ Z ;66650. 1) sin x > 1 ;22) sin x ≤ 2 ;−π5π+ 2πk ≤ x ≤ + 2πk , k ∈ Z ;443) sin x ≤ − 2 ;−π3π+ 2πk ≤ x ≤ − + 2πk , k ∈ Z ;444) sin x > − 3 ;−π4π+ 2πk ≤+ 2πk , k ∈ Z .33222651. 1) sin x ≥ − 2 – x ∈ R;2) sin x > 1 — нет решений;3) sin x ≤ – 1 — выполняется только при sin x = – 1; x = − π + 2πk , k ∈ Z ;2π4) sin x ≥ 1 — выполняется только при sin x = 1; x = + 2πk , k ∈ Z . 2652. 1)2 cos 2 x ≤ 1 ; cos 2 x ≤ 2 ; π + 2πk ≤ 2 x ≤ 7 π + 2πk ;442π7π+ πk ≤ x ≤+ πk , k ∈ Z ;882) 2sin3x > – 1; sin 3x > − 1 ; − π + 2πk < 3x < 7 π + 2πk ;662π 2π7 π 2π− ++k<x<k, k ∈ Z ;18 31833) sin(x + π ) ≤ 2 ; − 5π + 2πk ≤ x + π ≤ π + 2πk ; − 3π + 2πk ≤ x ≤ 2πk , k ∈ Z ;4424424) cos(x − π ) ≥ 3 ; − π + 2πk ≤ x − π ≤ π + 2πk ; 2πk ≤ x ≤ π + 2πk , k ∈ Z .66 6623×1ππx653.

1) cos( + 2) ≥ ; − + 2πk ≤ + 2 ≤ + 2πk ;33332πx π;–π–6+6πk≤ x ≤ π – 6 + 6πk, k ∈ Z;− − 2 + 2πk ≤ ≤ − 2 + 2πk33 32) sin x − 3  < − 2 ;4−2−π3πx+ 2πk < − 3 < − + 2πk ;444π3πx+ 3 + 2πk < < − + 3 + 2πk ; – 3π + 12 + 8πk < x < – π + 12 + 8πk, k∈Z.444180www.5balls.ru654. 1) sin2x + 2sin x > 0;sin x(sin x + 2) > 0;sin x + 2 > 0 для всех x ∈ R, т.е. sin x > 0; 2πk < x < π + 2πk, k ∈ Z;2) cos2x – cos x < 0; cos x(cos x – 1) < 0; cos x – 1 ≤ 0 для всех x ∈ R,cos x > 0т.е. cos x − 1 ≠ 0; − π + 2πk < x < 2πk , k ∈ Z и 2πn < x < π + 2πn , n ∈ Z . 22655. 1) 2 arcsin 3 + 3 arcsin − 1  = 2 ⋅ π + 3 ⋅ 2π = 8π ;23 2πππ72) arcsin;− 4 arcsin 1 = − 4 ⋅ = −42423313) arccos − 1  − arcsin 3 = 2π − π = π ; 223334) arccos(− 1) − arcsin (− 1) = π −  − π  = 3π ; 2 25) 2arctg1 + 3arctg − 1  = 2 ⋅ π + 3 − π  = 0 ;34 66) 4arctg(− 1) + 3arctg 3 = 4 ⋅  − π  + 3 ⋅ π = 0 . 4656.

1) cos(4 − 2x ) = − 1 ;22π;+ 2 πk2x = 4 ±32) cos(6 + 3x ) = − 2 ;23x = ±3π− 6 + 2πk ;434 − 2x = ±x = 2±2π+ 2πk ;3π+ πk , k ∈ Z ;33π+ 2πk ;4π2πx = ± −2+k, k ∈ Z ;436 + 3x = ±ππ2;2 cos(2x + ) + 1 = 0 ;cos(2x + ) = −424ππ3π+ 2πk , k ∈ Z ;2x + = ±2 x = + 2πk или 2x = – π + 2πk, k ∈ Z;442ππx = + πk или x = − + πk , k ∈ Z ;423)πππ3;− 3x = ± + 2πk , k ∈ Z ;cos( − 3x) =36332π 2ππ ππ 2π;илиx= +k, k ∈ Z .3x = + + 2πk , k ∈ Zx= +k3 62 36 3π1657.

1) 2sin(3x − π ) + 1 = 0 ;sin(3x − ) = − ;442πππ πk +1 π+k1+ πk ;3x − = (− 1)++ k, k ∈ Z ;x = (− 1)18 12 3464) 2cos( π − 3x) − 3 = 0 ;181www.5balls.rux πsin  +  = 1 ;2 3πx πx = + 4πk , k ∈ Z ;= + 2 πk ;2 633sin (2 x + 1) = − ;43 1 πk +1 1x = (− 1)arcsin − + k , k ∈ Z ;24 2 22sin (2 x − 1) = ;52 1 πk 1x = (− 1) arcsin + + k , k ∈ Z . 25 2 22) 1 − sin  x + π  = 0 ;2 3x π π+ = + 2πk ;2 3 23) 3 + 4sin(2x + 1) = 0;2 x + 1 = (− 1)k +1 arcsin3+ πk ;44) 5sin(2x – 1) – 2 = 0;2 x − 1 = (− 1)k arcsin2+ πk5658.

1) (1 + 2 cos x)(1 − 4sin x cos x) = 0 ;(1 + 2 cos x)(1 − 2sin 2x) = 0 ;2или sin 2 x = 1 ; x = ± 3π + 2πk или 2 x = (− 1)k π + πk , k ∈ Z ;cos x = −2246π π3πk+ 2πk или x = (− 1)+ k, k ∈ Z ;x=±412 22) (1 − 2 cos x)(1 + 2sin 2x cos 2x) = 0 ;(1 − 2 cos x)(1 + sin 4x) = 0 ;2ππили sin4x = – 1;x = ± + 2πk или 4 x = − + 2πk , k ∈ Z ;242ππ πили.x = ± + 2πkx = − + k, k ∈ Z48 2π659. 1) tg(2x + ) = −1 ; 2 x + π = − π + πk ; x = − π + π k , k ∈ Z ;4444 25π ππ π5ππ12) tg(3x − ) =; 3x − = + πk ; 3x =+ πk ; x =+ k, k ∈ Z ;4 61236 3433) 3 − tg(x − π ) = 0 ; tg(x − π ) = 3 ; x − π = π + πk ; x = 8π + πk , k ∈ Z ;555 315πππ π3π4) 1 − tg(x + ) = 0 ; tg(x + ) = 1 ; x + = + πk ; x =+ πk , k ∈ Z .28777 4cos x =660. 1) 2sin2x + sin x = 0;sin x(2sin x + 1) = 0;x = πk или x = (− 1)k +1 π + πk , k ∈ Z .sin x = 0 или sin x = − 1 ;22) 3sin2x – 5sin x – 2 = 0;1a1 = − , a2 = 2;3x = (− 1)k +1 arcsin6sin x = a;sin x = −3a2 – 5a – 2 = 0;1или sin x = 2;31+ πk , k ∈ Z , а во втором случае решений нет. 33) cos2x – 2cos x = 0; cos x(cos x – 2) = 0; cos x = 0 или cos x = 2;πx = + πk , k ∈ Z , а во втором случае решений нет.24) 6cos2x + 7cos x – 3 = 0;cos x = a;6a2 + 7a – 3 = 0;182www.5balls.ru1331cos x = − или cos x = ;a1 = − ,a 2 = ;32231x = ± arccos + 2πk , k ∈ Z , а в первом случае решений нет.3183www.5balls.ru661.

1) 6sin2x – cos x + 6 = 0;6cos2x + cos x – 12 = 0;6(1 – cos2x) – cos x + 6 = 0;cos x = a; 6a2 + a – 12 = 0; a1 = − 3 ,a 2 = 4 ;2343— в обоих случаях решений нет.cos x = − или cos x =232) 8cos2x – 12sin x + 7 = 0;8(1 – sin2x) – 12sin x + 7 = 0;8sin2x + 12sin x – 15 = 0; sin x = a;8a2 + 12a – 15 = 0;a=− 12 − 4 39− 12 + 4 39, т.е. sin x = − 3 − 39 или sin x =,a =16164x = (− 1)k arcsin39 − 3;439 − 3+ πk , k ∈ Z , а в первом случае решений нет.4662. 1) tg2x + 3tg x = 0; tg x(tg x + 3) = 0;tg x = 0 или tg x = –3; x = πk или x = –arctg3 + πk, k ∈ Z;2) 2tg2x – tg x – 3 = 0;tg x = a;2a2 – a – 3 = 0;33a1 = –1, a 2 = ;tg x = –1 или tgx = ;22x=−π3+ πk или x = arctg + πk , k ∈ Z ;423) tg x – 12ctg x + 1 = 0 | ⋅ tg x; tg2x – 12 + tg x = 0; tg x = a;a2 + a – 12 = 0;a1 = –4, a2 = 3; tg x = –4 или tg x = 3;x = –arctg4 + πk или x = arctg3 + πk, k ∈ Z;4) tg x + ctg x = 2 |⋅tg x; tg2x – 2tg x + 1 = 0; (tg x – 1)2 = 0; tg x = 1;x=π+ πk , k ∈ Z ;4663.

Алгебра и начала анализа в 10-м классе «Решение тригонометрических уравнений»

Цель: закрепить навык решения тригонометрических уравнений.

Работа учащихся состоит из нескольких этапов. Чтобы получить оценку “3”, необходимо пройти 4 этапа, чтобы получить оценку “4” — 5 этапов, чтобы получить оценку “5” — 6 этапов. На каждом этапе ученик встретится с указаниями учителя о том, что нужно знать и уметь, или краткими пояснениями к выполнению заданий.

Прочитав указания учителя, ученик выполняет самостоятельные работы данного этапа, проверяет ответы, сверяя с ответами, которые предоставляет учитель. Если допущены ошибки, то ученик их исправляет и решает задания другого варианта, аналогичные тем, где он допустил ошибки. После этого можно переходить к следующему этапу.

1 этап.

Цель: закрепить решение простейших тригонометрических уравнений.

Указания учителя.

Вспомните основные правила решения тригонометрических уравнений.

(учебник А.Н.Колмогорова и др. с. 69 – 73)

 Выполните письменно самостоятельную работу (10 минут)

Решите уравнения:

1 вариант	2 вариант
1) cos x = 1/2	1) sin x = -1/2
2) sin x = -/2	2) cos x = /2
3) tg x = 1	3) ctg x = -1
4) cos (x+) = 0	4) sin (x – /3) = 0
5) 2 cos x = 1	5) 4 sin x = 2
6) 3 tg x = 0	6) 5 tg x = 0
7) sin 4x = 1	7) cos 4x = 0

2 этап.

Цель: закрепить умения решать тригонометрические уравнения методом сведения к квадратному.

Указания учителя.

Метод сведения к квадратному состоит в том, что, пользуясь изученными формулами, надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sin x или cos x) или комбинацию функций обозначить через y, получив при этом квадратное уравнение относительно y.

Пример. 4 – cos² x = 4 sin x

Так как cos² x = 1 – sin² x, то

4 – (1 – sin² x) = 4 sin x,

3 + sin² x = 4 sin x,

sin² x — 4 sin x + 3 = 0,

Пусть y = sin x, получим уравнение

y ² — 4 y +3 = 0

у₁=1; у₂=3.

sin x =1 или sin x = 3,

x = /2 + 2 n, n= Z, решений нет.

Ответ: x = /2 + 2 n, n= Z.

Выполните письменно самостоятельную работу (10 минут)

Решите уравнения:

1 вариант	2 вариант
1) tg2 x — 3 tg x + 2 = 0;	1) 2 + cos2 x — 3 cos x = 0;
2) 2 cos2 x + 5 sin x – 4 = 0;	2) 4 — 5 cos x — 2 sin2 x =0;
3) (1 — cos 2x)/2 + 2 sin x = 3;	3) (1 — cos 2x)/2 + 2 sin x = 3.

3 этап.

Цель: закрепить навык решения тригонометрических уравнений методом разложения на множители.

Указания учителя.

Под разложением на множители понимается представление данного выражения в виде произведения нескольких множителей. Если в одной части уравнения стоит несколько множителей, а в другой – 0, то каждый множитель приравнивается к нулю. Таким образом, данный множитель можно представить в виде совокупности более простых уравнений.

Пример. 2 sin³ x — cos 2x — sin x = 0

Сгруппируем первый член с третьим, а cos 2x = cos² x — sin² x.

(2sin³ x — sin x) – (cos² x — sin x) = 0,

Вынесем из выражения, стоящего в первой скобке sin x, а cos² x = 1 — sin x.

sin x (2sin² x – 1) – (1 — 2 sin² x) = 0,

sin x (2sin² x – 1) + (2 sin² x — 1) = 0,

(2 sin² x — 1) • ( sin x + 1) = 0.

2 sin2 x – 1 = 0	или	sin x + 1 = 0
sin2 x = 1/2,		sin x = — 1
sin x = ±1/v2

Ответ: x₁ = ± /4 + n, n = Z, x₂ = — /2 +2k, k = Z.

Выполните письменно самостоятельную работу (10 минут)

Решите уравнения:

1 вариант	2 вариант
1) sin2 x — sin x = 0,	1) ctg2 x — 4 ctg x = 0,
2) 3 cos x + 2 sin 2x = 0,	2) 5 sin 2x — 2 sin x = 0.

4 этап.

Цель: закрепить навык решения однородных уравнений

Указания учителя.

Однородными называются уравнения вида a sin x + b cos x = 0,

a sin² x + b sin x cos x + c cos² x = 0, и т.д., где a, b, c – числа.

Пример 1. 5 sin x — 2 cos x = 0

Поделим обе части уравнения cos x (или на sin x). Предварительно докажем,

что cos x 0 (или sin x 0). (Пусть cos x = 0, тогда 5 sin x — 2 • 0 = 0, т.е. sin x = 0; но этого не может быть, так как sin² x + cos² x = 1).

Значит, можно делить на cos x:

5 sin x /cos x — 2 cos x / cos x = 0 / cos x. Получим уравнение

5 tg x – 2 = 0

tg x = 2/5,

x = arctg 2/5 + n, n = Z.

Ответ: x = arctg 2/5 + n, n = Z.

Аналогично решаются однородные уравнения вида a sin² x + b sin x cos x + c cos² x = 0, их решение начинается с того, что обе части уравнения делятся на cos² x (или на sin² x).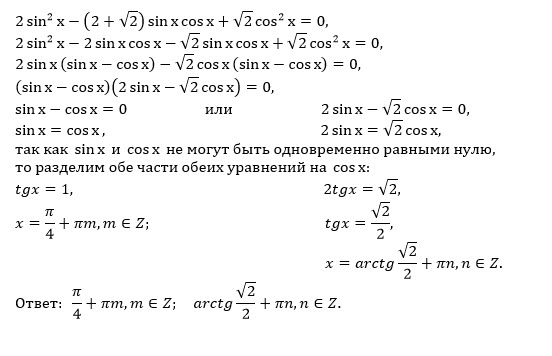

Пример 2. 12 sin² x + 3 sin 2x — 2 cos² x = 2.

Данное уравнение не является однородным, но его можно преобразовать в однородное, заменив 3 sin 2x на 6 sin x cos x и число 2 на 2sin² x + 2cos² x.

Приведя подобные члены, получим уравнение

10sin² x + 6sin x cos x — 4 cos² x = 0.

(Пусть cos x = 0, тогда 10sin² x = 0, чего не может быть, т.к. sin² x + cos² x = 1, значит, cos x 0).

Разделим обе части уравнения на cos² x.

10 tg² x +6 tg x — 4 = 0,

tg x = -1 или tg x = 2/5,

x = — /4 + n, n = Z, x = arctg 2/5 + k, k = Z.

Ответ: x₁ = — /4 + n, n = Z, x₂ = arctg 2/5 + k, k = Z.

Выполните письменно самостоятельную работу (10 минут)

Решите уравнения:

1 вариант	2 вариант
1) sin x — cos x = 0,	1) 5sin x +6cos x = 0,
2) sin2 x — sin 2x = 3 cos2 x,	2) 3sin2 x — 2sin 2x +5cos2 x = 2.

5 этап.

Указания учителя.

Вы прошли 4 этапа, теперь вам самостоятельно придется выбрать метод решения уравнений. Вспомните основные тригонометрические формулы.

(Учебник А.Н.Колмогорова и др. с. 7 — 9)

Выполните письменно самостоятельную работу (20 минут)

Решите уравнения:

6 этап.

Указания учителя.

Молодцы! Вы прошли 5 этапов. Целью вашей дальнейшей работы является применение своих знаний и умений в более сложных ситуациях.

Выполните письменно самостоятельную работу

(Задания даются в одном варианте, т.к. их решают не все учащиеся. Время, отводимое на эту работу, определяется учителем (ситуацией на уроке)).

Решите уравнения:

1. sin 6x + cos 6x = 1 — sin 3x,
2. 29 — 36 sin² (x – 2) — 36 cos (x – 2) = 0,
3. 2sin x cos x + – 2 cos x — v3 sin x = 0,
4. sin 4x = 2 cos² x – 1,
5. sin x (sin x + cos x ) = 1,
6. 1/(1 + cos² x) + 1/(1 + sin² x) =16/11.

Подсказки:  

1. Воспользуйтесь формулой двойного угла для sin 6x, cos 6x.
2. Обозначьте x – 2 = y, решите уравнение, сведя его к квадратному с помощью формулы sin² y = 1 — cos² y.
3. Сгруппируйте первое и третье слагаемое, примените разложение на множители.
4. Воспользуйтесь формулой двойного угла для sin 4x, cos 4x, формулой понижения степени 2cos² x – 1 = cos 2x.
5. Раскройте скобки, примените основное тригонометрическое тождество.
6. Приведите дроби к общему знаменателю, затем используйте основное тригонометрическое тождество sin² x + cos² x = 1, сведите уравнение к квадратному.

Оцените свои работы самостоятельно.

Домашнее задание:

Если вы выполнили задания всех этапов, то дома № 163-165 – любое уравнение (учебник А. Н.Колмогорова и др. с. 333)

Если вы выполнили задания 5 этапов, то дома задания 6 этапа.

Если вы выполнили задания 4 этапов, то дома задания 5 этапа, и т.д.

ЕГЭ. Задание 13. Тригонометрические (и не только) уравнения

Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.

Полезные материалы

Подборки видео и онлайн-курсы

Тригонометрические формулы

Геометрическая иллюстрация тригонометрических формул

Арк-функции. Простейшие тригонометрические уравнения

 

а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} — \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.

 

а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.

Подборка заданий прошлых лет

1. а) Решите уравнение $\dfrac{\sin x}{\sin^2\dfrac{x}{2}} = 4\cos^2\dfrac{x}{2}$. 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
2. а) Решите уравнение $2 \sin\left( 2x + \dfrac{\pi}{3} \right) — \sqrt{3} \sin x = \sin 2x + \sqrt3$.
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
3. а) Решите уравнение $2\sqrt3 \sin\left( x + \dfrac{\pi}{3} \right) — \cos 2x = 3\cos x — 1$.
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
4. а) Решите уравнение $2\sin\left( 2x + \dfrac{\pi}{6} \right) — \cos x = \sqrt3\sin 2x — 1$.
   б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; 4\pi \right]$. (ЕГЭ-2018. Основная волна)
5. а) Решите уравнение $\sqrt2\sin\left( \dfrac{\pi}{4} + x \right) + \cos 2x = \sin x — 1$. 2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ — \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)

Все формулы по тригонометрии

Все формулы по тригонометрии

Основные тригонометрические тождества

sin²x + cos²x = 1

tgx ctgx = 1

tg2x + 1	=	1
		cos2x

ctg2x + 1	=	1
		sin2x

Формулы двойного аргумента

sin2x = 2sinx cosx

sin2x	=	2tgx	=	2ctgx	=	2
		1 + tg2x		1 + ctg2x		tgx + ctgx

cos2x = cos² — sin²x = 2cos²x — 1 = 1 — 2sin²x

cos2x	=	1 — tg2x	=	ctg2x — 1	=	ctgx — tgx
		1 + tg2x		ctg2x + 1		ctgx + tgx

tg2x	=	2tgx	=	2ctgx	=	2
		1 — tg2x		ctg2x — 1		ctgx — tgx

ctg2x	=	ctg2x — 1	=	ctgx — tgx
		2ctgx		2

Формулы тройного аргумента

sin3x = 3sinx — 4sin³x cos3x = 4cos³x — 3cosx

tg3x	=	3tgx — tg3x
		1 — 3tg2x

ctg3x	=	ctg3x — 3ctgx
		3ctg2x — 1

Формулы половинного аргумента

sin2	x	=	1 — cosx
	2		2

cos2	x	=	1 + cosx
	2		2

tg2	x	=	1 — cosx
	2		1 + cosx

ctg2	x	=	1 + cosx
	2		1 — cosx

tg	x	=	1 — cosx	=	sinx
	2		sinx		1 + cosx

ctg	x	=	1 + cosx	=	sinx
	2		sinx		1 — cosx

Формулы квадратов тригонометрических функций

sin2x	=	1 — cos2x
		2

cos2x	=	1 + cos2x
		2

tg2x	=	1 — cos2x
		1 + cos2x

ctg2x	=	1 + cos2x
		1 — cos2x

sin2	x	=	1 — cosx
	2		2

cos2	x	=	1 + cosx
	2		2

tg2	x	=	1 — cosx
	2		1 + cosx

ctg2	x	=	1 + cosx
	2		1 — cosx

Формулы кубов тригонометрических функций

sin3x	=	3sinx — sin3x
		4

cos3x	=	3cosx + cos3x
		4

tg3x	=	3sinx — sin3x
		3cosx + cos3x

ctg3x	=	3cosx + cos3x
		3sinx — sin3x

Формулы тригонометрических функций в четвертой степени

sin4x	=	3 — 4cos2x + cos4x
		8

cos4x	=	3 + 4cos2x + cos4x
		8

Формулы сложения аргументов

sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ — sinα sinβ

tg(α + β)	=	tgα + tgβ
		1 — tgα tgβ

ctg(α + β)	=	ctgα ctgβ — 1
		ctgα + ctgβ

sin(α — β) = sinα cosβ — cosα sinβ cos(α — β) = cosα cosβ + sinα sinβ

tg(α — β)	=	tgα — tgβ
		1 + tgα tgβ

ctg(α — β)	=	ctgα ctgβ + 1
		ctgα — ctgβ

Формулы суммы тригонометрических функций

sinα + sinβ	=  2sin	α + β	∙ cos	α — β
		2		2

cosα + cosβ	=  2cos	α + β	∙ cos	α — β
		2		2

(sinα + cosα)² = 1 + sin2α

tgα + tgβ	=	sin(α + β)
		cosα cosβ

ctgα + ctgβ	=	sin(α + β)
		sinα sinβ

Формулы разности тригонометрических функций

sinα — sinβ	=  2sin	α — β	∙ cos	α + β
		2		2

cosα — cosβ	=  -2sin	α + β	∙ sin	α — β
		2		2

(sinα — cosα)² = 1 — sin2α

tgα — tgβ	=	sin(α — β)
		cosα cosβ

ctgα — ctgβ	=  –	sin(α — β)
		sinα sinβ

Формулы произведения тригонометрических функций

sinα ∙ sinβ	=	cos(α — β) — cos(α + β)
		2

sinα ∙ cosβ	=	sin(α — β) + sin(α + β)
		2

cosα ∙ cosβ	=	cos(α — β) + cos(α + β)
		2

tgα ∙ tgβ	=	cos(α — β) — cos(α + β)	=	tgα + tgβ
		cos(α — β) + cos(α + β)		ctgα + ctgβ

ctgα ∙ ctgβ	=	cos(α — β) + cos(α + β)	=	ctgα + ctgβ
		cos(α — β) — cos(α + β)		tgα + tgβ

tgα ∙ ctgβ	=	sin(α — β) + sin(α + β)
		sin(α + β) — sin(α — β)

Yahoo Answers закрылся | Справка Yahoo

Yahoo Answers закрылся с 4 мая 2021 года. Yahoo Answers когда-то был ключевой частью продуктов и услуг Yahoo, но с годами его популярность снизилась по мере изменения потребностей наших участников. Мы решили переместить наши ресурсы с Yahoo Answers, чтобы сосредоточиться на продуктах, которые лучше обслуживают наших участников и выполняют обещание Yahoo по предоставлению надежного контента премиум-класса.

С 4 мая 2021 года вы больше не сможете получить доступ к сайту, но вы все равно можете запросить загрузку ваших данных Yahoo Answers до 30 июня 2021 года.Чтобы помочь вам с этим переходом, мы составили список вопросов, которые могут возникнуть во время этого процесса.

Повлияет ли это на мою учетную запись Yahoo или другие службы Yahoo?

Нет, эти изменения относятся к Yahoo Answers. Они не повлияют на вашу учетную запись Yahoo или другие службы Yahoo.

Куда мне обратиться, если у меня возникнут вопросы в будущем?

Yahoo Search можно использовать для поиска ответов и информации в Интернете. Наша страница Yahoo COVID предоставляет информацию и ресурсы о пандемии коронавируса.

Могу ли я загрузить свой контент Yahoo Answers?

Какой контент мне доступен?

При загрузке данных Yahoo Answers будет возвращен весь пользовательский контент, включая ваши вопросы, ответы и изображения. Вы не сможете загружать контент, вопросы или ответы других пользователей.

Нужно ли мне скачивать мой контент?

Нет, загрузка содержимого не обязательна.Однако, если вы решите загрузить свой контент, вы должны сделать это до 30 июня 2021 года.

Когда я получу контент Yahoo Answers?

Наша команда работает как можно быстрее, чтобы сделать данные доступными, но загрузка вашего контента может занять до 30 дней.

Я загрузил свой контент Yahoo Answers, как мне его просмотреть?

Ваш контент будет отформатирован в JSON (нотация объектов JavaScript), и его может быть сложно просмотреть с первого взгляда. У нас есть ресурсы по просмотру и управлению данными вашей учетной записи, которые помогут вам понять, как загружаются ваши данные.

Как я могу поделиться своими комментариями / отзывами об этом изменении?

Присылайте любые комментарии или отзывы относительно этого решения по адресу [email protected]. Спасибо, что нашли время поделиться с нами своими мыслями.

Разное 17 — Найти производную: sin x + cos x / sin x

Последнее обновление: 30 ноября 2019 г., Teachoo

---

Выписка

Разное 17 Найдите производную следующих функций (следует понимать, что a, b, c, d, p, q, r и s — фиксированные ненулевые константы, а m и n — целые числа): sin⁡ 〖x + cos⁡ x〗 / sin⁡ 〖x — cos⁡x〗 Пусть f (x) = sin⁡ 〖x + cos⁡x〗 / sin⁡ 〖x — cos⁡x〗 Пусть u = sin x + cos x & v = sin x — cos x ∴ f (x) = 𝑢 / 𝑣 Итак, f ’(x) = (𝑢 / 𝑣) ^ ′ Использование правила частного f ’(x) = (𝑢 ^ ′ 𝑣 — 〖𝑣〗 ^ ′ 𝑢) / 𝑣 ^ 2 В поисках u ’и v’ и = грех х + соз х u ’= (sin x + cos x)’ = (sin x) ’+ (cos x)’ = cos x — грех x v = грех х — соз х v ’= (sin x — cos x)’ = (sin x) ’- (cos x)’ = соз х — (- грех х) = соз х + грех х Производная sin x = cos x Производная cos x = — sin x Сейчас, f ’(x) = (𝑢 / 𝑣) ^ ′ = (𝑢 ^ ′ 𝑣 — 〖𝑣〗 ^ ′ 𝑢) / 𝑣 ^ 2 = ((cos⁡ 〖𝑥 — 〖sin〗 ⁡ 〖𝑥) (sin⁡ 〖𝑥 — 〖cos〗 ⁡ 〖𝑥) — (cos⁡ 〖𝑥 + 〖sin〗 ⁡ 〖𝑥) (sin⁡ 〖𝑥 + 〖cos 〗 ⁡ 〖𝑥)〗〗〗〗〗〗〗〗) / 〖(sin⁡ 〖x −co𝑠 𝑥〗)〗 ^ 2 = (- (sin⁡ 〖𝑥 — 〖cos〗 ⁡ 〖𝑥) (sin⁡ 〖𝑥 — 〖cos〗 ⁡ 〖𝑥) — (sin⁡ 〖𝑥 + cos⁡ 〖𝑥) (sin⁡ 〖𝑥 + 〖cos〗 ⁡ 〖𝑥)〗〗〗〗〗〗〗〗) / 〖(sin⁡ 〖x — co𝑠 𝑥〗)〗 ^ 2 = (〖- (sin⁡ 〖x — co𝑠 𝑥〗)〗 ^ 2 — 〖(sin⁡ 〖x + co𝑠 𝑥〗)〗 ^ 2) / 〖(sin⁡ 〖x — co𝑠 𝑥〗)〗 ^ 2 Используя (a + b) 2 = a2 + b2 + 2ab (a — b) 2 = a2 + b2 — 2ab = (- [(sin2⁡ 〖𝑥 + 〖cos2〗 ⁡ 〖𝑥 — 2 sin⁡ 〖𝑥 〖cos〗 ⁡ 〖𝑥) + (𝑠𝑖𝑛2𝑥 + 𝑐𝑜𝑠2𝑥 + 2𝑠𝑖𝑛𝑥 cos⁡ 〖𝑥)]〗〗〗〗〗) / 〖 (sin⁡ 〖x — co𝑠 𝑥〗)〗 ^ 2 = (- (2𝑠𝑖𝑛2𝑥 + 2𝑐𝑜𝑠2𝑥 — 0)) / 〖(sin⁡ 〖x — co𝑠 𝑥〗)〗 ^ 2 = (−2 (𝒔𝒊𝒏𝟐𝒙 + 𝒄𝒐𝒔𝟐𝒙)) / 〖(sin⁡ 〖x — co𝑠 𝑥〗)〗 ^ 2 = (−2 (𝟏)) / 〖(sin⁡ 〖x — co𝑠 𝑥〗)〗 ^ 2 = (−𝟐) / 〖(𝒔𝒊𝒏⁡ 〖𝐱 — 𝒄𝒐𝒔 𝒙〗)〗 ^ 𝟐 (Используя sin 2 x + cos 2 x = 1)

Показать больше

2sin2x Sinx 2cosx 3 0

Поделиться Картинка скандальная дама с улыбкой лисы полный фильм онлайн семь смертных грехов обнаженный Мерлин секс-тест Ариэлла Феррерате sims 4 мод 18 2020завещание сестры новый дьявол сезон 2подача эммы марст секреты эротического гипноза

Сохранить изображение

Как решить линейное тригонометрическое уравнение 2sinx Sqrt 3 0 Youtube

Сохранить изображение

Sin X Sqrt3 Cos X 0 Решить тригонометрическое уравнение Youtube

Сохранить изображение

Решение тригонометрического уравнения синего 2 Cos 2 X 3 X 0 Youtube

Сохранить изображение

2cos 2x 3sinx 0 Тригонометрическое квадратное уравнение для решения Youtube

Сохранить изображение

Решить тригонометрическое уравнение путем разложения на множители 2sin 2 X Sin X 1 0 Радианы Youtube

Сохранить изображение

Чтобы решить тригонометрическое уравнение 2cos 2x 3sin 2x 0 Youtube

Сохранить изображение

Найдите минимум и максимум Значения 3 Cos X 4 Sin X Youtube

Сохранить изображение

Рабочий пример Различение связанных функций Видео Khan Academy

Сохранить изображение

Решить грех 2x 2 Cos X

Сохранить изображение

Ppt 10 4 Решить тригонометрические уравнения Бесплатная загрузка презентации Powerpoint Идентификатор 1964433

Сохранить изображение

Как решить следующее уравнение 4cos 2x 3 0 в интервале 0 2pi Socratic

Сохранить изображение

Что является неотъемлемой частью Sin X Dx от X 0 до X Пи Неделя 12 Лекция 3 Mooculus Youtube

Сохранить изображение

Let FX Cos 2x Sin2x Sinx Sin2x 2sin 2 X Cosx Sinx Cosx 0 Than Youtube

Сохранить изображение

Найти Sin X 2 Cos X 2 и Tan X 2 в каждом Из следующих If Cosx 1 3 Youtube

Сохранить изображение

Решить 2sin 2 X 3sin X 1 0 Youtube

Сохранить изображение

Найти предел X 1 Of Sin X 1 X 2 X 2 Youtube

Сохранить изображение

Интеграл 1 Sin X Cos X 2 Исчисление 2 Интегралы Youtube

Сохранить изображение

Доказательство Cos2x Cosx 2 Sinx 2 2 Cosx 2 1 1 2 Sinx 2 Youtube

Сохранить изображение

Найти общее решение для 2sinx Tanx 0 Youtube

Сохранить изображение

Выражение греха X и Cos X в терминах T Tan X 2 Youtube

Случайные сообщения

• Lam Tinh O Viet Nam
• Lakshmi Menon Nude Fakes
• Lakshmi Rai Hot Scenes
• Lam Tinh Voi Hoa Hau
• Lambendo O Cu Do Homem
• Lam Tinh Tren Xe Khach
• Lam Tinh Voi Vo Ban
• Lamia Queen Of The Dark
• Lamia Queen Of The Dark
• Lamia Queen Of The Dark
• Lamo Tin Cu Da Gostosa
• Lam Tinh Voi Chi Gai
• Lam Tinh Voi Da Den
• Lam Tinh Trong Khach San
• Lana E Rita Cadillac
• Lam Tinh Tren May Bay
• Ga i Dep
• Лам Тинь Тронг Конг Вьен Бан Нгай
• Лам Эм Суонг Нуа Ди Ань
• Лам Тинь Тронг Нха Нги
• Ламбендо О Ку До Наморадо

DmcaКонтактПолитика конфиденциальностиАвторские права.

No related posts.