Урок «Свойства арифметического квадратного корня. Урок №7»
Урок № 7 §2, п. 15
Тема: Свойства арифметического квадратного корня.
Цель урока:
Образовательная: изучить основные свойства квадратных корней, сформировать умение применять их для преобразования выражений, содержащих квадратные корни, научить вычислять значения квадратных корней.
Развивающая: развитие вычислительных умений и навыков.
Воспитательная: воспитание прилежности, аккуратности и творческого подхода к поставленной задаче.
Тип урока: урок усвоения новых знаний и умений
Оборудование: мел, доска, плакаты, учебник, карточки красные, зеленые и синие для проведения рефлексии
Х о д у р о к а
- Организационный момент.
— проверка готовности класса к уроку;
— проверка готовности учащихся к уроку;
— приветствие
- Мотивация урока.
Эпиграф нашего урока “О, сколько нам открытий чудных готовит просвещенья дух…”. А были ли открытия в вашей жизни? Что значат слова “Я сделал открытие”? Если человек своим трудолюбием, упорством достигает истины в чем-либо, то это и есть его открытие.
На сегодняшнем уроке мы тоже попытаеся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным
3. Проверка Д.З.
Анализ работ №454 и №449
Учитель: «Прежде чем перейти к новой теме, давайте обобщим и систематизируем теоретически знания, которые мы с вами имеем на данный момент».
Закрепление теоретического материала § 2,п.14.
1. Какие числа называют действительными?
2. Какие числа называют рациональными, какие иррациональными?
3.
Приведите примеры иррациональных чисел.
4. Бывают ли иррациональные числа отрицательными?
5. Является ли число 0 целым, рациональным, действительным?
6. Какие действия можно выполнять с иррациональными числами?
А с действительными числами?
7. Всегда ли сумма, разность, произведение или частное двух
иррациональных чисел — число иррациональное?
4.Объяснение нового материала
Задание классу (из предыдущего материала) – решите уравнение
х2 = 25,
корни уравнения х1 = 5 т.к. 52 = 25,
но и х2 = -5 т.к. (-5)2
Если учесть, что 5 = , а — 5 = — , то получается, что
(5)2 = ()2 и (-5)2 = (- )2
т.
е. 25 = ()2 и 25 = (- )2 следовательно
а = ()2
Примеры.
()2 = 6; ()2 = 18; ()2 = 3;
()2 = 3,2; = ; 2 = 0.
Верны также тождества:
плакат 1
- = ∙ , если a ≥ 0 и b ≥ 0;
- = , если a ≥ 0 и b > 0;
- = , если a ≥ 0 и k N.
- ()2 = , при допустимых a
Приведем доказательство первого равенства
()2 =
( ∙ )2 =()2 ∙ ()2 = ч.т.д.
Эти три теоремы кратко можно сформулировать так.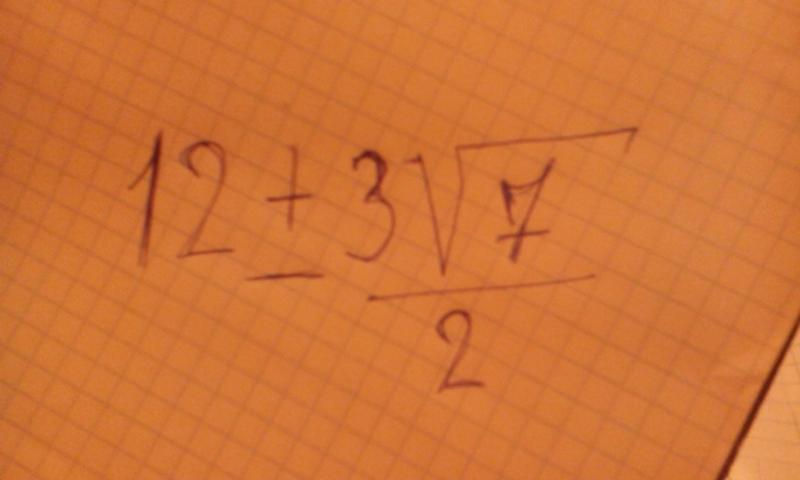
Плакат 2
1. Корень из произведения двух неотрицательных чисел равен произведению корней из этих чисел (теорема о корне из произведения).
2. Корень из дроби, числитель которой неотрицательный, а знаменатель положительный, равен корню из числителя, делённому на корень из знаменателя (теорема о корне из дроби).
3. Корень из степени , в котором числа а — неотрицательное и
Приводим для каждого свойства примеры:
= ∙ = 2 ∙ 3 = 6.
= = .
= = = = 8
Если эти тождества записать наоборот, то получим правила умножения, деления и представления любого выражения в виде квадрата.
Плакат 3
1. ∙ = , если a ≥ 0 и b ≥ 0;
2.
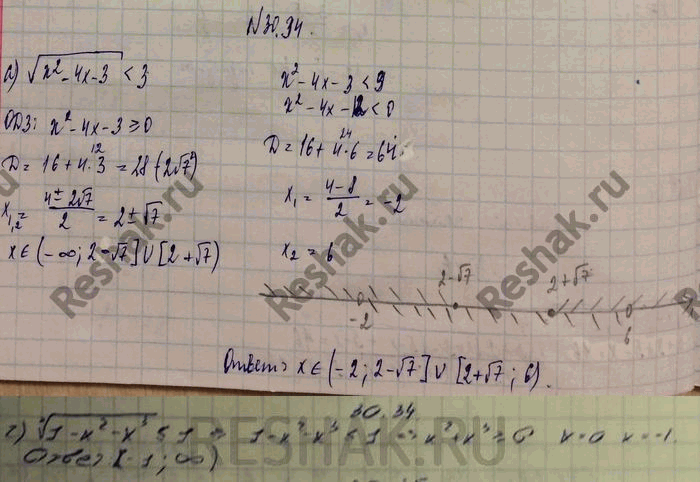= , если a ≥ 0 и b > 0;
3. = = ()2, если a ≥ 0 и k N.
Приведем примеры:
∙ = = = 4;
= = = 5;
= или = ()2 ;
13 = ()2 – умение представлять любое выражение и число в виде квадрата.
Из теоремы о корне из степени следует, что = а, если а ≥ 0. Если же а < 0, то равенство = а неверное, поскольку число неотрицательное и не может быть равным отрицательному числу а. Это равенство запишем в таком виде
= |а|
верное при каждом значении а, поскольку число |а|— неотрицательное и его квадрат равен а .
Например:
= |8| = |-7| = 7 = 3.
Запомним следующее
= |а|
()2 = а
Проблемная ситуация: если вдруг окажутся следующие типы заданий: , , , то необходимо воспользоваться определением арифметического значения квадратного корня, т.е.
= = 6.
= = .
= = 5 или = = 5.
4. Закрепление изученного материала.
Для закрепления знаний свойств квадратных корней в классе решить задания:
№471(1,4,7) и №471(2,5,8), №471(3,6,9) – три ученика
Релаксация.
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И вновь глазами
ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!
№472 — следующий ученик.
№473 – весь класс
Учитель регулирует и направляет ход решения каждого задания, а класс активно участвует во время обсуждения решений этих заданий.
- Итоги урока. Рефлексия.
Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал сегодня?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал сегодня?» и тот ответил: «А я добросовестно выполнял свою работу».
А третий улыбнулся, его лицо засветилось радостью и удовольствием. А я принимал участие в строительстве храма.
— Ребята, кто работал так, как первый человек, поднимите синие карточки.
-Кто работал как второй человек, поднимите зелёные карточки.
— Кто принимал участие в строительстве храма, поднимите красные карточки.
Подведение итогов и оценивание знаний учащихся.
5. Домашнее задание § 2, п. 15 № 472(2), 474 (1-12) и № 495 – на повторение.
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | Найти площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | | |
| 9 | Найти площадь | круг (3) | | |
| 10 9(1/2) | ||||
| 11 | Найти простую факторизацию | |||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найти том | сфера (2) | | |
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.
е. 1,45 .
Математические символы
| Символ | Название символа | Символ. | знак минус | вычитание | 1 1/2 — 2/3 |
|---|---|---|---|---|---|
| * | Asterisk | Умножение | 2/3 * 3/4 | 9000 | 5149599599599599595959595995959595959959595995995959959959599595959595959595959599595959595951 /3 × 5/6|
| : | division sign | division | 1/2 : 3 | ||
| / | division slash | division | 1/3 / 5 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Если вы съедите 2/3 оставшегося торта, сколько всего торта вы съедите?