Онлайн калькулятор алгоритмов: калькулятор алгоритмов

Содержание

Калькулятор НОД и НОК по алгоритму Евклида

Наибольший общий делитель (НОД) чисел a и b — это наибольшее число, на которое делятся без остатка числа a и b.

Среди всех способов нахождения наибольшего общего делителя для двух чисел алгоритм Евклида наиболее удобный и простой.

Нахождения НОД и НОК по алгоритму Евклида методом деления

Как известно, деление с остатком целых чисел a — делимое и b — делитель, где b ≠ 0, подразумевает нахождение таких целых чисел q и r, что выполняется равенство:
a = b ∙ q + r, где
q — называется неполным частным,
r — остаток от деления, который не может быть отрицательным числом и по модулю не может быть больше делителя.

Суть метода состоит в том, что сначала выбираем наибольшее из двух чисел, для которых требуется найти НОД и делим большее число на меньшее. Если остаток от деления не равен нулю, делим делитель на остаток от деления, так продолжаем до тех пор, пока остаток от деления не будет равен нулю.

Пример 1

Найдем НОД (36; 30), для этого сначала найдем остаток от деления 36 на 30
36 : 30 = 1 (остаток 6), так как 36 = 30 ∙ 1 + 6, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 30 на 6
30 : 6 = 5 (остаток 0) так как 30 = 6 ∙ 5 + 0, остаток от деления равен нулю, значит НОД равен предыдущему остатку от деление 6

Ответ: НОД (36; 30) = 6
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (36; 30) = (36 ∙ 30) : 6 = 180

Пример 2

Найдем НОД (176; 36), для этого сначала найдем остаток от деления 176 на 36
176 : 36 = 4 (остаток 32) так как 176 = 36 ∙ 4 + 32, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 36 на 32
36 : 32 = 1 (остаток 4) так как 36 = 32 ∙ 1 + 4, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 32 на 4
32 : 4 = 8 (остаток 0) так как 32 = 4 ∙ 8 + 0, остаток от деления равен нулю, значит НОД равен предыдущему остатку от деление 4
Ответ: НОД (176; 36) = 4
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (176; 36) = (176 ∙ 36) : 4 = 1584

Нахождения НОД и НОК по алгоритму Евклида методом вычитания

Суть метода вычитания состоит в том, что необходимо из большего числа вычитать меньшее, если результат вычитания не равен нулю, тогда уменьшаемое заменяем на получившуюся разность, если разность равна нулю, то НОД равен предыдущему значению разности.

Приведем примеры:

Пример 1

Найдем НОД (36; 30)
36 — 30 = 6
30 — 6 = 24
24 — 6 = 18
18 — 6 = 12
12 — 6 = 6
6 — 6 = 0
Ответ: НОД (36; 30) = 6
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (36; 30) = (36 ∙ 30) : 6 = 180

Пример 2

Найдем НОД (176; 36)
176 — 36 = 140
140 — 36 = 104
104 — 36 = 68
68 — 36 = 32

36 — 32 = 4
32 — 4 = 28
28 — 4 = 24
24 — 4 = 20
20 — 4 = 16
16 — 4 = 12
12 — 4 = 8
8 — 4 = 4
4 — 4 = 0
Ответ: НОД (176; 36) = 4
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (176; 36) = (176 ∙ 36) : 4 = 1584

Математический калькулятор в одну строку онлайн

Калькулятор математического выражения — это программа, позволяющая осуществлять арифметические операции, записывая команды в одну строку. Это удобный инструмент для проверки записи выражений, используемых в любых вычислительных программах от Excel и Matlab до вручную спрограммированных калькуляторов. Современные вычислительные машины производят сложнейшие вычисления за доли секунды, однако так было не всегда.

История создания калькуляторов

Калькулятор — это инструмент для автоматизации громоздких вычислений. В древнем мире не было речи об автоматизации, однако уже тогда ученые создали инструменты для упрощения счета. Первой помощницей античных математиков стала счетная доска — абак. Счетные доски использовались еще в Древнем Вавилоне: в то время абак представлял собой линованную доску, на которой математики раскладывали камни. Позднее абак был усовершенствован и превратился в счеты, которые широко распространились на территории России с 15-го века. Счеты — удобная вещь, которой до сих пор пользуются некоторые торговцы, однако инженерная мысль не стояла на месте и в 17-м веке появилась необходимость в создании калькуляторов.

Арифмометры

Первым калькулятором в истории Европы считается арифмометр Блеза Паскаля. Громоздкая суммирующая машина была выполнена в виде ящика со связанными шестеренками. Суммируемые числа вводились в машину при вращении наборных колесиков, каждое из которых соответствовало одному десятичному разряду числа. Совершив один полный оборот колесико сдвигало соседний разряд, увеличивая его на единицу. Крутить колесики можно было только в одну сторону, поэтому машина не работала с отрицательными числами. Тем не менее арифмометр использовался не только для суммирования чисел: операции умножения и деления выполнялись по алгоритмам повторного сложения.

Через пару десятилетий Вильгельм Лейбниц создал свой арифмометр. Он использовал принцип Паскаля, но вместе колесиков Лейбниц установил в машину специальные барабаны, а также рукоятку для удобства работы с арифмометром. Такая конструкция позволила ускорить вычисления, но и она была не слишком удобной для практического использования. В итоге было изготовлено всего 2 устройства по схеме Лейбница, одно из которых сегодня хранится в Ганноверском музее, а второе было утеряно.

Таким образом, арифмометры не смогли заменить банальные счеты. Машина Паскаля не получила широкого распространения, так как денежная система Франции была недесятичной, а «Паскалина» работала только с десятичными разрядами. Машина Лейбница разрабатывалась для сложных астрономических расчетов, но и она не дала той скорости вычислений, которую дает человеческий мозг.

Современные калькуляторы

Первые компактные вычислительные машины появились в шестидесятые годы 20-го века. Тогда началось массовое производство изящных электронных устройств, которые даже выдавали распечатку выполненных расчетов. Со временем вычислительная техника развивалась, и простые калькуляторы стали обыденной вещью. Началось производство специализированных устройств для инженерных, бухгалтерских, финансовых и статистических вычислений. Сегодня любой смышленый студент-программист может написать оболочку для выполнения простейших арифметических операций, а на просторах Сети легко отыскать сложные тематические калькуляторы, вычисления которых не ограничиваются арифметикой. В каталоге онлайн-инструментов можно найти налоговые, ипотечные, банковские, финансовые или бухгалтерские калькуляторы.

Калькулятор в одну строку

Математический калькулятор в одну строку — это удобный инструмент, позволяющий задать выражение так, как оно записывается при программировании или в некоторых вычислительных программах (Matlab, Excel). Основная проблема записи строчных калькуляторов состоит в учете знаков и скобок. Если выражение довольно громоздкое, потеря одной скобки приводит к ошибкам и неверной работе всей программы. Конечно, в программировании и Matlab в вычислениях используются переменные, а в Excel – ячейки. Но числовой вариант всегда можно проверить при помощи однострочного калькулятора.

Кроме того, такой калькулятор прекрасно подойдет школьникам и студентам для текущих расчетов. При использовании обыкновенного калькулятора или программы на мобильном телефоне достаточно сложно считать выражения по формулам. Обычный калькулятор не имеет функции скобок, поэтому при расчете по формулам, которые представляют собой многочлены или дроби, школьникам приходится вычислять поэтапно значения в скобках. Калькулятор математического выражения позволяет записать все числа и сразу же получить результат, избегая промежуточных расчетов.

Пример использования

Школьная задача

В задаче по физике требуется вычислить перемещение тела при равноускоренном движении. Это простая задача, даны все переменные, которые требуется подставить в формулу:

S = S0 + Vo × t + (a × t²)/2

С использованием обычного калькулятора потребовалось бы вначале вычислить значение (a× t²)/2, затем Vo × t и только потом суммировать все члены выражения. При помощи калькулятора в одну строку это сделать куда проще. Пусть в задаче начальная координата S0 = 2, начальная скорость Vo = 20 м/с, время движения t = 10 с, а ускорение тела составляет a= 2 м/с². Зная значения всех параметров мы можем записать эти значения в строку согласно формуле и произвести вычисления. Запишем это с учетом синтаксиса калькулятора, в котором знак умножения записывается как * (звездочка):

S = 2 + 20 * 10 + (2 * 10²) / 2 = 213

Калькулятор мгновенно рассчитал выражение, и мы вычислили, что тело совершило перемещение на 213 метров.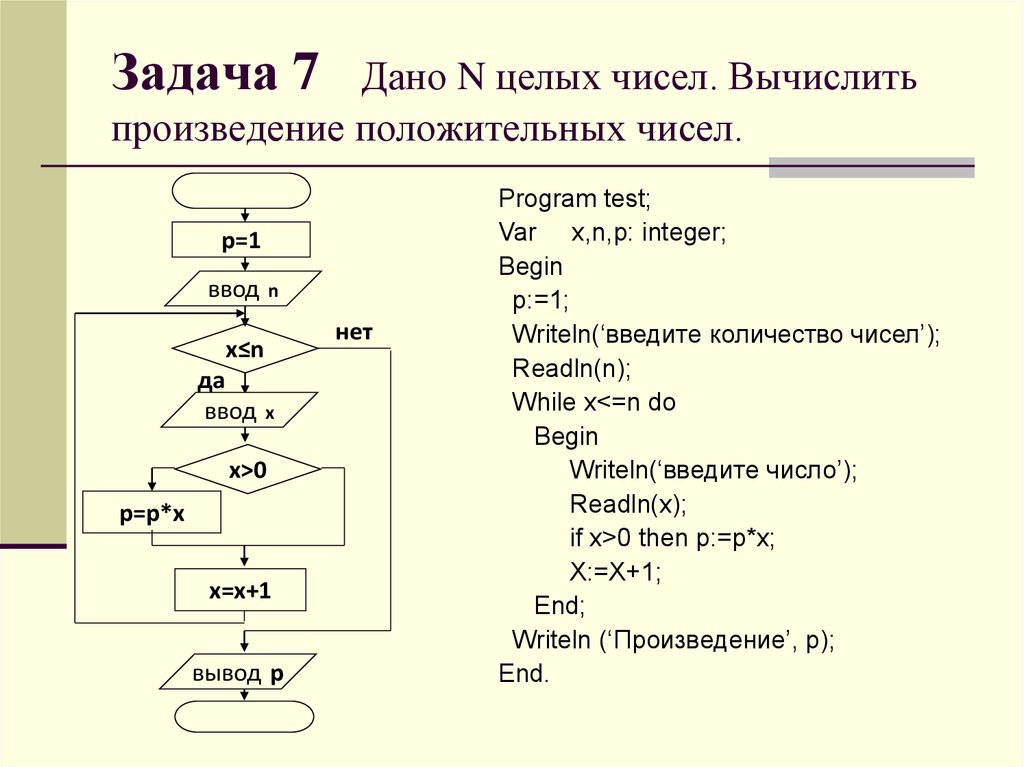

Заключение

Калькулятор математического выражения — это удобный инструмент, позволяющий быстро провести вычисления по заданной формуле. Используйте и другие калькуляторы из нашего каталога для упрощения или проверки своих выкладок.

Калькулятор алгоритма Евклида

перейти к калькулятору

перейти к основному содержанию

Базовый калькулятор

Алгоритм Евклида Калькулятор GCF

Значение 1:

Значение 2:

Ответ:

GCF(816, 2260) = 4

Решение

Задайте задачу на деление, где a больше, чем b.
a ÷ b = c с остатком R. Выполните деление. Затем замените a на b, замените b на R и повторите деление. Продолжайте процесс до тех пор, пока R = 0,

2260 ÷ 816 = 2 R 628 (2260 = 2 × 816 + 628)

816 ÷ 628 = 1 R 188 (816 = 1 × 628 + 188)

18 ÷ 98002 = 62003 18 98002 3 R 64 (628 = 3 × 188 + 64)

188 ÷ 64 = 2 R 60 (188 = 2 × 64 + 60)

64 ÷ 60 = 1 R 4 (64 = 1 × 60 + 4)

60 ÷ 4 = 15 R 0 (60 = 15 × 4 + 0)

Когда остаток R = 0, GCF является делителем b в последнем уравнении. GCF = 4

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.

Получить виджет для этого калькулятора

Поделитесь этим калькулятором и страницей

Калькулятор Используйте

Введите два целых числа, чтобы найти наибольший общий множитель ( GCF ). Посмотрите работу и узнайте, как найти GCF с помощью алгоритма Евклида.

Как найти

GCF Используя алгоритм Евклида

Даны два целых числа, где a больше b, разделить a ÷ b = c с остатком R.
Замените a на b, замените b на R и повторите деление.
Повторять шаг 2, пока R=0.

Когда R=0, делитель b в последнем уравнении является наибольшим общим множителем, GCF.

Поскольку наибольший общий делитель (НОД) и наибольший общий делитель (НОД) являются синонимами, алгоритм Евклида также работает для нахождения НОД.

Связанные калькуляторы

Чтобы найти GCF более двух значений, см. Калькулятор наибольшего общего фактора.

Для получения дополнительной информации и примеров использования алгоритма Евклида см. наш Калькулятор GCF и раздел, посвященный Алгоритм Евклида.

Ссылки

Бюро 42: Алгоритм Евклида: наибольшие общие факторы посредством вычитания.

Математический факультет Университета Рутгерса: Евклидов алгоритм.

Подписаться на CalculatorSoup:

Калькулятор расширенного алгоритма GCD — онлайн-поиск линейных комбинаций

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Расширенный алгоритм НОД

Инструмент для применения расширенного алгоритма НОД (метод Евклида) для нахождения значений коэффициентов Безу и значения НОД из 2 чисел.

Результаты

Расширенный алгоритм GCD — dCode

Теги: Арифметика

dCode и многое другое

Программа dCode бесплатна, а ее инструменты очень помогают в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Расширенный калькулятор НОД

Число A
Число B
Показать шаги алгоритма

См.

также: НОД (наибольший общий делитель) — Евклидово деление — тождество Безу

Ответы на вопросы (FAQ)

Что такое расширенный алгоритм GCD? (Определение)

Расширенный алгоритм Евклида является модификацией классического алгоритма НОД, позволяющей находить линейную комбинацию. Из двух натуральных чисел a и b его шаги позволяют вычислить их НОД и их коэффициенты Безу (см. тождество Безу).

Пример: $ a=12 $ и $ b = 30 $, поэтому $ gcd(12, 30) = 6 $

$$ 12 \times -10 + 30 \times 3 = 6 \\ 12 \times -3 + 30 \х 1 = 6 \ 12 \х 4 + 30 \х -1 = 6 \ 12 \х 11 + 30 \х -3 = 6 \ 12 \х 18 + 30 \х -5 = 6 \\ 12 \times −2+30 \times 1 = 6 $$

Как закодировать расширенный алгоритм НОД?

Вот реализация eGCD алгоритма псевдокода для нахождения линейной комбинации gcd(a,b) = a.u+b.v: function extended_gcd (a, b) {// a, b натуральные целые числа a < b r1 = b, r2 = a, u1 = 0, v1 = 1, u2 = 1, v2 = 0 в то время как (r2! = 0) do q = r1 ÷ r2 (целочисленное деление) r3 = r1 , u3 = u1, v3 = v1, r1 = r2, u1 = u2, v1 = v2, r2 = r3 - q * r2, u2 = u3 - q * u2, v2 = v3 - q * v2 end while return (r1, u1, v1) (r1 натуральное число и u1, v1 рациональные целые числа)

Значения таковы, что r1 = pgcd(a, b) = a * u1 + b * v1

Как алгоритм расширенного НОД работает с отрицательными числами?

Используя абсолютные значения для a и b, остальные вычисления идентичны благодаря свойству: $$ a(\text{sign}(a)\cdot x)+b(\text{sign}(b) \cdot y)=1 $$

Исходный код

dCode сохраняет за собой право собственности на исходный код «расширенного алгоритма GCD». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Расширенный алгоритм GCD», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Расширенного алгоритма GCD». Функции алгоритма (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Расширенного алгоритма GCD» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Расширенный алгоритм GCD» или любых его результатов разрешено, если вы цитируете dCode!
Экспорт результатов в виде файла .