3 х 2 график: Mathway | Популярные задачи

2

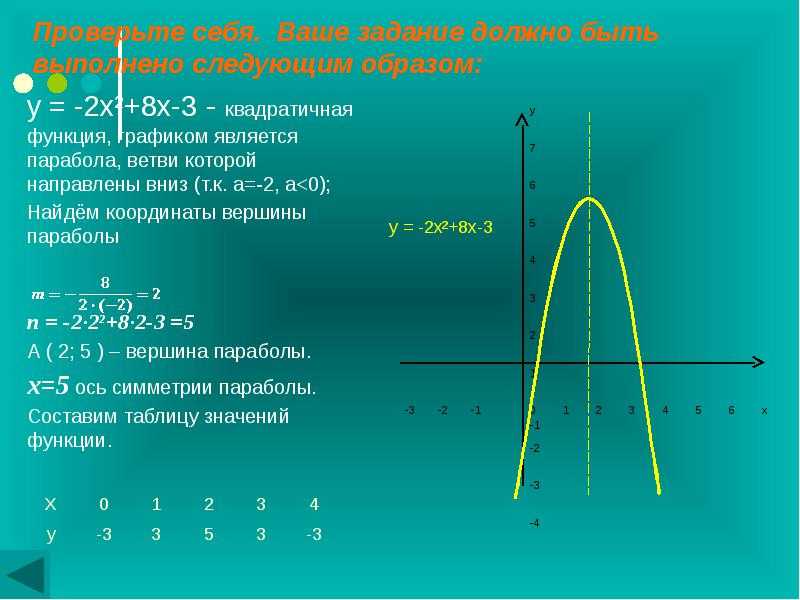
Постройте график функции y х2 3х 2. Квадратичная и кубическая функции

Разделы: Математика

Тема: “Построение графика квадратной функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)

Цель.

• Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
• Развить навыки построения графика функции, содержащей модуль.

Ход урока.

1. Этап актуализации знаний.

а) Проверка домашнего задания.

Пример 1. Построить график функции у = х 2 — 6х + 3. Найти нули функции.

Решение.

2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).

4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,

x 1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).

График на рис.1.

Алгоритм построения графика квадратной функции.

1. Определить направление “ветвей” параболы.

2. Вычислить координаты вершины параболы.

3. Записать уравнение оси симметрии.

4. Вычислить несколько точек.

б) Рассмотрим построение графиков линейных функций, содержащих модуль:

1. у = |х|. График функции на рисунке 2.

2.у = |х| + 1. График функции на рисунке 3.

3. у = |х + 1|. График функции рисунке 4.

Вывод.

1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.

2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.

2.Опирационно-исполнительная часть.

Этап исследовательской работы. Работа в группах.

Группа 1. Построить графики функций:

а) у = х 2 — 6|x| + 3,

б) у = |х 2 — 6х + 3|.

Решение.

1.Построить график функции у = х 2 -6х+3.

2. Отобразить его симметрично относительно оси Оу.

График на рисунке 5.

б) 1. Построить график функции у = х 2 — 6х + 3.

2. Отобразить его симметрично относительно оси Ох.

График функции на рисунке 6.

Вывод.

1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.

2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.

Группа 2.Построить графики функций:

а) у = |x 2 — 6|x| + 3|;

б) y = |x 2 — 6x + 3| — 3.

Решение.

1. График функции у = х 2 + 6x + 3 отображаем относительно оси Оу, получается график функции у = х 2 — 6|x| + 3.

2. Полученный график отображаем симметрично относительно оси Ох.

График функции на рисунке 7.

Вывод.

График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.

1. График функции у = х 2 — 6х + 3 отображаем относительно оси Ох.

2. Полученный график переносим на вектор {0;-3}.

График функции на рисунке 8.

Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.

Группа 3.Построить график функции:

а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.

Решение.

а) у = |x| (x — 6) + 3, имеем совокупность систем:

Строим график функции у = -х 2 + 6x + 3 при х

График функции на рисунке 9.

б) у = х |х — 6| + 3, имеем совокупность систем:

Строим график функции у = — х 2 + 6х + 3 при х 6.

2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).

3. Уравнение оси симметрии: х = 3.

4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.

Строим график функции у = х 2 — 6х + 3 при х = 7 у(7) = 10.

График на рис.10.

Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.

(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)

Получили сводную таблицу для графиков функций, содержащих модуль.

Таблица построения графиков функций, содержащих модуль.

Группа 4.

Построить график функции:

а) у = х 2 — 5x + |x — 3|;

б) у = |x 2 — 5x| + x — 3.

Решение.

а) у = х 2 — 5х + |х — 3|, переходим к совокупности систем:

Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по точкам у(4) = -3, у(5) = 2, у(6) = 9.

График функции на рисунке 11.

б) у = |х 2 — 5х| + х — 3, переходим к совокупности систем:

Строим каждый график на соответствующем интервале.

График функции на рисунке 12.

Вывод.

Выяснили влияние модуля в каждом слагаемом на вид графика.

Самостоятельная работа.

Построить график функции:

а) у = |х 2 — 5х + |x — 3||,

б) у= ||x 2 — 5x| + х — 3|.

Решение.

Предыдущие графики отображаем относительно оси Ох.

Группа.5

Построить график функции: у =| х — 2| (|x| — 3) — 3.

Решение.

Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.

Имеем совокупность систем уравнений:

Строим график на каждом из интервалов.

График на рисунке 15.

Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.

Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.

3.

Задание на дом.

Построить графики функций с различным расположением модуля:

1. у = х 2 + 4х + 2;

2. у = — х 2 + 6х — 4.

4. Рефлексивно – оценочный этап.

1.Оценки за урок складываются из отметок:

а) за работу в группе;

б) за самостоятельную работу.

2. Какой момент был наиболее интересен на уроке?

3. Трудное ли домашнее задание?

Построить функцию

Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру.

Преимущества построения графиков онлайн

• Визуальное отображение вводимых функций
• Построение очень сложных графиков
• Построение графиков, заданных неявно (например эллипс x^2/9+y^2/16=1)
• Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете
• Управление масштабом, цветом линий
• Возможность построения графиков по точкам, использование констант
• Построение одновременно нескольких графиков функций
• Построение графиков в полярной системе координат (используйте r и θ(\theta))

С нами легко в режиме онлайн строить графики различной сложности. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.

Квадратичная функция

Рис 1. Общий вид параболы

Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.

Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).

Основные свойства квадратичной функции

1. При х =0, у=0, и у>0 при х0

2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.

3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Если y=3×2+6x+2 отображается в плоскости xy, какая из следующих характеристик графика отображается как константа или коэффициент в уравнении?

Вопрос

Обновлено: 23. 05.2020

Рекомендуемые вопросы

9 видео

РЕКЛАМА

Текст Решение

A

Y-координата вершины 7 0 9090 9090 0906 Х-пересечение(я)

C

Y-точка

D

x-пересечение линии симметрии

Ответ

Правильный ответ C

Решение

Подстановка 0 вместо x в данном уравнении дает 2. Следовательно, график данного уравнения проходит через точку (0, 2), которая является точкой пересечения графика по оси y. Правая часть данного уравнения, y=3×2+6x+2, отображает константу 2, которая непосредственно соответствует y-координате точки пересечения y графика этого уравнения в плоскости xy.
Вариант А неверный. Координата y вершины графа равна −1, а не 3, 6 или 2. Вариант B неверен. Координаты x точек пересечения x графика примерно равны -1,577 и -0,423, а не 3, 6 или 2. Вариант D неверен. Координата х точки пересечения х линии симметрии равна −1, а не 3, 6 или 2. плоскость xy, то какая из следующих характеристик отображается как константа для эффективности в уравнении, если мы заменим 0 на X в данном уравнении, это будет читаться как bhai равно 3 x 0 весь квадрат + 6 x 0 плюс два скажи что-нибудь, но график данного уравнения проходит через точку ноль, к которой не что иное, как отсечение bhai отсечение, если мы рисуем график y + 3 X квадрат

+ 6 + 2 с помощью графического калькулятора с помощью программного обеспечения мы увидим, что данный график между разрезом по оси x в двух точках, которые — это 1 — 0,4 унции, а эта точка -1,5 77 Арджун Редди трейлер это -0,4 23, а это -1,577, это корни данного уравнения, поэтому ясно, что

выбор a неверен, потому что график данного уравнения между заданной вершиной как -1 справа минус один, но два — это точка пересечения, так что это не вариант пересечения X также неверен, потому что мы уже видели корни как -1,5 77 как второстепенные 0,423, и это не коррелирует с результатом, который был неверным, она верна и разбивает наш результат, найти хинди — это пересечение X линии симметрии это неправильная линия симметрии stx — это X равно минус единице, а не другим вариантам, поэтому это также неправильный вариант, поэтому единственный вариант — это вариант C, который соответствует нашему результату

Ответьте

Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

---

Похожие видео

В плоскости xy график y=3×2−14x пересекает график y = x в точках (0, 0) и (a, a). Какова ценность а?

181167185

Какое из следующих уравнений имеет график в плоскости xy, для которого y всегда больше или равно −1?

181172211

y=x2−6x+8
Приведенное выше уравнение представляет собой параболу в плоскости xy. Какая из следующих эквивалентных форм уравнения отображает точки пересечения параболы по оси x в виде констант или коэффициентов?

181172258

−2x+3y=6
В плоскости xy график какого из следующих уравнений перпендикулярен графику уравнения выше?

181173041

y=x2−a
В приведенном выше уравнении a является положительной константой, а график уравнения в плоскости xy представляет собой параболу. Что из следующего является эквивалентной формой уравнения?

181173099

Какая из следующих точек в плоскости xy является точкой пересечения графиков y=x+2 и y=x2+x−2?

185061334

Какое из следующих уравнений может быть уравнением графика в плоскости xy, показанной выше?

185062628

y=x2+16x+28
Уравнение выше представляет график параболы в плоскости xy.