Как развести бензин для бензопилы: официальный сайт Echotool.
Почему нужно смешивать масло и бензин
Для нормальной работы любому двигателю внутреннего сгорания нужны, как минимум, две вещи:
- Топливо — вернее топливовоздушная смесь, приготовленная карбюратором, попадает в камеру сгорания, воспламеняется, расширяется, и «толкает» поршень вниз, за счёт чего выполняется полезная работа.
- Смазка — необходима для уменьшения силы трения между соприкасающимися деталями двигателя.
В первую очередь, масло нужно для того, чтобы исключить так называемое «сухое» трение металла о металл. Из-за него контактирующие детали подвергаются критическому износу — появляются задиры, царапины, уменьшается компрессия, снижается ресурс. Также масло нужно для уплотнения зазоров.
Почему же нужно смешивать масло с топливом для бензопилы?
Это требование напрямую связано с особенностями устройства и принципом работы двухтактных двигателей, которыми оснащается данный инструмент.
Смазка деталей кривошипно-шатунного механизма и цилиндропоршневой группы здесь выполняется исключительно за счёт масла, находящегося в горючем. Благодаря особому устройству двигателя, топливовоздушная смесь попадает не только в камеру сгорания, но и в картер, где находится коленвал с шатуном. Таким образом, смазываются все трущиеся детали.
Соотношение количества масла и бензина для топливной смеси
Чтобы двухтактный двигатель бензопилы работал в оптимальном для него режиме, масло с бензином необходимо смешивать в определённых пропорциях. Они обычно указываются в инструкции к инструменту, а также на упаковках со смазкой. Рассмотрим вкратце, что будет, если рекомендуемых соотношений не соблюдать, или нарушать их по ошибке (незнанию).
Если масла добавить в бензин слишком мало, его концентрации не хватит для эффективной смазки трущихся деталей. Двигатель будет издавать звенящие звуки, чрезмерно греться, и быстро выйдет из строя.
Чтобы этих проблем избежать, масло с бензином надо смешивать в рекомендуемых производителем пропорциях. Указываются они в виде соотношений — 1:50, 1:40, 1:25 и так далее. Любая из этих пропорций говорит о том, сколько масла нужно лить на объём топлива. Например, для приготовления смеси по пропорции 1:25 понадобится 1 литр масла на 25 литров бензина.
Важно не перепутать! Довольно часто указанные пропорции воспринимаются пользователями наоборот. К примеру, 1:50 понимается, как на 1 литр бензина 50 миллилитров масла. Это грубая ошибка, которая приведёт к повышенной концентрации масла в горючем. На самом деле при таком соотношении на 1 литр масла нужно всего 20 миллилитров масла.
Как не запутаться в пропорциях? Ведь мало кому надо готовить 50, или даже 25 литров топливной смеси для бензопилы. Тем более, что хранить смешанный с маслом бензин долго нельзя. Обычно готовят столько, сколько потребуется на день-два. А с учётом небольшого расхода бензопилы это 1-5 литров.
Есть три способа, как правильно развести бензин для бензопилы в небольших объёмах:
- Поделить 1000 на вторую цифру в пропорции. К примеру, нужно приготовить смесь в соотношении 1:40. Делите 1000 на 40, получаете 25. Столько миллилитров масла льёте на 1 литр бензина.
- Решить пропорцию, как в школе. Для этого требуемый объём бензина в литрах делим на вторую цифру в пропорции. В результате получаем нужный объём масла в литрах. Переводим литры в миллилитры для удобства. Допустим, вам нужно 3 литра смеси в пропорции 1:50. Решаем: 3/50=0,06 л. Чтобы превратить литры в миллилитры, переносим запятую на три знака вправо, и получаем 60 миллилитров.

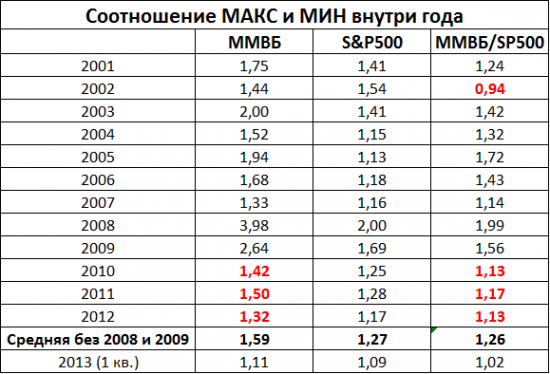
- Посмотреть в таблице. Это самый простой, быстрый и наглядный способ, если пропорции стандартные. Остальные два способа нужны для того, чтобы понять, почему при пропорции 1:50 нужно лить на литр бензина 20 миллилитров масла, а не 50.
| Пропорция | Масла на 1 л бензина (мл) |
| 1:20 | 50 мл |
| 1:25 | 40 мл |
| 1:30 | 33 мл |
| 1:35 | 28 мл |
| 1:40 | 25 мл |
| 1:45 | 22 мл |
| 1:50 | 20 мл |
Теперь кратко о том, почему у разных производителей отличаются пропорции и нет какого-то единого стандарта.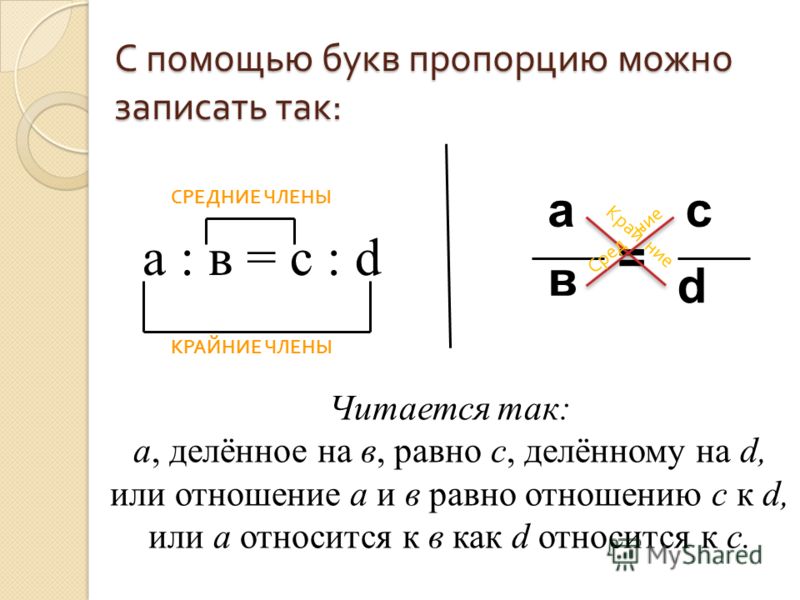 На это есть, как минимум, три причины. Во-первых, разные характеристики масел и бензина. Во-вторых, качество сборки двигателей (технологии, материалы) тоже отличается. В-третьих, режим эксплуатации инструмента. К примеру, для обкатки бензопил некоторых производителей рекомендуется добавлять в смесь на 20% больше масла.
На это есть, как минимум, три причины. Во-первых, разные характеристики масел и бензина. Во-вторых, качество сборки двигателей (технологии, материалы) тоже отличается. В-третьих, режим эксплуатации инструмента. К примеру, для обкатки бензопил некоторых производителей рекомендуется добавлять в смесь на 20% больше масла.
Пошаговая инструкция по заправке
Для приготовления топливной смеси и заправки бензопилы понадобится:
- мерная ёмкость;
- чистый бензин с октановым числом 92;
- специальное масло для двухтактных моторов с воздушным охлаждением;
- ёмкость для готовой смеси;
- воронка.
Для измерения объёмов можно использовать ёмкость, которыми обычно комплектуются бензиновые инструменты. Также можно купить специальные фирменные канистры с отделами и мерными приспособлениями.
Пошаговая инструкция:
- Приготовьте ёмкость для готовой топливной смеси.
 Её вместительности должно хватить и для бензина, и для масла.
Её вместительности должно хватить и для бензина, и для масла. - Посчитайте пропорцию смазки и бензина, исходя из руководства по эксплуатации, и воспользовавшись одним из способов выше.
- Отмерьте и налейте в ёмкость требуемый объём бензина.
- При помощи мерного стакана, штатной бутылочки или шприца отмерьте и добавьте в бензин нужный объём масла.
- Ёмкость для готовой смеси в итоге не должна быть полной под завязку.
- Надёжно закройте ёмкость крышкой, и несколько раз переверните её для того, чтобы масло смешалось с бензином.
- Заправьте приготовленную смесь в топливный бак бензопилы.
Вопреки гуляющему по Сети мнению, нет разницы, что первое заливать в ёмкость для приготовления смеси — бензин или масло. Главное, не забудьте тщательно перемешать. Вот чего на самом деле не стоит делать, так это готовить топливную смесь непосредственно в топливном баке бензопилы.
назад в блог
Золотое сечение как объяснение пропорций красоты
Главная Статьи Золотое сечение — пропорции красотыНад чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.
Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?
На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.
Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.
Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.
Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».
Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.
a : b = b : c или с : b = b : а.
Так что же особенного в этом соотношении?
Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:
То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).
Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».
Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».
В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.
Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился. Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».
История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д., известный, как ряд Фибоначчи.
Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.
В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.
Так в чём же ореол таинственности «золотого сечения»?
Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.
Паук плетёт паутину по спирали, ДНК человека закручено по спирали.
А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а
Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».
Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.
Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.
А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.
Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т.д.
Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.
Какие же пропорции в лице человека стремятся к «золотому сечению»?
Прежде всего, у людей с красивыми лицами наблюдается:
- Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка.
 Это соотношение называется «динамической симметрией» или «динамическим равновесием».
Это соотношение называется «динамической симметрией» или «динамическим равновесием». - Соотношение высоты верхней и нижней губы будет 1,618.
- Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
- Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
- Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
- Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
- Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».

Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.
В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.
Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».
Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».
Вот некоторые примеры соотношений размеров и расстояний между зубами:
- Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
- В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.

- Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.
- Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.
И этот список можно продолжить.
Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?
Разумеется, искать применение золотых пропорций в эстетической стоматологии.
Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».
Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.
А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.
И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.
Время работы
| Пн-Пт | 10:00 — 22:00 |
| Сб-Вс | 10:00 — 20:00 |
Калинина Елена Викторовна Врач-гигиенист
ПОСЛЕДНИЕ СТАТЬИ
Как соблюдать зубную гигиенуПротезирование зубов: металлокерамика и другие материалыПротезирование на имплантахИзготовление съемных зубных протезов и их ценаКак проходит процесс диагностики зубов
Что такое 1/3 как отношение? – Обзоры Вики
1: 3 = 2: 6 = 3: 9 = 4: 12 = 5: 15 = 6: 18 = 7: 21…. Все эти соотношения показывают одинаковую взаимосвязь. Упрощение отношений до простейшей формы может быть полезно при решении задач, связанных с отношениями.
Точно так же, что такое разведение от 1 до 3? Если у вас разведение 1:3, т.е. коэффициент разбавления 1:3, это означает, что вы добавить 1 единицу объема растворенного вещества (например, концентрата) к 3 единице объема растворителя (например, воды), что даст всего 4 единицы объема. … Возможно, вы уже используете коэффициент разбавления в своей повседневной жизни, даже не подозревая об этом!
… Возможно, вы уже используете коэффициент разбавления в своей повседневной жизни, даже не подозревая об этом!
Какова пропорция 1 стакана? 1:x означает 1 часть концентрата на x частей воды.
…
Диаграмма конверсии.
| 1 галлон = 128 унций | 1/4 чашки = 2 унции |
|---|---|
| 1 чашка = 8 унций | 2 пинты = 1 литр |
| 1/2 чашки = 4 унции | 4 кварты = 1 галлон |
Как рассчитать соотношение чашек? Поскольку в одной чашке 8 унций, 3 чашки равны 24 унциям:
- 3 чашки * 8 унций/чашка = 24 унции. Теперь два числа 3 чашки и 56 унций можно записать в виде следующего соотношения:
- от 24 унций до 56 унций,
- 0.21 = 21% = 21/100. к алгебраическим выражениям.
Во-вторых, что означает соотношение 1:1? соотношение 1:1 1 часть или 1 единица определенного количества. например, две бутылки воды содержат по 2 литра воды в каждой, соотношение будет 22=11=1:1. две коробки по 50 граммов масла в каждой, соотношение будет 5050=11=1:1.
две коробки по 50 граммов масла в каждой, соотношение будет 5050=11=1:1.
Как найти соотношение 1:1?
2 ответы
- две бутылки воды по 2 литра в каждой. соотношение будет 22 = 11 = 1: 1.
- две коробки по 50 граммов масла в каждой. соотношение будет 5050 = 11 = 1: 1.
тогда что такое соотношение 1 к 1 в выпечке? Фунт или бисквит – 1:1:1:1. Одно из самых простых соотношений для запоминания, фунт и бисквит требуют 1 часть муки, 1 часть яйца, 1 часть жира и 1 часть сахара..
Что такое соотношение 1/2? Соотношение 1:2 читается как «1 к 2». Это средство всего 3, одна часть стоит 1, а другая часть стоит 2. Чтобы преобразовать отношение частей к частям в дроби: Добавьте члены отношения, чтобы получить целое. Используйте это как знаменатель.
Что такое соотношение 3 к 2?
Например, соотношение 3:2 равно 6: 4 и 300: 200. Совет по точности. В подобном вопросе быстрая проверка заключается в следующем. пропорции суммируются с исходной суммой. 900 + 300 + 1200 = 2400.
900 + 300 + 1200 = 2400.
Каков размер 1 1? Соотношение 1:1. Соотношение 1:1 означает, что ширина и высота изображения равны, образуя квадрат. Некоторые распространенные соотношения 1:1 являются фото 8″x8″, изображение размером 1080 x 1080 пикселей или, как правило, любой шаблон изображения профиля на сайтах социальных сетей.
Как рассчитать 3 коэффициента?
Как рассчитать соотношение трех чисел
- Шаг 1: Найдите общее количество частей в соотношении, сложив числа в соотношении.
- Шаг 2: Найдите значение каждой части в соотношении, разделив полученное количество на общее количество частей.
- Шаг 3: Умножьте исходное соотношение на стоимость каждой части.
Как вы используете пропорции в выпечке?
Как работают пропорции выпечки. Пропорции выпечки основаны, как вы уже догадались, на математике.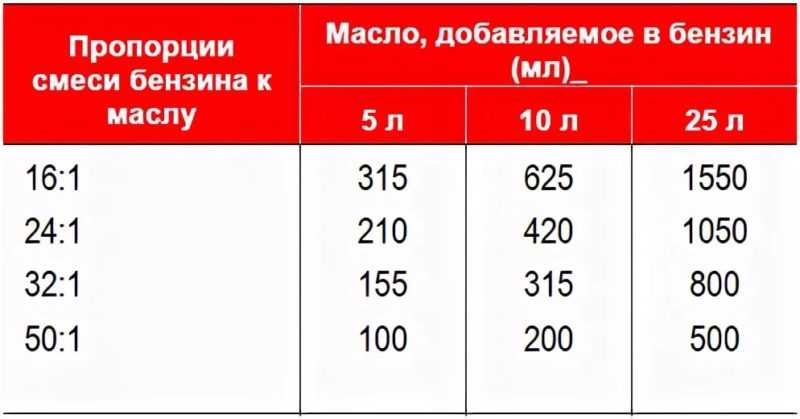 Чтобы все было кратко и сладко, пропорции выпечки разбивается на «части». Эти части описывают, сколько вам нужно каждого основного ингредиента (например, яиц, жидкости и муки), и все они должны измеряться в одной и той же единице измерения.
Чтобы все было кратко и сладко, пропорции выпечки разбивается на «части». Эти части описывают, сколько вам нужно каждого основного ингредиента (например, яиц, жидкости и муки), и все они должны измеряться в одной и той же единице измерения.
Какая пропорция для торта?
Но на самом деле, потому что соотношение для тортов 1: 1: 1: 1 (одна часть яиц на одну часть сахара на одну часть масла на одну часть муки). Когда все ингредиенты весят одинаково, у вас, по сути, есть пирог из фунта.
Каково соотношение 3 к 2? Например, соотношение 3:2 равно 6: 4 и 300: 200.
Равны ли отношения 1 к 2 и 2 к 3? Итак, умножим числитель и знаменатель так, чтобы знаменатель обеих этих дробей был равен 6. Отсюда можно сказать, что отношения 1:2 и 2:3 не эквивалентны.
Как разделить 3 соотношения?
Какое соотношение 4 к 1? Обратите внимание, что отношение 12 к 3 эквивалентно отношению 4 к 1, то есть 12:3 = 4: 1.
Как вы решаете проблемы соотношения?
Как решить задачу на соотношение
- Сложите доли коэффициента, чтобы найти общее количество долей.
- Разделите общую сумму на общее количество акций.
- Умножьте на необходимое количество акций.
Как рассчитать соотношение сторон? Как рассчитать соотношение сторон?
- Возьмите свой первоначальный рост. В нашем примере это будет 1200 пикселей.
- Возьмите исходную ширину. …
- Разделите высоту на ширину, например 1200/1600 = 0.75.
- Умножьте частное на предпочтительную ширину, например 0.75 * 300 = 225.
- Результирующая цифра — это ваша новая высота в пикселях.
Какое соотношение сторон 1200х628?
Рекомендуемый размер изображения: 1,200 x 628 пикселей. Соотношение изображения: 1.91:1.
Какой размер соответствует соотношению 4/3? Что такое соотношение сторон 4:3? В кино и на телевидении соотношение сторон 4:3 означает ширина и высота изображений 4 единицы в ширину и 3 единицы в высоту. Это слово также известно как 1.33:1 и часто произносится как «Четыре-три», «Четыре-к-трем» или «Четыре-на-три».
Это слово также известно как 1.33:1 и часто произносится как «Четыре-три», «Четыре-к-трем» или «Четыре-на-три».
Как решить проблему с соотношением сторон 3?
Как упростить 3 отношения? Чтобы упростить отношение с 3 числами, делите все 3 числа в соотношении на одну и ту же сумму, пока они не могут быть разделены точно дальше. Например, упростите соотношение с тремя числами 3:20:5. Каждое из 10, 20 и 5 можно разделить ровно на 10. Соотношение 5:20:5 упрощается до 10:4:1.
Что такое соотношение трех членов?
Трехчленное соотношение сравнивает три величины, измеренные в одних и тех же единицах. Соотношение красных и черных плиток к синим можно записать как 6:3:3 или 6 к 3 к 3. Соотношение в самом низком выражении равно 2:1:1 или 2 к 1 к 1. • Двухчленное соотношение сравнивает две величины, измеряемые в одних и тех же единицах.
Каково соотношение муки и сахара?
Сахар = Мука
A чашка сахара весит около 7 унций, а чашка универсальной муки весит около 4-1/2 унций. Итак, если мы создаем рецепт с 1 чашкой сахара, нам понадобится около 1-1/2 чашки муки (около 6-3/4 унций).
Что означает 1 1 в рецепте? Когда две величины взяты в одинаковой пропорции, говорят, что они находятся в соотношении 1:1. Например, 1 фунт кекса содержит муку и сахар в соотношении 1:1. Это означает, что в этой смеси оба элемента одинаково сбалансированы, на 100 грамм муки нужно добавить 100 грамм сахара.
Какое уравнение вы собираетесь использовать для преобразования вашего рецепта?
Современные страницы и веб-части полностью реагируют на различные устройства, поэтому масштаб изображений, используемых в веб-частях, зависит от того, где они показаны, какой макет используется и какое устройство их просматривает. Например, современные страницы прекрасно смотрятся на мобильных устройствах, а автоматическое масштабирование изображений помогает создать привлекательный вид.
Например, современные страницы прекрасно смотрятся на мобильных устройствах, а автоматическое масштабирование изображений помогает создать привлекательный вид.
Какие размеры изображений лучше всего работают?
Из-за быстрой компоновки страницы не существует определенной высоты или ширины в пикселях, что гарантирует сохранение определенной фигуры на разных устройствах и макетах. Изображения автоматически меняются и обрезаются, чтобы демонстрировать наилучший результат на различных устройствах и макетах. Однако существуют некоторые рекомендации, которые помогут вам убедиться, что изображения хорошо смотрятся на страницах.
Поиск изображений наилучшего размера зависит от указанных здесь факторов.
-
Пропорции:отношение между высотой и шириной изображений
org/ListItem»>
-
Макет веб-части:макет веб-части, в которой используется изображение
Макет столбца:тип и количество столбцов на странице
Пропорции
Пропорции — это отношение между шириной и высотой изображений. Обычно оно выражается в двух числах, таких как 3:2, 4:3 или 16:9. Ширина всегда является первым числом. Например, соотношение 16:9 может иметь ширину 1600 пикселей на 900 пикселей в высоту. Это может быть 1920 x 1080, 1280 x 720 или любые другие комбинации ширины и высоты, которые можно вычислить, равные 16:9. Калькуляторы пропорций можно найти в Интернете и некоторых средствах редактирования фотографий, чтобы определить пропорции изображений.
В большинстве случаев изображения в современных веб-частях лучше всего работают на разных макетах и устройствах с соотношением сторон 16:9 или 4:3 в зависимости от макета.
Макеты столбцов
На странице можно найти разделы с различными типами столбцов и макетами, такими как полно ширинные столбцы, один столбец, два столбца, три столбца, один третий левый и один третий правый столбец. Обычно изображения, которые должны заполнять ширину столбца, должны быть по крайней мере такой же ширины, как и в столбце, в котором они размещены. Например, изображение веб-части изображения в одном столбце должно иметь ширину не менее 1204 пикселей. Ниже указаны правила ширины для каждого макета столбца.
|
Макет |
Ширина в пикселях |
|
Столбец «Ширина» |
1920 |
|
Одна колонка |
1204 |
|
Два столбца |
586 в столбец |
|
Три столбца |
380 в столбец |
|
Третий левый столбец |
380 для левого столбца; 792 для правого столбца |
|
Один-третий правый столбец |
792 для левого столбца; 380 для правого столбца |
Из-за скорости реагирования страниц изображения в полношириных столбцах всегда будут отображаться на полноширивной странице с автоматической высотой в зависимости от размера экрана.
Высота изображений в других макетах столбцов будет зависеть от пропорций. Ниже указаны рекомендации по высоте и ширине для пропорций 16:9 и 4:3 (округлка вверх/вниз до ближайшего пикселя). Это помогает, например, сохранить ширину и высоту изображений с соответствующим масштабом для мобильных устройств.
|
ПРОПОРЦИИ МАКЕТ |
16 x 9 Ширина x высота в пикселях |
4 x 3 Ширина x высота в пикселях |
|---|---|---|
|
Одна колонка |
1204 x 677 |
1204 x 903 |
|
Два столбца |
586 x 330 |
586 x 439 |
|
Три столбца |
380 x 214 |
380 x 285 |
|
Третий левый столбец |
380 x 446 для левого столбца; 792 x 446 для правого столбца |
380 x 594 для левого столбца; 792 x 594 для правого столбца |
|
Один-третий правый столбец |
792 x 446 для левого столбца; 380 x 446 для правого столбца |
792 x 594 для левого столбца; 380 x 594 для правого столбца |
Макеты веб-части
Макеты в веб-частях, которые вы используете, также влияют на масштаб изображений. В следующих примерах различные веб-части и их макеты в одном столбце, а также пропорции, используемые в каждой из них.
В следующих примерах различные веб-части и их макеты в одном столбце, а также пропорции, используемые в каждой из них.
Рассмотрим это изображение с исходными пропорциами 16:9:
Ниже показаны примеры рисунка, показанного в макете страницы с одной колонкой в разных веб-частях и макетах.
|
Веб-часть «Главного сайта» |
Для макетов плиток и слоев имеются следующие пропорции:
Слои: индивидуальные шкалы слоев до пропорций 8:3, а изображения внутри каждой шкалы слоев — с соотношением сторон 16:9. Ниже показан пример изображения, показанного в макетах «Слои» (сверху) и «Плитки» (внизу).
|
|
Веб-часть «Выделенное содержимое» |
16:9 — пропорции для макетов «Карусель», «Пленка» и «Карточки». Ниже показан пример изображения, показанного в макетах «Пленка» (сверху) и «Карточки» (внизу).
|
|
Веб-часть «Изображение» |
Изображения будут расширяться по ширине раздела, содержащего веб-часть. Вы можете изменить пропорции или обрезать рисунок вручную с помощью панели инструментов «Изображение», а также увеличить или увеличить изображение с помощью хи24-часового режима. Ниже показан пример обрезных меток изображения (синие линии) в 4:3
|
|
Веб-часть «Галерея изображений» |
В разных макетах используются следующие пропорции:
В макете «Блок-блоки» пропорции всех показанных изображений: 16:9, 1:1, 4:3 и так далее. Ниже показан пример изображения, показанного в макетах «Плитки» (сверху) и «Мозаика» (внизу).
|
|
Веб-часть «Новости»: |
В зависимости от макета, изображения в веб-части «Новости» могут быть 4:3, 16:9 или 21:9. Вот пример изображений в верхней истории и макете карусель.
|
|
Область заголовка страницы |
Изображения лучше всего выглядят, когда они имеют альбомную или соотношение сторон 16:9 или больше и имеют размер не менее 1 МБ. Пример (исходное изображение 16:9) с фокальной точкой на динамике.
|
|
Эскиз страницы |
Эскизы страниц можно вывести в таких местах, как результаты поиска, выделенное содержимое, новости и другие. По умолчанию эскизы выводится из области заголовка страницы или веб-части, которая находится в первом порядке на странице (например, слева вверху). Вы можете переопременить заданный по умолчанию и изменить эскиз страницы. При этом лучше использовать изображение с пропорцией 16:9. Пример (исходное изображение 16:9)
|
|
Веб-часть «Быстрые ссылки» |
Веб-часть «Быстрые ссылки» имеет шесть разных макетов. Ниже советуем использовать пропорции.
Ниже показан пример изображения, показанного в макетах «Сжатая» (сверху) и «Пленка» (внизу).
|
Советы:
-
При добавлении изображения в область заголовка страницы или веб-части главного имиджегового рисунка также лучше всего установить его фокальной точкой.
 Дополнительные информацию о настройке фокальной точки для этих двух сценариев см. в веб-части «Изменение фокальной точки рисунка в веб-части «Главного имиджевного рисунка» и настройке области заголовка на странице.
Дополнительные информацию о настройке фокальной точки для этих двух сценариев см. в веб-части «Изменение фокальной точки рисунка в веб-части «Главного имиджевного рисунка» и настройке области заголовка на странице. -
Рекомендации по изображению в заглавной области сайта
Кроме страниц, может потребоваться добавить дополнительные логотипы или изображения. Ниже рекомендации по размеру этих элементов.
|
Элемент |
Описание |
Рекомендации Ширина x высота в пикселях |
|---|---|---|
|
Логотип сайта |
Логотип большего размера, который может быть не квадратным и прозрачным в зависимости от добавленного оформления |
192 x 64 Формат: PNG, JPEG, SVG (SVG не разрешено на сайтах, подключенных к группе) |
|
Эскиз логотипа сайта |
Эскиз квадратного логотипа, который используется при отправке логотипа сайта или в местах, где требуется использовать квадратный формат Это необходимый элемент. |
64 x 64 Формат: PNG, JPEG, SVG (SVG не разрешено на сайтах, подключенных к группе) |
|
Логотип сайта с расширенным макетом |
В расширенном макете загона имеется расширенная ширина логотипа сайта. |
300 x 64p Формат: JPEG, PNG, SVG |
|
Фоновое изображение расширенного макета |
Новое фоновое изображение, которое можно использовать с расширенным header. |
2560 x 164 Формат: JPEG, PNG |
Непрерывная пропорция
392.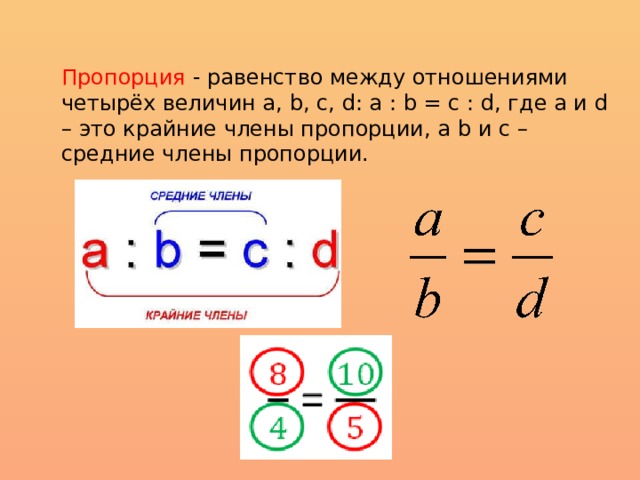 4} $
4} $
Когда некоторые величины находятся в непрерывной пропорции, количество пар, и, конечно, количество соотношений, на одно меньше количества величин. Таким образом пять пропорциональных величин a, b, c, d, e, образуют четыре пары и четыре соотношения и соотношение a:e равно соотношению a4:b4, то есть, соотношения первой величины в четвертой степени к второй величине в четвертой степени. Отсюда,
393. Если три величины пропорциональны, то первая пропорциональна третьей, так же как и квадрат первой к квадрату второй; или квадрат второй к квадрату третьей. Другими словами, отношение первой величины к третьей в два раза больше, чем соотношение первой ко второй. И наоборот, если первая из трёх величин относится к третьей, также как квадрат первой к квадрату второй, то при величины пропорциональны.
Если a:b = b:c, то a:c = a2:b2. Всегда,
394. Если несколько величин находятся в постоянной пропорции, то отношение первой величины к последней равно одному из промежуточных соотношений в степени с показателем степени на один меньше, чем количество величин.
Так, если имеются четыре члена пропорции a, b, c, d, то a:d = a3:b3
А если пять a, b, c, d, e; a:e = a4:b4, etc.
395. Если несколько величин находятся в непрерывной пропорции, то они будут также пропорциональны когда общий порядок будет обратным. Это уже было доказано относительно четырёх пропорциональных величин. (Статья 376.) Это может распространяться на любое количество величин.
Отношения между числами, 64, 32, 16, 8, 4,
равны 2, 2, 2, 2,
При размещении их в обратном порядке 4, 8, 16, 32, 64,
отношения равны ½, ½, ½, ½.
Поэтому если порядок любых пропорциональных величин инвертирован, то соотношения в первой последовательности будут обратными величинами к соотношениям во второй. Так при инверсии каждый предыдущий член соотношения становится последующим, и наоборот и отношение последующего к предыдущему члену обратно отношению предыдущего к последующему. (Статья 346.) То, что величины обратные равным между собой равны следует из Аксиомы 4.
(Статья 346.) То, что величины обратные равным между собой равны следует из Аксиомы 4.
396. Гармоническая пропорция это подвид геометрической пропорции. Она состоит из равных геометрических соотношений, но один или более членов является разностью двух величин.
Три или четыре величины называются гармонической пропорцией, то отношение первой к последней величины равно отношению разниц двух первых и двух последних величин.
Так, если три величины a, b, и c, составляют гармоническую пропорцию, то a:c = a-b:b-c.
Если величины a, b, c, и d are находятся в гармонической пропорции, то a:d = a-b:c-d.
Из этого следует, что числа 12, 8, 6, находятся в гармонической пропорции.
И четыре числа 20, 16, 12, 10, также составляют гармоническую пропорцию.
397. Если четыре величины находятся в гармонической пропорции и даны три из них, то последнюю можно найти. Так из пропорции
a:d = a-b:c-d,
при произведении крайних членов получаем ac — ad = ad — bd.
И это уравнение может быть упрощено для нахождения значения одной из переменных.
Таким образом, перенеся -ad, и разделив на a,
$c=\frac{2ad-bd}{a}$.
Пусть x= большая, и 49-x = меньшая.
Согласно предложенным условиям, x+6:38-x = 9:2
Сложим члены, (Статья. 385, 2.) x+6:44 = 9:11
Разделим знаменатели, (Статья. 378, 8.) x+6:4 = 9:1
Перемножим крайние члены и получается, что x+6 = 36. И x = 30.
2. Что за число, при добавлении порознь к которому 1, 5, и 13, первая сумма будет относится ко второй, как вторая к третьей?
Пусть x= нужное число.
Согласно предложенным условиям, x+1:x+5 = a+5:x+13
Отняв члены, (Статья. 385,2.) x+1:4 = x+5:8
Поэтому 8x+8 = 4x+20. И x = 3.
3. Разделить число 18 на две части таким образом, чтобы квадраты этих частей были бы в отношении 25 к 16.
Пусть x= большая часть, а 18 — x= меньшая часть.
Согласно условию, x2:(18-x)2 = 25:16
Квадратный корень, (Статья. 387,) x:18-x = 5:4
Сложив члены, x:18 = 5:9
Разделив члены, x:2 = 5:1
Поэтому, x = 10.
4. Если число разделено на две части так, что одна относится к другой в удвоенном соотношении 3 к 1, то какое число является средним пропорциональным между этими частями?
Пусть x= большая часть, и 20-x= меньшая.
Согласно условиям, x:20-x = 32:12 = 9:6
Сложив члены, x:20 = 9:10
Поэтому, x= 18. И 20-x = 2
Среднее пропорциональное между 18 и 2(Статья. 372.) =√2.18 = 6.
5. Есть два числа, произведение которых 135, а разница их корней относится к корню их разности, как 4 к 1. Найти числа?
Ответ: 15 и 9.
6. Найти числа, чья разность, сумма и произведение относятся как 2, 3, и 5, соответственно?
Ответ: 10 и 2.
7. Разделить число 24 на две такие части, что их произведение относилось к сумме их квадратов, как 3 к 10.
Ответ: 18 и 6.
8. В смеси рома и бренди, разница в количестве каждого относится к количеству бренди, как 100 относится к количеству галлонов рома и та же самая разность относится к количеству рома, как число 4 относится к количеству галлонов бренди. Сколько галлонов каждого компонента?
Ответ: 25 рома и 5 бренди.
9. Есть два числа, которые относятся друг к другу, как 3 к 2. Если прибавить 6 к большему числу и отнять от меньшего, тогда отношение суммы и разности будет 3 к 1. Найти эти числа.
Ответ: 24 и 16.
10. Есть два числа, произведение которых равно 320, а разница их кубов относится к кубу их разности, как 61 к 1. Каковы эти числа?
Ответ: 20 и 16.
11. Есть два числа, которые относятся друг к другу, как удвоенное отношение 4 к 3 и их среднее пропорциональное равно 24. Найти эти числа.
Найти эти числа.
Ответ: 32 и 18.
Что значит соотношение 1:1, 1:2 или 1:3 в рецептах?
Все вопросы → Домашний очаг → Рецепты
Спрашивает Марат Кунакбаевич 10 дек 2021
Как понять эти соотношения?
Ответы
Мне кажется, я правильно поняла автора вопроса. Поэтому попытаюсь донести свою точку зрения максимально-просто. И предельно-понятно))
Дело в том, что сегодня в кратких рецептах (в отличие от подробных!) чаще всего не указывается количество участвующих в том или ином блюде ингредиентов: в граммах, в миллиграммах и в килограммах. Это в старинных рецептах писалось примерно так: взять килограмм крепких сочных яблок и на этот килограмм добавить столько-то сахара и непременно столько-то имбиря и корицы положить…
Вот, если бы мне пришлось писать собственный рецепт бефстроганова, то (на старинный лад и со свойственной мне занудностью) я бы написала так: чтобы получить отличный бефстроганов, на один кэгэ говядины в нарезке положите не меньше одного кэгэ нарезанного репчатого лука. Ребята, только тогда будет вкусно, уж поверьте!..
Ребята, только тогда будет вкусно, уж поверьте!..
В то же время в кратком изложении мой рецепт имел бы право быть таким: бефстроганов – это говядина с репчатым луком 1:1 (один к одному). И — никаких установочных килограммов… Но! Для кого-то покажется, что лука многовато будет. Тогда он напишет свой рецепт, в котором лука добавит в два раза меньше))
Однако, стоп. Тут возникает закономерный вопрос: а зачем вообще указывать эти килограммы, если я, например, собираюсь готовить бефстроганов не из килограмма мяса, а из трёх кэгэ?.. И кто-то ещё вопрошает: а я буду готовить это же блюдо из тонны мяса, мне-то сколько лука потребуется?..
Вот тогда-то в рецептах люди и придумали указывать пропорции использованных продуктов, а не граммы с килограммами. То есть люди приноровились для упрощения отмечать не количество, а соотношение частей продуктов, участвующих в приготовлении блюда. Соотношение ингредиентов.
1 (один) – означает одну часть;
2 (две) – означает две части;
3 (три) – означает три части;
и так дальше…
На всякий случай. Посмотрите на сайте «Математика с нуля для начинающих». Пункт 24 «Соотношения», там всё подробно.
Посмотрите на сайте «Математика с нуля для начинающих». Пункт 24 «Соотношения», там всё подробно.
spacemath xyz
Jusha 11 дек 2021 11:21
★★★★★★★★★★
Если мы примемся разбираться, что же такое значит «соотношение», то обнаружим, что понятие «соотношение» имеет несколько значений и применяется в разных областях нашей жизни.
Для ответа на заданный вопрос из всего списка определений нам понадобится математическое определение соотношения. В математике также используются соотношения для разных целей: как взаимосвязь между двумя числами одного рода и как мера относительной величины двух количеств. Вот именно второй вариант нас и интересует.
Означает это понятие то, что количество одного вещества соотносится с количеством другого вещества. Единицы измерения количества вещества в данном случае должны использоваться одинаковые: килограммы, граммы, стаканы, чашки и тому подобное.
Если рассматривать соотношения в рецептах, то означать это будет следующее. Например, 1:1 (произносится «один к одному») означает, что для приготовления блюда нужно будет взять по 1 части обозначенных продуктов, то есть равное количество: по 1 килограмму помидоров и огурцов к салату или по 1 стакану сметаны и сахара для крема и так далее. Если указано соотношение 1:2, то это означает, что нужно взять 1 часть одного компонента, а 2 части второго. К примеру, 1 килограмм мяса и 2 килограмма картофеля для жаркого или какого-то другого блюда.
Например, 1:1 (произносится «один к одному») означает, что для приготовления блюда нужно будет взять по 1 части обозначенных продуктов, то есть равное количество: по 1 килограмму помидоров и огурцов к салату или по 1 стакану сметаны и сахара для крема и так далее. Если указано соотношение 1:2, то это означает, что нужно взять 1 часть одного компонента, а 2 части второго. К примеру, 1 килограмм мяса и 2 килограмма картофеля для жаркого или какого-то другого блюда.
Другие соотношения расшифровываются аналогичным образом. В рецепте может быть указано также соотношение не только двух продуктов, но и больше. К примеру, для какой-нибудь закуски на зиму, может быть указано такое соотношение: взять кабачок, морковь, болгарский перец и репчатый лук в соотношении 4:3:1:1, то есть по 4, 3 и 1 килограмму соответственно.
Enigma 26 янв 2022 13:49
★★★★★★★★★★
Соотношения в рецептах: 1:1, 1:3 и т.д.: как расшифровать и понять?
Такими значениями показывается взаимосвязь между двумя числами — величинами. Они могут измеряться и выражаться в самых разных характеристиках, например, обозначать массу, стоимость, объем, количество… Миллиграммы, граммы, килограммы…
Они могут измеряться и выражаться в самых разных характеристиках, например, обозначать массу, стоимость, объем, количество… Миллиграммы, граммы, килограммы…
В рецептах чаще всего пишут: 1 часть такого-то продукта и 2 части такого-то продукта, либо же такие-то продукты в указанном соотношении. Например, так: возьмите для соуса 1 часть сметаны и 2 части воды, либо же: для соуса понадобится сметана и вода в соотношении 1:2.
Вы можете взять любое количество сметаны, и взять воды вдвое больше. Тут уж, как говорится, придется работать «на глаз». Например, если вы взяли полстакана сметаны, понадобится стакан воды. Или 200 мл сметаны, и тогда берите 400 мл воды.
Очень часто я вижу, кстати, рецепты приготовления каши на упаковке с крупой. Но советую быть в отношении них очень осторожными, иногда производители указывают неверное соотношение. Однажды я по такому «рецепту» приготовила манную кашу, которая больше смахивала на мамалыгу. Так что этот момент перепроверяйте.
Главное, не перепутайте ингредиенты местами.
Нелли 27 янв 2022 00:03
★★★★★★★★★
Задать свой вопрос
Отношение к процентам — преобразование, формула, таблица, примеры
LearnPracticeDownload
В математике преобразование отношения к процентам очень полезно для сравнения каждой части с целым. Отношение сравнивает любые две части целого. Например, соотношение сахара и соли в растворе 3:1. Это говорит нам о том, что в растворе сахара в три раза больше, чем соли. Проценты — это очень специфический тип соотношения. Процент сравнивает любую часть целого с целым, вместо того, чтобы сравнивать отдельные части друг с другом. В том же примере процентное содержание сахара в растворе составляет 75 %, а процентное содержание соли — 25 %. Но как мы преобразовали 3:1 в проценты? Давайте узнаем о преобразовании соотношения в проценты в этой статье.
| 1. | Отношение к процентам Формула |
2. | Как преобразовать соотношение в проценты? |
| 3. | Отношение к процентной таблице |
| 4. | Часто задаваемые вопросы о соотношении к процентам |
Отношение к процентам Формула
Существует формула для преобразования соотношения в проценты. Его можно применять напрямую с любыми значениями, чтобы получить требуемый процент. Формула отношения к процентам приведена ниже:
Процент = Отношение × 100
Выражается символом процента (%).
Как преобразовать соотношение в проценты?
Прежде чем узнать о преобразовании отношений в проценты, давайте сначала кратко обсудим значение отношений и процентов. Соотношение — это отношение или сравнение между двумя величинами одного вида и одной и той же единицы. Существует три способа выражения отношения: отношение части к части, отношение части к целому и отношение целого к части. Соотношение частей к частям сравнивает количество двух частей друг с другом. Пример такой зависимости приведен в начале статьи (соотношение сахара и соли в растворе 3:1). Другим примером может быть соотношение количества мальчиков и девочек в классе — 2:3. Возьмем тот же пример, если мы представим соотношение количества мальчиков и общего числа учеников, соотношение будет 2:5 (в целом = общее количество частей = 2 + 3 = 5). Это пример отношения части к целому. То же самое соотношение, представленное как 5:2, является примером отношения «целое к части».
Соотношение частей к частям сравнивает количество двух частей друг с другом. Пример такой зависимости приведен в начале статьи (соотношение сахара и соли в растворе 3:1). Другим примером может быть соотношение количества мальчиков и девочек в классе — 2:3. Возьмем тот же пример, если мы представим соотношение количества мальчиков и общего числа учеников, соотношение будет 2:5 (в целом = общее количество частей = 2 + 3 = 5). Это пример отношения части к целому. То же самое соотношение, представленное как 5:2, является примером отношения «целое к части».
Чтобы преобразовать отношение в процентную форму, нам нужно сначала определить отношение. И затем мы можем применить это отношение в приведенной выше «формуле отношения к процентам», чтобы получить значение процента. Например, если известно, что соотношение яблок и апельсинов в корзине составляет 5:8, и нам нужно найти процентное соотношение яблок в корзине, то нам нужно сначала найти соотношение яблок и фруктов в корзине. Всего фруктов в корзине 5+8, то есть 13 фруктов. Итак, соотношение яблок и фруктов составляет 5:13. Теперь мы можем найти процент как,
Итак, соотношение яблок и фруктов составляет 5:13. Теперь мы можем найти процент как,
Процент = [Отношение × 100] %
Процент = 5/13 × 100
Процент = 38,46%
Таким же образом отношение апельсинов к фруктам составляет 8:13. Процент апельсинов в корзине равен [8/13 × 100]% = 61,54%. Посмотрите еще один пример преобразования 1:4 в проценты на изображении ниже.
В заключение, шаги по преобразованию отношения в проценты приведены ниже:
- Шаг 1: Определите отношение.
- Шаг 2: Выразите отношение a:b в виде дроби a/b.
- Шаг 3: Умножьте дробь на 100.
- Шаг 4: Упростите и запишите ответ с символом процента (%).
Отношение к процентной таблице
Таблица отношения к процентам — это быстрый способ указать процентные значения некоторых часто используемых отношений. Посмотрите на соотношение к процентной таблице, приведенной ниже.
Темы, связанные с отношением к процентам
Проверьте эти интересные статьи, похожие на концепцию отношения к процентам в математике.
- От дроби до процента
- Проценты в дроби
- Преобразование десятичной дроби в дробную
- Доля до десятичной дроби
- Десятичная дробь в процентах
- Проценты в десятичной дроби
Примеры отношения к процентам
Пример 1: Учащиеся начальных классов школы делятся на два дома — красный дом и синий дом. Если соотношение учеников синего дома к количеству учеников красного дома составляет 4:5, найдите процент учеников синего дома в школе, используя формулу преобразования отношения в процент.
Решение: Дано, что все ученики начальных классов школы разделены на два дома. Соотношение учеников синего дома и красного дома составляет 4:5. Итак,
Всего частей целого = 4 + 5 = 9
Отношение учеников синих домов к общему количеству учеников = 4/9
Итак, процент учеников синих домов в школе = 4/9 × 100 % = 44,44%
Следовательно, искомое процентное значение равно 44,44%.

Пример 2: Какова будет процентная доля пакетов апельсинового сока в ведре, содержащем пакеты сока, если его соотношение составляет 3:8?
Решение: Данное соотношение пакетов апельсинового сока в ведре, содержащем пакеты сока разных вкусов, составляет 3:8. Итак, используя формулу отношения к процентам — процент = [отношение × 100] %, мы получаем, процент = 3/8 × 100 %.
Доля пакетов апельсинового сока = 3/8 × 100 %
= 300/8 %
= 37,5 %
Таким образом, требуемый процент равен 37,5%.
Пример 3: Преобразуйте 3:1 в проценты, используя шаги преобразования соотношения в проценты.
Решение: Данное соотношение равно 3:1. Шаги преобразования этого соотношения в проценты приведены ниже:
Шаг 1: Запишите соотношение в дробной форме. Итак, 3:1 = 3/1.
Шаг 2: Умножьте полученную дробь на 100. Получается 3/1 × 100.
Шаг 3: Упростите и прикрепите к ответу знак процента.
 Итак, 3/1 × 100 = 300%.
Итак, 3/1 × 100 = 300%.Следовательно, 3:1 = 300%.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по отношению к процентам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о соотношении к процентам
Как преобразовать отношение в проценты?
Чтобы преобразовать отношение в процентную форму, есть два способа, которые поясняются ниже:
- Умножить антецедент и консеквент данного отношения на число так, чтобы консеквент стал равным 100. После этого антецедент будет равным 100. необходимый процент. Этот метод подходит для отношений, в которых консеквент равен 100. Если нет, то используйте метод, описанный ниже.

- Запишите отношение (a:b) в виде дроби (a/b) и умножьте его на 100. Упростите его и добавьте символ процента.
Как преобразовать проценты в отношение?
Чтобы преобразовать проценты в пропорции, выполните следующие действия:
- Удалите знак процента и разделите данное число на 100. Таким образом, x% = x/100.
- Упростите, если возможно.
- Запишите полученную дробь в виде соотношения. Итак, х/100 = х:100.
Каковы шаги для преобразования соотношения в проценты?
Шаги для преобразования отношения в проценты приведены ниже:
- Запишите соотношение в дробной форме.
- Умножьте это на 100.
- Упростите выражение и присоедините к ответу знак процента.
Что такое отношение к процентной формуле?
Формула отношения к процентам: Процент = Отношение × 100%. Эта формула помогает нам легко преобразовать любое отношение в процентную форму.
Какой процент соответствует соотношению 3 к 1?
Отношение 3 к 1 может быть записано как 3:1. Его можно записать в виде дроби 3/1. Умножьте это на 100. Это означает, что 3/1 × 100 = 300%. Следовательно, соотношение 3 к 1 эквивалентно 300%.
Его можно записать в виде дроби 3/1. Умножьте это на 100. Это означает, что 3/1 × 100 = 300%. Следовательно, соотношение 3 к 1 эквивалентно 300%.
Как преобразовать соотношение в проценты с тремя числами?
Если даны три количества, допустим, если соотношение количества яблок, апельсинов и дынь в корзине с фруктами составляет 3:2:4. Затем, чтобы найти процент яблок в корзине, мы сначала находим отношение яблок к общему количеству фруктов. Соотношение яблок к общему количеству плодов 3:9 или 1:3. Теперь 1:3 = 1/3 × 100% = 33,33%. Вот как мы конвертируем соотношение в проценты с тремя числами.
Скачать БЕСПЛАТНЫЕ учебные материалы
Отношение к процентам Рабочие листы
Рабочие листы по математике и
наглядная программа
Соотношения
Соотношение
сравнивает значений .Соотношение показывает, сколько одного предмета по сравнению с другим.
Есть 3 синих квадрата на 1 желтый квадрат
Соотношения могут отображаться по-разному:
| Используйте «:» для разделения значений: | 3 : 1 | |
| Или мы можем использовать слово «кому»: | от 3 до 1 | |
| Или напишите как дробь: | 3 1 |
Коэффициент можно увеличить:
Здесь также соотношение 3 синих квадрата к 1 желтому квадрату,
хотя квадратов больше.
Попробуйте сами
изображений/ratio-slider.js
Использование соотношений
Хитрость с отношениями заключается в том, чтобы всегда умножать или делить числа на одно и то же значение .
Пример:
4 : 5 совпадает с 4 × 2 : 5 × 2 = 8 : 10 |
Рецепты
Пример: В рецепте блинов используется 3 стакана муки и 2 стакана молока.
Таким образом, отношение муки к молоку составляет 3 : 2
Чтобы приготовить блины для МНОГО людей, нам может понадобиться в 4 раза больше, поэтому мы умножаем числа на 4:
3 ×4 : 2 × 4 = 12 : 8
Другими словами, 12 стаканов муки и 8 стаканов молока .
Соотношение остается прежним, поэтому блины должны быть такими же вкусными.
Соотношения «Часть к Части» и «Часть к Целому»
До сих пор примеры были «частичными» (сравнение одной части с другой частью).
Но отношение может также показать часть по сравнению с целой партией .
Пример: 5 щенков, 2 мальчика и 3 девочки девочек к мальчикам составляет 3:2 или
3 / 2Часть к целому:
Соотношение мальчиков к всем щенкам составляет 2:5 или 2 / 5
Соотношение девочек к всем щенкам составляет 90 3 / 5
Попробуйте сами
изображений/ratio.js
Масштабирование
Мы можем использовать пропорции для увеличения или уменьшения чертежа (посредством умножения или деления).
Отношение высоты индийского флага к ширине равно 9.0246 2:3 Таким образом, на каждые 2 (дюймов, метров и т. д.) высоты | |
Если мы сделали флаг высотой 20 дюймов, то он должен быть 30 дюймов в ширину. Если мы сделали флаг высотой 40 см, то ширина должна быть 60 см. (которое по-прежнему находится в соотношении 2:3) | |
Пример: чтобы нарисовать лошадь в масштабе 1/10 нормального размера,
умножьте все размеры на 1/10Эта лошадь в реальной жизни имеет высоту 1500 мм и длину 2000 мм, поэтому отношение ее высоты к длине равно
1500 : 2000
2 90 Какое это отношение? когда мы рисуем его в 1/10 нормального размера?
| 1500 : 2000 | = 1500 × 1/10 : 2000 × 1/10 | |
| = 150 : 200 |
Таким образом мы можем сделать любое уменьшение/увеличение, которое захотим.
Большая Нога?
Алли измерила свою ногу, и она оказалась 21 см в длину, а затем она измерила ногу своей матери, и она оказалась 24 см в длину. |
«Должно быть, у меня большие ступни, моя ступня почти такая же длинная, как у моей мамы!»
Но потом она решила измерить рост и обнаружила, что ее рост 133 см, а рост ее мамы 152 см.
В таблице это:
| Элли | Мама | |
| Длина стопы: | 21 см | 24 см |
| Высота: | 133 см | 152см |
Соотношение длины ноги к росту в виде дроби:
| Элли: | 21 133 | Мама: | 24 152 |
Мы можем упростить эти дроби следующим образом:
| Элли: | 21/7 133/7 | Мама: | 24/8 152/8 |
И мы получаем это (пожалуйста, проверьте правильность вычислений):
| Элли: | 3 19 | Мама: | 3 19 |
«О!» сказала она, «Соотношения одинаковые».
«Значит, моя нога такая большая, как должна быть для моего роста, и на самом деле не слишком большая.»
Практика
Вы можете попрактиковаться в своих пропорциях, приготовив шоколадные чипсы
1709, 1710, 1711, 1712, 1713, 1714, 1715, 1716, 3603, 3604
Как рассчитать отношение числа
Опубликовано Математика с мамой
ПримерВидеоВопросыУрок
Поделиться в Google Classroom
- В этом примере мы делим 50 фунтов стерлингов в соотношении 2:3, используя шаги.
- Шаг 1 заключается в том, чтобы найти общее количество частей в нашем соотношении.
- 2 + 3 = 5. Наше соотношение 2:3 содержит всего 5 частей.
- Шаг 2 заключается в том, чтобы найти значение одной части путем деления суммы на общее количество частей.

- 50 фунтов стерлингов ÷ 5 = 10 фунтов стерлингов.
- Шаг 3 заключается в увеличении исходного коэффициента на значение одной части коэффициента.
- 2:3 становится £20:£30, когда мы умножаем на £10.
- Один человек получает 20 фунтов стерлингов, а другой — 30 фунтов стерлингов. Эти значения добавляются к нашей общей сумме в 50 фунтов стерлингов.
Чтобы рассчитать соотношение суммы, мы делим сумму на общее количество частей в соотношении, а затем умножаем этот ответ на исходное соотношение.
- Мы хотим получить 20 долларов, разделенных в соотношении 1:3.
- Шаг 1 заключается в вычислении общего количества частей в соотношении.
- 1 + 3 = 4, поэтому отношение 1:3 содержит всего 4 части.
- Шаг 2 — разделить сумму на общее количество частей в пропорции.

- 20 $ ÷ 4 = 5 $.
- Каждая из четырех частей пропорции стоит 5 долларов.
- Шаг 3 заключается в увеличении исходного коэффициента на значение каждой части.
- 1:3, умноженное на 5 долларов, становится 5 долларов: 15 долларов.
- Один человек получает 5 долларов, а другой — 15 долларов.
- Мы можем проверить расчет коэффициента, добавив 5 и 15 долларов, чтобы получить общую сумму 20 долларов.
Что такое отношение?
Соотношения описывают, как разделить данную сумму, и записываются числами, разделенными двоеточиями. Количество чисел в соотношении говорит нам, на сколько групп распределяется количество. Размер каждого числа говорит нам о доле от общей суммы, которую получает каждая группа.
Например, в соотношении 1:3 есть два разных числа: «1» и «3».
Поскольку есть два числа, мы делим сумму между двумя людьми.
Это соотношение означает, что на каждую 1 часть, которую получает человек слева, человек справа получает 3. Человек справа получит в три раза больше, чем человек слева.
Человек слева получит 5 долларов, а человек справа — 15 долларов. Оба числа в сумме составляют 20 долларов, но 15 долларов в три раза больше, чем 5 долларов. Поэтому соотношение 1 к 3.
Как вычислить отношение числа в шагах
Чтобы вычислить отношение числа, выполните следующие 3 шага:
- Сложите части отношения, чтобы найти общее количество частей.
- Найдите значение каждой части отношения, разделив число на общее количество частей, рассчитанное на шаге 1.
- Умножьте каждую часть исходного коэффициента на значение каждой части, рассчитанное на шаге 2.
Например, разделите 20 долларов в соотношении 1:3.
Это означает, что в этой проблеме соотношения мы будем делить 20 долларов между двумя людьми, причем один человек получит в три раза больше, чем другой.
Мы следуем 3 шагам выше, чтобы выработать соотношение.
- Шаг 1: Найдите общее количество деталей
Глядя на соотношение 1:3, мы имеем:
1 + 3 = 4
Итак, у нас есть четыре части всего в нашем соотношении.
- Шаг 2: Разделите сумму на общее количество частей
Сумма 20 долларов, а общее количество деталей 4 .
20 ÷ 4 = 5
Каждая из четырех частей стоит 5 долларов .
- Шаг 3: Умножьте каждое число в пропорции на значение одной части
Всего у нас есть четыре части, и каждая из этих частей стоит 5 долларов.
Умножим оба числа в соотношении 1:3 на $5 .
1 х 5 долларов = 5 долларов
3 х 5 долларов = 15 долларов
Деньги делятся в соотношении $5:15 $.
Мы решили нашу проблему соотношения, чтобы найти, что один человек получает 5 долларов, а другой человек получает 15 долларов.
Чтобы проверить расчет отношения, добавьте окончательные значения, чтобы увидеть, равна ли общая сумма исходной сумме. Если общие суммы также можно упростить, чтобы получить приведенное соотношение, расчет правильный.
5 долларов + 15 долларов = 20 долларов — это сумма, с которой мы начали, поэтому мы можем быть уверены, что наши расчеты верны.
Чтобы подтвердить наш расчет соотношения, мы проверяем, что $5:15 упрощается, чтобы получить исходное соотношение.
Разделив 5 и 15 долларов на 5, мы получим 1:3, что является нашим исходным соотношением, а 15 долларов действительно в три раза больше, чем 5 долларов.
Теперь попробуйте наш урок на Разделение в соотношении между 3 людьми , где мы узнаем, как расширить наши шаги для расчета соотношения на примеры, где мы делим сумму между 3 людьми.
Калькулятор коэффициента разбавления
Создано Джоанной Михаловской, докторантом
Отзыв от доктора наук Доминика Черниа и Джека Боуотера
Последнее обновление: 10 марта 2022 г.
- Какова степень разбавления?
- Как рассчитать степень разбавления?
- Калькулятор коэффициента разбавления – практический пример
- Таблица разбавления
Калькулятор коэффициента разбавления подскажет, сколько растворенного вещества и растворителя необходимо для получения желаемого коэффициента разбавления . Наш инструмент имеет встроенное преобразование объема, поэтому вы сможете выполнять свои расчеты, используя любые единицы измерения! Ознакомьтесь со статьей ниже, чтобы ответить на вопрос » Как рассчитать степень разбавления? » и ознакомиться с нашей таблицей коэффициентов разбавления с примерами.
Обязательно попробуйте другие наши инструменты, которые могут оказаться полезными:
- Калькулятор разбавления раствора;
- Калькулятор коэффициента разбавления;
- Калькулятор серийного разведения;
- Калькулятор разбавления спирта; и
- Калькулятор соотношения компонентов смеси.

Какова степень разбавления?
Коэффициент разбавления отношение растворенного вещества (вещества, подлежащего разбавлению) к растворителю (например, воде) . Разбавленную жидкость необходимо тщательно перемешать для достижения истинного разбавления. Если у вас разбавление 1:3, т. е. отношение разбавления 1:3, это означает, что вы добавляете 1 единицу объема растворенного вещества (например, концентрата) к 3 единицам объема растворителя (например, воды), что даст общий 4 единицы объема.
Почему это полезно? Возможно, вы уже используете коэффициент разбавления в своей повседневной жизни, даже не подозревая об этом! Он может помочь вам приготовить идеальный рассол для домашнего варенья или подскажет количество концентрированного чистящего средства, которое вам нужно, если вы хотите повторно использовать бутылку (и, таким образом, использовать меньше пластика).
Как рассчитать степень разбавления?
Давайте познакомимся с математикой и наукой, лежащими в основе расчета коэффициента разбавления.
- Мы можем представить коэффициент разбавления следующим образом:
соотношение растворителя: соотношение растворенного вещества
Например:
5 : 1
- Расчет для растворенного вещества выглядит следующим образом:
объем растворенного вещества = конечный объем / (соотношение растворителя + соотношение растворенного вещества)
Например:
объем растворенного вещества = конечный объем / (5 + 1)
- Вычисление для растворителя можно выразить следующим образом:
объем растворителя = объем растворенного вещества * соотношение растворителей
Например:
объем растворителя = объем растворенного вещества * 5.
Как вы, наверное, заметили, в этих расчетах есть 5 различных переменных :
- Коэффициент растворения — который всегда равен 1 в нашем калькуляторе коэффициента разбавления;
- Коэффициент растворителя — может быть любым числом больше 0;
- Конечный объем — это желаемое количество разведенной жидкости, которую вы хотите получить;
- Объем растворенного вещества — количество использованного растворенного вещества; и
- Объем растворителя — количество использованного растворителя.
Соотношение растворенных веществ постоянно, поэтому у нас есть 4 неизвестных количества. Вам нужно только знать два из них , чтобы выполнять расчеты с помощью нашего калькулятора коэффициента разбавления.
Калькулятор коэффициента разбавления – практический пример
Теперь вы знаете все расчеты, поэтому давайте на практическом примере покажем, как работает калькулятор коэффициента разбавления.
Предположим, у вас есть контейнер объемом 1 литр. Вы хотите смешать концентрат чистящего средства с водой. Судя по этикетке, соотношение воды и концентрата должно быть равно 3:1 (то есть 3 части воды, 1 часть концентрата).
Рассчитать объем концентрата (объем растворенного вещества) .
объем растворенного вещества = конечный объем / (соотношение растворителя + соотношение растворенного вещества)
объем растворенного вещества = 1 литр / (3 + 1)
объем растворенного вещества = 1 литр / 4
объем растворенного вещества = 0,25 литра
- Теперь мы можем рассчитать объем воды (объем растворителя) .
объем растворителя = объем растворенного вещества * соотношение растворителей
объем растворителя = 0,25 * 3
объем растворителя = 0,75 литра
- Вот и все! Теперь вы знаете, что если желаемый коэффициент разбавления 1:3 и в вашем контейнере 1 литр, вам нужно использовать 0,25 литра концентрата и 0,75 литра воды.

Посмотрите нашу таблицу коэффициентов разбавления ниже, чтобы увидеть другие примеры!
Таблица разведения
Вы найдете примерные значения того, сколько растворенного вещества вам нужно, если вы знаете коэффициент разбавления и окончательный объем в таблице разбавления ниже. Допустим, вам нужен конечный объем 1 литр или 1 галлон США. Сколько концентрата нужно разбавить?
Считаете ли вы эту таблицу коэффициентов разбавления полезной? Наш калькулятор позволяет сделать еще больше!
Джоанна Михаловска, кандидат наук
💡 Введите любые два значения, чтобы получить результат.
Конечный объем
Коэффициент разбавления
: 1
Объем концентрата
Вода объем
Проверьте 24 аналогичные калькуляторы по экономике дома 🏡
Appliance ApplianceAppliance Palatchailback к школе… Еще 21
Dry Martini (3: 1 Коктейльный рецепт
Difford’s Guide
RATIN оценивать Добавить в список желаний персонализировать
Подавать в бокале
CoupeГарнир:
Охлажденные оливки на палочке или твист с лимонной цедрой.
Способ приготовления:
Смешайте все ингредиенты со льдом и процедите в охлажденный стакан.
| 2 выстрела | Сухой джин Рютте |
| 2 ⁄ 3 выстрел | Вермут Martini Extra Dry |
| 1 черточка | Апельсиновые биттеры от Angostura (по желанию) |
Загрузка… Порций | |
Прочтите о дозировках коктейлей и их измерении.
Купить напрямую у
Сухой джин Rutte, 70cl £ 33,95 2,95 фунта стерлингов за коктейль, получается 11,5 Вермут Martini Extra Dry, 75cl 10,45 фунтов стерлингов 0,28 фунта стерлингов за коктейль, всего 37
£ —
Минимум … коктейлей
Всего £ — за коктейль*
* Этот список может не включать все необходимые ингредиенты.
Цена за коктейль является оценочной, основанной на стоимости приготовления одного коктейля с доступными ингредиентами, указанными выше, и не включает почтовые расходы.
Оставьте первый комментарий
Нежный
Пьянящий
Сладкий
Сухой/кислый
Еще коктейли с таким же опьянением и сладостью/сухостью/кислотой
Обзор:
Три к одному могут быть несправедливыми шансами в бою, но вермут сияет в этом сухом мартини. В результате экспериментов мы обнаружили, что мартини 3:1 лучше размешивать, чем взбалтывать. И наоборот, мартини 15:1 лучше встряхивать, чем мешать.
И наоборот, мартини 15:1 лучше встряхивать, чем мешать.
История:
О происхождении мартини и о том, как лучше всего приготовить этот напиток, ведутся серьезные споры. Подробную информацию можно найти на нашем Драй Мартини стр.
Питание:
Одна порция Dry Martini (соотношение 3:1) содержит 151 калорий.
Содержание алкоголя:
Подробнее Классика/винтаж Коктейли
Подробнее В стиле мартини Коктейли
Подробнее Spirit-forward Коктейли
Путеводитель Difford остается бесплатным благодаря поддержке брендов, выделенных зеленым цветом выше. Значения, указанные для содержания алкоголя и калорий, а также количества напитков, приготовленных из ингредиента, следует считать приблизительными.
Предыдущий Коктейль
Порнозвезда Мартини
Next Cocktail
Dry Martini (соотношение 7:1) Embury’s
Купить напрямую у
Сухой джин Rutte, 70cl £ 33,95 2,95 фунта стерлингов за коктейль, получается 11,5 Вермут Martini Extra Dry, 75cl 10,45 фунтов стерлингов 0,28 фунта стерлингов за коктейль, всего 37
£ —
Минимум . .. коктейлей
.. коктейлей
Всего £ — за коктейль*
* Этот список может не включать все необходимые ингредиенты.
Цена за коктейль является оценочной, основанной на стоимости приготовления одного коктейля с доступными ингредиентами, указанными выше, и не включает почтовые расходы.
Предыдущий Коктейль
Порнозвезда Мартини
Следующий коктейль
Сухой мартини (соотношение 7:1) Embury’s
Коктейль Мартини и его эволюция
В своей простейшей и верной форме мартини представляет собой смесь джина и вермута, возможно, с щепоткой или двумя биттерами, и…
Вермут
Вермут — это крепленое вино из семейства «ароматизированных» вин, приправленное ароматными травами и специями. Это…
20 лучших коктейлей Angostura Bitters
Я слышал, что недавно открытый коктейль-бар успешен, когда ему нужна вторая бутылка Angostura….
20 лучших коктейлей с банановым ликером Crème de Banane
Аккуратно распакуйте бананы, чтобы получить здоровую и вкусную закуску, особенно если они перезрелые и для коктейлей. Сохраните свои бананы…
Сохраните свои бананы…
20 лучших коктейлей Whisk(e)y Sour
The Whiskey Sour или, в зависимости от происхождения вашего спиртного напитка, Whiskey Sour — один из лучших классических коктейлей….
20 лучших коктейлей Просекко
Шампанское со вкусом сухого бисквита предлагает изысканный декаданс, в то время как просекко легче, фруктовее и, возможно,…
Вы должны быть авторизованы чтобы отправить оценку
Нажмите здесь, чтобы войти Коэффициенты: что это такое? Как они работают?
ПропорцииПропорциональностьРешение словесных задачПохожие фигурыСолнечные лучи / Части
Purplemath
Что такое отношение?
«Отношение» — это просто сравнение или отношение двух разных вещей. Соотношения используются для создания пропорций путем установки двух соотношений, равных друг другу, и решения для некоторых неизвестных, а соотношения также могут использоваться для нахождения показателей на единицу, например, сколько миль автомобиль может проехать «на литр» или сколько часов средний студент данного вуза тратит на обучение «в неделю».
Содержимое продолжается ниже
MathHelp.com
Соотношения
Какой пример нахождения отношения?
В качестве примера отношения кто-то может посмотреть на группу людей, сосчитать носы и сослаться на «соотношение мужчин и женщин» в группе. Предположим, есть тридцать пять человек, пятнадцать из которых мужчины. Тогда остальные женщины, так что:
35 − 15 = 20
… в группе двадцать женщин. Языковое «отношение (этого) к (тому)» означает, что (это) предшествует (то) в сравнении. Таким образом, если бы нужно было выразить «соотношение мужчин и женщин», то соотношение, говоря английскими словами, было бы «15 мужчин к 20 женщинам» (или просто «15 к 20»).
Порядок элементов в соотношении очень важен и должен соблюдаться; какое бы слово ни стояло первым в соотношении (при выражении словами), его номер должен стоять первым в соотношении. Если бы выражение было «соотношение женщин и мужчин», то выражение внутри слов было бы «20 женщин к 15 мужчинам» (или просто «20 к 15»).
Выражение соотношения мужчин и женщин как «15 к 20» означает выражение соотношения словами. Есть два других обозначения для этого отношения «15 к 20»:
обозначение шансов: 15 : 20
дробное обозначение: 15 / 20
Вы должны уметь распознавать все три обозначения; вы, вероятно, должны знать их и то, как конвертировать между ними, на следующем тесте. Например:
Им нужно «отношение уток к гусям», поэтому число уток идет первым (или, для дробной формы, сверху). Итак, мой ответ:
На этот раз они хотят, чтобы я дал им «соотношение гусей и уток». Я буду использовать точно такие же числа, но в этом случае число гусей будет первым (или, для дробной формы, сверху). Итак, мой ответ:
Числа были одинаковыми в каждом из двух приведенных выше упражнений, но порядок , в котором они были перечислены, различался в зависимости от порядка, в котором были выражены элементы соотношения. В соотношениях очень важен порядок.
В соотношениях очень важен порядок.
Вернемся к 15 мужчинам и 20 женщинам в нашей исходной группе. Я выразил отношение дробью, а именно: 15 / 20 . Эта дробь сводится к 3 / 4 . Это означает, что мы также можем выразить соотношение мужчин и женщин в группе как 9.0385 3 / 4 , 3 : 4 или «от 3 до 4».
Это указывает на одну важную вещь, касающуюся отношений: числа, используемые в отношении, могут не быть абсолютными измеренными значениями. Соотношение «15 к 20» относится к абсолютным числам мужчин и женщин соответственно в группе из тридцати пяти человек. Упрощенное или сокращенное соотношение «3 к 4» говорит нам только о том, что на каждых трех мужчин приходится четыре женщины. Упрощенное соотношение также говорит нам о том, что в любом репрезентативном наборе из семи человек (3 + 4 = 7) из этой группы трое будут мужчинами. Другими словами, мужчины составляют 3 / 7 человек в группе. Эти отношения и рассуждения — то, что мы используем для решения многих текстовых задач:
Эти отношения и рассуждения — то, что мы используем для решения многих текстовых задач:
Соотношение «7 к 5» (или 7 : 5 или 7 / 5 ) говорит мне, что для каждой репрезентативной группы учащихся пять не удалось. Под «репрезентативной группой» я подразумеваю группу, в которой количество учеников такое же, как и во всем классе. Я могу вычислить размер этой группы, используя коэффициент, который они мне дали. Размер репрезентативной группы будет суммой ее частей:
7 + 5 = 12
Таким образом, в репрезентативной группе 12 студентов, из которых 7 сдали и 5 не сдали. В частности, доля группы, которая не сдала экзамен, определяется путем деления количества неуспевающих студентов на общее количество студентов в репрезентативной группе. То есть:
(не зачет)/(всего): 5 / 12
Итак, 5/12 группы завалили, а поскольку эта группа репрезентативна, 5/12 всего класса завалили. Это означает, что теперь я могу найти количество учеников во всем классе, которые завалили (это упражнение удручает!), умножив дробь из репрезентативной группы на размер всего класса:
( 5 / 12 )(36) = 15
Итак, из класса 36 учеников класс не прошел мимо:
15 учеников
9000 отношение от группы репрезентативной также использоваться для предоставления процентной информации.

Я уже знаю, что в репрезентативной группе 12 учеников, из которых 7 сдали класс. Преобразовав это в проценты (путем деления, а затем перемещения десятичной точки, как описано здесь), я получаю:
7/12 = 0,583333… = 58,3333…%
Они хотят, чтобы ответ был округлен до одного десятичного знака, поэтому мой ответ таков:
58,3% пройдено
Соотношение говорит мне, что для каждой репрезентативной группы из 16 + 9 = 25 птиц, 9 гусей. То есть 9 / 25 птиц — это гуси. Я могу использовать эту дробь из репрезентативной группы, чтобы найти ответ для всей группы:
(9/25)(300) = 108
Это число, которое им нужно. Во всем парке их:
108 гусей
Как правило, проблемы с соотношениями заключаются в простом указании соотношений или их упрощении. Например:
В этом упражнении мне нужно записать отношение в виде уменьшенной дроби. Итак, сначала я составлю дробь, а затем сделаю сокращение, которое приведет к «самой простой форме».
$ 10 / $ 45 = $ 2 / $ = 2 /
дробная форма. Итак, мой ответ:
Эта уменьшенная дробь представляет собой выражение отношения в простейшей дробной форме. Единицы (знаки «доллара») отменяются в дроби, потому что единицы (а именно, символы «$») были одинаковыми для обоих значений.
Если обе величины отношения имеют одну и ту же единицу измерения или обозначение, в сокращенной форме отношения не должно быть единиц измерения или обозначения. Единицы точно не являются факторами, но они сокращаются таким же образом, как и факторы.
Члены этого соотношения имеют разные единицы измерения, поэтому они не сокращаются; будут единицы по моему упрощенному соотношению. Мое упрощение выглядит так:
(240 миль) / (8 галлонов)
= (30 миль) / (1 галлон)
Это конкретное соотношение единиц «(мили)/(галлон)» имеет собственную упрощенную форму; а именно, «мили на галлон», сокращенно «миль на галлон». Итак, на стандартном английском языке мой ответ таков:
Итак, на стандартном английском языке мой ответ таков:
30 миль на галлон
В отличие от ответа на предыдущее упражнение, ответ в этом упражнении должен ли иметь единицы на нем, поскольку единицы на две части отношения ( а именно, «мили» и «галлоны») не были одинаковыми и, следовательно, не отменяли друг друга. Когда отношение заканчивается единицами (или измерениями), это отношение также может называться «скоростью». В случае вышеприведенного упражнения скорость представляла собой пройденное расстояние на единицу объема топлива.
Переводные коэффициенты — это упрощенные соотношения, поэтому их можно изучать примерно в то же время, когда вы изучаете отношения и пропорции. Например:
Какова длина в футах игровой площадки поля для американского футбола (т. е. длина поля без учета «конечных» зон)?
Я знаю, что длина поля для американского футбола, исключая «конечные» зоны, составляет 100 ярдов. Я также знаю, что 3 фута равны 1 ярду. Я могу установить это равенство как отношение. Поскольку они дали мне измерение в «ярдах», я хочу, чтобы единица измерения «ярды» сокращалась в моем умножении. Из-за этого я укажу свое отношение (ярдов к футам) с «футами» сверху:
Я также знаю, что 3 фута равны 1 ярду. Я могу установить это равенство как отношение. Поскольку они дали мне измерение в «ярдах», я хочу, чтобы единица измерения «ярды» сокращалась в моем умножении. Из-за этого я укажу свое отношение (ярдов к футам) с «футами» сверху:
(3 фута)/(1 ярд)
Теперь я могу умножить длину, которую они мне дали, на мой коэффициент преобразования (коэффициент выше) и упростить:
[(3 фута)/(1 ярд) ][100 ярдов]
= (3 фута)(100) = 300 футов
Это число, которое они хотят, поэтому мой ответ:
300 футов
Для получения дополнительной информации по этой теме см. Урок «Отмена / Преобразование единиц измерения».
Соотношения — это сравнение одной вещи с другой (мили к галлонам, футы к ярдам, утки к гусям и так далее). Но их истинная полезность заключается в установлении и решении пропорций.
Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в преобразовании коэффициентов, выраженных в виде «шансов», в дробную форму.


 Её вместительности должно хватить и для бензина, и для масла.
Её вместительности должно хватить и для бензина, и для масла. Это соотношение называется «динамической симметрией» или «динамическим равновесием».
Это соотношение называется «динамической симметрией» или «динамическим равновесием».
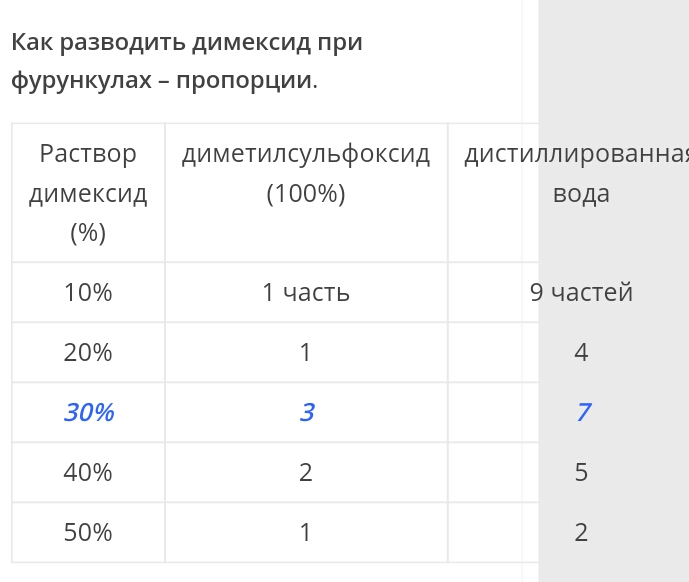

 Кроме того, не забудьте установить фокальной точкой, чтобы сохранить наиболее важную часть рисунка в представлении, особенно если рисунок используется в эскизах, макетах новостей и результатах поиска.
Кроме того, не забудьте установить фокальной точкой, чтобы сохранить наиболее важную часть рисунка в представлении, особенно если рисунок используется в эскизах, макетах новостей и результатах поиска.
 Дополнительные информацию о настройке фокальной точки для этих двух сценариев см. в веб-части «Изменение фокальной точки рисунка в веб-части «Главного имиджевного рисунка» и настройке области заголовка на странице.
Дополнительные информацию о настройке фокальной точки для этих двух сценариев см. в веб-части «Изменение фокальной точки рисунка в веб-части «Главного имиджевного рисунка» и настройке области заголовка на странице.

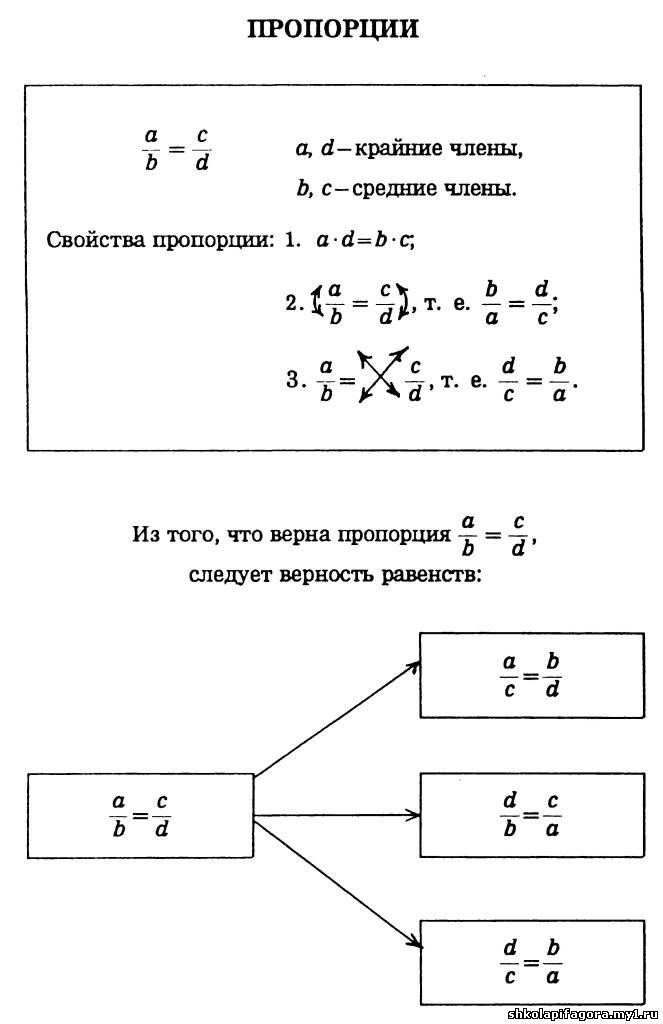 Итак, 3/1 × 100 = 300%.
Итак, 3/1 × 100 = 300%.