Вычисление матрицы онлайн: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

Содержание

Калькулятор определителя — вычислить определитель матрицы

Онлайн-калькулятор определителя поможет вам вычислить определитель матрицы заданных входных элементов. Калькулятор определяет значение определителя матрицы до размера матрицы 5 × 5. Он рассчитывается путем умножения его основных диагональных элементов и приведения матрицы к форме эшелона строк. У нас есть подробная информация о том, как рассчитать его вручную, определение, формулы и много других полезных данных, связанных с определителем матрицы. Наш калькулятор определяет результат с помощью следующих различных методов расчета:

Развернуть по столбцу.
Разверните по строке.
Формула Лейбница.
Правило треугольника.
Правило Сарруса.

Но давайте начнем с основ.

Читать дальше!

Что такое детерминант?

Это скалярное значение, которое получается из элементов квадратной матрицы и имеет определенные свойства линейного преобразования, описываемого матрицей. определитель матрицы калькулятор положительный или отрицательный, в зависимости от того, сохраняет ли линейное преобразование ориентацию векторного пространства или меняет ее на обратное. Это помогает нам найти обратную матрицу, а также то, что полезно в системах линейных уравнений, исчислении и многом другом. Он обозначается как det (A), det A или | A |.

Заметка:

Матрицы заключены в квадратные скобки, а определители обозначены вертикальными чертами. Матрица – это массив чисел, но определитель – одно число.

Как найти определитель матрицы онлайн вручную (шаг за шагом):

Определитель матриц можно вычислить разными методами. Здесь мы приводим подробные формулы для разного порядка матрицы, чтобы найти определитель разными методами:

Для умножения матриц 2×2:

Независимо от того, какой метод вы выбрали для расчетов, определитель матрицы онлайн A = (aij) 2 × 2 определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix} \\
$

$det⁡ A = ad-bc $

Пример:
Найти определитель матрицы калькулятор 2×2 A

$
det A =
\begin{vmatrix}
4 & 12 \\
2 & 7
\end{vmatrix} \\
$

Решение:

$
det A =
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix} \\
$

$|A| = (7)(4) – (2)(12)$
$|A| = 28 – 24$
$|A| = 4$

Для умножения матрицы 3×3:

Здесь обсуждаются расчеты для матриц 3×3 разными методами:

Развернуть по столбцу:

Для расчетов матрица A = (aij) 3 × 3 из разложения столбца определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
$

$det⁡ A= a\begin{vmatrix}
e & f \\h & i\end{vmatrix} – d\begin{vmatrix}b & c \\h & i\end{vmatrix}+g\begin{vmatrix}b & c \\e & f\end{vmatrix} $

Пример:
найти

$
det A =
\begin{vmatrix}
2 & 0 & 3\\1 & 4 & 1 \\0 & 4 & 7
\end{vmatrix} \\
$?

Решение:

$det⁡ A= 2\begin{vmatrix}
4 & 1 \\4 & 7\end{vmatrix} – 1\begin{vmatrix}0 & 3 \\4 & 7\end{vmatrix}+0\begin{vmatrix}0 & 3 \\4 & 1\end{vmatrix} $

$ det⁡ A = 2[(7)(4)-(4)(1)]-1[(4)(3)-(7)(0)]+ 0[(4)(3)-(1)(0)] $

$ det⁡ A = 2[28-4]-1[12-0]+ 0[12-0] $

$ det⁡ A = 2[24]-1[12]+ 0[12] $

$ det⁡ A = 48-12+ 0 $

$ det⁡ A = 36 $

Развернуть по строке:

Для вычислений матрица A = (aij) 3 × 3 из разложения строки определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
$

$det⁡ A= a\begin{vmatrix}
e & f \\h & i\end{vmatrix} – b\begin{vmatrix}d & f \\g & i\end{vmatrix}+c\begin{vmatrix}d & e \\g & h\end{vmatrix} $

Пример:

найти

$
det A =
\begin{vmatrix}
3 & 0 & 2\\1 & 4 & 1 \\7 & 0 & 4
\end{vmatrix} \\
$?

Решение:

$det⁡ A= 3\begin{vmatrix}
4 & 1 \\0 & 4\end{vmatrix} – 0\begin{vmatrix}1 & 1 \\7 & 4\end{vmatrix}+2\begin{vmatrix}1 & 4 \\7 & 0\end{vmatrix} $

$det⁡ A = 3[(4)(4)-(0)(1)]-0[(4)(1)-(7)(1)]+ 2[(0)(1)-(7)(4)]$
$det⁡ A = 3[16-0]-0[4-7]+ 2[0-28]$
$det⁡ A = 3[16]-0[-3]+ 2[-28]$
$det⁡ A = 48+0- 56$
$det⁡ A = -8$

Формула Лейбница:

Для расчетов матрица A = (aij) 3 × 3 по формуле Лейбница определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
$

$det⁡ A =(a*e*i)-(a*f*h)-(b*d*i)+(b*f*g)+(c*d*h)-(c*e*g) $

Пример:

найти

$
det A =
\begin{vmatrix}
2 & 3 & 8\\6 & 1 & 2 \\5 & 8 & 9
\end{vmatrix} \\
$?

Решение:

$
det A =
\begin{vmatrix}
2 & 3 & 8\\6 & 1 & 2 \\5 & 8 & 9
\end{vmatrix} \\
$
$det⁡ A = 2*1*9-2*2*8-3*6*9+3*2*5+8*6*8-8*1*5$

$det A =198$

Правило треугольника:

Для расчетов матрица A = (aij) 3 × 3 из правила Треугольника определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
$

Image

$det⁡ A =(a*e*i)-(a*f*h)-(b*d*i)+(b*f*g)+(c*d*h)-(c*e*g) $

Пример:

найти

$
det A =
\begin{vmatrix}
4 & 5 & 8\\0 & 4 & 9 \\1 & 2 & 3
\end{vmatrix} \\
$?

Решение:

$
det A =
\begin{vmatrix}
4 & 5 & 8\\0 & 4 & 9 \\1 & 2 & 3
\end{vmatrix} \\
$
$det⁡ A = 4*4*3+5*9*1+8*0*2-1*4*8-2*9*4-3*0*5$

$det A =-11$

Правило Сарруса:

Для расчетов матрица A = (aij) 3 × 3 по правилу Сарруса определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
$

Image

$det⁡ A =(a*e*i)-(a*f*h)-(b*d*i)+(b*f*g)+(c*d*h)-(c*e*g) $

Пример:

найти

$
det A =
\begin{vmatrix}
9 & 5 & 1\\3 & 5 & 7 \\4 & 8 & 6
\end{vmatrix} \\
$?

Решение:

$
det A =
\begin{vmatrix}
9 & 5 & 1\\3 & 5 & 7 \\4 & 8 & 6
\end{vmatrix} \\
$

$det⁡ A = 9*5*6+5*7*4+1*3*8-4*5*1-8*7*9-6*3*5$

$det A = -180$

Для матричного умножения 4×4:

Здесь обсуждаются расчеты для матриц 4х4 разными методами:

Развернуть по столбцу:

Для расчетов матрица A = (aij) 4 × 4 из разложения столбца определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c & d\\e & f & g &h \\i & j & k & l \\ m & n & o & p
\end{vmatrix} \\
$

$det⁡ A= a\begin{vmatrix}
f & g & h\\j & k & l\\n & o & p\end{vmatrix} – e\begin{vmatrix}b & c & d\\j & k & l\\ n & o & p\end{vmatrix}+i\begin{vmatrix}b & c & d \\f & g & h\\n & o & p\end{vmatrix}-m\begin{vmatrix}b & c & d\\f & g & h\\j & k & l\end {vmatrix}$

Затем просто определите определитель 3×3, используя приведенную выше формулу 3×3.

Пример:

найти

$
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
$?

Решение:

$det⁡ A= 1\begin{vmatrix}4 & 3 & 8\\4 & 3 & 2\\4 & 9 & 6\end{vmatrix} – 2\begin{vmatrix}8 & 7 & 2\\4 & 3 & 2\\ 4 & 9 & 6\end{vmatrix}+1\begin{vmatrix}8 & 7 & 2 \\4 & 3 & 8\\4 & 9 & 6\end{vmatrix}-1\begin{vmatrix}8 & 7 & 2\\4 & 3 & 8\\4 & 3 & 2\end {vmatrix}$

$det⁡ A=1( 4\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 3\begin{vmatrix}4 & 2 \\4 & 6\end{vmatrix}+8\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) -2( 8\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 7\begin{vmatrix}4 & 2 \\4 & 6\end{vmatrix}+2\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) +1( 8\begin{vmatrix}3 & 8 \\9 & 6\end{vmatrix} – 7\begin{vmatrix}4 & 8 \\4 & 6\end{vmatrix}+2\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) -1( 8\begin{vmatrix}
3 & 8 \\3 & 2\end{vmatrix} – 7\begin{vmatrix}4 & 8 \\4 & 6\end{vmatrix}+2\begin{vmatrix}4 & 3 \\4 & 3\end{vmatrix})$

$det⁡ A = 1[4(18-18)-3(24-8)+ 8(36-12)]-2[ 8(18-18)-7(24-8)+ 2(36-12)]+ 1[ 8(18-72)-7(24-32)+ 2(36-12)] -1[8(6-24)-7(8-32)+ 2(12-12)]$

$det⁡ A = 1[4(0)-3(16)+ 8(24)]-2[ 8(0)-7(16)+ 2(24)]+ 1[ 8(-54)-7(-8)+ 2(24)]-1[8(-18)-7(-24)+ 2(0)]$

$det⁡ A = 1[0-48+192]-2[0-112+48]+ 1[ -432+56+48]-1[-144+168+0]$

$det⁡ A = 1[144]-2[-64]+ 1[-328]-1[24]$

$det⁡ A = 144+128-328- 24$

$det⁡ A = -80$

Развернуть по строке:

Для вычислений матрица A = (aij) 4 × 4 из разложения строки определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c & d\\e & f & g &h \\i & j & k & l \\ m & n & o & p
\end{vmatrix} \\
$

$det⁡ A= a\begin{vmatrix}
f & g & h\\j & k & l\\n & o & p\end{vmatrix} – b\begin{vmatrix}e & g & h\\i & k & l\\ m & o & p\end{vmatrix}+c\begin{vmatrix}e & f & h \\i & j & l\\m & n & p\end{vmatrix}-d\begin{vmatrix}e & f & g\\i & j & k\\m & n & o\end {vmatrix}$

Затем просто определите определитель 3×3, используя приведенную выше формулу 3×3.
Пример:
найти

$
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
$?
Решение:

$det⁡ A= 1\begin{vmatrix}4 & 3 & 8\\4 & 3 & 2\\4 & 9 & 6\end{vmatrix} – 8\begin{vmatrix}2 & 3 & 8\\1 & 3 & 2\\ 1 & 9 & 6\end{vmatrix}+7\begin{vmatrix}2 & 4 & 8 \\1 & 4 & 2\\1 & 4 & 6\end{vmatrix}-2\begin{vmatrix}2 & 4 & 3\\1 & 4 & 3\\1 & 4 & 9\end {vmatrix}$

$det⁡ A=1( 4\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 3\begin{vmatrix}4 & 2 \\4 & 6\end{vmatrix}+8\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) -8( 2\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 3\begin{vmatrix}1 & 2 \\1 & 6\end{vmatrix}+8\begin{vmatrix}1 & 3 \\1 & 9\end{vmatrix}) +7( 2\begin{vmatrix}
4 & 2 \\4 & 6\end{vmatrix} – 4\begin{vmatrix}1 & 2 \\1 & 6\end{vmatrix}+8\begin{vmatrix}1 & 4 \\1 & 4\end{vmatrix}) -2( 2\begin{vmatrix}
4 & 3 \\4 & 9\end{vmatrix} – 4\begin{vmatrix}1 & 3 \\1 & 9\end{vmatrix}+3\begin{vmatrix}1 & 4 \\1 & 4\end{vmatrix})$

$det⁡ A = 1[4(18-18)-3(24-8)+ 8(36-12)]-8[ 2(18-18)-3(6-2)+ 8(9-3)]+ 7[ 2(24-8)-4(6-2)+ 8(4-4)]-2[2(36-12)-4(9-3)+ 3(4-4)] $
$det⁡ A = 1[4(0)-3(16)+ 8(24)]-8[ 2(0)-3(4)+ 8(6)]+ 7[ 2(16)-4(4)+ 8(0)]-2[2(24)-4(6)+ 3(0)]$
$det A = 1[0-48+192]-8[0-12+48]+ 7[ 32-16+0]-2[48-24+0]$
$det⁡ A = 1[144]-8[36]+ 7[16]-2[24]$
$det A = 144-288+112- 48 $
$det⁡ A = -80$

Формула Лейбница:

Для расчетов матрица A = (aij) 4 × 4 по формуле Лейбница определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c & d\\e & f & g &h \\i & j & k & l \\ m & n & o & p
\end{vmatrix} \\
$

$det A = a*f*k*p + a*j*o*h + a*n*g*l + e*b*o*l + e*j*c*p + e*n*k*d + i*b*g*p + i*f*o*d + i*n*c*h+ m*b*k*h + m*f*c*l + m*j*g*d − a*f*o*l – a*j*g*p – a*n*k*h − e*b*k*p – e*j*o*d -e*n*c*l− i*b*o*h – i*f*c*p – i*n*g*d − m*b*g*l – m*f*k*d – m*j*c*h$

Пример:
Find $
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
$?

Решение:

$
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
$
$1*4*3*6-1*4*2*9-1*3*4*6+1*3*2*4+1*8*4*9-1*8*3*4-8*2*3*6+8*2*2*9+8*3*1*6-8*3*2*1-8*8*1*9+8*8*3*1+7*2*4*6-7*2*2*4-7*4*1*6+7*4*2*1+7*8*1*4-7*8*4*1-2*2*4*9+2*2*3*4+2*4*1*9-2*4*3*1-2*3*1*4+2*3*4*1$
$=-80$

Для умножения матрицы 5×5:

Здесь обсуждаются расчеты для матриц 5×5 разными методами:

Развернуть по столбцу:

Для расчетов матрица A = (aij) 5 × 5 из разложения столбца определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c & d & e\\f & g & h & i & j\\k & l & m & n & o \\ p & q & r & s & t \\ u & v & w & x & y
\end{vmatrix} \\
$

$det⁡ A= a\begin{vmatrix}
g & h & i & j\\l & m & n & o\\q & r & s & t\\v & w & x & y\end{vmatrix} – f\begin{vmatrix}b & c & d & e\\l & m & n & o\\ q & r & s & t\\ v & w & x & y\end{vmatrix}+k\begin{vmatrix}b & c & d & e \\g & h & i & j\\q & r & s & t\\v & w & x & y\end{vmatrix}-p\begin{vmatrix}b & c & d & e\\g & h & i & j\\l & m & n & o\\q & r & s & t\end {vmatrix}$

Затем просто определите определитель 4×4, используя приведенную выше формулу 4×4.

Развернуть по строке:

Для расчетов матрица A = (aij) 5 × 5 из разложения строки определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a & b & c & d & e\\f & g & h & i & j\\k & l & m & n & o \\ p & q & r & s & t \\ u & v & w & x & y
\end{vmatrix} \\
$

$det⁡ A= a\begin{vmatrix}
g & h & i & j\\l & m & n & o\\q & r & s & t\\v & w & x & y\end{vmatrix} – b\begin{vmatrix}g & h & i & j\\k & m & n & o\\ p & r & s & t\\ u & w & x & y\end{vmatrix}+c\begin{vmatrix}f & g & i & j \\k & l & n & o\\p & q & s & t\\u & v & x & y\end{vmatrix}-d\begin{vmatrix}f & g & h & j\\k & l & m & o\\p & q & r & t\\u & v & w & y\end {vmatrix}+e\begin{vmatrix}f & g & h & i\\k & l & m & n\\p & q & r & s\\u & v & w & x\end {vmatrix}$

Затем просто определите определитель 4×4, используя приведенную выше формулу 4×4.

Формула Лейбница:

Для расчетов матрица A = (aij) 5 × 5 по формуле Лейбница определяется по следующей формуле:

$
det A =
\begin{vmatrix}
a11 & a12 & a13 & a14 & a15\\a21 & a22 & a23 & a24 & a25\\a31 & a32 & a33 & a34 & a35 \\ a41 & a42 & a43 & a44 & a45 \\ a51 & a52 & a53 & a54 & a55
\end{vmatrix} \\
$

Образ

Пример:
Find $
det A =
\begin{vmatrix}
1 & 8 & 7 & 2 & 8\\2 & 4 & 3 &8 & 3\\1 & 4 & 3 & 2 &1\\ 1 & 4 & 9 & 6 & 2 \\ 1 & 5 & 7 & 3 & 4
\end{vmatrix} \\
$?
Решение:
$
det A =
\begin{vmatrix}
1 & 8 & 7 & 2 & 8\\2 & 4 & 3 &8 & 3\\1 & 4 & 3 & 2 &1\\ 1 & 4 & 9 & 6 & 2 \\ 1 & 5 & 7 & 3 & 4
\end{vmatrix} \\
$
\( =1*4*3*6*4-1*4*3*2*3-1*4*2*9*4+1*4*2*2*7+1*4*1*9*3-1*4*1*6*7-1*3*4*6*4+1*3*4*2*3+1*3*2*4*4-1*3*2*2*5-1*3*1*4*3+1*3*1*6*5+1*8*4*9*4-1*8*4*2*7-1*8*3*4*4+1*8*3*2*5+1*8*1*4*7-1*8*1*9*5-1*3*4*9*3+1*3*4*6*7+1*3*3*4*3-1*3*3*6*5-1*3*2*4*7+1*3*2*9*5-8*2*3*6*4+8*2*3*2*3+8*2*2*9*4-8*2*2*2*7-8*2*1*9*3+8*2*1*6*7+8*3*1*6*4-8*3*1*2*3-8*3*2*1*4+8*3*2*2*1+8*3*1*1*3-8*3*1*6*1-8*8*1*9*4+8*8*1*2*7+8*8*3*1*4-8*8*3*2*1-8*8*1*1*7+8*8*1*9*1+8*3*1*9*3-8*3*1*6*7-8*3*3*1*3+8*3*3*6*1+8*3*2*1*7-8*3*2*9*1+7*2*4*6*4-7*2*4*2*3-7*2*2*4*4+7*2*2*2*5+7*2*1*4*3-7*2*1*6*5-7*4*1*6*4+7*4*1*2*3+7*4*2*1*4-7*4*2*2*1-7*4*1*1*3+7*4*1*6*1+7*8*1*4*4-7*8*1*2*5-7*8*4*1*4+7*8*4*2*1+7*8*1*1*5-7*8*1*4*1-7*3*1*4*3+7*3*1*6*5+7*3*4*1*3-7*3*4*6*1-7*3*2*1*5+7*3*2*4*1-2*2*4*9*4+2*2*4*2*7+2*2*3*4*4-2*2*3*2*5-2*2*1*4*7+2*2*1*9*5+2*4*1*9*4-2*4*1*2*7-2*4*3*1*4+2*4*3*2*1+2*4*1*1*7-2*4*1*9*1-2*3*1*4*4+2*3*1*2*5+2*3*4*1*4-2*3*4*2*1-2*3*1*1*5+2*3*1*4*1+2*3*1*4*7-2*3*1*9*5-2*3*4*1*7+2*3*4*9*1+2*3*3*1*5-2*3*3*4*1+8*2*4*9*3-8*2*4*6*7-8*2*3*4*3+8*2*3*6*5+8*2*2*4*7-8*2*2*9*5-8*4*1*9*3+8*4*1*6*7+8*4*3*1*3-8*4*3*6*1-8*4*2*1*7+8*4*2*9*1+8*3*1*4*3-8*3*1*6*5-8*3*4*1*3+8*3*4*6*1+8*3*2*1*5-8*3*2*4*1-8*8*1*4*7+8*8*1*9*5+8*8*4*1*7-8*8*4*9*1-8*8*3*1*5+8*8*3*4*1\)
$ =-248$

Заметка:

Правило Треугольника и Правило Сарруса применимо только к матрице до 3×3. Наш онлайн-калькулятор определителей матриц использует все эти формулы для точных вычислений определителей. Просто вы можете использовать наш онлайн-математический калькулятор, который поможет вам легко выполнять различные математические операции за короткий промежуток времени.

Как использовать этот онлайн-калькулятор определителя матрицы:

Наш онлайн-калькулятор помогает найти определитель матрицы калькулятор размером до 5×5 пятью различными методами. Просто следуйте пунктам для получения точных результатов.
Читать дальше!

Входы:

Прежде всего, выберите порядок матрицы из выпадающего списка калькулятора.
Затем введите значения матрицы в соответствующие поля.
Затем выберите метод, с помощью которого вы найдете определитель.
Наконец, нажмите кнопку “Рассчитать”.

Заметка:

Есть поле «номер столбца или строки», в которое вы вводите номер строки или номер столбца, которые необходимо развернуть. Кроме того, в нем есть поля для создания матрицы и очистки матрицы, он автоматически сгенерирует матрицу и очистит все значения из матрицы соответственно.

Выходы:

После заполнения всех полей калькулятор показывает:

Определитель матрицы.
Пошаговые расчеты.

Заметка:

Независимо от того, какой метод вы выберете для расчетов, онлайн-калькулятор определителя покажет вам результаты в соответствии с выбранным вариантом.

Детерминантные свойства:

Поскольку детерминанты обладают многими полезными свойствами, но здесь мы перечислили некоторые из их важных свойств:

Определитель произведения чисел равен произведению определителей чисел.
Если мы поменяем местами две строки и два столбца матрицы, то определитель останется тем же, но с противоположным знаком.
определитель матрицы онлайн равен транспонированной матрице.
определитель матрицы калькулятор 5 × 5 полезен в расширении Лапласа.
Если мы добавим те же две копии первой строки в любую строку (столбцы в любой столбец), то определитель не изменится.

Часто задаваемые вопросы (FAQ):

Для чего используются детерминанты?

Определитель полезен при определении решения линейных уравнений, фиксируя, как линейное преобразование изменяет объем или площадь и изменяет переменные в интегралах. Он отображается как функция, вход которой представляет собой квадратную матрицу, а выход представляет собой одно число.

Что означает определитель 0?

Определитель 0 означает, что объем равен нулю (0). Это может произойти только тогда, когда один вектор перекрывает один другой.

Может ли определитель быть отрицательным?

Поскольку это действительное число, а не матрица. Значит, это может быть отрицательное число. Определитель существует только для квадратных матриц (2 × 2, 3 × 3, … n × n).

Конечное примечание:

К счастью, вы узнали о детерминантах, о том, как их найти вручную, и о различных приложениях в математике, включая решение линейных уравнений; определить изменение объема или площади при линейном преобразовании и т. д. Когда дело доходит до решения определителя для матрицы более высокого порядка, это очень сложная задача. Просто попробуйте этот онлайн-калькулятор определителя, который позволяет вам найти определитель матриц с помощью различных методов расчета с полным расчетом. Как правило, студенты и профессионалы используют этот калькулятор определителя матрицы для решения своих математических задач.

Other languages: Determinant Calculator, Determinant Hesaplama, Kalkulator Wyznacznika Macierzy, Kalkulator Penentu Matriks, Determinanten Rechner, 行列式計算, 행렬식 계산기, Determinant Kalkulačka, Calculadora De Determinantes, Calcul Déterminant Matrice, Calculadora De Determinantes, Calcolo Determinante, حساب محدد, Determinantti laskin, Determinantberegner.

вычисление матриц

Вы искали вычисление матриц? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление матрицы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление матриц».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление матриц,вычисление матрицы,вычисление определителей онлайн,вычисление определителя 4 порядка онлайн,вычисление определителя 4 порядка онлайн с решением,вычисление определителя калькулятор онлайн,вычисление определителя матрицы,вычисление определителя матрицы калькулятор,вычисление определителя матрицы онлайн,вычисление определителя онлайн,вычисление определителя онлайн калькулятор,вычислите определитель 3 порядка,вычислите определитель матрицы онлайн,вычислитель определитель матрицы онлайн,вычислитель определителя онлайн,вычислить матрица,вычислить онлайн определитель 4 порядка,вычислить онлайн определитель второго порядка,вычислить определитель 2 порядка онлайн,вычислить определитель 4 го порядка онлайн,вычислить определитель 4 порядка калькулятор,вычислить определитель 4 порядка калькулятор онлайн,вычислить определитель 4 порядка онлайн,вычислить определитель 4 порядка онлайн калькулятор,вычислить определитель 4 порядка онлайн с подробным решением,вычислить определитель второго порядка онлайн,вычислить определитель второго порядка онлайн с решением,вычислить определитель используя свойства определителя онлайн,вычислить определитель калькулятор,вычислить определитель матрицы 4х4,вычислить определитель матрицы 4х4 онлайн с решением,вычислить определитель матрицы калькулятор,вычислить определитель матрицы калькулятор онлайн,вычислить определитель матрицы онлайн,вычислить определитель матрицы онлайн калькулятор,вычислить определитель матрицы онлайн с решением,вычислить определитель матрицы онлайн с решением подробно,вычислить определитель методом понижения порядка онлайн,вычислить определитель онлайн,вычислить определитель онлайн 4 порядка,вычислить определитель онлайн калькулятор,вычислить определитель онлайн с подробным решением,вычислить определитель онлайн с подробным решением онлайн,вычислить определитель с подробным решением онлайн,вычислить определитель третьего порядка,вычислить определитель четвертого порядка онлайн,вычислить определитель четвертого порядка онлайн с подробным решением,вычислить определитель четвертого порядка онлайн с решением,вычислить определитель четвертого порядка с решением онлайн,вычислить определить,вычислить определить онлайн,вычислить определить онлайн 4 на 4,детерминант матрицы 4 на 4,детерминант матрицы калькулятор,детерминант матрицы онлайн,детерминант матрицы онлайн калькулятор,детерминант онлайн,задачи определитель матрицы,используя свойства определителя вычислить определитель онлайн,как вычислить матрицу,как вычислить определитель 4 порядка онлайн с решением подробно,как вычислить определитель матрицы 4х4,как найти определитель матрицы,как найти определитель матрицы 4х4,как найти определитель матрицы 4х4 онлайн,как найти определитель матрицы 5х5,как посчитать матрицу 4 на 4,калькулятор визначників,калькулятор визначників онлайн,калькулятор вычисления определителя матрицы,калькулятор вычислить определитель,калькулятор вычислить определитель 4 порядка,калькулятор вычислить определитель 4 порядка онлайн,калькулятор вычислить определитель матрицы,калькулятор детерминант матрицы,калькулятор детерминанта матрицы,калькулятор для определителей,калькулятор матриц 4 порядка,калькулятор матриц матричный метод,калькулятор матриц матричным методом,калькулятор матриц онлайн определитель,калькулятор матриц онлайн определитель с решением,калькулятор матриц онлайн с решением определитель,калькулятор матриц определителей,калькулятор матриц определитель,калькулятор матриц определитель онлайн,калькулятор матрица определитель,калькулятор матрицы 4 порядка,калькулятор матрицы вычислить определитель,калькулятор матрицы вычислить определитель матрицы,калькулятор матрицы детерминант,калькулятор матрицы онлайн найти определитель,калькулятор матрицы определитель онлайн калькулятор с подробным решением,калькулятор матричный метод,калькулятор матричный метод онлайн,калькулятор матричный способ,калькулятор найти определитель матрицы,калькулятор онлайн вычисление определителя,калькулятор онлайн вычислить определитель матрицы,калькулятор онлайн вычислить определитель матрицы онлайн с решением,калькулятор онлайн матриц определитель,калькулятор онлайн матрица определитель,калькулятор онлайн матричный метод,калькулятор онлайн метод матричный,калькулятор онлайн найти определитель,калькулятор онлайн найти определитель матрицы,калькулятор онлайн обчислити визначник,калькулятор онлайн определителей,калькулятор онлайн определители,калькулятор онлайн определителя,калькулятор определения,калькулятор определителей,калькулятор определителей 4 порядка,калькулятор определителей матриц,калькулятор определителей матриц онлайн,калькулятор определителей матрицы,калькулятор определителей онлайн,калькулятор определители,калькулятор определители онлайн,калькулятор определитель,калькулятор определитель 4 порядка,калькулятор определитель матриц,калькулятор определитель матриц онлайн,калькулятор определитель матрицы,калькулятор определитель матрицы 4 порядка,калькулятор определитель третьего порядка онлайн с решением,калькулятор определителя,калькулятор определителя 4 порядка,калькулятор определителя 4 порядка онлайн,калькулятор определителя матрицы,калькулятор определителя матрицы онлайн,калькулятор определителя онлайн,калькулятор систем матриц,калькулятор союзной матрицы,линейная алгебра онлайн калькулятор,матрица 3 на 3 онлайн,матрица 4 порядка онлайн,матрица вычисление,матрица вычислить,матрица калькулятор онлайн определитель,матрица калькулятор определитель,матрица метод треугольника онлайн,матрица нахождение определителя,матрица онлайн калькулятор определитель,матрица онлайн определитель,матрица определитель калькулятор,матрица определитель калькулятор онлайн,матрица определитель онлайн,матрица определитель онлайн калькулятор,матрица четвертого порядка онлайн,матрицы onlinemschool,матрицы вычисление,матрицы калькулятор найти определитель матрицы,матрицы онлайн калькулятор найти определитель,матрицы определитель 4 порядка онлайн,матрицы считать,матричный калькулятор матричный способ,матричный калькулятор метод,матричный калькулятор онлайн матричный метод,матричный калькулятор онлайн метод матричный,матричный калькулятор определитель,матричный метод калькулятор,матричный метод калькулятор онлайн с подробным решением,матричный метод онлайн калькулятор с подробным решением,матричный способ калькулятор,матричный способ калькулятор онлайн,матричный способ онлайн калькулятор,метод матричный калькулятор,метод матричный онлайн калькулятор,метод матричный онлайн калькулятор с подробным решением,метод треугольника матрица онлайн,метод треугольника матрицы онлайн,метод элементарных преобразований матрицы онлайн калькулятор,модуль матрицы,найти детерминант матрицы онлайн,найти определитель калькулятор онлайн,найти определитель матрицы 3х3 онлайн,найти определитель матрицы 4х4,найти определитель матрицы 4х4 онлайн,найти определитель матрицы 4х4 онлайн с решением,найти определитель матрицы калькулятор онлайн,найти определитель матрицы онлайн,найти определитель матрицы онлайн 4х4,найти определитель матрицы онлайн калькулятор,найти определитель матрицы онлайн с подробным решением,найти определитель матрицы онлайн с решением,найти определитель матрицы с решением онлайн,найти определитель онлайн,найти определитель онлайн калькулятор,найти определить матрицы,нахождение детерминанта матрицы,нахождение определителя матрица,нахождение определителя матрицы 4 порядка онлайн,нахождение определителя матрицы онлайн,нахождение определителя матрицы онлайн с решением,нахождение определителя онлайн,обчислити визначник калькулятор онлайн,обчислити визначник онлайн калькулятор,онлайн вычисление определителей,онлайн вычисление определителя 4 порядка,онлайн вычисления определителя матрицы,онлайн вычислитель определителя,онлайн вычислить определитель четвертого порядка,онлайн детерминант,онлайн калькулятор визначників,онлайн калькулятор вычисление определителя,онлайн калькулятор вычислить определитель,онлайн калькулятор вычислить определитель 4 порядка,онлайн калькулятор вычислить определитель матрицы,онлайн калькулятор детерминант матрицы,онлайн калькулятор матриц определителей,онлайн калькулятор матриц определитель,онлайн калькулятор матриц определитель с решением,онлайн калькулятор матриц с решением определитель,онлайн калькулятор матрица определитель,онлайн калькулятор матрицы вычислить определитель,онлайн калькулятор матрицы детерминант,онлайн калькулятор матрицы найти определитель,онлайн калькулятор матричный метод,онлайн калькулятор матричный способ,онлайн калькулятор метод матричный,онлайн калькулятор метод саррюса,онлайн калькулятор найти определитель,онлайн калькулятор найти определитель матрицы,онлайн калькулятор обчислити визначник,онлайн калькулятор определение матрицы,онлайн калькулятор определителей,онлайн калькулятор определителей матриц,онлайн калькулятор определители,онлайн калькулятор определитель,онлайн калькулятор определитель 4 порядка,онлайн калькулятор определитель второго порядка,онлайн калькулятор определитель матриц,онлайн калькулятор определитель матрица,онлайн калькулятор определитель матрицы,онлайн калькулятор определитель матрицы 4 порядка,онлайн калькулятор определитель матрицы с подробным решением,онлайн калькулятор определитель матрицы с решением,онлайн калькулятор определителя,онлайн калькулятор определителя 4 порядка,онлайн калькулятор определителя матрицы,онлайн калькулятор присоединенная матрица,онлайн калькулятор решение определителей,онлайн матрица 3 на 3,онлайн определение определителя матрицы,онлайн определители,онлайн определители матриц,онлайн определитель 2 порядка,онлайн определитель 4 порядка,онлайн определитель матрицы 4 порядка,онлайн определитель матрицы 4х4,онлайн определитель матрицы с решением,онлайн определитель четвертого порядка,онлайн определить,онлайн подсчет определителя матрицы,онлайн расчет определителя матрицы,онлайн решение матриц 4 порядка,онлайн решение матриц методом,онлайн решение матрицы 3 на 3,онлайн решение матрицы определитель,онлайн решение определителей,онлайн решение определителей 4 порядка,онлайн решение определители,онлайн решение определитель,онлайн решение определитель матрицы,онлайн решение определителя,онлайн решение определителя 4 порядка,онлайн решить определитель,онлайн решить определитель 4 порядка,онлайн считать определитель,определение матрицы онлайн калькулятор,определение онлайн,определение определителя матрицы онлайн,определители 4 порядка онлайн,определители вычислить,определители калькулятор,определители калькулятор онлайн,определители матриц онлайн,определители онлайн,определители онлайн калькулятор,определители онлайн решение,определители решение онлайн,определитель 2 порядка онлайн,определитель 4 го порядка калькулятор онлайн,определитель 4 го порядка онлайн,определитель 4 порядка калькулятор,определитель 4 порядка калькулятор онлайн,определитель 4 порядка матрицы онлайн,определитель 4 порядка онлайн,определитель 4 порядка онлайн калькулятор,определитель 4 порядка онлайн с решением,определитель 4 порядка онлайн с решением подробно,определитель 4 порядка решить онлайн,определитель 5 порядка онлайн,определитель второго порядка онлайн калькулятор,определитель как считать,определитель калькулятор,определитель калькулятор матриц,определитель калькулятор онлайн,определитель матриц калькулятор,определитель матриц онлайн калькулятор,определитель матрица калькулятор онлайн,определитель матрица онлайн калькулятор,определитель матрицы 3х3 онлайн,определитель матрицы 4 порядка калькулятор,определитель матрицы 4 порядка онлайн,определитель матрицы 4 порядка онлайн калькулятор,определитель матрицы 4х4,определитель матрицы 4х4 найти,определитель матрицы 4х4 онлайн,определитель матрицы 4х4 формула,определитель матрицы 5х5,определитель матрицы калькулятор,определитель матрицы онлайн,определитель матрицы онлайн 4 порядка,определитель матрицы онлайн 4х4,определитель матрицы онлайн калькулятор,определитель матрицы онлайн калькулятор с подробным решением,определитель матрицы онлайн калькулятор с решением,определитель матрицы онлайн по строке,определитель матрицы онлайн решение,определитель матрицы онлайн с буквами,определитель матрицы онлайн с решением,определитель матрицы по строке онлайн,определитель матрицы рассчитать,определитель матрицы рассчитать онлайн,определитель матрицы решение онлайн,определитель матрицы с буквами онлайн,определитель матрицы с решением онлайн,определитель матрицы с решением онлайн калькулятор,определитель матрицы считать онлайн,определитель онлайн,определитель онлайн 2 порядка,определитель онлайн калькулятор,определитель онлайн решение,определитель онлайн решить,определитель посчитать,определитель решение матрицы онлайн,определитель решение онлайн,определитель решить,определитель решить онлайн,определитель считать,определитель считать онлайн,определитель третьего порядка онлайн калькулятор,определитель четвертого порядка калькулятор онлайн,определитель четвертого порядка онлайн,определить вычислить онлайн,определить матрицы калькулятор,определить матрицы онлайн,определить онлайн,определить онлайн матрицы,определить посчитать онлайн,подсчет определителя матрицы онлайн,поиск определителя матрицы онлайн,получить нули в строке матрицы онлайн калькулятор,посчитать детерминант матрицы онлайн,посчитать онлайн определитель,посчитать онлайн определитель 4 порядка,посчитать определитель,посчитать определитель 4 порядка онлайн,посчитать определитель матрицы,посчитать определитель матрицы онлайн,посчитать определитель онлайн,посчитать определить онлайн,приведение матрицы к диагональному виду онлайн,привести к диагональному виду матрицу онлайн,привести матрицу к диагональному виду онлайн,рассчитать определитель матрицы,рассчитать определитель матрицы онлайн,рассчитать определитель онлайн,расчет матрицы,расчет определителя матрицы онлайн,решение матриц 4 порядка онлайн,решение матриц 4х4,решение матриц методом онлайн,решение матриц онлайн 4 порядка,решение матриц онлайн методом,решение матрицы онлайн 3 на 3,решение матрицы онлайн определитель,решение матрицы определитель онлайн,решение онлайн матриц 4 порядка,решение онлайн определитель,решение онлайн определитель матрицы,решение онлайн определителя,решение определителей 4 порядка онлайн,решение определителей онлайн,решение определители онлайн,решение определитель матрицы онлайн,решение определитель онлайн,решение определителя 4 порядка онлайн,решение определителя онлайн,решить онлайн определитель,решить онлайн определитель 4 порядка,решить определитель 4 порядка онлайн,решить определитель онлайн,сделать линейные преобразования найти определитель,считать онлайн определитель,считать онлайн определитель матрицы,считать определитель,считать определитель матрицы онлайн,считать определитель онлайн,теорема лапласа онлайн калькулятор,упростить и вычислить определитель.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление матриц. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычисление определителей онлайн).

Решить задачу вычисление матриц вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Решение матриц — Онлайн калькулятор

Справочник
Онлайн-калькуляторы
Тесты с ответами

Калькулятор матриц онлайн предназначен для автоматизированного решения задач. В программу вычислений заложена формула, которая позволяет получить готовый ответ с подробным расчетом. Все промежуточные действия и преобразования доступны пользователю.

Для решения матрицы онлайн-калькулятором воспользуйтесь простым интерфейсом сервиса и получите:

экономию времени;
уверенность в точности вычислений;
наглядность и объяснение расчетов;
решение задачи за один клик.

Найти определитель матрицы онлайн-калькулятором, как и воспользоваться другими вычислениями на сайте, можно бесплатно и неограниченное количество раз.

Найти определитель матрицы
Найти обратную матрицу
Возведение матрицы в степень
Умножение матрицы на число
Умножение матриц
Транспонирование матрицы
Сложение и вычитание матриц
Ранг матрицы

К решению матриц онлайн чаще всего обращаются студенты с целью быстро узнать ответ. Если алгоритм расчета понятен, то данный способ подготовки к занятиям сокращает время и позволяет охватить больше заданий. Решить матрицу с онлайн-калькулятором также полезно тем, кто не разобрался в теме. С помощью полученных подробных вычислений можно самостоятельно вникнуть в суть расчетов и применять их при решении аналогичных задач.

Не всегда возможно найти ответ с помощью калькулятора. В некоторых заданиях требуется использовать также другие формулы. В таком случае обратитесь к консультанту на сайте:

для вас оперативно рассчитают стоимость услуги в зависимости от сложности задания, его объема и необходимого срока исполнения;
подберут надежного исполнителя из числа университетских преподавателей с учеными степенями;
решат задачи любой тематики и уровня сложности.

Оставляйте заявку, чтобы посчитать стоимость услуги. Для постоянных клиентов у нас действуют скидки.

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

Решение матриц
Точка, прямая, плоскость
Конвертеры
Объем фигур
Калькуляторы площади фигур
Решение уравнений
Операции над векторами
Периметр фигур

Популярные калькуляторы

Решение систем линейных уравнений методом Гаусса
Угол между векторами
Каноническое уравнение прямой проходящей через две точки
Решение систем линейных уравнений методом Крамера
Длина вектора. Модуль вектора
Площадь треугольника (по 3 сторонам)

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Вычисление определителя 4 порядка онлайн. Определитель матрицы

Второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: ; ; ; detA (детерминант).

Пример:
.

Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу

Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.

В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.

Пример:

Разложение определителя по элементам некоторой строки (столбца).

Минором М ij элемента а ij квадратной матрицы А называется определитель, составленный из элементов матрицы А , оставшихся после вычеркивания i- ой строки и j -го столбца.

Например, минором к элементу а 21 матрицы третьего порядка
будет определитель
.

Будем говорить, что элемент а ij занимает четное место, если i+j (сумма номеров строки и столбца на пересечении которых находится данный элемент) — четное число, нечетное место, если i+j — нечетное число.

Алгебраическим дополнением А ij элемента а ij квадратной матрицы А называется выражение (или величина соответствующего минора, взятого со знаком «+», если элемент матрицы занимает четное место, и со знаком «-», если элемент занимает нечетное место).

Пример:

а 23 = 4;

— алгебраическое дополнение элемента а 22 = 1.

Теорема Лапласа . Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.

Проиллюстрируем на примере определителя третьего порядка. Вычислить определитель третьего порядка разложением по первой строке можно следующим образом

Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.

Пример :

Таким образом, вычисление определителя 3-го порядка сводится к вычислению 3-х определителей второго порядка. В общем случае можно вычислить определитель квадратной матрицы n -го порядка, сводя его к вычислению n определителей (n-1 )-го порядка

Замечание. Не существует простых способов для вычисления определителей более высокого порядка, аналогичных способам вычисления определителей 2-го и 3-го порядка. Поэтому для вычисления определителей выше третьего порядка может использоваться только метод разложения.

Пример . Вычислить определитель четвертого порядка.

Разложим определитель по элементам третьей строки

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

4. Общий множитель всех элементов некоторой строки (столбца) определителя можно вынести за знак определителя.

5. Определитель не изменится, если к элементам одного из его столбцов (строки) прибавить соответствующие элементы любого другого столбца (строки), умноженные на некоторое число.

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи , то решайте их .»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

С каждой квадратной матрицей связывают число . Это число называется определителем матрицы. Определитель вычисляется по особым правилам и обозначается |A|, det A , ΔA.

Число строк (столбцов) определителя называется его порядком .

Определитель первого порядка матрицы равен элементу a 11: |A|=a 11

Не путать определитель первого порядка с модулем.

Определитель второго порядка обозначается символом

и равен |A|=a 11 a 22 -a 12 a 21

Определитель 3-го порядка обозначается символом

Для запоминания этой формулы используют схематические правила (правило треугольника или Саррюса )

Правило Саррюса.

Правило треугольника.

Посмотрим на примере, как используются эти правила.

ПРИМЕР:

Правило Саррюса

Допишем к определителю два первых столбца.

Правило треугольника

Такой способ вычисления определителей не подходит для определителей 4-го порядка и выше. Прежде чем указать правило, которое позволяет находить определители любого порядка, рассмотрим понятие алгебраического дополнения элемента матрицы.

Алгебраическим дополнением (А ij ) элемента а ij определителя матрицы А называется число, равное произведению (-1) i+j (в степени номер строки плюс номер столбца этого элемента) на определитель, который получается из данного в результате вычеркивания строки и столбца, где стоит этот элемент.

ПРИМЕР:

Вычислить алгебраическое дополнение А 21 элемента а 21 .

РЕШЕНИЕ:

По определению алгебраического дополнения

Вычисление определителя произвольного порядка. Определитель равен сумме произведений элементов любой его строки (или столбца) на соответствующие алгебраические дополнения.

, разложение определителя 4-го порядка по первой строке выглядит следующим образом:

Инструкция

Для вычисления детерминанта (Det A) матрицы размерностью 5х5 проведите элементов по первой строке. Для этого возьмите первый элемент данной строки и вычеркните из матрицы строку и столбец, на пересечении которых он находится. Запишите формулу произведения первого и определителя полученной матрицы 4 порядка: a11*detM1 – это будет первое слагаемое для нахождения Det A. В оставшейся четырехразрядной матрице М1 вам будет позже так же найти определитель (дополнительный минор).

Аналогичным образом, последовательно вычеркивайте столбец и строку, содержащие 2, 3, 4 и 5 элемент первой строки начальной матрицы, и находите для каждого из них соответствующую матрицу 4х4. Запишите произведения этих элементов на дополнительные миноры: a12*detM2, a13*detM3, a14*detM4, a15*detM5.

Найдите определители полученных матриц 4 порядка. Для этого проведите тем же методом понижение размерности. Первый элемент b11 матрицы M1 умножьте на определитель оставшейся матрицы 3х3 (C1). Детерминант же трехмерной матрицы можно легко по формуле: detC1 = c11* c22*c33 + c13* c21*c32 + c12* c23*c31 — c21* c12*c33 — c13* c22*c31 — c11* c32*c23, где cij – элементы полученной матрицы C1.

Далее рассмотрите аналогично второй элемент b12 матрицы М1 и вычислите его с соответствующим дополнительным минором detC2 полученной трехмерной матрицы. Таким же образом найдите произведения для 3 и 4 элемента первой матрицы 4 порядка. После чего определите искомый дополнительный минор матрицы detМ1. Для этого, согласно формуле разложения по строке, : detМ1 = b11*detC1 — b12*detC2 + b13*detC3 — b14*detC4. Вы получили первое слагаемое, необходимое для нахождения Det A.

Вычислите остальные слагаемые определителя матрицы пятого порядка, аналогичным образом понижая размерность каждой матрицы 4 порядка. Окончательная так: Det A = a11*detM1 — a12*detM2 + a13*detM3 — a14*detM4 + a15*detM5.

Инструкция

Самая простая и краткая формулировка этой операции такова: матрицы перемножаются по алгоритму «строка на столбец».

Теперь подробнее об этом правиле, а также о возможных ограничениях и особенностях.

Умножение на единичную матриц переводит исходную матрицы саму в себя (эквивалентно умножению чисел, где один из элементов 1). Аналогично, умножение на нулевую матрицу даёт нулевую матрицу.

Главное условие, накладываемое на участвующие в операции матрицы вытекает из способа выполнения : строк в первой матрице должно быть столько же, сколько столбцов во второй. Нетрудно догадаться, что в противном просто не на что.

Также стоит отметить ещё один важный момент: у умножения матриц нет коммутативности (или «перестановочности»), иначе говоря, А умножить на B не равняется B умножить на А. Запомните это и не путайте с правилом для умножения чисел.

Теперь, собственно сам процесс умножения.

Пусть мы умножаем матрицу А на матрицу B справа.

Берём первую строчку матрицы А и ее i-ый элемент умножаем на i-ый элемент первого столцба матрицы B. Все полученные складываем и записываем на место а11 в итоговую матрицу.

Затем также поступаем с первой строкой матрицы А и 3-им, 4-ым и т.д. столбцами матрицы Б, заполнив, таким образом, первую строчку итоговой матрицы.

Теперь переходим ко второй строке и снова перемножаем её последовательно на все столбцы, начиная с первого. Записываем результат во вторую строку итоговой матрицы.

Затем к 3-ей, 4-ой и т.д.

Повторяем , пока не перемножим все строки в матрице А со всеми столбцами матрицы В.

Матрицы — это эффективный способ представления числовой информации. Решение любой системы линейных уравнений можно записать в виде матрицы (прямоугольника, составленного из чисел). Умение перемножать матрицы — один из самых важных навыков, которым обучают на курсе «Линейной алгебры» в высших учебных заведениях.

Вам понадобится

Калькулятор

Инструкция

Для проверки этого условия проще всего воспользоваться следующим алгоритмом — запишите размерность первой матрицы как (a*b). Дальше размерность второй — (c*d). Если b=c — матрицы соразмерны, их можно перемножать.

Дальше произведите само перемножение. Помните — при перемножении двух матриц получается матрица. То есть, задача перемножения сводится к задаче нахождения новой, с размерностью (a*d). На СИ задачи перемножения матрицы выглядит следующим образом:
void matrixmult(int m1[n], int m1_row, int m1_col, int m2[n], int m2_row, int m2_col, int m3[n], int m3_row, int m3_col)
{ for (int i = 0; i for (int j = 0; j m3[i][j]=0;
for (int k = 0; k for (int i = 0; i for (int j = 0; j m3[i][k] += m1[i][j] * m2[j][k];
}

Проще говоря, новой матрицы — это сумма произведений элементов строки первой матрицы на элементы столбца второй матрицы. Если вы элемент третьей матрицы с номером (1;2), то вы должны просто умножить первую строку первой матрицы на второй столбец второй. Для этого считаете начальную сумму равной нулю. Дальше умножаете первый элемент первой строки на первый элемент второго столбца, значение добавляете в сумму. Делаете так: умножаете i-тый элемент первой строки на i-тый элемент второго столбца и добавляете результаты к сумме, пока не кончится строка. Итоговая сумма и будет искомым элементом.

После того, как вы нашли все элементы третьей матрицы, записываете ее. Вы нашли произведение матриц.

Источники:

Главный математический портал России в 2019
как находить произведение матриц в 2019

Определитель (детерминант) матрицы — одно из важнейших понятий линейной алгебры. Определитель матрицы представляет собой многочлен от элементов квадратной матрицы. Чтобы вычислить определитель четвертого порядка, нужно общим правилом вычисления определителя.

Вам понадобится

Инструкция

Квадратная матрица четвертого представляет из себя из четырех строк и четырех столбцов. (1+j))aij, то есть одного из членов перовой строки матрицы, взятого с положительным или знаком, на квадратную третьего порядка (минор квадратной матрицы).

Получившиеся миноры, которые представляют из себя матрицы третьего порядка, можно уже по известной частной формуле, без использования новых миноров. Определители квадратной матрицы третьего порядка можно рассчитать по так называемому «правилу треугольника». Формулу для расчета определителя в этом случае выводить не нужно, а можно запомнить ее геометрическую схему. Эта изображена на приведенном рисунке. В результате |А| = a11*a22*a33+a12*a23*a31+a13*a21*a32-a11*a23*a32-a12*a21*a33-a13*a22*a31.
Следовательно, миноры вычислены и определитель квадратной матрицы четвертого порядка может быть посчитан.

Источники:

как рассчитать определитель

Вам понадобится

— программа Microsoft Office Excel.

Инструкция

Запустите программу Microsoft Office Excel. В меню ввода данных впишите данную вам матрицу для последующего вычисления ее определителя. Выделите одну из незанятых ячеек таблицы, после чего введите следующую формулу: “=МОПРЕД(ak:fg)”. В данном случае ak будет означать координаты, соответствующие левому верхнему углу заданной матрицы, а fg – нижнему правому. Для получения определителя нажмите клавишу Enter. Нужное значение будет отображено в выбранной вами пустой ячейке.

Используйте функционал Excel для вычисления и других значений. В случае если вы не умеете использовать формулы в Microsoft Office Excel, скачайте специальную тематическую литературу, и после прочтения вам будет достаточно легко сориентироваться по данной программе.

Внимательно изучите наименования значений формул в данном программном обеспечении, поскольку при неправильном их вводе у вас могут испортиться сразу все результаты, в особенности это касается тех, кто выполняет сразу несколько одинаковых вычислений по одной одновременно.

Время от времени выполняйте проверку полученных в Microsoft Office Excel результатов вычисления. Это связано с тем, что в системе могли произойти какие-либо изменения со временем, в частности это относится к тем, кто выполняет работу по шаблона.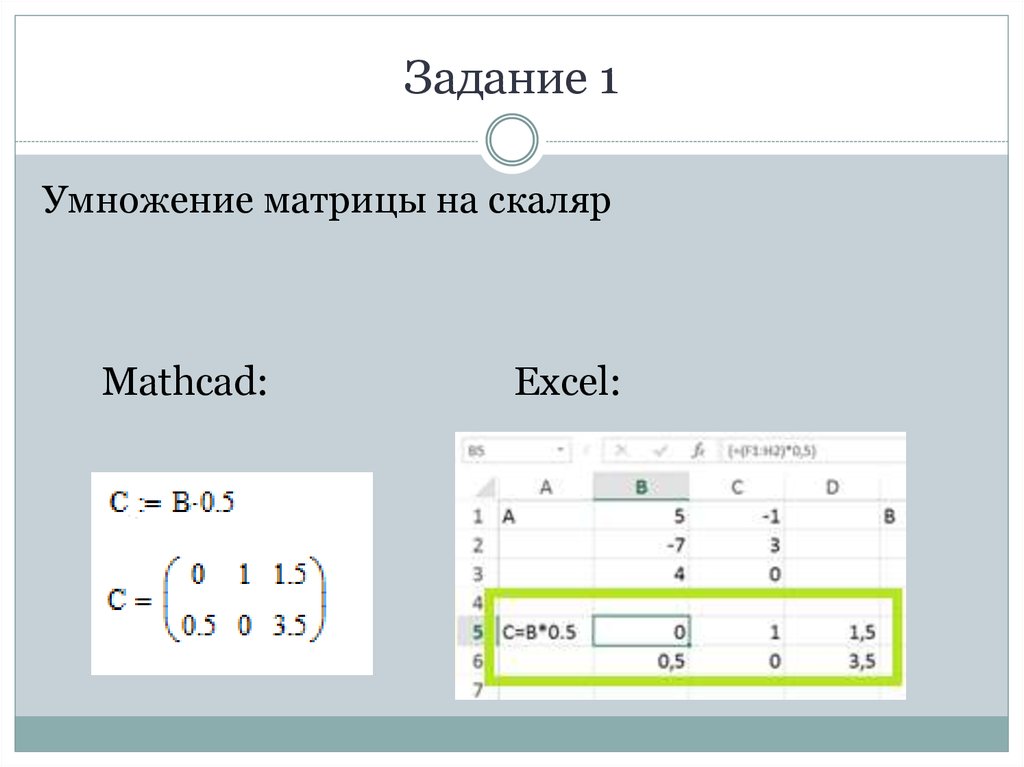 Всегда нелишним будет лишний раз сверить результаты сразу нескольких текущих вычислений.

Также при работе с формулами будьте крайне осторожны и не допускайте появления в вашем компьютере вирусов. Даже в случае если операции с формулами в Microsoft Office Excel понадобится вам единоразово, изучите функционал данной программы в большей степени, поскольку эти навыки помогут вам в дальнейшем лучше понимать автоматизацию учета и применять Excel для выполнения определенных заданий.

Определитель – одно из понятий матричной алгебры. Это квадратная матрица, состоящая из четырех элементов, а чтобы вычислить определитель второго порядка , нужно воспользоваться формулой разложения по первой строке.

Инструкция

Определитель квадратной – это , которое используется в различных расчетах. Он незаменим при нахождении обратной матрицы, миноров, алгебраических дополнений, операции деления , но чаще всего необходимость перехода к определителю возникает при решении систем линейных уравнений.

Матрица второго порядка представляет собой совокупность четырех элементов, расположенных на двух строках и столбцах. Эти числа соответствуют коэффициентам системы уравнений неизвестными, которые применяются при рассмотрении множества прикладных задач, например, экономических.

Переход к компактным матричным вычислениям помогает быстро две вещи: во-первых, имеет ли эта решение, во-вторых, найти его. Достаточным условием решения является

Лекция 6

Матрицы

6.1. Основные понятия

Определение 1. Матрицей называется прямоугольная таблица чисел.

Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:

Числа, составляющие матрицу, называются ее элементами , элементматрицырасположен в ее-й строке и-м столбце.

Числа и(число строк и столбцов матрицы) называются ее порядками.

Говорят также, что — матрица размером
.

Если
, матрицаназываетсяквадратной .

Для краткой записи используется также обозначение
(или
) и далее указывается, в каких пределах изменяютсяи, например,
,
,
. (Запись читается так: матрицас элементами,изменяется отдо,- отдо.)

Среди квадратных матриц отметим диагональные матрицы , у которых все элементы с неравными индексами (
) равны нулю:

Будем говорить, что элементы
расположены на главной диагонали.

Диагональная матрица вида

называется единичной матрицей.

В дальнейшем будут встречаться матрицы вида

и
,

которые называются треугольными матрицами, а также матрицы, состоящие из одного столбца:

и одной строки:

(матрица-столбец и матрица-строка ).

Матрица, все элементы которой равны нулю, называется нулевой.

6.2. Определители порядка n

Пусть дана квадратная матрица порядка :

. (6.1)

Составим всевозможные произведения элементов матрицы, расположенных в разных строках и разных столбцах, т. е. произведения вида

. (6.2)

Число произведений вида (6.2) равно (примем этот факт без доказательства).

Будем считать все эти произведения членами определителя порядка , соответствующего матрице (6.1).

Вторые индексы множителей в (6.2) составляют перестановку первых натуральных чисел
.

Говорят, что числа ив перестановке составляютинверсию , если
, а в перестановкерасположено раньше.

Пример 1. В перестановке шести чисел,
, числаи,и,и,и,исоставляют инверсии.

Перестановка называется четной , если число инверсий в ней четно, инечетной , если число инверсий в ней нечетно.

Пример 2. Перестановка
— нечетная, а перестановка
— четная (инверсий).

Определение 2. Определителем порядка , соответствующим матрице (6.1), называется алгебраическая сумма членов , составленная следующим образом : членами определителя служат всевозможные произведения элементов матрицы , взятых по одному из каждой строки и каждого столбца , причем слагаемое берется со знаком «+», если множество вторых индексов является четной перестановкой чисел
, и со знаком «–», если нечетной.

Обозначать определитель матрицы (6.1) принято так:

Замечание. Определение 2 для
и
приводит к уже знакомым нам определителям 2-го и 3-го порядка:

Транспонированием вокруг главной диагонали матрицыназывается переход к матрице
, для которой строки матрицыявляются столбцами, а столбцы — строками:

Будем говорить, что определитель
получен транспонированием определителя.

Свойства определителя порядка п:

1.
(определитель не меняется при транспонировании вокруг главной диагонали).

2. Если одна из строк определителя состоит из нулей, определитель равен нулю.

3. От перестановки двух строк определитель меняет лишь знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на число , определитель умножится на.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы -й строки определителя представлены в виде суммы
, то определитель равен сумме двух определителей, у которых все строки, кроме-й, такие же, как в исходном определителе, а-я строка в одном определителе состоит из, а в другом — из.

Определение 3. -я строка определителя называется линейной комбинацией остальных его строк , если такие , что, умножая -ю строку на, а затем складывая все строки , кроме -й , получаем -ю строку.

8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.

9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.

Замечание. Мы сформулировали свойства определителя для строк. В силу свойства 1 (
) они справедливы и для столбцов.

Все приведенные свойства были доказаны на практических занятиях для
; для произвольногопримем их без доказательства.

Если в определителе порядкавыбрать элементи вычеркнуть столбец и строку, на пересечении которых расположен, оставшиеся строки и столбцы образуют определитель порядка
, который называетсяминором определителя, соответствующим элементу.

Пример 3. В определителе

минором элемента
является определитель
.

Определение 4. Алгебраическим дополнением элементаопределителяназывается его минор , умноженный на
, где — номер строки , — номер столбца , в которых расположен выбранный элемент .

Пример 4. В определителе

алгебраическое дополнение
.

Теорема 1 (о разложении по строке). Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения.

Теорема 1 позволяет свести вычисление определителя порядка к вычислениюопределителей порядка
.

Пример 5 . Вычислить определитель четвертого порядка:

Воспользуемся теоремой 1 и разложим определитель по 4-й строке:

Замечание. Можно вначале упростить определитель, воспользовавшись свойством 9, а затем использовать теорему 1. Тогда вычисление определителя порядкасведется к вычислениювсего одного определителя порядка
.

Пример 6. Вычислить

Прибавим первый столбец ко второму и первый столбец, умноженный на (
), к третьему, в результате получим

Теперь применим теорему 1 и разложим по последней строке:

вычисление определителя 4-го порядка свелось к вычислению всего одного определителя 3-го порядка.

вычисление определителя третьего порядка свелось к вычислению всего одного определителя второго порядка.

Пример 7. Вычислить определитель порядка:

Первую строку прибавим ко второй, третьей и т.д. -й строке. Придем к определителю

Получен определитель треугольного вида.

Применим
раз теорему 1 (разложим по первому столбцу) и получим

Замечание. Определитель треугольного вида равен произведению элементов главной диагонали.

6.3. Основные операции над матрицами

Определение 5. Две матрицы
,
,
, и
,
,
, будем называть равными, если
.

Краткая запись:
.

Таким образом, две матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы равны.

Определение 6. Суммой двух матриц
,
,
, и
,
,
, называется такая матрица
,
,
, что
.

Иначе говоря, складывать можно только матрицы одних и тех же порядков, причем сложение осуществляется поэлементно.

Пример 8. Найти сумму матриц

и
.

В соответствии с определением 6 найдем

Правило сложения матриц распространяется на сумму любого конечного числа слагаемых.

Определение 7. Произведением матрицы
,
,
, на вещественное число называется такая матрица
,
,
, для которой
.

Иными словами, чтобы умножить матрицу на число, нужно умножить на это число все ее элементы и оставить полученные произведения на прежних местах.

Пример 9. Найти линейную комбинацию
матриц

и
.

Пользуясь определением 7, получаем

,
,

Свойства операций сложения матриц

и умножения на число:

1. Сложение коммутативно:
.

2. Сложение ассоциативно:.

3. Существует нулевая матрица
, удовлетворяющая условию
для всехА .

4. Для любой матрицы А существует противоположная матрицаВ , удовлетворяющая условию
.

Для любых матриц А иВ и любых действительных чисел
имеют место равенства:

5.
.

6.
.

7.
.

8.
.

Проверим свойство 1. Обозначим
,
. Пусть
,

,
. Имеем

и так как равенство доказано для произвольного элемента, в соответствии с определением 5
. Свойство 1 доказано.

Аналогично доказывается свойство 2.

В качестве матрицы возьмем матрицу порядка
, все элементы которой равны нулю.

Сложив с любой матрицейпо правилу, данному в определении 6, мы матрицуне изменим, и свойство 3 справедливо.

Проверим свойство 4. Пусть
. Положим
. Тогда
, следовательно, свойство 4 справедливо.

Проверку свойств 5 — 8 опустим.

Определение 8. Произведением матрицы
,
,
, на матрицу
,
,
, называется матрица
,
,
, с элементами
.

Краткая запись:
.

Пример 10. Найти произведение матриц

и
.

В соответствии с определением 8 найдем

Пример 11. Перемножить матрицы

и
.

Замечание 1. Число элементов в строке матрицыравно числу элементов в столбце матрицы(число столбцов матрицыравно числу строк матрицы).

Замечание 2. В матрице
строк столько же, сколько в матрице, а столбцов столько же, сколько в.

Замечание 3. Вообще говоря,
(умножение матриц некоммутативно).

Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.

Пример 12. Перемножим в обратном порядке матрицыииз примера 10.

таким образом, в общем случае
.

Отметим, что в частном случае равенство
возможно.

Матрицы и, для которых выполняется равенство
, называютсяперестановочными, иликоммутирующими .

Упражнения.

1. Найти все матрицы, перестановочные с данной:

а)
; б)
.

2. Найти все матрицы второго порядка, квадраты которых равны нулевой матрице.

3. Доказать, что
.

Свойства умножения матриц:

Умножение дистрибутивно.

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.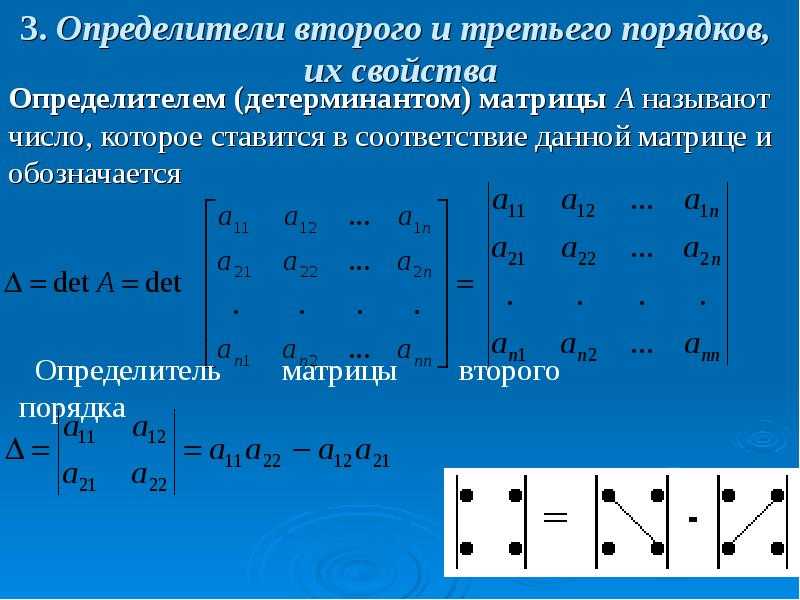

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ . Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Определитель, детерминант матрицы — онлайн справочник для студентов

ОПРЕДЕЛЕНИЕ

Определителем или определителем квадратной матрицы $\ A=\left\|a_{i j}\right\|_{n \times n} $ является число, присвоенное этой матрице.

Определитель матрицы $\ A $ обозначается вертикальными полосами $\ |A| $ или греческой буквой $\ \Delta $ или $\ \operatorname{det} A $.

Способы вычисления определителя матрицы

Определителем матрицы второго порядка является число, равное

$\ \left|\begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right|=a_{11} \cdot a_{22}-a_{21} \cdot a_{12} $

ПРИМЕР 1

Задача

Вычислить определитель второго порядка

$\ \Delta=\left|\begin{array}{cc}{1} & {-1} \\ {2} & {3}\end{array}\right| $

Решение

По определению определитель второго порядка

$\ \Delta=\left|\begin{array}{cc}{1} & {-1} \\ {2} & {3}\end{array}\right|=1 \cdot 3-2 \cdot(-1)=3+2=5 $

Ответ

$\ \Delta=5 $

Определитель матрицы третьего порядка

Определитель матрицы третьего порядка может быть вычислен с использованием правила треугольника или правила Сарруса.

Правило треугольника. Определитель матрицы третьего порядка можно вычислить по формуле

$\ \left|\begin{array}{lll}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=a_{11} \cdot a_{22} \cdot a_{33}+a_{31} \cdot a_{12} \cdot a_{23}+a_{21} \cdot a_{13} \cdot a_{32}-a_{31} \cdot a_{22} \cdot a_{13}-a_{21} \cdot a_{12} \cdot a_{33}-a_{11} \cdot a_{23} \cdot a_{32} $

Это правило можно схематически изобразить следующим образом.

ПРИМЕР 2

Задача

Вычислить определитель третьего порядка по правилу треугольника

$\ \Delta=\left|\begin{array}{ccc}{1} & {2} & {-4} \\ {2} & {3} & {1} \\ {3} & {-1} & {2}\end{array}\right| $

Решение

Согласно правилу треугольника определитель третьего порядка равен

$\ \Delta=\left|\begin{array}{ccc}{1} & {2} & {-4} \\ {2} & {3} & {1} \\ {3} & {-1} & {2}\end{array}\right|=1. 3 \cdot 2+3 \cdot 2 \cdot 1+2 \cdot(-4) \cdot(-1)-3 \cdot 3 \cdot(-4)-2 \cdot 2 \cdot 2-1 \cdot 1 \cdot(-1)=49 $

Ответ

$\ \Delta=49 $

Правило Сарруса. Чтобы вычислить детерминант третьего порядка, мы добавим первые два столбца и умножим диагональные элементы, взяв произведение со знаком плюс, если диагональ является главной или параллельной ему и взяв произведение с знаком минус, если диагональ равна стороны или параллели, мы получаем

ПРИМЕР 3

Задача

Вычислить определитель третьего порядка из примера 2 в соответствии с правилом Сарруса

$\ \Delta=\left|\begin{array}{ccc}{1} & {2} & {-4} \\ {2} & {3} & {1} \\ {3} & {-1} & {2}\end{array}\right| $

Решение.

Согласно правилу Сарруса, необходимо написать первые два столбца этого определителя справа от вычисленного определителя и умножить диагональные элементы. Взяв эти произведения с соответствующими знаками, получим, что искомый определитель третьего порядка

$\ \Delta= \begin{array}{|ccc|cc}{1} & {2} & {-4} & {1} & {2} \\ {2} & {3} & {1} & {2} & {3} \\ {3} & {-1} & {2} & {3} & {-1}\end{array}=1 \cdot 3 \cdot 2+2 \cdot 1 \cdot 3+(-4) \cdot 2 \cdot(-1)-3 \cdot 3 \cdot(-4)-(-1) \cdot 1 \cdot 1-2 \cdot 2 \cdot 2=49 $

Ответ

$\ \Delta=49 $

Вычисление детерминантов более высокого порядка

Для расчета детерминантов высших порядков используется метод разложения определителя в строке или столбце. Это позволяет нам представить детерминант квадратной матрицы как сумму произведений элементов любой из ее строк или столбцов для их алгебраических дополнений. В этом случае вычисление детерминанта n-го порядка сводится к вычислению детерминантов n-1-го порядка.

Теорема

Теорема о разложении определителя на элементы строки. Детерминант матрицы $\ \mathrm{A} $ равен сумме произведений элементов строки и их алгебраических дополнений.

$\ \operatorname{det} A=a_{i 1} A_{i 1}+a_{i 2} A_{i 2}+\ldots+a_{i n} A_{i n} $

Теорема

Теорема о разложении определителя на элементы столбца. Определитель матрицы $\ \mathrm{A} $ равен сумме произведений элементов столбца и их алгебраических дополнений.

$\ \operatorname{det} A=a_{1 j} A_{1 j}+a_{2 j} A_{2 j}+\ldots+a_{n j} A_{n j} $

ПРИМЕР 4

Задача

Вычислить определитель 4-го порядка двумя способами:

а) выкладка на 1-й линии;

б) расширение на 1-й столбец

$\ \Delta=\left|\begin{array}{cccc}{2} & {1} & {0} & {2} \\ {3} & {2} & {1} & {0} \\ {-1} & {0} & {1} & {3} \\ {-1} & {2} & {1} & {3}\end{array}\right| $

Решение

а) По теореме о разложении определителя на элементы строки этот определитель разбивается на первую строку следующим образом

$\ \Delta=a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}+a_{14} A_{14} $

С учетом формулы для вычисления алгебраических дополнений $\ A_{i j}=(-1)^{i+j} M_{i j} $ Здесь $\ M_{i j} $ является минором элемента $\ a_{i j} $ , равным определителю, полученному из данного определителя, путем пересечения i-й строки и j-го столбца. {1+4}\left|\begin{array}{ccc}{3} & {2} & {1} \\ {-1} & {0} & {1} \\ {-1} & {2} & {1}\end{array}\right|=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{3} & {1} & {0} \\ {-1} & {1} & {3} \\ {-1} & {1} & {3}\end{array}\right|-2 \cdot\left|\begin{array}{ccc}{3} & {2} & {1} \\ {-1} & {0} & {1} \\ {-1} & {2} & {1}\end{array}\right| \)

Полученные детерминанты третьего порядка вычислимы по правилу треугольника $\ \Delta=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{3} & {1} & {0} \\ {-1} & {1} & {3} \\ {-1} & {1} & {3}\end{array}\right|-2 \cdot\left|\begin{array}{ccc}{3} & {2} & {1} \\ {-1} & {0} & {1} \\ {-1} & {2} & {1}\end{array}\right|=2(6+6+0-0-0-6)-(9-3+0-0+3-9)-2(0-2-2-0+2-6)= $

б) По теореме о разложении определителя на элементы столбца этот определитель разбивается на первый столбец следующим образом

$\ \Delta=a_{11} A_{11}+a_{21} A_{21}+a_{31} A_{31}+a_{41} A_{41}=2 \cdot(-1)^{1+1}\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|+3 \cdot(-1)^{2+1}\left|\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|+(-1) \cdot(-1)^{3+1}\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {2} & {1} & {3}\end{array}\right|+ $

$\ +(-1) \cdot(-1)^{4+1}\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {0} & {1} & {3}\end{array}\right|=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-3 \cdot\left|\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {2} & {1} & {3}\end{array}\right|+\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {0} & {1} & {3}\end{array}\right| $

Полученные детерминанты третьего порядка вычислимы по правилу треугольника

$\ \Delta=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-3 \cdot\left|\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {2} & {1} & {3}\end{array}\right|+\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {0} & {1} & {3}\end{array}\right|=2 \cdot(6+6+0-0-0-6)- 3 \cdot(3+0+0-4-0-3)-(3+0+4-4-0-0)+(3+0+4-0-0-0)=28 $

Ответ

$\ \Delta=28 $

Свойства определителя матрицы

Определитель любого порядка может быть вычислен с использованием свойств определителя:

детерминант не изменяется при элементарных преобразованиях строк или столбцов;

при перестановке строк или столбцов знак детерминанта меняется на обратный;

Определитель треугольной матрицы равен произведению элементов, расположенных на диагонали. Например, для верхней треугольной матрицы

$\ A=\left(\begin{array}{cccc}{a_{11}} & {a_{12}} & {\dots} & {a_{1 n}} \\ {0} & {a_{22}} & {\dots} & {a_{2 n}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {0} & {0} & {\dots} & {a_{n n}}\end{array}\right) $

детерминантом является $\ \operatorname{det} A=a_{11} \cdot a_{22} \cdot \ldots \cdot a_{n n} $

ПРИМЕР 5

Задача

Вычислить определитель 4-го порядка, используя свойства определителя

$\ \Delta=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {-2} & {1} & {5} & {6} \\ {-3} & {-5} & {1} & {7} \\ {-4} & {-6} & {-7} & {1}\end{array}\right| $

Решение.

Приведем этот определитель, используя элементарные преобразования в верхнюю треугольную форму. Для этого добавьте первый, умноженный, соответственно, на 2, 3 и 4 на вторую, третью и четвертую строки.

$\ \Delta=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {-2} & {1} & {5} & {6} \\ {-3} & {-5} & {1} & {7} \\ {-4} & {-6} & {-7} & {1}\end{array}\right|=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {5} & {11} & {14} \\ {0} & {1} & {10} & {19} \\ {0} & {2} & {5} & {17}\end{array}\right| $

Измените вторую и третью строки в некоторых местах, а знак детерминанта изменится на противоположное

$\ \Delta=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {5} & {11} & {14} \\ {0} & {1} & {10} & {19} \\ {0} & {2} & {5} & {17}\end{array}\right|=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {5} & {11} & {14} \\ {0} & {2} & {5} & {17}\end{array}\right| $

Рядом с третьей строкой добавьте вторую, умноженную на (-5), а на четвертую добавьте вторую, умноженную на (-2). Получите

$\ \Delta=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {5} & {11} & {14} \\ {0} & {2} & {5} & {17}\end{array}\right|=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {0} & {-39} & {-81} \\ {0} & {0} & {-15} & {-21}\end{array}\right| $

Добавьте к последней строке третий, умноженный на $\ (-38) $

Теперь определитель равен произведению элементов на главной диагонали

$\ \Delta=-\left(1 \cdot 1 \cdot(-39) \cdot \frac{396}{39}\right)=396 $

Ответ

$\ \Delta=396 $

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Умножение матриц Сравнение бесконечно малых функций Бесконечно малые функции Непрерывность функции в точке и на промежутке

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Калькулятор матриц.

Решение матриц онлайн. Решение матричных уравнений

Решение матриц онлайн является одним из самых востребованных запросов в интернете среди студентов, причём сервисов, где можно решить онлайн матрицу, практически нет. И снова на помощь придёт многофункциональный математический калькулятор. В его арсенал входит калькулятор матриц онлайн, который выполняет все основные операции над матрицами!

Матрица — это совокупность значений, записанных в прямоугольную таблицу. Каждый элемент матрицы имеет двойной порядковый номер в этой таблице, а именно номер столбца и номер строки. Размер матрицы определяется количеством строк и столбцов в таблице. Например, размер матрицы 3 на 5 значит, что она состоит из трёх строк и пяти столбцов.

Обратите внимание, 5 x 5 — это максимальный размер матрицы, которую может решить бесплатный калькулятор, предлагаемый на нашем сайте.

Как решать матрицы в онлайн калькуляторе

Чтобы вызвать калькулятор матриц, нажмите кнопку Matrix.

Кнопка, открывающая калькулятор матриц

Панель управления дополнится инструментами, с помощью которых выполняется решение матриц онлайн.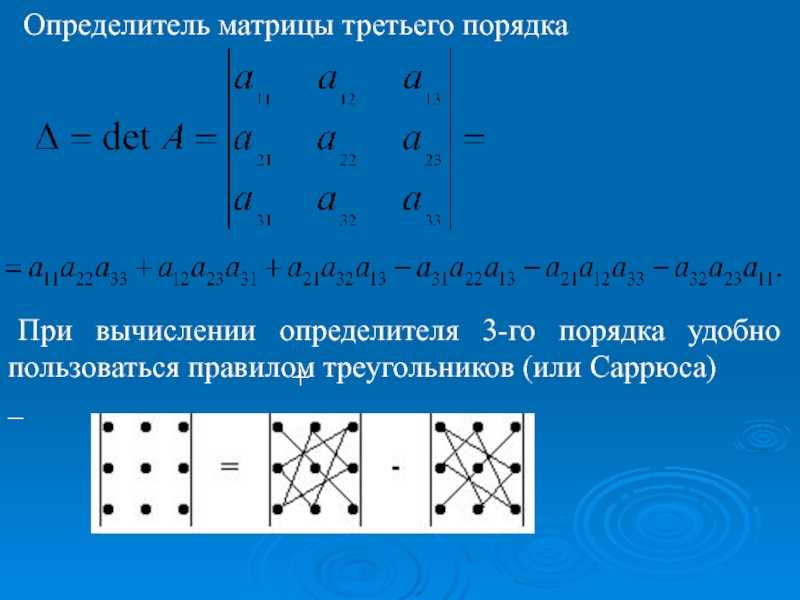 Калькулятор позволяет выполнять следующие онлайн действия над матрицами: вычитание, сложение и умножение матриц, векторное произведение, решение матричных уравнений, транспонирование, нахождение обратной матрицы и вычисление определителя матрицы.

Кнопки калькулятора, выполняющие основные действия над матрицами

Помимо панели с кнопками онлайн калькулятор матриц содержит удобную форму для быстрого ввода выражения. В левой и правой частях задаются матрицы, их размер выбирается из выпадающего списка. В середине выпадающее меню для выбора операции, которую нужно выполнить калькулятору с заданными матрицами. Другие возможности калькулятора можно посмотреть здесь Функции калькулятора.

Вычисление матриц онлайн с помощью формы быстрого ввода

Если элемент матрицы не указан, онлайн калькулятор подставляет значение «0».

Обратите внимание, при вызове меню решения матриц вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I», чтобы увидеть дисплей в полный размер.

Вектор столбец

Матрица, состоящая только из одной строки или одного столбца, называется вектор-строкой или вектор-столбцом соответственно. В калькуляторе предусмотрены отдельные кнопки для ввода матрицы, число столбцов которой равно 1. Используйте эти клавиши, чтобы записать вектор-столбец из 3,4 или 5 строк соответственно.

Кнопки калькулятора для ввода вектора

(2, 6, 8)

Вектор-столбец из 3х строк

Квадратная матрица

Матрица называется квадратной, если число её строк равно числу столбцов. Следует отметить, что только у квадратной матрицы может быть главная диагональ матрицы — линия, проходящая через элементы матрицы с одинаковыми индексами, начиная с ячейки первой строки первого столбца и заканчивая элементом, стоящем в последнем столбце последней строки.

Для быстрой записи квадратных матриц 2, 3 или 4-го порядка используйте специальные кнопки, которые предлагает калькулятор онлайн.

Кнопки калькулятора для ввода квадратных матриц

[[ 8, 4, 1, 8][ 7, 1, 8, 8][ 8, 4, 1, 6][ 4, 8, 3, 1]]

Пример квадратной матрицы 4 порядка

Квадратные матрицы, у которых все элементы, исключая элементы главной диагонали, равны нулю, называются диагональные матрицы. Симметричная матрица чисел представляет собой таблицу, в которой все элементы, симметричные относительно главной диагонали, равны.

[[ 1, 2, 8, 11][ 2, 3, 24, 5][ 8, 24, 6, 4][ 11, 5, 4, 9]]

Пример симметричной матрицы

Есть ещё такие виды матриц в математике.

Единичная матрица чисел — это таблица, в которой элементы главной диагонали равны единице, а все остальные элементы являются нулевыми.

[[ 1, 0, 0, 0][ 0, 1, 0, 0][ 0, 0, 1, 0][ 0, 0, 0, 1]]

Пример единичной матрицы

Таблица, у которой значение всех элементов равно 0, называется нулевая матрица.

[[ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0]]

Пример нулевой матрицы

Матрицы и действия над ними

Сложение и вычитание матриц онлайн

С помощью калькулятора можно произвести сложение матриц онлайн, а также найти разность матриц онлайн. Чтобы вычислить сумму матриц или найти их разность, выполняются соответствующие операции над их элементами. Например, найти сумму матриц значит определить такую матрицу, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.

Найти сумму элементов матриц или их разность можно только в том случае, если исходные матрицы одинакового размера, т. е. число их строк и столбцов соответственно равно. Вычитание и сложение матриц разного размера невозможно.

Для выполнения этих операций в калькуляторе используйте форму быстрого ввода или запишите выражение вручную.

Сложение матриц примеры

[[1, 2, 3][3, 1, 2][5, 0, 6]]+[[1, 2, 5][6, 3, 2][9, 9, 9]]

Сложение двух матриц

[[2, 7][4, 5]]+[[2, 10][6, 8]]

Сумма двух матриц

Векторное произведение матриц

Для выполнения этой операции используйте клавишу Cross Product.

(2, 6, 4)#(8, 2, 5)

Пример произведения векторов

Умножение матриц

Умножение матриц онлайн калькулятор производит с помощью клавиши Vector/Matrice-Multiplication.

Перемножение матриц возможно только в том случае, если количество столбцов одной матрицы равняется количеству строк другой. Чтобы матрицу умножить на число, нужно каждый элемент матрицы умножить на это число.

[[2, 8][4, 2]]*[[8, 8][7, 1]]

Умножение матриц пример

[[5, 6][7, 8]]*9

Умножение матрицы на число онлайн

Решение матричных уравнений

Эта функция калькулятора позволяет находить неизвестные матрицы, которые описаны уравнением зависимости одной матрицы от другой. Решение матричных уравнений осуществляется с помощью кнопки Solve Ecuation System.

[[6, 1, 8],[7, 5, 3],[2, 9, 4]]*x=(1, 2, 3)

Пример решения системы уравнений матриц

Транспонирование матрицы

Используйте клавишу Matrix Transponent, когда нужно выполнить транспонирование матрицы — действие, в котором строки со столбцами меняются местами. Таким образом, транспонированная матрица получается путем замены строк на столбы в исходной матрице.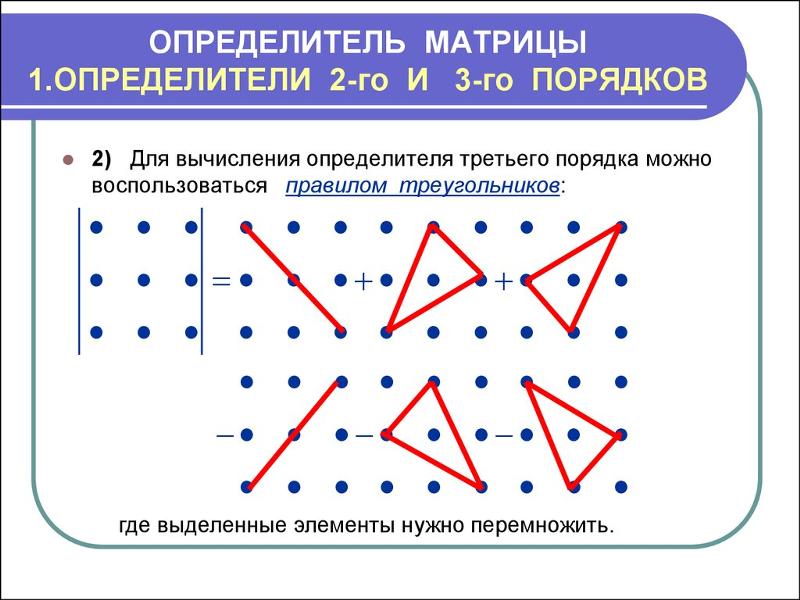 -1

Нахождение обратной матрицы пример

Нахождение определителя матрицы

В калькуляторе матриц нет специальной кнопки для того, чтобы найти определитель матрицы. Но вычислить его можно, написав в поле ввода специальную функцию — оператор det(Determinant).

det( [ [-2, 2, -3], [-1, 1, 3], [2, 0, -1] ] )

Пример, как найти определитель матрицы онлайн

Бесплатный калькулятор онлайн может не только решить онлайн матрицу, в его возможностях также: возведение в степень, калькулятор корней, тригонометрические функции, решение логарифмов и другие дополнительные функции.

Калькулятор Инструкция — обзор всех функций калькулятора и общее описание, как пользоваться калькулятором.

Умножение матриц — Онлайн математические инструменты

Скоро в продаже Эти математические инструменты уже в пути

Функции построения графиков

Рисовать графики математических функций.

Рисование формулы LaTeX

Создание изображения из выражения LaTeX.

Найти n-ю цифру

Вычислить n-ю цифру числа Эйлера.

Найти n-ю цифру золотого сечения

Вычислить n-ю цифру золотого сечения.

Найти n-ю цифру числа пи

Вычислите n-ю цифру константы Пи.

Вычислить сумму e цифр

Найти сумму e цифр.

Вычислить сумму цифр золотого сечения

Найти сумму цифр золотого сечения.

Вычислить сумму пи цифр

Найти сумму пи цифр.

Генерировать цифры Чамперноуна

Генерировать цифры константы Чамперноуна.

Найти n-ю цифру Чамперноуна

Вычислить n-ю цифру константы Чамперноуна.

Декодировать последовательность «посмотри и скажи»

Выполни обратную операцию над последовательностью «посмотри и скажи».

Создание P-адических расширений

Вычисление p-адических расширений произвольных чисел.

Создать последовательность панцифровых чисел

Создать список панцифровых чисел.

Создать последовательность номеров Стэнли

Создать список номеров Стэнли.

Создать последовательность номеров звонков

Создать список номеров звонков.

Создать последовательность чисел Кармайкла

Создать список чисел Шармишеля.

Создать последовательность каталонских номеров

Создать список каталонских номеров.

Создать последовательность треугольных чисел

Создать список треугольных чисел.

Создать последовательность составных чисел

Создать список составных чисел.

Создать последовательность секущих чисел

Создать список секущих чисел.

Создать последовательность чисел Голомба

Создать список чисел Голомба-Сильвермана.

Создать последовательность чисел Эйлера Тотиент

Создать список фи-чисел Эйлера.

Создать последовательность номеров жонглеров

Создать список номеров жонглеров.

Создать последовательность счастливых номеров

Создать список счастливых номеров.

Создать последовательность номеров Моцкина

Создать список номеров Моцкина.

Создать последовательность номеров Padovan

Создать список номеров Padovan.

Генерация псевдосовершенной числовой последовательности

Создать список полусовершенных чисел.

Создать последовательность номеров Ulam

Создать список номеров Ulam.

Создать последовательность странных чисел

Создать список странных чисел.

Создать последовательность суперсовершенных чисел

Создать список суперсовершенных чисел.

Продолжить числовую последовательность

Найти закономерность в числовой последовательности и расширить ее.

Разбить число

Найти все разбиения данного целого числа.

Создать последовательность номеров разделов

Создать список функциональных номеров разделов.

Создание арифметической прогрессии

Создание арифметической последовательности чисел.

Создание геометрической прогрессии

Создание геометрической последовательности чисел.

Создание полиномиальной прогрессии

Создание полиномиальной последовательности чисел.

Создать последовательность натуральных чисел

Создать список натуральных чисел.

Генерировать степени двойки

Создать список чисел степеней двойки.

Создание степеней десяти

Создание списка чисел в степени десятка.

Создание плотной матрицы

Создание матрицы с очень небольшим количеством нулевых элементов.

Создать разреженную матрицу

Создать матрицу с очень небольшим количеством ненулевых элементов.

Умножение матрицы на скаляр

Умножение всех элементов матрицы на число.

Проверить, является ли матрица единственной

Определить, является ли матрица вырожденной.

Найти матрицу кофакторов

Для заданной матрицы найти ее матрицу кофакторов.

Найдите вспомогательную матрицу

По заданной матрице найдите ее дополнение.

LU Factor a Matrix

Разложить матрицу на LU-факторы.

Найти собственные значения матрицы

Найти собственные значения матрицы.

Украсьте матрицу

Украсьте матрицу, аккуратно выровняв все ее столбцы.

Переформатировать матрицу

Преобразование матрицы одного формата в другой формат.

Рисование архимедовой спирали

Создание архимедовой спирали.

Рисование спирали Эйлера

Создание кривой спирали Корню (полиномиальной спирали).

Рисование спирали Фибоначчи

Создание кривой спирали Фибоначчи.

Рисование спирали Теодора

Создание спирали квадратного корня.

Нарисуйте спираль Ферма

Создайте кривую в виде параболической спирали.

Рисование прямоугольников Фибоначчи

Создание рисунка прямоугольников Фибоначчи.

Нарисуйте головку семени Фибоначчи

Создайте головку цветка Фибоначчи.

Нарисовать фрактал Падована

Создать фрактал равнобуквенных треугольников Падована.

Нарисуйте аполлонову прокладку

Создайте фрактал аполлоновой прокладки.

Нарисовать фрактал Мандельброта

Создать фрактал Мандельброта.

Нарисовать фрактал Юлии

Создать фрактал Джулии.

Нарисовать фрактал Рози

Создать фрактал Рози.

Нарисовать кривую фрактала Бланманже

Создать фрактал Бланманже.

Рисование функции Вейерштрасса

Создание фрактала Вейерштрасса.

Нарисовать кривую Минковского в виде вопросительного знака

Создать фрактал Минковского в виде вопросительного знака.

Нарисуйте функцию Тома

Создайте функцию Тома (также известную как функция попкорна или капли дождя).

Нарисуйте функцию Дирихле

Создать функцию Дирихле.

Нарисуйте рог Гавриила

Нарисуйте геометрическую фигуру с бесконечной площадью поверхности и конечным объемом.

Преобразование слов в числа

Преобразование чисел из английского текста в реальные цифры.

Преобразование чисел в слова

Преобразование чисел в письменный текст на английском языке.

Преобразование десятичной записи в экспоненциальную запись

Преобразование чисел, записанных в десятичной форме, в экспоненциальную форму.

Преобразование научного представления в десятичное представление

Преобразование чисел, записанных в научной форме, в десятичную форму.

Округление чисел вверх

Применение операции ceil к числам.

Округление чисел в меньшую сторону

Применить операцию пола к числам.

Анализ чисел

Подсчитайте, сколько раз встречается каждое число.

Преобразование числа в виде суммы

Создайте сумму, которая в сумме равна заданному числу.

Создать таблицу умножения

Нарисовать таблицу умножения n×m.

Нарисовать круговую диаграмму

Нарисовать круговую диаграмму и показать относительные размеры данных.

Визуализация процентов

Нарисуйте диаграмму, показывающую проценты.

Подбрось монетку

Подбрось монетку и выпадет орел или решка.

Бросьте кубик

Бросьте кубик и получите число на его стороне.

Калькулятор матриц — Примеры, Калькулятор матриц онлайн

Калькулятор матриц вычисляет результирующую матрицу, когда к двум заданным матрицам применяются определенные арифметические операции. В математике матрица — это функция сетки или прямоугольный массив, в котором числа расположены в упорядоченных строках и столбцах.

Что такое матричный калькулятор?

Калькулятор матриц — это онлайн-инструмент, который помогает выполнять различные матричные операции с матрицами 2 × 2, т. е. сложение матриц, вычитание матриц и умножение матриц. Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной матрицей. Чтобы использовать этот матричный калькулятор , введите числа в поле ввода.

Калькулятор матриц

ПРИМЕЧАНИЕ. Введите не более трех цифр.

Как пользоваться калькулятором матриц?

Чтобы найти окончательную матрицу с помощью онлайн-калькулятора матриц, выполните следующие шаги:

Шаг 1: Перейдите к онлайн-калькулятору матриц Cuemath.
Шаг 2: Введите значения матриц 2 × 2 в поля ввода и выберите операцию, которую необходимо выполнить, из раскрывающегося списка.
Шаг 3: Нажмите кнопку «Вычислить» , чтобы найти результирующую матрицу.
Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает матричный калькулятор?

Размеры матрицы обычно представляются как m x n. Здесь m обозначает количество строк, а n представляет количество столбцов в этой матрице. Таким образом, матрица 2×2 будет иметь 2 строки и 2 столбца. С матрицами можно выполнять вычитание, сложение и умножение. Методы вычисления результата для этих арифметических операций приведены ниже:

1. Сложение матриц — Если две матрицы имеют одинаковое количество строк и столбцов, то можно выполнить сложение. Чтобы сложить две матрицы, элементы каждой строки и столбца одной матрицы добавляются к соответствующим элементам другой матрицы.

A + B = $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} +\begin{bmatrix} b_{11} & b_ {12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11} + b_{11} & a_{12} + b_{12}\\ a_{21} + b_{21}& a_{22} + b_{22} \end{bmatrix}$

2. Вычитание матриц — Подобно сложению, мы можем вычесть две матрицы, только если они имеют одинаковое количество строк и столбцов. Вычитаем элементы каждой строки и столбца одной матрицы из соответствующих элементов предыдущей матрицы.

A — B = $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} -\begin{bmatrix} b_{11} & b_ {12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11} — b_{11} & a_{12} — b_{12}\\ a_{21} — b_{21}& a_{22} — b_{22} \end{bmatrix}$

3. Умножение матриц — Для умножения двух матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Умножение матриц можно выполнить следующим образом:

A × B = $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \times \begin {bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11}b_{11} + a_{12}b_{21 } & a_{11}b_{12} + a_{12}b_{22}\\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{ 22}b_{22} \end{bmatrix}$

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Решенные примеры на калькуляторе матриц

Пример 1:

Сложите две матрицы $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ & $\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}$ и проверьте это с помощью калькулятора матриц.

Решение:

Матрица 1 + Матрица 2 = $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 2 & 1\\ 4 & 2 \end {bmatrix} = \begin{bmatrix} 3 и 3 \\ 7 и 6 \end{bmatrix}$

Пример 2:

Вычтите две матрицы $\begin{bmatrix} 1 и 2 \\ 3 & 4 \end{bmatrix}$ & $\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}$ и проверьте это с помощью калькулятора матриц.

Решение:

Матрица 1 — Матрица 2 = $\begin{bmatrix} 1 и 2 \\ 3 и 4 \end{bmatrix} + \begin{bmatrix} 2 и 1\\ 4 & 2 \end{bmatrix} = \ begin{bmatrix} -1 & 1 \\ -1 & 2 \end{bmatrix}$

Точно так же вы можете попробовать матричный калькулятор для сложения, вычитания и умножения следующих матриц:

Matrices = $\begin {bmatrix} 2 и 1 \\ 4 и 2 \end{bmatrix}$ & $\begin{bmatrix} 3 и 3 \\ 7 и 6 \end{bmatrix}$
Матрицы = $\begin{bmatrix} 5 и 8 \\ 10 и 16 \end{bmatrix}$ & $\begin{bmatrix} 8 и 2 \\ 1 и 3 \end{bmatrix}$

☛ Статьи по теме:

Матрицы
Добавление матриц

☛ Математические калькуляторы:

Калькулятор умножения матриц — Выполнение умножения матриц

Позволяет этому калькулятору умножения матриц находить произведение двух матриц, которые либо содержат комплексные числа, либо не содержат их в секундах.

Здесь мы будем обсуждать условия умножения матриц онлайн. Более того, мы увидим, как мгновенно умножать матрицы с помощью этого бесплатного калькулятора произведения матриц. Поэтому для правильного понимания всего сценария сохраняйте концентрацию.

Давайте начнем с основного определения.

Что такое матрица?

В контексте математики:
«Говорят, что прямоугольный массив или набор действительных чисел, скажем, 1 2 3 и 4 6 7, заключенный в квадратную скобку [ ], образует матрицу»

Например:

Представим все упомянутые выше числа в матричной форме ниже:

$$ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\\end{bmatrix} $$

Точно так же у нас есть некоторые другие матрицы, как показано ниже:

$$ \begin{bmatrix}10 & 10 \\ 8 & 8 \\\end{bmatrix} \hspace{0.25in} \begin{bmatrix} 6 \\ 3 \\\end{bmatrix} \hspace{0.25in} \begin{bmatrix} 2 \\\end{bmatrix} $$

Обобщение:

Предположим, что у нас есть две матрицы как $M_{1}$ и \ (М_{2}\). Теперь, если мы их перемножим, мы получим новую матрицу $M_{3}$. Умножение матриц — это произведение и сложение элементов обеих матриц $M_{1}$ и $M_{2}$. Все это обобщение состоит в следующем:

$$ M_1 = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \ vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} $$

$$ M_2 = \begin{bmatrix} b_{11 } & b_{12} & \cdots & b_{1p} \\ b_{21} & b_{22} & \cdots & b_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ b_{ n1} & b_{n2} & \cdots & b_{np} \end{bmatrix} $$

$$ M_1 \cdot M_2 = \begin{bmatrix} a_{11}b_{11} +\cdots + a_{1n}b_{n1} & a_{11}b_{12} +\cdots + a_{1n} b_{n2} & \cdots & a_{11}b_{1p} +\cdots + a_{1n}b_{np} \\ a_{21}b_{11} +\cdots + a_{2n}b_{n1} & a_{21}b_{12} +\cdots + a_{2n}b_{n2} & \cdots & a_{21}b_{1p} +\cdots + a_{2n}b_{np} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{11} +\cdots + a_{mn}b_{n1} & a_{m1}b_{12} +\cdots + a_{mn}b_{n2 } & \cdots & a_{m1}b_{1p} +\cdots + a_{mn}b_{np} \end{bmatrix} $$

Теперь, если вы хотите вычислить положение элемента в матрице $M_{3}$, выполните следующие действия:

Посмотрите, в какой строке и столбце находится элемент
Зная это, выберите эту строку из первой матрицы $M_{1}$ и этот столбец из второй матрицы $M_{2}$
После того, как вы выберете строку и столбец, умножьте каждый присутствующий в них объект один на один
Среди этих сущностей также лежит желаемое значение элемента, которое можно определить мгновенно

Кроме того, источник калькулятора-онлайн разработал бесплатный онлайн-калькулятор матриц для определения позиции любого элемента в матрице.

Основные условия умножения матриц:

Итак, как сделать умножение матриц, если числа комплексные? Это довольно просто, так как мы собираемся обсудить следующие шаги, которые также помогут вам решить такие проблемы. К ним относятся:

Количество столбцов в первой матрице должно быть равно количеству строк во второй матрице
После умножения окончательная матрица будет содержать строки, равные первой матрице, и столбцы, равные второй матрице
Например; если вы найдете произведение матрицы порядка ‘n’ на ‘k’ с другой матрицей порядка ‘k’ на ‘m’ , порядок конечной матрицы будет ‘n’ на ‘m’

Это может вас немного запутать, но мы проясним это с помощью следующих матриц ниже:

$$ \begin{bmatrix}10 & 10 \\ 8 & 8 \\\end{bmatrix} \hspace {0,25 дюйма} \begin{bmatrix}9\\ 5 \\\end{bmatrix} $$

Теперь, если вы видите обе эти матрицы, вы ясно увидите, что первая матрица имеет два столбца, а вторая матрица состоит из двух строк. Поскольку они выполняют условие, они идеально подходят для умножения. Теперь, когда вы перемножите их, вы получите следующую матрицу:

$$ \begin{bmatrix}140 \\ 112 \\\end{bmatrix} $$

Теперь, если вы проверите порядок, это 2 на 1 , который указывает, что его строки равны первой матрице, а столбцы равны второй матрице.

Кроме того, вы можете ускорить свои вычисления, используя наш лучший калькулятор умножения матриц.

Свойства умножения матриц:

Умножение матриц обладает частыми свойствами, перечисленными ниже:

Переместительное свойство:

Умножение матриц не обладает свойством перестановочности.

AB≠BA

Ассоциативное свойство:

Умножение матриц следует ассоциативному закону произведения:

(ab) c = a (bc)

Распределительное свойство:

A (B+C) = AB+AC Lever Distribute Law
(A+B) C = AC+BC Право распределяет. Закон

Этим законам распределения также удовлетворяют действительные числа, которые также можно проверить с помощью калькулятора свойств распределения.

IA = A или AI = A

Мультипликативное свойство с нулем:

Если мы умножим матрицу на нулевую матрицу (матрицу, все сущности которой равны нулю), мы получим нулевую матрицу.

AO = OA= O

Как умножать матрицы?

Давайте разберем пример, чтобы вы могли правильно понять умножение матриц. Оставайся сфокусированным!

Пример № 01:

Как умножить матрицу на единичную матрицу, приведенную ниже:

$$ \begin{bmatrix} 5 \\ 4 \\\end{bmatrix} $$

Решение:

Поскольку данная матрица имеет только один столбец, то и единичная матрица должна содержать только одну строку и выглядит следующим образом:

$$ \begin{bmatrix}1 & 0 \\\end{bmatrix} $$

Умножение матриц:

$$ \begin{bmatrix} 5 \\ 4 \\\end {bmatrix} \cdot \begin{bmatrix}1 & 0 \\\end{bmatrix} $$

$$ \begin{bmatrix} ( 5*1 ) ( 5*0 ) \\ ( 4*1 ) ( 4 *0 ) \\\end{bmatrix} $$

$$ \begin{bmatrix}(5 ) (0 ) \\ (4 ) (0 ) \\\end{bmatrix} $$

$$ \begin{bmatrix} 5 & 0 \\ 4 & 0 \ \\end{bmatrix} $$

Несомненно, ручное вычисление матриц выглядит устрашающе, использование бесплатного калькулятора умножения матриц здесь имеет большой смысл.

Это может занять у вас много времени. Вот почему вам также следует воспользоваться бесплатным калькулятором матриц умножения.

Как работает калькулятор умножения матриц?

Позвольте этому бесплатному умножителю матриц определять произведение двух матриц, идеально подходящих для умножения. Давайте перейдем к изучению его использования!

Ввод:

Прежде всего, выберите количество строк и столбцов для первой матрицы
Теперь сделайте то же самое для второй матрицы. Но учтите, что количество ее строк должно быть равно количеству столбцов первой матрицы
Теперь нажмите «Установить матрицы», чтобы получить нужные макеты матриц
После получения макетов введите все значения для обеих матриц
Нажмите кнопку расчета

Вывод:

Калькулятор матриц с умножением выполняет следующие вычисления:

Определяет умножение матриц
Показывает пошаговые расчеты задействованных шагов

Часто задаваемые вопросы:

Как мгновенно умножить матрицы 2×2?

Если вы ищете прямое произведение этих матриц, воспользуйтесь нашим бесплатным онлайн-калькулятором умножения матриц.

Можно ли умножать матрицы, имеющие следующий порядок: 2 на 3 и 4 на 3

Нет, умножение невозможно. Это связано с тем, что количество столбцов первой матрицы не равно количеству строк второй матрицы.

Каков порядок умножения матрицы?

Предположим, вы собираетесь перемножить две матрицы, удовлетворяющие условиям произведения. Вы всегда будете начинать с самого левого объекта и продвигаться к правому. Таким образом, порядок умножения матриц всегда слева направо, что также можно получить с помощью бесплатного онлайн-калькулятора умножения матриц.

Что такое умножение матрицы на скаляр?

При скалярном умножении вы просто берете одно скалярное число и умножаете его на каждую единицу матрицы, с помощью которой предполагается получить произведение.

Какие еще калькуляторы можно использовать для различных матричных расчетов?

Мы разработали различные матричные калькуляторы, так как это основа алгебры. Вы можете использовать калькуляторы ниже, чтобы определить различные факторы с помощью наших калькуляторов, связанных с матрицей:

Чтобы определить определитель любой матрицы, коснитесь калькулятора определителя
Чтобы найти собственное значение любой матрицы, коснитесь калькулятора собственных значений.
Если вы хотите определить матрицу нулевого пространства, попробуйте использовать калькулятор нулевого пространства

Вывод:

Итак, мы поняли все основы матричных произведений в прочитанном, мы надеемся, что вы не испытаете затруднений при использовании калькулятора умножения матриц для определения результатов.

Ссылки:

Из источника Википедии: Умножение матриц, Фундаментальные приложения, Общие свойства, Квадратные матрицы

Из источника академии хана: Нулевые и единичные матрицы, Стратегии, Реальные приложения

Из источника люмен обучение: Введение в матрицы, скалярное умножение, умножение матриц

Калькулятор матрицы Гессе + онлайн-решатель с бесплатными шагами

Калькулятор матрицы Гессе используется для расчета матрицы Гессе для функции с несколькими переменными путем решения всех вычислений, необходимых для проблема. Этот калькулятор очень удобен, так как Матрица Гессе — длинная и суматошная задача, и калькулятор предлагает решение одним нажатием кнопки.

Что такое калькулятор матрицы Гессе?

Калькулятор матрицы Гессе — это онлайн-калькулятор, предназначенный для поиска решений задач с матрицей Гессе.

Матрица Гессе представляет собой сложную задачу исчисления и используется в основном в области искусственного интеллекта и машинного обучения .

Таким образом, этот калькулятор очень полезен. Он имеет поле ввода для ввода вашей проблемы и одним нажатием кнопки может найти решение вашей проблемы и отправить его вам. Еще одна замечательная особенность этого калькулятора заключается в том, что вы можете использовать его в своем браузере, ничего не загружая.

Как пользоваться калькулятором матрицы Гессе?

Чтобы использовать калькулятор матрицы Гессе , вы можете ввести функцию в поле ввода и нажать кнопку отправки, после чего вы получите решение для вашей функции ввода. Следует отметить, что этот калькулятор может рассчитать только Матрица Гессе для функции с максимум тремя переменными.

Теперь мы предоставим вам пошаговые инструкции по использованию этого калькулятора для получения наилучших результатов.

Шаг 1

Вы начинаете с постановки задачи, для которой хотите найти Матрицу Гессе .

Шаг 2

Вы вводите функцию с несколькими переменными, для которой хотите получить решение, в поле ввода.

Шаг 3

Для получения результатов нажмите 9Кнопка 0331 Отправить открывает решение в интерактивном окне.

Шаг 4

Наконец, вы можете решить больше задач на матрицу Гессе, введя условия задачи в интерактивное окно.

Как работает калькулятор матрицы Гессе?

A Калькулятор матрицы Гессе работает, решая частные производные второго порядка входной функции и затем находя из них результирующую матрицу Гессе .

Матрица Гессе

A Гессе или Матрица Гессе соответствует квадратной матрице, полученной из частных производных второго порядка функции. Эта матрица описывает локальные кривые, вырезанные функцией, и используется для оптимизации результатов, полученных от такой функции.

A Матрица Гессе вычисляется только для функций со скалярными составляющими, которые также называются скалярными полями . Первоначально он был выдвинут немецким математиком Людвиг Отто Гессе в 1800-х годах .

Вычисление матрицы Гессе

Чтобы вычислить матрицу Гессе , нам сначала потребуется функция многих переменных такого рода:

f(x, y)

функционал максимум для трех переменных.

Получив функцию с несколькими переменными, мы можем двигаться вперед, взяв частные производные первого порядка от этой функции:

\[\frac{\partial f(x, y)}{\partial x}, \frac{ \partial f(x, y)}{\partial y}\] 92 x \end{matrix} \bigg ] \]

Список математических калькуляторов

‎Матричный калькулятор

в App Store

Описание

Матричный калькулятор

. Калькулятор вычитания
4×4 Matrix Addition & Subtraction Calculator
4×4 Matrix Multiplication Calculator
4×4 Inverse Matrix Calculator
Squared Matrix Calculator
Transpose Matrix Calculator
4×4 Matrix Determinant Calculator
Cramer’s Rule Determinant Calculator
Gauss Matrix Elimination Calculator

inverse matrix calculator
matrix solver
inverse матричный
обратный калькулятор матрицы
калькулятор умножения матриц
обратный калькулятор
обратная матрица
обратная матрица
калькулятор rref
генератор матриц
обратная матрица
онлайн калькулятор матриц
обратимая матрица
обратная матрица 3×3
расширенный калькулятор матриц
калькулятор матриц онлайн
обратная матрица 3×3
калькулятор сокращения строк
обратная матрица 3×3
вычислитель определителя матрицы
обратная матрица 2×2
обратная матрица 2×2
калькулятор сокращения матрицы
обратная матрица 3×3
инвертор матрицы
формула матрицы
онлайн-решатель матриц
обратный калькулятор матрица
калькулятор собственных значений
2×2 обратная матрица
найти обратную матрицу калькулятора матриц 3×3
обратный калькулятор матриц
обратный мультипликативный калькулятор
калькулятор определителя 3×3
калькулятор обратной матрицы 3×3
найти обратную матрицу
калькулятор матрицы
онлайн-решатель матриц
обратная матрица 3×3
обратная матрица 3×3 калькулятор
калькулятор алгебры матриц
калькулятор решения матрицы
онлайн-калькулятор матриц
решить матричный калькулятор
калькулятор матриц rref
нахождение обратной матрицы
обратная матрица онлайн
калькулятор сложных матриц
калькулятор матриц 3×3
калькулятор матриц
формула обратной матрицы
калькулятор с матрицей
онлайн матрица
калькулятор ранга матрицы
калькулятор операций с матрицами
метод обращения матрицы
калькулятор сопряженной матрицы
обратная матрица 3×3
калькулятор решения матриц матрица онлайн
Метод обратной матрицы
Калькулятор обратной матрицы 3×3
Решатель математической матрицы
Калькулятор матрицы кофактора
калькулятор матричных произведений
3×3 обратная матрица
поиск обратной матрицы 3×3
обращение матрицы
матричные компьютеры
обратная матрица 2 на 2
определитель решателя
решение матриц онлайн
найти обратный калькулятор
онлайн обратная матрица
9 графический калькулятор
найти обратную матрицу калькулятор
найти обратную матрицу 3×3
научный калькулятор
калькулятор собственных векторов
генератор матриц онлайн
калькулятор уменьшения строки матрицы
калькулятор диагонализации
калькулятор переходной матрицы
обратная матрица 2×2
решить матрицу онлайн
калькулятор определительной матрицы
калькулятор диагонализации матрицы
математический калькулятор

Поддерживаемые операции с матрицами:
— Обратная матрица.
— Определитель матрицы.
— Матричное скалярное умножение.
— Добавление матрицы.
— Вычитание матриц.
— Умножение матриц.
— Транспозиция матриц.

Приложение может работать с:
— Целые числа (-2, -1, 0, 1, 2 и т. д.).
— Десятичные дроби (1,5, 3,14 и т. д.).
— Простые дроби (1/2, 3/4, 7/3 и т.д.).
— Комплексные числа (i, 1+i, 1/2-2i, 0,5+2/3i и т. д.).

Проверьте результаты матриц 2×2, 3×3, 4×4, nxn или матриц сложения, вычитания, умножения, определителя, обратной или транспонированной матрицы или выполните такие вычисления с помощью этих формул и калькуляторов. Основная цель этих матричных инструментов — помочь студентам, специалистам и исследователям быстро выполнить такие расчеты или проверить результаты таких расчетов для анализа, определения и решения линейных функций и уравнений. Эти матричные формулы и калькуляторы могут дать ответы на многие сложные алгоритмы обработки цифровой информации, изображений и видео.

7 сентября 2021 г.

Версия 1.5

Исправления ошибок, обновление библиотеки и повышение производительности.

Разработчик Sunnykumar Mavani указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Данные, используемые для отслеживания вас

Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:

Покупки
Расположение
Пользовательский контент
Идентификаторы
Данные об использовании
Диагностика
Другие данные

Данные, связанные с вами

Следующие данные могут быть собраны и связаны с вашей личностью:

Покупки
Расположение
Пользовательский контент
Идентификаторы
Данные об использовании
Диагностика
Другие данные

Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше

Информация

Продавец: Сунникумар Мавани
Размер: 2,7 МБ
Категория: Утилиты
Возрастной рейтинг: 4+
Цена: Бесплатно

Сайт разработчика
Тех. поддержка
Политика конфиденциальности

Еще от этого разработчика

Калькулятор нормы матрицы

Добро пожаловать в калькулятор нормы матрицы . Мы рассмотрим теорию матричных норм и то, что они собой представляют, а также упрощенные выражения для хорошо известных норм, таких как 1-норма, 2-норма и норма Фробениуса матрицы. С помощью нашего калькулятора вы можете вычислить норму для любой матрицы размером до 3×33\times33×3. Итак, возьмите бутерброд с арахисовым маслом и начнем!

Что такое норма матрицы?

Начнем с оговорки : норма матрицы не представляет величину , как норма вектора. Вместо этого норма 90 331 матрицы 90 332 AAA (иногда называемая 90 331 индуцированной матричной нормой ) представляет максимальную величину, на которую единичный вектор x⃗\vec{x}x растягивается на на при умножении на AAA. Мы можем обозначить это определение с матричной нормой ∥A∥\Vert A\Vert∥A∥ следующим образом:

∥A∥=max⁡∥x⃗∥=1∥Ax⃗∥\Vert A\Vert=\max_{\Vert \vec{x}\Vert=1}\Vert A\vec{x}\Vert∥A∥=∥x

∥=1max∥Ax

∥

В этом определении AAA представляет собой m×nm\ матрица, умноженная на nm×n, а x⃗\vec{x}x — единичный вектор размера n×1n\times1n×1. В соответствии с правилами умножения матриц мы получаем A⋅x⃗A\cdot\vec{x}A⋅x как вектор m×1m\times 1m×1. Следовательно, ∥A⋅x⃗∥\Vert A\cdot\vec{x}\Vert ∥A⋅x∥ является векторной нормой A⋅x⃗A\cdot\vec{x}A⋅x.

Как и в случае с векторными нормами, существует более одной матричной нормы . Какую норму матрицы мы вычисляем выше, зависит от того, какую векторную норму мы используем для A⋅x⃗A\cdot\vec{x}A⋅x.

Итак, в этом определении мы выбираем ∥⋅∥\Vert \cdot\Vert ∥⋅∥ в качестве одной конкретной векторной нормы. Например, если мы выберем ∥⋅∥\Vert \cdot\Vert ∥⋅∥ в качестве 2-нормы ∥⋅∥2\Vert \cdot\Vert _{2}∥⋅∥2, то мы будем вычислять 2-норма матрицы, ∥A∥2\Vert A\Vert _2∥A∥2. Вот почему мы называем многие матричные нормы «индуцированные матричные нормы» , поскольку они индуцируются при использовании сопровождающей их векторной нормы на A⋅x⃗A\cdot\vec{x}A⋅x.

Матричные нормы имеют много смежных применений. Наиболее часто он используется при вычислении номера условия матрицы , который основан на том факте, что нормы матрицы представляют величину растяжения вектора .

Как вычислить норму матрицы?

Математическое определение ценно в теории, но было бы трудно вычислить его напрямую . К счастью для нас, мы можем упростить формулу для различных матричных норм . Мы рассмотрим следующие нормы:

1-норма , ∥A∥1\Vert A\Vert _1∥A∥1;
норма бесконечности , ∥A∥∞\Vert A\Vert _∞∥A∥∞;
2-норма , ∥A∥2\Vert A\Vert _2∥A∥2;
Норма Фробениуса , ∥A∥F\Vert A\Vert _F∥A∥F; и
Максимальная норма , ∥A∥max⁡\Vert A\Vert _{\max}∥A∥max. 9T\!\cdot\!A)}∥A∥F=trace(AT⋅A)

Наконец, максимальную норму AAA можно получить, просто взяв наибольшее значение в AAA:
∥A∥max⁡=max⁡i,j∣ai,j∣\Vert A\Vert_{\max} = \max_{i,j} |a_{i,j}|∥A∥max=i,jmax ∣ai,j∣
Как пользоваться калькулятором нормы матрицы?
Вычисление матричных норм может быть утомительным выполнять снова и снова — вот почему мы сделали этот калькулятор матричных норм! Вот как им пользоваться :
1. Выберите размерность вашей матрицы . Вы можете выбрать что угодно до 3×33\×33×3.
2. Введите элементы вашей матрицы построчно.
3. Найдите норму своей матрицы в самом низу! Это 1-норма, бесконечная норма, 2-норма, норма Фробениуса и максимальная норма. Вы можете взглянуть выше на их формулы.
Как вычислить норму матрицы? – Пример
Воспользуемся этими формулами и посмотрим как рассчитать все эти нормы матрицы на практике. Рассмотрим нашу матрицу 3×33\times33×3 AAA:
A=[226139610]A = \begin{bmatrix} 2 и 2 и 6 \\ 1 и 3 и 9 \\ 6 и 1 и 0 \\ \end{bmatrix}A=⎣
⎡216231690⎦
⎤
Мы можем вычислить 1-норму матрицы по , суммируя каждый столбец и сумму, выбирая максимальный столбец . Итак,
∥A∥1=max⁡(2 ⁣+ ⁣1 ⁣+ ⁣6, 2 ⁣+ ⁣3 ⁣+ ⁣1, 6 ⁣+ ⁣9⁣+ ⁣0)=max⁡(9, 6, 15)=15\begin{split} \Верт А\Верт_1 &= \max(2\!+\!1\!+\!6,\ 2\!+\!3\!+\!1,\ 6\!+\!9\!+\!0) \ \ &= \max(9,\ 6,\ 15) \\ &= 15 \end{split}∥A∥1=max(2+1+6, 2+3+1, 6+9+0)=max(9, 6, 15)=15
Точно так же мы можем вычислить норму бесконечности матрицы на , суммируя каждую строку и , выбирая максимальную сумму строки . Следовательно,
∥A∥∞=max⁡(2 ⁣+ ⁣2 ⁣+ ⁣6, 1 ⁣+ ⁣3 ⁣+ ⁣9, 6 ⁣+ ⁣1 ⁣+ ⁣0)=max,⁡1,⁣0)=max,⁡1 7)=13\начать{разделить} \Верт А\Верт_\infty &= \max(2\!+\!2\!+\!6,\ 1\!+\!3\!+\!9Т\cточка А) \\ =&\41+14+117\ = &\ 172 \end{split}== trace(AT⋅A) 41+14+117 172
Наконец, максимальная норма — это просто наибольшее значение в AAA. Следовательно, ∥A∥max⁡=9\Vert A\Vert_{\max} = 9∥A∥max=9.
Вот и все! Мы определили каждую норму для матрицы 3×33×33×3.
Часто задаваемые вопросы
Что такое норма Фробениуса единичной матрицы?
‖I _n×n ‖ _F = √n . Норма Фробениуса n×n единичная матрица равна √n , потому что I ^T = I , а затем I ^T · I = I . We can therefore conclude that
‖I‖ _F = √trace(I ^T ·I)
‖I‖ _F = √trace(I)
‖I‖ _F = √n
как I состоит только из 1 по диагонали.
Имеют ли прямоугольные матрицы нормы?
Все матрицы имеют нормы . Нормы, которые используют операции, исключительные для квадратных матриц, такие как собственные значения и трассы, выполняют их над квадратными матрицами, полученными из исходной матрицы. Следовательно, квадратная матрица или нет, не имеет значения для матричных норм.
Что означает «А» в матрицах?
‖A‖ — это обозначение для матричной нормы . Точная норма обычно указывается в виде нижнего индекса нормы, например ‖A‖ ₂ . Это означает, что мы использовали векторную 2-норму, чтобы найти максимальное растяжение. Не путайте обозначение матричной нормы 9.1314 ‖A‖ с обозначением определителя матрицы |A| .
Может ли норма матрицы быть меньше 1?
Да. Если матрица сжимает векторное пространство вместо его растяжения, норма матрицы будет меньше 1 , чтобы отразить это сжатие.
No related posts.

Калькулятор определителя — вычислить определитель матрицы

вычисление матриц

Решение матриц — Онлайн калькулятор

Вычисление определителя 4 порядка онлайн. Определитель матрицы

Определитель, детерминант матрицы — онлайн справочник для студентов

Калькулятор матриц.

Как решать матрицы в онлайн калькуляторе

Вектор столбец

Квадратная матрица

Матрицы и действия над ними

Сложение и вычитание матриц онлайн

Векторное произведение матриц

Умножение матриц

Решение матричных уравнений

Транспонирование матрицы

Нахождение определителя матрицы

Умножение матриц — Онлайн математические инструменты

Калькулятор матриц — Примеры, Калькулятор матриц онлайн

Что такое матричный калькулятор?

Калькулятор матриц

Как пользоваться калькулятором матриц?

Как работает матричный калькулятор?

Решенные примеры на калькуляторе матриц

Калькулятор умножения матриц — Выполнение умножения матриц

Что такое матрица?

Обобщение:

Основные условия умножения матриц:

Свойства умножения матриц:

Переместительное свойство:

Ассоциативное свойство:

Распределительное свойство:

Мультипликативное свойство с нулем:

Как умножать матрицы?

Как работает калькулятор умножения матриц?

Часто задаваемые вопросы:

Как мгновенно умножить матрицы 2×2?

Можно ли умножать матрицы, имеющие следующий порядок: 2 на 3 и 4 на 3

Каков порядок умножения матрицы?

Что такое умножение матрицы на скаляр?

Какие еще калькуляторы можно использовать для различных матричных расчетов?

Вывод:

Ссылки:

Калькулятор матрицы Гессе + онлайн-решатель с бесплатными шагами

Что такое калькулятор матрицы Гессе?

Как пользоваться калькулятором матрицы Гессе?

Шаг 1

Шаг 2

Шаг 3

Шаг 4

Как работает калькулятор матрицы Гессе?

Матрица Гессе

Вычисление матрицы Гессе

Список математических калькуляторов

‎Матричный калькулятор

Описание

Данные, используемые для отслеживания вас

Данные, связанные с вами

Информация

Еще от этого разработчика

Вам также может понравиться

Калькулятор нормы матрицы

Что такое норма матрицы?

Как вычислить норму матрицы?

Как пользоваться калькулятором нормы матрицы?

Как вычислить норму матрицы? – Пример

Часто задаваемые вопросы

Что такое норма Фробениуса единичной матрицы?

Имеют ли прямоугольные матрицы нормы?

Что означает «А» в матрицах?

Может ли норма матрицы быть меньше 1?

Добавить комментарий Отменить ответ