Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не \(12\) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3.
В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. {o}}=\frac{a\sqrt{3}}{2}\)
Радиус вписанной окружности равностороннего треугольника
\(r=\frac{a\sqrt{3}}{6}\)
Это уже теперь должно быть совсем ясно:
Бонус 2: Вебинары о треугольниках, чтобы набить руку в решении задач
А в этих видео из нашего курса подготовки к ЕГЭ по математике вы можете потренироваться, решая задачи вместе с нашим репетитором Алексеем Шевчуком.
Это не просто вебинары, «бла-бла-бла» о теории математики. Это разбор задач в режиме реального времени.
Вы точно научитесь решать любые задачи на эти темы, если их прослушаете.
Хотите получить максимум от этих вебинаров? Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.

Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но в этом видео мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
На этом уроке мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Также мы научимся решать и «обычные» треугольники. Убедимся в утверждении из прошлого урока — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Итак, задача 16 профильного ЕГЭ.
Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Медиана равностороннего треугольника Калькулятор | Вычислить Медиана равностороннего треугольника
✖Длина ребра равностороннего треугольника равна длине одной из сторон равностороннего треугольника.
В равностороннем треугольнике все три стороны равны.ⓘ Длина ребра равностороннего треугольника [le] AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр
+10%
-10%
✖Медиана равностороннего треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны, таким образом делящий эту сторону пополам.
ⓘ Медиана равностороннего треугольника [M]
AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр
⎘ копия
👎
Формула
сбросить
👍
Медиана равностороннего треугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Длина ребра равностороннего треугольника: 8 метр —> 8 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
6.92820323027551 метр —> Конверсия не требуется
< 2 Равносторонний треугольник Калькуляторы
Медиана равностороннего треугольника формула
Медиана равностороннего треугольника = (sqrt(3)*Длина ребра равностороннего треугольника)/2
M = (sqrt(3)*le)/2Что такое равносторонний треугольник?
Равносторонний треугольник в геометрии — это треугольник, у которого все три стороны имеют одинаковую длину. В знакомой евклидовой геометрии равносторонний треугольник также является равноугольным; то есть все три внутренних угла также конгруэнтны друг другу и равны 60 ° каждый.

Что такое медиана равностороннего треугольника и как ее вычислить?
Медиана равностороннего треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны, таким образом делящий эту сторону пополам. В равностороннем треугольнике длины всех трех сторон треугольника равны, а все углы равны 60 градусов. Его медиана вычисляется по формуле M = √3a/2, где M — медиана равностороннего треугольника, а a — длина стороны равностороннего треугольника.
Share
Copied!
формула нахождения, свойства, известные следствия
Геометрия
12.11.21
13 мин.
Пожалуй, каждый хоть раз сталкивался с геометрическими вычислениями. Одной из самых распространённых фигур является многоугольник. Его особенность заключается в свойствах, благодаря которым можно легко и быстро определить нужные параметры.
Часто при расчётах приходится использовать медиану. В равностороннем треугольнике она разбивает фигуру на две равные площади. При этом она и центр тяжести, чем зачастую и пользуются при решении задач.
Оглавление:
- Свойства и виды треугольников
- Особенности медианы
- Решение задачи
- Онлайн-расчёты на калькуляторе
Свойства и виды треугольников
Многоугольник с тремя углами называют треугольником. Образуется он тремя отрезками, соединяющими 3 точки, располагающиеся на разных прямых. Эти точки называются вершинами, а замкнутые линии — сторонами. Площадь, заключённую сторонами, называют внутренней.
Вершины фигуры принято обозначать большими латинскими буквами A, B, C. Углы же греческими символами α, β, γ. Треугольники принято различать по видам. Они бывают:
- остроугольными — все углы в фигуре имеют разворот меньше 90 градусов;
- тупоугольными — один из углов треугольника больше 90 градусов;
- прямоугольными — 2 стороны фигуры образуют прямой угол.

Кроме этого, их разделяют по числу равных сторон на разносторонние, равнобедренные и равносторонние (правильные). В треугольнике можно построить так называемые замечательные прямые. Отрезок, проведённый из середины вершины к противолежащей стороне, является медианой. В любом виде фигуры может быть построено 3 таких прямых. Они будут пересекаться в центре внутренней площади треугольника, а их общая точка являться центром массы.
Кроме медианы, может быть отложена высота и биссектриса. Первая это перпендикуляр, опущенный из угла на противоположное основание, а вторая — линия, проходящая из угла и делящая противоположную сторону пополам.
Зная высоту или биссектрису, найти медиану равностороннего треугольника очень просто. Всё дело в том, что для него все 3 линии полностью совпадают. Это и есть одно из замечательных свойств равносторонней фигуры,поэтому знание этого параметра позволяет находить много различных размеров многоугольника.
В треугольник можно вписать окружность и описать её вокруг него. Радиус вписанной фигуры находится из отношения площади фигуры к полупериметру, а описанной — как произведение сторон, делённое на 4 площади. Внутреннее пространство для равносторонней фигуры можно определить по формуле: S = (a2 √3) / 4. При этом углы любого равностороннего треугольника будут равны 60 градусам.
Особенности медианы
С латинского «медиана» переводится как «средняя», поэтому так называют отрезок, соединяющий вершину с серединой противоположного углу отрезка. Точку, в которой она соприкасается с прямой, называют основанием медианы. Существуют свойства, характерные только для рассматриваемой прямой. Так, можно, зная медиану, найти сторону треугольника, его площадь или угол вершины.
К свойствам отрезков, делящих сторону пополам в произвольном треугольнике, относят:
- деление медиан в точке их пересечения в отношении 2:1;
- разделение фигуры на 2 треугольника с равными площадями, то есть являющимися равновеликими;
- если построить 3 медианы, то треугольник окажется разделённым на 6 одинаковых фигур;
- зная значения сторон, длину параметров можно вычислить по следующей формуле: m = √(2b2 + 2c2 — a2) / 2.
Для доказательства равенства площадей нужно построить треугольник и провести медиану, например, из вершины B. Точку пересечения с противоположной стороной можно обозначить буквой D. Площадь новых фигур будет равняться: S1 = (AD * BE) / 2 и S2 = (DC * BE) / 2. Так как ограниченная прямая — это медиана, то AD = DC. Отсюда следует, что фигура делится на 2 равные части. Значит, S1 = S2, что и нужно было доказать.
Доказательство равенства 6 фигур при построении трёх медиан: пусть одна из полученных фигур будет иметь вершины A, O, F. Если из угла опустить перпендикуляр на линию BF, будет верным равенство: S = (OF * AK) / 2 = (BF * AK) / 6 = S / 3. Беря во внимание свойства, что линия рассекает фигуру на 2 равные части, можно утверждать о справедливости записи: Sabf = Sabc / 2 → Saof = Sabf / 3 = Sabc / 6. Свойство доказано.
В равнобедренном треугольнике медиана совпадает с высотой. Доказать это утверждение просто. Пусть есть многоугольник ABC. Из вершины B опущена высота BD.
Полученные 2 фигуры равны: ABD = CDB, значит, их сторона BD — общая и является катетом. Следовательно, AD = CD. Так как гипотенузы треугольников равны, AB = BC. Замечательное свойство доказано.
Существуют 2 следствия из свойств:
- если вокруг прямоугольного треугольника описать круг, его центр совпадёт с серединой гипотенузы;
- треугольник, где медиана равна половине длины стороны, к которой её построили, будет прямоугольным.
Эти свойства и следствия очень важны. Зная их и формулы нахождения площади, решить большинство задач не составит труда. Но при этом часто приходится использовать формулу нахождения длины медианы.
Решение задачи
Для закрепления теоретического материала преподаватель учащимся предлагает решить ряд задач. Самостоятельное вычисление ответа позволяет не только научиться применять знания на практике, но и разобраться в различных тонкостях. Вот одна из таких задач, рассчитанная на школьников среднего уровня подготовки.
Дан равносторонний треугольник ABC. Длина медианы BH, проведённой на основание AC, составляет 9 * √3. Определить, чему равны стороны фигуры. Перед тем как непосредственно перейти к решению, нужно обратить внимание, что все стороны у фигуры будут одинаковые, при этом углы также равны. По сути, равносторонний многоугольник является равнобедренным, поэтому медиана является и высотой, а значит, угол H будет составлять 90 градусов. При этом все остальные углы равны 60 градусам.
Решить задачу можно двумя способами:
- Первый предполагает решение через тригонометрические функции. Так как известен острый угол в прямоугольном треугольнике ABH, используя синус (значение противолежащего катета к гипотенузе) можно записать: sin BAH = BH / AB. Отсюда AB = BH / sin BAH = (9 * √3) / (√3 / 2) = 9 * 2 = 18.
- В основе второго способа лежит теорема Пифагора. Сторона AB — это гипотенуза. Для удобства её можно обозначить как х. Так как медиана делит сторону пополам, то AH = x / 2.
По теореме: AB2 = Ah3 + Bh3. Подставив известные значения в формулу, можно получить выражение: x2 = (x/2)2 + (9 * √3)2 = (x2 / 4) + 81 * 3 = 81 * 4. Отсюда x = √ 81 * √ 4 = 9 * 2 = 18.
Это классические методы, с помощью которых можно найти сторону треугольника, если известна медиана. Какой из них выбрать, зависит от предпочтения решающего задачу. Конечно же, первый занимает меньше времени, но требует знаний хотя бы основ тригонометрии.
Следует отметить, что формула: m = a √3 / 2 называется выражением медианы через высоту. И находится она как раз по теореме Пифагора. Это позволяет, зная лишь высоту или биссектрису, находить не только величину сторон, но и площадь фигуры, радиусы вписанной и описанной окружностей. При этом эта формула работает и в обратном направлении. Так, сторона будет равна: а = m / (√3 / 2).
Онлайн-расчёты на калькуляторе
Найти медиану в треугольнике при известных размерах сторон или площади фигуры довольно просто.
В школьных задачах обычно подбираются исходные данные так, что при решении не нужно пользоваться калькулятором или делать сложные расчёты. Ответ часто получается в удобной форме в виде десятичных чисел.
Но на практике начальные данные, используемые для нахождения медианы, могут представлять коренные, степенные, дробные выражения, поэтому приходится выполнять громоздкие вычисления, которые могут занять много времени. При этом существует риск допустить оплошность, приводящую к неправильному ответу.
В интернете существуют математические онлайн-калькуляторы. Это сервисы, предлагающие услуги по автоматическому нахождению ответа в различных заданиях. Чтобы воспользоваться сайтом, пользователю даже не нужно знать формулы. Всё что от него требуется, это просто указать значения сторон в предложенной форме и нажать кнопку «Рассчитать» или «Вычислить». При этом эти сервисы бесплатны и не требуют даже регистрации.
Из онлайн-калькуляторов, существующих в русском сегменте интернета, можно отметить следующие:
- Allcalc.
Настоящий комбайн вычислений. Сайт содержит несколько сотен математических калькуляторов и конвертеров. Пользователь также может скачать бесплатное приложение для системы Android.
- Planetcalc. Отличается удобной навигацией и интуитивно понятным интерфейсом. Работу того или иного калькулятора можно оценить в комментариях.
- Geleot. Позиционируется не только как онлайн-расчётчик, но и как справочник.
Кроме быстрого и правильного расчёта, сайты могут предложить пользователю различный теоретический материал, касающийся вычислений. На их страницах приведены не только формулы, используемые для нахождения ответа, но и их объяснения. При этом расчёт сопровождается комментариями и подробными действиями.
Использовать онлайн-калькулятор для вычисления медианы не зазорно, особенно в процессе обучения. Благодаря ему можно не только проверить ответ, но и в случае ошибки быстро её найти и разобраться в причинах появления, поэтому ими часто пользуются не только школьники, но и инженеры, выполняющие сложные геометрические расчёты.
Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
\[{\Large{\text{Медиана}}}\]
Теорема
В любом треугольнике медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Доказательство
Пусть \(AD\) и \(BE\) – медианы в треугольнике \(ABC\), \(O\) – точка пересечения \(AD\) и \(BE\).
\(DE\) – средняя линия в треугольнике \(ABC\), тогда \(DE\parallel AB\), значит \(\angle ADE = \angle BAD\), \(\angle BED = \angle ABE\), следовательно, треугольники \(ABO\) и \(DOE\) подобны (по двум углам).
Из подобия треугольников \(ABO\) и \(DOE\): \(\dfrac{BO}{OE} = \dfrac{AB}{DE} = \dfrac{2}{1}\).
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию: \(S_{ABC} = 0,5\cdot AC\cdot h\).
Пусть \(BD\) – медиана в треугольнике \(ABC\), тогда \(AD = DC\).
\(S_{ABD} = 0,5\cdot AD\cdot h\),
\(S_{BCD} = 0,5\cdot DC\cdot h\).
Так как \(AD = DC\), то \(S_{ABD} = S_{BCD}\), что и требовалось доказать.
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
1) Докажем, что если \(\triangle ABC\) – прямоугольный, то \(BM=\frac12AC\), где \(M\) – середина гипотенузы \(AC\).
Достроим треугольник \(ABC\) до прямоугольника \(ABCD\) и проведем диагональ \(BD\).
\circ\), чтд.
\[{\Large{\text{Биссектриса}}}\]
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC\cdot CD}{CB\cdot CD} = \dfrac{AC}{CB}\]
С другой стороны, \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{0,5\cdot AD\cdot h}{0,5\cdot DB\cdot h}\), где \(h\) – высота, проведённая из точки \(C\), тогда \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AD}{DB}\).
В итоге \(\dfrac{AD}{DB} = \dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC}{CB}\), откуда \(\dfrac{AD}{AC} = \dfrac{DB}{BC}\), что и требовалось доказать.
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
{2} \cdot \sqrt{3}}{4}=\frac{12 \sqrt{3}}{4}=3 \sqrt{3}$ (м2)
Ответ. $\mathrm{S}_{\Delta A B C}=3 \sqrt{3}$ (м2)
Остались вопросы?
Здесь вы найдете ответы.
Как можно вычислить площадь равсностороннего треугольника?
Согласно формуле, по которой вычисляется площадь S треугольника с равными сторонами, она равна:
S = √3/4*а, в которой а – это длина стороны фигуры.
Площадь можно также найти следующим образом:
S = a*h/2, где h – это высота.
Высоту можно вычислить, используя теорему Пифагора:
h = а² — (а/2)².
Как можно рассчитать площадь равностороннего треугольника, если известно, что площадь треугольной фигуры, отсекаемой от него средней линией, составляет 6 см. кв.?
Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим как МК.
Тогда Sмвк = 6 см. кв.
В случае с равносторонним треугольником:
S = а²√3/4
Зная свойство средней линии треугольника, можно записать следующее равенство:
МК = АС/2 = а/2.
В этом случае площадь отсекаемого треугольника равна:
Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.
В условии дано, что Sмвк = 6 см.кв., тогда:
а²√3/16 = 6
а² = 96/√3.
Площадь равностороннего треугольника:
S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.
Как можно вычислить площадь равностороннего треугольника при условии, что его периметр составляет 24 см.?
Найдем сторону равносторонней треугольной фигуры, разделив его периметр на 3:
а = 24:3 = 8 см.
Тогда площадь этой фигуры равна:
S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.
Что представляет собой формула площади равностороннего треугольника?
Обозначив одну из сторон равносторонней треугольной фигуры как а, а высоту, проведенную к ней, — как h, то формула расчета площади этой фигуры будет выглядеть так:
S=ah/2.
Принимая во внимание то, что все стороны данной треугольной фигуры равны, то его высоту можно выразить через сторону и вычислить, используя теорему Пифагора:
h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4
h = (а√3)/2
Тогда площадь данной фигуры равна:
S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4
Как выразить длину стороны а из формулы площади равностороннего треугольника?
Для расчета площади треугольника, длины всех сторон которого равны, используется формула:
S=a²√3/4
Перенесем 4 в правую часть равенства:
4S=a²√3.
Тогда:
a² = 4S/√3
а = √4S/√3.
Какая формула используется для вычисления площади равностороннего треугольника с длиной стороны а?
Если известно, что сторона равносторонней треугольной фигуры равна а, то его площадь рассчитывается так:
S = а²√3/4.
Каким образом можно привести доказательство теоремы о площади равностороннего треугольника?
Треугольник имеет два катета – АВ и ВС.
Его гипотенуза – ВС. Так как фигура является равносторонней, то АВ = АС.
Требуется доказать, что площадь треугольной фигуры, стороны которой одинаковы, равна произведению длин его катетов, разделенному на два.
Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его углов, и получим что:
ΔВАС = ΔВСD.
Площадь квадрата равна:
S = а*b.
Диагональ квадрата ВС является гипотенузой треугольника, которая делит квадрат на 2 равные части. Из этого следует, что площадь треугольника равна половине площади квадрата. Что и требовалось доказать.
Как вычислить площадь равностороннего треугольника со стороной длиной 9 см.?
Имеется треугольник АВС с равным сторонами.
ВН = 9 см.
Площадь данной фигуры находится по формуле:
S=1/2*АС*ВН,
в которой АС – основание треугольной фигуре, по длине равное любой из сторон (равносторонний Δ), ВН – высота.
Предположим, что АС = 2а см.
Тогда:
АН = АС/2 = ½*2а = а см.
Согласно теореме Пифагора:
АВ² = ВН²+АН².
В данном случае:
(2а)² = 9²+а²
Переносим а² в правую часть уравнения:
4а²-а² = 81
Упрощаем:
3а² = 81.
Отсюда:
а² = 81/3 = 27
а=√27=√9×3=3√3 см.
Теперь можно найти площадь:
S=1/2*9*3√3=1/2*27/√3=27√3/2=13,5√3 см.кв.
Какому числу равна площадь равностороннего треугольника с основанием длиной 6 см.?
Известна формула расчета площади треугольника:
S=1/2*h*b.
Проведем высоту h, которая в равностороннем треугольнике представляет собой также биссектрису и медиану.
Воспользуемся теоремой Пифагора для вычисления высоты:
h = √(36-9) = √27 см.
Тогда:
S = h*3 = 3√27 см.кв.
Возможно ли привести доказательство того, что площадь равностороннего треугольника равна √3*a²/4, в которой длина его стороны обозначена как а?
Доказать, что приведенное в задании утверждение является верным, можно, если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь которого равна произведению длины стороны и высоты.
2√3/4?
Известно, что площадь любого треугольника можно найти по формуле:
S = 1/2*a*b*sinA,
в которой стороны треугольника обозначены как а и b, а угол, образованный ими, — как А.
Доказано, что каждый угол равносторонней треугольной фигуры составляют 60 градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если подставить эти значения в формулу, то получим:
S = a22√3/4.
Как найти площадь равностороннего треугольника при условии, что длина каждой его стороны составляет 12 см.?
Площадь треугольника с равными сторонами вычисляется по формуле:
S = √3/4*a².
В данном случае:
S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.
Согласно формуле Герона:
S = √(р(р-а)(р-a)(p-a))
Для данного треугольника:
Р = 12*3 = 36 см.
Р = р/2 = 36/2 = 18 см.
Тогда:
S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.
Как вычислить площадь правильного равностороннего треугольника, зная радиус круга R?
Площадь треугольника с одинаковыми сторонами считается как:
S = a²√3/4.
Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:
а = 2√3r.
Считаем площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильной треугольной фигуры, равен a/√3. Следовательно, а = R√3.
В этом случае:
S = R²*3√3/4 = 3√3R²/4.
Известно, что площадь правильного треугольника равна 100√3 м.кв. Как вычислить его сторону?
Площадь треугольника равна:
(a²√3)/4.
В данном случае:
100√3=(a²√3)/4
Тогда:
a²√3=400√3.
Находим а:
a²√3 = 400√3
a² = 400
a = 20 см.
Чему равна площадь правильного треугольника при условии, что диаметр окружности, вписанной в него, = 10 см.?
Если d = 10 см., то r = 10/2 = 5 см.
Известно, что:
r = а√3/6, где а – это длина стороны правильного Δ.
Значит:
5 = а√3/6.
Отсюда:
а = 30/√3 = 10√3 см.
Тогда:
SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см.
кв.
Чему равна площадь правильного треугольника со стороной 4 дм.?
Известно, что:
S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.
Площадь также можно найти так:
S = a²√3/4 = 16√3/4 = 4√3 дм.кв.
Как найти площадь правильного треугольника, зная, что длина описанной около него окружности равна 4Пи см.?
Длина окружности через радиус находится так:
L=2πR.
Значит:
R=L/2π=4π/2π=2 у.е.
Имеем правильный треугольник, значит длина его стороны:
a=R*√3=2√3 у.е.
Можем найти SΔ:
S = √3/4a² = √3/43*3 = 3√3 у.е.кв.
Чему равна площадь правильного треугольника и его стороны, если его высота = 14 см.?
В правильном треугольнике длины всех сторон одинаковы. Это значит, что каждую из них можно обозначить как х. Тогда:
Р (периметр) = х + х + х = 3х см.
Площадь будет равна:
S = 1/2 h * x = 14/2*x = 7х см.кв.
Как найти площадь правильного треугольника с равными сторонами при условии, что радиус круга R?
Площадь треугольной фигуры с равными сторонами считается как:
S = a²√3/4.
Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.
Находим площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильного Δ, составляет a/√3. Это означает, что а = R√3.
Теперь можем высчитать площадь треугольника:
S = R²*3√3/4 = 3√3R²/4.
Как найти площадь правильного треугольника при условии, что расстояние от его центра до вершины составляет 2 м.?
Центр правильно треугольной фигуры также является центральной точкой описанной около нее окружности. Ее радиус представляет собой расстояние от центра до вершины фигуры:
а=R√3=2√3
Все углы в правильном треугольнике являются одинаковыми и равны по 60 градусов (180/3).
Площадь треугольной фигуры рассчитывается как:
а²sin60°/2=(2√3)²√3/2/2=6√3 м.кв.
Как найти площадь правильного треугольника, если определено, что сторона имеет длину, аналогичную длине стороны ромба с диагоналями 10 см.
и 12 см.?
Предположим, что BD = 10 см., а АС = 12 см.
Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь в определенной точке.
ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.
Согласно теореме Пифагора:
АВ = √(АО² + ВО²) = √(36 + 25) = √41.
Треугольник имеет равные стороны, длина каждой из которых аналогична длине стороны ромба:
а = √41.
Тогда:
SΔ = a²√3/4 = 41√3/4 см.кв.
Как найти площадь правильного треугольника периметром 6 см.?
Если длина стороны правильного треугольника указана, то его площадь вычисляется следующим образом:
S = a²√3/4.
Согласно определению правильного треугольника, длины всех его сторон одинаковые. Исходя из этого можно найти его сторону, разделив периметр на три:
а = 6/3 = 2 см.
Ищем площадь, подставив в равенство значение а:
S = 2²√3/4 = S 4√3/4 = √3 см.кв.
Как найти площадь правильного треугольника при условии, что окружность, которая вписана в него, имеет радиус длиной 4 см.
?
Площадь треугольника, имеющего стороны одинаковой длины, может быть рассчитана через длину его стороны без применения формулы радиуса окружности, которая вписана в него. Для данной фигуры верно утверждение о том, что высота, биссектриса и медиана делятся в точке пересечения в отношении 2:1. При схематичном изображении можно увидеть, что треугольная фигура АВС включает 6 треугольников с прямыми углами, которые имеют одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь треугольника АВС будет представлять собой сумму площадей всех 6 треугольников, формирующих его.
Какова формула вычисления площади равностороннего треугольника со стороной а?
Если сказано, что сторона равносторонней треугольной фигуры равна а, то его площадь можно найти:
S = a²√3/4.
Как определить, чему равна длина стороны треугольника с равными сторонами, зная формулу, по которой вычисляется площадь равностороннего треугольника (S=√3/4 а²) и то, что она равна 9√3см²?
Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².
Выразим а²:
а² = 9√3:√3/4 = 9√3 x 4√3 = 36
а = +-√36 = +- 6.
Так как длина стороны не может быть отрицательным числом, то a = 6 см.
Какой вид имеет формула, которая отражает зависимость площади равностороннего треугольника от длины его сторон?
Доказано, что равносторонний треугольник имеет равные углы по 60 градусов. Также известна формула вычисления площади данной фигуры путем умножения длин двух его сторон и синуса угла, который они образуют:
S = 1/2*a*a*sin 60 = a²√3/4 см.кв.
Чему равна площадь равностороннего треугольника и длина его медианы, если известно, что его сторона составляет а?
Если указано, что длина стороны равностороннего треугольника составляет а, то его площадь равна:
S=a²√3/4.
Медиана, проведенная в треугольнике с равными сторонами, также представляет собой его биссектрису и высоту. Из этого следует, что:
h=a√3/2.
Ответ: Площадь треугольника = a²√3/4 см.
кв., его медиана = a√3/2 см.
Как определить площадь равностороннего треугольника со стороной, длина которой составляет 8√2 см?
В случае с треугольником с равными сторонами, высота представляет собой также медиану, делящую на две равные части сторону, на которую она опущена. Если применить в данном случае теорему Пифагора, то высота равна:
h = √((8√2)²-(4√2)²)=4√6 см.
Теперь есть возможность найти площадь:
S = (1/2)*8√2*4√6 = 32√3 см. кв.
Площадь также можно найти по формуле для треугольника с равными сторонами:
S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.
Дано два равносторонних треугольника, площадь одного из которых превышает площадь другого в три раза. Чему будет равна сторона второго равностороннего треугольника, при условии, что сторона первого из них составляет 1 см.?
Для расчета площади треугольника с равными сторонами есть формула:
S = a²√3/4.
Найдем площадь меньшего из треугольников, подставив значение а:
S₁ = 12 √3/4 = √3/4 см.
кв.
Известно, что площадь второго треугольника больше площади первой фигуры в три раза. Тогда:
S₂ = 3√3/4.
Очевидно, что сторона большего треугольника составляет √3 см.
Сторона равностороннего треугольника равна 14 см. Чему будет равна его площадь, умноженная на √3?
Формула площади для треугольника с равными сторонами:
S = а²*√3/4.
Подставляем значение а:
S = 14²*√3/4 = 49√3 см. кв.
Умножаем полученное число на √3:
49√3*√3 = 49*3 = 147 см.
Читать дальше: как найти площадь круга.
треугольник, радиус вписанной и описанной окружностей
Все формулы для треугольника, как найти сторону, биссектрису, медиану, высоту, угол…
Найти длину биссектрисы в треугольнике
L — биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC, разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
Биссектриса прямоугольного треугольника
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
Длина биссектрисы равнобедренного треугольника
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L — высота=биссектриса=медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол вершины
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Найти медиану=биссектрису=высоту равностороннего треугольника
Формула для вычисления высоты= биссектрисы= медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — стороны треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Найти длину медианы треугольника по формулам
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a , b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Длина медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам. Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b. c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
Формулы высоты прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
*Внимательно, при подстановке в формулу, для тупого угла ( α90), сosα,принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (c, a, b):
Все формулы радиуса описанной окружности
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
h — высота
p = (a+d+c)/2
Формула радиуса описанной окружности трапеции, (R)
Радиус описанной окружности правильного многоугольника
a — сторона многоугольника
N — количество сторон многоугольника
Радиус описанной окружности правильного многоугольника, (R):
Радиус описанной окружности правильного шестиугольника
a — сторона шестиугольника
d — диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Радиус описанной окружности прямоугольника по стороне
a, b — стороны прямоугольника
d — диагональ
Радиус описанной окружности прямоугольника (R):
Найти радиус описанной окружности около квадрата
a — сторона квадрата
d — диагональ
Радиус описанной окружности квадрата (R):
Найти радиус описанной окружности треугольника, формула
a, b, c — стороны треугольника
p — полупериметр,
p= (a+b+c)/2
Формула радиуса описанной окружности треугольника, (R):
Найти радиус описанной окружности равностороннего треугольника по стороне
a — сторона треугольника
Радиус описанной окружности равностороннего треугольника (R):
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Найти радиус описанной окружности прямоугольного треугольника по катетам
a, b — катеты прямоугольного треугольника
c — гипотенуза
Радиус описанной окружности прямоугольного треугольника (R):
Все формулы радиуса вписанной окружности
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
Радиус вписанной окружности в правильный многоугольник
a — сторона многоугольника
N — количество сторон многоугольника
Радиус вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Формула радиуса вписанной окружности в ромб, (r):
Радиус вписанной окружности в квадрат
a — сторона квадрата
Радиус вписанной окружности в квадрат (r):
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиус вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Радиус вписанной окружности в прямоугольный треугольник (r):
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Радиус вписанной окружности в равнобедренный треугольник (r):
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
Радиус вписанной окружности в равносторонний треугольник (r):
Радиус вписанной окружности в треугольник
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Радиус вписанной окружности в треугольник (r):
Медианы треугольника: определение, свойства
- Автор Rachana
- Последнее изменение 19-07-2022
- Автор Рачана
- Последнее изменение 19-07-2022
Медианы треугольника: Треугольник — это трехсторонний многоугольник, имеющий три стороны, три угла и три вершины.
Это одна из самых фундаментальных геометрических форм. Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны, тем самым делящий эту сторону пополам. Для каждого треугольника есть три медианы, по одной из каждой вершины.
Эти медианы пересекаются в точке, которая известна как центроид треугольника и обозначается буквой G. Центроид треугольника — это место, в котором соединяются его медианы, и он (центроид) делит каждую медиану в отношении 2:1. Embibe предоставляет рекомендации от предметных экспертов, чтобы студенты могли тщательно изучить темы. В этой статье будут рассмотрены медианы, их характеристики и решенные экземпляры.
Медиана треугольника — это отрезок, соединяющий вершину с серединой другой стороны треугольника. Треугольник содержит три медианы, по одной из каждой вершины. Три медианы совпадают в точке, называемой центром тяжести треугольника.
Здесь \(DM,\,EN\) и \(LF\) медианы, пересекающие друг друга в центроиде \(G\).
Центроид делит медиану в отношении \(2:1.\)
Высота: Высота треугольника, перпендикулярная вершине к противоположной стороне треугольника, называется высотой. Треугольник содержит три высоты, по одной из каждой вершины. Три высоты совпадают в точке, называемой ортоцентром треугольника.
Здесь \(DL\) — высота от вершины \(D\) до ее противоположной стороны \(EF\).
Медианы треугольника: параллельные
Точка, в которой пересекаются или встречаются непараллельные прямые линии, называется точкой пересечения.
Медианы треугольника совпадают. Точка совпадения медиан называется центром тяжести треугольника. Медианы треугольника совпадают во внутренней части треугольника. Центроид разделяет медианы на соотношение \(2:1\).
Узнать о центроиде треугольника
Доказательство совпадения медиан треугольника:
На первом рисунке выше \(QE\) и \(DR\) являются медианами на \(PR\) и \(PQ\) соответственно.
Итак, \(D\) и \(E\) являются серединами на \(PQ\) и \(PR\) соответственно.
Следовательно, \(DE\,{\rm{||}}\,QR\) и \(DE\, = \,\frac{1}{2}\,QR\) [теорема о средней точке]
\( \frac{{DE}}{{QR}}\, = \,\frac{1}{2} – – – – – ({\rm{I}})\)Теперь рассмотрим \(\Delta \,DEG\) и \(\Delta \,QGR\)
\(\angle GQR = \,\angle GED\, = \,y\) и \(\angle RDE = \,\угол DRQ\, = \,x\)Следовательно, из \(AA\) критерия подобия \(\Delta DEG \sim \Delta QGR.\)
Тогда \(\frac{{EG}}{{GQ}} = \frac{{DG}}{{GR}} = \frac{{DE}}{{QR}} – – – – ({\ м{II}})\)
Из уравнения \(({\rm{I}})\) и \(({\rm{II}})\)
\(\frac{{EG}}{{GQ}} = \frac{{DG}}{{GR}} = \frac{{DE}}{{QR}} = \frac{1}{2} – – – – ({\rm{III}})\)
Аналогично из второго рисунка получаем \(\Delta PQG \sim \Delta FEG.\)
\(\frac{{EG}}{{GQ}}\, = \,\frac{{EF}}{{PQ}}\, = \,\frac{{FG}}{{GP}}\ , = \,\frac{1}{2} – – – – ({\rm{IV}})\) 92}}}{4}} \)
\(a,b\) и \(c\) — три стороны треугольника.Центроид формулы треугольника
Центроид треугольника берет среднее значение координат \(x\) и координат \(y\) всех трех вершин. Таким образом, формула центроида может быть математически сформулирована как \(G(x,y) = \left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\,\frac{{ {y_1} + {y_2} + {y_3}}}{3}} \справа)\)
Свойства медианы треугольника
Свойства медиан треугольника следующие:
- Медиана треугольника далее делит треугольник на два треугольника, имеющие точное измерение площади.
- Для данного треугольника вторая медиана делит треугольник, образованный первой медианой, в отношении \(1:2.\)
- Каждый треугольник имеет три медианы, по одной из каждой вершины. Точка пересечения трех медиан образует центр тяжести треугольника.
- Независимо от формы или размера треугольника, три его медианы сходятся в одной точке.
- Каждая медиана треугольника делит треугольник на два меньших треугольника с равными площадями.
Три медианы делят треугольник на \(6\) меньших треугольников одинаковой площади.
- Сумма двух сторон треугольника больше медианы, проведенной из вершины, что и ожидалось.
Медианы равностороннего треугольника равны
Длина медиан в равностороннем треугольнике всегда равна. Поскольку длины всех сторон равностороннего треугольника одинаковы, длины медиан, делящих эти стороны пополам, равны.
Здесь медианы \(AE,\,BD\) и \(CF\) равны
Медианы треугольника Примечания
- Медиана любого треугольника делит его пополам на два равновеликих треугольника.
- Центроид (точка, где они встречаются) является центром тяжести треугольника.
- Сумма медиан треугольника: Сумма квадратов медиан треугольника равна трем четвертям суммы квадратов сторон треугольника.
- Граница треугольника больше суммы их трех медиан.
- Эквивалентные стороны, границы, медианы и высоты будут находиться в одинаковом соотношении для двух подобных треугольников.
- Середина отрезка делит его на две конгруэнтные части, тогда как медиана треугольника делит его на два конгруэнтных треугольника.
- Кроме того, если два треугольника конгруэнтны, медианы конгруэнтных треугольников равны, поскольку соответствующие части конгруэнтных треугольников конгруэнтны.
- Центроид любого треугольника является точкой трех секторов всех медиан.
- Центр тяжести треугольника любого типа всегда лежит внутри треугольника.
Решенные примеры — медианы треугольника
Q.1. \(PM\) является медианой \(\Delta PQR\). \(PM\) расширяется до \(N\) так, что \(PM = MN\) — точка \(MN\) и если площадь \(\Delta PQR\) равна \(40\,{\rm{sq}}{\rm{.cm}}\) , затем найдите площадь \(\Delta QOM\) .
Ответ: \(PM\) является медианой \(\Delta PQR\).
\(\следовательно \,\,\влево( {\Delta PQM} \right) = \frac{1}{2}ar\left( {\Delta PQR} \right) = \frac{1}{2} \times 40\,{\rm{sq}}{\rm{.cm}}\,{\rm{=}}\,{\rm{20}}\,{\rm{sq}}{\rm {.см}}\)
Опять же, \(QM\) является медианой \(\Delta PQN\).
\(\следовательно \,\,ar\left( {\Delta QMN} \right) = \frac{1}{2}ar\left( {\Delta PQN} \right) = \frac{1}{2 } \times 40\,{\rm{sq}}{\rm{.cm}}\,{\rm{=}}\,{\rm{20}}\,{\rm{sq}}{\ rm{.cm}}\)
Теперь \(QO\) является медианой \(\Delta QMN\).
\(ar\left( {\Delta QOM} \right) = \frac{1}{2}ar\left( {\Delta QMN} \right) = \frac{1}{2} \times 20\, {\ rm {sq}}. {\ rm {см}} \, {\ rm { = }} \, {\ rm {10}} \, {\ rm {sq}} {\ rm {.}} \ ,{\rm{cm}}\)
Следовательно, требуемая площадь равна \({\rm{10}}\,{\rm{sq}}{\rm{.}}\,{\rm{.}}\,{\rm{см} }\).Q.2. \(E\) является серединой медианы \(AD\) \(\Delta ABC\) .
Докажите, что \(\Delta BED = \frac{1}{4}\Delta ABC\)
Ответ:
Доказательство\(AD\) является медианой \(\Delta ABC\)
\(\следовательно \Delta ABD = \frac{1}{2}\Delta ABC – – – – – ({\rm{I}} )\)
( \(\следовательно \) медиана каждого треугольника делит его пополам на два треугольника равновеликих площадей.)
Опять же, \(E\) является серединой \(AD.\)
\(\следовательно BE\) является медианой \(\Delta ABD\).
\(\следовательно \Delta BED = \frac{1}{2}\Delta ABD = \frac{1}{2} \times \frac{1}{2}\Delta ABC\) (по \(({ \rm{I}})\))
\( = \,\frac{1}{4}\Delta ABC\)
\(\следовательно \,\Delta BED\, = \,\frac{1}{ 4}\Дельта АВС\)Q.3. Для данного \(\Delta PQR,\,G\) является центром тяжести и \(QR\, = \,12\) \({\rm{единицы} }\).
Определить длину \(MR\).
Здесь \(PM,\,QN,\) и \(RL\) — медианы \(\Delta PQR,\,M\) — середина \(QR\), поскольку \(PM\) — это медиана \(QR\, = 12\,{\rm{единиц}},\,MR = 6\,{\rm{единиц}}\). Следовательно, \(MR\,\, = \,6\,{\rm{единицы}}\).
Q.4. Вычислить координаты центра тяжести треугольника, вершины которого равны \((2,\,6),\,(8,\,12)\,и\,(8,\,0)\ ) .
Ответ: Мы знаем, что координаты центра тяжести треугольника, угловые точки которого равны
\(({x_1},\,{y_1}),\,({x_2},\,{y_2}),\,({x_3 },\,{y_3})\) являются \(\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\,\frac{{{y_1} + {y_2 } + {y_3}}}{3}} \right)\)
Следовательно, координаты центра тяжести треугольника, вершины которого равны \((2,\,6),\,(8,\,12 )\) и \((8,\,0)\) равны \(\left( {\ frac {{2 + 8 + 8}} {3},\, \ frac {{6 + 12 + 0}} {3}} \right) = (6,\,6)\)
Следовательно, центр тяжести треугольника для данных вершин равен \((6,\,6)\).Q.5. Докажите, что если любые две медианы треугольника равны, то это равнобедренный треугольник.
Ответ: Дано: Пусть медианы \(BE\) и \(CF\) вектора \(\Delta ABC\) равны, т. е. \(BE\, = \,CF\)Чтобы доказать: \(\Delta ABC\) равнобедренный треугольник.
Доказательство. Пусть \(BE\) и \(CF\) пересекаются друг с другом в точке \(G.\). Мы знаем, что три медианы треугольника пересекаются в трехсекторной точке внутри него, \(\следовательно, EG\ , = \,\frac{1}{3}\,BE\) и \(FG\, = \,\frac{1}{3}CF\)
Но \(BE\, = \,CF\,\,\поэтому \,EG\, = \,FG\, – – – – ({\rm{I}})\) и \(BG\, = \,CG\, – – – – ({\rm{II}})\)
Теперь в \(\Delta BGF\) и \(\Delta CGE\), \(FG\, = \,EG \) ( by \(({\rm{I}})\)), \(BG\, = \,CG\) (by \(\left( {{\rm{II}}} \right)\ ))
И \(\угол BGF\, = \,\угол CGE\) (\(\следовательно\) это противоположные углы)
\(\следовательно \,\Delta BGF\, \cong \,\Delta \ ,CGE\) (по условию \(SAS\) конгруэнтности)
\(\следовательно, BF = CE\) (\(\следовательно\) это подобные стороны конгруэнтных треугольников)
или \(\frac{1}{2}AB = \frac{1}{2}AC\) (\(\следовательно\) \(F\) и \(E\) являются серединами \ (AB\) и \(AC\) соответственно) или \(AB\, = \,AC\)
\(\следовательно \,\Delta ABC\) равнобедренный треугольник.
Значит, доказано.Резюме
В этой статье мы узнали о медианах определения треугольника, медианы треугольника совпадают, медианы формулы треугольника, медианы свойств треугольника, медианы треугольника равны, медианы треугольника, отмечены решенные примеры по медианам треугольника. треугольник и часто задаваемые вопросы о медианах треугольника.
Результатом изучения этой статьи является то, что мы узнали о связи между медианами треугольника и их сторонами, а также о связи между площадью треугольника и его медианами.
Узнайте о свойствах треугольника
Часто задаваемые вопросы (FAQ) о медианах треугольникаQ.1 : Какими свойствами обладает медиана треугольника ?
Ответ: Свойства медиан треугольника следующие:
1. Медиана треугольника далее делит треугольник на два треугольника, имеющие точное измерение площади.
2. Для определенного треугольника вторая медиана разделяет треугольник, созданный первой медианой, в отношении \(1:2\)
3. Каждый треугольник имеет три медианы, по одной из каждой вершины. Точка пересечения трех медиан образует центр тяжести треугольника.
4. Независимо от формы или размера треугольника, три его медианы совпали в одной точке.
5. Каждая медиана треугольника делит его на два меньших треугольника с равными площадями. Три медианы делят треугольник на \(6\) меньших треугольников одинаковой площади.
6. Сумма двух сторон треугольника больше медианы, проведенной из вершины, что и ожидалось.Q.2 : Медианы треугольника равны ?
Ответ: Длина медиан в равностороннем треугольнике всегда равна. Поскольку длины всех сторон равностороннего треугольника равны, отсюда следует, что длина медиан, делящих эти стороны пополам, равна.Q.
3: 92}}}{4}} \)
\(a,\,b\) и \(c\) — три стороны треугольника.Q.4: Что означает медиана в треугольнике ?
Ответ: Медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны треугольника, называется медианой. Треугольник содержит три медианы, по одной из каждой вершины.Q.5: Что такое центр тяжести треугольника ?
Ответ: Медианы треугольника совпадают (они пересекаются в одной общей точке). Точка совпадения медиан называется центром тяжести треугольника.
Центроид треугольника содержит среднее значение координат \(x\) и координат \(y\) всех трех вершин. Таким образом, формула центроида может быть математически сформулирована как \(G(x,\,y)\, = \,\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3}, \frac{{{y_1} + {y_2} + {y_3}}}{3}} \right)\)Мы надеемся, что эта подробная статья о медианах треугольника помогла вам в ваших исследованиях.
Если у вас есть какие-либо сомнения, вопросы или предложения относительно этой статьи, не стесняйтесь спрашивать нас в разделе комментариев, и мы будем более чем рады помочь вам. Приятного обучения!
Практические вопросы о треугольниках с советами и решениями
Свойства равносторонних треугольников | Brilliant Math & Science Wiki
Содержание
- Удостоверение личности
- Основные свойства
- Расширенные свойства
- Теоремы о равносторонних треугольниках
- Смотрите также
Самый простой способ определить равносторонний треугольник — сравнить длины сторон. Если длины трех сторон равны, то структура треугольника определена (следствие конгруэнтности SSS).
Однако, это не всегда возможно. 9{\ circ} 60∘.
Примечательно, что равносторонний треугольник является уникальным многоугольником, для которого знание длины только одной стороны позволяет определить полную структуру многоугольника. Например, существует бесконечно много четырехугольников с равными длинами сторон (ромбов), поэтому вам нужно знать хотя бы еще одно свойство, чтобы определить его полную структуру. Таким образом, равносторонний треугольник находится в компании с кругом и сферой, полная структура которых определяется указанием только радиуса.
Поскольку равносторонний треугольник в некотором смысле является простейшим многоугольником, многие обычно важные свойства легко вычисляются. Например, для равностороннего треугольника со стороной s\color{#D61F06}{s}s мы имеем следующее:
- Высота, медиана, биссектриса угла и биссектриса для каждой стороны представляют собой одну и ту же прямую. .
- Эти 3 линии (по одной на каждую сторону) также являются линиями симметрии треугольника.
92\sqrt{3}}{4}4s23.
- Ортоцентр, центр описанной окружности, центр вписанной окружности, центроид и девятиточечный центр являются одной и той же точкой. Линия Эйлера вырождается в одну точку.
- Радиус описанной окружности равностороннего треугольника равен s33\frac{s\sqrt{3}}{3}3s3. Обратите внимание, что это 23\frac{2}{3}32 длины высоты, потому что каждая высота также является медианой треугольника.
- Радиус равностороннего треугольника равен s36\frac{s\sqrt{3}}{6}6s3. Обратите внимание, что внутренний радиус равен 13\frac{1}{3}31 длины высоты, потому что каждая высота также является медианой треугольника. Также внутренний радиус равен 12\frac{1}{2}21 длины описанной окружности.
Пусть aaa — площадь равностороннего треугольника, а bbb — площадь другого равностороннего треугольника, вписанного в окружность, вписанную в первый треугольник. Что такое ab\frac{a}{b}ba?
Также стоит отметить, что шесть конгруэнтных равносторонних треугольников могут быть сложены в правильный шестиугольник, что позволяет легко обнаружить некоторые свойства правильных шестиугольников.
2\sqrt{3}} {2}6⋅4с23=23с23.
Во-первых, стоит отметить, что радиус описанной окружности ровно в два раза больше внутреннего радиуса, что важно, поскольку R≥2rR \geq 2rR≥2r согласно неравенству Эйлера. Равносторонний треугольник обеспечивает случай равенства, как и в более сложных случаях, таких как неравенство Эрдоса-Морделла.
Если PPP является любой точкой внутри равностороннего треугольника, сумма расстояний от нее до трех сторон равна длине высоты треугольника:
Сумма трех цветных длин — это длина высоты, независимо от положения P 9{\circ}15∘
Также стоит отметить, что помимо равностороннего треугольника на рисунке выше есть еще три треугольника с площадями X, YX, YX, Y и ZZZ (((с наибольшим ZZZ).) .). Они удовлетворяют соотношению 2X=2Y=Z ⟹ X+Y=Z2X=2Y=Z \ подразумевает X+Y=Z 2X=2Y=Z⟹X+Y=Z. Фактически X+Y=ZX+Y=ZX+Y=Z верно для любого прямоугольника, описанного вокруг равностороннего треугольника, независимо от ориентации.
Стороны прямоугольника ABBCDABCDABCD имеют длины 101010 и 111111. Начерчен равносторонний треугольник так, что ни одна точка треугольника не лежит вне ABDABCDABCD. Максимально возможная площадь такого треугольника может быть записана в виде pq−rp\sqrt{q}-rpq−r, где p,q,p, q,p,q и rrr — положительные целые числа, а qqq — не делится на квадрат любого простого числа. Найдите p+q+r.p+q+r.p+q+r. 92,PA2=PB2+PC2,
найти меру ∠BPC\угла BPC∠BPC в градусах.
Другим свойством равностороннего треугольника является теорема Ван Шутена:
Если ABCABCABC — равносторонний треугольник, а MMM — точка на дуге BCBCBC описанной окружности треугольника ABC, ABC, ABC, то
MA=MB+MC.MA=MB+MC.MA=MB+MC.
Используя теорему Птолемея о вписанном четырехугольнике ABMCABMCABMC, мы имеем
MA⋅BC=MB⋅AC+MC⋅ABMA\cdot BC= MB\cdot AC+MC\cdot ABMA⋅BC=MB⋅AC+MC⋅AB
или
МА=МБ+МС. □MA=MB+MC.\ _\squareMA=MB+MC. □
Вот пример, связанный с координатной плоскостью.
Докажите, что на плоскости нет равностороннего треугольника, вершины которого имеют целые координаты.
Предположим, что на плоскости есть равносторонний треугольник, вершины которого имеют целочисленные координаты.
Формула определителя площади рациональна, поэтому, если все три точки являются рациональными точками, то площадь треугольника также рациональна. 92a2 — целое число, а 3\sqrt{3}3 — иррациональное число.
Это противоречие. □_\квадрат□
Теорема Морли утверждает, что три точки пересечения трех смежных углов образуют равносторонний треугольник (розовый треугольник на рисунке справа).
На самом деле эта теорема обобщает: оставшиеся точки пересечения определяют еще четыре равносторонних треугольника. Кроме того, расширение этой теоремы дает в общей сложности 18 равносторонних треугольников. Однако первое (как показано) является наиболее важным.
Теорема Наполеона утверждает, что если на сторонах любого треугольника построить равносторонний треугольник, центры этих трех треугольников сами образуют равносторонний треугольник.
Если треугольники развернуты наружу, как на изображении слева, треугольник известен как внешний треугольник Наполеона . В противном случае, если треугольники развернуты внутрь, треугольник известен как внутренний треугольник Наполеона . Разница между площадями этих двух треугольников равна площади исходного треугольника.
Внутренний и внешний треугольники Наполеона имеют один и тот же центр, который также является центром тяжести исходного треугольника.
- Свойства равнобедренных треугольников
Процитировать как: Свойства равносторонних треугольников. Brilliant.org . Извлекаются из https://brilliant.
org/wiki/properties-of-equilateral-triangles/
Равносторонний треугольник — калькулятор геометрии
Геометрия | Формы | Контакты и конфиденциальность Геометрические калькуляторы Немецкий: Geometriechner, Formen 1DЛиния, дуга окружности, парабола, спираль, кривая Коха 2D Правильные многоугольники:
Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольникаДругие многоугольники:
треугольник, прямоугольный треугольник, равнобедренный треугольник, ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадрат, прямой змей, воздушный змей, правильная трапеция, равнобедренная трапеция, трехравносторонняя трапеция, трапеция, тупая трапеция, циклический четырехугольник, касательный четырехугольник, наконечник стрелки, вогнутый четырехугольник, Перекрещенный прямоугольник, антипараллелограмм, форма дома, симметричный пятиугольник, восьмиугольник, разделенный пополам по диагонали, прямоугольник с вырезом, вогнутый пятиугольник, вогнутый правильный пятиугольник, вытянутый пятиугольник, прямой восьмиугольник, разделенный пополам, вытянутый шестиугольник, симметричный шестиугольник, параллелогон, вогнутый шестиугольник, шестиугольник со стрелкой, прямоугольный шестиугольник , L-образная форма, острый излом, T-образная форма, усеченный квадрат, вытянутый восьмиугольник, рамка, открытая рамка, сетка, крест, X-образная форма, H-образная форма, три звезды, F наша звезда, пентаграмма, гексаграмма, уникурсальная гексаграмма, октаграмма, звезда Лакшми, многоугольник с двойной звездой, полиграмма, многоугольникКруглые формы:
3Д Platonic Solids:
Круг, Полукруг, Круглый сектор, Круглый сегмент, Круглый слой, Круглый центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Заостренный овал, Два круга, Стрельчатая арка, Холм , Кольцо, Сектор кольца, Изогнутый прямоугольник, Скругленный многоугольник, Скругленный прямоугольник, Эллипс, Полуэллипс, Эллиптический сегмент, Эллиптический сектор, Эллиптическое кольцо, Стадион, Спираль, Бревно.Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Tetrahedron, Cube, Octahedron, Dodecahedron, IcosahedronArchimedean Solids:
Truncated Tetrahedron, Cuboctahedron, Truncated Cube, Truncated Octahedron, Rhombicuboctahedron, Truncated Cuboctahedron, Icosidodecahedron, Truncated Dodecahedron, Truncated Icosahedron, Snub Cube, Rhombicosidodecahedron , Truncated Icosidodecahedron, Snub DodecahedronCatalan Solids:
Triakis Tetrahedron, Rhombic Dodecahedron, Triakis Octahedron, Tetrakis Hexahedron, Deltoidal Icositetrahedron, Hexakis Octahedron, Rhombic Triacontahedron, Triakis Icosahedron, Pentakis Dodecahedron, Pentagonal Icositetrahedron, Deltoidal Hexecontahedron, Hexakis Icosahedron, Пятиугольный шестигранникJohnson Solids:
Pyramids, Cupolae, Rotunda, Elongated Pyramids, Gyroelongated Pyramids, Bipyramids, Elongated Bipyramids, Gyroelongated Square Dipyramid, Gyrobifastigium, Disheptahedron, Snub Disphenoid, Sphenocorona, DisphenocingulumOther Polyhedrons:
Cuboid, Square Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдрКруглые формы:
4Д Тессеракт, Гиперсфера
Сфера, полусфера, сферический угол, цилиндр, срезанный цилиндр, наклонный цилиндр, изогнутый цилиндр, эллиптический цилиндр, обобщенный цилиндр, конус, усеченный конус, косой круговой конус, эллиптический конус, усеченный эллиптический конус, общий конус , Общий усеченный конус, двояконус, усеченный двояконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферическая крышка, сферический сегмент, сферический центральный сегмент, двойной калот, сферический клин, полуцилиндр, диагонально разделенный пополам Цилиндр, Цилиндрический клин, Цилиндрический сектор, Цилиндрический сегмент, Цилиндр с плоским концом, Полуконус, Конический сектор, Конический клин, Сферическая оболочка, Полусферическая оболочка, Цилиндрическая оболочка, Вырезанная цилиндрическая оболочка, Наклонная цилиндрическая оболочка, Полый конус, Усеченный полый конус, Сферический Кольцо, тор, тор веретена, тороид, сектор тора, сектор тора, арка, тетраэдр Рело, капсула, сегмент капсулы, двойная точка, антиконус, усеченный антиконус, Sphe повторный цилиндр, линза, вогнутая линза, бочонок, форма яйца, параболоид, гиперболоид, олоид, тела Штейнмеца, тело вращенияAnzeige
Вычисления в равностороннем треугольнике или правильном треугольнике.
Это самый простой правильный многоугольник (многоугольник с равными сторонами и углами). Введите одно значение и выберите количество знаков после запятой. Затем нажмите Рассчитать.
Формулы:
h = √3 / 2 * a
p = 3 * a
A = a² * √3 / 4
r c = √3 / 3 = 6 * a
i r 906†1 3 / 6 * a
Угол: 60°
0 диагоналиДлина, высота, периметр и радиус имеют одну и ту же единицу измерения (например, метр), площадь имеет эту единицу в квадрате (например, квадратный метр).
Anzeige
Высоты, биссектрисы, медианы, биссектрисы и оси симметрии совпадают. Для них равносторонний треугольник осесимметричен. Они встречаются с центром тяжести, описанной окружностью и центром вписанной окружности в одной точке. К этому равносторонний треугольник осесимметричен при вращении на 120 ° или кратно этому.
периметр p, площадь A5 окружность
высота h a , h b , h c
углы и биссектрисы
срединные линии
перпендикулярные биссектрисыПоделиться:
© Jumk.
de Веб-проекты | Онлайн калькуляторы
Anzeige
Высота и медиана треугольника: определение и свойства
Высота и медиана треугольника — это два разных понятия, которые часто путают, чтобы они были равными или одинаковыми. Хотя оба они имеют одинаковое значение при изучении различных аспектов треугольников, они не являются одним и тем же, а не в редком случае. Медиана начинается с вершины, тогда как высота часто упоминается как начинающаяся со стороны треугольника. Но и медиана, и высота касаются вершины и стороны треугольника. Некоторые факторы делают медиану и высоту интересными частями треугольника.
Table of Content
- Triangle
- Altitude of a triangle
- Median of a triangle
- Properties of median and altitude
- Things to Remember
- Примеры вопросов
Ключевые термины: треугольник, перпендикулярная линия, высота, медиана, высота, площадь треугольника
Треугольник
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Треугольник — это замкнутая геометрическая фигура с тремя сторонами.
Точки, в которых встречаются стороны, известны как вершины (множественное число, вершины). Треугольник может образовывать любые углы при вершинах, но сумма всех углов будет равна 180°. С помощью длины стороны и высоты можно измерить площадь треугольника.
Читайте также: Треугольник и его виды
Высота треугольника
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Высота — это перпендикулярная линия, проведенная от вершины к противоположной стороне треугольника. Перпендикулярная линия всегда будет составлять 90° со стороной, на которой она пересекается. Поскольку у треугольника три стороны и три вершины, у треугольника будет 3 высоты. Высота помогает вычислить площадь треугольника,
Площадь треугольника = ½ x Основание x Высота
Медиана треугольника
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Медиана треугольника — это отрезок, проведенный из вершины в другую точку на противоположной стороне этой вершины так, что отрезок делит противоположную сторону на две половины.
На приведенном выше рисунке AR — это отрезок, который делит сторону BC на две половины, то есть BR и RC. Точно так же все три медианы делят стороны на равные половины.
С помощью длин сторон мы можем найти длину медианы, используя следующую формулу:
Длина медианы = √(2b²+ 2c²- a²)/4
Где a, b и c — стороны треугольника, а «a» — сторона, к которой проведена медиана.
Свойства медианы и высоты
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Высота и медиана треугольника имеют разные свойства как части треугольника. Свойства могут быть разными для разных видов треугольников, но есть некоторые особенности или ключевые свойства, которые делают их узнаваемыми.
- Как и медиана, в треугольнике будет 3 высоты. Другими словами, количество сторон в треугольнике будет равно количеству высот.
- Угол, который образует высота с противоположной стороной, всегда будет 90 градусов.
- Если одновременно провести все высоты треугольника, то три высоты наверняка пересекутся в точке, называемой ортоцентром.
- Высота — это часть треугольника, которая не обязательно должна находиться внутри сторон треугольника.
- Высота — это основной компонент, который помогает вычислить площадь треугольника.
- В равностороннем треугольнике высота совпадает с медианой.
Существуют некоторые свойства медианы, которые можно определить как ее характеристики. К этим свойствам относятся:
- Высота начинается из вершины треугольника и заканчивается в точке противоположной стороны, которая делит противоположную сторону поровну.
- Площадь двух частей, образованных медианой (которая будет двумя треугольниками), всегда будет равна.
- Количество медиан в треугольнике всегда будет равно количеству вершин в треугольнике.
- Если одновременно провести три медианы, они обязательно пересекутся в одной точке треугольника.( Центроид )
- Площади числа меньших частей, которые медиана образует внутри треугольника, всегда будут равны.
- В равностороннем треугольнике медиана равна высоте.
Что нужно помнить
[Нажмите здесь, чтобы просмотреть примеры вопросов]
- Высота треугольника — это перпендикулярная линия , проведенная из вершины треугольника к противоположной стороне. Другими словами, высота представляет собой высоту треугольника.
- Высота используется для расчета площади треугольника вместе с длиной основания, к которому относится высота.
- Медиана — это отрезок, проведенный от центра стороны треугольника к противоположной вершине. Другими словами, медиана делит сторону на две половины.
Длина медианы может быть рассчитана по формуле
Длина медианы = √ (2b²+ 2c²- a²)/4
Где a, b и c — стороны треугольника, а «a» это сторона, к которой проведена медиана.
- В случае равностороннего треугольника медиана треугольника совпадает с высотой треугольника.
Читайте также: Равносторонний треугольник
Примеры вопросов
Вопрос.
В чем основная разница между высотой и медианой треугольника? ( 1 балл )
Ответ. Высота — это линия, представляющая собой перпендикулярную линию, проведенную от стороны треугольника к вершине, противоположной этой стороне. Высота называется высотой треугольника. Тогда как медиана — это линия, проведенная для вершины к точке на противоположной стороне, которая делит сторону на две равные части.
Вопросы. Как называются точки пересечения медиан и точек пересечения высот? ( 2 балла )
Отв. В треугольнике должно быть 3 медианы, которые всегда лежат внутри треугольника. Когда все эти три медианы треугольника рисуются одновременно, они пересекаются в общей точке, называемой центроидом.
Высоты треугольника также пересекаются с общей точкой треугольника, которая не всегда может быть внутренней по отношению к треугольнику.
Эта точка называется ортоцентром треугольника.
Вопросы. Назовите некоторые интересные свойства медианы треугольника. ( 3 балла )
Отв. Медиана — это линия, проведенная от вершины треугольника к центру противоположной стороны. Вот некоторые интересные особенности медианы:
- Медиана делит противоположную сторону на две равные части.
- Как и противоположная линия, площади двух образованных треугольников всегда будут равны.
- Количество медиан в треугольнике всегда равно трем или равно количеству вершин в треугольнике.
- Если одновременно провести три медианы, они обязательно пересекутся в центре треугольника.
- Количество меньших треугольников, образуемых тремя медианами внутри треугольника, всегда будет одинаковой площади.
Вопрос. Объясните шаг за шагом, что происходит с площадью треугольника, когда проводится каждая медиана.
( 3 балла )
Отв.
Рассмотрим треугольник ABC.
При проведении медианы AR треугольник ABC делится на два треугольника (Δ ABR и Δ ACR).
Площадь Δ ABR = Площадь Δ ACR.
Аналогично, когда мы рисуем медиану BQ,
Площадь Δ BAQ = площадь Δ BCQ.
Кроме того, когда мы проводим медиану CP,
Площадь Δ CBP = Площадь Δ ABQ.
Таким образом, при проведении всех трех медиан весь треугольник будет разделен на.
Вопросы. Треугольник ABC имеет основание BC, а высоту OA. Если дополнительно указать, что ВС = 12 см, а ОА в 2 раза больше 3/4 th Британской Колумбии, поможет ли это рассчитать площадь этого треугольника? ( 3 балла )
Отв.
Площадь треугольника = ½ x основание x высота
При заданном Δ ABC,
Основание, BC = 12 см
Высота, OA = 2 x ¾ x BC
= 2 x ¾ x 12
= 18 см
Следовательно, площадь Δ ABC = ½ x BC X OA
= ½ x 12 x 18
= 108 см²
Запрос.
В треугольнике DEF DE = EF = ED. Если бы DE было равно 12 см, какой была бы высота этого треугольника? ( 4 балла )
Отв.
Дано в ΔDEF, стороны DE = EF = ED= 12см.
Следовательно, Δ DEF — равносторонний треугольник.
Площадь равностороннего треугольника = a² x √3/2
Где, a = длина сторон
Площадь Δ DEF = 12 2
= 176,36 см²
Кроме того, площадь треугольника = ½ х основание х высота
Здесь 176,36 = ½ х 12 х высота
Следовательно, , Высота = 29,39 см
Вопрос. Δ GHI имеет стороны GH = 3 см, HI = 4 см, IG = 4,5 см. Тогда какова будет длина медианы IO? ( 5 баллов )
Ответ.
Длина медианы = √(2b²+ 2c²- a²)/4
Где a, b и c — стороны треугольника, а «a» — сторона, к которой проведена медиана.
В Δ GHI,
a = GH = 3 см
b = 4 см
c = 4,5 см
(Примечание: значения b и c взаимозаменяемы). — 3] / 4
= √ [52,25 – 3] / 4
= 1,75 см
Запросы. Медиана треугольника АВС равна 4 см. Если АВ = 34 см, а ВС = 23 см, какова будет длина СА, к которой проведена медиана? ( 5 баллов )
Ответ.
Длина медианы = √(2b²+ 2c²- a²)/ 4
Где a, b и c — стороны треугольника, а «a» — сторона, к которой проведена медиана.
Здесь 4 см = √ (2b²+ 2c²- a²)/4
→ 4 см = √ (2 x 34²+ 2 x 23²- a²)/4
→ 4 см = √ (3370-a ² )/4
→ a = 42,05 см
Запросы. Площадь треугольника равна 24 см². Чему равна высота, если длина основания 32 см? ( 3 балла )
Отв.

Площадь треугольника = ½ x основание x высота
Здесь площадь треугольника = 24 см ²
основание = 32 см
т.е. высота = 24 x 2/32
= 1,5 см
Вопрос. В треугольнике ABC медиана АО = 4 см, а линия под углом 90 градусов, проведенная из вершины В к медиане, равна 3,4 см. Тогда какова будет площадь треугольника BAO? ( 3 балла )
Отв.
Медиана AO разделит Δ ABC на два равных треугольника, Δ AOB и Δ AOC.
Учитывая Δ AOB,
AO = основание = 4 см
Высота = 3,4 см (перпендикуляр к основанию)
Следовательно, площадь Δ AOB = ½ x 4 x 3,4
= 908 см² Поскольку медиана делит треугольник на два равных треугольника,
Площадь Δ AOB = площадь Δ AOC
Следовательно,
Площадь Δ ABC = 2 x площадь Δ AOB
= 2 x 6,8
= 13,6 см²
Также читайте:
900Вопрос задан: г-жа Теодора Рунольфссон
Оценка: 4,8/5 (57 голосов)
В случае некоторых треугольников, таких как равносторонний треугольник, медиана и высота совпадают.
В треугольнике 3 медианы. Медиана также может быть определена как линия от середины стороны до противоположного внутреннего угла треугольника . Медианы совпадают в центроиде.
Одинаковы ли медиана и высота в равностороннем треугольнике?
Ответ: Нет. Высота и медиана в треугольнике не одно и то же. … Однако в случае равностороннего треугольника медиана и высота всегда одинаковы .
Как называется медиана в равностороннем треугольнике?
Ответ: В равностороннем треугольнике медиану также называют вершина .
Является ли медиана равностороннего треугольника также биссектрисой угла?
Следовательно, биссектриса этого угла также является высотой . – Если высота, проведенная из вершины А, также является медианой, то треугольник равнобедренный, так что АВ = АС, а ВС – основание. Следовательно, эта высота также является биссектрисой угла. … В равностороннем треугольнике каждая высота, медиана и биссектриса угла, проведенные из одной вершины, перекрываются.
В равностороннем треугольнике медиана перпендикулярна основанию?
В треугольнике линия, соединяющая один угол (или вершину) с серединой противоположной стороны, называется медианой. Свойство равнобедренных треугольников , которое легко доказать с помощью сравнения треугольников, состоит в том, что в равнобедренном треугольнике медиана основания перпендикулярна основанию.
Медиана формулы треугольника, примеры задач, свойства, определение, геометрия, середина и центры
Найдено 29 связанных вопросов
Медиана перпендикулярна противоположной стороне?
Отрезок, соединяющий вершину с серединой противоположной стороны, называется медианой.
Перпендикуляр от вершины к противоположной стороне называется высотой . Прямая, проходящая через середину отрезка и перпендикулярная отрезку, называется биссектрисой отрезка.
Что такое срединный треугольник?
Медиана треугольника — это отрезок, проведенный из вершины к середине противоположной стороны вершины .
Что такое средний пример?
Медиана: среднее число; можно найти, упорядочив все точки данных и выбрав ту, которая находится посередине (или, если есть два средних числа, взяв среднее значение этих двух чисел). Пример: Медиана 4, 1 и 7 равна 4, потому что, если расположить числа в порядке (1 , 4, 7), число 4 окажется в середине.
В чем разница между медианой и высотой треугольника?
Ответ: Разница между медианами и высотами в том, что медиана проведена из вершины треугольника к середине противоположной стороны , а высота проведена из вершины треугольника к противоположной стороне перпендикулярно ей.
Должен ли равносторонний треугольник быть равноугольным?
Равносторонний треугольник — это треугольник, все стороны которого равны. Это особый вид равнобедренного треугольника, основание которого равно каждому катету, а угол при вершине равен углам его основания. … Следовательно, каждый равносторонний треугольник также является равноугольным .
Что такое теорема о медиане?
В треугольнике отрезок, соединяющий вершину и середину противоположной стороны, называется медианой. … Теорема о медиане утверждает, что медианы треугольника пересекаются в точке, называемой центроидом , который составляет две трети расстояния от вершин до середины противоположных сторон.
Что называют медианой?
Медиана — это среднее число в отсортированном списке чисел . … Если имеется нечетное количество чисел, медианное значение — это число, которое находится посередине, с одинаковым количеством чисел ниже и выше.
Может ли прямоугольный треугольник быть равносторонним?
Нет, прямоугольный треугольник не может быть равносторонним .
По определению, прямоугольный треугольник — это треугольник, содержащий прямой угол, где прямой…
Сколько высот имеет равносторонний треугольник?
Три высоты имеют одинаковую длину.
В каком треугольнике медиана и высота совпадают?
Медианы равностороннего треугольника совпадают с высотой треугольника.
Имеет ли равносторонний треугольник 3 равные величины угла?
Равносторонний. Равносторонний треугольник имеет три равные стороны и углы. Он всегда будет иметь углов по 60° в каждом углу .
Может ли средний сегмент быть медианой?
Это отличается от медианы, которая соединяет вершину с серединой противоположной стороны. Чтобы построить средний отрезок, найдите середины двух сторон . Это можно сделать, проведя биссектрису на одной стороне треугольника. … Медиана будет содержать вершину, а середина — нет.
Может ли быть треугольник с двумя прямыми углами?
Нет, в треугольнике не может быть двух прямых углов .
У треугольника ровно 3 стороны, а сумма внутренних углов равна 180°. Итак, если треугольник имеет два прямых угла, третий угол должен быть равен 0 градусов, что означает, что третья сторона будет пересекаться с другой стороной.
Что такое ортоцентр треугольника?
Ортоцентр можно определить как точку пересечения высот, проведенных перпендикулярно от вершины к противоположным сторонам треугольника. Ортоцентр треугольника равен точка пересечения всех трех высот треугольника .
Как иначе называется медиана?
Некоторые распространенные синонимы медианы: среднее, среднее и норма. Хотя все эти слова означают «нечто, представляющее среднюю точку», медиана применяется к значению, представляющему точку, в которой выше столько же экземпляров, сколько и ниже.
Чем полезна медиана?
Использование. Медиана может использоваться как 90 548 мера местоположения, когда крайним значениям придается меньшее значение , как правило, из-за того, что распределение асимметрично, экстремальные значения неизвестны или выбросы ненадежны, т.
е. могут быть ошибками измерения/транскрипции.
Что говорит вам медиана?
ЧТО МЕДИАНА МОЖЕТ ВАМ СКАЗАТЬ? Медиана обеспечивает полезную меру центра набора данных . Сравнивая медиану со средним значением, вы можете получить представление о распределении набора данных. Когда среднее значение и медиана совпадают, набор данных более или менее равномерно распределяется от самых низких до самых высоких значений.
Какими свойствами обладает медиана треугольника?
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой его противоположной стороны. Медиана треугольника делит пополам противоположную сторону, деля ее на две равные половины, и делит пополам угол, из которого она возникает, на два равных угла .
Что такое медиана прямоугольного треугольника?
Медиана треугольника — это линия, проведенная от одной из вершин к середине противоположной стороны. Медиана гипотенузы прямоугольного треугольника равна 9.
0548 то свойство, что его длина равна половине длины гипотенузы .
Может ли быть треугольник с двумя тупыми углами?
У нас есть свойство, что сумма углов треугольника всегда равна 180∘ . Тупой угол – это угол, величина которого больше 90∘. Таким образом, добавив только два угла, мы получим 180∘ или больше. … Следовательно, имея два тупых угла, построение треугольника вообще невозможно .
Похожие вопросы
- 23Как образуется равносторонний треугольник?
- 41Кто равноугольный и равносторонний?
- 26Was значит равносторонний?
- 32Является ли равносторонний треугольник равнобедренным?
- 24Всегда ли равносторонние треугольники равноугольные?
- 40Может ли равносторонний треугольник создать мозаику?
- 20Почему треугольник равносторонний прямоугольный?
- 24В треугольнике abc и bde есть два равносторонних треугольника?
- 29Почему всякий равносторонний треугольник остроугольный?
- 16Может ли прямоугольный треугольник быть равносторонним треугольником?
Реклама
Популярные вопросы
- 26Следовало определение?
- 32 Пенни Маршалл была замужем?
- 42Как хранить ловушку?
- 15Когда Брайан О’Дрисколл ушел на пенсию?
- 18Что означает роговой?
- 31Чем заменить фундук?
- 45Смысл в грамматике?
- 41Как отрегулировать парфокальное?
- 41Откуда произошло слово вытесняющий?
- 43Где находятся клетки эпидермиса?
Как найти длину стороны равностороннего треугольника
Все ресурсы по геометрии среднего уровня
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Промежуточная справка по геометрии » Плоская геометрия » Треугольники » Равнобедренные треугольники » Как найти длину стороны равностороннего треугольника
Площадь равностороннего треугольника , какова длина каждой стороны?
Возможные ответы:
Правильный ответ:
Пояснение:
Равносторонний треугольник можно разбить на 2 прямоугольных треугольника 30-60-90 (см.
рисунок). Длина стороны (основания) в 2 раза больше, а высота равна . Площадь треугольника можно рассчитать с помощью следующего уравнения:
Следовательно, если равно длине стороны:
Длина боковой стороны равна 2x:
Сообщайте об ошибке
Что такая из этого.
Возможные ответы:
Правильный ответ:
Объяснение:
Мы знаем формулу площади равностороннего треугольника:
, если это сторона треугольника.
Итак, поскольку нам это сказали, мы можем подставить вместо и найти площадь треугольника:
Сообщить об ошибке
Найти, равен ли периметр этого треугольника.
Возможные ответы:
Правильный ответ:
Пояснение:
Этот треугольник равносторонний; мы можем сказать, потому что каждая из его сторон имеет одинаковую длину.
Чтобы найти длину одной стороны, нам нужно разделить периметр на :
Сообщить об ошибке
Чему равна сторона, если периметр этого треугольника равен ?
Возможные ответы:
Правильный ответ:
Пояснение:
Поскольку все стороны этого треугольника равны по длине, он равносторонний. Чтобы найти длину одной стороны равностороннего треугольника, нам нужно разделить периметр на .
Сообщить об ошибке
Высота треугольника – футы.
Какова длина основания треугольника с точностью до десятых?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку это равносторонний треугольник, линия, представляющая высоту, делит его пополам на треугольник 30-60-90.
Здесь вы можете использовать и найти гипотенузу, чтобы найти одну из сторон треугольника.
Используйте определение равностороннего треугольника, чтобы знать, что ответ гипотенузы также относится к основанию треугольника.
Следовательно,
Сообщить об ошибке
Высота равностороннего треугольника равна 5. Какова длина его сторон?
Возможные ответы:
Правильный ответ:
Пояснение:
Высота равностороннего треугольника, показанная пунктирной линией, также является одной из сторон прямоугольного треугольника:
Гипотенуза равна х, длина каждой стороны в этом равностороннем треугольнике, а другой катет равен половине этой, 0,5х.
Чтобы найти x, используйте теорему Пифагора:
возведите члены слева
объедините одинаковые члены, вычитая 0,25 x в квадрате с обеих сторон
разделите обе стороны на 0,75
возьмите квадратный корень из обеих сторон
Сообщить об ошибке
Равносторонний треугольник расположен поверх квадрата, как показано на рисунке ниже.
Найдите периметр фигуры.
Возможные ответы:
Правильный ответ:
Объяснение:
Напомним, что периметр — это сумма всех внешних сторон фигуры. Стороны, которые составляют периметр, выделены красным цветом.
Так как равносторонний треугольник имеет общую сторону с квадратом, каждая из пяти обведенных сторон имеет одинаковую длину.
Напомним, что высота равностороннего треугольника разбивает треугольник на конгруэнтные треугольники.
Затем мы можем использовать высоту, чтобы найти длину стороны треугольника.
Вспомним, что у треугольника отношение сторон равно . Наименьшая сторона на данном рисунке — это основание, вторая по длине сторона — это высота, а самая длинная сторона — это сторона самого треугольника.
Таким образом, мы можем использовать соотношение и длину высоты, чтобы составить следующее уравнение:
Подставьте значение высоты, чтобы найти длину стороны.
Теперь, поскольку периметр фигуры состоит из этих сторон, мы можем использовать следующее уравнение, чтобы найти периметр.
Сообщить об ошибке
Равносторонний треугольник расположен поверх квадрата, как показано на рисунке ниже.
Найдите периметр фигуры.
Возможные ответы:
Правильный ответ:
Объяснение:
Напомним, что периметр — это сумма всех внешних сторон фигуры. Стороны, которые составляют периметр, выделены красным цветом.
Так как равносторонний треугольник имеет общую сторону с квадратом, каждая из пяти обведенных сторон имеет одинаковую длину.
Напомним, что высота равностороннего треугольника разбивает треугольник на конгруэнтные треугольники.
Затем мы можем использовать высоту, чтобы найти длину стороны треугольника.
Вспомним, что у треугольника отношение сторон равно . Наименьшая сторона на данном рисунке — это основание, вторая по длине сторона — это высота, а самая длинная сторона — это сторона самого треугольника.
Таким образом, мы можем использовать отношение и длину высоты, чтобы составить следующее уравнение:
Подставьте заданную высоту, чтобы найти длину стороны.
Теперь, поскольку периметр фигуры состоит из этих сторон, мы можем использовать следующее уравнение, чтобы найти периметр.
Сообщить об ошибке
Равносторонний треугольник расположен поверх квадрата, как показано на рисунке ниже.
Найдите периметр фигуры.
Возможные ответы:
Правильный ответ:
Объяснение:
Напомним, что периметр — это сумма всех внешних сторон фигуры.
Стороны, которые составляют периметр, выделены красным цветом.
Так как равносторонний треугольник имеет общую сторону с квадратом, каждая из пяти обведенных сторон имеет одинаковую длину.
Напомним, что высота равностороннего треугольника разбивает треугольник на конгруэнтные треугольники.
Затем мы можем использовать высоту, чтобы найти длину стороны треугольника.
Вспомните, что у треугольника отношение сторон равно . Наименьшая сторона на данном рисунке — это основание, вторая по длине сторона — это высота, а самая длинная сторона — это сторона самого треугольника.
Таким образом, мы можем использовать отношение и длину высоты, чтобы составить следующее уравнение:
Подставьте заданную высоту, чтобы найти длину стороны.
Теперь, поскольку периметр фигуры состоит из этих сторон, мы можем использовать следующее уравнение, чтобы найти периметр.
Сообщить об ошибке
Равносторонний треугольник расположен поверх квадрата, как показано на рисунке ниже.
Найдите периметр фигуры.
Возможные ответы:
Правильный ответ:
Объяснение:
Напомним, что периметр — это сумма всех внешних сторон фигуры. Стороны, которые составляют периметр, выделены красным цветом.
Поскольку равносторонний треугольник имеет общую сторону с квадратом, каждая из пяти обведенных сторон имеет одинаковую длину.
Напомним, что высота равностороннего треугольника разбивает треугольник на конгруэнтные треугольники.
Затем мы можем использовать высоту, чтобы найти длину стороны треугольника.
Вспомним, что у треугольника отношение сторон равно . Наименьшая сторона на данном рисунке — это основание, вторая по длине сторона — это высота, а самая длинная сторона — это сторона самого треугольника.
Таким образом, мы можем использовать соотношение и длину высоты, чтобы составить следующее уравнение:
Подставьте заданную высоту, чтобы найти длину стороны.

 {o}}=\frac{a\sqrt{3}}{2}\)
{o}}=\frac{a\sqrt{3}}{2}\)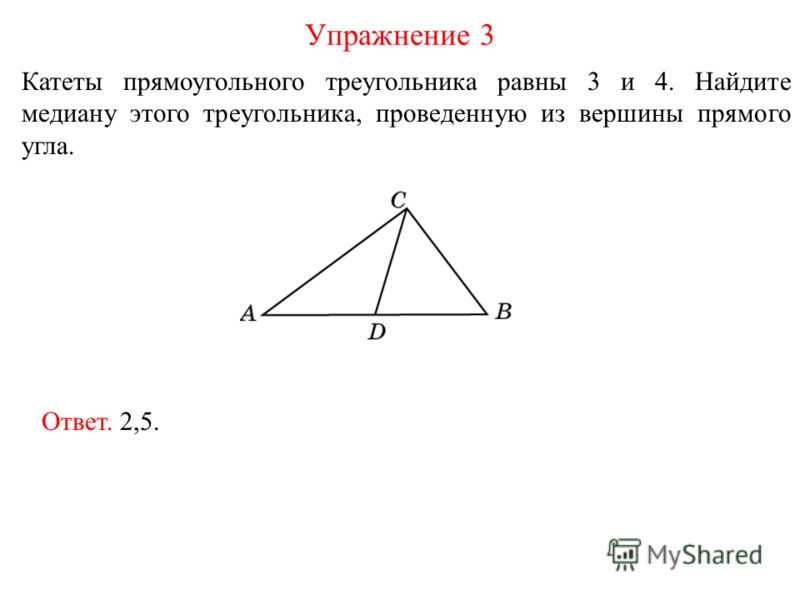
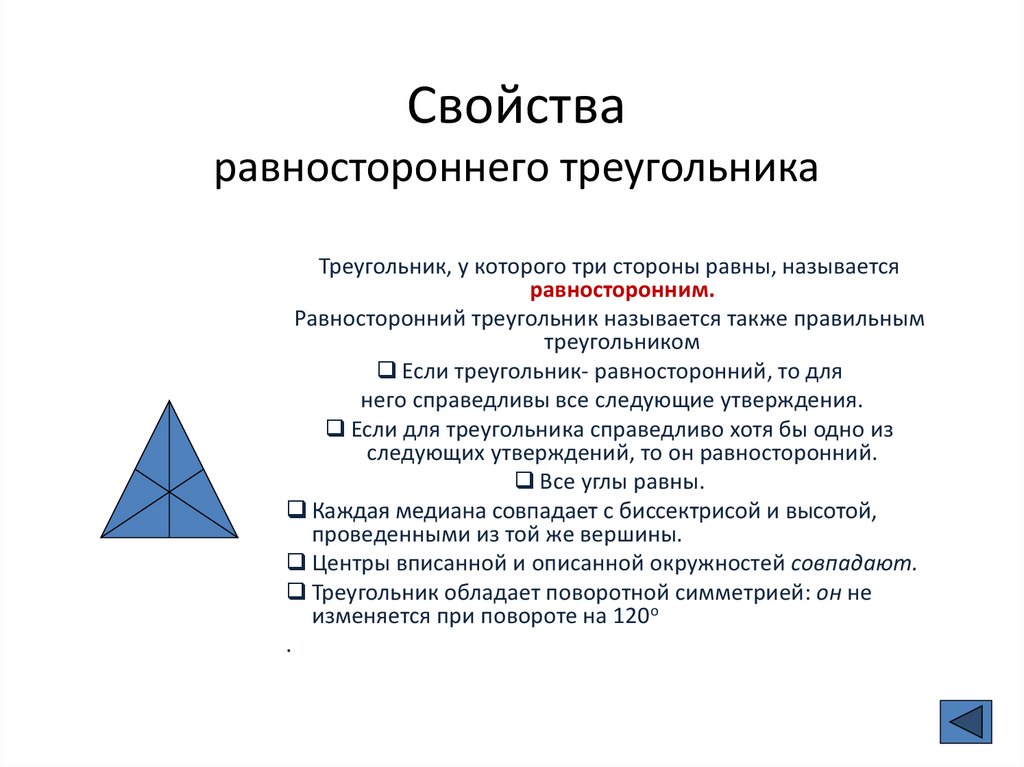 Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
 ⓘ Медиана равностороннего треугольника [M]
ⓘ Медиана равностороннего треугольника [M]
 Преобразование входов в базовый блок
Преобразование входов в базовый блок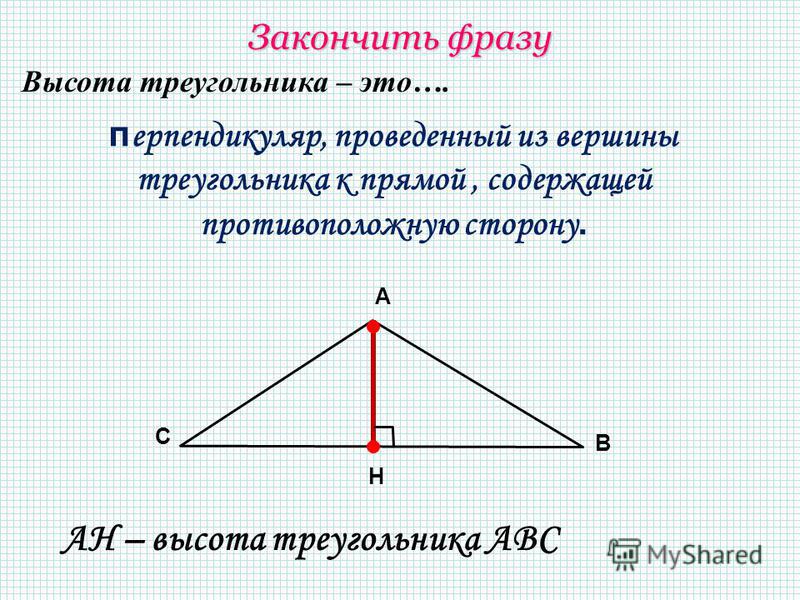
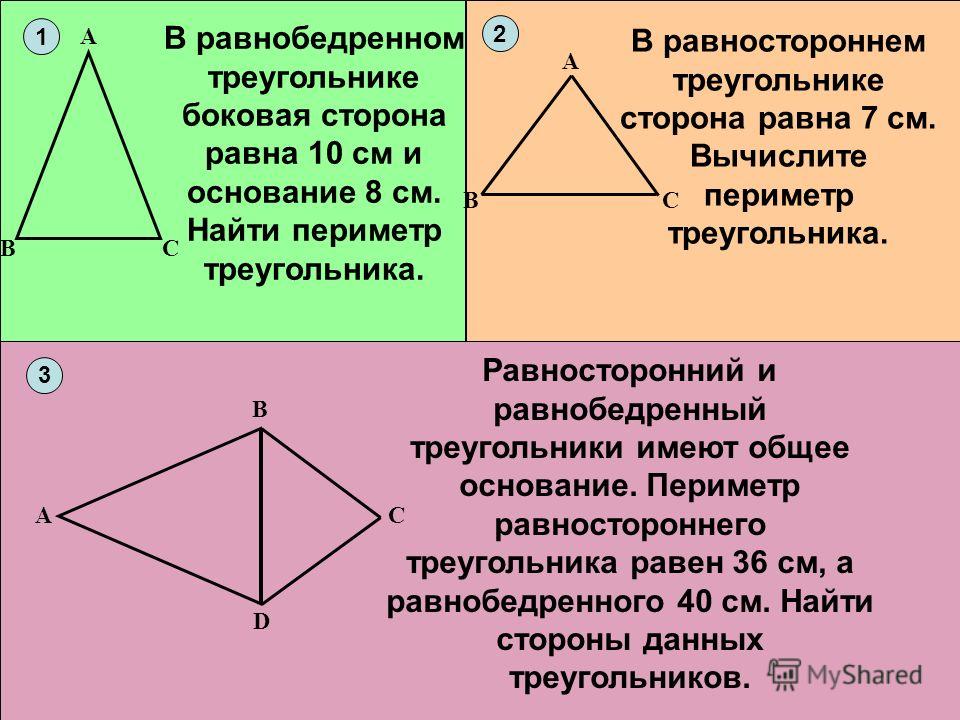 Часто при расчётах приходится использовать медиану. В равностороннем треугольнике она разбивает фигуру на две равные площади. При этом она и центр тяжести, чем зачастую и пользуются при решении задач.
Часто при расчётах приходится использовать медиану. В равностороннем треугольнике она разбивает фигуру на две равные площади. При этом она и центр тяжести, чем зачастую и пользуются при решении задач.
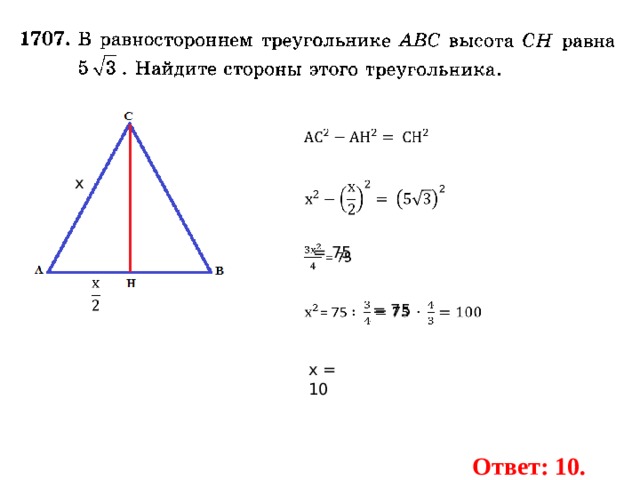

 Полученные 2 фигуры равны: ABD = CDB, значит, их сторона BD — общая и является катетом. Следовательно, AD = CD. Так как гипотенузы треугольников равны, AB = BC. Замечательное свойство доказано.
Полученные 2 фигуры равны: ABD = CDB, значит, их сторона BD — общая и является катетом. Следовательно, AD = CD. Так как гипотенузы треугольников равны, AB = BC. Замечательное свойство доказано.
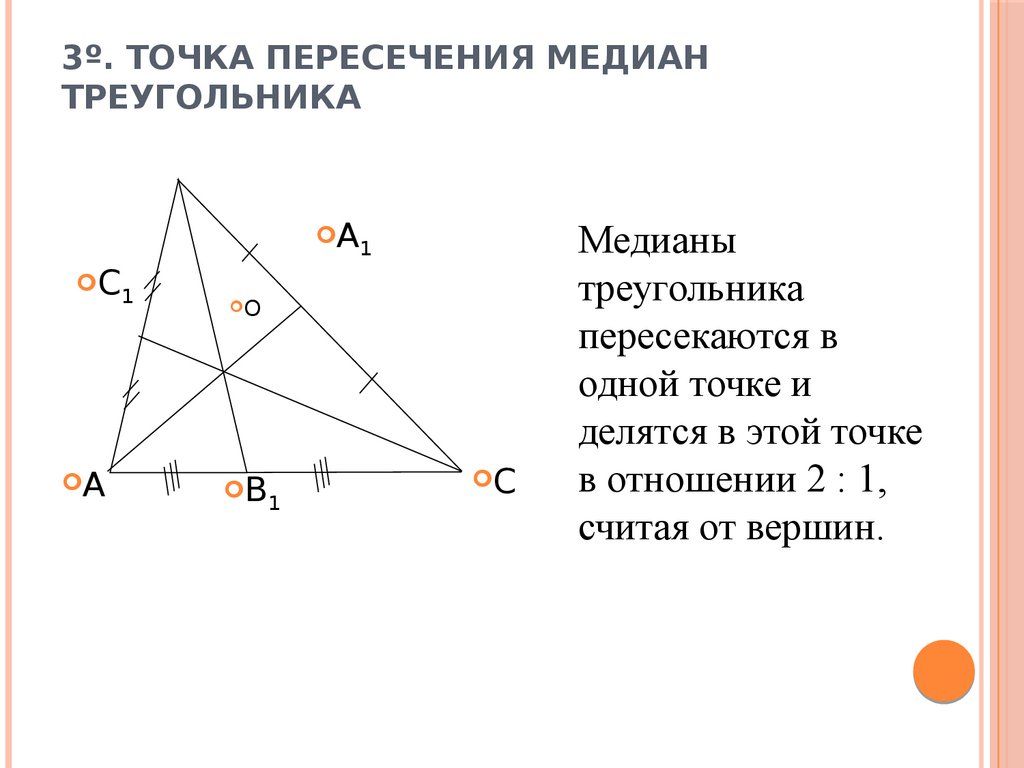 По теореме: AB2 = Ah3 + Bh3. Подставив известные значения в формулу, можно получить выражение: x2 = (x/2)2 + (9 * √3)2 = (x2 / 4) + 81 * 3 = 81 * 4. Отсюда x = √ 81 * √ 4 = 9 * 2 = 18.
По теореме: AB2 = Ah3 + Bh3. Подставив известные значения в формулу, можно получить выражение: x2 = (x/2)2 + (9 * √3)2 = (x2 / 4) + 81 * 3 = 81 * 4. Отсюда x = √ 81 * √ 4 = 9 * 2 = 18.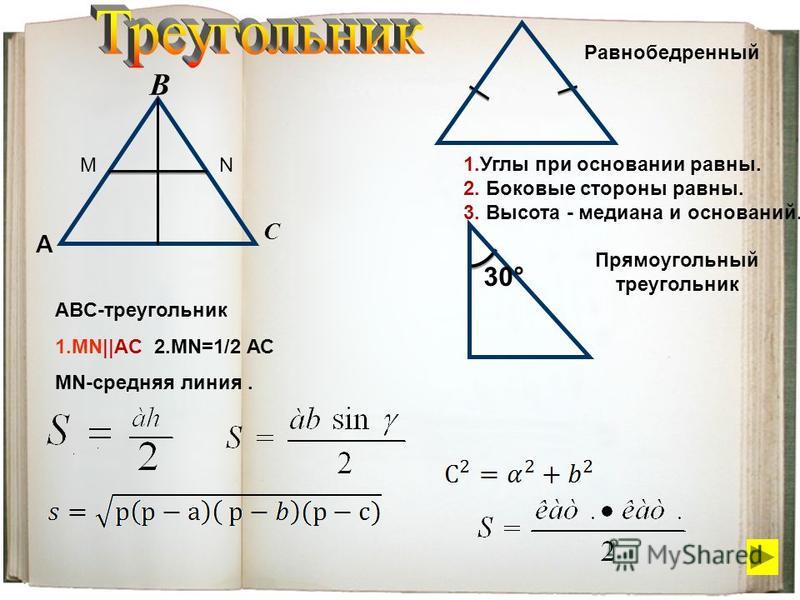 В школьных задачах обычно подбираются исходные данные так, что при решении не нужно пользоваться калькулятором или делать сложные расчёты. Ответ часто получается в удобной форме в виде десятичных чисел.
В школьных задачах обычно подбираются исходные данные так, что при решении не нужно пользоваться калькулятором или делать сложные расчёты. Ответ часто получается в удобной форме в виде десятичных чисел.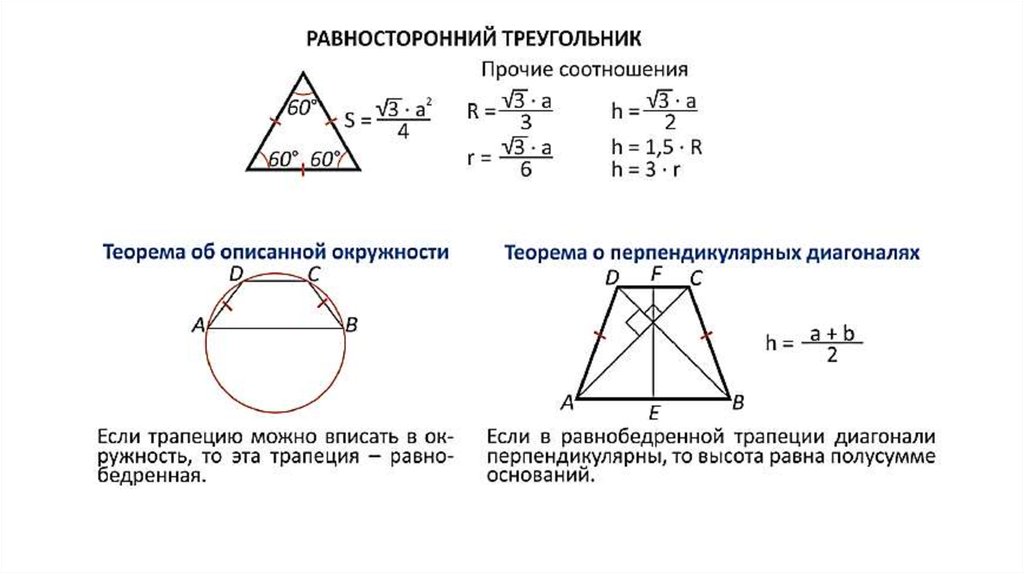 Настоящий комбайн вычислений. Сайт содержит несколько сотен математических калькуляторов и конвертеров. Пользователь также может скачать бесплатное приложение для системы Android.
Настоящий комбайн вычислений. Сайт содержит несколько сотен математических калькуляторов и конвертеров. Пользователь также может скачать бесплатное приложение для системы Android.


 \circ\), чтд.
\circ\), чтд. {2} \cdot \sqrt{3}}{4}=\frac{12 \sqrt{3}}{4}=3 \sqrt{3}$ (м2)
{2} \cdot \sqrt{3}}{4}=\frac{12 \sqrt{3}}{4}=3 \sqrt{3}$ (м2)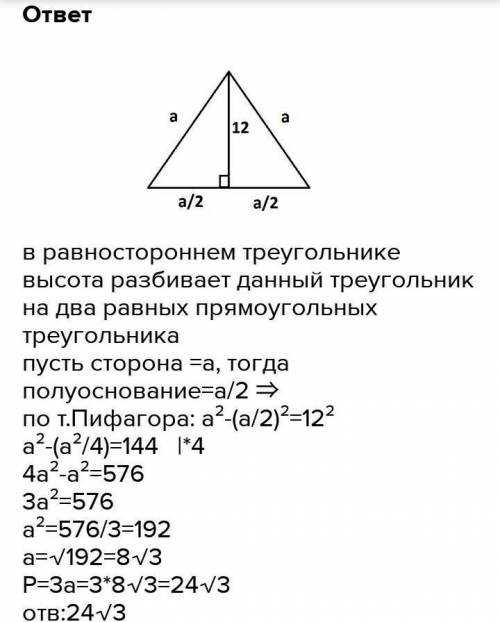 Тогда Sмвк = 6 см. кв.
Тогда Sмвк = 6 см. кв.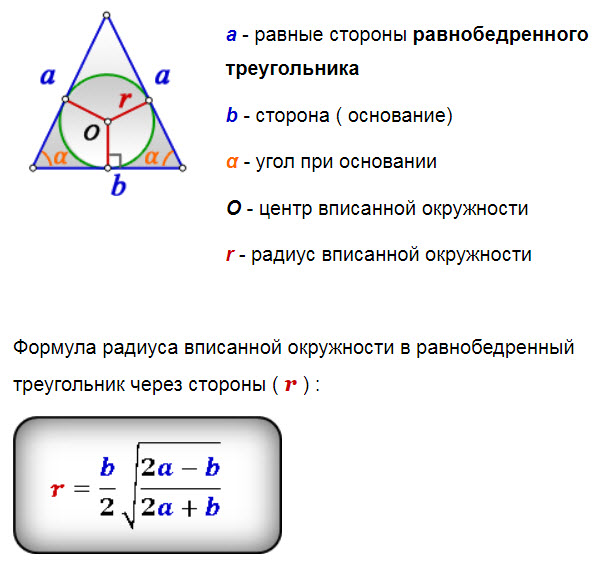
 Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС.
Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС. Тогда:
Тогда: 2√3/4?
2√3/4?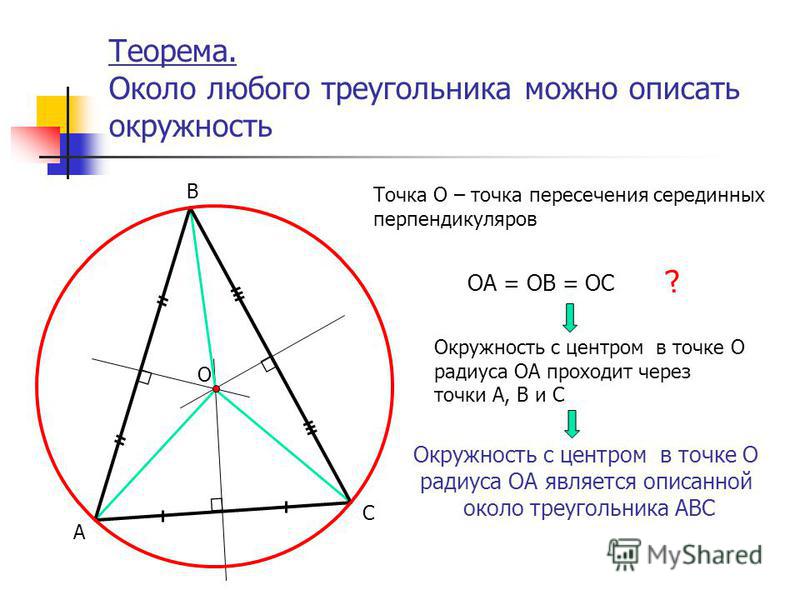
 кв.
кв.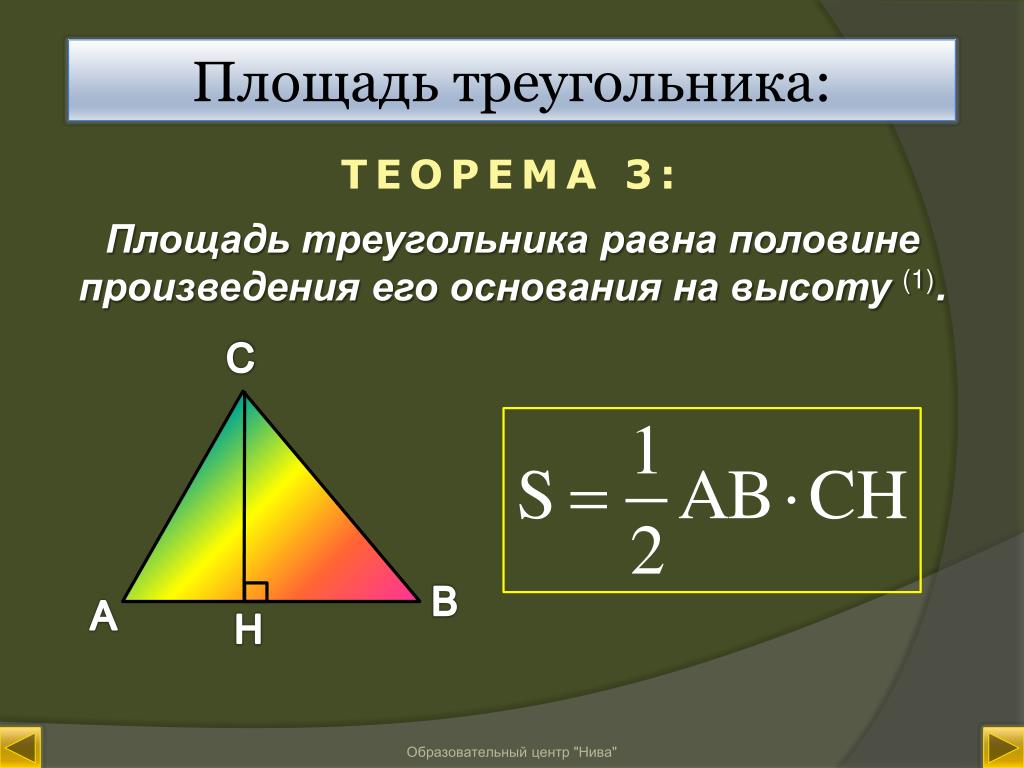
 и 12 см.?
и 12 см.? ?
?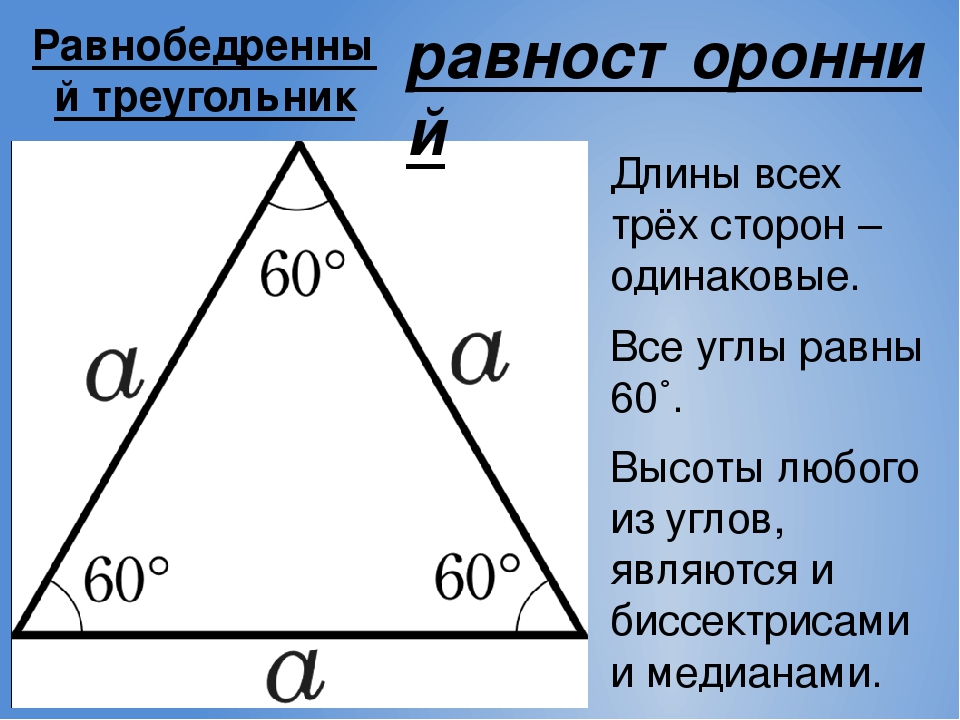
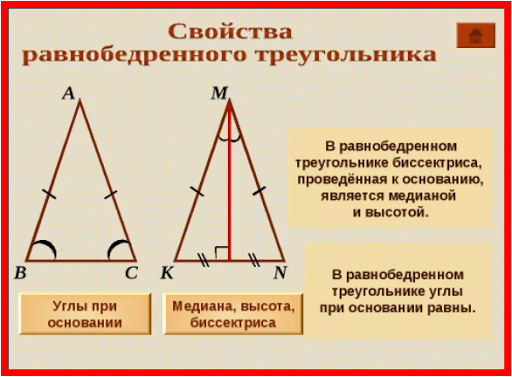 кв., его медиана = a√3/2 см.
кв., его медиана = a√3/2 см. кв.
кв.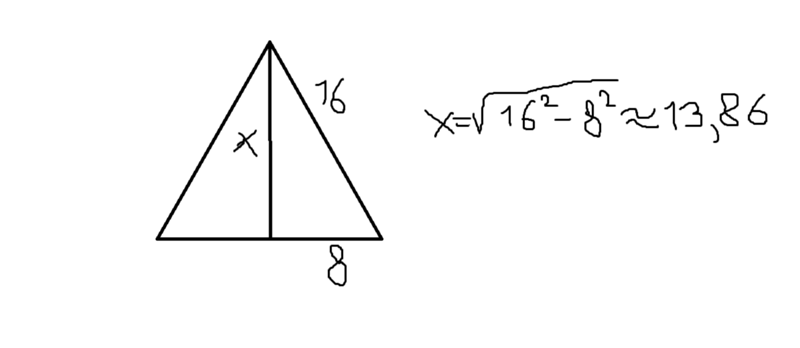

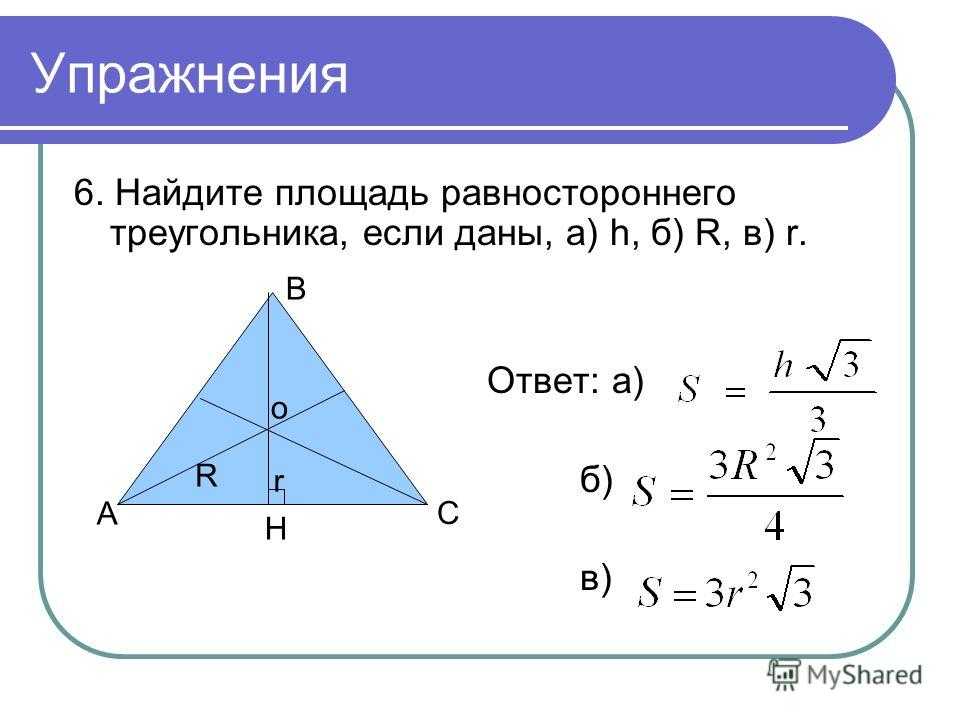 Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.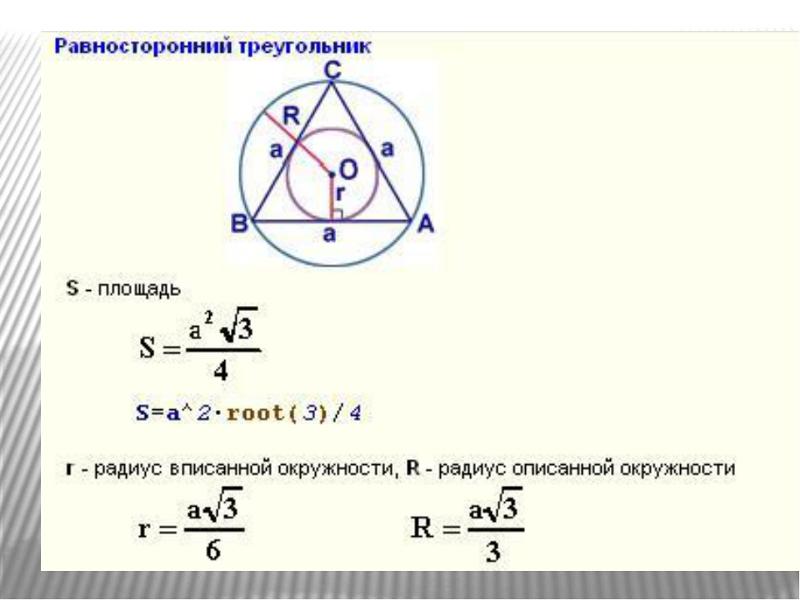 Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.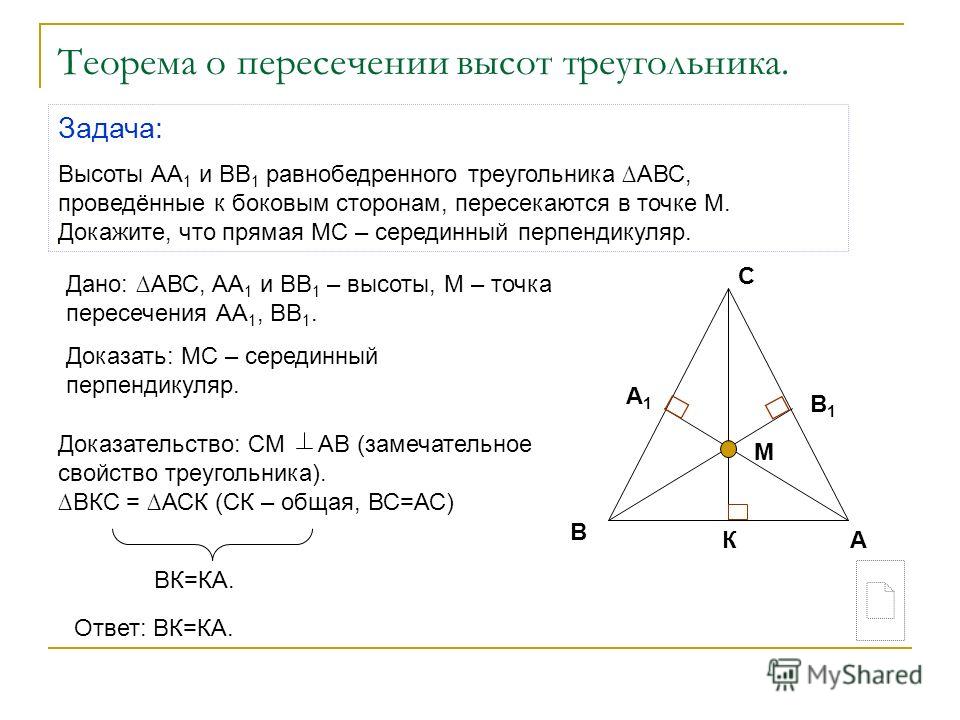
 Это одна из самых фундаментальных геометрических форм. Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны, тем самым делящий эту сторону пополам. Для каждого треугольника есть три медианы, по одной из каждой вершины.
Это одна из самых фундаментальных геометрических форм. Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны, тем самым делящий эту сторону пополам. Для каждого треугольника есть три медианы, по одной из каждой вершины.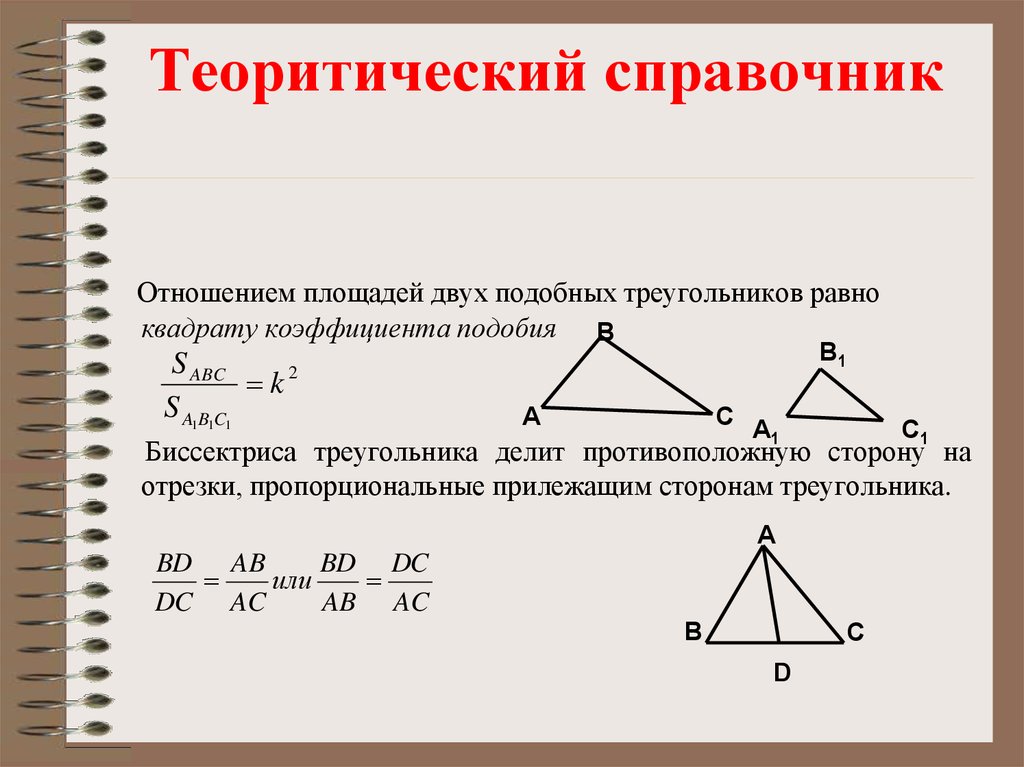
 Итак, \(D\) и \(E\) являются серединами на \(PQ\) и \(PR\) соответственно.
Итак, \(D\) и \(E\) являются серединами на \(PQ\) и \(PR\) соответственно.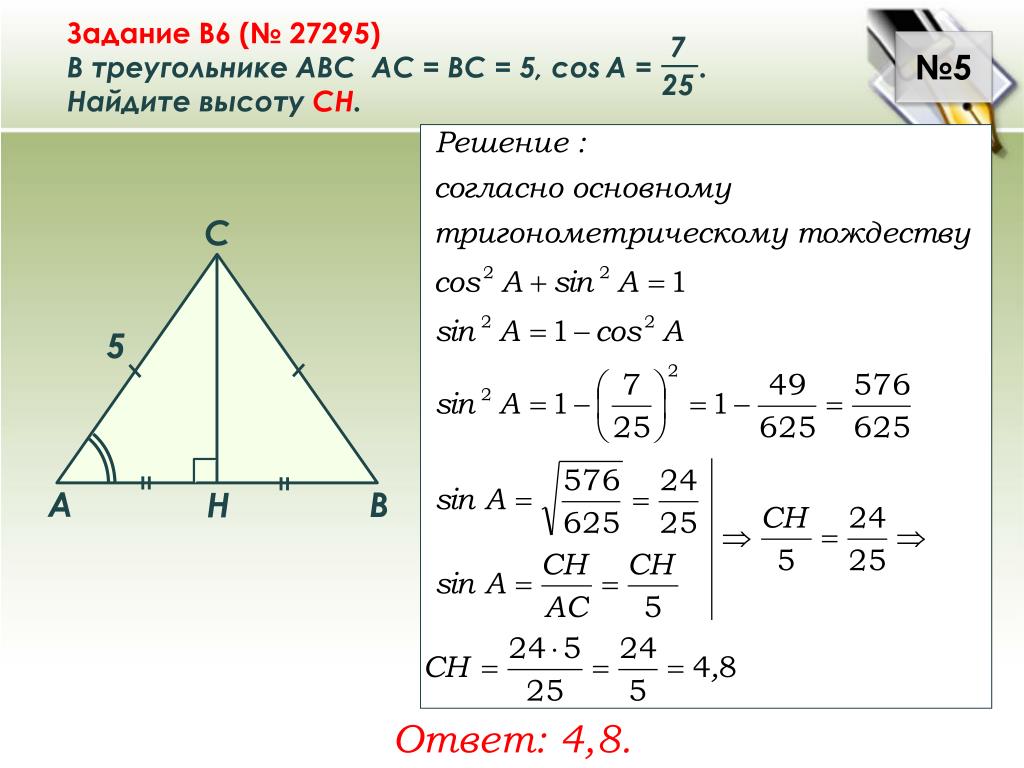
 Три медианы делят треугольник на \(6\) меньших треугольников одинаковой площади.
Три медианы делят треугольник на \(6\) меньших треугольников одинаковой площади.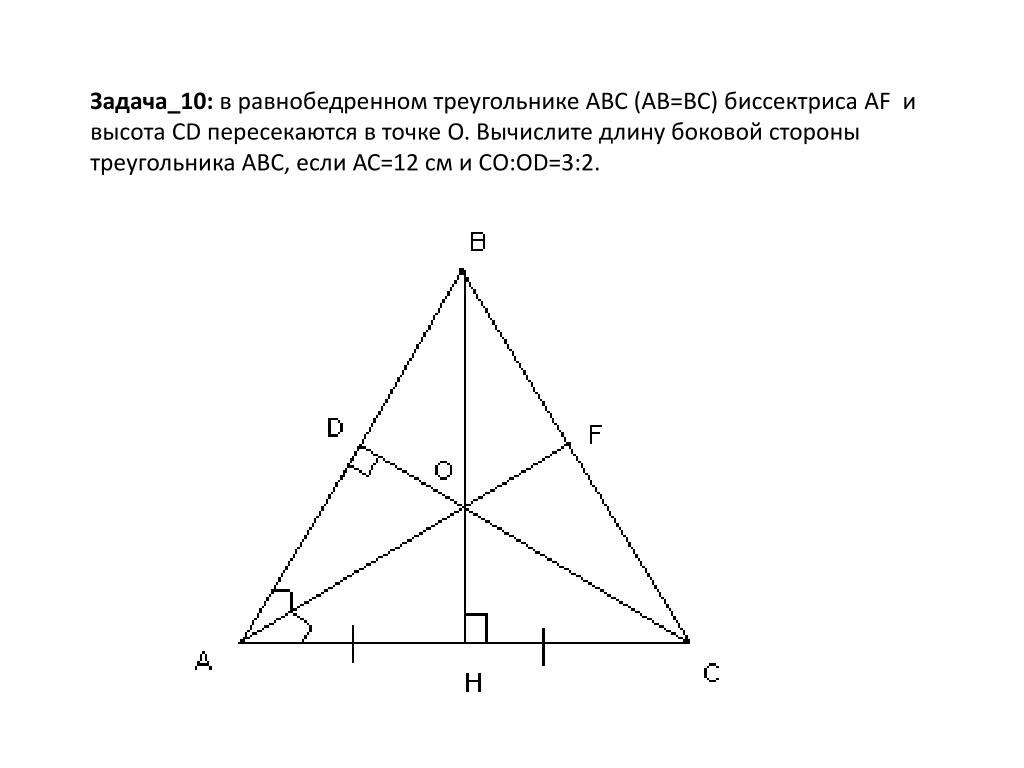

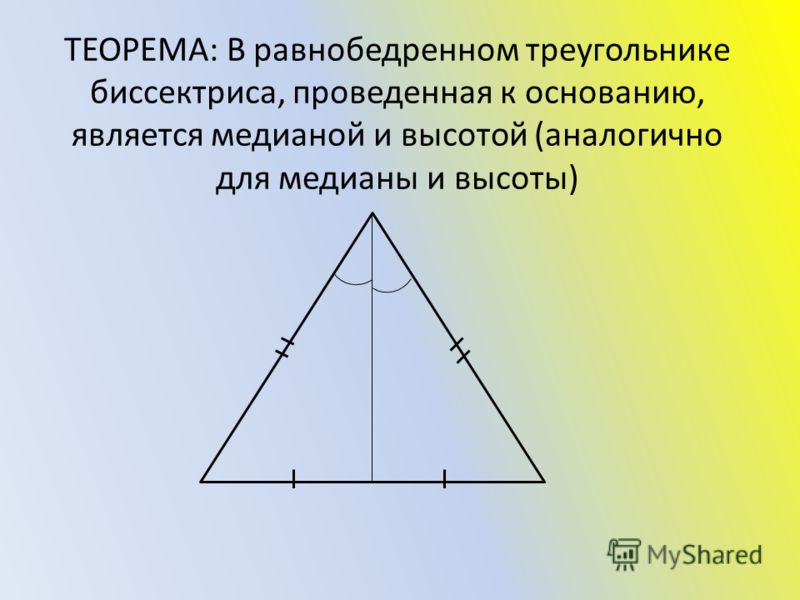 Докажите, что \(\Delta BED = \frac{1}{4}\Delta ABC\)
Докажите, что \(\Delta BED = \frac{1}{4}\Delta ABC\)  Определить длину \(MR\).
Определить длину \(MR\). 


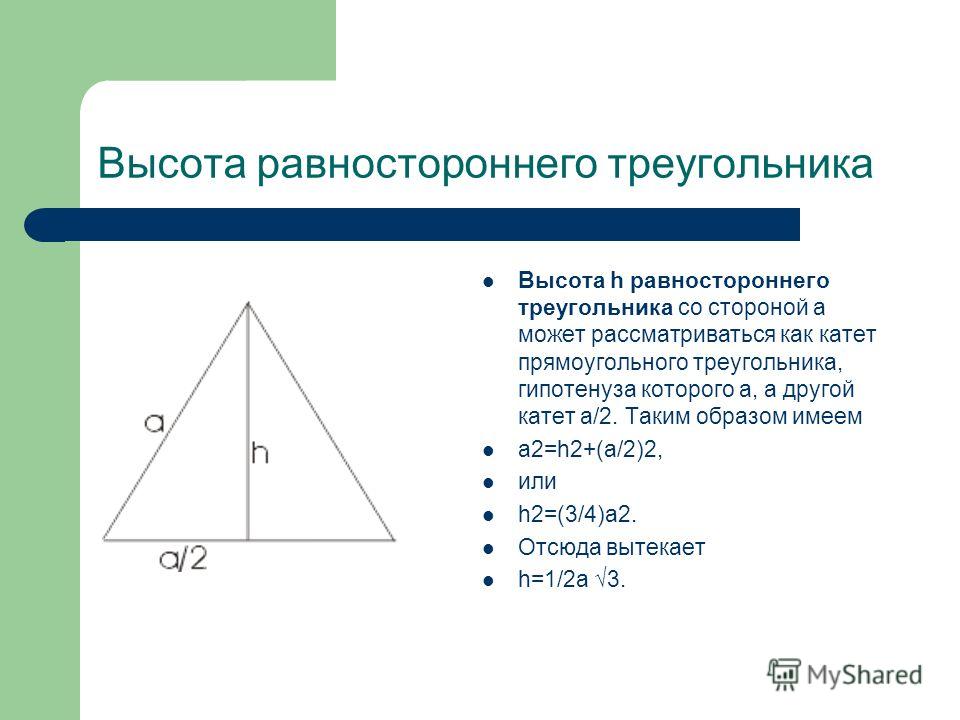 3: 92}}}{4}} \)
3: 92}}}{4}} \)  Если у вас есть какие-либо сомнения, вопросы или предложения относительно этой статьи, не стесняйтесь спрашивать нас в разделе комментариев, и мы будем более чем рады помочь вам. Приятного обучения!
Если у вас есть какие-либо сомнения, вопросы или предложения относительно этой статьи, не стесняйтесь спрашивать нас в разделе комментариев, и мы будем более чем рады помочь вам. Приятного обучения! 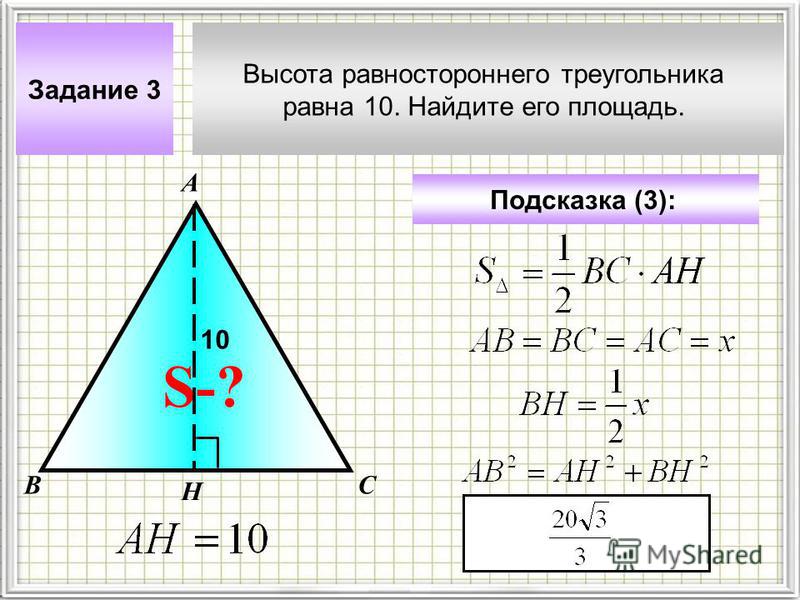 Однако, это не всегда возможно. 9{\ circ} 60∘.
Однако, это не всегда возможно. 9{\ circ} 60∘.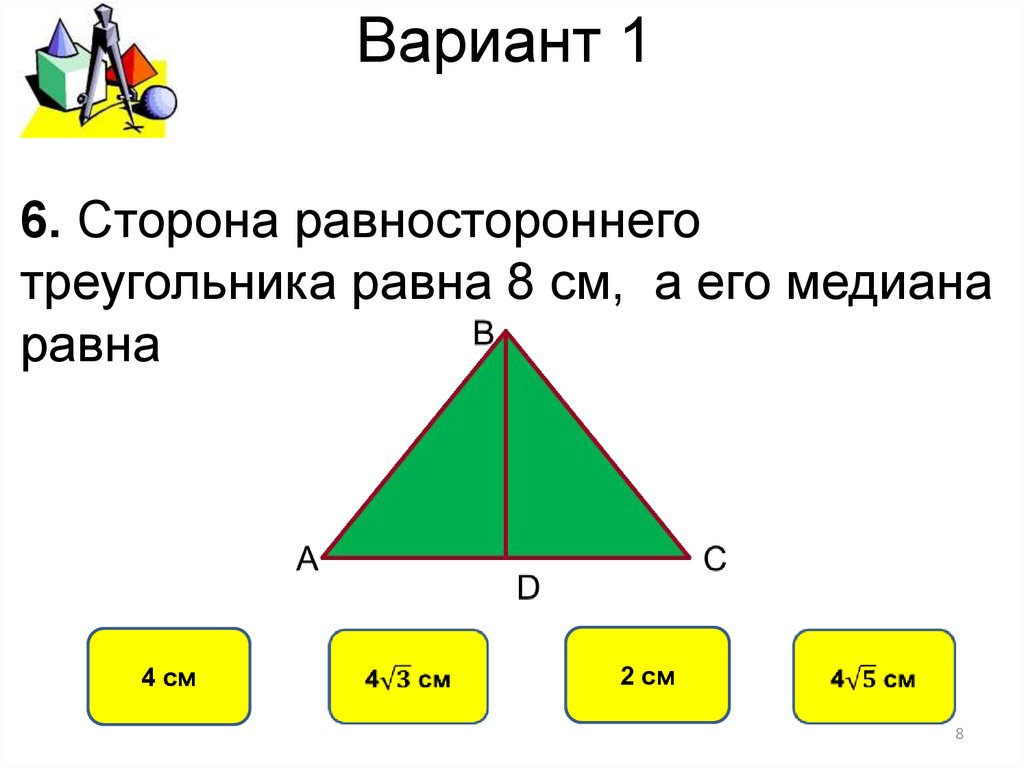 92\sqrt{3}}{4}4s23.
92\sqrt{3}}{4}4s23. 2\sqrt{3}} {2}6⋅4с23=23с23.
2\sqrt{3}} {2}6⋅4с23=23с23.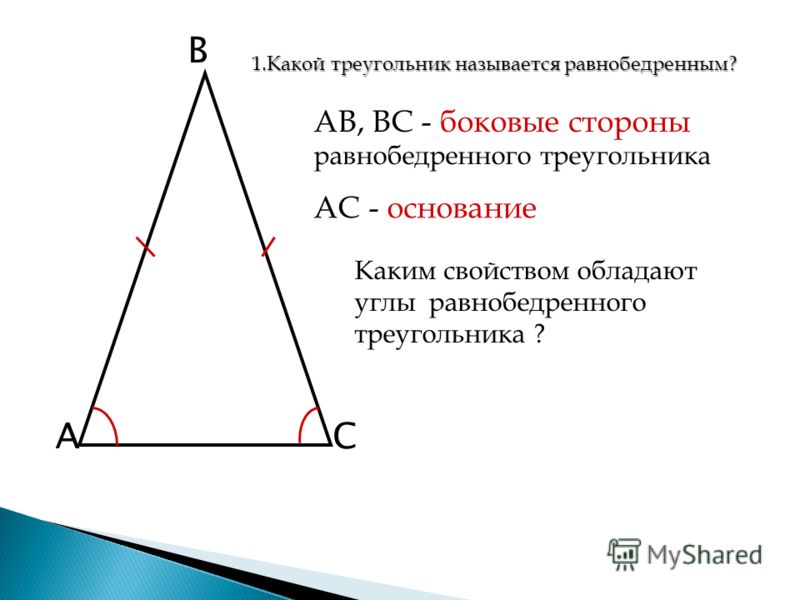
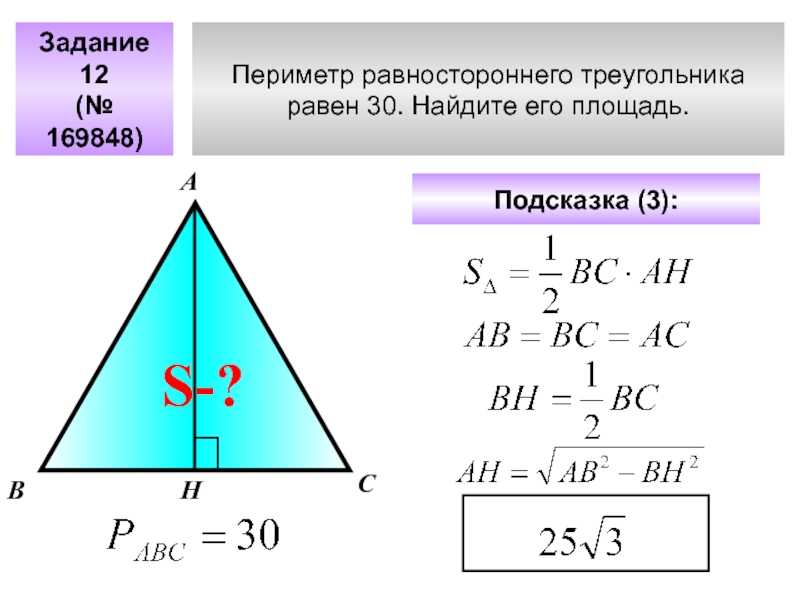

 org/wiki/properties-of-equilateral-triangles/
org/wiki/properties-of-equilateral-triangles/ Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник  Это самый простой правильный многоугольник (многоугольник с равными сторонами и углами). Введите одно значение и выберите количество знаков после запятой. Затем нажмите Рассчитать.
Это самый простой правильный многоугольник (многоугольник с равными сторонами и углами). Введите одно значение и выберите количество знаков после запятой. Затем нажмите Рассчитать. de Веб-проекты | Онлайн калькуляторы
de Веб-проекты | Онлайн калькуляторы
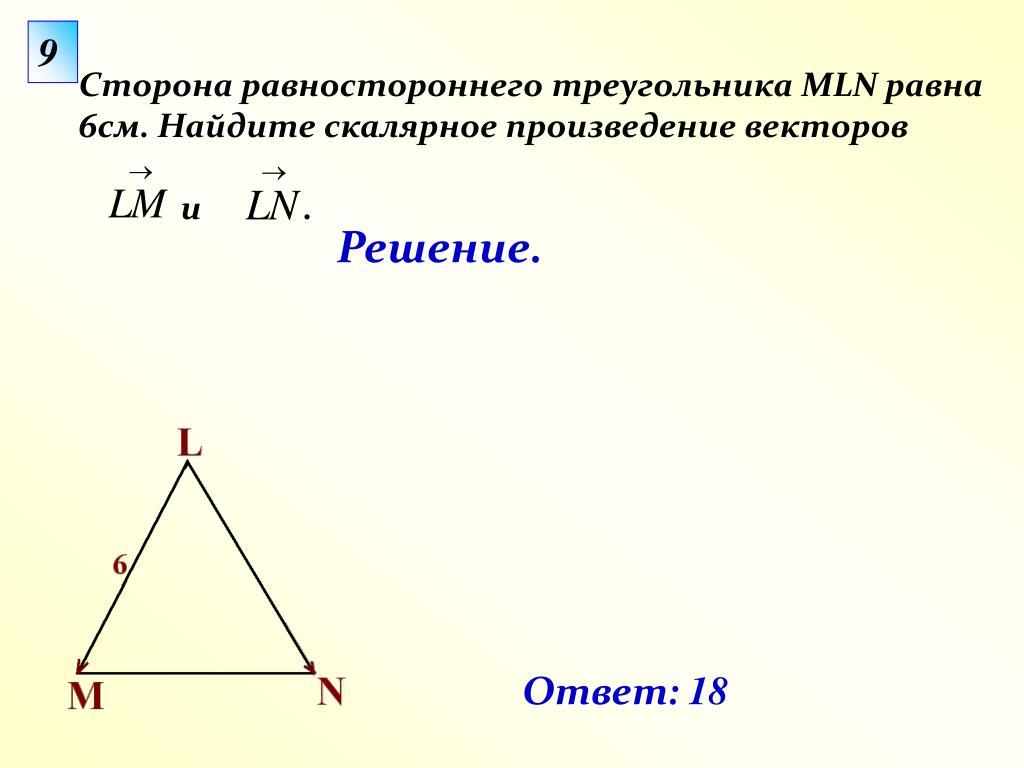
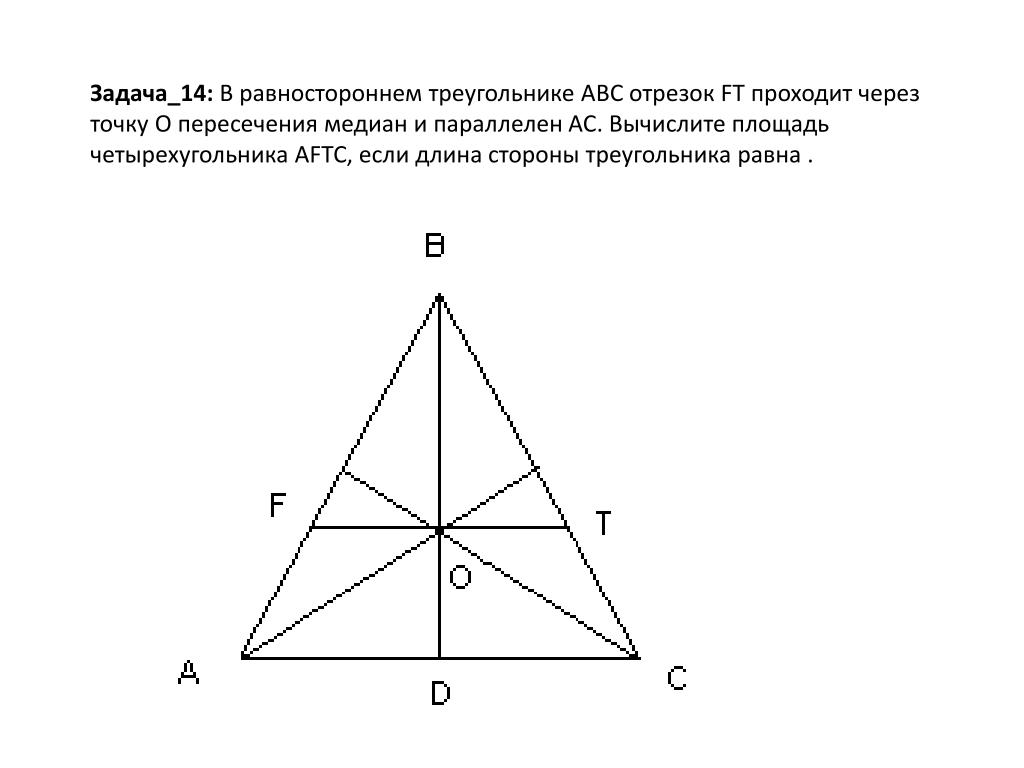
 В чем основная разница между высотой и медианой треугольника? ( 1 балл )
В чем основная разница между высотой и медианой треугольника? ( 1 балл )  Эта точка называется ортоцентром треугольника.
Эта точка называется ортоцентром треугольника. ( 3 балла )
( 3 балла )  В треугольнике DEF DE = EF = ED. Если бы DE было равно 12 см, какой была бы высота этого треугольника? ( 4 балла )
В треугольнике DEF DE = EF = ED. Если бы DE было равно 12 см, какой была бы высота этого треугольника? ( 4 балла ) 
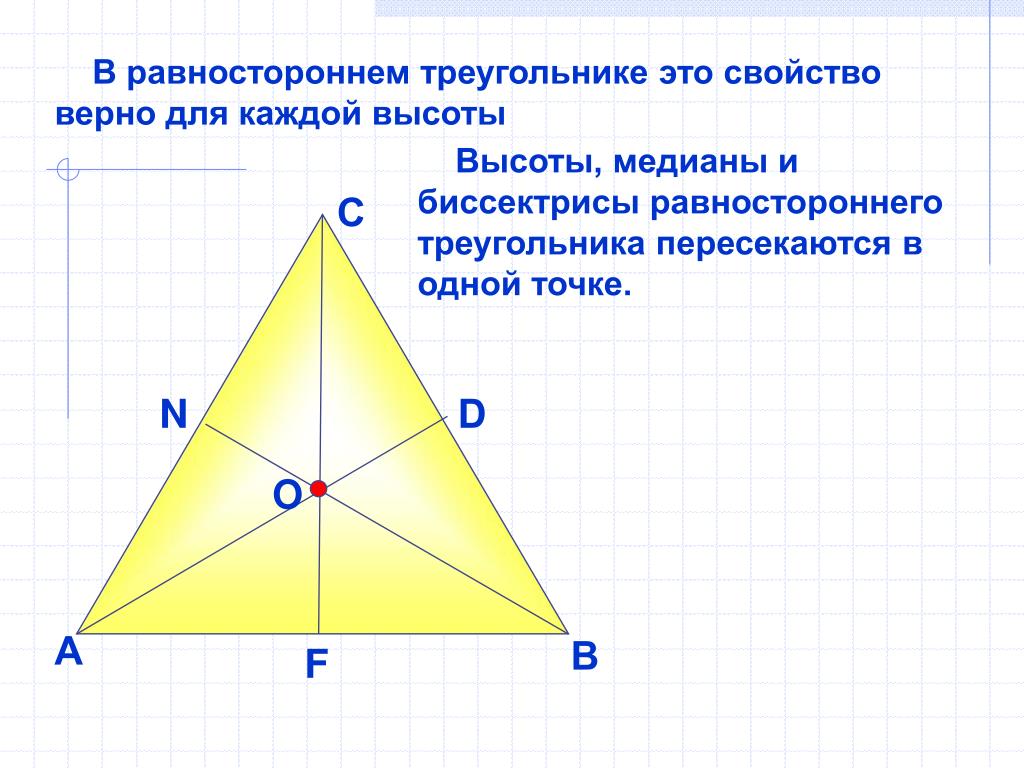
 В треугольнике 3 медианы. Медиана также может быть определена как линия от середины стороны до противоположного внутреннего угла треугольника . Медианы совпадают в центроиде.
В треугольнике 3 медианы. Медиана также может быть определена как линия от середины стороны до противоположного внутреннего угла треугольника . Медианы совпадают в центроиде.
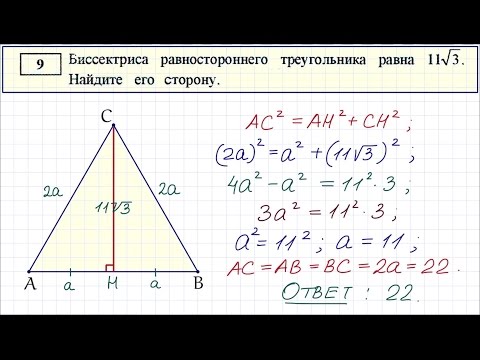 Перпендикуляр от вершины к противоположной стороне называется высотой . Прямая, проходящая через середину отрезка и перпендикулярная отрезку, называется биссектрисой отрезка.
Перпендикуляр от вершины к противоположной стороне называется высотой . Прямая, проходящая через середину отрезка и перпендикулярная отрезку, называется биссектрисой отрезка.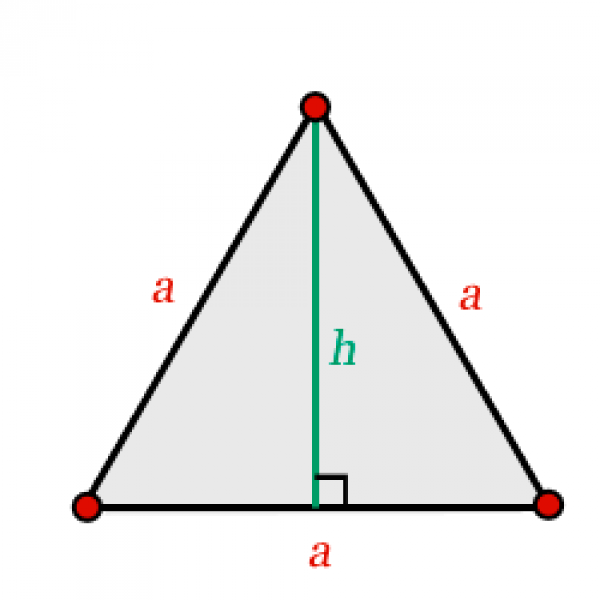
 По определению, прямоугольный треугольник — это треугольник, содержащий прямой угол, где прямой…
По определению, прямоугольный треугольник — это треугольник, содержащий прямой угол, где прямой…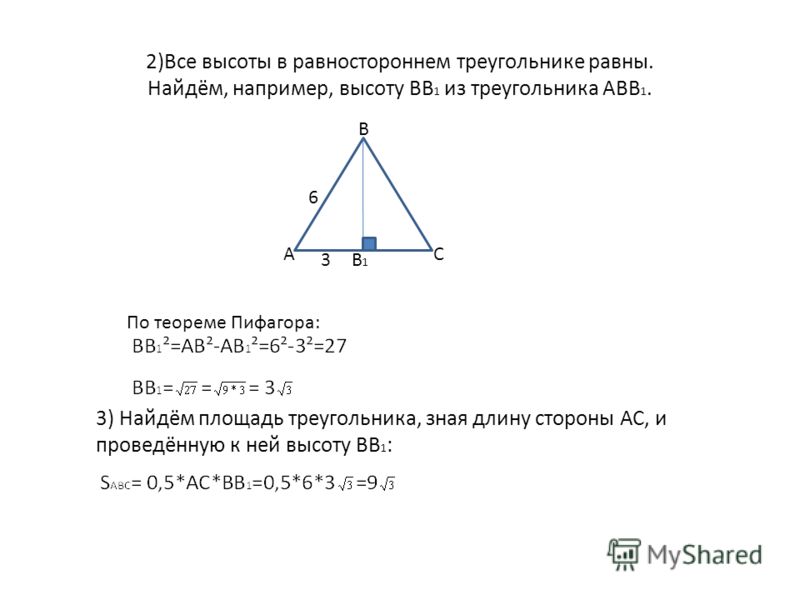 У треугольника ровно 3 стороны, а сумма внутренних углов равна 180°. Итак, если треугольник имеет два прямых угла, третий угол должен быть равен 0 градусов, что означает, что третья сторона будет пересекаться с другой стороной.
У треугольника ровно 3 стороны, а сумма внутренних углов равна 180°. Итак, если треугольник имеет два прямых угла, третий угол должен быть равен 0 градусов, что означает, что третья сторона будет пересекаться с другой стороной. е. могут быть ошибками измерения/транскрипции.
е. могут быть ошибками измерения/транскрипции. 0548 то свойство, что его длина равна половине длины гипотенузы .
0548 то свойство, что его длина равна половине длины гипотенузы .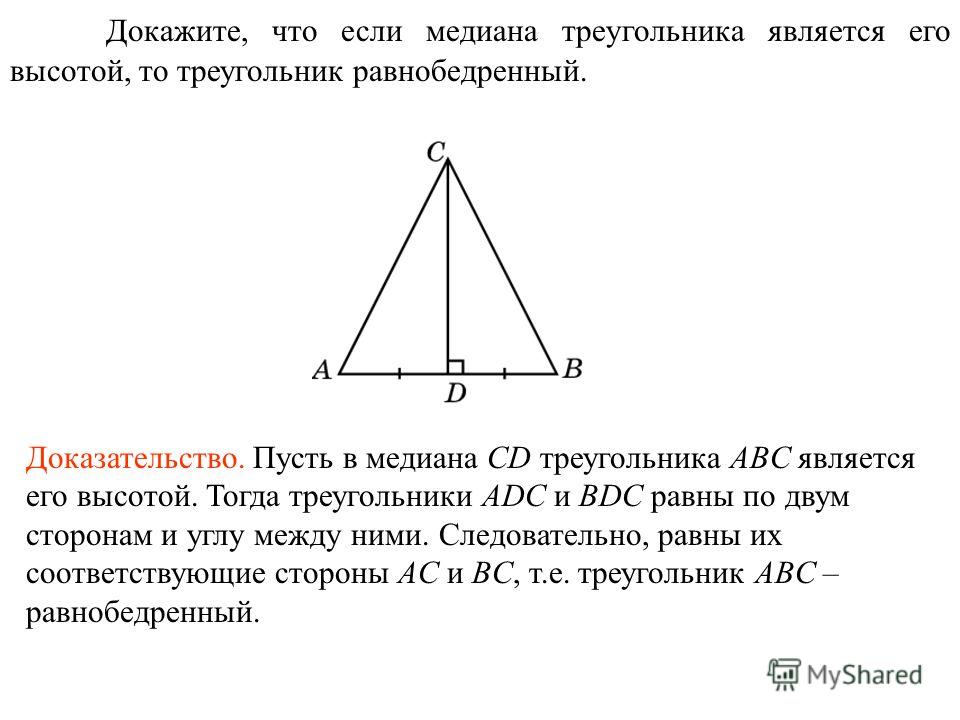 рисунок). Длина стороны (основания) в 2 раза больше, а высота равна . Площадь треугольника можно рассчитать с помощью следующего уравнения:
рисунок). Длина стороны (основания) в 2 раза больше, а высота равна . Площадь треугольника можно рассчитать с помощью следующего уравнения: Чтобы найти длину одной стороны, нам нужно разделить периметр на :
Чтобы найти длину одной стороны, нам нужно разделить периметр на :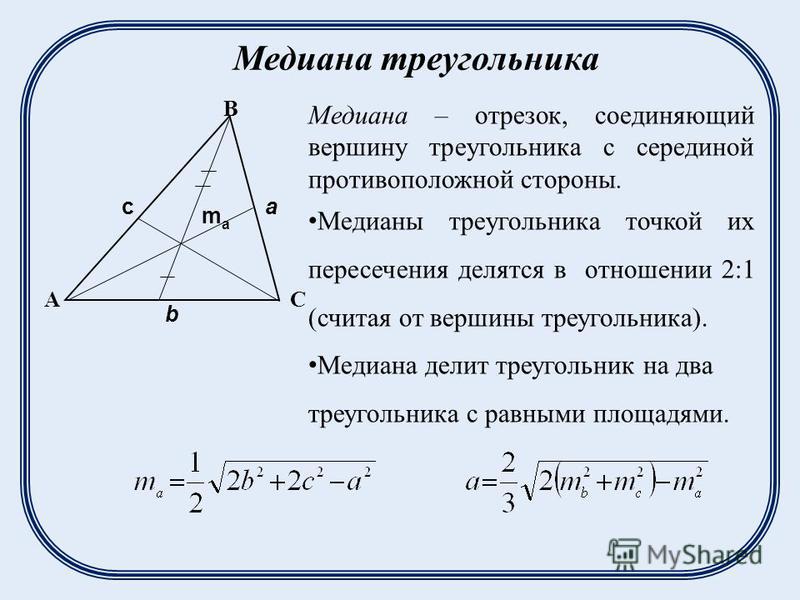


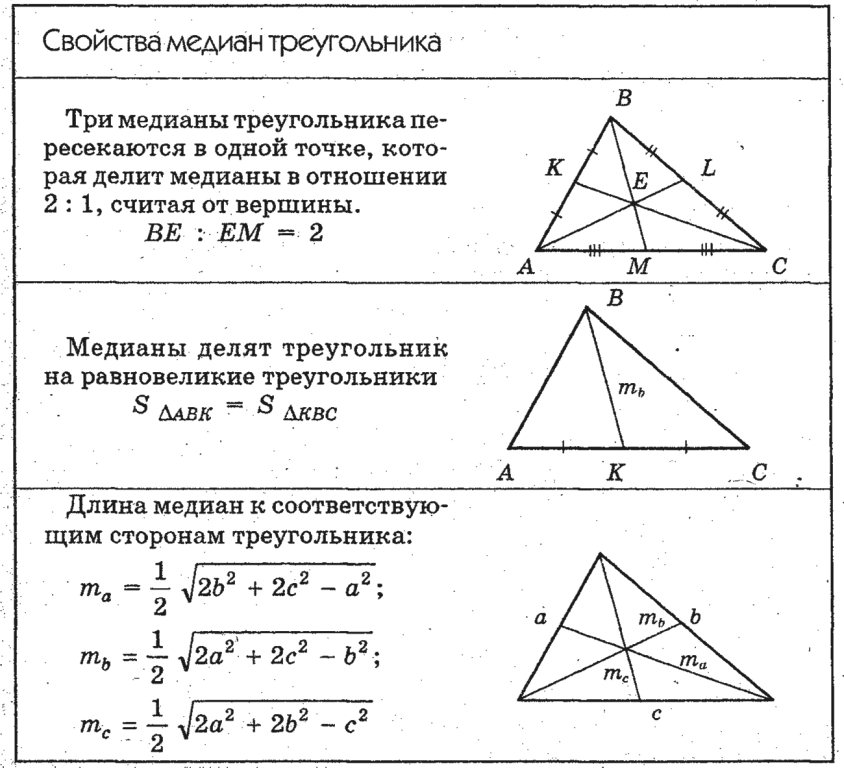
 Стороны, которые составляют периметр, выделены красным цветом.
Стороны, которые составляют периметр, выделены красным цветом.
