Перевод обыкновенной дроби в десятичную и наоборот ⋆ СПАДИЛО
теория по математике 🎲 числа и вычисления
При решении различных вычислительных заданий требуется произвести перевод десятичной дроби в обыкновенную или наоборот. В частности, в бланках ответов первой части ОГЭ (и ЕГЭ) нельзя записывать обыкновенную дробь, так как поле для этой дроби просто не существует.
Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель.
Как перевести обыкновенную дробь в конечную десятичную дробь?Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель (устно или в столбик).
Пример №1. ½ = 0,5 так как 1:2=0,5
Пример №2. ¾ = 0,75 так как 3:4=0,75
Пример №3. Так как 18:25=0,72, то
Если дана смешанная дробь, то целая часть уже есть, делим числитель на знаменатель и добавляем в часть после запятой. Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель. Строгого правила для способа выполнения данного действия нет.
Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель. Строгого правила для способа выполнения данного действия нет.
Пример №4.
здесь целая часть 14 уже есть, пишем ее и ставим запятую. Затем делим 3 на 50 и получаем 0,06. Приписываем десятичную часть 06 после запятой к числу 14 и получаем 14,06.
Пример №5.
в данном случае сначала перевели смешанное число в неправильную дробь (знаменатель умножается на целую часть и прибавляется числитель – это число записывается в числитель неправильной дроби), а затем разделили числитель 703 на знаменатель 50 и получили 14,06.
Как перевести десятичную дробь (конечную) в обыкновенную?Чтобы перевести десятичную дробь в обыкновенную, нужно в числитель записать цифры из десятичной части дроби (которые стоят после запятой), а в знаменателе написать столько нулей, сколько цифр получилось в числителе. Затем, по возможности сократить данную дробь.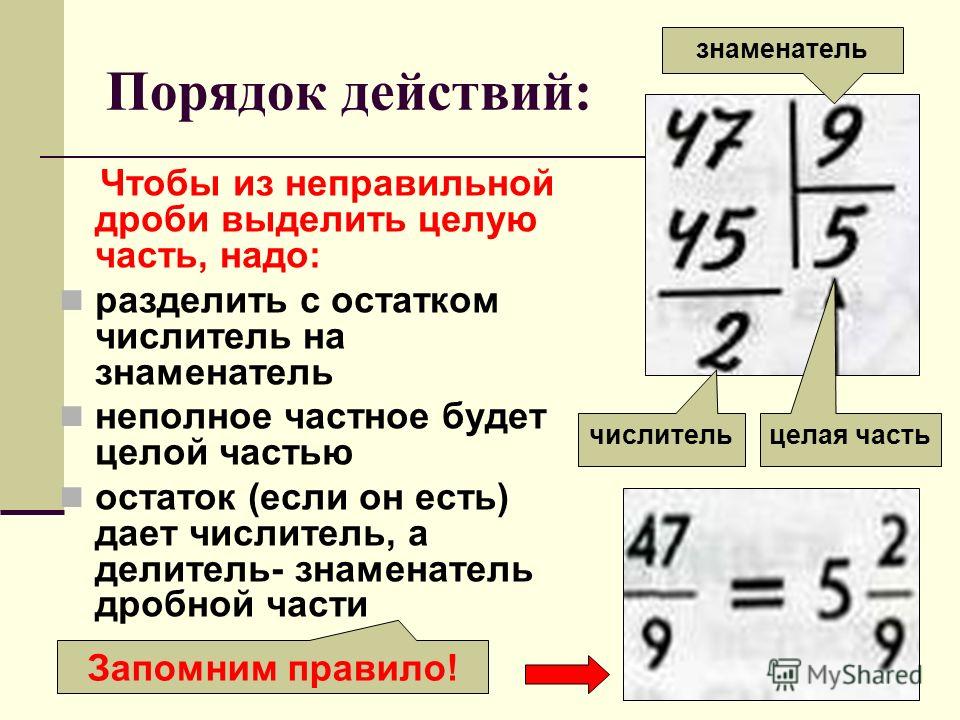
Пример №6.
целая часть равна нулю, нуль перед обыкновенной дробью не пишется, 17 записали в числитель, а 100 в знаменатель, так как в числе 17 две цифры, как у сотни два нуля.
Пример №7.
целая часть равна 5, поэтому записали ее перед дробью, 34 пошло в числитель, а знаменатель соответственно равен 100 (по количеству цифр в числе 34). Здесь видно, что получилась сократимая дробь, так как числитель и знаменатель оба делятся на 2. Выполняем сокращение дробной части и получаем новую дробь
Задание 7OM21R На координатной прямой отмечены точки А, В, С и D. Одна из них соответствует числу 10713… Какая это точка?- точка А
- точка В
- точка С
- точка D
Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0705oОдно из чисел отмечено на прямой точкой.
Какое это число?
Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат.
Итак, выделяем целые части:
Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.
У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0704oНа координатной прямой отмечена точка А:
Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?
- 181/16
- √37
- 0,6
- 4
Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду.
Оцениваем 181/16 – можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.
Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.
Оцениваем √37 – самое близкое значение, из которого вычисляется квадратный корень – это 36, значит √37 – это 6 и что-то еще, что вычислять нам не обязательно. Данное значение нам подходит, так как лежит чуть правее середины отрезка 0-10, как и точка А.
Посмотрим на вариант 0,6 – это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет.
Вариант с ответом 4 также не подойдет по вышеуказанной причине.
Ответ: √37pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0701oКакое из следующих чисел заключено между числами 8/3 и 11/4 ?
- 2,7
- 2,8
- 2,9
- 3
В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:
Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:
Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0604o Найдите значение выражения: ¼ + 0,07К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
0,25 + 0,07 = 0,32
Ответ: 0,32pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM0601o Найдите значение выражения:Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
4,5 • 2,5
Можно произвести вычисления в столбик, тогда получим:
4,5 • 2,5 = 11,25
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Алла Василевская | Просмотров: 7. 4k | Оценить:
4k | Оценить:
Как перевести десятичную дробь в обыкновенную: 3 способа
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
\[0,75=\frac{3}{4};\quad 1,33=1\frac{33}{100};\quad -7,41=-7\frac{41}{100}\]
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
- Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу. При этом знак исходного числа также помещается в числитель. Например:
\[0,75=\frac{0,75}{1};\quad 1,33=\frac{1,33}{1};\quad -7,41=\frac{-7,41}{1}\]
- Умножаем числитель и знаменатель полученной дроби на 10 до тех пор, пока в числителе не исчезнет запятая. Напомню: при каждом умножении на 10 запятая сдвигается вправо на один знак. Разумеется, поскольку знаменатель тоже умножается, там вместо числа 1 будут появляться 10, 100 и т.д. Примеры: Алгоритм перехода к обычным дробям
- Наконец, сокращаем полученную дробь по стандартной схеме: делим числитель и знаменатель на те числа, которым они кратны. Например, в первом примере 0,75=75/100, при этом и 75, и 100 делятся на 25.
 Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)
Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:
Примеры перехода от десятичной записи дробей к обычнойКонечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.
Более быстрый способ
В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
- Посчитать, сколько цифр стоит после запятой.
 {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.Наконец, последний пример:
\[1,88=\frac{188}{100}=\frac{47}{25}=\frac{25+22}{25}=1\frac{22}{25}\]
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88.
 Она легко преобразуется:
Она легко преобразуется:\[0,88=\frac{88}{100}=\frac{22}{25}\]
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
\[\frac{22}{25}\to 1\frac{22}{25}\]
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
\[\begin{align}& 2,15\to 0,15=\frac{15}{100}=\frac{3}{20}\to 2\frac{3}{20}; \\& 13,8\to 0,8=\frac{8}{10}=\frac{4}{5}\to 13\frac{4}{5}. \\\end{align}\]
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных».
 Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Так или иначе, ключевое слово — «тысячных», т.е. 1000.Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
\[0,004=4:1000=\frac{4}{1000}=\frac{1}{250}\]
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
\[2,5=2\frac{5}{10}=2\frac{1}{2}\]
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
\[1,125=1\frac{125}{1000}=1\frac{1}{8}\]
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 103, а 10 = 2 ∙ 5, поэтому
\[\begin{align}& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end{align}\]
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.

На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».
Смотрите также:
- Сравнение дробей
- Периодические десятичные дроби
- Тригонометрические функции
- Что такое числовая дробь
- Задачи на проценты считаем проценты с помощью формулы
- Более сложные задачи на производительность
Перевод в неправильную дробь примеры. Как сделать из неправильной дроби правильную
Нехитрые математические правила и приемы, если они не используются постоянно, забываются быстрее всего. Еще быстрее уходят из памяти термины.
Одно из таких простых действий – преобразование неправильной дроби в правильную или, по-другому – смешанную.
Неправильная дробь
Неправильной называется дробь, у которой числитель (число над дробной чертой) больше или равно знаменателю (число под чертой). Такая дробь получается при сложении дробей или умножении дроби на целое число.
 По правилам математики такую дробь обязательно нужно превратить в правильную.
По правилам математики такую дробь обязательно нужно превратить в правильную.Правильная дробь
Логично предположить, что правильными называются все остальные дроби. Строгое определение – правильной называется дробь, у которой числитель меньше знаменателя. Дробь, у которой есть целая часть иногда называется смешанной.
Преобразование неправильной дроби в правильную
- Первый случай: числитель и знаменатель равны друг другу. В результате преобразования любой такой дроби получится единица. Неважно, три третьих это или сто двадцать пять сто двадцать пятых. По сути, такая дробь обозначает действие деления числа на само себя.
- Второй случай: числитель больше знаменателя. Здесь нужно вспомнить метод деления чисел с остатком.
Для этого нужно найти самое близкое к значению числителя число, которое делится на знаменатель без остатка. Например, у вас есть дробь девятнадцать третьих. Наиболее близкое число, которое можно разделить на три – это восемнадцать. Получится шесть. Теперь отнимите от числителя полученное число. Получим единицу. Это и есть остаток. Запишите результат преобразования: шесть целых и одна треть.
Получится шесть. Теперь отнимите от числителя полученное число. Получим единицу. Это и есть остаток. Запишите результат преобразования: шесть целых и одна треть.
Но прежде чем приводить дробь к правильному виду, нужно проверить, можно ли её сократить.
Сокращение дроби возможно, если у числителя и знаменателя есть общий делитель. То есть такое число, на которое и то, и другое делится без остатка. Если таких делителей несколько, нужно найти наибольший.
Например, у всех четных чисел такой общий делитель – двойка. А у дроби шестнадцатых двенадцатых, есть еще один общий делитель – четверка. Это наибольший делитель. Разделите числитель и знаменатель на четыре. Результат сокращения: четыре третьих. А теперь, в качестве тренировки, преобразуйте эту дробь в правильную.Инструкция
Найдите числитель результирующей дроби, который должен остаться после выделения из нее целой части. Для этого умножьте вычисленную целую часть (20) на знаменатель (23) и отнимите результат (20*23=460) от числителя исходной дроби (475).
 Эту операцию тоже можно проделать в уме, столбиком или с помощью калькулятора (475-460=15).
Эту операцию тоже можно проделать в уме, столбиком или с помощью калькулятора (475-460=15).Соберите вычисленные данные в одну запись в форме смешанной дроби — сначала напишите целую часть (20), затем , потом поставьте правильную с числителем (15) и (23). Для использованного в качестве образца примера преобразование неправильной дроби в правильную (точнее — в смешанную) можно записать так: 475/23=20 15/23.
Часто приходится делить на части что-либо, и те части, на которые поделено целое, являются дробями. В математике существует несколько видов дробей: десятичные (0,1; 2,5 и так далее) и обыкновенные (1/3; 5/9; 67/89 и так далее). Именно обыкновенные дроби бывают правильными и неправильными.
Инструкция
Обыкновенная дробь называется правильной, если число, стоящее в ее числителе, меньше числа, стоящего в знаменателе. Сокращение дробей производится для работы с наименее большими числами.
Дробь представляет собой число, которое состоит из одной или нескольких долей единицы.
 В математике существует три вида дробей: обыкновенные, смешанные и десятичные.
В математике существует три вида дробей: обыкновенные, смешанные и десятичные.
Обыкновенные дроби
Обыкновенная дробь записывается как соотношение, в котором в числителе отражается, сколько взято частей от числа, а знаменатель показывает, на сколько частей разделена единица. Если числитель меньше знаменателя, то перед нами правильная дробь.Например: ½, 3/5, 8/9.
Если числитель равен знаменателю или больше его, то мы имеем дело с неправильной дробью. Например: 5/5, 9/4, 5/2 При делении числителя может получиться конечное число. Например, 40/8 = 5. Следовательно, любое целое число может быть записано в виде обыкновенной неправильной дроби или ряда таких дробей. Рассмотрим записи одного и того же числа в виде ряда различных .
- Смешанные дроби
В общем виде смешанная дробь может быть представлена формулой:
Таким образом, смешанная дробь записывается как целое число и обыкновенная правильная дробь, а под такой записью понимают сумму целого и его дробной части.

- Десятичные дроби
Десятичная дробь – это особая разновидность дроби, у которой знаменатель может быть представлен как степень числа 10. Существуют бесконечные и конечные десятичные дроби. При записи этой разновидности дроби сначала указывается целая часть, затем через разделитель (точку или запятую) фиксируется дробная часть.
Запись дробной части всегда определяется ее размерностью. Десятичная запись выглядит следующим образом:
Правила перевода между различными видами дробей
- Перевод смешанной дроби в обыкновенную
Смешанную дробь можно перевести только в неправильную. Для перевода необходимо целую часть привести и тому же знаменателю, что и дробную. В общем виде это будет выглядеть следующим образом:
Рассмотрим использование этого правила на конкретных примерах:- Перевод обыкновенной дроби в смешанную
Неправильную обыкновенную дробь можно превратить в смешанную путем простого деления, в результате которого находится целая часть и остаток (дробная часть).

Для примера переведем дробь 439/31 в смешанную:
- Перевод обыкновенной дроби
В некоторых случаях перевести дробь в десятичную достаточно просто. В этом случае применяется основное свойство дроби, числитель и знаменатель умножаются на одно и то же числу, для того, чтобы привести делитель к степени числа 10.
Например:
В некоторых случаях может понадобиться найти частное путем деления уголком или с помощью калькулятора. А некоторые дроби невозможно привести к конечной десятичной дроби. Например, дробь 1/3 при делении никогда не даст конечный результат.
Перевести неправильную дробь в правильную можно путем деления числителя такой дроби на знаменатель — таким образом мы получим правильную дробь. По другому неправильную дробь можно записать в виде простого десятичного числа.
неправильная дробь — дробь, у которой числитель больше знаменателя. правильная — та дробь, у которой, соответственно, числитель меньше знаменателя. неправильную дробь превратить в правильную никак нельзя, но зато ее можно представить в виде смешанного числа, состоящего из двух частей (одна часть будет целым числом, а другая — как раз правильной дробью).

например 5/2=2+1/2 (только пишут дробь обычно сразу после целого числа без знака quot;плюсquot;)
здесь нужно числитель неправильной дроби разделить на знаменатель. записываем целую часть от деления (в нашем случае 2). затем остаток от деления (то есть 1) записываем как числитель дроби, которую мы записываем рядом с двойкой.
Из школьного курса математики мы знаем. что неправильная дробь представляет собой дробь у которой числитель больше, чем ее знаменатель. Чтобы перевести ее в правильную дробь, нужно числитель такой дроби разделить на ее знаменатель. Все очень просто, таким образом она станет правильной, либо десятичной дробью.
Неправильная дробь например: 9/5 выделим у нее целую часть это будет: 1 4/5 теперь она немного похоже на правильную только с целой частью это единица.
Можно и превратить ее в десятичную дробь в нашем случае будет 1.8
Чтобы решить поставленную задачу, сначала нужно четко уяснить для себя, что такое правильная дробь, а что такое неправильная.

Начнем с того, что утверждение
верно далеко не для всех чисел на числовой оси.
числитель равен (-10), знаменатель равен (-4)
аналогичное утверждение
верно также не всегда
числитель равен 2, знаменатель равен (-3)
Неправильную дробь можно записать с помощью суммы целого числа и правильной дроби (смешанной дроби) и для этого нужно:
разделить числитель на знаменатель, полученное целое число записать в целой части, остаток в числителе, знаменатель оставить без изменений
в числителе (-15), в знаменателе 2, минус вынесем за пределы дроби — (15/2), 15 разделим на 2, целое число 7 ставим в целую часть дроби, остаток от деления 1 запишем в числителе, а знаменатель 2 оставим без изменений.
Для того чтобы преобразовать неправильную дробь в правильную для начала необходимо сказать:
У неправильной дроби числитель (верхнее число в дроби) больше знаменателя ил равна ему;
У правильной дроби все наоборот.
Процесс преобразования разберем на примере дроби 260/7:
1) Сначала делим 260 на 7, получаем число 37,14.
 .
.2) Число 37 будет стоять впереди дроби как целое число
3) Теперь 37 * 7 = 259
4) От числителя отнимаем получившееся число 260 — 259 = 1 — это число и будет в числители нашей правильной дроби.
5) При записи новой дроби знаменатель остается неизменной. В данном случае это 7. Правильная дробь будет выглядит следующим образом:
Проверка преобразованной дроби:
Целое число умножаем на знаменатель и прибавляем числитель 37 * 7 + 1 = 260.
Правильной дробью называется такая дробь, у которой знаменатель больше числителя. Это говорит о том, что эта дробь показывает какую-то часть целого. Например дробь 1/2 говорит о том что у нас есть половина например арбуза, а дробь 7/9 — что у нас осталось семь кусочков арбуза разрезанного на 9 частей. Две части кто-то съел.
Если же дробь неправильная, то есть числитель больше знаменателя, то совершенно непонятно, какая у нас часть целого, но разрезанного арбуза и сколько еще целых арбузов в наличии.
 Поэтому приходится перевести неправильную дробь в правильную. при этом мы получим какое-то целое число и остаток — именно правильную дробь.
Поэтому приходится перевести неправильную дробь в правильную. при этом мы получим какое-то целое число и остаток — именно правильную дробь.Для перевода делим числитель на знаменатель в столбик. Пример: 7/4. Семь на четыре дает единицу и остаток 3/4. Вот мы и перевели дробь в правильную — ответ 1 и 3/4.
Неправильной дробью называют такую дробь, у которой числитель больше знаменателя . Значит правильная дробь та, у которой числитель меньше знаменателя. Чтобы превратить неправильную дробь в правильную можно представить в виде десятичного числа. Например 17/8 можно записать так: 2,125. Или записать так: 2 1/8.
Правильной дробью принято считать такую, у которой знаменатель выше числителя. Для того чтобы неправильную дробь перевести в правильную, надо разделить числитель неправильной дроби на ее знаменатель, результатом будет число с остатком.
Например 4 целых и три одиннадцатых, мы 4 умножаем на 11 и +3 , потом мы делим на 11 , получается 44 +3 и делим на 11 , и получим дробь 47/11 .
 Неправильная дробь это когда есть целое число например 5,10 , то есть пять целых и 10/100 , пять мы умножаем 100 и +10 , получается 10/500 . Так же если например 6,6 , тут проще, 6 умножаем на 6 и +6 получается 12/6 , сокращаем на два, получается шесть третьих, шесть третьих мы сокращаем на три получается две первых, два делим на один получается два. То есть 6,6 =2.
Неправильная дробь это когда есть целое число например 5,10 , то есть пять целых и 10/100 , пять мы умножаем 100 и +10 , получается 10/500 . Так же если например 6,6 , тут проще, 6 умножаем на 6 и +6 получается 12/6 , сокращаем на два, получается шесть третьих, шесть третьих мы сокращаем на три получается две первых, два делим на один получается два. То есть 6,6 =2.Само слово — дробь означает, что число дробное, оно меньше целого (как минимум единицы).
Следовательно, необходимо выделить целое число из числителя. Например, число 30/4 — дробь неправильная, поскольку 30 больше, чем 4. Значит, нужно просто разделить 30 на 4 и получим число до запятой — 7, его то и ставим перед дробью. Умножим 7 на 4 и вычтем это число из 30 — получится 2 — оно будет в числителе дроби. Итог — 7 2/4, сокращаем — 7 1/2. В вашем примере, ответ — 2 3/4.
Для того необходимо чтслитель: на знаменатель.
То целое, что получилось — пишите в числитель. Знаменатель тот, что был. Когда поделите — записывайте в целую часть.

11:4=2 (3 остаток).
Получаем правил-ую дробь: 2 — целых 34
Чтобы сделать из неправильной дроби правильную, нужно выявить целые части и отнять их из неправильной дроби. В нашем случае неправильная дробь 11/4. Целых частей будет две (2). Вычитаем их и получаем правильную дробь: две целых три четвртых (2 целых 3/4).
Неправильную дробь, в нашем случае 11/4 нужно перевести в правильную, т.е. в этом случае смешанную дробь. Если по-простому, то дробь неправильная, потому что в ней помимо дроби есть и целое число. Это как стоит в холодильнике тортик непочатый, хоть и порезанный, а на столе — осталось несколько кусочков от второго. Когда говорим об 11/4, то мы уже не знаем о двух целых тортах, видим лишь одиннадцать крупных кусков. 11 разделили на 4, получили 2, а остаток 11-8=3. Итак, 2 целых 3/4, теперь дробь правильная, в ней числитель поменьше знаменателя будет, но смешанная, так как без целых единиц расчет не обошелся.
Чтобы из неправильной дроби сделать правильную, надо числитель разделить на знаменатель.
 Полученное целое число выносим перед дробью, а остаток вписываем в числитель. Знаменатель не изменяется.
Полученное целое число выносим перед дробью, а остаток вписываем в числитель. Знаменатель не изменяется.Например: дробь 11/4 — неправильная, где числитель равен 11, а знаменатель — 4.
Сначала 11 делим на 4, получим 2 целых и 3 остаток. Выносим 2 перед дробью, а остаток 3 пишем в числитель 3/4. Таким образом дробь становится правильной — 2 целых и 3/4.
У неправильной дроби знаменатель оказывается меньше числителя, что говорит о том, что в этой дроби имеются целые части, которые можно выделить и получить правильную дробь с целым числом.
Самый простой способ поделить числитель на знаменатель. Полученное целое число ставим слева от дроби, а остаток пишем в числитель, знаменатель остается тем же самым.
Например 11/4. Делим 11 на 4 и получаем 2 и остаток 3. Двойка -это число, которое ставим рядом с дробью, а тройку пишем в числитель дроби. Выходит 2 и 3/4.
Чтобы ответить на этот несложный вопрос, можно решить такую же несложную задачку:
Петя и Валя пришли в компанию сверстников.
 Всех вместе их стало 11. У Вали были с собой яблоки (но не много) и чтобы угостить всех Петя разрезал каждое на четыре части и раздал. Хватило всем и даже пять кусочков осталось.
Всех вместе их стало 11. У Вали были с собой яблоки (но не много) и чтобы угостить всех Петя разрезал каждое на четыре части и раздал. Хватило всем и даже пять кусочков осталось.Сколько яблок раздал Петя и сколько яблок осталось? Сколько их было всего?
А можно записать это математически
11 кусочков яблока это в нашем случае 11/4 — получили неправильную дробь, так как числитель больше знаменателя.
Чтобы выделить целую часть (преобразовать неправильную дробь в правильную), нужно числитель разделить на знаменатель , неполное частное (в нашем случае это 2) записать слева, остаток (3)оставить в числителе а знаменатель не трогать.
В результате получим 11/4 = 11:4 = 2 3/4 яблока раздал Петя.
Аналогично 5/4 = 1 1/4 яблок осталось.
(11+5)/4 = 16/4 = 4 яблока принесла Валя
Как перевести обыкновенную дробь в десятичную: 2 способа
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.
 ru Математика Алгебра Перевод обыкновенной дроби в десятичную
ru Математика Алгебра Перевод обыкновенной дроби в десятичнуюВ данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно перевести в десятичную (конечную и бесконечную). Также разберем решение примеров для лучшего понимания изложенного материала.
- Преобразование обыкновенной дроби в десятичную
- Способ 1
- Способ 2
Чтобы перевести простую дробь в десятичную, можно воспользоваться одним из двух способов ниже:
Способ 1
И числитель, и знаменатель умножаем на одно и то же число. При этом число должно быть таким, чтобы знаменатель новой дроби делился нацело на 10, 100, 1000, 10000 и т.д.
Условие: данный способ подойдет только для таких дробей, знаменатель которых раскладывается на простые множители 2 или 5 (могут повторяться). В результате будет получена конечная десятичная дробь. В остальных случаях для перевода нужно воспользоваться Способом 2, описанным ниже.

Пример 1:
Представим дробь
3/20
в виде десятичной.
Решение3/20
=
3⋅5/20⋅5
=
15/100
= 0,15
Пример 2:Превратим дробь
7/12
в десятичную.
РешениеЗаданную дробь нельзя преобразовать в конечную десятичную дробь, т.к. знаменатель 12 раскладывается на простые множители: 2, 2 и 3. А это противоречит упомянутому выше условию.
Способ 2
Этот способ значительно популярнее первого. Алгоритм действий следующий:
- Сначала выполняем деление числителя на знаменатель как обычно (в столбик).
- Как только мы столкнемся с тем, что остаток от деления больше не делится нацело на делитель, значит:
- в частном ставим запятую;
- к остатку добавляем ноль и продолжаем делить полученное число на делитель, записывая результат уже справа от запятой.
 И так далее, пока мы не получим остаток, равный нулю (для конечных десятичных дробей) или требуемое количество цифр после запятой (для бесконечных дробей).
И так далее, пока мы не получим остаток, равный нулю (для конечных десятичных дробей) или требуемое количество цифр после запятой (для бесконечных дробей). - Примечание: Если числитель больше знаменателя, значит десятичная дробь будет больше одного, если меньше – целая часть десятичной дроби равна нулю (следовательно, в частном пишем 0, ставим запятую и продолжаем выполнять деление, записывая полученные цифры в дробной части).
ВАЖНО: Смешанную дробь перед превращением в десятичную необходимо представить в виде неправильной.
Пример 1:
Представим дробь
16/5
в виде десятичной.
РешениеТ.е. дробь
16/5
равняется 3,2.
Пример 2:Переведем дробь
3/20
в десятичную.
РешениеТ.
 е. дробь
е. дробь 3/20
равняется 0,15.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Mathway | Популярные задачи
1 Множитель x^2-4 2 Множитель 4x^2+20x+16 3 График y=-x^2 4 Вычислить 2+2 5 Множитель x^2-25 6 Множитель x^2+5x+6 7 Множитель x^2-9 8 Множитель x^3-8 9 Вычислить квадратный корень из 12 10 Вычислить квадратный корень из 20 11 Вычислить квадратный корень из 50 12 Множитель x^2-16 13 Вычислить квадратный корень из 75 14 Множитель x^2-1 15 Множитель x^3+8 16 Вычислить -2^2 17 Вычислить квадратный корень из (-3)^4 18 Вычислить квадратный корень из 45 19 Вычислить квадратный корень из 32 20 Вычислить квадратный корень из 18 21 Множитель x^4-16 22 Вычислить квадратный корень из 48 23 Вычислить квадратный корень из 72 24 Вычислить квадратный корень из (-2)^4 25 Множитель x^3-27 26 Вычислить -3^2 27 Множитель x^4-1 28 Множитель x^2+x-6 29 Множитель x^3+27 30 Множитель x^2-5x+6 31 Вычислить квадратный корень из 24 32 Множитель x^2-36 33 Множитель x^2-4x+4 34 Вычислить -4^2 35 Множитель x^2-x-6 36 Множитель x^4-81 37 Множитель x^3-64 38 Вычислить 4^3 39 Множитель x^3-1 40 График y=x^2 41 Вычислить 2^3 42 Вычислить (-12+ квадратный корень из -18)/60 43 Множитель x^2-6x+9 44 Множитель x^2-64 45 График y=2x 46 Множитель x^3+64 47 Вычислить (-8+ квадратный корень из -12)/40 48 Множитель x^2-8x+16 49 Вычислить 3^4 50 Вычислить -5^2 51 Множитель x^2-49 52 Вычислить (-20+ квадратный корень из -75)/40 53 Множитель x^2+6x+9 54 Множитель 4x^2-25 55 Вычислить квадратный корень из 28 56 Множитель x^2-81 57 Вычислить 2^5 58 Вычислить -8^2 59 Вычислить 2^4 60 Множитель 4x^2-9 61 Вычислить (-20+ квадратный корень из -50)/60 62 Вычислить (-8+ квадратный корень из -20)/24 63 Множитель x^2+4x+4 64 Множитель x^2-10x+25 65 Вычислить квадратный корень из -16 66 Множитель x^2-2x+1 67 Вычислить -7^2 68 График f(x)=2^x 69 Вычислить 2^-2 70 Вычислить квадратный корень из 27 71 Вычислить квадратный корень из 80 72 Множитель x^3+125 73 Вычислить -9^2 74 Множитель 2x^2-5x-3 75 Вычислить квадратный корень из 40 76 Множитель x^2+2x+1 77 Множитель x^2+8x+16 78 График y=3x 79 Множитель x^2+10x+25 80 Вычислить 3^3 81 Вычислить 5^-2 82 График f(x)=x^2 83 Вычислить квадратный корень из 54 84 Вычислить (-12+ квадратный корень из -45)/24 85 Множитель x^2+x-2 86 Вычислить (-3)^3 87 Множитель x^2-12x+36 88 Множитель x^2+4 89 Вычислить квадратный корень из (-8)^2 90 Множитель x^2+7x+12 91 Вычислить квадратный корень из -25 92 Множитель x^2-x-20 93 Вычислить 5^3 94 Множитель x^2+8x+15 95 Множитель x^2+7x+10 96 Множитель 2x^2+5x-3 97 Вычислить квадратный корень квадратный корень из 116 98 Множитель x^2-x-12 99 Множитель x^2-x-2 100 Вычислить 2^2 примеры перевода для обыкновенных дробей и целых чисел
Содержание:
- Общие сведения о дробях
- Формы дробной записи
- Понятие смешанного числа
- Как соотносятся между собой неправильные дроби и смешанные числа
-
Необходимость и алгоритм преобразования
- Как перевести смешанное число в неправильную дробь
- Как выделить из неправильной дроби целую часть
Содержание
- Общие сведения о дробях
- Формы дробной записи
- Понятие смешанного числа
- Как соотносятся между собой неправильные дроби и смешанные числа
-
Необходимость и алгоритм преобразования
- Как перевести смешанное число в неправильную дробь
- Как выделить из неправильной дроби целую часть
Общие сведения о дробях
Определение
Дробь — форма записи рационального числа в виде доли целого.

В стандартном виде дроби записываются так: \( \frac mn.\)
Число над чертой называется числителем, под ней — знаменателем. Такую запись можно передать словами, как m частей из n, причем \(\frac nn\) равняется единице.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Например, \(\frac67\) — это 6 частей из 7.
В такой форме можно записать любое рациональное число, в том числе целое. При этом в качестве знаменателя может выступать любое натуральное число.
Так, единицу можно представить как \(\frac88,\;\frac{13}{13},\;\frac{857}{857}\) и так далее.
Для записи чисел больше одного в дробной форме необходимо это число умножить на числитель:
\(2=2\cdot1=2\cdot\frac55=\frac{10}5.\)
Существует понятие правильных и неправильных дробей.
Определение
Правильной называют дробь, у которой модуль числителя меньше модуля знаменателя.

Соответственно, у неправильной дроби числитель больше или равен знаменателю. Из приведенных выше примеров\( \frac67\) — правильная дробь, а \(\frac88,\;\frac{13}{13},\;\frac{857}{857}\) и \(\frac{10}5\) — неправильные.
Формы дробной записи
Как уже описывалось выше, стандартный способ записи обыкновенных дробей — через горизонтальную черту. Числитель помещается сверху, знаменатель — под чертой: \(\frac mn.\)
Также распространена строчная форма записи через наклонную черту: . Так, числитель оказывается слева, знаменатель — справа.
Один из самых распространенных и часто используемых на практике методов записи дробей — десятичная дробь. В этом случае число записывается как результат деления числителя на знаменатель. При этом, целая часть отделяется от остаточной при помощи запятой (в стандарте стран СНГ) или точкой.
Десятичные дроби могут быть конечными и бесконечными. У конечных ограниченное количество знаков после запятой: 0,15; 7,1; 871,986 и т.
 д. Пример бесконечной десятичной дроби — число \( \mathrm\pi\). В обычной форме оно выглядит, как \(\frac{22}7\), в десятичной: 3,1415926535897…
д. Пример бесконечной десятичной дроби — число \( \mathrm\pi\). В обычной форме оно выглядит, как \(\frac{22}7\), в десятичной: 3,1415926535897…По своей сути, все десятичные дроби являются смешанными числами.
Понятие смешанного числа
Определение
Смешанное число — комбинация целочисленной и дробной форм записи рациональных чисел.
По сути, смешанное число — это упрощенный вид записи суммы целого числа и правильной дроби. Например, \(2\frac57\) можно обозначить, как \(2+\frac57\). Читаться такая запись будет так: «две целых, пять седьмых».
Как соотносятся между собой неправильные дроби и смешанные числа
Неправильные дроби отличаются от правильных тем, что в них числитель больше знаменателя. То есть, если представлять их буквально как операцию деления, то делимое больше делителя. Это значит, что в них содержится целая часть, выделив которую можно получить смешанное число.

Необходимость и алгоритм преобразования
В первую очередь, выделение целой части повышает удобство чтения записанных нецелых чисел и позволяет лучше понимать их значение. Это можно оценить на простом примере: \(\frac{12}5=2\frac25\). Можно пойти дальше и перевести смешанное число в десятичную дробь: \(2\frac25=2,4\).
При решении задач зачастую необходимо преобразовать смешанные числа в дробные, так как с ними проще проводить вычисления.
Как перевести смешанное число в неправильную дробь
Чтобы записать смешанное число в форме неправильной дроби необходимо выполнить два действия: умножить целую часть на знаменатель и прибавить полученный результат к числителю.
Пример:
\(4\frac78=\frac{4\cdot8+7}8=\frac{32+7}8=\frac{39}8\)
Этот упрощенный способ преобразования работает на том принципе, что любое целое число можно представить в виде произведения этого числа на единицу. Единицу же в свою очередь можно представить в виде дроби, где числитель равен знаменателю.
 Разберем предыдущий пример более подробно:
Разберем предыдущий пример более подробно:\(4\frac78=4+\frac78=4\cdot1+\frac78=4\cdot\frac88+\frac78=\frac{32}8+\frac78=\frac{39}8\)
Как выделить из неправильной дроби целую часть
Обратное преобразование работает на принципе, согласно которому, при делении двух некратных друг другу чисел, делимое можно представить в виде суммы кратного делителю числа и некоего остатка. В качестве примера возьмем число из предыдущего пункта:
\(\frac{39}8=\frac{32}8+\frac78=4+\frac78=4\frac78\)
В этом преобразовании можно пойти дальше и представить смешанное число в виде десятичной дроби. Для этого целая часть отделяется запятой, а операция деления продолжается с остатком, умноженным на 10. Само деление продолжается до тех пор, пока остаток не окажется равен нулю.
\(4\frac78=4,0+\frac{7\cdot10}8=4,0+\left(\frac{64}8+\frac68\right)=4,8+\frac{6\cdot10}8=4,8+\left(\frac{56}8+\frac48\right)=4,87+\frac{40}8=4,875\)
В случае с бесконечными десятичными дробями, деление продолжается до тех пор, пока число знаков после запятой не удовлетворит условие задачи.
 В таком случае, последняя цифра округляется согласно установленным правилам.
В таком случае, последняя цифра округляется согласно установленным правилам.Насколько полезной была для вас статья?
Рейтинг: 1.50 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Неправильные дроби
7 4 (семь четвертей или семь четвертей) Неправильная дробь имеет первое число больше (или равно) нижнему числу.
Обычно » »Другие примеры
3 2 7 3 16 15 15 15 100 5 Видите, как верхнее число больше (или равно) нижнего числа?
Это делает его неправильной дробью (но в неправильных дробях нет ничего плохого).
Три типа дробей
Существуют три типа дробей:
Дроби
Дробь (например, 7 / 4 ) имеет два числа:
Числитель Знаменатель
Верхнее число 90 (числитель частей9)
Нижнее число (знаменатель) — это число частей, которое делится на .Пример: 7 / 4 означает:
- У нас есть 7 детали
- Каждая часть равна квартал ( 1 / 4 ) целого
Итак, мы можем определить три типа дробей следующим образом:
Правильные дроби: Числитель меньше знаменателя Примеры: 1 / 3 , 3 / 4 , 2 / 7 Неправильные дроби: Числитель больше (или равен) знаменателю Примеры: 4 / 3 , 11 / 4 , 7 / 7 Смешанные фракции: Целое число и правильная дробь вместе Примеры: 1 1 / 3 , 2 1 / 4 , 16 2 / 5 Неправильная дробь
Таким образом, неправильная дробь — это дробь, в которой верхнее число (числитель) больше или равно нижнему числу (знаменатель): это верхнее тяжелое .

4 4Могут быть равны
Что делать, если числитель равен знаменателю? Например 4 / 4 ?
Ну, в целом то же самое, но записывается в виде дроби, поэтому большинство людей согласны с тем, что это разновидность неправильной дроби.
Неправильные или смешанные дроби
Мы можем использовать либо неправильную дробь, либо смешанную дробь, чтобы показать одну и ту же сумму.
Например, 1 3 4 = 7 4 , как показано здесь:
1 4 3 0012 7 4 = Преобразование неправильных дробей в смешанные
Чтобы преобразовать неправильную дробь в смешанную, выполните следующие действия.

- Разделить числитель на знаменатель.
- Запишите целое число ответ
- Затем запишите любой остаток выше знаменателя.
Пример: Преобразуйте
11 4 в смешанную дробь.Разделить:
11 ÷ 4 = 2 с остатком 3
Запишите 2, а затем запишите остаток (3) над знаменателем (4).
Ответ:
2 3 4
Этот пример можно записать так:
Пример: Преобразуйте
10 3 в смешанную дробь.Ответ:
3 1 3
Преобразование смешанных дробей в неправильные дроби
- Умножить целую часть числа на знаменатель дроби.
- Добавьте это к числителю
- Затем запишите результат над знаменателем.

Пример: Преобразуйте 3
2 5 в неправильную дробь.Умножьте целую часть числа на знаменатель:
3 × 5 = 15
Добавьте это к числителю:
15 + 2 = 17
Затем запишите этот результат над знаменателем:
17 5
Мы можем сделать числитель за один раз:
Пример: Преобразовать 2
1 9 в неправильную дробь.Плохие ли неправильные дроби?
НЕТ, они неплохие!
Для математики они на самом деле лучше , чем смешанные дроби. Потому что смешанные дроби могут сбивать с толку, когда мы пишем их в формуле: следует ли складывать или умножать две части?
Смешанная фракция: Что такое: 1 + 2 1 4 ? Это: 1 + 2 + 1 4 = 3 1 4 ? Или это: 1 + 2 × 1 4 = 1 1 2 ? Неправильная дробь: Что такое: 1 + 9 4 ? Это: 4 4 + 9 4 = 13 4 Но для повседневного использования люди лучше понимают смешанные дроби.

Пример: Легче сказать «Я съел 2 1 4 сосисок», чем «Я съел 9 4 сосиски»
Рекомендуем:
- Для математики: неправильные дроби
- Для повседневного использования: смешанные фракции
4.2. Правильные дроби, неправильные дроби и смешанные числа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48851
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады 901 901 08X через OpenStax
Цели обучения
- уметь различать правильные дроби, неправильные дроби и смешанные числа
- уметь преобразовывать неправильную дробь в смешанное число
- уметь преобразовывать смешанное число в неправильную дробь
Теперь, когда мы знаем, что такое положительные дроби, рассмотрим три типа положительных дробей: правильные дроби, неправильные дроби и смешанные числа.

Положительные правильные дроби
Определение: Положительная правильная дробь
Дроби, в которых целое число в числителе строго меньше целого числа в знаменателе, называются положительными правильными дробями . На числовой прямой правильные дроби располагаются в промежутке от 0 до 1. Положительные правильные дроби всегда меньше единицы.
Закрашенный кружок 0 означает, что 0 включен, а открытый кружок 1 означает, что 1 не включен.
Некоторые примеры положительных правильных дробей:
\(\dfrac{1}{2}\), \(\dfrac{3}{5}\), \(\dfrac{20}{27}\), и \(\dfrac{106}{255}\)
Обратите внимание, что \(1 < 2\), \(3 < 5\), \(20 < 27\) и \(106 < 225\).
Положительные неправильные дроби
Определение: Положительные неправильные дроби
Дроби, в которых целое число в числителе больше или равно целому числу в знаменателе, называются положительными неправильными дробями . На числовой прямой неправильные дроби лежат справа от 1 (включительно).
 Положительные неправильные дроби всегда больше или равны 1.
Положительные неправильные дроби всегда больше или равны 1.Некоторые примеры положительных неправильных дробей:
\(\dfrac{3}{2}\), \(\dfrac{8}{5}\), \(\dfrac{4}{4}\) и \(\dfrac{105}{16 }\)
Обратите внимание, что \(3 \ge 2, 8 \ge 5, 4 \ge 4\) и \(105 \ge 16\).
Положительные смешанные числа
Определение: Положительные смешанные числа
Число вида \(\text{ненулевое целое число} + \text{правильная дробь}\) называется положительным смешанным числом . Например, 2\(\dfrac{3}{5}\) — смешанное число. На числовой прямой смешанные числа расположены в промежутке справа от 1 (включительно). Смешанные числа всегда больше или равны 1.
Связь положительных неправильных дробей и положительных смешанных чисел
Связь между неправильными дробями и смешанными числами подтверждается двумя фактами. Во-первых, неправильные дроби и смешанные числа располагаются на одном и том же интервале числовой прямой.
 Второй факт, что смешанные числа представляют собой сумму натурального числа и дроби, можно увидеть, сделав следующие наблюдения.
Второй факт, что смешанные числа представляют собой сумму натурального числа и дроби, можно увидеть, сделав следующие наблюдения.Разделите целое количество на 3 равные части.
Теперь рассмотрим следующие примеры, наблюдая за соответствующими заштрихованными областями.
В заштрихованной области 2 трети, или \(\dfrac{2}{3}\).
\(2 (\dfrac{1}{3}) = \dfrac{2}{3}\)
Есть 3 трети, или \(\dfrac{3}{3}\), или 1.
\(3(\dfrac{1}{3}) = \dfrac{3}{3}\) или 1
Таким образом,
\(\dfrac{3}{3} = 1\ )
Неправильная дробь = целое число.
Есть 4 трети, или \(\dfrac{4}{3}\), или 1 и \(\dfrac{1}{3}\).
\(4(\dfrac{1}{3}) = \dfrac{4}{3}\) или 1 и \(\dfrac{1}{3}\)
Члены 1 и \(\ dfrac{1}{3}\) можно представить как \(1 + \dfrac{1}{3}\) или \(1 \dfrac{1}{3}\)
Таким образом,
\(\ dfrac{4}{3} = 1 \dfrac{1}{3}.\)
правильная дробь = смешанное число.
Есть 5 третей, или \(\dfrac{5}{3}\), или 1 и \(\dfrac{2}{3}\).

\(5(\dfrac{1}{3}) = \dfrac{5}{3}\) или 1 и \(\dfrac{2}{3}\)
Члены 1 и \(\ dfrac{2}{3}\) можно представить как \(1 + \dfrac{2}{3}\) или \(1\dfrac{2}{3}\).
Таким образом,
\(\dfrac{5}{3} = 1 \dfrac{2}{3}\).
Неправильная дробь = смешанное число.
Есть 6 третей, или \(\dfrac{6}{3}\), или 2.
\(6(\dfrac{1}{3}) = \dfrac{6}{3 } = 2\)
Таким образом,
\(\dfrac{6}{3} = 2\)
Неправильная дробь = целое число.
Следующий важный факт иллюстрируется предыдущими примерами.
Смешанное число = Натуральное число + Правильная дробь
Смешанные числа — это сумма натурального числа и правильной дроби. Смешанное число = (натуральное число) + (правильная дробь)Например, \(1 \dfrac{1}{3}\) можно выразить как \(1 + \dfrac{1}{3}\) Дробь \ (5 \dfrac{7}{8}\) можно выразить как \(5 + \dfrac{7}{8}\).
Важно отметить, что такое число, как \(5 + \dfrac{7}{8}\), не , а указывает на умножение.
 Чтобы указать умножение, нам нужно будет использовать символ умножения (например, \(\cdot\))
Чтобы указать умножение, нам нужно будет использовать символ умножения (например, \(\cdot\))Пример \(\PageIndex{1}\)
\(5 \dfrac{7}{8}\) означает \(5 + \dfrac{7}{8}\) и , а не \(5 \ cdot \dfrac{7}{8}\), что означает 5 умножить на \(\dfrac{7}{8}\) или 5 умножить на \(\dfrac{7}{8}\).
Таким образом, смешанные числа могут быть представлены неправильными дробями, а неправильные дроби могут быть представлены смешанными числами.
Преобразование неправильных дробей в смешанные числа
Чтобы понять, как можно преобразовать неправильную дробь в смешанное число, рассмотрим дробь \(\dfrac{4}{3}\).
\(\ begin {array} {rcl} {\ dfrac {4} {3}} & = & {\ underbrace {\ dfrac {1} {3} + \ dfrac {1} {3} + \ dfrac{1}{3}}_{1} + \dfrac{1}{3}} \\ {} & = & {1 + \dfrac{1}{3}} \\ {} & = & {1 \dfrac{1}{3}} \end{array}\)
На этом примере можно проиллюстрировать процедуру преобразования неправильной дроби в смешанное число. Однако преобразование 90 756 проще, чем 90 010, путем деления числителя на знаменатель и использования результата для записи смешанного числа.

Преобразование неправильной дроби в смешанное число
Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель.Целая часть смешанного числа является частным.
Дробная часть смешанного числа – это остаток, написанный над делителем (знаменателем неправильной дроби).Набор образцов A
Преобразуйте каждую неправильную дробь в соответствующее смешанное число.
\(\dfrac{5}{3}\) Разделите 5 на 3.
Решение
Неправильная дробь \(\dfrac{5}{3} = 1 \dfrac{2}{3}\).
Набор образцов A
\(\dfrac{46}{9}\) Разделите 46 на 9.
Решение
\dfrac{1}{9}\).
Образец набора A
\(\dfrac{83}{11}\) Разделите 83 на 11.
Решение
\dfrac{6}{11}\).
Набор образцов A
\(\dfrac{104}{4}\) Разделите 104 на 4. 0}{4} = 26
Неправильная дробь \(\dfrac{104}{4} = 26\).

Практический набор A
Преобразуйте каждую неправильную дробь в соответствующее смешанное число.
\(\dfrac{9}{2}\)
- Ответить
\(4\dfrac{1}{2}\)
Тренировочный набор A
\(\dfrac{11}{3}\)
- Ответить
\(3\dfrac{2}{3}\)
Тренировочный набор A
\(\dfrac{14}{11}\)
- Ответить
\(1\dfrac{3}{11}\)
Тренировочный набор A
\(\dfrac{31}{13}\)
- Ответить
\(2\dfrac{5}{13}\)
Тренировочный набор A
\(\dfrac{79}{4}\)
- Ответить
\(19\dfrac{3}{4}\)
Тренировочный набор A
\(\dfrac{496}{8}\)
- Ответить
62
Преобразование смешанных чисел в неправильные дроби
Чтобы понять, как преобразовать смешанное число в неправильную дробь, вспомним
смешанное число = (натуральное число) + (правильная дробь)
и рассмотрим следующую диаграмму.

Напомним, что умножение описывает многократное сложение.
Обратите внимание, что \(\dfrac{5}{3}\) можно получить из \(1 \dfrac{2}{3}\) с помощью умножения следующим образом.
Умножить: \(3 \cdot 1 = 3\)
Сложить: \(3 + 2 = 5\). Поместите 5 над 3: \(\dfrac{5}{3}\)
В этом примере показана процедура преобразования смешанного числа в неправильную дробь.
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь,Умножьте знаменатель дробной части смешанного числа на целую часть числа.
К этому произведению прибавьте числитель дробной части.
Поместите этот результат над знаменателем дробной части.Набор образцов B
Преобразуйте каждое смешанное число в неправильную дробь.
\(5 \dfrac{7}{8}\)
Решение
- Умножить: \(8 \cdot 5 = 40\)
- Добавить: \(40 + 7 = 47\)
- Место 47 вместо 8: \(\dfrac{47}{8}\)
Таким образом, \(5 \dfrac{7}{8} = \dfrac{47}{8}\).

Набор образцов B
\(16 \dfrac{2}{3}\)
Решение
- Умножьте: \(3 \cdot 16 = 48\).
- Добавить: \(48 + 2 = 50\)
- Поместите 50 на 3: \(\dfrac{50}{3}\)
Таким образом, \(16 \dfrac{2}{3} = \dfrac{50}{3}\)
Тренировочный набор A
Преобразуйте каждое смешанное число в соответствующую ему неправильную дробь.
\(8 \dfrac{1}{4}\)
- Ответить
\(\dfrac{33}{4}\)
Тренировочный набор A
\(5 \dfrac{3}{5}\)
- Ответить
\(\dfrac{28}{5}\)
Тренировочный набор A
\(1 \dfrac{4}{15}\)
- Ответить
\(\dfrac{19}{15}\)
Тренировочный набор A
\(12 \dfrac{2}{7}\)
- Ответить
\(\dfrac{86}{7}\)
Упражнения
В следующих 15 задачах определите каждое выражение как правильную дробь, неправильную дробь или смешанное число.

Упражнение \(\PageIndex{1}\)
\(\dfrac{3}{2}\)
- Ответить
неправильная дробь
Упражнение \(\PageIndex{2}\)
\(\dfrac{4}{9}\)
Упражнение \(\PageIndex{3}\)
\(\dfrac{5}{7}\)
- Ответить
правильная дробь
Упражнение \(\PageIndex{4}\)
\(\dfrac{1}{8}\)
Упражнение \(\PageIndex{5}\)
\(6 \dfrac{1}{4}\)
- Ответить
смешанный номер
Упражнение \(\PageIndex{6}\)
\(\dfrac{11}{8}\)
Упражнение \(\PageIndex{7}\)
\(\dfrac{1,001}{12}\)
- Ответить
неправильная дробь
Упражнение \(\PageIndex{8}\)
\(191 \dfrac{4}{5}\)
Упражнение \(\PageIndex{9}\)
\(1 \dfrac{9}{13}\)
- Ответить
смешанный номер
Упражнение \(\PageIndex{10}\)
\(31 \dfrac{6}{7}\)
Упражнение \(\PageIndex{11}\)
\(3 \dfrac{1}{40}\)
- Ответить
смешанный номер
Упражнение \(\PageIndex{12}\)
\(\dfrac{55}{12}\)
Упражнение \(\PageIndex{13}\)
\(\dfrac{0}{9}\)
- Ответить
правильная дробь
Упражнение \(\PageIndex{14}\)
\(\dfrac{8}{9}\)
Упражнение \(\PageIndex{15}\)
\(101 \dfrac{1}{11}\)
- Ответить
смешанный номер
В следующих 15 задачах преобразуйте каждую неправильную дробь в соответствующее смешанное число.

Упражнение \(\PageIndex{16}\)
\(\dfrac{11}{6}\)
Упражнение \(\PageIndex{17}\)
\(\dfrac{14}{3}\)
- Ответить
\(4 \dfrac{2}{3}\)
Упражнение \(\PageIndex{18}\)
\(\dfrac{25}{4}\)
Упражнение \(\PageIndex{19}\)
\(\dfrac{35}{4}\)
- Ответить
\(8 \dfrac{3}{4}\)
Упражнение \(\PageIndex{20}\)
\(\dfrac{71}{8}\)
Упражнение \(\PageIndex{21}\)
\(\dfrac{63}{7}\)
- Ответить
9
Упражнение \(\PageIndex{22}\)
\(\dfrac{121}{11}\)
Упражнение \(\PageIndex{23}\)
\(\dfrac{165}{12}\)
- Ответить
\(13 \dfrac{9}{12}\) или \(13 \dfrac{3}{4}\)
Упражнение \(\PageIndex{24}\)
\(\dfrac{346}{15}\)
Упражнение \(\PageIndex{25}\)
\(\dfrac{5,000}{9}\)
- Ответить
\(555 \dfrac{5}{9}\)
Упражнение \(\PageIndex{26}\)
\(\dfrac{23}{5}\)
Упражнение \(\PageIndex{27}\)
\(\dfrac{73}{2}\)
- Ответить
\(36 \dfrac{1}{2}\)
Упражнение \(\PageIndex{28}\)
\(\dfrac{19}{2}\)
Упражнение \(\PageIndex{29}\)
\(\dfrac{316}{41}\)
- Ответить
\(7 \dfrac{29}{41}\)
Упражнение \(\PageIndex{30}\)
\(\dfrac{800}{3}\)
В следующих 15 задачах преобразуйте каждое смешанное число в соответствующую ему неправильную дробь.

Упражнение \(\PageIndex{31}\)
\(4 \dfrac{1}{8}\)
- Ответить
\(\dfrac{33}{8}\)
Упражнение \(\PageIndex{32}\)
\(1 \dfrac{5}{12}\)
Упражнение \(\PageIndex{33}\)
\(6 \dfrac{7}{9}\)
- Ответить
\(\dfrac{61}{9}\)
Упражнение \(\PageIndex{34}\)
\(15 \dfrac{1}{4}\)
Упражнение \(\PageIndex{35}\)
\(10 \dfrac{5}{11}\)
- Ответить
\(\dfrac{115}{11}\)
Упражнение \(\PageIndex{36}\)
\(15 \dfrac{3}{10}\)
Упражнение \(\PageIndex{37}\)
\(8 \dfrac{2}{3}\)
- Ответить
\(\dfrac{26}{3}\)
Упражнение \(\PageIndex{38}\)
\(4 \dfrac{3}{4}\)
Упражнение \(\PageIndex{39}\)
\(21 \dfrac{2}{5}\)
- Ответить
\(\dfrac{107}{5}\)
Упражнение \(\PageIndex{40}\)
\(17 \dfrac{9}{10}\)
Упражнение \(\PageIndex{41}\)
\(9 \dfrac{20}{21}\)
- Ответить
\(\dfrac{209}{21}\)
Упражнение \(\PageIndex{42}\)
\(5 \dfrac{1}{16}\)
Упражнение \(\PageIndex{43}\)
\(90 \dfrac{1}{100}\)
- Ответить
\(\dfrac{9001}{100}\)
Упражнение \(\PageIndex{44}\)
\(300 \dfrac{43}{1,000}\)
Упражнение \(\PageIndex{45}\)
\(19 \dfrac{7}{8}\)
- Ответить
\(\dfrac{159}{8}\)
Упражнение \(\PageIndex{46}\)
Почему \(0 \dfrac{4}{7}\) не считается смешанным числом?
Подсказка:
См.
 определение смешанного числа.
определение смешанного числа.Упражнение \(\PageIndex{47}\)
Почему 5 считается смешанным числом?
Подсказка:
См. определение смешанного числа.
- Ответить
… потому что это может быть записано как \(5 \dfrac{0}{n}\), где \(n\) — любое положительное целое число.
Задачи с калькулятором
В следующих 8 задачах используйте калькулятор для преобразования каждого смешанного числа в соответствующую ему неправильную дробь.Упражнение \(\PageIndex{48}\)
\(35 \dfrac{11}{12}\)
Упражнение \(\PageIndex{49}\)
\(27 \dfrac{5}{61}\)
- Ответить
\(\dfrac{1,652}{61}\)
Упражнение \(\PageIndex{50}\)
\(83 \dfrac{40}{41}\)
Упражнение \(\PageIndex{51}\)
\(105 \dfrac{21}{23}\)
- Ответить
\(\dfrac{2,436}{23}\)
Упражнение \(\PageIndex{52}\)
\(72 \dfrac{605}{606}\)
Упражнение \(\PageIndex{53}\)
\(816 \dfrac{19}{25}\)
- Ответить
\(\dfrac{20,419}{25}\)
Упражнение \(\PageIndex{54}\)
\(708 \dfrac{42}{51}\)
Упражнение \(\PageIndex{55}\)
\(6,012 \dfrac{4,216}{8,117}\)
- Ответить
\(\dfrac{48,803,620}{8,117}\)
Упражнения для обзора
Упражнение \(\PageIndex{56}\)
Округлите 2 614 000 до ближайшей тысячи.

Упражнение \(\PageIndex{57}\)
Найдите продукт. \(1,004 \cdot 1,005\)
- Ответить
1 009 020
Упражнение \(\PageIndex{58}\)
Определить, делится ли число 41 826 на 2 и 3.
Упражнение \(\PageIndex{59}\)
Найдите наименьшее общее кратное чисел 28 и 36.
- Ответить
252
Упражнение \(\PageIndex{60}\)
Укажите числитель и знаменатель дроби \(\dfrac{12}{19}\).
Эта страница под названием 4.2: Правильные дроби, неправильные дроби и смешанные числа распространяется по лицензии CC BY, ее автор, ремикширование и/или куратор — Денни Бурзински и Уэйд Эллис-младший (OpenStax CNX).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Денни Бурзински и Уэйд Эллис-младший
- Лицензия
- СС BY
- Показать страницу Содержание
- нет
- Теги
- неправильные дроби
- смешанные числа
- натуральные числа
- положительные неправильные дроби
- положительные правильные дроби
- правильные дроби
Преобразование десятичных, неправильных дробей и смешанных чисел (видео)
mp4″ src=»https://player.vimeo.com/video/566639397?app_id=122963&h=f39b954b7e» frameborder=»0″ allow=»autoplay; fullscreen; picture-in-picture» allowfullscreen=»»>TranscriptPractice
Здравствуйте! Добро пожаловать в это видео о преобразовании десятичных, неправильных дробей и смешанных чисел! В этом видео мы рассмотрим шаги по преобразованию десятичной дроби в дробь и смешанного числа в неправильную дробь и наоборот. Давайте узнаем о преобразовании десятичных дробей в дроби и смешанных чисел в неправильные дроби!
Мы ежедневно используем дроби и десятичные числа. Все наши денежные операции выполняются в десятичной форме. Когда мы печем, мы используем полстакана и треть стакана. Умение конвертировать десятичную дробь в дробь — это математический навык, который вы будете использовать каждый божий день.
В таблице показаны десятичная, неправильная дробь и смешанное число, которые эквивалентны друг другу.
Decimal \ (3,25 \) Неправильная фракция \ (\ frac {13} {4} \) Смешанный номер \ (3 \ frac 4}\) Преобразование десятичной дроби в дробь:
Преобразование десятичной дроби в дробь начинается с умножения десятичной дроби на дробь, эквивалентную 1, поэтому значение десятичная не меняется.
 Например, если после запятой стоит только одно число (другими словами, число в десятом разряде), число будет умножено на \(\frac{10}{10}\). Если после запятой два числа (последняя цифра стоит в сотых), мы должны умножить число на \(\frac{100}{100}\) и так далее. После умножения упрощаем дробь.
Например, если после запятой стоит только одно число (другими словами, число в десятом разряде), число будет умножено на \(\frac{10}{10}\). Если после запятой два числа (последняя цифра стоит в сотых), мы должны умножить число на \(\frac{100}{100}\) и так далее. После умножения упрощаем дробь.Давайте рассмотрим пример.
Преобразуем 5,85 в дробную форму. Так как после запятой 2 числа, мы умножим 5,85 на \(\frac{100}{100}\).
\(5,58\times \frac{100}{100}=\frac{585}{100}\)
Чтобы упростить дробь, мы начнем с разбиения числа на его множители. Тогда мы сократим общие множители в числителе и знаменателе. Оба числа имеют коэффициент 5, поэтому \(\frac{585}{100}\) можно упростить до \(\frac{117}{20}\).
\(\frac{585}{100}=\frac{5\times 3\times 3\times 13}{5\times 5\times 2\times 2}=\frac{117}{20}\ )
Дробь, эквивалентная 5,85, равна \(\frac{117}{20}\), которую также называют неправильной дробью.
 Теперь превратим неправильную дробь в смешанное число.
Теперь превратим неправильную дробь в смешанное число.Преобразование неправильной дроби в смешанное число:
Мы преобразуем неправильную дробь \(\frac{117}{20}\) в смешанное число, разделив сначала числитель на знаменатель. Целое число становится числом перед дробью, остаток становится числителем дроби, а знаменатель дроби остается прежним. Следовательно, \(\frac{117}{20}\), преобразованное в смешанное число, равно \(5\frac{17}{20}\).
Вот пример того, как мы используем конверсии в реальной жизни.
Сэмм владеет пекарней. У нее \(5\frac{3}{4}\) кг сахара. Она покупает еще один мешок с 10,75 кг сахара. Каково общее количество сахара в килограммах, которое есть у Сэмма для выпечки? Дайте ответ в виде дроби.
Во-первых, мы начнем с преобразования 10,75 в дробную форму, умножив его на \(\frac{100}{100}\), что равно \(\frac{1,075}{100}\). Как только дробь упростится, мы получим \(\frac{43}{4}\), что при преобразовании в смешанное число равно \(10\frac{3}{4}\).

Теперь, когда оба числа представлены в форме смешанных чисел, мы можем легко объединить их, чтобы найти общее количество сахара, которое Сэмм приготовила для выпечки. Итак, все, что мы собираемся сделать, это добавить \(5\frac{3}{4}+10\frac{3}{4}\). Когда мы складываем смешанные числа, мы хотим начать со сложения дробных частей, поэтому давайте сделаем \(\frac{3}{4}+\frac{3}{4}\). Это дает нам \(\frac{6}{4}\), потому что мы добавляем наши числители, а наш знаменатель остается прежним. Теперь, если вы заметили, у нас есть неправильная дробь. Итак, давайте преобразуем это в смешанное число. Если мы разделим числитель на знаменатель, мы получим \(1\frac{2}{4}\), что можно упростить до \(1\frac{1}{2}\). Теперь мы добавим эту часть к нашим частям целых чисел из предыдущих. Итак, \(5+10=15+1\frac{1}{2}=16\frac{1}{2}\). Итак, у Сэмма есть \(16\frac{1}{2}\) кг сахара для выпечки.
Надеюсь, это видео о преобразовании десятичных дробей, неправильных дробей и смешанных чисел было полезным.
 Спасибо за просмотр и удачной учебы!
Спасибо за просмотр и удачной учебы!Вопрос № 1:
Преобразуйте десятичное число 6,8 в смешанное число.\(6\frac{4}{5}\)
\(6\frac{3}{4}\)
\(6\frac{5}{8}\)
\(6 \frac{1}{2}\)
Показать ответ
Ответ:
Смешанное число — это целое число, рядом с которым стоит правильная дробь.
Шаг 1. Преобразуйте десятичное число в неправильную дробь, умножив его на некоторую форму единицы, чтобы значение десятичного числа не изменилось. Число 8 после запятой стоит на десятом месте, поэтому мы можем умножить наше десятичное число на \(\frac{10}{10}\), чтобы преобразовать его в неправильную дробь.
\(6.8\times\frac{10}{10}=\frac{68}{10}\)
Шаг 2. Сократите неправильную дробь, полностью разложив числитель и знаменатель на множители, затем сократив все общие факторы между ними.

\(\frac{68}{10}=\frac{2\times 2\times 17}{2\times 5}=\frac{34}{5}\)
Шаг 3. Преобразование неправильная дробь в сокращенной форме до смешанного числа путем деления числителя на знаменатель.
\ (\ phantom {0} 6 \) \ (5 \) \ (34 \) \ ( — \) \ (30 \) \(4\)
Смешанное число записывается с использованием частного, остатка и делителя. Целое число для нашего смешанного числа есть частное \(6\). Числитель правильной дроби — это остаток от \(4\), а знаменатель — делитель \(5\). Итак, \(\frac{34}{5}=6\frac{4}{5}\).Таким образом, \(6.8=6\frac{4}{5}\).
Скрыть ответ
Вопрос № 2:
Преобразуйте десятичное число 3,25 в смешанное число.\(3\frac{1}{8}\)
\(3\frac{1}{4}\)
\(3\frac{2}{5}\)
\(3 \frac{3}{4}\)
Показать ответ
Ответ:
Смешанное число – это целое число, рядом с которым стоит правильная дробь.

Шаг 1. Преобразуйте десятичное число в неправильную дробь, умножив его на некоторую форму единицы, чтобы значение десятичного числа не изменилось. Число 5 после запятой стоит в сотых, поэтому мы можем умножить наше десятичное число на \(\frac{100}{100}\), чтобы преобразовать его в неправильную дробь.
\(3.25\times\frac{100}{100}=\frac{325}{100}\)
Шаг 2. Сократите неправильную дробь, полностью разложив числитель и знаменатель на множители, затем сократив все общие факторы между ними.
\(\frac{325}{100}=\frac{5\times5\times13}{2\times2\times\times5}=\frac{13}{4}\)
Шаг 3. Преобразование неправильная дробь в сокращенной форме до смешанного числа путем деления числителя на знаменатель.
\(\фантом{0}3\) \(4\) \(13\) \(–\) \(12\)
Смешанное число записывается с использованием частного, остатка и делителя. Целое число для нашего смешанного числа — это частное 3. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{13}{4}=3\frac {1}{4}\).
Целое число для нашего смешанного числа — это частное 3. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{13}{4}=3\frac {1}{4}\).Таким образом, \(3,25=3\frac{1}{4}\).
Скрыть ответ
Вопрос № 3:
Преобразуйте десятичное число 8,275 в смешанное число.\(8\frac{25}{49}\)
\(8\frac{22}{45}\)
\(8\frac{11}{40}\)
\(8 \frac{29}{40}\)
Показать ответ
Ответ:
Смешанное число — это целое число, рядом с которым стоит правильная дробь.
Шаг 1. Преобразуйте десятичное число в неправильную дробь, умножив его на некоторую форму единицы, чтобы значение десятичного числа не изменилось. Число 5 после запятой стоит в тысячных, поэтому мы можем умножить наше десятичное число на \(\frac{1{,}000}{1{,}000}\), чтобы преобразовать его в неправильную дробь.

\(8.275\times\frac{1{,}000}{1{,}000}=\frac{8{,}275}{1{,}000}\)
Шаг 2. Уменьшить неправильную дробь, полностью разложив числитель и знаменатель на множители, а затем сократив любые общие множители между ними.
\(\frac{8{,}275}{1{,}000}=\frac{5\times5\times331}{2\times2\times2\times5\times5\times5}=\frac{331}{ 40}\)
Шаг 3. Преобразуйте сокращенную неправильную дробь в смешанное число, разделив числитель на знаменатель.
\ (\ Phantom {00} 8 \) \ (40 \) \ (331 \) \ ( — \) \ (320 \) \ ( — \) \ (320 \) \(11\)
Смешанное число записывается с использованием частного, остатка и делителя. Целое число для нашего смешанного числа — это частное 8. Числитель правильной дроби — остаток от 11, а знаменатель — делитель 40. Итак, \(\frac{331}{40}=8\frac {11}{40}\).
Таким образом, \(8,275=8\frac{11}{40}\).
Скрыть ответ
Вопрос № 4:
Рецепт морса, приготовленного из нескольких видов фруктов, смешивают с 20 унциями воды, 10,2 унциями яблочного сока и \(\frac{13}{ 5}\) унций лимонного сока. Сколько жидкости нужно для рецепта?\(32\frac{4}{5}\text{ унций}\)
\(32\frac{1}{5}\text{ унций}\)
\(32\frac{1} {4}\text{ унций}\)
\(32\frac{3}{4}\text{ унций}\)
Показать Ответ
Ответ:
Нам нужно объединить количество воды, яблочного сока и лимонного сока, чтобы найти общее количество жидкости, необходимое для смешивания фруктового напитка. Мы сначала преобразуем количество яблочного сока и лимонного сока в смешанные числа, прежде чем объединять все количества жидкости. Смешанное число — это целое число и правильная дробь рядом с ним.

Шаг 1. Преобразуйте десятичное число 10,2 в неправильную дробь, умножив его на некоторую форму единицы, чтобы значение десятичного числа не изменилось, прежде чем преобразовать его в смешанное число. Число 2 после запятой стоит на десятом месте, поэтому мы можем умножить наше десятичное число на \(\frac{10}{10}\), чтобы преобразовать его в неправильную дробь.
\(10,2\times\frac{10}{10}=\frac{102}{10}\)
Шаг 2. Сократите неправильную дробь, полностью разложив числитель и знаменатель на множители, затем сократив все общие факторы между ними.
\(\frac{102}{10}=\frac{2\times51}{2\times5}=\frac{51}{5}\)
Шаг 3. Преобразуйте неправильную дробь в уменьшенную образуют смешанное число путем деления числителя на знаменатель.
\(10\) \ (5 \) \ (51 \) \ ( — \) \ (50 \) \ (1 \)
записано с использованием частного, остатка и делителя. Целое число для нашего смешанного числа — это частное 10. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 5. Итак, \(\frac{51}{5}=10\frac {1}{5}\).
Целое число для нашего смешанного числа — это частное 10. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 5. Итак, \(\frac{51}{5}=10\frac {1}{5}\).Шаг 4. Затем преобразуйте \(\frac{13}{5}\) в смешанное число, разделив числитель на знаменатель.
\ (\ Phantom {0} 2 \) \ (5 \) \ (13 \) \ ( — \) \ (10 \) \(3\) Смешанное число записывается с использованием частного, остатка и делителя. Целое число для нашего смешанного числа — это частное 2. Числитель правильной дроби — остаток от 3, а знаменатель — делитель 5. Итак, \(\frac{13}{5}=2\frac {3}{5}\).
Шаг 5. Теперь, когда мы преобразовали количество яблочного сока и лимонного сока в смешанные числа, мы можем объединить 3 количества, складывая правильные дроби для смешанных чисел, а затем добавляя целые числа для каждого смешанного числа.

\(20+10\frac{1}{5}+2\frac{3}{5}=32\frac{4}{5}\)
Таким образом, всего \(32\ frac{4}{5}\) унций жидкости, необходимой для рецепта фруктового напитка.
Скрыть ответ
Вопрос №5:
Вы на рыбалке в надежде поймать определенную рыбу. Суточный лимит веса для содержания рыбы составляет \(9\frac{1}{2}\) фунтов. Вы ловите две рыбы, одна весом 4,75 фунта, а другая весом \(\frac{9}{2}\) фунтов. Вам нужно будет отпустить одну из рыб обратно в воду из-за превышения дневного лимита веса?Да, так как общий вес пойманной рыбы составляет \(9\frac{3}{4}\) фунтов, что превышает дневной лимит веса \(9\frac{1}{2}\) фунты.
Да, так как общий вес пойманной рыбы составляет \(9\frac{1}{4}\) фунтов, что превышает дневной лимит веса в \(9\frac{1}{2}\) фунтов.
Нет, так как общий вес пойманной рыбы составляет \(9\frac{1}{4}\) фунтов, что меньше дневного лимита веса в \(9\frac{1}{2}\) фунты.

Нет, так как общий вес пойманной рыбы составляет \(9\frac{3}{4}\) фунтов, что меньше дневного лимита веса в \(9\frac{1}{2}\) фунты.
Показать Ответ
Ответ:
Мы объединим общий вес двух пойманных вами рыб, используя смешанные числа, и сравним его с дневным лимитом веса, чтобы определить, нужно ли выпускать одну из рыб. Смешанное число — это целое число и правильная дробь рядом с ним.
Шаг 1. Преобразуйте вес рыбы, заданный в виде десятичного числа, в неправильную дробь, умножив его на некоторую форму единицы, чтобы значение десятичного числа не изменилось, прежде чем преобразовать его в смешанное число. Число 5 после запятой находится в сотых разрядах, поэтому мы можем умножить наше десятичное число на \(\frac{100}{100}\), чтобы преобразовать его в неправильную дробь.
\(4,75\times\frac{100}{100}=\frac{475}{100}\)
Шаг 2. Сократите неправильную дробь, полностью разложив числитель и знаменатель на множители, затем сократив все общие факторы между ними.

\(\frac{475}{100}=\frac{5×5×19}{2×2×5×5}=\frac{19}{4}\)
Затем преобразуем неправильную дробь , в сокращенной форме, до смешанного числа путем деления числителя на знаменатель.
\ (4 \) \ (4 \) \ (19 \) \ ( — \) \ (16 \) 19 \ (16 \) 19 4 \ (16 \) 19 4. 3\)
Смешанное число записывается с использованием частного, остатка и делителя. Целое число для нашего смешанного числа — это частное 4. Числитель правильной дроби — остаток от 3, а знаменатель — делитель 4. Итак, \(4,75=\frac{19{4}=4\frac{3}{4}\).Шаг 3. Преобразуйте вес рыбы, заданный в виде неправильной дроби, в смешанное число, разделив числитель на знаменатель.
\ (4 \) \ (2 \) \ (9 \) \ ( — \) \ (8 \) 19 \ (8 \) 19 4 \ (8 \) 1\) Смешанное число записывается с использованием частного, остатка и делителя.
 Целое число для нашего смешанного числа — это частное 4. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 2. Итак, \(\frac{9{2}=4\frac{1}{2}\).
Целое число для нашего смешанного числа — это частное 4. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 2. Итак, \(\frac{9{2}=4\frac{1}{2}\).Шаг 4. Теперь, когда мы преобразовали веса двух пойманных рыб в смешанные числа, мы можем объединить их, сложив соответствующие дроби для каждого смешанного числа, а затем сложив целые числа для каждого смешанного числа.
\(4\frac{3}{4}+4\frac{1}{2}=4\frac{3}{4}+4\frac{2}{4}=8\frac{5} {4}\)
Поскольку дробная часть смешанного числа является неправильной дробью, нам нужно преобразовать ее в смешанное число и прибавить к 8, чтобы определить общий вес пойманной рыбы как правильное смешанное число.
Мы можем преобразовать \(\frac{5}{4}\) в смешанное число, разделив числитель на знаменатель.
\ (1 \) \ (4 \) \ (5 \) \ ( — \) \ (4 \) 19 \ (4 \) 19 4 \ (4 \) 1\)
Смешанное число записывается с использованием частного, остатка и делителя. Целое число для нашего смешанного числа — это частное от 1. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{5}{4}=1\frac {1}{4}\).
Целое число для нашего смешанного числа — это частное от 1. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{5}{4}=1\frac {1}{4}\).Следовательно, правильное смешанное число:
\(8\frac{5}{4}=8+1\frac{1}{4}=9\frac{1}{4}\)
общий вес двух пойманных вами промысловых рыб составляет \(9\frac{1}{4}\) фунтов. Суточный лимит веса промысловой рыбы составляет \(9\frac{1}{2}\) фунтов или \(9\frac{2}{4}\) фунтов. Поскольку ваш общий вес пойманной рыбы меньше дневного лимита веса, вам не нужно выпускать какую-либо рыбу.
Скрыть ответ
Вернуться к конверсиям Видео
696924
Простые дроби, правильные дроби, неправильные дроби, смешанные числа — Полный курс арифметики
Навыки
в н
А Р И Т Х М Е Т И КСодержание | Главная | Введение
Урок 19
Под натуральным числом мы подразумеваем совокупность неделимых.

Натуральное число состоит только из определенных частей. 6, например, имеет только половину, третью часть и шестую часть. Натуральное число 1 не имеет частей — мы не можем взять половину 1 человека!
Но если мы теперь подумаем о 1 как о длине,
, то у него будет любая часть — половина, третья, четвертая, пятая, миллионная!
Это порождает новый вид числа — дробь. Это число нам нужно для измерения, а не для подсчета. Тогда мы можем сказать, что определенная длина, например, равна 5¼ см. И так то, что мы называем правильная дробь является числом меньше 1.
Дроби принадлежат тому, что непрерывно, а не дискретно. См. Эволюция действительных чисел , Урок 3.
Мы увидим, что все, что мы узнали о соотношениях, применимо и к дробям, потому что, как мы увидим, каждый числитель имеет отношение к своему знаменателю. А сама дробь представляет собой число , имеющее отношение к 1,9.
 0023
0023 В этом уроке мы ответим на следующие вопросы:
- Что такое обыкновенная дробь ?
- Что такое правильная дробь ?
- Как узнать правильную дробь?
- Как называются правильные дроби?
- Какое отношение имеет каждая дробь к 1?
- Что такое смешанный номер ?
- Что такое неправильная дробь?
- Как представить неправильную дробь в виде смешанного числа?
- Как представить смешанное число в виде неправильной дроби?
1. Что такое обыкновенная дробь ? Число, записанное с числителем и знаменателем, в котором оба являются натуральными числами. Пример 1. 
3
10– обыкновенная дробь. Это в отличие от . 3, то есть десятичная дробь или просто десятичная дробь.
Числитель из 3
10равно 3. Знаменатель равен 10. Это членов дроби. Мы увидим, что они соответствуют условиям соотношения.
2. Что такое правильная дробь ? Дробь, которая на меньше , чем 1. 3. 
Как распознать правильную дробь? Числитель меньше знаменателя. 2
3(«две трети») – правильная дробь. Меньше 1. На числовой прямой он падает слева от 1. В частности, 2
3это две трети из 1, как мы сейчас увидим.
4. Как называются правильные дроби? То же, что отношение числителя к знаменателю. 
Пример 2. Число, которое мы записываем как 1 над 2 — 1
2— называется «половина» из-за отношения 1 к 2. 1 половина от 2.
Пишем название числа через дефис —
половина — но имя соотношения без дефиса. Очевидно, нужно сначала понять, что значит сказать, что число составляет половину от 1. То есть сначала нужно понять отношение.Пример 3. Почему этот номер 3
4называется «три четверти»? Ответ. Из-за отношения 3 к 4.
 3 равно три четверти от 4.
3 равно три четверти от 4.Это название верно для английского языка. Испанский гораздо более скрупулезно отличает названия дробей от названий соотношений. Эта дробь, например, называется un dozavo , а отношение 1 к 12 — la duodécima parte .
Отношение — это отношение между числами; числа имеют отношение друг к другу. Мы сохраним это различие, написав название числа, дробь через дефис, а отношение без дефиса. Это разделение числа и соотношения дает жизнь вопросу: может ли «отношение двух длины » (что бы это ни значило) всегда должны быть названы? Есть ли число ? Ибо числа имеют имена. 1, 9 . 6, , . число, то мы упустим один из самых интригующих и тревожных вопросов в математике
.Заинтересованного студента отсылают к книге «Эволюция действительных чисел».
Пример 4. Прочитайте это номера:
«Пять восьмых» «Шестнадцать третей» Неправильные дроби (см.  ниже) называются так же, как и правильные дроби.
ниже) называются так же, как и правильные дроби.«Девять половинок» (Не «Девять двойки».) «27 на 39» При больших числах не надо говорить «27 тридцать девятых». «56 тысячных» Однако когда знаменатель представляет собой степень числа 10, мы всегда произносим десятичное имя. (Урок 2) «5 и 79 сотых» Это смешанное число; Смотри ниже. 
Отношение к 1
Дробь — это число, и, как и любое число, мы знаем его относительно 1.
Как мы понимаем «2»? Это в два раза больше, чем 1. Что такое «3»? Это трижды 1.
Каждое число имеет отношение к 1. Именно в соответствии с этим отношением мы знаем каждое число.
Какое же отношение имеет ½ к 1?
½ равно половина из 1.
½ имеет такое же отношение к 1, как числитель к знаменателю.
5. Какое отношение имеет каждая дробь к 1? Отношение числителя к знаменателю такое же. Пример 5.  Какое отношение имеет
Какое отношение имеет2
3до 1? Ответить . Число, которое мы записываем как 2 над 3 — 2
3— это две трети от 1. Это то же отношение, что 2 к 3.
2
3равнозначно 1 как 2 равно 3. На место 2
3в числовой строке мы должны отрезать длину, соответствующую 1 .на три равные части. Обратите внимание, что для того, чтобы разрезать эту единицу на трети, мы разрезаем ее только дважды.
 «Одна треть, две трети».
«Одна треть, две трети».Поскольку числитель относится к знаменателю в том же отношении, что и два натуральных числа, дроби также называют рациональными числами.
Пример 6. Это число ¼ называется «одна четверть» или «одна четвертая», потому что числитель равен одной четверти знаменателя, а сама ¼ составляет одну четверть 1.
Чтобы поставить ¼ на числовой строке, мы обрезаем линию на единицу меньше, чем название детали. Чтобы разделить 1 на четвертей , разрежьте линию три раз.
Пример 7. Какое число указано на стрелке?
Ответ. Единица была разрезана пять раз — на шесть равных частей.
Это число 5
6. Правильные дроби являются частями числа 1.
Дробь ½ составляет только половину от 1. Но отношение к половине относится ко многим числам.
 «5 — это половина 10». «6 — это половина от 12». И так далее. Написать «6 — это ½ от 12», как, к сожалению, делают некоторые, — вульгарно.
«5 — это половина 10». «6 — это половина от 12». И так далее. Написать «6 — это ½ от 12», как, к сожалению, делают некоторые, — вульгарно.6. Что такое смешанное число? Целое число плюс правильная дробь . Пример 8. 2 1
3— «2 и одна треть» — смешанное число. Это 2 плюс .1
3. и в «2 и одна треть» означают плюс.
На место 2 1
3в числовой строке нужно отрезать единицу между 2 и 3 на трети.
 Разрезаем леску дважды.
Разрезаем леску дважды.Проблема. Ответьте смешанным числом или целым числом и остатком, в зависимости от того, что имеет смысл.
а) Сколько баскетбольных команд — по 5 в команде — можно составить из 23
а) студенты?б) Вы собираетесь проехать 23 мили и прошли пятую часть
б) расстояние. Как далеко вы зашли?Ответы .
7. Что такое неправильная дробь? Дробь больше или равна 1. Мы можем распознать неправильную дробь, если числитель больше или равен знаменателю.
Пример 9.  С 90 005
С 90 0053
3равно , равному и 1, тогда 8
3больше 1. 8
3это неправильная дробь.
3
3также называют неправильной дробью. Теперь мы ясно увидим, почему мы используем черту деления для обозначения дроби.
8. Как представить неправильную дробь в виде смешанного числа или целого числа? Разделите числитель на знаменатель.  Запишите частное (4), а остаток (1) запишите как числитель дроби; знаменатель остается прежним.
Запишите частное (4), а остаток (1) запишите как числитель дроби; знаменатель остается прежним.Пример 10. 43
5= 8 3
5«5 входит в число 43 восемь (8) раз (40) с остатком 3.»
Учащийся не должен писать разделительную рамку. (Урок 12.)
Пример 11. 32
9= 3 5
9«9 входит в число 32 три (3) раза (27) с остатком 5.»
Остаток — это то, что мы должны прибавить к 27, чтобы получить 32. (Урок 10.)
Пример 12. 
28
4= 7 «4 входит в число 28 ровно семь (7) раз.»
9. Как представить смешанное число в виде неправильной дроби? Умножьте целое число (4) на знаменатель (2) и добавьте числитель (1).
Запишите эту сумму (9) как числитель неправильной дроби. Знаменатель остается прежним.Примеры. 2 3
5= 13
5«5 умножить на 2 будет 10, плюс 3 будет 13; больше 5.
 »
»3 5
8= 29
8«8 умножить на 3 будет 24, плюс 5 будет 29; больше 8.»
Подводя итог: Дроби, которые на меньше меньше 1, называются правильными, а дроби больше или равные 1 – неправильными. Неправильные дроби эквивалентны смешанным числам или целым числам.
Пожалуйста, «переверните» страницу и выполните несколько Задач.
или
Перейти к следующему уроку.
Введение | Главная | Содержание
www.proyectosalonhogar.com
Преобразование смешанных чисел в дроби
Форма поиска
Поиск
Пример 1: Каждые полчаса звонит школьный звонок. Если он просто звонил, то сколько раз он будет звонить в следующие три с половиной часа?
Анализ: Эта задача спрашивает: Сколько половин в три с половиной?
Шаг 1: Давайте воспользуемся фигурами для представления смешанного числа три с половиной.

Шаг 2:
Решение:
В примере 1 мы использовали фигуры, чтобы решить задачу. Давайте посмотрим на пример 2.
Пример 2: Школьный звонок звонит каждые полчаса. Если он просто звонил, то сколько раз он будет звонить в следующие девять с половиной часов?
Анализ: Использование фигур для решения этой задачи нецелесообразно. Нам нужно найти другой метод.
Напомним, что смешанное число состоит из целой части и дробной части . Например:
Процедура: Чтобы записать смешанное число в виде неправильной дроби:
- Запишите целую часть в виде неправильной дроби, используя знаменатель дробной части .
- Добавьте результат шага 1 к дробной части смешанного числа.
Воспользуемся приведенной выше процедурой для решения задачи из примера 2.
Пример 2: Школьный звонок звонит каждые полчаса.
 Если он просто звонил, то сколько раз он будет звонить в следующие девять с половиной часов?
Если он просто звонил, то сколько раз он будет звонить в следующие девять с половиной часов?Анализ:
Шаг 1:
Шаг 2:
Solution: The School Will Will 1
.
Рассмотрим еще несколько примеров записи смешанного числа в виде неправильной дроби.
Пример 3: Запишите две и три четверти как неправильную дробь.
Анализ:
Шаг 1:
Шаг 2:
Решение:
Пример 4: . Врушивайте шесть и двух-тит.
Анализ:
Шаг 1:
Шаг 2:
Раствор:
. шаблон? Вы видите более простой способ записать смешанное число в виде неправильной дроби?
Примеры с 1 по 4 Для записи смешанного числа в виде неправильной дроби можно использовать сокращенный вариант: Если умножить знаменатель на целую часть, а затем добавить числитель, то в результате получится числитель неправильной дроби.
 Это показано ниже для смешанного числа две и три четверти.
Это показано ниже для смешанного числа две и три четверти.Повторяя примеры с 1 по 4, получаем:
Смешанный номер Преобразован в Неправильная дробь Рассмотрим еще несколько примеров записи смешанного числа в виде неправильной дроби с помощью этого сокращения.

Пример 5: Запишите одиннадцать и три пятых как неправильную дробь.
Анализ:
Шаг 1:
Решение:
Пример 6: . Напишите четверо и один-тел.
Анализ:
Шаг 1:
Решение:
Этот ярлык использует только один шаг и упрощает преобразование больших смешанных чисел в неправильные дроби.
Резюме: Существует несколько способов преобразования смешанного числа в неправильную дробь. Используйте тот, который подходит для данной проблемы.
Упражнения
В упражнениях с 1 по 5 щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать сначала, нажмите ОЧИСТИТЬ. Примечание. Чтобы написать неправильную дробь пять третей, введите 9.
 0028 5/3 в форму.
0028 5/3 в форму.1. Запишите одну и три четверти как неправильную дробь. ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ:
2. Запишите четыре и одну пятую как неправильную дробь. ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ:
3. Запишите пять и семь восьмых в виде неправильной дроби. 
ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ:
4. Запишите пятнадцать и две трети как неправильную дробь. ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ:
5. Рецепт требует две и три четверти чашки молока. Если мерный стакан вмещает только одну четверть стакана, то сколько раз вам придется его наполнить? ОКНО ОТВЕТОВ: раз ОКНО РЕЗУЛЬТАТОВ:
Уроки дробей 1. 
Знакомство с дробями 2. Классификация фракций 3. Эквивалентные дроби 4. Упрощение дробей 5. Сравнение дробей 6. Заказ фракций 7. Преобразование дробей в смешанные числа 8. Преобразование смешанных чисел в дроби 9. Практические упражнения 10. Упражнения с вызовом 11. Решения Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Адрес электронной почты *
Что такое неправильные дроби? Значение, определение, примеры, факты
Дроби часто называют числами между числами.
 Дроби — это числовые значения, которые представляют собой часть или часть целого. Например, посмотрите на пиццу ниже.
Дроби — это числовые значения, которые представляют собой часть или часть целого. Например, посмотрите на пиццу ниже.Эта пицца разрезана на 4 равные части. Таким образом, каждый кусок пиццы представляет собой 1 из 4 равных частей. Таким образом, математически мы можем представить каждую часть как $\frac{1}{4}$. Это число называется дробью.
Число под чертой, представляющее общее количество равных частей, на которые делится целое, называется знаменателем.
И число вверху, которое представляет количество равных частей, которое мы рассматриваем, называется числителем.
Что такое неправильная дробь?
Прежде чем обсуждать неправильную дробь, нам сначала нужно понять правильные дроби.
Правильные дроби: Дроби, у которых числитель меньше знаменателя, называются правильными дробями. Например, если вы заказываете пиццу и разрезаете ее на 4 равные части, а затем съедаете один кусок, оставшаяся часть пиццы может быть выражена как $\frac{3}{4}$ всей пиццы.
 Здесь, поскольку 3 меньше 4, дробь правильная.
Здесь, поскольку 3 меньше 4, дробь правильная.Неправильные дроби: Неправильными дробями считаются дроби, у которых числитель больше знаменателя. Давайте возьмем пример неправильной дроби, представьте, что вы заказываете пиццу, состоящую из 4 кусочков. Твои друзья съели все 4 ломтика. И ты понимаешь, что ничего не получил. Вы заказываете еще одну пиццу. Съев 1 ломтик из него, вы понимаете, что закончили есть. Итак, сколько всего пиццы съели ваши друзья и вы?
У ваших друзей сначала были все 4 куска 1 пиццы, а потом у вас был 1 кусок того же размера от второй пиццы.
Итак, общее количество съеденной пиццы равно $\frac{5}{4}$ кусочков пиццы. И это неправильная дробь, у которой числитель больше знаменателя.
Смешанные числа: Смешанные числа — это просто еще один способ записи дробей, больших, чем целое. Смешанное число состоит из целой части и дробной части, которая на самом деле является правильной дробью.
Возьмем тот же пример, что и выше. Вы и ваши друзья съели одну целую пиццу и четверть пиццы.
 В виде смешанной дроби мы можем записать это как $1$ и $\frac{1}{4}$ пиццы или $1\frac{1}{4}$ пиццы.
В виде смешанной дроби мы можем записать это как $1$ и $\frac{1}{4}$ пиццы или $1\frac{1}{4}$ пиццы.Преобразование дроби
Неправильная дробь в смешанное число
Неправильная дробь может быть преобразована в смешанную дробь, а смешанная дробь может быть преобразована в неправильную дробь.
Допустим, мы хотим преобразовать дробь $\frac{7}{2}$ в смешанное число.
Шаг 1: Найдите частное и остаток, разделив числитель на знаменатель.
Шаг 2: Частным будет количество целых чисел в смешанном числе. Остаток будет числителем дробной части, а знаменатель останется прежним.
Итак, смешанная числовая форма $\frac{7}{2}$ будет:
Смешанное число в неправильную дробь
Любое смешанное число можно преобразовать в неправильную дробь.
Допустим, мы хотим преобразовать смешанное число $1\frac{3}{4}$ в неправильную дробь.
Шаг 1: Умножьте знаменатель на целое. Затем прибавьте к произведению числитель.

Шаг 2: Сохраните знаменатель и найдите числитель.
Следовательно, неправильная дробь для смешанного числа $1\frac{3}{4}$ будет равна $\frac{7}{4}$.
Решенные примеры
Пример 1. Определите неправильные дроби:
$\frac{1}{5}$, $2\frac{7}{5}$, $\frac{3}{2 }$, $\frac{1}{3}$, $\frac{5}{4}$, $6 \frac{1}{6}$
Решение: $\frac{2}{3} $ и $\frac{5}{4}$ являются неправильными дробями, так как значение числителя больше значения знаменателя для обеих этих дробей.
Пример 2. Запишите $4\frac{2}{7}$ как неправильную дробь.
Решение: Преобразование $4\frac{2}{7}$ в неправильную дробь,
$4 \frac{2}{7}$ = $\frac{(7\times4) + 2}{7 }$ = $\frac{30}{7}$
Пример 3. Запишите $2\frac{9}{6}$ как неправильную дробь.
Решение: При делении 29 на 6 частное и остаток равны 4 и 5 соответственно.

Итак, $\frac{29}{6}$, записанное как смешанное число, равно $ 4 \frac{5}{6}$ .Преобразование $3\frac{1}{5}$ в неправильную дробь:
Практические задачи
Смешанная дробь
Неправильная дробь
Правильная дробь
Единичная дробь
Правильный ответ: Неправильная дробь
Поскольку значение числителя больше знаменателя, данная дробь является неправильной дробью.$\frac{18}{5}$
$\frac{16}{5}$
$\frac{1}{15}$
$\frac{14}{5}$
Правильный ответ: $\frac{16}{5}$
Преобразование $3\frac{1}{5}$ в неправильную дробь:
$3\frac{1}{5}$ = $\frac{(5\times 3) + 1}{5}$ = $1\frac{6}{5}$$\frac{2}{7 }$
$\frac{11}{22}$
$\frac{14}{15}$
$\frac{12}{11}$
Правильный ответ: $\frac{12} {11}$
Значение числителя больше значения знаменателя в $\frac{12}{11}$. Следовательно, это неправильная дробь.$2\frac{1}{2}$
$1\frac{1}{2}$
$1\frac{2}{4}$
Ничего из вышеперечисленного
Правильный ответ: $2\ гидроразрыв{1}{2}$
Разделив 5 на 2, мы получим частное и остаток как 2 и 1 соответственно.
Частное становится целым числом, остаток становится числителем дробной части, а знаменатель остается прежним.Часто задаваемые вопросы
Что легче считать: неправильные дроби или смешанные дроби?
С неправильными дробями легко выполнять арифметические операции сложения, вычитания, умножения и деления. Смешанные дроби легче понять и представить в цифрах.
Почему важны дроби?
Каждое количество не может быть выражено целыми числами. Дроби используются для обозначения определенной части или части любого элемента. Они являются фундаментальной концепцией в вычислениях и применяются в алгебре, соотношениях и некоторых других концепциях в математике и других областях.
Как десятичные дроби связаны с дробями?
Дроби и десятичные дроби — это оба способа представления величин или чисел. Десятичные дроби — это не что иное, как другой способ представления дробей, знаменатель которых равен 10 или степени 10.


 Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)
Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:) {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ. Она легко преобразуется:
Она легко преобразуется: Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Так или иначе, ключевое слово — «тысячных», т.е. 1000.
 По правилам математики такую дробь обязательно нужно превратить в правильную.
По правилам математики такую дробь обязательно нужно превратить в правильную. Получится шесть. Теперь отнимите от числителя полученное число. Получим единицу. Это и есть остаток. Запишите результат преобразования: шесть целых и одна треть.
Получится шесть. Теперь отнимите от числителя полученное число. Получим единицу. Это и есть остаток. Запишите результат преобразования: шесть целых и одна треть. Эту операцию тоже можно проделать в уме, столбиком или с помощью калькулятора (475-460=15).
Эту операцию тоже можно проделать в уме, столбиком или с помощью калькулятора (475-460=15). В математике существует три вида дробей: обыкновенные, смешанные и десятичные.
В математике существует три вида дробей: обыкновенные, смешанные и десятичные.
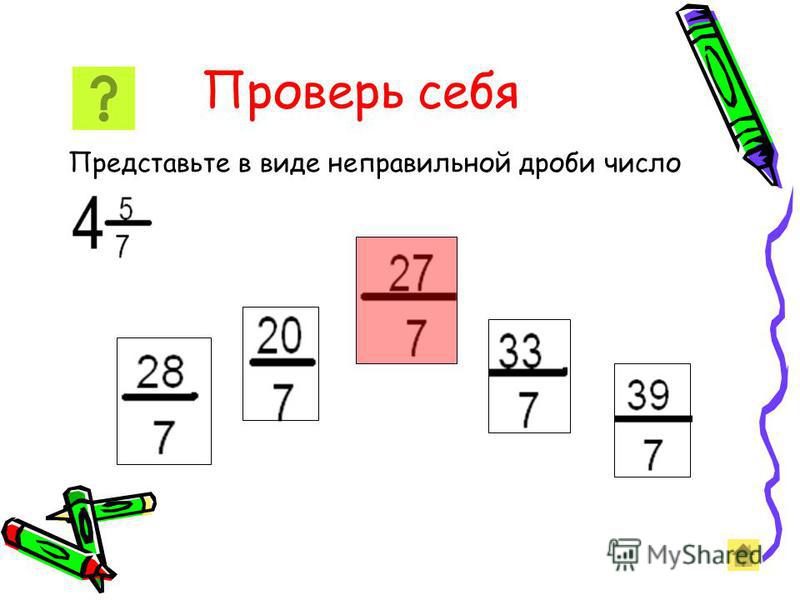
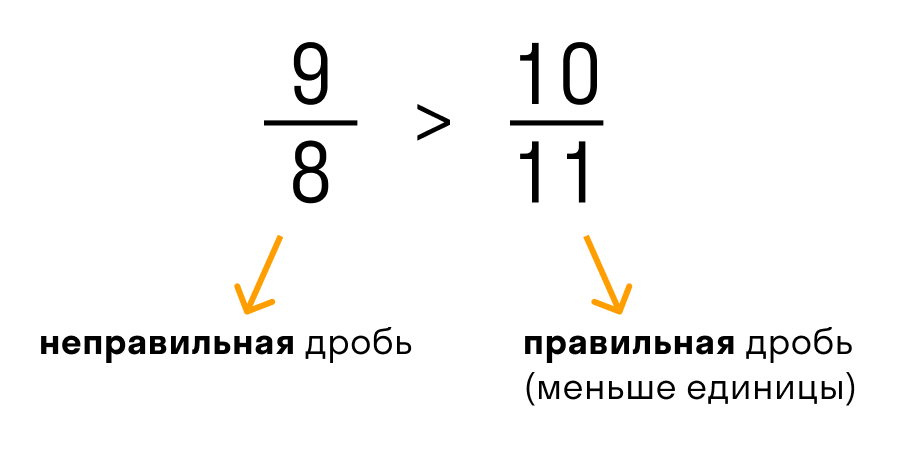

 .
. Поэтому приходится перевести неправильную дробь в правильную. при этом мы получим какое-то целое число и остаток — именно правильную дробь.
Поэтому приходится перевести неправильную дробь в правильную. при этом мы получим какое-то целое число и остаток — именно правильную дробь. Неправильная дробь это когда есть целое число например 5,10 , то есть пять целых и 10/100 , пять мы умножаем 100 и +10 , получается 10/500 . Так же если например 6,6 , тут проще, 6 умножаем на 6 и +6 получается 12/6 , сокращаем на два, получается шесть третьих, шесть третьих мы сокращаем на три получается две первых, два делим на один получается два. То есть 6,6 =2.
Неправильная дробь это когда есть целое число например 5,10 , то есть пять целых и 10/100 , пять мы умножаем 100 и +10 , получается 10/500 . Так же если например 6,6 , тут проще, 6 умножаем на 6 и +6 получается 12/6 , сокращаем на два, получается шесть третьих, шесть третьих мы сокращаем на три получается две первых, два делим на один получается два. То есть 6,6 =2.
 Полученное целое число выносим перед дробью, а остаток вписываем в числитель. Знаменатель не изменяется.
Полученное целое число выносим перед дробью, а остаток вписываем в числитель. Знаменатель не изменяется. Всех вместе их стало 11. У Вали были с собой яблоки (но не много) и чтобы угостить всех Петя разрезал каждое на четыре части и раздал. Хватило всем и даже пять кусочков осталось.
Всех вместе их стало 11. У Вали были с собой яблоки (но не много) и чтобы угостить всех Петя разрезал каждое на четыре части и раздал. Хватило всем и даже пять кусочков осталось. ru Математика Алгебра Перевод обыкновенной дроби в десятичную
ru Математика Алгебра Перевод обыкновенной дроби в десятичную
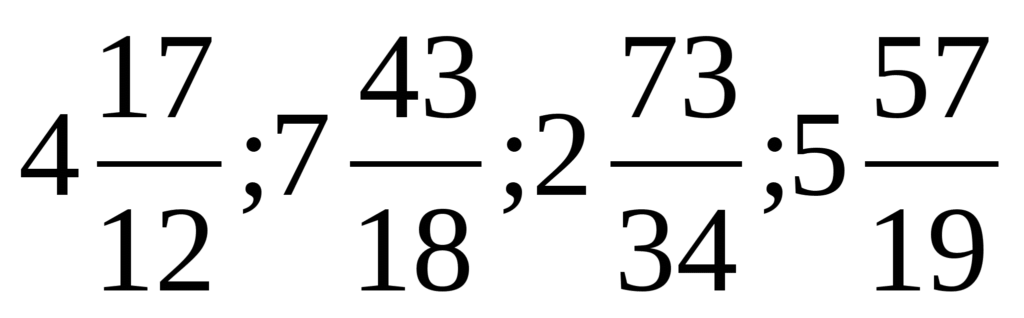 И так далее, пока мы не получим остаток, равный нулю (для конечных десятичных дробей) или требуемое количество цифр после запятой (для бесконечных дробей).
И так далее, пока мы не получим остаток, равный нулю (для конечных десятичных дробей) или требуемое количество цифр после запятой (для бесконечных дробей). е. дробь
е. дробь 

 д. Пример бесконечной десятичной дроби — число \( \mathrm\pi\). В обычной форме оно выглядит, как \(\frac{22}7\), в десятичной: 3,1415926535897…
д. Пример бесконечной десятичной дроби — число \( \mathrm\pi\). В обычной форме оно выглядит, как \(\frac{22}7\), в десятичной: 3,1415926535897…
 Разберем предыдущий пример более подробно:
Разберем предыдущий пример более подробно: В таком случае, последняя цифра округляется согласно установленным правилам.
В таком случае, последняя цифра округляется согласно установленным правилам.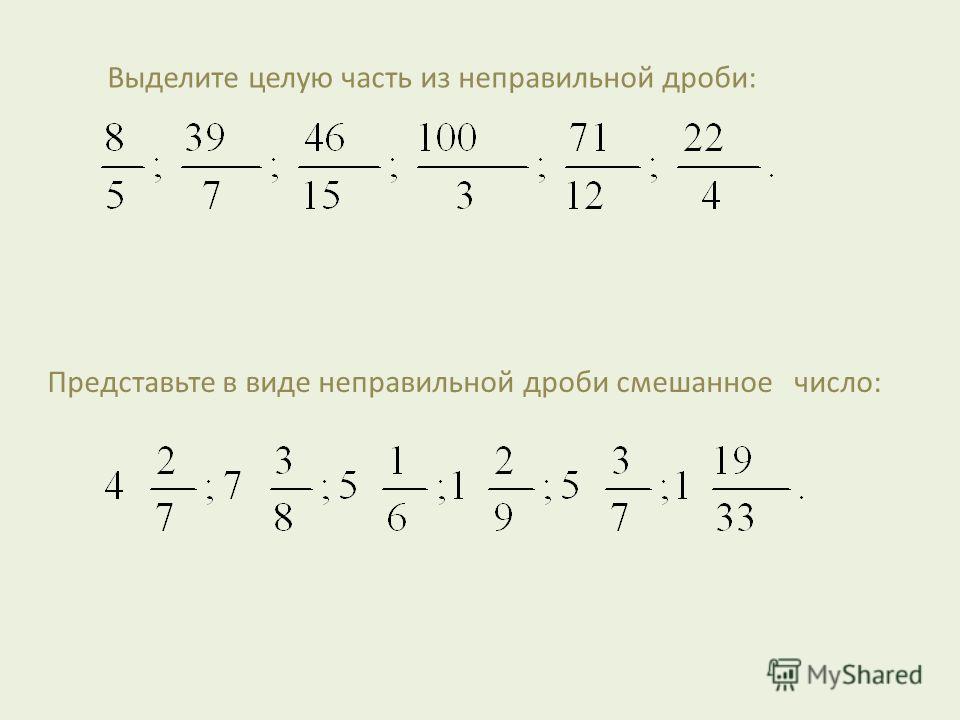

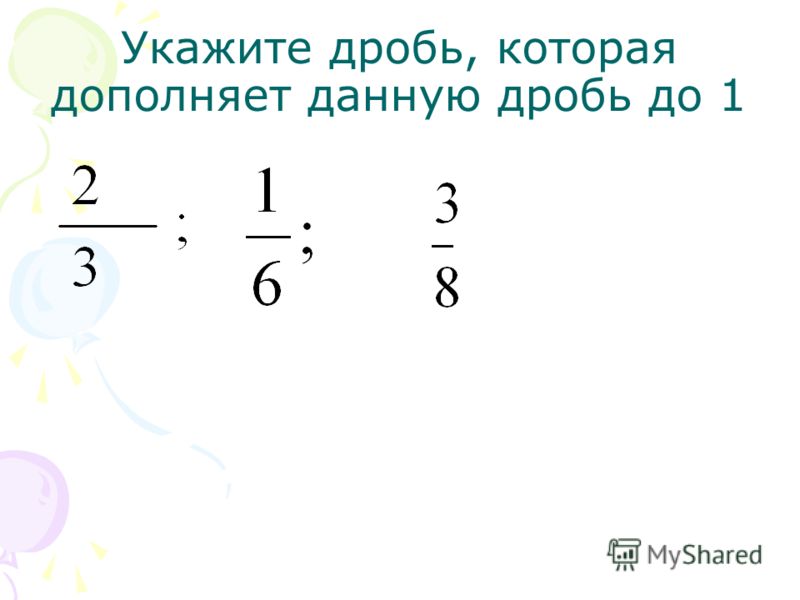

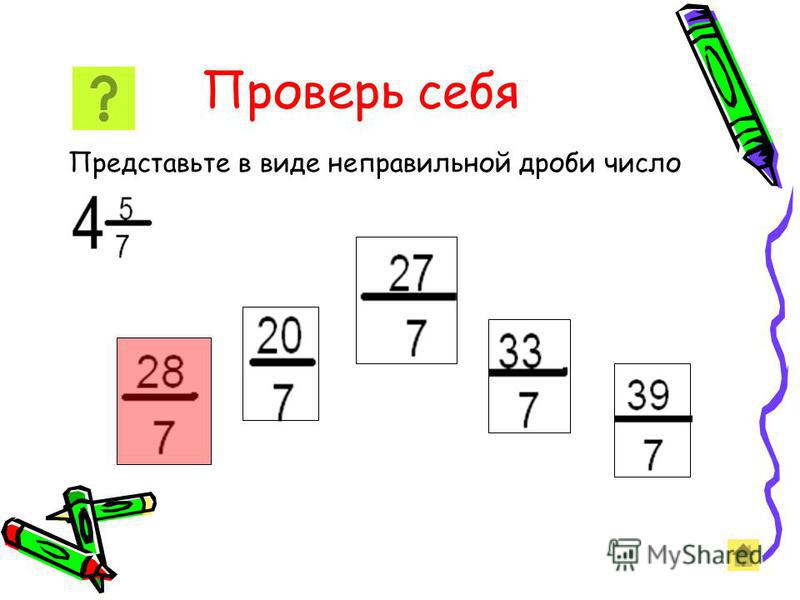

 Положительные неправильные дроби всегда больше или равны 1.
Положительные неправильные дроби всегда больше или равны 1. Второй факт, что смешанные числа представляют собой сумму натурального числа и дроби, можно увидеть, сделав следующие наблюдения.
Второй факт, что смешанные числа представляют собой сумму натурального числа и дроби, можно увидеть, сделав следующие наблюдения.
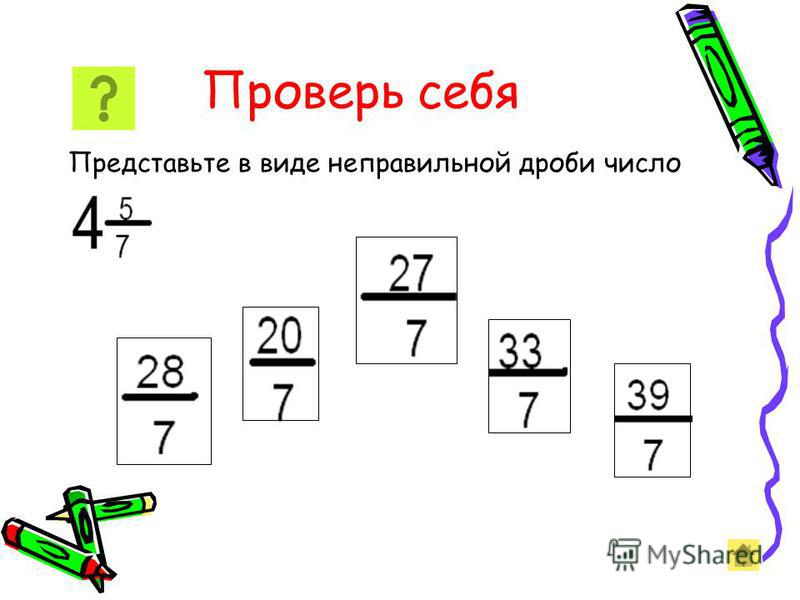 Чтобы указать умножение, нам нужно будет использовать символ умножения (например, \(\cdot\))
Чтобы указать умножение, нам нужно будет использовать символ умножения (например, \(\cdot\))






 определение смешанного числа.
определение смешанного числа.
 Например, если после запятой стоит только одно число (другими словами, число в десятом разряде), число будет умножено на \(\frac{10}{10}\). Если после запятой два числа (последняя цифра стоит в сотых), мы должны умножить число на \(\frac{100}{100}\) и так далее. После умножения упрощаем дробь.
Например, если после запятой стоит только одно число (другими словами, число в десятом разряде), число будет умножено на \(\frac{10}{10}\). Если после запятой два числа (последняя цифра стоит в сотых), мы должны умножить число на \(\frac{100}{100}\) и так далее. После умножения упрощаем дробь. Теперь превратим неправильную дробь в смешанное число.
Теперь превратим неправильную дробь в смешанное число.
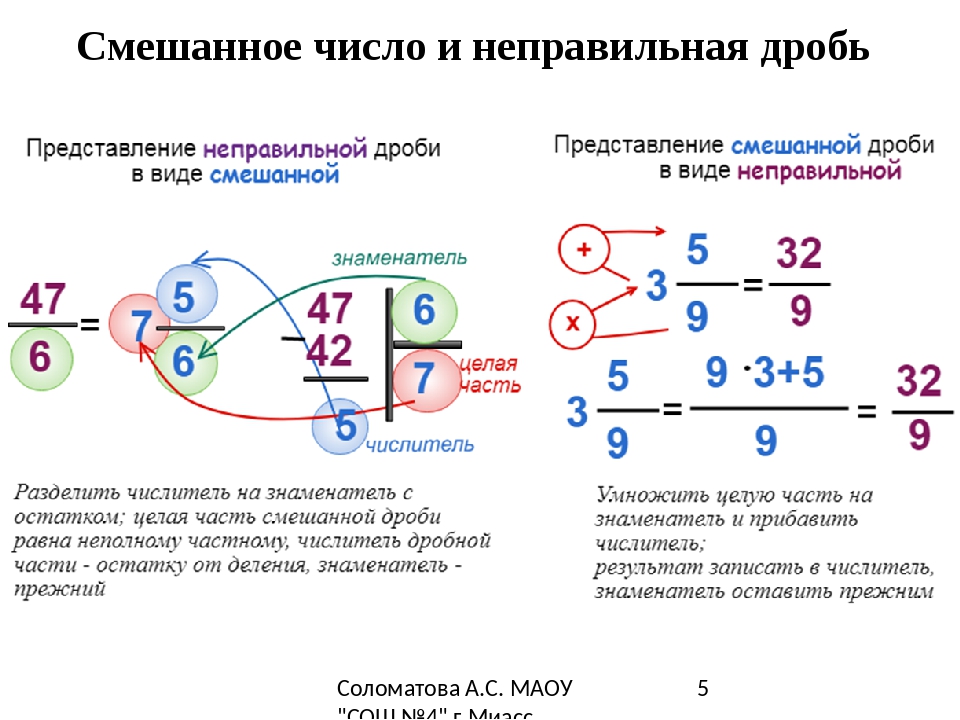 Спасибо за просмотр и удачной учебы!
Спасибо за просмотр и удачной учебы!
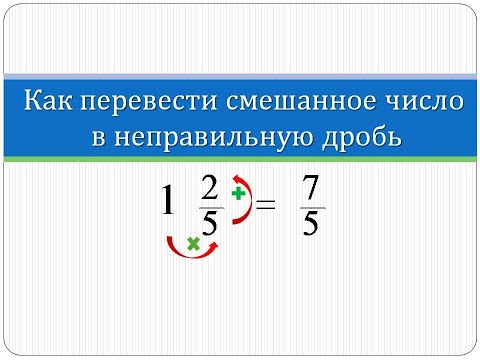
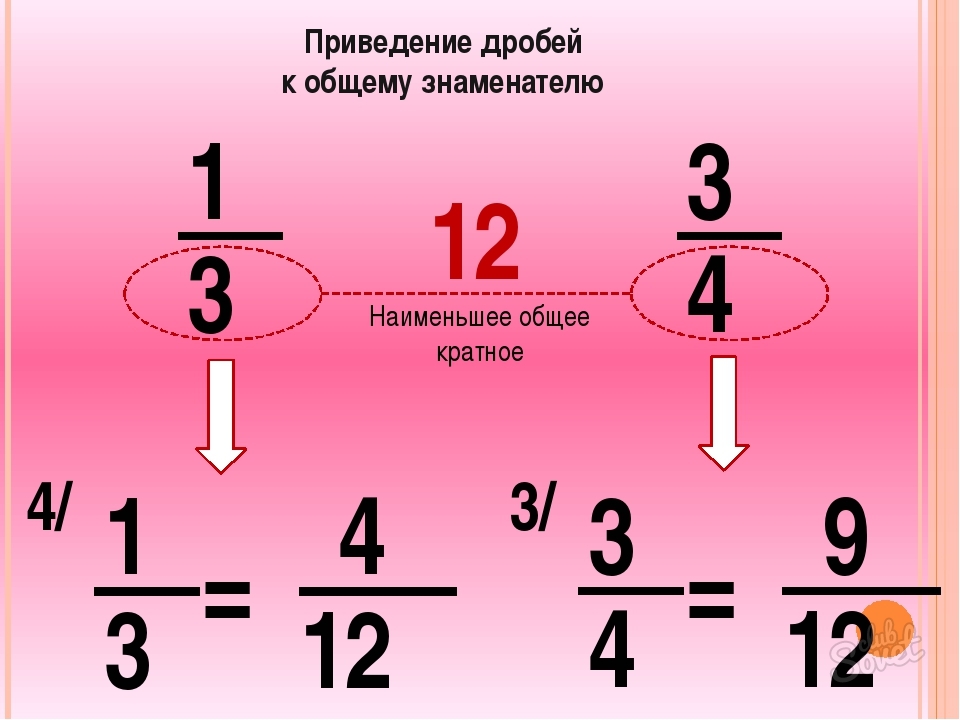 Целое число для нашего смешанного числа — это частное 3. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{13}{4}=3\frac {1}{4}\).
Целое число для нашего смешанного числа — это частное 3. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{13}{4}=3\frac {1}{4}\).
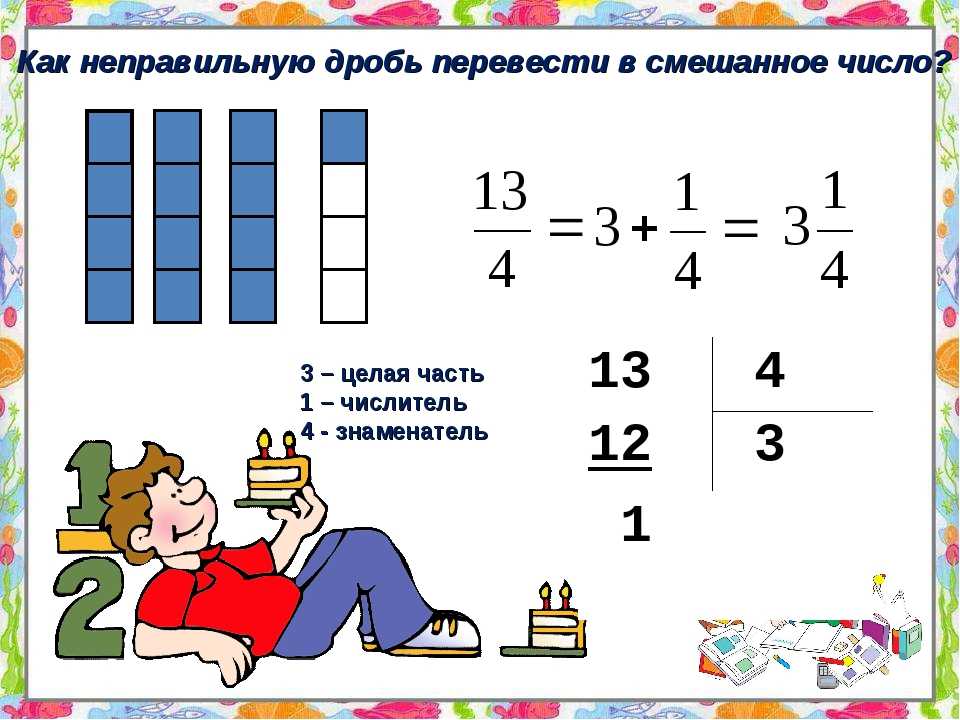

 Целое число для нашего смешанного числа — это частное 10. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 5. Итак, \(\frac{51}{5}=10\frac {1}{5}\).
Целое число для нашего смешанного числа — это частное 10. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 5. Итак, \(\frac{51}{5}=10\frac {1}{5}\).


 Целое число для нашего смешанного числа — это частное 4. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 2. Итак, \(\frac{9{2}=4\frac{1}{2}\).
Целое число для нашего смешанного числа — это частное 4. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 2. Итак, \(\frac{9{2}=4\frac{1}{2}\). Целое число для нашего смешанного числа — это частное от 1. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{5}{4}=1\frac {1}{4}\).
Целое число для нашего смешанного числа — это частное от 1. Числитель правильной дроби — остаток от 1, а знаменатель — делитель 4. Итак, \(\frac{5}{4}=1\frac {1}{4}\).
 0023
0023 


 3 равно три четверти от 4.
3 равно три четверти от 4. ниже) называются так же, как и правильные дроби.
ниже) называются так же, как и правильные дроби.
 Какое отношение имеет
Какое отношение имеет «Одна треть, две трети».
«Одна треть, две трети». «5 — это половина 10». «6 — это половина от 12». И так далее. Написать «6 — это ½ от 12», как, к сожалению, делают некоторые, — вульгарно.
«5 — это половина 10». «6 — это половина от 12». И так далее. Написать «6 — это ½ от 12», как, к сожалению, делают некоторые, — вульгарно. Разрезаем леску дважды.
Разрезаем леску дважды. С 90 005
С 90 005 Запишите частное (4), а остаток (1) запишите как числитель дроби; знаменатель остается прежним.
Запишите частное (4), а остаток (1) запишите как числитель дроби; знаменатель остается прежним.
 »
»
 Если он просто звонил, то сколько раз он будет звонить в следующие девять с половиной часов?
Если он просто звонил, то сколько раз он будет звонить в следующие девять с половиной часов? Это показано ниже для смешанного числа две и три четверти.
Это показано ниже для смешанного числа две и три четверти.
 0028 5/3 в форму.
0028 5/3 в форму.

 Дроби — это числовые значения, которые представляют собой часть или часть целого. Например, посмотрите на пиццу ниже.
Дроби — это числовые значения, которые представляют собой часть или часть целого. Например, посмотрите на пиццу ниже. Здесь, поскольку 3 меньше 4, дробь правильная.
Здесь, поскольку 3 меньше 4, дробь правильная. В виде смешанной дроби мы можем записать это как $1$ и $\frac{1}{4}$ пиццы или $1\frac{1}{4}$ пиццы.
В виде смешанной дроби мы можем записать это как $1$ и $\frac{1}{4}$ пиццы или $1\frac{1}{4}$ пиццы.


