3 корень квадратный 2: сколько будет 3 корня из 2 в квадрате

Математический анализ. (Виленкин)

Математический анализ. (Виленкин)

Виленкин Н.Я., Шварцбурд С.И. Математический анализ. Учебное пособие для IX—X классов средних школ с математической специализацией. M., Просвещение, 1969 г. Учебное пособие для школ с математической специализацией, снабженное большим количеством задач и упражнений. Как и вышедшая ранее (1968 г.) книга «Алгебра» того же авторского коллектива, может быть использована преподавателями и учащимися общеобразовательной школы. Оглавление ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ ВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств. 8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2. Метод разложения на множители. 3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 3. Сокращение показателей и приведение корней к общему показателю. 4. Извлечение корня из произведения и степени. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень. 6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений. 8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 2. Выражение степенных сумм 3. Основная теорема о симметрических многочленах от двух переменных. 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения. § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости. § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 3. Разложение на множители многочленов с действительными коэффициентами. 4. Краткие исторические сведения. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2. Комбинаторные задачи. Продолжение § 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения

Является ли 2 корень 2 рациональным или иррациональным? – Обзоры Вики

Таким образом, 2 корень 2 является иррациональное число.

Отсюда, как вы меняете корень 2 на десятичную? √2 = 1.414

С помощью метода длинного деления вы найдете значения несовершенных квадратных значений, таких как корень 3, корень 5 и т. д.

Как найти квадратный корень из 2? Квадратный корень из 2, округленный до 10 знаков после запятой, равен 1. 4142135624. Это положительное решение уравнения x ² = 2 .
…
Корень квадратный из 2 в радикальной форме: √2.

1.	Что такое квадратный корень из 2?
2.	Является ли квадратный корень из 2 рациональным или иррациональным?
3.	Важные примечания относительно квадратного корня из 2

Дополнительно Является ли 2 идеальным квадратом? Например, произведение числа 2 само по себе равно 4. В этом случае 4 называется полным квадратом. Квадрат числа обозначается как n × n. Точно так же экспоненциальное представление квадрата числа равно n ² , обычно произносится как «n» в квадрате.
…
Пример 1.

Целое	Идеальный квадрат
2 х 2	4
3 х 3	9
4 х 4	16
5 х 5	25

Что такое рационализация знаменателя? Рационализация знаменателя означает процесс перемещения корня, например, кубический или квадратный корень из нижней части дроби (знаменатель) в верхнюю часть дроби (числитель). Таким образом, мы приводим дробь к простейшей форме, благодаря чему знаменатель становится рациональным. Иррациональный знаменатель.

Какое значение имеет 2 корень 2?

Значение 2√2 равно 2.828. Следовательно, 2√2 = 2(1.414) = 2.828.

Как добавить корень 2 и корень 2? √2 + √2 = 2√2 = √(2² x 2) = √8. Какой ответ я должен получить при добавлении root 2 и root 2? √2 + √2 = 2√2.

Является ли квадратный корень из 3 рациональным числом? Квадратный корень из 3 — это положительное действительное число, которое при умножении само на себя дает число 3… Квадратный корень из 3 равен иррациональное число.

2 — квадратное число — да или нет?

Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на само, полученное произведение называется квадратным числом, или точным квадратом, или просто «квадратом». Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — квадратные числа.

Также Почему в квадрате 2? Возведение числа n в степень 2 называется «возведением в квадрат», потому что полученное число n²соответствует площади квадрата со сторонами длиной n. Функция квадрата — чрезвычайно полезная функция в алгебре, тригонометрии и физике.

Что такое квадратный корень?

Квадратный корень числа равен обратная операция возведения числа в квадрат. Квадрат числа — это значение, которое получается, когда мы умножаем число само на себя, а квадратный корень числа — это коэффициент числа, который при умножении на себя дает исходное число.

Что означает сопряжение в математике? Математическое сопряжение формируется путем изменения знака между двумя членами в биноме. Например, сопряжение x + y равно x – y. Мы также можем сказать, что x + y сопряжено с x – y. Другими словами, два бинома сопряжены друг с другом.

Как рационализировать дроби?

Итак, чтобы рационализировать знаменатель, нам нужно избавиться от всех радикалов, которые находятся в знаменателе.

1. Шаг 1. Умножьте числитель и знаменатель на радикал, чтобы избавиться от радикала в знаменателе. …
2. Шаг 2: Убедитесь, что все радикалы упрощены. …
3. Шаг 3: При необходимости упростите дробь.

Как складывать дроби?

Чтобы сложить дроби, есть три простых шага:

1. Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают.
2. Шаг 2: сложите верхние числа (числители), поставьте полученный ответ над знаменателем.
3. Шаг 3: Упростите дробь (если возможно)

Чему равно 2 корня из 2 всего квадрата? Квадратный корень из 2 или корень из 2 представляется с помощью символа квадратного корня √ и записывается как √2, значение которого равно 1.414. Это значение широко используется в математике.
…
Похожие темы:

Таблица квадратного корня	Квадратный корень от 1 до 25
Квадратный корень из 3	Поиск квадратного корня
Уловки с квадратным корнем	Квадратный корень и кубический корень

Можно ли умножить 2 квадратных корня?

Умножение квадратных корней: пример вопроса № 2

При умножении квадратных корней вам разрешено умножать числа внутри квадратного корня. Затем упростите, если необходимо.

Чему равна сумма корня 2 корня 2? Сумма √2 и -√2 равна ноль (0).

2 корень 3 рациональный или иррациональный?

Следовательно, 2 + √3 является иррациональное число.

Является ли 3.14 рациональным числом? 3.14 можно записать в виде дроби двух целых чисел: 314100 и поэтому рационально. π нельзя записать в виде дроби от двух целых чисел.

Является ли квадратный корень из 3 2 рациональным?

Нет! √3/2 не является рациональным числом… Рациональное число определяется как число, которое может быть представлено как p/q, где p и q — целые числа, но q не равно нулю.

Является ли 2 совершенным числом? совершенное число, положительное целое число, равное сумма собственных делителей. Наименьшее совершенное число — 6, которое представляет собой сумму 1, 2 и 3. Другие совершенные числа — 28, 496 и 8,128.

Как выглядит 2 в квадрате?

Квадратное число — это число, умноженное само на себя. Это также можно назвать «числом в квадрате».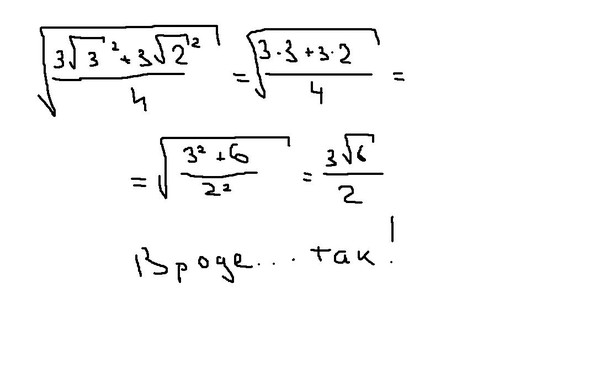 Символ квадрата — ².

Является ли произведение двух квадратных чисел квадратным числом? да. Пусть, согласно вопросу, «а» и «b» — квадратные числа. Следовательно, произведение 2 квадратных чисел тоже квадратное число.

Как бы вы алгебраически решили такие вопросы, как площадь в 3 раза больше квадратного корня из 2 + 5?

Алгебра 2 Радикалы

Сидней Л.

спросил 25.01.13

? Мой учитель научил нас делать это двумя разными способами, например, складывать и извлекать квадратный корень на калькуляторе, затем снова извлекать квадратный корень и извлекать квадратный корень из каждого из вариантов, пока они не совпадут. Пожалуйста помоги!

Подписаться І 7

Подробнее

Отчет

5 ответов от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Джордж С. ответил 25.01.13

Репетитор

5 (2)

Выпускник Университета Гумбольдта и Джорджтауна 9(1/2)?

Плохо представлен.

 

Голосовать за 2 голос против

Подробнее

Отчет

Билл Д. ответил 24.07.13

Репетитор

4.2 (6)

Репетиторство по математике и физике – учиться может каждый!

Посмотреть таких репетиторов

Смотрите таких репетиторов

При работе с радикалами (также известными как квадратные корни) правило стандартного арифметического процесса одинаково для выражений в скобках и радикалов. Я изучил этот процесс как:

«Пожалуйста, извините, моя дорогая тетя Салли»  для упрощения выражений

«Скобки, экспоненты, умножение, деление, сложение, вычитание»

Формулируемая задача может быть записана как:

3 X √(2 + 5). Чтение выражения слева направо,

1-й Упростите выражения в скобках, в данном случае 2 + 5 = 7,

Теперь наше исходное выражение: 3 X √7

Как учитель я принимаю 3√7 как упрощенный ответ.

Для цифрового ответа, теперь, когда мы заполнили все скобки, будем смотреть слева направо для всех экспоненциальных выражений.

Мы знаем, что √7 можно записать как 7 ^(1/2) ; Решая получаем 2,645751311.

Наше исходное выражение теперь равно 3 X 2645751311, что при умножении дает нам:

Ответ =   7,93725933

Голосовать за 1 голос против

Подробнее

Отчет

Дерон Т. ответил 19.06.13

Репетитор

Новое в Византе

ОБУЧЕНИЕ MADE EASY EASY

Смотрите таких репетиторов

Смотрите таких репетиторов

Мы ничего не спекулируем и не предполагаем в математике. Вы должны четко понимать, о чем проблема и что вам нужно найти. Мы можем предположить, что это круг, квадрат, прямоугольник или параллелограмм, но мы не отвечаем на вопросы. Пожалуйста, отправьте повторно с подробностями.

Голосовать за 0 голос против

Подробнее

Отчет

Сэм М. ответил 31.03.13

Репетитор

4,8 (121)

Мистер Добивается Результатов

Смотрите таких репетиторов

Смотрите таких репетиторов

Вот что вы делаете.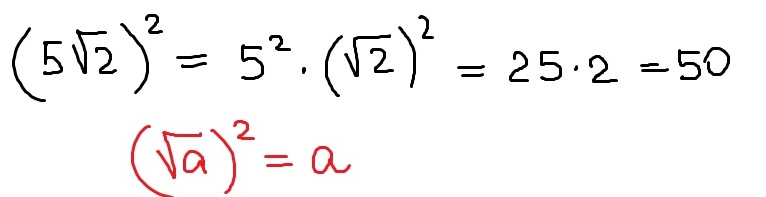 Говорят, что ПЛОЩАДЬ в 3 раза больше квадратного корня из 2 + 5. Я предполагаю, что под 2 + 5 вы подразумеваете 7. Если число 5 НЕ в радикале, то все это будет 5 + 3sqrt (2), но я интерпретировал это как 3(sqrt(7)).

Теперь, зная, что площадь этой фигуры равна 3sqrt(7), способ, которым вы вычисляете другие измерения фигуры, зависит от того, какой она формы. Если это круг, то вы можете найти радиус, и вы получите (3(sqrt(7))/pi. Затем возьмите квадратный корень из ЭТОГО числа, и у вас будет точный радиус, насколько точно вы хотите его округлить. Боже, благослови калькуляторы. Ответ около 1,59.. Это радиус круга. Его диаметр составляет около 3,18, а окружность около 9,99. Вы можете понять все это с помощью шпаргалки по геометрии.

С другой стороны, если вы ищете квадрат, то вы просто берете квадратный корень. Не беспокойтесь о числе пи. Это просто квадратный корень из 3sqrt(7). Это примерно 2,82. 2,82 — это размер (приблизительно) каждой из четырех сторон квадрата. Кстати, периметр квадрата в сумме составляет около 11,27.

Если фигура представляет собой прямоугольник, то вы просто берете ЛЮБУЮ пару чисел, которые вам нравятся, и пока они имеют произведение 3squrt(7), все в порядке. Вы можете начать с 1 и 3sqrt(7) и, конечно же, получите именно такую ​​площадь. Периметр такого прямоугольника будет разным, но всегда будет больше 11,27. Я знаю это, потому что (11.27) — это периметр квадрата, а квадрат — это четырехсторонняя фигура, которая МАКСИМАЛЬНО увеличивает площадь при заданной длине периметра.

Престижность и не останавливайтесь на достигнутом

Мистер Добивается Результатов

Голосовать за 0 голос против

Подробнее

Отчет

Шейла М. ответил 26.01.13

Репетитор

4.9 (63)

Дружелюбный профессор математики колледжа — понимает опасения студентов по поводу математики 92) = sqrt (3 рад 2 + 5)

x = sqrt (3 рад 2 + 5)

Внимательно используйте калькулятор, чтобы определить ответ.
Надеюсь, это помогло.

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

квадратный корень из 12 — Googlesuche

AlleBilderShoppingVideosMapsNewsBücher

suchoptionen

квадратный корень(12) =

3. 46410162

Ähnliche Fragen

Что такое упрощенный квадратный корень из 12?

Что такое 12 квадратный корень из 2 упрощенно?

Почему квадратный корень из 12?

Как найти квадратный корень из 12? — Cuemath

www.cuemath.com › алгебра › квадратный корень из 12

Квадратный корень из 12 выражается как √12 в радикальной форме и как (12)½ или (12)0,5 в экспоненте форма. Квадратный корень из 12, округленный до 5 десятичных знаков …

Рациональный корень из 12… · Как найти корень квадратный…

Корень квадратный из 12 — YouTube

www.youtube.com › смотреть

26.07.2021 · В этом видео я показать, как упростить квадратный корень из 12, оценку и квадратный корень до 5 знаков.
Dauer: 1:54
Прислан: 26.07.2021

квадратный корень из 12 — YouTube

www.youtube.com › смотреть

29.01.2019 · Колледж Алгебра. квадратный корень из 12. 33K показов 4 года назад Алгебра в колледже · Math Guy Zero . ..
Дауэр: 1:18
Gepostet: 29.01.2019

Bilder

Alle Angeigen

Alle Anzeigen

кв. корень из 12 представлен в радикальной форме как √12, что равно 2√3. Так как 2√3 не может быть далее упрощено, следовательно, такие корни …

Простые числа от 1 до 50: делимые числа
Латинские буквы от 1 до 100: длина окружности
Рациональные числа: угол рефлекса
График обратных тригонометрических функций: тождества по математике для 9 класса

Квадратный корень из 12 — значение, метод расчета, примеры решения

www.vedantu.com › математика › квадратный корень из -12

Квадратный корень из 12: 3,4641016151377544 · Квадратный корень из 12 в экспоненциальной форме: (12)½ или (12)0,5 · Квадратный корень из 12 в радикальной форме: √12 или 2 √3 …

Квадрат Root Of 12 — Osmo

www.playosmo.com › … › Квадратный корень

Следовательно, квадратный корень из 12 равен 3,464. Как найти квадратный корень из минус 12? Квадратный корень из 12 до 10 знаков после запятой равен 3,4641016151.