3 сигма: Правило трех сигм (3-sigma rule) · Loginom Wiki

Правило трёх сигм | это… Что такое Правило трёх сигм?

ТолкованиеПеревод

Правило трёх сигм

Стандартное отклонение (иногда среднеквадратичное отклонение) — в теории вероятности и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно её математического ожидания. Измеряется в единицах измерения самой случайной величины. Равен корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

где  — стандарт, стандартное отклонение, несмещенная оценка среднеквадратического отклонения случайной величины X относительно её математического ожидания;  — дисперсия;  — i-й элемент выборки;  — среднее арифметическое выборки;  — объём выборки.

Следует отметить отличие стандарта (в знаменателе n − 1) от корня из дисперсии(среднеквадратического отклонения)(в знаменателе n), при малом объёме выборки оценка дисперсии через последнюю величину является несколько смещенной, при бесконечно большом объёме выборки разница между указанными величинами исчезает. Выборка — лишь часть генеральной совокупности. Генеральная совокупность — абсолютно все возможные результаты. Получить результат, не входящий в генеральную совокупность абсолютно невозможно в принципе. Для случая с бросанием монетки генеральной совокупностью является : решка, ребро, орел. а вот пара орел-решка уже лишь выборка. Для генеральной совокупности математическое ожидание совпадает с истинным значением оцениваемого параметра. А вот для выборки не факт. Математическое ожидание выборки имеет смещение относительно истинного значения параметра. В силу этого, среднеквадратичная ошибка больше чем дисперсия, так как дисперсия — математическое ожидание квадрата отклонения от среднего значения, а среднеквадратичное отклонение — математическое ожидание отклонения от истинного значения.

Разница в том, от чего ищем отклонение, когда дисперсия, то от среднего и не важно истинное это среднее или ошибочно, а когда среднеквадратичное отклонение, то ищем отклонение от истинного значения.

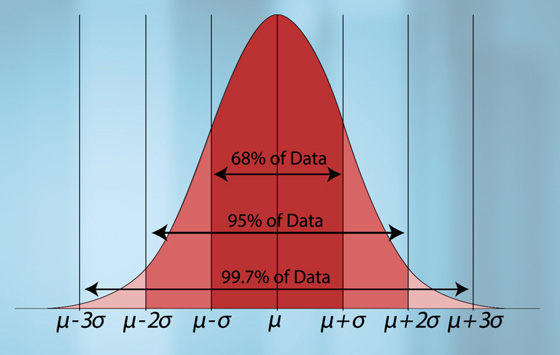
Правило 3-х сигм () — практически все значения нормально распределённой случайной величины лежат в интервале . Более строго — не менее чем с 99,7 % достоверностью, значение нормально распределенной случайной величины лежит в указанном интервале. При условии что величина истинная, а не полученная в результате обработки выборки. Если же истинная величина неизвестна, то следует пользоваться не σ, а s. Таким образом, правило 3-х сигм преобразуется в правило трех s

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать реферат

• Правило умножения
• Правило фаз Гиббса

Полезное

Правила 2 и 3 сигма

Правила 2 и 3 сигма полезно знать. Они часто используются на практике. Смысл этих правил состоит в том, что если от точки среднего или от точки максимума плотности нормального распределения отложить вправо и влево соответственно два и три стандартных отклонения (2 и 3 сигма), то площадь под графиком нормальной плотности, подсчитанная по этому промежутку, будет соответственно равна 95,45% и 99,73% всей площади под графиком.

Другими словами, это можно выразить следующим образом: 95,45% и 99,73% всех независимых наблюдений из нормального распределения лежат в пределах двух и трех стандартных отклонений от среднего значения.

Это правило также легко проверить с помощью вероятностного калькулятора. Выберите нормальное распределение в списке распределений, задайте, например, стандартные параметры: среднее = 0, стандартное отклонение = 1, пометьте опцию

Two-tailed (Двухсторонний), в строке X задайте 2 (два стандартных отклонения), нажмите Compute, в строке р появится значение 0,9545 (рисунок 2.6).

В поле Density Function (Функция плотности) вероятностного калькулятора показана заштрихованная площадь под графиком плотности, в поле р показано значение 0,9545.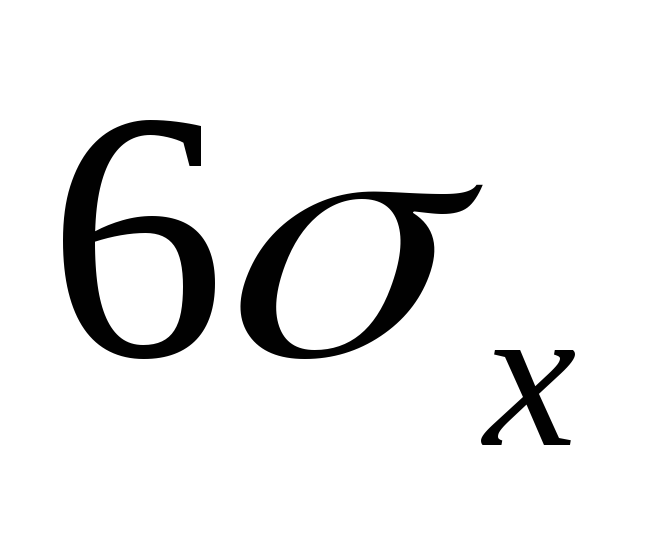 Переходя к процентам, имеем 95,45%. Заштрихованная площадь составляет 95,45% всей площади под графиком.

Рисунок 2.6 – Иллюстрация к правилу 2 сигм

Выберите нормальное распределение, задайте стандартные параметры: среднее = 0, стандартное отклонение = 1, пометьте опцию Two-tailed

в строке X задайте 3 (три стандартных отклонения), нажмите Compute, в строке р появится значение 0,9973 (рисунок 2.7).

Рисунок 2.7 – Иллюстрация к правилу 3 сигм

Данные правила действуют при любых значениях среднего и стандартного отклонения нормального закона.

Логарифмически-нормальное распределение

Плотность распределения имеет одно максимальное значение и несимметрично. График плотности логарифмически-нормального распределения показан на рисунке 2.8 а.

В списке распределений вероятностного калькулятора выберите Log-Normal (Логнормальное распределение), рисунок 2. 8 б).

а) б)

Рисунок 2.8 – Логарифмически-нормальное распределение в вероятностном калькуляторе: а) задание; б) плотность распределения

Задания для выполнения

1. С помощью вероятностного калькулятора вычислите вероятности при заданном среднем и стандартном отклонении (таблица 2.1).

2. Дайте объяснение полученным результатам.

Таблица 2.1 – Задание для выполнения расчетов

№ варианта	Среднее	Стандартное отклонение	Минимум	Максимум
1	10	8	8	12
2	10	5	8	12
3	10	3	8	12
4	10	1	8	12
5	10	0,5	8	12
6	20	5	8	12
7	15	5	8	12
8	10	5	8	12
9	5	5	8	12
10	1	5	8	12

Статистический расчет пределов трех сигм на примере

По

Уилл Кентон

Полная биография

Уилл Кентон — эксперт в области экономики и инвестиционного законодательства. Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.

Узнайте о нашем редакционная политика

Обновлено 31 мая 2022 г.

Рассмотрено

Эми Друри

Рассмотрено Эми Друри

Полная биография

Эми является членом ACA, генеральным директором и основателем OnPoint Learning, финансовой обучающей компании, проводящей обучение финансовых специалистов. Она имеет почти двадцатилетний опыт работы в финансовой отрасли и в качестве финансового инструктора для профессионалов отрасли и частных лиц.

Узнайте о нашем Совет финансового контроля

Факт проверен

Кирстен Рорс Шмитт

Факт проверен Кирстен Рорс Шмитт

Полная биография

Кирстен Рорс Шмитт — опытный профессиональный редактор, писатель, корректор и специалист по проверке фактов. У нее есть опыт в области финансов, инвестиций, недвижимости и всемирной истории. На протяжении всей своей карьеры она писала и редактировала контент для многочисленных потребительских журналов и веб-сайтов, составляла резюме и контент для социальных сетей для владельцев бизнеса, а также создавала материалы для академических кругов и некоммерческих организаций. Кирстен также является основателем и директором Your Best Edit; найдите ее на LinkedIn и Facebook.

Узнайте о нашем редакционная политика

Инвестопедия / Джули Бэнг

Что такое предел трех сигм?

Пределы трех сигм — это статистический расчет, при котором данные находятся в пределах трех стандартных отклонений от среднего значения. В бизнес-приложениях три сигмы относятся к процессам, которые работают эффективно и производят товары высочайшего качества.

Пределы трех сигм используются для установки верхнего и нижнего контрольных пределов в диаграммах статистического контроля качества.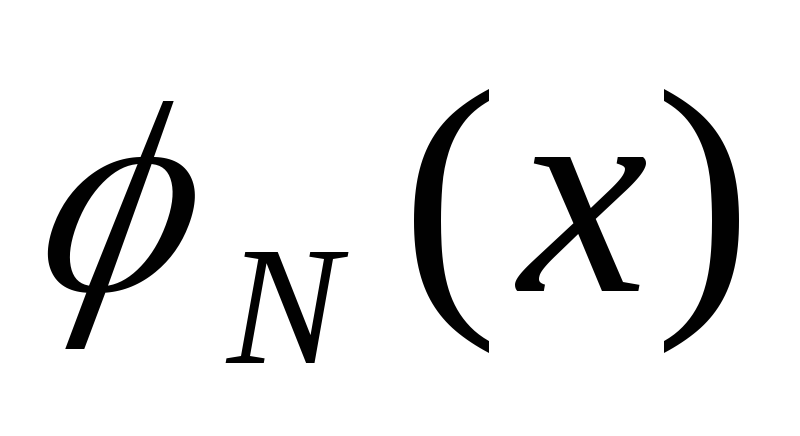 Контрольные карты используются для установления ограничений для производственного или бизнес-процесса, находящегося в состоянии статистического контроля.

Основные выводы:

• Пределы трех сигм (пределы трех сигм) — это статистический расчет, который относится к данным в пределах трех стандартных отклонений от среднего значения.
• Пределы трех сигм используются для установки верхнего и нижнего контрольных пределов в диаграммах статистического контроля качества.
• На колоколообразной кривой данные, лежащие выше среднего и за линией трех сигм, представляют менее 1% всех точек данных.

Понимание пределов трех сигм

Контрольные карты, также известные как карты Шухарта, названы в честь Уолтера А. Шухарта, американского физика, инженера и статистика (1891–1967). Контрольные карты основаны на теории о том, что даже идеально спроектированным процессам присуща определенная степень изменчивости выходных измерений.

Контрольные карты определяют, есть ли контролируемые или неконтролируемые изменения в процессе. Говорят, что изменения в качестве процесса, вызванные случайными причинами, находятся под контролем; К неконтролируемым процессам относятся как случайные, так и особые причины изменчивости. Контрольные карты предназначены для определения наличия особых причин.

Для измерения вариаций статистики и аналитики используют показатель, известный как стандартное отклонение, также называемое сигмой. Сигма — это статистическое измерение изменчивости, показывающее, насколько сильно отличается среднестатистическое значение.

Сигма измеряет, насколько сильно наблюдаемые данные отклоняются от среднего или среднего; инвесторы используют стандартное отклонение для оценки ожидаемой волатильности, известной как историческая волатильность.

Чтобы понять это измерение, рассмотрим нормальную кривую нормального распределения, которая имеет нормальное распределение. Чем дальше вправо или влево точка данных записана на кривой нормального распределения, тем выше или ниже, соответственно, данные, чем среднее значение. С другой точки зрения, низкие значения указывают на то, что точки данных близки к среднему; высокие значения указывают на то, что данные широко распространены и не близки к среднему значению.

Пример расчета предела трех сигм

Давайте рассмотрим производственную фирму, которая проводит серию из 10 тестов, чтобы определить, есть ли различия в качестве ее продукции. Точки данных для 10 тестов: 8,4, 8,5, 9,1, 9,3, 9,4, 9,5, 9,7, 9,7, 9,9 и 9,9.

1. Сначала рассчитайте среднее значение наблюдаемых данных. (8,4 + 8,5 + 9,1 + 9,3 + 9,4 + 9,5 + 9,7 + 9,7 + 9,9 + 9,9) / 10, что равно 93,4 / 10 = 9,34.
2. Второй, вычислить дисперсию набора. Дисперсия — это разброс между точками данных, который рассчитывается как сумма квадратов разницы между каждой точкой данных и средним значением, деленная на количество наблюдений. Первый квадрат разности будет рассчитан как (8,4 — 9,34) ² = 0,8836, второй квадрат разности будет равен (8,5 — 9,34) ² = 0,7056, третий квадрат может быть рассчитан как (9,1 — 9,34) ² = 0,0576 и так далее. Сумма различных квадратов всех 10 точек данных равна 2,564. Таким образом, дисперсия составляет 2,564/10 = 0,2564.
3. В-третьих, вычислить стандартное отклонение, которое представляет собой просто квадратный корень из дисперсии. Итак, стандартное отклонение = √0,2564 = 0,5064.
4. В-четвертых, вычислить три сигмы, что на три стандартных отклонения выше среднего. В числовом формате это (3 x 0,5064) + 9,34 = 10,9. Поскольку ни один из данных не находится на таком высоком уровне, процесс производственного тестирования еще не достиг уровня качества «три сигмы».

Особые указания

Термин «три сигмы» указывает на три стандартных отклонения. Шухарт установил пределы трех стандартных отклонений (3 сигмы) в качестве рационального и экономичного ориентира для минимальных экономических потерь. Пределы трех сигм устанавливают диапазон для параметра процесса на уровне контрольных пределов 0,27%. Контрольные пределы по трем сигмам используются для проверки данных, полученных в процессе, и проверки того, находятся ли они в пределах статистического контроля. Это делается путем проверки того, находятся ли точки данных в пределах трех стандартных отклонений от среднего значения. Верхний контрольный предел (UCL) устанавливается на три сигма выше среднего, а нижний контрольный предел (LCL) устанавливается на три сигма ниже среднего.

Поскольку около 99,73% контролируемого процесса будет происходить в пределах плюс-минус три сигмы, данные процесса должны аппроксимировать общее распределение вокруг среднего значения и в заранее определенных пределах. На колоколообразной кривой данные, лежащие выше среднего и за линией трех сигм, представляют менее 1% всех точек данных.

Источники статей

Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем редакционная политика.

1. Национальный центр биотехнологической информации. «Уолтер А. Шухарт, 1924 год, и фабрика в Хоторне».

Объяснение: Сигма | Новости Массачусетского технологического института

Это вопрос, который возникает практически при каждом крупном новом открытии в науке или медицине: что делает результат достаточно надежным, чтобы его можно было воспринимать всерьез? Ответ связан со статистической значимостью, а также с суждениями о том, какие стандарты имеют смысл в данной ситуации.

Единицей измерения, обычно используемой, когда речь идет о статистической значимости, является стандартное отклонение, выражаемое строчной греческой буквой сигма (σ). Этот термин относится к степени изменчивости в заданном наборе данных: сгруппированы ли все точки данных вместе или сильно разбросаны.

Во многих случаях результаты эксперимента следуют так называемому «нормальному распределению». Например, если вы подбросите монету 100 раз и подсчитаете, сколько раз она выпадет орлом, средний результат будет 50. Но если вы проведете этот тест 100 раз, большинство результатов будет близко к 50, но не точно. Вы получите почти столько же случаев с 49, или 51. Вы получите немало 45-х или 55-х, но почти не 20-х или 80-х. Если вы нанесете свои 100 тестов на график, вы получите хорошо известную форму, называемую колоколообразной кривой, которая выше в середине и сужается с обеих сторон. Это нормальное распределение.

Отклонение показывает, насколько данная точка данных удалена от среднего значения. В примере с монетой результат 47 имеет отклонение в три раза от среднего (или «среднего») значения 50. Стандартное отклонение — это просто квадратный корень из среднего значения всех квадратов отклонений. Одно стандартное отклонение или одна сигма, нанесенное выше или ниже среднего значения на этой кривой нормального распределения, будет определять область, которая включает 68 процентов всех точек данных. Две сигмы выше или ниже включают около 95 процентов данных и три сигмы будут включать 99,7 процента.

Итак, когда конкретная точка данных или результат исследования считается значимым? Стандартное отклонение может служить критерием: если точка данных отличается от тестируемой модели на несколько стандартных отклонений, это является убедительным доказательством того, что точка данных не согласуется с этой моделью. Однако, как использовать этот критерий, зависит от ситуации. Джон Цициклис, профессор электротехники Кларенса Дж. Лебеля в Массачусетском технологическом институте, который читает курс «Основы теории вероятностей», говорит: «Статистика — это искусство, в котором много места для творчества и ошибок». Часть искусства сводится к тому, чтобы решить, какие меры имеют смысл для данной ситуации.

Например, если вы проводите опрос о том, как люди планируют голосовать на выборах, принято считать, что два стандартных отклонения выше или ниже среднего, что дает 95-процентный уровень достоверности, являются разумными. Именно этот интервал в две сигмы имеют в виду социологи, когда указывают в своих выводах «границу погрешности выборки», например 3 процента.

Это означает, что если вы задали вопрос опроса всему населению и получили определенный ответ, а затем задали тот же вопрос случайной группе из 1000 человек, есть 95-процентная вероятность того, что результаты второй группы окажутся в пределах двух сигм от первого результата. Если опрос покажет, что 55 % всего населения поддерживает кандидата А, то в 95 % случаев результат второго опроса будет где-то между 52 и 58 %.

Конечно, это также означает, что в 5% случаев результат будет за пределами диапазона двух сигм. Такая большая неопределенность хороша для опроса общественного мнения, но, возможно, не для результата важного эксперимента, бросающего вызов ученым в понимании важного явления, такого как объявление прошлой осенью о возможном обнаружении нейтрино, движущихся быстрее скорости света в эксперименте. в Европейском центре ядерных исследований, известном как ЦЕРН.

Шесть сигм все еще могут быть ошибочными

Технически результаты этого эксперимента имели очень высокий уровень достоверности: шесть сигм. В большинстве случаев результат с пятью сигмами считается золотым стандартом значимости, что соответствует примерно одному шансу на миллион того, что результаты являются просто результатом случайных вариаций; Шесть сигм означают один шанс из полумиллиарда, что результат является случайным совпадением. (Популярная стратегия управления бизнесом под названием «Шесть сигм» происходит от этого термина и основана на введении строгих процедур контроля качества для сокращения потерь.)

Но в этом эксперименте ЦЕРН, который мог перевернуть столетние общепризнанные законы физики, подтвержденные тысячами различных тестов, этого все еще недостаточно. Во-первых, предполагается, что исследователи провели анализ правильно и не упустили из виду некоторый систематический источник ошибок. И поскольку результат был таким неожиданным и таким революционным, большинство физиков думает, что произошло именно это — какой-то необнаруженный источник ошибки.

Интересно, что другой набор результатов, полученных на одном и том же ускорителе частиц в ЦЕРН, интерпретировался совершенно по-разному.

В прошлом году также было объявлено о возможном обнаружении так называемого бозона Хиггса — теоретической субатомной частицы, которая поможет объяснить, почему частицы весят что-то, а не ничего. Этот результат имел уровень достоверности всего 2,3 сигма, что соответствует примерно одному шансу из 50 того, что результат был случайной ошибкой (98-процентный уровень достоверности). Тем не менее, поскольку он соответствует ожиданиям, основанным на современной физике, большинство физиков считают, что результат, вероятно, будет правильным, несмотря на гораздо более низкий уровень статистической достоверности.

Значимый, но ложный

Но в других областях все становится сложнее. «То, где этот бизнес становится действительно сложным, — это социальные и медицинские науки», — говорит Цициклис. Например, широко цитируемая статья 2005 года в журнале Public Library of Science под названием «Почему большинство опубликованных результатов исследований ошибочны» содержит подробный анализ множества факторов, которые могут привести к необоснованным выводам. Однако они не учитываются в типичных используемых статистических показателях, включая «статистическую значимость».

В документе отмечается, что, рассматривая большие наборы данных с разных точек зрения, легко найти примеры, соответствующие обычным критериям статистической значимости, даже если на самом деле это просто случайные вариации. Помните пример с опросом, где один раз из 20 результат просто случайным образом выходит за эти границы «значимости»? Что ж, даже при уровне значимости в пять сигм, если компьютер будет перебирать миллионы возможностей, будут обнаружены некоторые совершенно случайные паттерны, соответствующие этим критериям. Когда это происходит, «вы не публикуете те, которые не проходят» тест значимости, говорит Цициклис, но некоторые случайные корреляции будут создавать видимость реальных результатов — «так что в конечном итоге вы просто публикуете случайности».

Один из примеров: во многих опубликованных за последнее десятилетие статьях утверждается о значительной корреляции между определенными видами поведения или мыслительных процессов и изображениями мозга, полученными с помощью магнитно-резонансной томографии или МРТ.