3 sin 1 x pi: Mathway | Популярные задачи — Таловская средняя школа

36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x 13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град.

2+n-72)=1/(n+9)

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x

92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

ГЛАВА 2 Обратные тригонометрические функции

Доступ к ответам NCERT.

1. Найдите значение tan ^-1 [tan (5π/6)] + cos ^-1 [cos (13π/6)]

Solution:

We know that,

tan ^-1 tan x = x, x ∈ (-π/2, π/2)

And, here

TAN ^-1 TAN (5π/6). ^-1 потому что х = х; x ∈ [0, π]

Итак,

COS ^-1 COS (13π/6) ≠ 13π/6 AS 13π/6 ∉ [0, π]

теперь,

^{9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999919. ^{919 ^{19 9 ^{919 ^{919. 5π/6)] + cos ^-1 [cos (13π/6)]}}}}}
= tan ^-1 [tan (π – π /6)] + cos ^-1 [cos ( 2π + π/6)]
= tan ^-1 [ -tan π /6] + cos ^-1 [ -cos (7π/6)]

619 = – tan ^-1 [tan π /6] + cos ^-1 [cos (π/6)]

= – π /6 + π /6

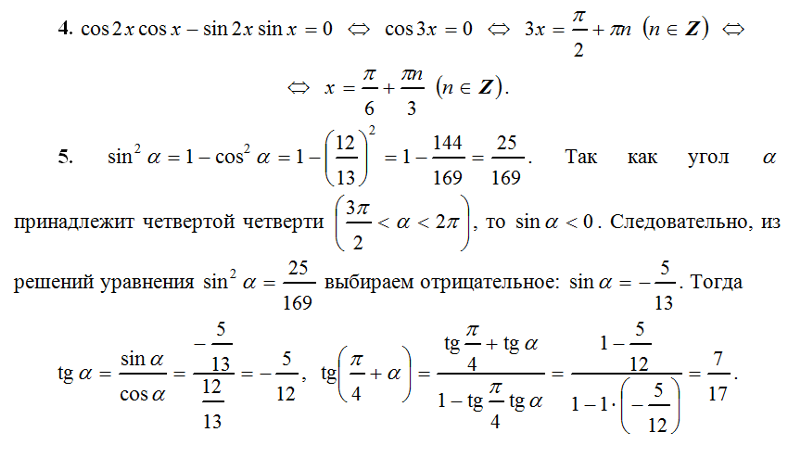2. Evaluate cos[cos ^-1 (-√3/2) + π/6]

Solution:

3 , Докажите, что кроватка (π/4 – 2 кроватка ^-1 3) = 7

Решение:

Re-writing the given,

L.H.S = R.H.S

– Hence Proved

4. Найдите значение tan ^-1 (-1/√3) + cot ^-1 (1/√3) + tan ^-1 (sin (-π/2))

Решение :

Дано,

tan ^-1 (-1/√3) + cot ^-1 (1/√3) + tan ^-1 (sin (-π/2))

08
08

5. Найдите значение тангенса ^-1 (тангенс 2π/3).

Решение:

Мы знаем,

TAN ^-1

TAN -1

6. Show that 2 tan ^-1 (-3) = – π/2 + tan ^-1 (-4/3)
Solution:
Принимая LHS = 2 tan ^-1 (-3) = -2 tan ^-1 3 (∵ tan ^-1 (-x) = – tan ^-1 x, x ∈ R)

= правая сторона
– Отсюда доказано.

7. Find the real solution of the equation
Solution:
Given equation,

Hence, действительные решения данного тригонометрического уравнения равны 0 и -1.

8. Найдите значение выражения sin (2 tan ^-1 1/3) + cos (tan ^-1 2√2).
Решение:
.
9. Если 2 тангенс ^-1 (cos θ) = тангенс ^-1 (2 cosec θ), то покажите, что θ = π/4.
Решение:
Дано, 2 тангенс ^-1 (cos θ) = тангенс ^-1 (2 cosec θ)
So,

10. Show that cos (2 tan ^-1 1/7) = sin (4 tan ^-1 1/3).
Solution:
Taking L.H.S, we have

Thus, L.H.S = R. H.S
– Отсюда доказано
11. Решить уравнение cos (tan ^-1 x) = sin (cot ^-1 3/4).
Solution:
Given equation, cos (tan ^-1 x) = sin (cot ^-1 3/4)
Taking L.H.S,

На квадрат с обеих сторон,
16(x ² + 1) = 25
16x ² + 16 = 25
16x ² = 9
x ² = 9/16
Therefore, x = ± 3/4

12. Prove that
Solution:

Taking L. H.S,

= R.H.S
– Hence Proved
13. Find the simplified form of cos ^-1 [3/5 cos x + 4/5 sin x], x ∈ [-3π/4, π/4].
Решение:
У нас есть,
cos ^-1 [3/5 cos x + 4/5 sin x], x ∈ [-3π/4, π/4]
Теперь пусть cos α = 3/5

Итак, sin α = 4/5 и tan α = 4/3
cos ^-1 [3/5 cos x + 4/5 sin x]
⇒
1 [3/5 cos x + 4/5 sin x] = cos ^-1 [cos α cos x + sin α sin x]
= cos ^-1 [cos (α – x )]
= α -x
= TAN ^-1 4/3 -x
. 3/5 = SIN ^-1 77/85
Решение:
. 3/5
= желто-коричневый ^-1 8/15 + tan ^-1 3/4

– Hence proved
15. Show that sin ^-1 5/13 + cos
— 1 3/5 = tan ^-1 63/16
Solution:
Here, sin ^-1 5/13 = tan ^-1 5/12
А,
cos ^-1 3/5 = tan ^-1 4/3
Taking the L.H.S, we have

Thus, L.H.S = R.H.S
– Hence Proved
16. Prove that tan ^-1 1/4 + tan ^-1 2/9 = sin ^-1 1/√5
Solution :
Taking the LHS,

tan ^-1 1/4 + tan ^-1 2/9

= RHS
– Hence Proved
17. Find the value of 4 tan ^-1 1/5 – tan ^-1 1/239
Solution:
4 tan ^-1 1/5 – желто-коричневый ^-1 1/239
= 2 (tan ^-1 1/5) – tan ^-1 1/239

= 2 tan ^-1 5/12 – tan ^-1 1/239

Thus,
4 tan ^-1 1/5 – tan ^-1 1/239 = π/4
18. Покажите, что загар ^-1 (1/2 sin ^-1 3/4) = (4 – √7)/3 и обоснуйте, почему игнорируется другое значение (4 + √7)/3.
Solution:
We have, tan ^-1 (1/2 sin ^-1 3/4)
Let ½ sin ^-1 ¾ = θ ⇒ sin ^-1 ¾ = 2θ ⇒ sin 2θ = ¾
2 tan θ/ 1 + tan ² θ = ¾
3 tan ² θ – 8 tan θ + 3 = 0

Hence,

19. If a ₁ , a ₂ , a ₃ , …., a _n является арифметической прогрессией с общей разностью d, то оцените следующее выражение.

Решение:
Поскольку а ₁ , а ₂ , а ₃ , …. , а _n представляет собой арифметическую прогрессию с общей разностью d.
d = a ₂ – a ₁ = a ₃ – a ₂ = a ₄ – a ₃ = …… = a _n – a _{n- 1}
Итак,

06 20. Что из нижеперечисленного является основной ветвью cos-1 x?
(а) [-π/2, π/2] (б) (0, π) (в) [0. π] (d) [0, π] – {π/2}
Решение:
(c) [0. π]
Как мы знаем, ветвь главного значения cos ^-1 x равна [0, π].
21. Что из нижеперечисленного является основной ветвью cosec ^-1 х?
(а) (-π/2, π/2) (б) [0, π] – {π/2} (в) [-π/2, π/2] (г) [ -π/2, π/2] – {0}
Решение:
(d) [-π/2, π/2] – {0}
Поскольку главная ветвь cosec ^-1 x есть [-π/2, π/2] – {0}.
22. Если 3 tan ^-1 x + cot ^-1 x = π, то x равно
(a) 0 (b) 1 (c) -1 (d) ½
Solution:
(b) 1
Given, 3 tan ^-1 x + cot ^-1 x = π
2 tan ^-1 x + tan ^-1 x + cot ^-1 x = π
2 tan ^{— 1} x + π/2 = π (As tan ^-1 + cot ^-1 = π/2)
2 tan ^-1 x = π/2
tan ^-1 x = π/4
x = 1
23. The value of sin ^-1 cos 33π/5 равно
(a) 3π/5 (b) -7π/5 (c) π/10 (d) -π/10
Решение :
(г) -π/10

24. Область определения функции cos-1 (2x – 1) равна
(a) [0, 1] (b) [-1, 1] (c) [-1, 1 ] (d) [0, π]
Решение:
(a) [0, 1]
6 1, 1]
Таким образом, f(x) = cos-1 (2x – 1) определяется, если0906 0 ≤ 2x ≤ 2
Следовательно,
0 ≤ ≤ 1 0 ≤ 1
0 ≤ 1
9
9.
6
9
6
9 0 ≤ ≤ 1 0. √(x – 1) равно
(a) [1, 2] (b) [-1, 1] (c) [0, 1] (d) ни один из этих
Решение:
(a) [1, 2]
Мы знаем, что грех ^-1 x определено для x ∈ [-1, 1]
Итак, f(x) = sin ^-1 √(x – 1) определено, если ≤ √(x – 1) ≤ 1
0 ≤ x – 1 ≤ 1
1 ≤ x ≤ 2
Hence,
x ∈ [ 1, 2]
26. Если cos (sin ^-1 2/5 + cos ^-1 x) = 0, то x равен
(a) 1/5 (b) 2/5 (c) 0 (d) 1
Solution:
(b) 2/5
Given,
cos (sin ^-1 2/5 + cos ^-1 x) = 0
So, this can be rewritten as
sin ^-1 2/5 + cos ^-1 x = cos ^-1 0
sin ^-1 2/5 + cos ^-1 x = π/2
cos ^-1 x = π/2 – sin ^-1 2/5
cos ^-1 x = cos ^-1 2/5 [Since, cos ^-1 x + sin ^-1 x = π/2]
Следовательно,
x = 2/5
27.
No related posts.