Линейное уравнение с одной переменной 7 класс
Тема 2. МОДЕЛЬ ОФОРМЛЕНИЯ СЦЕНАРИЯ ДИСТАНЦИОННОГО УРОКА.
Краткая аннотация: Определение уравнения. Понятие решить уравнение. Определение корней уравнения. Правила нахождения компонентов уравнения. Первоначальное понятие равносильного уравнения. На данном уроке с помощью решения задач наглядно показывается целесообразность изучения уравнений.
Предмет Алгебра
Класс: 7
Тема: Линейное уравнение с одной переменной.
Тип урок: комбинированный
Форма урока: изучение нового материала
Необходимое оборудование и материалы для дистанционного урока: (компьютер с выходом в интернет, веб-камера, микрофон, презентация).
Требования к уровню ИКТ компетентности обучающихся (умение пользоваться электронной почтой, скайпом)
Тип доставки учебного материала (форма доставки материала — диалог — специально организованная интерактивная беседа учащегося с преподавателем посредством электронной почты, скайпа; вид доставки — виртуальный источник (материал получается из сети Интернет), технологии доставки – локальные телекоммуникационные сети). )
)
Цель урока:
1. Формировать умения и навыки решать уравнения, находить его корни
2. Развивать логическое мышление, познавательный интерес , а также навыки контроля и самоконтроля.
3. Приучать ученика к эстетическому оформлению записи, умению выслушивать и умению общаться.
Задачи урока:
— Образовательные задачи урока: усвоить определение уравнения и понятия «корни уравнения», уметь решать уравнения, содержащие 2-3 действия. Учить решать задачи с помощью уравнений.
— Воспитательные задачи урока: формировать привычку правильно, аккуратно записывать решение уравнений и задач. Учить самостоятельности и умению работать индивидуально.
— Развивающие задачи урока: при решении уравнений учить ученика использовать грамотно термины и понятия, выделять главное, анализировать, делать выводы и сравнивать.
Учебно-методическое обеспечение (указать авторов учебников, учебно-методических комплексов)
Время реализации занятия – 45 минут
Примерная структура дистанционного урока
№ | Название модуля | Дидактические функции | Деятельность учащегося | Время |
1. | Организационный момент. | Проверка готовности детей к уроку. Проведение релаксации и дыхательных упражнений. | Выполняют дыхательные упражнения | 3мин |
2. | Постановка целей урока. | Умение анализировать и делать выводы | Использование терминов и понятий данного урока | 3 мин |
3. | Актуализация опорных знаний и устная работа. | Устный опрос | Повторение пройденного материала | 5 мин |
4. | Объяснение нового материала | Усвоение определения «корня уравнения», «равносильных уравнений2. | Отвечает на проблемные вопросы | 10 мин |
5. | Физминутка | Зарядка для глаз | Выполняет упражнения | 4 мин |
6. | Тестирование | Закрепление знаний, умений, навыков | Выполняют тест | 8 мин |
7. | Самостоятельно | Проверка знаний, умений, навыков | решает не только простые уравнения в одно действие, но и в 2-3 действия, а также простейшие уравнения, которые либо не имеют корней, либо имеют бесконечно много корней | 9 мин |
8. | Д/зад. | Закрепление знаний, умений, навыков при решении уравнений | Записывают домашнее задание. | 1 мин |
9. | Итоги урока | Рефлексия учащегося | Самоанализ работы на уроке | 2 мин |
Технологии, методы:
Методы обучения: словесные, практические, наглядные.
Технология: Личностно-ориентированный подход к обучению
Создание ситуации успеха и сотрудничества.
Занимательная деятельность, способствующая формированию внутренней мотивации и, как следствие, стимулирование развития памяти, мышления.
Ход занятия.
Организационный момент:
— Придумано кем-то
Просто и мудро
При встрече здороваться:
-Доброе утро.
-Доброе утро!
-Солнцу и птицам.
— Доброе утро!
— Улыбчивым лицам.
— И каждый становится
Добрым, доверчивым…
Пусть доброе утро
Длится до вечера.
-Тема нашего урока « Уравнение и его корни ».
-Итак, начнём урок. Соберёмся с силами. В четыре приёма глубоко вдохнём воздух через нос и в пять приёмов с силой выдохнем, задувая воображаемую свечку. Повторим это 3 раза.
2.Постановка цели урока:
Целью сегодняшнего нашего урока будет — научиться находить корни уравнения, ввести определение равносильных уравнений, научиться заменять данное уравнение более простым уравнением, равносильным ему.
3.Актуализация опорных знаний:
А) Этап повторения теоретического материала.
-Учитель опрашивает ученика по теории,:
1.Как найти неизвестное слагаемое?
2.Как найти неизвестное уменьшаемое?
3.Как найти неизвестное вычитаемое?
4.Правило раскрытия скобок.
Б) Актуализация прежних знаний и способов действий:
1) Ребята разбирают решения уравнений и находят ошибки в уравнениях:
а) Y + 32 = 152 б) Х – 38 = 142
Y = 152 + 32 – неверно Х = 142 + 38
Y= 184 – неверно Х = 180 — верно
Ответ: 120 Ответ: 180
в) Х – 25 = 125 г) 518 – Z = 400
Х = 125 – 25 – неверно Z = 518 — 400
Х = 120 – неверно Z = 118 — верно
Ответ: 150 Ответ: 118
2)Ученик разбирает решение задачи из теоретического материала курса Алгебра. Первый год обучения сайта http://iclass.home-edu.ru.:
Первый год обучения сайта http://iclass.home-edu.ru.:
-Рассмотрим следующую задачу.
В классе девочек вдвое больше, чем мальчиков. Если из этого класса уйдут три девочки и придут три мальчика, то девочек будет на 4 больше, чем мальчиков. Сколько учеников в данном классе?
-Решим эту задачу.
Пусть x — число мальчиков в классе, тогда 2x — число девочек. Если уйдут три девочки, то останется (2x — 3) девочек. Если придут три мальчика, то станет (x + 3) мальчиков. По условию девочек будет тогда на 4 больше, чем мальчиков, отсюда составим уравнение:
(2x — 3) — (x + 3) = 4.
Чтобы найти неизвестное число мальчиков, мы составили равенство, содержащее переменную. Такие равенства называют уравнениями с одной переменной. Нам надо найти число, при подстановке которого вместо x в уравнение (2x — 3) — (x + 3) = 4 получается верное равенство.
Используя известные правила решения уравнений, последовательно получаем:
2x — 3 — x — 3 = 4; (раскрыли скобки)
x — 6 = 4; (привели подобные слагаемые)
x = 6 + 4;
x = 10.
Число 10 называют корнем уравнения.
4.Изучение нового материала:
Учитель: Что называют уравнением?
Ученик: Уравнением называют равенство, содержащее букву, значение которой надо найти.
Учитель: Что такое корень уравнения?
Ученик: Корнем уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.
Учитель: Давай вспомним стих про корень уравнения (Эмоциональная разрядка чтением стихотворения):
Когда уравненье решаешь дружок,
Ты должен найти у него корешок.
Значение буквы проверить не сложно,
Подставь в уравненье его осторожно.
Коль верное равенство выйдет у вас,
То корнем значенье зовите тот час.
Учитель: А теперь рассмотрим примеры уравнений, которые содержат: один корень уравнения; более одного корня; не имеют корней уравнения; бесконечно много корней уравнения:
Пример 1
Уравнение x + 1 = 6 имеет один корень — число 5.
Пример 2
Уравнение (x — 1)(x — 5)(x — 8) = 0 имеет три корня: 1, 5 и 8. Каждое из этих значений x обращает произведение (x — 1)(x — 5)(x — 8) в ноль, а при любых других значениях x ни один из множителей не равен нулю, а значит, не равно нулю их произведение.
Пример3
Уравнение x = x + 4 не имеет корней, так как значение его левой части меньше значения правой части на 4 при любом значении x.
Пример 4
Уравнение 3(x + 5) = 3x + 15 имеет бесконечно много корней, так как в силу распределительного свойства умножения значение его левой части равно значению правой части при любом значении x.
Учитель: Введем теперь понятие равносильности уравнений.
Ученик: Уравнения называются равносильными, если они имеют одни и те же корни или не имеют корней.
Учитель: В процессе решения уравнений всегда стремятся данное уравнение заменить более простым уравнением, равносильным ему. При этом используются следующие свойства:
При этом используются следующие свойства:
1) из данного уравнения получается равносильное ему уравнение, если перенести слагаемое из одной части уравнения в другую, изменив его знак;
2) из данного уравнения получается равносильное ему уравнение, если обе части умножить или разделить на одно и то же число, отличное от нуля.
Пример
Решим уравнение 4 + 16x = 21 – (3 + 12x).
Решение:
1) 4 + 16x = 21 – 3 – 12x – раскрыли скобки в правой части уравнения.
2) 16x + 12x = 21 – 3 – 4 – перенесли слагаемые с неизвестным в левую часть, а числовые слагаемые — в правую.
3) 28x = 14 – привели подобные слагаемые.
4) x = 14 : 28 — разделили на 28 обе части уравнения.
5) x = 0,5 — корень уравнения.
Все пять уравнений, полученные при решении данного уравнения, являются равносильными ему и имеют решением один и тот же корень: 0,5.
Ответ: 0,5.
5.Физминутка. «Повторяй! Не зевай!»
6.Тестирование.
(После самостоятельного решения теста, демонстрация решений в презентации)
Тест «Уравнение и его корни»
Начало формы
Question1
Баллов: —/2
Корнем уравнения называется значение , при котором уравнение обращается в числовое равенство.
Question2
Баллов: —/1
Уравнения называются равносильными, если они имеют или не имеют корней.
Question3
Баллов: —/4
В процессе решения уравнений всегда стремятся данное уравнение заменить более простым уравнением, равносильным ему. При этом используются следующие свойства:
1) из данного уравнения получается равносильное ему уравнение, если слагаемое из одной части уравнения в другую, его знак;
2) из данного уравнения получается равносильное ему уравнение, если обе части умножить или разделить на , .
Question4
Баллов: —/5
Является ли число 6 корнем данных уравнений?
2х — 6 = 0 | |
9 — х = 3 | |
0,5х + 1,2 = 42 | |
4(х — 5) — 0,6 = 3,4 | |
х — 1 = 4 |
Question5
Баллов: —/5
Сколько корней имеет каждое уравнение?
0,4 — 6х = 8 | |
х(х — 3)(1,2 — 2х) = 0 | |
2х — 3 = 2х | |
9х — (3х + 5) = 0 | |
3(х — 1) = 0 |
7. Самостоятельная работа
Самостоятельная работа
(После самостоятельного решения заданий, демонстрация решений в презентации)
8. Дом.задание: Сегодня домашнее задание – задание для самостоятельного решения (урок №5, уровень Б — курс алгебра 7 сайта http://iclass.home-edu.ru)
9. Итоги урока:
Вот и подошел урок к концу. Что же мы сегодня выучили на уроке? А что понравилось больше всего? Решение уравнений – важная тема, и мы на протяжении всей школьной жизни будем к ней постоянно возвращаться. А теперь выставим оценки.
упростить вычисление квадратного корня — Googlesuche
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
Упрощение радикальных, рациональных выражений с помощью Step-by-Step … — QuickMath
quickmath.com › 904 радикальные выражения с помощью нашего бесплатного пошагового математического калькулятора.
Калькулятор квадратного корня
www. calculatorsoup.com › Алгебра
calculatorsoup.com › Алгебра
Используйте этот калькулятор для нахождения главного квадратного корня и корней из действительных чисел. Входными данными для подкоренного числа x могут быть положительные или отрицательные действительные числа. Ответ …
Калькулятор квадратного корня и решатель
www.mathwarehouse.com › арифметика › квадратный корень…
Калькулятор квадратного корня и решатель. Бесплатный калькулятор сводит квадратные корни к простейшей радикальной форме. Рабочий лист Упрощение радикалов.
Решить — Упрощение калькулятора квадратных корней — Алгебратор
softmath.com › факторинг-выражения › упрощение-квадра…
Упрощение калькулятора квадратных корней. Посетители Google нашли наш веб-сайт вчера, введя следующие термины алгебры: симметрия бесплатных распечаток; Как разместить …
Калькулятор квадратных корней — Symbolab
www.symbolab.com › … › Экспоненты и радикалы
Бесплатный калькулятор квадратных корней — Находите квадратные корни любого числа шаг за шагом.
Упрощенный калькулятор квадратного корня
online-calculator.org ›simplify-square-root-calculator
Упрощенный калькулятор квадратного корня, чтобы найти простейшую форму квадратного корня любого числа. Калькулятор упрощения радикалов покажет вам шаг за шагом …
Калькулятор квадратного корня — MathCracker.com
mathcracker.com › Калькулятор квадратного корня
Этот калькулятор позволяет упростить и вычислить любое допустимое выражение квадратного корня, показывая все шаги. Вам необходимо предоставить действительное выражение, включающее …
Онлайн-калькулятор квадратного корня — Simplify_surd — Solumaths
www.solumaths.com › калькулятор › расчет › упрощение…
Упростите surd, онлайн-исчисление. Резюме : онлайн-калькулятор surds, который позволяет производить расчеты в точной форме с квадратными корнями: сумма, …
Калькулятор квадратного корня. Извлечение квадратного корня одним простым действием
www. omnicalculator.com › математика › извлечение квадратного корня
omnicalculator.com › математика › извлечение квадратного корня
06.04.2022 · В следующем тексте вы найдете подробное объяснение различных свойств квадратного корня, например, как упростить квадратные корни, с …
TI 84 Plus CE Упрощение квадратных корней и других радикалов — YouTube
www.youtube.com › смотреть
28.03.2018 · Как упростить квадратные корни, кубические корни и другие радикалы. Купите TI84 Plus CE на …
Dauer: 8:28
Gepostet: 28.03.2018
ähnliche tushanfragen
Упрощайте калькулятор квадратного корня с шагами
Спроф -калькулятор корневой корневой. Символ квадратного корня
Вычислить квадратный корень вручную
Решить для x
как упростить-квадратный корень — Googlesuche
AlleVideosBilderShoppingMapsNewsBücher
suchoptionen
Чтобы упростить квадратный корень, вам просто нужно разложить число на множители и извлечь корни всех найденных идеальных квадратов из знака радикала.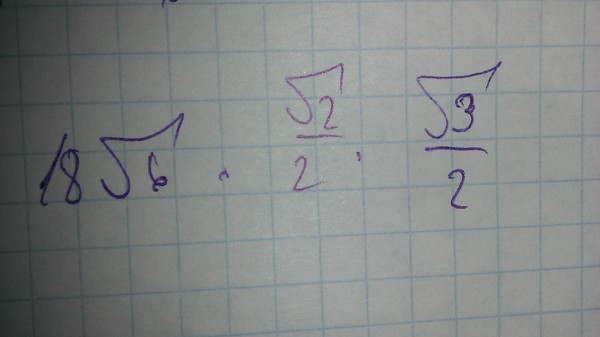
√72 = √(9 х 8)
√72 = √(9 х 4 х 2)
√72 = √(0 х 9) х 3
√72 = 3 х 2 х √2.
√72 = 6√2.
3 способа упростить квадратный корень — wikiHow
www.wikihow.com › … › Алгебра › Экспоненты и логарифмы
Hervorgehobene Snippets
How To Simplify Square Roots — YouTube
www.youtube.com › смотреть
25.11.2018 · В этом видеоуроке по математике объясняется, как упростить квадратные корни. Моя электронная книга: https:// amzn.to …
Добавлено: 10:46
Прислан: 25.11.2018
Как упростить квадратные корни (обзор) (статья) | Khan Academy
www.khanacademy.org › математика › алгебра › упрощение…
Упрощение квадратных корней обзор… Узнайте, как переписать квадратные корни (и содержащие их выражения), чтобы в корне не было полного квадрата. Для …
Упрощение квадратных корней | Алгебра (видео) — Khan Academy
www. khanacademy.org › математика › алгебра › упрощение
khanacademy.org › математика › алгебра › упрощение
09.08.2016 · Он пытается упростить. 5•3•√13 сложнее, чем 15•√13. Первый состоит из 3 этапов…
Dauer: 3:09
Прислан: 09.08.2016
Упрощение квадратных корней — математика — это весело
www.mathsisfun.com . Чтобы упростить квадратный корень: сделайте число внутри квадратного корня как можно меньшим (но все же целым числом): …
ACT Math: Как упростить квадратный корень — Varsity Tutors
www.varsitytutors.com › act_math-help › How-to-si…
Чтобы упростить квадратный корень, вы должны ищите пары. Всякий раз, когда есть пара множителей (например, две двойки), вы вытягиваете один из …
GRE Math: как упростить квадратные корни — Varsity Tutors
www.varsitytutors.com › gre_math-help › как -to-si…
Самый простой способ упростить: перевести в экспоненциальное представление. √0,0000490= √4,9 х 10-5. найти квадратный корень из четной степени несложно, а 49 — идеальный . ..
..
Как упростить квадратный корень | Алгебра — Study.com
study.com › навык › выучить › как упростить квадрат…
Упрощение квадратного корня… Шаг 1. Найдите простые множители числа внутри радикала подписать. Шаг 2: Сгруппируйте факторы в пары. Шаг 3. Вытащите один …
Узнайте, как упростить квадратный корень за 2 простых шага — алгебра, класс
www.алгебра-класс.com › как упростить-квадрат-…
Обучение тому, как упростить квадратный корень, можно разбить на 2 простых шага. Сначала подумайте о факторах и определите, является ли один из них идеальным …
Упрощение квадратных корней – методы и примеры
www.storyofmathematics.com › упрощение-квадрат-…
Bewertung 5,0
(24)
Чтобы упростить выражение, содержащее квадратный корень, находим множители числа и группируем их по парам. Например, число 16 имеет 4 копии .