Как пользоваться треугольником паскаля: Треугольник Паскаля — урок. Алгебра, 11 класс.

Треугольник Паскаля

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Родионова А.В. 1Федоров Г.Д. 1

---

1МБОУ Лицей №40 при УлГУ

Гуськова А.Г. 1

---

1МБОУ Лицей №40 при УлГУ

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Замечательная геометрическая фигура и самая популярная в школьной программе геометрии — это треугольник. Но треугольники «поселились» не только на страницах учебника геометрии. В данной работе мы рассмотрим не обычный треугольник, а треугольник, состоящий из чисел – треугольник Паскаля, его свойства, связь с числами Фибоначчи и биномиальными коэффициентами.

Цель работы:

Познакомиться с таким математическим объектом, как треугольник Паскаля

Задачи:

Пополнить запас научных знаний.

Продолжить знакомство с основными историческими этапами возникновения и развития математической науки, судьбами открытий, именами людей, творивших науку. В первую очередь с биографией ученого Блеза Паскаля.

Самостоятельно попытаться составить данный треугольник.

Рассмотреть свойства треугольника Паскаля.

Определить значимость открытия треугольника Паскаля.

Сформулировать вывод и итоги исследования.

Гипотеза:

Треугольник Паскаля обладает рядом замечательных свойств, поэтому и носит имя одного из выдающихся людей.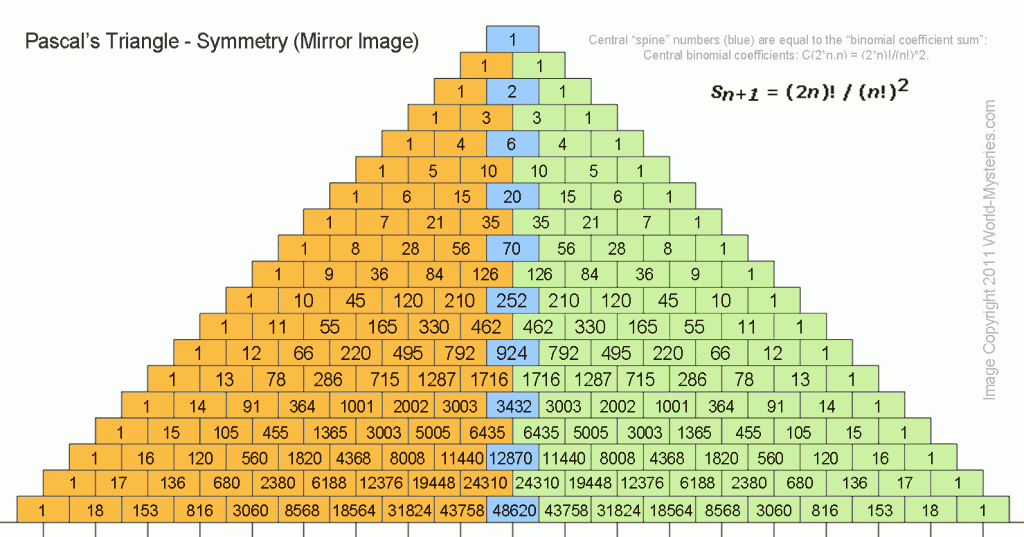

Актуальность:

Актуальность данной работы не вызывает сомнения, поскольку обусловлена, с одной стороны большим интересом к теме «Треугольник Паскаля» в современной науке, с другой стороны, её недостаточной разработанностью.

Навыки решения задач с применением треугольника Паскаля помогут в рамках изучения школьного курса математики, при решении олимпиадных задач.

Предмет исследования:

Треугольник Паскаля

Этапы исследования:

Сбор первоначальных сведений о треугольнике в энциклопедической и учебно-научной литературе.

Построение треугольник Паскаля.

Выявление «волшебных» свойств чисел треугольника.

Изучение возможностей применения треугольника Паскаля.

Формулирование итогов и выводов.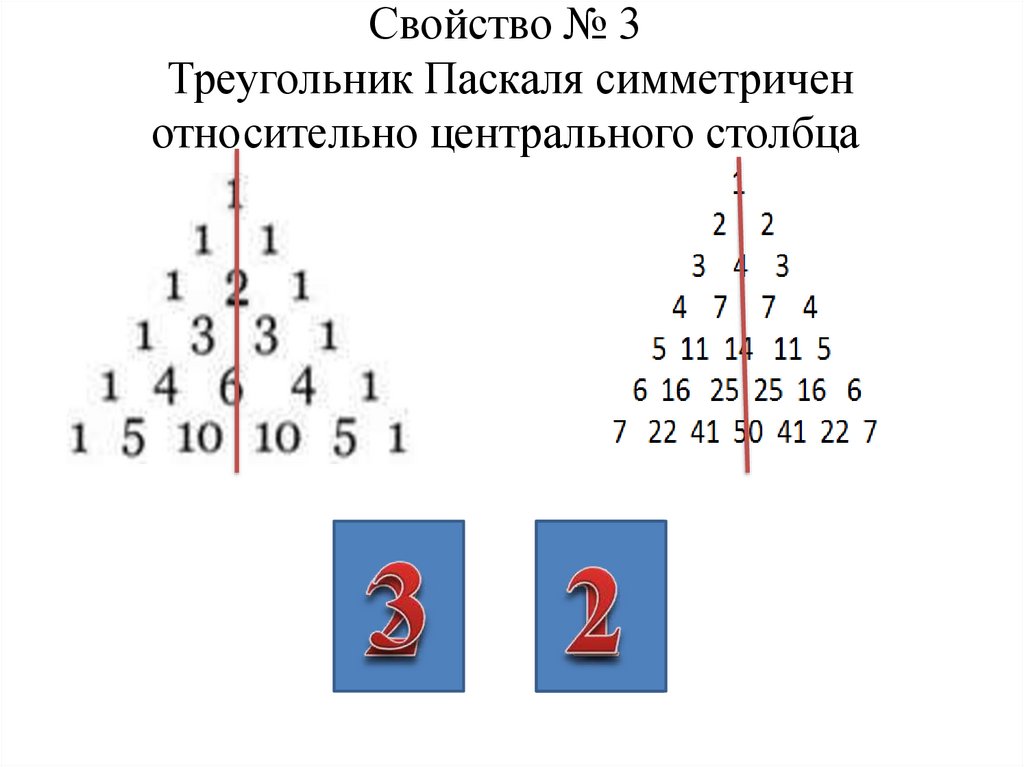

Методы исследования:

аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;

поиск информации в интернет — ресурсах.

1.Биография Блеза Паскаля

Прогресс человечества во многом связан с открытиями, сделанными гениями.

Одним из них является Блез Паскаль — французский математик, физик, философ и мастер прозы.

Родился Блез Паскаль в 1623 г. 19 июня в Клермон — Ферране, в семье председателя суда города Этьена Паскаля.

Род Паскалей отличали незаурядные способности, а Блеза одаренность посетила с раннего детства. Этьен Паскаль уделил много внимания развитию умственных способностей сына и уже в 16 лет Блез сочинил труд под названием «Опыт о конических сечениях» в котором содержалась теорема известная, как теорема Паскаля.

Вклад Паскаля в науках очень велик. Вот лишь некоторые из них: заложил основы современной теории вероятностей и математического анализа, сформулировал основной закон гидростатики, написал множество трудов по философии, изобрел шприц,создал гидравлический пресс и вычислительное устройство «Паскалин» (прототип калькулятора), изобрел тачку, придумал омнибус — конные экипажи с фиксированными маршрутами, ставшие впоследствии первым видом регулярного общественного транспорта и пр.

Умер Блез Паскаль 19 августа 1662 года.

Вследствие его больших вкладов в изучение давления в физике, в честь Паскаля назвали единицу измерения давления (Па). Так же в честь Паскаля назвали язык программирования Pascal.

2.Определение и основные свойства треугольника Паскаля.

2.1 История треугольника.

Треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике» Блеза Паскаля

Похожий треугольник представлен в качестве иллюстрации в книге китайского математика Яна Хуэя, изданной в 1303 году.

О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.

2.2 Построение треугольника Паскаля.

«Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике» (Мартин Гарднер).

Треугольником Паскаля называется бесконечная треугольная таблица, в которой (рис.1):

на вершине и по боковым сторонам стоят единицы,

-каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.

Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Продолжать треугольник можно бесконечно.

2.3 Основные свойства треугольника Паскаля.

Для любой строки под номером n (n = 0, 1, 2…) верно:

Первое и последнее числа – 1; второе и предпоследнее – n.

Строки треугольника симметричны относительно вертикальной оси треугольника.

Сумма чисел n-й строки треугольника Паскаля равна  (рис.2)

Первая диагональ — это натуральные числа, идущие по порядку (рис.3).

Вторая диагональ — это «треугольные» числа(Рис.3). Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде.

 

 

Третья диагональ — это «пирамидальные» числа (один шар мы можем положить на три — итого четыре, под три подложим шесть — итого десять, и так далее) (рис.4).

 

 

Четвертая диагональ – это «фигурные числа» в четырехмерном измерении. Это можно представить только в виртуальном мире. Один шар касается четырех, а те, в свою очередь, десяти…

Каждое число треугольника Паскаля равно сумме чисел предыдущей диагонали, стоящей над этим числом.

В каждой строке сумма чисел на нечётных местах равна сумме чисел на чётных местах.

Если номер строки – простое число, то все числа этой строки, кроме 1, делятся на это число.

Каждое число, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм, ограниченный правыми и левыми диагоналями, на пересечении которых стоит это число.

Бином Ньютона – возведение выражения (a + b) в степень. При возведении в степень получаются коэффициенты, равные числам в треугольнике Паскаля.

Сумма чисел n-й восходящей диагонали, проведенной через строку треугольника с номером n − 1, есть n-е число Фибоначчи (число равно сумме двух предыдущих чисел) (рис.5).

Если нечётное число в треугольнике Паскаля заменить на точки контрастного цвета, а чётные — белого цвета, то треугольник Паскаля разобьётся на более мелкие треугольники, образующие изящный узор. Удивительное свойство треугольника Паскаля.

3. Применение треугольника Паскаля.

Где же применяется треугольник Паскаля?

При решении комбинаторных задач.

Треугольник Паскаля используется для решения различных задач в области физики:

принцип минимума потенциальной энергии;

материальные точки и центр тяжести;

центр тяжести системы двух материальных точек;

центр тяжести стержня с многими грузами;

невозможность вечного двигателя.

С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.

Вот далеко не полный перечень свойств чисел треугольника Паскаля и его многочисленных применений.

4. Применение свойств треугольника Паскаля в решении математических задач.

Свойства треугольника Паскаля, наверное, были бы не столь значимы, если бы на их основе нельзя было решать математические задачи. Такие задачи можно встреть в ОГЭ, ЕГЭ и в олимпиадных задачах старшего школьного уровня. Треугольник Паскаля используется при решении комбинаторных задач, для решения различных задач в области физики. С построением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении программирования.

Задача 1.

Найдите сумму первых 8 треугольных чисел.

Решение:

Найдем сумму первых восьми чисел 3 диагонали треугольника Паскаля. (рис.6) Получится 120.

Ответ: 120

Задача 2.

Вася построил из шариков пирамиду. Известно, что на её строительство ушло 286 шариков, сколько «этажей» в Васиной пирамиде?

Решение:

В данной задаче нам известно, что на строительство пирамиды ушло 286 шариков. Найдем решение с помощью треугольника Паскаля, в котором количество прямоугольников, пересеченных зеленой линией, будет наш ответ. (рис. 7)

Ответ: 11 «этажей».

Задача 3.

В магазине «Теплица» продается 6 различных сортов помидор. Сколькими способами можно выбрать из них 3 сорта помидор?

Решение:

В данной задаче нам даны различные сорта, поэтому повторений не будет и порядок выбора сортов нам неважен, нам важно количество, а именно 3. Найдем решение с помощью нашего треугольника Паскаля, в котором пересечении 3-й диагонали и 6 строки будет наш ответ (рис.8).

Ответ: 20.

Задача 4.

На плоскости даны 11 точек, из которых никакие три не лежат на одной прямой и никакие четыре не лежат на одной окружности. Сколько существует окружностей, каждая из которых проходит через три данные точки

Решение:

Ответ находится на пересечении 11 ряда и 3 диагонали: Это число – 165 (рис.9).

Ответ: 165 окружностей.

З адача 5.

Танк может двигаться по квадратам, видимым на карте, размером 4 на 4 только вправо или вниз. Он стоит в точке А. Из штаба пришло задание прибыть в точку В. Сколько маршрутов передвижения может использовать экипаж?

 

Рис.10(а)

Решение:

 

Рис. 10(б)

В квадраты a2, a3, a4, а1, b1, c1, d1 танк попадёт 1 способом, в квадрат b2 может добраться 2 способами (рис.10(а)). В квадрат с2 и b3 — 3 способами, d2 и b4 — 4 способами, в c3 – 6 способами, d3, c4 – 10 способами и в квадрат d4 (точка В) – 20 способами. (рис.10(б))

Ответ: 20 способов.

Решив задачу, мы замечаем, что полученные на «карте» числа образуют треугольник Паскаля. Таким образом, можно сделать вывод, что число в треугольнике Паскаля показывает количество способов передвижения от вершины треугольника до данного числа.

Задача 6.

Из пункта А по сети дорог идет группа из человек. На каждом перекрестке, начиная с А, пришедшие туда люди делятся пополам – половина идет по направлению l, половина – по направлению m (рис.11). Сколько человек придет в пункты В, С, D, …, I соответственно?

Решение:

Количество людей, пришедших в искомые точки соответствует числам n-ой строки. В данном случае, n = 7, следовательно¸ искомое количество людей на каждом перекрестке соответствует 7 строке треугольника Паскаля (рис.12).

Ответ: 1, 7, 21, 35, 35, 21, 7, 1.

Задача 7.

Возведите в степень: (u — v) ⁵

Решение:

У нас есть (a + b) ⁿ , где a = u, b = -v, и n = 5. Мы используем 5-й ряд треугольника Паскаля:

1 5 10 10 5 1

Тогда у нас есть:

(u — v)⁵ = (u + (-v))⁵ = 1(u)⁵ + 5(u) ⁴ (-v)¹ + 10(u) ³ (-v)² + 10(u)² (-v)³ + 5(u) (-v)⁴ +1(-v)⁵ = u⁵ — 5u⁴v + 10u³v² — 10u²v³ + 5uv⁴ — v⁵.

Заключение.

В ходе исследования мы убедились, что треугольник Паскаля, несмотря на кажущуюся простоту, действительно обладает рядом замечательных свойств, знание которых будет полезно. Этот треугольник широко используется в математике для решения различных видов задач. Треугольник Паскаля имеет применение не только в математике, но и в физике, информатике.

Изучение темы «Треугольник Паскаля» оказалось очень интересной и необычной. Работа над проектом показала, что математика – это не только точная, но и красивая наука.

Список литературы.

Гиндикин, С.Г. Рассказы о физиках и математиках/ С.Г.Гиндикин. – М.: Терра, 2013. – 480с.

Энциклопедия для детей Аванта+: В 57 т. Т. 11. Математика/ под ред. М. Аксёновой, В. Володина, М. Самсоновф – М.: Аванта+, 2003. — 688 с.

Корбалан, Ф. Мир математики: В 40 т. Т.1. Золотое сечение, математический язык красоты/ Пер. с исп. — М.: DeAgostini, 2014. — 164 с.: ил.

Гарднер, М. Математические новеллы. (Mathematics Games) / Пер. с англ. Ю.А.Данилова; под ред. Я.А. Смородинского — М.: Мир, 1974. — 456 с.

Успенский, В.А. Треугольник Паскаля. Популярные лекции по математике. Выпуск 43/ ред. В.В. Донченко — 2-е изд. доп. — М.: Наука, 1979. — 48 с.: ил.

Картинки [Электронный ресурс]. — Режим доступа: http://arbuz.uz/u_treug.html

Блез Паскаль: биография, мысли, изобретения, открытия, арифмометр [Электронный ресурс]. — Режим доступа: http://www.iqfun.ru/articles/pascal.shtml

Левченков С.И. — Краткий очерк истории химии: Дополнения. Биографии великих учёных. Паскаль (Pascal), Блез. Учебное пособие для студентов химфака РГУ [Электронный ресурс]. — Режим доступа: http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Pascal.html

Биография математика, физика, философа и писателя Блеза Паскаля [Электронный ресурс]. — Режим доступа: http://to-name.ru/biography/blez-paskal.htm

Блез Паскаль — великий ученый. [Электронный ресурс]. — Режим доступа: http://znaniya-sila.narod.ru/people/013_00.htm

Швец А.Н. Информатика -54 Глава 10. Треугольник Паскаля [Электронный ресурс]. — Режим доступа: http://mech.math.msu.su/~shvetz/54/inf/perl-problems/chPascalTriangle.xhtml

Биография Паскаля [Электронный ресурс]. — Режим доступа: http://phyart-pascal.narod.ru/biography.html

Просмотров работы: 6736

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Формулы сокращенного умножения

      Для того, чтобы получить треугольник Паскаля, перепишем Таблицу 1 из раздела «Формулы сокращенного умножения: степень суммы и степень разности» в следующем виде (Таблица П.):

      Таблица П. – Натуральные степени бинома   x + y

№	Степень	Разложение в сумму одночленов
0	(x + y)0 =	1
1	(x + y)1 =	1x + 1y
2	(x + y)2 =	1x2 + 2xy + 1y2
3	(x + y)3 =	1x3 + 3x2y + 3xy2 + 1y3
4	(x + y)4 =	1x4 + 4x3y + 6x2y2 + 4xy3 + 1y4
5	(x + y)5 =	1x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + 1y5
6	(x + y)6 =	1x6 + 6x5y + 15x4y2 + 20x3y3 + + 15x2y4 + 6xy5 + 1y6
…	…	…

      Теперь, воспользовавшись третьим столбцом Таблицы П. , составим следующую Таблицу — Треугольник Паскаля:

Степень 0: (x + y)0 = Разложение в сумму одночленов: 1

Степень 1: (x + y)1 = Разложение в сумму одночленов: 1x + 1y

Степень 2: (x + y)2 = Разложение в сумму одночленов: 1x2 + 2xy + 1y2

Степень 3: (x + y)3 = Разложение в сумму одночленов: 1x3 + 3x2y + 3xy2 + 1y3

Степень 4: (x + y)4 = Разложение в сумму одночленов: 1x4 + 4x3y + 6x2y2 + + 4xy3 + 1y4

Степень 5: (x + y)5 = Разложение в сумму одночленов: 1x5 + 5x4y + 10x3y2 + + 10x2y3 + 5xy4 + 1y5

Степень 6: (x + y)6 = Разложение в сумму одночленов: 1x6 + 6x5y + 15x4y2 + + 20x3y3 + + 15x2y4 + + 6xy5 + 1y6

…

      Теперь, записыая только коэффициенты разложений степеней бинома в сумму одночленов, получим следующую Таблицу — Треугольник Паскаля:

      Таблица — Треугольник Паскаля

№	Треугольник Паскаля
0	1
1	1     1
2	1     2     1
3	1     3     3     1
4	1     4     6     4     1
5	1     5     10     10     5     1
6	1     6     15     20     15     6     1
…	…

      На всякий случай напомним, что Блез Паскаль – это знаменитый физик и математик, живший во Франции более трех веков назад.

      В треугольнике Паскаля каждая строка соответствует строке с тем же номером в Таблице П. Однако в каждой строке треугольника Паскаля, в отличие от Таблицы П., записаны только коэффициенты разложения в сумму одночленов соответствующей степени бинома   x + y .

      Заполнив сначала строки треугольника Паскаля с номерами   0   и   1,   рассмотрим строки с номерами   2   и далее.

      Основным свойством треугольника Паскаля, позволяющим последовательно, начиная со строки с номером   2,   заполнять его строки, является следующее свойство:

      Каждая из строк, начиная со строки с номером   2,   во-первых, начинается и заканчивается числом   1,   а, во-вторых, между числами   1   стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.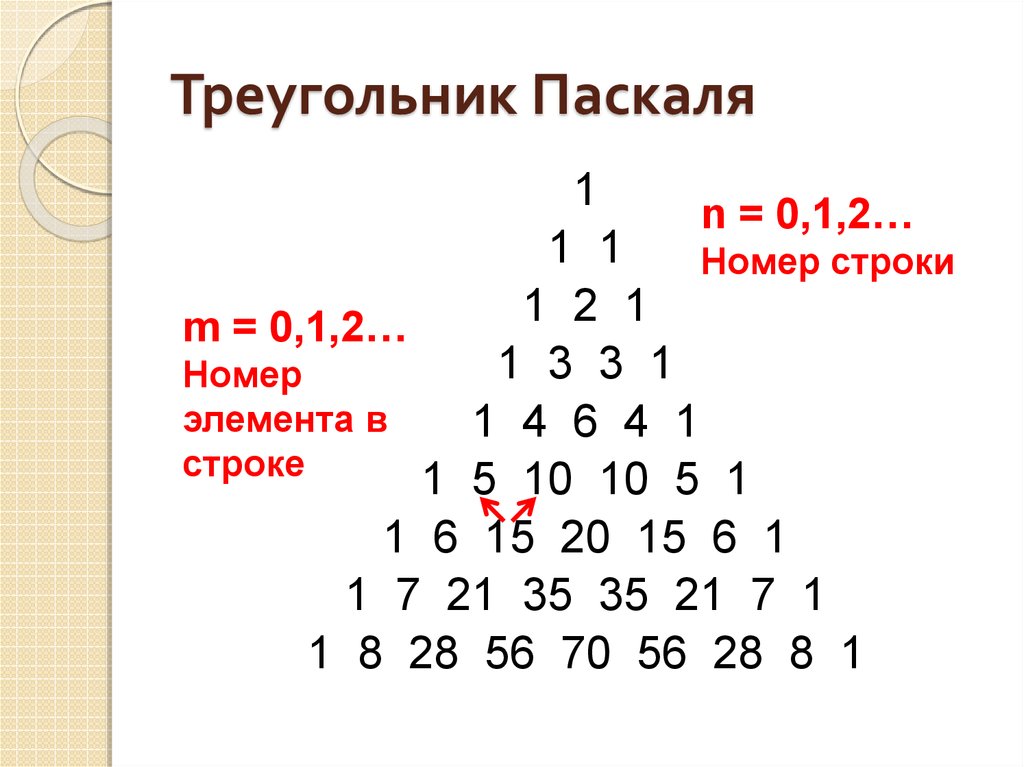

      Действительно, число   2,   стоящее в строке с номером два, равно сумме чисел   1   плюс   1,   стоящих в первой строке. Точно так же, числа   3   и   3,   стоящие в строке с номером три, равны соответственно сумме чисел   1   плюс   2   и сумме чисел   2   плюс   1,   стоящих во второй строке.

      Также и для других строк.

      Таким образом, свойство треугольника Паскаля позволяет, заполнив одну из строк, легко заполнить и следующую за ней, т.е. получить необходимые коэффициенты разложения в сумму одночленов следующей степени бинома   x + y .

      Пример. Написать разложение вида:

(x + y)⁷ .

      Решение. Воспользовавшись строкой треугольника Паскаля с номером   6   и применив основное свойство треугольника Паскаля, получим строку с номером   7:  

6	1    6    15    20    15    6    1
7	1    7    21    35    35    21    7    1

      Следовательно,

(x + y)⁷ = x⁷ + 7x⁶y +
+ 21x⁵y² + 35x⁴y² +
+ 35x³y⁴ +
+ 21x²y⁵ + 7xy⁶ + y⁷ .

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Треугольник Паскаля: определение, вычисление комбинаций

Определения статистики > Треугольник Паскаля

Треугольник Паскаля представляет собой числовой образец в форме (что неудивительно!) треугольника.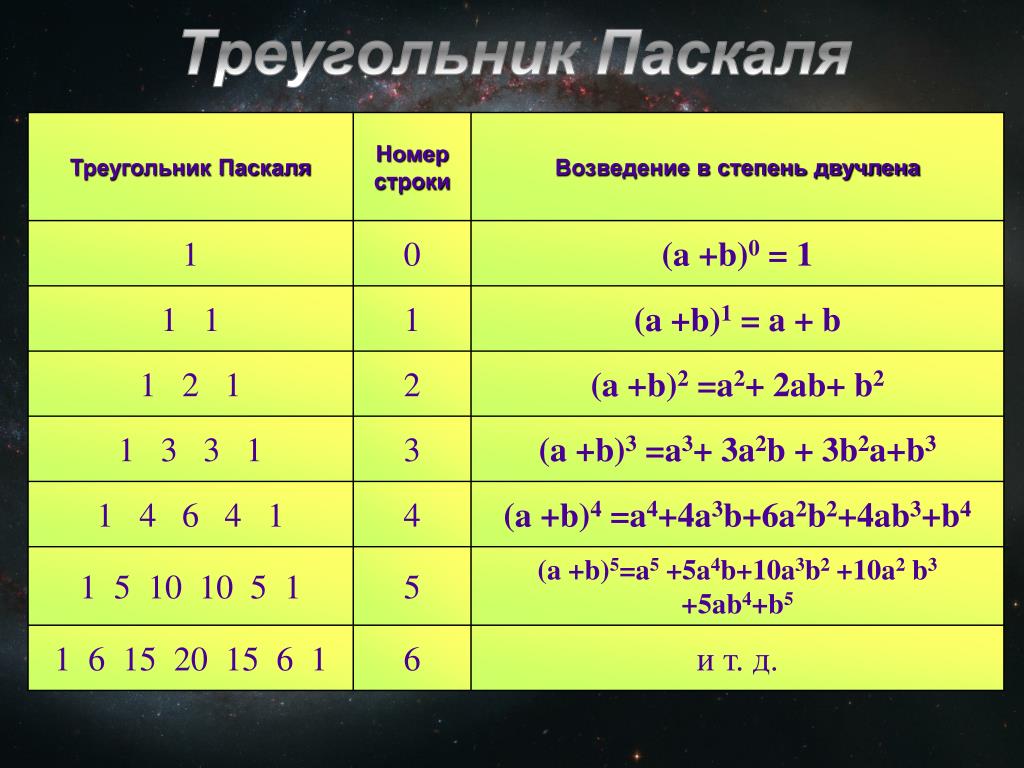 Он назван в честь французского математика Блеза Паскаля. Треугольник Паскаля имеет множество применений в математике и статистике, в том числе помогает вычислять комбинации.

 Ряд 0 1
   Ряд 1 1 1
   Ряд 2 1 2 1
   Ряд 3 1 3 3 1
   Ряд 4 1 4 6 4 1
   Ряд 5 1 5 10 10 5 1
   Ряд 6 1 6 15 20 15 6 1
   Ряд 7 1 7 21 35 35 21 7 1
 

Каждое число в треугольнике является суммой двух чисел над ним. Например, в центре строки 4 есть
: это сумма 3 и 3 в строке выше. Самое первое и самое последнее число в любой строке всегда будет 1.

Треугольник Паскаля Изображение: Hersfold | Викисклад.

Как находить комбинации с помощью треугольника Паскаля

Треугольник Паскаля можно использовать для поиска комбинаций. Верхняя строка в треугольнике Паскаля — это нулевая строка, а первый элемент в любой строке (единицы) — это нулевой элемент в этой строке. Например, допустим, мы хотели найти 6_C_4. Посмотрите в строке 6, на пункт номер 4. ответ 15.

Другое применение

Помимо вероятности, треугольник Паскаля также используется для:

• Алгебры, где можно использовать коэффициент полиномов для нахождения чисел в треугольнике Паскаля. Алгебра выходит за рамки этого сайта, но вы можете найти отличное объяснение этой концепции на сайте Dr. Math.
• Нахождение треугольных чисел (1, 3, 6, 10, 15, 21, 28, 36, 45, …). Треугольные числа — это «точки», из которых состоит треугольник. Например, вы можете сделать очень простой треугольник из 3 точек, по одной на каждом углу. Чтобы узнать больше о треугольных числах, ознакомьтесь с Math is Fun.

В треугольнике можно найти множество других интересных моделей, включая простые числа, каталонские числа и последовательность Фибоначчи. Страница Дж. Уилсона на веб-сайте Университета Джорджии содержит превосходное краткое изложение множества числовых моделей, скрытых в треугольнике Паскаля.

Посетите наш канал YouTube, где вы найдете сотни видеороликов со статистикой!

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Треугольник Паскаля: определение, вычисление комбинаций» С StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.