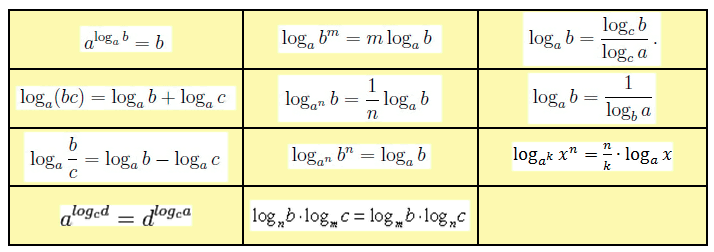Корни, степени и логарифмы. | Тест по алгебре (10 класс) на тему:
Опубликовано 23.03.2015 — 14:51 — Мельникова Мария Николаевна
Задание с вариантами ответов для двух вариантов.
Скачать:
Предварительный просмотр:
Тематический контроль
МАТЕМАТИКА
Раздел: Корни, степени и логарифмы.
Критерии оценки выполнения работы
Число баллов, которое надо набрать для получения оценки | ||||
Зачёт (удовлетворительно) | Хорошо (4) | Отлично (5) | ||
Обязательная часть | 5 | 5 | 6 | 6 |
Дополнительная часть | — | 3 | 2 | 4 |
Итого | 5 | 8 | 8 | 10 |
Выполните задания 1–4 и запишите правильный ответ.
Вариант 3
Обязательная часть
- (1 балл) Установите с помощью стрелок соответствие межу числами
и арифметическими квадратными корнями из этих чисел:
А)64 1)0
Б)0,25 2)8
В)1 3)1
Г)0 4)0,5
- (1 балл) Выберите букву, соответствующую варианту правильного ответа. Какое из равенств является верным:
А) (√а2)2=а
Б) √а=а2
В) √а= а1/2
Г) √а=а
- (1 балл) Выберите букву, соответствующую варианту правильного ответа. Иррациональным является число:
А) √64
Б) -81
В) 0,65
Г) √7
- (1 балл) Выберите букву, соответствующую варианту правильного ответа. Какое уравнение не имеет решений :
А) х2=8
Б) х2=0
В) х2=-64
Г) х2=81
При выполнении заданий 5–8 запишите ход решения и полученный ответ.
5.(2 балла) Найдите корень уравнения:
Log3(2x-5)=1.
Дополнительная часть
6.(2 балла) Найдите х, если:
lgx=1/2 lg16+2 lg5
7.(2 балла) Упростите выражение и найдите его значение:
√18+√50-2√2
8.(2 балла) Найдите значение выражения:
Log3 (m3), если log3m=-4,5.
№ заданий | Критерии оценивания выполнения заданий | Баллы |
5. | Уравнение решено и верно найден его корень | 2 |
Способ решения данного уравнения верен, но получен неверный ответ | 1 | |
Уравнение не решено или решено неверно | 0 | |
6. | Верно применены свойства логарифмов и найден корень уравнения | 2 |
Верно применены свойства логарифмов, но не найден корень уравнения | 1 | |
Не применены свойства логарифмов и не найден корень уравнения | 0 | |
7. | Упрощение проведено верно и найдено значение выражения | 2 |
Упрощение проведено верно , но не найдено значение выражения | 1 | |
Упрощение проведено неверно и не найдено значение выражения | 0 | |
8. | Правильно применено свойство логарифмов и найдено значение выражения | 2 |
Правильно применено свойство логарифмов, но не найдено значение выражения | 1 | |
Неправильно применено свойство логарифмов и не найдено значение выражения | 0 |
Предварительный просмотр:
Тематический контроль
МАТЕМАТИКА
Раздел: Корни, степени и логарифмы.
Критерии оценки выполнения работы
Число баллов, которое надо набрать для получения оценки | ||||
Зачёт (удовлетворительно) | Хорошо (4) | Отлично (5) | ||
Обязательная часть | 5 | 5 | 6 | 6 |
Дополнительная часть | — | 3 | 2 | 4 |
Итого | 5 | 8 | 8 | 10 |
Выполните задания 1–4 и запишите правильный ответ.
Вариант 4
Обязательная часть
- (1 балл) Установите с помощью стрелок соответствие межу числами
и арифметическими квадратными корнями из этих чисел:
А)0,16 1)0
Б)0 2)5
В)1 3)0,4
Г)25 4)0
- (1 балл) Выберите букву, соответствующую варианту правильного ответа. Какое из равенств является верным:
А) (√а)2=а2
Б) √а=а
В) √а= а1/2
Г) √а=а2
- (1 балл) Выберите букву, соответствующую варианту правильного ответа. Иррациональным является число:
А) √16
Б) 0,36
В) √2
Г) -45
- (1 балл) Выберите букву, соответствующую варианту правильного ответа. Какое уравнение не имеет решений :
А) х2=0
Б) х2=-25
В) х2=0,16
Г) х2=11.
При выполнении заданий 5–8 запишите ход решения и полученный ответ.
5.(2 балла) Найдите корень уравнения:
Log3(3x-5)=0.
Дополнительная часть
6.(2 балла) Найдите х, если:
lgx=1/2 lg25+ lg20
7.(2 балла) Упростите выражение и найдите его значение:
√48+√75-√3
8.(2 балла) Найдите значение выражения:
log2 (16m), если log2m=-3,4.
№ заданий | Критерии оценивания выполнения заданий | Баллы |
5. | Уравнение решено и верно найден его корень | 2 |
Способ решения данного уравнения верен, но получен неверный ответ | 1 | |
Уравнение не решено или решено неверно | 0 | |
6. | Верно применены свойства логарифмов и найден корень уравнения | 2 |
Верно применены свойства логарифмов, но не найден корень уравнения | 1 | |
Не применены свойства логарифмов и не найден корень уравнения | 0 | |
7. | Упрощение проведено верно и найдено значение выражения | 2 |
Упрощение проведено верно , но не найдено значение выражения | 1 | |
Упрощение проведено неверно и не найдено значение выражения | 0 | |
8. | Верно применено свойство логарифмов и найдено значение выражения | 2 |
Верно применено свойство логарифмов, но не найдено значение выражения | 1 | |
Не применено свойство логарифмов и не найдено значение выражения | 0 |
По теме: методические разработки, презентации и конспекты
Методическая разработка открытого урока «Корни, степени,логарифмы»
.
Аннотация (методическое обоснование темы урока) Методическая разработка открытого урока «Степени. Корни. Логарифмы»» демонстрирует возможности формирования общих компетенций студенто…
ПЛАН-КОНСПЕКТ учебного занятия по учебной дисциплине ОУДу.03 Математика. Тема: Корни, степени, логарифмы
Цель занятия: расширение представления обучающихся о степенных зависимостях, формирование понятий: степень, корень, логарифм, применение полученных знаний для решения задач….
Методическая разработка урока по теме: «Корни, степени, логарифмы».
Цель урока: создать условия для систематизации изученного материала, выявления уровня овладения системой знаний и умений.Задачи:— обучающие: закрепить умение работы с корнями, степеням…
Контрольная работа по теме «Корни, степени, логарифмы»
Контрольная работа по теме «Корни, степени, логарифмы» 4 варианта…
План-конспект учебного занятия «Корни. Степени. Логарифмы»
Преподавателям для проведения учебного занятияпо ОУДу.
04 Математика…
Практические работы «Корни степени и логарифмы»
В разработке представлены практические работы по теме «Корни степени и логарифмы». Работы составлены в 6 вариантах. Может быть использовано для проведенеия контроля знаний на занятиях или в …
Практические работы «Корни степени и логарифмы»
В разработке представлены практические работы по теме «Корни степени и логарифмы». Работы составлены в 6 вариантах. Может быть использовано для проведенеия контроля знаний на занятиях или в …
Поделиться:
3-8
Решение степени трех с помощью JavaScript и логарифмов | by Jackson Beytebiere
Сила трех — классический вопрос для начинающих программистов.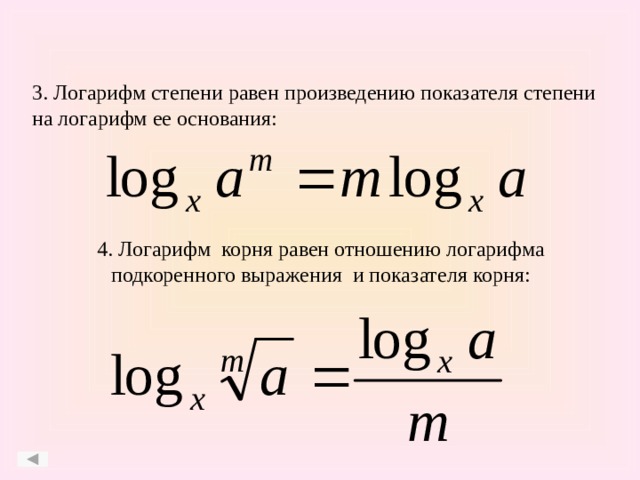
Вопрос звучит так: задано число n, вернуть true, если это степень числа три, или false, если нет. Предположим, что n больше 0. Его просто решить, но самое оптимальное решение довольно крутое, поскольку его время выполнения постоянно. Решения с постоянным временем великолепны, потому что они будут выполнять заданное количество операций независимо от того, насколько велик входной параметр n. Сначала я расскажу о простом восходящем решении, а затем о логарифмах. Далее я объясню решение с постоянным временем и то, как оно работает. Нажмите на строку ниже, чтобы перейти к наиболее интересующей вас части:
Восходящее решение
Объяснение логарифмов
Постоянные решения времени выполнения
Чтобы решить на калькуляторе, вы можете просто взять 3 и умножить его на 3. Продолжайте умножать это число на 3, пока не достигнете или не превзойдете введенное число . Если вы дойдете до введенного числа, это степень числа 3. Если вы превысите число, это не так. Также любое число в 0-й степени будет 1.
Поместите в JavaScript решение, которое будет выглядеть так:
const isPowerThree = (n) => {
if(n===1) return true for(let i=3; i<=n; i*=3){ if (i === n) return true } return false} Это решение имеет среду выполнения сложность O(N). Эта среда выполнения хороша, но могла бы быть и лучше. Как и во многих других задачах, в «Силе трех» есть аккуратное решение с постоянным временем. Это связано с использованием логарифмов.
Логарифмы обратны экспоненциальным функциям. Вот пример:
Экспоненциальная функция: 10²=100
Логарифмическая функция: log(100)=2
Приведенный выше логарифм имеет основание десять. Это база по умолчанию для большинства калькуляторов. Основание — это число, которое возводится в степень в экспоненциальной функции, обратной логарифму (10 в приведенном выше примере с экспонентой). Если общие функции логарифма и экспоненты положить на график рядом, легко увидеть, как они обратны друг другу:
источник Чтобы решить эту задачу с помощью логарифмов, мы можем использовать основание 3 вместо 10 ( базой по умолчанию в JavaScript является число e или число Эйлера).
Math.log(y)/Math.log(x)
Чтобы найти ответ, возьмите логарифм по основанию 3 вашего заданного числа, и если возвращаемое значение является целым числом, это степень трех.
Звучит достаточно просто, однако если вы запустите Math.log(27)/Math.log(3), например, вы получите 3,0000000000000004. Это связано с ошибками точности с плавающей запятой. Вы можете прочитать больше об ошибках точности с плавающей запятой здесь. Однако вам нужно знать только об ошибках для этой проблемы. Есть несколько способов обойти эту проблему. Один из способов — взять логарифм и преобразовать его в строку. Затем отрежьте конец строки и преобразуйте его обратно в число с плавающей запятой. После этого проверьте, является ли это число целым, проверив, равен ли остаток по модулю 1 0.
const isPowerThree = (n) => {return( parseFloat((Math.log(n)/Math.log(3)).toString().substr(0,15))%1 ===0
) } Другой способ решения с использованием логарифмов состоит в том, чтобы преобразовать журнал обратно в число, возведя 3 в логарифм и проверив, соответствует ли оно заданному числу n.
const isPowerThree = (n) => {return parseInt(3**parseInt((Math.log(num)/Math.log(3))))===num} Эти решения также можно использовать для работать для любого вопроса «Является ли сила X?», просто заменив 3 аргументом функции следующим образом:
const isPowerOf = (exp,num) => {return parseInt(exp**parseInt((Math.log(num)/Math.log(exp))))===num} Интересно, если бы вы чтобы поместить эти решения в LeetCode, можно сказать, что восходящее решение имеет наилучшее время выполнения. Возможно, это связано с тем, как работает Math.log, или с неожиданной сложностью запуска parseInt. Однако логарифмическое решение, преобразованное в Ruby, при отправке LeetCode утверждает, что решение находится в верхней части 0,001% скорости выполнения решения.