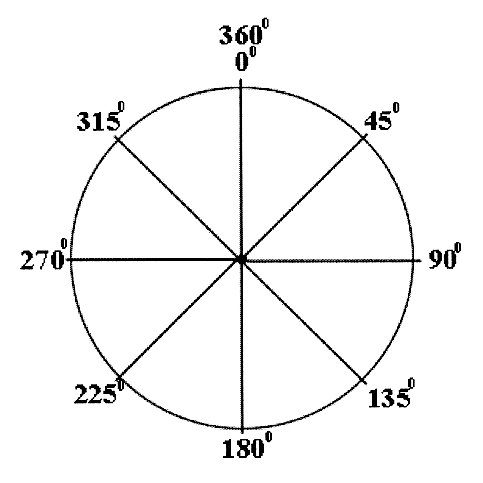
Полный угол – градус
4.6
Средняя оценка: 4.6
Всего получено оценок: 139.
4.6
Средняя оценка: 4.6
Всего получено оценок: 139.
Полный угол – это одна из разновидностей углов в целом. Что такое угол, какие виды углов бывают, почему они так называются и что вообще значат углы – говорим далее.
Что такое угол?
Угол это геометрическая фигура, состоящая из двух лучей, исходящих из одной точки. Фигура намеренно чертится из двух лучей, так как лучи сами по себе не имеют размерности, потому единственной определяющей такой фигуры будет именно величина угла.
Что показывает величина угла? Один луч всегда остается на месте, а вот другой поворачивается вокруг точки, откуда исходят оба луча. Тогда получается, что угол показывает величину поворота одного луча относительно другого.
В геометрических фигурах всегда отображается лишь часть угла, ограниченная границами самой фигуры, что тем не менее не мешает использовать углы и знания о них при решении геометрических задач.
Виды углов
Разделяют несколько видов углов:
- Острый, то есть угол, градусная мера которого меньше 90 градусов. Такое название угол берет за острый носик, который чем-то напоминает наконечник копья.
- Тупой, то есть угол, градусная мера которого больше 90 градусов. Если копье оббить до состояния, когда им проколоть ничего не получится, то его наконечник можно будет назвать тупоугольным.
- Прямой, то есть угол, градусная мера которого равняется 90 градусам. Прямой угол во всем мире считается красивым и правильным. Обратите внимание, сколько мебели в классе или любой комнате сделано из досок под прямыми углами: шкафы, столы, подоконники, кухонные уголки и многое другое.
- Развернутый, то есть угол, градусная мера которого равняется 180 градусам. Если угол развернуть до такой степени, что оба луча станут совпадать, то есть лежать на одной прямой, то получится именно развернутый угол.

- Полный угол, градусная мера которого равняется 360 градусов. Именно об этом типе углов мы поговорим подробнее.
Полный угол
Мы уже решили, что угол это мера поворота одного луча вокруг начала двух лучей при условии сохранения одного луча неподвижным. А что будет, если провернуть один луч до такой степени, что оба луча совпадут? Получится тот самый полный угол, мера которого составляет 360 градусов. Внешне такой угол похож на луч, но представляет собой два совпавших луча.
А что будет, если на каком-то расстоянии от начала лучей прикрепить карандаш, а потом провернуть луч на полный угол? Получится окружность.
Полный угол с градусной мерой в 360 градусов и нулевой угол с градусной мерой в 0 градусов выглядят одинаково. Но, если полный угол – это луч, провернутый до совпадения со вторым лучом, то нулевой угол – это два луча, ни один и которых еще не поворачивали.
Что мы узнали?
Мы рассмотрели, какие бывают углы. Выделили основные виды углов, в отдельности рассмотрели полный угол и градус полного угла.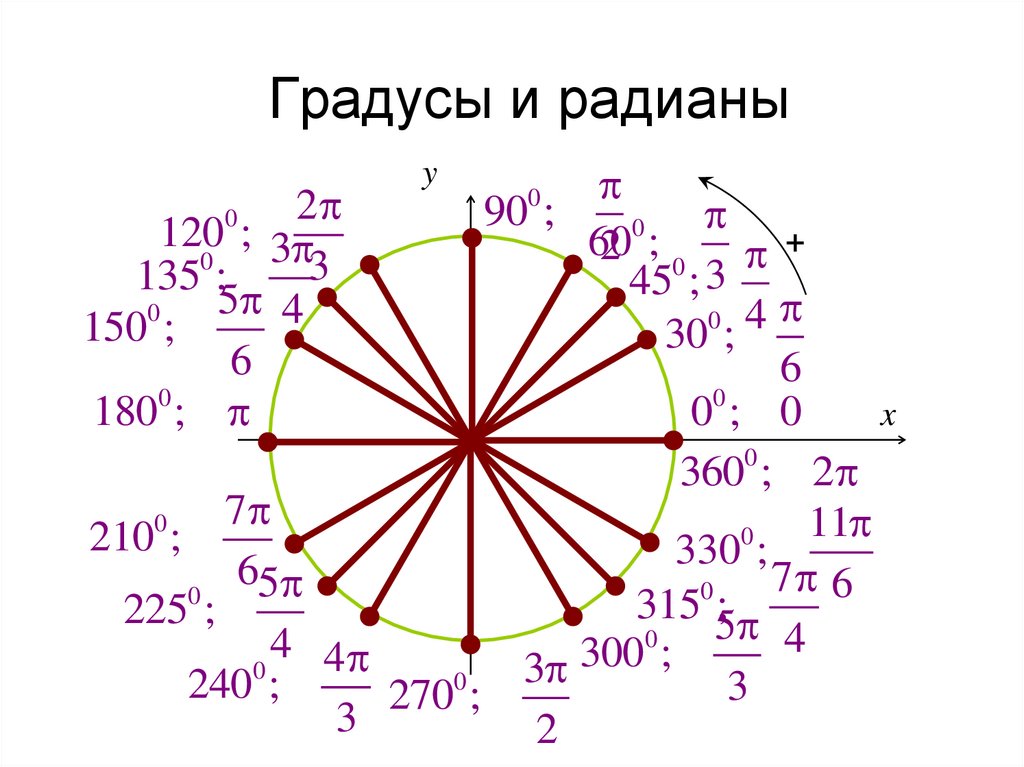 А также сравнили полный угол с нулевым углом.
А также сравнили полный угол с нулевым углом.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Анна Ножеева
4/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 139.
А какая ваша оценка?
Преобразовать угол больший 360 градусов или меньше -360 градусов онлайн
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор находит наименьший положительный, либо отрицательный угол для углов больших 360 градусов.
Введите целое значение угла
Идет расчет …
Как найти наименьший положительный (отрицательный) угол
Для преобразования угла большего или меньшего 360° градусов, необходимо значение данного угла разделить на 360 с остатком.
В результате деления с остатком – неполное частное будет соответствовать числу полных оборотов, а остаток от деления значению угла.
Приведем примеры:
Пример 1. Найдем наименьший положительный угол для угла 1267° градусов.
Разделим 1267 на 360 с остатком:
Следовательно, наименьший положительный угол равен 187° градусов.
Пример 2. Найдем наименьший отрицательный угол для угла -745° градусов.
Разделим 745 на 360 с остатком:
Следовательно, наименьший отрицательный угол равен -25° градусов.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Угол 360 градусов — построение, определение, шаги по рисованию и измерению
LearnPracticeDownload
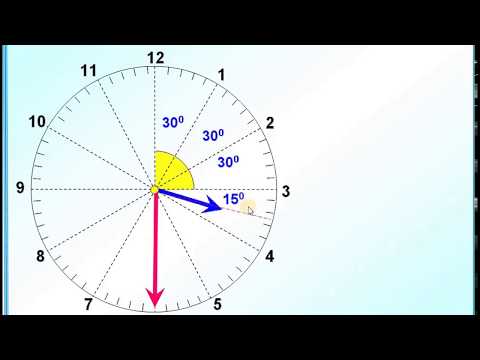
Угол 360 градусов — это полный угол или полный угол, поскольку он образует окружность вокруг точки. Это ровно вдвое больше прямого угла (угол 180 градусов). Если говорить о реальном примере угла в 360 градусов, то прекрасным примером является угол между двумя стрелками часов в положении 12 часов.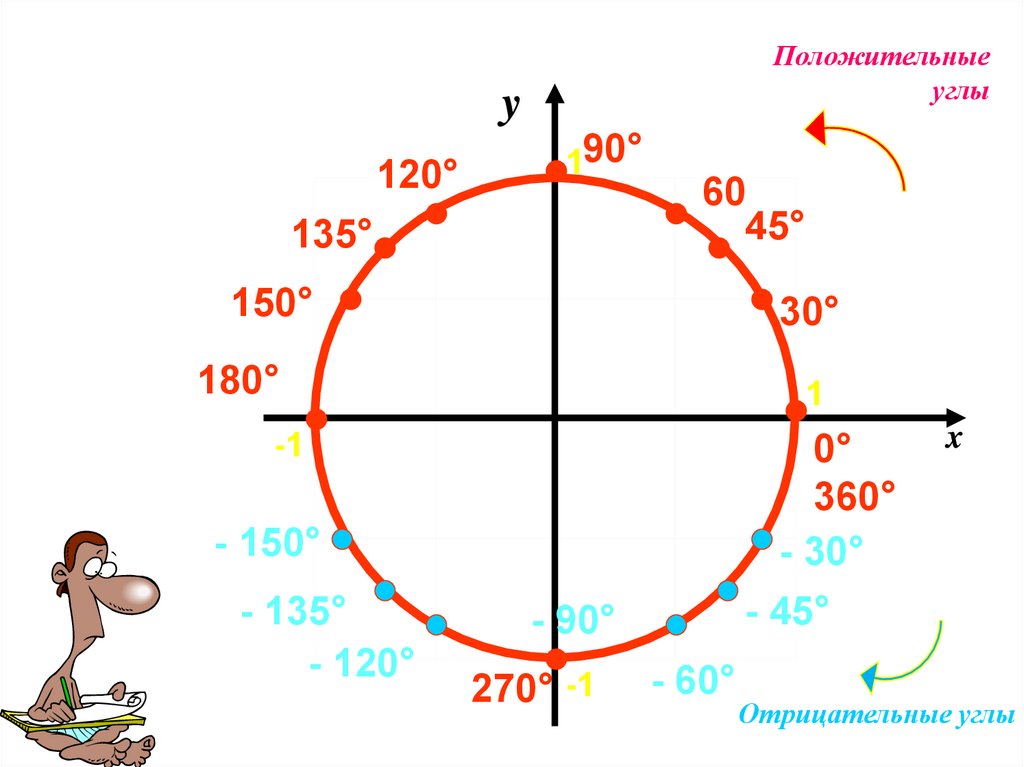 Угол между двумя стрелками часов составляет 360°, потому что они образуют полный оборот или круг. Обе руки будут перекрывать друг друга под углом 12, что представляет собой угол в 360 градусов.
Угол между двумя стрелками часов составляет 360°, потому что они образуют полный оборот или круг. Обе руки будут перекрывать друг друга под углом 12, что представляет собой угол в 360 градусов.
| 1. | Что такое угол 360 градусов? |
| 2. | Угол 360 градусов Название |
| 3. | Как нарисовать угол 360 градусов? |
| 4. | Часто задаваемые вопросы |
Что такое угол 360 градусов?
Угол в 360 градусов является полным углом и равен обороту. Его еще называют полным углом. Два плеча угла, составляющего 360 градусов, перекрывают друг друга из общей вершины. Угол в 360 градусов не меняет направление точки или линии. Посмотрите на изображение, приведенное ниже, показывает, как выглядит угол 360 градусов.
Из изображения выше видно, что угол в 360 градусов образует полный круг. Это шесть раз угол 60 градусов, четыре раза прямой угол и дважды прямой угол.
Это шесть раз угол 60 градусов, четыре раза прямой угол и дважды прямой угол.
Угол 360 градусов Название
Угол, равный 360 градусам, называется полным углом . Всякий раз, когда мы строим угол в 360 градусов, он всегда образует круг, поэтому он известен как полный угол. Существуют разные названия углов разных измерений. Например, половина угла в 360 градусов, то есть угол в 180 градусов, известен в геометрии как прямой угол. Точно так же одна четвертая часть 360 градусов, то есть 9Угол 0 градусов известен как прямой угол. Углы, которые меньше 360 градусов, но больше 180 градусов, относятся к категории рефлекторных углов.
Как нарисовать угол 360 градусов?
Угол 360 градусов можно нарисовать с помощью транспортира и циркуля.
Рисование угла в 360 градусов с помощью транспортира
Чтобы нарисовать угол в 360 градусов с помощью транспортира, имеется транспортир на 360 градусов круглой формы. У него есть центр посередине, который можно проследить, чтобы нарисовать угол в 360 градусов.
Построение угла в 360 градусов с помощью компаса
Выполните указанные действия, чтобы построить угол в 360 градусов с помощью компаса.
- Шаг 1: Начертите с помощью линейки луч и назовите его AB.
- Шаг 2: Поместите кончик компаса в точку A и выберите подходящую ширину на компасе.
- Шаг 3: Поместите кончик карандаша где-нибудь между A и B на луче AB и начните рисовать дугу.
- Шаг 4: Остановитесь, когда снова достигнете той же точки. Это необходимый угол 360°.
Важные примечания
- Угол в 360 градусов также называют полным углом.
- Угол вокруг центральной точки окружности составляет 360 градусов.
Связанные статьи об угле 360 градусов
Ознакомьтесь с этими интересными статьями, посвященными углам 360 градусов.
- Угол 45 градусов
- Уголки
- Угол 60 градусов
- Тупой угол
- Угол 180 градусов
- Угол рефлекса
- Угол 30 градусов
- Угол 90 градусов
Примеры угла 360 градусов
Пример 1: Можете ли вы помочь Джозефу найти разницу между углом 180° и углом 360°?
Решение: Угол в 180 градусов представляет собой прямую линию, известную как полуокружность.
 Он изменяет направление линии или луча. Угол в 360 градусов образует круг. Два плеча угла, образующего 360 градусов, перекрывают друг друга.
Он изменяет направление линии или луча. Угол в 360 градусов образует круг. Два плеча угла, образующего 360 градусов, перекрывают друг друга.Пример 2: Если угол в 360 градусов разделить на четыре части так, что сумма трех частей равна 270 градусам, то чему равен четвертый угол?
Решение: Пусть неизвестный угол равен x.
сумма трех других углов + x = 360°
270° + х = 360°
х = 360° — 270° = 90°
Следовательно, четвертый угол равен 90°. Это прямой угол.Пример 3: Есть три угла, образующих вместе полный угол: угол A, угол B и угол C. Если угол A = 130 градусов, угол B = 90 градусов, то какова величина угла C?
Решение: Мы знаем, что полный угол равен 360 градусам. Это означает, что угол A + угол B + угол C = 360 градусов.
130° + 90° + С = 360°
C = 360° — (90° + 130°) = 140°Таким образом, угол C равен 140 градусам.

перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по углу 360 градусов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об угле 360 градусов
Как называется угол 360 градусов?
Угол в 360 градусов называется полным углом, полным углом или полным поворотом. Он образует круг вокруг точки. Прекрасным примером угла в 360 градусов являются две стрелки часов в положении 12 часов.
Как выглядит угол 360 градусов?
Угол в 360 градусов выглядит как круг, поскольку он совершает полный оборот или оборот вокруг точки.
Как нарисовать угол 360 градусов?
Чтобы построить угол в 360 градусов, нарисуйте луч с помощью линейки. Поместите кончик циркуля в конечную точку и нарисуйте дугу, начинающуюся и заканчивающуюся в одной и той же точке луча. Этот угол и будет искомым.
Поместите кончик циркуля в конечную точку и нарисуйте дугу, начинающуюся и заканчивающуюся в одной и той же точке луча. Этот угол и будет искомым.
Сколько прямых углов составляют угол 360 градусов?
Прямой угол равен 90 градусам. Чтобы найти количество прямых углов, необходимых для угла в 360 градусов, нам нужно разделить 360 на 90. Итак, 360/90 = 4. Следовательно, 4 прямых угла составляют угол в 360 градусов.
Как нарисовать угол 360 градусов с помощью транспортира?
Транспортир на 360 градусов имеет форму круга. Итак, чтобы составить угол в 360 градусов с помощью транспортира, нарисуйте линию, луч или отрезок. Поместите центральную точку этого транспортира в любую конечную точку линии. Проследите окружность, заданную в центре, вокруг конечной точки. Это и будет искомый угол 360 градусов.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Рабочие листы с углами 360 градусов
Рабочие листы по математике и
визуальные учебные программы
Типы углов
Существует довольно много различных типов углов
что вам нужно знать. Изучение этих специальных типов углов полезно
потому что они помогают вам использовать приемы, которые могут сделать вашу жизнь намного проще, когда
вы делаете расчеты. Если вы знаете, под каким углом вы смотрите
вы сможете решить, какой трюк использовать, чтобы облегчить вашу работу.
Изучение этих специальных типов углов полезно
потому что они помогают вам использовать приемы, которые могут сделать вашу жизнь намного проще, когда
вы делаете расчеты. Если вы знаете, под каким углом вы смотрите
вы сможете решить, какой трюк использовать, чтобы облегчить вашу работу.
Острые углы
Углы меньше 90°. меньший что’ часть важна — 90 градусов сами по себе , а не острый угол.
Рекламные ссылки
Прямые углы
Углы 90 градусов получили свое особое название — они известны как прямых углов . Они также получают свой собственный специальный символ угла. — вместо того, чтобы рисовать изогнутую линию для обозначения угла, вы рисуете маленькую рамку вот так:
Тупые углы
Итак, имена звучат довольно странно, но поскольку это то, что все используют, вы должны их изучить. Тупые углы между 90° и 180°.
Прямые углы
Есть специальное название для углов, которые точно
180°. Их называют прямыми углами . На этот раз имя делает
в полном смысле — когда вы рисуете этот угол, вы рисуете прямую линию!
Их называют прямыми углами . На этот раз имя делает
в полном смысле — когда вы рисуете этот угол, вы рисуете прямую линию!
Углы рефлекса
Что ж, остаются только углы между 180 и 360 градусов. Эти углы называются углы рефлекса .
360 градусов
Угол, равный 360 градусам, часто называют оборотом . Одна из очень важных вещей, которые нужно знать об угле, равном 360 градусам, это что это то же самое, что и угол 0 градусов. Это потому, что когда вы вращаетесь на 360 градусов, вы возвращаетесь к тому, с чего начали, то есть к 0 градусов:
Это правило также применяется для углов больше 360°. Например, скажем, я повернулся на 372°. Это тот же угол, что и 12 градусов, как видно:
Простой способ упростить любой угол свыше 360 градусов. состоит в том, чтобы продолжать отнимать от него 360, пока угол не будет между 0 и 360 градусов. Например, если бы мне дали 800 градусов, я бы сделал так:
440° больше, чем 360°, поэтому мне нужно сохранить вычитая из него 360:
Бинго – угол 800° равен углу 80°.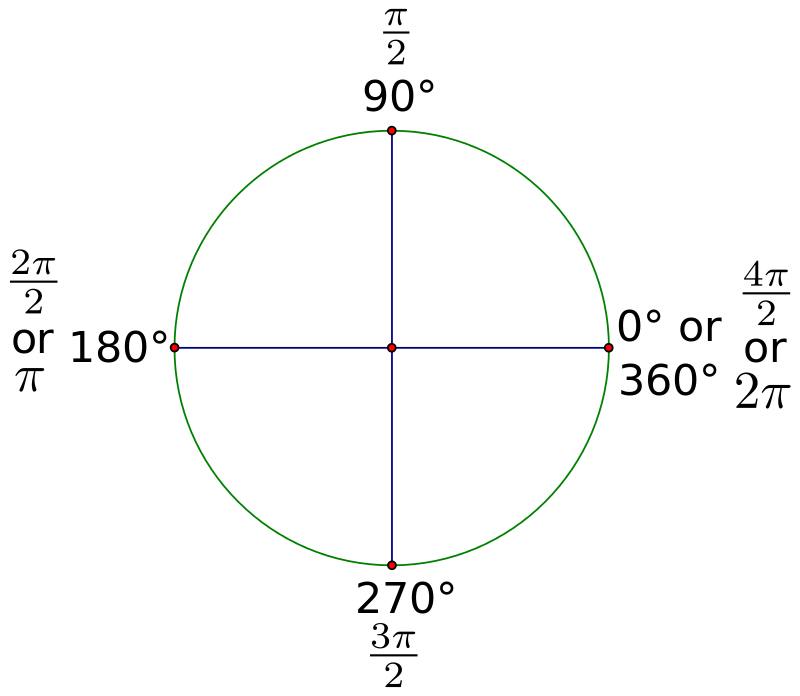
Когда не упрощать углы больше 360 градусов
В некоторых ситуациях углы больше 360 градусов может иметь смысл. Например, скажем, вы смотрите автомобильные гонки по телевизору. и машина теряет управление и дважды полностью переворачивается. Если бы ты был описывая это кому-нибудь позже, вы могли бы сказать что-то вроде: «Машина потеряла управление и вращается на 720 градусов». Говоря 720 градусов, вы сообщаете человека, что машина сделала два полных оборота – с одного полного оборота или вращение 360 градусов.
Скейтбордисты, сноубордисты, вейкбордисты, серферы, лыжники и многие другие экстремальные спортсмены часто используют такие термины чтобы описать специальные трюки, которые они делают. Простой трюк на доске для серфинга называется «360», при котором во время катания на волне серфер вращает доску на 360 градусов. градусов – отсюда и название «360».
Дополнительные углы
Когда кто-то говорит о дополнительных углах они говорят не об одном, а о двух ракурсах. Дополнительные углы складываются
90°. Например, 50° и 40° являются дополнительными углами. Поскольку дополнительные
углы в сумме дают 90°, вы знаете, что ни один из них не может быть больше 90°.
Дополнительные углы обычно легко заметить, потому что вместе они составляют 90 209 прямых.
угол . Взгляните, например, на эту диаграмму:
Дополнительные углы складываются
90°. Например, 50° и 40° являются дополнительными углами. Поскольку дополнительные
углы в сумме дают 90°, вы знаете, что ни один из них не может быть больше 90°.
Дополнительные углы обычно легко заметить, потому что вместе они составляют 90 209 прямых.
угол . Взгляните, например, на эту диаграмму:
Первое, на что следует обратить внимание, это три углы на схеме. Есть угол 53°, угол x° и прямой угол. Также обратите внимание, что для 53° и x° я не удосужился нарисовать кривую. линия, показывающая угол – для такой простой диаграммы довольно ясно, что каждый угол соответствует .
Скажем, мне нужно было вычислить, чему равен «x». Сейчас,
как на экзамене, чтобы отработать ответ, наверное нужно что-то использовать
что вы только недавно узнали. Мы только что говорили о дополнительных
углы, так как насчет того, чтобы попытаться использовать это в наших интересах. Глядя на
диаграмме вы можете видеть, что прямой угол равен , составленному из 53° и
х°. Другими словами:
Другими словами:
Мы должны думать об угле, который при добавлении к 53° дает нам 90°. Это не так уж сложно, если вы немного подумаете об этом, вы должны получаем:
Это означает, что x равно 37.
Дополнительные углы
Они очень похожи на дополнительные углы, за исключением того, что в сумме они должны составлять 180°, а не 90°. Так, например, 60° и 120° дополнительных углов. Другой способ сказать это: «120 градусы являются дополнением к 60 градусам».
Дополнительные углы легко заметить на диаграммах потому что они образуют прямой угол. Вот схема, показывающая два дополнительные углы:
На этой диаграмме t° и 141° являются дополнительными углов, так как вместе они составляют прямой угол, или 180 градусов в других слова. Если мы запишем это математически, то это будет выглядеть так:
значение ‘t’, которое сделает это уравнение равным верно . Если вы думаете о
на какое-то время вы должны получить:
Если вы думаете о
на какое-то время вы должны получить:
и вычислить, что t равно 39.
Вертикально противоположно углов
Допустим, я нарисовал две прямые линии, которые пересекаются, и обозначьте четыре образовавшихся угла:
Обратите внимание, что каждый угол имеет угол , противоположный . например, напротив «а» стоит «с», а напротив «d» — «б». Эти две пары углов известны как по вертикали напротив углов . Вертикально противоположные углы равны по величине, поэтому на этой диаграмме «а» имеет тот же размер, что и «с» и «d» такие же, как «b». Это очень полезно, когда у вас есть ситуации примерно так:
Поскольку «а» и 121° вертикально противоположны, вы можно сразу понять, что «а» тоже равно 121°.
Описание углов
Любой угол измеряется между двумя различными
направления. Обычно на диаграмме эти направления изображают линиями,
иногда со стрелками на них.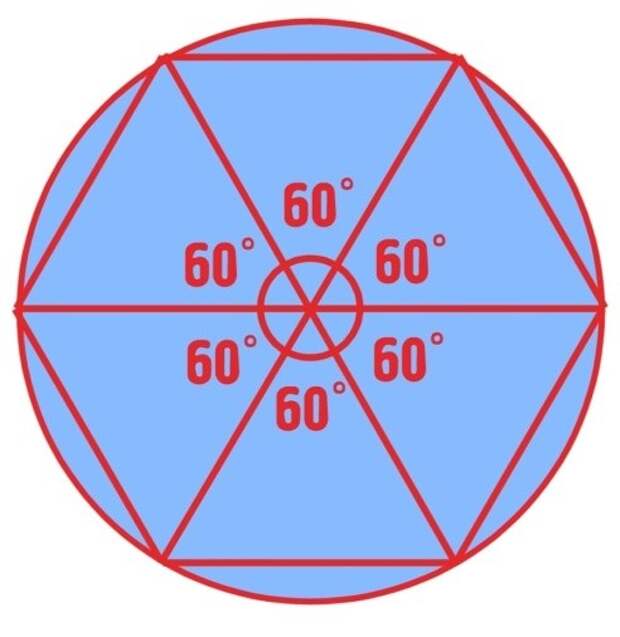

 Он изменяет направление линии или луча. Угол в 360 градусов образует круг. Два плеча угла, образующего 360 градусов, перекрывают друг друга.
Он изменяет направление линии или луча. Угол в 360 градусов образует круг. Два плеча угла, образующего 360 градусов, перекрывают друг друга.