 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Конспект урока по алгебре в 10 классе: «Числовая окружность»
Тема:«Числовая окружность»
Цель урока:
- способствовать формированию умения записывать множество чисел, соответствующих на числовой окружности точке;
- способствовать формированию умения находить на числовой окружности точку, соответствующую данному числу.
- способствовать формированию навыков работать в коллективе способствовать развитию коммуникативных компетенций.
- способствовать развитию креативных способностей учащихся
- способствовать формированию элементов информационной культуры.
- способствовать самореализации учеников.
Тип урока: Комбинированный
Возраст учащихся: 10 класс
Обучающие задачи:
- познакомиться с числовой окружностью;
- научиться находить на числовой окружности точки соответствующие заданному числу.

- научиться переходить от градусной системы счисления к радианной и наоборот.
- научиться выделять на числовой окружности дугу соответствующей заданному интервалу.
- научиться по заданной дуге записывать аналитическое выражение.
- сделать самоанализ урока.
Развивающие задачи:
- способствовать формированию навыков работать в коллективе при выполнении групповых заданий;
- способствовать развитию коммуникативных компетенций при работе в группах;(при выполнении в группах практического задания)
- способствовать развитию креативных способностей учащихся при решении нестандартных задач;
- способствовать совершенствованию аналитических навыков учащихся при решении задач;
- способствовать формированию навыков и умений использовать различные способы решения задач.
- способствовать развитию пространственного воображения, умению работать с интерактивной доской,
- развивать логическое мышление, вычислительные навыки, память, внимание, повышение мотивации к изучению математики
Воспитывающие задачи :
- воспитывать ответственность за свои действия.

Оборудование и методические материалы: компьютер, проектор, экран, демонстрационный круг ,веревка, маркер.
Этапы урока:
1. Организационный момент.
2. Актуализация знаний учащихся.
3. Изучение нового материала.
4. Закрепление знаний, умений и навыков.
5. Домашнее задание.
6. Подведение итогов урока.
7. Рефлексия.
Ход урока
1. Организационный момент
1) Учитель приветствует учащихся.
2) Учитель выявляет отсутствующих, выясняет причину отсутствия.
3) Проверка готовности учащихся к уроку (внешний вид, рабочая поза, состояние рабочего места).
4) Проверка подготовленности классного помещения к уроку (чистая доска, мел, тряпка, порядок в классе).
5) Организация внимания.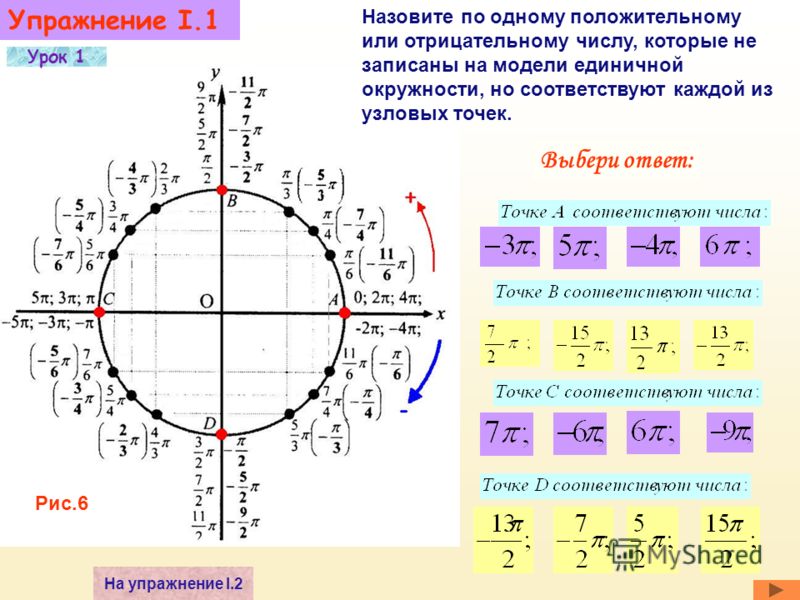
Учитель: Ребята, сегодня мы с вами начинаем изучать большой раздел в математике — тригонометрические функции. Отнеситесь к её изучению очень внимательно, поскольку, как показывает опыт, обучающиеся, хорошо овладевший понятием «числовая окружность», достаточно уверенно обращается и с тригонометрическими функциями.
Зачем нам нужна тригонометрия?(Слайды №1-8)
Восход и заход солнца, изменение фаз луны, чередование времен года, биение сердца, циклы в жизнедеятельности организма, вращение колеса, морские приливы и отливы — модели этих многообразных процессов описываются тригонометрическими функциями.
Звук, электрический ток, радиоволны так же представляют собой колебания различной частоты и амплитуды.
Если бы зрение людей обладало способностью видеть звуковые, электромагнитные и радиоволны, то мы видели бы вокруг многочисленные синусоиды всевозможных видов.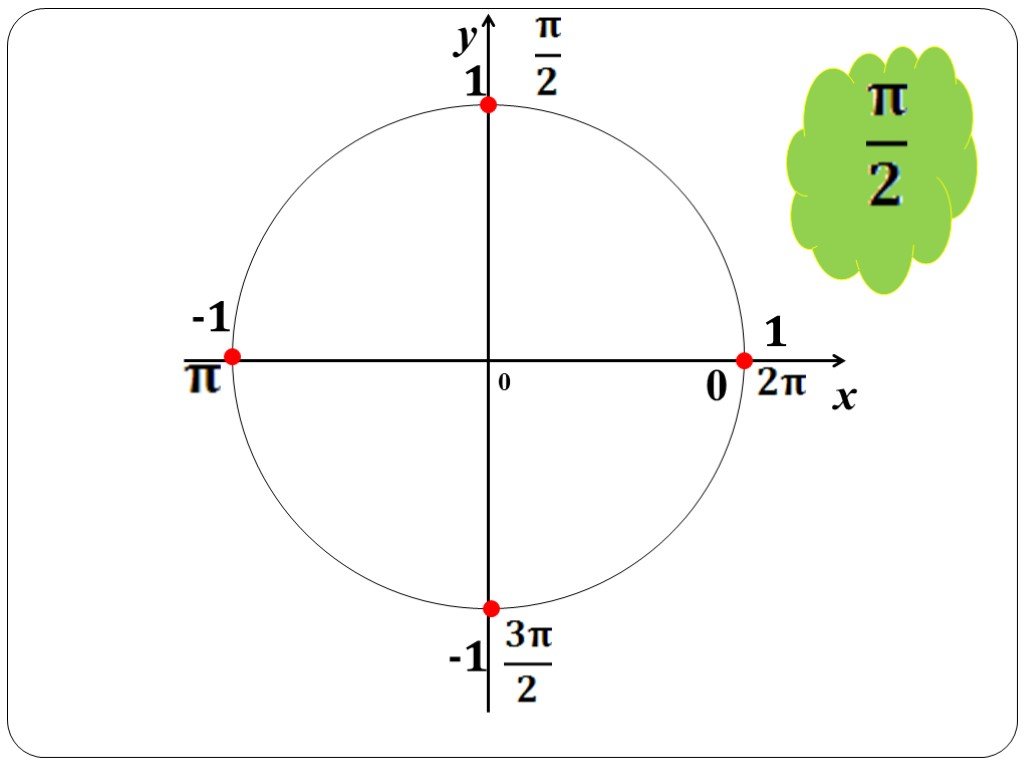
Таким образом многие процессы происходящие в природе и технических системах описываются тригонометрическими функциями, которые служат основой их математических моделей.
2. Актуализация знаний учащихся
Учитель: Внимание, на доске обозначены вопросы для повторения, они помогут вам в изучении нового материала. Обучающимся дается несколько минут на обдумывание ответа. Затем к доске вызывается один из учеников и отвечает на них. Правильность ответа контролируют обучающиеся, они могут задать дополнительные наводящие вопросы, если не согласны с ответом или считают, что ответ неполный. Учитель контролирует всех. В конце опроса выставляется оценка за ответ. Слайд № 9,10.
Устная работа.
Учитель: Что называется числовой прямой?
Ученики: Это прямая, на которой заданы начальная точка О, масштаб (единичный отрезок) и положительное направление.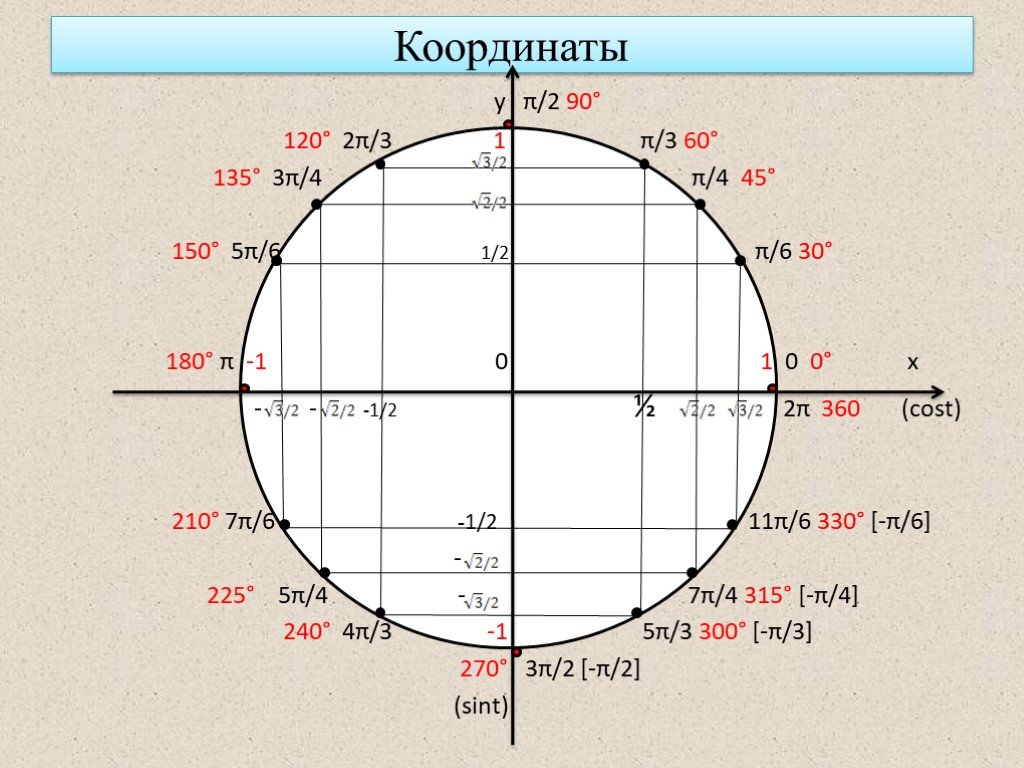
Учитель: Сколько действительных чисел можно поставить в соответствие каждой точке числовой прямой?
Ученики: Каждой точке соответствует только одно действительное число.
Учитель То есть числовая прямая – это взаимно однозначное соответствие между всеми точками прямой и всеми действительными числами.
Учитель Что называется окружностью?
Ученики: Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной точки.
Учитель: Как найти длину окружности?
Ученики: Длина окружности равна :L=2 пr.
Учитель: А что такое пи?
Ученики: Пи — математическая константа, выражающая отношение длины окружности к длине её диаметра. Эта константа приближенно равна 3,14.
Учитель: Чему будет равна L при R=1.
Ученики: L=2П или 6,28.
Учитель: Отметьте на числовой прямой точки П и 2П.(Слайд №9,10,11 )
3. Изучение нового материала.
Учитель: В реальной жизни приходится двигаться не только по прямой, но и по окружности.
В принципе любую окружность можно рассматривать как числовую, но удобнее всего использовать для этой цели единичную окружность — окружность радиусом 1. Исходя из основной формулы длины окружности при радиусе равном 1 получаем длину единичной окружности равной 2П, что составляет примерно 6,28. Соответственно половина длины окружности равна П, четверть П/2 и три четверти окружности равны 3П/2.(Слайд№ 12)
На числовой окружности принято условно называть дугу от 0 до П/2 первой четвертью, дугу от П/2 до П – второй четвертью, от П до 3П/2 3 четвертью и от 3П/2 до 2П 4-й четвертью.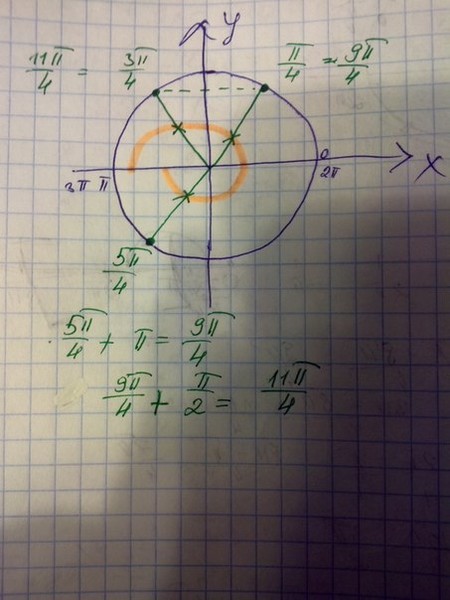 При этом, как правило, речь идет об открытых дугах, т.е. о дугах без их концов: например, первая четверть — это дуга от 0 до П/2, без точек 0 и П/2.
При этом, как правило, речь идет об открытых дугах, т.е. о дугах без их концов: например, первая четверть — это дуга от 0 до П/2, без точек 0 и П/2.
Рассмотрим следующее определение.
Учитель :Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
И самое главное необходимо запомнить что положительное значение откладывается против часовой стрелки , а отрицательное по часовой стрелке
(Слайд 12,13).
Любому действительному числу можно сопоставить единственную точку на прямой и наоборот (любая точка прямой соответствует единственному числу).
Числу 0 соответствует начальная точка О.
Если t>0, то, двигаясь по прямой из точки О в положительном направлении, необходимо пройти путь длиной t.
Если t<0, то, двигаясь по прямой из точки О в отрицательном направлении, необходимо пройти путь длиной |t|.
Проведем горизонтальный и вертикальный диаметры CA и BD. (Слайд№14)
Учитель: Разделим первую четверть на три равные части. Чему раны длины полученных дуг?(Слайд№14)
Ученики: П/6
Учитель: А если возьмем две части?
Ученики: П/3
Учитель: Найдите на числовой окружности точки симметричные точкам П/6 и П/3 относительно диаметров. Чему они равны?
Ученики: П/6, 5П/6, 7П/6, 11П/6. П/3, 2П/3,4П/3, 5П/3. (Слайды№15,16)
Учитель: Разделим первую четверть на две равные части. Чему раны длины полученных дуг? (Слайд№17)
Ученики: П/4
Учитель: Найдите на числовой окружности точки симметричные точке П/4 относительно диаметров. Чему они равны?
Ученики: П/4, 3П/4, 5П/4, 7П/4.
Учитель: Подумайте как найти точки: 21П/4, 13П/6, 19П/6.(Слайд№18) Использовать демонстрационный круг ,веревка, маркер
Ученики:
4. . Закрепление знаний, умений и навыков.
Учитель: Обозначьте на числовой окружности точку, которая
соответствует данному числу:
Ученики: Отмечаю в тетради заданные точки, результат сверяют по
слайду№20.
Учитель: Какой четверти числовой окружности принадлежит точка, соответствующая числу: 2; 5; -5; -9; -17; 31; -95.?
Ученики: Производят необходимые расчеты в тетради и отвечают на вопрос.(Слайд№21)
Учитель: Как расположены на координатной прямой и на числовой окружности точки, соответствующие числам: a) t и –t; б) t и t+2πk, kÎZ;
в) t и t+π; г) t+π и t-π.
Ученики: Выполняют задание в тетради, результат сверяют по Слайду№22.
Учитель: Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству.
Ученики: Выполняют задание в тетради, результат сверяют по Слайду№23.
Учитель: Найдите все числа t, которым на числовой окружности соответствуют точки, принадлежащие открытой дуге АВ, DC, PR .(Слайд№24)
Ученики: Выполняют задание в тетради, результат сверяют по Слайду.
Учитель: Выполним самостоятельную работу.(Слайд№25)
Учащиеся самостоятельно выполняют работу с последующей проверкой и отметкой за урок.. На начальном этапе выполнения задания, учитель контролирует и консультирует обучающихся. Затем в роли консультантов выступают обучающиеся справившиеся с заданием раньше.
Дополнительное задание (если останется время): Приложение№1.
Слайд №26,27,28.
5. Домашнее задание.
П2. 9-13(в, г) — 24.25(в, г).
6. Подведение итогов урока.
Учитель: Молодцы ребята, очень хорошо потрудились, хорошо решали задачи, внимательно слушали и принимали активное участие.
Давайте подведем итоги. В начале урока мы задали следующие вопросы.
1)Что называется числовой окружностью?
2)Как найти точки на числовой окружности, соответствующие заданным числам?
3)Как выделять на числовой окружности дугу соответствующей заданному интервалу.
4)Как по заданной дуге записывать аналитическое выражение.
Теперь вы можете ответить на них.
7. Рефлексия.
Продолжите фразы:
— сегодня на уроке я узнал …
— сегодня на уроке я научился…
— сегодня на уроке я повторил…
— сегодня на уроке я познакомился…
— сегодня на уроке мне понравилось
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | ||
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
какова площадь круга с окружностью 3 пи дюйма?
Вот ответ на такие вопросы, как: как найти площадь круга с окружностью 3 пи дюйма?
Калькулятор окружности
| ||||||||||||
Площадь круга с окружностью 3π равна 7,069 | |
Изображение кружка = 1,5d = 3C = 9,43 | А = πr 2 = π(d2) 2 А = С 2 4π π = 3,1415A = площадь C = окружность или периметр r = радиус , d = диаметр |
Площадь круга относительно радиуса
:Площадь = π·r 2 = 3,14·1,5 2 = 7,07 квадратных дюйма (*)
Площадь круга относительно
диаметра :Площадь = π·(d2) 2 = 3,14·(32) 2 = 3,14·(1,5) 2 = 7,07 квадратных дюйма (*)
Площадь круга в пересчете на
длины окружности :Площадь = С 2 4π = 9,43 2 4π = 88,83(4·3,14) = 88,8312,56 = 7,07 квадратных дюйма (*)
(*) 7,068583470577 дюйма, точно или ограничено точностью этого калькулятора (13 знаков после запятой).
Примечание: для простоты указанные выше операции были округлены до 2 знаков после запятой, а число π округлено до 3,14.
Окружность радиусом = 1,5, или диаметром = 3, или окружностью = 9,425 дюйма имеет площадь: см²)
Используйте приведенный ниже калькулятор площади круга, чтобы найти площадь круга по длине окружности или другим параметрам. Для расчета площади вам достаточно ввести положительное числовое значение в одно из 3-х полей калькулятора. Вы также можете увидеть в нижней части калькулятора пошаговое решение.
Формула площади круга
Вот три способа нахождения площади круга (формулы):
Формула площади круга по радиусу
A = πr 2
Формула площади круга по диаметру
A = π(d2) 2
Формула площади круга по длине окружности
2 4π
См. ниже некоторые определения, связанные с формулами:
ниже некоторые определения, связанные с формулами:
Окружность
Окружность – это линейное расстояние вокруг края круга.
Радиус
Радиусом круга является любой из отрезков от его центра до периметра. Радиус равен половине диаметра или r = d2.
Диаметр
Диаметр окружности — это любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности. Диаметр в два раза больше радиуса или d = 2·r.
Греческая буква π
π обозначает число Пи, которое определяется как отношение длины окружности к ее диаметру или π = Cd . Для простоты можно использовать Pi = 3,14 или Pi = 3,1415. Пи — иррациональное число. Первые 100 цифр числа Пи: 3,14159.26535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 …
Note:
If you input the radius in centimeters, you will get the answer in square centimeters (cm²), if in inches, will get the answer in square inches (дюйм²) и т.


