Задачи по теме «Классические вероятности» (9 класс)
Классические вероятности
1. Задание 9 № 149
На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.
Решение.
Сергей выучил 25 − 3 = 22 вопроса. Поэтому вероятность того, что ему попадётся выученный билет равна
Ответ: 0,88.
Ответ: 0,88
2. Задание 9 № 132728
Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
Решение.
Всего трехзначных чисел 900. На пять делится каждое пятое их них, то есть таких чисел Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел:
Ответ: 0,2.
Примечание.
Количества чисел можно было не
находить: искомая вероятность равна одной пятой потому, что пятая часть
чисел делится на 5.
Ответ: 0,2
3. Задание 9 № 132730
Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.
Решение.
Количество каналов, по которым не идет кинокомедий Вероятность того, что Маша не попадет на канал, по которому идут кинокомедии равна отношению количества каналов, по которым не идут кинокомедии к общему числу каналов:
Ответ: 0,85.
Ответ: 0,85
4. Задание 9 № 132732
На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение.
Вероятность того, что будет выбран пирожок с вишней равна отношению количества пирожков с вишней к общему количеству пирожков:
Ответ:0,25
Ответ: 0,25
5. Задание
9 № 132734
Задание
9 № 132734
В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Решение.
Вероятность того, что приедет желтая машина равна отношению количества желтых машин к общему количеству машин:
Ответ: 0,2.
Ответ: 0,2
6. Задание 9 № 132736
В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
Решение.
Так как в каждой десятой банке кофе есть приз, то вероятность выиграть приз равна Поэтому, вероятность не выиграть приз равна
Ответ:0,9.
Ответ: 0,9
7. Задание 9 № 132738
Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.
Решение.
Вероятность того, что подойдет красная кабинка равна отношению количества красных кабинок к общему количеству кабинок на колесе обозрения. Всего красных кабинок: Поэтому искомая вероятность
Ответ: 0,5.
Ответ: 0,5
8. Задание 9 № 132740
У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Решение.
Вероятность того, что чай нальют в
чашку с синими цветами равна отношению количества чашек с синими
цветами к общему количеству чашек. Всего чашек с синими цветами: Поэтому
искомая вероятность
Всего чашек с синими цветами: Поэтому
искомая вероятность
Ответ: 0,75.
Ответ: 0,75
9. Задание 9 № 132744
Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
Решение.
Вероятность получить пазл с машиной равна отношению числа пазлов с машиной к общему числу закупленных пазлов, то есть .
Ответ: 0,6.
Ответ: 0,6
10. Задание 9 № 132748
В среднем из каждых 80 поступивших в продажу аккумуляторов 76 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.
Решение.
Из каждых 80 аккумуляторов в
среднем будет 80 − 76 = 4 незаряженных. Таким образом, вероятность
купить незаряженный аккумулятор равна доле числа незаряженных аккумуляторов
из каждых 80 купленных, то есть .
Ответ: 0,05.
Ответ: 0,05
11. Задание 9 № 311324
Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
Решение.
Всего было подготовлено 50 билетов. Среди них 9 были однозначными. Таким образом вероятность того, что наугад взятый учеником билет имеет однозначный номер равна
Ответ: 0,18
12. Задание 9 № 311336
В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
Решение.
Всего в мешке 50 жетонов. Среди них 45 имеют двузначный номер. Таким образом, вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число равна
Ответ: 0,9
13. Задание 9 № 311359
В денежно-вещевой лотерее на 100
000 билетов разыгрывается 1300 вещевых и 850 денежных выигрышей.
Решение.
Вероятность получить вещевой выигрыш равна отношению количества вещевых выйграшей к общему количеству выйгрышей
Ответ: 0,013
14. Задание 9 № 311415
Из 900 новых флеш-карт в среднем 54 не пригодны для записи. Какова вероятность того, что случайно выбранная флеш-карта пригодна для записи?
Решение.
Из 900 карт исправны 900 − 54 = 846 шт. Поэтому вероятность того, что случайно выбранная флеш-карта пригодна для записи равна:
.
Ответ: 0,94.
Ответ: 0,94
15. Задание 9 № 311505
В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?
Решение.
Каждая команда попадет в группу
с вероятностью 0,25. Таким образом, вероятность того, что команда не
попадает в группу равна 1-0,25=0,75.
Таким образом, вероятность того, что команда не
попадает в группу равна 1-0,25=0,75.
Ответ: 0,75
16. Задание 9 № 311512
В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по-английски, трое только по-французски, двое по-французски и по-английски. Какова вероятность того, что случайно выбранный турист говорит по-французски?
Решение.
Количество туристов, говорящих по-французски, равно 5. Поэтому вероятность того, что случайно выбранный турист говорит по-французски равна
Ответ: 0,25
17. Задание 9 № 311525
В коробке 14 пакетиков с чёрным чаем и 6 пакетиков с зелёным чаем. Павел наугад вынимает один пакетик. Какова вероятность того, что это пакетик с зелёным чаем?
Решение.
Всего в коробке 14+6=20 пакетиков. Вероятность того, что Павел вытащит пакетик с зелёным чаем равна
Ответ: 0,3
18. Задание 9 № 311767
Задание 9 № 311767
Стас, Денис, Костя, Маша, Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
Решение.
Вероятность события равна отношению количества благоприятных случаев к количеству всех случаев. Среди пяти детей одна девочка. Поэтому вероятность равна
Ответ: 0,2.
Ответ: 0,2
19. Задание 9 № 311919
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.
Решение.
Рассмотрим все возможные исходы жеребьёвки.
· Команда А в матче в обоих матчах первой владеет мячом.
· Команда А в
матче в обоих матчах не владеет мячом первой.
· Команда А в матче с командой В владеет мячом первой, а в матче с командой С — второй.
· Команда А в матче с командой С владеет мячом первой, а в матче с командой В — второй.
Из четырех исходов один является благоприятным, вероятность его наступления равна 0,25.
Ответ: 0,25.
Ответ: 0,25
20. Задание 9 № 315159
В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
Решение.
Всего спортсменов 11 + 6 + 3 = 20 человек. Поэтому вероятность того, что первым будет стартовать спортсмен из России равна
Ответ: 0,55.
Ответ: 0,55
21. Задание 9 № 315173
В лыжных гонках участвуют 11
спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите
вероятность того, что первым будет стартовать спортсмен не из России.
Порядок, в котором спортсмены стартуют, определяется жребием. Найдите
вероятность того, что первым будет стартовать спортсмен не из России.
Решение.
Всего спортсменов 11 + 6 + 3 = 20 человек. Поэтому вероятность того, что первым будет стартовать спортсмен не из России равна
Ответ: 0,45.
Ответ: 0,45
22. Задание 9 № 315195
Из каждых 1000 электрических лампочек 5 бракованных. Какова вероятность купить исправную лампочку?
Решение.
Вероятность купить исправную лампочку равна доле исправных лампочек в общем количестве лампочек:
Ответ: 0,995.
Ответ: 0,995
23. Задание 9 № 316328
Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Решение.
Вероятность события равна отношению
количества благоприятных случаев к количеству всех случаев. Благоприятными
случаями являются 3 случая, когда игру начинает Петя, Игорь или Антон,
а количество всех случаев 6. Поэтому искомое отношение равно
Благоприятными
случаями являются 3 случая, когда игру начинает Петя, Игорь или Антон,
а количество всех случаев 6. Поэтому искомое отношение равно
Ответ: 0,5.
Ответ: 0,5
24. Задание 9 № 325436
Из 1600 пакетов молока в среднем 80 протекают. Какова вероятность того, что случайно выбранный пакет молока не течёт?
Решение.
Вероятность того, что пакет молока протекает равна Поэтому вероятность того, что случайно выбранный пакет молока не течёт равна
Ответ: 0,95.
Ответ: 0,95
25. Задание 9 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна
Ответ: 0,3.
Ответ: 0,3
26. Задание 9 № 325453
Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.
Решение.
При бросании кубика равновозможны шесть различных исходов. Событию «выпадет нечётное число очков» удовлетворяют три случая: когда на кубике выпадает 1, 3 или 5 очков. Поэтому вероятность того, что на кубике выпадет нечётное число очков равна
Ответ: 0,5.
Ответ: 0,5
27. Задание 9 № 325481
Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.
Решение.
При бросании кубика равновозможны
шесть различных исходов. Событию «выпадет не больше трёх очков»
удовлетворяют три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет не больше трёх очков
равна
Поэтому вероятность того, что на кубике выпадет не больше трёх очков
равна
Ответ: 0,5.
Ответ: 0,5
28. Задание 9 № 325482
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно 1 раз.
Решение.
Всего возможны четыре исхода: решка-решка, решка-орёл, орёл-решка, орёл-орёл. Орёл выпадает ровно один раз в двух случаях, поэтому вероятность того, что орёл выпадет ровно один раз равна
Ответ: 0,5.
Ответ: 0,5
29. Задание 9 № 325491
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
Решение.
При бросании кубика равновозможны
шесть различных исходов. Событию «выпадет больше трёх очков» удовлетворяют
три случая: когда на кубике выпадает 4, 5, или 6 очков. Поэтому вероятность
того, что на кубике выпадет не больше трёх очков равна Таким
образом, при одном бросании кубика с одинаковой вероятностью реализуется
либо событие А — выпало число, большее 3, либо событие Б — выпало
число не больше 3. То есть равновероятно реализуются четыре события:
А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что оба раза выпало число,
большее 3 равна
То есть равновероятно реализуются четыре события:
А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что оба раза выпало число,
большее 3 равна
Ответ: 0,25.
Ответ: 0,25
30. Задание 9 № 325540
Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
Решение.
Вероятность промаха равна 1 − 0,5 = 0,5. Вероятность того, что стрелок первые три раза попал в мишени равна 0,53 = 0,125. Откуда, вероятность события, при котором стрелок сначала три раза попадает в мишени, а четвёртый раз промахивается равна 0,125 · 0,5 = 0,0625.
Ответ: 0,0625.
Ответ: 0,0625
31. Задание 9 № 325560
В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
Номер стрелка | Число выстрелов | Число попаданий |
1 | 42 | 28 |
2 | 70 | 20 |
3 | 54 | 45 |
4 | 46 | 42 |
Тренер решил послать на соревнования
того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите в ответе его номер.
Кого из стрелков выберет тренер? Укажите в ответе его номер.
Решение.
Найдём относительную частоту попаданий каждого из стрелков:
Заметим, что Приведём и к общему знаменателю и сравним: Таким образом, наибольшая относительная частота попаданий у четвёртого стрелка.
Ответ: 4.
Ответ: 4
32. Задание 9 № 325580
В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку.
Решение.
Найдём количество чёрных ручек: Вероятность того, что Алиса вытащит наугад красную или чёрную ручку равна
Ответ: 0,56.
Ответ: 0,56
33. Задание 9 № 341531
В среднем из 100 карманных
фонариков, поступивших в продажу, восемь неисправных. Найдите вероятность
того, что выбранный наудачу в магазине фонарик окажется исправен.
Найдите вероятность
того, что выбранный наудачу в магазине фонарик окажется исправен.
Решение.
Из 100 фонариков 100 − 8 = 92 исправны. Значит, вероятность того, что выбранный наудачу в магазине фонарик окажется одним из них равна
Ответ: 0,92.
Ответ: 0,92
Задачи по теме «Вероятность». 9 класс — 4ЕГЭ
Теория вероятности в задачах ОГЭ по математике. 49 задач с ответами.
tv49.docx
1. Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 50.
2. Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 11.
3. На тарелке 10 пирожков: 2 с мясом, 6 с капустой и 2 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
4. На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Вова наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
5. В фирме такси в данный момент свободно 30 машин: 7 черных, 6 желтых и 17 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
6. В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Петя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Петя не найдет приз в своей банке.
7. Игорь с папой решили покататься на колесе обозрения. Всего на колесе двадцать кабинок, из них 3 — синие, 14 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Игорь прокатится в красной кабинке.
8. Петя с папой решили покататься на колесе обозрения. Всего на колесе двенадцать кабинок, из них 3 — синие, 6 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке.
9. У дедушки 10 чашек: 7 с красными цветами, остальные с синими. Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
10. У бабушки 20 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
11. На экзамене 50 билетов. Петя не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.
12. На экзамене 50 билетов. Петя не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет.
13. Родительский комитет закупил 10 пазлов для подарков детям на окончание года, из них 2 с машинами и 8 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с машиной.
14. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 22 с машинами и 3 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной.
15. В среднем на 100 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
16. В среднем на 75 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
17. В среднем из каждых 100 поступивших в продажу аккумуляторов 91 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
18. В среднем из каждых 80 поступивших в продажу аккумуляторов 68 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
19. Саша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 6.
20. Определите вероятность того, что при бросании кубика выпало нечетное число очков.
21. Определите вероятность того, что при бросании кубика выпало 1.
22. Одновременно бросают две симметричные монеты. Какова вероятность того, что выпадут орел и решка?
23. Одновременно бросают три симметричные монеты. Какова вероятность того, что выпадут два орла и одна решка?
24. В классе 21 учащийся, среди них два друга — Петя и Вася. На уроке физкультуры класс случайным образом разбивают на 7 равных групп. Найдите вероятность того, что Петя и Вася попали в одну группу.
В классе 21 учащийся, среди них два друга — Петя и Вася. На уроке физкультуры класс случайным образом разбивают на 7 равных групп. Найдите вероятность того, что Петя и Вася попали в одну группу.
25. Перед началом футбольного матча судья бросают монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть три матча — с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах владение мячом первыми будет принадлежать команде А.
26. В соревнованиях по толканию ядра участвуют 6 спортсменов из Греции, 4 спортсмена из Болгарии, 3 спортсмена из Румынии и 7 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Венгрии.
27. В соревнованиях по толканию ядра участвуют 4 спортсмена из Дании, 8 спортсменов из Швеции, 4 спортсмена из Румынии и 9 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
28. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
29. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
30. На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Треугольники», равна 0,5. Вероятность того, что это окажется задача на тему «Окружность» равна 0,25. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
31. На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Окружность», равна 0,45. Вероятность того, что это окажется задача на тему «Углы» равна 0,5. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
32. Стрелок четыре раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
33. Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
34. Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
35. Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
36. В девятом экономическом классе учатся 24 мальчика и 6 девочек. По жребию они выбирают одного дежурного по классу.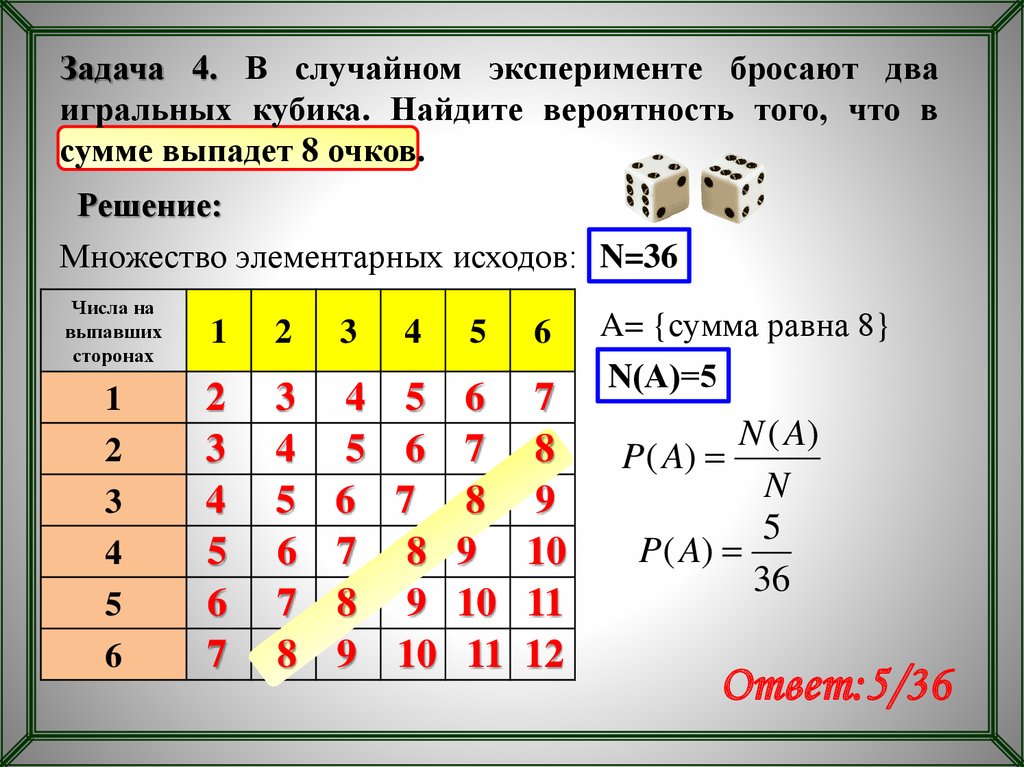 Какова вероятность того, что это будет мальчик?
Какова вероятность того, что это будет мальчик?
37. В девятом математическом классе учатся 2 мальчика и 23 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет девочка?
38. Вероятность того, что новый компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
39. Вероятность того, что новый сканер прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
40. Какова вероятность того, что случайно выбранное натуральное число от 25 до 39 делится на 5?
41. Какова вероятность того, что случайно выбранное натуральное число от 15 до 36 делится на 2?
42. На олимпиаде по химии участников рассаживают по трем аудиториям. В первых двух по 180 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
43. На олимпиаде по математике участников рассаживают по трем аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 300 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
44. Вероятность того, что на тесте по физике Петя верно решит больше 11 задач, равна 0,65. Вероятность того, что он верно решит больше 10 задач, равна 0,71. Найдите вероятность того, что Петя верно решит ровно 11 задач.
45. Вероятность того, что на тесте по математике Вася верно решит больше 12 задач, равна 0,7. Вероятность того, что он верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что Вася верно решит ровно 12 задач.
46. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 22 пассажиров, равна 0,86. Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21.
Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21.
47. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,96. Вероятность того, что окажется меньше 11 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 11 до 20.
48. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
49. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Ответы
1. 0,02
2. 0,09
3. 0,2
4. 0,3
5. 0,2
6. 0,9
7. 0,15
8. 0,25
9. 0,3
10. 0,8
11. 0,82
12. 0,98
13. 0,2
14. 0,88
15. 0,93
16. 0,92
17. 0,09
18. 0,15
19. 0,1
20. 0,5
21. 1/6
22. 0,5
23. 0,375
24. 0,1
25. 0,125
26. 0,35
27. 0,32
28. 0,11
29. 0,13
30. 0,75
31. 0,95
32. 0,0625
33. 0,063
34. 0,243
35. 0,375
36. 0,8
37. 0,92
38. 0,14
39. 0,09
40. 0,2
41. 0,5
42. 0,2
43. 0,2
44. 0,06
45. 0,09
46. 0,36
47. 0,45
48. 0,078
49. 0,0776
практических задач на вероятность | Класс 9 Математика
Вероятность простыми словами — это предсказание наступления события до того, как оно уже произошло. Мы делаем предсказания во многих вещах в нашей повседневной жизни, например:
Мы делаем предсказания во многих вещах в нашей повседневной жизни, например:
1) Предсказываем погоду перед тем, как отправиться на пикник.
2) Предсказать исход выборов.
3) Угадайте, кто выиграет жеребьевку.
Во всех этих ситуациях мы пытаемся найти вероятность или шансы наступления события, рассматривая все условия, благоприятствующие этому событию. Из приведенного выше обсуждения вероятность может быть определена математически как:
Вероятность — это раздел математики, который говорит нам, каковы шансы того, что событие произойдет. Вероятность события представляет собой число от 0 до 1, где 0 указывает на невозможность события, а 1 на достоверность. Следовательно, 0 ≤ P(E) ≤ 1, , где P(E) = вероятность возникновения события.
Некоторые основные термины, используемые в теории вероятностей:
1. Эксперимент: Эксперимент известен как событие, в котором ожидается некоторый четко определенный результат. Также известен как пространство выборки. Например, выборочное пространство S равно S = {H, T}, где H относится к голове, а T относится к хвосту.
Также известен как пространство выборки. Например, выборочное пространство S равно S = {H, T}, где H относится к голове, а T относится к хвосту.
2. Испытание: Испытание известно как единичное событие, которое проводится для определения результата.
3. Результат: Итоги — это результаты эксперимента. Например, выигрыш/проигрыш — это возможные исходы матча по крикету.
4. Случайный эксперимент: Случайный эксперимент — это эксперимент, результат которого нельзя предсказать заранее. Это может быть повторено при многочисленных условиях.
5. Невозможное событие: Когда вероятность события равна 0, это событие называется невозможным.
6. Верное событие: Когда вероятность события равна 1, это событие называется достоверным.
Формула вероятности
Экспериментальная или эмпирическая вероятность события составляет событие, которое произойдет
N(E) = общее количество благоприятных исходов
N(S) = общее количество всех возможных исходов
Теперь давайте перейдем к решению задач и лучшему пониманию вероятности.
Примеры задач
Вопрос 1. Сумит играет в крикет со своими друзьями, чтобы решить, кто будет бить, нужно подбросить монету, и тот, кто выиграет бросок, бьет первым. Предположим, что Сумит и Мохит являются капитанами двух команд, выбравших соответственно орла и решку. Найдите шансы Сумита ударить первым.
Решение:
Мы знаем, что есть только два возможных результата подбрасывания: орел или решка.
Таким образом, выборочное пространство (я) = общее количество возможных исходов = {H, T}
Для выигрыша в жеребьевке сумме требуется решка, поэтому возможен только один благоприятный исход. 0,5 Найдите вероятность того, что сумма баллов будет простым числом?
Решение:
Так как подбрасываются две кости, то общее количество комбинаций = n(S) = (6 x 6) = 36 комбинаций.
Пусть E будет событием, когда сумма является простым числом.
Все благоприятные исходы (E) = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 5), (3, 2), (3, 4), (4, 1) (6, 5)}
Следовательно, n(E) = 15
Вероятность того, что результат будет простым числом = n(E)/n(S) = 15/36 = 5/12
Вопрос 3.
В лотерейном ящике лежат 10 призов и 25 бланков. Из лотерейной коробки случайным образом вытягивается талон. Какова вероятность получить приз?
Решение:
Дано: Общее количество призов = 10
Общее количество пробелов = 25
Итак, общее количество возможных исходов (т. е. n(S)) равно 10 + 25 = 35
Общее количество призов, n(E) = 10
По формуле
P(E) = n(E)/n(S) = 1035 = 27
Вопрос 4. В мешке 8 синих шарики и несколько розовых шариков. Если вероятность вытащить розовый шар вдвое меньше вероятности вытащить синий шар, то найти количество розовых шаров в мешке.
Решение:
Предположим, что количество розовых шаров равно n.
Количество синих шаров = 8.
Следовательно, общее количество шаров в мешке = n + 8.
Теперь вероятность вытащить розовый шар, т.е. P(X) = n/n + 8
вероятность вытащить синий шар, т.е.
P(B) = 8/n + 8
Согласно вопросу, вероятность вытащить розовый
шар равна половине вероятности вытянуть синий шар
Итак, P(X) = P(B)/2
n = 4.
Итак, количество розовых шаров в мешке равно 4.
Вопрос 5. Карты с номерами от 1 до 20 смешиваются, затем случайным образом вытягивается карта. Какова вероятность того, что номер вытянутой карты кратен 3 или 5?
Решение:
Карточки пронумерованы от 1 до 20, поэтому n(S) = {1, 2, 3, 4, …., 19, 20}.
Пусть E будет событием получения числа, кратного 3 или 5
Итак, n(E) = {3, 6, 9, 12, 15, 18, 5, 10, 20}.
По формуле
P(E) = n(E)/n(S) = 9/20.
Вопрос 6. Из колоды в 52 карты вытягивается одна карта, хорошо перетасованная. Вычислите вероятность того, что карта
(i) будет тузом,
(ii) не будет тузом.
Решение:
Перетасовка обеспечивает равновероятные результаты.
(i) В колоде 4 туза.
Пусть E будет событием, когда вынутая карта окажется тузом.
Количество благоприятных исходов события E = 4
Количество возможных исходов = 52
Следовательно, P(E) = 4/52 = 1/13
(ii) Пусть F будет событием «карта не туз»
число благоприятных исходов к F = 52 – 4 = 48
Число возможных исходов = 52
Следовательно, P(F) = 48/52 = 12/13
Вопрос 7. При одновременном броске пары кости. Найдите вероятность получить в сумме больше 7.
Решение:
Общее количество комбинаций для пары игральных костей равно = n(S) = (6 x 6) = 36
Будем считать E событием получения суммы более 7
= {(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4),
(5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Следовательно, P(E) = n( E)/n(S)
= 15/36 = 5/12.
Вопрос 8.
В компании из 364 рабочих 91 состоит в браке. Найти вероятность выбора работника, не состоящего в браке.
Решение:
Дано,
Общее количество рабочих (т.е. пространство выборки) = n(S) = 364
Общее количество женатых рабочих = 91
Теперь общее количество незамужних рабочих = n(4E) = 3 – 91 = 273
Метод 1: Итак, вероятность неженатого рабочего P(NM) = n(E)/n(S) = 273/364 = 0,75
Метод 2: P(M) + P(NM) = 1
Здесь P(M) = 91/364 = 0,25
Итак, 0,25 + P(NM) = 1
P(NM) = 1 – 0,25 = 0,75
Вопрос 9. Из мешка с желтыми и коричневыми шарами вероятность вытащить красный шар равна х/2. Найдите «х», если вероятность вытащить коричневый шар равна 2/3.
Решение:
Дано, в мешочке только желтые и коричневые шарики.
P(выбор желтого шара) + P(выбор коричневого шара) = 1
x/2 + 2/3 = 1
3x + 4 = 6
3x = 2
Или, x = 2/ 3
Вопрос 10.
Две монеты подбрасываются одновременно 360 раз. Количество раз, когда появлялось «2 хвоста», было три раза, когда появлялось «Без хвоста», а количество раз, когда появлялось «1 хвост», было вдвое больше, чем количество раз, когда появлялось «Без хвоста». Найдите вероятность выпадения «двух решек».
Решение:
Общее количество исходов = 360
Предположим, что количество раз, когда выпадало «Нет решки», равно z
Тогда количество раз, когда выпадало «Две решки» = 3z
Количество раз Появилась «1 решка» = 2z
Теперь z + 2z + 3z = 360
6z = 360
z = 60
Следовательно, вероятность выпадения «двух решек» = (3 x 60)/360 = 1 /2
Важные вопросы для CBSE Класс 9 Математика Вероятность
Важные вопросы для CBSE Математика класса 9 Глава 8 Вероятность
Темы и подтемы в Решениях NCERT для класса 9 Математика Глава 15 Вероятность:
ВАЖНЫЕ ВОПРОСЫ
- Вероятность
- Введение
- Вероятность — экспериментальный подход
- Резюме
ОЧЕНЬ КРАТКИЕ ОТВЕТЫ ВОПРОСЫ
1.В коробке 50 болтов и 150 гаек. При проверке коробки обнаружилось, что половина болтов и половина гаек заржавели. Если наугад выбран один предмет, найти вероятность того, что он ржавый. [CBSE-15-NS72LP7]
Ответ.2. Кости бросают определенное количество раз, и результаты записываются следующим образом:
Найдите вероятность того, что выпадет нечетное число. [CBSE-15-NS72LP7]
Ответ. Общее количество исходов = 250
Общее количество исходов получения нечетных чисел = 35 + 50 + 53 = 138
.-. P(получение нечетного числа) = 138/250=69/125Дополнительные ресурсы для CBSE Class 9
- Решения NCERT
- Решения NCERT, класс 9, математика
- Решения NCERT, класс 9, наука
- Решения NCERT, класс 9, социальные науки
- Решения NCERT, класс 9, английский язык
- Решения NCERT, класс 9, хинди
- Решения NCERT, класс 9, санскрит
- Решения NCERT, класс 9 IT
- Решения RD Sharma класса 9
3.
Если P (событие E) = 0,47, то найти P(не E).
Ответ. P(не E) = 1 – P(E)
=> 1 – 0,47 = 0,534. Вероятность угадать правильный ответ на заданный вопрос равна x/ 2.Если вероятность не угадать правильный ответ равно 2/3, найдите х. [CBSE-14-ERFKZ8H], [CBSE-14-17DIG1U]
Ответ.5. Кость подбрасывают шесть раз, и число на нем записывается следующим образом:
Вычислите вероятность выпадения простого числа. [Пример задачи NCERT]
Ответ. Здесь в 6 испытаниях каждое число встречается один раз, а все простые числа, т. е. 2, 3, 5 встречаются один раз каждое
Следовательно, количество простых чисел = 3
Вероятность получения простого числа = 3/6 = 1/26. При обследовании 364 детей в возрасте 19-36 месяцев было установлено, что 91 любит есть картофельные чипсы. Если ребенок выбран случайным образом, вычислите вероятность того, что он/она не любит есть картофельные чипсы.
[Пример задачи NCERT]
Ответ. Всего детей = 364
Количество детей, которым нравятся картофельные чипсы = 91
.-. Количество детей, не любящих чипсы = 364 – 91 = 273 273
Требуемая вероятность = 273 / 364 = 0,757. При медицинском осмотре учащихся класса регистрируются следующие группы крови:
Учащийся выбирается случайным образом из класса. Найдите вероятность того, что у него/нее группа крови B. [Пример задачи NCERT]
Ответ. Общее количество студентов = 10 + 13 + 12 + 5 = 40
Количество студентов с группой крови «В» = 12
Требуемая вероятность = 12 / 40 = 3 / 108. Две монеты подбрасываются 1000 раз и результаты записываются следующим образом:
Основываясь на этой информации, найдите вероятность выпадения не более одного орла.
Ответ. Требуемая вероятность = P(0 голов) + P(1 голова)
= 250/1000 + 550/1000 = 800/1000 =4/5 =0,89.
В мешке лежат x белых, y красных и z синих шаров. Наугад извлекается шар, какова вероятность того, что выпадет синий шар.
Ответ. Количество синих шаров = z
Всего шаров = x + y + z
, следовательно, P(aсиний шар)= z /(x+y+z )10. При бросании игральной кости найдите вероятность того, что он не выпадет 4 или 5.
Ответ. Требуемая вероятность = 1 – P(4) – P(5)
\(\)=1- 1/6 – 1/6 = 4/6 = 2/311. При выборочном исследовании 642 человек было установлено, что 514 человек имеют аттестат зрелости. Если человек выбран случайным образом, найдите вероятность того, что у него есть аттестат о среднем образовании.
Ответ. Общее количество человек = 642
Количество лиц со средним школьным аттестатом = 514
Следовательно, требуемая вероятность = 514 / 642 = 0,8012. В классе x девочек и y мальчиков, ученик выбирается случайным образом , то найти вероятность выбора мальчика.

Ответ. Количество мальчиков = y
Всего учеников = (x + y)
Таким образом, P(aboy)= y/(x+y)13. Три монеты подбрасываются одновременно 200 раз со следующей частотой различных исходов;
Если одновременно снова подбросить три монеты, вычислите вероятность того, что выпадет 2 орла. [CBSE, март 2012 г.]
Ответ. Общее количество шансов = 23 + 72 + 77 + 28 = 200
Количество шансов выпадения 2 решек = 72
, следовательно, P( приход 2 головы) = 514 / 642 = 9/ 25КРАТКИЕ ОТВЕТЫ НА ВОПРОСЫ ТИПА-I
14. 750 семей с 3 детьми были выбраны случайным образом, и были записаны следующие данные
Если член семьи выбран случайным образом, вычислите вероятность того, что он имеет:
(i) нет мальчика
(ii) нет девочки [CBSE-15-6DWMW5A]
Ответ.(i) P (отсутствие мальчиков) = 100 / 750 = 2/15
(ii) P (нет девочек) = 120/750 =4/25Найдите вероятность победы в гонке. [CBSE-15-6DWMW5A]
Ответ. Пусть вероятность победы в гонке равна p Вероятность проигрыша в гонке = 1 – p Согласно постановке вопроса имеем
p = 2 (1 – p) – 1/6
=>6p=12-12p-1
=>18p=11
=>p=11 / 18
Следовательно, вероятность победы в гонке равна 11 / 18 .16. Две монеты подбрасываются одновременно 360 раз. Количество раз, когда появлялось «2 хвоста», было три раза, когда появлялось «Без хвоста», а количество раз, когда появлялось «1 хвост», было вдвое больше, чем количество раз, когда появлялось «Без хвоста». Найдите вероятность выпадения «двух решек». [CBSE-14-ERFKZ8H], [CBSE-14-17DIG1U]
Ответ. Общее количество исходов = 360
Пусть количество раз, когда выпало «Нет хвоста», будет x
Тогда количество раз, когда выпало «2 решки» = 3x
Количество раз, когда выпало «1 решка» = 2x
Теперь х + 2х + 3х = 360
=> 6х = 360
=> х = 60
Р (двух решек) = (3 х 60)/360 = 1/217.
Три монеты подбрасываются одновременно 200 раз со следующей частотой различных исходов:
Если три монеты подбрасываются снова одновременно, вычислите вероятность того, что выпадет менее трех решек. [Образец задачи NCERT].
Ответ. Дано, что монета подбрасывается 200 раз Общее количество попыток = 200
Количество событий для выпадения менее трех решек = 68 + 82 + 30 = 180
Вероятность выпадения менее трех решек = 180 / 200 = 9 / 1018. Игральная кость была брошена 100 раз и число раз , 6 подошли было отмечено. Если экспериментальная вероятность, рассчитанная на основе этой информации, равна 2/5, то сколько раз выпадет 6? Обосновать ответ. [CBSE, март 2013 г.]
Ответ.КРАТКИЕ ОТВЕТЫ НА ВОПРОСЫ II ТИПА
19. В таблице представлены оценки, полученные учащимся за модульные тесты из 50 :
Найдите вероятность того, что учащийся наберет 70% или более баллов в следующем модульном тесте.Также вероятность того, что студент получит меньше 70%. [CBSE-14-GDQNI3W]
Ответ.20. Книги уложены стопками по 20 книг в каждой. Тридцать пять стопок были проверены на наличие дефектных книг, и результаты приведены в следующей таблице:
Одна стопка была выбрана случайным образом. Какова вероятность того, что он имеет:
(i) нет дефектных книг?
(ii) более 0, но менее 4 дефектных книг?
(iii) более 4 дефектных книг? [CBSE-15-NS72LP7]
Ответ.21. В данной таблице указан месяц рождения 40 учащихся IX класса определенного отделения школы.
Если наугад выбран один учащийся, найдите вероятность того, что этот учащийся родится:
(a) во второй половине года
(b) в месяце из 31 дня
(c) в месяце из 30 дней [CBSE-14-17DIG1U]
Ответ.
22. Два игральных кубика подбрасываются одновременно 500 раз. Каждый раз сумма двух чисел, выпадающих на них, отмечается и записывается в следующую таблицу:
Из приведенных данных какова вероятность получения суммы:
(i) больше 10 (ii ) между 8 и 12. [Пример задачи NCERT]
Ответ.
ПОДРОБНЫЕ ВОПРОСЫ
23. Ежедневная стоимость молока (в рупиях), поставляемого в 25 домов населенного пункта, указана ниже:
вероятность того, что ;
(a) счет дома за молоко составляет от 60 до 80 рупий.
(b) дом платит не более 69 рупий за счет за молоко.
(c) счет за молоко дома меньше 50 рупий. [CBSE-14-ERFKZ8H]
Ответ.24. Туристическая компания имеет 100 водителей для вождения автобусов по различным туристическим направлениям.
Ниже приведена таблица времени отдыха водителей после преодоления определенного расстояния (в км).
Какова вероятность того, что случайно выбранный водитель
(a) остановится, проехав 80 км?
(b) останавливается после прохождения 115 км ?
(c) останавливается после преодоления 155 км ?
(d) останавливается после преодоления 200 км ? [CBSE-15-6DWMW5A]
Ответ.25. Проведен опрос 2000 человек разных возрастных групп для выяснения их предпочтений в просмотре фильмов разного типа:
Тип I —> Семейный
Тип II —> Комедия и Семейный
Тип III —> Романтика, Комедия и Семейный
Тип IV —> Боевик, Романтика, Комедия и Семейный
Найдите вероятность того, что случайно выбранный человек:
(а) в возрасте от 18 до 29 лет и любит фильмы второго типа
(б) старше 50 лет и любит все жанры фильмов
(c) в возрасте 30-50 лет и любит фильмы типа I.[CBSE-14-GDQNI3W]
Ответ.
Вопросы, основанные на ценности
1. Страховая компания отобрала 2000 водителей случайным образом (т. е. без предпочтения одного водителя другому) в определенном городе, чтобы найти связь между возрастом и авариями. Полученные данные приведены в следующей таблице:
Найти вероятность следующих событий для водителя, выбранного наугад из города:
(i) в возрасте 18-29 лет, попавшего ровно в 3 аварии за один год.
(ii) в возрасте 30-50 лет и с одним или несколькими несчастными случаями в год.
(iii) ни одного несчастного случая в течение одного года.
(iv) Какое значение вы хотите запомнить из этих данных?
Ответ.
(iv) Наибольшее количество людей в Индии погибло или получило ранения в результате несчастных случаев по сравнению с любой другой страной.Итак, мы должны соблюдать правила дорожного движения, поскольку жизнь очень ценна.
2. Есть группа из 130 человек патриотически настроенных, 50 человек верящих в насилие. Какова вероятность того, что люди верят в ненасилие 7 Какие ценности вы разовьете в своем характере?
Ответ.
Для мирной обстановки необходимы обе ценности: патриотизм и ненасилие. Только патриотизм с насилием очень опасен.3. 100 растений были посеяны в шести различных колониях A, B, C, D, E и E. Через 31 день число выживших растений было следующим:
Какова вероятность того, что:
(i) в колонии выжило более 80 растений?
(ii) в колонии выжило менее 82 растений ?
(iii) какие значения изображены из приведенных выше данных?
Ответ.4. Для передвижения 1500 человек используются следующие виды транспорта:
Найдите вероятность количества людей:
(i) только подержанный автомобиль и скутер?
(ii) используется только цикл ?
(iii) использовали хотя бы один вид транспорта?
(iv) какое значение вы бы узнали из приведенных выше данных?
Ответ.

 В лотерейном ящике лежат 10 призов и 25 бланков. Из лотерейной коробки случайным образом вытягивается талон. Какова вероятность получить приз?
В лотерейном ящике лежат 10 призов и 25 бланков. Из лотерейной коробки случайным образом вытягивается талон. Какова вероятность получить приз? P(B) = 8/n + 8
P(B) = 8/n + 8
 В компании из 364 рабочих 91 состоит в браке. Найти вероятность выбора работника, не состоящего в браке.
В компании из 364 рабочих 91 состоит в браке. Найти вероятность выбора работника, не состоящего в браке. Две монеты подбрасываются одновременно 360 раз. Количество раз, когда появлялось «2 хвоста», было три раза, когда появлялось «Без хвоста», а количество раз, когда появлялось «1 хвост», было вдвое больше, чем количество раз, когда появлялось «Без хвоста». Найдите вероятность выпадения «двух решек».
Две монеты подбрасываются одновременно 360 раз. Количество раз, когда появлялось «2 хвоста», было три раза, когда появлялось «Без хвоста», а количество раз, когда появлялось «1 хвост», было вдвое больше, чем количество раз, когда появлялось «Без хвоста». Найдите вероятность выпадения «двух решек». В коробке 50 болтов и 150 гаек. При проверке коробки обнаружилось, что половина болтов и половина гаек заржавели. Если наугад выбран один предмет, найти вероятность того, что он ржавый. [CBSE-15-NS72LP7]
В коробке 50 болтов и 150 гаек. При проверке коробки обнаружилось, что половина болтов и половина гаек заржавели. Если наугад выбран один предмет, найти вероятность того, что он ржавый. [CBSE-15-NS72LP7]  Если P (событие E) = 0,47, то найти P(не E).
Если P (событие E) = 0,47, то найти P(не E).  [Пример задачи NCERT]
[Пример задачи NCERT]  В мешке лежат x белых, y красных и z синих шаров. Наугад извлекается шар, какова вероятность того, что выпадет синий шар.
В мешке лежат x белых, y красных и z синих шаров. Наугад извлекается шар, какова вероятность того, что выпадет синий шар. 
 (i) P (отсутствие мальчиков) = 100 / 750 = 2/15
(i) P (отсутствие мальчиков) = 100 / 750 = 2/15  Три монеты подбрасываются одновременно 200 раз со следующей частотой различных исходов:
Три монеты подбрасываются одновременно 200 раз со следующей частотой различных исходов:  Также вероятность того, что студент получит меньше 70%. [CBSE-14-GDQNI3W]
Также вероятность того, что студент получит меньше 70%. [CBSE-14-GDQNI3W] 