Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры
Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.
Перевод обыкновенных дробей в десятичные
Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.
Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.
Приступим!
Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби
Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.
Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.
Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?
Правило перевода обыкновенных правильных дробей в десятичные- Записываем 0 и ставим после него запятую.

- Записываем число из числителя, которое получилось после дописывания нулей.
Теперь перейдем к примерам.
Пример 1. Перевод обыкновенных дробей в десятичныеПереведем обыкновенную дробь 39100 в десятичную.
Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно — количество цифр в числителе совпадает с количеством нулей в знаменателе.
Следуя правилу, записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,39.
Разберем решение еще одного примера по этой теме.
Пример 2. Перевод обыкновенных дробей в десятичныеЗапишем дробь 10510000000 в виде десятичной дроби.
Количество нулей в знаменателе равно 7, а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля:
000010510000000
Теперь записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,0000105.
Рассмотренные во всех примерах дроби — обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.
Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.
- Записываем число, которое находится в числителе.
- Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.
Ниже приведем пример на использование этого правила.
Пример 3. Перевод обыкновенных дробей в десятичныеПереведем дробь 56888038009100000 из обыкновенной неправильной в десятичную.
Сначала запишем число из числителя:
56888038009
Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе — пять). Получим:
568880,38009
Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом.
- Выполняем подготовку дробной части числа, если это необходимо.
- Записываем целую часть исходного числа и ставим после него запятую.
- Записываем число из числителя дробной части вместе с дописанными нулями.
Обратимся к примеру.
Пример 4. Перевод смешанных чисел в десятичные дробиПереведем смешанное число 231710000 в десятичную дробь.
В дробной части имеем выражение 1710000. Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: 001710000.
Теперь записываем целую часть числа и ставим после него запятую: 23,..
После запятой записываем число из числителя вместе с нулями. Получаем результат:
231710000=23,0017
Перевод обыкновенных дробей в конечные и бесконечные периодические дроби
Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д.
Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.
Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.
Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно.
Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности.
Числитель при делении представляется в виде десятичной дроби — справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров.
Пример 5. Перевод обыкновенных дробей в десятичныеПереведем обыкновенную дробь 6214 в десятичный вид.
Представим число 621 из числителя в виде десятичной дроби, добавив после запятой несколько нулей. 621=621,00
621=621,00
Теперь разделим столбиком 621,00 на 4. Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим.
Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом.
В итоге мы получаем десятичную дробь 155,25, которая и является результатом обращения обыкновенной дроби 6214
6214=155,25
Рассмотрим решение еще одного примера, чтобы закрепить материал.
Пример 6. Перевод обыкновенных дробей в десятичныеОбратим обыкновенную дробь 21800.
Для этого в столбик разделим дробь 21,000 на 800. Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю.
В результате мы получили: 21800=0,02625.
Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.
В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.
Обратим обыкновенную дробь 1944 в десятичную. Для этого выполним деление столбиком.
Мы видим, что при делении повторяются остатки 8 и 36. При этом в частном повторяются цифры 1 и 8. Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки.
Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь.
1944=0,43(18).
Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие — в бесконечные периодические?
Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000.
Подытожим сказанное:
- Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
- Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.
Приведем пример.
Пример 8. Перевод обыкновенных дробей в десятичныеКакая из данных дробей 4720, 712, 2156, 3117 переводится в конечную десятичную дробь, а какая — только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.
Дробь 4720, как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100.
4720=235100. Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.
Разложение знаменателя дроби 712 на множители дает 12=2·2·3. Так как простой множитель 3 отличен от 2 и от 5, данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.
Дробь 2156, во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 38, разложение знаменателя которой на множители дает 8=2·2·2. Следовательно, это конечная десятичная дробь.
В случае с дробью 3117 разложение знаменателя на множители представляет собой само простое число 17. Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.
Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь
Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?
Отвечаем: нет!
Важно!При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.
Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:
- Мы получаем в остатке 0, и на этом деление заканчивается.
- Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.
Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?
Правило перевода десятичных дробей в обыкновенные дроби- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.

- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение данного правила на примерах.
Пример 8. Перевод десятичных дробей в обыкновенныеПредставим число 3,025 в виде обыкновенной дроби.
- В числитель записываем саму десятичную дробь, отбросив запятую: 3025.
- В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 30251000.
- Полученную дробь 30251000 можно сократить на 25, в результате чего мы получим: 30251000=12140.
Переведем дробь 0,0017 из десятичных в обыкновенные.
- В числителе запишем дробь 0,0017, отбросив запятую и нули слева. Получится 17.
- В знаменатель записываем единицу, а после нее пишем четыре нуля: 1710000. Данная дробь несократима.

Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?
Сформулируем еще одно правило.
Правило перевода десятичных дробей в смешанные числа.- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Обратимся к примеру
Пример 10. Перевод десятичной дроби в смешанное числоПредставим дробь 155,06005 в виде смешанного числа.
- Записываем число 155, как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Поучаем смешанное число: 1556005100000
Дробную часть можно сократить на 5. Сокращаем, и получаем финальный результат:
155,06005=155120120000
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.
Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.
Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример 11. Перевод периодической десятичной дроби в обыкновеннуюОбратим периодическую дробь 3,75(0).
Отбросив нули справа, получим конечную десятичную дробь 3,75.
Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:
3,75(0)=3,75=375100=154.
Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:
0,(74)=0,74+0,0074+0,000074+0,00000074+..
Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0<q<1, то сумма равна b1-q.
Рассмотрим несколько примеров с применением данной формулы.
Пример 12. Перевод периодической десятичной дроби в обыкновеннуюПусть у нас есть периодическая дробь 0,(8) и нам нужно перевести ее в обыкновенную.
Запишем:
0,(8)=0,8+0,08+0,008+..
Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0,8 и знаменателем 0,1.
Применим формулу:
0,(8)=0,8+0,08+0,008+..=0,81-0,1=0,80,9=89
Это и есть искомая обыкновенная дробь.
Для закрепления материала рассмотрим еще один пример.
Пример 13. Перевод периодической десятичной дроби в обыкновеннуюОбратим дробь 0,43(18).
Сначала записываем дробь в виде бесконечной суммы:
0,43(18)=0,43+(0,0018+0,000018+0,00000018..)
Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:
0,0018+0,000018+0,00000018..=0,00181-0,01=0,00180,99=189900.
Полученное прибавляем к конечной дроби 0,43=43100 и получаем результат:
0,43(18)=43100+189900
После сложения данных дробей и сокращения получим окончательный ответ:
0,43(18)=1944
В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Перевести десятичную дробь в обыкновенную. Калькулятор онлайн.
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор может перевести десятичную дробь в обыкновенную и дать подробное решение.
 Так же калькулятор может преобразовать математическое выражение в обыкновенную дробь.
Так же калькулятор может преобразовать математическое выражение в обыкновенную дробь.Введите десятичную дробь или выражение, например 0.5, (1/3)+7 и т.д.
Как представить десятичную дробь в виде обыкновенной
Для того, чтобы записать десятичную дробь в виде обыкновенной, необходимо обратить внимайте на числа, стоящие до и после запятой.
Например, число 4,075 читается как «четыре целых семьдесят пять тысячных». Число, стоящее до запятой необходимо записать как целую часть дроби, в данном примере 4 является целой частью. В качестве числителя необходимо записать число 75, которое идет после запятой, а для записи знаменателя необходимо посчитать количество знаков в десятичной дроби после запятой. В нашем примере у десятичной дроби после запятой стоит три знака, значит знаменатель дроби можно записать как 1 и три ноля 1000. Получаем:
4.075 =
4
75
1000
=
Можно сделать вывод, что для записи знаменателя необходимо записать после единицы столько нолей, сколько знаков после запятой у десятичной дроби.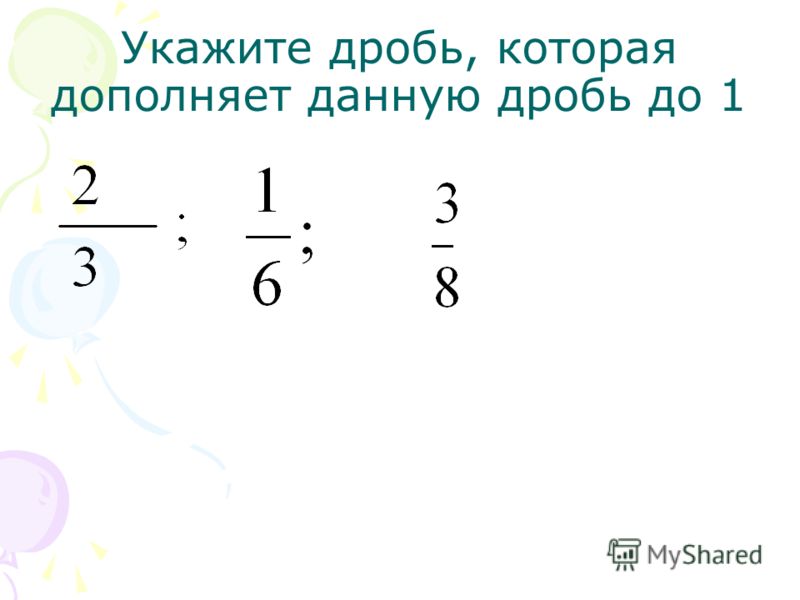 Более подробно о десятичных дробях можно прочитать в данной статье.
Более подробно о десятичных дробях можно прочитать в данной статье.
| Вам могут также быть полезны следующие сервисы |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
простое правило, примеры преобразования, онлайн-конвертер
Математика
12.11.21
12 мин.
При изучении математики важно не только знать, как перевести десятичную дробь в обыкновенную, но и уметь применять полученные знания на практике. Обучают этой науке в четвертом классе средней школы. Преобразование выражений позволяет упрощать различные задачи, делая решение простым и понятным. Сама операция несложная, но требует понимания смысла использования дробных чисел. Лишь в этом случае действие можно будет довести до автоматизма и выполнять устно.
Сама операция несложная, но требует понимания смысла использования дробных чисел. Лишь в этом случае действие можно будет довести до автоматизма и выполнять устно.
Оглавление:
- Виды дробей
- Алгоритм преобразования
- Решение примеров
- Использование онлайн-конвертера
Виды дробей
Дробь — это число, в состав которого входит одна доля или несколько её частей, поделенных на равные части. По сути, это отношение двух значений. Обыкновенное дробное выражение записывают с помощью натуральных чисел, разделённых горизонтальной чертой. Называется она винкулумом. В литературе можно встретить и другой тип записи с наклонной чертой (солидус).
Верхнее число, или стоящее слева от черты, называют числителем или делимым, а нижнее — знаменателем (делителем). Что такое дробь, удобнее всего объяснить на примере. Пусть на столе стоит тарелка, на которой лежит пирог. Он один и целый. Можно взять нож и разделить его на шесть равных частей.
Он один и целый. Можно взять нож и разделить его на шесть равных частей.
По сути, количество пирога не изменится, поэтому, с математической точки зрения, на тарелке будет всё так же находиться целый пирог. Если с неё взять два куска, то целостность нарушится. Записывают это действие с помощью дроби: 2/6. То есть внизу указывают число, обозначающее, на сколько поделили пирог, а сверху — сколько кусков забрали.
Дробь — это число, обозначающее часть целого предмета. При этом дробное отношение всегда будет меньше единицы. Существующие отношения принято разделять на следующие виды:
- Правильные — отношения, в которых числитель меньше знаменателя.
- Неправильные — дроби, где делимое по величине превышает делитель.
- Смешанные — состоящие из суммы натурального и дробного числа.
- Десятичные — в знаменателе которых стоит натуральное число с размерностью кратной десяти.
- Составные — состоящие из нескольких черт дроби.

С дробными отношениями можно выполнять любые математические действия. Их складывают, вычитают, умножают, возводят в степень. Замечательным свойством дробей есть возможность их преобразования из одного вида в другой. Например, можно перевести обычную дробь в десятичную, неправильную — в смешанную. При этом операции возможны как в одну, так и другую сторону.
Существует и так называемое основное свойство отношений. Оно позволяет над числителем и знаменателем проводить одинаковые операции
. Например, делитель и делимое можно возвести в одинаковую степень, поделить или умножить на одно и то же число. Это свойство позволяет упрощать выражения, делая их простыми и удобными для восприятия.
Алгоритм преобразования
Действие по переводу десятичной дроби в простую относится к элементарным операциям. Существует несколько способов перевода. Какой из них выполнять, зависит от личных предпочтений решающего. Например, выражение 3,2 можно записать и как 16/5.
Какой из них выполнять, зависит от личных предпочтений решающего. Например, выражение 3,2 можно записать и как 16/5.
Другими словами, математики договорились, что в случае простых чисел нули опускаются, а вместо них ставится запятая, отделяющая целую часть. Это было сделано для удобства восприятия записи и облегчения счёта.
Правило наиболее часто используемого способа перевода следующее. Если в знаменателе стоит число, кратное десяти, то нужно просто переписать числитель, а затем отсчитать число цифр, совпадающих с разрядностью числа в знаменателе, и поставить после них запятую. Счёт числа отделяемых цифр нужно начинать с правой стороны. При этом если количество нулей превышает число цифр в делителе, то недостающее их количество записать перед числом.
При преобразовании смешанного числа в десятичное действие немного изменяется. Вначале нужно записать целую часть отношения. После него поставить запятую, а уже затем написать число из делимого дробной части с учётом недостающих нулей.
Проводимые операции, кроме получения периодической дроби, можно выполнять и в обратную сторону. Остаток при делении должен всегда быть меньше делителя. Поэтому, если при действии получается ноль, деление прекращается, а если остаток — бесконечная периодическое отношение.
Чаще всего для того, чтобы преобразовать простую дробь в десятичную, необходимо выполнить три шага:
- Сократить выражение, требующее преобразования.
- Разделить удобным способом числитель на знаменатель. В зависимости от величины значений, стоящих в числителе и знаменателе, это можно сделать столбиком или в уме. Если при делении остаток выходит отличным от нуля, то поставить запятую и продолжить искать частное.
- Записать найденный результат с использованием запятой.
Нужно отметить, что алгоритм, объясняющий правило того, как перевести обыкновенную дробь в десятичную, подходит лишь для случаев, когда знаменатель раскладывается на множители пять и два.
В иных случая получится периодическое десятичное число.
Решение примеров
Порой теоретическая информация довольно трудно воспринимается без применения её на практике. Поэтому крайне важно не только посмотреть, как делает преобразование учитель, но и самостоятельно выполнить перевод. Обычно хватает трех-четырех примеров для каждого типа преобразований, чтобы закрепить материал и освоить практическое применение.
Существуют определённые сборники заданий, предназначенные для самостоятельного решения учащимися. Вот некоторые наиболее интересные примеры из них:
- Преобразовать: 1/1000; 34/10; 78954/10; 186/100; 959/10000. Алгоритм действия определяется правилом отсчитывания запятой. В задании три нуля, но в числителе только один знак. Поэтому на недостающих местах следует поставить нули. Отсюда следует что 1/1000 = 0,001. По аналогии нужно решать и следующие примеры.
 В итоге должно получиться: 34/10 = 3,4; 78954/10 = 7895,4; 186/100 = 1,86; 959/10000 = 0,0959.
В итоге должно получиться: 34/10 = 3,4; 78954/10 = 7895,4; 186/100 = 1,86; 959/10000 = 0,0959. - Записать выражения в обыкновенном виде: 0,59; 34,78; 0,00078; 767,009. В соответствии с правилом в числителе записывают исходное число, а в знаменатель ставят единицу: 0,59 = 0,59/1. Для избавления от запятой делимое и делитель умножают на сто, так как по условию после запятой стоит два знака: (0,59 * 100) / (1 * 100) = 59/100. Аналогично решают и оставшиеся примеры: 34,78 = 34,78/1 = 34,78 * 100/ 100 = 3478/100; 0,00078 = 78/100000 = 39/50000; 767,009 = 767 + 0,009= 767 9/1000.
- Перевести выражения в десятичный вид: 5/2; ¼; 34/81; 456/1245; 1245/456. Преобразование таких примеров можно выполнить путём деления числителя на знаменатель для нахождения частного. В первом случае пять нужно разделить на два. Используя деление в столбик, можно опередить, что целым будет число два (2 * 2 = 4). Так как в остатке получается единица, то в частном ставят запятую, а к остатку дописывают ноль.
 То есть, 5/2 = 2,5. Таким же образом переводят и другие примеры: ¼ = 0,25; 34/81 = 0,420; 456/1245 = 0,366; 1245/456 = 2,73.
То есть, 5/2 = 2,5. Таким же образом переводят и другие примеры: ¼ = 0,25; 34/81 = 0,420; 456/1245 = 0,366; 1245/456 = 2,73.
Эти задания затрагивают преобразование как в одну, так и в другую сторону. После первичного перевода не стоит забывать об упрощении полученного результата. Его нужно делать всегда, чтобы в дальнейшем при решении сложных задач последующие действия становились проще.
Использование онлайн-конвертера
Десятичные дроби могут состоять из довольно больших чисел. Поэтому не всегда их можно быстро преобразовать. При этом любая невнимательность может привести к ошибке, что повлечёт неверный как промежуточный, так и итоговый результат. В таких случаях есть резон использовать так называемый конвертер дробей.
Это интернет-сервис, предоставляющий услуги по автоматическому преобразованию дробей из одного вида в другой. Для того чтобы воспользоваться его возможностями, пользователю даже необязательно понимать принцип перевода выражений. От него требуется лишь ввести исходные данные в предлагаемую форму и нажать кнопку «Рассчитать».
Таких математических сервисов в интернете довольно много. Русскоязычные конвертеры не требуют регистрации и указания каких-либо персональных данных. При этом свои услуги они предоставляют бесплатно. Согласно отзывам пользователей, можно выделить следующие онлайн-калькуляторы:
- 0oq;
- onlinemschool;
- naobumium;
- allcalc;
- webmath.
Нужно отметить, что приведенные сайты являются настоящими математическими комбайнами-решателями. Они умеют не только конвертировать дроби, но и выполнять с ними любые действия. Например, складывать, делить, умножать, извлекать корень и возводить в степень. Кроме этого, на их страницах содержится теоретический материал и подробное описание решений.
Чему равно 4 разделить на 3 в виде дроби? – Обзоры Вики
Используя калькулятор, если вы введете 4, разделенные на 3, вы получите 1. 3333. Вы также можете выразить 4/3 как смешанную дробь: 1 1/3.
3333. Вы также можете выразить 4/3 как смешанную дробь: 1 1/3.
Точно так же, как вы делите 4 на 3? 4 разделить на 3 равно 1 с остатком 1 (4/3 = 1р.1). Когда вы разделите 4 на 3, у вас не останется равное количество групп, потому что 3…
Чему равно ¼ разделить на 4? Другими словами – одна четверть, деленная на четыре = одна шестнадцатая.
Как разделить 3 1 4? Другими словами – три разделить на одну четверть = двенадцать.
Во-вторых Сколько 4 разделить пополам? Другими словами – четыре разделить на одну половину = 8.
Какая половина делится на 4 в виде дроби?
(1/2): 4 = 18 = 0.125.
тогда что такое 4 с половиной как неправильная дробь? Правильный ответ на это 9/2. Чтобы узнать ответ, нужно сначала умножить целое число на знаменатель. (4×2) = 8.
Сколько будет 3 разделить пополам? Другими словами, три разделить на половину = шесть.
Чем деление на 3 равносильно умножению на 1 3?
В этом примере мы поменяем местами числитель и знаменатель дроби, на которую мы делим: 1/3. Таким образом, 1/3 становится 3/1. Это называется нахождением обратной или мультипликативной обратной дроби. … Это потому, что умножение обратно делению.
Таким образом, 1/3 становится 3/1. Это называется нахождением обратной или мультипликативной обратной дроби. … Это потому, что умножение обратно делению.
Какое отношение эквивалентно отношению 3 4? Эквивалентные соотношения 3:4
| 3:4 (м 1 = 1) | 6:8 (м 2 = 2) | 12: 16 (m 4 = 4) |
|---|---|---|
| 33:44 (м 11 = 11) | 36:48 (м 12 = 12) | 42:56 (м 14 = 14) |
| 48:64 (м 16 = 16) | 51:68 (м 17 = 17) | 57:76 (м 19 = 19) |
| 63:84 (м 21 = 21) | 66:88 (м 22 = 22) | 72:96 (м 24 = 24) |
| 78:104 (м 26 = 26) | 81:108 (м 27 = 27) | 87:116 (м 29 = 29) |
Что такое половина от 3/4 в виде дроби?
Половина 3/4 — это 3/8.
Сколько будет 3 разделить на половину? Если мы делим 3 на 1/2, то ставим знак умножения и делаем обратное число 1/2, которое равно 2/1 или 2.. так что 3 × 2= 6.. Сколько половинок в трех??
Как решить дроби?
Что такое 3 и 3/4 как неправильная дробь?
33/4 как неправильная дробь
Следовательно, несобственная дробь равна 15/4.
Как решать неправильные дроби? Чтобы преобразовать смешанную дробь в неправильную, выполните следующие действия:
- Умножьте целую числовую часть на знаменатель дроби.
- Добавьте это в числитель.
- Затем напишите результат над знаменателем.
Сколько 2 разделить на XNUMX/XNUMX?
Ответ: 3/4 деленное на 2 в дроби равно 3/8.
Какова обратная величина 3/4 в виде дроби?
Обратная величина 3/4 ≈ 1.333333333333
Совет: как вы, возможно, поняли из нашего руководства выше, вы можете быстро получить обратную величину любой дроби, например 3/4, поменяв местами числитель и знаменатель.
Какое правило деления дробей? Правило деления дробей таково. вы берете первую дробь и умножаете ее на обратную величину второй дроби.
Как выглядит разделить на?
Знак деления напоминает тире или двойное тире с точкой вверху и точкой внизу (÷). Это эквивалентно словам «разделить на». Этот символ встречается в основном в арифметических текстах на уровне начальной школы.
Какие дроби равны 3 4? Таблица преобразования десятичных и дробных чисел
| Доля | Эквивалентные дроби | |
|---|---|---|
| 2/3 | 4/6 | 8/12 |
| 1/4 | 2/8 | 4/16 |
| 3/4 | 6 /8 | 12/16 |
| 1/5 | 2/10 | 4/20 |
Какая формула соотношения?
Формула отношения
Общая форма представления отношения между двумя величинами, скажем, «а» и «b», представляет собой отношение : b, которое читается как «а к b». Дробная форма, которая представляет это соотношение, — a/b. Чтобы еще больше упростить отношение, мы следуем той же процедуре, которую используем для упрощения дроби. а:б = а/б.
Дробная форма, которая представляет это соотношение, — a/b. Чтобы еще больше упростить отношение, мы следуем той же процедуре, которую используем для упрощения дроби. а:б = а/б.
Что получится, если перевести 3/4 в проценты? Ответ: 3/4 выражается как 75% в процентном отношении.
Какая половина 3/4 стакана в чашках?
Половина 3/4 стакана будет 1 / 4 чашки плюс 2 столовые ложки или 6 столовых ложек.
Что такое половина три четверти чашки?
Половина 3/4 стакана = 6 ст.л.. 1/2 стакана = 8 ст.
Как умножать дроби? Есть 3 простых шага для умножения дробей
- Умножьте верхние числа (числители).
- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | minus sign | subtraction | 1 1/2 — 2/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | asterisk | multiplication | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2/3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Смешанные дроби — определение, преобразование, примеры.Смешанная дробь – это дробь, в которой есть целая и дробная части. Например, \(3\dfrac{1}{7}\) — это смешанная дробь. Его также называют смешанным числом.
Что такое смешанные фракции?Смешанная дробь определяется как дробь, образованная путем объединения целого числа и дроби. Например, если 8 — целое число, а \(\dfrac{1}{2}\) — дробь, то 8\(\dfrac{1}{2}\) — смешанная дробь. Преобразование неправильной дроби в смешанную дробьНеправильная дробь — это дробь, числитель которой больше или равен знаменателю и которую нельзя упростить дальше. Например, 13/5 — неправильная дробь. Давайте узнаем, как преобразовать эту неправильную дробь в смешанную дробь.
Преобразование смешанной дроби в неправильную дробь Смешанная дробь также может быть преобразована в неправильную дробь.
Операции со смешанными дробямиПодобно тому, как мы складываем, вычитаем, умножаем и делим числа, точно так же мы можем применять арифметические операции и к смешанным дробям. Сложение смешанных дробейЧтобы сложить смешанные дроби, выполните следующие действия:
Пример: добавим \(1\dfrac{1}{2}\) и \(2\dfrac{1}{2}\). Вычитание смешанных дробейЧтобы вычесть смешанные дроби, выполните следующие шаги:
Пример. Вычтем \(2\frac{1}{3}\) из \(3\frac{2}{3}\). Умножение смешанных дробейЧтобы умножить смешанные дроби, выполните следующие шаги:
Пример. Перемножим \(2\frac{2}{5}\) и \(3\frac{1}{5}\). Разделение смешанных фракцийЧтобы разделить смешанные дроби, выполните следующие действия:
Пример. Разделим \(1\frac{1}{5}\) на \(3\frac{4}{5}\). Смешанные эквивалентные фракции Две дроби называются эквивалентными, если они обе равны при сведении к простейшим формам. Например, 1/3 и 2/6 — эквивалентные дроби. Точно так же дроби 7/2 и 14/4 при преобразовании в смешанные дроби эквивалентны. Когда 7/2 преобразуется в смешанную дробь, мы получаем \(3\frac{1}{2}\), а когда мы конвертируем 14/4, мы получаем \(3\frac{2}{4}\). Здесь \(3\frac{1}{2}\) и \(3\frac{2}{4}\) называются смешанными эквивалентными дробями, поскольку в дроби \(3\frac{2}{4}\) , дробную часть 2/4 можно упростить до 1/2. Похожие темы Проверьте эти интересные статьи, связанные с концепцией смешанных дробей.
Часто задаваемые вопросы о смешанных фракцияхЧто такое смешанная фракция?Целое число вместе с дробной частью составляет смешанную дробь. Их также называют «смешанными числами». Например, если 2 — целое число, а 1/5 — дробь, то 2\(\dfrac{1}{5}\) — смешанная дробь. Что такое неправильная дробь?Неправильная дробь — это дробь, в которой числитель больше или равен знаменателю. Например 13/5. Как преобразовать неправильную дробь в смешанную дробь? Чтобы преобразовать неправильную дробь в смешанную, мы делим числитель на знаменатель и выражаем его в виде ‘Частное \(\dfrac{Остаток}{Знаменатель}\). Как преобразовать смешанную дробь в неправильную дробь?Чтобы преобразовать смешанную дробь в неправильную, мы умножаем знаменатель на целое число, затем прибавляем произведение к числителю и записываем сумму как числитель со знаменателем. Например, преобразуя \(3\frac{2}{3}\) в неправильную дробь, мы получаем 11/3. Как складывать смешанные дроби?Чтобы сложить смешанные дроби с одинаковыми знаменателями, мы сначала преобразуем их в неправильные дроби, а затем запишем сумму числителей над общим знаменателем. Если знаменатели не равны, то находим НОК знаменателей и делаем их общими. Затем складываем числители так, чтобы знаменатель остался тем же. Например, \(2\frac{1}{2}\) и \(3\frac{1}{2}\). Во-первых, преобразуем дроби в неправильные дроби, которые у нас получились, 5/2 и 7/2. Сложив 5/2 и 7/2, мы получим 12/2. Тогда при дальнейшем упрощении 12/2 получаем 6. Следовательно, \(2\frac{1}{2}\) + \(3\frac{1}{2}\) = 6, Как вычитать смешанные дроби? Чтобы вычесть смешанные дроби с одинаковыми знаменателями, мы сначала преобразуем их в неправильные дроби, а затем вычтем числители. Правильные и неправильные дроби и смешанные числа (видео)TranscriptFAQsPractice Привет! Добро пожаловать в этот обзор дробей и смешанных чисел! Прежде чем углубиться, давайте рассмотрим основные части дроби . Помните, дробь просто представляет собой часть целого. У него есть числитель и знаменатель, которые говорят нам, что такое «часть» и что такое «целое».
Очень важно помнить, что знаменатель числа 4 не представляют значение 4. Знаменатель 4 представляет значение 1, которое делится на 4 равные части или четверти. Этот тип дроби представляет собой значение, меньшее, чем одно целое. \(\frac{3}{4}\) не совсем 1. Если бы у нас было \(\frac{4}{4}\), это было бы эквивалентно единице, но у нас есть только 3 части из 4. Мы постоянно видим и используем дроби, которые меньше единицы, в нашей повседневной жизни, будь то для таких вещей, как рецепты или учет времени. Рецепты часто требуют количества, такого как «1/2 чайной ложки соли», и мы часто отслеживаем время с точки зрения четверти часа, например, «четверть третьего» для 3:15. Рассмотрим следующий сценарий. Вы заказываете пиццу для большого праздника. На этом торжестве будет много голодных гостей, поэтому вы заказываете 3 пиццы. Каждая пицца разрезана на 6 кусочков. Это означает, что каждая пицца состоит из 6 равных частей, и в качестве дроби 6 будет считаться нашим «целым» или нашим знаменателем. Если ваш первый гость съест 2 ломтика, мы представим это как дробь \(\frac{2}{6}\). Две части, всего 6 частей. Но что, если первый гость был очень голоден и съел 7 ломтиков? Опять же, каждая пицца была разрезана на 6 равных кусочков, поэтому 6 остается нашим «целым» или знаменателем. Но на этот раз наша «часть» равна 7: \(\frac{7}{6}\). В этом сценарии наш числитель больше нашего знаменателя. Дроби, числитель которых больше знаменателя, называются неправильными дробями . По сути, неправильные дроби равны значению, которое больше единицы. Например, неправильную дробь \(\frac{7}{6}\) также можно записать как смешанное число \(1\frac{1}{6}\). Смешанные числа и неправильные дроби показывают одну и ту же сумму, но в смешанном числе «части» собираются и объединяются в как можно больше групп из 1 целого. Например, \(\frac{4}{4}\) будет сгруппировано вместе как 1. \(\frac{7}{7}\) также будет сгруппировано как 1. Любое значение, где числитель эквивалентен знаменатель будет выражен просто как 1, В нашем примере с пиццей гость взял 7 ломтиков из группы пицц, которые были нарезаны на шестые части. Преобразование неправильных дробей в смешанные числаДавайте попробуем еще несколько примеров. Запишем следующие неправильные дроби в виде смешанных чисел: \(\frac{4}{3}\) и \(\frac{3}{2}\). \(\frac{4}{3}\) можно представить как \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{ 1}{3}\). Мы знаем, что \(\frac{3}{3}\) равно 1, поэтому давайте сгруппируем 3 из этих «третей» вместе. Теперь у нас осталось \(1\frac{1}{3}\) в качестве нашего смешанного числа. \(\frac{3}{2}\) можно представить как \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}\). Попробуем еще один пример: \(\frac{7}{4}\) \(\frac{7}{4}\) равно \(\frac{1}{4}+\ frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{ 4}\). Теперь мы знаем, что \(\frac{4}{4}\) сгруппировано как одно целое. Таким образом, эти \(\frac{4}{4}\) подтянуты, чтобы равняться 1. И у нас осталось \(\frac{3}{4}\). \(\frac{7}{4}\), записанное как смешанное число, равно \(1\frac{3}{4}\). Этот процесс будет выполняться в обратном порядке, чтобы преобразовать смешанное число в неправильную дробь. Преобразование смешанных чисел в неправильные дроби Например, если мы начали со смешанного числа \(1\frac{3}{4}\) и хотели преобразовать его в эквивалентную неправильную дробь, мы бы посмотрели в целое число , в данном случае это 1. Это целое число действительно представляет наш знаменатель, который находится в дроби. Вот и все! Я надеюсь, что это видео было полезным. Спасибо за просмотр и удачной учебы! Часто задаваемые вопросыQКакие примеры правильной дроби?AПравильная дробь — это дробь, не имеющая целой части и числитель которой меньше знаменателя. Некоторые примеры правильных дробей: \(\frac{1}{4}\),\(\frac{7}{9}\),\(\frac{12}{13}\),\(\frac{ 23}{25}\) и \(\frac{17}{76}\). QЧто такое правильная и неправильная дробь?AПравильная дробь — это дробь, не имеющая целой части и числитель которой меньше знаменателя. Неправильная дробь — это дробь, у которой числитель больше знаменателя, и она представляет собой число больше единицы. Примеры правильных дробей: \(\frac{1}{2}\), \(\frac{1}{6}\), \(\frac{2}{5}\), \(\frac{ 13}{14}\), \(\frac{7}{11}\) Примеры неправильных дробей: \(\frac{16}{11}\), \(\frac{12}{7}\ ), \(\frac{6}{4}\), \(\frac{3}{2}\), \(\frac{8}{3}\) QПример неправильной дроби?A \(\frac{17}{11}\) является примером неправильной дроби, поскольку ее числитель больше знаменателя, что означает, что она представляет собой значение больше единицы. QЧто такое пример смешанного числа?AСмешанное число — это число, состоящее из целой части числа и правильной дробной части. \(4\frac{1}{3}\) является примером смешанного числа, поскольку оно состоит из целой части \((4)\) и правильной дробной части \((\frac{1}{3} )\). QКак превратить неправильную дробь в смешанное число?AЧтобы превратить неправильную дробь в смешанное число, подсчитайте, сколько раз знаменатель может вписаться в числитель, а затем сколько числителя осталось. Затем количество раз, когда знаменатель вписывается в числитель, становится целой частью смешанного числа, а оставшееся число является числителем дробной части исходного знаменателя. пр. Преобразуйте \(\frac{17}{4}\) в смешанное число. QКак смешанное число превратить в неправильную дробь?A Чтобы превратить смешанное число в неправильную дробь, умножьте целую часть числа на знаменатель и прибавьте числитель. пр. Преобразуйте \(3\frac{5}{7}\) в неправильную дробь. \(3\frac{5}{7}=\frac{3\times7+5}{7}=\frac{21+5}{7}=\frac{26}{7}\) Практические вопросыВопрос №1: \(\frac{5}{3},\frac{7}{5},\text{ и }\frac{2}{2}\) \(\frac{3}{5}, \frac{7}{5},\text{ и }\frac{3}{2}\) \(\frac{5}{3},\frac{7}{5},\text{ и }\frac{3}{2}\) \(\frac{5}{5},\frac{7}{7},\text{ и }\frac{3}{3}\) Показать ответ Ответ: правильный ответ: C: \(\frac{5}{3},\frac{7}{5},\text{ и }\frac{3}{2}\). Если у дроби числитель больше знаменателя, общее значение больше одного целого. Такие дроби, как \(\frac{3}{3}, \frac{5}{5}, \text{ и }\frac{7}{7}\), равны одному целому. Скрыть Ответ Вопрос № 2: \(\frac{8}{3}\) \(\frac{5}{3}\) \(\frac{7}{3}\) \(\frac{4 }{3}\) Показать ответ Ответ: Правильный ответ: C: \(\frac{7}{3}\). \(2\frac{1}{3}\) эквивалентно \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{ 1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\). Это представляет семь групп \(\frac{1}{3}\) или неправильную дробь, \(\frac{7}{3}\). Скрыть ответ Вопрос №3: \(1\frac{2}{3}\) \(1\frac{3}{4}\) \(2\frac{1}{3}\) \(2 \frac{2}{3}\) Показать ответ Ответ: Правильный ответ: A: \(1\frac{2}{3}\). \(\frac{5}{3}\) можно рассматривать как \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac {1}{3}+\frac{1}{3}\). Мы можем объединить три группы \(\frac{1}{3}\), чтобы создать \(\frac{3}{3}\) или одно целое. Осталось еще две трети, поэтому наше смешанное число равно \(1\frac{2}{3}\). Скрыть ответ Вопрос № 4: \(\frac{7}{11}\) \(\frac{11}{28}\) \(\frac{11}{15}\) \(\frac{ 11}{12}\) Показать ответ Ответ: Правильный ответ: D: \(\frac{11}{12}\). Восемь подложек, разрезанных на три части каждая, образуют двадцать четыре бутерброда меньшего размера. Сын мистера Джонса съедает два таких куска, или \(\frac{2}{24}\) от общего количества еды. Это означает, что осталось двадцать две части, или \(\frac{22}{24}\). Если числитель и знаменатель делятся на два, упрощенная дробь становится \(\frac{11}{12}\). \(\frac{11}{12}\) от общего количества еды еще осталось. Скрыть ответ Вопрос № 5: \(1\frac{1}{4}\) кварт воды \(1\frac{1}{2}\) кварт воды \(2\frac{1}{2}\ ) кварт воды \(\frac{1}{2}\) кварт воды Показать ответ Ответ: Правильный ответ: B: \(1\frac{1}{2} \) литров воды. Если Кристина выпивает \(\frac{1}{4}\) литра воды на каждую милю, она, по сути, выпивает \(\frac{1}{4}+\frac{1}{4}+\frac {1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}\) кварт воды. Сумма этого списка дробей равна \(1\frac{2}{4}\) или, в простейшей форме, \(1\frac{1}{2}\). Скрыть ответ
Вернуться к видео по основам арифметики 211077972516728606 обыкновенные и десятичные дроби — Студенты | Британика КидсВведениеЕсть много способов получить сдачу за доллар: два полдоллара, четыре четверти, десять десятицентовиков, 20 пятицентовых монет или 100 пенни. Независимо от того, как производится сдача, доллар разбивается — «раскалывается» — на несколько частей. Эти части называются фракциями, от того же латинского слова ( fractus, означает «сломанный»), от которого происходит разлом. Все дроби представляют собой части целого. Типы дробей В повседневной математике есть два типа дробей: обыкновенные и десятичные. Единственная разница между ними заключается в том, как они написаны. Все дроби записываются с использованием тех же символов, которые используются для записи целых чисел, но символы используются по-другому. Простые дроби записываются как 4 / 10 или 7 / 100 : четыре больше десяти и семь больше ста. В обыкновенной дроби число под чертой является знаменателем, а число над чертой — числителем. При чтении обыкновенной дроби первым ставится числитель. Таким образом, 2 / 3 читается как две трети. Любое число, кроме нуля, может быть как знаменателем, так и числителем. В обыкновенной дроби выражается не только количество, но и отношение: отношение одной величины к другой. Например, дробь 1 / 2 выражает отношение один к двум: Отношение один к двум состоит в том, что один равен половине двух. Использование коэффициента довольно распространено. Когда пекарь делает пирог, он может использовать две чашки сахара на каждые три чашки муки: соотношение два к трем, и оно может быть выражено дробью, 2 / 3 . Десятичные дроби называются так потому, что они основаны на десятичной или десятичной системе счисления (см. В обыкновенных дробях любое число может быть знаменателем. Но в десятичных дробях неписаный знаменатель всегда равен 10 или некоторой степени 10, такой как 100, 1000, 10000 и так далее. Это означает, что преобразовать десятичную дробь в обыкновенную просто, поставив правильный знаменатель под числом справа от десятичной точки. Чтобы превратить обыкновенную дробь в десятичную, надо числитель разделить на знаменатель. Таким образом, 3 / 4 можно изменить на десятичное число 0,75. Однако не все обыкновенные дроби можно преобразовать в такие точные десятичные дроби: 2 / 3 , поскольку десятичная дробь представляет собой бесконечный ряд шестерок справа от запятой. Обыкновенные дроби.Обыкновенные дроби бывают четырех видов: правильные, неправильные, смешанные и сложные. У правильной дроби числитель меньше знаменателя, например 3 / 4 . Поэтому значение правильной дроби всегда меньше единицы. В неправильных дробях числитель больше или равен знаменателю, как 4 / 4 или 6 / 5 . Таким образом, все неправильные дроби равны или больше единицы. Смешанная дробь, также называемая смешанным числом, состоит из целого числа и дроби, например 2 1 / 3 . Сложные дроби, используемые в высшей математике, не состоят из натуральных чисел. Например, квадратный корень из двух на квадратный корень из пяти считается сложной дробью: Точно так же использование смешанных дробей как для числителя, так и для знаменателя создаст сложную дробь: Десятичные дроби . Смешанные десятичные числа, известные как смешанные десятичные числа, возникают, если число содержит цифры как слева, так и справа от десятичной точки. Примером может служить число 2,38: оно читается как «две и тридцать восемь сотых». Слово «и» используется только там, где стоит десятичная точка, чтобы отделить целое число от десятичной дроби. Во избежание путаницы при чтении десятичных дробей обычно говорят «точка» вместо «и». Неправильных десятичных дробей быть не может, потому что ни один числитель (десятичное число) никогда не может превышать понимаемый знаменатель (десятые, сотые и т. д.). Все, что больше десятичной дроби, будет смешанным или целым числом. Также было бы невозможно выразить сложную дробь в виде десятичной с какой-либо точностью. Вычисления с десятичными дробями Дроби можно складывать, вычитать, умножать и делить так же, как и целые числа. Эти операции легче выполнять с десятичными дробями, потому что процедуры очень похожи на использование целых чисел. Разница заключается в запоминании правильного размещения десятичной точки. Необходимо также отметить, что при сложении или вычитании каждое из чисел должно иметь одинаковое количество знаков после запятой. Чтобы добавить или вычесть нечетные десятичные дроби, возможно, придется добавить нули к одному из чисел. Например, чтобы прибавить 3,68 к 7,5, необходимо поставить ноль в конце второго десятичного знака, чтобы получилось 7,50. Те же принципы применяются при вычитании десятичных дробей, и операция идентична вычитанию целых чисел, за исключением наличия десятичной точки. Если бы вышеупомянутую задачу нужно было решить как вычитание, она выглядела бы точно так же; только результат будет другим: Обратите внимание, что ноль должен быть помещен в конце 7,5, чтобы было из чего вычесть 8. Умножать десятичные дроби не сложнее, чем целые числа, за исключением того, что нужно помнить о правильном расположении десятичной точки. Основное отличие от сложения и вычитания состоит в том, что для заполнения десятичной дроби не нужно добавлять нули. Это связано с тем, что добавление нулей может привести к путанице в расположении десятичной точки. Существуют определенные правила умножения с десятичными дробями, которые помогают правильно расставить запятую. Правило 1. Если десятичная дробь умножается на целое число, количество знаков после запятой в произведении равно количеству знаков после запятой в умножаемом числе. Задача умножения десятичных шестидесятых (0,6) на четыре (4) выглядит следующим образом: Обратите внимание, что десятичная точка ставится перед 4 в произведении, потому что в произведении был только один десятичный знак. число умножается (0,6). Правило 2. Если целое число умножается на десятичную, количество знаков после запятой в произведении равно количеству знаков после запятой в множителе. (Обратите внимание, что это противоположно правилу 1, но принцип тот же самый.) Чтобы умножить 32 на 2,5, задача ставится следующим образом: Еще раз обратите внимание на размещение десятичной дроби. В множителе (2,5) был только один десятичный знак, поэтому в произведении (80,0) появляется только один. Однако в этом случае десятичную дробь можно исключить, поскольку 80 — это целое число. Правило 3. При умножении десятичной дроби на десятичную дробь количество знаков после запятой в произведении равно количеству знаков после запятой в множителе плюс количество знаков после запятой в умножаемом числе. Если множитель и число, умноженные вместе, имеют в общей сложности четыре знака после запятой, в произведении будет четыре знака после запятой. (Любые нули в конце можно, конечно, исключить.) Задача умножения 0,56 на 0,44 ставится следующим образом: Сумма показывает четыре десятичных знака, потому что множитель и число, умноженные вместе, имеют четыре десятичных знака. При умножении смешанных десятичных дробей применяется тот же принцип. Произведение 33,5 × 6,055 равно 202,8425 с четырьмя знаками после запятой. Процесс деления десятичных дробей такой же, как и целых чисел, но необходимо особенно внимательно относиться к расстановке десятичной точки. Правило 1. Если десятичная дробь делится на целое число, количество знаков после запятой в ответе равно количеству знаков после запятой в делимом десятичном числе. Таким образом, если 0,06 разделить на 2, ответ будет 0,03. Правило 2. При делении целого числа на десятичную дробь необходимо сначала преобразовать десятичную дробь в целое, переместив запятую вправо. Затем десятичная точка в делимом числе должна быть перемещена на такое же количество знаков вправо и при необходимости добавлены нули. Затем десятичная точка в ответе ставится непосредственно над десятичной точкой в делимом числе: Правило 3. При делении десятичного числа на десятичное число снова преобразуется в целое число, при этом десятичная точка в числе делится, а десятичная точка в ответе перемещается соответственно. Вычисления с обыкновенными дробямиЭта процедура несколько сложнее, чем с десятичными дробями. Но его можно упростить, если не забыть сделать так, чтобы все дроби имели одинаковый знаменатель. Это легко сделать, потому что деление или умножение обоих членов дроби на одно и то же число не меняет его значения. Поэтому добавить 2 / 3 и 3 / 4 , необходимо найти общий знаменатель. В данном случае это 12. Задача принимает вид 8 / 12 + 9 / 12 . Результат находится путем сложения числителей (8 + 9), чтобы получить 17 / 12 . Этот ответ можно изменить на смешанную дробь или десятичную. Процесс вычитания аналогичен. Найдите общий знаменатель, затем вычтите один числитель из другого: При работе со смешанными фракциями, такими как 2 1 / 3 +3 3 / 4 , измените их на неподготовленные фракции: | 2, изменение их на неподготовленные фракции:
| Числитель: |
| Знаменатель: |
| Эквивалентные дроби для 4/3: |
Важно: 43 выглядит как дробь, но на самом деле это неправильная дробь. Существует бесконечное количество эквивалентных дробей до 43. Чтобы найти эквивалентную дробь до 43, или любой другой дроби, нужно просто умножить (или разделить, если дробь еще не уменьшена) оба числителя а знаменатель данной дроби на любое ненулевое натуральное число. Например: Умножая исходную дробь на 2, мы получаем: 4 × 2 3 × 2 = 86 Вот полный список эквивалентных дробей до 43. 43, 86, 129, 1612, 2015, 2418, 2821, 3224, 3627, 4030, 4433, 4836, 5239, 5642, 6045, 6448, 6851, 7254, 7657, 8060. Подробнее о том, как найти 4 эквивалентные дроби /3 или любую другую дробь, указанную ниже на этой странице. Упрощенный список для копирования и вставки: 4/3, 8/6, 12/9, 16/12, 20/15, 24/18, 28/21, 32/24, 36/27, 40/30, 44/33, 48/36, 52/39, 56/42, 60/45, 64/48, 68/51, 72/54, 76/57, 80/60… |
Вот ответ на такие вопросы, как: 4/3 или Какие числа эквивалентны 4/3?
Этот калькулятор эквивалентных дробей шаг за шагом покажет вам эквивалентные дроби для любой введенной вами дроби.
См. ниже пошаговое решение, как найти эквивалентные дроби.
Как найти эквивалентные дроби?
Две дроби эквивалентны, если они обе равны при записи в наименьшем выражении. Дробь 86 равна 43 при сокращении до наименьших членов. Чтобы найти равнозначные дроби, нужно просто умножить числитель и знаменатель той сокращенной дроби (43) на одно и то же натуральное число, т. е. умножить на 2, 3, 4, 5, 6…
Важно: 43 выглядит как дробь, но на самом деле это неправильная дробь.
- 86 эквивалентно 43, потому что 4 × 23 × 2 = 86
- 129 эквивалентно 43, потому что 4 × 33 × 3 = 129
× 9 эквивалентно 4 × 1 12482 9 = 1612
- 2015 эквивалентно 43, потому что 4 × 53 × 5 = 2015
- и так далее…
получить одно и то же значение, показывающее, что они эквивалентны. Если данная дробь не приводится к наименьшему члену, вы можете найти другие эквивалентные дроби, разделив числитель и знаменатель на одно и то же число.
Что такое эквивалентная дробь? Как узнать, равны ли две дроби?
Нахождение эквивалентных дробей может быть легким, если вы используете это правило:
Определение эквивалентных дробей: две дроби ab и cd эквивалентны, только если произведение (умножение) числителя (a) первой дроби и знаменателя (d ) другой дроби равно произведению знаменателя (b) первой дроби на числитель (c) другой дроби.
Другими словами, если вы перемножите (ab и cd) равенство останется, т. е. a.d = b.c. Итак, вот несколько примеров:
е. a.d = b.c. Итак, вот несколько примеров:
- 86 эквивалентно 43, потому что 8 × 3 = 6 × 4 = 24
- 129 эквивалентно 43, потому что 12 × 3 = 9 × 4 = 36 1121100 9 эквивалентно 43, потому что 16 × 3 = 12 × 4 = 48
Таблица/таблица эквивалентных дробей
Эта таблица/таблица эквивалентных дробей содержит общепринятые практические дроби. Вы можете легко конвертировать дроби в десятичные, а также из долей дюймов в миллиметры.
| 1 / 64 | 1 / 32 | 1 / 16 | 1 / 8 | 1 / 4 | 1 / 2 | Десятичный | мм | |
|---|---|---|---|---|---|---|---|---|
| 1 / 64 | 0,015625 | 0,397 | ||||||
| 2 / 64 | 1 / 32 | 0,03125 | 0,794 | |||||
| 3 / 64 | 0,046875 | 1. 191 191 | ||||||
| 4 / 64 | 2 / 32 | 1 / 16 | 0,0625 | 1,588 | ||||
| 5 / 64 | 0,078125 | 1,984 | ||||||
| 6 / 64 | 3 / 32 | 0,09375 | 2,381 | |||||
| 7 / 64 | 0,109375 | 2,778 | ||||||
| 8 / 64 | 4 / 32 | 2 / 16 | 1 / 8 | 0,125 | 3,175 | |||
| 9 / 64 | 0,140625 | 3,572 | ||||||
| 10 / 64 | 5 / 32 | 0,15625 | 3,969 | |||||
| 11 / 64 | 0,171875 | 4,366 | ||||||
| 12 / 64 | 6 / 32 | 3 / 16 | 0,1875 | 4,763 | ||||
| 13 / 64 | 0,203125 | 5. 159 159 | ||||||
| 14 / 64 | 7 / 32 | 0,21875 | 5,556 | |||||
| 15 / 64 | 0,234375 | 5,953 | ||||||
| 16 / 64 | 8 / 32 | 4 / 16 | 2 / 8 | 1 / 4 | 0,25 | 6,35 | ||
| 17 / 64 | 0,265625 | 6,747 | ||||||
| 18 / 64 | 9 / 32 | 0,28125 | 7.144 | |||||
| 19 / 64 | 0,296875 | 7,541 | ||||||
| 20 / 64 | 10 / 32 | 5 / 16 | 0,3125 | 7,938 | ||||
| 21 / 64 | 0,328125 | 8. 334 334 | ||||||
| 22 / 64 | 11 / 32 | 0,34375 | 8.731 | |||||
| 23 / 64 | 0,359375 | 9.128 | ||||||
| 24 / 64 | 12 / 32 | 6 / 16 | 3 / 8 | 0,375 | 9,525 | |||
| 25 / 64 | 0,3 | 9.922 | ||||||
| 26 / 64 | 13 / 32 | 0,40625 | 10.319 | |||||
| 27 / 64 | 0,421875 | 10.716 | ||||||
| 28 / 64 | 14 / 32 | 7 / 16 | 0,4375 | 11. 113 113 | ||||
| 29 / 64 | 0,453125 | 11.509 | ||||||
| 30 / 64 | 15 / 32 | 0,46875 | 11.906 | |||||
| 31 / 64 | 0,484375 | 12.303 | ||||||
| 32 / 64 | 16 / 32 | 8 / 16 | 4 / 8 | 2 / 4 | 1 / 2 | 0,5 | 12,7 | |
| 33 / 64 | 0,515625 | 13.097 | ||||||
| 34 / 64 | 17 / 32 | 0,53125 | 13. 494 494 | |||||
| 35 / 64 | 0,546875 | 13.891 | ||||||
| 36 / 64 | 18 / 32 | 9 / 16 | 0,5625 | 14.288 | ||||
| 37 / 64 | 0,578125 | 14.684 | ||||||
| 38 / 64 | 19 / 32 | 0,59375 | 15.081 | |||||
| 39 / 64 | 0,609375 | 15.478 | ||||||
| 40 / 64 | 20 / 32 | 10 / 16 | 5 / 8 | 0,625 | 15. 875 875 | |||
| 41 / 64 | 0,640625 | 16.272 | ||||||
| 42 / 64 | 21 / 32 | 0,65625 | 16.669 | |||||
| 43 / 64 | 0,671875 | 17.066 | ||||||
| 44 / 64 | 22 / 32 | 11 / 16 | 0,6875 | 17.463 | ||||
| 45 / 64 | 0,703125 | 17.859 | ||||||
| 46 / 64 | 23 / 32 | 0,71875 | 18.256 | |||||
| 47 / 64 | 0,734375 | 18. 653 653 | ||||||
| 48 / 64 | 24 / 32 | 12 / 16 | 6 / 8 | 3 / 4 | 0,75 | 19.05 | ||
| 49 / 64 | 0,765625 | 19.447 | ||||||
| 50 / 64 | 25 / 32 | 0,78125 | 19.844 | |||||
| 51 / 64 | 0,796875 | 20.241 | ||||||
| 52 / 64 | 26 / 32 | 13 / 16 | 0,8125 | 20.638 | ||||
| 53 / 64 | 0,828125 | 21. 034 034 | ||||||
| 54 / 64 | 27 / 32 | 0,84375 | 21.431 | |||||
| 55 / 64 | 0,859375 | 21.828 | ||||||
| 56 / 64 | 28 / 32 | 14 / 16 | 7 / 8 | 0,875 | 22.225 | |||
| 57 / 64 | 0,8 | 22.622 | ||||||
| 58 / 64 | 29 / 32 | 0, | 23.019 | |||||
| 59 / 64 | 0,5 | 23.416 | ||||||
| 60 / 64 | 30 / 32 | 15 / 16 | 0,9375 | 23. 813 813 | ||||
| 61 / 64 | 0,953125 | 24.209 | ||||||
| 62 / 64 | 31 / 32 | 0,96875 | 24.606 | |||||
| 63 / 64 | 0,984375 | 25.003 | ||||||
| 64 / 64 | 32 / 32 | 16 / 16 | 8 / 8 | 4 / 4 | 2 / 2 | 1 | 25,4 |
Ссылка:
- [1] Как найти эквивалентные дроби
Equivalent Fractions — Samples
- Equivalent fraction for 27/3
- Equivalent fraction for 23/11
- Equivalent fraction for 20/26
- Equivalent fraction for 24/18
- Equivalent fraction for 17/24
- Эквивалентная дробь для 13/24
- Эквивалентная дробь для 11/21
- Эквивалентная дробь для 1/27
- Эквивалентная дробь для 15/8
- Эквивалентная дробь для 29/7
- Эквивалентная фракция для 21/6
- Эквивалентная фракция для 16/19
- Эквивалентная фракция для 25/5
- Эквивалентная фракция для 25/3
- Эквивалентная фракция для 26/23
Deckamer
, По мнению всех усилий
, По мнению всех усилий
, По мнению все усилия
.





 В иных случая получится периодическое десятичное число.
В иных случая получится периодическое десятичное число. В итоге должно получиться: 34/10 = 3,4; 78954/10 = 7895,4; 186/100 = 1,86; 959/10000 = 0,0959.
В итоге должно получиться: 34/10 = 3,4; 78954/10 = 7895,4; 186/100 = 1,86; 959/10000 = 0,0959. То есть, 5/2 = 2,5. Таким же образом переводят и другие примеры: ¼ = 0,25; 34/81 = 0,420; 456/1245 = 0,366; 1245/456 = 2,73.
То есть, 5/2 = 2,5. Таким же образом переводят и другие примеры: ¼ = 0,25; 34/81 = 0,420; 456/1245 = 0,366; 1245/456 = 2,73. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. Какую часть составляют девочки?
Какую часть составляют девочки?
 Для этого выполните шаги, указанные ниже. Поясним это на примере смешанной дроби 2\(\dfrac{4}{5}\). Здесь 2 — целое число, 4 — числитель, 5 — знаменатель.
Для этого выполните шаги, указанные ниже. Поясним это на примере смешанной дроби 2\(\dfrac{4}{5}\). Здесь 2 — целое число, 4 — числитель, 5 — знаменатель.



 Если знаменатели не равны, то находим НОК знаменателей и делаем их общими. Затем вычитаем числители так, чтобы знаменатель остался тем же. Например, чтобы вычесть \(3\frac{1}{3}\) из \(4\frac{2}{3}\), преобразуйте дроби в неправильные дроби, которые мы получим, 10/3 из 14/3. Если из 14/3 вычесть 10/3, получится 4/3. Затем, переводя 4/3 в смешанную дробь, мы получаем \(1\frac{1}{3}\).
Если знаменатели не равны, то находим НОК знаменателей и делаем их общими. Затем вычитаем числители так, чтобы знаменатель остался тем же. Например, чтобы вычесть \(3\frac{1}{3}\) из \(4\frac{2}{3}\), преобразуйте дроби в неправильные дроби, которые мы получим, 10/3 из 14/3. Если из 14/3 вычесть 10/3, получится 4/3. Затем, переводя 4/3 в смешанную дробь, мы получаем \(1\frac{1}{3}\). Давайте посмотрим на дробь \(\frac{3}{4}\) в качестве примера. Мы видим, что 3 — это наш числитель, а 4 — наш знаменатель. Таким образом, дробь \(\frac{3}{4}\) на самом деле означает 3 части из 4 частей. Также может быть полезно визуализировать \(\frac{3}{4}\) как просто
Давайте посмотрим на дробь \(\frac{3}{4}\) в качестве примера. Мы видим, что 3 — это наш числитель, а 4 — наш знаменатель. Таким образом, дробь \(\frac{3}{4}\) на самом деле означает 3 части из 4 частей. Также может быть полезно визуализировать \(\frac{3}{4}\) как просто Хотя мы очень часто наблюдаем этот тип дроби в нашей повседневной жизни, это не единственный тип дроби.
Хотя мы очень часто наблюдаем этот тип дроби в нашей повседневной жизни, это не единственный тип дроби.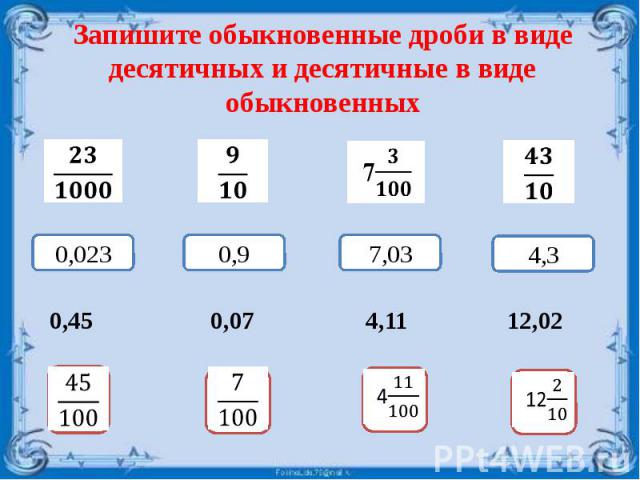 Одна целая пицца будет представлена \(\frac{6}{6}\) или «шесть шестых». \(\frac{7}{6}\) представляет «семь шестых», то есть больше, чем одна пицца. Это можно представить как \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6} }+\frac{1}{6}+\frac{1}{6}=7\). Его также можно записать в другой форме, называемой 9.1237 смешанный номер . Неправильная дробь и смешанное число будут представлять одну и ту же сумму, но просто будут записаны в другой форме.
Одна целая пицца будет представлена \(\frac{6}{6}\) или «шесть шестых». \(\frac{7}{6}\) представляет «семь шестых», то есть больше, чем одна пицца. Это можно представить как \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6} }+\frac{1}{6}+\frac{1}{6}=7\). Его также можно записать в другой форме, называемой 9.1237 смешанный номер . Неправильная дробь и смешанное число будут представлять одну и ту же сумму, но просто будут записаны в другой форме. Мы сказали, что это можно выразить как неправильную дробь \(\frac{7}{6}\) или визуализировать как \(\frac{1}{6}+\frac{1}{6}+\frac{ 1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\). В качестве смешанного числа мы бы сгруппировали 6 таких «шестых», чтобы сформировать \(1\frac{6}{6}\), или 1 целое. Сгруппировав \(\frac{6}{6}\) вместе, мы можем увидеть, что \(\frac{1}{6}\) остался сам по себе. Мы запишем наше смешанное число как \(1\frac{1}{6}\).
Мы сказали, что это можно выразить как неправильную дробь \(\frac{7}{6}\) или визуализировать как \(\frac{1}{6}+\frac{1}{6}+\frac{ 1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\). В качестве смешанного числа мы бы сгруппировали 6 таких «шестых», чтобы сформировать \(1\frac{6}{6}\), или 1 целое. Сгруппировав \(\frac{6}{6}\) вместе, мы можем увидеть, что \(\frac{1}{6}\) остался сам по себе. Мы запишем наше смешанное число как \(1\frac{1}{6}\). Тогда мы знаем, что \(\frac{2}{2}\) составляет одно целое. И у нас осталось \(\frac{1}{2}\). Итак, \(\frac{3}{2}\) как смешанное число равно \(1\frac{1}{2}\).
Тогда мы знаем, что \(\frac{2}{2}\) составляет одно целое. И у нас осталось \(\frac{1}{2}\). Итак, \(\frac{3}{2}\) как смешанное число равно \(1\frac{1}{2}\). В данном случае это 4, поэтому 1 равно \(\frac{4}{4}\). Когда мы объединяем эти четыре четверти с \(\frac{3}{4}\), мы получаем всего семь четвертей, или \(\frac{7}{4}\).
В данном случае это 4, поэтому 1 равно \(\frac{4}{4}\). Когда мы объединяем эти четыре четверти с \(\frac{3}{4}\), мы получаем всего семь четвертей, или \(\frac{7}{4}\).
 Это становится новым числителем над исходным знаменателем.
Это становится новым числителем над исходным знаменателем. Дроби, у которых числитель меньше знаменателя, представляют значения, которые меньше одного целого. \(\frac{5}{3}, \frac{7}{5}, \text{ и }\frac{3}{2}\) — неправильные дроби, представляющие суммарные значения, превышающие одно целое.
Дроби, у которых числитель меньше знаменателя, представляют значения, которые меньше одного целого. \(\frac{5}{3}, \frac{7}{5}, \text{ и }\frac{3}{2}\) — неправильные дроби, представляющие суммарные значения, превышающие одно целое.
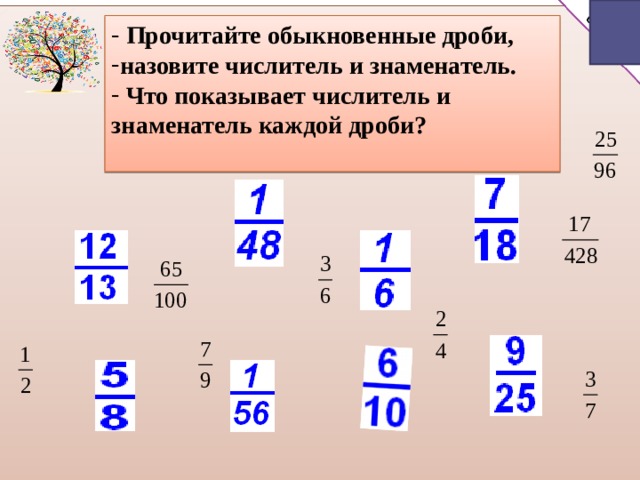

 Давно удобно и принято делить вещи на сегменты. Часы делятся на 60 минут каждый. Сутки делятся на 24 часа, а годы на 12 месяцев. Мили делятся на футы, а километры на метры. Каждый из этих сегментов может быть представлен в виде дроби. Один дюйм составляет одну двенадцатую часть или одну двенадцатую фута. Дроби очень полезны, потому что они делают возможными измерения не в целых числах, таких как 1, 2 или 5. Измерения с помощью дробей часто могут быть более точными: точнее сказать «четыре и одна десятая галлона», чем «немного более четырех галлонов».
Давно удобно и принято делить вещи на сегменты. Часы делятся на 60 минут каждый. Сутки делятся на 24 часа, а годы на 12 месяцев. Мили делятся на футы, а километры на метры. Каждый из этих сегментов может быть представлен в виде дроби. Один дюйм составляет одну двенадцатую часть или одну двенадцатую фута. Дроби очень полезны, потому что они делают возможными измерения не в целых числах, таких как 1, 2 или 5. Измерения с помощью дробей часто могут быть более точными: точнее сказать «четыре и одна десятая галлона», чем «немного более четырех галлонов». Одни и те же числа, представленные в виде десятичных дробей, будут 0,4 и 0,07. Обычно их читали как «четыре точки» и «ноль семь». Они выражают одинаковые суммы.
Одни и те же числа, представленные в виде десятичных дробей, будут 0,4 и 0,07. Обычно их читали как «четыре точки» и «ноль семь». Они выражают одинаковые суммы. Системы счисления и числа). Иногда называемые просто «десятичными», все десятичные дроби состоят из одного или нескольких чисел, которым предшествует точка, называемая десятичной запятой: например, 0,4 читается как четыре десятых. Если справа от запятой стоит только одна цифра, дробь всегда читается как «десятые». При наличии двух цифр дробь читается как «сотые», а при наличии трех – как «тысячные». Другими словами, десятичные дроби следуют той же последовательности, что и целые числа, где первая цифра находится в столбце «десятки», вторая — в «сотнях» и так далее (см. Арифметика). Например, десятичная дробь 0,075 читается как «семьдесят пять тысячных», а дробь 0,3852 — как «три тысячи восемьсот пятьдесят две десятитысячных».
Системы счисления и числа). Иногда называемые просто «десятичными», все десятичные дроби состоят из одного или нескольких чисел, которым предшествует точка, называемая десятичной запятой: например, 0,4 читается как четыре десятых. Если справа от запятой стоит только одна цифра, дробь всегда читается как «десятые». При наличии двух цифр дробь читается как «сотые», а при наличии трех – как «тысячные». Другими словами, десятичные дроби следуют той же последовательности, что и целые числа, где первая цифра находится в столбце «десятки», вторая — в «сотнях» и так далее (см. Арифметика). Например, десятичная дробь 0,075 читается как «семьдесят пять тысячных», а дробь 0,3852 — как «три тысячи восемьсот пятьдесят две десятитысячных». Таким образом, 0,85 становится обыкновенной дробью 85 / 100 .
Таким образом, 0,85 становится обыкновенной дробью 85 / 100 . Любую смешанную дробь можно превратить в неправильную, умножив целое число на знаменатель, прибавив результат к числителю и поместив сумму над исходным знаменателем. Таким образом 2 1 / 3 можно заменить на 7 / 3 .
Любую смешанную дробь можно превратить в неправильную, умножив целое число на знаменатель, прибавив результат к числителю и поместив сумму над исходным знаменателем. Таким образом 2 1 / 3 можно заменить на 7 / 3 . Число 2,38 будет читаться как «два целых три десятых восемь».
Число 2,38 будет читаться как «два целых три десятых восемь». А при сложении или вычитании десятичные запятые всегда должны стоять в прямой колонке. Для выполнения этого сложения цифры должны быть записаны так:
А при сложении или вычитании десятичные запятые всегда должны стоять в прямой колонке. Для выполнения этого сложения цифры должны быть записаны так:
 Если бы множитель был равен 2,6, произведение было бы 83,2, смешанное десятичное число, и десятичная точка была бы сохранена.
Если бы множитель был равен 2,6, произведение было бы 83,2, смешанное десятичное число, и десятичная точка была бы сохранена. При делении следует помнить один главный момент: положение запятой в ответе определяется положением запятой в делимом числе. Как и в умножении, здесь могут помочь определенные правила.
При делении следует помнить один главный момент: положение запятой в ответе определяется положением запятой в делимом числе. Как и в умножении, здесь могут помочь определенные правила. Следовательно, ответ, полученный при делении 6,816 на 2,13, равен 3,2 с одним десятичным знаком, полученным по этому правилу.
Следовательно, ответ, полученный при делении 6,816 на 2,13, равен 3,2 с одним десятичным знаком, полученным по этому правилу.

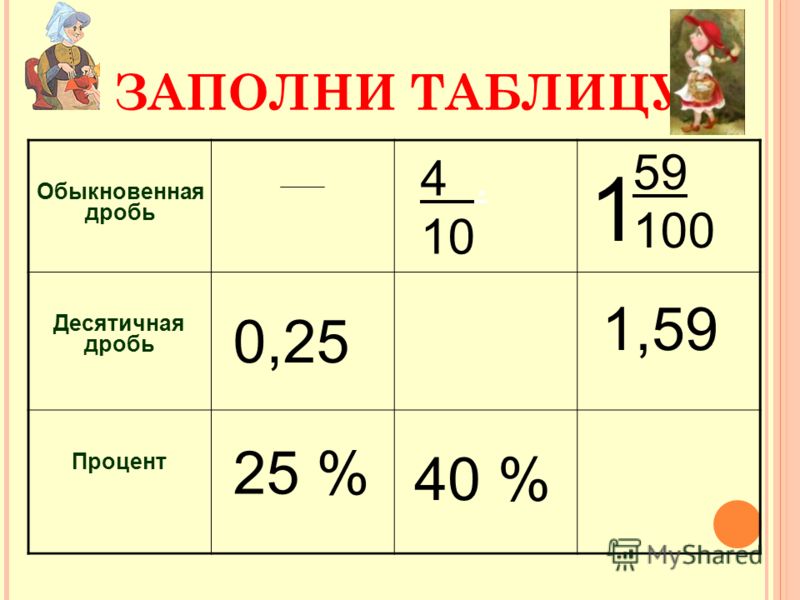 ..
..