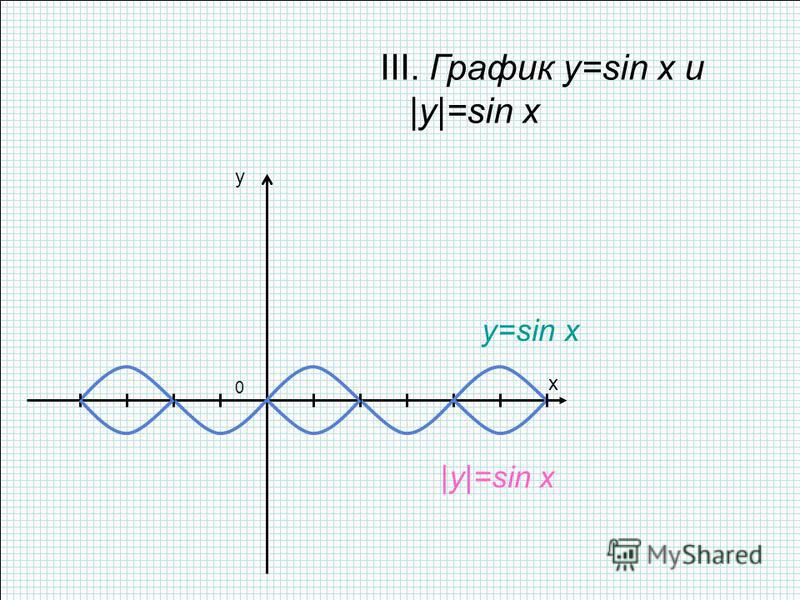
Графики тригонометрических функций кратных углов. График функции y=sin x График функции y sin x 2
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
«Йошкар-Олинский техникум сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
/методическая разработка/
Йошкар – Ола
Тема . Построение и исследование графика тригонометрической функции y = sinx в табличном процессоре MS Excel
Тип урока – интегрированный (получение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции y = sinx в зависимости от коэффициентов с помощью компьютера
Обучающие:
1.
2. Показать внедрение компьютерных технологий в обучение математике, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерных технологий на уроках математики
4. Закрепить навыки исследования функций и построения их графиков
Развивающие:
1. Развивать познавательный интерес учащихся к учебным дисциплинам и умение применять свои знания в практических ситуациях
2. Развивать умения анализировать, сравнивать, выделять главное
3. Способствовать повышению общего уровня развития студентов
Воспитывающие :
1. Воспитывать самостоятельность, аккуратность, трудолюбие
2. Воспитывать культуру диалога
Формы работы на уроке – комбинированная
Дидактическое оснащение и оборудование:
1. Компьютеры
2. Мультимедийный проектор
Мультимедийный проектор
4. Раздаточный материал
5. Слайды презентации
Ход урока
I . Организация начала урока
· Приветствие студентов и гостей
· Настрой на урок
II . Целеполагание и актуализация темы
Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Сегодня мы научимся строить графики тригонометрических функций в среде табличного процессора MS Excel 2007.
Тема нашего занятия «Построение и исследование графика тригонометрической функцииy = sinx в табличном процессоре»
Из курса алгебры нам известна схема исследования функции и построения ее графика. Давайте вспомним как это сделать.
Слайд 2
Схема исследования функции
1. Область определения функции (D(f))
2. Область значения функции Е(f)
3. Определение четности
Определение четности
4. Периодичность
5. Нули функции (y=0)
6. Промежутки знакопостоянства (у>0, y
7. Промежутки монотонности
8. Экстремумы функции
III . Первичное усвоение нового учебного материала
Откройте программу MS Excel 2007.
Построим график функции y=sinx
Построение графиков в табличном процессоре MS Excel 2007
График данной функции будем строить на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом, чтобы график получился более точным.
Т. к. редактор работает с числами, переведем радианы в числа, зная что
1. Находим значение функции в точке х=-2П. Для остальных значение аргумента соответствующие значения функции редактор вычисляет автоматически.
2. Теперь у нас имеется таблица со значениями аргумента и функции. С помощью этих данных мы должны построить график этой функции с помощью мастера диаграмм.
3. Для построения графика надо выделить нужный диапазон данных, строки со значениями аргумента и функции
4..jpg»>
Выводы записываем в тетрадь (Слайд 5)
Вывод. График функции вида у=sinx+k получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОУ на k единиц
Если k >0, то график смещается вверх на k единиц
Если k
Построение и исследование функции вида у= k *sinx, k — const
Задание 2. На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.(Чтобы заново не задавать значение аргумента давайте скопируем имеющиеся значения. Теперь вам надо задать формулу, и по полученной таблице построить график.)
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и проследите как изменяется вид графика.
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
Выводы записываем в тетрадь (Слайд 11)
Вывод. График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график смещается вправо вдоль оси ОХ
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием на построение и исследование функции при помощи графика
Y=6 *sin(x) | Y= 1-2 sin х | Y= — sin (3х+ ) | |
1. | |||
2. Область значения | |||
3. Четность | |||
4. Периодичность | |||
5. Промежутки знакопостоянства | |||
6. Промежутки монотонности | |||
Функция возрастает | |||
Функция убывает | |||
7. | |||
Минимум | |||
Максимум |
V . Организация домашнего задания
Построить график функции y=-2*sinх+1 , исследовать и проверить правильность построения в среде электронной таблицы Microsoft Excel. (Слайд 12)
VI . Рефлексия
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).

- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.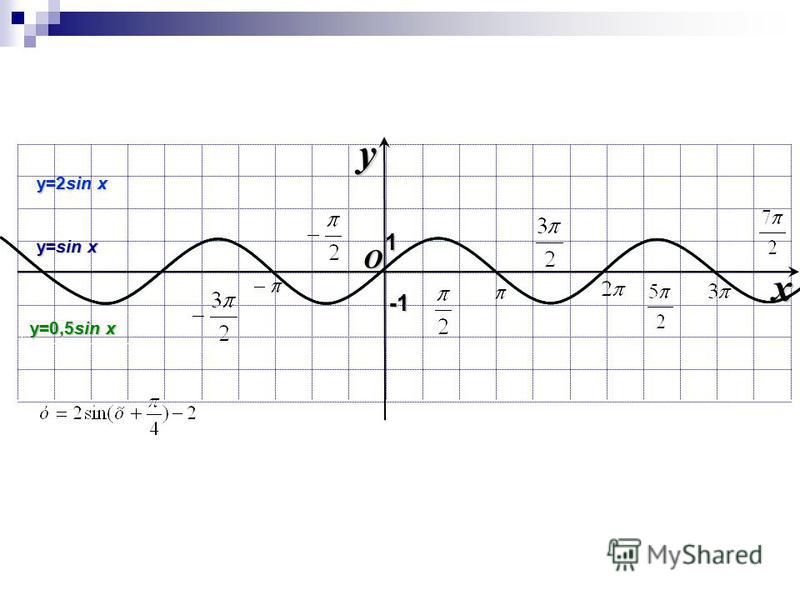
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375484 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.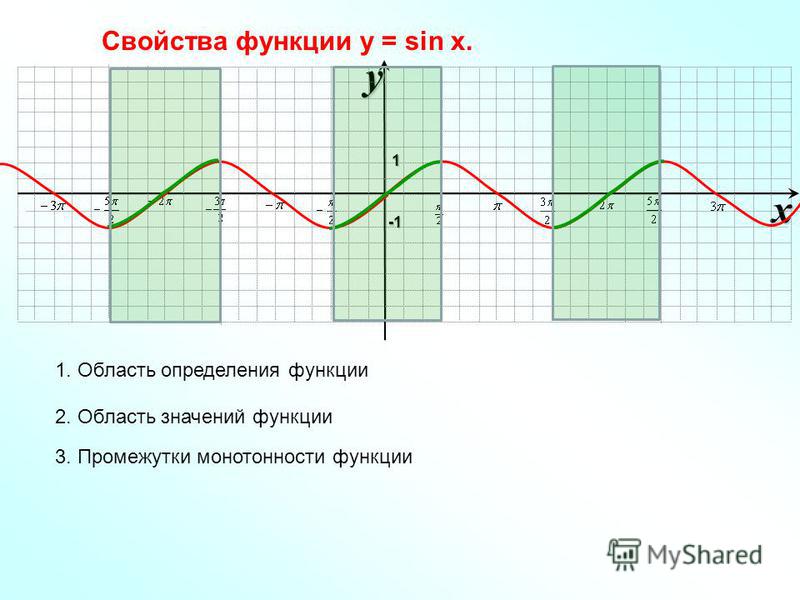 В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Свойства функции y = sin x и ее график
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
y
— 2π
-π
0
π
2π
x
1
2. Свойства функции
1.D(y)
2.E(y)
3. Четность функции
4. Периодичность функции
5.Нули функции
6.
 Наибольшее значение
Наибольшее значение7. Наименьшее значение
8. Положительные значения
9. Отрицательные значения
10. Возрастание функции
11. Убывание функции
2
3. y = sin x
yy = sin x
1
D (y)
x
0
xЄR
-1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
3
x
4. y = sin x
yy = sin x
E (y)
1
0
[ -1; 1]
y
x
-1
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
4
x
5. y = sin x
yy = sin x
1
Четность функции
Функция нечетна, т.к. sin(-x)=-sin x,
график симметричен относительно
(0;0)
0
x
-1
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
5
x
6. y = sin x
yy = sin x
1
Периодичность функции
0
Период функции Т=2π,
sin(x+2π)=sin x
x
-1
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
6
x
7.
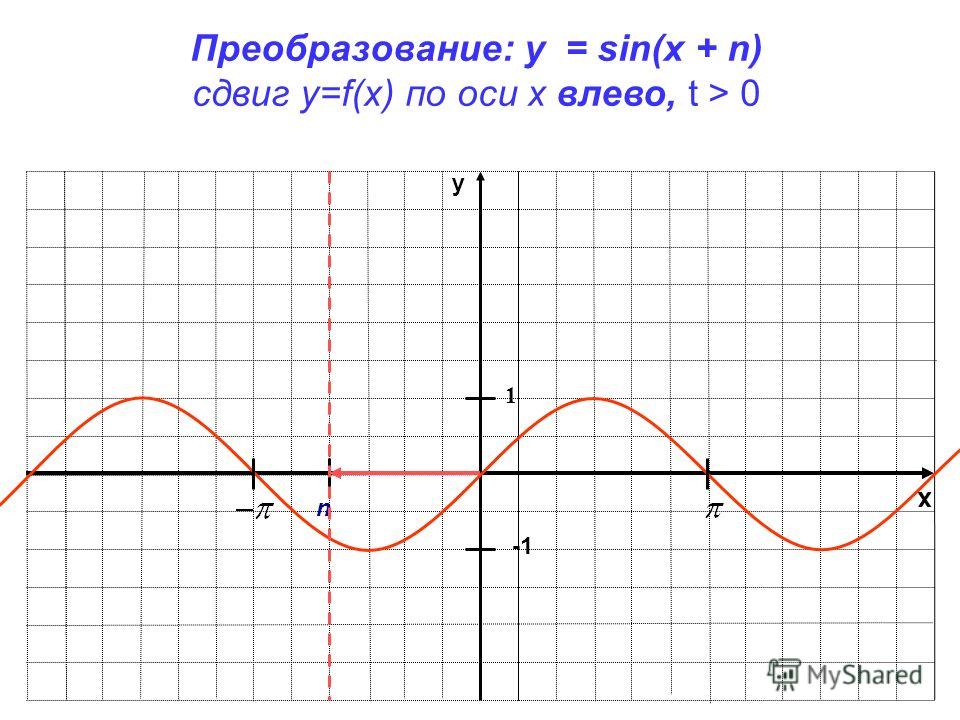 y = sin xy
y = sin xyy = sin x
1
Нули функции sin x = 0
при x = πk
0
y
x
-1
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
7
x
8. y = sin x
y1
y = sin x
0
Наибольшее значение sin x = 1
при х= π/2+2πk
y
x
-1
х= π/2
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
8
x
9. y = sin x
yy = sin x
1
Наименьшее значение sin x = -1
при х= -π/2+2πk
0
y
x
-1
х= 3π/2
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
x
2π
-1
9
10. y = sin на отрезке
Построение графика функцииy = sin на отрезке
y
0, 2
3
4
6
sin(π/6)=0,5
x
sin(π/4) 0,7
y
sin(π/3) 0,866
1
— 3π/2
-π
— π/2
0
6 4 3
π/2
π
3π/2
2π
-1
10
x
График функции на отрезке
;
y
у = sin x
x
y
— 3π/2
-π
— π/2
0
π/2
π
x
3π/2
11
12.
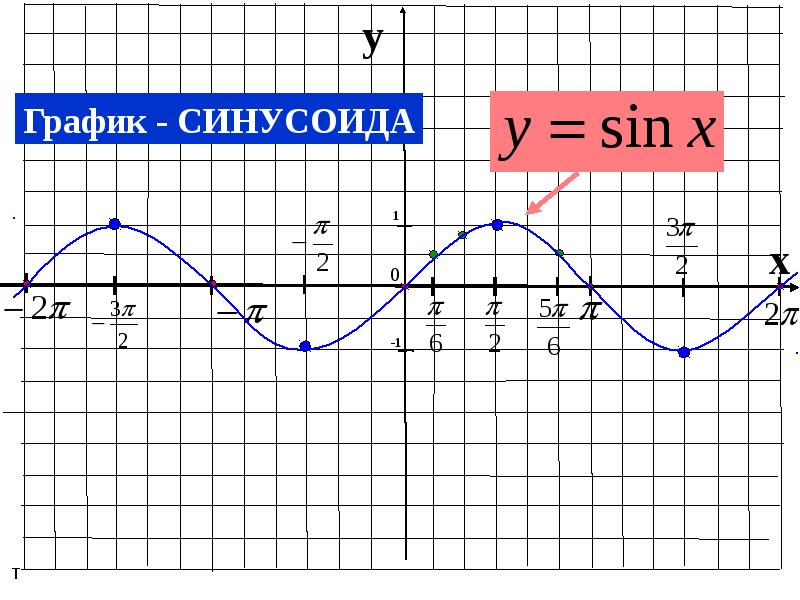 y = sin xy
y = sin xyy = sin x
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
12
x
13. y = sin x
График функции y=sin x называется синусоидаy
1
-2π
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
5π/2 x
-1
13
14. y = sin x
Промежутки знакопостоянстваy
y = sin x
+
+
Положительные значения sin x>0
на отрезке (2πk; π+2πk), k
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
14
x
15. y = sin x
.y
Промежутки знакопостоянства
y = sin x
Отрицательные значения sin x<0
–
на отрезке (π+2πk; 2π+2πk). k
x
–
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
15
x
16. y = sin x
Промежутки возрастанияy
y = sin x
Функция возрастает
на отрезке [-π/2+2πk; π/2+2πk]
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
x
2π
-1
16
17.
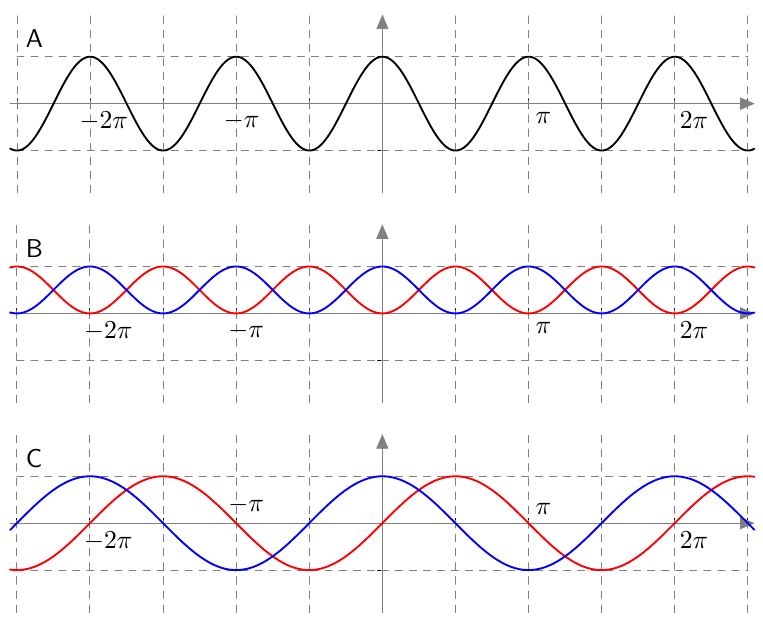 y = sin x Промежутки убывания
y = sin x Промежутки убыванияy
y = sin x
Функция убывает
на отрезке [π/2+2πk; 3π/2+2πk]
x
y
1
— 3π/2
-π
— π/2
0
π/2
π
3π/2
2π
-1
17
x
Задача
Сравнить числа
Так как
= 3,14,
< 2 < 3 <
sin 2
2
и
1,57
sin 3
, то
2
Из графика видно, что на отрезке ;
2
функция у=sinх убывает.
Ответ: sin 2 > sin 3.
18
Преобразование графика
y = sinx
4,5
Построить график
функции
у=sinх+3
y = sinx + 3
4
3,5
3
3
2,5
2
1,5
y = sinx
1
+
Сдвиг вдоль оси ординат
0,5
вверх
0
2
-0,5
-1
-1,5
1,5
Построить график
функции
у=sinх-3
1
0,5
0
-0,5
-1
-2
-2,5
-3
—
y = sinx — 3
-1,5
-3
-3,5
вниз
-4
-4,5
19
Сдвиг вдоль оси абсцисс
Построить график функции
у=sin(х — 4 )
1,5
+
y = sin x
1
y = sin(x —
0,5
4
)
π/
0
Сдвиг влево
-0,5
-1
-1,5
Построить
график функции
у=sin(х+ )
—
4
1,5
y = sinx
1
y = sin(x +
4
)
0,5
0
-0,5
—
-1
Сдвиг вправо
-1,5
20
Сжатие и растяжение к оси абсцисс
Построить график
функции у= 3 sinх
K >1
растяжение
У = 3 sin x
3,5
3
2,5
2
1,5
1
0,5
0
-0,5
-1
-1,5
-2
-2,5
-3
-3,5
1,5
Построить график 1
функции у=1/ 3 sinх0,5
у = 1/3 sin x
0
0< K <1
сжатие
-0,5
-1
-1,5
21
Сжатие и растяжение к оси ординат
Построить график
функции
у = sin2х
1,5
У =sin 2х
1
0,5
0
K >1
-0,5
сжатие
Построить
график функции
у = sin х
2
-1
-1,5
У = sin
y
1,5
х
2
1
0,5
0
x
0
-0,5
0< K <1
растяжение
-1
-1,5
— π/2
π/2
π
3π/2
2
π
22
English Русский Правила
 ru 🎓
ru 🎓1
Первый слайд презентации: Функция y=sin x, ее свойства и график
Математика 10 класс МБОУ СШ №12 Учитель: Шудраков Николай Николаевич
Изображение слайда
2
Слайд 2: Свойства функции y=sin x
Свойство 1. Область определения D(f)=(-∞;+ ∞ ) Найти: sin 35 sin 23 /3 sin -15 /4
Изображение слайда
3
Слайд 3: Свойства функции y=sin x
Свойство 2. Четность y=sin x — нечетная функция sin (-x)= — sin x Найти: sin (-24) sin (-17 /3 )
Изображение слайда
4
Слайд 4: Свойства функции y=sin x
Свойство 3.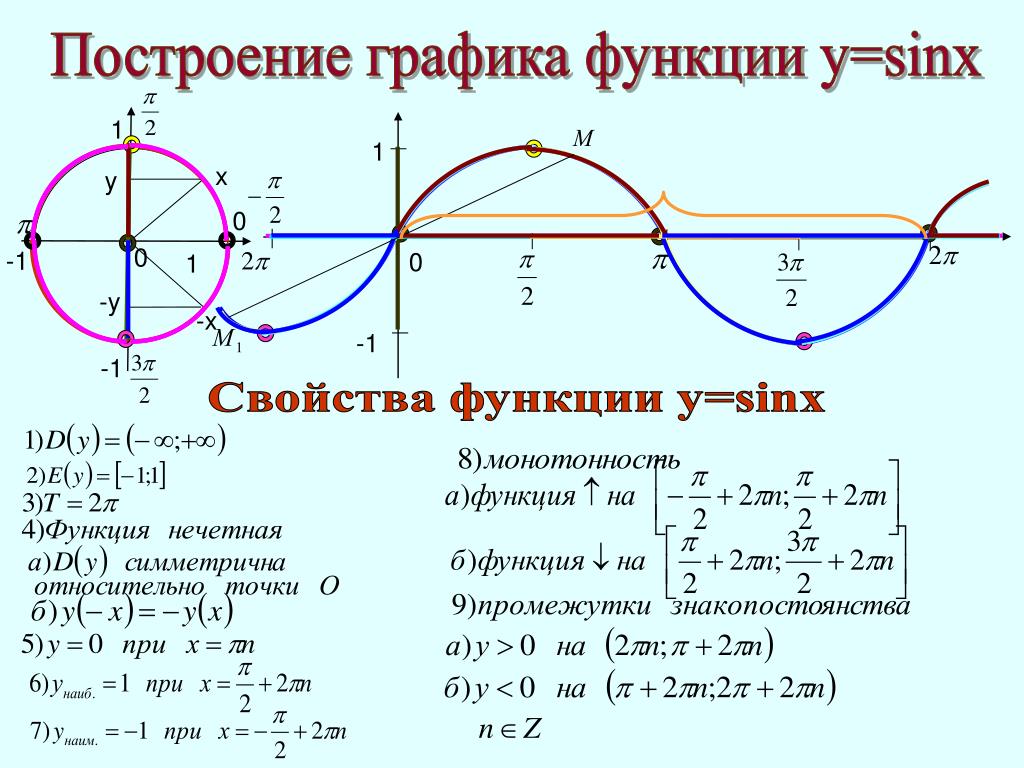 Возрастание и убывание
Возрастает на промежутке
[0 ; /2]
Убывает на промежутке
[ /2 ; ]
Возрастание и убывание
Возрастает на промежутке
[0 ; /2]
Убывает на промежутке
[ /2 ; ]
Изображение слайда
5
Слайд 5: Свойства функции y=sin x
Свойство 4. Ограниченность Функция ограничена снизу и сверху -1 ≤ sin x ≤ 1
Изображение слайда
6
Слайд 6: Свойства функции y=sin x
Свойство 5. Наименьшее и наибольшее значение функции y наим = -1 (в любой точке вида x = — π /2+2 π k) y наиб = 1 (в любой точке вида x = π /2+2 π k) Найти наименьшее и наибольшее значение: 1+ sin x 2 sin x — 3
Изображение слайда
7
Слайд 7: График функции y=sin x
x 0 π /6 π /3 π /2 2 π /3 5 π /6 π y 0 1/2 √ 3/2 1 √ 3/2 1/2 0
Изображение слайда
8
Слайд 8: График функции y=sin x
x [ — π ; π ] Волна синусоиды
Изображение слайда
9
Слайд 9: График функции y=sin x
Синусоида
Изображение слайда
10
Слайд 10: График функции y=sin x
Полуволна синусоиды
Изображение слайда
11
Слайд 11: Свойства функции y=sin x
Свойство 6. Функция y=sin x возрастает на любом отрезке вида
[ — π /2 + 2 π k ; π /2+2 π k ]
и убывает на любом отрезке вида
[ π /2 + 2 π k ; — π /2+2 π k ]
Функция y=sin x возрастает на любом отрезке вида
[ — π /2 + 2 π k ; π /2+2 π k ]
и убывает на любом отрезке вида
[ π /2 + 2 π k ; — π /2+2 π k ]
Изображение слайда
12
Слайд 12: Свойства функции y=sin x
Свойство 7. Непрерывность Функция y=sin x непрерывна на всей области определения
Изображение слайда
13
Слайд 13: Свойства функции y=sin x
Свойство 8. Область значений функции Е (f)=[ -1 ; 1 ]
Изображение слайда
14
Слайд 14: Пример 1
Решите графически уравнение sin x = x — π
Изображение слайда
15
Слайд 15: Пример 2
Постройте график функции y=sin (x — π /3)+2
Изображение слайда
16
Слайд 16: Пример 2
Постройте график функции y=sin (x — π /3)+2
Изображение слайда
17
Слайд 17: Пример 3
Найдите наибольшее и наименьшее значение функции y=sin x на отрезке [5 π / 6 ; 2 π]
Изображение слайда
18
Последний слайд презентации: Функция y=sin x, ее свойства и график: Домашнее задание
10.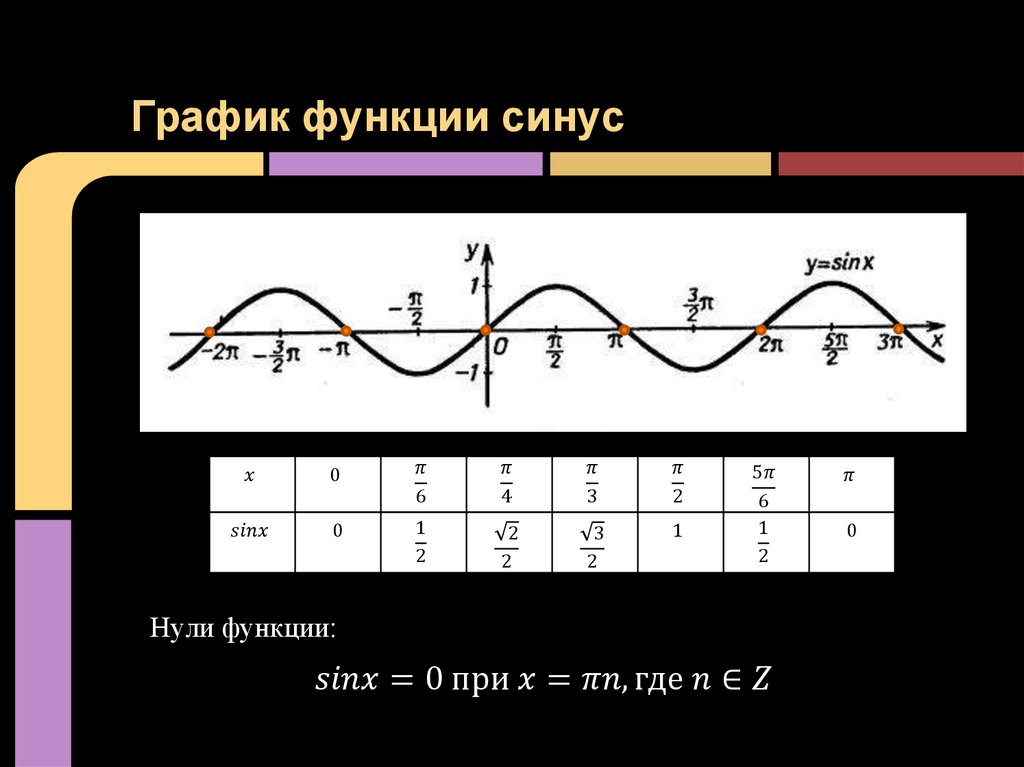 7 а
10.8 в
10.11 а,б
____________
10.9 б
10.10а
7 а
10.8 в
10.11 а,б
____________
10.9 б
10.10а
Изображение слайда
График sin x 2. Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.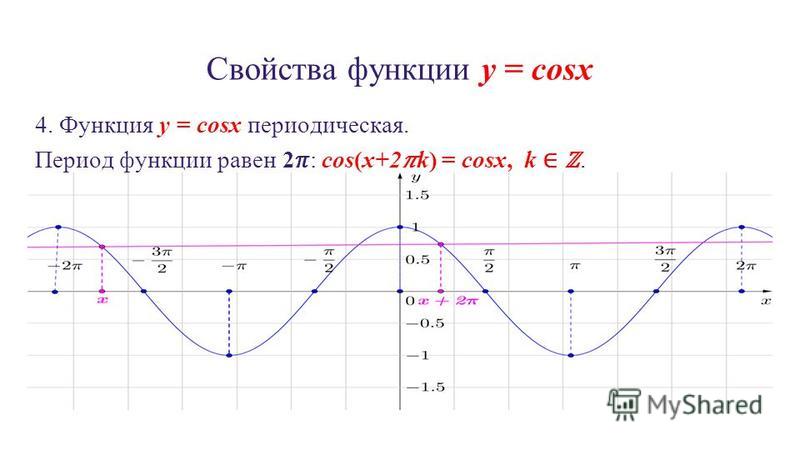
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.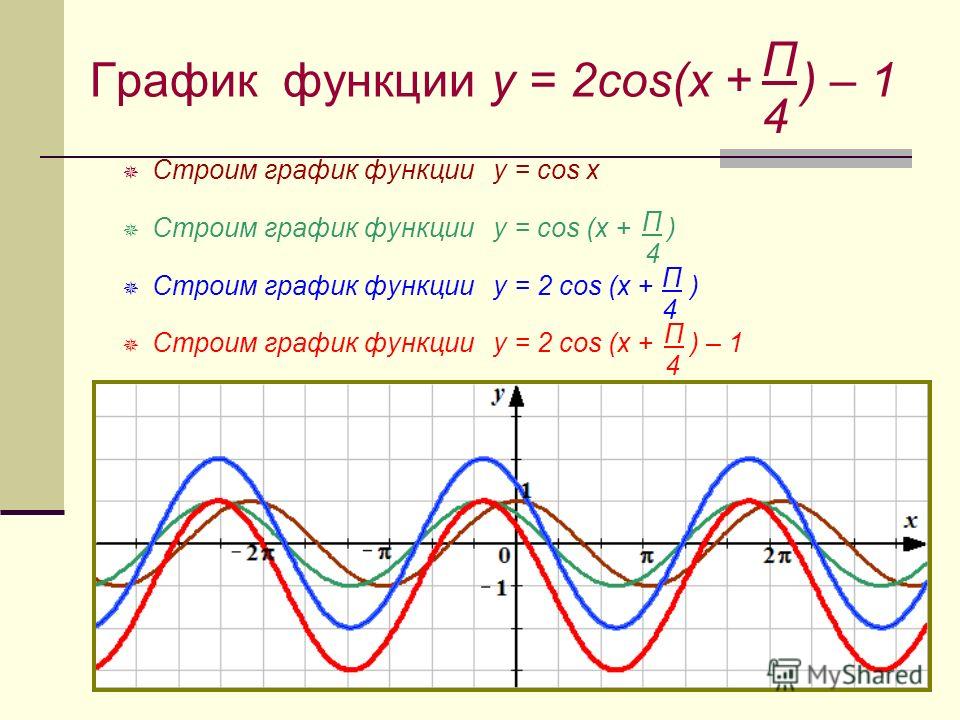
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.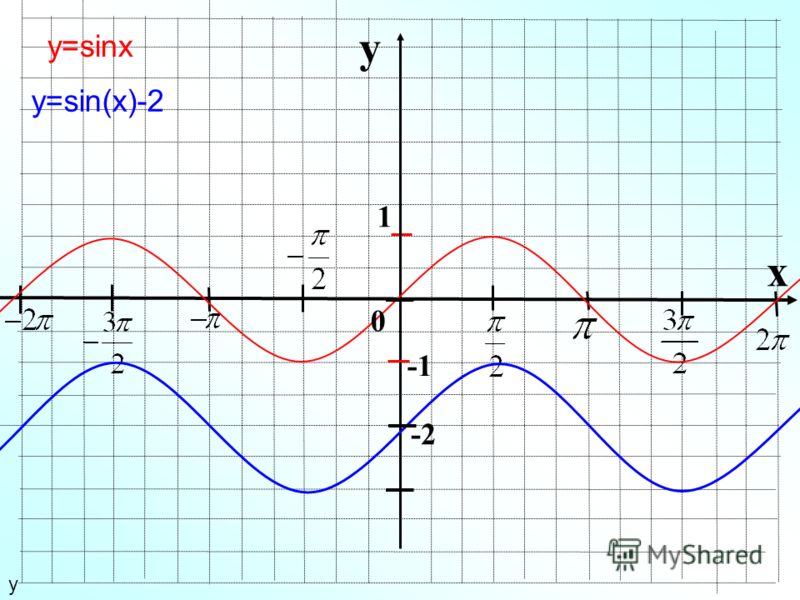
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .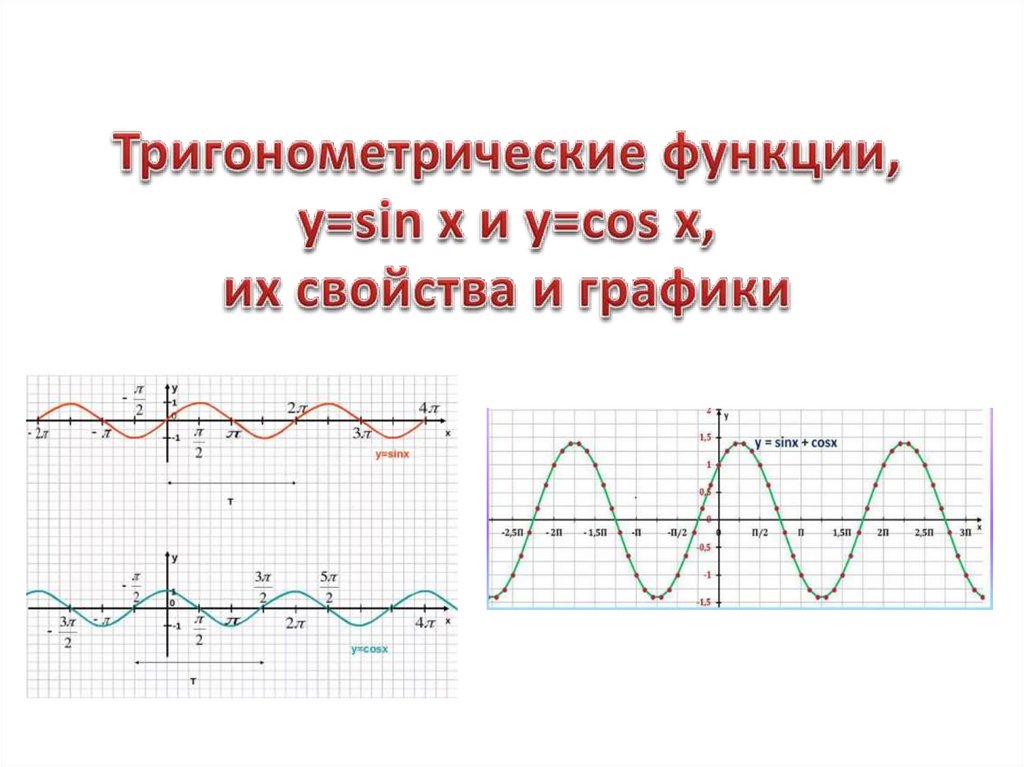
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
«Йошкар-Олинский техникум сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
/методическая разработка/
Йошкар – Ола
Тема . Построение и исследование графика тригонометрической функции y = sinx в табличном процессоре MS Excel
Тип урока – интегрированный (получение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции y = sinx в зависимости от коэффициентов с помощью компьютера
Обучающие:
1. Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
2. Показать внедрение компьютерных технологий в обучение математике, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерных технологий на уроках математики
4. Закрепить навыки исследования функций и построения их графиков
Развивающие:
1. Развивать познавательный интерес учащихся к учебным дисциплинам и умение применять свои знания в практических ситуациях
2. Развивать умения анализировать, сравнивать, выделять главное
3. Способствовать повышению общего уровня развития студентов
Воспитывающие :
1. Воспитывать самостоятельность, аккуратность, трудолюбие
2. Воспитывать культуру диалога
Формы работы на уроке – комбинированная
Дидактическое оснащение и оборудование:
1. Компьютеры
2. Мультимедийный проектор
Мультимедийный проектор
4. Раздаточный материал
5. Слайды презентации
Ход урока
I . Организация начала урока
· Приветствие студентов и гостей
· Настрой на урок
II . Целеполагание и актуализация темы
Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Сегодня мы научимся строить графики тригонометрических функций в среде табличного процессора MS Excel 2007.
Тема нашего занятия «Построение и исследование графика тригонометрической функцииy = sinx в табличном процессоре»
Из курса алгебры нам известна схема исследования функции и построения ее графика. Давайте вспомним как это сделать.
Слайд 2
Схема исследования функции
1. Область определения функции (D(f))
2. Область значения функции Е(f)
3. Определение четности
Определение четности
4. Периодичность
5. Нули функции (y=0)
6. Промежутки знакопостоянства (у>0, y
7. Промежутки монотонности
8. Экстремумы функции
III . Первичное усвоение нового учебного материала
Откройте программу MS Excel 2007.
Построим график функции y=sinx
Построение графиков в табличном процессоре MS Excel 2007
График данной функции будем строить на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом, чтобы график получился более точным.
Т. к. редактор работает с числами, переведем радианы в числа, зная что П ≈ 3,14 . (таблица перевода в раздаточном материале).
1. Находим значение функции в точке х=-2П. Для остальных значение аргумента соответствующие значения функции редактор вычисляет автоматически.
2. Теперь у нас имеется таблица со значениями аргумента и функции. С помощью этих данных мы должны построить график этой функции с помощью мастера диаграмм.
3. Для построения графика надо выделить нужный диапазон данных, строки со значениями аргумента и функции
4..jpg»>
Выводы записываем в тетрадь (Слайд 5)
Вывод. График функции вида у=sinx+k получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОУ на k единиц
Если k >0, то график смещается вверх на k единиц
Если k
Построение и исследование функции вида у= k *sinx, k — const
Задание 2. На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
(Чтобы заново не задавать значение аргумента давайте скопируем имеющиеся значения. Теперь вам надо задать формулу, и по полученной таблице построить график.)
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и проследите как изменяется вид графика.
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
Выводы записываем в тетрадь (Слайд 11)
Вывод. График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график смещается вправо вдоль оси ОХ
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием на построение и исследование функции при помощи графика
Y=6 *sin(x) | Y= 1-2 sin х | Y= — sin (3х+ ) | |
1. | |||
2. Область значения | |||
3. Четность | |||
4. Периодичность | |||
5. Промежутки знакопостоянства | |||
6. Промежутки монотонности | |||
Функция возрастает | |||
Функция убывает | |||
7. | |||
Минимум | |||
Максимум |
V . Организация домашнего задания
Построить график функции y=-2*sinх+1 , исследовать и проверить правильность построения в среде электронной таблицы Microsoft Excel. (Слайд 12)
VI . Рефлексия
«Функция y=sin x, ее свойства и график»
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.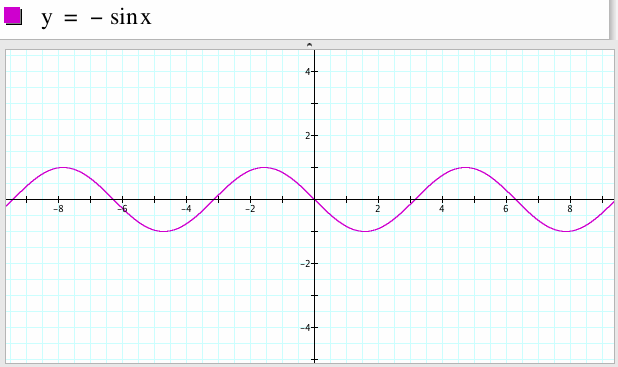
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис.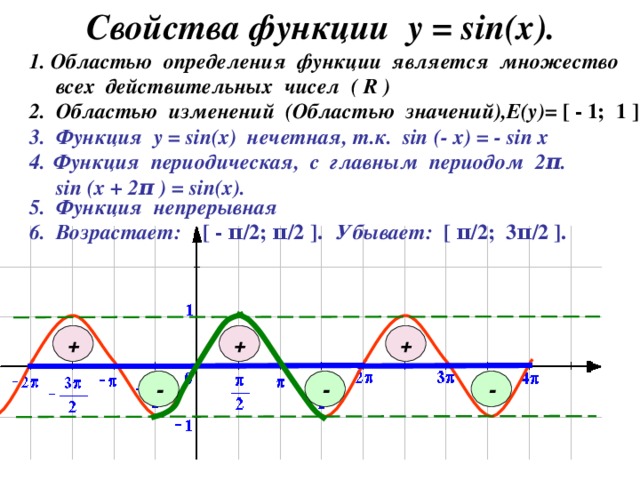 2)
2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Урок и презентация на тему: «Функция y=sin(x). Определения и свойства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.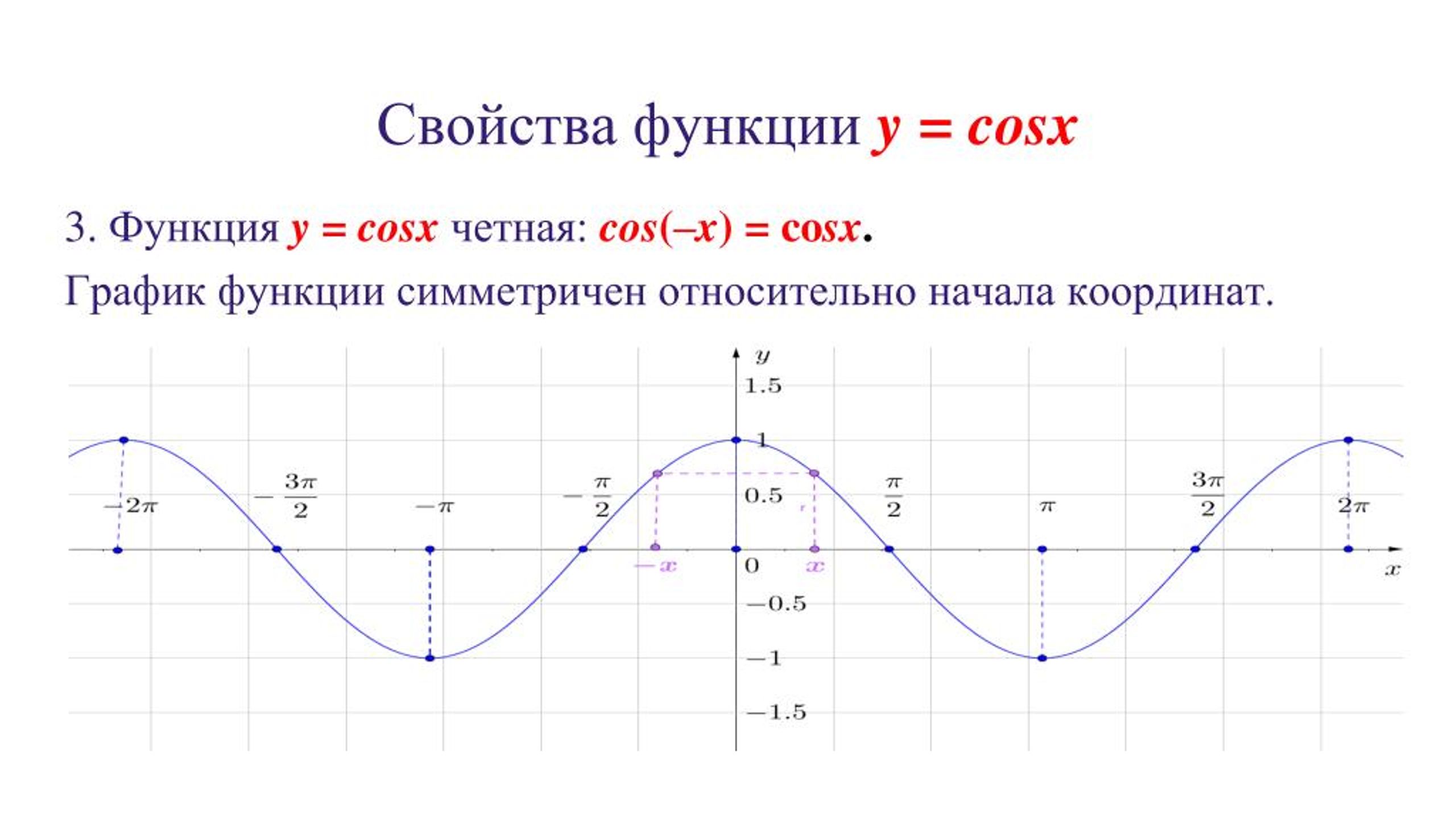 1″
1″
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk).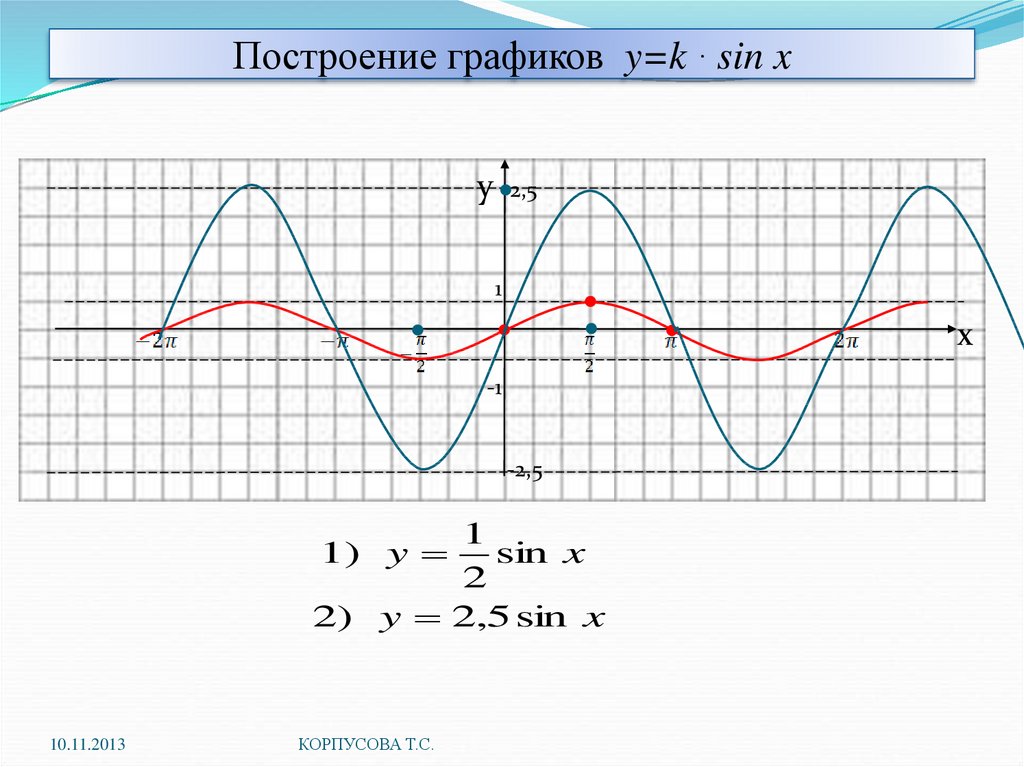 Наибольшее значение функции равно 1 (при х = π/2+ πk).
Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
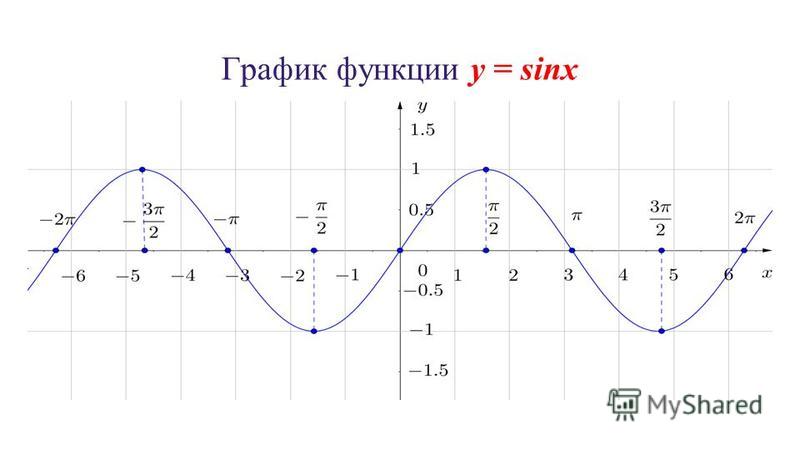
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
Свойства функции y = sin x :
3) Это нечетная функция. 4) Это непрерывная функция.
6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках функция принимает положительные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. |
Для построения графика функции y = sin x удобно применять следующие масштабы:
На листе в клетку за единицу отрезка примем длину в две клетки.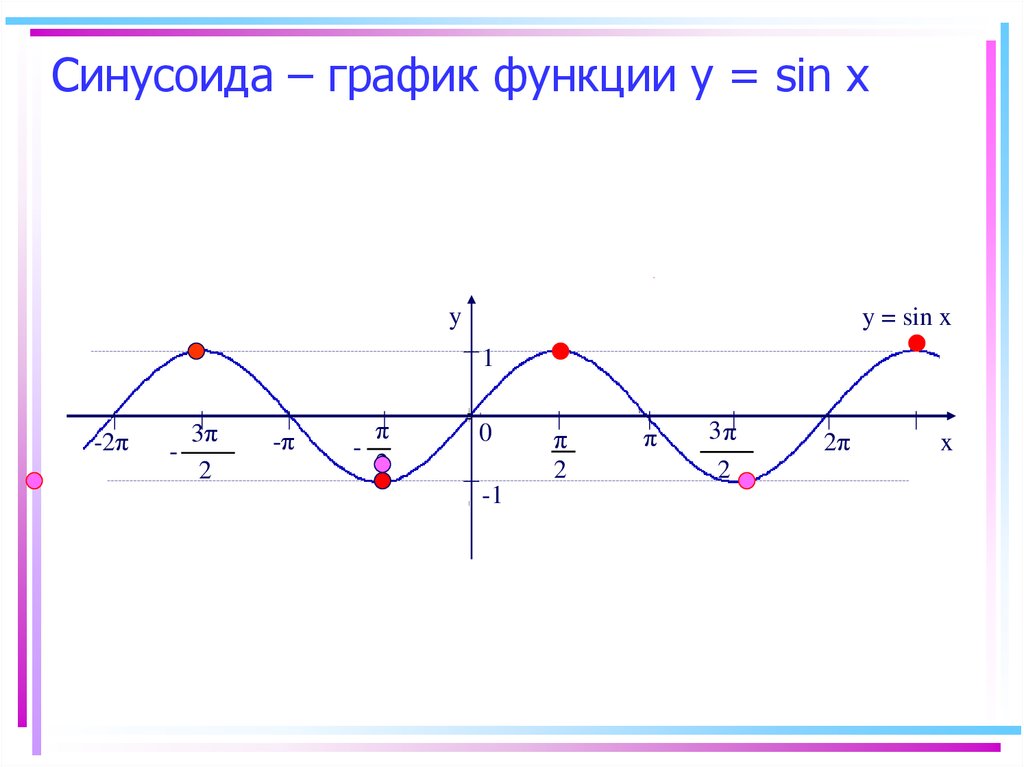
На оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x .
На оси y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x :
√3 | √3 |
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1).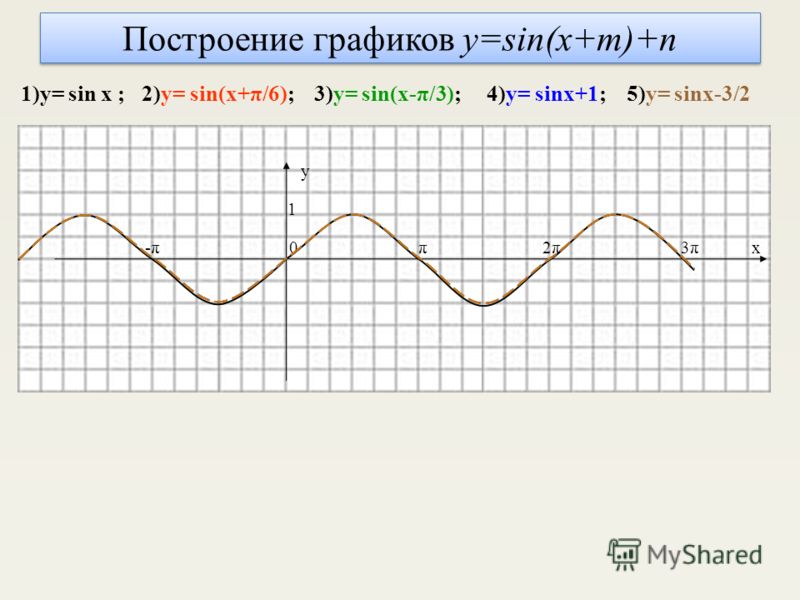 Это график функции y = sin x на отрезке . Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].
Это график функции y = sin x на отрезке . Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
Функция y = cos x .
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x :
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: 6) На отрезке функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. 9) Точки минимума функции: π + 2πn. 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, 11) Это периодическая функция с периодом 2π (Т = 2π) |
Функция y = mf (x ).
Возьмем предыдущую функцию y = cos x . Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f (kx ).
Если функция y = mf (x ) приводит к растяжению синусоиды от оси x либо сжатию к оси x , то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y .
Причем k – любое действительное число.
При 0 k y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x .
Графиком функции y = tg x является тангенсоида.
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.
Свойства функции y = tg x :
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
Свойства функции y = ctg x :
3-8преобразования синус-графа
Мы собираемся изучить графики
y = a sin(bx + c) для различных значений a, b и c и изучить влияние каждого из этих параметров.
Прежде чем я попрошу студентов изучить преобразования синусоидального графика, я попрошу их изучить преобразования функции для повторения.
Обзор: Нарисуйте график следующих функций и запишите свои наблюдения для каждой из них.
Для этого исследования я бы порекомендовал учащимся использовать какое-либо программное обеспечение для графического калькулятора. Я буду использовать программное обеспечение Graphing Calculator 4.0. Студенты могут использовать графические калькуляторы, но эти преобразования гораздо легче увидеть на экране компьютера. Function Flyer — это бесплатный апплет от Shodor, который также могут использовать студенты. Этот апплет доступен по адресу http://www.shodor.org/interactivate/activities/FunctionFlyer/
. Кроме того, этот апплет называется Math Flyer в App Store и доступен по цене 0,9 доллара США.9. Преподаватель потенциально может предложить своим ученикам выполнить это исследование с помощью своих смартфонов.
Мы хотим изучить графики
y = a sin(bx + c) и влияние параметров a, b и c.К этому моменту учащиеся должны знать, как выглядит график y = sin(x).
Фиолетовая кривая — это график синусоиды.
Красная кривая — трансформация.у = 2 sin(x)
у = ½ sin(x)
Обратите внимание, что минимальное и максимальное значения функции увеличились с -1 и 1 до -2 и 2.
Обратите внимание, что минимальное и максимальное значения функции уменьшились с -1 и 1 до -1/2 и 1/2. 909:10 На этих графиках представлены изменения амплитуды.Абсолютное значение параметра a представляет собой амплитуду графика.
= Амплитуда
Для дальнейшего изучения предложите учащимся изучить преобразования, когда a
< 0.
Из наших знаний об единичной окружности мы знаем, что период y = sin(x) равен 2π. Функция синуса начинает повторяться каждые 2π единиц. Таким образом, он завершает один цикл от 0 до 2π, другой от 2π до 4π и т. д.
у = грех(2х)
График y = sin(2x) выглядит так, будто его сжали с боков, как пружину.
Мы видим, что y=sin(2x) совершает два цикла в интервале от 0 до 2π вместо одного.у = sin(½x)
График y = sin(½x) выглядит так, как будто он растянут с боков.909:10 Мы видим, что y = sin(½x) завершает половину цикла в интервале от 0 до 2π вместо одного.
Параметр b относится к периоду синусоиды. Итак, период синусоиды равен (2π/b)
.
Обратите внимание, что на анимации выше при увеличении значения b от 0 до 5 график сжимается, а период синусоиды уменьшается.
На анимации выше обратите внимание, что при уменьшении значения b от 0 до -5 график растягивается, а период синусоиды увеличивается.Что происходит с периодом функции, когда b
< 0? Как вы думаете, как будут выглядеть графики функции y = sin(5x) и y = sin(-5x)?
у = грех(х + 2)
y = sin(x — 2)
Обратите внимание, что на графике y = sin(x + 2) синусоида сдвинута на две единицы влево.На графике y = sin(x — 2) синусоида сместилась вправо на две единицы.
Эти преобразования часто называют горизонтальными или фазовыми сдвигами.
Параметр c представляет фазовый сдвиг (также называемый сдвигом средней линии).
Я считаю, что проще сначала выполнить изменение периода, но нет определенного порядка, в котором должны выполняться эти преобразования.
b = 4, поэтому период функции равен (2π/4) = (1/2π). у = грех(4х)
Теперь давайте возьмем график выше и выполним фазовый сдвиг.c = -1, поэтому график сместился вправо на 1. y = sin(4x -1)
Наконец, давайте учтем изменение амплитуды.
a = 3, поэтому минимальное и максимальное значения равны -3 и 3. y = 3 sin(4x -1)
Следовательно, мы построили график y = 3 sin(4x -1).
Для дальнейшего исследования попросите учащихся сделать еще один шаг и предсказать влияние параметра d на графике y = a sin(bx + c) + d
Нажмите здесь, чтобы вернуться на домашнюю страницу Лейси
Тригонометрические функции
Тригонометрические функцииПроизвольные углы и единичная окружность
До сих пор мы использовали единичный круг для определения тригонометрических функций для острых углов. В следующем разделе, где мы рассмотрим косые треугольники, нам понадобятся не только острые углы. Некоторые косые треугольники тупые, и нам нужно знать синус и косинус тупых углов. Пока мы это делаем, мы также должны определить триггерные функции для углов, превышающих 180°, и для отрицательных углов. Во-первых, нам нужно понять, что такое такие углы. Древнегреческие геометры рассматривали только углы между 0° и 180°, и они не считали ни прямой угол 180°, ни вырожденный угол 0° углами.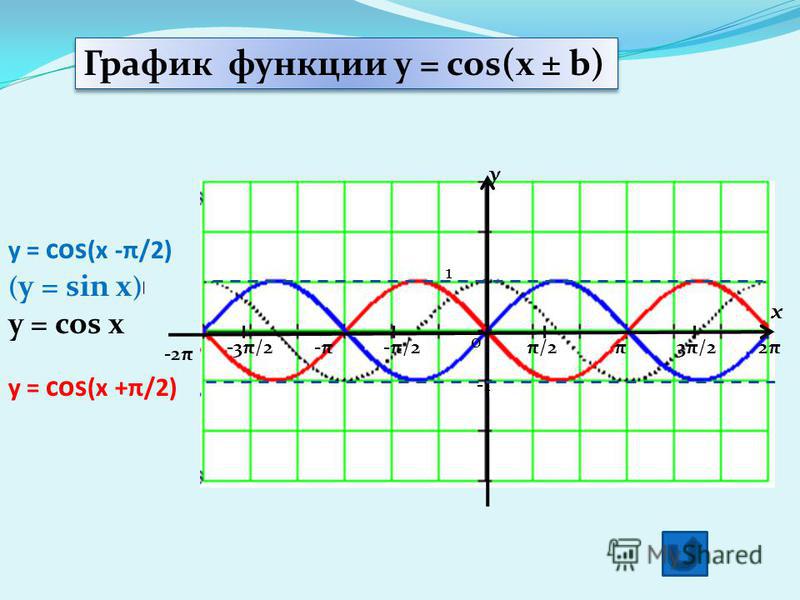 Полезно не только считать эти частные случаи углами, но также включать углы от 180° до 360°, иногда называемые «рефлекторными углами». С применением тригонометрии к предметам исчисления и дифференциальных уравнений также стали приняты углы за пределами 360 ° и отрицательные углы.
Полезно не только считать эти частные случаи углами, но также включать углы от 180° до 360°, иногда называемые «рефлекторными углами». С применением тригонометрии к предметам исчисления и дифференциальных уравнений также стали приняты углы за пределами 360 ° и отрицательные углы.
Рассмотрим единичный круг. Обозначим его центр (0,0) как O, , а точку (1,0) на нем как A. Как движущаяся точка B движется по единичной окружности, начиная с A и против часовой стрелки, угол AOB как угол 0° и увеличивается. Когда B пройдет весь круг и вернется к A, , тогда угол AOB будет равен 360°. Конечно, это тот же угол, что и угол 0°, поэтому мы можем идентифицировать эти два угла. Как B продолжаем второй раз по кругу, получаем углы от 360° до 720°. Это те же ракурсы, которые мы видели в первый раз, но у нас для них разные названия. Например, прямой угол называется либо 90°, либо 450°. Каждый раз по кругу мы получаем другое название угла.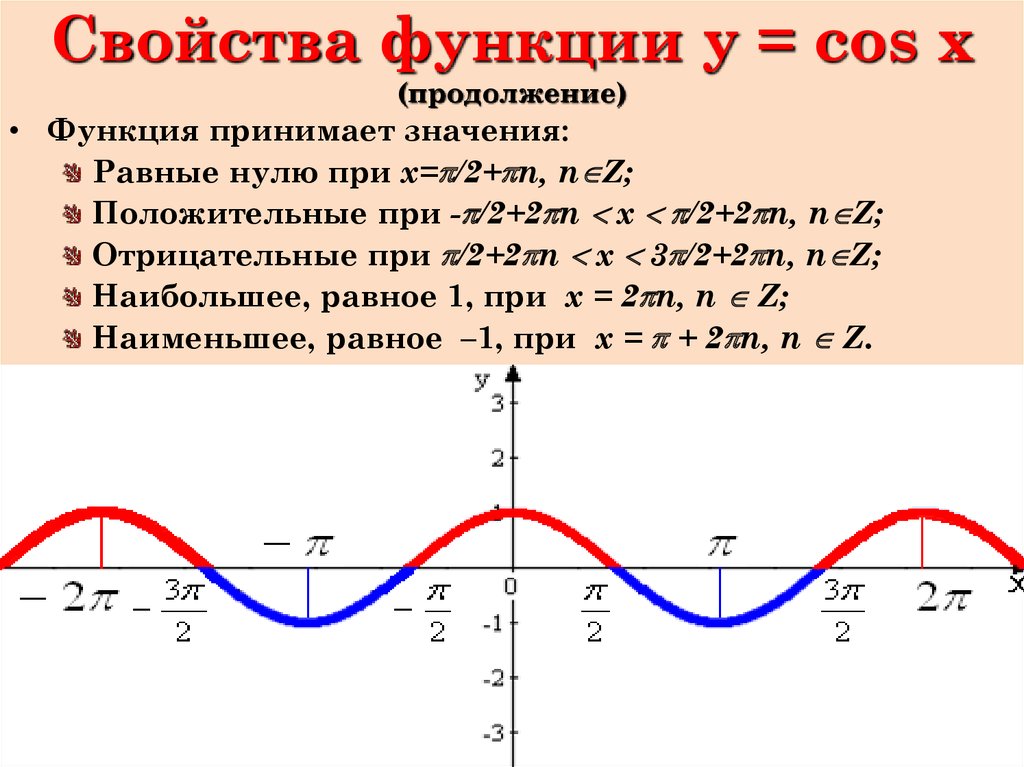 Таким образом, 90°, 450°, 810° и 1170° обозначают один и тот же угол.
Таким образом, 90°, 450°, 810° и 1170° обозначают один и тот же угол.
Если B начинается в той же точке A и движется по часовой стрелке, то мы получим отрицательные углы, а точнее имена в отрицательных градусах для тех же самых углов. Например, если вы пройдете четверть круга по часовой стрелке, угол AOB обозначен как –90°. Конечно, это то же самое, что угол 270°.
Таким образом, любой угол имеет бесконечное множество названий, но все они отличаются друг от друга на кратное 360°.
Синусы и косинусы произвольных углов
Теперь, когда мы задали произвольные углы, мы можем определить их синусы и косинусы. Пусть угол расположен так, что его вершина находится в центре единичной окружности O = (0,0), а первая сторона угла расположена вдоль x -ось. Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B для определения косинуса угла и синуса угла. В частности, координата x координаты B является косинусом угла, а координата y координатой B является синусом угла.
В частности, координата x координаты B является косинусом угла, а координата y координатой B является синусом угла.Свойства синусов и косинусов, вытекающие из этого определения
Есть несколько свойств, которые мы можем легко вывести из этого определения. Некоторые из них обобщают тождества, которые мы уже видели для острых углов.- Синус и косинус являются периодическими функциями периода 360°, то есть периода 2 π . Это потому, что синусы и косинусы определяются в терминах углов, и вы можете добавить числа, кратные 360°, или 2 π , и это не изменит угол. Таким образом, для любого угла θ ,
sin ( θ + 360°) = sin θ, и cos ( θ + 360°) = cos θ.
Многие из современных приложений тригонометрии вытекают из использования тригонометрического исчисления, особенно те приложения, которые имеют дело непосредственно с тригонометрическими функциями.
 Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается какsin ( θ + 2 π ) = sin θ, и cos ( θ + 2 π ) 9 1 = 101 θ1 θ1 θ1 θ1 θ1
- Синус и косинус дополняют друг друга:
cos θ = sin ( π /2 – θ ) sin θ = cos ( π /2 – θ )
Мы видели это раньше, но теперь у нас есть это для любого угла θ. Это правда, потому что когда вы отражаете плоскость через диагональную линию y = x, угол заменяется его дополнением.
- Тождество Пифагора для синусов и косинусов следует непосредственно из определения. Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 =1.
 Но координаты косинус и синус, так что делаем вывод
Но координаты косинус и синус, так что делаем выводsin 2 θ + cos 2 θ = 1, Теперь мы готовы рассмотреть синус и косинус как функции.
- Синус — нечетная функция, а косинус — четная функция. Возможно, вы не встречали этих прилагательных «нечетный» и «четный» применительно к функциям, но знать их важно. Функция f называется нечетной функцией , если для любого числа x, f (– x ) = – f ( x ). Функция f называется четной функцией , если для любого числа x, f (– x ) = f ( x ). Большинство функций не являются ни нечетными, ни четными функциями, но некоторые из наиболее важных функций являются либо теми, либо другими. Любой полином только с нечетными степенями является нечетной функцией, например, f ( x ) = x 5 + 8 x 3 – 2 x.
 (Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5.
(Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5.Синус — нечетная функция, а косинус — четная
sin (– θ ) = –sin θ, и cos (– θ ) = cos θ.
Эти факты следуют из симметрии единичного круга относительно оси x . Угол — t — это тот же угол, что и t , за исключением того, что он находится на другой стороне оси x . Переворот точки ( x,y ) на другую сторону оси x превращает ее в ( x,–y ), поэтому координата y инвертируется, то есть синус инвертируется , но x -координата остается прежней, то есть косинус не меняется.
- Очевидным свойством синусов и косинусов является то, что их значения лежат в диапазоне от –1 до 1.
 Каждая точка на единичной окружности удалена от начала координат на 1 единицу, поэтому координаты любой точки также находятся в пределах 1 от 0.
Каждая точка на единичной окружности удалена от начала координат на 1 единицу, поэтому координаты любой точки также находятся в пределах 1 от 0.
Графики функций синуса и косинуса
Возьмем t в качестве переменного угла. Вы можете думать о и и как об угле, и как о времени. Хороший способ для человека понять функцию — посмотреть на ее график. Начнем с графика sin т. Возьмите горизонтальную ось за ось t (а не ось x , как обычно), возьмите вертикальную ось за ось y и постройте уравнение y = sin t . Выглядит так. Во-первых, обратите внимание, что это периодический период 2 π . Геометрически это означает, что если вы возьмете кривую и сдвинете ее 2 π влево или вправо, то кривая вернется сама на себя. Во-вторых, обратите внимание, что график находится в пределах одной единицы т -ось. Мало что еще очевидно, за исключением того, где оно увеличивается и уменьшается. Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Далее давайте посмотрим на график косинуса. Снова возьмем горизонтальную ось за ось t , но теперь возьмем вертикальную ось за ось x и нарисуем уравнение 9.1101 x = cos t.
Обратите внимание, что он выглядит точно так же, как график sin t , за исключением того, что он сдвинут влево на π /2. Это из-за тождества cos t = sin ( π /2 + t ). Хотя мы раньше не встречались с этим тождеством, оно легко следует из тех, что мы видели: π /2 + t ).
Графики функций тангенса и котангенса
График функции тангенса имеет вертикальную асимптоту при x = π /2. Это связано с тем, что тангенс стремится к бесконечности, когда t приближается к π /2. (На самом деле, оно приближается к минус бесконечности, поскольку t приближается к π /2 справа, как вы можете видеть на графике.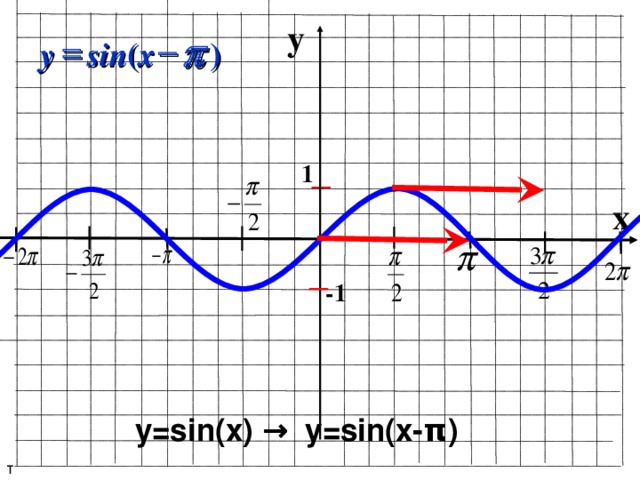
Вы также можете видеть, что тангенс имеет период π ; есть также вертикальные асимптоты через каждые π единиц слева и справа. Алгебраически эта периодичность выражается как тангенс ( t + π ) = тангенс t.
График для котангенса очень похож.
Это сходство просто потому, что котангенс t является тангенсом дополнительного угла π – t.
Графики функций секанса и косеканса
Секанс является обратной величиной косинуса, и поскольку косинус принимает значения только между –1 и 1, следовательно, секанс принимает значения только выше 1 или ниже –1, как показано на графике. Также секанс имеет период 2 π .Как и следовало ожидать, график косеканса очень похож на график секанса.
Графики функций синуса и косинуса · Алгебра и тригонометрия
Графики функций синуса и косинуса · Алгебра и тригонометрияВ этом разделе вы:
- Графические варианты
y=sin(x)
и
y=cos(x).

- Использовать фазовые сдвиги синусоидальных и косинусоидальных кривых.
Белый свет, такой как свет солнца, на самом деле вовсе не белый. Вместо этого это композиция всех цветов радуги в виде волн. Отдельные цвета можно увидеть, только когда белый свет проходит через оптическую призму, которая разделяет волны в соответствии с их длинами волн, образуя радугу.
Световые волны могут быть представлены графически с помощью функции синуса. В главе о тригонометрических функциях мы рассмотрели тригонометрические функции, такие как функция синуса. В этом разделе мы будем интерпретировать и создавать графики функций синуса и косинуса.
График функций синуса и косинуса
Напомним, что функции синуса и косинуса связывают действительные числовые значения с координатами x и y точки на единичной окружности. Так как же они выглядят на графике в координатной плоскости? Начнем с функция синуса .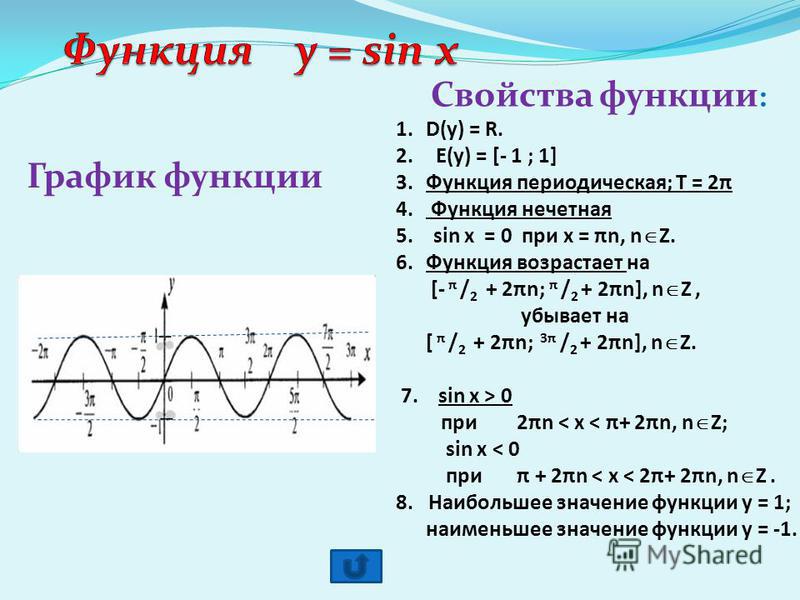 Мы можем создать таблицу значений и использовать их для построения графика. [ссылка] перечисляет некоторые значения функции синуса на единичном круге.
Мы можем создать таблицу значений и использовать их для построения графика. [ссылка] перечисляет некоторые значения функции синуса на единичном круге.
|
х| 0
| |
sin(x)| 0
Нанесение точек из таблицы и продолжение вдоль оси x дает форму функции синуса. См. [ссылка].
Обратите внимание, что значения синуса положительны между 0 и π,
, которые соответствуют значениям функции синуса в квадрантах I и II на единичной окружности, а значения синуса отрицательны между π
и 2π,
, которые соответствуют значениям функции синуса в квадрантах III и IV на единичной окружности. См. [ссылка].
Теперь давайте аналогично посмотрим на функцию косинуса . Опять же, мы можем создать таблицу значений и использовать их для построения графика. [ссылка] перечисляет некоторые значения функции косинуса на единичном круге.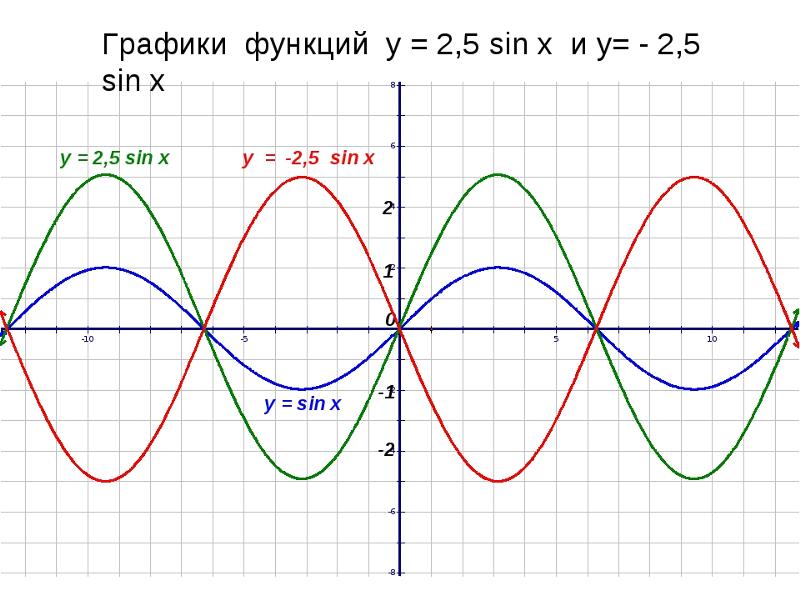
| кос(х) |
Как и в случае функции синуса, мы можем нанести точки на график функции косинуса, как показано в [ссылка].
Поскольку мы можем вычислить синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Думая о значениях синуса и косинуса как о координатах точек на единичной окружности, становится ясно, что диапазоном обеих функций должен быть интервал [−1,1].
На обоих графиках форма графика повторяется через 2π,
, что означает периодичность функций с периодом 2π.
Периодическая функция — это функция, для которой определенное горизонтальное смещение , P приводит к функции, равной исходной функции: f(x+P)=f(x)
для всех значений x
в области f.
Когда это происходит, мы называем наименьшее такое горизонтальное смещение с P>0
период функции.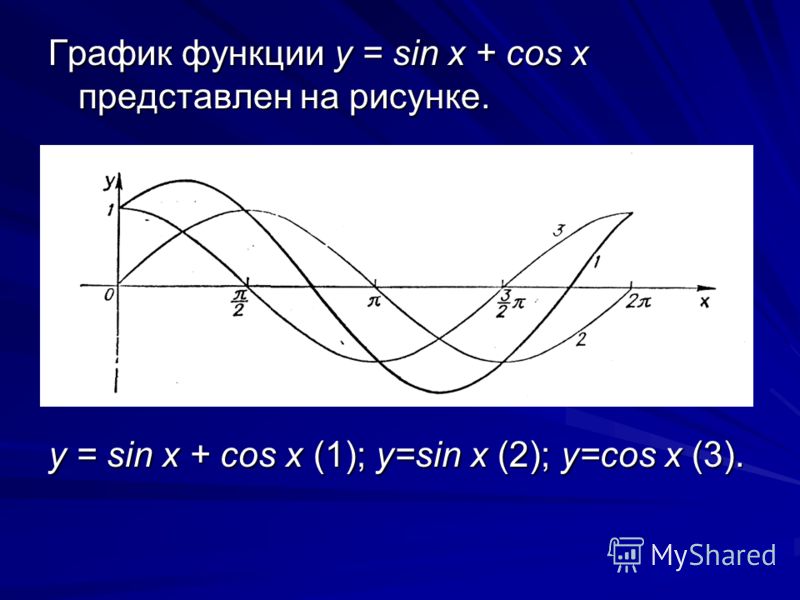 [ссылка] показывает несколько периодов функций синуса и косинуса.
[ссылка] показывает несколько периодов функций синуса и косинуса.
Повторный взгляд на функции синуса и косинуса в области с центром на оси y помогает обнаружить симметрию. Как мы видим в [ссылка], синусоидальная функция симметрична относительно начала координат. Напомним из книги «Другие тригонометрические функции», что мы определили по единичному кругу, что синусоидальная функция является нечетной функцией, поскольку sin(−x)=−sin x.
Теперь мы можем ясно увидеть это свойство на графике.
[ссылка] показывает, что функция косинуса симметрична относительно оси и . Опять же, мы определили, что функция косинуса является четной функцией. Теперь из графика видно, что cos(−x)=cos x.
Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько различных характеристик:
- Они являются периодическими функциями с периодом
2π.

- Домен каждой функции
(−∞,∞)
и диапазон
[−1,1]. - График y=sin x 90 947 симметрична относительно начала координат, потому что это нечетная функция.
- График
y=cos x
симметричен относительно
ось y-, потому что это четная функция.
Исследование синусоидальных функций
Как мы видим, функции синуса и косинуса имеют правильный период и диапазон. Если мы понаблюдаем за океанскими волнами или рябью на пруду, мы увидим, что они напоминают функции синуса или косинуса. Однако они не обязательно идентичны. Некоторые выше или длиннее других. Функция, которая имеет ту же общую форму, что и синус или 9Функция косинуса 1495 известна как синусоидальная функция . Общие формы синусоидальных функций
y=Asin(Bx−C)+D andy=Acos(Bx−C)+D
Определение периода синусоидальных функций
Глядя на формы синусоидальных функций, мы можем видеть, что они являются преобразованиями функций синуса и косинуса.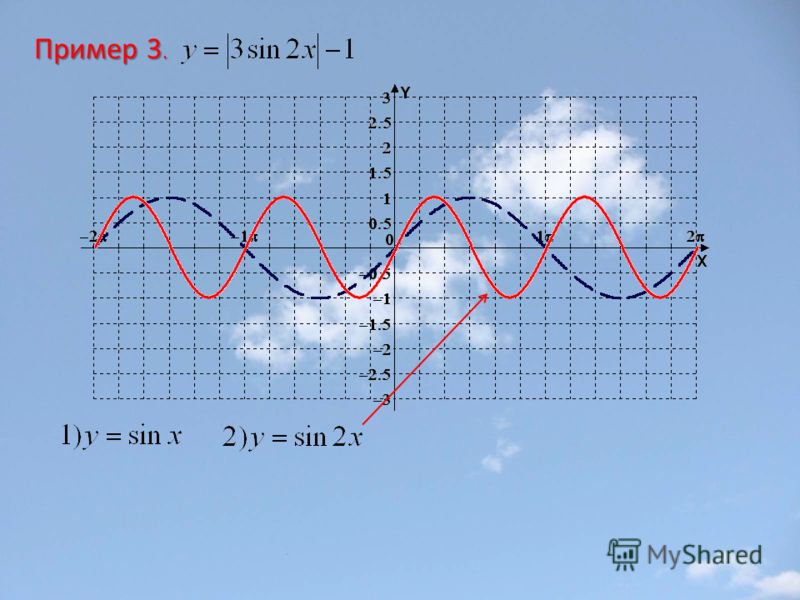 Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле B
связано с периодом соотношением P=2π\|B\|.
Если \|B\|>1,
, то период меньше 2π
и функция подвергается горизонтальному сжатию, тогда как если \|B\|<1,
, то период больше 2π
, и функция подвергается горизонтальному растяжению. Например, f(x)=sin(x),
B=1,, поэтому период равен 2π,
., который мы знали. Если f(x)=sin(2x),
, тогда B=2,
, поэтому период π
.и график сжат. Если f(x)=sin(x2),
, тогда B=12,
, поэтому период 4π
.и график растянут. Обратите внимание на [ссылка], как период косвенно связан с \|B\|.
Период синусоидальных функций
Если положить C=0
и D=0
в уравнениях синуса и косинуса общего вида, то получим формы
y=Asin(Bx)
(Bx)
Период равен 2π\|B\|.
Определение периода функции синуса или косинуса
Определение периода функции f(x)=sin(π6x).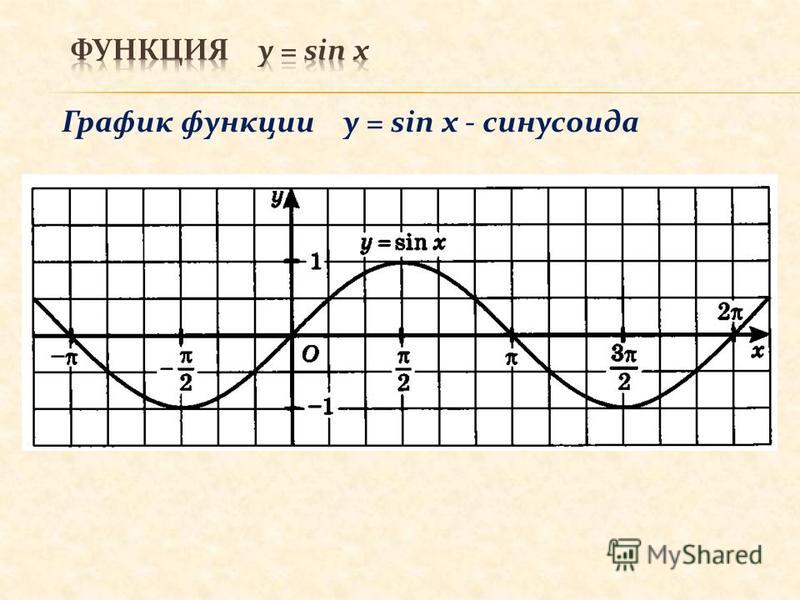
Начнем со сравнения уравнения с общей формой y=Asin(Bx).
В данном уравнении B=π6,
, поэтому период будет равен
P=2π\|B\| =2ππ6 =2π⋅6π =12
Определите период функции g(x)=cos(x3).
6π
Определение амплитуды
Возвращаясь к общей формуле для синусоидальной функции, мы проанализировали, как переменная B
относится к периоду. Теперь обратимся к переменной A
., поэтому мы можем проанализировать, как это связано с амплитудой или наибольшим расстоянием от покоя. А
представляет коэффициент вертикального растяжения, а его абсолютное значение \|A\|
— это амплитуда. Локальные максимумы будут на расстоянии \|A\|
выше горизонтальной средней линии графика, которая представляет собой линию y=D;
, потому что D=0
в данном случае средняя линия это x -ось. Локальные минимумы будут на таком же расстоянии ниже средней линии.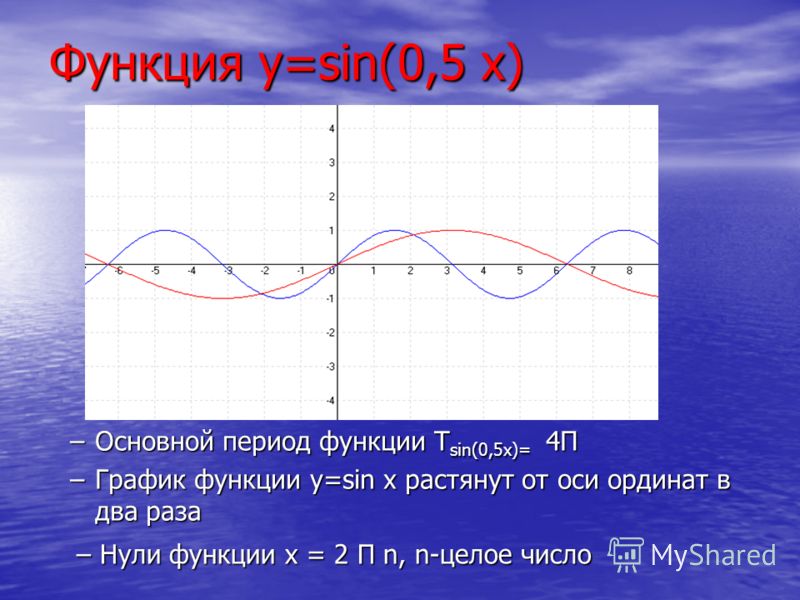 Если \|A\|>1,
Если \|A\|>1,
функция растянута. Например, амплитуда f(x)=4 sin x
в два раза больше амплитуды f(x)=2 sin x.
Если \|А\|<1,
функция сжата. [ссылка] сравнивает несколько синусоидальных функций с разными амплитудами.
Амплитуда синусоидальной функции
Если в уравнениях синусоидальной и косинусоидальной функций общего вида положить C=0
и D=0
, то получим формы
y=Asin(Bx) и y=Acos(Bx)
Амплитуда равна A,
, а высота по вертикали от средней линии равна \|A\|.
Кроме того, обратите внимание, что в примере
\|A\| = амплитуда = 12\|максимум – минимум\|
Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции f(x)=−4sin(x)?
Функция растянута или сжата по вертикали?
Начнем со сравнения функции с упрощенной формой y=Asin(Bx).
В заданной функции A=−4,
, поэтому амплитуда равна \|A\|=\|−4\|=4.
Функция растянута.
Анализ
Отрицательное значение A
приводит к отражению по оси x синусоидальной функции , как показано на [ссылка].
Какова амплитуда синусоидальной функции f(x)=12sin(x)?
Функция растянута или сжата по вертикали?
12
сжатый
Анализ графиков вариаций
y = sin x и y = cos xТеперь, когда мы понимаем, как A
и В
относятся к уравнению общей формы для функций синуса и косинуса, мы будем исследовать переменные C
и Д.
Вызов общей формы:
y=Asin(Bx−C)+D и y=Acos(Bx−C)+Dory=Asin(B(x−CB))+D и y=Acos(B(x−CB))+D
Значение CB
для синусоидальной функции называется фазовым сдвигом или горизонтальным смещением основного синуса или косинусной функцией . Если C>0,
Если C>0,
график смещается вправо. Если C<0,
график смещается влево. Чем больше значение \|C\|,
, тем больше сдвигается график. [ссылка] показывает, что график f(x)=sin(x−π)
сдвигается вправо на π
единиц, что больше, чем мы видим на графике f(x)=sin(x−π4),
, что сдвигается вправо на π4
единиц.
Пока C
относится к сдвигу по горизонтали, D
указывает вертикальное смещение от средней линии в общей формуле для синусоидальной функции. См. [ссылка]. Функция y=cos(x)+D
имеет среднюю линию в точке y=D.
Любое значение D
, кроме нуля, сдвигает график вверх или вниз. [ссылка] сравнивает f(x)=sin x
с f(x)=sin x+2,
, который смещен на 2 единицы вверх на графике.
Вариации функций синуса и косинуса
Для данного уравнения в форме f(x)=Asin(Bx−C)+D
или f(x)=Acos(Bx−C)+D,
CB
это фазовый сдвиг и D
это вертикальный сдвиг .
Определение фазового сдвига функции
Определите направление и величину фазового сдвига для f(x)=sin(x+π6)−2.
Начнем с сравнения уравнения с общей формой y=Asin(Bx−C)+D.
Обратите внимание, что в данном уравнении B=1
и C=−π6.
Таким образом, фазовый сдвиг равен
CB=-π61 =-π6
или π6
единиц влево.
Анализ
Мы должны обратить внимание на знак в уравнении для общего вида синусоидальной функции. Уравнение показывает знак минус перед C.
Следовательно, f(x)=sin(x+π6)−2
можно переписать как f(x)=sin(x−(−π6))−2.
Если значение C
отрицательный, сдвиг влево.
Определите направление и величину фазового сдвига для f(x)=3cos(x−π2).
№2;
справа
Определение вертикального сдвига функции
Определите направление и величину вертикального сдвига для f(x)=cos(x)−3.
Начнем со сравнения уравнения с общей формой y=Acos(Bx−C)+D.
В приведенном уравнении D=−3
, поэтому сдвиг составляет 3 единицы вниз.
Определите направление и величину вертикального смещения для f(x)=3sin(x)+2.
2 шт. до
Дана синусоидальная функция в виде f(x)=Asin(Bx−C)+D,
определить срединную линию, амплитуду, период и фазовый сдвиг.
- Определите амплитуду как \|А\|.
- Определить период как Р=2π\|В\|.
- Определите фазовый сдвиг как КБ.
- Определите среднюю линию как у=Д.
Идентификация вариаций синусоидальной функции из уравнения
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции y=3sin(2x)+1.
Начнем с сравнения уравнения с общей формой y=Asin(Bx−C)+D.
A=3,
, значит, амплитуда \|A\|=3.
Далее, B=2,
, поэтому период равен P=2π\|B\|=2π2=π.
В скобках нет добавленной константы, поэтому C=0
, а фазовый сдвиг CB=02=0.
Наконец, D=1,
, поэтому средняя линия y=1.
Анализ
Изучая график, мы можем определить, что период равен π,
, средняя линия y=1,
, а амплитуда равна 3. См. [ссылка].
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции y=12cos(x3−π3).
средняя линия: y=0;
амплитуда: \|A\|=12;
период: P=2π\|B\|=6π;
фазовый сдвиг: CB=π
Определение уравнения для синусоидальной функции на графике
Определите формулу для функции косинуса в [ссылка].
Чтобы определить уравнение, нам нужно идентифицировать каждое значение в общем виде синусоидальной функции.
y=Asin(Bx-C)+Dy=Acos(Bx-C)+D
График может представлять функцию синуса или косинуса , которая сдвинута и/или отражена. При x=0,
график имеет крайнюю точку, (0,0).
Поскольку функция косинуса имеет крайнюю точку при x=0,
, запишем наше уравнение в терминах функции косинуса.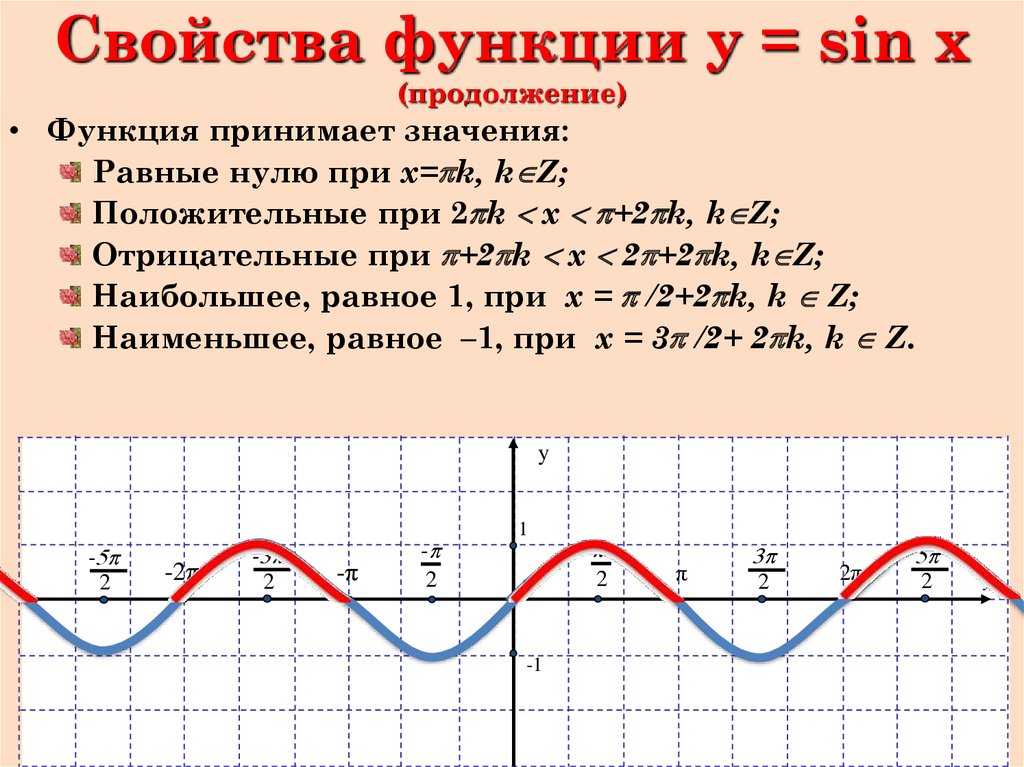
Начнем со средней линии. Мы видим, что график поднимается и опускается на одинаковое расстояние выше и ниже y=0,5.
Это значение, которое является средней линией, равно D
в уравнении, поэтому D=0,5.
Наибольшее расстояние выше и ниже средней линии — это амплитуда. Максимумы на 0,5 единицы выше средней линии, а минимумы на 0,5 единицы ниже средней линии. Значит \|А\|=0,5.
Другой способ определить амплитуду — это признать, что разница между высотой локальных максимумов и минимумов равна 1, поэтому \|A\|=12=0,5.
Кроме того, график отражается относительно оси x , так что A=-0,5.
График не растягивается и не сжимается по горизонтали, поэтому B=1;
, а график не смещен по горизонтали, поэтому C=0.
Собираем все вместе,
g(x)=−0,5cos(x)+0,5
Определите формулу для функции синуса в [ссылка].
f(x)=sin(x)+2
Определение уравнения для синусоидальной функции на графике
Определите уравнение для синусоидальной функции в [ссылка].
При максимальном значении 1 и наименьшем значении −5
средняя линия будет на полпути между −2.
So D=−2.
Расстояние от средней линии до самого высокого или самого низкого значения дает амплитуду \|A\|=3.
Период графика равен 6, который можно измерить от пика при x=1
до следующего пика при x=7,
или от расстояния между нижними точками. Следовательно, P=2π\|B\|=6.
Используя положительное значение для B,
, мы находим, что
B=2πP=2π6=π3
На данный момент наше уравнение имеет вид либо y=3sin(π3x−C)−2
, либо y=3cos(π3x −С)−2.
Для формы и смещения у нас есть более одного варианта. Мы могли бы записать это как любое из следующего:
- косинус, сдвинутый вправо
- отрицательный косинус сдвинут влево
- синус смещен влево
- отрицательный синус сдвинут вправо
Хотя любое из этих значений было бы правильным, в данном случае с косинусными сдвигами работать легче, чем с синусоидальными, поскольку они включают целые числа.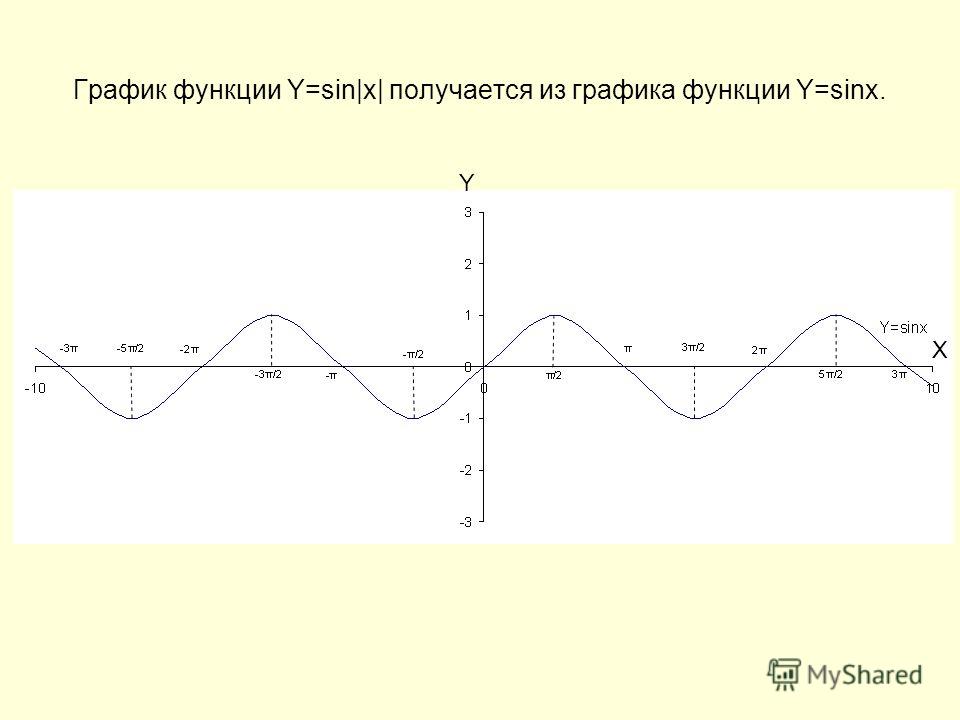 Таким образом, наша функция принимает вид
Таким образом, наша функция принимает вид
y=3cos(π3x−π3)−2 или y=−3cos(π3x+2π3)−2
Опять же, эти функции эквивалентны, поэтому обе дают один и тот же график.
Напишите формулу для функции, изображенной на [ссылка].
две возможности: y=4sin(π5x−π5)+4
или y=−4sin(π5x+4π5)+4
Графические варианты
y = sin x и y = cos xВ этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков. Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общей формы
y=Asin(Bx−C)+D и y=Acos(Bx−C)+D,
мы допустим C=0
и D=0
и работать с упрощенной формой уравнений в следующих примерах.
**Для функции y=Asin(Bx),
нарисуйте ее график.**
- Определите амплитуду,
\|А\|.

- Определите период, Р=2π\|В\|.
- Начать с исходной точки, функция увеличивается вправо, если
A
положительно или уменьшается, если
Аотрицательный.
- В
х=π2\|В\|
есть локальный максимум для
A>0или минимум для
А<0,с
у=А. - Кривая возвращается к оси x в точке х=π\|В\|.
- Существует локальный минимум для
A>0
(максимум для
A<0) в
х=3π2\|В\|с
у=-А. - Кривая снова возвращается к x — ось на х=2π\|В\|.
Построение графика функции и определение амплитуды и периода
Нарисуйте график f(x)=−2sin(πx2).
Давайте начнем со сравнения уравнения с формой y=Asin(Bx).
- Шаг 1. Из уравнения видно, что
A=−2,
, поэтому амплитуда равна 2,
.
\|А\|=2
- Шаг 2. Уравнение показывает, что
В=π2,
, значит период
P=2ππ2 =2π⋅2π =4
- Шаг 3. Потому что
A
отрицательно, график опускается по мере продвижения вправо от начала координат.
- Шаги 4–7. Отрезки размером x находятся в начале одного периода,
x=0,
горизонтальные средние точки находятся на
x=2и в конце периода
х=4.
Четверть точек включает минимум при x=1
и максимум при x=3.
Локальный минимум будет на 2 единицы ниже средней линии, при x=1,
, а локальный максимум будет на 2 единицы выше средней линии, при x=3.
[ссылка] показывает график функции.
Нарисуйте график g(x)=−0,8cos(2x).
Определение средней линии, амплитуды, периода и фазового сдвига.
средняя линия: y=0;
амплитуда: \|A\|=0,8;
период: P=2π\|B\|=π;
фазовый сдвиг: CB=0
или нет
Дана синусоидальная функция со сдвигом по фазе и по вертикали, нарисуйте ее график.
- Выразите функцию в общем виде y=Asin(Bx−C)+D или y=Acos(Bx−C)+D.
- Определить амплитуду, \|А\|.
- Определите период, Р=2π\|В\|.
- Определить фазовый сдвиг, КБ.
- Нарисуйте график
f(x)=Asin(Bx)
сдвинут вправо или влево на
CBи вверх или вниз на
Д.
Построение преобразованной синусоиды
Нарисуйте график f(x)=3sin(π4x−π4).
- Шаг 1. Функция уже написана в общем виде:
f(x)=3sin(π4x−π4).
Этот график будет иметь форму синусоидальной функции , начиная со средней линии и увеличиваясь вправо.
- Шаг 2.
 \|А\|=\|3\|=3.
\|А\|=\|3\|=3.Амплитуда равна 3.
- Шаг 3. С
\|B\|=\|π4\|=π4,
период определяем следующим образом.
P=2π\|B\|=2ππ4=2π⋅4π=8
Период равен 8.
- Шаг 4. С
C=π4,
фазовый сдвиг равен
КБ=π4π4=1.
Фазовый сдвиг составляет 1 единицу.
- Шаг 5. [ссылка] показывает график функции.
Нарисуйте график зависимости g(x)=−2cos(π3x+π6).
Определение средней линии, амплитуды, периода и фазового сдвига.
средняя линия: y=0;
амплитуда: \|A\|=2;
период: P=2π\|B\|=6;
фазовый сдвиг: CB=−12
Идентификация свойств синусоидальной функции
Дано y=−2cos(π2x+π)+3,
определить амплитуду, период, фазовый сдвиг и сдвиг по горизонтали. Затем постройте график функции.
Начните со сравнения уравнения с общей формой и выполните шаги, описанные в [ссылка].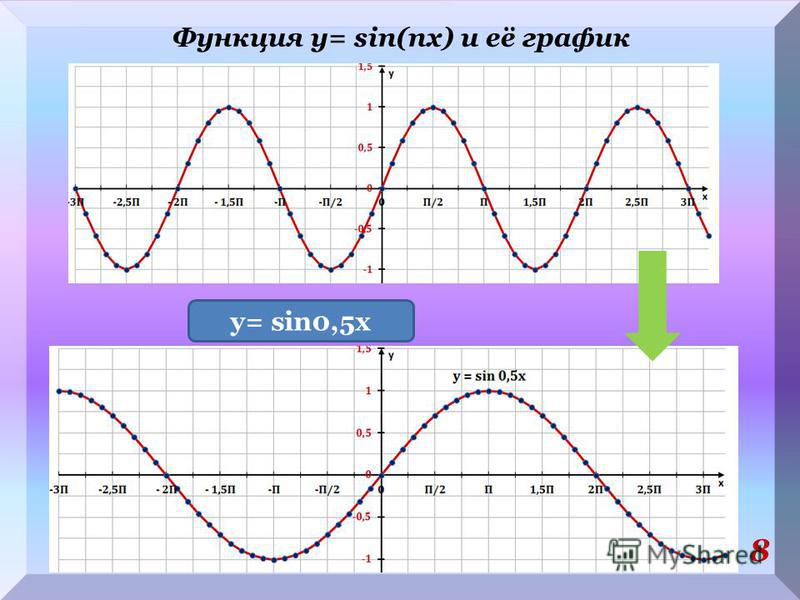
y=Acos(Bx−C)+D
Поскольку A
отрицательно, график функции косинуса отражается относительно оси x .
[ссылка] показывает один цикл графика функции.
Использование преобразования функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение может быть смоделировано с помощью функции синуса или косинуса .
Нахождение вертикальной составляющей кругового движения
Точка вращается вокруг окружности радиуса 3 с центром в начале координат. Нарисуйте график зависимости координаты y точки от угла поворота.
Напомним, что для точки на окружности радиусом r координата y точки равна y=r sin(x),
, поэтому в этом случае мы получаем уравнение y(x) =3 sin(x).
Константа 3 вызывает вертикальное растяжение y -значений функции в 3 раза, что мы можем видеть на графике в [ссылка].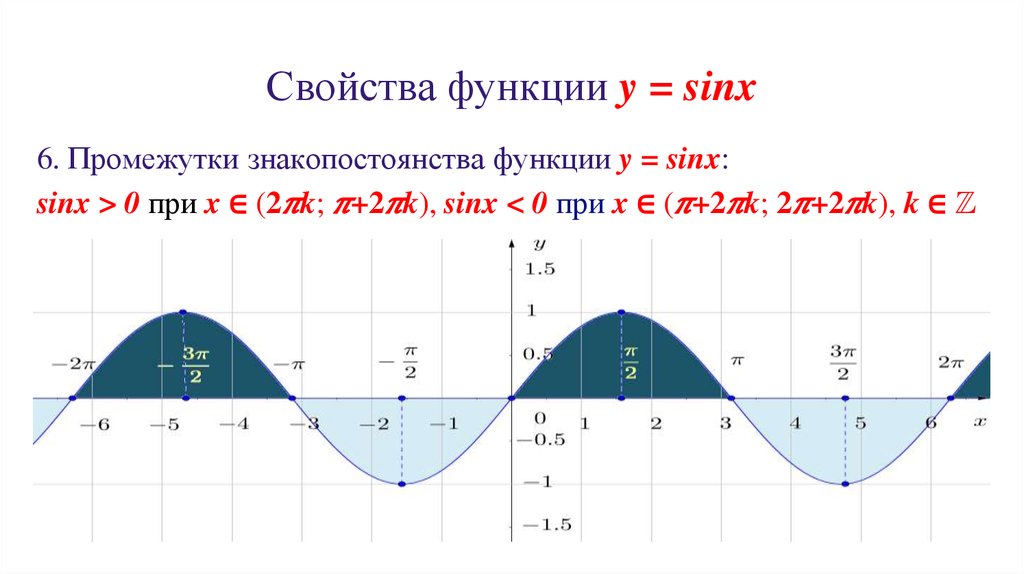
Анализ
Обратите внимание, что период функции по-прежнему 2π;
, путешествуя по кругу, мы возвращаемся в точку (3,0)
for x=2π,4π,6π,….
Поскольку выходные данные графика теперь будут колебаться между –3
и 3,
амплитуда синусоиды равна 3,
Какова амплитуда функции f(x)=7cos(x)?
Нарисуйте график этой функции.
7
Нахождение вертикальной составляющей кругового движения
Окружность радиусом 3 фута установлена так, что ее центр находится на расстоянии 4 фута от земли. Ближайшая к земле точка помечена P , как показано на [ссылка]. Нарисуйте график высоты над землей точки P
при вращении окружности; затем найдите функцию, которая дает высоту через угол поворота.
Зарисовывая высоту, мы отмечаем, что она начинается на 1 футе над землей, затем увеличивается до 7 футов над землей и продолжает колебаться на 3 фута выше и ниже центрального значения 4 фута, как показано на [ ссылка на сайт].
Хотя мы могли бы использовать преобразование функции синуса или косинуса, мы начнем с поиска характеристик, которые облегчили бы использование одной функции по сравнению с другой. Давайте воспользуемся функцией косинуса, поскольку она начинается с наибольшего или наименьшего значения, а Функция синуса начинается со среднего значения. Стандартный косинус начинается с самого высокого значения, а этот график начинается с самого низкого значения, поэтому нам нужно включить вертикальное отражение.
Во-вторых, мы видим, что график колеблется на 3 выше и ниже центра, а базовый косинус имеет амплитуду 1, поэтому этот график вертикально растянут на 3, как в последнем примере.
Наконец, чтобы переместить центр круга на высоту 4, график был сдвинут по вертикали вверх на 4. Объединяя эти преобразования, мы находим, что
у=-3cos(x)+4
Груз прикреплен к пружине, которая затем подвешена к доске, как показано на [ссылка]. Когда пружина колеблется вверх и вниз, положение y
Когда пружина колеблется вверх и вниз, положение y
груза относительно доски изменяется от –1
дюймов (в момент времени x=0)
до –7
дюймов (в момент времени x=π )
под платой. Предположим, что положение y
задано как синусоидальная функция x.
Нарисуйте график функции, а затем найдите функцию косинуса, которая дает положение y
в пересчете на x.
y=3cos(x)−4
Определение роста наездника на колесе обозрения
Лондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся с платформы на высоте 2 метра над землей. Выразите высоту всадника над землей как функцию времени в минутах.
При диаметре 135 м колесо имеет радиус 67,5 м. Высота будет колебаться с амплитудой 67,5 м выше и ниже центра.
Посадка пассажиров на высоте 2 м над уровнем земли, поэтому центр колеса должен располагаться 67,5+2=69,5
м над уровнем земли. Средняя линия колебаний будет на высоте 69,5 м.
Средняя линия колебаний будет на высоте 69,5 м.
Колесу требуется 30 минут, чтобы совершить 1 оборот, поэтому высота будет колебаться с периодом 30 минут.
И наконец, поскольку всадник садится в самую нижнюю точку, высота начинается с наименьшего значения и увеличивается в соответствии с формой вертикально отраженной косинусоидальной кривой.
- Амплитуда:
67,5
, значит
А=67,5 - Средняя линия:
69,5
, значит
Д=69,5 - Период:
30
, значит
В=2π30=π15 - Форма: −cos(t)
Уравнение для роста всадника будет следующим:
y=-67,5cos(π15t)+69,5
, где t
в минутах, а y
в метрах.
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с графиками функций синуса и косинуса.
- Амплитуда и период синуса и косинуса
- Преобразование синуса и косинуса
- Графические преобразования синуса и косинуса
- График функции синуса
Ключевые уравнения
Ключевые понятия
- Периодические функции повторяются после заданного значения. Наименьшей такой величиной является период. Основные функции синуса и косинуса имеют период 2π.
- Функция
sin x
нечетно, поэтому его график симметричен относительно начала координат. Функция
cos xчетно, поэтому его график симметричен относительно оси y .
- График синусоидальной функции имеет ту же общую форму, что и синусоидальная или косинусоидальная функция.
- В общей формуле синусоидальной функции период равен
Р=2π\|В\|.
См. [ссылка].
- В общей формуле синусоидальной функции
\|А\|
представляет амплитуду. Если
\|A\|>1,функция растягивается, тогда как если
\|A\|<1,функция сжата. См. [ссылка].
- Значение
CB
в общей формуле для синусоидальной функции указывает на фазовый сдвиг.
 См. [ссылка].
См. [ссылка]. - Значение
D
в общей формуле синусоидальной функции указывает на сдвиг по вертикали от средней линии. См. [ссылка].
- Комбинации вариаций синусоидальных функций могут быть обнаружены из уравнения. См. [ссылка].
- Уравнение синусоидальной функции можно определить по графику. См. [ссылка] и [ссылка].
- График функции можно изобразить, определив ее амплитуду и период. См. [ссылка] и [ссылка].
- Функцию также можно изобразить в виде графика, определив ее амплитуду, период, фазовый сдвиг и сдвиг по горизонтали. См. [ссылка].
- Синусоидальные функции можно использовать для решения реальных задач. См. [ссылка], [ссылка] и [ссылка].
Секционные упражнения
Устный
Почему функции синуса и косинуса называются периодическими функциями?
Функции синуса и косинуса обладают тем свойством, что f(x+P)=f(x)
для определенного P.
Это означает, что значения функции повторяются для каждого P
единиц по оси x .
Как график y=sin x
сравнивается с графиком y=cos x?
Объясните, как можно горизонтально перевести график y=sin x
, чтобы получить y=cos x.
Для уравнения A cos(Bx+C)+D,
какие константы влияют на диапазон функции и как они влияют на диапазон?
Абсолютное значение константы A
(амплитуда) увеличивает общий диапазон и константу D
(сдвиг по вертикали) сдвигает график по вертикали.
Как диапазон переведенной синусоидальной функции связан с уравнением y=A sin(Bx+C)+D?
Как можно использовать единичный круг для построения графика f(t)=sin t?
В точке, где конечная сторона t
пересекает единичную окружность, можно определить, что sin t
равно y -координате точки.
Графический
Для следующих упражнений нарисуйте два полных периода каждой функции и укажите амплитуду, период и среднюю линию. Укажите максимум и минимум y -значений и соответствующие им x -значения на одном периоде для x>0.
При необходимости округлить ответы до двух знаков после запятой.
f(x)=2sin x
f(x)=23cos x
амплитуда: 23;
период: 2π;
средняя линия: y=0;
максимум: y=23
происходит при x=0;
минимум: y=−23
происходит при x=π;
за один период, график начинается с 0 и заканчивается на 2π
f(x)=−3sin x
f(x)=4sin x
амплитуда: 4; период: 2π;
средняя линия: y=0;
максимум y=4
происходит при x=π2;
минимум: y=−4
происходит при x=3π2;
один полный период происходит от x=0
до x=2π
f(x)=2cos x
f(x)=cos(2x)
амплитуда: 1; период: π;
средняя линия: y=0;
максимум: y=1
происходит при x=π;
минимум: y=−1
происходит при x=π2;
один полный период построен на графике от x=0
до x=π
f(x)=2 sin(12x)
f(x)=4 cos(πx)
амплитуда: 4; период: 2; средняя линия: y=0;
максимум: y=4
происходит при x=0;
минимум: y=−4
происходит при x=1
f(x)=3 cos(65x)
y=3 sin(8(x+4))+5
амплитуда: 3; период: π4;
средняя линия: y=5;
максимум: y=8
происходит при x=0,12;
минимум: y=2
встречается при x=0,516;
сдвиг по горизонтали: −4;
вертикальное перемещение 5; один период происходит от x=0
до x=π4
y=2 sin(3x−21)+4
y=5 sin(5x+20)−2
амплитуда: 5; период: 2π5;
средняя линия: y=−2;
максимум: y=3
происходит при x=0,08;
минимум: y=−7
происходит при x=0,71;
фазовый сдвиг: −4;
вертикальное перемещение: −2;
один полный период можно изобразить на графике x=0
до x=2π5
Для следующих упражнений нарисуйте один полный период каждой функции, начиная с x=0.
Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x за один период для x>0.
Укажите фазовый сдвиг и вертикальное смещение, если применимо. При необходимости округлить ответы до двух знаков после запятой.
f(t)=2sin(t−5π6)
f(t)=−cos(t+π3)+1
амплитуда: 1 ; период: 2π;
средняя линия: y=1;
максимум: y=2
происходит при x=2,09;
максимум: y=2
происходит при t=2,09;
минимум: y=0
происходит при t=5,24;
фазовый сдвиг: −π3;
вертикальное перемещение: 1; один полный период от t=0
до t=2π
f(t)=4cos(2(t+π4))−3
f(t)=−sin(12t+5π3)
амплитуда: 1; период: 4π;
средняя линия: y=0;
максимум: y=1
происходит при t=11,52;
минимум: y=−1
происходит при t=5,24;
фазовый сдвиг: −10π3;
вертикальное смещение: 0
f(x)=4sin(π2(x−3))+7
Определите амплитуду, среднюю линию, период и уравнение, включающее функцию синуса, для графика, показанного на [ссылка].
амплитуда: 2; средняя линия: y=-3;
период: 4; уравнение: f(x)=2sin(π2x)−3
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на [ссылка].
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на [ссылка].
амплитуда: 2; период: 5; средняя линия: y=3;
уравнение: f(x)=−2cos(2π5x)+3
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на [ссылка].
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на [ссылка].
амплитуда: 4; период: 2; средняя линия: y=0;
уравнение: f(x)=−4cos(π(x−π2))
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на [ссылка].
Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на [ссылка].
амплитуда: 2; период: 2; срединная линия y=1;
уравнение: f(x)=2cos(πx)+1
Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на [ссылка].
Алгебраический
Для следующих упражнений пусть f(x)=sin x.
On [0,2π),
решить f(x)=0.
On [0,2π),
решить f(x)=12.
№6,5π6
Вычислить f(π2).
On [0,2π),f(x)=22.
Найти все значения x.
π4,3π4
On [0,2π),
максимальное значение(я) функции происходит(я) при каком x -значении?
On [0,2π),
минимальное значение(я) функции происходит(ются) при каком x — значение(я)?
3π2
Покажите, что f(−x)=−f(x).
Это означает, что f(x)=sin x
является нечетной функцией и обладает симметрией относительно ________________.
Для следующих упражнений пусть f(x)=cos x.
On [0,2π),
решить уравнение f(x)=cos x=0.
π2,3π2
On [0,2π),
решить f(x)=12.
On [0,2π),
найти x -пересечений f(x)=cos x.
№2,3π2
On [0,2π),
найти x -значений, при которых функция имеет максимальное или минимальное значение.
On [0,2π),
решают уравнение f(x)=32.
№6,11π6
Технология
График h(x)=x+sin x
on [0,2π].
Объясните, почему график выглядит именно так.
График h(x)=x+sin x
on [−100,100].
Отобразился ли график так, как предполагалось в предыдущем упражнении?
График кажется линейным. Линейные функции преобладают в форме графика при больших значениях x.
График f(x)=x sin x
on [0,2π]
и опишите, как график отличается от графика f(x)=sin x.
График f(x)=x sin x
в окне [−10,10]
и объясните, что показывает график.
График симметричен относительно оси y и не имеет амплитуды, поскольку функция не является периодической.
График f(x)=sin xx
в окне [−5π,5π]
и объясните, что показывает график.
Реальные приложения
Колесо обозрения имеет диаметр 25 метров и садится на платформу, которая находится на высоте 1 метр над землей. Шесть часов на колесе обозрения находятся на одном уровне с грузовой платформой. Колесо совершает 1 полный оборот за 10 минут. Функция h(t)
дает рост человека в метрах над землей t минуты после начала вращения колеса.
- Найдите амплитуду, среднюю линию и период ч(т).
- Найдите формулу для функции высоты ч(т).
- На какой высоте над землей находится человек через 5 минут?
- Амплитуда: 12,5; период: 10; средняя линия: у=13,5;
- h(t)=12,5sin(π5(t−2,5))+13,5;
- 26 футов
Глоссарий
- амплитуда
- вертикальная высота функции; постоянная
A
появляется в определении синусоидальной функции
- средняя линия
- горизонтальная линия
y=D,
, где
Dпоявляется в общей форме синусоидальной функции
- периодическая функция
- а функция
f(x)
, что удовлетворяет
f(x+P)=f(x)для конкретной константы
Pи любое значение
х
- фазовый сдвиг
- горизонтальное смещение основной функции синуса или косинуса; постоянная КБ
- синусоидальная функция
- любая функция, которая может быть выражена в виде
f(x)=Asin(Bx−C)+D
или
f(x)=Acos(Bx−C)+D
Эта работа находится под лицензией Creative Commons Attribution 4.
 0 International License.
0 International License.Вы также можете скачать бесплатно по адресу http://cnx.org/contents/[email protected]
Атрибуция:
- По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
- Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом: Колледж OpenStax, алгебра и тригонометрия. OpenStax CNX. http://cnx.org/contents/[email protected].
- Если вы распространяете этот учебник в печатном формате, вы должны указать на каждой физической странице следующее указание авторства: «Скачать бесплатно на http://cnx.org/contents/[email protected].»
- Если вы повторно распространяете часть этого учебника, вы должны сохранять при каждом просмотре страницы в цифровом формате (включая, помимо прочего, EPUB, PDF и HTML) и на каждой физической печатной странице следующее указание авторства:
«Загрузите бесплатно по адресу http://cnx.
 org/contents/[email protected]».
org/contents/[email protected]».
Графики синуса, косинуса
Графики синуса, косинуса| Графики синусоиды и косинуса |
График синусоидальных кривых
Основная синусоида: f(x) = sin x .
Поскольку мера радиана представляет длину, а также вращение (углы),
мы выражаем наши значения x в радианах и наши значения y в значениях sin x .
Используя этот подход, мы можем построить графики триггерных функций.
Из значений x и y из единичный круг мы знаем:
| sin 0 = 0 | sin или /2 = 1 | sin или = 0 | sin 3 o /2 = -1 |
Здесь мы видим два цикла f(x) = sin x .
Этот шаблон будет бесконечно повторяться вправо и влево.
Как видите, домен — это R , диапазон — это [-1, 1].
Существует бесконечно много нулей , каждый из которых расположен в середине
между ближайшим максимумом и минимумом .
Свойства циклических триггерных графов по-прежнему включают в себя все элементы прежнего списка (то есть: домен, диапазон, максимум, минимум, возрастание, убывание и знаки), но также включают:
амплитуда, период, частота, фазовый сдвиг и вертикальное смещение.
(информацию см. в файле урока tr4.2 свойства синусоидальных кривых)
Пример 1: Построим график f(x) = 2 sin 4(x + o /2) + 1
| амплитуда: 2 | период: | 2 о/4 | = о/2 | фазовый сдвиг: -о/2 | вертикальный перевод: 1 |
| начальная точка = (- o /2, 1) | г макс = 3 | y min = -1 | |
Как видно из графика, линия y = 1 образует горизонтальную ось кривой.
Находим начальную и конечную точки цикла, делим интервал
на 4 равные части, затем нарисуйте кривую.
Примечание : Чтобы разделить интервал на 4 равные части, найдите начальную и конечную точки, найдите их середину, затем найдите оставшиеся 2 средние точки.
Пример 2: Построим еще одну синусоиду.
График f(x) = -4 sin 3(x — o /3) — 2
| амплитуда: 4 | период: | 2 о/3 | = 2o/3 | фазовый сдвиг = o /3 | вертикальный перевод: -2 |
| начальная точка = ( o /3, -2) | г макс = 2 | y мин = -6 | |
, так как a < 0, кривая уменьшится до своего минимального значения, прежде чем подняться до максимального.
Отдельная точка = ( O /3, -2), ПЕРИОД = 2 O 9299 /3, 9294 O 9299 /3, 9294 O 9299 /3, 9294 O 9299 /3, 9294 O 9299 /3, 9294 O 9299 /3, 9294 O 9299 /3, 9294 . о /3 = о .
Прим.2995 /6 , поэтому мы просто добавляем или /6 к каждому значению x.
Середина между началом и концом равна
(o/6 + o/3 = o/2) и (o/6 + 2 o/3 = 5 o/6).
Вертикальное смещение равно -2, поэтому горизонтальной осью кривой является линия y = -2.
.
.
График косинусоидальных кривых:
Кривая функции косинуса изоморфна кривой синусоидальной функции, которая была сдвинута назад или сдвинута по фазе на o /2 единиц влево. Другими словами, кривая косинуса начинается с максимального или минимального значения. Давайте посмотрим на y = cos x , а затем обсудим свойства функции.
Давайте посмотрим на y = cos x , а затем обсудим свойства функции.
Как видите, кривая начинается с максимума, если a > 0 .
Если a < 0, кривая начинается с минимума.
Период, амплитуда, фазовый сдвиг и вертикальное смещение идентичны синусоиде.
(информацию см. в файле урока tr4.2 свойства синусоидальных кривых)
.
Построим график y = -3 cos 2(x + o /3) — 1 .
| ампер : 3 | период: или | фазовый сдвиг: — или /3 | верт. транс: -1 |
| максимальное значение y = 2 | минимальное значение у = -4 | начальная точка: (- o /3, -4) | конечная точка: (2 или /3, -4) |
* Примечание : параметр b не влияет на кривую так же, как на синусоиду.
Поскольку cos x является положительным ( > 0) в 1-м и 4-м квадратах, когда b является отрицательным, это не меняет форму или начальную точку кривой косинуса.
.
Практика
1/ Нарисуйте один цикл функции f(x) = 4 sin ( = x + o /8) + 3 .
Перечислите амплитуду, период, фазовый сдвиг, максимум, минимум и вертикальное смещение.
.
2/ Нарисуйте один цикл функции g(x) = — 3 cos (2x + o ) — 5 .
Перечислите амплитуду, период, фазовый сдвиг, максимум, минимум и вертикальное смещение.
( для дополнительной практики см. файл урока tr536qz: викторина по триггерам в Trig MathRoom)
.
Решения
1/ f(x) = 4 sin ( = x + o /8) + 3 становится f(x) = 4 sin ¼ ( x + o /2) + 3
| amp : 4, сначала вверх | период: 8 или | фазовый сдвиг: -о/2 | верт. |

 Область определения
Область определения 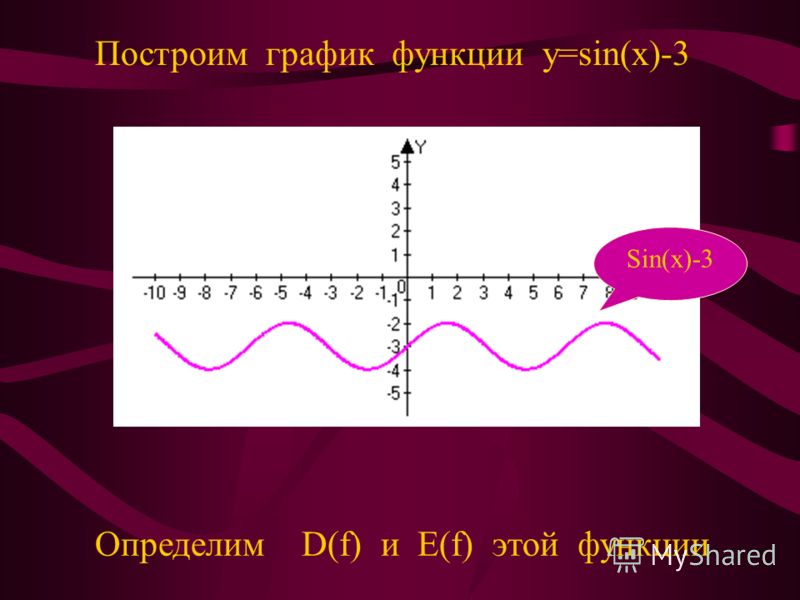 Экстремумы функции
Экстремумы функции 
 RU
RU
 Область определения
Область определения  Экстремумы функции
Экстремумы функции 
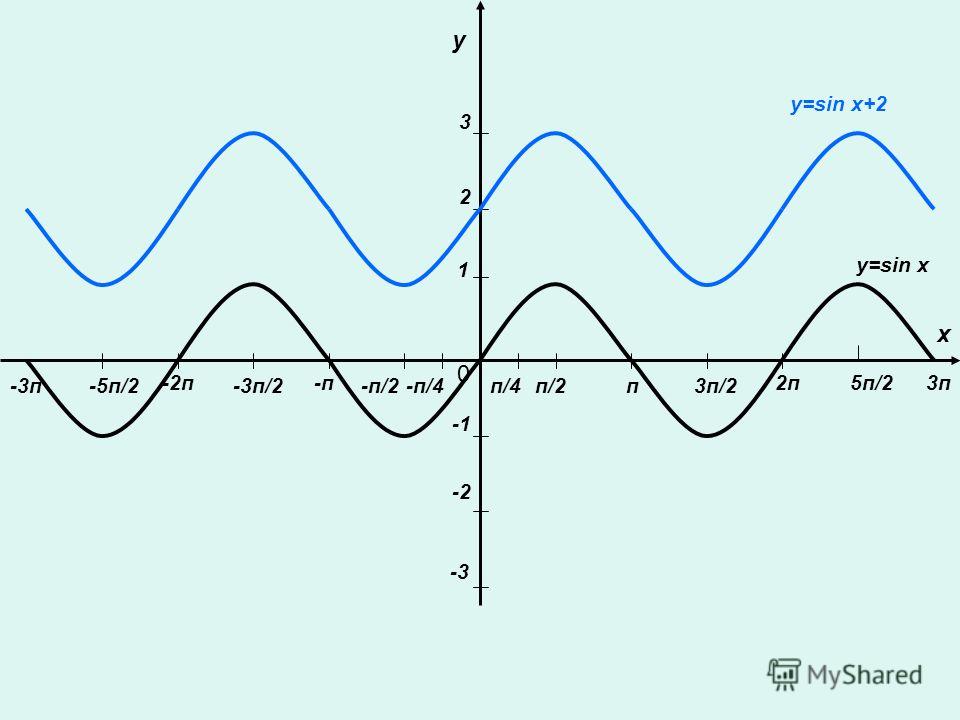


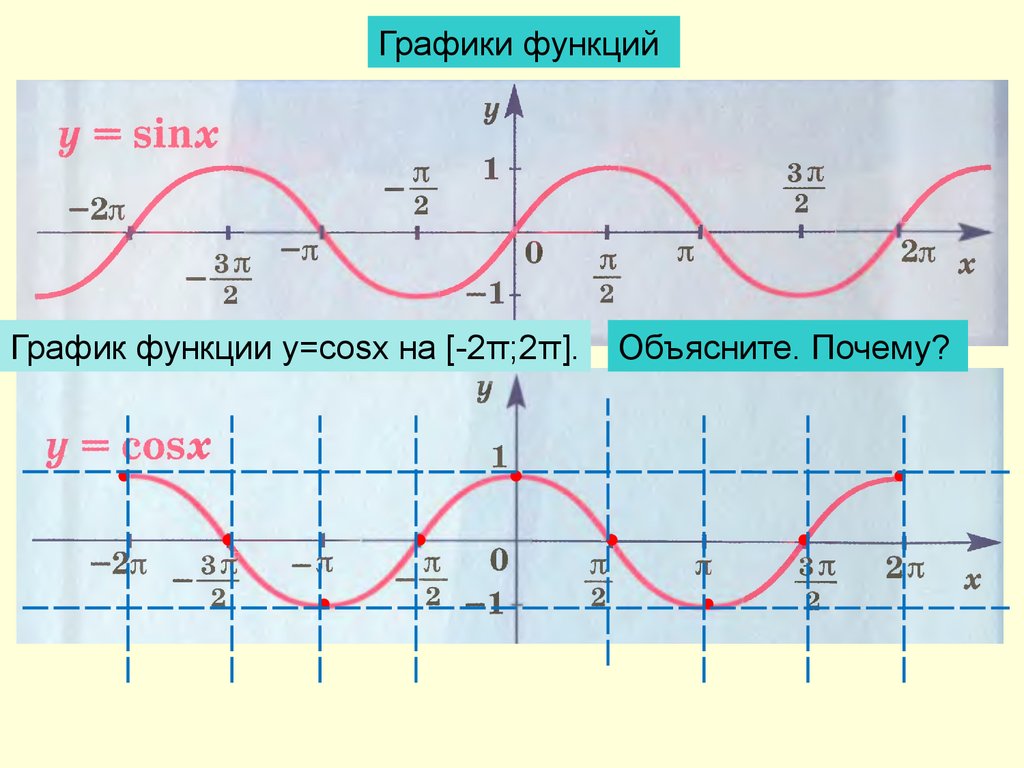 909:10 Мы видим, что y = sin(½x) завершает половину цикла в интервале от 0 до 2π вместо одного.
909:10 Мы видим, что y = sin(½x) завершает половину цикла в интервале от 0 до 2π вместо одного. 
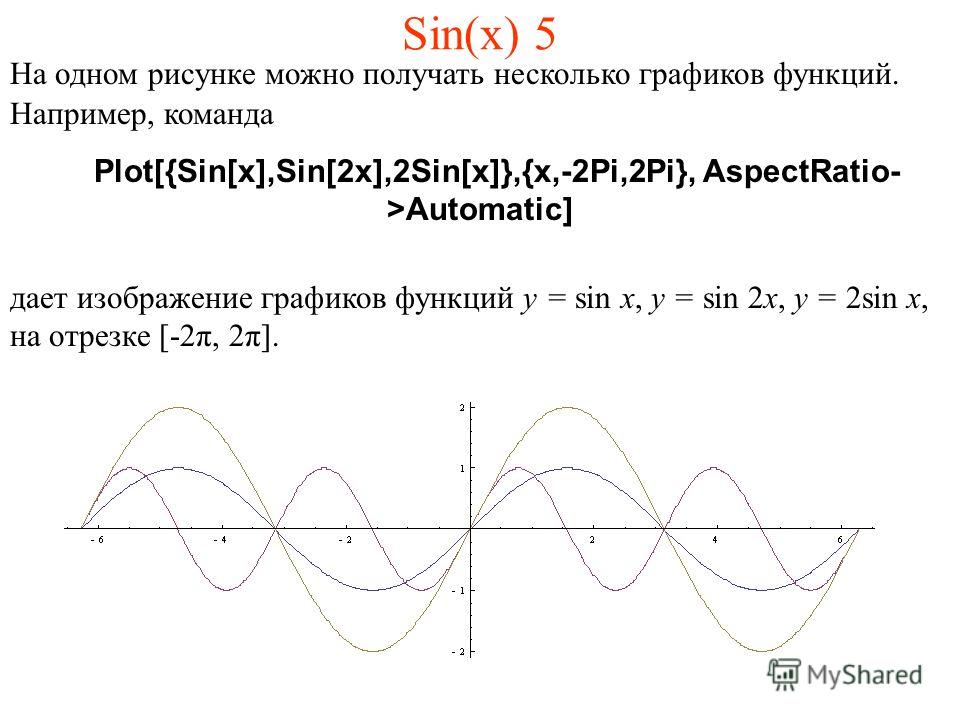
 Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается как Но координаты косинус и синус, так что делаем вывод
Но координаты косинус и синус, так что делаем вывод (Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5.
(Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5. Каждая точка на единичной окружности удалена от начала координат на 1 единицу, поэтому координаты любой точки также находятся в пределах 1 от 0.
Каждая точка на единичной окружности удалена от начала координат на 1 единицу, поэтому координаты любой точки также находятся в пределах 1 от 0.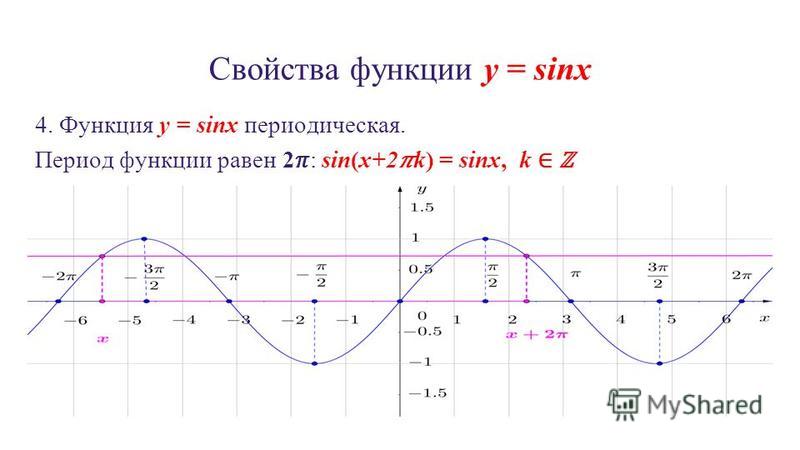


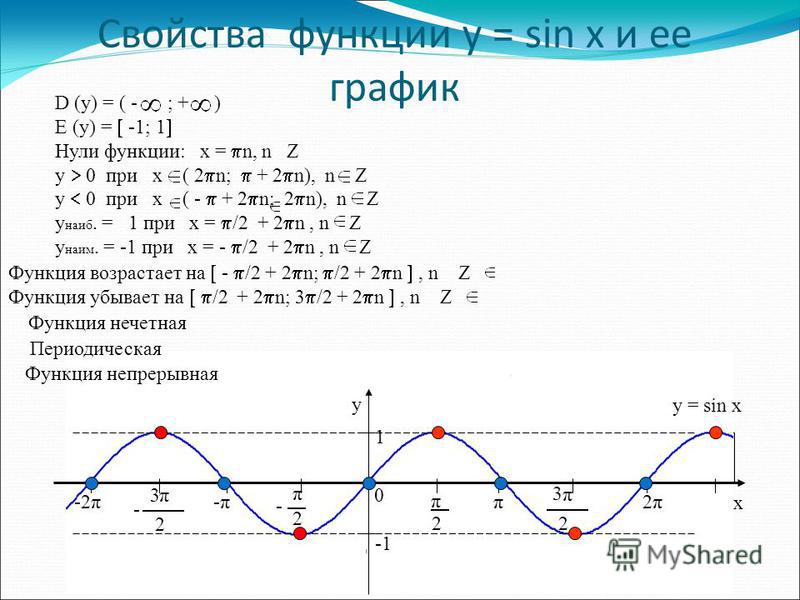
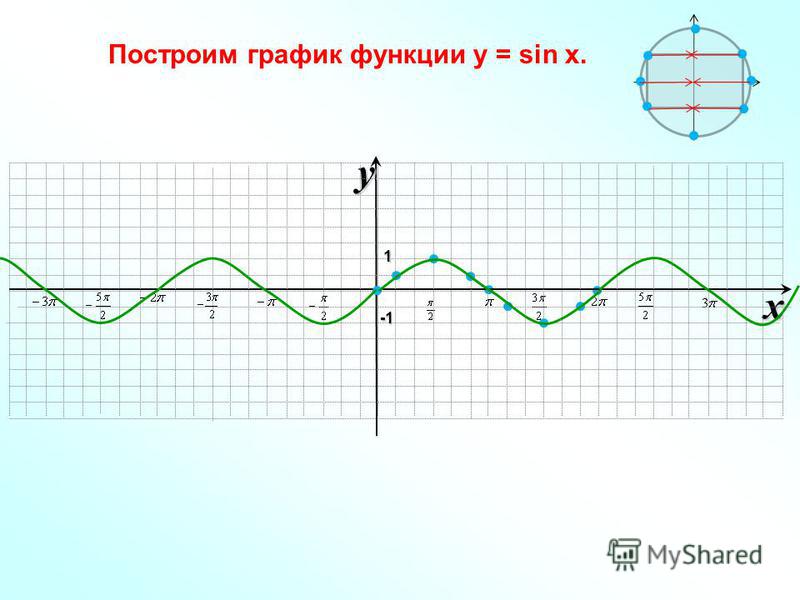 \|А\|=\|3\|=3.
\|А\|=\|3\|=3.