VII.1. Формы записи комплексных чисел и действия над ними
(схема 43)
Комплексным числом называется выражение вида z=x+iy, (7.1) где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы i2=–1. (7.2) Если x=0, то число 0+iy=iy называется чисто мнимым; если y=0, то число x+i∙0=x отождествляется с действительным числом x, а это означает, что множество  Число x называется действительной частью комплексного числа z и обозначается x=Re z, а y – мнимой частью комплексного числа z и обозначается y=Im z. Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются равными (z1=z2) тогда, когда равны их действительные и мнимые части: x1=x2, y1=y2. В частности, комплексное число z=x+iy равно нулю, когда x=y=0. Понятия «больше» и «меньше» для комплексных чисел не вводятся. Числа z=x+iy и называются комплексно сопряженными. Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости x0y такой,
что x=Re z, y=Im z. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z=x+0∙y= Комплексное
число z=x+iy можно задавать с помощью радиус-вектора . Длина вектора , изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r. Величина
угла между положительным направлением действительной оси и вектором называется аргументом комплексного
числа, обозначается Arg z или φ. Для комплексного числа z=0 аргумент не определен. Аргумент комплексного числа – величина многозначная и определяется с точностью до слагаемого 2πk (k=0;–1;1;–2;2…): , где arg z – главное значение аргумента , заключенное в промежутке (–π;π). Иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0;2π). Алгебраической формой комплексного числа называется запись числа z в виде z=x+iy. Модуль r и аргумент φ можно рассматривать как полярные координаты вектора , изображающего комплексное число z=x+iy (см. рис. 7.1). Тогда из соотношений сторон в прямоугольном треугольнике получаем . Следовательно, комплексное число z=x+iy можно записать в виде или . Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r=|z| однозначно определяется по формуле . (7.4) Аргумент определяется из формул: . (7.5) При переходе от
алгебраической формы комплексного числа к тригонометрической достаточно
определить главное значение аргумента комплексного числа z, то есть
считать φ=arg z. Знаки полученных значений cos φ и sin φ по
формулам (7. Используя формулу Эйлера , (7.6) комплексное число можно записать в так называемой показательной (или экспоненциальной) форме z=reiφ, (7.7) где r=|z| — модуль комплексного числа, а угол (k=0; Функция eiφ – периодическая с основным периодом 2π, поэтому для записи комплексного числа в показательной форме по формуле 7. Пример 7.1. Записать комплексные числа в тригонометрической и показательной формах. Решение. Для z1 имеем . Поэтому . Для действительного числа . Поэтому На множестве комплексных чисел определен ряд операций. 1. Суммой двух комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством . (7.8) Из (7.8) следует, что геометрически комплексные числа складываются как
векторы, причем сумма комплексных чисел интерпретируется как диагональ
параллелограмма, построенного на векторах, представляющих слагаемые (рис. 2. Вычитание комплексных чисел определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число z1, то есть z= z1 – z2 (7.9) Из равенства (7.9) следует, что геометрически
комплексные числа вычитаются как векторы. При этом число z= z1 – z2 изображается вектором, соединяющим концы векторов , и исходящим из конца
вычитаемого в конец уменьшаемого (см. 3. Произведением комплексных чисел z1=x1+iy1 и z2=x2+iy2 называется комплексное число, определяемое равенством . (7.11) Из (7.11) следует важнейшее соотношение i2= –1. Действительно, . Найдем произведение комплексных чисел и . . (7.12) Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень: . (7.13) (7.13)
называется первой формулой Муавра. Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид: . (7.14) 4. Частным двух комплексных чисел z1 и называется комплексное число z, которое, будучи умноженным на z2, дает число z1, то есть , если . Пусть , тогда с использованием этого определения получаем: . (7.15) На практике при нахождении частного двух комплексных чисел
удобно умножить числитель и знаменатель дроби на число, сопряженное
знаменателю, с дальнейшим применением равенства i2= –1 и формулы разности квадратов. Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула: . (7.16) Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно. Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид: . (7.17) Пример 7.2. Найти сумму, разность, произведение и частное комплексных чисел . Решение. По формуле (7.8) сумма заданных чисел равна . Согласно формуле (7.9) разность заданных чисел равна . Пользуясь формулой (7.11), вычислим их произведение . На основании формулы (7. Пример 7.3. Найти произведение и частное комплексных чисел , представив их в тригонометрической и показательной форме. Решение. Используя (7.4) и (7.5), получаем: . Следовательно, на основе формул (7.3) и (7.7) число z1 имеет тригонометрическую и показательную форму . Аналогично, для z2 можно записать: . Отсюда . По формулам (7.12) и (7.16) получим в тригонометрической форме: Пользуясь формулами (7.14) и (7.17), получим в показательной форме: 5. Извлечение корня n-ой степени – операция, обратная возведению в натуральную степень, определенному ранее формулой (7.13). Корнем n-ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωn=z, то есть , если ωn=z. Пусть , тогда по данному определению и формуле (7.13) Муавра можно записать: . Сравнивания части этого равенства, получим: . Отсюда (корень арифметический). Окончательно получаем: . (7.18) (7.18) называется второй формулой Муавра. Видно, что для любого корень n-ой степени из комплексного числа z имеет равно n различных значений. Пример 7.4. Найти все корни уравнения z4+16=0. Решение. Запишем уравнение в виде z4=–16+0∙i. Отсюда по формуле (7.18) получим: . Рассмотрим различные значения k=0;1;2;3. Корни z1 и z4, а также z2 и z3 являются
комплексно сопряженными.
Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел. Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами степени n>0 существует точка , в которой P(z0)=0 Приведем еще одну теорему, имеющую место над множеством комплексных чисел. Теорема 7.2. Если многочлен Pn(x) с действительными коэффициентами имеет комплексный корень a+ib, то он имеет и сопряженный корень a–ib В разложение
многочлена комплексные корни
входят сопряженными парами. Пусть корни многочлена x1=a+ib и x2=a–ib. Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Вопросы для самопроверки |
Часть 3. Комплексные числа
Федеральное агентство по образованию РФ |
|
|
ГОУВПО «Удмуртский государственный университет» | УДК | 511.147 |
Факультет информационных технологий | ББК | 22.151 |
и вычислительной техники |
| Г 60 |
| Рецензенты: доцент Е. | |
|
| к.ф.-м.н. В.И. Родионов |
В.В. Головизин |
| Головизин В.В. |
| Г60 | Основные задачи курса «Алгебра и геометрия». |
|
| Часть 3: Комплексные числа: учеб.-метод. пособие. |
|
| Ижевск, 2009. 59 с. |
Основные задачи курса «Алгебра и геометрия». |
|
|
Часть 3. Комплексные числа | Третья часть учебно-методического пособия предна- | |
| значена для студентов, изучающих комплексные числа в | |
| рамках любого курса высшей математики. Пособие может | |
| быть полезно преподавателям при проведении практиче- | |
Учебно-методическое пособие | ских занятий и при подготовке индивидуальных заданий | |
| студентам. | |
| Пособие содержит решения задач на отработку техники | |
| действий с комплексными числами. Задачи тематически | |
| разбиты на 4 главы и имеют сквозную нумерацию. Номера | |
упражнений, помещенных в конце пособия, совпадают с номерами соответствующих задач.
УДК 511.147 ББК 22.151
Ижевск 2009
© Головизин В.В., 2009
2
Предисловие
Третья часть учебно-методического пособия посвящена комплексным числам. Это тема является традиционно трудной для студентов, и этому есть, на взгляд автора, ряд объективных причин. Во-первых, то обстоятельство, что комплексное число есть принципиально новый вид числа. Если действительные числа сопровождают человека повсюду в его обыденной жизни, то этого нельзя утверждать для комплексных чисел. От студента требуется определенный уровень даже не столько знаний, сколько способности абстрактного мышления. Во-вторых, геометрическая интерпретация комплексного числа, как точки плоскости, связана с совмещением двух принципиально различных систем координат на плоскости – прямоугольной декартовой и полярной, последняя из которых является новой для студентов. Кроме того, комплексное число изображается на плоскости с помощью вектора, поэтому от студента требуются устойчивые знания основ векторной алгебры. В- третьих, активно используется тригонометрия, которая сама по себе является «крепким орешком» для многих выпускников школ. И, наконец, принятая символика для обозначения корней из комплексных чисел остается прежней, как и для действительных чисел, а, по сути, обозначает принципиально иное, что часто вводит студентов в заблуждение. Освоить весь этот материал за короткий срок является весьма трудоемкой задачей. Помочь студенту справиться с этой задачей, получить устойчивые практические навыки при работе с комплексными числами – вот цели, которые автор ставил в этой части пособия.
Во-вторых, геометрическая интерпретация комплексного числа, как точки плоскости, связана с совмещением двух принципиально различных систем координат на плоскости – прямоугольной декартовой и полярной, последняя из которых является новой для студентов. Кроме того, комплексное число изображается на плоскости с помощью вектора, поэтому от студента требуются устойчивые знания основ векторной алгебры. В- третьих, активно используется тригонометрия, которая сама по себе является «крепким орешком» для многих выпускников школ. И, наконец, принятая символика для обозначения корней из комплексных чисел остается прежней, как и для действительных чисел, а, по сути, обозначает принципиально иное, что часто вводит студентов в заблуждение. Освоить весь этот материал за короткий срок является весьма трудоемкой задачей. Помочь студенту справиться с этой задачей, получить устойчивые практические навыки при работе с комплексными числами – вот цели, которые автор ставил в этой части пособия.
3
СПИСОК ЗАДАЧ
Глава 20. Действия с комплексными числами
Действия с комплексными числами
валгебраической форме записи
164.Найти сумму и разность двух комплексных чисел.
165.Найти произведение двух комплексных чисел.
166.Найти частное двух комплексных чисел.
167.Найти комплексное число, сопряженное данному.
Глава 21. Комплексная плоскость
и тригонометрическая форма комплексного числа
168.Построить комплексное число, заданное в алгебраической форме записи, на комплексной плоскости.
169.Построить комплексное число и сопряженное ему на комплексной плоскости.
170.Найти модуль и аргумент комплексного числа, заданного в алгебраической форме.
171.Записать тригонометрическую форму комплексного числа, заданного в алгебраической форме.
172.Найти модуль и аргумент комплексного числа, сопряженного данному.
173.Записать алгебраическую форму комплексного числа, заданного в тригонометрической форме.
174.Найти произведение двух комплексных чисел, заданных в тригонометрической форме.
175.Найти частное двух комплексных чисел, заданных в тригонометрической форме.
176.Найти целую степень комплексного числа, заданного в тригонометрической форме.
177.Найти расстояние между двумя точками на комплексной плоскости.
178.Изобразить все точки на комплексной плоскости, удаленные от данной на заданное расстояние.
4
179.Изобразить на комплексной плоскости все комплексные числа, имеющие постоянный заданный аргумент.
180.Изобразить множество точек z комплексной плоскости, удовлетворяющих заданным условиям.
181.Из всех комплексных чисел, удаленных от заданного комплексного числа на заданное расстояние, найти комплексное число с наименьшим модулем.
Глава 22. Корни из комплексных чисел
182.Вычислить квадратный корень из отрицательного действительного числа.
183.Решить в поле комплексных чисел квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом.
184.Вычислить квадратный корень из комплексного числа.
185.Решить квадратное уравнение с комплексными коэффициентами.
186.Найти все корни данной натуральной степени из данного комплексного числа и изобразить их на комплексной плоскости.
187.Разложить многочлен на линейные множители.
Глава 23. Корни из единицы
188.Найти все корни n-й степени из 1 и изобразить их на комплексной плоскости.
189.Записать все корни n-ой степени из 1 в виде степеней одного корня.
190.Построить таблицу умножения для всех корней n-ой степени из 1.
191.Разложить многочлен xn −1 на линейные множители.
192.Разложить многочлен на неприводимые множители над полем действительных чисел.
5
Глава 20. Действия с комплексными числами в алгебраической форме записи
Задача 164. Найти сумму и разность двух комплексных чисел.
Решение. Пусть
z1 = x1 +iy1, z2 = x2 +iy2
– два произвольных комплексных числа. Тогда
z1 +z2 = (x1 + x2 ) +i (y1 + y2 ), z1 −z2 = (x1 −x2 ) +i (y1 − y2 ) .
Пример. | Пусть | z1 = (2 +3i), z2 = −1+5i, z3 = −2i, z4 = 7 . | ||
Вычислить: а) z1 +z2 ; б) z1 −z2 ; | в) z1 +z3 ; | г) z2 −z3 ; | ||
д) z3 +z4 ; е) z1 −z4 . |
|
| ||
Решение. |
|
|
| |
а) z1 +z2 | = (2 +3i) +(−1+5i) = (2 −1) +i (3 +5) =1+8i ; | |||
б) z1 −z2 | = (2 +3i) −(−1+5i) = (2 +1) +i (3 −5) = 3 −2i ; | |||
в) z1 +z3 | = (2 +3i) +(−2i) = 2 +i ; |
|
| |
г) z2 −z3 | = (−1+5i) −(−2i) = −1+7i ; |
|
| |
д) z3 +z4 | = (−2i) +7 = 7 −2i ; е) z1 −z4 = (2 +3i) −7 = −5 +3i . | |||
Ответ: а) 1+8i ; | б) 3 −2i ; в) 2 +i ; | г) −1+7i ; | д) 7 −2i ; | |
е) −5 +3i . |
|
|
| |
Задача 165. Найти произведение двух комплексных чисел.
Решение. Пусть z1 = x1 +iy1, z2 = x2 +iy2 – два произвольных комплексных числа. Тогда
z z | 2 | = (x | 1 | +iy ) (x | 2 | +iy | 2 | ) = x | x | 2 | +ix | y | 2 | +ix | 2 | y +i2 y y | 2 | = | ||
1 |
| 1 |
|
| 1 |
| 1 |
|
| 1 | 1 |
| ||||||||
|
|
|
|
| = (x1x2 − y1y2 ) +i (x1y2 + x2 y1 ) , |
|
|
| ||||||||||||
где мы воспользовались равенством i2 | = −1 . |
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| |
Пример. Пусть z1 = 2 +3i, z2 = −1+5i, z3 = −2i, z4 = 7 . Вычислить: а) z1z2 ; б) z1z3 ; в) z1z4 ; г) z3z4 ; д) z12 ;
е) 4z −3z | 2 | +(z | z | 4 | )2 . |
1 | 2 | 3 |
|
|
Решение.
а) z1z2 = (2 +3i)(−1+5i) = −2 +10i −3i +15i2 = −17 +7i ; б) z1z3 = (2 +3i) (−2i) = −4i −6i2 = 6 −4i ;
в) z1z4 = (2 +3i) 7 =14 +21i ; г) z3z4 = (−2i) 7 = −14i ;
д) z12 = (2 +3i)2 = 4 +12i +9i2 = 4 −9 +12i = −5 +12i ; е) 4z1 −3z22 +(z3z4 )2 = 4(2 +3i) −3(−1+5i)2 +(−14i)2 =
=8 +12i −3(1−10i +25i2 ) +196i2 =
=8 +12i −3(−24 −10i) −196 = −116 +42i .
Ответ: а) −17 +7i ; б) 6 −4i ; в) 14 +21i ; г) −14i ;
д) −5 +12i ; е) | −116 +42i . |
|
|
|
|
| ||||
Задача 166. Найти частное двух комплексных чисел. | ||||||||||
Решение. Пусть z1 = x1 +iy1, z2 = x2 +iy2 | – два произ- | |||||||||
вольных комплексных числа. Тогда |
| |||||||||
| z1 | = | x1 +iy1 | = | (x1 +iy1 ) (x2 −iy2 ) | = | ||||
| z2 |
| x2 +iy2 |
| (x2 +iy2 ) (x2 −iy2 ) |
| ||||
|
| = | x1x2 + y1y2 | +i | x2 y1 −x1y2 | . |
| |||
|
|
|
|
| ||||||
|
|
|
| x22 + y22 |
|
| x22 + y22 |
| ||
Правило деления комплексных чисел в алгебраической форме записи можно сформулировать словами:
для того, чтобы разделить одно комплексное число на другое нужно числитель и знаменатель дроби умножить на комплексное число, комплексно сопряженное знаменателю дроби.
7
Этим достигается то, что в знаменателе дроби остается действительное число.
Пример. Пусть z1 = 2 +2i, z2 | = −1+i, | z3 = −i, | z4 = −3 . Вы- | ||||||||||||||||||||||||||||||||
числить: | а) |
| z |
| ; |
| б) |
| z | 2 | ; |
| в) | z | 2 |
| ; г) | z |
| ; | д) | z2 | . | ||||||||||||
| 1 |
|
|
|
|
|
|
|
| 4 | 2 | ||||||||||||||||||||||||
Решение. |
|
| z2 |
|
|
| z3 |
|
|
|
| z4 |
|
|
| z3 |
|
| z3 |
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
а) | z |
| = | 2 +2i | = | (2 +2i) (−1 | −i) | = |
| −2(1 | +i)2 | = | −2(2i) | = −2i ; | |||||||||||||||||||||
1 | −1 | +i | (−1+i) (−1 | −i) |
| (−1)2 −i2 |
|
| |||||||||||||||||||||||||||
z2 |
| 2 |
| ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||
б) | z | 2 |
|
| = | −1 | +i | = | (−1 | +i)i | = | −i +i2 |
| = −1−i ; |
|
|
|
| |||||||||||||||||
z3 |
|
| −i |
|
| −i2 |
|
| 1 |
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
в) | z2 |
| = | −1+i | = | 1 − | 1 i ; г) |
| z4 |
| = | −3 = | (−3)i | = | −3i | = −3i ; | |||||||||||||||||||
z4 |
| −3 | z3 |
| (−i)i | −i2 | |||||||||||||||||||||||||||||
|
|
|
|
|
|
| 3 |
| 3 |
|
|
|
|
|
|
|
|
| −i |
|
|
| |||||||||||||
| z | 2 |
|
|
|
| (−1+i)2 |
|
| 1−2i +i2 |
| −2i |
|
|
|
|
|
|
|
|
|
| |||||||||||||
д) |
| 2 |
| = |
| −i |
|
| = |
|
| −i |
|
| = |
| −i | = 2 . |
|
|
|
|
|
|
| ||||||||||
z3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
Ответ: а) −2i ; | б) −1−i ; | в) | 1 | − | 1 i ; | г) −3i ; д) 2. |
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
| 3 |
|
|
|
|
|
|
|
| ||
Задача 167. Найти комплексное число, сопряженное данному.
Решение. Пусть дано произвольное комплексное число z = x +iy . Тогда по определению z = x −iy есть комплекс-
ное число, комплексно сопряженное данному комплексному числу z.
Пример. Найти z , если z = (2 +i)2 −(1+2i)3 . Решение. (2 +i)2 = 4 +4i +i2 =3 +4i ,
Решение. (2 +i)2 = 4 +4i +i2 =3 +4i ,
(1+2i)3 =13 +3 12 (2i) +3 1 (2i)2 +(2i)3 =
=1+6i +12i2 +8i3 = −11−2i . 8
Отсюда, z =3 +4i −(−11−2i) =14 +6i, z =14 −6i .
Замечание. Можно использовать свойства комплексно сопряженных чисел:
z1 +z2 = z1 +z2 , z1z2 = z1 z2 .
Тогда этот же пример можно решить по-другому.
z= (2 +i)2 −(1+2i)3 = (2 +i)2 −(1+2i)3 = (2 +i)2 −(1+2i)3 =
=(2 −i)2 −(1−2i)3 = 4 −4i +i2 −(1−2i)2 (1−2i) =
=3 −4i −(1−4i +4i2 ) (1−2i) = 3 −4i −(−3 −4i) (1−2i) =
=3 −4i +(3 +4i) (1−2i) = 3 −4i +3 −2i −8i2 =14 −6i .
Ответ: 14 −6i .
Глава 21. Комплексная плоскость и тригонометрическая форма комплексного числа
Задача 168. Построить комплексное число, заданное в алгебраической форме записи, накомплексной плоскости.
Решение. Каждому комплексному числу z = x +iy ста-
вится во взаимно однозначное соответствие точка на координатной плоскости Оху с координатами (x, y) , которую
мы будем отождествлять с данным комплексным числом. Поэтому для решения данной задачи нужно просто отметить эту точку на координатной плоскости.
Поэтому для решения данной задачи нужно просто отметить эту точку на координатной плоскости.
| у |
|
|
|
|
| z = x +iy | ||
у |
| |||
|
|
|
| |
O | х |
| х |
|
|
|
| ||
| Рис. 1. |
|
|
|
Определение. Комплексной плоскостью называется прямоугольная декартовая система координат на плоскости, каждая точка которой отождествлена с комплексным числом.
Каждой точке координатной плоскости ставится во взаимно однозначное соответствие ее радиус-вектор, координаты которого совпадают с координатами точки. Отсюда следует, что каждому комплексному числу также ставится во взаимно однозначное соответствие радиус-вектор. Поэтому комплексное число можно также изображать на комплексной плоскости радиус-вектором точки, с которой оно отождествлено. Смотрите рисунок 1.
Отсюда следует, что каждому комплексному числу также ставится во взаимно однозначное соответствие радиус-вектор. Поэтому комплексное число можно также изображать на комплексной плоскости радиус-вектором точки, с которой оно отождествлено. Смотрите рисунок 1.
Пример. Следующие комплексные числа изобразить на
комплексной плоскости:
z =1+i, z =1−i, z = −1+i, z = −1−i .
|
| у |
|
|
z = −1+i | 1 |
| z =1+i |
|
|
|
| ||
|
|
|
|
|
–1 | О | 1 | х | |
| ||||
z = −1−i |
| –1 | z =1−i |
|
| Рис. |
|
| |
Ответ: рисунок 2.
Задача 169. Построить комплексное число и комплексно сопряженное ему на комплексной плоскости.
Решение. Из определения комплексно сопряженного числа следует, что комплексное число и комплексно сопряженное ему имеют одинаковую вещественную часть и противоположные мнимые части, поэтому соответствующие им точки на комплексной плоскости будут симметричны относительно оси абсцисс, смотрите рисунок 3.
|
| у |
|
|
|
|
| у |
| z = x +iy | |||
|
|
|
|
|
| |
| O | х |
|
| х |
|
|
|
|
|
| ||
–у |
|
| = x −iy | |||
| z | |||||
|
|
|
|
|
|
|
Рис. 3.
3.
11
В примере предыдущей задачи (рисунок 2) на комплексной плоскости построены две пары комплексно сопряженных чисел:
z =1+i, z =1−i и z = −1+i, z = −1−i .
Задача 170. Найти модуль и аргумент комплексного числа, заданного в алгебраической форме.
Определение. Модулем комплексного числа называется расстояние от начала координат до точки комплексной плоскости, отождествленной с этим числом.
Определение. Аргументом комплексного числа называется угол поворота оси абсцисс вокруг начала координат против часовой стрелки до совпадения с радиус-вектором точки, отождествленной с этим комплексным числом.
Обозначение: | модуль комплексного числа | обозначается |
| z | , а его аргумент обозначается arg z . |
| |
Замечание. | Из определения следует, что | | z | [0; ∞) , |
arg z [0; 2π) . Часто полагают, что arg z (−π; π], считая,
Часто полагают, что arg z (−π; π], считая,
как в тригонометрии, отрицательным углом поворота поворот по часовой стрелке. Аргумент нуля по определению полагают равным нулю: arg0 = 0 .
Введем на комплексной плоскости полярную систему координат, стандартным образом совмещенную с прямоугольной системой координат, т.е. полюс поместим в начало координат, а полярную ось совместим с положительной полуосью оси абсцисс. Тогда можно дать следующее определение модуля и аргумента комплексного числа.
12
(x, y)
3) x > 0, y < 0 . Точка
Определение. Модулем комплексного числа называется полярный радиус точки комплексной плоскости, отождествленной с этим числом, а аргументом комплексного числа называется полярный угол этой точки.
| у |
|
|
|
у | | z | ϕ | z = x +iy | ||
|
| х |
| |
O | х |
|
| |
|
|
| ||
| Рис. |
|
|
|
Здесь arg z обозначен буквой ϕ.
Таким образом, задача нахождения модуля и аргумента комплексного числа, заданного в алгебраической форме записи, сводится к задаче нахождения полярных координат точки по известным ее декартовым координатам. Эта задача была уже решена в данном пособии, смотрите часть 1, главу 4, задачу 20.
Приведем для удобства читателя основные формулы, с помощью которых можно решить данную задачу.
Пусть z = x +iy . Тогда | z | = x2 + y2 . Для вычисления
аргумента комплексного числа нам необходимо знать, в какой четверти комплексной плоскости находится соответствующая точка, отождествленная с данным комплексным числом. Ниже мы полагаем, что arg z [0; 2π) .
Если точка находится на одной из осей координат, то угол поворота легко определяется без всяких формул, поэтому полагаем, что и действительная часть комплексного числа и его мнимая часть отличны от нуля:
x = Rez ≠ 0 ≠ Im z = y .
13
1) x > 0, y > 0 . Точка (x, y) лежит в первой четверти. Тогда, смотрите рисунок 4:
arg z = arctg xy .
2) x < 0, y < 0 . Точка (x, y) лежит в третьей четверти. Тогда arg z = arctg xy +π.
лежитвчетвертойчетверти. Тогда arg z = arctg xy +2π.
4) x < 0, y > 0 . Точка (x, y) лежитвовторойчетверти. Тогда arg z = arctg xy +π.
Пример. Найти модуль и аргумент следующих комплекс-
ных чисел: z = ±1, z = ±i, z = ±1±i 3 .
Решение. Отметим на комплексной плоскости первые 4 числа z = ±1, z = ±i .
| у |
|
|
|
|
|
z = −1 | z =i |
|
|
|
|
|
|
|
|
|
|
| |
| О | z = | 1 | х |
|
|
z = −i |
|
|
| |||
|
|
|
|
|
| |
| Рис. |
|
|
|
|
|
Легко видеть, что |1| =| −1| =| i | =| −i | =1 , |
| |||||
arg1 = 0, arg(−1) = π, arg i = π | , arg(−i) = | 3π. | ||||
|
| 2 |
|
|
| 2 |
14
Отметим на комплексной плоскости числа z = ±1±i | 3 : | ||||||||
|
|
| у | z =1+i | 3 |
|
|
| |
z = −1+i 3 |
|
|
|
|
| ||||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
| х |
|
|
|
z = −1−i 3 |
|
| z =1−i 3 |
|
|
| |||
|
| Рис. |
|
|
|
|
|
| |
Модуль находим по формуле | z | = | x2 + y2 : |
|
|
|
| ||||
| ±1±i 3 | = (±1)2 +(± 3)2 = 2 . |
|
|
| ||||||
Находим аргументы данных комплексных чисел: |
|
|
| ||||||
arg(1+i | 3) = arctg | 3 = π , |
|
|
|
| |||
|
|
|
|
| 3 |
|
|
|
|
arg(−1−i 3) = arctg | (− 3) | = arctg | 3 = π +π = | 4π | , | ||||
|
| (−1) |
|
| 3 |
|
| 3 |
|
arg(1−i | 3) = arctg(− | 3) = −π | +2π = | 5π | , |
|
| ||
|
|
|
| 3 |
| 3 |
|
|
|
arg(−1+i | 3) = arctg(− | 3) = − | π +π = | 2π . |
|
| |||
|
|
|
|
| 3 | 3 |
|
|
|
Задача 171. Записать тригонометрическую форму комплексного числа, заданного в алгебраической форме.
Решение. Пусть комплексное число дано в алгебраической форме записи: z = x +iy . Тогда (x, y) – его декарто-
вые координаты на комплексной плоскости. Пусть (r,ϕ) –
полярные координаты комплексного числа z на комплексной плоскости. Тогда r =| z |, ϕ = arg z .
15
Декартовые и полярные координаты связаны друг с другом соотношением:
x = r cos ϕy = r sin ϕ.
Отсюда получаем
z = x +iy = r cos ϕ+ir sin ϕ = r (cos ϕ+isin ϕ)
или
z=| z | (cos ϕ+i sin ϕ)
–тригонометрическая форма записи комплексного числа,
где ϕ= arg z .
Таким образом, для решения данной задачи нужно найти модуль и аргумент комплексного числа, т. е. задача сводится к предыдущей задаче 170.
е. задача сводится к предыдущей задаче 170.
Пример. Записать следующие комплексные числа в тригонометрической форме:
z = ±1, z = ±2i, z = − 3 −3i, z = 3 −4i .
Решение. Как в задаче 170, находим модули и аргументы данных комплексных чисел. Запишем сразу ответ.
Ответ: 1 = cos 0 +isin 0 , −1 = cos π+isin π, |
|
|
|
| |||||||
2i = 2(cos | π +i sin | π) , | −2i = 2(cos 3π | +isin 3π) , | |||||||
| 2 | 2 |
|
|
| 2 |
|
|
| 2 | |
− | 3 −3i = 2 3 (cos | 4π +isin 4π) , |
|
| |||||||
|
|
|
| 4 |
| 3 | 3 |
| 4 |
| |
|
|
|
|
|
|
|
|
| |||
3 −4i = | 5(cos arctg | − |
|
| +i sin arctg | − |
| ) . | |||
3 | 3 | ||||||||||
|
|
|
|
|
|
|
|
| |||
Задача 172. Найти модуль и аргумент комплексного
числа, сопряженного данному. |
|
| ||
Решение. | Пусть | дано | комплексное | число |
z = x +iy =| z | (cosϕ+isin ϕ) , где | z | | – его модуль, | ϕ = arg z | ||
|
| 16 |
|
|
– его аргумент. Пусть ϕ = arg z [0, 2π) . Так как модули
комплексно сопряженных чисел равны, то задача заключается внахождении аргумента комплексно сопряженного числа.
Заметим сразу, что если мнимая часть комплексного числа Im z = y = 0 , то есть arg z = 0 или arg z = π, то z = z и
их аргументы равны.
В силу симметрии чисел z = x +iy и z = x −iy на ком-
плексной плоскости относительно оси абсцисс, их радиус векторы также симметричны относительно оси абсцисс. Поэтому угол поворота оси абсцисс до совпадения с ради-
ус-вектором точки z = x −iy будет противоположен углу
поворота оси абсцисс до совпадения с радиусом-вектором точки z = x +iy .
у
z = x +iy
arg z
х
arg z = −arg z
z = x −iy
Рис. 7.
Если arg z [0; 2π) и нам нужно, чтобы arg z [0; 2π) , тогда полагаем
arg z = −arg z +2π.
Если arg z (−π; π) , тогда arg z = −arg z (−π; π) . Если най-
денный аргумент комплексно сопряженного числа получился при этом отрицательный, то, прибавив 2π, мы помещаем его на промежуток [0; 2π) .
17
Пример. Найдите модули и аргументы комплексных чисел, комплексно сопряженных следующим комплексным числам:
z = cos π +isin | π, z | 2 | = cos | 3π +isin 3π, z | 3 | = cos 7π +isin 7π, | ||||||||||
1 | 4 |
| 4 |
|
| 4 | 4 |
|
| 6 |
| 6 | ||||
|
|
|
|
|
|
|
|
| ||||||||
z4 | = cos | 11π | +isin | 11π | , z5 |
| − | 5π |
|
| − | 5π | ||||
6 |
| 6 | = cos | 6 |
|
| +i sin | . | ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| 6 | |||
Решение. Модули всех данных комплексных чисел равны 1. Аргументы первых четырех данных комплексных чисел лежат на промежутке [0; 2π) , поэтому
arg |
|
|
| = −arg z |
|
| +2π, k =1, 2,3, 4 : | arg |
|
| = −π | +2π = 7π , | ||||||||||||||||||||||||||||||||||||
z | k | k | z | |||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
| 4 |
|
|
| 4 |
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
| arg |
|
| = −3π +2π = | 5π | , |
|
|
|
| arg |
|
| = − | 7π | +2π = 5π | , |
|
| |||||||||||||||||||||||||||
|
| z2 |
|
| z3 | |||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
| 6 |
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| arg |
|
|
| = −11π | +2π = | π . |
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| z4 |
|
|
|
|
|
|
|
| |||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5π |
|
|
|
|
|
|
| 6 |
|
|
| 5π |
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
| ||||||
Так как | arg z5 = − | , то |
| arg |
|
|
| = | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||
| z5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
| 7π |
|
|
| 6 |
|
|
|
|
|
|
|
| 5π |
|
|
|
|
| 5π |
| |||||
Ответ: |
|
| | z |
| | =1, |
|
|
| arg |
|
| = |
| , |
|
| arg |
|
|
| = | , | arg |
|
| = | , | |||||||||||||||||||||
|
| k |
|
| z |
|
|
| z | 2 |
| z | 3 | |||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
| 4 |
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
| 6 |
| ||||||||||||||
|
|
|
|
| π, |
|
|
|
|
|
|
|
| 5π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
arg |
| = | arg |
|
| = |
| . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||
z4 | z5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
Задача 173. Записать алгебраическую форму комплексного числа, заданного в тригонометрической форме.
Записать алгебраическую форму комплексного числа, заданного в тригонометрической форме.
Решение. Пусть комплексное число задано в тригонометрической форме z =| z | (cos ϕ+i sin ϕ) . Раскроем скобки: z =| z | cos ϕ+i | z | sin ϕ.
Получили алгебраическую форму записи данного комплексного числа. Если аргумент ϕ относится к табличным
значениям тригонометрических углов, тогда мы можем заменить cos ϕ и sinϕ на их соответствующие значения.
18
Пример. Найти алгебраическую форму записи следующих комплексных чисел:
|
|
|
|
| z |
| = cos π +isin | π, |
| z | 2 |
| = cos 3π | +isin 3π , |
| ||||||||||||||||
|
|
|
|
| 1 |
|
|
|
| 4 |
|
|
|
| 4 |
|
|
|
|
|
|
| 4 |
|
| 4 |
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| z3 = | 2 |
|
| 17π | +isin | 17π |
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
| cos |
| 16 |
|
| 16 | , |
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
| z4 = cos | 1 | +isin | 1 | , |
| z5 |
|
|
|
|
|
| − | 5π | +isin |
| − | 5π | |||||||||||
|
| 6 | 6 |
| = cos |
|
| 6 | . | ||||||||||||||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
z | = | 2 |
| +i |
|
| 2 | , | z |
| = − |
|
| 2 |
| +i |
| 2 | , z |
| = 2cos 17π +i2sin 17π , | ||||||||||
|
|
|
|
| 2 |
|
|
|
|
| 3 | ||||||||||||||||||||
1 | 2 |
|
|
|
| 2 |
|
|
|
|
| 2 |
|
|
| 2 |
|
|
|
| 16 |
|
|
| 16 | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
z4 | = cos | 1 | +isin | 1 | , z5 = − |
| 3 |
| − | 1 i . |
|
|
|
|
|
|
| ||||||||||||||
6 | 6 |
| 2 |
|
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
| |||||
Задача 174. Найти произведение двух комплексных чисел, заданных в тригонометрической форме.
Решение. Чтобы перемножить два числа в тригонометрической форме, нужно перемножить их модули, а аргументы сложить.
Пусть z1 =| z1 | (cos ϕ1 +isin ϕ1 ) , z2 =| z2 | (cos ϕ2 +isin ϕ2 ) .
Тогда
z1z2 =| z1 | | z2 | (cos(ϕ1 +ϕ2 ) +isin(ϕ1 +ϕ2 )) .
Замечания. 1) Прежде чем применить это правило, нужно убедиться, что числа даны в тригонометрической форме, т.е. аргументы, стоящие под знаком косинуса и синуса, равны и перед мнимой единицей i стоит знак плюс.
2) Число ϕ1 +ϕ2 может оказаться вне промежутка [0; 2π) или (−π; π] . В этом случае используем периодичность функций синуса и косинуса, чтобы аргумент полученного
19
произведения лежал в одном из указанных промежутков. Для этого достаточно к числу ϕ1 +ϕ2 прибавить 2π или
(−2π) .
Пример. Найти произведение чисел и записать его в тригонометрической форме:
а) z | = 3(cos 11π | +i sin 11π), |
| z | 2 | = 2(cos 4π | +isin 4π) ; | ||||||||||||||||||
1 | 6 |
|
| 6 |
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
| 3 |
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
б) z | = 3(cos 5π +isin 5π), |
| z | 2 | = 2(cos 5π −isin π) . |
| |||||||||||||||||||
1 | 6 |
|
| 6 |
|
|
|
|
|
|
|
| 3 |
| 3 |
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
| 11π |
|
| 4π |
|
|
| 11π |
|
|
| 4π | |||||||||
Решение. | = 6 (cos |
|
|
|
|
| + |
|
|
| +isin |
|
|
| + |
|
|
| ) = | ||||||
6 |
|
|
|
| 3 | ||||||||||||||||||||
|
|
|
|
|
|
|
|
| 3 |
|
|
| 6 |
|
|
| |||||||||
| = 6(cos | 19π | +isin | 19π | ) = 6(cos | 7π |
| +isin |
| 7π | ) . | ||||||||||||||
|
|
|
| 6 | |||||||||||||||||||||
|
|
| 6 |
| 6 |
|
|
|
|
|
| 6 |
|
|
|
|
|
| |||||||
б) Здесь число z | 2 записано не в тригонометрической фор- | |||||||||||||||||||
ме, как нужно. Выполним преобразования: |
|
|
|
|
|
|
| |||||||||||||
cos | 5π | 5π |
|
|
| − | π |
| , | −sin | π |
|
|
| − | π | ||||
3 | = cos |
| 3 |
| −2π | = cos | 3 |
| 3 | =sin | 3 | . | ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
Отсюда следует | 5π |
| π |
|
|
|
|
| π |
|
|
| π |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
z2 = 2(cos |
|
|
| −isin |
| ) = 2(cos |
| − | +isin | − |
| ) |
| |||||||
| 3 |
| 3 | 3 |
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
| |||
– тригонометрическая форма комплексного числа z2 . Здесь
Здесь
мы воспользовались свойством нечетности синуса. |
|
| |||||||||||||
Теперь перемножаем по правилу: |
|
|
|
|
|
| |||||||||
5π |
| π | 5π |
| π |
|
| π |
| π |
| ||||
z1z2 = 6( cos |
| − |
| +isin |
| − |
| ) = 6(cos |
| +isin |
| ) . | |||
6 | 3 |
| 3 | 2 | 2 | ||||||||||
|
|
| 6 |
|
|
|
|
|
| ||||||
Ответ: а) 6(cos | 7π | +isin | 7π) ; б) | 6(cos | π | +isin | π) . |
|
| ||||||
| 6 |
|
|
| 6 |
|
|
|
| 2 |
| 2 |
|
|
|
|
|
|
|
| 20 |
|
|
|
|
|
|
|
|
| |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Калькулятор комплексных чисел с решением
Теория
Сложение двух комплексных чисел, представленных в алгебраической форме.
Сложение вещественного и комплексного числа, представленного в алгебраической форме.
Вычитание двух комплексных чисел, представленных в алгебраической форме.
Вычитание комплексного числа из вещественного числа.
Вычитание вещественного числа из комплексного числа.
Умножение двух комплексных чисел, представленных в алгебраической форме.
Умножение вещественного и комплексного числа, записанного в алгебраической форме.
Деление двух комплексных чисел, представленных в алгебраической форме.
Деление комплексного числа, представленного в алгебраической форме на вещественное число.
Деление вещественного числа на комплексное число, представленного в алгебраической форме.
Сложение комплексных чисел, представленных в тригонометрической форме.
Вычитание комплексных чисел, представленных в тригонометрической форме.
Умножение комплексных чисел, представленных в тригонометрической форме.
Деление комплексных чисел, представленных в тригонометрической форме.
Сложение комплексных чисел, представленных в показательной форме.
Вычитание комплексных чисел, представленных в показательной форме.
Умножение комплексных чисел, представленных в показательной форме.
Деление комплексных чисел, представленных в показательной форме.
Модуль комплексного числа.
Аргумент комплексного числа.
Представление комплексного числа, записанного в алгебраической форме в тригонометрической форме.
Представление комплексного числа, записанного в алгебраической форме в показательной форме.
Представление комплексного числа, записанного в тригонометрической форме в алгебраической форме.
Представление комплексного числа, записанного в тригонометрической форме в показательной форме.
Представление комплексного числа, записанного в показательной форме в тригонометрической форме.
Представление комплексного числа, записанного в показательной форме в алгебраической форме.
Сопряженное число комплексного числа, записанного в алгебраической форме.
Сопряженное число комплексного числа, записанного в тригонометрической форме.
Сопряженное число комплексного числа, записанного в показательной форме.
Обратная величина комплексного числа, записанного в алгебраической форме.
Обратная величина комплексного числа, записанного в тригонометрической форме.
Обратная величина комплексного числа, записанного в показательной форме.
Аддитивная инверсия комплексного числа.
Извлечение корня n−й степени из комплексного числа, записанного в алгебраической форме.
Извлечение корня n−й степени из комплексного числа, записанного в тригонометрической форме.
Извлечение корня n−й степени из комплексного числа, записанного в показательной форме.
Сложение двух комплексных чисел, представленных в алгебраической форме
Для того, чтобы сложить два комплексных числа представленных в алгебраической форме, нужно сложить их вещественные и мнимые части:
(a + bi) + (c + di) = (a + c) + (b + d)i
Приведем примеры:
Пример 1. Сложим два комплексных числа 2 + 3i и 1.6 + 7i
(2 + 3i) + (1.6 + 7i) = (2 + 1.6) + (3 + 7)i = 3.6 + 10i
Пример 2. Сложим два комплексных числа 3 + 4i и 8 − 6i
Сложим два комплексных числа 3 + 4i и 8 − 6i
(3 + 4i) + (8 − 6i) = (3 + 8) + (4 − 6i) = 11 − 2i
Сложение вещественного и комплексного числа, представленного в алгебраической форме
Чтобы сложить комплексное число a + bi и вещественное число c, необходимо прибавить к вещественной части комплексного числа вещественное число:
(a + bi) + с = (a + c) + bi
Приведем примеры:
Пример 1. Сложим комплексное число 2 + 3i и вещественное число 10
(2 + 3i) + 10 = (2 + 10) + 3i = 12 + 3i
Пример 2. Сложим комплексное число −6 + 3i и вещественное число -23
(−6 + 3i) + (−23) = (−6 + (−23)) + 3i = −29 + 3i
Вычитание двух комплексных чисел, представленных в алгебраической форме
Для того, чтобы вычесть два комплексных числа представленных в алгебраической форме, нужно вычесть их вещественные и мнимые части:
(a + bi) − (c + di) = (a − c) + (b − d)i
Приведем примеры:
Пример 1. Вычтем два комплексных числа 3 + 9i и 5 + 6i
Вычтем два комплексных числа 3 + 9i и 5 + 6i
(3 + 9i) − (5 + 6i) = (3 − 5) + (9 − 6)i = −2 + 3i
Пример 2. Вычтем два комплексных числа 6 + 23i и 57 + 68i
(6 + 23i) − (57 + 68i) = (6 − 57) + (23 − 68)i = −51 − 45i
Вычитание комплексного числа из вещественного числа
Чтобы вычесть из вещественного числа a комплексное число c + di, необходимо воспользоваться формулой, приведенной ниже:
a − (c + di) = (a − c) − di
Приведем примеры:
Пример 1. Вычтем из вещественного числа 6 комплексное число 1 + 7i
6 − (1 + 7i) = (6 − 1) + 7i = 5 − 7i
Пример 2. Вычтем из вещественного числа -15 комплексное число 1 + (−7)i
−15 − (1 + (−7)i) = (−15 − 1) − (−7)i = −16 + 7i
Вычитание вещественного числа из комплексного числа
Чтобы вычесть из комплексного числа a + bi вещественное число c, необходимо вычесть из действительной части комплексного числа вещественное число:
(a + bi) − с = (a − c) + bi
Приведем примеры:
Пример 1. Вычтем из комплексного числа 5 + 12i вещественное число 8
Вычтем из комплексного числа 5 + 12i вещественное число 8
(5 + 12i) − 8 = (5 − 8) + 12i = −3 + 12i
Пример 2. Вычтем из комплексного числа −1 + (−5)i вещественное число −3
(−1 + (−5)i) − (−3) = (−1 − (−3)) + (−5)i = 2 − 5i
Умножение двух комплексных чисел, представленных в алгебраической форме
Для того чтобы умножить два комплексных числа записанных в алгебраической форме, необходимо воспользоваться формулой, приведенной ниже:
(a + bi) × (c + di) = ac + adi + bci + bdi2 = (ac + bdi2) + (bc + ad)i = (ac − bd) + (bc + ad)i
Приведем примеры:
Пример 1. Умножим два комплексных числа 2 + 5i и 3 + 7i
Решение 1
(2 + 5i) × (3 + 7i) = ((2 × 3) − (5 × 7)) + ((5 × 3) + (2 × 7))i = (6 − 35) + (15 + 14)i = −29 + 29i
Решение 2
(2 + 5i) × (3 + 7i) = (2 × 3) + (2 × 7i) + (5i × 3) + (5i × 7i) = 6 + (14i) + (15i) + (35i2) = 6 + (29i) + (35 × (−1)) = −29 + 29i
Пример 2. Умножим два комплексных числа 0.4 + (−2)i и 3.023 + 0.25i
Умножим два комплексных числа 0.4 + (−2)i и 3.023 + 0.25i
Решение 1
(0.4 + (−2)i) × (3.023 + 0.25i) = ((0.4 × 3.023) − (−2 × 0.25)) + (((−2) × 3.023) + (0.4 × 0.25))i = (1.2092 − (−0.5)) + (−6.046 + 0.1)i = 1.7092−5.946i
Решение 2
(0.4 + (−2)i) × (3.023 + 0.25i) = (0.4 × 3.023) + (0.4 × 0.25i) + ((−2)i × 3.023) + ((−2)i × 0.25i) = 1.2092 + (0.1i) + (−6.046i) + (−0.5i2) = 1.2092 + (−5.946i) + ((−0.5 × (−1))) = 1.7092 − 5.946i
Умножение вещественного и комплексного числа, записанного в алгебраической форме
Для того чтобы умножить вещественное число a на комплексное число c + di, необходимо вещественную и комплексную части числа c + di умножить на это число:
a × (c + di) = ac + adi
Приведем примеры:
Пример 1. Умножим комплексное число 3 + 4i и вещественное число 1
1 × (3 + 4i) = (1 × 3) + (1 × 4)i = 3 + 4i
Пример 2. Умножим комплексное число −5 + 4i и вещественное число −74
−74 × (−5 + 4i) = (−74 × (−5)) + (−74 × 4)i = 370 − 296i
Деление двух комплексных чисел, представленных в алгебраической форме
Для того чтобы разделить два комплексных числа записанных в алгебраической форме, необходимо воспользоваться формулой, приведенной ниже:
| a + bi | = | |
| c + di |
| (a + bi) × (c − di) | = | |
| (c + di) × (c − di) |
| ac + bd | + | |
| c2 + d2 |
| bc − ad | |
| c2 + d2 |
Приведем примеры:
Пример 1. Разделим комплексное число 4 + 3i на комплексное число 5 + 8i
Разделим комплексное число 4 + 3i на комплексное число 5 + 8i
| (4 + 3i) | = | |
| (5 + 8i) |
| (4 + 3i) × (5 − 8i) | = | |
| (5 + 8i) × (5 − 8i) |
| (4 × 5) + (3 × 8) | + | |
| (52 + 82) |
| (3 × 5) − (4 × 8) | |
| (52 + 82) |
| (20 + 24) | + | |
| (25 + 64) |
| 15 − 32 | |
| 25 + 64 |
| 44 | + | |
| 89 |
= 0. 49438202247191−0.191011235955056i 49438202247191−0.191011235955056i | ||
Пример 2. Разделим комплексное число 6 + (−2)i на комплексное число −4 + 7i
| (6 + (−2)i) | = | |
| (−4 + 7i) |
| (6 + (−2)i) × (−4 − 7i) | = | |
| (−4 + 7i) × (−4 − 7i) |
| (6 × (−4)) + (−2 × 7) | + | |
| (−42 + 72) |
| (−2 × (−4)) − (6 × 7) | |
| (−42 + 72) |
| (−24 + (−14)) | + | |
| (16 + 49) |
| 8 − 42 | |
| 16 + 49 |
| −38 | + | |
| 65 |
= −0. 584615384615385−0.523076923076923i 584615384615385−0.523076923076923i | ||
Деление комплексного числа, представленного в алгебраической форме на вещественное число
Для того чтобы разделить комплексное число a + bi на вещественное число c, необходимо вещественную часть комплексного числа разделить на вещественное число и мнимую часть комплексного числа разделить на вещественное число:
| a + bi | = | |
| c |
Приведем пример:
Разделим комплексное число 3 + 6i на вещественное число 7
| (3 + 6i) | = | |
| 7 |
| = 0.428571428571429 + 0.857142857142857i | ||
Деление вещественного числа на комплексное число, представленного в алгебраической форме
Для того чтобы разделить вещественное число a на комплексное число c + di, необходимо воспользоваться формулой, приведенной ниже:
| a | = | |
| c + di |
| a × (c − di) | = | |
| (c + di) × (c − di) |
| ac | − | |
| c2 + d2 |
| ad | |
| c2 + d2 |
Приведем пример:
Разделим вещественное число 5 на комплексное число 2 + 9i
| 5 | = | |
| (2 + 9i) |
| 5 × (2 − 9i) | = | |
| (2 + 9i) × (2 − 9i) |
| 5 × | − | |
| (22 + 92) |
| 5 × | |
| (22 + 92) |
| 10 | − | |
| (4 + 81) |
| 45 | |
| 4 + 81 |
| 10 | − | |
| 85 |
= 0. 117647058823529−0.529411764705882i 117647058823529−0.529411764705882i | ||
Сложение комплексных чисел, представленных в тригонометрической форме
Для того чтобы сложить два комплексных числа записанных в тригонометрической форме, необходимо воспользоваться формулой приведенной ниже:
z1 + z2 = (|z1| × (cos α + i sin α)) + (|z2| × (cos β + i sin β)) = ((|z1| × cos α) + (|z2| × cos β)) + i((|z1| × sin α) + (|z2| × sin β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Сложим два комплексных числа √13 (cos 48° + i sin 48°) и √25 (cos 69° + i sin 69°)
√13 (cos 48° + i sin 48°) + √25 (cos 69° + i sin 69°) = ((√13 × cos(48°)) + (√25 × cos(69°))) + i((√13 × sin(48°)) + (√25 × sin(69°))) = (2.41258471120918 + 1.7918397477265) + (2.67944677335447 + 4. 667902132486)i = 4.20442445893568 + 7.34734890584047i
667902132486)i = 4.20442445893568 + 7.34734890584047i
Вычитание комплексных чисел, представленных в тригонометрической форме
Для того чтобы вычесть два комплексных числа записанных в тригонометрической форме, необходимо воспользоваться формулой приведенной ниже:
z1 − z2 = (|z1| × (cos α + i sin α)) − (|z2| × (cos β + i sin β)) = ((|z1| × cos α) − (|z2| × cos β)) + i((|z1| × sin α) − (|z2| × sin β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Вычтем из два комплексного числа 1/2 (cos π/2 + i sin π/2) число 1/3 (cos π/3 + i sin π/3)
1/2 (cos π/2 + i sin π/2) − 1/3 (cos π/3 + i sin π/3) = ((1/2 × cos((π/2))) − (1/3 × cos((π/3)))) + i((1/2 × sin((π/2))) − (1/3 × sin((π/3)))) = (0 − 0.166666666666666) + (0.5 − 0.288675134594813)i = −0.166666666666666 + 0. 211324865405187i
211324865405187i
Умножение комплексных чисел, представленных в тригонометрической форме
Для того чтобы умножить два комплексных числа записанных в тригонометрической форме, необходимо воспользоваться формулой приведенной ниже:
z1 × z2 = (|z1| × |z2|) × (cos(α + β) + i × sin(α + β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Умножим два комплексных числа 2 (cos π/2 + i sin π/2) и 2 (cos π/3 + i sin π/3)
2 (cos π/2 + i sin π/2) × 2 (cos π/3 + i sin π/3) = (2 × 2) × (cos(π/2 + (π/3)) + i × sin(π/2 + (π/3))) =
16
× (cos(5π/6) + i × sin(5π/6)) =
16
× (cos(150°) + i × sin(150°))
Деление комплексных чисел, представленных в тригонометрической форме
Для того чтобы разделить два комплексных числа записанных в тригонометрической форме, необходимо воспользоваться формулой приведенной ниже:
z1 ÷ z2 = (|z1| ÷ |z2|) × (cos(α − β) + i × sin(α − β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Разделим два комплексных числа 3 (cos 45° + i sin 45°) и 2 (cos 37° + i sin 37°)
3 (cos 45° + i sin 45°) ÷ 2 (cos 37° + i sin 37°) = (3 ÷ 2) × (cos(45° − 37°) + i × sin(45° − 37°)) =
2. 25
25
× (cos(8°) + i × sin(8°))=
2.25
× (cos(2π/45) + i × sin(2π/45))
Сложение комплексных чисел, представленных в показательной форме
Для того чтобы сложить два комплексных числа записанных в показательной форме, необходимо воспользоваться формулой приведенной ниже:
|z1| eiα + |z2| eiβ = (|z1| × (cos α + i sin α)) + (|z2| × (cos β + i sin β)) = ((|z1| × cos α) + (|z2| × cos β)) + i((|z1| × sin α) + (|z2| × sin β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Сложим два комплексных числа 3 × e(π/2)i и 2 × e(3π/2)i
3 × e(π/2)i + 2 × e(3π/2)i = ((3 × cos((π/2))) + (2 × cos((3π/2)))) + i((3 × sin((π/2))) + (2 × sin((3π/2)))) = (0 + 0) + (3 + (−2))i = 0 + 1i
Вычитание комплексных чисел, представленных в показательной форме
Для того чтобы вычесть два комплексных числа записанных в показательной форме, необходимо воспользоваться формулой приведенной ниже:
|z1| eiα − |z2| eiβ = (|z1| × (cos α + i sin α)) − (|z2| × (cos β + i sin β)) = ((|z1| × cos α) − (|z2| × cos β)) + i((|z1| × sin α) − (|z2| × sin β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Вычтем из числа 3 × e(π/2)i число 2 × e(3π/2)i
3 × e(π/2)i — 2 × e(3π/2)i = ((3 × cos((π/2))) − (2 × cos((3π/2)))) + i((3 × sin((π/2))) − (2 × sin((3π/2)))) = (0 − 0) + (3 − (−2))i = 0 + 5i
Умножение комплексных чисел, представленных в показательной форме
Для того чтобы умножить два комплексных числа записанных в показательной форме, необходимо воспользоваться формулой приведенной ниже:
|z1| eiα × |z2| eiβ = (|z1| × |z2|) × (cos(α + β) + i × sin(α + β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Умножим два комплексных числа 3 × e(π/2)i и 2 × e(3π/2)i
(3 × e(π/2)i) × (2 × e(3π/2)i) = (3 × 2) × (cos(π/2 + (3π/2)) + i × sin(π/2 + (3π/2))) =
36
× (cos(360°) + i × sin(360°)) = 6 + 0i
Деление комплексных чисел, представленных в показательной форме
Для того чтобы разделить два комплексных числа записанных в показательной форме, необходимо воспользоваться формулой приведенной ниже:
|z1| eiα ÷ |z2| eiβ = (|z1| ÷ |z2|) × (cos(α − β) + i × sin(α − β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2
Приведем пример:
Разделим два комплексных числа 3 × e(π/2)i и 2 × e(3π/2)i
(3 × e(π/2)i) ÷ (2 × e(3π/2)i) = (3 ÷ 2) × (cos(π/2 − (3π/2)) + i × sin(π/2 − (3π/2))) =
2. 25
25
× (cos(−180°) + i × sin(−180°)) =
2.25
× (cos(−π) + i × sin(−π)) = −1.5 + 0i
Модуль комплексного числа
Модуль комплексного числа равен расстоянию от точки на комплексной плоскости до начала координат и обозначается |z|.
Модуль комплексного числа z вычисляется по формуле:
|z| =
a2 + b2
Приведем пример:
Найдем модуль комплексного числа 1 + 3i
|1 + 3i| =
12 + 32
=
1 + 9
=
10
= 3.16227766016838
Аргумент комплексного числа
Аргументом ненулевого комплексного числа называется угол φ между радиус−вектором соответствующей точки и положительной вещественной полуосью.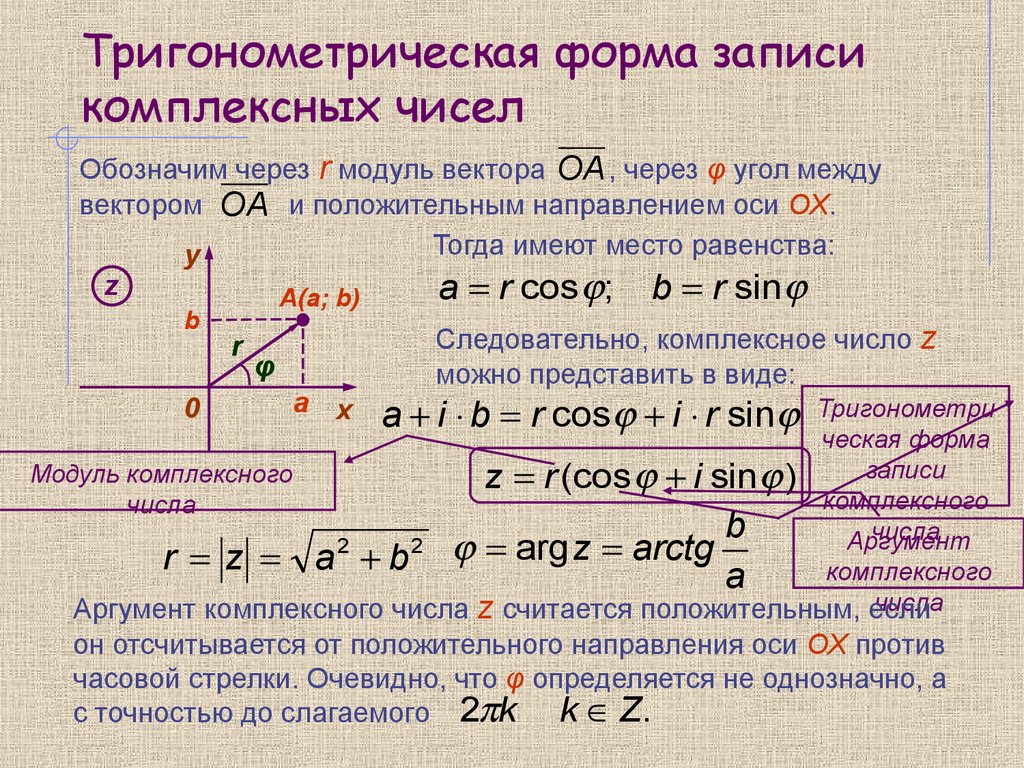 Аргумент числа z обозначается Arg(z).
Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:
Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента, должно принимать такое значение, что −π < arctg(b/a) ⩽ π. Калькулятор вычисляет именно главное значение аргумента.
Приведем пример:
Найдем аргумент комплексного числа −4 + 7i
Arg(−4 + 7i) = arctg(7/(−4)) + π = 2.08994244104142 радиан
Arg(−4 + 7i) = 119.744881296942° градусов
Представление комплексного числа, записанного в алгебраической форме в тригонометрической форме
Для того, чтобы представить комплексное число, записанное в алгебраической форме в тригонометрической форме, необходимо найти модуль и аргумент данного комплексного числа.
z = a + bi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Модуль комплексного числа равен расстоянию от точки на комплексной плоскости до начала координат и обозначается |z|.
Модуль комплексного числа z вычисляется по формуле:
|z| =
a2 + b2
Приведем пример:
Представим число 2 + 3i в тригонометрической форме
|2 + 3i| =
22 + 32
=
4 + 9
=
13
= 3.60555127546399
Аргументом ненулевого комплексного числа называется угол φ между радиус−вектором соответствующей точки и положительной вещественной полуосью. Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:
Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента, должно принимать такое значение, что −π < arctg(b/a) ⩽ π. Калькулятор вычисляет именно главное значение аргумента.
Arg(2 + 3i) = arctg(3/2) = 0.982793723247329 радиан
Arg(2 + 3i) = arctg(3/2) = 56.3099324740202° градусов
Теперь можно записать комплексное число z в тригонометрической форме:
z = 2 + 3i =
13
× (cos(arctg(3/2)) + sin(arctg(3/2))i) = 3.60555127546399 × (cos(56.3099324740202°) + sin(56.3099324740202°)i)
Представление комплексного числа, записанного в алгебраической форме в показательной форме
Для того, чтобы представить комплексное число, записанное в алгебраической форме в показательной форме, необходимо найти модуль и аргумент данного комплексного числа.
z = a + bi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Модуль комплексного числа равен расстоянию от точки на комплексной плоскости до начала координат и обозначается |z|.
Модуль комплексного числа z вычисляется по формуле:
|z| =
a2 + b2
Приведем пример:
Представим число 2 + 2i в показательной форме
|2 + 2i| =
22 + 22
=
4 + 4
=
8
= 2.82842712474619
Аргументом ненулевого комплексного числа называется угол φ между радиус−вектором соответствующей точки и положительной вещественной полуосью. Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:
Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента, должно принимать такое значение, что −π < arctg(b/a) ⩽ π. Калькулятор вычисляет именно главное значение аргумента.
Arg(2 + 2i) = arctg(2/2) = 0.785398163397448 радиан
Arg(2 + 2i) = arctg(2/2) = 45° градусов
Теперь можно записать комплексное число z в показательной форме:
z = 2 + 2i =
8
× e0.785398163397448i =
8
× e45°i =
8
× e(π/4)i
Представление комплексного числа, записанного в тригонометрической форме в алгебраической форме
Чтобы представить комплексное число записанное в тригонометрической форме в алгебраической форме z = a + bi, необходимо вещественную часть a представить как cos φ умножить на модуль |z|, а мнимую часть b как sin φ умножить на модуль |z| комплексного числа z.
|z| (cos φ + i sin φ) = (|z| × (cos φ)) + (|z| × (sin φ)i) = a + bi, где
a = |z| × cos φ
b = |z| × sin φ
Приведем пример:
Представим число 2 × (cos(60°) + sin(60°)i) в алгебраической форме
2 × (cos(60°) + sin(60°)i) = 2 × (0.5 + 0.86602540378444i) = (2 × 0.5) + (2 × 0.86602540378444i) = 1 + 1.73205080756888i
Представление комплексного числа, записанного в тригонометрической форме в показательной форме
Для того, чтобы представить комплексное число, записанное в тригонометрической форме в показательной форме, необходимо воспользоваться формулой приведенной ниже:
|z| × (cos φ + i sin φ) = |z| eφi, где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Приведем пример:
Представим число 2 × (cos(60°) + sin(60°)i) в показательной форме
2 × (cos(60°) + sin(60°)i) = 2 × e60°i = 2 × e(π/3)i
Представление комплексного числа, записанного в показательной форме в тригонометрической форме
Для того, чтобы представить комплексное число, записанное в показательной форме в тригонометрической форме, необходимо воспользоваться формулой приведенной ниже:
|z| eφi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Приведем пример:
Представим число 2 × e(π/3)i в тригонометрической форме
2 × e(π/3)i = 2 × (cos((π/3)) + sin((π/3))i)
Представление комплексного числа, записанного в показательной форме в алгебраической форме
Для того, чтобы представить комплексное число, записанное в показательной форме в алгебраической форме, следует сначала это число представить в тригонометрической форме.
|z| eφi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Чтобы представить комплексное число записанное в тригонометрической форме в алгебраической форме z = a + bi, необходимо вещественную часть a представить как cos φ умножить на модуль |z|, а мнимую часть b как sin φ умножить на модуль |z| комплексного числа z.
|z| (cos φ + i sin φ) = (|z| × (cos φ)) + (|z| × (sin φ)i) = a + bi, где
a = |z| × cos φ
b = |z| × sin φ
Приведем пример:
Представим число 2 × e(π/3)i в алгебраической форме
2 × e(π/3)i = 2 × (cos((π/3)) + sin((π/3))i) = 2 × (0.5 + 0.86602540378444i) = (2 × 0.5) + (2 × 0.86602540378444i) = 1 + 1.73205080756888i
Сопряженное число комплексного числа, записанного в алгебраической форме
Два комплексно−сопряжённые числа обладают одинаковыми действительными частями и противоположными по знаку мнимыми частями.
Число сопряженное числу z, обозначается как z.
Для z = a + bi сопряженным число является z = a − bi.
Приведем пример:
Найдём сопряженное число для числа 2 + 3i
2 + 3i = 2 − 3i
Сопряженное число комплексного числа, записанного в тригонометрической форме
Два комплексно−сопряжённые числа обладают одинаковыми действительными частями и противоположными по знаку мнимыми частями.
Число сопряженное числу z, обозначается как z.
Для z = |z| (cos φ + i sin φ) сопряженным число является z = |z| (cos φ − i sin φ).
Приведем пример:
Найдём сопряженное число для числа 2(cos((π/3)) + sin((π/3))i)
2(cos((π/3)) + sin((π/3))i) = 2(cos((π/3)) − sin((π/3))i)
Сопряженное число комплексного числа, записанного в показательной форме
Два комплексно−сопряжённые числа обладают одинаковыми действительными частями и противоположными по знаку мнимыми частями.
Число сопряженное числу z, обозначается как z.
Для z = |z| eiφ сопряженным число является z = |z| e−iφ.
Приведем пример:
Найдём сопряженное число для числа 2 × e(π/3)i
2 × e(π/3)i = 2 × e − (π/3)i
Обратная величина комплексного числа, записанного в алгебраической форме
Для каждого комплексного числа, отличного от нуля существует обратное число. Чтобы найти обратное число для числа a + bi, необходимо единицу разделить на это число. Так как в качестве делимого выступает единица, то формула для деления упрощается и принимает вид:
| 1 | = | |
| a + bi |
| 1 × (a − bi) | = | |
| (a + bi) × (a − bi) |
| a | − | |
| a2 + b2 |
| b | |
| a2 + b2 |
Приведем пример:
Найдём обратную величину для числа 2 + 3i
| 1 | = | |
| (2 + 3i) |
| 2 | − | |
| (22 + 32) |
| 3 | |
| (22 + 32) |
| 2 | − | |
| (4 + 9) |
| 3 | |
| 4 + 9 |
| 2 | − | |
| 13 |
= 0. 153846153846154−0.230769230769231i 153846153846154−0.230769230769231i | ||
Обратная величина комплексного числа, записанного в тригонометрической форме
Чтобы вычислить обратное число для числа, представленного в тригонометрической форме, необходимо воспользоваться формулой, приведенной ниже:
1/z = 1/|z| × (cos φ − i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Приведем пример:
Найдём обратную величину для числа 2(cos((π/2)) + sin((π/2))i)
1/z = 1/2 × (cos (π/2) − i sin π/2) =
0.25
× (cos(π/2) − i × sin(π/2))
Обратная величина комплексного числа, записанного в показательной форме
Чтобы вычислить обратное число для числа, представленного в показательной форме, необходимо воспользоваться формулой, приведенной ниже:
1/z = (1/|z|)e−iφ, где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Приведем пример:
Найдём обратную величину для числа 2 × ei(π/2)
1/z = 1/2 × e−i (π/2) =
0. 25
25
× e−i (π/2)
Аддитивная инверсия комплексного числа
Аддитивная инверсия комплексного числа – это такое число, которое при добавлении к нему исходного числа дает ноль. Аддитивная инверсия комплексного числа представляет собой число в котором действительные и мнимые части умножаются на −1. Для того чтобы умножить число −1 на комплексное число a + bi. необходимо вещественную и комплексную части числа a + bi умножить на это число:
−1 × (a + bi) = (−1 × a) + (−1 × bi)
Приведем пример:
Найдём аддитивную инверсию для числа z = 2 + 3i
−z = (−1 × 2) + (−1 × 3)i = −2−3i
Извлечение корня n−й степени из комплексного числа, записанного в алгебраической форме
Извлечем корень 3 степени из числа 3 + 2i
Чтобы извлечь корень n−й степени из ненулевого комплексного числа. необходимо сначала данное число представить в тригонометрической форме.
необходимо сначала данное число представить в тригонометрической форме.
Для того, чтобы представить комплексное число, записанное в алгебраической форме в тригонометрической форме, необходимо найти модуль и аргумент данного комплексного числа.
z = a + bi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
Модуль комплексного числа равен расстоянию от точки на комплексной плоскости до начала координат и обозначается |z|.
Модуль комплексного числа z вычисляется по формуле:
|z| =
a2 + b2
|3 + 2i| =
32 + 22
=
9 + 4
=
13
= 3.60555127546399
Аргументом ненулевого комплексного числа называется угол φ между радиус−вектором соответствующей точки и положительной вещественной полуосью. Аргумент числа z обозначается Arg(z).
Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:
Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента, должно принимать такое значение, что −π < arctg(b/a) ⩽ π. Калькулятор вычисляет именно главное значение аргумента.
Arg(3 + 2i) = arctg(2/3) = 0.588002603547568 радиан
Arg(3 + 2i) = arctg(2/3) = 33.6900675259798° градусов
Теперь можно записать комплексное число z в тригонометрической форме:
z = 3 + 2i =
13
× (cos(arctg(2/3)) + sin(arctg(2/3))i) = 3.60555127546399 × (cos(33.6900675259798°) + sin(33.6900675259798°)i)
Применим формулу Муавра чтобы извлечь корень n−й степени:
n√z = n√|z| × (cos (φ + 2πk)/n + i sin (φ + 2πk)/n)), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
n – степень корня (количество корней)
k – принимает значения 0, 1, 2, … n−1
z1 = 3
3. 60555127546399
60555127546399
× (cos((33.6900675259798° + (2 × 180 × 0))/3) + i sin ((33.6900675259798° + (2 × 180 × 0))/3)) = 1.53340623701639 × (cos((33.6900675259798° + 0)/3) + i sin ((33.6900675259798° + 0)/3)) = (1.53340623701639 × (cos 11.2300225086599°)) + (1.53340623701639 × (sin 11.2300225086599°))i = 1.50404648119798 + 0.298628314325244i
z2 = 3
3.60555127546399
× (cos((33.6900675259798° + (2 × 180 × 1))/3) + i sin ((33.6900675259798° + (2 × 180 × 1))/3)) = 1.53340623701639 × (cos((33.6900675259798° + 360)/3) + i sin ((33.6900675259798° + 360)/3)) = (1.53340623701639 × (cos 131.23002250866°)) + (1.53340623701639 × (sin 131.23002250866°))i = −1.01064294709398 + 1.15322830402742i
z3 = 3
3.60555127546399
× (cos((33.6900675259798° + (2 × 180 × 2))/3) + i sin ((33.6900675259798° + (2 × 180 × 2))/3)) = 1.53340623701639 × (cos((33. 6900675259798° + 720)/3) + i sin ((33.6900675259798° + 720)/3)) = (1.53340623701639 × (cos 251.23002250866°)) + (1.53340623701639 × (sin 251.23002250866°))i = −0.493403534104007 − 1.45185661835266i
6900675259798° + 720)/3) + i sin ((33.6900675259798° + 720)/3)) = (1.53340623701639 × (cos 251.23002250866°)) + (1.53340623701639 × (sin 251.23002250866°))i = −0.493403534104007 − 1.45185661835266i
z1 = 1.50404648119798 + 0.298628314325244i
z2 = −1.01064294709398 + 1.15322830402742i
z3 = −0.493403534104007 − 1.45185661835266i
z1 = 1.53340623701639 × (cos(11.2300225086599°) + i sin(11.2300225086599°))
z2 = 1.53340623701639 × (cos(131.23002250866°) + i sin(131.23002250866°))
z3 = 1.53340623701639 × (cos(251.23002250866°) + i sin(251.23002250866°))
Извлечение корня n−й степени из комплексного числа, записанного в тригонометрической форме
Извлечем корень 3 степени из числа 3(cos((π/5)) + sin((π/5))i)
Применим формулу Муавра чтобы извлечь корень n−й степени:
n√z = n√|z| × (cos (φ + 2πk)/n + i sin (φ + 2πk)/n)), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
n – степень корня (количество корней)
k – принимает значения 0, 1, 2, … n−1
z1 = 3
3
× (cos((36° + (2 × 180 × 0))/3) + i sin ((36° + (2 × 180 × 0))/3)) = 1. 44224957030741 × (cos((36° + 0)/3) + i sin ((36° + 0)/3)) = (1.44224957030741 × (cos 12°)) + (1.44224957030741 × (sin 12°))i = 1.41073295685556 + 0.299860546743801i
44224957030741 × (cos((36° + 0)/3) + i sin ((36° + 0)/3)) = (1.44224957030741 × (cos 12°)) + (1.44224957030741 × (sin 12°))i = 1.41073295685556 + 0.299860546743801i
z2 = 3
3
× (cos((36° + (2 × 180 × 1))/3) + i sin ((36° + (2 × 180 × 1))/3)) = 1.44224957030741 × (cos((36° + 360)/3) + i sin ((36° + 360)/3)) = (1.44224957030741 × (cos 132°)) + (1.44224957030741 × (sin 132°))i = −0.965053329500603 + 1.07180030522094i
z3 = 3
3
× (cos((36° + (2 × 180 × 2))/3) + i sin ((36° + (2 × 180 × 2))/3)) = 1.44224957030741 × (cos((36° + 720)/3) + i sin ((36° + 720)/3)) = (1.44224957030741 × (cos 252°)) + (1.44224957030741 × (sin 252°))i = −0.445679627354959 − 1.37166085196474i
z1 = 1.41073295685556 + 0.299860546743801i
z2 = −0.965053329500603 + 1.07180030522094i
z3 = −0.445679627354959 − 1.37166085196474i
z1 = 1. 44224957030741 × (cos(12°) + i sin(12°))
44224957030741 × (cos(12°) + i sin(12°))
z2 = 1.44224957030741 × (cos(132°) + i sin(132°))
z3 = 1.44224957030741 × (cos(252°) + i sin(252°))
Извлечение корня n−й степени из комплексного числа, записанного в показательной форме
Извлечем корень 3 степени из числа 2 × e45°i
Чтобы извлечь корень n−й степени из ненулевого комплексного числа. необходимо сначала данное число представить в тригонометрической форме,
Для того, чтобы представить комплексное число, записанное в показательной форме в тригонометрической форме, необходимо воспользоваться формулой приведенной ниже:
|z| eφi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
2 × e45°i = 2 × (cos(45°) + sin(45°)i)
Применим формулу Муавра чтобы извлечь корень n−й степени:
n√z = n√|z| × (cos (φ + 2πk)/n + i sin (φ + 2πk)/n)), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
n – степень корня (количество корней)
k – принимает значения 0, 1, 2, … n−1
z1 = 3
2
× (cos((45° + (2 × 180 × 0))/3) + i sin ((45° + (2 × 180 × 0))/3)) = 1. 25992104989487 × (cos((45° + 0)/3) + i sin ((45° + 0)/3)) = (1.25992104989487 × (cos 15°)) + (1.25992104989487 × (sin 15°))i = 1.2169902811787 + 0.326091563038355i
25992104989487 × (cos((45° + 0)/3) + i sin ((45° + 0)/3)) = (1.25992104989487 × (cos 15°)) + (1.25992104989487 × (sin 15°))i = 1.2169902811787 + 0.326091563038355i
z2 = 3
2
× (cos((45° + (2 × 180 × 1))/3) + i sin ((45° + (2 × 180 × 1))/3)) = 1.25992104989487 × (cos((45° + 360)/3) + i sin ((45° + 360)/3)) = (1.25992104989487 × (cos 135°)) + (1.25992104989487 × (sin 135°))i = −0.890898718140328 + 0.89089871814034i
z3 = 3
2
× (cos((45° + (2 × 180 × 2))/3) + i sin ((45° + (2 × 180 × 2))/3)) = 1.25992104989487 × (cos((45° + 720)/3) + i sin ((45° + 720)/3)) = (1.25992104989487 × (cos 255°)) + (1.25992104989487 × (sin 255°))i = −0.326091563038355 − 1.2169902811787i
z1 = 1.2169902811787 + 0.326091563038355i
z2 = −0.890898718140328 + 0.89089871814034i
z3 = −0.326091563038355 − 1.2169902811787i
z1 = 1. 25992104989487 × (cos(15°) + i sin(15°))
25992104989487 × (cos(15°) + i sin(15°))
z2 = 1.25992104989487 × (cos(135°) + i sin(135°))
z3 = 1.25992104989487 × (cos(255°) + i sin(255°))
Комплексные числа это, операции с комплексными числами
Комплексные числа (от латинского complexus — связь, сочетание) — это числа вида a+bi, где a, b — вещественные числа, i — мнимая единица, то есть число, для которого выполняется равенство: i² = -1. Число a называется действительной частью комплексного числа, число b называется мнимой частью комплексного числа.
Комплексные числа не так сложны, как могло бы показаться. В начале они назывались невозможными числами. Также их еще называли мнимыми или воображаемыми, поскольку действительно чтобы их представить, требуется немного воображения. В данном обзоре постараемся в доступной форме с наглядными примерами разобраться с данными числами.
Комплексные числа — простое объяснение
Для того, чтобы разобраться с комплексными числами, следует для начала рассмотреть множество действительных чисел. К этому множеству относятся целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.
К этому множеству относятся целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.
Рассмотрим две точки на прямой А = 1 и Б = 2. Сложим эти две точки. Их сумма эта третья точка В = 1+2 = 3.
Точки также можно перемножать. Посмотрим, например, как действует умножения на минус 2. Данное действие преобразует точку 1 в минус 2. Если мы снова умножим на минус 2, то нужно будет повторить аналогичное передвижение на прямой, поменять стороны относительно начала координат и удвоить расстояние до него. В результате получим 4.
Умножение на минус 1 устроено просто. Каждая точка переходит в симметричную ей относительно начала координат. Другими словами нужно сделать пол оборота (повернуть на 180°). Повторение умножения на минус 1 приводит в исходное положение. Умножение на минус 1 переводит 1 в минус 1. Если еще раз умножить на минус 1, мы вернемся обратно в 1.
На данном этапе можно выделить правило, что если умножить число на себя, результат всегда будет положительным. Другими словами минус 1 не имеет квадратного корня. Но только не в случае с комплексными числами.
Другими словами минус 1 не имеет квадратного корня. Но только не в случае с комплексными числами.
В начале 19 века Робер Арган высказал следующую идею. Поскольку умножить на минус 1 означает повернуть на 180°, то квадратный корень из минус 1 означает повернуть на половину (90°). Если повернуть дважды на четверть оборота, вы сделаете пол оборота. Квадрат четверти оборота — это пол оборота (минус 1). То есть квадратный корень из минус 1 отвечает точке, в которую минус 1 переходит при повороте на 90°. Поскольку такое построение, выходящее за пределы горизонтальной прямой, выглядит странным, говорят, что такая точка, являющаяся квадратным корнем из минус 1 — это мнимое число. И в математике оно обозначается — i.
С выходом за пределы прямой, все последующие действия производятся легко. Можно отметить числа 2i, 3i и так далее. Каждой точке плоскости отвечает комплексное число. И наоборот — всякое комплексное число задает точку на плоскости.
Операции с комплексными числами
Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания, умножения и деления. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел. Например, нельзя указать, какое из двух комплексных чисел больше или меньше.
Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел. Например, нельзя указать, какое из двух комплексных чисел больше или меньше.
Сложение и вычитание комплексных чисел
Комплексные числа могут складываться и вычитаться как обычные.
Рассмотрим точку, обозначающую число 1+2i. Прибавим к нему число 3+1i. Можно сложить столбиком и получить 4+3i. Геометрически это обычное сложение векторов.
Разность комплексных чисел, записанных в алгебраической форме, представляет собой комплексное число, действительная часть которого и коэффициент при мнимой части равны соответственно разности действительных частей и разности коэффициентов при мнимой части уменьшаемого и вычитаемого.
В общем виде вычитание комплексных чисел z1 = a+bi и z2 = c+di можно записать так: z1-z2 = (a+bi)-(c+di) = (a-c)+(b-d)i.
Несколько примеров вычитания:
- (5+9i)-(3+24i) = (5-3)+(9-24)i = 2-15i.
- (-4+16i)-(11-8i) = (-4-11)+(16+8)i = -15+24i.

Умножение и деление комплексных чисел
Комплексные числа перемежаются точно также, как и действительные числа. Рассмотрим несколько примеров.
2×(1+1i) = 2+2i. Геометрически умножение на два выглядит как растягивание прямой с точкой на плоскости в два раза.
Умножать на i также не сложно. Известно, что i отвечает четверти оборота. Например, чтобы умножить 3+1i на i, достаточно повернуть точку на четверть оборота. Получаем -1+3i.
Умножим два комплексных числа 2+1,5i и -1+2,4i:
Сначала нужно умножить (-1+2,4 i) на два, затем на 1,5i. Далее складываются результаты. (2+1,5i)×(-1+2,4i) = 2(-1+2,4i)+1,5i(-1+2,4i) = -2+4,8i-1,5i+3,6×i×i. i в квадрате равно минус 1. Соответственно -2+4,8i-1,5i+3,6×i×i = -2+4,8i-1,5i-3,6 = -5,6+3,3i.
Частное комплексных чисел z1 = x1+y1i и z2 = x2+y2i в алгебраической форме находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:
z1÷z2 = (x1+y1i)÷(x2+y2i) = ((x1+y1i)×(x2-y2i))÷((x2+y2i)×(x2-y2i)) = ((x1×x2+y1×y2)÷(x2²+y2²)) + (i×(x2×y1-x1×y2)÷(x2²+y2²)).
Рассмотрим пример деления -1+3i на 1+2i. Используя формулу для нахождения частного, получаем:
z1÷z2 = (-1+3i)÷(1+2i) = ((-1+3i)×(1-2i))÷((1+2i)×(1-2i)) = ((-1×1+3×2)÷(1²+2²))+(i×(3×1+(-1)×(-2))÷(1²+2²)) = 5÷5+i×5÷5 = 1+i.
Комплексные числа — тригонометрическая форма
Казалось бы, плоскость двухмерная, так как для описания произвольной точки нужны два числа. На самом же деле можно обойтись одним числом. Для этого используется тригонометрическая форма представления. То есть z = a+bi можно представить как z = [z]×(cosφ+i×sinφ), где:
- [z] — модуль комплексного числа. Это расстояние от соответствующей точки до начала координат на плоскости. Например, модуль 2 + 1,5i = 2,5.
- φ (argz) — аргумент комплексного числа. Он находится измерением угла между осью абсцисс и прямой, соединяющей начало координат с точкой, отвечающей числу. Аргумент 2 + 1,5i = 36,8°.
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: [z] = √(a²+b²). Данная формула справедлива для любых значений a и b.
Данная формула справедлива для любых значений a и b.
Для нахождения аргумента (φ или argz) нужно воспользоваться следующими формулами:
- Если a>0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле argz = arctg(b/a).
- Если a<0, b>0 (2-я координатная четверть), то аргумент нужно находить по формуле argz = π+arctg(b/a).
- Если a<0, b<0 (3-я координатная четверть), то аргумент нужно находить по формуле argz = -π+arctg(b/a).
Как видно, комплексные числа не так сложны, как могло бы показаться на первый взгляд. Ознакомившись с простым объяснением и методикой работы с ними, вы научитесь складывать, вычитать, умножать и делить комплексные числа. Также вы сможете переводить комплексные числа из алгебраической формы в тригонометрическую.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 12Следующая ⇒
3.1. Даны комплексные числа и . Вычислить . 3.2. Даны числа: , . Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме. 3.3. Даны числа . Вычислить . 3.4. Решить уравнение .
Краткие теоретические сведения для выполнения контрольной работы № 3 и решение типовых задач
Действия над комплексными числами В алгебраической форме
Выражение вида (1) где х и у – произвольные действительные числа, i – мнимая единица, удовлетворяющая условию , называется алгебраической формой записи комплексного числа. Число х называется действительной частью комплексного числа z и обозначается , число у называется мнимой частью комплексного числа z и обозначается . При число совпадает с вещественным числом х, если число называется чисто мнимым. Два комплексных числа называются равными, если у них равны соответственно действительные и мнимые части: . Комплексные числа называются сопряженными, если у них равны действительные части, а мнимые противоположны по знаку; сопряженные числа обозначают . Определим основные действия над комплексными числами и , заданными в алгебраической форме. Суммой двух комплексных чисел называется комплексное число , т.е. при сложении комплексных чисел складываются действительные и мнимые части соответственно. Разностьюкомплексных чисел называется комплексное число , которое удовлетворяет равенству . Очевидно: . При нахождении разности из действительной и мнимой частей уменьшаемого z1 вычитаются соответственно действительная и мнимая части вычитаемого z2. Произведением комплексных чисел называется комплексное число . Частным от деления называется такое комплексное число z, которое удовлетворяет уравнению . Для частного имеет место формула: Чтобы разделить число z1 на z2 , следует числитель и знаменатель дроби умножить на число , сопряженное знаменателю. Возведение комплексного числа z в степень n – это нахождение произведения n сомножителей, каждый из которых равен z, т.е. . При возведении в степень n используется правило возведения в степень двучлена , в общем случае применяется формула бинома Ньютона.
Пример Даны комплексные числа . Вычислить . Решение , , , , , Тригонометрическая и показательная формы комплексного числа
Комплексное число изображается на плоскости Оху точкой М с координатами (х;у), либо вектором, начало которого находится в точке О(0;0), а конец – в точке (рис.
у=Im z
М(х,у) r j 0 х=Re z Рис. 1
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось Ох – действительной осью, ось Оу – мнимой осью. Число r – длина радиус-вектора точки (расстояние точки М от начала координат) называется модулем комплексного числа . ( 2 ) Угол j, который образован вектором с осью Ох и отсчитываемый от положительного направления оси Ох, называется аргументомкомплексного числа и обозначается Arg z. Аргумент комплексного числа определен с точностью до слагаемого, кратного : где – главное значение аргумента, определяемое условием . Аргумент числа неопределен. Если вектор расположен в верхней полуплоскости, то угол j отсчитывается от положительного направления оси Ох против часовой стрелки до направления вектора , в данном случае . Если вектор расположен в нижней полуплоскости, то угол j отсчитывается от положительного направления оси Ох по ходу часовой стрелки до направления вектора , в данном случае . Если , то будем считать, что . Существует несколько подходов к определению аргумента. Один из них состоит в следующем. Если , то аргумент , где . Учитывая, что , получим — ( 3 ) тригонометрической форма записи комплексного числа.
Используя формулу Эйлера , получим показательную форму комплексного числа: , ( 4 ) где – модуль, – аргумент комплексного числа. Пример Даны комплексные числа: , . Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме.
Решение (рис. 2) у
7 z5 5,5 z3 z6 2 z2z1 -7 -5,5 -3,5 0 2 6 12,1 х -2 z8 -6 z4
z7 -12,1
Рис.
1. Найдем модуль и аргумент для комплексного числа . Подставляя модуль и аргумент в формулы (3) и (4), получим . 2. Для имеем: Следовательно: .
3. Для имеем:
Следовательно: . 4. Для имеем:
Следовательно: . 5. Для имеем: Следовательно: . 6. Для имеем: Следовательно: .
7. Для имеем: , Следовательно: . 8. Для имеем: . Следовательно: .
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
|||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Value of I — Наиболее часто используемые значения i
Комплексные числа являются одними из самых интересных и забавных разделов математики. Чтобы правильно понимать комплексные числа, необходимо знать основы системы счисления. Эта статья была написана для того, чтобы рассказать вам о значении i. Существует распространенное мнение, что комплексные числа трудно понять и они очень запутаны. Это далеко от истины, потому что мы можем гарантировать, что комплексные числа очень забавны и просты для понимания.
Действительное число обозначается действительным числом, а мнимая часть комплексного числа обозначается буквой i. Эта статья о том же i. Он сообщает вам, каково точное значение i и имеет ли оно точное измеримое значение или нет. Добавление мнимой части к числу делает число комплексным. Это очень простая тема, которая требует серьезного внимания с самого начала, так что расслабьтесь, расслабьтесь и наслаждайтесь этой веселой статьей от Vedantu о ценности i.
Добавление мнимой части к числу делает число комплексным. Это очень простая тема, которая требует серьезного внимания с самого начала, так что расслабьтесь, расслабьтесь и наслаждайтесь этой веселой статьей от Vedantu о ценности i.
Значение i или понятие i используется для объяснения и выражения комплексных чисел. Комплексные числа — это числа, у которых есть действительная и мнимая части. Мнимая часть определяется с помощью i. По сути, «i» — это мнимая часть, которую также называют йотой.
Значение i равно √-1 Отрицательное значение внутри квадратного корня означает мнимое значение. Все основные арифметические операторы применимы к мнимым числам. При возведении в квадрат мнимого числа мы получаем отрицательное значение.
При изучении комплексных чисел «i» имеет большое значение. Мы попытаемся понять сложности, связанные со значением i, на нескольких примерах. Мы также подробно обсудим высшие степени «i». Благодаря лучшему пониманию этих концепций учащиеся могут с большей легкостью решать сложные числовые задачи.
Каково значение i?
Заявление было предложено в начале этой статьи. Утверждение было о точном значении или измерении того, что означает i. Эта часть статьи посвящена этому и объясняет, имеет ли оно конкретное значение или нет.
Мнимая часть комплексного числа определяется как «йота». Для вычисления значения мнимого числа мы используем обозначение йота или «i». Квадратный корень из отрицательного числа дает нам мнимое число.
Значение i = √-1
Мы используем это значение i для понимания концепций комплексных чисел.
Для квадратного уравнения x2 + 1 = 0
x2 = -1
x = √-1
Здесь √-1 — мнимая часть.
я = √-1
i2 = -1
Как обсуждалось ранее, возведение в квадрат мнимого числа дает нам отрицательное значение.
i = √-1
Возведение в квадрат с обеих сторон
i2 = -1
Любое комплексное число представляет собой комбинацию действительного числа и мнимого числа. Все недействительные значения представлены йотой или «i».
Все недействительные значения представлены йотой или «i».
Примеры действительных чисел: 10, -20, √3 и т. д.
Примеры мнимых чисел: 2i, √-5, -i и т. д.
Комплексные числа имеют форму a + ib, где i означает мнимое часть. Ноль тоже комплексное число. В комплексном числе к действительной части можно прибавлять или вычитать только действительную часть, а к мнимой можно прибавлять или вычитать только мнимую часть.
Значение i
Теперь попробуем понять значение i в комплексном числе. Для любого комплексного числа
a + ib, a и b — действительные числа, где i означает мнимую часть. Значение i в квадрате
i2 = -1 дает нам отрицательное число.
При умножении отрицательного целого числа на это значение мы получаем
-i2 = 1
Если мы умножаем i на i2, мы получаем
i x i2 = i(-1)= -i
При дальнейшем умножении мы получит
-i x i = -i2 = -(-1)=1
Ниже приведена таблица с часто используемыми значениями i. Учащиеся могут обращаться к этим значениям при решении задач с комплексными числами.
Учащиеся могут обращаться к этим значениям при решении задач с комплексными числами.
Values of i
Degree | Mathematical Calculation | Value | |||||
i2 | i * i | -1 | |||||
i3 | i * i * i | -i | |||||
i4 | i * i * i * i | 1 | |||||
i5 | i * i * i * i * i | i | |||||
i6 | i * i * i * i * i * i | -1 | |||||
i0 | I1-1 | 1 | |||||
I-1 | 1/I = I/I2 = I/-1 | -I | -I | 9008||||
-I | 9008|||||||
-I | 9008-I | 9008-I | 9008-I | 18-I | 9008. | 1/i2 = 1/-1 | -1 |
i-3 | 1/ i3 = 1/-i | i |
Запоминание всех этих значений может сбивать с толку и утомлять! Есть трюк для решения более высоких степеней i. Значения i следуют круговому шаблону. Давайте посмотрим на этот шаблон:
i4n = 1
i4n+1 = i
i4n+2 = -1
i4n+3 = -i
Используя этот круг формул, учащиеся могут вычислить значения i.
. i7 = -1
i8 = -i
При n = 2,
i9 = 1
i10 = i
i11 = -1
i12 = -i
Значение высших степеней i следует этой круговой формуле. Математика — это концептуальное и прикладное исследование. Это не способствует изучению ценностей. Знакомство с концепциями поможет вам лучше понять математические приложения.
Знакомство с концепциями поможет вам лучше понять математические приложения.
Комплексные числа являются фундаментальной темой изучения. Понятие мнимых чисел составляет значительную его часть. Студенты могут прояснить свои концепции, пройдя эти решенные примеры.
Найдите значение 1 + √-3.
Ответ: 1 + √-3 — комплексное число с действительной и мнимой частями.
Мы знаем, что
√-1 = i. Подставляя это значение, мы получаем
1 + 3i
Это упрощенная форма уравнения.
Заключение
Мы надеемся, что эта статья смогла подробно объяснить, что такое значение i, и облегчила вам тему комплексных чисел. Целью статьи было предложить иной подход к теме комплексных чисел. Подход, который может дать вам очень четкое и уникальное понимание темы. Веданту стремится дать своим ученикам только самое лучшее, и статья о ценности i была еще одной нашей попыткой сделать то же самое.
Комплексные числа: степени и корни
Комплексные числа: степени и корни Степени комплексных чисел — это просто частные случаи произведений, когда мощность — целое положительное число. Мы уже изучили мощности воображаемой единицы и и обнаружили, что они совершают цикл в периоде длины 4.и так далее. Причины заключались в том, что (1) абсолютное значение | и | число i было единицей, поэтому все его степени также имеют абсолютное значение 1 и, следовательно, лежат на единичной окружности, и (2) аргумент arg( i ) числа i было равно 90°, поэтому его n -я степень будет иметь аргумент n 90°, и эти углы будут повторяться в периоде длины 4, поскольку 4 · 90° = 360°, полный круг.
В более общем случае вы можете найти z n как комплексное число (1), абсолютное значение которого равно | из | n , n th степень абсолютного значения z , и (2) чей аргумент равен n раз больше аргумента z.
На рисунке вы видите комплексное число z , абсолютное значение которого составляет корень шестой степени из 1/2, то есть | из | = 0,89, а аргумент равен 30°. Здесь единичный круг закрашен черным, а за пределами единичного круга — серым, поэтому z находится в черной области. Поскольку | из | меньше единицы, его квадрат находится на 60° и ближе к 0. Каждая высшая степень дальше на 30° и даже ближе к 0. Первые шесть степеней отображаются, как вы можете видеть, в виде точек на спирали. Эта спираль называется геометрический или экспоненциальный спиральный.
Корни.
Обратите внимание, что в последнем примере z 6 находится на отрицательной действительной оси примерно на -1/2. Это означает, что z примерно равно одному из корней шестой степени из -1/2. На самом деле существует шесть корней шестой степени любого комплексного числа. Пусть z — комплексное число, а z — любой его корень шестой степени. С по 6 = w, следует, что
С по 6 = w, следует, что
- абсолютное значение w , | с | есть | из | 6 , так что | из | = | с | 1/6 и
- 6 arg( z ) равно arg( w ), поэтому arg( z )=arg( w )/6.
Например, возьмем w как -1/2, зеленую точку на рисунке справа. Затем | с | равно 1/2, а arg( w ) равно 180°. Пусть z — корень шестой степени из w. Затем (1) | из | есть | с | 1/6 , что примерно 0,89. Кроме того, (2) аргументом w является arg( w ) = 180°. Но один и тот же угол мог быть назван любым из

Если мы возьмем 1/6 каждого из этих углов, то у нас будут возможные аргументы для z :
Так как каждый из углов для z отличается на 360°, то каждый из возможных углов для z будет отличаться на 60°. Эти шесть шестых корней из -1/2 показаны на рисунке синими точками.
Больше корней единства.
Напомним, что « n -й корень из единицы» — это просто другое название n -го корня из единицы. Четвертые корни составляют ± 1, ± 90 287 i, 90 288, как отмечалось ранее в разделе об абсолютном значении. Мы также увидели, что восемь восьмых корней из единицы, когда мы смотрели на умножение, были ± 1, ± 90 287 i, 90 288 и ± √ 2/2 ± 90 287 i 90 288 √ 2/2. Рассмотрим теперь шестые корни из единицы. Они будут размещены по кругу с интервалом в 60°. Два из них, конечно, ±1. Пусть w — с аргументом 60°. Треугольник с вершинами 0, 1 и w 90 288 является равносторонним треугольником, поэтому легко определить координаты 90 287 w.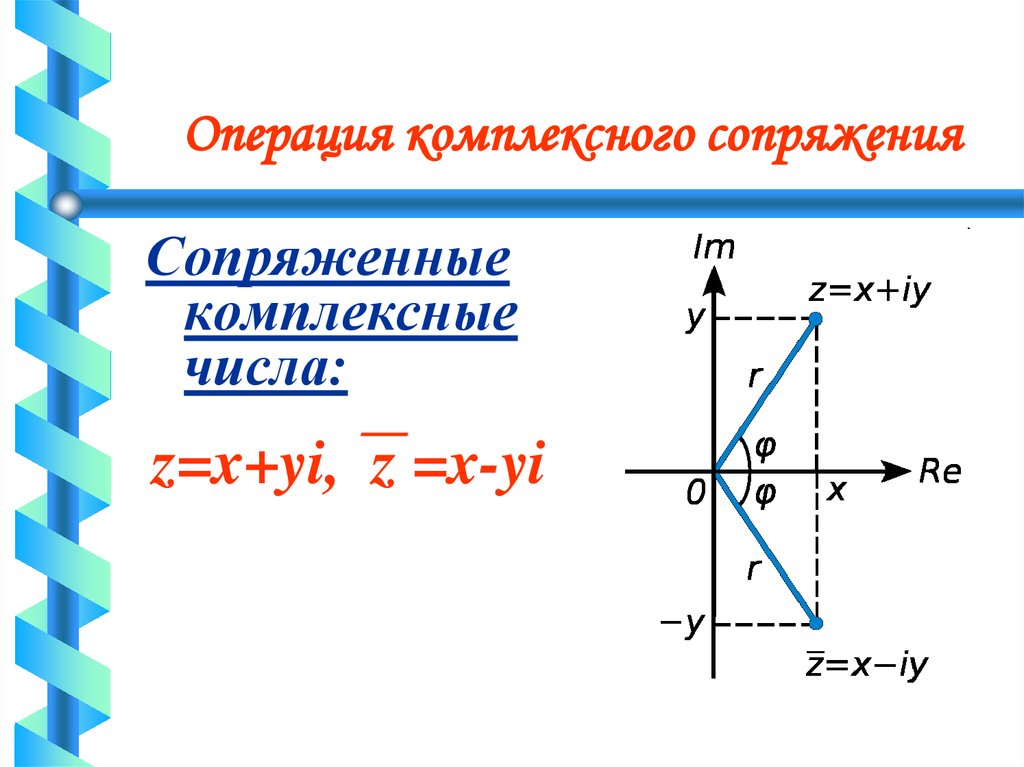 Координата x равна 1/2, а координата y равна √3/2. Следовательно, w равно (1 + i √3)/2. Остальные корни шестой степени являются отражением w в действительной и мнимой осях. Таким образом, шесть шестых корней из единицы равны ± 1 и (± 1 ± 90 287 i 90 288 √ 3)/2 (где + и можно брать в любом порядке).
Координата x равна 1/2, а координата y равна √3/2. Следовательно, w равно (1 + i √3)/2. Остальные корни шестой степени являются отражением w в действительной и мнимой осях. Таким образом, шесть шестых корней из единицы равны ± 1 и (± 1 ± 90 287 i 90 288 √ 3)/2 (где + и можно брать в любом порядке).
Некоторые из этих шестых корней также являются нижними корнями из единицы. Число 1 представляет собой квадратный корень из единицы, (1 ± i √3)/2 являются кубическими корнями из единицы, а сама 1 считается кубическим корнем, квадратным корнем и «первым» корнем (любым является первым корнем самого себя). Но оставшиеся два корня шестой степени, а именно (1 ± i √3)/2, являются корнями шестой степени, а не нижними корнями из единицы. Такие корни называются примитивными , , поэтому (1 ± i √3)/2 — это два примитивных корня шестой степени из единицы.
Забавно находить корни единства, но мы уже нашли большинство самых простых.
мнимых чисел — Расчет | Значение in в математике
Греческий математик по имени Герой Александрийский первым изобрел мнимые числа. Позже, в 1572 году, итальянский математик Джероламо Кардано разработал правила умножения мнимых чисел. Эти числа помогают находить квадратные корни отрицательных чисел.
Давайте узнаем больше о мнимых числах вместе с их определением, примерами и геометрической интерпретацией. Кроме того, давайте посмотрим, как выполнять вычисления с этими числами.
| 1. | Что такое мнимые числа? |
| 2. | Геометрическая интерпретация мнимых чисел |
| 3. | я по математике |
| 4. | Вычисление мнимых чисел |
| 5. | Советы и рекомендации по мнимым числам |
| 6. | Часто задаваемые вопросы о мнимых числах |
Что такое мнимые числа?
Мнимые числа — это числа, которые при возведении в квадрат дают отрицательное число. Они также определяются как квадратный корень из отрицательных чисел. Мнимое число — это произведение ненулевого действительного числа и мнимой единицы «i» (известной также как «йота»), где i = √(-1) (или) i 2 = -1.
Они также определяются как квадратный корень из отрицательных чисел. Мнимое число — это произведение ненулевого действительного числа и мнимой единицы «i» (известной также как «йота»), где i = √(-1) (или) i 2 = -1.
Попробуем возвести в квадрат некоторые действительные числа:
(−2) 2 = −2×−2 = 4
5 2 = 5×5 = 25
(1,3) 2 = 1,3×1,3 = 1,69
13 Is любой из результатов отрицательное число? Нет. Это означает, что квадрат любого действительного числа всегда положителен. Тогда какое число дает отрицательный квадрат? Это мнимое число. В математике мы много раз сталкиваемся с квадратным корнем из отрицательных чисел, особенно в случае решения квадратных уравнений по квадратной формуле. В таких случаях использование мнимых чисел обязательно. Вот несколько примеров мнимых чисел:- √(-4) = √(-1) · √4 = i (2) = 2i
- √(-3) = √(-1) · √3 = я √3
В приведенных выше примерах 2i и i √3 — мнимые числа. Мы видим, что каждое из этих чисел является произведением ненулевого действительного числа и i. Таким образом, мы можем вывести правило для мнимых чисел:
Мы видим, что каждое из этих чисел является произведением ненулевого действительного числа и i. Таким образом, мы можем вывести правило для мнимых чисел:
- √(-x) = i √x
Это часть комплексных чисел, где комплексное число представляет собой сумму действительного числа и мнимого числа. т. е. комплексное число имеет форму a + ib, где и «a», и «b» — действительные числа, а здесь bi — мнимое число.
Геометрическая интерпретация мнимых чисел
Обычно мы представляем комплексное число a+bi точкой (a, b) на плоскости Аргана. Например, комплексное число 1-3i представляет точку (1, -3) на плоскости Аргана. Таким образом, мнимое число bi (которое можно записать как 0 + bi) представляет собой точку (0, b) на плоскости и, следовательно, является точкой на вертикальной оси (воображаемой оси). Таким образом, мнимые числа всегда лежат на вертикальной оси плоскости Аргана. Вот несколько примеров.
я по математике
Что такое член i в комплексном числе x+iyx+iy, соответствующий точке P(x, y)? Ясно, что «i» не может быть действительным числом, потому что если бы i было действительным, то x+iyx+iy также было бы действительным и лежало бы на самой действительной оси. Таким образом, если бы i было реальным, то x+iy представляли бы только точки на действительной оси, а не точки на плоскости.
Таким образом, если бы i было реальным, то x+iy представляли бы только точки на действительной оси, а не точки на плоскости.
Если мы хотим представить точки на плоскости с помощью чисел, i должно быть недействительным числом в том смысле, что оно не должно принадлежать множеству вещественных чисел. Мы интерпретируем i в математике следующим образом: «i — одна единица в направлении, перпендикулярном действительной оси». На приведенном выше рисунке мы видим, что точка (0, 1) — это не что иное, как «i».
Таким образом, в комплексном числе x+iy член iy становится недействительным числом: он представляет y, умноженное на i, то есть y единиц в направлении i. Следовательно, x+iy представляет собой точку, до которой можно добраться, переместив x единиц в реальном направлении и y единиц в направлении i (от начала координат):
Значение i
Получается, что арифметически i 2 = −1. Другими словами, значение i равно квадратному корню из −1. Пока не спрашивайте как! Как мы уже говорили ранее, различные части головоломки комплексных чисел встанут на свои места по мере того, как вы углубитесь в эту тему.
Пока не спрашивайте как! Как мы уже говорили ранее, различные части головоломки комплексных чисел встанут на свои места по мере того, как вы углубитесь в эту тему.
На этом этапе просто имейте в виду, что:
i — недействительное число (оно лежит вне множества Real).
i представляет одну единицу, перпендикулярную реальному направлению.
yi представляет единицы y, перпендикулярные реальному направлению
x+iy представляет точку (x, y)
i — это квадратный корень из −1, или i 2 = −1.
Когда мы говорим, что i — ненастоящее число, мы не имеем в виду, что i не существует или является плодом нашего воображения. Мы хотим сказать, что i нереален в том смысле, что ему не нравится набор Real. Однако это вполне допустимая математическая сущность. я также известен под именем «йота».
Вычисление мнимых чисел
Мы можем производить все вычисления с мнимыми числами так же, как и с действительными числами. Давайте посмотрим, как мы их делаем.
Давайте посмотрим, как мы их делаем.
Сложение/вычитание мнимых чисел
Сложение или вычитание мнимых чисел точно так же, как мы комбинируем одинаковые термины в алгебре. Например:
- 2i + 3i = 5i
- 2i — 3i = -i
Умножение мнимых чисел
Мы умножаем мнимые числа точно так же, как мы умножаем термины в алгебре. Здесь нам, возможно, придется использовать правило показателей степени a m × a n = a m+n . Но здесь мы должны позаботиться о том, что i 2 = -1. Вот несколько примеров.
- 2i × 3i = 6i 2 = 6(-1) = -6
- 3i 2 × -5i 3 = -15i 5 = -15 (i 2 ) 2 i = -15 (-1) 2 i = -15i
Нам может показаться, что упростить возможности йоты сложно. Вот несколько правил, которые облегчают процесс нахождения степеней i при умножении комплексных чисел.
- я 4k = 1
- i 4k+1 = 1
- i 4k+2 = -1
- я 4k+3 = -я
где k — целое число. Эти правила гласят, что «i», возведенное в число, равно «i», возведенному в число, которое является остатком, полученным от деления исходного числа на 4. Например:
Эти правила гласят, что «i», возведенное в число, равно «i», возведенному в число, которое является остатком, полученным от деления исходного числа на 4. Например:
- я 4 = я 0 = 1
- я 17 = я 1 = я
Любая степень i равна одной из 1, i, -i и -1 после упрощения. Мы можем понять это из рисунка ниже.
Эти правила действительно очень упростили вычисление произведения мнимых чисел.
Деление мнимых чисел
При делении мнимых чисел мы используем правило показателей степени a m / a н = а м-н . В результате после деления мы обычно не оставляем «i» в знаменателе. Если получается, то используем правило 1/i = -i (это потому, что 1/i = 1/i · i/i = i/i 2 = i/(-1) = -i). Вот несколько примеров:
- 4i/2i = 2
- 3i 3 / 4i 6 = 3/(4i 3 ) = 3/(4(i 2 )(i)) = -3/(4i) = (-3/4)(- и) = 3i/4
Советы и рекомендации по мнимым числам
- Когда знак минус выходит из квадратного корня, он становится i, потому что значение i в математике равно i = √(-1).

- \(\sqrt[n]{x}\) можно упростить, используя мнимые числа, где x отрицательное, а n четное число.
- Когда «i» является знаменателем (или в случае отрицательных степеней i), используйте правило 1/i= -i.
- i n = i r , где r — остаток от деления n на 4. Тогда можно применить одно из правил: i 2 = -1, i 3 = -i, i 4 = 1.
Часто задаваемые вопросы о мнимых числах
Что такое определение мнимых чисел?
Мнимое число — это число, являющееся произведением ненулевого действительного числа и йоты «i». Здесь i = √(-1) или i 2 = -1. Эти числа помогают найти квадратный корень из отрицательных чисел. Некоторые примеры мнимых чисел: -4i, 6i, i и т. д.
Каково значение i в математике?
«i» в математике известен как воображаемая единица. Его значение равно √-1. Он используется для вычисления квадратных корней отрицательных чисел. Это также часть комплексных чисел.
Это также часть комплексных чисел.
Что такое процесс упрощения мнимых чисел?
Чтобы сложить/вычесть мнимые числа, мы просто складываем/вычитаем их коэффициенты. Например, -2i + 8i — 4i = i. Мы умножаем/делим мнимые числа точно так же, как мы делаем это с терминами в алгебре. Но мы используем факты i 2 = -1 и 1/i = -i при умножении/делении мнимых чисел.
В чем разница между мнимыми числами и комплексными числами?
Мнимое число имеет форму bi, тогда как комплексное число имеет форму a+bi, где a и b — действительные числа. Все мнимые числа являются комплексными числами (поскольку «а» может быть 0), но все комплексные числа могут не быть мнимыми числами.
В чем разница между мнимыми числами и реальными числами?
Вещественное число может быть натуральным, целым, целым, рациональным или иррациональным числом. Но мнимое число — это произведение действительного числа и «i», где i = √(-1). Мы используем мнимые числа для вычисления квадратного корня из отрицательных чисел. Например, √(-9) = √(-1) . √9 = я (3) = 3я.
Например, √(-9) = √(-1) . √9 = я (3) = 3я.
Что такое правила мнимых чисел?
Вот несколько правил, которые помогут вычислить мнимые числа.
- я = √(-1)
- я 2 = -1
- я 3 = -я
- я 4 = 1
- i n = i r , где r — остаток от деления n на 4.
- 1/i = -i, и это правило полезно для вычисления отрицательных степеней i.
Как записать действительное число через i в математике?
Любое действительное число x может быть записано как x + i0. Другими словами, действительное число также можно рассматривать как комплексное число, в котором недействительная часть равна 0. Таким образом, каждое действительное число является комплексным числом. Иными словами, реальное множество является подмножеством сложного множества. Это также должно быть очевидно геометрически: реальная линия является подмножеством комплексной плоскости.
Каково применение мнимых чисел?
- Мнимые числа используются для упрощения извлечения квадратных корней из отрицательных чисел.

- Используются при решении квадратных уравнений.
- Используются при формировании комплексных чисел.
- Они используются в физике и в сложных вычислениях.
Является ли 0 мнимым числом?
Хотя 0 можно записать как 0i, это не мнимое число, поскольку оно не связано с квадратным корнем любого отрицательного числа. Вот почему мы четко указываем в определении мнимого числа, что оно имеет форму bi, где b — ненулевое действительное число. 92\cdot i=-i$.
$\sqrt{a}\sqrt{b}=\sqrt{ab}$ гарантируется только для положительных действительных $a$ и $b$.
$\endgroup$
0
$\begingroup$
Мы не можем сказать, что $\sqrt{a}\sqrt{b}=\sqrt{ab}$ для отрицательных $a$ и $b$. Если бы это было так, то $1=\sqrt{1}=\sqrt{\left(-1\right)\cdot\left(-1\right)} = \sqrt{-1}\sqrt{-1}= i\cdot i=-1$. Поскольку это неверно, мы должны сказать, что $\sqrt{a}\sqrt{b}\neq\sqrt{ab}$ вообще, когда мы расширяем его для приема отрицательных чисел.
$\endgroup$
$\begingroup$
Я уверен, что все правильно ответили на вопрос. Но вот мои 2 цента:
С точки зрения плоскости Аргана, умножение комплексного числа на $i$ эквивалентно повороту его по окружности (радиус = модуль комплексного числа) против часовой стрелки на 90 градусов. Поэтому спросите себя, где вы окажетесь, если возьмете $i$ и дважды умножите на $i$.
$\endgroup$
1 92=а$. Оно определяется не однозначно, так как если $b$ — корень, то и $-b$ — корень (а они совпадают только при $a=0$ или характеристике $2$). Теперь правильное утверждение:
- Если $\sqrt{a}$ и $\sqrt{b}$ являются корнями $a$ соответственно. $b$, то $\sqrt{a}\sqrt{b}$ является корнем $ab$.
Если мы определим $\sqrt{a}$ как набор из всех корней $a$, то $\sqrt{ab}=\sqrt{a}\sqrt{b}$ верно даже дословно. Например, $\sqrt{-1}=\{\pm i\}$ тогда и $\sqrt{(-1) (-1)} = \sqrt{-1} \sqrt{-1}$ так как обе стороны равны $\{\pm 1\}$. 93 = -i$, как показано на следующем рисунке $b$, поэтому его нельзя использовать с комплексными числами.
Например, $\sqrt{-1}=\{\pm i\}$ тогда и $\sqrt{(-1) (-1)} = \sqrt{-1} \sqrt{-1}$ так как обе стороны равны $\{\pm 1\}$. 93 = -i$, как показано на следующем рисунке $b$, поэтому его нельзя использовать с комплексными числами.
$\endgroup$
$\begingroup$
$\sqrt[n]z$ возвращает не одно значение, а n комплексных значений. Отсюда ваша путаница, поскольку и i , и $-i$ входят в число квадратных корней из $-1$.
$\endgroup$ 92$ вы получите $(-1)\cdot i =-i$
это простой трюк.
$\endgroup$
1
$\begingroup$
Кто-то ранее писал, что это i x i x i, что равно -1 x i, т.е. -i (но сообщение, кажется, было удалено!
Но это все, что нужно сказать. Неважно, что представляет i, алгебра Но чтобы доказать это, подставив значение i, т.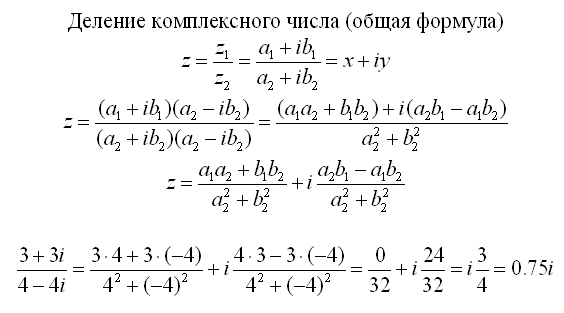 е. (√-1), вы получите
е. (√-1), вы получите
√-1 x √-1 x √-1 = -1 х √-1 = -(√-1) = -я
Однако стоит отметить, что i не является комплексным числом, как предполагалось, — это иррациональное число. Комплексное число имеет вид (x +iy)
. $\endgroup$
2
Комплексные или мнимые числа — Полный курс алгебры
Навыки
в
A L G E B R A
Содержание | Дом
30
Квадратный корень из отрицательного числа
Определяющее свойство i
Полномочия и
Алгебра с комплексными числами
Действительные и мнимые компоненты
Комплексные конъюгаты
ЧТО НАсчет квадратного корня из отрицательного числа? ?
Не может быть 2, потому что 2 в квадрате равно +4, и не может быть -2, потому что -2 в квадрате также равно +4. На самом деле не существует ни положительного, ни отрицательного числа, квадрат которого отрицателен.
Однако, если мы хотим сказать, что у этого уравнения есть решение,
х 2 + 4 = 0
, то мы должны сказать, что это число . Для этого уравнения реализуется
х 2 = −4,
x = ±.
не настоящее число. Мы называем это комплексным или мнимым числом.
Таким образом, такие символы, как , , , и т. д. — квадратные корни отрицательных чисел — мы теперь будем называть комплексными числами. Наше знание комплексного числа при возведении в квадрат дает подкоренное число. , при возведении в квадрат дает -3. Итак, ничто не мешает нам пользоваться этими числами и использовать их в расчетах. Они будут подчиняться всем правилам, которые мы обычно связываем с числом. Мы можем их складывать, вычитать, умножать и так далее.
Теперь, если a — положительное число, то − a = −1 · a . Следовательно, по теореме:
= = .
Квадратный корень из отрицательного числа всегда приводит к множителю . Отсюда будет удобно положить равным i .
= i .
Мы называем и сложной единицей.
я 2 = −1.
Это основное алгебраическое свойство i .
пример 1
Пример 2. −5 i · 6 i = −30 i 2 = 30,
Видим:
Фактор i 2 меняет знак продукта.
Проблема 1. Оцените следующее.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
| а) | i 2 = −1 | б) | i · 2 i = 2 i 2 = 2(−1) = −2 | |
| в) | (3 i ) 2 = 3 2 i 2 = −9 | г) | -5 i · 4 i = -20 i 2 = 20 | |
Пример 3. | = | и | |
| = | я = 2 я | ||
| = | я = 2 я | ||
Квадратный корень из − из равен i , умноженному на квадратный корень из из .
Задача 2. Выразите каждое из следующих чисел в терминах i .
| а) | = я | б) | = 3 i | в) | = 7 i | |||
| г) | = я | д) | = я | е) | = 2 i | |||
| г) | = 3 i | ч) | = 5 i | я) | = 7 i | |||
Примечание: Чтобы умножить комплексные числа, мы должны сначала выразить их через i .
= i · и = −.
Правило не выполняется, когда оба числа a и b отрицательны.
Полномочия и
Начнем с i 0 , что равно 1. (Любое число с показателем степени 0 равно 1.) Каждую степень i можно получить из предыдущей степени, умножив ее на i . У нас есть:
| я 0 | = | 1 |
| i 1 | = | и |
| i 2 | = | −1 |
| i 3 | = | −1 · i = − i |
| i 4 | = | − i · i = — i 2 = -(-1) = 1 |
Поскольку мы вернулись к 1, цикл сил повторится. Любая степень и будут либо
Любая степень и будут либо
1, i , -1 или — i
— по остатку от деления показателя степени n на 4.
Пример 4.
| и 9 | = | i , потому что при делении 9 на 4 остаток равен 1. | |
| я 9 = я 1 . | |||
| i 18 | = | −1, потому что при делении 18 на 4 остаток равен 2. | .|
| и 35 | = | − i , потому что при делении 35 на 4 остаток равен 3. | |
| i 35 = i 3 . | |||
| i 40 | = | 1, потому что при делении 40 на 4 остаток равен 0. | |
| i 40 = i 0 . | |||
Примечание: Четные степени числа i будут равны 1 или −1, в зависимости от того, кратен ли показатель степени 4 или на 2 больше, чем кратен 4. Нечетные степени будут либо i , либо − я .
Задача 3. Оцените каждую степень числа i .
| а) i 3 = − i | б) i 4 = 1 | в) i 6 = i 2 = −1 | ||
| г) i 9 = i 1 = | д) i 12 = я 0 = 1 | е) i 17 = я 1 = я | ||
| г) i 27 = я 3 = — я | ч) i 30 = i 2 = −1 | i) i 100 = я 0 = 1 | ||
Задача 4. |
Алгебра с комплексными числами
Комплексные числа подчиняются тем же правилам, что и действительные числа. Например, чтобы умножить
(2 + 3 i ) (2 − 3 i )
учащийся должен распознать форму ( a + b )( a − b ), которая даст разницу в два квадрата. Следовательно,
| (2 + 3 и ) (2 − 3 и ) | = | 4 − 9 и 2 |
| = | 4 − 9(−1) | |
| = | 4 + 9 | |
| = | 13. | |
Опять же, множитель i 2 меняет знак члена.
Задача 5. Умножение.
Умножение.
а) (1 + i )(1 − i ) = 1 − 2 и 2 знак равно 1 + 2 = 3
| б) (3 − i ) 2 | = | 9 − 6 и + 2 и 2 , | при возведении бинома в квадрат, |
| = | 9 − 6 и − 2 | ||
| = | 7 − 6 и | ||
| в) (2 + 3 i )(4 − 5 i ) | = | 8 − 10 i + 12 i − 15 i 2 |
| = | 8 + 2 и + 15 | |
| = | 23 + 2 и | |
Задача 6. ( x + 1 + 3 i )( x + 1 − 3 i )
а) Какая форма будет получена? Разность двух квадратов.
Урок 19.
б) Умножить.
| ( x + 1 + 3 i )( x + 1 − 3 i ) | = | ( x + 1) 2 − 9 i 2 |
| = | х 2 + 2 х + 1 + 9 | |
| = | x 2 + 2 x + 10 | |
| в) | ( x — 2 — i ) ( x — 2 + i ) | = | ( x − 2) 2 − 2 i 2 |
| = | x 2 − 4 x + 4 + 2 | ||
| = | x 2 − 4 x + 6 | ||
Действительные и мнимые компоненты
Вот то, что сейчас называется стандартной формой комплексного числа:
а + би .
Это действительное число a плюс комплексное число, которое равно bi .
Например,
3 + 2 и .
a — то есть 3 в примере — называется действительной составляющей (или действительной частью). b (2 в примере) называется мнимой составляющей (или мнимой частью).
Компоненты настоящие.
Задача 7. Назовите действительную компоненту a и мнимую компоненту b .
| а) | 3 − 5 i a = 3, b = −5. | б) | 1 + i a = 1, b = . | |
| в) | i a = 0, b = 1. | г) | −6 a = −6, b = 0, | |
Комплексно-сопряженные соединения
Комплексное сопряжение a + bi равно a − bi . Суть сопряженной пары в том, что при их умножении —
Суть сопряженной пары в том, что при их умножении —
( a + до ) ( a − до )
— произведение является положительным вещественным числом. Эта форма представляет собой разность двух квадратов:
( a + bi )( a − bi ) = a 2 − b 2 i 2 = a 2 + b 2
Произведение комплексно сопряженной пары
равно сумме квадратов компонентов.
Задача 8. Вычислите положительное действительное число, которое получается в результате умножения каждого из следующих чисел на его комплексно-сопряженное число.
а) 2 + 3 i
(2 + 3 i )(2 − 3 i ) = 2 2 + 3 2 = 4 + 9 = 13,
б) 3 − i .
(3 − i ) (3 + i ) =
3 2 + () 2 = 9 + 2 = 11.
c) u + iv . .
г) 1 + i . (1 + i ) (1 − i ) = 1 2 + 1 2 = 2.
д) − i . (− я ) ( я ) = − i 2 = 1,
Следующий урок: прямоугольные координаты
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Основные сведения о комплексных числах
Основные сведения о комплексных числах Комплексные числа используются во множестве интересных реальных приложений, таких как
как анализ электронных схем, высокоскоростного обтекания реактивного самолета,
и так далее. Они также являются сердцем и душой некоторых фракталов, таких как этот
недавно обнаруженный четырехмерный объект природы, представленный союзом
множеств Мандельброта и Жюлиа.
Этот сайт знакомит с основной идеей комплексных чисел: откуда откуда они берутся, как их добавить и так далее? Если вы уже знакомы с комплексными числами, вы можете сразу перейти к ним. разделы, которые вы хотели бы освежить:
- Основные определения
- Нанесение комплексных чисел на комплексную плоскость
- Добавление комплексных чисел
- Вычитание комплексных чисел
- Умножение комплексных чисел
- Возведение комплексных чисел в степень
- Использование комплексных чисел для нахождения N-го корня чего-либо в мире
Вперед
В математике, как и в жизни, мы часто натыкаемся на стену, где что-то просто кажется невозможно или нереально. Однако в математике работа с «нереальным» часто приводит к очень реальным результатам. полученные результаты. Комплексные числа — отличный пример этого явления.
Квадратный корень из отрицательной единицы кажется невозможным, нереальным. Но это на самом деле
очень реальное и чрезвычайно важное число в математике. Итак, даем ему имя: i.
Итак, даем ему имя: i.
- ВООБРАЖАЕМАЯ ЕДИНИЦА: Пусть i = воображаемая единица, определенная таким образом, что я 2 = -1.
- КОМПЛЕКСНЫЕ ЧИСЛА: Имеют как действительную, так и мнимую части. Примеры:
- 3+6i (3 — действительная часть, 6i — мнимая часть)
- 4-2и
- х+уи
- ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА: Когда мнимая часть комплексного числа равна нулю, вы получаете
настоящий номер! Примеры:
- 5
- 87
- квадратный корень из 97.3
- ЧИСТО ВООБРАЖАЕМЫЕ ЧИСЛА: Это комплексные числа, действительная часть которых равна нулю. Примеры:
- 5и
- -2,75i
- АМПЛИТУДЫ И МОДУЛИ КОМПЛЕКСНЫХ ЧИСЕЛ: Это будет легче объяснить в следующем разделе о графическом представлении комплексных чисел в сложная плоскость.
Назад к началу
Назад на страницу определений
Графический комплекс
чисел выполняется так же, как и построение точки (x, y) в
прямоугольные координаты; основное отличие состоит в том, что ось Y теперь представляет
ВООБРАЖАЕМЫЕ числа, а не ДЕЙСТВИТЕЛЬНЫЕ, как при построении точек в прямоугольных
координаты. Ниже приведен график, демонстрирующий некоторые цифры (точки)
в комплексной плоскости:
Ниже приведен график, демонстрирующий некоторые цифры (точки)
в комплексной плоскости:
Переслать
Назад
Назад к началу
Назад на страницу определений
Вы добавляете комплексные числа, добавляя действительные части, а затем добавляя воображаемые части. Примеры:
- (3+2i) + (1+3i) = 4+5i
- (-1-i) + (1-2i) = 0-3i
Вот как это выглядит в комплексной плоскости:
Вперед
Назад
Назад к началу
Назад на страницу определений
Чтобы вычесть комплексные числа, мы вычитаем действительные части и мнимые части. Примеры:
- (3+2i) — (1+3i) = (3-1)+i(2-3) = 2-i
- (-2-i) — (2+3i) = (-2-2)+i(-1-3) = -4-4i
Вот как это выглядит в комплексной плоскости — обратите внимание, что это то же самое, что и добавление, кроме того, что сначала мы должны повернуть назад «стрелку» что мы вычитаем:
Вперед
Назад
Назад к началу
Назад на страницу определений
Ну, есть алгебраический способ сделать это и изобразительный способ сделать это. Алгебраический метод использует старый добрый метод «ФОЛЬГА» (умножить первое
термины, затем внешние термины, затем внутренние термины, затем последние термины).
Главное помнить, что я 2 =-1. Примеры:
Алгебраический метод использует старый добрый метод «ФОЛЬГА» (умножить первое
термины, затем внешние термины, затем внутренние термины, затем последние термины).
Главное помнить, что я 2 =-1. Примеры:
- (1+i)*(2-i) = 1*2 + 1*(-i) + i*2 + i*-i = 2-i+2i-i 2 = 2-i+ 2я+1 = 3+я
- (1+i)*(-1+i) = -1 + i — i + i 2 = -1 -1 = -2
Показать, что происходит в комплексной плоскости, довольно сложно, но я уверен, вы согласитесь, что красота в этом определенно стоит усилий!
В принципе, включает три шага:
- Нарисуйте свои комплексные числа в виде стрелок, затем обратитесь к своим триггерным заметкам. (или приведенные ниже формулы), чтобы найти длину каждой стрелки и угол от каждого до оси абсцисс. Это «сложная часть».
- Чтобы получить длину ответа, умножьте длину вашего маленького стрелки! (Напомним, что это называется нормой или амплитудой)
- Чтобы увидеть, куда указывает стрелка ответа, сложите углы вашего маленького стрелки! Напомним, что это называется модулем)
Ну, как сказал бы Билл Най, разве это не дико? Сделаем пример. Покажем, что:
Покажем, что:
Вот пошаговая инструкция:
91/2 = 2! Итак, у нас есть растяжка стрелок
и поворот в комплексной плоскости. Аккуратно, а?
Кстати, обратите внимание, что мы только что проверили
графически результат, который мы получили ранее, используя
Метод ФОЛЬГИ!
Прежде всего, вот отличное практическое правило, которое вы можете запомнить на все времена: Неважно, о каком числе вы говорите, если вы извлекаете из него корень энной степени, их n! значит 9-1 г/х .
Чтобы показать вам, как это работает, лучше пять
nipziff примеры были разработаны, которые вы
можно кликнуть и посмотреть.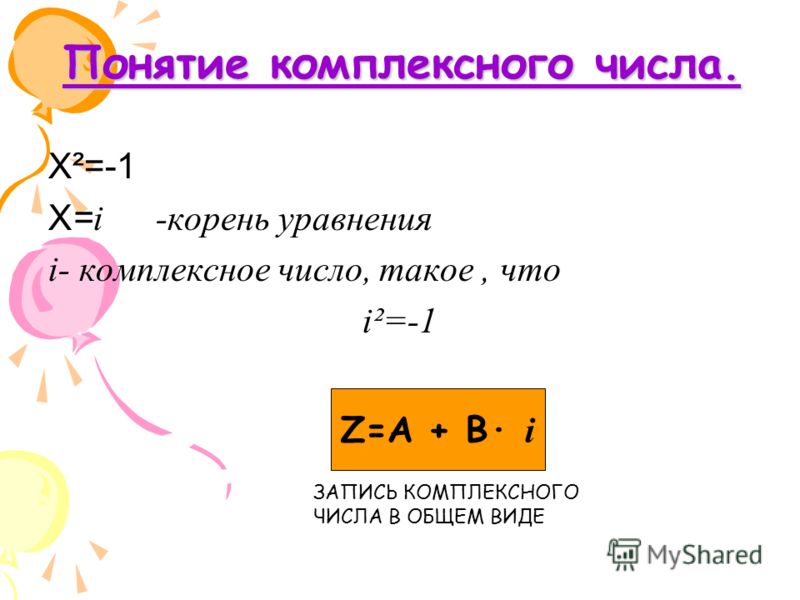

 Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа z=x+iy (рис. 7.1).
Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа z=x+iy (рис. 7.1).
 (7.3)
(7.3)
 7 достаточно найти главное значение его аргумента, то есть считать φ=arg z.
7 достаточно найти главное значение его аргумента, то есть считать φ=arg z. 7.2).
7.2).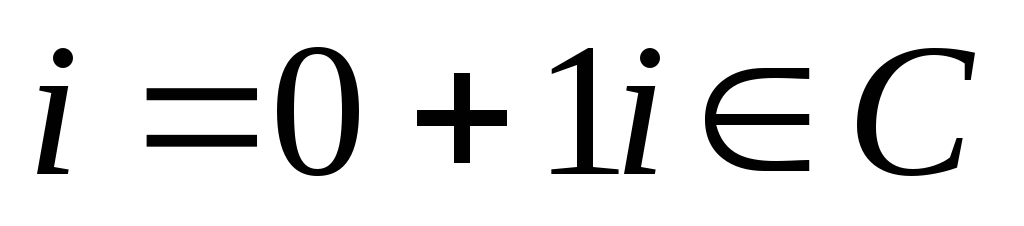 рис. 7.2).
Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости:
рис. 7.2).
Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости: Производя все необходимые выкладки согласно формуле (7.11),
получим формулу
Производя все необходимые выкладки согласно формуле (7.11),
получим формулу 

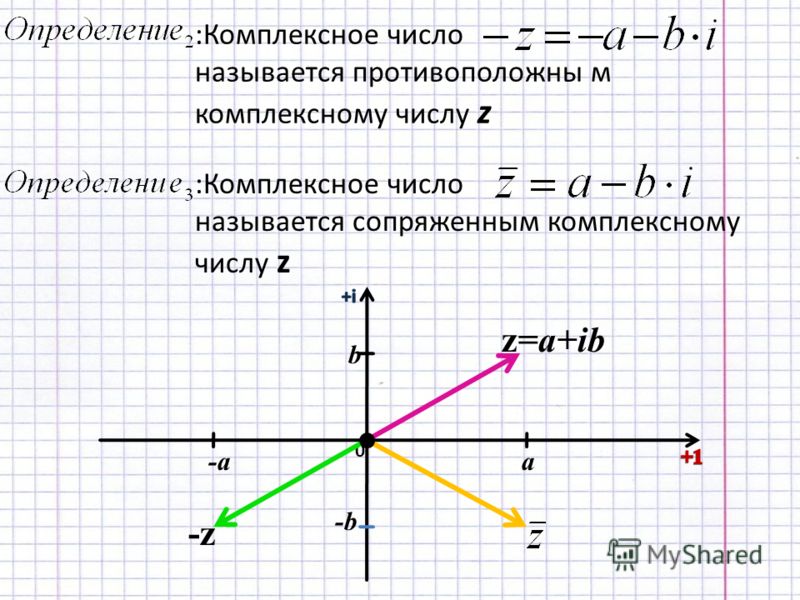 14) вычислим их частное
14) вычислим их частное
 Таким образом, корнями заданного уравнения z4+16=0
являются комплексные числа
Таким образом, корнями заданного уравнения z4+16=0
являются комплексные числа  Перемножив линейные множители
разложения , получим трехчлен второй степени с действительными
коэффициентами x2+px+q и
отрицательным дискриминантом. Действительно,
Перемножив линейные множители
разложения , получим трехчлен второй степени с действительными
коэффициентами x2+px+q и
отрицательным дискриминантом. Действительно, В. Новикова
В. Новикова
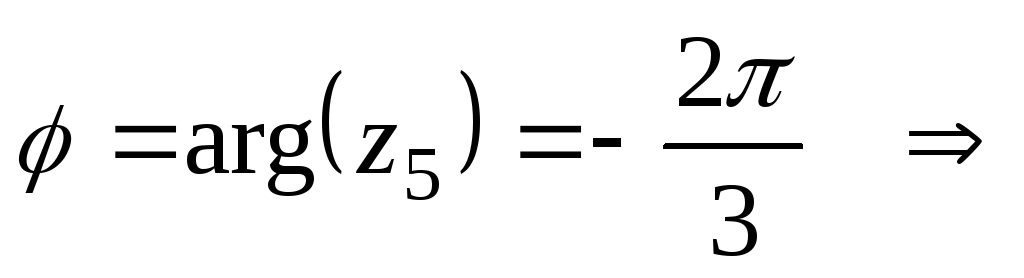






 4.
4. 5.
5. 6.
6.



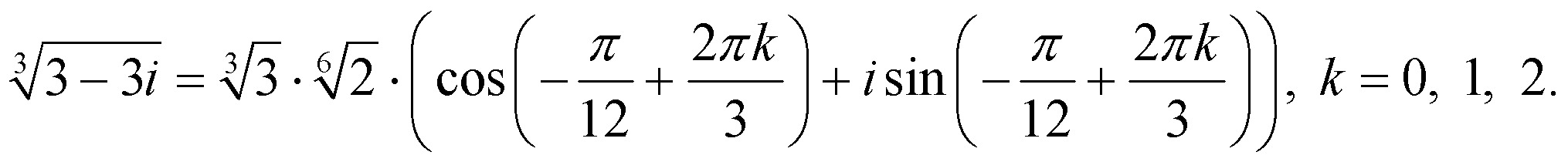




 а) z1z2
а) z1z2
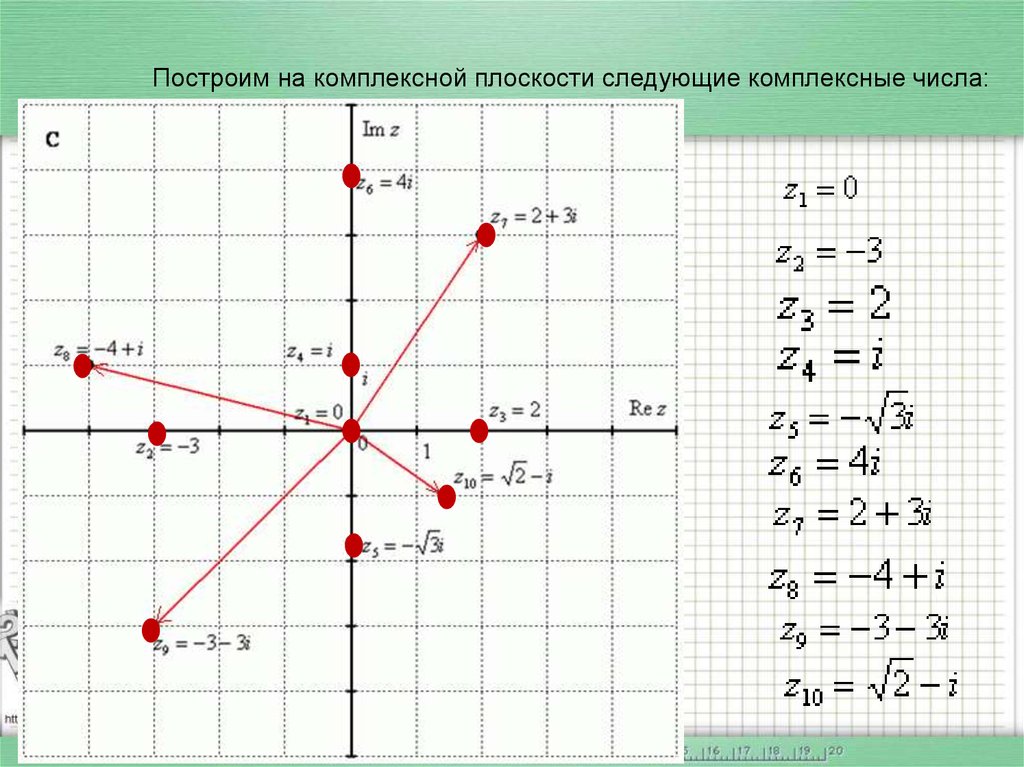


 Комплексные числа.
Комплексные числа.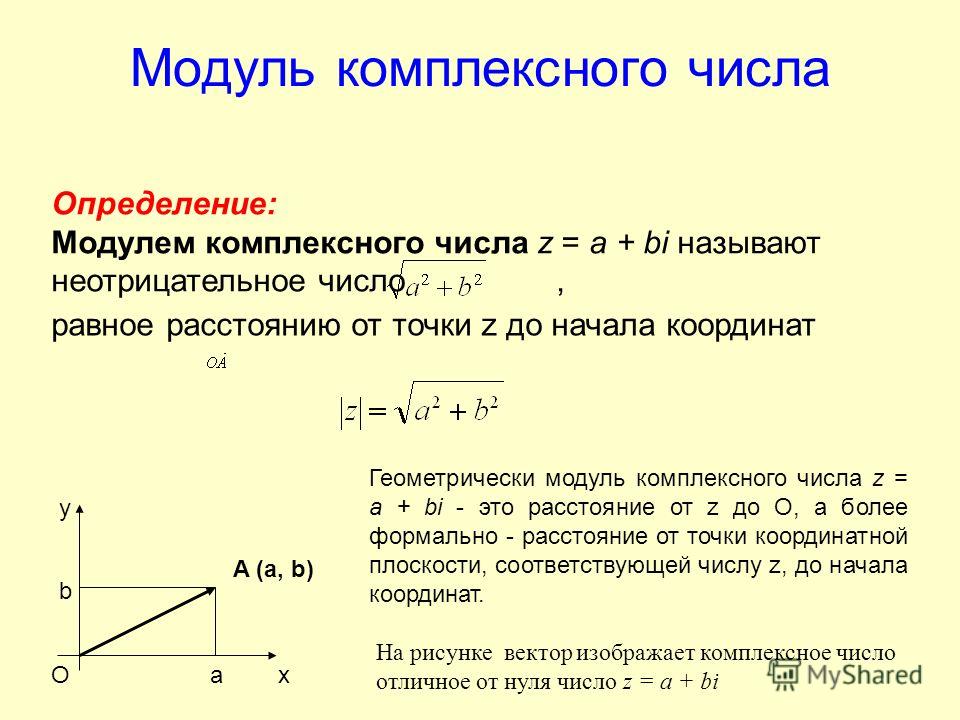 Все правила по сольфеджио
Все правила по сольфеджио

 Комплексные числа перемножаются как двучлены, при этом учитывается, что .
Комплексные числа перемножаются как двучлены, при этом учитывается, что . 1).
1).
 2.
2. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.027 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.027 с.)
