Арабские цифры | это… Что такое Арабские цифры?
Арабские цифры (шрифт без засечек)
Арабские цифры — традиционное название набора из десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; ныне использующегося в большинстве стран для записи чисел в десятичной системе счисления.
История
Арабские цифры. Цифры 4, 5 и 6 существуют в двух вариантах, слева — арабский, справа — персидский.
Индийские цифры возникли в Индии не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья), которое позволило перейти к позиционной записи чисел.
Арабские и индо-арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму[1].
Индийскую систему записи широко популяризировал учёный ал-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра».
Арабские цифры стали известны европейцам в X веке. Благодаря тесным связям христианской Барселоны (Барселонское графство) и мусульманской Кордовы (Кордовский халифат), Сильвестр II (папа римский с 999 по 1003 годы) имел возможность доступа к научной информации, которой не имел никто в тогдашней Европе. В частности, он одним из первых среди европейцев познакомился с арабскими цифрами, понял удобство их употребления по сравнению с римскими цифрами и начал всячески пропагандировать их внедрение в европейскую науку.
| Арабские цифры, используемые в арабских странах Африки (кроме Египта) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Индо-арабские цифры, используемые в арабских странах Азии и в Египте | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Персидские цифры | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Индийские цифры (в письме деванагари), используемые в Индии | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Цифры в письме гуджарати | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ |
| Цифры в письме гурмукхи | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ |
| Цифры в письме лимбу (Limbu) | ᥆ | ᥇ | ᥈ | ᥉ | ᥊ | ᥋ | ᥌ | ᥍ | ᥎ | ᥏ |
| Цифры в бенгальском письме | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Цифры в письме ория | ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ |
| Цифры в письме телугу | ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ |
| Цифры в письме каннада | ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ |
| Цифры в письме малаялам | ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ |
| Цифры в тамильском письме | ೦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
| Цифры в тибетском письме | ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ |
| Цифры в бирманском письме | ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ |
| Цифры в тайском письме | ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ |
| Цифры в кхмерском письме | ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ |
| Цифры в лаосском письме | ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ |
Одна из легенд происхождения начертания современных арабских цифр[2]. Количество углов соответствует числовому значению цифры.
Количество углов соответствует числовому значению цифры.
Название «арабские цифры» образовалось исторически, из-за того что именно арабы распространяли десятичную позиционную систему счисления. Цифры, которые используют в арабских странах, по начертанию сильно отличаются от используемых в европейских странах.
Примечания
- ↑ وجهات النظر حول أصل الأرقام ا&# … (ар.)
- ↑ Florian Cajori A History of Mathematical Notations. — Cosimo, Inc., 2007. — Vol. I. — P. 64-66. — ISBN 9781602066847
Ссылки
- Арабские цифры // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
- «Арабские цифры» в Большой советской энциклопедии
- Титло — переводчик национальных начертаний арабских и других чисел
- Арабские цифры, использующиеся при датировке ковров
Арабские цифры от 1 до 10
Цифры и буквы являются народным достоянием и имеют большую историю во всех народах мира. Самые распространенные на сегодняшний день числовые знаки — это арабские и римские. И те, и другие используют для создания списков в русском языке, для счета предметов и для математических вычислений. Из этой статьи вы узнаете все об арабских цифрах в диапазоне от 1 до 10.
Самые распространенные на сегодняшний день числовые знаки — это арабские и римские. И те, и другие используют для создания списков в русском языке, для счета предметов и для математических вычислений. Из этой статьи вы узнаете все об арабских цифрах в диапазоне от 1 до 10.
Содержание
- История появления арабских цифр
- Откуда взялись современные числовые знаки от 1 до 10
- Особенности арабской цифры 0 (ноль)
- Использование нуля в расчетах
История появления арабских цифр
Арабские числовые знаки были выдуманы и записаны в Индии, произошло это около 5 века. В это время был определен отсчет чисел при перечислении. Отправной точкой был ноль (оригинальное название шунья). Это число позволило сформировать нынешний порядок чисел при счете. Популяризацией арабских цифр занимался индийский ученый того времени Абу Аль-Хорезми, который создал несколько книг на эту тему. От одной из них произошло сегодняшнее название школьного предмета — алгебра. Предоставленный ученым способ записи числовых значений использовал десятичную систему.
Предоставленный ученым способ записи числовых значений использовал десятичную систему.
Археологи находили разные работы древних математиков и археологов, которые использовали арабские цифры для своих работ. Эти работы были созданы предположительно в 8-9 веке. Сегодня большинство арабских стран используют отличительную от привычной всем записи чисел в европейских и других регионах. Более того, на Востоке принято писать порядок чисел с права налево.
Существует множество мнений, что в формировании цифр арабского происхождения, которыми пользуемся сегодня мы — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, были использованы не только арабские цифры древней Индии. Посмотрев на таблицу арабских цифр в диапазоне от 1 до 10 старого и нового представления, можно найти множество сходств. Например, 1, 2, 3, 4 в начальном представлении — это те же знаки, только повернутые на 90 градусов.
Читайте также: Рандомайзер чисел онлайн.
Откуда взялись современные числовые знаки от 1 до 10
Зарождение арабских цифр относят к древней южной Индии. Во многих древних странах, когда еще не было письма, использовались для счета палочки. Одна палочка обозначала 1, две — 2 и так далее. Такой способ записи навеян зарубками. Именно отсюда и происходят числа в римском представлении (для цифр 1, 2, 3). Индийские цифры позаимствовали некоторые элементы буквы из разных стран того времени.
Во многих древних странах, когда еще не было письма, использовались для счета палочки. Одна палочка обозначала 1, две — 2 и так далее. Такой способ записи навеян зарубками. Именно отсюда и происходят числа в римском представлении (для цифр 1, 2, 3). Индийские цифры позаимствовали некоторые элементы буквы из разных стран того времени.
В цифрах встречаются признаки букв арамейского, греческого и финикийского алфавитов. Предположительно числовые знаки начали зарождаться во 2 веке до нашей эры, в то время, когда существовало Индо-греческое царство.
В отличие от счета в русском языке — один (1), два (2), три (3), арабские цифры имеют свое название:
- 1 (один) — 1 Уахид;
- 2 (два) — 2 Итнан;
- 3 (три) — 3 Талата;
- 4 (четыре) — 4 Арба-а;
- 5 (пять) — 5 Хамиза;
- 6 (шесть) — 6 Ситта;
- 7 (семь) — 7 Саба-а;
- 8 (восемь) — 8 Таманиа;
- 9 (девять) — 9 Тизза;
- 10 (десять) — 10 Ашара.
Особенности арабской цифры 0 (ноль)
Ноль понимается как отсутствие числового значения или разряда. Ноль — очень полезная цифра хотя бы тем, что позволяет производить вычисления в столбик. Ни в одной другой числовой системе нет возможности это сделать. Чтобы убедиться в этом, попробуйте сделать расчет в столбик, используя римские цифры. Ноль придумали тоже индийцы и названа была эта цифра «сунья». На индийском значит — «пустой». В древних арабских странах этот знак еще называли cifra.
Ноль — очень полезная цифра хотя бы тем, что позволяет производить вычисления в столбик. Ни в одной другой числовой системе нет возможности это сделать. Чтобы убедиться в этом, попробуйте сделать расчет в столбик, используя римские цифры. Ноль придумали тоже индийцы и названа была эта цифра «сунья». На индийском значит — «пустой». В древних арабских странах этот знак еще называли cifra.
Российский математик и педагог Магницкий называет ноль также — цифра или ничто. Часто её название использовали для первой страницы книг. Есть и другие источники, в которых можно найти старое название 0 — цифра. Чаще всего оно встречается в рукописях русских и европейских ученых 17-18 века.
Это может быть полезным: Лучшие генераторы случайных чисел для конкурса.
Использование нуля в расчетах
Детей в школе учат начинать отсчет с единицы. Но большинство программистов используют вычисления, где отсчет всегда начинается с нуля. Такая запись всех 10 чисел удобна тем, что для их представления используется только 1 символ. А экономия в программировании является неотъемлемой его частью. Если мы начнем отсчет с нуля, записывать цифру 10 нам не нужно. Её место занимает девятка.
А экономия в программировании является неотъемлемой его частью. Если мы начнем отсчет с нуля, записывать цифру 10 нам не нужно. Её место занимает девятка.
Ноль обладает другими интересными свойствами при взаимодействии с числами. Так, если вы попытаетесь прибавить к нулю или отнять ноль от какого-нибудь числа — оно не изменится. Когда производится умножение на это число — вы получите 0 во всех случаях. При возведении каждого числа в ноль, получится единица. А также на ноль (0) нельзя разделить другое целое или дробное число.
Существует Закон Бенфорда. Если не вдаваться в подробности с рассмотрением формул и таблиц, он гласит, что в реальной жизни цифры от 1 до 4 встретить гораздо вероятнее, чем цифры от 5 до 9. Сюда можно отнести номера домов улиц, различную статистику и тому подобное. Есть у этого закона и практическое применение. Используя его, можно проверять бухгалтерские отчетности, результаты голосований, подсчет расходов.
В некоторых американских штатах несоответствие каких-либо расчетов по Закону Бенфорда является уликой, имеющей вес в судебном процессе. Все расчеты по этому закону производятся в десятичной системе. Таким образом, арабские цифры в границе от 1 до 10 являются самыми распространенными во всем мире.
Все расчеты по этому закону производятся в десятичной системе. Таким образом, арабские цифры в границе от 1 до 10 являются самыми распространенными во всем мире.
Дизайн циферблата — Цифры. SpbluxWatches
Цифры нельзя назвать неотъемлемой частью циферблата, ведь время можно указывать не только ими, но и часовыми метками, одной отметкой на 12 часов или вовсе обойтись без них. Но все же именно цифры придают циферблату особый стиль и являются важной составляющей дизайна часов, а потому мы решили углубиться в историю их возникновения и причины выбора тех или иных обозначений.
Начало
Первым отметкам, обозначающим количество, уже больше 30 000 лет. Но в том далеком прошлом они представляли не что иное, как засечки на прочном материале: дереве, камне или кости. Они не имели численного значения, а лишь количественное. Первые же числа пришли к нам от шумеров, базирующихся в современном Ираке. Эти архаичные и клинописные символы не нашли свое место на циферблатах, однако они дали нам намного больше — их математически счет положен в основу шестнадцатеричной системы счисления. Именно шумерская, а затем и вавилонская способы счета объясняют, почему у нас 60 секунд в минуте, 60 минут в часе и 360 градусов по кругу.
Они не имели численного значения, а лишь количественное. Первые же числа пришли к нам от шумеров, базирующихся в современном Ираке. Эти архаичные и клинописные символы не нашли свое место на циферблатах, однако они дали нам намного больше — их математически счет положен в основу шестнадцатеричной системы счисления. Именно шумерская, а затем и вавилонская способы счета объясняют, почему у нас 60 секунд в минуте, 60 минут в часе и 360 градусов по кругу.
Вавилонские цифры
Рим
Римские цифры стали появляться на часах раньше прочих — примерно в IX веке до н. э. Существует две теории их происхождения. Одна говорит, что они базируются на старых начертаниях и стали их логическим развитием. Вторая теория исходит из их физического обозначения — пальцами одной руки, именно этим объясняется группировка по 5 знаков. И несмотря на сложность их использования для арифметики, римские цифры широко использовались вплоть до XV века.
В современном дизайне их используют, чтобы придать дизайну некий классицизм. Интересно, что цифра 4, которая обычно выглядит как IV, на циферблатах встречается чаще в виде IIII. И на этот счет есть также несколько объяснений. Одни говорят, что символ IV был древним сокращением для Юпитера, а часовые мастера не хотели ставить на 4 место главного бога. Но эта теория довольно спорная и рождает больше вопросов, нежели ответов, ведь если бы это было настолько важно, использование такого обозначения и вовсе запретили. Более разумное объяснение кроется в эстетическом балансе, где 4 сравнивается с 8 на противоположной стороне циферблата. Можно заметить, что большинство римских цифр состоят из V или X, имеющих в своем начертании жирную и тонкую линии. Восьмерка имеет 4 жирные и одну тонкую линию, а вот классическая IV только две жирные и одну тонкую. Ее смена на IIII сохраняет баланс между двумя сторонами циферблата. А то, что вариант написания варьируется, еще раз подтверждает стилистические мотивы.
Индия
Успех арабских цифр связан прежде всего с их десятичной системой, кроме того их происхождение не исламское, а индуистское. Они произошли от Брахми, восходящих к 300 году до н. э., но это были не десятичные, а позиционные числа и до 400 года н. э. они не менялись. Только в 628 году индийский математик и астроном Брахмагупта совершил открытие и определил в арифметике ноль, чем внес невообразимый вклад в математику и подарил индуистской системе счисления ее силу и долговечность.
Естественным образом индуистские числа распространялись по Шелковому пути на запад, но принять их помогли работы Аль-Хорезми и Аль-Кинди. Стилистическое написание чисел разделилось на два лагеря: арабские цифры, которые мы знаем и используем до сих пор — «западно-арабские цифры», и те, что используются в современном арабском письме — «восточно-арабские цифры».
К середине XVI века арабские цифры сменили римские в их обычном использовании. Стимулом к этому послужила географическая близость, которая перенесла западный стиль в Средневековую Европу, познакомив их с научными работами Аль-Хорезми, объясняющими использование цифр. И даже термин «алгебра» произошел из названия математического трактата ученого — «Китаб аль-джебр ва-ль-мукабала»./
Стимулом к этому послужила географическая близость, которая перенесла западный стиль в Средневековую Европу, познакомив их с научными работами Аль-Хорезми, объясняющими использование цифр. И даже термин «алгебра» произошел из названия математического трактата ученого — «Китаб аль-джебр ва-ль-мукабала»./
В последнее время встретить восточно-арабские цифры, или цифры хинди, как их еще называют, на циферблатах часов можно в качестве дизайнерского приема. И прежде всего это связано с ориентированностью на вкусы рынка. Например, Rolex M228206-0025 в платине 2016 года украшены именно такими цифрами. Это своего рода отсылка к старой модели Day-Date, выпускавшейся с конца 50-х до конца 70-х. На более ранних моделях такие обозначения встречаются очень редко, однако маркеры в форме шеврона на карманных часах для турецкого османского рынка, на самом деле представляют собой стилизованную версию восточно-арабских цифр.
Самый широко распространенный стиль арабских цифр нашел себя во французском начертании и их лицом стали цифры Breguet. Они украшают не только собственные часы мануфактуры, но и циферблаты от Seiko до Patek Philippe. Чем при их создании в 1790 году вдохновлялся мастер, мы не имеем никакого представления, но судя по подписи А.-Л. Бреге, цифры написаны его рукой. А благодаря их эстетизму в сочетании с разборчивостью дизайнеры со всего мира очарованы ими уже больше 200 лет.
Они украшают не только собственные часы мануфактуры, но и циферблаты от Seiko до Patek Philippe. Чем при их создании в 1790 году вдохновлялся мастер, мы не имеем никакого представления, но судя по подписи А.-Л. Бреге, цифры написаны его рукой. А благодаря их эстетизму в сочетании с разборчивостью дизайнеры со всего мира очарованы ими уже больше 200 лет.
Другие алфавиты
Может показаться, что существует только два вида цифр: арабские и римские, но это не так. Причина их преобладания на циферблатах кроется в сосредоточении исторических часовых мастерских в Западной Европе. Конечно, со временем производство распространилось и в другие регионы, но к тому времени арабские цифры уже успели стать общепринятыми.
Не стоит забывать и про кириллические цифры. Хотя благодаря реформам Петра Великого они вышли из постоянного использования, их все еще можно встретить на некоторых современных моделях часов русских мастеров. Однако они больше напоминают буквы, нежели цифры, а потому выступают скорее в качестве дизайнерского приема для создания стиля.
До Китая и Японии арабские цифры дошли намного раньше часового производства, но это не помешало Bovet, мануфактуре, начавшей производить часы для китайского рынка одной из первых, использовать на циферблатах римские цифры. Они же первыми использовали и китайские иероглифы для обозначения часовых меток моделей из лимитированных коллекций. Но ограниченные тиражи с использованием Hanzi и Kanji для китайского и японского рынков выпускают многие бренды: Rolex, Nomos, Bovet, Graham. Как правило, эти модели посвящены культурным событиям, к примеру, Nomos выпустил коллекцию Tangente для дня культуры Японии, а Bovet и Graham создали циферблаты Hanzi.
Сейчас цифры в дизайне циферблатов используются так же часто, как и их отсутствие, но все же они прочно укоренились в нашей культуре и психике, а потому выбор стиля и начертания — лучший способ выразить особый стиль каждой конкретной модели или подчеркнуть эстетику часовой мануфактуры в целом.
арабские цифры — frwiki.wiki
Для более общей статьи см. Рисунок .
Эти арабские цифры в текущем языке, то графические западные десять цифры (1, 2, 3, 4, 5, 6, 7, 8, 9, 0) и система позиционных обозначений десятичным , что сопровождает их. Этот принцип зародился в Индии и его индийская система счисления , затем он достиг средневекового Запада в контакте с арабскими математиками через андалузскую цивилизацию. Таким образом, европейское написание происходит от написания западного средневекового арабского мира, отсюда и название арабских цифр. Поскольку эта терминология неоднозначна, у них также есть другие названия, позволяющие избежать путаницы, но некоторые из которых относятся к обработке данных: «цифры ASCII», ссылаясь на древнюю историю их кодирования, «европейские цифры», «латинские цифры», в отношении набора символов, с которым они были связаны, «западные цифры».
Название «арабские цифры» иногда также относится к числам, используемым в арабском письме.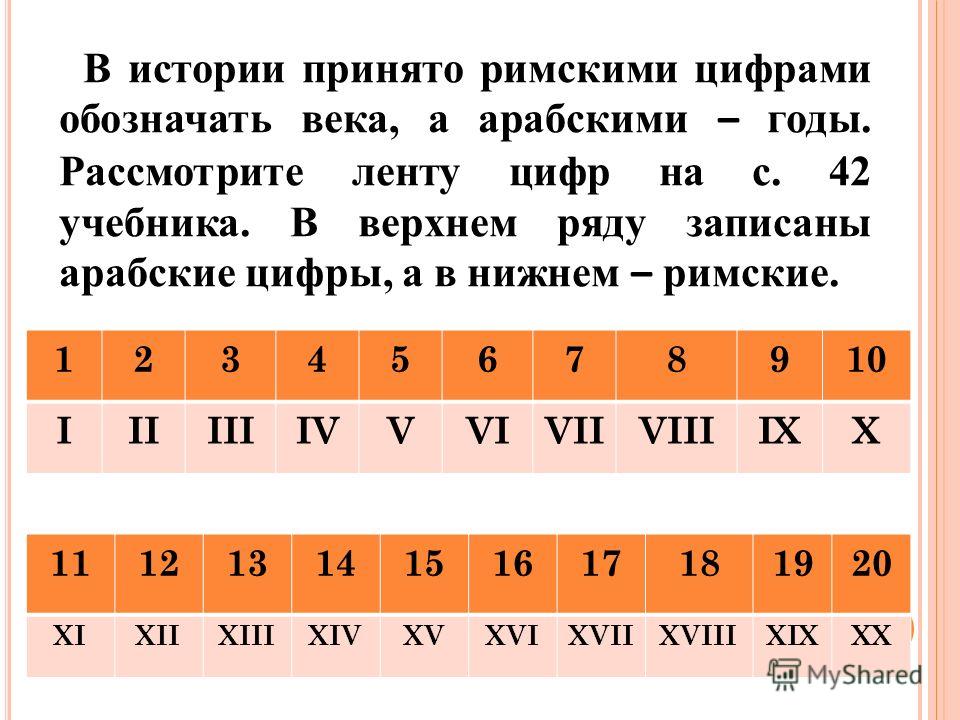 Сегодня стандарт Unicode и стандарт ISO / IEC 10646 допускают три нотации для последнего. Также включены различные записи индийских и персидских чисел.
Сегодня стандарт Unicode и стандарт ISO / IEC 10646 допускают три нотации для последнего. Также включены различные записи индийских и персидских чисел.
Резюме
- 1 История
- 2 Этимология
- 3 Орфография общего происхождения
- 4 варианта графики в почерке
- 5 Примечания и ссылки
- 6 См. Также
- 6.1 Связанные статьи
Исторический
Первые арабские цифры, известные на Западе, появляются в Codex Vigilanus 976 года, монастыре Святого Мартина де Альбеда, Королевство Памплона .
Написание арабских цифр может нарисовать десятичной позиционной нумерации не индийскую знакомства с III — го века до нашей эры. Н.э. , число Брахми .
Свидетельство их использование в Индии было найдено в Сирии на фоне VII — го века, в комментарии епископа Тяжелого Sebôkht на греческой науке и восточных науках. Они подхватили арабские математики и описаны в книге IX — го века математик персидская Аль-Хорезми на позиционной десятичной системе счисления.
Они подхватили арабские математики и описаны в книге IX — го века математик персидская Аль-Хорезми на позиционной десятичной системе счисления.
Арабские цифры достигли Европу в X — го столетия на Пиренейский полуостров , а затем под доминированием Омейядов . Затем их распространение на остальной части Запада продолжалось различными способами.
Некоторые сосредоточиться на работе Герберт d’Орийака (940-1003), будущий папа Сильвестр II, который, по преданию, учился в университете Аль Quaraouiyine в Фесе в Марокко , изучая науки и исламские методы , изучая математику и астрономию ; более вероятно, что он просто посетил Кордову и опирался на каталонские источники, напрямую контактируя с арабо-мусульманским миром. Последний написал работу о делении Libellus de numerorum Divisione, Regulae de Divisionibus , где Герберт изобрел метод евклидова деления, о котором сообщил Бернелин (Bernélinus или Bernelinus) из Парижа, один из его учеников; и трактат об умножении Libellus multiplicationum , который предписывает древнее умножение пальцами (цифровое исчисление).
Другие приписывают важную роль итальянскому математику Леонардо Фибоначчи (1175 — 1250), который учился у мусульманских профессоров в Бежайе (на территории современного Алжира ), привез в Пизу в 1198 году часть своих знаний и опубликовал в 1202 году: абака Liber ( Книга расчета ), трактат по расчетам и бухгалтерский учет на основе расчета десятичного.
В конце концов, трудно установить, кто из этих двух ученых больше всего способствовал распространению арабской математики на Западе, но факт остается фактом: Гербер д’Орийак, а позже Фибоначчи были авторами основных популярных работ. Так называемый арабский язык цифры.
Леди Арифметик , арбитраж соревнования между Боэцием , использующим арабское письмо и цифры, и Пифагором , использующим абак . Она смотрит в сторону Боэция , который, кажется, в значительной степени поддерживает ее. Конечно, исторически Боэций не мог знать арабских цифр.
Как и многие решения, которые кажутся нам простыми, полезными и гениальными, потому что они нам знакомы, распространение арабских цифр столкнулось с традиционными привычками, и их усвоение было постепенным. Во Флоренции (Италия) купцам впервые запретили использовать их в договорах и официальных документах. В 1299 году они были запрещены повсеместно, в том числе на частных счетах флорентийских банкиров и купцов. Пока операции остаются простыми, достаточно использовать счет для расчета и римские цифры для графического изображения. Начиная с эпохи Возрождения, с экспоненциальным развитием торговли, а затем и наук, в частности астрономии и баллистики, потребность в мощной и быстрой системе вычислений стала существенной: индо-арабские цифры окончательно исключают своих римских предшественников. Их окончательный маршрут, стандартизирован, засвидетельствован с XV — го века .
Во Флоренции (Италия) купцам впервые запретили использовать их в договорах и официальных документах. В 1299 году они были запрещены повсеместно, в том числе на частных счетах флорентийских банкиров и купцов. Пока операции остаются простыми, достаточно использовать счет для расчета и римские цифры для графического изображения. Начиная с эпохи Возрождения, с экспоненциальным развитием торговли, а затем и наук, в частности астрономии и баллистики, потребность в мощной и быстрой системе вычислений стала существенной: индо-арабские цифры окончательно исключают своих римских предшественников. Их окончательный маршрут, стандартизирован, засвидетельствован с XV — го века .
Этимология
Слово « число» происходит от арабского صفر ( ṣifr ), означающего «ноль», по образцу санскритского «шунья», обозначающего пустоту, а также «ноль». Ноль, будучи самым важным нововведением в системе счисления, стал обозначать все числа. «Ноль» также происходит от итальянского слова «zefiro», что означает «пустой», которое происходит от того же арабского слова صفر ( ṣifr ).
«Ноль» также происходит от итальянского слова «zefiro», что означает «пустой», которое происходит от того же арабского слова صفر ( ṣifr ).
Правописание общего происхождения
Написание «западных» арабских цифр, известных как «губар», отличается от их правильных арабских предков и их индийских эквивалентов.
Вот быстрое сравнение между нынешними графиками так называемых «арабских» чисел, используемых, в частности, на Западе, по сравнению с числами, которые сегодня используют некоторые арабские страны (числа на хинди), и числами, нанесенными на график в нескольких индийских писаниях.
| След | Система письма | Символы | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Западные / магрибские / андалузцы | Арабский / латинский | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Араб | Восточный арабский (кроме персидского и урду) | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Персидский | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | |
| Урду | |||||||||||
| Индийский | Бенгальский | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Деванагари | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ | |
| Гуджарати | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ | |
| Гурмукхи | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ | |
Стилизованные числа (восточный алфавит), обычно используемые на циферблатах, особенно персидские
Страны Магриба используют только современные маршруты, в отличие от стран Машрика (или Ближнего Востока ), которые используют оба. Этот тип европейского маршрута, вероятно, был изобретен в Испании, вероятно, в Аль-Андалусе .
Этот тип европейского маршрута, вероятно, был изобретен в Испании, вероятно, в Аль-Андалусе .
Развитие десятичных цифр в Европе до XVIII — го века показано на рисунке ниже из Монтюкла , который был опубликован в 1758 году в своей истории математики :
Сравнение рейтингов. Для пояснения щелкните документ.
Графические варианты в почерке
- Компьютерные специалисты и военные иногда представляют цифру ноль , «0», перечеркнув ее косой чертой, чтобы избежать путаницы с буквой « О », которая приближает ее к скандинавской букве « Ø ».
- Франкоязычные и европейцы в целом очень часто пишут цифру « 1 » с короткой косой чертой, спускающейся слева сверху, а также с короткой горизонтальной чертой внизу числа (« 1 »). Англофонам и франкофонам в Северной Америке часто достаточно вертикальной черты (|). В информатике чаще всего используется франкоязычная форма (« 1 »), поскольку она позволяет избежать путаницы с заглавной буквой I.

- Франкоязычные и европейцы в целом часто пишут цифру « 7 » с помощью средней перекладины (более или менее напоминающей «
7»), что позволяет избежать путаницы с их цифрой « 1 ». Это очень редко встречается среди англоязычных и франкоязычных в Северной Америке.
- Открытый графический вариант 4 обычно используется в почерке.
Примечания и ссылки
- ↑ Згиби Рашид, « Компьютерное кодирование арабского письма: от ASMO 449 к Unicode и ISO / IEC 10646 », Цифровой документ , Lavoisier , vol. 6,, стр. 155-182 ( DOI 10.3166 / dn.6.3-4.155-182 , читать онлайн , по состоянию на 7 апреля 2015 г. )
- ↑ (in) Дж.
 Дж. О’Коннор и Э. Ф. Робертсон, « Индийские цифры » , в архиве истории математики MacTutor ,(по состоянию на 20 июля 2019 г. )
Дж. О’Коннор и Э. Ф. Робертсон, « Индийские цифры » , в архиве истории математики MacTutor ,(по состоянию на 20 июля 2019 г. ) - ↑ Жорж Ифра , Универсальная история фигур , Seghers, 1981, с. 466 .
- ↑ Жорж Ифра , Универсальная история фигур , Seghers, 1981, с. 493 .
- ↑ « История: Папа Сильвестр II, лауреат премии« Аль-Карауайин »у истоков крестовых походов? » , На Yabiladi.com (по состоянию на 15 июля 2020 г. ) .
- ↑ Герберт также является источником особого типа счётов , счётов Герберта, где несколько счетчиков заменены одним жетоном с так называемым «арабским» числом: семь счетчиков в столбце единиц заменены на жетон с номером 7, три жетона в столбце десять — жетон с номером 3 и т.
 д. Согласно Жаку Хальбронну (Mathematics Divinatories, Paris, La Grande Conjonction -Trédaniel, 1983), было бы целесообразно приблизить написание этих чисел к ивритской скорописи, в частности, буквы Daleth, Tsadé, Samekh, Vav, Zayin для обозначения 2, 3, 0, 1 и 5; из которого остальные пять получаются путем добавления строки: 4, 9, 8, 7 и 6.
д. Согласно Жаку Хальбронну (Mathematics Divinatories, Paris, La Grande Conjonction -Trédaniel, 1983), было бы целесообразно приблизить написание этих чисел к ивритской скорописи, в частности, буквы Daleth, Tsadé, Samekh, Vav, Zayin для обозначения 2, 3, 0, 1 и 5; из которого остальные пять получаются путем добавления строки: 4, 9, 8, 7 и 6. - ↑ . Несомненно, потому что очень легко добавить ноль, чтобы получить, например, сумму от ста до тысячи (риск мошенничества или ошибки, который существует и сегодня). Следовательно, обязательство, все еще действующее , вписать в договорах сумму как цифрами, так и прописью.
- ↑ Джон Д. Барроу, Пи в небе .
- ↑ Смотрите этимологию слова в TLFi
- ↑ (in) Дэвид Юджин Смит и Луи Чарльз Карпински Индо-арабские цифры с. 58
- ↑ Ложные углы и арабские цифры
Смотрите также
Статьи по Теме
- Индийский граф
- Арабская нумерация
- Аль-Хорезми
- Десятичная система
- Система счисления
- Номера: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9
- Цифры в мире
- Цифры на французском
- Индо-арабская система счисления
Системы счисления | |
|---|---|
| Арабо-индейцы |
|
| Позиционный |
|
| Восточная Азия |
|
| По алфавиту |
|
| Добавки |
|
арабские цифры | |
|---|---|
| 0 · 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 |
<img src=»//fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Читать онлайн «Тайна русской истории», Анатолий Фоменко – ЛитРес, страница 4
5.2. Как появились арабские цифры для позиционной записи чисел
Д.Я. Стройк пишет: «Весьма разнообразны знаки, которые применялись для записи цифр в позиционной системе, но имеются два главных типа: индийские обозначения, которые применялись восточными арабами, и так называемые цифры «гобар» (или «губар»), которые применялись западными арабами в Испании. Знаки первого типа и сейчас еще применяются в арабском мире, но наша современная система, по-видимому, произошла из системы «гобар»» [821], с. 89.
ВОПРОС О ПРОИСХОЖДЕНИИ «АРАБСКИХ ЦИФР» ОСТАЕТСЯ В СКААИГЕРОВСКОЙ ИСТОРИИ НАУКИ ДО СИХ ПОР ОТКРЫТЫМ. Существуют различные теории на сей счет. Например, теория Вепке. Согласно которой, эти знаки проникли на Запад якобы в V веке н. э. из Александрии через неопифагорейцев [821], с. 90. Есть и другая теория – H.М. Бубнова. Согласно ей, знаки «гобар» произошли из давних римско-греческих символов [821], с. 90. Но ни в том, ни в другом случае, не приводятся РОДОНАЧАЛЬНИКИ хорошо всем знакомых арабских цифр. В качестве таких прародителей объявляются давние (в смысле ЗАБЫТЫЕ) римско-греческие символы. Или «александрийские символы». Тоже забытые. А потому сегодня неизвестные. Никому, даже историкам.
Согласно ей, знаки «гобар» произошли из давних римско-греческих символов [821], с. 90. Но ни в том, ни в другом случае, не приводятся РОДОНАЧАЛЬНИКИ хорошо всем знакомых арабских цифр. В качестве таких прародителей объявляются давние (в смысле ЗАБЫТЫЕ) римско-греческие символы. Или «александрийские символы». Тоже забытые. А потому сегодня неизвестные. Никому, даже историкам.
Известный русский историк математики В.В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕЕ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ С ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метода внушения, впечатление КАК БЫ ЧЕГО-ТО ДОКАЗАННОГО». Цит. по [989], с. 53. Авторы Энциклопедии [989], после изложения различных теорий происхождения арабских цифр, делают следующий многозначительный вывод. «Таким образом, МЫ ДО СИХ ПОР НЕ ИМЕЕМ ИСТОРИЧЕСКИ ОБОСНОВАННОЙ ГИПОТЕЗЫ, КОТОРАЯ ДОСТАТОЧНО УДОВЛЕТВОРИТЕЛЬНО ОБЪЯСНЯЛА БЫ ПРОИСХОЖДЕНИЕ НАШИХ ЦИФР» [989], с. 52.
Нам представляется, что дело намного проще. Стоит лишь задаться этим вопросом и отрешиться от неправильных скалигеровских датировок, как происхождение «арабских цифр» становится в общем-то очевидным. И весьма естественным. Как мы сейчас покажем, ВСЕ «АРАБСКИЕ ЦИФРЫ» ПРОИЗОШЛИ ИЗ ПРЕДШЕСТВУЮЩЕЙ ПОЛУ-ПОЗИЦИОННОЙ СЛАВЯНО-ГРЕЧЕСКОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем, будет явно видно, что использовался именно СЛАВЯНСКИЙ ВАРИАНТ букв-символов. Источником послужила русская скоропись шестнадцатого века. ПРОИЗОШЛО ВСЕ ЭТО, СКОРЕЕ ВСЕГО, В XVI ВЕКЕ. То есть в эпоху изобретения позиционной системы, см. выше. Перейдем к подробностям.
Стоит лишь задаться этим вопросом и отрешиться от неправильных скалигеровских датировок, как происхождение «арабских цифр» становится в общем-то очевидным. И весьма естественным. Как мы сейчас покажем, ВСЕ «АРАБСКИЕ ЦИФРЫ» ПРОИЗОШЛИ ИЗ ПРЕДШЕСТВУЮЩЕЙ ПОЛУ-ПОЗИЦИОННОЙ СЛАВЯНО-ГРЕЧЕСКОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем, будет явно видно, что использовался именно СЛАВЯНСКИЙ ВАРИАНТ букв-символов. Источником послужила русская скоропись шестнадцатого века. ПРОИЗОШЛО ВСЕ ЭТО, СКОРЕЕ ВСЕГО, В XVI ВЕКЕ. То есть в эпоху изобретения позиционной системы, см. выше. Перейдем к подробностям.
До позиционной системы счисления и арабских цифр на Руси использовалась полу-позиционная система, где для каждой десятичной цифры имелось три различных значка [782], вып. 1, с. 16. А именно, один значок для изображения цифры в рязряде единиц. Другой – для изображения той же цифры, но в разряде десятков. И, наконец, третий – для изображения цифры в разряде сотен, рис. 1.36. Ноль отсутствовал. Но поскольку в разных разрядах обозначение цифры было разным, то само обозначение сразу указывало на разряд, в котором стояла данная цифра. С помощью такой системы можно было производить все обычные арифметические действия с целыми числами в пределах от единицы до тысячи. Для чисел, больших тысячи, приходилось применять специальные дополнительные значки, рис. 1.36. Для этого использовались буквы кириллицы.
С помощью такой системы можно было производить все обычные арифметические действия с целыми числами в пределах от единицы до тысячи. Для чисел, больших тысячи, приходилось применять специальные дополнительные значки, рис. 1.36. Для этого использовались буквы кириллицы.
Поясним таблицу на рис. 1.36. Например, цифра «один» изображалась тремя способами.
1) Буквой А, если единица стояла в разряде единиц, то есть в первом разряде.
2) Буквой I, если единица стояла в разряде десятков, то есть во втором разряде.
3) Буквой Р, если единица стояла в разряде сотен, то есть в третьем разряде.
Скажем, число РА означало 101. В нашей современной позиционной системе при записи числа 101 используется ноль, так как здесь отсутствует цифра во втором разряде. В старой же славянской полу-позиционной записи нуля не было. Но само обозначение единиц буквами указывало, что одна из них стоит в первом, а другая – в третьем разряде. То есть цифра во втором разряде здесь отсутствует.
Рис. 1.36. Старая славяно-греческая полу-позиционная система записи цифр. Взято из [782], выпуск 1, с. 16
1.36. Старая славяно-греческая полу-позиционная система записи цифр. Взято из [782], выпуск 1, с. 16
Таким образом, для записи целых чисел от единицы до тысячи использовались не ДЕВЯТЬ символов, как сегодня (не считая нуля), а в ТРИ РАЗА БОЛЬШЕ. А именно, ДВАДЦАТЬ СЕМЬ букв кириллицы. НА КАЖДУЮ ЦИФРУ ПРИХОДИЛОСЬ ТЕМ САМЫМ ПО ТРИ БУКВЫ. В таблице на рис. 1.36 двадцать семь кириллических букв расположены в трех верхних строках. Под каждой арабской цифрой мы видим три различные буквы кириллицы. Остальные четыре строки таблицы на самом деле повторяют первую строку, но снабжены специальными дополнительными символами, чтобы обеспечить следующие разряды от тысячи до миллиона. Новых букв тут не появляется.
Зададимся вопросом. Что должно было произойти, когда решили заменить указанную систему обозначений на полностью позиционную? То есть с нулем. Для этого следовало оставить вместо двадцати семи цифр всего лишь девять. Требовалось каким-то образом выбрать девять цифр-букв из двадцати семи. Например, из трех обозначений-букв для единицы нужно было оставить только одну кириллическую букву. То же самое для двойки. И так далее до девятки.
Например, из трех обозначений-букв для единицы нужно было оставить только одну кириллическую букву. То же самое для двойки. И так далее до девятки.
Оказывается, именно эту простую процедуру и проделали. Как мы сейчас увидим, в результате получились привычные нам сегодня «арабские цифры», которыми все пользуются до сегодняшнего дня. Что сразу же делает очевидным тот факт, что люди, впервые придумавшие «арабские цифры», пользовались до этого именно славяногреческой полу-позиционной системой счисления. Причем, для «арабских цифр» были использованы во многих случаях РУССКИЕ СКОРОПИСНЫЕ формы кириллических букв XVI века. Что может означать лишь одно. Люди, придумавшие «арабские цифры» хорошо читали и писали по-русски. Для них РУССКАЯ СКОРОПИСЬ XVI ВЕКА была хорошо знакомым, привычным почерком.
В частности, исчезает «великая загадка» скалигеровской истории – откуда же взялись «арабские цифры»? Наш ответ таков. Они произошли из славяно-греческих цифр-букв в русской скорописи XVI века. Кроме того, и другие детали, о которых мы ниже расскажем, однозначно показывают, что использовалась именно РУССКАЯ, А НЕ ГРЕЧЕСКАЯ азбука XVI века. Эти азбуки несколько отличаются.
Кроме того, и другие детали, о которых мы ниже расскажем, однозначно показывают, что использовалась именно РУССКАЯ, А НЕ ГРЕЧЕСКАЯ азбука XVI века. Эти азбуки несколько отличаются.
Обратимся теперь к таблице на рис. 1.37. Обсудим каждую цифру отдельно.
1) ЕДИНИЦА. Из трех обозначений единицы выбрали букву I из второго разряда, как наиболее простую из трех. Получилась «индо-арабская» единица.
2) ДВОЙКА. Для двойки избрали не букву В (то есть вторую букву греческой азбуки), а букву Б – вторую букву славянской азбуки. При этом взяли скорописную форму этой буквы и зеркально отразили, рис. 1.37. Получилась привычная нам сегодня «индо-арабская» двойка. В данном случае автор новых обозначений явно показал свое предпочтение славянской азбуке перед греческой. В греческой азбуке буквы Б нет. Она пропущена, и сразу после А идет В.
Тройку мы пока пропустим, так как ее обозначение переставлено с семеркой.
4) ЧЕТВЕРКА. У четверки есть две формы: открытая и закрытая. Закрытая форма «домиком» получается из славянской буквы Д, обозначавшей четверку в первом разряде. Открытая же форма получается из славянской буквы У, обозначавшей четверку в третьем разряде, рис. 1.37. Получилась «индо-арабская» четверка.
Открытая же форма получается из славянской буквы У, обозначавшей четверку в третьем разряде, рис. 1.37. Получилась «индо-арабская» четверка.
Рис. 1.37. Наша таблица происхождения арабских цифр из славянских цифр-букв предшествующей полу-позиционной системы счисления. Обратите внимание, что во многих случаях ДЛЯ АРАБСКИХ ЦИФР БЫЛИ ВЗЯТЫ РУССКИЕ СКОРОПИСНЫЕ ФОРМЫ КИРИЛЛИЧЕСКИХ БУКВ
Пятерку, шестерку и семерку мы пока пропустим, так как их обозначения переставлены. Подробнее об этом – ниже.
8) ВОСЬМЕРКА. Она получается из славянской буквы «омега», обозначавшей восьмерку в третьем разряде. Буква повернута на девяносто градусов, рис. 1.37. Получилась «индо-арабская» восьмерка.
9) ДЕВЯТКА. Здесь для «индо-арабской» цифры употребили нестандартную, ЧИСТО РУССКУЮ форму девятки в третьем разряде. Обычно в славяно-греческих обозначениях для этого использовалась буква Ц. Однако на Руси употребляли также букву Я для обозначения девятки в третьем разряде. Мы видим, что ее скорописная форма – это в точности «индо-арабская» девятка с приделанной палочкой. Палочку отбросили. Получилась хорошо знакомая нам сегодня «индо-арабская» цифра девять, рис. 1.37. Эта скорописная форма буквы Я была, с небольшими изменениями, канонизирована во время петровской реформы и используется до сих пор. На рис. 1.38 приведен образец русской скорописи начала XVII века [791], выпуск 19, форзац. Здесь написано русское слово «знамя». В его конце стоит буква Я.
Палочку отбросили. Получилась хорошо знакомая нам сегодня «индо-арабская» цифра девять, рис. 1.37. Эта скорописная форма буквы Я была, с небольшими изменениями, канонизирована во время петровской реформы и используется до сих пор. На рис. 1.38 приведен образец русской скорописи начала XVII века [791], выпуск 19, форзац. Здесь написано русское слово «знамя». В его конце стоит буква Я.
Перейдем теперь к «индо-арабским» цифрам: ТРОЙКА, ПЯТЕРКА, ШЕСТЕРКА И СЕМЕРКА.
3 и 7) ТРОЙКА и СЕМЕРКА. Для «индо-арабской» тройки была использована русская скорописная форма буквы 3, обозначавшая семерку в первом разряде, рис. 1.37. Формы русской скорописной буквы 3 и «индо-арабской» тройки полностью идентичны! И наоборот, для «индо-европейской» семерки взяли скорописную форму русской буквы Т, обозначающую тройку в третьем разряде, рис. 1.39. Таким образом, обозначения для тройки и семерки были почему-то ПЕРЕСТАВЛЕНЫ местами.
5 и 6) ПЯТЕРКА и ШЕСТЕРКА. Для «индо-арабской» пятерки была использована скорописная форма русской буквы «зело», обозначавшая шестерку в первом разряде, рис. 1.37. И наоборот, для «индо-арабской» шестерки взяли скорописную форму славянской буквы Е, обозначавшую пятерку в первом разряде. Эта форма, кстати, очень близка к современной форме рукописной буквы Е. Создатели «индо-арабских» цифр просто зеркально отразили славянскую букву Е и получили шестерку. На рис. 1.40 приведен образец русской скорописи начала XVII века, где буква Е в конце слова «великие» написана как зеркально отраженная шестерка [787], выпуск 7. Таким образом, обозначения для пятерки и шестерки почему-то ПЕРЕСТАВИЛИ местами. Как и в случае тройки и семерки.
1.37. И наоборот, для «индо-арабской» шестерки взяли скорописную форму славянской буквы Е, обозначавшую пятерку в первом разряде. Эта форма, кстати, очень близка к современной форме рукописной буквы Е. Создатели «индо-арабских» цифр просто зеркально отразили славянскую букву Е и получили шестерку. На рис. 1.40 приведен образец русской скорописи начала XVII века, где буква Е в конце слова «великие» написана как зеркально отраженная шестерка [787], выпуск 7. Таким образом, обозначения для пятерки и шестерки почему-то ПЕРЕСТАВИЛИ местами. Как и в случае тройки и семерки.
0) НОЛЬ. Вопрос о НУЛЕ особенно интересен. Поскольку именно изобретение нуля позволило ввести НОВУЮ СИСТЕМУ СЧИСЛЕНИЯ. В этой, общепринятой сегодня системе счисления, ноль обозначает ОТСУТСТВУЮЩУЮ ЦИФРУ. То есть говорит о том, что В ДАННОМ РАЗРЯДЕ ЦИФРЫ НЕТ.
Рис. 1.38. Скорописная форма славянской буквы Я в конце слова «знамя». Ясно видно, что если отбросить верхнюю палочку, то получится «ИНДО-АРАБСКАЯ» ДЕВЯТКА. Взято из [791], выпуск 19
Взято из [791], выпуск 19
И ее пустое место обозначает 0 = ноль. Скорее всего, 0 = «ноль», это сокращение какого-то слова. Зададимся вопросом, какого именно? Оказывается, это очень легко объяснить в предположении, что слово было славянским. Как сообщает В. Даль, слово или предлог О в русском языке раньше могло употребляться вместо предлога ОТ [223], т. 2, столбец 1467. А предлог ОТ в русском языке означает ОТСУТСТВИЕ чего-либо. Этимологический словарь сообщает, что ОТ – это «глагольная приставка – обозначает прекращение, завершение действия; удаление, устранение чего-либо» [955], т. 1, с. 610. Таким образом, отсутствующую цифру вполне естественно было обозначить символом, похожим на букву О. По-видимому, именно так и возник ноль = 0.
Возможно и другое объяснение. Слово НОЛЬ могло произойти от старого русского слова НОЛИ или НОЛЬНО. Сегодня оно уже забыто, но раньше, до XVII века, часто использовалось в русском языке. Об этом говорят многочисленные примеры его употребления в старых текстах, приведенные в Словаре Русского Языка XI–XVII веков [789], с. 420–421. Слово НОЛЬНО, или НОЛЬНЫ, НОЛЬНЕ, НОЛЬ НА использовалось, в частности, как ограничительная частица, в смысле «не прежде чем, только когда» [789], с. 421. Но ведь и ноль в десятичной записи числа можно рассматривать, как ограничительный знак, «не пускающий» цифру соседнего разряда на место отсутствующей цифры данного разряда. Дело в том, что в предшествующей славяно-греческой полу-позиционной системе счисления если значащей цифры в том или ином разряде не было, то цифры соседних разрядов сдвигались друг к другу, занимая пустое место отсутствующей цифры. Именно поэтому и приходилось обозначать цифры разных разрядов по-разному, чтобы как-то различать их. В позиционной системе этого не происходит, потому что на «пустое» место цифры других разрядов «не пускает» ноль. Поэтому ноль могли первое время рассматривать как ограничительный знак, а значит и его название вполне могло произойти от ограничительной частицы НОЛЬНО в старом русском языке. Нольно – ноль.
420–421. Слово НОЛЬНО, или НОЛЬНЫ, НОЛЬНЕ, НОЛЬ НА использовалось, в частности, как ограничительная частица, в смысле «не прежде чем, только когда» [789], с. 421. Но ведь и ноль в десятичной записи числа можно рассматривать, как ограничительный знак, «не пускающий» цифру соседнего разряда на место отсутствующей цифры данного разряда. Дело в том, что в предшествующей славяно-греческой полу-позиционной системе счисления если значащей цифры в том или ином разряде не было, то цифры соседних разрядов сдвигались друг к другу, занимая пустое место отсутствующей цифры. Именно поэтому и приходилось обозначать цифры разных разрядов по-разному, чтобы как-то различать их. В позиционной системе этого не происходит, потому что на «пустое» место цифры других разрядов «не пускает» ноль. Поэтому ноль могли первое время рассматривать как ограничительный знак, а значит и его название вполне могло произойти от ограничительной частицы НОЛЬНО в старом русском языке. Нольно – ноль.
Рис. 1.39. Скорописная форма славянской буквы Т в начале слова.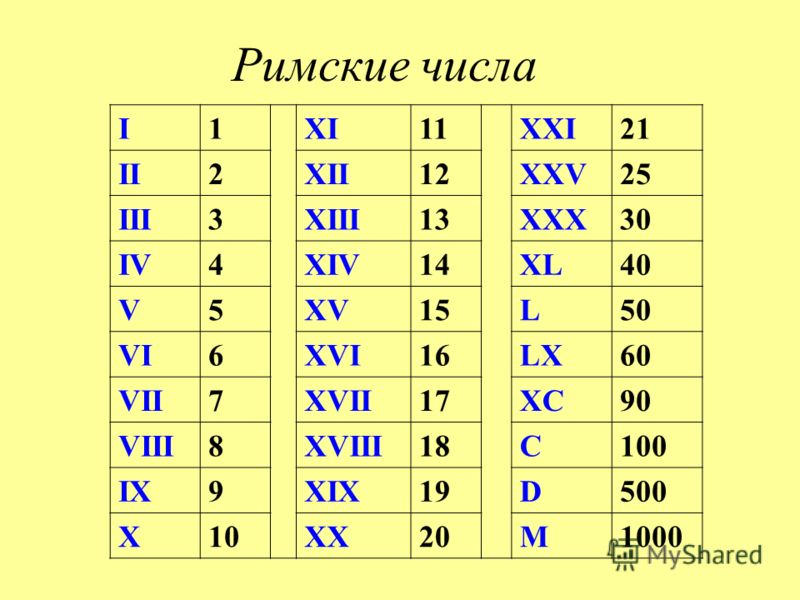 Ясно видно, что это в точности «ИНДО-АРАБСКАЯ» СЕМЕРКА. Взято из [791], выпуск 19
Ясно видно, что это в точности «ИНДО-АРАБСКАЯ» СЕМЕРКА. Взято из [791], выпуск 19
Рис. 1.40. Скорописная форма славянской буквы Е в конце слова великие». Ясно видно, что «ИНДО-АРАБСКАЯ» ШЕСТЕРКА получается из этой буквы Е зеркальным отражением. Взято из [787], выпуск 7
Кроме того, слово НОЛИ в старом русском языке употреблялось также и для обозначения неосуществившейся возможности: «помышляль есмь въ себе:… ноли буду лучии тогда, но худъ есмь и боленъ» [789], с. 420. В современном переводе: «я думал про себя: может быть («ноли») буду лучше тогда, но [это не осуществилось] я плох и болен». Этот смысл старого слова НОЛИ тоже, по-видимому, подходил для нового знака – нуля в позиционной системе. Ведь цифра ноль тоже как бы обозначает неосуществившуюся возможность – а именно, возможность поставить значащую цифру в данном разряде. Ноль говорит, что значащей цифры в данном разряде нет, хотя она МОГЛА БЫ здесь быть.
Возможно, конечно, попытаться произвести обозначение нуля = 0 из латинского слова OB, одним из значений которого было «в ОБМЕН на» [237], с. 684. Но не произошло ли само это «античное» латинское слово из славянской приставки ОБ в слове ОБМЕН? О том, что в фундаменте «древней латыни» лежит славянский язык, мы подробно говорим в книге «Русские корни «древней» латыни».
684. Но не произошло ли само это «античное» латинское слово из славянской приставки ОБ в слове ОБМЕН? О том, что в фундаменте «древней латыни» лежит славянский язык, мы подробно говорим в книге «Русские корни «древней» латыни».
Итак, название новой цифры НОЛЬ, позволившей ввести новую для того времени позиционную систему счисления, возникло, скорее всего, на основе именно русского языка. Так же как и новые обозначения «индо-арабских» цифр появились в результате легкого видоизменения старых русских цифр-букв. Все это происходило, как мы выяснили, не так уж давно – скорее всего, не ранее конца XVI века. А не в далеком средневековье, как это ошибочно утверждает скалигеровская хронология.
В заключение отметим, что в принципе можно пытаться искать буквы, похожие на «индо-арабские» цифры, и в других азбуках. Однако важно подчеркнуть, что для выяснения происхождения «индо-арабских» цифр подходит ДАЛЕКО НЕ ВСЯКАЯ АЗБУКА. Ведь требуется найти не просто какие-то буквы, «похожие на цифры», что иногда удается. Необходимо найти буквы-цифры, ДЕЙСТВИТЕЛЬНО ИСПОЛЬЗОВАВШИЕСЯ В СРЕДНИЕ ВЕКА В КАЧЕСТВЕ ОБОЗНАЧЕНИЙ ЦИФР. Причем, в силу естественной консервативности обозначений, цифровые значения старых цифр-букв должны в основном сохраняться и в новой системе счисления. Как это имеет место для славянско-греческой азбуки и «индо-арабских цифр». Азбуки же, не использовавшиеся для обозначения цифр, привлекать не имеет смысла.
Необходимо найти буквы-цифры, ДЕЙСТВИТЕЛЬНО ИСПОЛЬЗОВАВШИЕСЯ В СРЕДНИЕ ВЕКА В КАЧЕСТВЕ ОБОЗНАЧЕНИЙ ЦИФР. Причем, в силу естественной консервативности обозначений, цифровые значения старых цифр-букв должны в основном сохраняться и в новой системе счисления. Как это имеет место для славянско-греческой азбуки и «индо-арабских цифр». Азбуки же, не использовавшиеся для обозначения цифр, привлекать не имеет смысла.
С нашим выводом о том, что ноль изобретен только в конце XVI века, прекрасно согласуется и следующий известный в истории факт. Он поразителен с точки зрения скалигеровской хронологии. Нам предлагают считать, что ноль был известен еще в глубокой древности. Однако в то же время, отмечается, что математики, даже в XVI веке еще НЕ РАССМАТРИВАЛИ КОРНИ УРАВНЕНИЙ, РАВНЫЕ НУЛЮ [219], с. 153. Кроме того, как сообщают историки науки, естественная идея – оставить в правой части уравнения НОЛЬ, появилась лишь в конце XVI – начале XVII века [219], с. 153. Хотя ноль, как нас уверяют, к тому времени уже давным-давно известен, якобы несколько сотен лет. Цитируем: «Идея приравнивания уравнения нулю БЫЛА ЧУЖДА МАТЕМАТИКЕ ВОЗРОЖДЕНИЯ. ВПЕРВЫЕ КАНОНИЧЕСКУЮ ФОРМУ УРАВНЕНИЯ привел англичанин Т. Гэрриот (1580–1621) в книге «Применение аналитического искусства»» [219], с. 153. Но это, конечно же, означает, что обозначения для нуля не существовало вплоть до конца XVI века. Другое объяснение вряд ли возможно.
Цитируем: «Идея приравнивания уравнения нулю БЫЛА ЧУЖДА МАТЕМАТИКЕ ВОЗРОЖДЕНИЯ. ВПЕРВЫЕ КАНОНИЧЕСКУЮ ФОРМУ УРАВНЕНИЯ привел англичанин Т. Гэрриот (1580–1621) в книге «Применение аналитического искусства»» [219], с. 153. Но это, конечно же, означает, что обозначения для нуля не существовало вплоть до конца XVI века. Другое объяснение вряд ли возможно.
5.3. Явные следы переделки шестерки в пятерку на старых документах
Обратимся, например, к известной гравюре «Меланхолия» знаменитого средневекового художника Альбрехта Дюрера, жившего якобы в 1471–1528 годах, рис. 1.41. В правом верхнем углу гравюры он нарисовал так называемый магический квадрат размером 4 на 4. То есть, четыре строки и четыре столбца. Сумма чисел, стоящих в каждой строке, и сумма чисел, стоящих в каждом столбце, здесь одна и та же, и равняется 34. На рис. 1.42 мы приводим увеличенное изображение этого квадрата. А на рис. 1.43 показана первая клетка во втором ряду. Тут стоит цифра 5. И она действительно ДОЛЖНА здесь стоять, потому что иначе квадрат перестанет быть «магическим». Но достаточно вглядеться в изображение, чтобы стало совершенно очевидно, что эта пятерка получилась ИСПРАВЛЕНИЕМ стоявшей тут раньше цифры ШЕСТЬ, рис. 1.43.
Но достаточно вглядеться в изображение, чтобы стало совершенно очевидно, что эта пятерка получилась ИСПРАВЛЕНИЕМ стоявшей тут раньше цифры ШЕСТЬ, рис. 1.43.
Картина полностью ясна. Сегодняшнюю ШЕСТЕРКУ сначала, то есть в эпоху XVI века, воспринимали как пятерку. И наоборот, сегодняшнюю ПЯТЕРКУ тогда еще воспринимали как шестерку. В этих старых, первоначальных обозначениях и был нарисован «магический квадрат» у Дюрера. Но когда через некоторое время обозначения поменяли, то в новых обозначениях квадрат перестал быть магическим. Пришлось переправить рисунок. Может быть, это сделал сам Дюрер. Возможно, это сделали уже после его смерти – ученики или последователи. Наверное, меняли цифры не только на гравюрах Дюрера. Но во всяком случае, на его гравюре «Меланхолия» сохранились совершенно отчетливые следы ПЕРЕДЕЛКИ ЦИФР в XVI–XVII веках.
5.4. Переделка старых дат в семнадцатом веке
То обстоятельство, что в начале XVII века значения «индоарабских» цифр еще не устоялись, по-видимому, использовали скалигеровские историки для фальсификации дат, относящихся к началу XVII века. Пусть в каком-то документе дата начала XVII века, например, ТЫСЯЧА ШЕСТЬСОТ ЧЕТЫРНАДЦАТЫЙ ГОД была записана еще по-старому, то есть как 1514 год, где символ 5, в виде буквы ЗЕЛО, обозначал цифру ШЕСТЬ.
Пусть в каком-то документе дата начала XVII века, например, ТЫСЯЧА ШЕСТЬСОТ ЧЕТЫРНАДЦАТЫЙ ГОД была записана еще по-старому, то есть как 1514 год, где символ 5, в виде буквы ЗЕЛО, обозначал цифру ШЕСТЬ.
Рис. 1.41. Гравюра «Меланхолия» Альбрехта Дюрера. Взято из [1232], номер 23
Рис. 1.42. Фрагмент гравюры А. Дюрера «Меланхолия» с изображением «магического квадрата». Взято из [1232]
Рис. 1.43. Откровенно переделанная цифра в «магическом квадрате» гравюры А. Дюрера «Меланхолия». Цифру 6 переделали на цифру 5. Взято из [1232]
Затем цифровое значение этого символа изменилось и стало ПЯТЬ. Если забыть, что цифровое значение символа 5 менялось, то теперь дату 1514 год мы прочтем «по-новому» (и ошибочно): как ТЫСЯЧА ПЯТЬСОТ ЧЕТЫРНАДЦАТЫЙ ГОД. Вместо подлинного исходного значения – тысяча шестьсот четырнадцатого года. Как мы видим, дата удревнилась на СТО ЛЕТ. Тем самым, таким простым приемом можно было опустить вниз даты многих старых документов начала XVII века. По-видимому, скалигеровские историки XVII–XVIII веков этим лукавым «методом» широко пользовались. В результате они отодвинули в прошлое лет на сто многие события XVI–XVII веков. И в самом деле, мы уже хорошо знакомы со столетним хронологическим сдвигом в европейской и, в частности, русской истории.
По-видимому, скалигеровские историки XVII–XVIII веков этим лукавым «методом» широко пользовались. В результате они отодвинули в прошлое лет на сто многие события XVI–XVII веков. И в самом деле, мы уже хорошо знакомы со столетним хронологическим сдвигом в европейской и, в частности, русской истории.
Не исключено, что перестановка цифровых значений «индоарабских» цифр-букв, – пятерку поменяли с шестеркой, а тройку с семеркой, – была отнюдь не случайной. Вероятно, преследовали цель – СКРЫТЬ ПРОИСХОЖДЕНИЕ «индо-арабских» цифр-букв из прежних славяно-греческих обозначений. Скорее всего, это происходило уже в эпоху распада Великой = «Монгольской» Империи, то есть, начиная с XVII века. Когда в Западной Европе стали писать «новую историю» не только далеких веков, но и совсем недавнего прошлого. Как мы обсуждаем в книге «Освоение Америки Русью-Ордой», одним из пунктов западно-европейской государственной программы независимости было создание новых языков, новых правил чтения и т. п. Немаловажное место в ряду этих реформаторских мероприятий занимало преднамеренное искажение прежних цифровых обозначений. Стремились отделиться от традиций Великой Империи не только в языковом и культурном отношении, но и в «цифровом» тоже. Для этого переставили ПЯТЬ и ШЕСТЬ, а также ТРИ и СЕМЬ. В результате связь славянских обозначений-цифр с новыми западно-европейскими стала не так сильно бросаться в глаза. Чтобы ее обнаружить, сегодня потребовалась определенная работа. А без таких перестановок эта связь сразу обращала бы на себя внимание. Была бы очевидной. Хотя бы на примере ТРОЙКИ, которая ДО СИХ ПОР ПИШЕТСЯ НЕОТЛИЧИМО ОТ СЛАВЯНСКОЙ БУКВЫ 3.
Стремились отделиться от традиций Великой Империи не только в языковом и культурном отношении, но и в «цифровом» тоже. Для этого переставили ПЯТЬ и ШЕСТЬ, а также ТРИ и СЕМЬ. В результате связь славянских обозначений-цифр с новыми западно-европейскими стала не так сильно бросаться в глаза. Чтобы ее обнаружить, сегодня потребовалась определенная работа. А без таких перестановок эта связь сразу обращала бы на себя внимание. Была бы очевидной. Хотя бы на примере ТРОЙКИ, которая ДО СИХ ПОР ПИШЕТСЯ НЕОТЛИЧИМО ОТ СЛАВЯНСКОЙ БУКВЫ 3.
Надо четко сказать, что из обнаруженного нами факта не следует, что «индо-арабские» цифры придуманы именно на Руси, то есть в метрополии Империи. Может быть, что это сделали в какой-то имперской провинции. Например, в Египте или в Западной Европе в конце XVI – начале XVII века. Ведь в те годы Великая Империя была еще единой и разные ее земли исполняли разные функции. Это было удобно и разумно. В одних регионах ордынские цари-ханы развивали кораблестроение, в других – науку, в третьих – изящные искусства, в четвертых – медицину. Все достижения и открытия тут же становились общим достоянием «Монгольской» Империи, «шли в общий котел». В этом смысле, владельцем всех плодов интеллектуальной, производственной и т. п. деятельности считался имперский двор в метрополии Империи и лично Великий царь-хан, Император. Лишь после раскола Империи в XVII веке возник ранее неизвестный эффект. Появилась и пышно расцвела обостренная региональная конкуренция – чья наука или чья медицина лучше. Ранее такой вопрос просто не возникал. А теперь, одни стали гордиться – у нас, дескать, лучшие корабли, а другие отвечали – зато у нас лучшие пушки. Забыв, что не так давно и корабли и пушки были общими, имперскими и производились в том или ином месте в соответствии с общим хозяйственным планом, составленным в канцелярии Великого Императора.
Все достижения и открытия тут же становились общим достоянием «Монгольской» Империи, «шли в общий котел». В этом смысле, владельцем всех плодов интеллектуальной, производственной и т. п. деятельности считался имперский двор в метрополии Империи и лично Великий царь-хан, Император. Лишь после раскола Империи в XVII веке возник ранее неизвестный эффект. Появилась и пышно расцвела обостренная региональная конкуренция – чья наука или чья медицина лучше. Ранее такой вопрос просто не возникал. А теперь, одни стали гордиться – у нас, дескать, лучшие корабли, а другие отвечали – зато у нас лучшие пушки. Забыв, что не так давно и корабли и пушки были общими, имперскими и производились в том или ином месте в соответствии с общим хозяйственным планом, составленным в канцелярии Великого Императора.
Поэтому, повторим, «индо-арабские» цифры могли быть изобретены в том регионе Империи, где в ту эпоху решили организовать научные центры, направить туда дополнительное финансирование. Но мы утверждаем, что В ОСНОВЕ ЭТОГО ИЗОБРЕТЕНИЯ ЛЕЖИТ ИМЕННО СТАРАЯ СЛАВЯНСКАЯ ТРАДИЦИЯ ЗАПИСИ ЦИФР ПРИ ПОМОЩИ БУКВ. Как мы показали выше, только внутри этой традиции и могли возникнуть «индо-арабские» обозначения цифр. Если их придумали в Европе, то это означает лишь, что в Европе до этого пользовались славянскими буквами и языком. А если их придумали на Руси, то это значит, что Западная Европа просто воспользовалась новыми обозначениями, возможно видоизменив их. Переставив пятерку с шестеркой и тройку с семеркой.
Как мы показали выше, только внутри этой традиции и могли возникнуть «индо-арабские» обозначения цифр. Если их придумали в Европе, то это означает лишь, что в Европе до этого пользовались славянскими буквами и языком. А если их придумали на Руси, то это значит, что Западная Европа просто воспользовалась новыми обозначениями, возможно видоизменив их. Переставив пятерку с шестеркой и тройку с семеркой.
Нас могут спросить: а где же в таком случае ПЕРВИЧНЫЕ «индо-арабские» цифры в старых русских документах? Ответ следующий. По-видимому, «индо-арабские» цифры вошли во всеобщее употребление – в документацию и т. п., в Западной Европе в XVII веке. И вскоре после этого, в эпоху Петра I, были приняты и на Руси. Здесь нужно отделять этап ИЗОБРЕТЕНИЯ «индоарабских» цифр в конце XVI – начале XVII века, и этап их широкого ВНЕДРЕНИЯ в делопроизводство. ВНЕДРЕНИЕ «индоарабских» цифр происходило уже в XVII веке, ПОСЛЕ РАСКОЛА ИМПЕРИИ. Когда русское общество, при Романовых, уже было поставлено в вынужденную культурную зависимость от Западной Европы. Поэтому на новой романовской Руси и цифры приняли именно в том виде, в каком они НЕЗАДОЛГО ДО ТОГО начали употребляться в Западной Европе.
Поэтому на новой романовской Руси и цифры приняли именно в том виде, в каком они НЕЗАДОЛГО ДО ТОГО начали употребляться в Западной Европе.
Но если, как мы видим, «индо-арабские» цифры внедрены лишь в начале XVII века, а в своем окончательном виде, где-то в середине XVII века, то следовательно, все записи, использующие «индо-арабские» цифры в их современном виде, нельзя датировать эпохой ранее конца XVI века. Если нам сегодня говорят, что на некоем документе современником поставлена дата в принятой сегодня форме: 1250 год, или 1460 год, или даже 1520 год, то ПОДДЕЛКА. Либо подделан документ, либо подделана дата, то есть проставлена задним числом. А в случае дат якобы шестнадцатого века, как мы уже говорили, вероятно, некоторые из них относятся на самом деле к СЕМНАДЦАТОМУ ВЕКУ. Сегодня их неправильно интерпретируют, объявляя старый символ 5 – современной пятеркой, а не старой ШЕСТЕРКОЙ, как это было первоначально.
В связи с этим следует заново вернуться к вопросу – когда на самом деле жили известные нам сегодня деятели якобы XV–XVI веков. Например, нас уверяют, будто знаменитый художник Альбрехт Дюрер жил в 1471–1528 годах. Усомнимся. Скорее всего, на самом деле он жил в конце XVI – начале XVII века. Поскольку старый смысл дат вида 15(…) год, проставленных на его картинах и рисунках, был 16(…) год. А следовательно, и его известные гравюры, звездные карты к птолемеевскому Альмагесту и т. д., изготовлены не в начале XVI века, как нам сегодня говорят, а в начале XVII века. Напомним, что наш анализ Альмагеста показал, что эта книга в своем современном виде, появилась не ранее начала XVII века. См. «Звезды свидетельствуют». А следовательно, и дюреровские звездные карты к Альмагесту изготовлены примерно в это же время. А не на сто лет раньше.
Например, нас уверяют, будто знаменитый художник Альбрехт Дюрер жил в 1471–1528 годах. Усомнимся. Скорее всего, на самом деле он жил в конце XVI – начале XVII века. Поскольку старый смысл дат вида 15(…) год, проставленных на его картинах и рисунках, был 16(…) год. А следовательно, и его известные гравюры, звездные карты к птолемеевскому Альмагесту и т. д., изготовлены не в начале XVI века, как нам сегодня говорят, а в начале XVII века. Напомним, что наш анализ Альмагеста показал, что эта книга в своем современном виде, появилась не ранее начала XVII века. См. «Звезды свидетельствуют». А следовательно, и дюреровские звездные карты к Альмагесту изготовлены примерно в это же время. А не на сто лет раньше.
Приведем теперь примеры записи дат на старых картинах и рисунках нескольких известных художников средневековья. После всего сказанного выше становится понятным, что эти работы следует датировать ПРИМЕРНО СТА ГОДАМИ ПОЗЖЕ, чем принято считать сегодня.
На рис. 1.44 приведен автопортрет А. Дюрера. Над головой художника крупно проставлена дата, рис. 1.45. Сегодня считается, что здесь написан 1493 год. Однако обратите внимание на форму второй слева цифры, якобы четверки. Не получена ли она легким искажением славянской буквы Е? То есть прежней старой ПЯТЕРКИ. Если это так, то дата на автопортрете Дюрера окажется следующей: 1593 год. Получается самый конец ШЕСТНАДЦАТОГО ВЕКА. На сто лет позже, чем принято думать сегодня.
Дюрера. Над головой художника крупно проставлена дата, рис. 1.45. Сегодня считается, что здесь написан 1493 год. Однако обратите внимание на форму второй слева цифры, якобы четверки. Не получена ли она легким искажением славянской буквы Е? То есть прежней старой ПЯТЕРКИ. Если это так, то дата на автопортрете Дюрера окажется следующей: 1593 год. Получается самый конец ШЕСТНАДЦАТОГО ВЕКА. На сто лет позже, чем принято думать сегодня.
На рис. 1.46 приведена одна из гравюр А. Дюрера. Наверху проставлена дата, рис. 1.47. Сегодня нам говорят, что тут стоит 1494 год. Однако всмотримся внимательнее в так называемую «четверку». Она написана практически так же, как и славянское рукописное Е. То есть, как ПЯТЕРКА в старых обозначениях. Если это так, то данный рисунок А. Дюрера датируется не 1494 годом, а 1595 годом. То есть, концом XVI века.
На рис. 1.48 приведена картина А. Дюрера с проставленной датой, рис. 1.49. Сегодня считается, что это 1499 год. Однако опять-таки мы видим здесь «четверку», являющуюся просто повернутой славянской буквой Е. То есть, на самом деле это ПЯТЕРКА в старых обозначениях. Следовательно, данная картина, скорее всего, датируется не 1499 годом, а 1599 годом. Концом XVI века.
То есть, на самом деле это ПЯТЕРКА в старых обозначениях. Следовательно, данная картина, скорее всего, датируется не 1499 годом, а 1599 годом. Концом XVI века.
Рис. 1.44. Автопортрет А. Дюрера, датируемый якобы 1493 годом.
На самом деле это, скорее всего, 1593 год. То есть на сто лет ближе к нам. Взято из [1232], картина 1
Рис. 1.45. Фрагмент с датой на автопортрете А. Дюрера
Рис. 1.46. Гравюра А. Дюрера «Битва морских богов». Наверху проставлена дата якобы 1494 год. На самом деле это, скорее всего, 1595 год. То есть, на сто лет ближе к нам. Взято из [1232], номер 4
Рис. 1.47. Фрагмент с датой на гравюре А. Дюрера «Битва морских богов». Взято из [1232], номер 4
Рис. 1.48. Картина А. Дюрера, датируемая якобы 1499 годом. На самом деле это, скорее всего, 1599 год. То есть на сто лет ближе к нам. Взято из [1232], номер 11
Рис. 1.49. Фрагмент с датой на картине А. Дюрера якобы 1499 года
На рис. 1.50 приведена гравюра А. Дюрера. На ней, внизу, проставлена дата, рис. 1.51. Сегодня нам говорят, что это 1502 год. Однако, как мы объяснили выше, скорее всего, здесь символ 5 обозначал старую ШЕСТЕРКУ. Следовательно, это 1602 год. То есть, начало XVII века. На сто лет позже, чем считается сегодня. Кстати, такая великолепная техника исполнения рисунка, как теперь становится понятно, возникла лишь в XVII веке.
1.50 приведена гравюра А. Дюрера. На ней, внизу, проставлена дата, рис. 1.51. Сегодня нам говорят, что это 1502 год. Однако, как мы объяснили выше, скорее всего, здесь символ 5 обозначал старую ШЕСТЕРКУ. Следовательно, это 1602 год. То есть, начало XVII века. На сто лет позже, чем считается сегодня. Кстати, такая великолепная техника исполнения рисунка, как теперь становится понятно, возникла лишь в XVII веке.
На рис. 1.52 приведена картина А. Дюрера. Над головой женщины проставлена дата, рис. 1.53. Сегодня нас уверяют, будто это очевидно 1505 год. Но в свете того, что нам стало известно, это, скорее всего, 1606 год. Поскольку старое цифровое значение символа 5 было ШЕСТЬ. Кроме того, в данной дате первая единица обозначена буквой X, а не буквой I, рис. 1.53. Но ведь буква X – это первая буква имени Христос. Это в точности отвечает нашей мысли, что в начале даты раньше ставили первую букву имени Иисус или имени Христос. И лишь потом эту букву объявили обозначением «тысячи». Между прочим, в данном случае, на картине А. Дюрера, буква X в дате записана в форме характерной именно для КИРИЛЛИЦЫ.
Дюрера, буква X в дате записана в форме характерной именно для КИРИЛЛИЦЫ.
Рис. 1.50. Рисунок А. Дюрера, датируемый якобы 1502 годом. На самом деле это, скорее всего, 1602 год. То есть на сто лет ближе к нам. Взято из [1232], номер 12
Рис. 1.51. Фрагмент с датой на рисунке А. Дюрера, датируемом якобы 1502 годом
Рис. 1.52. Картина А. Дюрера, датируемая якобы 1505 годом. На самом деле это, скорее всего, 1606 год. То есть на сто лет ближе к нам. Кроме того, первая цифра «один» записана явно как кириллическое X. То есть, как первая буква имени Христос. Взято из [1232], номер 16
Рис. 1.53. Фрагмент с датой на картине А. Дюрера, датируемой якобы 1505 годом
Все сказанное применимо отнюдь не только к Альбрехту Дюреру. Но и ко всем художникам и скульпторам, на картинах которых стоят даты, относимые сегодня к XV–XVI векам. То же самое следует сказать и о датах, проставленных на «старых» книгах. В том числе, и на «старых» Библиях.
На рис. 1.54 приведена картина Ганса Фриза «Усекновение головы Иоанна Крестителя». Внизу проставлена дата, рассматриваемая сегодня как 1514 год, рис. 1.55. Однако, как мы уже объяснили, старое цифровое значение символа 5 было ШЕСТЬ. Так что, скорее всего, это 1614 год или 1615 год. Обратите также внимание на запись первой цифры «один». Это – явное «И с точкой», то есть i. Кроме того, впереди поставлена еще одна точка. Итак, в качестве «первой цифры» мы видим I, то есть первую букву имени Иисус. Это в точности отвечает нашей реконструкции.
Рис. 1.54. Картина Ганса Фриза «Усекновение головы Иоанна Крестителя». Базельский художественный музей.
Она датируется якобы 1514 годом. Однако, скорее всего, это 1614 или 1615 год. То есть, на сто лет ближе к нам. Обратите внимание, что первая «цифра» записана как буква I (с точкой/), то есть как первая буква имени Иисус. Взято из [104], номер 10
Рис. 1.55. Фрагмент с датой на картине Ганса Фриза «Усекновение головы Иоанна Крестителя»
Неустойчивость форм «индо-арабских» цифр в эпоху XVI – начала XVII века ярко проявляется, например, на картинах знаменитого средневекового художника Луки Кранаха. Сегодня считается, что он жил в 1472–1553 годах [797], с. 643. Например, одна и та же цифра 5, – означающая у Кранаха, скорее всего, ШЕСТЬ, а не пять, как сегодня, – НА РАЗНЫХ ЕГО КАРТИНАХ ВЫГЛЯДИТ СОВЕРШЕННО ПО-РАЗНОМУ. Поскольку, как мы теперь понимаем, Лука Кранах жил, скорее всего, не в XV–XVI веках, а в XVI–XVII веках, то такие колебания в написании им цифр в датах на картинах, указывают, что еще и в XVII веке правила изображения «индо-арабских» цифр еще не устоялись.
Сегодня считается, что он жил в 1472–1553 годах [797], с. 643. Например, одна и та же цифра 5, – означающая у Кранаха, скорее всего, ШЕСТЬ, а не пять, как сегодня, – НА РАЗНЫХ ЕГО КАРТИНАХ ВЫГЛЯДИТ СОВЕРШЕННО ПО-РАЗНОМУ. Поскольку, как мы теперь понимаем, Лука Кранах жил, скорее всего, не в XV–XVI веках, а в XVI–XVII веках, то такие колебания в написании им цифр в датах на картинах, указывают, что еще и в XVII веке правила изображения «индо-арабских» цифр еще не устоялись.
Проект по математике «Арабские числа» (6 класс)
Содержание
Введение……………………………………………………………………… 3
1.Знакомство с древними цифрами………………………………………… 4
2. Арабские цифры – их написание ……………………………………… 5
3. Арабские цифры — история и развитие ………………………………… 6
4. Арабские цифры в Европе ……………………………………………… 8
Заключение………………………………………………………………… 9
Список литературы………………………………………………………… 10
Введение.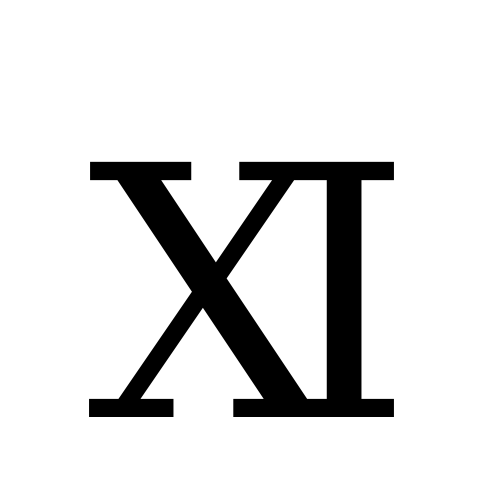
История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно как они произошли. Одно точно известно, что именно благодаря древним астрономам, а именно их точным расчетам мы и имеем наши числа. Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией. Они переняли шестидесятеричную систему и круглый греческий нуль. Индийцы соединили принципы греческой нумерации с десятичной мультипликативной системой взятой из Китая. Так же они стали обозначать цифры одним знаком, как было принято в древнеиндийской нумерации брахми. Блестящая Севильи перевел на латынь эту книгу, и индийская система счета широко распространилась по всей Европе.
Цифры
возникли в Индии, не позднее V века. Тогда же было открыто и формализовано
понятие нуля (шунья). Арабские цифры возникли в Индии, не позднее V века. Тогда
же было открыто и формализовано понятие нуля, которое позволило перейти к
позиционной записи. Арабские цифры стали известны европейцам в X вв. Благодаря
тесным связям христианской Барселоны и мусульманской Кордовы, Сильвестр имел возможность
доступа к научной информации, которой не имел никто в тогдашней Европе. В
частности он одним из первых среди европейцев познакомился с арабскими цифрами,
понял удобство их употребления по сравнению с римскими и начал их внедрять в
европейскую науку.
Благодаря
тесным связям христианской Барселоны и мусульманской Кордовы, Сильвестр имел возможность
доступа к научной информации, которой не имел никто в тогдашней Европе. В
частности он одним из первых среди европейцев познакомился с арабскими цифрами,
понял удобство их употребления по сравнению с римскими и начал их внедрять в
европейскую науку.
Название «арабские цифры» – результат исторической ошибки. Придумали эти знаки для записи числа отнюдь не арабы. Ошибка была исправлена лишь в XVIII веке стараниями Г.Я.Кера – русского ученого-востоковеда. Именно он впервые высказал мысль, что цифры, традиционно именуемые арабскими, родились в Индии.
1. Знакомство с древними цифрами
Традиционное
название десяти математических знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С помощью
них по десятичной системе счисления записываются любые числа. В течение
тысячелетий люди использовали пальцы рук для обозначения числа. Так, один
предмет они, также как и мы, показывали одним пальцем, три – тремя. С помощью
руки можно было показать до пяти единиц. Для выражения большего количества
использовались обе руки, а в некоторых случаях и обе ноги. Сейчас мы постоянно
пользуемся числами. Используем их, чтобы измерять время, покупать и продавать,
звонить по телефону, смотреть телевизор, водить автомобиль. К тому же у каждого
человека есть различные числа, идентифицирующие лично его. Например, в
удостоверении личности, в банковском счете, в кредитной карточке и т.д. Более
того, в компьютерном мире вся информация, и этот текст в том числе, передается
посредством числовых кодов.
В течение
тысячелетий люди использовали пальцы рук для обозначения числа. Так, один
предмет они, также как и мы, показывали одним пальцем, три – тремя. С помощью
руки можно было показать до пяти единиц. Для выражения большего количества
использовались обе руки, а в некоторых случаях и обе ноги. Сейчас мы постоянно
пользуемся числами. Используем их, чтобы измерять время, покупать и продавать,
звонить по телефону, смотреть телевизор, водить автомобиль. К тому же у каждого
человека есть различные числа, идентифицирующие лично его. Например, в
удостоверении личности, в банковском счете, в кредитной карточке и т.д. Более
того, в компьютерном мире вся информация, и этот текст в том числе, передается
посредством числовых кодов.
Мы
встречаемся с числами на каждом шагу и настолько к ним привыкли, что почти не
отдаем себе отчета, насколько важную роль они играют в нашей жизни. Числа
составляют часть человеческого мышления. На протяжении истории каждый народ
писал числа, считал, вычислял с их помощью. Первые написанные цифры, о которых
мы имеем достоверные свидетельства, появились в Египте и Месопотамии около пяти
тысяч лет назад. Хотя эти две культуры находились очень далеко друг от друга,
их числовые системы очень похожи, как будто представляют один метод –
использование засечек на дереве или камне для записи прошедших дней. Египетские
жрецы писали на папирусе, а в Месопотамии на мягкой глине. Конечно, конкретные
формы их цифр различны, но и в той, и в другой культуре использовали простые
черточки для единиц и другие метки для десятков и более высоких порядков. Кроме
того, в обеих системах писали желаемую цифру, повторяя черточки и метки нужное
число раз.
Первые написанные цифры, о которых
мы имеем достоверные свидетельства, появились в Египте и Месопотамии около пяти
тысяч лет назад. Хотя эти две культуры находились очень далеко друг от друга,
их числовые системы очень похожи, как будто представляют один метод –
использование засечек на дереве или камне для записи прошедших дней. Египетские
жрецы писали на папирусе, а в Месопотамии на мягкой глине. Конечно, конкретные
формы их цифр различны, но и в той, и в другой культуре использовали простые
черточки для единиц и другие метки для десятков и более высоких порядков. Кроме
того, в обеих системах писали желаемую цифру, повторяя черточки и метки нужное
число раз.
2. Арабские цифры — их написание.
1) Написание арабских цифр состояло из отрезков прямых линий, где
количество углов соответствовало
величине знака. Вероятно, кто-то из арабских математиков когда-то предложил
Вероятно, кто-то из арабских математиков когда-то предложил
идею — связать числовое значение цифры с количеством углов в ее начертании.
2) Дело в том, что именно арабы первыми познакомились с десятичными цифрами, которые в свою очередь возникли в Индии. Арабы по достоинству оценили десятичную систему счисления и начали использовать при подсчетах в торговых операциях. Именно арабы завезли эту систему счисления в Европу. Будучи проще и удобнее остальных систем, она достаточно быстро вытеснила все другие способы записи чисел. С тех пор цифры, используемые для записи чисел в десятичной системе счисления, называют арабскими.
3) Арабы переняли те
цифры, что называются теперь «арабскими» у индусов, а европейцы уже
заимствовали эти цифровые символы у арабов в конце средневековья.
Существует одна из гипотез, что некий арабский математик древности предложил связать
количество углов написанной цифры с её числовым значением.
Очертания всех
арабских цифр состояли из отрезков, при соединении дававших определённое
количество углов.
Не имеет углов только цифра «ноль» (придуманная гораздо позже остальных цифр),
поэтому она единственная изображается в виде овала.
4) Таблица, из которой видно, как постепенно видоизменялись цифры, употреблявшиеся арабами, пока они не приняли современные формы. Эти цифры называются цифрами «губар».
3.Арабские цифры — история и развитие.
А сейчас я бы хотел вам рассказать, что означали цифры у Арабов:
0 — это цифра без единого угла в начертании;
1 — это цифра содержащая один острый угол;
2 — это цифра содержащая два острых угла;
3 — это цифра содержащая три острых угла;
4 — это цифра содержащая 4 прямых угла;
5 — это цифра содержащая 5 прямых углов;
6 — это цифра содержащая 6 прямых углов;
7 — это цифра содержащая 7 прямых и острых углов;
8 — это цифра содержащая 8 прямых углов;
9 — это цифра содержащая 9 прямых углов.
Цифры, которыми мы
привыкли пользоваться, считаются Арабскими, на самом деле они происходят из древней
Индии. С VIII по XIII века арабский мир бурно развивался, большое внимание
уделялось астрономии, математике и другим наукам, Багдад был научным и
культурным центром Ближнего Востока. Находясь в выгодном географическом
положении, арабы использовали все полезное от Европейских и Азиатских
достижений. В Багдаде собирались ученые из Индии Китая, обменивались знаниями,
делали доклады, по своим исследованиям пользуясь своей системой исчисления, так
в 711 году у Индии была заимствована система исчисления из десяти знаков. Арабы
сразу оценили ее преимущество перед греческой и римской системой, которой в то
время пользовались европейцы, считая ее самой совершенной в мире. Стало
очевидным, что десятью знаками можно гораздо рациональнее отобразить огромные
значения численности. Достоинство арабских чисел не в том, что их удобно
писать, а в самой системе исчисления, где положение цифры определяет значение
числа. В последствии от арабов эта методика исчисления и записи попала в
Европу, совершенствовалась, знаки изменяли свои формы, но принцип десятичной
системы оставался неизменным.
В последствии от арабов эта методика исчисления и записи попала в
Европу, совершенствовалась, знаки изменяли свои формы, но принцип десятичной
системы оставался неизменным.
Даже само слово
цифра имеет арабское происхождение, арабы перевели значение знака с индийского
на свой язык, это звучало как «сифр» в последствии «цифр» более знакомое
произношение для нас, так постепенно десятичная система исчисления с востока
распространилась по всему миру. Надо отметить, что современные обозначения,
существенно отличаются от тех, которыми пользовались древние люди на востоке.
Как формировалось написание цифр, однозначно сейчас ни кто сказать не может,
почему 7 или 8 выглядят так, а не иначе, из каких соображений исходили древние,
когда придавали им подобные формы, существует много гипотез объясняющих эти
факты. Одна из таких гипотез наиболее правдоподобная, для более удобного
запоминания и логического соответствия математическому значению для цифры
выбирали такую фигуру, количество острых углов которой соответствует ее
обозначению.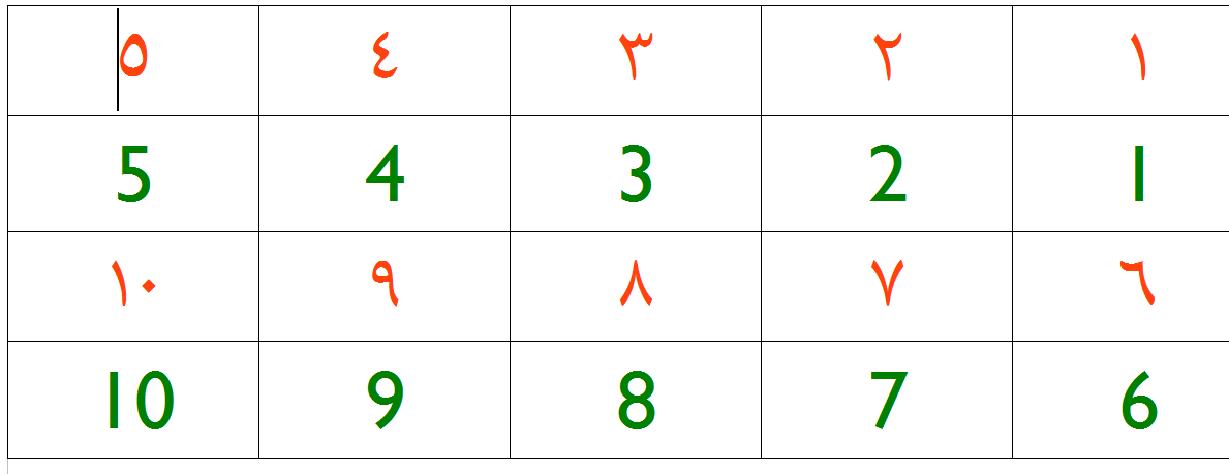 Если сравнить древние записи, то мы увидим, что все цифры имеют
угловатые контуры, кроме нуля, таким образом, восьмерка имеет 8 углов, семерка
с горизонтальной планкой поперек основания будет иметь 7 углов и такая аналогия
проглядывается на многих знаках. Самые древние упоминания о цифрах этой системы
обнаружены в Индии, они относятся к V веку, тогда же индийскими математиками
было определено понятие нуля. Писали 0 по разному, пропускали место,
ставили точку, и рисовали круг, последняя фигура утвердилась и дошла до наших
времен.
Если сравнить древние записи, то мы увидим, что все цифры имеют
угловатые контуры, кроме нуля, таким образом, восьмерка имеет 8 углов, семерка
с горизонтальной планкой поперек основания будет иметь 7 углов и такая аналогия
проглядывается на многих знаках. Самые древние упоминания о цифрах этой системы
обнаружены в Индии, они относятся к V веку, тогда же индийскими математиками
было определено понятие нуля. Писали 0 по разному, пропускали место,
ставили точку, и рисовали круг, последняя фигура утвердилась и дошла до наших
времен.
6) Со временем углы сгладились, и цифры приобрели привычный нам вид. Вот уже много столетий весь мир пользуется арабской системой записи чисел. Этими десятью значками можно легко выразить огромные значения.
7) Кстати, слово «цифра» тоже арабское. Арабские математики перевели
индийское слово «сунья» по смыслу на свой язык. Вместо «сунья» они стали
говорить «сифр» или «цифр», а это уже знакомое нам слово. Так слово «цифра» по наследству от арабов досталось и
нам.
Вместо «сунья» они стали
говорить «сифр» или «цифр», а это уже знакомое нам слово. Так слово «цифра» по наследству от арабов досталось и
нам.
Индия – родина цифр
Точно сказать, когда именно в Индии
появились цифры, невозможно, но с VI века они уже встречаются в документах.
Происхождение начертания цифр имеет два
объяснения.
Возможно, цифры происходят от букв алфавита
девангари, используемого в Индии. С этих букв начинались соответствующие
числительные на санскрите.
Согласно другой
версии, изначально числовые знаки состояли из отрезков, соединяющихся под
прямым углом. Это отдаленно напоминало очертания тех цифр, которыми сейчас
пишут индекс на почтовых конвертах. Отрезки образовывали углы, и их количество
у каждого знака соответствовало числу, которое он обозначал. У единицы угол был
один, у четверки – четыре и т.д., а нуль вообще углов не имел.
О нуле следует
сказать особо. Это понятие – под названием «шунья» – тоже ввели индийские
математики. Благодаря введению нуля родилась позиционная запись чисел. То был
истинный прорыв в математике!
Благодаря введению нуля родилась позиционная запись чисел. То был
истинный прорыв в математике!
Как индийские цифры стали арабскими
О том, что цифры были не изобретены арабами, а заимствованы,
говорит хотя бы тот факт, что буквы они пишут справа налево, а цифры – слева
направо.
С индийскими цифрами арабский мир познакомил
средневековый ученый Абу Джафар Мухаммад ибн Муса аль-Хорезми (783-850). Один
из его научных трудов так и называется – «Книга об индийском счете». В этом
трактате аль-Хорезми описал и цифры, и десятичную позиционную систему.
Постепенно цифры утратили первоначальную
угловатость, приспосабливаясь к арабскому письму, приобрели округлую форму.
4. Арабские цифры в Европе
Средневековая Европа пользовалась римскими
цифрами. Насколько это было неудобно, говорит, например, письмо итальянского
математика, адресованное отцу его ученика. Учитель советует отцу отправить сына
в Болонский университет: может, там парня научат умножению и делению, сам учитель
за такое сложное дело не берется.
Между тем, контакты с арабским миром у европейцев были, а значит – была возможность позаимствовать научные достижения. Большую роль сыграл в этом Герберт Орильякский (946-1003). Этот ученый и религиозный деятель изучал математические достижения математиков Кордовского Халифата, расположенного на территории современной Испании, что и позволило ему познакомить Европу с арабскими цифрами.
Нельзя сказать, что европейцы сразу приняли арабские цифры с восторгом. В университетах ими пользовались, а вот в повседневной практике – остерегались. Опасение было связано с легкостью подделок: единицу очень просто исправить на семерку, еще проще приписать лишнюю цифру – с римскими цифрами подобные махинации невозможны. Во Флоренции в 1299 году арабские цифры даже запретили.
Но постепенно достоинства арабских цифр становились очевидными для всех. К XV веку Европа практически полностью перешла на арабские цифры и пользуется ими до сих пор.
Заключение.
Подводя итог, надо отметить: несмотря на то что ответ на вопрос, сколько арабских цифр существует в настоящее время, очень прост, позиционная цифровая система прошла длинный путь становления. Так, символы, т. е. цифры, однажды созданные выдающимися индийскими учеными, сначала заняли свое место в арабской культуре, а только затем начали распространяться во всем цивилизованном мире. Создание такой цифровой системы позволило значительно ускорить темпы развития как науки, так и техники. Главной причиной быстрого распространения и адаптации арабских цифр на мировом уровне стали миграция и появление книгопечатания, благодаря которым удалось познакомить с ними жителей всех континентов.
Список литературы:
1. В мире чисел. (И.Я.
Депман, составитель Ю.И. Смирнов)
В мире чисел. (И.Я.
Депман, составитель Ю.И. Смирнов)
2. Энциклопедия.
3. сайт:http://ru.wikipedia.org/wiki/
Арабские цифры
Как считать на современном стандартном арабском языке (اللغة العربية الفصحى), универсальном языке арабоязычного мира. Примечание : цифры в арабском языке пишутся слева направо, а буквы — справа налево.
Если какие-либо из номеров являются ссылками, вы можете прослушать запись, нажав на них. Если вы можете предоставить записи, пожалуйста, свяжитесь со мной.
| Число | Кардинал | Порядковый номер |
|---|---|---|
| 0 (٠) | (ṣifr) صفر | |
| 1 (١) | (ваид) واحد | m — (awwal) اول f — (ūla) اولى |
| 2 (٢) | (инан) إثنان | (alṯani) الثّاني |
| 3 (٣) | (ṯālaṯa) ثلاثة | (alṯalṯu) الثّالِثُ |
| 4 (٤) | (арбаа) أربعة | (alrab’eu) الرّابِعُ |
| 5 (٥) | (хамса) خمسة | (альамсу) الْخامِسُ |
| 6 (٦) | (ситта) ستة | (алсадсу) السّادِسُ |
| 7 (٧) | (саба) سبعة | (альсабеу) السابعُ |
| 8 (٨) | (самания) ثمانية | (аламну) الثّامِنُ |
| 9 (٩) | (тис’а) تسعة | (altas’eu) التّاسِعُ |
| 10 (١٠) | (ашра) عشرة | (аль-ашру) الْعاشِرُ |
| 11 (١١) | إحدى عشر (ахада ашар) | м — (альхади ашар) الحادِيَ عَشَرَ f — (альхадиата ашар) الحادية عَشْرةَ |
| 12 (١٢) | إثنا عشر (ина ашар) | м — (alṯani ашар) الثانيَ عَشَرَ f — (alṯania ашар) الثانيةَ عَشْرةَ |
| 13 (١٣) | ثلاثة عشر (ṯālatha ‘ashar) | (alṯaleṯ ‘ашар) الثالثَ عَشَرَ f — (alṯaleṯata ‘ашар) الثالثةَ عَشْرةَ |
| 14 (١٤) | أربعة عشر (арбаа ашар) | м — (альрабе ашар) الرابعَ عَشَرَ f — (альрабе ашар) الرابعةَ عَشْرةَ |
| 15 (١٥) | خمسة عشر (хамса ашар) | м — (алхамс ашар) الخامِسَ عَشَرَ f — (альхамст ашар) الخامسةَ عَشْرةَ |
| 16 (١٦) | ستة عشر (ситта ашар) | м — (алсадис ашар) السادِسَ عَشَرَ f — (алсадст ашар) السادسةَ عَشْرةَ |
| 17 (١٧) | سبعة عشر (саб’а ашар) | м — (альсабе ашар) السابعَ عَشَرَ f — (альсабет ашар) السابعةَ عَشْرةَ |
| 18 (١٨) | ثمانية عشر (самания ашар) | m — (alṯamn ‘ашар) الثامنَ عَشَرَ f — (alṯamnt ‘ашар) الثامنةَ عَشْرةَ |
| 19 (١٩) | تسعة عشر (тис’а ‘ашар) | m — (altase ‘ашар) التاسعَ عَشَرَ f — (altaset ‘ашар) التاسعةَ عَشْرةَ |
| 20 (٢٠) | عشرون (‘ишрун) | (алейшрун) العِشرونَ |
| 21 (٢١) | واحد و عشرون (wāḫed wa-’ishrun) | |
| 22 (٢٢) | إثنان وعشرون (iṯnāne wa-’ishrun) | |
| 23 (٢٣) | ثلاثة و عشرون (ṯālaṯa wa-’ishrun) | |
| 24 (٢٤) | أربعة و عشرون (arba’a wa-’ishrun) | |
| 25 (٢٥) | خمسة و عشرون (ḫamsa wa-’ishrun) | |
| 26 (٢٦) | ستة و عشرون (sitta wa-’ishrun) | |
| 27 (٢٧) | سبعة وعشرون (саб’а ва-’ишрун) | |
| 28 (٢٨) | ثمانية و عشرون (ṯamāniya wa-’ishrun) | |
| 29 (٢٩) | تسعة و عشرون (тис’а ва-’ишрун) | |
| 30 (٣٠) | (ṯālaṯun) ثلاثون | |
| 40 (٤٠) | (арбаун) أربعون | |
| 50 (٥٠) | (амсун) خمسون | |
| 60 (٦٠) | (ситтун) ستون | |
| 70 (٧٠) | (саб’ун) سبعون | |
| 80 (٨٠) | (ṯamānun) ثمانون | |
| 90 (٩٠) | (тис’ун) تسعون | |
| 100 (١٠٠) | (миа) مائة | |
| 1000 (١٠٠٠) | (альф) или | |
| 2 000 (٢٠٠٠) | (альфаин) ألفين | |
| 100 000 (١٠٠٠٠٠) | (миат альф) مائة ألف | |
| 1 миллион (١٠٠٠٠٠٠) | (млн. ) مليون ) مليون |
Послушайте арабские цифры:
Если вы хотите внести какие-либо исправления или дополнения на эту страницу или если вы можете предоставить записи, пожалуйста, свяжитесь со мной.
Информация об арабских числах
http://arabic.speak7.com/arabic_numbers.htm
http://userpages.umbc.edu/~samir1/620_Project_2/L3T1_1.htm
https://www.rocketlanguages.com/ арабский/уроки/цифры-в-арабском
http://www.learnarabiconline.com/arabic-numbers.shtml
http://allthearabicyouneverlearnedthefirsttimearound.com/p3/p3-ch4/arabic-numbers/
Информация об арабском языке | Фразы | Числа | Вавилонская башня | Статьи | Ссылки | Учебные материалы | Книги об арабской графике | Арабские электронные словари и переводчики
Амхарский, арабский (чадский), арабский (египетский), арабский (хиджази), арабский (ливийский), арабский (современный стандарт), арабский (марокканский), Иврит, мальтийский, Тигре, Тигриня, Turoyo
Числа на других языках
Алфавитный указатель | Индекс языковой семьи
[сверху]
Почему бы не поделиться этой страницей:
Изучайте языки бесплатно на Duolingo
Если вам нравится этот сайт и вы считаете его полезным, вы можете поддержать его, сделав пожертвование через PayPal или Patreon или пожертвовав другим способом. Омниглот — это то, как я зарабатываю на жизнь.
Омниглот — это то, как я зарабатываю на жизнь.
Примечание : все ссылки на этом сайте на Amazon.com, Amazon.co.uk и Amazon.fr являются партнерскими ссылками. Это означает, что я получаю комиссию, если вы нажимаете на любой из них и что-то покупаете. Таким образом, нажав на эти ссылки, вы можете помочь поддержать этот сайт.
[сверху]
Арабские цифры — О языках и числах
Обзор языков
Арабский язык ( Al-ʻarabiyyah , العَرَبِيَّة ) — центрально-семитский язык афро-азиатской семьи. Официальный или соофициальный язык в 26 странах, на нем говорят около 422 миллионов человек. Это также литургический язык ислама. Его современная стандартная арабская форма, образованная от классического арабского языка, является лингва-франка, поскольку включает в себя множество диалектных разновидностей. Арабский язык пишется справа налево в абджаде, системе письма, в которой каждый символ обозначает согласную.
Из-за отсутствия данных мы можем точно сосчитать только до 1 000 000 на арабском языке. Пожалуйста, свяжитесь со мной, если вы можете помочь мне подсчитать от этого предела.
Пожалуйста, свяжитесь со мной, если вы можете помочь мне подсчитать от этого предела.
Список арабских номеров
- 1 — ١ Wahid (واحد)
- 2 — ٢ ithnan (إثنان)
- 3 — ٣ Thalatha (ثلاثة 50408 40407 (خمسة)
- 6 — ٦ Sitta (ستة)
- 7 — ٧ Sab’a (سبмяте)
- 8 — ٨ Thamaniya (ثمانية)
- 9 — ٩ Tis’a (#تрединил.0407 10 — ١٠ ‘Ashra (عشرة)
- 11 — ١١ ahada’ ashar (احد عشر)
- 12 — ١٢ Ithna ‘Ashar (اثنا عشر)
- 13 — ١٣ ١٣ vtyر)
- 13 — ١٣ ش v) Arba’a ‘Ashar (اربعة عشر)
- 15 — ١٥ Khamsa’ Ashar (خمسة عشر)
- 16 — ١٦ Sitta ‘Ashar (ستة عشر)
- 17 17 — ١٧ Sab’a’ Ashar (® عشر)
- 17 — ١٧ Sab’a ‘Ashar (® عشe) — ١٨ Thamaniya ‘Ashar (ثمانية عشر)
- 19 — ١٩ Tis’a’ Ashar (تسstة عشر)
- 20 — ٢٠ ‘Ishrun (عشرون)
- 30 — ٣٠ Thalathun (عشرون)
- 30 — ٣٠ ٣٠ ٣٠ ٣٠’ thalathun (ваш)
- 30 — ٣٠0408
- 40 — ٤٠ arba’un (أربعون)
- 50 — ٥٠ Khamsun (خمسون)
- 60 — ٦٠ Sittun (ستو едлее)
- 70 — ٧٠ Sab’un (سب408
- 70 — ٧٠ Sab’un (سب408
- 70 — ٧٠ Sab’un (سب408
- 70 —
- 90 – ٩٠ tis’un (تسعون)
- 100 – ١٠٠ mi’a (مئة)
- 1,000 – ١٠٠٠ alf (ألف)
- one million – malioun (مَلِيُوْن)
- one billion – maliâr (مَلِيَار)
Арабские цифры
То, что широко известно как «арабские цифры» и реже индийско-арабские цифры, представляет собой набор символов или графем, которые представляют цифры от 0 до 9, а также привязанная к нему позиционная десятичная система. Эти цифры, изобретенные в Индии примерно в III -м -м веках до нашей эры, прошли через арабскую цивилизацию с IX -го -го века до прибытия в Европу в X -м -м веке. В странах Машрека, то есть в основном в Ираке, Сирии, Ливане, Иордании и Палестине, индуистские цифры используются в сочетании с западными цифрами.
Эти цифры, изобретенные в Индии примерно в III -м -м веках до нашей эры, прошли через арабскую цивилизацию с IX -го -го века до прибытия в Европу в X -м -м веке. В странах Машрека, то есть в основном в Ираке, Сирии, Ливане, Иордании и Палестине, индуистские цифры используются в сочетании с западными цифрами.
0
1
2
3
4
5
6
7
8
9
Правила арабской нумерации
Теперь, когда вы ознакомились с наиболее полезными числами, давайте перейдем к правилам написания десятков, составных чисел, а почему не сотен, тысяч и выше (если возможно).
- Цифры от нуля до девяти являются определенными словами, а именно sifr (صِفْرٌ) [0], вахид (وَاحِدٌ) [1], ithnan (اِثْ) [ن9ْْن]0397 Thalatha (ثَلَاثَةٌ) [3], Arba’a (أَرْبَعٌ) [4], KHAMSA (خَمْ профессия) [5], SITTA (خَمْ®) [5], SITTA (خَمْ®) [5], SITTA (خَمْ®).
 [7], тамания (ثَمَانِيَةٌ) [8] и тис’а (تِسْعَةٌ) [9].
[7], тамания (ثَمَانِيَةٌ) [8] и тис’а (تِسْعَةٌ) [9]. - Десятки основаны на корне имен цифр с суффиксом и (ون), за исключением десяти: ‘ашра (عَشَرَةٌ) [10], ‘ишрун (عِشْرُونَ) [20397 ‘ишрун (عِشْرُونَ) [200397 ‘ашра (عَشَرَةٌ) (ثَلَاثُونَ) [30], Arba’un (أَرْبَعُون вероятно) [40], KHAMSUN (خَمْونَ) [50], SITTUN (سِتُّونَ) [60], SABIN (سِتُّونَ) [60], SABLIN (سِتُّونَ). [80] и тис’ун (تَسْعَوْنَ) [90].
- От одиннадцати до девятнадцати составные числа образуются путем указания единицы измерения, а затем формы слова, обозначающего десять: ахада ‘ашар (إِحْدَى عَشَرٍ) [11], итна ‘ашар (اِثْنَا عَشَ) [1َشَا عَشٍ]. талата ‘ашар (ثَلَاثَةَ عَشَرَ) [13], Arba’a ‘Ashar (أَرْبَعَةَ عَشَرَ) [14], KHAMSA’ ASHAR (خَمْ читал (15], Sitta ‘ASHAR (щал ASH’THçtّة عt -Ash’TsTRITHARش عt -عtrشt -َsTRI -→ ASHARI -َ vt’TRITHAR’T.
 عَشَرَ) [17], тамания ‘ашар (ثَمَانِيَةَ عَشَرَ) [18] и тис’а ‘ашар (تِسْعَةَ عَشَ 19).
عَشَرَ) [17], тамания ‘ашар (ثَمَانِيَةَ عَشَرَ) [18] и тис’а ‘ашар (تِسْعَةَ عَشَ 19). - Свыше двадцати одного составные числа образуются путем указания единицы, а затем десяти, связанных с помощью соединителя слов и ( wa-, وَ). Отсюда получаем: талатха ва-хамсун (ثَلَاثَةُ وَ خَمْسُونَ) [53], саб’а ва-тис’ун (سَبْعَةُ وَ تٳعَ7).
- Сотни образуются путем указания цифры множителя перед словом сотни, за исключением самой сотни: ми’а (مِئَةٌ) [100], итнан ми’а (مِائَتَانِ) [200], талатха ми’ A (ثَلَاثَةَ مِئَةَ) [300], Arba’a Mi’a (أَرْبَعَةَ مِئَةَ) [400], Khamsa Mi’a (خَمْ® .0398 (سِتَّةَ مِئَةَ) [600], Sab’a Mi’a (سَبْعَةَ مِئَةَ) [700], Thamaniya mi’a (ثَمَانِеся ة гать 800398 (ثَمَانِيَةَ مِئَة выполнен), и (ثَمَانِеся ة م 400398. مِئَةَ) [900].
- Слово для тысячи — alf (أَلْفٌ). Две тысячи используют двойную форму тысячи: alfain (أَلْفَيْنِ) [2,000].
 Выше двух тысяч используется форма множественного числа тысячи: талата алааф (ثَلَاثَةُ آلَافٍ) [3,000], арбаа алааф (أربَعة آلَافٍ) [9,000],0397 KHAMSA ALAAF (خَمْسَةُ أَﻟﺎف) [5000], Sitta Alaaf (سِتَّةُ أَﻟﺎف) [6000], Sab’a Alaaf (щал ( (щал. . и тис’а алааф (ﺗﺴِﻌﺔ أَﻟﺎف) [9000].
Выше двух тысяч используется форма множественного числа тысячи: талата алааф (ثَلَاثَةُ آلَافٍ) [3,000], арбаа алааф (أربَعة آلَافٍ) [9,000],0397 KHAMSA ALAAF (خَمْسَةُ أَﻟﺎف) [5000], Sitta Alaaf (سِتَّةُ أَﻟﺎف) [6000], Sab’a Alaaf (щал ( (щал. . и тис’а алааф (ﺗﺴِﻌﺔ أَﻟﺎف) [9000]. - Миллион — это малиун (مَلِيُوْن) [1 миллион, 10 6 ], а слово для миллиарда — малиар (مَلِيَار) [1 миллиард, 10 9 9 ].
Напишите число полностью на арабском языке
Давайте теперь перейдем к практике правил нумерации в арабском языке. Угадаете, как написать число полностью? Введите число и попробуйте записать его в уме или, может быть, на листе бумаги, прежде чем отображать результат.
Книги
Оксфордский арабский словарь
Карин С. Райдинг, редакторы Oxford University Press (2014)
[ Amazon. com, Kindle — Amazon.com]
com, Kindle — Amazon.com]
Справочник по грамматике современного стандартного арабского языка
редакторы Cambridge University Press (2005)
[ Amazon.com ]
Arabic Voices 1: Аутентичные практики чтения и прослушивания на современном стандартном арабском языке и разговорных диалектах
Мэтью Олдрич, редакторы Лингвализм (2014)
[ Amazon.com, Kindle — Amazon.com]
As-saqiya A1, Lengua árabe
editors Albujayra (2015)
[ Amazon.com ]
Gramática Árabe Comentada
Антонио Моралес Дельгадо, редакторы Albujayra (2014)
[ Amazon.com ]
Alatul Iniciación a la lengua árabe
by Victoria Aguilar, editors Herder (2010)
[ Amazon.com ]
Матье Гидер, редакторы Ellipses (2015)
[ Amazon.com ]
Путеводитель по арабской литературе
Ханса Леу, редакторы Ассимил (2011)
[Amazon.com]
Manuel d’arabe moderne
Люка-Вилли Дехевеля, редакторы L’Asiathèque (2008)
[ Amazon.com ]
Статьи
Семитские языки
Амхарский, арабский, иврит и мальтийский.
Другие поддерживаемые языки
Поскольку других поддерживаемых в настоящее время языков слишком много, чтобы перечислять их здесь, выберите язык из полного списка поддерживаемых языков.
Арабские цифры — [Полное руководство для начинающих]
الأرقَامُ في اللغةِ العربيةِ Чувствуете себя подавленным из-за всех правил, касающихся арабских цифр? Это простое, но исчерпывающее изложение всех правил, которые вам нужно знать.
Имейте в виду, что в арабском языке у каждого числа есть мужской и женский варианты.
Вот цифры от 1 до 10 на арабском языке. Цифры указаны словами рядом с символом для каждого:
| 1 | ١ | |
| 2 | إثْنانِ | ٢ |
| 3 | ثَلاثَةٌ | ٣ |
| 4 | أَرْبَعَةٌ | ٤ |
| 5 | خَمْسَةٌ | å |
| 6 | سِتَّةٌ | æ |
| 7 | Номер телефона | ٧ |
| 8 | ثَمَانِيَةٌ | ٨ |
| 9 | تِسْعَةٌ | ٩ |
| 10 | Номер телефона | ١٠ |
В арабском языке есть определенные правила работы с числами. Они основаны на самом числе, а также на поле субъекта.
Они основаны на самом числе, а также на поле субъекта.
Грамматика чисел на арабском языке
Мы можем разделить эти правила на четыре набора
Правила, относящиеся к:
1-العَدَدُ المُف нравится-единственные номера
Числа от 3 до 10-1000-ficeete. 1000…. и т. д.
ال Обеспечение المُرَكَبَب-2-составные номера
Числа от 11 до 19
ألفاظ العقود-3
, которые 20-30-40…. цифры
т.е. Числа от 1 до 9 с одним из чисел العُقُود
Это означает, что он имеет букву вав (от 21 до 99).
Правила для чисел 1 и 2Числа 1 и 2 всегда соответствуют роду существительного, к которому они относятся. То есть их форма мужского рода с существительными мужского рода и женского рода с существительными женского рода. Это اِثْنَان/ وَاحِد с существительными мужского рода и وَاحِدَة / اِثْنَتَان с существительными женского рода, как в следующих примерах: один день
ُ حُجرَةٌ وَاحِدَةٌ | одна комната
جَاءَ عَالِمَان اِثْنَان | Пришли два ученых
Я прочитал две буквы
Помните: цифры 1 и 2 в арабском языке следуют за существительным, которое они модифицируют, и согласуются с ним по падежу и роду.
Для чисел 3-9 мы используем существительные во множественном числе, не согласуясь с родом существительного. Существительные, которые следуют за этими числами, должны быть в неопределенном родительном падеже множественного числа, как в этих примерах:
سَبْعَةُ كُتُبٍ| семь книг
تِسْعُ سَيَّارَاتٍ | девять машин
Имейте в виду, что числа 3–10 становятся мужскими, если в конце просто убрать «та», маркер женского рода. (ة )
Просто помните, число имеет противоположный род существительного в единственном числе.
Правила числа 10:Когда 10 используется отдельно (не в сочетании с 1-9), оно следует обратному правилу согласования. Если составить от 1 до 9, оно должно быть согласовано с предшествующим ему существительным.
Обратите внимание, что для عشرة мужская форма не только опускает ة, но и требует добавления сукууна ْ над ش, поэтому вы получаете عَشْرٌ
عَشَرَةُ أَهْدَافٍ | десять голов
عَشْرُ لَاعِبَاتٍ | Десять игроков женского пола
Правила для чисел 11 и 12 Когда число 11 изменяет слово мужского рода, то число единиц َ أ حَد , так и число десятков عَشر являются мужскими.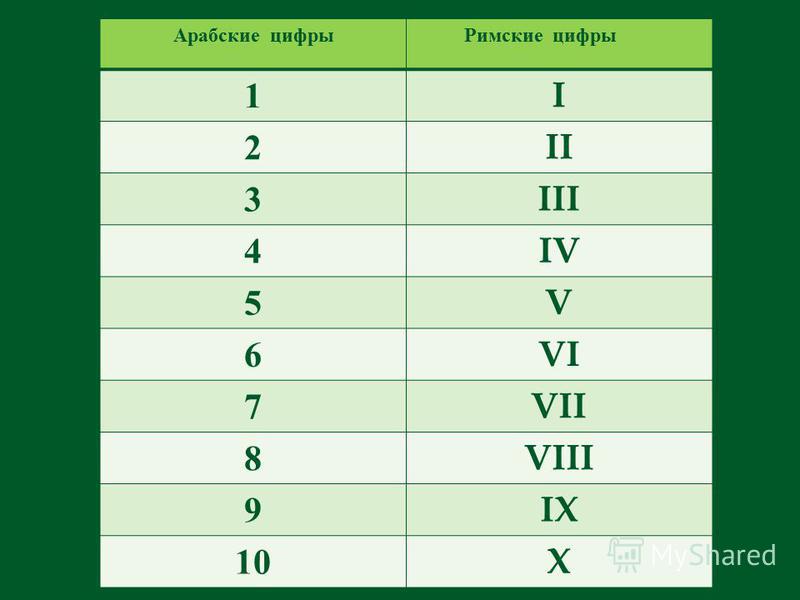 Однако они оба стоят в винительном падеже без нунации 9.0003 (تنوين). Исчисляемое существительное будет следовать за числом и будет стоять в единственном числе и в винительном падеже с нунтацией.
Однако они оба стоят в винительном падеже без нунации 9.0003 (تنوين). Исчисляемое существительное будет следовать за числом и будет стоять в единственном числе и в винительном падеже с нунтацией.
Например, «одиннадцать книг» — это أَحَدَ عَشَرَ كِتَابًا.
Если исчисляемое существительное женского рода, то обе части числа 11 преобразуются в женский род. Женский род слова أَحَدَ — это إِحْدَى, и, поскольку إحْدَى оканчивается на alif maqsuura ى, это не показывает случай. Однако женский род عَشرَ покажет винительный падеж без нунации. Женский род عَشر — عَشْرَة Обратите внимание, что сукуун ставится над ش в женском роде.
Например, «Одиннадцать романов» — это إِحْدَى عَشْرَة روايًة. Поскольку رواية женского рода, оба слова, использованные в этом числе, также женского рода.
По сути, 12 работает так же, как 11, но с небольшим отличием. Во-первых, сходство: исчисляемое существительное всегда в единственном и винительном падежах с нунацией. Оба элемента числа двенадцать согласуются с существительным в роде. Второй член числа, عشر или عشرة, всегда винительный без нунации.
Второй член числа, عشر или عشرة, всегда винительный без нунации.
Разница между 11 и 12 заключается в первом элементе числа. Первый элемент в числе 12 — إثْنَا для именительного падежа мужского рода, но إِثْنَىْ — для винительного и родительного падежей. То же самое верно, когда первый элемент женского рода. Женский род إثْنَتا для именительного падежа и إِثْنَتَيْ для винительного падежа. Например
двенадцать мужчин и двенадцать женщин в мечети.
Правила для чисел от 13 до 19Для чисел 13-19 правила следующие:
1. Второй элемент (عَشر или عَشرة) согласуется с исчисляемым существительным в роде.
2. Первый элемент (ثلاثة, اربعة… и т. д.) показывает обратную согласованность, которую мы видели для чисел 3-10.
3. Оба элемента номера всегда винительный падеж без нунации.
4. Исчисляемое существительное в единственном числе, винительный и имеет нунацию.
Например:
ثَلاثَةَ عَشَرَ دَرْسًا | тринадцать уроков
ً خَمْسَ عَشْرَةَ تفاحَة | пятнадцать яблок
обратите внимание, что харака буквы ش в числе عشرة будет следующей:
- составное число, то ش будет с фатхой, как в этих аятах:
وَبَعَثْنَا مِنهُمُ اثْنَيْ عَشَرَ نَقِيبًا
سورة المائدة : 12
مَن جَاء بِالْحَسَنَةِ فَلَهُ عَشْرُ أَمْثَالِهَا
سورة الأنعام : 160
- If عشرة came как женский род, то если оно в единственном числе, то ش будет быть с фатхой, а если это составное число, то ش будет Будьте с Sukoon, как в этих Ayat:
فَانفَجَرَتْ مِنْهُ اثْنَتَا عَشْرَةَ
سورة البقs: 60 9
سورة البقs: 60 9
سورة البقs: 60 9
нибудь البقرة. 0005
0005
تِلْك® عَشَرَةٌ كَامِلَةٌ
سورة البقرة: 196
Правила для числа 20-99ниже это цифры на арабском для десятков.
| Кардинальный номер | Именительный | Арабские символы |
| 20 | عِشْرُونَ | № |
| 30 | ثَلاثُونَ | номер |
| 40 | أَرْبَعُونَ | номер |
| 50 | خَمْسُونَ | номер |
| 60 | سِتُّونَ | № |
| 70 | سَبْعونَ | номер |
| 80 | ثَمَانُونَ | номер |
| 90 | تِسْعُونَ | ٩٠ |
Эти числа легко запомнить, так как они представляют собой числа от 3 до 10 во множественном числе. Эти числа уменьшаются по падежу, как и множественное число мужского рода. Существительные, которые они изменяют, имеют форму единственного числа, винительного падежа и нунацию. У этих чисел нет женских версий. Таким образом, «50 мальчиков» — это خَمْسُونَ ولدًا, а 50 девочек — это خَمْسُونَ بنتًا.
Существительные, которые они изменяют, имеют форму единственного числа, винительного падежа и нунацию. У этих чисел нет женских версий. Таким образом, «50 мальчиков» — это خَمْسُونَ ولدًا, а 50 девочек — это خَمْسُونَ بنتًا.
Для получения таких чисел, как 21, 22, 23….99, вы используете числа от 1 до 9 вместе с числом десятков. وَ используется для соединения числа единиц с числом десятков. Обратите также внимание, что число для 1 может быть либо وَاحِد, либо его аналогом женского рода وَاحِدَة, либо أحد и его аналогом женского рода إحْدَى.
Номера единиц один и два согласуются с существительным так же, как и сами по себе.
Например, «двадцать одна книга» — это و وَاحِدٌ و عِشرُونَ كتابًا или أحَدٌ وعشرون كتابًا. «Двадцать одна буква» — это وَاحِدَةُ وعِشْرُونَ رسالةً или إحْدَى وعِشرونَ رسالة.
То же соглашение имеет место всякий раз, когда два сочетаются с одним из десятков.
Для номеров 3-9, при использовании в
комбинации с десятками принцип обратного согласования применяется точно так же, как
это происходит, когда эти числа используются сами по себе. Например:
Например:
«Сорок три учителя мужского пола»-это ثَلَاثَةٌ و вероятное слово: وَاحِد/وَاحِدَة، اِثْنَان/اِثْنَتَان . И это происходит независимо от того, являются ли они «независимыми» (1, 2) или составными (11, 12, 21, 22, 31, 32….)
- 2 рассматривается как любое двойное слово: اِثْنَان в номинативном случае, и اِثْنَتَين в (родительный средний), и он теряет свою монахиню, когда в структуре Идаафа с 3ASHRA: اِثْنَا رَ رجلجلجلج Цинаафы и اِثْنَت вероятно.
- 10 принимает противоположный род слова: عَشْرُ نساء ٍ وعَشَرَةَ رجالٍ
- 3 – 9 также принимает противоположный род. Как в аяте Корана: ٍ في سِتَةِ أيام (Аллах создал мир за шесть дней).
- 11-12: follow the gender – أَحَدَ عَشَرَ رَجُلاً وإحْدَى عَشْرَةَ اِمْرَأَةٍ، اِثْنَا عَشَرَ رَجُلاً واِثْنَتَا عَشْرَةَ اِمْرَأَة
- 13-19: Ten следует за полу, а номер блока не-ثَلَاثُ عَشْرَةَ يَومًا وخَمْسَةَ عَشرَ لَيْلَة
- 20, 30, 40, 40, 4040: 4040:.

- 23, 24, 25… 33, 34,…93, 94… : (3-9) принимает противоположный род слова, в то время как 30, 40….90 (10-й разряд) остается постоянным رَجُلاً وثَلَاثٌ وعشرُونَ اِمرَأ®
مِئَة всегда останутся тем же, независимо от того, является ли существенным, является мужским или феминином.
Слово «сто» — مِئة. Иногда пишется иначе – مائة. Однако оба написания произносятся как «миа». И в Священном Коране это всегда произносится как مِئة, а не مائة,
«сто человек» — это مِئَةَ رَجُلٍ.
Поскольку مِئَة — существительное, нам не нужно беспокоиться об обратном соглашении. Оно всегда будет женского рода, даже если за ним следует существительное женского рода. Таким образом, «сто женщин» — это مِئَةُ امرأةٍ, а двести — это مِئَتَان.
Чтобы сказать «сто один», мы используем مِئَةٌ وَ وَاحِد (или واحدة для женского рода). То же самое верно и для «сто двух» مِئَةٌ وَ إثْنَان (или إثْنتان для женского рода).
Для всех чисел от 103 до 999 падеж и число исчисляемого существительного зависят от последнего слова в числе. Таким образом, «сто четыре мальчика» — это مِئَةٌ وَ أَرْبَعَة اولاد, а «сто пятьдесят три мальчика» — это مِئةٌ وَ ثَلَاثَةٌ وَ خَمَاوُن. В первом примере последним словом было اربعة. Поскольку 3-9 всегда находятся в конструкции идаафа, показывают обратное согласование и за ними следует существительное во множественном числе. Слово ولد во множественном числе и в родительном падеже. А число اربعة женского рода.
Во втором примере слово «пятьдесят» является последней цифрой. Поскольку خَمْسُون всегда сопровождается единственным, неопределенным и винительным существительным, ولد написан ولدًا
для четырехсот шестидесяти семи мальчиков, мы можем сказать,
وَرْبَعُمَاмобильный ٌ و вероятное esshinْ® و etshetrْ® و etshetrْ® وminine? et-Fasteminْ® stes. те же самые правила, о которых мы упоминали).
Остальные сотни сами являются идаафами для чисел 3-9, написанных перед مِئَة. Поскольку مِئَة — существительное, числа будут мужского рода. Однако مئة останется в единственном числе. «Триста» — это ثَلَاثُمِئَة. Числа (300 400 500,… 900) остаются одинаковыми независимо от пола. Например: سَبْعُمَائَة كتاب و سَبْعُمَائَة فكرة
Поскольку مِئَة — существительное, числа будут мужского рода. Однако مئة останется в единственном числе. «Триста» — это ثَلَاثُمِئَة. Числа (300 400 500,… 900) остаются одинаковыми независимо от пола. Например: سَبْعُمَائَة كتاب و سَبْعُمَائَة فكرة
Слово «тысяча» — ألْفٌ. Как и مئة, это существительное. И всегда остается одинаковым независимо от пола.
Тысяча стран: اَلْفُ بَلَدٍ/ M
Тысяча приключений: أَلْفُ مغامرةٍ /F
В отличие от مئة это мужской род; поэтому, когда ему предшествуют числа 3-9, это число женского рода и используется множественное число от ألْف. Четыре тысячи ручек: ثَلَاثَةُ ألآف قلم
Когда ألْف предшествует число больше десяти, оно остается в единственном числе и изменяется на винительный падеж, как и любое существительное. Таким образом, «двадцать тысяч» — это عِشرُونَ ألْفاً
. Обратите внимание, что когда ألْف стоит в единственном или двойном числе, оно работает точно так же, как مئة. «Тысяча путей» — это ألفُ طريقةٍ. «Тысяча и один путь» — это ألْفُ طَرِيقةٍ وَ طَريقة. «Тысяча и два пути» — это ألْفُ طريقةٍ وطريقتان. «Две тысячи способов: ألْفَا طَرِيقةٍ
«Тысяча путей» — это ألفُ طريقةٍ. «Тысяча и один путь» — это ألْفُ طَرِيقةٍ وَ طَريقة. «Тысяча и два пути» — это ألْفُ طريقةٍ وطريقتان. «Две тысячи способов: ألْفَا طَرِيقةٍ
1985 :
َسنَةَ ألْفٍ وَ تٌسْعُمَائَةٍ وَ خَمْسٍ وَ ثَمَانِين
1440:
ألْف وأرْبَعُمَائَةٍ وَ أرْبَعُون
Millions and BillionsAnd finally, the word for “million” is مِلْيُون It works exactly as does ألْف . Множественное число — مَلَايين, а слово «миллиард» — مِلْيَار.
БесконечностьДля бесконечности мы говорим:
ما لا نهاية
Что буквально означает «То, что не имеет конца»
Бонус: числа в КоранеВот некоторые аяты из Священного Корана, в которых упоминаются числа. Изучите их, чтобы практиковать числовые правила, которые вы только что выучили!
- قُلْ إِنَّمَا هُوَ إِلَٰهٌ وَاحِدٌ وَإِنَّنِي بَرِيءٌ مِمَّا تُشْرِكُونَ ﴿19﴾ الانعام
- وَالَّذِينَ يَرْمُونَ أَزْوَاجَهُمْ وَلَمْ يَكُن لَّهُمْ شُهَدَاءُ إِلَّا أَنفُسُهُمْ فَشَهَادَةُ أَحَدِهِمْ أَرْبَعُ شَهَادَاتٍ بِاللَّهِ ۙ إِنَّهُ لَمِنَ الصَّادِقِينَ (6) النور
- إِذْ قَالَ يُوسُفُ لِأَبِيهِ يَا أَبَتِ إِنِّي رَأَيْتُ أَحَدَ عَشَرَ كَوْكَبًا وَالشَّمْسَ وَالْقَمَرَ رَأَيْتُهُمْ لِي سَاجِدِينَ ﴿4﴾يوسف
- حَتَّىٰ إِذَا بَلَغَ أَشُدَّهُ وَبَلَغَ أَرْبَعِينَ سَنَةً (15) الاحقاف
- فَأَمَاتَهُ اللَّهُ مِائَةَ عَامٍ (259) سورة البقرة
- يَوَدُّ أَحَدُهُمْ لَوْ يُعَمَّرُ أَلْفَ سَنَةٍ(96)سورة البقرة
- عَلَيْهَا تِسْعَةَ عَشَرَ ﴿30﴾المدثر
- فَكَفَّارَتُهُ إِطْعَامُ عَشَرَةِ مَسَاكِينَ(89) المائدة
Арабские цифры и цифры, 0-10
Стандарт
Автор:
DWD
Если вам нужны более высокие номера, они здесь.
Таким образом, я несколько ввожу в заблуждение с этим заголовком поста, поскольку то, что мы действительно собираемся изучать, — это арабские цифры Eastern ; по-видимому, любой, кто читает это, уже знает западные арабские числительные, поскольку мы используем их в английском языке. Арабы взяли индийскую систему счисления, внесли некоторые изменения, а затем передали вариант этой системы европейцам, поэтому мы называем их «арабскими цифрами», а не «индийскими цифрами», несмотря на то, что в конечном итоге они пришли из Индии. В арабских странах Магриба (в основном вся Северная Африка к западу от Египта) используются именно такие числительные. В Египте и указывает на восток, однако, используются разные (но связанные, вы можете видеть сходство) числительные, которые по-арабски называются أرقام هِندية ( arqāmhinīyah ), или «индийские цифры» («числительное» — رُقْم ruqm , множественное число أرقام arqām ). В таблице ниже показаны названия и цифры для чисел от 0 до 10 (подросткам придется подождать до другого раза).
Помимо رُقْم, «число» также может быть переведено как عَدَد ( ʿadad ), множественное число أعداد ( aʿdād ).
Английское название | Западная арабская цифра | Восточно-арабская цифра | Арабское имя | Арабское имя в транслитерации |
ноль | 0 | ۰ | Номер | Шифр |
один | 1 | ۱ | Номер | вахид |
два | 2 | ۲ | إثْنان | ишнан |
три | 3 | ۳ | ثَلاثة | талатах |
четыре | 4 | ٤ (вариант: ۴) | Номер | арбах |
пять | 5 | ۵ | Номер | хамса |
шесть | 6 | ٦ (вариант: ۶) | Номер | ситтах |
семь | 7 | ۷ | Номер | сабах |
восемь | 8 | ۸ | ثَمانية | тамания |
девять | 9 | ۹ | Номер | тиша |
десять | 10 | ۱۰ | Номер | Ашра |
Обратите внимание, что 4 и 6 имеют альтернативные формы; они чаще встречаются на персидском языке, но могут быть найдены и на арабском языке.
К сожалению, считать от 1 до 10 немного сложно. Ну, я должен сказать, что считать вещи от 3 до 10 сложно; для 1 чего-то вы просто использовали существительное в единственном числе, с номером 1, если хотите подчеркнуть его единственность, а для 2 чего-то вы используете специальную двойную форму существительного. Например:
- كتاب (китаб) или واحد كتاب (ваид китаб) = «одна книга»
- كتابان (kitābān) = «две книги»
Однако от 3 до 10 вы должны использовать форму множественного числа существительного, и по какой-то причине вы должны соответствовать противоположному роду существительного (не спрашивайте меня). Таким образом, «четыре книги» были бы أربعة كُتُب ( Arbaʿhah Kutub ) с числом в женском, но четыре журнала (единственный مَجَلّة, Majallah ) будет أربt in in number in in in in in in in in in in in in in in ج ج ج ج ج ج ج ج in in ج ج ج in in in ج in in in in ج in in in in in in in in in in in in in in in in in in in ج in in in in in in in ج in in ج in in in in ج in in in ج in in. .
.
Нравится:
Нравится Загрузка…
%d блоггерам нравится это:
A: Арабские цифры
Ниже приводится обзор системы счисления в современном стандартном арабском языке и ее грамматического использования. Обсуждение ниже будет охватывать как количественные, так и порядковые числа, а также некоторые другие детали. Большая часть того, что ниже, можно найти в главах 15 и 21 первого тома документа EMSA , но информация включена сюда для полноты картины.
Вообще грамматика, связанная с числами в арабском языке, считается самой сложной вещью в языке. На самом деле он считается настолько сложным, что многие учителя утверждают, что даже арабы не используют его правильно, поэтому американцам не следует его учить должным образом. Это верно. Это также неверно.
Когда кто-то говорит на современном стандартном арабском языке и начинает использовать числа, говорящий имеет тенденцию переходить к разговорному использованию и произношению. Однако в письменном арабском языке используется только стандарт. Поэтому, если вы хотите уметь правильно читать числа (и правильно их писать), вам необходимо ознакомиться с изложенным ниже материалом. Кроме того, поскольку вы можете не знать разговорного арабского языка, вам понадобятся правила и произношение из стандарта, когда вы хотите использовать числа в речи. Поэтому вам действительно необходимо знать этот материал .
Однако в письменном арабском языке используется только стандарт. Поэтому, если вы хотите уметь правильно читать числа (и правильно их писать), вам необходимо ознакомиться с изложенным ниже материалом. Кроме того, поскольку вы можете не знать разговорного арабского языка, вам понадобятся правила и произношение из стандарта, когда вы хотите использовать числа в речи. Поэтому вам действительно необходимо знать этот материал .
Также важно отметить, что система счисления, хотя и представляет свои трудности, по сути не слишком сложна. Несколько правил охватывают практически все, что вам нужно знать при использовании чисел. Как только вы привыкнете к правилам, у вас не будет особых трудностей. Чтобы привыкнуть к правилам, требуется около часа практики (если вы уже научились считать) и периодического повторения.
Приведенная ниже обработка будет чередовать количественные числительные (один, два, три) и порядковые числительные (первый, второй, третий). Например, сначала я расскажу о кардиналах от 1 до 10, а затем приведу порядковый номер. Постарайтесь усвоить весь этот раздел по крупицам. Если вы будете идти шаг за шагом, у вас не будет особых проблем.
Постарайтесь усвоить весь этот раздел по крупицам. Если вы будете идти шаг за шагом, у вас не будет особых проблем.
Числа: 1 – 10
Это числа от 1 до 10 на арабском языке. Цифры выписываются полностью рядом с символом для каждой цифры.
1 | واحِدٌ | и |
2 | إثْنانِ | и |
3 | ثَلاثَةٌ | и |
4 | أَرْبَعةٌ | и |
5 | خَمْسةٌ | и |
6 | سِتّةٌ | и |
7 | سَبْعةٌ | и |
8 | ثَمانِيةٌ | и |
9 | تِسْعةٌ | и |
10 | عَشرَةٌ | и |
Прежде всего, вы должны уметь без запинки произносить эти числа по порядку. Научите их себе сейчас, прежде чем продолжать. Вы также должны уметь сразу распознавать символы, так что учите их себе прямо сейчас. Затем продолжайте.
Научите их себе сейчас, прежде чем продолжать. Вы также должны уметь сразу распознавать символы, так что учите их себе прямо сейчас. Затем продолжайте.
Я сказал, что вы должны уметь легко произносить приведенные выше числа и узнавать их символы. Так что вернитесь и сделайте это.
Ладно — теперь обсудим эти цифры дальше. Начнем с числа 1. Число 1 на арабском языке — это واحِد , а ١ — его символ. Если вы хотите сказать «одна книга» на арабском языке, у вас есть два варианта. Первый — просто сказать «книга», كتابٌ Это означает и «книга», и «одна книга». Однако واحِد может следовать за существительным для выделения. Таким образом, «одну книгу» можно перевести как كتابٌ واحدٌ . Поскольку واحد является прилагательным, оно будет иметь тот же падеж, что и существительное, которое оно изменяет. Если существительное женского рода, то واحد делается женского рода.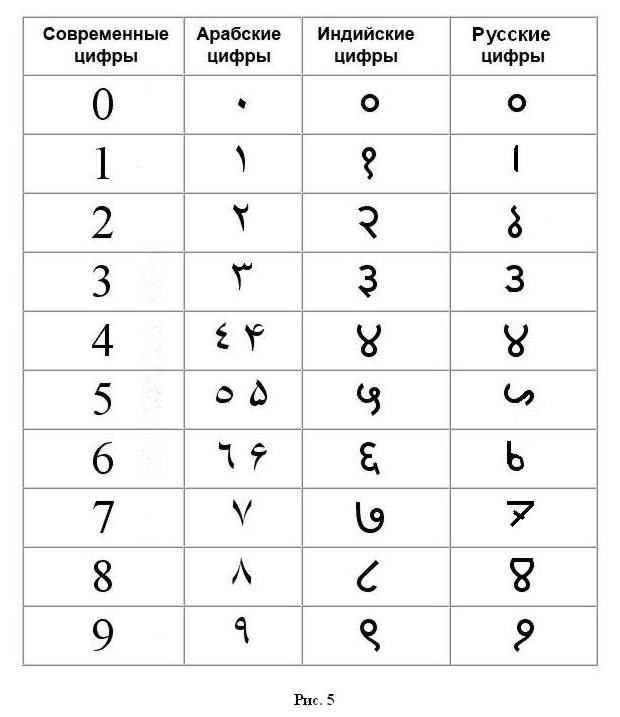 «Одна буква» رسالةٌ واحدةٌ
«Одна буква» رسالةٌ واحدةٌ
Чтобы сказать «две книги», вы можете либо поставить существительное в двойственной форме отдельно, либо добавить إثْنان для акцента. Таким образом, вы можете сказать либо كتابانِ , либо كتابان إثنانِ . «Я прочитал две книги» — это قرأتُ كتابينِ اثْنَيْنِ . (Конечно, اثْنَيْنِ не является обязательным.) إثْنان становится إثْنَتانِ в женском роде. Поэтому, сказав «две буквы», вы получите رسالتان اثْنَتانِ ». .
Теперь самое интересное, цифры 3-10. Хотя числа являются прилагательными, 3-10 всегда ставятся в идаафа с исчисляемым существительным 9.0003 после номер. Исчисляемое существительное будет во множественном числе. Например, множественное число от مدرس равно مدرسون . Мы хотим сказать «три учителя», поэтому получаем ثلاثة مدرسين . Так как у нас есть идаафа, второй термин стоит в родительном падеже. Обратите внимание, что это число ثلاثة женского рода. Вот самое интересное. Число женского рода, если единственное число исчисляемого существительного мужского рода. Поскольку единственное число مدرسون — это مدرس, которое является словом мужского рода, любое кардинальное число от 3 до 10, используемое с ним, должно быть женского рода. Этот принцип известен как «обратное соглашение». Некоторые изучающие арабский язык называют его по-другому.
Так как у нас есть идаафа, второй термин стоит в родительном падеже. Обратите внимание, что это число ثلاثة женского рода. Вот самое интересное. Число женского рода, если единственное число исчисляемого существительного мужского рода. Поскольку единственное число مدرسون — это مدرس, которое является словом мужского рода, любое кардинальное число от 3 до 10, используемое с ним, должно быть женского рода. Этот принцип известен как «обратное соглашение». Некоторые изучающие арабский язык называют его по-другому.
Теперь возьмем слово مُدَرِّسة «учительница». Теперь мы хотим сказать «три учительницы». Единственное слово женского рода, поэтому мы будем использовать МУЖСКУЮ форму числа. Результат: ثلاث مدرساتٍ
Этот принцип обратного согласования применим ко всем существительным (это означает все, не большинство, большинство или почти все). Неважно, относится ли существительное к человеку или к чему-то нечеловеческому. Просто помните, что число имеет противоположный род существительного в единственном числе.
Просто помните, что число имеет противоположный род существительного в единственном числе.
Этот принцип справедлив для чисел от 3 до 10. Вот еще несколько примеров использования чисел от 1 до 10 с существительными. Сначала посмотрите на английский и попытайтесь предсказать арабский. Тогда посмотрите на арабские ответы. Кстати, числа от 3 до 10 становятся мужскими, если просто опустить ة. Для عشرة мужская форма не только опускает ة, но и требует добавления сукууна над ش , поэтому вы получаете عَشْرٌ
| Четыре студента (мужского рода) | أربعةُ طلابٍ |
| Четыре ученика (женщины) | ارْبَعُ طالباتٍ |
| Десять автомобилей | عَشْرُ سياراتٍ |
| Шесть фанатиков | ستّةُ متطرّفين |
| Две ручки | قلمانِ اثْنانِ |
| Восемь глупых репортеров (мужской род) | ثمانيةُ مراسلين سُخفاء |
| Восемь превосходных отчетов (женских) | ثماني مراسلاتٍ ممتازاتِ |
Обратите внимание на слово «восемь» на арабском языке. Это происходит от дефектного корня. Когда число женское, оно обычное. Однако, когда оно мужского рода (как в случае с последним примером выше), оно будет работать как любое дефектное слово, используемое в идаафа или ставшее определенным. То есть у него не будет падежа для именительного или родительного падежа, но будет отображаться фатха для винительного падежа. Таким образом, «Я прочитал восемь скучных статей о числах» равно 9.0003 قرأتٌ ثمانيَ مقالاتٍ مملةٍ عن الارقام .
Это происходит от дефектного корня. Когда число женское, оно обычное. Однако, когда оно мужского рода (как в случае с последним примером выше), оно будет работать как любое дефектное слово, используемое в идаафа или ставшее определенным. То есть у него не будет падежа для именительного или родительного падежа, но будет отображаться фатха для винительного падежа. Таким образом, «Я прочитал восемь скучных статей о числах» равно 9.0003 قرأتٌ ثمانيَ مقالاتٍ مملةٍ عن الارقام .
Числа от 3 до 10 часто используются в словосочетаниях с существительными прилагательными «три книги», «эти четыре танка» и т. д. Принцип обратного согласования по-прежнему будет применяться, но теперь число будет следовать за существительным, как и любое прилагательное. . «Три книги» — это الكتبُ الثلاثةُ . «Эти четыре танка» — это هذا الدبابات الاربعُ
Более редкое использование чисел с существительными для выражения «три книги» и т. д. выглядит следующим образом: الثلاثةُ كتبٍ .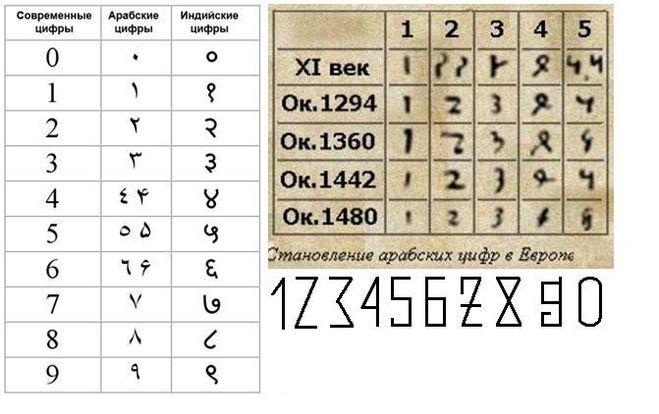 Здесь число определено и показывает обратное согласие. Однако исчисляемое существительное без определенного артикля, в родительном падеже и имеет нунацию. Это использование, за вычетом падежных окончаний, обычно используется в разговорном арабском языке, но редко в MSA.
Здесь число определено и показывает обратное согласие. Однако исчисляемое существительное без определенного артикля, в родительном падеже и имеет нунацию. Это использование, за вычетом падежных окончаний, обычно используется в разговорном арабском языке, но редко в MSA.
Вы обнаружите, что большую часть времени, когда вы используете числа, вы будете использовать числа от 1 до 10. Таким образом, если вы знакомы с вышеизложенным материалом, вы знаете многое из того, что будете использовать на регулярной основе.
В следующем разделе рассматриваются порядковые номера 1-10. Если вы хотите остаться с кардиналами, пропустите следующий раздел и перейдите к следующему разделу, в котором рассматриваются количественные числа 11-19..
Порядковые номера: 1 – 10
Порядковые номера – это прилагательные, которые следуют за изменяемым существительным. Поскольку они обычно являются определенными, в приведенном ниже списке они указаны с прикрепленным определенным артиклем. Запомните приведенный ниже список, а затем прочитайте комментарии, которые следуют.
Запомните приведенный ниже список, а затем прочитайте комментарии, которые следуют.
| Первый | ألأَوَّلُ (أٌولى женский род) |
| Второй | الثّاني |
| Третий | الثّالِثُ |
| Четвертый | الرّابِعُ |
| Пятый | الْخامِسُ |
| Шестой | السّادِسُ |
| Седьмой | السابعُ |
| Восьмой | الثّامِنُ |
| Девятый | التّاسِعُ |
| Десятый | الْعاشِرُ |
Порядковый номер для «первого» не связан с واحد , но происходит от другого корня. Его женское начало такое же, как и у родственного женского рода; Например, كبْرى из ( أكْبَرُ ).
Его женское начало такое же, как и у родственного женского рода; Например, كبْرى из ( أكْبَرُ ).
Порядковый номер слова «второй» является дефектным прилагательным. Без определенного артикля ثانٍ . Это слово имеет те же характеристики, что и дефектные слова, которые вы изучали во второй главе части II, такие слова, как قاضٍ . Когда становится определенным, ثانٍ становится الثاني точно так же, как قاضٍ становится القاضي В именительном и родительном падежах это слово не показывает падеж, но оно будет иметь фатху в винительном падеже. Это точно так же, как и в случае таких слов, как القاضي . Обратите внимание, что قاضٍ является активным причастием. ثانٍ также является активным причастием.
При преобразовании в женский род ثانٍ становится ثانية и всегда будет иметь обычные падежные окончания.
Чтобы сказать «первая книга», вы получите الكتابُ الأَوَّلُ . Порядковый номер следует за существительным и согласуется с ним по определенности, роду и падежу. «Первое письмо» — الرسالةُ الأولى . Как вы знаете, слова, оканчивающиеся на alif maqsuura, не имеют падежа, поэтому маркера падежа أولى никогда не бывает.
«Вторая книга» — это الكتابُ الثاني (на кардинале нет дела, потому что оно бракованное). «Вторая буква» — الرسالة الثانية .
Все порядковые номера от 3 до 10 являются образцом активного причастия. Обратите внимание, что порядковый номер «шестого» — السادِس . Это слово — единственное из порядковых чисел от 3 до 10, которое значительно отклоняется от количественного числительного.
Обратите внимание, что порядковый номер «восьмерки» не дефектный, в отличие от кардинального. Следовательно, женская форма также не будет иметь дефектных и . Женская форма — الثامنة .
Женская форма — الثامنة .
Обычно все порядковые числительные следуют за изменяемым существительным и согласуются с ним по определенности, падежу и роду. Ниже приведены несколько примеров. Закрой арабский, прочитай английский и попробуй сгенерировать арабский.
| Четвертый корпус | البناءُ الرابِعُ |
| Девятый вагон | السيارةُ التاسعةُ |
| День десятый | اليوم العاشِرُ |
| Шестая страница | الصفحةُ السادِسةُ |
Иногда эти порядковые номера ставятся перед существительным в конструкции идаафа с тем же значением. Таким образом, «первая книга» — это أَوَّلُ كتابٍ , а «в третий раз» — ثالث مرةٍ . Обратите внимание, что у существительного нет определенного артикля, но перевод определён. Это похоже на ситуацию с использованием относительного падежа, за которым следует существительное, как в 9.0003 أطوَلُ نهر «самая длинная река».
Таким образом, «первая книга» — это أَوَّلُ كتابٍ , а «в третий раз» — ثالث مرةٍ . Обратите внимание, что у существительного нет определенного артикля, но перевод определён. Это похоже на ситуацию с использованием относительного падежа, за которым следует существительное, как в 9.0003 أطوَلُ نهر «самая длинная река».
Эти порядковые числительные принимают множественное число в словосочетаниях существительное-прилагательное. Таким образом, «первые студенты» — это الطلابُ الأولون
В следующем разделе будут рассматриваться количественные числительные от 11 до 19. Если вы хотите продолжить только с порядковыми числительными, пропустите следующий раздел и перейдите к разделу, который следует за ним. В этом разделе рассматриваются порядковые числа от 11 до 19.
Кардинальные числа: 11 – 19
Ниже приведены количественные числительные от 11 до 19.вместе с арабскими символами. Запомните их, а затем прочитайте комментарии, которые следуют.
| Кардинальный номер | Мужской род | Женственность | Символ |
| 11 | أحَدَ عَشَرَ | إِحْدى عَشْرةَ | и |
| 12 Именительный падеж | إثْنا عَشَرَ | إثْنَتا عَشْرةَ | и |
| 12 Акк./Общ. | إثْنَىْ عَشَرَ | إِثْنَتَيْ عَشْرةَ | и |
| 13 | ثلاثةَ عَشَرَ | ثلاثَ عَشْرةَ | и |
| 14 | أَرْبَعةَ عَشَرَ | أرْبعَ عَشْرةَ | и |
| 15 | خَمْسةَ عَشَرَ | خِمْسَ عَشْرةَ | и |
| 16 | سِتّةَ عَشَرَ | سِتَّ عَشْرةَ | и |
| 17 | سَبْعةَ عَشَرَ | سِبْعَ عَشْرةَ | и |
| 18 | ثَمانيةَ عَشَرَ | ثمانيَ عَشْرةَ | и |
| 19 | تِسْعةَ عَشَرَ | تِسْعَ عَشْرةَ | и |
Сначала посмотрите на символы для чисел. Хотя арабский язык идет справа налево, числа расположены в том же порядке, что и в английском языке, столбец десятков находится слева от столбца одиночных цифр.
Хотя арабский язык идет справа налево, числа расположены в том же порядке, что и в английском языке, столбец десятков находится слева от столбца одиночных цифр.
А теперь еще больше удовольствия. Мы начнем с чисел 11 и 12, так как они представляют собой самую захватывающую задачу.
Когда число 11 изменяет слово мужского рода, как число единиц أحد , так и число десятков عَشرَ являются мужскими. Тем не менее, они оба В винительном падеже БЕЗ НУНАЦИИ так же, как они представлены в списке выше. Исчисляемое существительное будет следовать за числом и будет стоять в ЕДИНСТВЕННОМ ПАДЕЖЕ И В АККУЗАТИВНОМ ПАДЕЖЕ С НУНАЦИЯ . Например, «одиннадцать книг» — это أحدَ عَشَرَ كتاباً . Помните, что существительное всегда в единственном числе, винительном падеже и имеет нунацию.
Если исчисляемое существительное женского рода, то обе части числа 11 преобразуются в женский род. Женский род أحد равен إحدى 9. 0004 Поскольку إحدى оканчивается на alif maqsuura, регистр не отображается. Однако женский род , عَشرَ покажет винительный падеж без нунации. Женский род عَشرَ равен عَشرَة Обратите внимание, что сукуун ставится над ش в женском роде. «Одиннадцать букв» — это إحدى عَشرَة رسالة . Поскольку رسالة женского рода, оба слова, используемые в числе, также женского рода.
0004 Поскольку إحدى оканчивается на alif maqsuura, регистр не отображается. Однако женский род , عَشرَ покажет винительный падеж без нунации. Женский род عَشرَ равен عَشرَة Обратите внимание, что сукуун ставится над ش в женском роде. «Одиннадцать букв» — это إحدى عَشرَة رسالة . Поскольку رسالة женского рода, оба слова, используемые в числе, также женского рода.
Опять же, оба элемента числа будут в винительном падеже (кроме إحدى , который не может отображать регистр) и не будет иметь нунацию. Оба элемента числа согласуются с исчисляемым существительным в роде. Исчисляемое существительное всегда будет единственного числа, винительного падежа и будет иметь нунацию.
Если вы думаете, что 11 было весело, теперь мы подошли к 12. Посмотрите на примеры ниже, а затем прочтите мои комментарии.
| двенадцать книг | إثْنا عَشرَ كتاباً |
| Я прочитал двенадцать книг | قرأتُ إثْنىْ عَشرَ كتاباً |
| двенадцать букв | إثْنَتا عشرةَ رسالةً |
| Я прочитал двенадцать букв | قرأتُ إثْنىْ عَشرةَ رسالةَ |
По сути, 12 работает так же, как 11, но с уникальными особенностями. Во-первых, сходство. Исчисляемое существительное всегда в единственном и винительном падежах с нунацией. Оба элемента числа двенадцать согласуются с существительным в роде. Второй член числа عشر или عشرة , всегда винительный падеж без нунации.
Во-первых, сходство. Исчисляемое существительное всегда в единственном и винительном падежах с нунацией. Оба элемента числа двенадцать согласуются с существительным в роде. Второй член числа عشر или عشرة , всегда винительный падеж без нунации.
Разница между 11 и 12 заключается в первом элементе числа. Первый элемент в числе 12 равен إثْنا для именительного падежа мужского рода, но إِثْنَىْ для винительного и родительного падежей. Таким образом, первый элемент действительно склоняется к регистру. То же самое верно, когда первый элемент женского рода. Женский род إثْنَتا для именительного падежа и إِثْنَتَيْ для винительного падежа.
Теперь мы подходим к числам 13-19, и все становится намного проще. Для 13-19 правила следующие:
1. Второй элемент ( عشر или عشرة ) согласуется с исчисляемым существительным в роде.
2. Первый элемент ( ثلاثة, اربعة и т. д.) показывает обратную согласованность, которую мы видели для чисел 3-10.
Первый элемент ( ثلاثة, اربعة и т. д.) показывает обратную согласованность, которую мы видели для чисел 3-10.
3. Оба элемента числа всегда винительный падеж без нунации.
4. Исчисляемое существительное в единственном числе, винительном падеже и имеет нунацию.
5. В бейсболе слишком много дивизий, и нужно избавиться от джокера.
Ниже приведены некоторые примеры. Закройте арабский язык и попытайтесь воспроизвести его, глядя на английский язык. Тогда посмотрите на арабский, чтобы проверить себя. Когда вы это сделаете, просмотрите четыре приведенных выше правила по одному и посмотрите, как они применимы к каждому приведенному ниже примеру.
| пятнадцать профессоров (мужского рода) | خَمْسةَ عَشرَ أستاذاً |
| шестнадцать профессоров (женщина) | سِتَّ عَشْرَةَ استاذةً |
| девятнадцать дебилов (мужского рода) | تِسْعةَ عَشرَ بليداً |
| восемнадцать окон | ثمانيةَ عَشرَ شباكاً |
| семнадцать самолетов | سَبْعَ عَشرةَ طائرةً |
| четырнадцать солдат (мужской род) | اربعةَ عَشرَ جندياً |
Если вы все правильно поняли, вы освоили большую часть грамматики, связанной с арабскими числами. Как всегда есть еще. Продолжайте улыбаться.
Как всегда есть еще. Продолжайте улыбаться.
Как бы вы сказали «четырнадцать отличных студентов»? «Четырнадцать студентов (маск.)» — это أربعةَ عشرَ طالبا . Слово «отличный» مُمتاز будет использоваться для модификации طالبا . Таким образом, мы получаем اربعة عشرَ طالبا ممتازا . Прилагательное остается в единственном числе и согласуется с существительным в падеже.
Как бы вы сказали «Четырнадцать замечательных студентов пошли в библиотеку?» Если глагол стоит первым, он, как обычно, будет единственного числа. Однако, если четырнадцать студентов стоят перед глаголом, тогда глагол будет во множественном числе. Таким образом, اربعةَ عشرَ طالبا ممتازا ذهبوا الى المكتبة
Мне это нравится.
«Четырнадцать студентов» — это الطلابُ الاربعةَ عَشرَ Теперь существительное стоит во множественном числе. Номер единицы показывает обратное согласие, является винительным падежом и имеет определенный артикль. Число десятков показывает истинное согласие, является винительным и не имеет определенного артикля.
Число десятков показывает истинное согласие, является винительным и не имеет определенного артикля.
Теперь мы подходим к порядковым номерам с 11 по 19. Если вы хотите пропустить их, перейдите к следующему разделу.
Порядковые номера: 11-19
Ниже приведен список порядковых номеров от 11 до 19. Наслаждайтесь ими, а затем прочитайте комментарии, которые следуют.
| Порядковый номер | Мужской род | Женственность |
| одиннадцатый | الحادِيَ عَشَرَ | الحادية عَشْرةَ |
| двенадцатый | الثانيَ عَشَرَ | الثانيةَ عَشْرةَ |
| тринадцатый | الثالثَ عَشَرَ | الثالثةَ عَشْرةَ |
| четырнадцатый | الرابعَ عَشَرَ | الرابعةَ عَشْرةَ |
| пятнадцатый | الخامِسَ عَشَرَ | الخامسةَ عَشْرةَ |
| шестнадцатый | السادِسَ عَشَرَ | السادسةَ عَشْرةَ |
| семнадцатый | السابعَ عَشَرَ | السابعةَ عَشْرةَ |
| восемнадцатый | الثامنَ عَشَرَ | الثامنةَ عَشْرةَ |
| девятнадцатый | التاسعَ عَشَرَ | التاسعةَ عَشْرةَ |
Порядковые числа от 11 до 19 всегда стоят в винительном падеже, как и количественные. Порядковые числа работают как обычные прилагательные с точки зрения гендерного соглашения. Следовательно, если существительное мужского рода, обе части порядкового числа будут мужского рода. Если существительное женского рода, обе части будут женского рода. Только первый элемент будет иметь определенный артикль. Второй элемент никогда не делает этого. Заметьте также, что слово «одиннадцатый» имеет другой корень, чем слово «один» 9.0003 واحد или слово «первый» أَوَّل .
Порядковые числа работают как обычные прилагательные с точки зрения гендерного соглашения. Следовательно, если существительное мужского рода, обе части порядкового числа будут мужского рода. Если существительное женского рода, обе части будут женского рода. Только первый элемент будет иметь определенный артикль. Второй элемент никогда не делает этого. Заметьте также, что слово «одиннадцатый» имеет другой корень, чем слово «один» 9.0003 واحد или слово «первый» أَوَّل .
Для «семнадцатой книги» вы говорите الكتابُ السابعَ عَشرَ Обратите внимание, что порядковый номер стоит в винительном падеже, а существительное в именительном. «Семнадцатая буква» — الرسالةُ السابعةَ عَشرَةَ
Порядковые числа от 1 до 12 используются для определения времени. См. раздел об определении времени в следующей главе.
Теперь мы подошли к количественным числам от 20 до 99. Если вы хотите пропустить их, перейдите к следующему разделу, чтобы продолжить с порядковыми номерами.
Числа: 20-99
Ниже приведены числа на арабском языке для десятков. Запомните их сейчас.
| Кардинальный номер | Именительный | Акк./Общ. | |
| 20 | عِشْرونَ | عِشْرينَ | и |
| 30 | ثَلاثونَ | ثَلاثينَ | и |
| 40 | أَرْبَعونَ | أَرْبَعينَ | и |
| 50 | خَمْسونَ | خَمْسينَ | и |
| 60 | ستّونَ | ستّينَ | и |
| 70 | سَبْعونَ | سَبْعينَ | и |
| 80 | ثَمانونَ | ثَمانينَ | и |
| 90 | تِسْعونَ | تِسْعينَ | и |
Эти числа легко запомнить, поскольку они представляют собой числа от 3 до 10 во множественном числе. Эти числа уменьшаются по падежу, как и множественное число мужского рода. Существительные, которые они изменяют, стоят в единственном числе, в винительном падеже и имеют нунацию. У этих чисел нет женских версий. Таким образом, «50 студентов мужского пола» — это خَمْسونَ طالبا , а 50 студенток — خَمْسونَ طالبة
Эти числа уменьшаются по падежу, как и множественное число мужского рода. Существительные, которые они изменяют, стоят в единственном числе, в винительном падеже и имеют нунацию. У этих чисел нет женских версий. Таким образом, «50 студентов мужского пола» — это خَمْسونَ طالبا , а 50 студенток — خَمْسونَ طالبة
.вместе с десятками. Взгляните на примеры ниже.
| Двадцать один | واحِدٌ وعِشْرونَ
|
| Двадцать два | إثْنانِ وعِشرْونَ |
| Тридцать шесть | سِتّةٌ وثلاثونَ |
| Девяносто восемь | ثمانيةٌ وتِسعونَ |
Обратите внимание, что وَ используется для соединения числа единиц с числом десятков. Заметьте также, что число для 1 может быть либо . واحد и его женский аналог واحدة или أحد и его женский аналог إحْدى .
Заметьте также, что число для 1 может быть либо . واحد и его женский аналог واحدة или أحد и его женский аналог إحْدى .
Теперь вопрос согласования. Числа единиц один и два согласуются с существительным так же, как и сами по себе. Например, «двадцать одна книга» — это واحدٌ وعشرون 9.0004 كتابا или أحدٌ وعشرون كتابا . «Двадцать одна буква» — это واحدةُ وعشرونَ رسالةً или إحْدى وعِشرونَ رسالة . То же самое соглашение имеет место всякий раз, когда два соединяются с одним из десятков. Элемент unit будет отображать обычные регистровые окончания, за исключением إحدى, которое, как вы знаете, не показывает регистр. Единица десятков показывает падежи так же, как и множественное число мужского рода.
Для чисел от 3 до 9, когда они используются в сочетании с десятками, применяется принцип обратного согласования точно так же, как и при использовании этих чисел сами по себе. Номера единиц будут показывать обычные окончания падежей. Таким образом, «сорок три книги» — это ثلاثةٌ واربعون كتابا . Сорок три буквы» — это ثلاث واربعون كتابا
Номера единиц будут показывать обычные окончания падежей. Таким образом, «сорок три книги» — это ثلاثةٌ واربعون كتابا . Сорок три буквы» — это ثلاث واربعون كتابا
Счетное существительное для всех чисел от 11 до 19 всегда единственное, неопределенное и винительный падеж с нунацией.
Ниже приведены примеры использования чисел от 1 до 99 с исчисляемыми существительными. Посмотрите на английский слева и переведите его на арабский. Затем проверьте свою работу, взглянув на арабский язык справа.
семьдесят две книги | إثْنان وسَبْعونَ كتابا |
тридцать восемь дебилов | ثمانيةٌ وثلاثونَ بليدا |
Я прочитал двадцать три письма | قرأتُ ثلاثا وعشرينَ رسالةً |
Я видел шестерых учителей | شاهدتُ ستَّ مدرساتٍ |
девятнадцать офисов | تِسْعةَ عَشرَ مكتبا |
семьдесят два слова | إثْنتانِ وسبعون كلمةً |
сорок восемь часов | ثمان وأربعون ساعةً* (см. |
одиннадцать автомобилей | إحدى عَشرةَ سيارةً |
четыре дня | أربعةُ أيامٍ |
восемь школ | ثماني مدارسَ |
Надеюсь, вы все правильно поняли. Если нет, убедитесь, что вы понимаете, почему вы сделали ошибки, которые вы сделали. Ниже у вас будет больше возможностей искупить свою вину.
Эти составные числа также можно сделать определенными, как в «двадцати трех книгах», что составляет الكتبُ الثلاثُ والعشرون . Оба элемента сделаны определенными. Первый элемент принимает характерное для него согласование, обычное для 1 и 2, обратное для 3–9.
В следующем разделе рассматриваются порядковые номера от 20 до 99. Вы можете пропустить его, если хотите продолжить работу с кардиналами.
Порядковые числительные: 20-99
Порядковые числительные для четных десятков такие же, как количественные с добавлением определенного артикля. Таким образом, العِشرونَ — «двадцатый», а التِسعونَ — «девяностый». Эти порядковые номера не будут уменьшаться по полу, но будут уменьшаться по регистру.
Составные порядковые номера использовали те же самые порядковые номера для одиночных цифр, как вы видели ранее. И элемент одиночных чисел, и элемент десятков будут иметь определенный артикль. Элемент singles будет согласовываться в роде и падеже. Элемент десятков согласится только в случае. Обратите внимание, что для «первого» здесь используется الحادي, как и в случае с «одиннадцатым». Вот несколько примеров.
| двадцать первый день | اليومُ الحادي والعِشْرونَ |
| двадцать первый час | الساعةُ الحاديةُ والعشرون |
| пятьдесят шестая страница | الصفحةُ السادسةُ والخمسون |
| сорок пятая минута | الدقيقةُ الخامسةُ والاربعون |
| Я прочитал тридцать девятую страницу | قرأتُ الصفحةَ التاسعةَ والثلاثين |
Теперь мы перейдем к последнему разделу о количественных числах. За ним сразу последует заключительный раздел, посвященный порядковым номерам.
За ним сразу последует заключительный раздел, посвященный порядковым номерам.
Числовые числа: от 100 до бесконечности, насколько я хочу получить0003 مائة . Однако оба написания произносятся как «миа». Слово является существительным и используется в idaafa с исчисляемым существительным, следующим за ним в единственном числе. Таким образом, «сто человек» — это مئة رجل . Поскольку مئة — это существительное, нам не нужно беспокоиться об обратном согласовании. Оно всегда будет женского рода, даже если за ним следует существительное женского рода. Таким образом, «сто женщин» — это مئة امرأةٍ
, «двести» — это مئتانِ . Двойное окончание أنِ просто добавляется к 9.0003 مئة . Это слово склоняется по падежу, как и любое двойное существительное, и при использовании в идаафа падает ن . «Двести человек» — это مئتا رجلٍ . В винительном/родительном падеже это будет مئتيْ رجلٍ
Остальные сотни сами по себе являются идаафами, состоящими из чисел от 3 до 9, написанных перед مئة . Поскольку مئة — существительное, числа будут мужского рода. Однако مئة останется в единственном числе. «Триста» — это 9.0003 ثلاث مئة Часто к مئة присоединяются числа от 3 до 9, но у вас все равно будет идаафа. Таким образом, «триста» также можно записать как ثلاثمئةٍ Обратите внимание, что ثلاث по-прежнему склоняется для падежа. Этот последний способ делать сотни кажется более распространенным. «Триста человек» — это ثلاثمئتِ رجلٍ . Вот и все сотни.
Поскольку مئة — существительное, числа будут мужского рода. Однако مئة останется в единственном числе. «Триста» — это 9.0003 ثلاث مئة Часто к مئة присоединяются числа от 3 до 9, но у вас все равно будет идаафа. Таким образом, «триста» также можно записать как ثلاثمئةٍ Обратите внимание, что ثلاث по-прежнему склоняется для падежа. Этот последний способ делать сотни кажется более распространенным. «Триста человек» — это ثلاثمئتِ رجلٍ . Вот и все сотни.
| сто | مِئة или مائة (оба произносятся как «ми»а) | Номер |
| двести | مئتانِ / مئتين в род./соотв.) | и |
| триста | ثلاثُمئةٍ или ثلاثُ مئةٍ | и |
| четыреста | أرْبَعُمئةٍ или أَرْبَعُ مئةٍ | и |
| пятьсот | خَمْسُمئةٍ или خَمسُ مئةٍ | и |
| шестьсот | سِتُّمئةٍ или سِتُّ مئةٍ | ٦٠٠ |
| семьсот | سَبعُمئةٍ или سَبعُ مئةٍ | ٧٠٠ |
| восемьсот | ثَمانيمئةٍ или ثَماني مئةٍ | ٨٠٠ |
| девятьсот | تِسْعُمئةٍ или تِسْعُ مئةٍ | и |
Напомним, что слово «восемь» ошибочно. Следовательно, ي на ثماني не будет показывать падежа в именительном и родительном падежах, но будет показывать фатху в винительном падеже.
Следовательно, ي на ثماني не будет показывать падежа в именительном и родительном падежах, но будет показывать фатху в винительном падеже.
Чтобы сказать «сто один», вы используете مئة وواحد (или واحدة для женского рода). То же самое верно и для «сто два» مئة وإثْنان (или إِثْنتان для женского рода). Однако, если вы упоминаете исчисляемое существительное, вы не используете واحد или اثنان . «Сто один человек» — это مئة رجلٍ ورجل «Сто два человека» — это مئة رجلٍ ورجلان
103-109 все имеют предшествующие числа 900ة04. «Сто пять» — это مئة وخمسة
Для всех чисел от 103 до 999 падеж и число исчисляемого существительного следуют правилам, регулирующим последнее числительное в числе. Таким образом, «сто три человека» — это مئة ثلاثة رجال , но «сто пятьдесят три человека» — это مئةٌ وثلاثةٌ وخَمْسون رجلا . Поскольку от трех до девяти всегда находятся в идаафе, показывают обратное согласие и за ними следует существительное во множественном числе, слово رجل делается во множественном числе и стоит в родительном падеже, а число ثلاثة — женского рода.
Поскольку от трех до девяти всегда находятся в идаафе, показывают обратное согласие и за ними следует существительное во множественном числе, слово رجل делается во множественном числе и стоит в родительном падеже, а число ثلاثة — женского рода.
Во втором примере слово «пятьдесят» является последней цифрой. Поскольку за خَمْسون всегда следует неопределенное существительное в единственном числе, винительный падеж, رجل пишется رجلا
Ниже приведены дополнительные примеры. Посмотрите на английский слева и посмотрите, сможете ли вы воспроизвести арабский справа. Тогда посмотрите на арабский, чтобы проверить себя.
двести пять книг | مئتان وخمسةُ كتبٍ |
четыреста сорок четыре дня | اربعمئةٍ واربعةٌ وارْبعون يوماً |
пятьсот семнадцать человек | خمسُمئةٍ وسبعةَ عشرَ رجلا |
(восемьсот двадцать один студент (маска | ثمانيمئةٍ وواحدٌ وعشرونَ طالباً |
(шестьсот восемь учителей (жен. | ستُمئةٍ وثماني مدرساتٍ |
Слово «тысяча» — ألْفٌ . Как и مئة , это существительное. В отличие от مئة это мужской род. Когда ему предшествуют числа от трех до десяти, чтобы сказать «три тысячи» и т. д., это число женского рода и используется множественное число от الف , آلاف . Таким образом, чтобы сказать «три тысячи человек», вы производите ثلاثةُ آلافِ رجلٍ .
Вы видите, что у вас есть трехчленная идаафа.
Когда ألْف предшествует число больше десяти, оно остается в единственном числе и ставится в винительный падеж, как любое существительное. Таким образом, «двадцать тысяч» — это 9.0003 عشرون ألْفاً Если после ألف следует исчисляемое существительное , الف будет в идаафа с этим существительным. «Двадцать тысяч человек» — это عشرون ألفَ رجلٍ
. «Тысяча ночей» — это الفُ ليلةٍ . «Тысяча одна ночь» — это الفُ ليلة وليلة . «Тысяча две ночи» — это الفُ ليلةٍ وليلتان «Две тысячи ночей» — это الفا ليلةٍ
«Тысяча ночей» — это الفُ ليلةٍ . «Тысяча одна ночь» — это الفُ ليلة وليلة . «Тысяча две ночи» — это الفُ ليلةٍ وليلتان «Две тысячи ночей» — это الفا ليلةٍ
Слово «миллион» — это مِليون . Оно работает точно так же, как ألْف . Его множественное число — ملايين . Слово для миллиарда — مليار . Не путайте это слово с مليون . مليار принимает множественное число женского рода, но работает во всех отношениях так же, как الف и مليون . Теперь, просто чтобы вы не думали, что все это было слишком просто — имейте в виду, что «миллиард» также отображается как بِلْيون , который имеет بَلايين во множественном числе. Он также работает как الف и مليون .
«Три миллиона человек» — ثلاثةُ ملاين رجلٍ , а «три миллиарда человек» — ثلاثةُ ملياراتِ رجلٍ или ثلاثةُ بلايэй رجلٍ .
Порядковые числительные от 100 до бесконечности, насколько я хочу получить «Сотая книга»
الكتابُ المئةُ . «Миллионная книга» — это الكتابُ المليون . Эти слова не изменяются для женского рода.«Тысячная ночь» — это الليلة الألْفُ
Если вы можете делать порядковые числа от 11 до 99, вы сможете делать порядковые числа от 101 до 1 меньше бесконечности. Начиная с مئة , الف и т. д., не меняйте, все, что вам нужно запомнить, это правила для 11-99.
Если вы помните, «тридцать седьмой урок» — это الدرس السابع والثلاثون . «Тридцать седьмая буква» — это الرسالة السابعة والثلاثون . Сказать «Сто тридцать седьмой книги».
Единственное гендерное соглашение, о котором вам нужно беспокоиться, касается единицы. Остальные единицы соглашаются только в случае. Если порядковый номер, который вы используете, содержит что-то в подростковом возрасте, тогда вам нужно беспокоиться об этом немного больше, так как слово عشرة также согласуется в роде, но оно не принимает определенный артикль. Например, «миллион семнадцатая ошибка» — это 9.0003 الخطأ المليون والسابعَ عشرَ
Например, «миллион семнадцатая ошибка» — это 9.0003 الخطأ المليون والسابعَ عشرَ
Примечание 1. Помните, что слово «восемь», ثمانٍ / дефектное слово 90يمان Следовательно, окончание ي появится только в том случае, если слово находится в идаафа, как в последнем примере выше, или используется с определенным артиклем или с суффиксом местоимения. (Это не относится к порядковому «восьмому», الثامن , как я указал в предыдущем разделе.)
| СЕМАНТИЧЕСКИЕ ЗАГАДКИ Почему арабские цифры так называются, если они совсем не похожи на арабские цифры? Гарри Копе, Виктория, Канада
| ||||||||||||||||||||||||||||


 Дж. О’Коннор и Э. Ф. Робертсон, « Индийские цифры » , в архиве истории математики MacTutor ,(по состоянию на 20 июля 2019 г. )
Дж. О’Коннор и Э. Ф. Робертсон, « Индийские цифры » , в архиве истории математики MacTutor ,(по состоянию на 20 июля 2019 г. )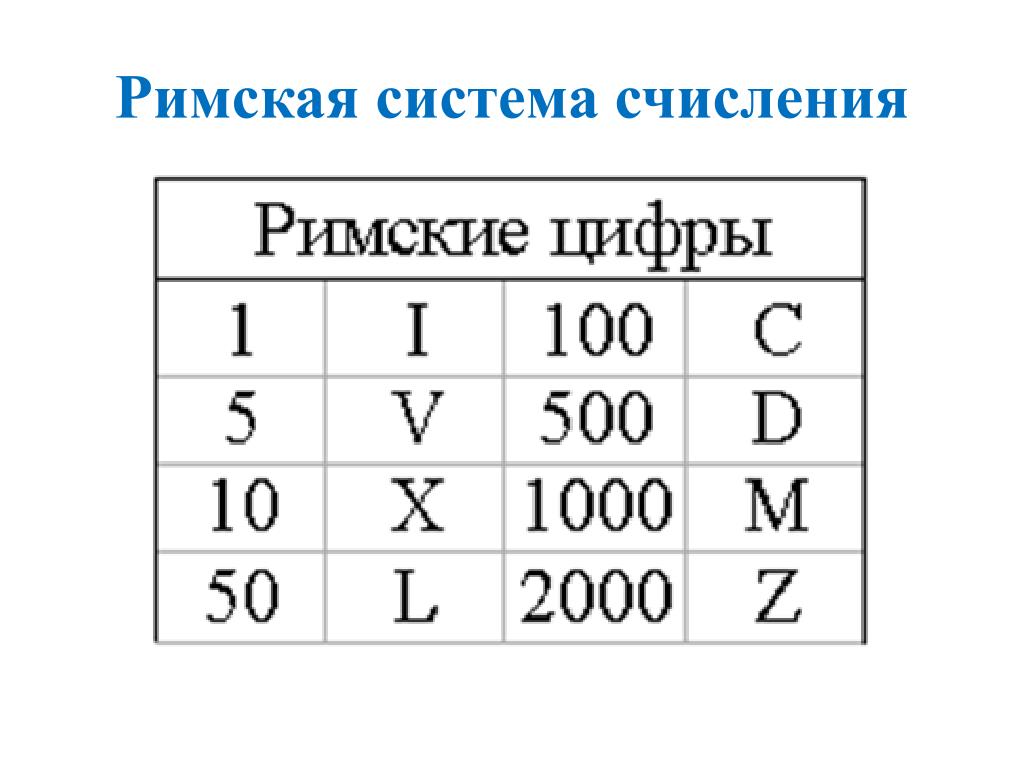 д. Согласно Жаку Хальбронну (Mathematics Divinatories, Paris, La Grande Conjonction -Trédaniel, 1983), было бы целесообразно приблизить написание этих чисел к ивритской скорописи, в частности, буквы Daleth, Tsadé, Samekh, Vav, Zayin для обозначения 2, 3, 0, 1 и 5; из которого остальные пять получаются путем добавления строки: 4, 9, 8, 7 и 6.
д. Согласно Жаку Хальбронну (Mathematics Divinatories, Paris, La Grande Conjonction -Trédaniel, 1983), было бы целесообразно приблизить написание этих чисел к ивритской скорописи, в частности, буквы Daleth, Tsadé, Samekh, Vav, Zayin для обозначения 2, 3, 0, 1 и 5; из которого остальные пять получаются путем добавления строки: 4, 9, 8, 7 и 6.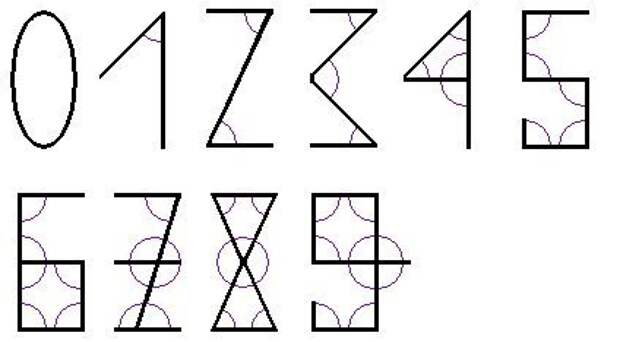 [7], тамания (ثَمَانِيَةٌ) [8] и тис’а (تِسْعَةٌ) [9].
[7], тамания (ثَمَانِيَةٌ) [8] и тис’а (تِسْعَةٌ) [9]. عَشَرَ) [17], тамания ‘ашар (ثَمَانِيَةَ عَشَرَ) [18] и тис’а ‘ашар (تِسْعَةَ عَشَ 19).
عَشَرَ) [17], тамания ‘ашар (ثَمَانِيَةَ عَشَرَ) [18] и тис’а ‘ашар (تِسْعَةَ عَشَ 19). Выше двух тысяч используется форма множественного числа тысячи: талата алааф (ثَلَاثَةُ آلَافٍ) [3,000], арбаа алааф (أربَعة آلَافٍ) [9,000],0397 KHAMSA ALAAF (خَمْسَةُ أَﻟﺎف) [5000], Sitta Alaaf (سِتَّةُ أَﻟﺎف) [6000], Sab’a Alaaf (щал ( (щал. . и тис’а алааф (ﺗﺴِﻌﺔ أَﻟﺎف) [9000].
Выше двух тысяч используется форма множественного числа тысячи: талата алааф (ثَلَاثَةُ آلَافٍ) [3,000], арбаа алааф (أربَعة آلَافٍ) [9,000],0397 KHAMSA ALAAF (خَمْسَةُ أَﻟﺎف) [5000], Sitta Alaaf (سِتَّةُ أَﻟﺎف) [6000], Sab’a Alaaf (щал ( (щал. . и тис’а алааф (ﺗﺴِﻌﺔ أَﻟﺎف) [9000].