Видео с вопросами: Определение и запись квадратичных функций на графике
Стенограмма видео
Для функции 𝑓 от 𝑥 равно 𝑥 в квадрате минус четыре 𝑥 плюс три, ответьте на следующие вопросы. Во-первых, найти, разложив на множители нули функции. Во-вторых, определите график 𝑓.
Есть еще две детали для этот вопрос. Итак, во-первых, нас просят найти нули этой функции. И метод, который нам говорят использовать, факторинг. Поэтому нам нужно написать наш квадратичный как произведение двух линейных множителей. Поскольку коэффициент при квадрате 𝑥 равен one, мы знаем, что первый член в каждой из наших скобок будет 𝑥. Затем мы ищем два числа чья сумма является коэффициентом 𝑥, это минус четыре, и чье произведение является постоянный член, это положительная тройка.
Ну, два числа, которые подходят обоим
из этих критериев отрицательный один и отрицательный три.
Нам нужно использовать эту факторизованную форму
для определения нулей функции, которые, как мы помним, являются 𝑥-значениями такими, что
𝑓 из 𝑥 равно нулю. Если мы установим эту факторизованную форму равной
к нулю, мы тогда вспоминаем, что для того, чтобы произведение двух вещей было равно нулю, по крайней мере один
из них сами должны быть равны нулю. Таким образом, мы можем взять каждый фактор по очереди
и приравняем его к нулю, получив два простых линейных уравнения. Первую можно решить, добавив
по одному с каждой стороны, чтобы получить 𝑥 равно единице, а второе можно решить, добавив три
в каждую сторону, чтобы получить 𝑥 равно трем.
Теперь, во второй части вопрос, нас просят определить график нашей функции 𝑓. И мы видим, что мы были Даны три возможности: синяя, красная и зеленая. Теперь мы только что обнаружили, что наш график имеет нули на единице и тройке. И помните, эти нули значений 𝑥, при которых график пересекает ось 𝑥. Итак, если наш график пересекает 𝑥-ось в один и три, мы можем видеть из рисунка, что остаются только красный и зеленый графики. Синий график пересекает ось 𝑥 или имеет нули при значениях отрицательной единицы и отрицательной тройки.
Теперь нам просто нужно выбрать между
красный и зеленый графики, которые мы видим, являются зеркальным отображением друг друга. Одна из них представляет собой восходящую параболу,
а другой — парабола, изогнутая вниз. Напомним, что тип параболы
у нас будет определяться значением 𝑎.
Оставшиеся две части вопрос, который я изначально не записал, потому что игру отдают за предыдущая часть есть. Напишите уравнение для 𝑔, функция, описывающая синий график. И напишите уравнение для ℎ, функция, описывающая зеленый график.
Давайте сначала посмотрим на этот синий график
всего тогда. Мы уже говорили, что он имеет нули
при отрицательной единице и отрицательной тройке.
Это означает, что в его факторизованном
форме, у него есть множители 𝑥 плюс один и 𝑥 плюс три. Но может быть и фактор
𝑎, на которое мы умножаем. Чтобы определить, является ли значение
𝑎 является тем или иным, мы рассматриваем 𝑦-перехват графа, который мы можем
см. совпадает с 𝑦-перехватом красного графика. Это три. Когда мы умножаем эти два фактора
вместе, постоянный член будет один, умноженный на три, что действительно
три. Таким образом, это говорит нам о том, что значение
из 𝑎 просто один. Наша функция 𝑔 в факторизованном
Форма тогда равна 𝑥 плюс один, умноженный на 𝑥 плюс три. Если мы раскроем скобки,
у нас есть 𝑔 из 𝑥 равно 𝑥 в квадрате плюс четыре 𝑥 плюс три.
Для зеленого графика имеет
те же нули, что и наша функция 𝑓. Так что это можно записать как 𝑎
умножить на 𝑥 минус один умножить на 𝑥 минус три.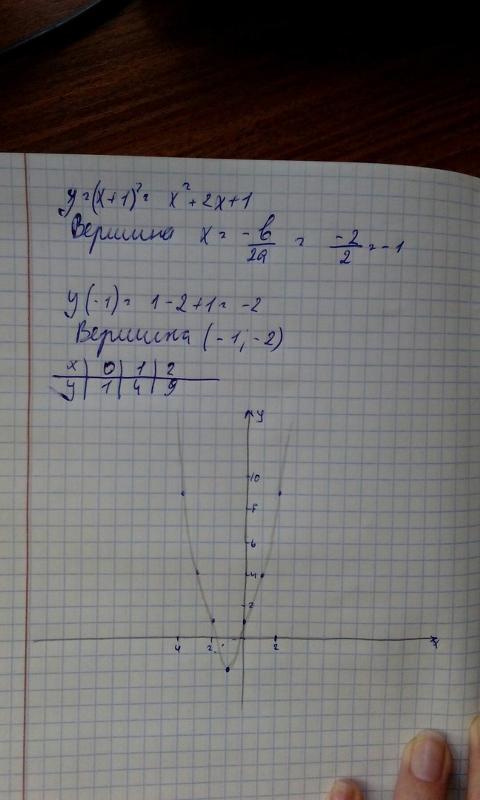
И снова нам нужно определить
является ли значение 𝑎 одним или чем-то другим. Ну, 𝑦-перехват для
зеленый график отрицательный три. Если мы умножим вместе отрицательное
единица и отрицательная тройка, мы получаем значение положительной тройки. И поэтому для обеспечения
𝑦-перехват, постоянный член в расширенной форме ℎ из 𝑥, равен трем отрицательным,
нам нужно, чтобы значение 𝑎 было отрицательным.
Уравнение ℎ для 𝑥 тогда отрицательное 𝑥 минус один, умноженное на 𝑥 минус три. По сути, это полная отрицательное значение нашей функции 𝑓 от 𝑥, что мы также можем видеть, потому что они отражения друг друга по оси 𝑥. Мы можем написать уравнение ℎ для 𝑥 тогда как полное отрицание нашей функции 𝑓 от 𝑥. ℎ из 𝑥 равно отрицательному 𝑥 в квадрате минус четыре 𝑥 плюс три.
Завершение квадрата — это метод, который можно использовать для преобразования квадратного уравнения в стандартной форме в вершинную форму. Способ заполнения квадрата состоит из нескольких простых шагов. Основное упрощение, которое мы стремимся сделать, — это свернуть термин Другими словами, эти два термина равны друг другу, поэтому мы можем преобразовать один в другой. Шаги для завершения квадрата можно обобщить следующим образом:
Мы проиллюстрируем каждый из шагов по заполнению квадрата на следующем примере: у = 2 х 2 — 8 х + 10, типичное квадратное уравнение в стандартной форме. Чтобы завершить квадрат этого уравнения, мы должны сначала выделить члены, включающие x как, г — 10 = 2 х 2 − 8 х . Затем мы делаем старший коэффициент 1 путем деления обеих частей уравнения на 2 как, Теперь возьмем половину коэффициента x , возведем его в квадрат и прибавим к обеим сторонам как Обратите внимание, что у нас есть правая часть формы, , где к = -4. Мы сворачиваем правую сторону 9от 0077 до как, х 2 — 4 х + 4 = ( х — 2) 2 . Итак, имеем Решение для y дает, Следовательно, мы преобразовали уравнение y = 2 x 2 — 8 x + 10 в стандартную форму к вершинной форме как, Мы можем расширить уравнение y = 2( x − 2) 2 + 2, чтобы проверить наше преобразование, Заполнение квадрата для решения квадратных уравнений. Заполнение квадрата также можно использовать для решения квадратных уравнений. Например, предположим, вас попросили решить уравнение .Решить приведенное выше уравнение означает найти значения x , которые делают это утверждение верным. Один из способов сделать это — заполнить квадрат. Вы должны выполнить те же четыре шага, сначала изолировав все термины, включающие x , .Затем мы делаем старший коэффициент равным 1, умножая обе части уравнения на 2, так как х 2 + 6 х = 16. Теперь возьмите половину коэффициента x возведите его в квадрат и добавьте к обеим частям уравнения как Обратите внимание, что у нас есть левая часть формы, . Сворачиваем левую часть до как, Чтобы найти x , мы возьмем квадратный корень из обеих сторон как .Таким образом, мы находим решения нашего уравнения как, х + = 5 — 3 = 2, х — = -5 — 3 = -8. Заполнение квадрата для помощи в построении графика квадратичной функции Любую квадратичную функцию, не являющуюся вершинной, можно привести к вершинной форме, дополнив квадрат. Приняв вершинную форму, квадратное уравнение можно легко построить, вспомнив графические преобразования. Функция задана, y ( x ) = a ( x − h ) 2 + k , можно изобразить путем преобразования базовой функции f ( x ) = x 2 . г ( х ) = 3 ( х + 1) 2 − 7 связано с графиком f ( x ) = x 2 посредством основных преобразований. В частности, график г ( x ) выглядит как график f ( x ), перенесенный влево на 1 единицу, растянутый по вертикали в 3 раза и, наконец, сдвинутый вниз в 7 раз. Область определения всех квадратных уравнений состоит из всех действительных чисел. Знание того, где находится вершина параболы, также позволяет определить диапазон этой квадратичной функции. В частности, если парабола направлена вверх, диапазон квадратичной функции f ( х ) = ах 2 + бх + с есть, Если парабола направлена вниз, диапазон квадратичной функции f ( x ) составляет В качестве конкретного примера график функции f ( x ) = −2 x 2 − 4 x + 1 имеет вершину, Поскольку эта парабола направлена вниз (т. |
Приняв форму вершины, квадратное уравнение легко построить или решить.
Например,