Теория параллельных прямых. Теория треугольника, страница 14
Если при пересечении двух прямых секущей сумма внутренних односторонних углов не равна 180°, то прямые не параллельны, то есть при достаточном продолжении пересекаются.
Доказательство. Если бы эти прямые не пересекались, то они были бы параллельны, и тогда сумма внутренних односторонних углов равнялась бы 180°, что противоречит условию. Теорема доказана.
Сформулируйте обратную теорему.
Мы изучили различные случаи взаимного расположения двух и трёх прямых на плоскости. Теперь изучим взаимное расположения четырёх прямых на плоскости. Изобразим разные случаи.
а) две пересекающиеся прямые пересекают две другие пересекающиеся прямые:
Рис.3.22
б) каждая из двух пересекающиеся прямых пересекает две параллельные прямые:
Рис.3.23
в) две параллельные прямые пересечены двумя параллельными прямыми:
Рис.
г) три параллельные прямые пересечены третьей прямой:
Рис.3.24
д) все четыре прямые параллельны:
Рис.3.25
Какие фигуры вы можете увидеть на этих рисунках? Например, на рис.3.23, слева, видна фигура, состоящая из четырех отрезков, два из которых параллельны. На рис.3.23 видно, что при пересечении двух параллельных прямых двумя другими параллельными прямыми получилась фигура, у которой противоположные стороны попарно параллельны и равны. Докажем это.
Лемма 1. При пересечении двух параллельных прямых двумя другими параллельными между собой прямыми получается фигура, у которой противоположные стороны параллельны.
Доказательство. Пусть параллельные между собой прямые a, b и параллельные между собой прямые c, d пересекаются в точках A, B, C, D (рис.3.26).
Докажем, что АВ=СD и АD=ВС. Проведём
отрезок АС (рис.3.27, а). Для начала докажем, что АВ=СD.
Проведём
отрезок АС (рис.3.27, а). Для начала докажем, что АВ=СD.
Углы ÐACD иÐСAB равны как внутренние накрест лежащие при параллельных прямых a и b и секущей AC. Углы ÐDAC иÐACB равны как внутренние накрест лежащие при параллельных прямых c и d и секущей AC.
На луче АВ отложим отрезок АЕ, равный отрезку CD (рис.3.27, б). Углы ÐACD иÐСAE равны, значит, их соответственные поперечины AD и CE равны. То есть АЕ и DC – соответственные поперечины углов ÐDAC иÐACB, но они равны по построению, а значит, угол ÐACЕ равен углу ÐDAC. Но угол ÐDAC равен углу ÐACB. Это означает, что равны углы Ð

Итак мы доказали, что равны отрезки АВ и СD. Отрезки AD и CB равны как соответственные поперечины равных углов. Утверждение леммы 1 доказано.
Следствие 5: Противоположные углы фигуры ABCD равны (рис.3.27).
Если 2 параллельные прямые пересечены. Параллельные прямые
Опре-де-ле-ние:
Две пря-мые на-зы-ва-ют-ся па-рал-лель-ны-ми , если они не пе-ре-се-ка-ют-ся (Рис. 1). Обо-зна-ча-ет-ся это так: .
Через точку, не ле-жа-щую на дан-ной пря-мой, про-хо-дит толь-ко одна пря-мая, па-рал-лель-ная дан-ной(Рис. 2).
Cледствия из аксиомы
След-ствие 1:Если пря-мая пе-ре-се-ка-ет одну из па-рал-лель-ных пря-мых, то она пе-ре-се-ка-ет и дру-гую.
Дано: .
До-ка-зать: .
До-ка-за-тель-ство:
Будем до-ка-зы-вать от про-тив-но-го. Пред-по-ло-жим, что с не пе-ре-се-ка-ет пря-мую b (Рис. 4).
4).
Тогда:(по усло-вию), (по пред-по-ло-же-нию). То есть через точку М про-хо-дят две пря-мые (а и c ), па-рал-лель-ные пря-мой b . А это про-ти-во-ре-чит ак-сио-ме. Зна-чит, наше пред-по-ло-же-ние невер-ное. Тогда пря-мая c пе-ре-се-чет пря-мую b .
След-ствие 2:
Если две пря-мые па-рал-лель-ны тре-тьей пря-мой, то они па-рал-лель-ны (Рис. 5).
Дано: .
До-ка-зать: .
До-ка-за-тель-ство:
Будем до-ка-зы-вать от про-тив-но-го. Пред-по-ло-жим, что пря-мые
Таким об-ра-зом, по-лу-ча-ем про-ти-во-ре-чие с ак-си-о-мой: через точку М про-хо-дят две пря-мые, од-но-вре-мен-но па-рал-лель-ные тре-тьей пря-мой.
Сле-до-ва-тель-но, наше пред-по-ло-же-ние невер-но. Тогда .
Теоремы о свойствах параллельных прямы
Тео-ре-ма 1:
Если две пря-мые пе-ре-се-че-ны се-ку-щей, то на-крест ле-жа-щие углы равны (Рис.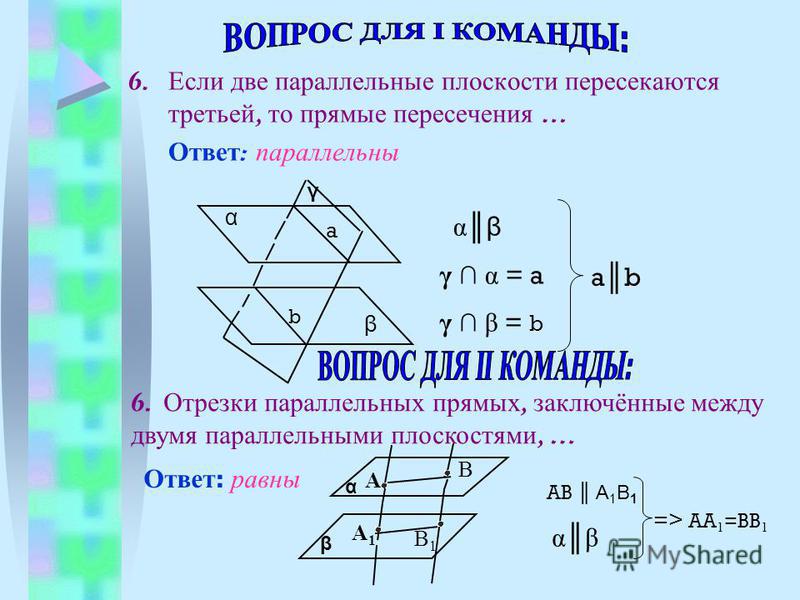 7).
7).
Дано: .
До-ка-зать: .
До-ка-за-тель-ство:
Будем до-ка-зы-вать от про-тив-но-го. Пред-по-ло-жим, что: .
Тогда от луча MN можно от-ло-жить един-ствен-ный угол ∠ PMN , ко-то-рый будет равен ∠ 2 (Рис. 7). Но тогда ∠ PMN и ∠ 2 — на-крест ле-жа-щие и равны. Тогда пря-мые PM и b — па-рал-лель-ны. Тогда через точку М про-хо-дят две пря-мые, па-рал-лель-ные тре-тьей. А имен-но:
По-лу-ча-ем про-ти-во-ре-чие с ак-си-о-мой. Зна-чит, наше пред-по-ло-же-ние невер-но. То есть: .
След-ствие:
Если пря-мая пер-пен-ди-ку-ляр-на одной из па-рал-лель-ных пря-мых, то она пер-пен-ди-ку-ляр-на и вто-рой.
Дано:
До-ка-зать:
До-ка-за-тель-ство:
1. с пе-ре-се-ка-ет а , а зна-чит, и пе-ре-се-ка-ет па-рал-лель-ную ей пря-мую, то есть b . Тогда с — се-ку-щая по от-но-ше-нию к а и b .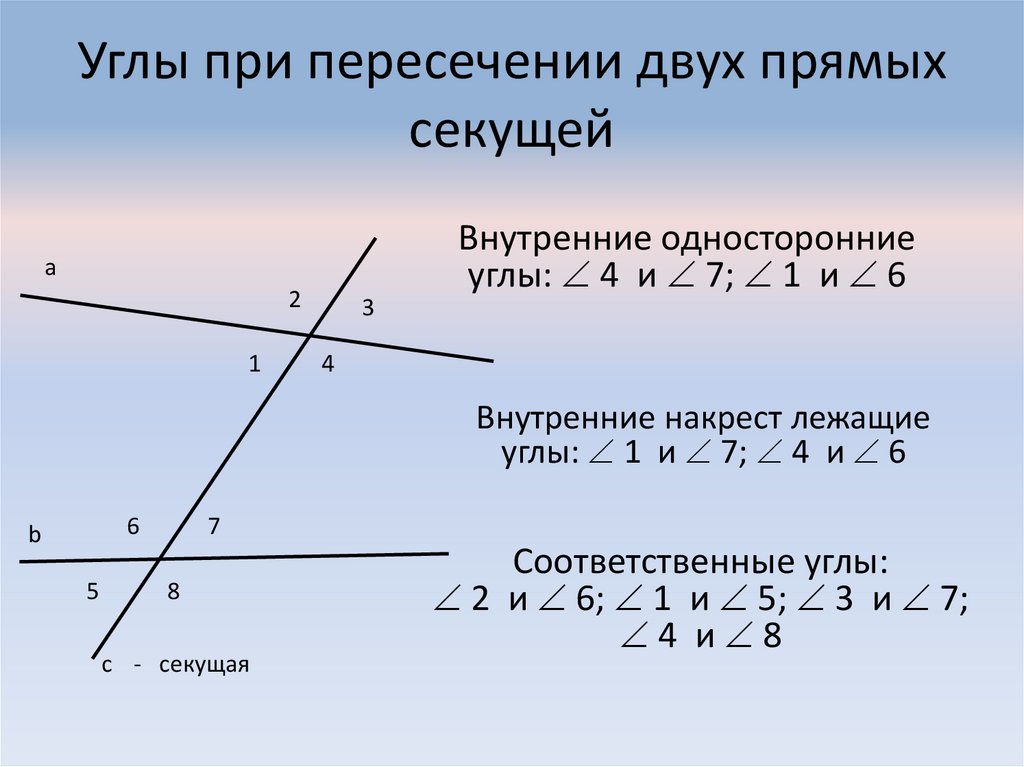
2. по-сколь-ку они яв-ля-ют-ся на-крест ле-жа-щи-ми. Тогда . То есть.
Тео-ре-ма 2:
Если две па-рал-лель-ные пря-мые пе-ре-се-че-ны се-ку-щей, то со-от-вет-ствен-ные углы равны.
Дано: — се-ку-щая.
До-ка-зать: (Рис. 9).
До-ка-за-тель-ство:
Если , то из преды-ду-щей тео-ре-мы сле-ду-ет, что на-крест ле-жа-щие углы равны. То есть .
AB и С D пересечены третьей прямой MN , то образовавшиеся при этом углы получают попарно такие названия:
соответственные углы : 1 и 5, 4 и 8, 2 и 6, 3 и 7;
внутренние накрест лежащие углы : 3 и 5, 4 и 6;
внешние накрест лежащие углы : 1 и 7, 2 и 8;
внутренние односторонние углы : 3 и 6, 4 и 5;
внешние односторонние углы : 1 и 8, 2 и 7.
Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.
Следовательно, ∠ 2 =∠ 8.
3.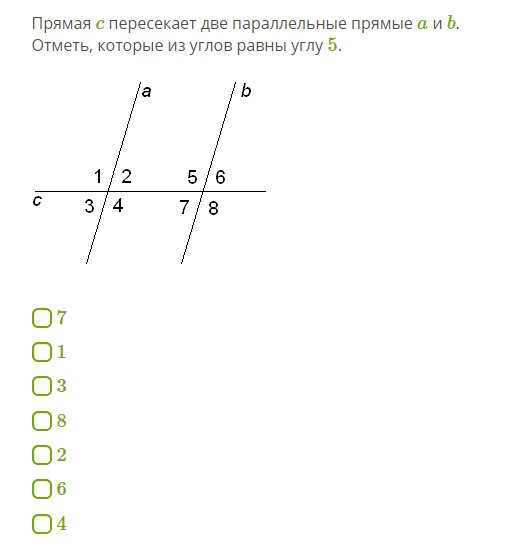 Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.
Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.
4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.
5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам , как углы вертикальные .
Из выше доказанного обоснования получаем обратные теоремы.
Когда при пересечении двух прямых произвольной третьей прямой получим, что:
1. Внутренние накрест лежащие углы одинаковы;
или 2. Внешние накрест лежащие углы одинаковые;
или 3. Соответственные углы одинаковые;
или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;
или 5. Сумма внешних односторонних равна 2d = 180 0 ,
то первые две прямые параллельны.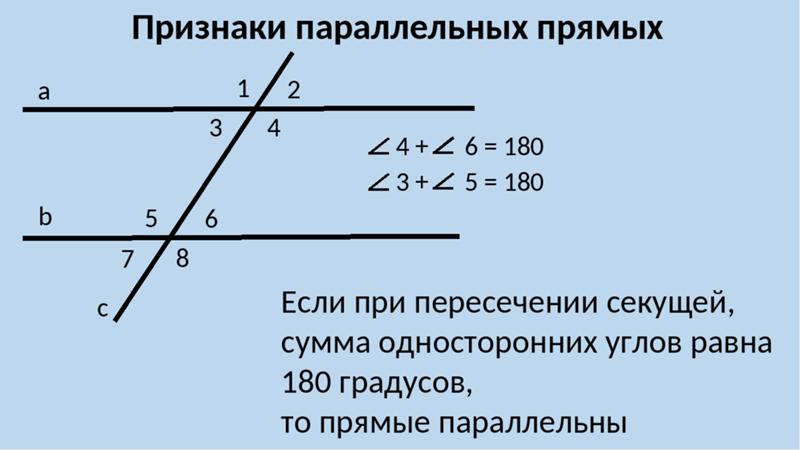
ГЛАВА III.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
§ 38. ЗАВИСИМОСТЬ МЕЖДУ УГЛАМИ,
ОБРАЗОВАННЫМИ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ И СЕКУЩЕЙ.
Мы знаем, что две прямые параллельны, если при пересечении их третьей прямой равны соответственные углы, или внутренние, или внешние накрест лежащие углы, или сумма внутренних, или сумма внешних односторонних углов равна 2d . Докажем, что верны и обратные теоремы, а именно:
Если две параллельные прямые пересечены третьей, то:
1) соответственные углы равны;
2) внутренние накрест лежащие углы равны;
3) внешние накрест лежащие углы равны;
4) сумма внутренних односторонних углов равна 2 d ;
5) сумма внешних односторонних углов равна 2 d .
Докажем, например, что если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.
Пусть прямые АВ и СD параллельны, а МN — их секущая (черт. 202). Докажем, что соответственные углы 1 и 2 равны между собой.
Докажем, что соответственные углы 1 и 2 равны между собой.
Допустим, что / 1 и / 2 не равны. Тогда при точке О можно построить / МОК, соответственный и равный / 2 (черт. 203).
Но если / МОК = / 2, то прямая ОК будет параллельна СD (§ 35).
Получили, что через точку О проведены две прямые АВ и ОК, параллельные прямой СD. Но этого быть не может (§ 37).
Мы пришли к противоречию, потому что допустили, что / 1 и / 2 не равны. Следовательно, наше допущение является неправильным и / 1 должен быть равен / 2, т. е. соответственные углы равны.
Установим соотношения между остальными углами. Пусть прямые АВ и СD параллельны, а МN — их секущая (черт. 204).
Мы только что доказали, что в этом случае соответственные углы равны. Положим, что какие-нибудь два из них имеют по 119°. Вычислим величину каждого из остальных шести углов. На основании свойств смежных и вертикальных углов мы получим, что четыре угла из восьми будут иметь по 119°, а остальные — по 61°.
Оказалось, что как внутренние, так и внешние накрест лежащие углы попарно равны, а сумма внутренних или внешних односторонних углов равна 180° (или 2d ).
То же самое будет иметь место и при любом другом значении равных соответственных углов.
Следствие 1. Если каждая из двух прямых АВ и СD параллельна одной и той же третьей прямой МN, то первые две прямые параллельны между собой (черт. 205).
В самом деле, проведя секущую ЕF (черт. 206), получим:
а) / 1 = / 3, так как АВ || МN; б) / 2 = / 3, так как СО || МN.
Значит, / 1 = / 2, а это углы соответственные при прямых АВ и СD и секущей ЕF, следовательно, прямые АВ и СD параллельны.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (черт. 207).
В самом деле, если ЕF _|_ АВ, то / 1 = d ; если АВ || СD, то / 1 = / 2.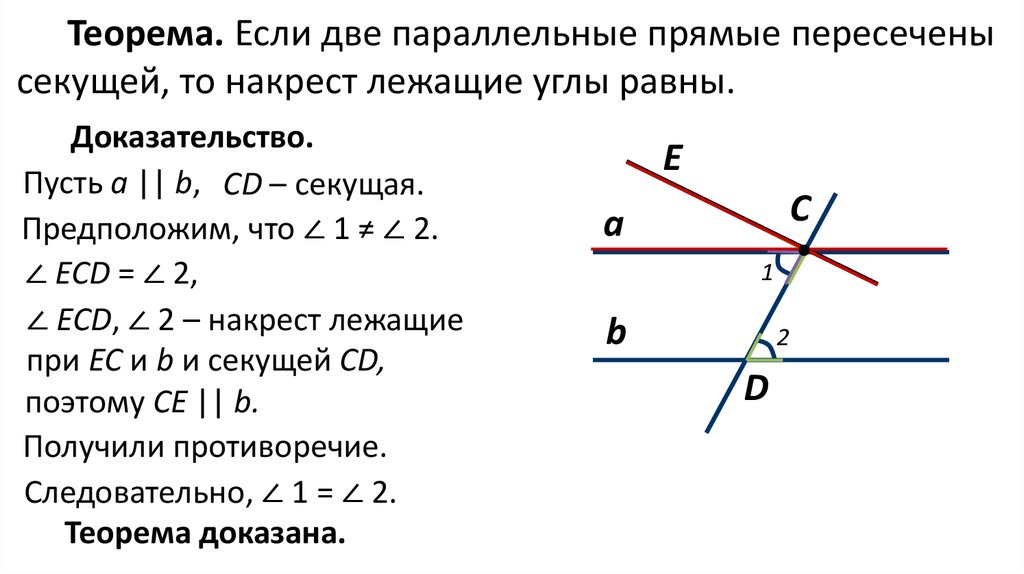
Следовательно, / 2 = d т. е. ЕF _|_ СD .
Признаки параллельности двух прямых
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1 . Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.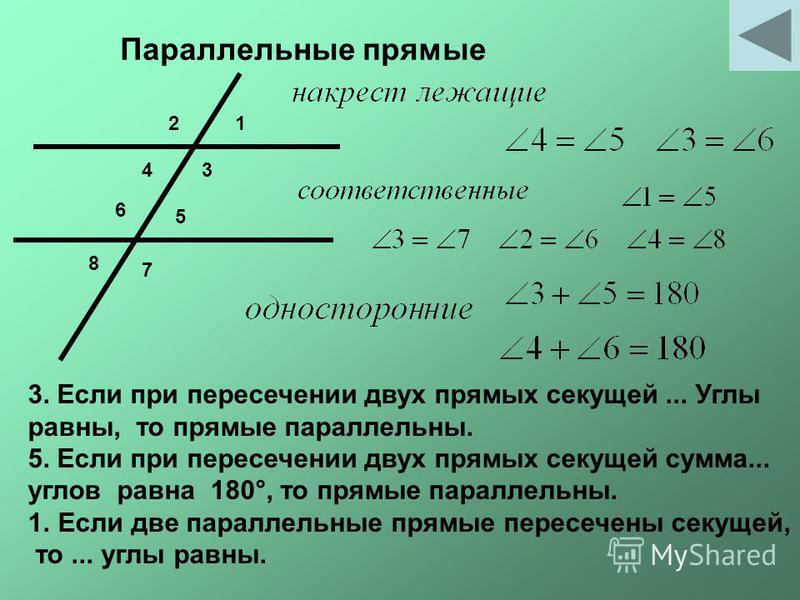 2).
2).
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной .
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Если при пересечении двух прямых секущей сумма внутренних односторонних углов не равна 180°, то прямые не параллельны, то есть при достаточном продолжении пересекаются.
Доказательство. Если бы эти прямые не пересекались,
то они были бы параллельны, и тогда сумма внутренних односторонних углов
равнялась бы 180°, что противоречит
условию.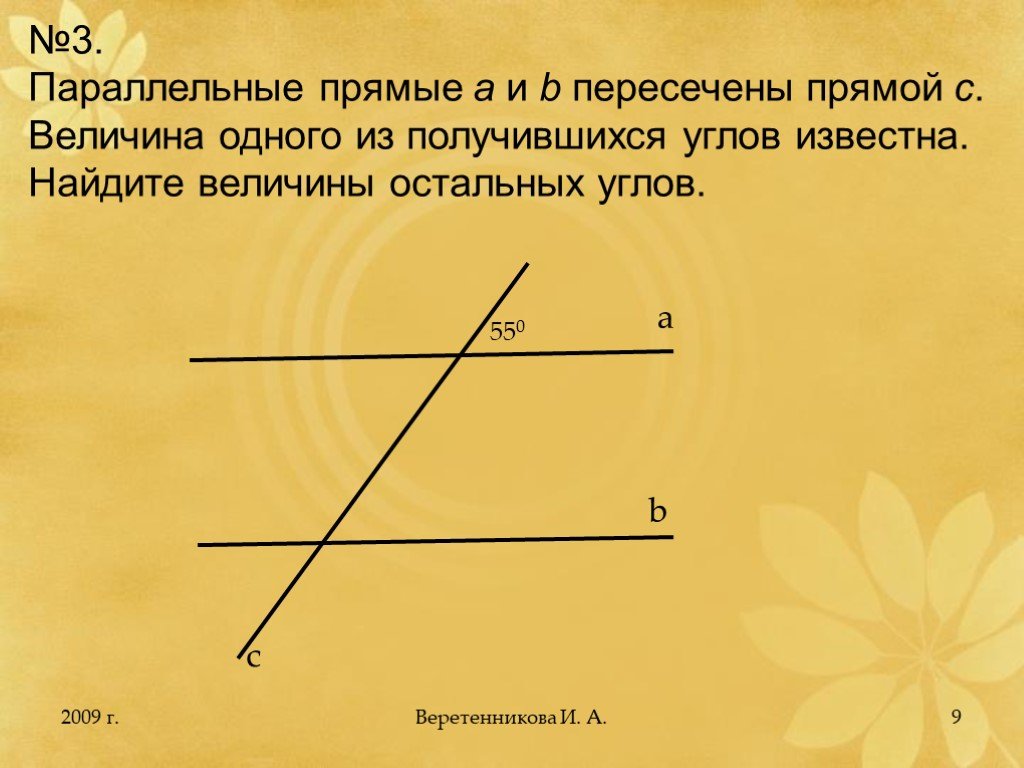 Теорема доказана.
Теорема доказана.
Сформулируйте обратную теорему.
3.3. Взаимное расположение четырех прямых.
Мы изучили различные случаи взаимного расположения двух и трёх прямых на плоскости. Теперь изучим взаимное расположения четырёх прямых на плоскости. Изобразим разные случаи.
а ) две пересекающиеся прямые пересекают две другие пересекающиеся прямые:
б) каждая из двух пересекающиеся прямых пересекает две параллельные прямые:
в) две параллельные прямые пересечены двумя параллельными прямыми:
г) три параллельные прямые пересечены третьей прямой:
д) все четыре прямые параллельны:
Какие фигуры вы можете увидеть на этих рисунках? Например,
на рис.3.23, слева, видна фигура, состоящая из четырех отрезков, два из которых
параллельны. На рис.3.23 видно , что при пересечении двух параллельных прямых
двумя другими параллельными прямыми получилась фигура, у которой
противоположные стороны попарно параллельны и равны. Докажем это.
Докажем это.
Лемма 1. При пересечении двух параллельных прямых двумя другими параллельными между собой прямыми получается фигура, у которой противоположные стороны параллельны.
Доказательство. Пусть параллельные между собой прямые a, b и параллельные между собой прямые c, d пересекаются в точках A, B, C, D (рис.3.26).
Докажем, что АВ=С D и А D=ВС. Проведём отрезок АС (рис.3.27, а). Для начала докажем, что АВ=С D .
Углы ÐACD иÐС AB a и b и секущей AC. Углы ÐDAC иÐ ACB равны как внутренние накрест лежащие при параллельных прямых c и d и секущей AC.
На луче АВ отложим отрезок АЕ , равный отрезку CD (рис.3.27, б). Углы ÐACD иÐС AE равны, значит, их
соответственные поперечины AD и CE равны. То есть АЕ и DC – соответственные поперечины углов ÐDAC иÐ ACB, но
они равны по построению, а значит, угол Ð ACЕ равен углу ÐDAC. Но угол ÐDAC равен углу Ð ACB. Это означает, что равны углы Ð ACЕ иÐ ACB, то
есть точка Е лежит на луче СВ . По построению точка Е лежит
на луче АВ . Но эти лучи пересекаются в точке В, то есть точки В и Е совпадают и АВ=АЕ= CD .
То есть АЕ и DC – соответственные поперечины углов ÐDAC иÐ ACB, но
они равны по построению, а значит, угол Ð ACЕ равен углу ÐDAC. Но угол ÐDAC равен углу Ð ACB. Это означает, что равны углы Ð ACЕ иÐ ACB, то
есть точка Е лежит на луче СВ . По построению точка Е лежит
на луче АВ . Но эти лучи пересекаются в точке В, то есть точки В и Е совпадают и АВ=АЕ= CD .
Итак мы доказали, что равны отрезки АВ и С D . Отрезки AD и CB равны как соответственные поперечины равных углов. Утверждение леммы 1 доказано.
Следствие 5: Противоположные углы фигуры ABCD равны (рис.3.27).
Теорема о трех параллельных прямых | Помощь по геометрии
Главная » Прямые и углы » Параллельные прямые » Теорема о трех параллельных прямых
Последнее обновление: Идо Сариг · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности
Теорема о трех параллельных пересечение параллельных прямых, аналогично теореме о пересечении.
В нем говорится, что если три прямые, параллельные друг другу, пересекаются двумя поперечными прямыми, то отрезки прямых пересечения, пересекаемые параллельной линией, имеют равные пропорции:
|AB|/|BC|=|DE|/|EF|
Задача
Две поперечные прямые пересекают три параллельные прямые x, y, и z в точках A,B,C и D,E,F соответственно. Покажите, что |AB|/|BC|=|DE|/|EF|
Стратегия
Эта теорема очень похожа на теорему о перехвате, и рисунок очень похож на рисунок теоремы о перехвате:
Итак, давайте посмотрим, сможем ли мы использовать эту теорему в нашем доказательстве. Проведем прямую, параллельную DF, через точку A (помните аксиому: «для каждой прямой и каждой точки, не лежащей на этой прямой, через эту точку проходит одна прямая, параллельная первой прямой»).
Левая сторона рисунка в точности соответствует теореме о пересечении. Непосредственно используя это, мы имеем |AB|/|BC|=|AG|/|GH|.
Но поскольку x, y и z параллельны, а AH параллелен DF по построению, ADEG и GEFH являются параллелограммами. А в параллелограмме противоположные стороны равны, поэтому |AG|=|DE| и |GH|=|EF|. Подставляя, получаем нужный результат: |AB|/|BC|=|AG|/|GH|=|DE|/|EF|
Вот как мы доказываем теорему о трех параллельных прямых.
Пруф
(1) х || у || z //Дано
(2) AH||DF // Конструкция
(3) |AB|/|BC|=|AG|/|GH| // Теорема о перехвате
(4) |AG|=|DE| //(1), (2), Противоположные стороны параллелограмма равны
(5) |GH|=|EF| //(1), (2), Противоположные стороны параллелограмма равны
(6) |AB|/|BC|=|DE|/|EF| //(3), (4), (5) , Транзитивность равенства
Следствие
Следствием является предложение, которое следует из только что доказанного доказательства. Следствием теоремы о трех параллельных прямых является то, что если три параллельные прямые отсекают конгруэнтные сегменты на одной поперечной прямой, то они отсекают конгруэнтные сегменты на каждой поперечной из этих трех прямых.
Это следствие следует непосредственно из того, что мы доказали выше. Мы показали, что при наличии трех параллельных прямых отношения отрезков, отсеченных на поперечных прямых, одинаковы: |AB|/|BC|=|DE|/|EF|. Отсюда следует, что если AB и BC конгруэнтны, то |AB|/|BC|=1, поэтому |DE|/|EF| = 1. И это верно для любой поперечной прямой с отрезками DE и EF, отсекаемыми тремя параллелями.
Интересным применением этого следствия является то, что если вы возьмете блокнот, страницы которого разлинованы, и проведете любую прямую линию через направляющие, то все отрезки этой прямой линии, отсекаемые направляющими, будут равны:
Это связано с тем, что направляющие расположены на одинаковом расстоянии друг от друга. Таким образом, расстояние между любыми двумя соседними прямыми одинаково. Расстояние — это длина перпендикулярной линии от одной параллельной прямой до другой. Например, красная линия на левом поле рисунка выше.
Итак, любые три соседние строки имеют отношение |AB|/|BC|=1. И по следствию, приведенному выше, 3 параллельные прямые будут отсекать конгруэнтные сегменты на каждом пересечении этих трех прямых.
И по следствию, приведенному выше, 3 параллельные прямые будут отсекать конгруэнтные сегменты на каждом пересечении этих трех прямых.
Об авторе
Идо Сариг — руководитель отдела высоких технологий со степенью бакалавра вычислительной техники. Его цель — помочь вам разработать лучший подход к решению геометрических задач. Вы можете связаться с ним по телефону [email protected]
4.3: Переходы к трем параллельным линиям
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34137
- Генри Африк
- CUNY Технологический колледж Нью-Йорка через Технологический колледж Нью-Йорка в CUNY Академические работы
В главе 1 мы определили секущую как линию, которая пересекает две другие прямые. Теперь мы расширим определение до линии, которая пересекает три другие прямые. На рисунке \(\PageIndex{1}\) \(AB\) представляет собой пересечение трех линий.
Теперь мы расширим определение до линии, которая пересекает три другие прямые. На рисунке \(\PageIndex{1}\) \(AB\) представляет собой пересечение трех линий.
Если три прямые параллельны и у нас есть две такие секущей, мы можем сформулировать следующую теорему:
Теорема \(\PageIndex{1}\)
Отрезки, образованные двумя секущими, пересекающими три параллельные прямые, пропорциональны.
На рисунке \(\PageIndex{2}\), \(\dfrac{a}{b} = \dfrac{c}{d}\).
Рисунок \(\PageIndex{2}\): Отрезки прямых, образованные секущими, пропорциональны.Пример \(\PageIndex{1}\)
Найти \(x\):
Решение
\[\begin{array} {rcl} {\dfrac{x}{3}} & = & {\dfrac{8}{4}} \\ {4x} & = & {24} \\ {x} & = & {6} \end{массив}\]
Проверить:
Ответ : \(х = 6\).
Доказательство теоремы \(\PageIndex{1}\)
Нарисуйте \(GB\) и \(HC\) параллельно \(DF\) (рисунок \(\PageIndex{3}\)). 2 — 5x — 6} & = & {0} \\ {(x — 2)(4x + 3)} & = & {0} \end{array} \)
2 — 5x — 6} & = & {0} \\ {(x — 2)(4x + 3)} & = & {0} \end{array} \)
\(\begin{массив} {rcl} {x — 2} & = & {0} \\ {x} & = & {-2} \end{массив}\) или \(\begin{массив} {rcl} {4x + 3} & = & {0} \\ {4x} & = & {-3} \\ {x} & = & {-\dfrac{3}{4}} \end{array} \)
Мы отвергаем \(x = -\dfrac{3}{4}\), потому что \(BC = x\) не может быть отрицательным.
Проверка, \(x = 2\):
Ответ: \(x = 2\).
1 — 6. Найдите \(x\):
1.
2.
3.
4.
5.
6.
Эта страница под названием 4.3: Переходы к трем параллельным линиям распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Генри Африком (Нью-Йоркский технологический колледж в CUNY Academic Works) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
