Окружность и круг – различия (6 класс, математика)
4.7
Средняя оценка: 4.7
Всего получено оценок: 755.
4.7
Средняя оценка: 4.7
Всего получено оценок: 755.
Окружность и круг – это две разные фигуры, которые частенько путают в математике 6 класса. Поэтому имеет смысл обсудить эту тему более подробно.
Определения
Круг – это часть пространства, ограниченная окружностью. Окружность – это множество точек, равноудаленных от одной точке, называемой центром окружности.
Различия
Окружность – это линия. Круг – это плоская фигура. Окружность не может иметь площади, тогда как круг ее имеет.
Рис. 1. Круг и окружность.На этом, пожалуй, различия круга и окружности заканчиваются. Но стоит сказать еще и о том, что в геометрии чаще звучит название окружности.
Круг имеет площадь, но в задачах мы чаще ищем длину окружности. На длину окружности завязаны некоторые свойства вписанной и описанной окружности треугольника, поэтому сложилась некая традиция использования окружности вместо круга.
Вспомним, что
$R={D\over{2}}$-то есть радиус равен половине диаметра. Соответственно это равенство можно подставить в формулу площади и получить еще одну формулу. Или просто найти диаметр или радиус через эту формулу и подставить в уже приведенную формулу.
Существует формула, которая позволяет найти длину окружности. Что такое длина окружности? Если условно распрямить линию окружности, то получится прямая, длину которой можно найти по формуле:
$L=\pi*d$ – диаметр, так же, как и в площади можно заменить диаметром.
Рис. 2. Длина окружности.Окружность и прямая
Положение окружности и прямой на плоскости это отдельная тема для разговора. Прямая на плоскости может:
- Пересекать окружность
- Не пересекать окружность
- Касаться окружности
Прямая, пересекающая окружность зовется секущей и имеет две общие точки с окружностью.
Отдельный интерес имеет касательная прямая, то есть прямая, которая имеет одну общую точку с окружностью.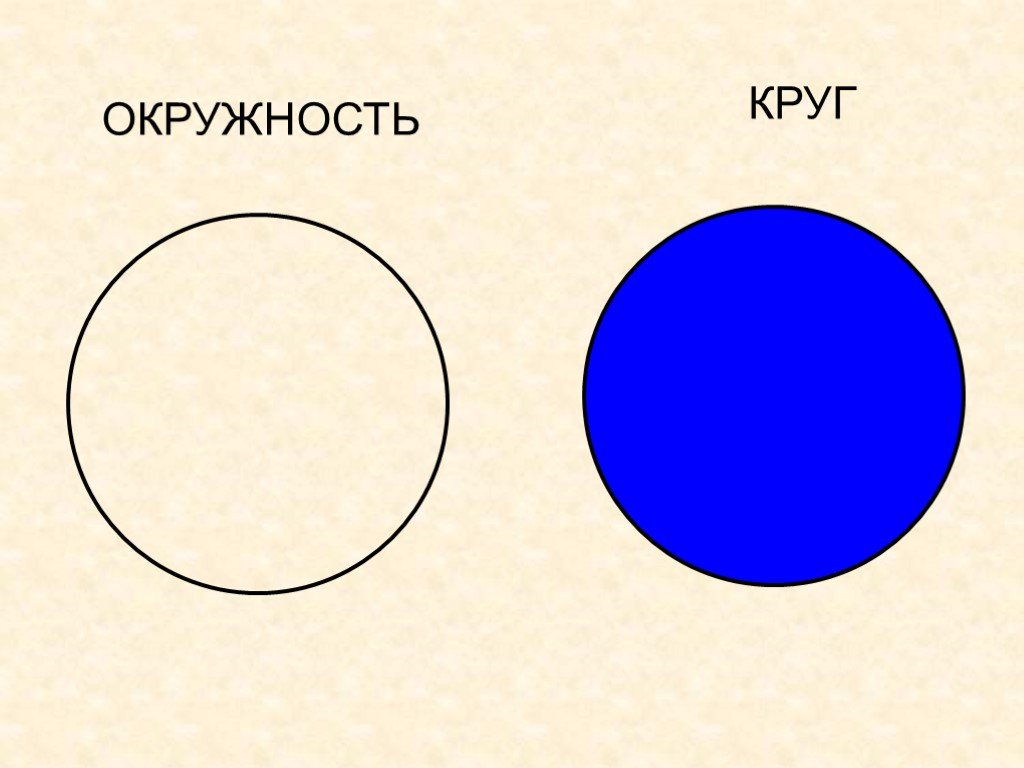
Запомните, радиус, проведенный в точку касания перпендикулярен касательной.
Рис. 3. Окружность и прямая.Окружность и угол
Окружность и угол связаны, потому как окружность это наиболее яркий пример полного угла. То есть, если провести какой либо отрезок и повернуть его вокруг своего начала на 360 градусов, то получится окружность.
Углом в окружности измеряется дуга. Дуга это часть окружности, ограниченная двумя радиусами. Два радиуса и дуга представляют собой сектор.
Что мы узнали?
Из статьи мы узнали о том, что круг – это плоская фигура, а окружность – это линия. Мы познакомились с характеристиками этих понятий и узнали свойства круга и окружности.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Владимир Найда
10/10
Вет Громов
9/10
Шварева Наталья
8/10
Ольга Журавлёва
10/10
Оценка статьи
4.
7
Средняя оценка: 4.7
Всего получено оценок: 755.
А какая ваша оценка?
Чем отличается окружность от круга
В обычной жизни нам приходится замечать множество предметов, которые по своей форме напоминают окружности и круги, но редко кто задумывается о том, чем окружность отличается от круга и что у них общего.
Окружность – это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Окружностью называют линию, которая ограничивает круг. Правильную окружность можно изобразить с помощью циркуля. Ножку с иголкой нужно установить в задуманную точку, и тогда ножка с карандашиком начертит замкнутую линию. Эта линия разделяет плоскость на две части: внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, т. к. плоскость в общем понимании не имеет границ. Для отличия, можно заштриховать внутреннюю область. Часть, которая осталась внутри, называется кругом.
Окружность имеет центр — это начальная точка нарисования циркулем.
Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.
Круг – является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Пространство, закрепленное границей, включая центр круга принадлежит кругу. Если провести линию от одной точки на границе круга до другой через центр, то такое расстояние будет называться диаметром круга. Если от центра круга провести прямую линию до любой отметки на его границе, то это расстояние называется радиус. Два радиуса, равноудалённые от центра круга, будут соответствовать его диаметру.
Следовательно, диаметр в два раза больше радиуса. Если от одной точки круга провести хорду, то хорда и соответствующая ей дуга будет образовывать сегмент круга. Окружность и круг имеют общий радиус и диаметр.
Отличие окружности и круга
Окружность, как любая линия имеет длину, а круг, как любая геометрическая фигура имеет площадь. Круг имеет площадь, но её нет у окружности. Круг содержит центр окружности, а окружность, содержит сам круг. Без окружности не было бы круга, но она существует самостоятельно. Окружность проводит границу круга снаружи, а круг – внутренняя часть окружности. И круг, и окружность имеют одинаковый центр.
Выводы:
- Окружность представляет собой замкнутую линию.
- Круг, это пространство, ограниченное окружностью.
- Радиус окружности, равен радиусу круга.
-
Диаметр делит окружность и круг на два равных полукруга.
- Окружность является границей круга.
- Если начертить заштрихованную окружность, то её можно считать кругом и наоборот.
- Круг и окружность имеют единый центр.
- У окружности есть длина, а у круга её нет.
Ресурсы:
- Большой энциклопедический словарь (БЭС)
Окружность круга — определение, формула и примеры ola
Что такое окружность?
Окружность — это расстояние по окружности. Мы можем найти длину окружности, используя либо диаметр, либо радиус окружности.
О фигурах, состоящих из прямых линий, мы говорим, что они имеют периметр. Для кругов периметр получает название окружности.
Что такое окружность — определение Не имеет значения, является ли круг частью сферы (как земной экватор) или плоской, как место сбора короля Артура для всех его рыцарей, если мы знаем либо диаметр, либо радиус, мы можем найти окружность круга.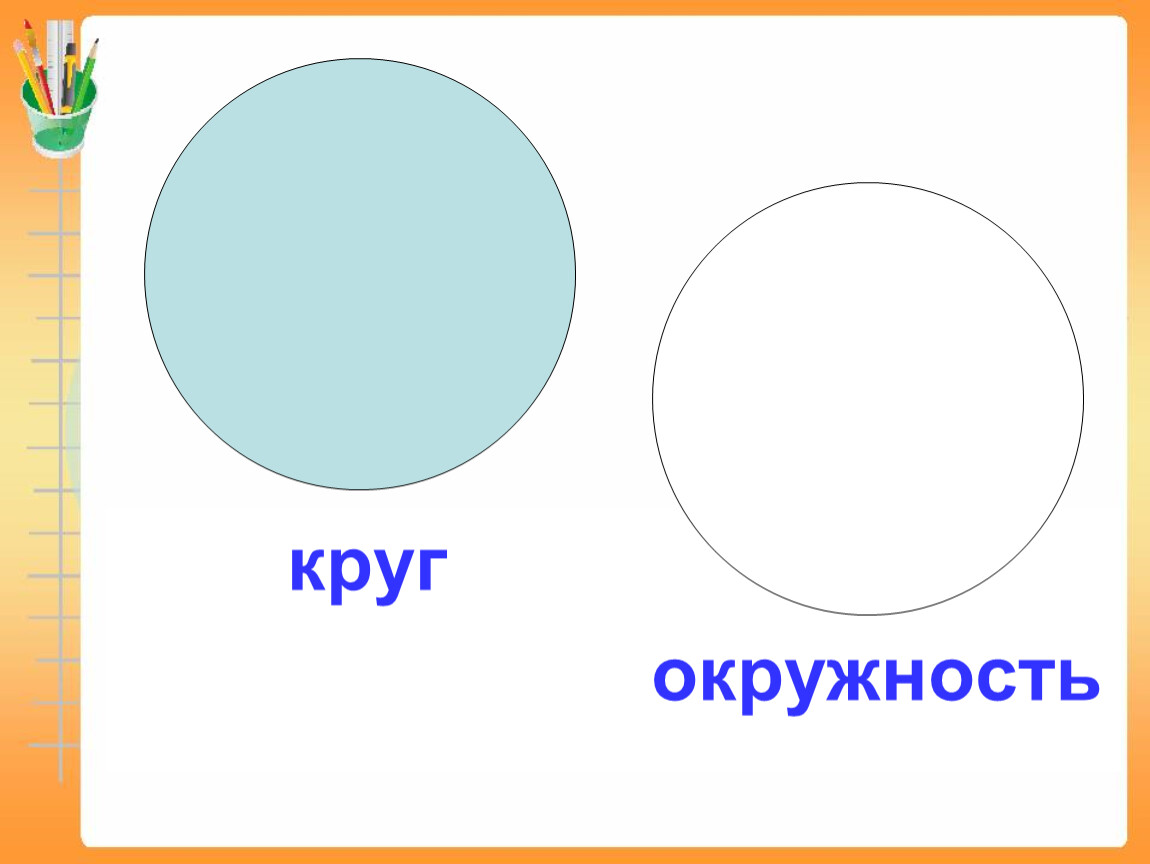
Бьюсь об заклад, король Артур приветствовал бы сэра Камференса за своим Круглым столом.
Части круга
Окружность (множество всех точек, равноудаленных от данной точки) состоит из многих частей, но в этом уроке основное внимание будет уделено трем:
Окружность – Расстояние по окружности (периметр окружности).
Диаметр – Расстояние от окружности через центр окружности до окружности на противоположной стороне. (удвоенный радиус)
Радиус – Расстояние от центра окружности до окружности (половина диаметра). Нарисуйте отрезок из центра круга в любую часть круга, и вы получите радиус.
Формула длины окружности
Для нахождения длины окружности используются две формулы, C , в зависимости от предоставленной информации. В обеих формулах длины окружности используется иррациональное число Пи, которое обозначается греческой буквой π . Пи — математическая константа, а также отношение длины окружности к диаметру.
Диаметр относительно длины окружности
Если вам известен диаметр окружности, d , затем используйте эту формулу длины окружности:
Формула радиуса окружности
Если вам дан радиус, r , вы все равно можете найти длину окружности. Если вы знаете радиус, формула длины окружности:
Вы всегда можете найти длину окружности, если знаете диаметр или радиус.
Как найти длину окружности
Допустим, у нас есть круг с заданным диаметром 12 756,274 км . Чтобы найти длину окружности, умножьте это время измерения на π :
. Мы выбрали диаметр не случайно. С точностью до трех знаков после запятой это окружность земного экватора.
Пример окружности — диаметр землиБританская энциклопедия сообщает нам, что исторический Круглый стол, по слухам, принадлежавший королю Артуру, имеет радиус 2,75 метра . Чтобы найти длину окружности стола короля Артура, воспользуемся формулой радиуса:
Это массивный стол.
Артур предположительно собрал 25 рыцарей, поэтому со всеми 26 мужчинами, собравшимися вокруг, у каждого было только 69 сантиметров края стола. Они были бы локтем к локтю, эти рыцари.
Вы также можете найти длину окружности через площадь круга.
Найдите диаметр по окружности
То же уравнение C = πd можно использовать для нахождения диаметра окружности, если известна длина окружности. Просто разделите обе части на иррациональное число 9.0029 № .
Предположим, что длина окружности равна 339,292 фута . Каков диаметр круга?
Нет, этот диаметр не случайный; это размер сарсенового каменного кольца в Стоунхендже.
От длины окружности до диаметраНайдите радиус от окружности
Уравнение окружности с использованием радиуса C = 2πr также можно использовать для нахождения радиуса окружности, если вы знаете длину окружности.
Допустим, у нас есть круг с длиной окружности 40,526 м ; каков его радиус? Мы снова разделим обе части на π , но нам также нужно исключить 2 , поэтому разделим обе части на 2π :
Конечно, это не случайное число.
Это размер знаменитого Южного окна-розы собора Нотр-Дам. Это огромный большой витраж!
Этот урок предоставил вам много информации о длине окружности круга и о способе найти любую меру любой части, если у вас есть другое измерение. Попутно вы также немного изучили географию и историю, которые тоже могут вам пригодиться.
Окружность круга — Common Core: Математика для 7-го класса
All Common Core: Математические ресурсы для 7-го класса
7 Диагностических тестов 110 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Common Core: Справка по математике для 7-го класса » Геометрия » Знать и использовать формулы площади и длины окружности: CCSS.Math.Content.7.GB.4 » Окружность круга
Какова длина окружности с радиусом, равным ?
Возможные ответы:
Правильный ответ:
Объяснение:
Длина окружности может быть определена с помощью следующего уравнения:
Сообщить об ошибке
Радиус окружности равен .
Выразите длину окружности в терминах .
Возможные ответы:
Правильный ответ:
Объяснение:
Длина окружности может быть рассчитана как , где — радиус окружности.
Сообщить об ошибке
Какова длина окружности с радиусом ?
Возможные ответы:
Правильный ответ:
Объяснение:
Длина окружности может быть определена с помощью следующего уравнения:
Сообщить об ошибке
Если этот круг имеет диаметр 12 дюймов, какова его окружность?
Возможные ответы:
ни один из этих ответ:
Объяснение:
Знайте, что формула для длины окружности такова, где C — длина окружности, а D — диаметр.
Дано, что диаметр 12 дюймов. Следовательно, длина окружности равна 9 0003
Сообщить об ошибке
Если площадь круга равна , какова длина окружности круга?
Возможные ответы:
Правильный ответ:
Объяснение:Формула площади круга: πr 2 . Площадь этого конкретного круга равна 81π, поэтому 81π = πr 2 . Разделите обе части на π, и у нас останется r 2 = 81. Извлеките квадратный корень из обеих сторон, чтобы найти r = 9.. Формула длины окружности: 2πr = 2π(9) = 18π. Правильный ответ 18π.
Сообщить об ошибке
Если площадь круга равна , какова длина окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
Для круга формула площади равна , а формула длины окружности – , где по которой это диаметр.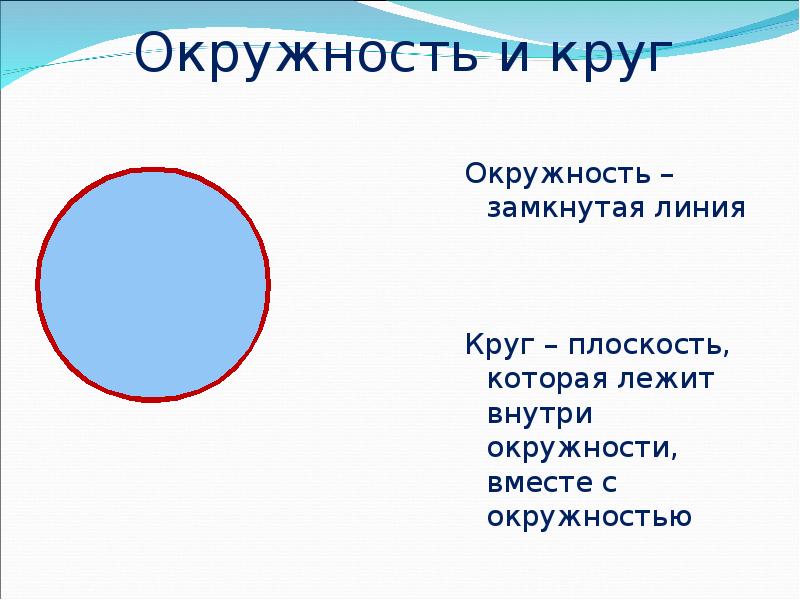
Подставьте известные величины в формулу площади и найдите радиус:
Теперь подставьте это значение в формулу длины окружности, чтобы решить:
Сообщить об ошибке
Найдите длину окружности с радиусом .
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните формулу для нахождения длины окружности:
Мы можем подставить значение радиуса, чтобы найти длину окружности рассматриваемого круга.
Решить.
Упрощение.
Сообщить об ошибке
Найдите длину окружности радиусом .
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните формулу для нахождения длины окружности:
Мы можем подставить значение радиуса, чтобы найти длину окружности рассматриваемого круга.
Решить.
Упрощение.
Сообщить об ошибке
Найдите длину окружности радиусом .
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните формулу для нахождения длины окружности:
Мы можем подставить значение радиуса, чтобы найти длину окружности рассматриваемого круга.
Решить.
Упрощение.
Сообщить об ошибке
Найдите длину окружности радиусом .
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните формулу для нахождения длины окружности:
Мы можем подставить значение радиуса, чтобы найти длину окружности рассматриваемого круга.