4 класс примеры на сложение: 4 класс. Задачи на сложение и вычитание чисел. Сложение и вычитание многозначных чисел в столбик. Скачать pdf

Конспект урока по математике 4 класс » Сложение и вычитание многозначных чисел»

Конспект урока по математике 4 класс

« Сложение и вычитание многозначных чисел.»

ТЕМА

Сложение и вычитание многозначных чисел.

Цели:

• ввести прием сложения и вычитания многозначных чисел; закрепить изученные приемы сложения и вычитания трехзначных чисел; продолжить работу над изучением устной нумерации многозначных чисел;

• создать условия ощущения радости у детей в процессе обучения с помощью выполнения упражнений, эффективных для сохранения и укрепления здоровья;

— развивать мышление, речь, творческие способности, культуру здоровья, сотрудничать в групповой и парной деятельности.

ЗАДАЧИ:

• познакомить учащихся с темой «Сложение и вычитание многозначных чисел»путём

• активизировать знания нумерации многозначных чисел: чтение, запись, сравнение; представление его в виде разрядных слагаемых.

• продолжить формирование новых компетенций, знаний и умений, способов деятельности путём использования современных технологий обучения.

• способствовать повышению мотивации обучения посредством тематического отбора и представления учебного материала в интересной, интерактивной и максимально понятной для обучающихся форме.

• содействовать формированию навыков самоорганизации путём создания ситуаций для самостоятельного принятия решений и проявления инициативы.

• развивать познавательную активность обучающихся и познавательный интерес к предмету путём создания и решения в сотрудничестве проблемной ситуации.

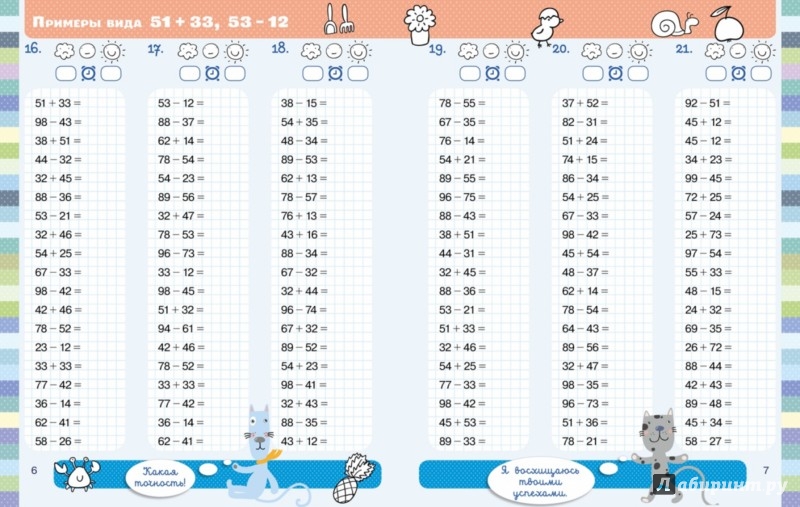
• проверить уровень самостоятельности мышления обучающихся по применению знаний в различных ситуациях.

1. Активизация знаний

Одна хорошая минута

Сделала одно хорошее дело,

Десять хороших минут

Сделали десять хороших дел.

А сколько хороших дел

Можно сделать за целый урок? (40)

2 Математическая разминка

1. Числа больше трёхзначных называются … (Многозначные)

2. Для того чтобы правильно читать и записывать многозначные числа, их разбили на … (Классы)

3. с какими классами вы познакомились: (Класс единиц, класс тысяч, класс миллионов, миллиардов …)

4. Сколько разрядов в каждом классе? (3)

5. Как называются единицы 2–го разряда? (Десятки)

№3 устно

а) На доске записаны многозначные числа.

Необходимо числа расставить в порядке возрастания.

98, 4295, 3846, 20000, 34295, 45348, 1309400, 923527, 500004

(98, 3846, 4295, 20000, 34295, 45348, 500004, 923527, 1309400)

В

С

Е

Л

Е

Н

Н

А

Я

— Назовите число, которое стоит после числа 20000.

— Назовите число, в котором 295 единиц первого класса.

— Назовите число, в котором 3 единицы класса тысяч.

— Назовите соседей числа 923527.

Перевернув цифры, мы получим слово. (Вселенная)

— Что такое Вселенная? (Космическое пространство, и всё, что его заполняет)

б) Числа записаны в виде суммы разрядных слагаемых.

Необходимо определить, какие это числа, и мы узнаем диаметры некоторых планет Вселенной.

6000+700+90=6790 км — диаметр Марса

10000+2000 +100=12100 км — диаметр Венеры

10000+2000+700+40+2= 12742 км — диаметр Земли

50000+4000= 54000 км — диаметр Урана

40000+9000+ 500= 49500 км – диаметр Нептуна

— Диаметр, какой планеты больше?Урана

— Диаметр, какой планеты меньше?Марса

— сравните

— На какой планете мы живём? (Земля)

12 742

• назовите число, которая обозначает разряд сотен 1 класса.

• назовите число, которая обозначает, если какой-либо разряд в числе отсутствует.

— назовите число, которая обозначает разряд единиц 2 класса.

— назовите число, которая обозначает разряд десятков 1 класса.

7, 0, 2, 4.

1 в. Составьте из этих цифр самое большое четырёхзначное число, чтобы цифры не повторялись. (7420)

2 в. Составьте из этих цифр самое маленькое четырёхзначное число, чтобы цифры не повторялись. (2047)

числа мы умеем читать,сравнивать,представлять в виде суммы разрядных слагаемых

А если я предложу вам сложить их вы сможете?

Какие знания помогут вам выполнить сложения?(сложения и вычитание 3-х чисел)

кто попробует выполнить сложение у доски?

Что изменилось в алгоритме сложения многозначных чисел по сравнению с 3-х значными числами?-один разряд добавился

сможем выполнить вычитание чисел как вы это выполните?алгоритм вычитания 3-х значных

Что изменилось в алгоритме вычитания многозначных чисел по сравнению с 3-х значными числами?-один разряд добавился трудности возникли при решении примеров?

Какой вывод можем сделать о + — многозначных чисел?

Кто догадался о чем пойдет речь на уроке?какая у нас тема?

Проверим наше предположение прочитаем правило на стр 68

Закрепление с 68 №4выпоним в учебнике.

Проверка.

№6

при решении алгоритмом каким воспользуемся?

Решаю 2 столбик какое свойство сложения вспомним,для удобного решения примера?

1-девочки

2-мальчики

взаимопроверка

3. Решение задачи

• Возьмите листы с текстами и найдите среди них задачу.

• Почему вы решили,что это задача?

1. Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам.

1. Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам. Чему равна длина окружности Марса?

2. Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам.

На сколько километров ошиблись древние учёные?

Анализ задачи, решение самостоятельное. За доской ученик Как выполнять решение будем?

столбиком

Проверка: 40 075- 39 690=385 (км)

Итак: — Кто испытывал затруднения при решении задачи?

-В чём были затруднения?

Внимание на доску.

Записаны примеры все ли правильно записаны и решены В чем ошибка?

Запишите правильные варианты решения к себе в тетрадь Еще раз запомните как правильно записываем в столбик многозначные числа

683159 — 2304__ 452759 Ошибка

683159 — 2304 680855 Верно

34981 + 40075 389885 Ошибка

34981 + 40075 75056 Верно

Как правильно записываем примеры в столбик?

В заключении урока я предлагаю вам выполнить задание на листках.

1. Укажи правильную запись числа: девять тысяч пятнадцать.

а) 9015
б) 90015
в) 9150
г) 915

2. Какое число следует за числом 24567?

а) 24667
б) 24568
в) 25567
г) 24566

3. Какое число представлено в виде суммы разрядных слагаемых:

40000+5000+ 600+50+4

а) 405654
б) 4565
в) 45654
г) 54654

4. Какая цифра стоит в разряде сотен в записи числа 432567?

а) 4
б) 3
в) 2
г) 5

5. Какое число содержит 572 единицы первого класса и 400 единиц второго класса.

а) 572400
б) 572
в) 400
г) не знаю
д) 400572

Правильный ответ обводим кружочком. Проверка

Вы слышали что математику называют царицей всех наук

почему так называют?

Люди в жизни где используют + и — многозначных чисел?

Вызвал ли у вас алгоритм + и — многозначных чисел затруднения?

В чем отличие сложения и вычитания трехзначных чисел от многозначных?

д.з с 70 №11 в ученике

98
В
4295
Е
3846
С
20000
Л
34295
Е
45348
Н
500004
Н
923527
А
1309400
Я

1. Укажи правильную запись числа: девять тысяч пятнадцать.

а) 9015
б) 90015
в) 9150
г) 915

2. Какое число следует за числом 24567?

а) 24667
б) 24568
в) 25567
г) 24566

3. Какое число представлено в виде суммы разрядных слагаемых:

40000+5000+ 600+50+4

а) 405654
б) 4565
в) 45654
г) 54654

4. Какая цифра стоит в разряде сотен в записи числа 432567?

а) 4
б) 3
в) 2
г) 5

5. Какое число содержит 572 единицы первого класса и 400 единиц второго класса.

а) 572400
б) 572
в) 400
г) не знаю
д) 400572

1.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам.

2.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам. Чему равна длина окружности Марса?

3.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам. На сколько километров ошиблись древние учёные?

1.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам.

2.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам. Чему равна длина окружности Марса?

3.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам. На сколько километров ошиблись древние учёные?

1.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам.

2.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам. Чему равна длина окружности Марса?

3.Древние учёные в Греции рассчитали длину окружности Земли, которая составила 39 690 километров. Измерения в наше время равно — 40075 километрам. На сколько километров ошиблись древние учёные?

1- а

2 — б

3- в

4- г

5- д

ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

❤️️Ответ к странице 60. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.

Номер 260.

(Устно.) Вычисли наиболее лёгким способом.

Ответ:

2 + 96 + 98 + 904 = (2 + 98) + (96 + 904) = 100 + 1000 = 1100 257 + 18 + 12 + 3 + 40 = (257 + 3) + (18 + 12) + 40 = 260 + 30 + 40 = (260 + 40) + 30 = 300 + 30 = = 330 48 + 530 + 70 + 52 = (48 + 52) + (530 + 70) = 100 + 600 = 700 33 + 34 + 35 + 36 + 37 =(33 + 37) + (34 + 36) + 35 =70 + 70 + 35 = 140 + 35 = 175

Объясни, как выполнено сложение и вычитание.

Ответ:

При записи столбиком сложения и вычитания чисел с большим количеством разрядов пользуются правилом: единицы записываются под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч и так далее.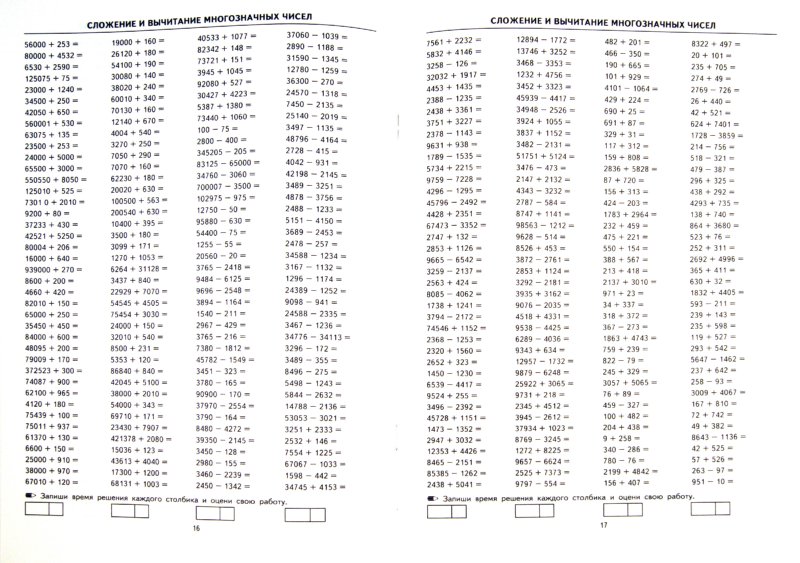
Первый пример:

Записываем разряды под разрядами и приступаем к сложению. Складываем единицы: шесть плюс два будет восемь. Складываем десятки: два плюс девять будет одиннадцать. Пишем единицу, а 1 десяток запоминаем. Складываем сотни: один плюс два будет три, да еще один-четыре. Складываем единицы тысяч: три плюс четыре получится 7. Читаем ответ: семь тысяч четыреста восемнадцать.
Второй пример: Записываем разряды под разрядами. Видим, что данный пример на вычитание. Приступаем к решению. Вычитаем единицы: от шести семь не отнимешь, значит, занимаем десяток. Шестнадцать минус семь будет девять. Вычитаем десятки: было четыре стало три, потому что заняли десяток. Три минус ноль будет три. Вычитаем сотни: от трех четыре не отнимешь, значит, занимаем десяток. Тринадцать минус четыре будет девять. Вычитаем единицы тысяч: было 5, занимали единицу, осталось 4.
От 4 отнять 3 получится 1. Сносим десятки тысяч в ответ. Читаем ответ: двадцать одна тысяча девятьсот тридцать девять.

Номер 261.

Объясни, что означают записи в рамках на полях.

Ответ:

1) b + 0 = b, если к любому числу прибавить 0, то получится это же число. 2) 0 + c = c, если к нулю прибавить любое число, то получится прибавленное число. 3) a – 0 = a, если из любого числа вычесть 0, то получится это же число. 4) k – k = 0, если из любого числа вычесть себя же, то получится 0.

Номер 262.

Вычисли, записывая решение столбиком, и проверь сложение вычитанием, а вычитание сложением.

Ответ:

Номер 263.

В соревнования участвовало 18 семей, состоящих из 3 человек, и 16 семей, состоящих из 4 человек. Сколько это всего человек?

Ответ:


1) 3 ∙ 18 = 54 (чел. ) – в 18 семьях. 2) 4 ∙ 16 = 64 (чел.) – в 16 семьях. 3) 54 + 64 = 118 (чел.) 3 ∙ 18 + 4 ∙ 16 = 118 (чел.) Ответ: 118 человек всего.

Номер 264.

После того как школьникам было выдано 327 книг, в библиотеке осталось на 246 книг меньше, чем было выдано. Сколько всего книг в библиотеке?

Ответ:


1) 327 − 246 = 81 (кн.) – осталось. 2) 327 + 81 = 408 (кн.) Ответ: 408 книг было в библиотеке.

Номер 265.

Составь задачу по выражению: 100 − (68 + 14)

Ответ:

На склад привезли 100 игрушек, из них 14 кукол и 68 мячей, а остальные игрушки были машинки. Сколько было машинок?
Всего – 100 шт. Куклы – 14 шт. Мячи – 68 шт. Машинки – ? шт. 100 − (68 + 14) = 18 (шт.) Ответ: 18 машинок.

Номер 266.

(Устно.)

Ответ:

999 + 1 = 1000 1000 − 1 = 999
10000 − 1 = 9999 9999 + 1 = 10000
50000 − 1 = 49999 80000 − 1 = 79999

Задание внизу страницы

Вычисли.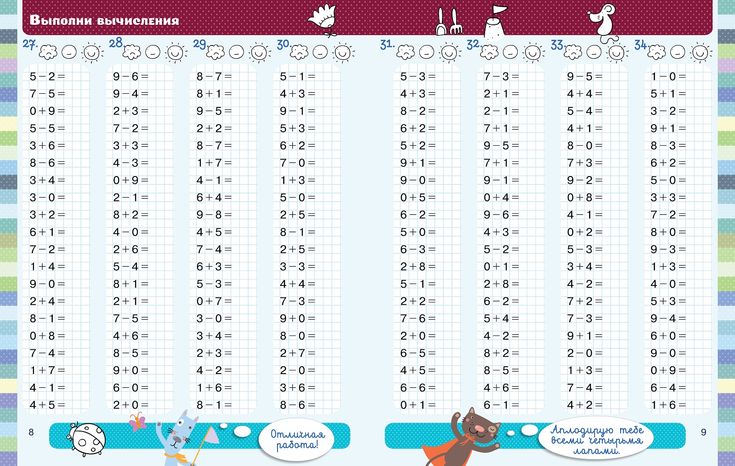

Ответ:

1050 − 50 = 1000 20000 + 800 = 20800 35840 − 840 = 35000

Задание на полях страницы

Ребус.

Ответ:

394 − 285 = 109

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Таблицы сложения многозначных чисел

Сложение многозначных чисел

Сложение двухзначных чисел (без перегруппировки)

Таблицы сложения на этой странице не перегруппированы и не переносятся.
Прибл. уровни: 1-й класс, 2-й класс

Двузначное сложение (с перегруппировкой)

Рабочие листы с двузначным сложением на этой странице требуют, чтобы учащиеся носили их с собой или перегруппировывали. Включает математику на миллиметровой бумаге, Scoot! Игра и рабочие листы с текстовыми задачами.
Прибл. уровни: 1-й класс, 2-й класс

3-значное сложение

Эти печатные рабочие листы и игры имеют задачи на сложение с 3-значным сложением. Включает в себя математические загадки, игру с волшебными цифрами, математические кроссворды и рабочие листы для сложения столбцов.
Прибл. Уровень: 2-й класс, 3-й класс

4-значное сложение

На этой странице представлены ресурсы для обучения сложению с 4-значным сложением. Действия на этой странице включают в себя: упражнения на сложение столбцов, кроссворд на сложение, карточки с заданиями и текстовые задачи.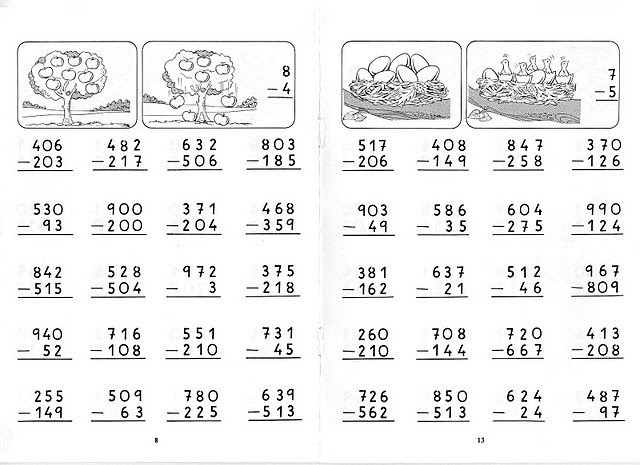
Прибл. уровень: 3-й класс, 4-й класс

5-значное сложение

Используйте эти материалы для печати, чтобы изучать, повторять и практиковать сложение с 5-значными сложениями.
Прибл. уровень: 4-й класс, 5-й класс

Сложение с 3 или более дополнениями

Когда вы распечатаете эти задания, вы заметите, что задачи имеют 3, 4 или 5 дополнений. Включает в себя 1, 2, 3 и 4-значные числа.

Прибавление 10 и числа, кратного 10

На этой странице есть карточки с заданиями и рабочие листы для обучения учащихся прибавлению 10 или числа, кратного 10, к любому двузначному числу.

Сложение десятичных дробей, денег и дробей

Сложение дробей

На этих листах учащиеся будут практиковаться в сложении дробей и смешанных чисел. Включает дроби с одинаковым знаменателем и разными знаменателями.
Прибл. уровни: 3-й, 4-й, 5-й и 6-й классы

Десятичное сложение и вычитание

Найдите суммы и разности для пар десятичных знаков на этих рабочих листах. Эти практические страницы имеют десятичные доли в десятых, сотых и тысячных долях.

Сложение денег

В этих печатных формах есть задачи на сложение денег по горизонтали и вертикали, а также задачи со словами.

Еще Сложение

Сложение и вычитание целых чисел
(Положительные и отрицательные числа)

Практика нахождения сумм и разностей положительных и отрицательных целых чисел.

Свойства сложения

Узнайте о коммутативных и ассоциативных свойствах сложения с этими печатными формами.
Прибл. уровни: 3-й, 4-й, 5-й

Базовое сложение

Базовое сложение (сложение 0-5; суммирует до 10)

Эти базовые задачи на сложение имеют слагаемые до 5 и суммируют до 10. Включает головоломки, рабочие листы, карточные игры, иллюстрированные концептуальные листы , и более. (примеры: 4+1=5, 2+3=5)


Прибл. уровень: детский сад и 1-й класс

Базовое сложение (сложение 0-10; суммирование до 20)

На этой странице есть множество упражнений, которые можно использовать при обучении основам сложения. Включает игру на запоминание, игры в кости, бинго, рабочие листы для упражнений, карточки, упражнения с числовыми линиями и многое другое. Все факты имеют слагаемые от 0 до 10. (примеры: 9+8=17, 8+6=14)
Прибл. уровни: 1-й и 2-й классы

Основы сложения и вычитания (смешанный)

Рабочие листы, которые вы найдете здесь, сочетают в себе основы сложения и вычитания.
Прибл. класс: Детский сад, 1-й класс, 2-й класс

Базовое сложение: Составление 10 (сумма 10)

Эти рабочие листы и задания помогут учащимся находить пары слагаемых с суммой 10.

Базовое сложение: удвоение фактов

Выучить основное сложение удваивает факты . Это задачи на сложение, в которых вы добавляете число к самому себе.
(примеры: 3+3=6, 5+5=10, 7+7=10)

Базовое сложение: удвоение +1 Факты

Рабочие листы на этой странице могут быть использованы для обучения учащихся решению удвоений +1 факты . Это задачи на сложение, в которых учащиеся удваивают число, а затем прибавляют единицу.
(примеры: 2+3=5, 5+6=11, 8+9=17)

Семейства фактов (сложение/вычитание)

В этом разделе есть несколько рабочих листов для обучения семействам фактов. (Также известны как числовые связи или числовые семейства.) Прибл. уровни: 1-й и 2-й классы

Sum Game

На этой странице есть много разных версий STW Addition Sum Game. В этой игре учащиеся по очереди обводят пары чисел, которые в сумме составляют заданную сумму.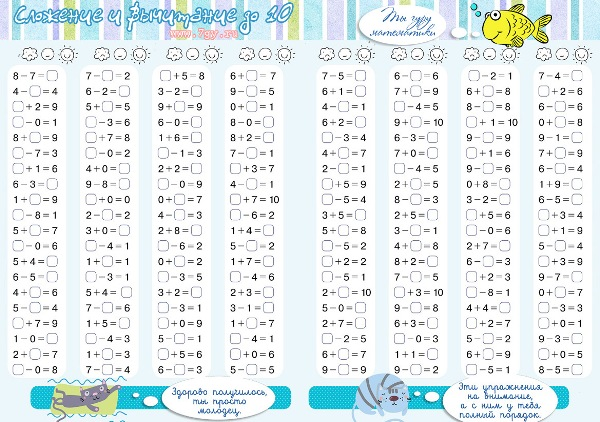 Например, они могут искать пары чисел, сумма которых составляет 17.
Прибл. уровень: 1 класс, 2 класс, 3 класс

Головоломки с квадратами

Смогут ли ваши ученики решить эти сложные логические головоломки? Есть три уровня: базовый, средний и продвинутый.

См. также:

Рабочие листы математических загадок

На нашей странице математических загадок также есть много дополнительных рабочих листов. На этих листах учащиеся могут расшифровать ответ на забавную загадку, решая арифметические задачи.

Math Mystery Pictures

В этом разделе сайта есть ссылки на множество базовых таблиц сложения однозначных чисел. Учащиеся решают задачи на сложение, а затем раскрашивают загадочную картинку в соответствии с цветовым ключом внизу страницы.

Проблемы с несколькими шаговыми словами

Учащиеся используют сложение, вычитание, умножение и/или деление для решения этих многоэтапных математических задач.

Использование числовых рядов

Научитесь складывать и вычитать с помощью числовых рядов.

Какие существуют типы стратегий и методов сложения? (Примеры)

• Введение в сложение
• Стратегии операции сложения
• Сложение с использованием открытой числовой строки
• Сложение с использованием частичной суммы
• Сложение с использованием перегруппировки
• Сложение с использованием метода компенсации
• Сложение с использованием блочных моделей
• Решаемые примеры
• Часто задаваемые вопросы

Введение в метод сложения

. Когда вы складываете два числа вместе, вы считаете их одним большим числом. В реальной жизни сложение происходит часто.

Что, если бы, например, было еще три яблока?

Как видите, если вы начнете с двух яблок и добавите еще три, у вас будет пять яблок. Вы можете выразить это так:

Сложение можно представить в виде уравнения: 2 + 3 = 5. Его можно записать как два плюс три равно пяти. Математическое уравнение — это математическое предложение. Вместо слов используются цифры и символы. При записи уравнений сложения мы используем два символа: « + » и « = ». Знак плюс (+) обозначает добавление двух элементов. Вот почему мы поместили его в середину яблок. Мы начали с двух яблок, а затем добавили еще три.

Знак равенства (=) является другим символом в уравнении. В уравнении знак равенства указывает на то, что два или более элемента равны или эквивалентны. Эквивалентные вещи не всегда выглядят или звучат одинаково, но означают одно и то же. Знак равенства в математике указывает на то, что два числа или выражения означают одно и то же, несмотря на их внешний вид.

Любая операция сложения может быть выражена письменно. Допустим, вы пригласили 12 друзей на празднование дня рождения. Вы приглашаете еще четырех человек в последнюю минуту. Вы можете написать что-то вроде этого, чтобы получить общее количество гостей, приходящих в ваш дом:

Это выражение просто еще один способ продемонстрировать ситуацию: вечеринка по случаю дня рождения будет проводиться для 12 друзей плюс еще четверо.

Стратегии операции сложения

Определенные стратегии используются для фиксированного выполнения операций. Используя эти стратегии, мы можем легко и эффективно выполнять математические операции. Существует пять основных стратегий сложения. Давайте рассмотрим эти стратегии:

1. Сложение с использованием открытой числовой строки

2. Addition using partial sum

3. Addition using regrouping

4. Addition using the compensation method

5. Addition using models

Addition using an open number line

На открытой числовой строке нет цифр или маркировки. Открытые числовые строки удобны для работы с разрядными значениями при добавлении чисел.

 

Давайте рассмотрим несколько способов применения этой стратегии.

Рассмотрим 17 + 38 для следующих случаев:

Например,

• Линия 1:

9000 2

9000 2

, за которыми следуют единицы (7 + 8). Числовой ряд начинается с 10 (десятки от первого числа) и продолжается до 40 путем добавления трех десятков от второго числа. Затем мы сложили 7 + 8, чтобы получить 15. Затем два результата суммировались, чтобы получить 55.

 

• Числовая строка 2:  

 

Мы должны оставить 17 в целом и добавить три десятка из второго числа. Затем 8 единиц были разбиты на 3 + 5. Затем из 3 единиц было получено 47 + 3 = 50. Наконец, мы добавили последние пять, чтобы получить 50 + 5 = 55. :  

 

Мы знаем, что 38 можно разбить на 30 + 8. Кроме того, 8 можно разбить на 3 + 5, так что 38, наконец, равно 30 + 3 + 5. Теперь мы взяли три единицы из 8 в 38. Затем к 17 прибавляется три, чтобы получить 20 (17 + 3 = 20). Затем мы взяли три десятка из 30, чтобы получить 50. Наконец, мы добавили оставшиеся 5 к общему количеству 55.

Сложение с использованием частичной суммы

По сравнению со всеми другими методами сложения метод частичной суммы является самым простым.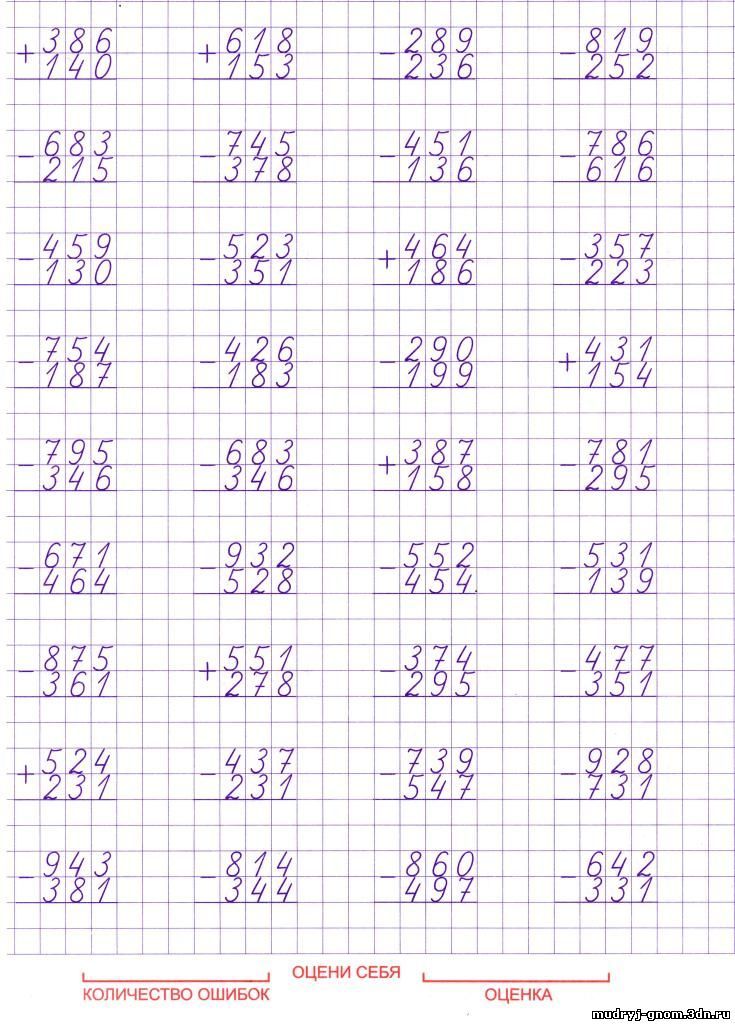 Метод частичной суммы, как следует из названия, одновременно вычисляет частичные суммы для разных столбцов разряда. Затем мы складываем все частичные суммы, чтобы найти общую сумму.

 

Частично добавленные суммы можно добавлять в любом порядке, но наиболее распространенный способ — слева направо. Поскольку мы читаем слева направо, такой порядок кажется естественным, и он также отдает приоритет наиболее важному разряду, с которого следует начинать в сложениях, например, тысячи перед сотнями, сотни перед десятками и так далее.

 

Для ментальной арифметики можно легко адаптировать метод сложения частичных сумм.

 

Например, сложение 7701 и 243.

 

 

Сложение с использованием перегруппировки

При сложении с перегруппировкой может быть использована техника сложения двух или более чисел любого размера, сложение двух или более чисел. Он используется с методом сложения столбцов, который упорядочивает суммы по вертикали и складывает числа по одному. Перегруппировку иногда называют «переносом». Когда вы складываете все числа в столбце вместе, и в сумме получается десять или более, число в разряде десятков переносится в следующий столбец разряда.

 

Например, если столбец единиц содержит 2 и 9, общее количество будет 11. Вы должны поместить 1 в столбец единиц, а затем перенести 1 в столбец десятков.

 

Когда сумма значений в одном столбце разряда превышает девять, применяется перегруппировка.

 

Нет необходимости использовать метод перегруппировки, если сумма значений в каждом столбце разряда равна девяти или меньше.

 

Например, рассмотрим уравнение сложения 28 + 14,9.0005

 

Как и в случае любого сложения с помощью метода столбца, мы можем выстроить эти числа вертикально в столбцах их позиционных значений.

 

 

 

Затем числа в столбце единиц можно добавить. Это крайний правый столбец, который содержит 8 и 4. Эти два числа в сумме дают 12. Мы напишем 2 в столбце единиц под чертой и перенесем 1 в столбец десятков, написав его над цифрой. два других числа, следуя методу перегруппировки. После этого этапа у вас должно получиться что-то похожее на это:

 

 

 

После этого вы можете сложить вместе цифры из столбца десятков – 2 и 1 из исходных чисел, а также 1, которую вы только что перенесли. Тогда вы получите 4 как ответ из суммы 1 + 2 + 1. Это должно быть записано в колонке десятков вашего ответа.

 

 

Так работает метод перегруппировки. Ответ на этот вопрос: 42.

Дополнение компенсационным методом

Округление числа (для упрощения сложения) и последующее вычитание лишнего числа после завершения вычисления называется «компенсацией».

Например,

Добавление 29 и 16.

Написание этого в качестве выражения, 29 + 16

Проще разрешить 30 + 16 = 46.

. что превратило 29 в 30, чтобы получить 45.

 

Например,

 

Складываем 695 и 116. 

В виде выражения имеем 695 + 116

. получите 811.

Полезные ресурсы для детей

Повторите математические формулы и важные понятия, используя наши рабочие листы по математике! Эти рабочие листы помогают учащимся развивать математические навыки в увлекательной и интересной форме. Нажмите на ссылку ниже, чтобы получить все простые для понимания математические калькуляторы и рабочие листы.

Сложение с использованием блочных моделей

Блоки с основанием 10 — это визуальные представления, которые помогают нам понять систему с основанием 10, представляя разрядное значение чисел. Мы используем эти блоки для визуализации процесса перегруппировки, чтобы мы могли полностью понять распространенные способы сложения чисел. Этот метод также помогает нам выявлять ошибки в дополнение.

 

Давайте разберемся в этом, используя модели.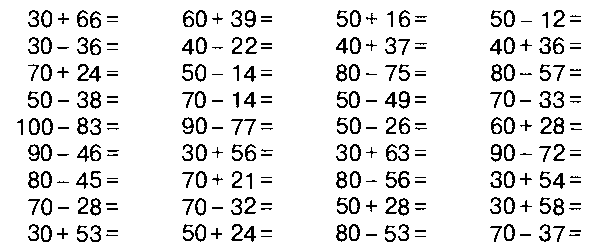 Каждый куб является единицей. Этот стек содержит десять единиц.

 

 

Предположим, что всего имеется десять стеков.

 

 

Десять стопок по десять штук в каждой равно ста.

1 сотня = 10 десятков = 100.

. , группа детей бросает монету. У них 13 орлов и 32 решки. Сколько раз они подбросили монету?

 

Решение: Добавьте 13 и 32, чтобы узнать, сколько раз была подброшена монета. Используйте открытую числовую строку для работы над сложением чисел 13 и 32. Когда числа в операции сложения более простые, мы можем использовать метод числовой строки для сложения.

 

 

Сначала прибавлялись десятки (10 + 30), а затем единицы (3 + 2). Числовая строка начинается с 10 (десятки от первого числа) и продолжается до 40, добавляя три десятка от второго числа. Затем мы добавили 3 + 2, чтобы получить 5, а затем добавили к 40, чтобы получить 45.

 

Следовательно, они подбросили монету 45 раз.

 

2) В одном озере 1525 лягушек, а в другом озере 251. Сколько всего лягушек?

 

Решение: Добавление 1525 и 251 лягушек, чтобы найти всех лягушек. Для этого вопроса можно использовать метод частичной суммы, поскольку он упрощает расчеты за счет использования частичных сумм по одному столбцу разряда за раз. Затем он складывает все частичные суммы, чтобы найти общую сумму. Когда нам нужно разделить большие числа, мы должны использовать метод частичной суммы.

 

 

Следовательно, общее количество лягушек в обоих озерах равно 1776.

 

деревьев, которые он посадил?

 

Решение: Добавьте 16 и 18, чтобы найти общее количество деревьев, посаженных Джозефом. Когда сумма значений в одном столбце разряда превышает девять, используется перегруппировка.

 

Здесь сумма значений в одном разряде = 6 + 8 = 14, что превышает девять. Поэтому используется метод перегруппировки.

 

Как и в случае любой операции сложения, включающей метод столбцов, мы можем выстроить эти числа вертикально в соответствии со столбцами их позиционных значений.

 

 

 

Затем числа в столбце единиц можно добавить. Это крайний правый столбец, который содержит 6 и 8. Эти два числа в сумме дают 14. Мы напишем 4 в столбце единиц под чертой и перенесем 1 в столбец десятков, написав его над цифрой. два других числа, следуя методу перегруппировки. После этого этапа у вас должно получиться что-то похожее на это:

 

 

Теперь вы можете сложить вместе цифры из столбца десятков – 1 и 1 из исходных чисел, а также 1, которую вы только что перенесли. Вы получите 3 как ответ из суммы 1 + 1 + 1. Это должно быть записано в колонке десятков вашего ответа.

 

 

 

Таким образом, всего Иосиф посадил 34 дерева.

..»> Учебная программа по математике для всех классов

Наши онлайн-уроки по математике специально разработаны с учетом возраста и академического уровня вашего ребенка. Нажмите на ссылки ниже, чтобы узнать больше о наших онлайн-классах по математике для 1–8 классов.

Часто задаваемые вопросы о методах и стратегиях сложения

Какие стратегии можно использовать для сложения двух чисел?

• Счет от однозначного числа
• Техника прыжков
• Счет до десяти
• Сколько длятся десятки? (разбить большие числа на десятки и единицы, добавить единицы, затем добавить десятки)
• Поставьте цель десять (когда число близко к десяти, мы можем «позаимствовать» у другого числа, чтобы оно достигло десяти)
• Стратегия компенсации
• Когда числа совпадают, удвойте их.
• Если числа близки, удвойте их, а затем зафиксируйте.

 

Как компенсация упрощает сложение?

С некоторыми числами работать легче, чем с другими.