«Решение уравнений вида х + 15 = 68 : 2». 4-й класс
Тип урока: урок изучения нового материала.
Основные понятия: уравнение, алгоритм, компоненты действия, результат действия, выражения.
Ресурсы.
Информационный материал: учебник “Математика”, ч. 1; памятка “Алгоритм решения уравнений”; раздаточный материал — тесты.
Демонстрационный материал: карточки уравнений; карточки с геометрическим материалом;
Интерактивный материал: компьютер, мультимедиа проектор, презентация Power Point.
Ход урока
1. Организационный этап. (Мотивация к учебной деятельности)
Я рада видеть каждого из вас!
И пусть нам холодом зима в окошко дышит.
Нам будет здесь уютно, ведь наш класс
Друг друга любит, чувствует и слышит!
Ученик:
Мы рады приветствовать вас в нашем классе.
Возможно, есть классы и лучше и краше.
Но пусть в нашем классе вам будет светло.
Пусть будет уютно и очень легко!
Учитель:
Пусть сегодня для нас всех,
На уроке сопутствует успех!
2. Актуализация опорных знаний.
— Ребята, сегодня я приглашаю Вас в путешествие, но не обычное, а математическое — путешествие за новыми знаниями. Нас ждут в пути испытания, но я верю, что вы их легко преодолеете. Готовы? Тогда вперёд! И пусть девизом нашего урока станут слова “Думаю, знаю, могу!”.
Не бойтесь ошибаться. Мы учимся, и каждый из вас имеет право на ошибку.
Итак, испытание 1: “Я это знаю”.
1) К нам в гости пожаловал Мистер Х.
— Из каких геометрических фигур он составлен?
— Каких геометрических фигур взято больше?
— Сколько всего их потребовалось?
Число геометрических фигур увеличьте в 100 раз и
полученный результат уменьшите на 110.
Какое число получилось? (890)
Что вы можете о нём рассказать?
Чистописание.
Откройте тетради, запишите число.
Это чистописание сегодняшнего урока.
2) Запишите только ответы.
— Первое слагаемое 380, второе 120. Чему равна сумма?
— Я задумала число. Когда я к нему прибавила 250, у меня получилось число 1000. Какое число я задумала?
— Первое слагаемое 900. Сумма равна 1200. Чему равно 2-е слагаемое?
— Каковы ваши ответы? Проверяем. (500, 750, 300)
— Что общего у этих чисел?
— Чем они различаются?
— Какие компоненты арифметических действий вы находили? Каким правилом пользовались?
3) На доске записаны математические выражения.
— На какие группы их можно разбить? (Числовые выражения, буквенные выражения, уравнения)
| а + c | 7 • 3 — 10 |
| 3 • 100 | x + 15 = 64 : 2 |
| х + 10 = 135 | k • d |
— Прочитайте только уравнения и докажите, что
эти записи являются уравнением.
— Что такое уравнение? (Равенство с переменой, значение которой надо найти)
— Что значит “решить уравнение”? (Найти значение этой переменной)
3. Постановка проблемы, определение темы урока, целеполагание
— Следующее наше испытание “Я это умею!”.
Решим уравнение х + 10 = 135.
Вспомним алгоритм решения простых уравнений.
Решим уравнение с объяснением. (Ученик отвечает)
— Можете ли мне ответит быстро, чему равно значение х в уравнении х + 15 = 64 : 2?
— Почему возникли затруднения? (Мы не решали уравнения такого вида)
— Какова же тема нашего урока математики?
— Какие задачи мы поставим перед собой? (Обсудите это в парах)
4.
Физкультминутка.
5. Совместное “открытие” новых знаний.
— Итак, друзья мои, у нас уравнение х + 15 = 64 : 2.
— Чем оно отличается от тех, которые мы умеем решать?
— Какие варианты решения вы предлагаете? (Сначала найти значение выражения справа. Получается простое уравнение, которое мы умеем решать. Дальше рассуждаем по алгоритму).
(Решение с объяснением у доски)
6. Закрепление новых знаний
а) Работа по учебнику.
Стр.64. под красной чертой. Работаем в парах.
— Что главное при работе а парах? (Уметь слушать и помочь своему товарищу.)
— Объясните друг другу, как решали уравнения.
— Объясните решение уравнения 24 + х = 79 — 30.
б) Самостоятельная работа по решению уравнения нового вида.
Стр. 64, № 310 (уравнение 2).
— Какие шаги вы сделали, чтобы найти корень уравнения? (Алгоритм)
в) Введение новых знаний в решение задачи.
Стр.64, № 311. (Решение с объяснением)
— Ну, что же, ребята, наше путешествие в Страну новых знаний подходит к концу. Осталось последнее испытание “Я это могу!” У вас на парте лежат тесты. Выполнив их, мы сможем подвести итог нашего урока.
Тест
1. Выбери правильный ответ.
а) Уравнение – это пример, в котором пропущено число.
б) Уравнение – это выражение с неизвестным компонентом.
в) Уравнение – это равенство с переменной, значение которой нужно найти.
2. Реши уравнение устно и выбери, чему равен корень этого уравнения.
1 вариант х + 5 = 100 : 10
2 вариант х + 4 = 18 : 2
а) 5; б) 2; в) 8.
— Проверим.
7. Итог урока. Рефлексия.
Итак, друзья, преодолев немало испытаний,
Вы оказались у двери в мир Знаний.
“Входите в неё!” — я вам говорю,
За труд на уроке всех вас хвалю.
Оценки за урок.
— Какую главную задачу мы перед собой ставили?
— Удалось ли нам её выполнить?
Оцените свою работу на уроке.
— Вам было всё понятно? Вы научились решать уравнения и можете помочь другим?
— Вы считаете, что научились решать уравнения, но ещё всё-таки вам нужна помощь?
— Вы считаете, что на уроке было трудно?
И последнее: Прочитайте слово на экране. Спасибо!
Его можно произносить холодно, тепло, резко, ласково.
Но волшебным оно становится только в том случае, если в нём звучат нотки искренней благодарности.
Спасибо! Пусть это слово звучит сегодня и каждый день. И пусть на душе у вас будет светло и радостно.
Будет усилена борьба с диверсионной деятельностью
Депутаты Государственной Думы на пленарном заседании приняли во втором чтении блок законопроектов, направленных на защиту нашей страны и граждан от террористической и диверсионной угроз.
Их авторами стали Председатель ГД Вячеслав Володин Володин
Вячеслав Викторович
Председатель Государственной Думы Федерального Собрания Российской Федерации восьмого созыва.
Избран по избирательному округу № 163 (Саратовский — Саратовская область)
, все депутаты от фракции «Единая Россия», а также руководители других фракций.
«Учитывая, что Российская Федерация проводит специальную военную операцию и одновременно принимает беженцев, остается открытой для въезда и выезда иностранных граждан, принятие законопроектов — принципиально важный шаг, необходимый для защиты нашей страны. Это общее мнение всех фракций Государственной Думы. Авторами инициатив выступили более 380 депутатов, — говорил ранее Вячеслав Володин. — Наказание для диверсантов будет максимально жестким».
Поправки предлагается внести в Уголовный кодекс РФ, установив уголовную ответственность за содействие диверсионной деятельности, вовлечение, призывы и склонение к финансированию диверсионных актов.
Также предполагается сделать уголовно наказуемым обучение диверсионным актам и создание всякого рода преступных сообществ с целью совершения диверсий.
Так, согласно законопроекту за склонение, вербовку или иное вовлечение в диверсионную деятельность, а равно финансирование диверсии будет грозить лишение свободы вплоть до пожизненного. Такое же наказание в случае окончательного принятия законопроекта предусмотрено за прохождение обучения для совершения диверсии.
Создание диверсионного сообщества также будет наказываться пожизненным заключением. За участие в таком сообществе будет грозить до 10 лет лишения свободы, а за пособничество в совершении диверсии — от 10 до 20 лет.
Вносятся изменения и в другие законодательные акты, в частности в закон «Об информации, информационных технологиях и о защите информации». Это позволит оперативно блокировать материалы, содержащие инструкции о способах и методах незаконного изготовления боеприпасов, — эта информация будет признана запрещенной.
По действующему законодательству уже запрещено распространение информации о способах и методах самодельного изготовления взрывчатых веществ и взрывных устройств, а также об изготовлении, о переделке, ремонте огнестрельного оружия и его основных частей.
Кроме того, приняты во втором чтении поправки в закон о противодействии легализации средств, добытых преступным путем, а также используемых для финансирования терроризма: счета тех, кто финансирует диверсионную деятельность, будут блокироваться по аналогии с мерами, которые сейчас предусмотрены в отношении финансирующих терроризм.
Упрощение: x-8/5=2/4 Tiger Algebra Solver
Преобразование:
Преобразование уравнения путем вычитания того, что находится справа от знака равенства из обеих частей уравнения:
x-8/5- (2/4)=0
Пошаговое решение:
Шаг 1 :
1
Упростить —
2
Уравнение в конце шага 1 :
8 1
(х - -) - - = 0
5 2
Шаг 2 :
8
Упростить —
5
Уравнение в конце шага 2 :
8 1
(х - -) - - = 0
5 2
Шаг 3
х = — = —————
1 5
Эквивалентная дробь: Сгенерированная таким образом дробь выглядит иначе, но имеет то же значение, что и целое число
Общий знаменатель: Эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель знаменатель
Соедините числители, подставьте сумму или разность к общему знаменателю, затем приведите к наименьшему числу, если возможно:
x • 5 - (8) 5x - 8
знак равно
5 5
Уравнение в конце шага 3 :
(5x - 8) 1
———————— - — = 0
5 2
Шаг 4:
Расчет наименьшего распространенного множественного:
4.
1. Наименование наименьшего количества множественных
Левый знаменатель: 5
Правый знаменатель: 2
| Prime Factor | Left Denominator | Right Denominator | L.C.M = Max {Left,Right} |
|---|---|---|---|
| 5 | 1 | 0 | 1 |
| 2 | 0 | 1 | 1 |
| Продукт всех Prime Factors | 5 | 2 | 10 |
Наименее распространенное множество:
10
0014 Расчет мультипликаторов:
4.2 Расчет мультипликаторов для двух фракций
Обозначайте наименьшее распространенное множественное множество по L.C.M
Обозначите левый мультипликатор левым_м
обозначает правое множитель на правой right_m
.
Left_M = L.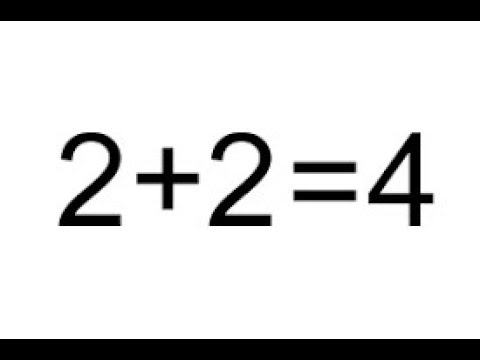
C.M / L_Deno = 2
Right_M = L.C.M / R_Deno = 5
Составление эквивалентных дробей:
4.3 Преобразуйте две дроби в эквивалентные дроби0005
Две дроби называются эквивалентными, если они имеют одинаковое числовое значение.
Например: 1/2 и 2/4 эквивалентны, y/(y+1) 2 и (y 2 +y)/(y+1) 3 также эквивалентны.
Чтобы рассчитать эквивалентную дробь, умножьте числитель каждой дроби на соответствующий множитель.
Л. Мульти. • L. Num. (5x-8) • 2
знак равно
LCM 10
Р. Мульт. • R.Число. 5
знак равно
LCM 10
Сложение дробей, имеющих общий знаменатель:
4.4 Сложение двух эквивалентных дробей
(5x-8) • 2 - (5) 10x - 21
знак равно
10 10
Уравнение в конце шага 4 :
10x - 21
———————— = 0
10
Шаг 5 :
Когда дробь равна нулю :
5.1 Когда дробь равна нулю ...
Если дробь равна нулю, ее числитель, часть, которая находится над дробной чертой, должна равняться нулю.
Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
Вот как:
10x-21
—————— • 10 = 0 • 10
10
Теперь в левой части 10 уравновешивает знаменатель, а в правой части ноль, умноженный на что-либо, по-прежнему равен нулю.
Теперь уравнение принимает форму:
10x-21 = 0
Решение уравнения с одной переменной :
5.2 Решение : 10x-21 = 0
Добавить 21 к обеим сторонам уравнения:
10x = 21
Разделите обе стороны уравнения на 10:
x = 21/10 = 2,100
Было обнаружено одно решение:
x = 21/10 = 2,1008
.
2 + 2 не всегда равно 4
Викисклад 2 + 2 = ? кажется, одна из самых простых задач в математике, и это, вероятно, одна из первых, с которыми вы когда-либо сталкивались.
Если у Кати 2 яблока и Мэтт дает ей еще 2 яблока, то у нее 4 яблока. Очевидно.
Но что, если мы скажем вам, что 2 + 2 = ? ставит в тупик даже самых умных математиков, потому что оно не обязательно должно равняться 4?
Вам, наверное, интересно, как это возможно.
Но сначала пример
Поговорим о часах.
Я прихожу на работу в 7 часов утра. Вот так выглядят мои часы. Впервые в этот день меньшая стрелка часов достигает отметки 7 на циферблате.
SPCCПозже днем я ухожу с работы в 5 часов дня. Когда я смотрю на свое запястье, мои часы выглядят так. Это второй раз, когда меньшая стрелка часов достигает отметки 5 на циферблате часов. Первый раз был в 5 утра.
SPCC Другими словами, меньшая стрелка моих часов прошла все 12 цифр на циферблате, а затем снова начала с 1.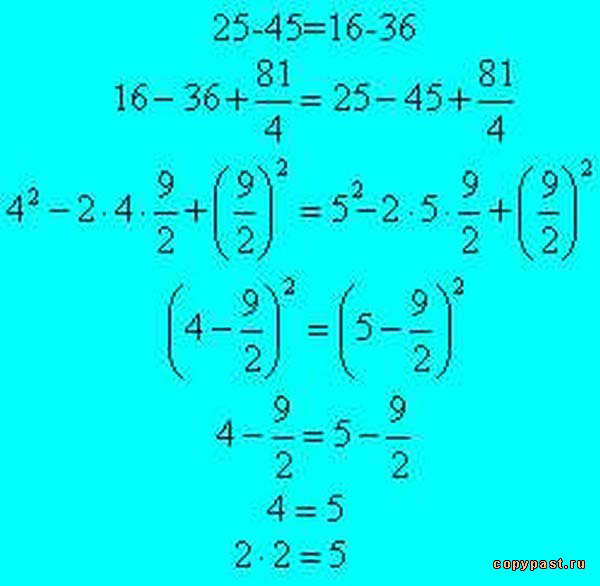
Мы можем представить 13:00 как 13 часов; 14:00 как 14 часов; и 5 вечера как 17 часов.
Однако большинство людей не говорят: «Я закончу работу в 17». Обычно они говорят: «Я закончу в 5». Если вы сделаете это, вы на самом деле решаете сложную математическую задачу, даже не осознавая этого.
Часы работают в определенной системе
Происходит следующее: стрелки часов работают в системе (циферблате), которая имеет 12 чисел, но стрелки часов пытаются представить систему, которая имеет более 12 чисел ( в этом случае система представляет собой сутки, в которых 24 часа).
Мы собираемся классифицировать систему часов по модулю 12, что означает, что 12 — это максимальное число, которое мы можем иметь на часах, состоящее из чисел 1, 2, 3, 4… вплоть до 12. (Не t псих! Модуль — это просто причудливый математический термин для математики, которую мы делаем).
В результате, чтобы понять, как 17 -й -й час дня представлен на часах, нужно сделать 17 (число вне модуля 12) минус 12 (максимальное число по модулю 12), что равно 5 ( которое является числом по модулю 12 для представления числа вне по модулю 12).
Другими словами, в системе часов мы можем сказать, что 12 + 5 = 5, потому что 5 представляет 17.
Еще более странно, даже если вы думаете, что 13 + 4 = 17, в этой системе по модулю 12, 14 +4 = 6, потому что 18:00 означает «18 часов».
Теперь вернемся к 2+2
Используя то, что мы здесь узнали, давайте вернемся к 2 + 2 = ?.
Хотите верьте, хотите нет, но вы действительно можете создать модульную систему с любыми числами. Его не нужно ограничивать модулем 12, как в случае с часами с числами от 1 до 12.
Теперь наша новая система будет иметь модуль 3 с числами 0, 1, 2. Это немного отличается от смотреть, потому что часы не имеют 0. Давайте быстро освежим, что это значит.
Модуль 3 с числами 0, 1, 2 означает, что после того, как мы достигнем третьего числа в нашем наборе чисел, мы снова начнем считать с первого числа. В этом случае, после того, как мы достигнем 2, мы снова начнем с 0. Это точно так же, как с часами, когда после того, как мы достигли 12, мы снова начали с 1.