4 умножить на 4 корня из 2: 2 корень из 2 умножить на 4

2

2 целых умножить на 3 10. Извлечение корня из числа

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x 2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1 / x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления.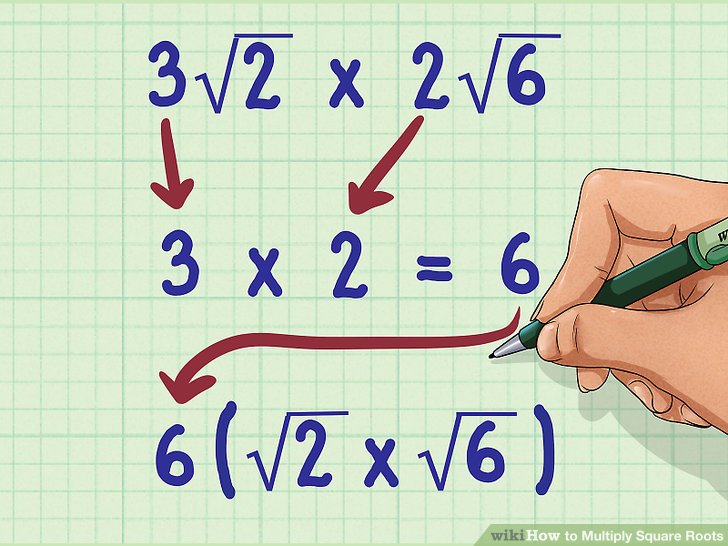 Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Возведение в квадрат целого числа { (3) 2 = 9 }

Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }

Перевод в десятичные дроби.

Вычисление процентов от числа

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Таблица умножения — базовое понятие в математике, с которым мы знакомимся еще в начальной школе и которое потом используем всю жизнь вне зависимости от профессии. Вот только дети не спешат заучивать бесконечные столбики наизусть, особенно если задание пришлось на каникулы.

сайт даст советы, как легко выучить таблицу вместе с детьми и сделать этот процесс увлекательным.

Таблица Пифагора

Несмотря на то что задача — выучить, то есть заучить, таблицу наизусть, прежде всего важно понять суть самого действия. Для этого можно заменить умножение сложением: одинаковые числа складываются столько раз, на сколько мы умножаем. Например, 6×8 — это сложить 8 раз по 6.

Выделяем цветом одинаковые значения

Отличным помощником для изучения умножения станет таблица Пифагора, которая также демонстрирует некоторые закономерности. Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.

Начинать изучение таблицы Пифагора лучше с самых простых и понятных частей: умножения на 1, 2, 5 и 10. При умножении на единицу число остается неизменным, а умножение на 2 дает нам удвоенное значение. Все ответы умножения на 5 оканчиваются либо на 0, либо на 5. А вот умножив на 10, в ответе мы получим двузначное число из цифры, которую умножали, и нуля.

Таблица для закрепления результата

Для закрепления результатов нарисуйте с ребенком пустую таблицу Пифагора и предложите ему заполнить клеточки правильными ответами. Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строчку и крайний левый столбик числами от 1 до 9, пропустив первую клетку.

Конечно, все дети индивидуальны и универсального рецепта не существует. Главная задача родителя — найти подход и поддержать свое чадо, ведь все мы когда-то начинали с таких одновременно простых и сложных шагов.

С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!

Учить таблицу умножения — игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Смотрите ниже шпаргалки в полной форме.

Умножение прямо на сайте (онлайн)

*

Таблица умножения (числа от 1 до 20)

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

мнимых и комплексных чисел

мнимых и комплексных чисел

---

Мнимые числа В конце концов, вы столкнетесь с ситуацией, когда вам придется иметь дело с квадратными корни отрицательных чисел. Как это может быть сделано ? В конце концов, положительное число в квадрате или отрицательное число в квадрате всегда будет равняться положительному числу. Математики выделили особое число i, равное квадратному корню из минус 1. Отсюда следует, что i 2 = -1. Чтобы определить квадратный корень из отрицательного числа (например, -16), возьмите квадратный корень из абсолютного значения числа (квадратный корень из 16 = 4), а затем умножить его на ‘я’. Итак, квадратный корень из -16 равен 4i. В качестве двойной проверки мы можем возвести в квадрат 4i (4*4 = 16 и i*i =-1), что дает -16. Все отрицательные квадратные корни вызываются «мнимые числа» (теперь вы знаете, откуда взялась эта буква «i»). Комплексные числа Когда число имеет форму a + bi (действительное число плюс мнимое число), оно называется «комплексное число». Как комплексные числа «возникают» в математике? Хорошим примером будет корни квадратного уравнения x 2 -6x + 25 = 0, где 2 корня равны 3 + 4i и 3 — 4и. Можем ли мы быть уверены, что это корни уравнения? В качестве перепроверки, используя эти корни, мы можем «перестроить» исходное уравнение с помощью (X — 3 -4i) * (X — 3 + 4i) = X 2 -3x +4Xi -3X +9 -12i -4Xi +12i -(4i) 2 Это сводится к: X 2 -3x -3X +9 -(16)*i 2 Так как i 2 = -1, то -(16)*i 2 становится -(-16) = 16 и так: Х 2 -6Х +25 =0 Умножение комплексных чисел Сложение и вычитание комплексных чисел в значительной степени следуют правилам базовой арифметики и так что мы не будем обсуждать это. Умножение начинает становиться немного сложнее. Учтите: (5 + 6i) * (7 + 8i) Это равно 35 + 40i + 42i + 48i 2 Как мы видели выше, i 2 = -1, поэтому 48i 2 = -48 Итак, ответ = -13 + 82i Комплексный номер отдела Вы задавались вопросом — деление сложнее, чем умножение? Уверенный. Сначала мы должны определить новый термин — , сопряженный , в силу чего сопряженный а + би = а-би. Пример — сопряженным (3 + 4i) является (3 — 4i). Главный принцип, который следует помнить при делении комплексных чисел, заключается в том, что умножаем «верх» и «низ» дроби на сопряженное знаменателю . Время для примера: разделим (9+3i) на (7+5i) (9+3i) ————— (7 + 5i) Знаменатель равен (7 + 5i), а его сопряженное число равно (7-5i) . Умножение верхнего и нижнего на сопряженное: ((9 + 3i)* (7 — 5i)) ————————— ((7 + 5i) * (7 — 5i)) Что равно (78 — 24 i) ————— 74 Что равно 78                   24i ——   минус —— 74                   74 9 0004 Что равно Ответ = 1. 054054054054054 & -0.32432432432432434 i Квадратный корень из комплексного числа Теперь переходим к еще большей сложности. Пришло время определить еще один термин — модуль , где модуль комплексного числа a + bi равен квадратному корню из ( 2 + б 2 ). Модуль комплексного числа обычно обозначается буквой «r», поэтому: r = квадратный корень (a 2 + b 2 ) Далее мы определим эти 2 величины: y = Квадратный корень ((r-a)/2) x = b/2y Наконец, 2 квадратных корня комплексного числа: корень 1 = x + yi root 2 = -x — yi Пример должен сделать эту процедуру более понятной. Найдите квадратный корень из 12 + 16i r = Квадратный корень (12 2 + 16 2 ) r = квадратный корень (144 + 256) = 20 y = квадратный корень ((20-12)/2) = 2 x = 16/(2*2) = 4 корень 1 = 4 + 2i корень 2 = -4 — 2i Даже если у вас есть калькулятор, который может сделать эти расчеты для Вы, теперь вы знаете процедуры для арифметики комплексных чисел. Вернуться к калькулятору

---

Вернуться на главную страницу

Авторское право © 1999 — 1728 программных систем

Рационализация знаменателя с более высокими корнями — Концепция

Когда знаменатель имеет более высокий корень, умножение на подкоренное не удаляет корень. Вместо этого, чтобы рационализировать знаменатель , мы умножаем на число, которое даст новый член, который может исходить из корня. Например, умножьте кубический корень на число, которое даст кубическое число, такое как 8, 27 или 64.

рационализация знаменателя более высокий корень

Рационализация знаменателя — это, по сути, способ сказать, что нужно извлечь квадратный корень из нижней части. Хорошо. Мы можем спросить, почему он внизу. Не совсем уверен, почему, но по какой-то причине мы не можем, и когда мы это делаем, нам нужно умножить на что-то, чтобы избавиться от квадратного корня.
Итак, мы собираемся сделать пример, будем надеяться, что вы помните, как это сделать. И это будет 4 больше квадратного корня из 8, хорошо? Мы могли бы умножить его на квадратный корень из 8 на квадратный корень из 8, тогда квадратный корень из 8 отменяется, оставляя нас с 8. Но я хочу, чтобы вы привыкли делать это искать, есть ли способ что мы можем сначала упростить знаменатель. Хорошо? Под этим я подразумеваю, что нужно сделать так, чтобы у нас был меньший квадратный корень, чем тот, с которым мы имеем дело. Квадратный корень из 8 — это то же самое, что квадратный корень из 4, умноженный на квадратный корень из 2, который всего лишь умножает на 2 корень из 2. Итак, это выражение — то же самое, что 4, 2, корень из 2. Хорошо? Так что упростите это, и теперь нас интересует только квадратный корень из 2, то есть в знаменателе. Люди часто хотят умножить на весь знаменатель. Не надо, не надо этого делать. Корень 2 — единственное, что создает проблему, поэтому вы можете оставить 2 прямо там, как есть. Хорошо?
Таким образом, чтобы рационализировать знаменатель, умножьте корень 2 на корень 2. Наш числитель станет 4, корень 2, наша 2 все еще там, и тогда у нас есть корень 2, умноженный на корень 2, что равно 2. Вы можете упростить это до 4 на 2. умножить на 2, они все отменяются, оставляя нас с квадратным корнем из 2, хорошо. Так что, надеюсь, это не слишком ново для вас.
Сейчас я хочу поговорить в основном о знаменателе, когда вы имеете дело с корнем, отличным от 2. Итак, этот пример, о котором мы говорим, — это кубический корень. И одна распространенная ошибка заключается в том, что люди хотят умножить на кубический корень из 2, а не на кубический корень из 2. Хорошо? Когда мы умножаем радикалы, мы [IB] основываем корни одинаковыми. Мы совмещаем это. Таким образом, мы на самом деле получаем здесь кубический корень из 2 в квадрате или из 4. Это нам совсем не помогает, потому что кубический корень из 4 мы не знаем.