4 в степени 2 и в степени 2: как посчитать 4 в степени 3/2 — Спрашивалка

3 = 164 = 0.015625.

Чему равна 4 мощность? Полномочия 4

Питания	Силовая математика	Значение мощности
4	4 4	256
5	4 5	1024
6	4 6	4096
7	4 7	16384

Дополнительно Как вы решаете 4 в 4-й степени? Ответ: Значение 4 в 4-й степени, т.е. 4⁴ is 256. Вычислим значение 4 в 4-й степени, т. Е. 4⁴, Таким образом, 4⁴ можно записать как 4 × 4 × 4 × 4 = 256.

Чему равна 4-я степень числа 3? Ответ: 3 в 4-й степени равно числу 3, умноженному на себя четыре раза, и в результате получается ответ 81.

1/4 это четверть?

Доля одной четверти, одна четверть, 25% золото 0. 4 = 625.

Какой показатель у 4?

Таблицы экспонент и паттерны

Полномочия 2	Полномочия 3	Полномочия 4
24 = 16	34 = 81	44 = 256
25 = 32	35 = 243	45 = 1024
26 = 64	36 = 729	46 = 4096
27 = 128	37 = 2187	47 = 16384

Как называется 4-я сила? Альтернативные синонимы к слову «четвертая сила»:

биквадрат; биквадратный; квартик; номер.

Каким будет 1 2 в степени 4 в виде дроби?

Ответ: 1/2 в степени 4 равно (1/2)⁴ = 1/16. Разберемся с решением.

Что такое 2 в степени 5?

Ответ: 2 в степени 5 можно выразить как 2⁵ = 2 × 2 × 2 × 2 × 2 = 32.

Что до четвертого? Когда говорят, что число находится «в четвертой степени», это просто означает, что вы нужно умножить число само на себя в четыре раза.

Что такое 1/4 в целом числе? Ответ: число 1/4, которое также можно записать как 0.25. Следовательно, число 1/4, округленное до ближайшего целого числа, будет равно 0.

Что означает ¼?

одна из четырех равных или эквивалентных частей, на которые что-либо делится или может быть разделено. 2. четвертая часть, сп. из одного (¼).

Как вы записываете 1/4 как неправильную дробь?

1^1/4 как неправильная дробь

Следовательно, несобственная дробь равна 5/4.

Что такое 1/3 в степени 3?

Ответ: 1/3 в степени 3 представляется как 1/27 как дробь. Давайте разберемся с решением. Пояснение: Если мы должны представить (1/3)³ как дробь, мы должны вычислить куб 1/3.

Какова мощность числа 4? Силы числа 4

Питания	Силовая математика	Значение мощности
1	4 1	4
2	4 2	16
3	4 3	64
4	4 4	256

Какова ценность Силы 4?

«Пятая степень» числа — это число, умноженное само на себя в четыре раза. Напишите его с выпуклым числом 4 (показатель степени) рядом с основным числом. «количество⁴«Или« 5⁴»Или« 8⁴»Являются примерами использования показателя степени 4. Как сказать« 3 в степени 4 »или« 3 »⁴ то же самое, что сказать 3 раза 3 раза 3 раза 3 (равно 81).

1, 2, 3, 4 степени ожирения и их лечение

• Ожирение
• Диагностика
• Степени заболевания
• Причины
• Лечение
• Ожирение у детей
• Осложнения

Под ожирением понимается заболевание, которое развивается по причине неправильного течения обменных процессов в организме. Спровоцировать подобные нарушения могут гиподинамия, вызванная малоподвижным образом жизни, злоупотребление жирами животного происхождения и углеводной пищей, курение и присутствие алкогольных напитков в рационе. Под действием упомянутых факторов масса жировой ткани начинает увеличиваться, что не только создает эстетический дефект, но и представляет большую опасность для работы сердечно-сосудистой системы в частности, способствуя повышению артериального давления, вызывая ишемическую болезнь сердца, венозную недостаточность и другие болезни.

В зависимости от толщины жировой прослойки и стадии развития патологии принято выделять несколько степеней ожирения:

1. Первая степень характеризуется избыточной массой, нормативные показатели которой обычно высчитываются исходя из индекса массы тела (сокр.
   ИМТ). В процентном соотношении фактический вес превышает идеальный не более, чем на 29%. Такие изменения существенным образом не сказываются на самочувствии пациента, работоспособность сохраняется, признаки патологий со стороны сердца и других органов отсутствуют.
2. Вторая степень ожирения предполагает значительное увеличение жировой ткани, при которой порог допустимой для роста человека массы тела превышен на 30-49%. Отмечаются повышенная утомляемость, общая слабость, снижение внимания, ухудшение памяти и другие проявления плохого самочувствия, появляются признаки сердечной недостаточности.
3. Третья степень диагностируется в случае, если избыточная масса тела отличается от нормы более, чем на 50%. Одышка возникает как при минимальных физических нагрузках, так и в состоянии покоя. Повышенная утомляемость приводит к резкому снижению умственного труда. Человек утрачивает способность выполнять работу, которая требует внимания или физических усилий.
4. О четвертой степени можно говорить при увеличении массы тела двое и более. Тяжелое физическое состояние пациента отягощается болями в области сердца, головокружением, учащенным сердцебиением. В качестве осложнений прогрессируют такие заболевания, как атеросклероз, сахарный диабет второго типа, наблюдаются патологии в работе печени, желчевыводящих путей и других внутренних органов.

Последняя степень ожирения представляет опасность для жизни человека. Больные часто теряют контроль над негативными эмоциями и без причины выходят из себя. С физиологической точки зрения патология дает о себе знать усилением чувства голода, пациента нередко мучает жажда. Обильное поглощение жидкости приводит к нагрузке на почки. Они перестают в полном объеме выполнять свою функцию, вследствие чего возникает отечность, которая сначала проявляется на лице, а потом и по всему телу. Большая масса тела, которая оказывает непосредственное давление на суставы, провоцирует развитие заболеваний опорно-двигательного аппарата. Со временем болевой синдром только усиливается.

Лечение ожирения также проводится с учетом его степени.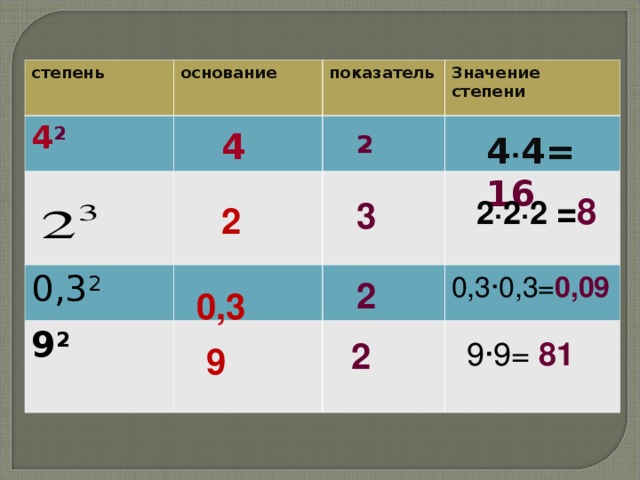 На начальных стадиях бывает достаточно скорректировать питание, подобрать комплекс необходимых физических упражнений и провести медикаментозное лечение. При развитии заболевания порой требуется комплексная терапия, направленная на устранение осложнений. Бариатрическая хирургия, например, шунтирование или бандажирование желудка, также может применяться для лечения патологии.

Как представить число в степени двойки?

Математика касается не только чисел, но и различных вычислений с использованием чисел и переменных. Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Числа могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.

Экспоненты и степени

Экспоненты и степени — это основные операторы, используемые в математических вычислениях, экспоненты используются для упрощения сложных вычислений, включающих многократное самоумножение, самоумножение — это в основном числа, умноженные сами на себя.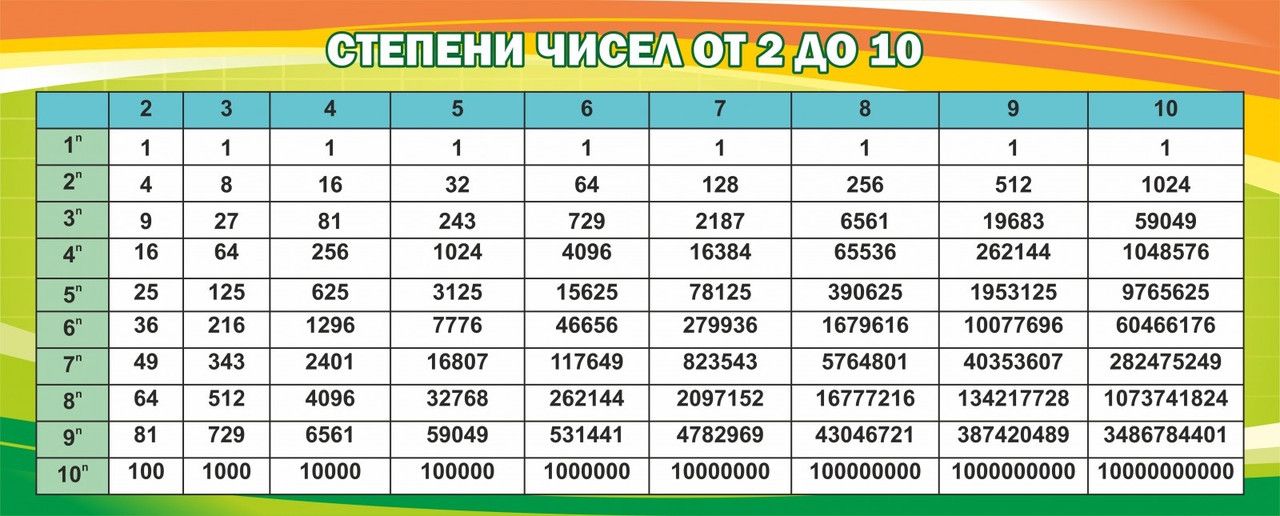 Например, 7 × 7 × 7 × 7 × 7 можно просто записать как 7 ⁵ . Здесь 7 — базовое значение, 5 — показатель степени, а значение равно 16807. 11 × 11 × 11 можно записать как 11 ³ , здесь 11 — базовое значение, а 3 — показатель степени или степень числа 11. Значение 11 ³ равно 1331.

Показатель степени определяется как степень, заданная числу, сколько раз оно умножается само на себя. Если выражение записано как cx ^y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как

p × p × p × p … n раз = p ⁿ

Основные правила экспонент с другими математическими операциями, например, если есть произведение двух показателей, его можно упростить, чтобы упростить вычисления, и оно известно как правило произведения, давайте рассмотрим некоторые из основных правил показателей,

• Правило продукта ⇢ A ^N + A ^M = A ^{N + M}
• Правило коэффициента ⇢ ^N / A ^M = A ^{N — M}
• Правило мощности ⇢ (A A A A ^{N — M}
• ^N ) ^M = A ^{N × M} или ^M √a ^N = A ^N/M
• Отрицательное правило показания ⇢ ^-M = 1/A ^M
• Нулевое правило ⇢ a ⁰ = 1
• Одно правило ⇢ a ¹ = a

Как представить число в степени двойки?

Решение:

Любое число, имеющее степень двойки, можно представить в виде квадрата этого числа. Квадрат числа — это число, умноженное само на себя, квадрат числа представлен как показатель степени 2 этого числа. Если нужно записать квадрат x, это будет x ² . Например, квадрат 5 представлен как 5 ² и равен 5 × 5 = 25. Другим примером может быть квадрат 12, представленный как 12 ² равно 12 × 12 = 144. Возьмем число 3, теперь 3, поскольку степень двойки будет представлена ​​как

3 ² = 3 × 3

= 9

Следовательно, 9 является второй степенью числа 3.

Следовательно, можно сделать вывод, что любое число в степени числа 2 можно представить в виде квадрата этого числа.

Пример вопроса

Вопрос 1: Решите выражение, 5

2 – 3 ² .

Решение:

Чтобы решить выражение, сначала решите 2 ^и степени чисел, а затем вычтите второй член из первого члена. Однако ту же задачу можно решить проще, просто применив формулу:

x ² – y ² = (x + y)(x – y)

5 ² – 3 ² = (5 + 3)(5 – 3)

= 8 × 2

= 16

Вопрос 2: Решите выражение, 10 ² – 6 ² .

No related posts.