Решение уравнений с дробями 5 класс
Обыкновенные дроби
часть 3
5 класс
— Сложение дробей с одинаковыми знаменателями.
— Вычитание дробей с одинаковыми знаменателями.
— Решение уравнений.
— Решение задач.
Сложение дробей с одинаковыми знаменателями.
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить прежним.
3
3+1
1
4
=
+
=
8
8
8
8
1
8
3
3+5
5
=
=
+
=
8
8
8
8
Вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
3
3-1
1
2
=
=
8
8
8
8
0
3
3
—
=
8
8
Решение уравнений.
При решении уравнений необходимо пользоваться правилами решения уравнений, свойствами сложения и вычитания.
Решение уравнений с применением свойств.
Решение уравнений с использованием правил.
Решите уравнение.
Подсказка 1
Выражение в левой части уравнения является суммой.
51
32
=
;
х
+
85
85
32
51
Подсказка 2
слагаемое + слагаемое = сумма.
х
=
—
;
85
85
19
х
=
.
85
Подсказка 3
Чтобы найди неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
19
Ответ:
85
Решите уравнение.
Выражение в левой части уравнения является разностью.
Подсказка 1
12
78
=
;
у
—
90
90
12
78
Подсказка 2
уменьшаемое – вычитаемое = разность
у
=
—
;
90
90
66
у
=
.
90
Чтобы найди неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Подсказка 3
66
Ответ:
90
Решите уравнение.
Выражение в левой части уравнения является разностью.
Подсказка 1
8
11
а
=
—
;
25
25
8
11
Подсказка 2
уменьшаемое – вычитаемое = разность
а
=
+
;
25
25
19
а
=
.
Чтобы найди неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Подсказка 3
25
19
Ответ:
25
Решите уравнение.
(
7
3
18
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
+
х
+
=
(
;
19
19
19
В левой части уравнения выражение является суммой.
Подсказка 1
3
18
7
+
=
х
;
—
19
19
19
3
11
=
х
+
Подсказка 2
;
Неизвестное содержится в слагаемом.
19
19
11
3
х
=
;
—
19
19
8
8
х
.
=
Ответ:
19
19
Решите уравнение.
(
5
37
17
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
—
у
=
(
+
;
44
44
44
В левой части уравнения выражение является разностью.
Подсказка 1
5
37
17
=
у
+
;
—
44
44
44
5
20
=
у
+
Подсказка 2
;
Неизвестное содержится в вычитаемом.
44
44
20
5
у
=
;
—
44
44
15
15
у
.
=
Ответ:
44
44
Решите уравнение.
18
8
21
ИСПОЛЬЗОВАНИЕ ПРАВИЛ РЕШЕНИЯ УРАВНЕНИЙ.
b
+
=
—
;
73
73
73
Подсказка 1
В левой части уравнения выражение является разностью.
18
8
21
b
+
;
=
+
73
73
73
29
18
=
+
Подсказка 2
Неизвестное содержится в уменьшаемом.
b
;
73
73
29
18
=
b
;
—
73
73
11
11
b
Ответ:
.
=
73
73
Решите уравнение.
(
7
3
18
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
+
х
+
=
(
;
19
19
19
В левой части уравнения можно применить сочетательное свойство сложения .
Подсказка 1
7
3
18
+
;
+
=
х
19
19
19
10
18
=
х
+
Подсказка 2
;
Чтобы к числу прибавить сумму , можно к этому числу прибавить сначала одно слагаемое, а потом другое.
19
19
18
10
х
=
;
—
19
19
8
8
х
.
=
Ответ:
19
19
Решите уравнение.
(
5
37
17
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
—
у
=
(
+
;
44
44
44
В левой части уравнения можно применить свойство вычитания суммы из числа. .
Подсказка 1
37
5
17
—
;
—
=
у
44
44
44
32
17
=
у
—
Подсказка 2
;
Чтобы из числа вычесть сумму, можно вычесть сначала одно слагаемое, а потом другое.
44
44
32
17
у
=
;
—
44
44
15
15
у
.
=
Ответ:
44
44
Решите уравнение.
8
18
21
ПРИМЕНЕНИЕ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
+
b
=
—
;
73
73
73
Подсказка 1
В левой части уравнения можно применить свойство вычитания числа из суммы.
18
21
8
—
;
+
=
b
73
73
73
10
21
=
b
+
Подсказка 2
Чтобы вычесть число из суммы, можно сначала вычесть это число из одного слагаемого, а потом прибавить другое.
;
73
73
21
10
=
b
;
—
73
73
11
11
b
.
=
Ответ:
73
73
2
В первый день Саша прочитал книги, а во второй день — книги. Сколько страниц прочитал Саша за два дня, если в книге 144 страницы?
9
4
9
144 стр.
4
2
9
9
2
4
6
1) + = (книги) – прочитал Саша за 2 дня.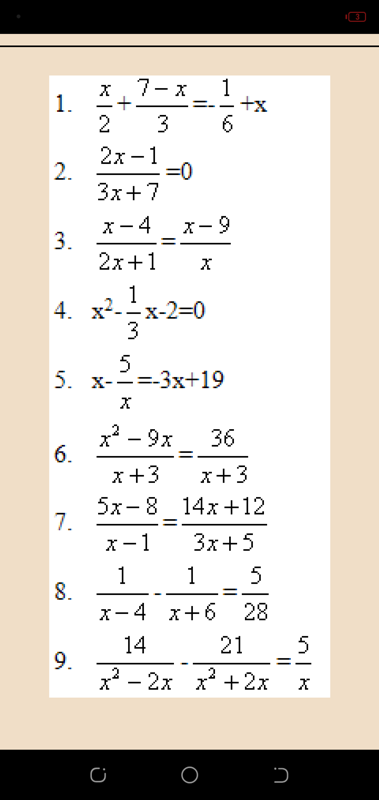
9
9
9
2) 144 : 9 ∙ 6 = 96 (стр.)
Ответ: За 2 дня Саша прочитал 96 страниц.
Решение задач.
5
В первый день Маша прочитала книги, а во второй день — книги. Сколько страниц в книге, если Маша за два дня прочитала 36 страниц?
12
4
12
36 стр.
4
5
12
12
5
4
9
1) + = (книги) – прочитала Маша за 2 дня.
12
12
12
2) 36 : 9 ∙ 12 = 48 (стр.)
Ответ: В книге 48 страниц.
Контрольные работы для 5 класса по математике, составленные по критериям воспроизведение, применение, интеграция
Контрольная работа по математике №1. 5 класс.
Цель: проверить уровень усвоения ГОСО по курсу математики 4 класса:
-решение задачи на нахождение скорости, времени, расстояния;
-выполнение арифметических действий с многозначными числами;
-знание порядка действий;
-знание формул для нахождения периметра и площади прямоугольника и умение применять их при решении геометрической задачи;
-умение
находить неизвестный компонент уравнения.
1 вариант
1. Реши задачу:
1. Выполни действия:
5847 + 6132 18619 х 39
49524 – 2615 19776 : 309
2. Реши уравнение:
х – 135 = 5095 : 5
3. Выполни порядок действий:
(450 – 230) : 20 + 49 х 3
4.Из пункта А одновременно в противоположных направлениях выехали два велосипедиста. Скорость первого велосипедиста 23 км/ч, а скорость другого 36 км/ч. На каком расстоянии друг от друга будут велосипедисты через 7 часов?
5. Дан квадрат со стороной 12 см. Найдите ширину прямоугольника, площадь которого равна площади квадрата, а длина прямоугольника на 3 см меньше стороны квадрата.
2 вариант
1. Реши задачу:
1. Выполни действия:
80256 : 192 56789 — 2374
72512 х 27 2894 + 8972
2. Реши уравнение:
х + 137 = 1485 : 5
3. Выполни порядок действий:
Выполни порядок действий:
270 : (120 – 90) + 140 х 4
4. Из двух городов, находящихся на расстоянии 540 км друг от друга, выехали одновременно навстречу друг другу велосипед и мотоцикл. Они встретились через 18 часов. Велосипед шел со скоростью 11 км/ч. С какой скоростью ехал мотоцикл?
5. Дан прямоугольник, длина которого 60 см, а ширина 15 см. Найди длину другого прямоугольника, площадь которого равна площади данного, а его ширина на 5 см меньше ширины первого прямоугольника.
Критерии оценивания | |
«5» | 22-23 баллов |
«4» | 16-21 балла |
«3» | 13-15 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Действия с многозначными числами | №1, | №3 |
| 40 % |
Уравнение | №2 | №4 |
| 40% |
Площади |
|
| №5 | 20% |
Итого | 40 % | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполненное задание |
1 | Выполнение действий с многозначными числами | Выполнение сложения Выполнение вычитания Выполнение умножения Выполнение деления | 1 1 1 1
| 4 |
2 | Решение уравнения | Нахождение
неизвестного члена уравнения. | 2
2 | 4 |
3 | Выполнение действий с многозначными числами | Знание порядка действий Выполнение сложения Выполнение вычитания Выполнение умножения Выполнение деления | 1 1 1 1 1 | 5 |
4 | Решение задач | Краткая запись условия задачи Решение задачи Запись ответа | 1 3 1 | 5 |
5 | Решение задачи | Знание формулы вычисления площади прямоугольника, квадрата Умение выражать неизвестную длину (ширину) через известную площадь Вычислительные навыки | 2
2
1 | 5 |
Контрольная
работа по математике №2. 5 класс.
5 класс.
Тема: Буквенные выражения. Уравнения.
Цель: проверить уровень усвоения ГОСО по следующим вопросам:
-буквенные выражения и нахождение их значений
-решение уравнений
-упрощение выражений
-действия с натуральными числами
Текст работы:
Вариант 1
1. Найдите значение выражения: а+37+в при а=13 ,в=28 2. Упростить выражение: (23х-81+42Х)∙3 3. Упростите выражение 39х+18х-27х+56 и найдите его значение при х=12
4. Решите задачу, составив уравнение: Папа, сын и дочка собрали 99 кг свеклы. Сын собрал в два раза больше, чем дочь, а папа в три раза больше, чем сын. Сколько кг свеклы собрал каждый из них. 5. Длина прямоугольной ванной комнаты равна 4 м, ширина в два раза меньше длины, а высота на 50 см больше ширины. Сколько штук облицовочной плитки понадобится для стены, если размер плитки 50х50 см? | Вариант 2
1. Найдите значение выражения: а+87+в при а=21, в=47 2. Упростить выражение: 4∙(31Х-17+54х) 3.Упростите выражение 43у-14у+39у-18 и найдите его значение при у=12
4. Решите задачу, составив уравнение: Петя, Костя и Гена нашли 112 грибов. Петя нашел в три раза меньше, чем Костя и в четыре раза меньше, чем Гена. Сколько грибов нашел каждый мальчик 5.Решите задачу: Ширина кабинета 4м, а длина на 2м 60см больше ширины, а высота на 3м 60 см меньше длины. Сколько рулонов обоев понадобится для оклеивания стен, если в одном рулоне 10 квадратных метров обоев? |
Критерии оценивания | |
«5» | 20-21 баллов |
«4» | 16-19 баллов |
«3» | 11-15 баллов |
Распределение заданий по содержанию и уровню сложности.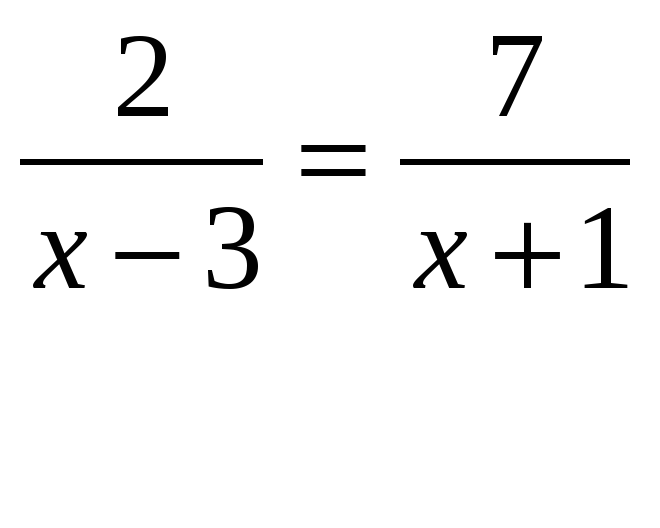
Содержание | Воспроизведение знаний | Применение знаний | Интеграция | % |
Буквенные выражения | №1, №2 | №3 |
| 60%
|
Уравнение |
| №4 |
| 20% |
Формулы |
|
| №5 | 20% |
Итого |
40% |
40% |
20% |
100% |
Критерий
оценивания по проверяемым элементам.
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
1 | Упрощение выражений | Подстановка численных значений Вычислительные навыки | 1 2 | 3
|
2 | Упрощение выражений | Применение распределительного закона умножения Приведение подобных | 2
2 |
4 |
3 | Упрощение выражений | Приведение подобных Вычислительные навыки | 2 2 | 4
|
4 | Задача на составление уравнения | Составление уравнения Решение уравнения Запись ответа | 2 2 1 | 5
|
5 | Задача на нахождение площади | Знание формулы площади прямоугольника Решение задачи Вычислительные навыки | 1
2 2 | 5 |
Контрольная работа № 3. 5
класс
5
класс
Тема: Угол. Окружность. Круг.
Цель: проверить уровень усвоения ГОСО:
-знание понятий угол, окружность, круг;
-измерять величину угла с помощью транспортира;
-строить угол заданной величины;
Текст работы:
Вариант 1 |
| Вариант 2 | |||||||||||
| |||||||||||||
№ 1. Начерти в тетради, обозначь углы и запиши их градусную меру: острый угол и прямой тупой и развёрнутый | |||||||||||||
№2. Реши задачу: Диаметр окружности равен 8 см, Радиус окружности равен 3см Найди длину радиуса и начерти Найди длину диаметра и начерти окружность. №3.Выполни: | |||||||||||||
Угол АОВ- развёрнутый, Найдите градусную меру угла EFK, АОС = 500. Найти градусную меру угла если угол EFN прямой, а угол KFN = 550 СОВ. Определите вид угла. Определите вид угла. C K N
А О В Е F | |||||||||||||
| |||||||||||||
|
|
| |||||||||||
№ 4. АВС – прямой угол(рис. А) СВD – прямой угол (рис. Б) начертите рисунок в тетради. А Д С Д 350 Е | |||||||||||||
200 | |||||||||||||
В 150 С | А В Е | ||||||||||||
| |||||||||||||
№5. Угол MOK равен 1200, внутри угла Угол АОВ равен 1500, внутри угла проведен луч OD. проведен луч OD. Угол MOD больше угла DOK на 500. Угол АОК больше угла DOK на 400. Сколько градусов содержит угол DOK? Сколько градусов содержит угол DOK? А М Д Д В К О О | |||||||||||||
|
|
| |||||||||||
Критерии оценивания | |
«5» | 22-23 баллов |
«4» | 16-21 балла |
«3» | 12-15 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Угол | №1 | №3, №4 | №5 | 80 % |
Окружность и круг | №2
|
|
| 20 % |
Итого | 40 % | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполненное задание |
1 | Изображение угла и запись в градусной мере | Знание понятий угол Умение построить угол Умение изображать угол Умение измерять величину угла | 1 1 1 1 | 4 |
2 | Построение окружности, измерение радиуса и диаметра | Знание
понятия окружность, радиус, диаметр. Умение изображать окружность. | 2
2
| 4 |
3 | Вычисление градусной меры угла | Знание видов углов и их градусных мер Вычисление градусной меры | 2 2 | 4 |
4 | Решение геометрической задачи | Знание видов углов. Нахождение суммы двух данных углов. Нахождение искомого угла | 1
2 2 | 5 |
5 | Решение геометрической задачи с помощью уравнения | Краткая
запись условия задачи. Составление уравнения по условию задачи. Решение уравнения. Запись ответа | 1
2
2 1 | 6 |
Контрольная работа №4 по теме «Делители чисел» , 5 класс
Цель: проверить уровень усвоения ГОСО:
-знание понятий делители чисел
-знание понятий кратные чисел
-знание понятий простые числа
-знание понятий составные числа
-знание понятий чётные и нечетные числа
— знание признаков делимости на 2 3 5 9
— знание свойства деления суммы на число
-умение применять свойства деления суммы на число
Текст работы:
Вариант 1 |
| Вариант 2 |
| |||||||||||
№1 а) Запишите все делители чисел 6, 11, 23, 38, 62 7, 14, 25, 45, 84 |
| |||||||||||||
б) Подчеркните простые числа 21,13,72,19,81,23 34,29,31,49,11,18 |
| |||||||||||||
№3 а) Какие из чисел 896, 975, 1002, 2379, 4568, 9694, 9999 являются чётными нечётными б) Выпишите из чисел 94673, 28624, 33460, 54745, 63785, 73688, 83840 числа, делящиеся на 5 на 2 в) Выпишите числа, делящиеся на 9 на 3 из чисел 8568, 7776, 5306, 8694, 9963, 9087, 7031, 9648 |
| |||||||||||||
№ 4. а) Делится ли сумма (68 + 40) на 4 или 5? а) Делится ли сумма (63 + 54) на 7 или на 9? б) Делится ли произведение 60·28 на 5? б) Делится ли произведение 45·91 на 3? |
| |||||||||||||
№ 5.Решите задачу
|
| |||||||||||||
|
| |||||||||||||
|
|
|
| |||||||||||
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Делители чисел Кратные чисел | №1(а), №2(а) |
|
| 20 % |
Простые и составные числа | №1(б), №2(б) |
|
| 20 % |
Признаки дели-мости на 2, 3, 5 ,9 |
| №3 | №5 | 40 % |
Свойства деления суммы на число |
| №4 |
| 20 % |
Итого | 40 % | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполненное задание |
1 | Делители чисел | Нахождение делителей числа Нахождение простых чисел | 2 1 | 3 |
2 | Кратные чисел | Нахождение кратных чисел Понятие составного числа Решение неравенства | 2 1 1 | 4 |
3 | Признаки делимос-ти на 2 и 5,на 3 и 9 | Знание признаков делимости Вычисления | 3 1 | 4 |
4 | Свойства деления суммы и разности на число | Знание свойства деления суммы и разности на число Умение применять свойства деления суммы на число Запись ответа | 2
2
1 | 5 |
5 | Четные и нечетные числа | Знание формул четного и нечетного чисел Способ решения задачи Запись ответа | 2
2 1 | 5 |
Контрольная работа №5. 5 класс.
5 класс.
Тема: НОД и НОК.
Цель: проверить уровень усвоения ГОСО:
-знание понятий простых и составных чисел;
-знание понятий наибольшего общего делителя и наименьшего общего кратного;
— знание понятия степени;
-умение находить НОД и НОК
Текст работы:
Вариант 1 |
| Вариант 2 | ||
| ||||
№ 1 Разложи на простые множители
число
402
число 705.
| ||||
№ 2. Найдите НОД и НОК данных чисел:
2 . 3 . 3 . 5 и 2 . 2 . 3 . 3 2 . 2 . 2 . 3 . 7 и 2 . 3 . 3 . 7.
№ 3.Найдите
а)наибольший общий делитель чисел 27 и 45; а) наибольший общий делитель чисел 32 ,48; б) наименьшее общее кратное чисел 15 и 18. б) наименьшее общее кратное чисел 16 и 20
| ||||
№ 4. Решите задачу: Алла и
Маша идут рядом. Аллы 40 см, а Маши-60 см . Какое расстояние одного шага Армана 50 см, а Серика пройдут девочки, когда их шаги совпадут? 80 см. Какое расстояние пройдут | ||||
|
| мальчики, когда их шаги совпадут? | ||
№5. Решите уравнение: | ||||
х ·33=15 · 32 |
| 23 · х=24 ·19 | ||
Критерии оценивания | |
«5» | 23-25 баллов |
«4» | 18-22 балла |
«3» | 13-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Наибольший общий делитель | №1, №2 |
| №5 | 60 % |
Наименьшее общее кратное |
| №3, №4 |
| 40 % |
Итого | 40 % | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполненное задание |
1 | Разложение на простые множители
| Знание понятий простых и составных чисел Умение раскладывать на простые простые множители | 1
2
| 3 |
2 | Нахождение НОД и НОК чисел разложенных на простые множители | Нахождение НОДа Нахождение НОКа Вычислительные навыки | 1 1 1
| 3 |
3 | Нахождение НОД и НОК двух чисел | Разложение чисел на простые множители Нахождение НОД двух чисел Нахождение НОК двух чисел Вычисления | 2
1 1 1 | 5 |
4 | Решение задач с использованием понятий НОД и НОК | Краткая запись условия задачи Разложение чисел на простые множители Нахождение НОК двух чисел Запись ответа | 1
1 2 1 | 5 |
5 | Решение уравнений с использованием понятия степени | Нахождение неизвестного компонента уравнения Знание понятия степени Вычисления |
2 2 1 | 5 |
Контрольная работа по математике №6. 5 класс.
5 класс.
Тема: Обыкновенные дроби. Смешанные числа.
Цель: проверить уровень усвоения ГОСО:
-знание понятий правильной и неправильной дроби;
-знание и понятие смешанного числа;
-умение переводить неправильную дробь в смешанное число;
-умение изображать обыкновенную дробь на координатном луче;
-умение решать основные задачи на дроби.
Текст работы:
Вариант 1 |
| Вариант 2 | ||||
| ||||||
№ 1. Представь в виде смешанного числа неправильную дробь | ||||||
|
|
| ||||
№
2.
При каких натуральных х дробь При каких натуральных х дробь х/5 будет правильной? х/8 будет правильной?
| ||||||
№ 3. Реши задачу: | ||||||
Книга стоит 225 тенге, а цена тетради составляет стоимости книги. Сколько надо заплатить за 2 книги и 5 тетрадей? |
| Кукла стоит 216 тенге, а цена машинки составляет стоимости куклы. Сколько надо заплатить за 3 куклы и 2 машинки? | ||||
№ 4. | ||||||
На числовом луче, выбрав единичный отрезок, отметь точки, соот-ветствующие числам Запиши числа в порядке убывания |
| На числовом луче, выбрав единичный отрезок, отметь точки, соответствующие числам Запиши числа в порядке возрастания | ||||
№5Реши уравнение:
| ||||||
= |
| = | ||||
Критерии оценивания | |
«5» | 23-25 баллов |
«4» | 18-22 балла |
«3» | 13-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Смешанные числа | №1 |
|
| 20 % |
Дроби | №2 |
| №5 | 40 % |
Обыкновенные дроби |
| №3 |
| 20% |
Координатный луч |
| №4 | 20% | |
Итого | 40% | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполненное задание |
1 | Запись неправильной дроби в виде смешанного числа | Знание понятий правильной и неправильной дроби Алгоритм перевода дроби в смешанное число Применение алгоритма | 1
2
2 | 5 |
2 | Понятие дроби | Правильная дробь
Умение записывать дробь
Запись ответа | 2
1
3 | 5 |
3 | Решение задач | Краткая запись условия задачи Решение задачи Запись ответа | 1 3 1 | 5 |
4 | Изображение обыкновенных дробей на координатном луче | Выбор единичного отрезка Изображение обыкновенных дробей Расположение дробей в заданном порядке | 1 2
2 | 5 |
5 | Решение уравнения | Знание основного свойства дроби Составление уравнения Решение уравнения Вычисления | 2
1 1 1 | 5 |
Контрольная работа по математике № 7. 5 класс.
5 класс.
Тема: Сложение и вычитание обыкновенных дробей, смешанных чисел.
Цель: проверить уровень усвоения ГОСО:
-знание понятий правильной и неправильной дроби;
-знание правил сравнения дробей;
-умение выполнять сложение и вычитание обыкновенных дробей и смешанных чисел;
-умение изображать обыкновенные дроби на координатном луче.
Текст работы:
Вариант 1 |
| Вариант 2 | |||
| |||||
№ 1. Из данных дробей | |||||
а) выпишите неправильные дроби | |||||
б) запишите их в виде смешанного числа | |||||
, , , , |
| , , , , | |||
№ 2. | |||||
а) и б) и в) и |
| а) и б) и в) и | |||
№ 3. Выполните действие: | |||||
а) +
б) 2 + 3
в) 6 — — |
| а) + б) 2 + 1 в) 5 — — | |||
№ 4. Решите задачу: | |||||
Ученики
в первый день очистили части земельного участка,
выделенного им, во второй день – на части больше, чем в
первый день. |
| Читатель в первый день прочитал части книги, за второй день – на часть меньше, чем в первый день. Какую часть книги прочитал читатель за два дня? | |||
№ 5. | |||||
а) Отметьте на координатном луче точки, соответствующие числам | |||||
, , , |
| , , ,
| |||
б) Запишите эти числа в порядке | |||||
возрастания |
| убывания | |||
Критерии оценивания | |
«5» | 23-25 баллов |
«4» | 18-22 балла |
«3» | 13-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Обыкновенная дробь | №1, №2 |
| №5 | 60 % |
Сложение и вычитание обыкновенных дробей |
| №3, №4 |
| 40 % |
Итого | 40 % | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполненное задание |
1 | Запись неправильной дроби в виде смешанного числа | Знание понятий правильной и неправильной дроби Алгоритм перевода дроби в смешанное число Применение алгоритма | 1
2 2 | 5 |
2 | Сравнение обыкновенных дробей | Знание правил сравнения дробей с одинаковыми знаменателями Знание правил сравнения дробей с одинаковыми числителями Знание правил сравнения дробей с разными знаменателями и числителями | 1
1
3 | 5 |
3 | Сложение и вычитание обыкновенных дробей | Знание алгоритма приведения к наименьшему общему знаменателю Сложение и вычитание обыкновенных дробей Вычитание дроби из целого числа Сокращение дробей Сложение смешанных чисел | 1
1
1 1 1 | 5 |
4 | Решение задач | Краткая запись условия задачи Решение задачи Запись ответа | 1 3 1 | 5 |
5 | Изображение обыкновенных дробей на координатном луче | Выбор единичного отрезка Изображение обыкновенных дробей Расположение дробей в заданном порядке | 1 2 2 | 5 |
Контрольная
работа по математике № 8. 5 класс.
5 класс.
Тема: Умножение и деление обыкновенных дробей, смешанных чисел
Цель: определить уровень усвоения государственного стандарта по теме умножение и деления обыкновенных дробей, нахождение дроби от числа и числа по его дроби:
— умение находить число обратное данному;
— умение умножать обыкновенную дробь на дробь, натуральное и смешанное число;
— уметь решать задачи на нахождение дроби от числа, числа по его дроби;
— умение делить, умножать обыкновенные дроби, находить число по за данному значению его дроби;
— умение выполнять все действия с обыкновенными дробями и применять эти умения при решении задач
Текст работы:
Вариант 1 1. Найдите
число, обратное данному числу: 2 , , 13, . 2. Вычислите: 3.Для пошива одного платья нужно м ткани. Сколько метров ткани нужно для пошива 6 таких платьев? 4.Путешественники преодолели 90 км расстояния. Это составляет всего пути, который они должны преодолеть. Сколько километров должны пройти путешественники? 5. Вычислить и ответы записать в порядке возрастания:
|
Вариант 2 1. Найдите число, обратное данному числу: , 2 , 9, 2.Вычислите: 3.В одном пакете кг конфет. Сколько килограммов конфет в 20 таких пакетах? 4.В классе учится 18 девочек, это составляет всего количества учеников класса. Сколько мальчиков учится в классе? 5. Вычислить и ответы записать в порядке убывания:
|
Критерии оценивания | |
«5» | 24-25 баллов |
«4» | 18-23 балла |
«3» | 13-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Умножение и деление обыкновенных дробей | №1,№2 | №4, №3 | №5 | 100 % |
Итого | 40 % | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ п/п | Характеристика задания | Проверяемые элементы | Баллы за выполнение проверяемых элементов | Балл за выполнение задания |
1 | Число обратное данному | Применение правила Стандартная запись дроби | 3 2 | 5 баллов |
2 | Умножение
и деление обыкновенных дробей. | Умножение дроби на натуральное число Умножение обыкновенных дробей Умножение смешанных чисел Деление дроби на натуральное число Деление смешанных чисел | 1 1 1 1 1 | 5 баллов |
3 | Решение задачи | Краткая запись условия задачи Применение правила умножения запись ответа | 2 балла 2 балла 1 балл | 5 баллов |
4 | Решение задачи | Краткая запись условия задачи Применение правила нахождения числа по его дроби запись ответа | 2 балла 2 балла 1 балл | 5 баллов |
5 | Все действия с обыкновенными дробями | 1) Сложение и вычитание смешанных чисел 2)
Умножение и деление дробей. 3) запись ответа | 2балл 2 балл 1 балл | 5 баллов |
Контрольная работа по математике №9. 5 класс.
Тема: Десятичная дробь. Сложение и вычитание десятичных дробей.
Цель: определить уровень усвоения государственного стандарта по теме десятичная запись дробных чисел, сложение и вычитание десятичных дробей
— умение записывать частное двух чисел в виде десятичной дроби;
— умение складывать и вычитать десятичные дроби и применять эти умения при решении задач;
— умение решать уравнения
— умения сравнивать десятичные дроби.
Текст работы:
Вариант 1 1. 27:10; 81:100; 319:100; 919: 100 2. Вычислите: а) 2,83 + 15,2; в) 45,6 + 7,35; б) 19 – 5,86; г) 15,7 – 9,85. 3. Для пошива платья нужно 2,35 м ткани, а для пошива рубашки нужно на 1,2 м меньше ткани. Сколько метров ткани нужно для пошива рубашки?
4. Решите уравнение 80,6-(х-7,98)=63,4 5. Замени все звездочки одной и той же цифрой так, чтобы оба неравенства были верны: 0,*8 0,8* и 0,*5 0,5*
| Вариант 2 1. Запишите в виде десятичных дробей частное: 29:10; 91:100; 461:100; 817: 100. 2. Вычислите: а) 3.18 + 17,3; в) 54,8 + 8,25; б) 18 – 4,15; г) 16,7 – 8,95. 3. Рабочие в первый день отремонтировали 4,85 км дороги, во второй день – на 1,26 км больше, чем в первый день. Сколько километров дороги отремонтировали рабочие за 2 дня? 4. (52,3-х)-4,08=17,3 5. Замени все звездочки одной и той же цифрой так, чтобы оба неравенства были верны: 0,*6 0,6* и 0,3* 0,*3 |
Критерии оценивания | |
«5» | 22-23 баллов |
«4» | 16-21 балла |
«3» | 12-15 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроизведение знаний | Применение знаний | интеграция | % отношение |
Действия сложен ия и вычитания десятичных дробей | №1,№2 | №3 |
| 60 % |
Уравнение |
| №4 |
| 20 % |
Сравнение дробей |
|
| №5 | 20 % |
Итого | 40 % | 40 % | 20 % | 100 % |
Содержательная матрица и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
1 | Запись десятичной дроби | Запись десятичной дроби | 1 1 1 1 |
4 |
2 | Сложение и вычитания дробей | Сложение десятичных дробей Вычитание десятичных дробей | 2 2 |
4 |
3 | Решение задачи | Краткая запись условия задачи Решение задачи Запись ответа | 1 3 1 |
5 |
| Решение уравнений | Алгоритм решения уравнения Оформление уравнения Сложение и вычитание десятичных дробей | 2 1 2 |
5 |
6 | Сравнение десятичных дробей | Правила сравнения дробей Решение первого неравенства Решение второго неравенства Запись ответа | 1 1 1 2 | 5 |
Контрольная
работа по математике №10 .
5 класс.
Тема: Умножение и деление десятичных дробей
Цель: определить уровень усвоения государственного стандарта по теме умножение и деление десятичных дробей, округление чисел, среднее арифметическое нескольких чисел.
— умения умножать десятичные дроби
— умения делить десятичные дроби
-умения решать задачи на умножение и деление десятичных дробей
Текст работы:
Вариант 1 1.Вычислите: а) г) 2,7 : 9 б) д) 7,28 : 0,1; в) 57 ∙ 0,01 е) 5,85 : 3,25; 2.Света собрала 2,56 кг лекарственных трав, а Айман в 3 раза меньше. Сколько килограммов лекарственных трав собрали девочки?
3. 1 кг
слив стоит 320 тг, что составляет 0,4 стоимости 1кг груш.
4. Решите уравнение 6х-2х+3,4=9,2
5.Если в некоторой десятичной дроби перенести запятую на два знака влево, то дробь уменьшится на 51,183. Найдите эту дробь. | Вариант 2 1. Вычислите: а) 31,25∙4; г) 1,8 : 3; б ) 5,4∙ 0,01; д) 5,67 : 0,1; в) 2.47 ∙0,5 е) 3,29 : 2,35;
2. В первом бидоне 8,2 литров масла, а во втором в 3 раза больше. Сколько литров масла в обоих бидонах?
3. 1 кг винограда стоит 350 тг, что составляет 0,2 стоимости 1кг ананасов. Сколько стоит 1 кг ананасов?
4. Решите уравнение 3х+3х-1,4=4,7
5. Если в некоторой десятичной дроби перенести запятую на два знака вправо, то дробь увеличится на 53,361. Найдите эту дробь.
|
Критерии оценивания | |
«5» | 22-23 баллов |
«4» | 16-21 балла |
«3» | 12-15 баллов |
Распределение
заданий по содержанию и уровню сложности .
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % |
Десятичные дроби | №1 |
| №5 | 40% |
Решение задачи | №2 | №3 |
| 40% |
Решение уравнений |
| №4 |
| 20% |
Итого |
40% |
40% |
20% |
100% |
Содержательная матрица и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
1 | Умножение и деление десятичных дробей | Умножение десятичной дроби на натуральное число Умножение десятичной дроби на разрядную единицу Умножение десятичной дроби на десятичную дробь Деление десятичной дроби на натуральное число Деление десятичной дроби на разрядную единицу Деление
десятичной дроби на десятичную дробь. | 1
1
1
1
1 1 |
6 |
2 | Задача | Краткая запись условия Решение задачи | 1 2 |
3 |
3 | Задача | Краткая запись условия Нахождения числа по его дроби Деление десятичных дробей | 1 1 1 | 3 |
4 | Решение уравнений | Применение распределительного закона Алгоритм решения уравнений Вычислительные навыки |
1 2 2 |
5 |
5 | Задача на составление уравнения | Составление уравнения по условию задачи Решение уравнения | 3
2 |
5 |
Контрольная
работа по математике №11. 5 класс.
5 класс.
Тема: Действия с десятичными и обыкновенными дробями. Среднее арифметическое чисел. Мода, размах, медиана.
Цель: определить уровень усвоения государственного стандарта по темам «Совместные действия с десятичными и обыкновенными дробями. Среднее арифметическое чисел. Мода, размах, медиана. »
-умения выполнять совместные действия с обыкновенными и десятичными дробями
— умения умножать десятичные дроби
— умения делить десятичные дроби
-умения округлять десятичные дроби
-умения находить среднее арифметическое чисел
Текст работы:
Вариант 1
1. Округлите числа: а) до десятых 0,821; б) до тысячных 0,9385. 2. Найдите размах ряда чисел и моду чисел: 9,57; 4,9; 8,3; 4,9; 7,8;
3. :1,2+3,5- 4.Велосипедист в первый час ехал со скоростью 11 км/ч, во второй час со скоростью 10,8 км/ч, в третий час – 11,5 км\ч. Найдите среднее арифметическое скоростей велосипедиста. 5. Найдите наименьшее натуральное число при делении которого на3,6 и 2получаются натуральные числа | Вариант 2
1. Округлите числа: а) до десятых 0,679; б) до тысячных 0,8275. 2. Найдите размах ряда чисел и моду чисел: 8,131; 5,8; 7,1; 5,8; 8.
3. Вычислите: 4.Автобус в первый час ехал со скоростью 45 км/ч, во второй час со скоростью 52,3 км/ч, в третий час – 47,5 км/ч. Найдите среднее арифметическое скоростей автобуса. 5. Найдите наименьшее натуральное число при делении которого на2,4 и 1 получаются натуральные числа |
Критерии оценивания | |
«5» | 21-22 баллов |
«4» | 14-20 баллов |
«3» | 11-13 баллов |
Распределение
заданий по содержанию и уровню сложности .
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % |
Десятичные дроби | №1 |
| №5 | 40% |
Округление чисел | №2 |
|
| 20% |
Размах и мода |
| №3 |
| 20% |
Среднее арифметическое |
| №4 |
| 20% |
Итого |
2 – 40% |
2 – 40% |
2 – 20% |
100% |
Содержательная матрица и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
1 | Округление чисел | Знание разрядных единиц Применение правила округления
| 2 2 |
4 |
2 | Размах и мода | Знание
определений «размах». Вычитание десятичных дробей | 2
1 | 3 |
3 | Совместные действия с десятичными и обыкновенными дробями | Сложение дробей Вычитание дробей Умножение дробей Деление дробей Перевод одного вида дробей в другой | 1 1 1 1 1 | 5 |
4 | Среднее арифметическое | Правило нахождения среднего арифметического Перевод обыкновенной дроби в десятичную дробь Действия с десятичными дробями | 1
2
2 |
5 |
5 | Совместные действия с десятичными и обыкновенными дробями | Выбор способа решения задачи Умение делить натуральное число на дробь Нахождение НОК | 2 1
2
|
5 |
Контрольная
работа по математике № 12 .
5 класс.
Тема: Проценты.
Цель: определить уровень усвоения государственного стандарта по теме проценты, углы, диаграммы
— умение записывать дроби в виде процентов, находить процент от числа и число по заданному значению процента;
— умение применять формулы объёма;
— умение строить круговую диаграмму и выполнять действия с десятичными дробями.
Текст работы:
Вариант 1
1 .Запишите дроби в виде процентов: 0,2; 0,8; 0,75; 2,3.
2.В библиотеке 35000 книг. Из них 22% составляют художественные книги. Сколь-ко художественных книг в библиотеке?
3.Со склада выгрузили 244,8 тонн угля, после чего на складе осталось 55% угля. Сколько тонн угля было на складе первоначально?
4.
5.Сколько кубов с ребром 3см необходимо для построения куба с ребром 15см?
| Вариант 2
1. Запишите дроби в виде процентов: 0,5; 0,4; 0,15;1,25.
2.В школе 1500 учеников. Из них 42% составляют мальчики. Сколько мальчиков в школе?
3. Истратив на посев 65% имевшегося в запасе зерна, фермер обнаружил, что у него осталось 197,4 кг зерна. Сколько кг зерна было у фермера первоначально?
4. 80% всех книг школьной библиотеки составляют учебники, а остальное – худо-жественные книги. Начертите круговую диаграмму книг в школьной библиотеке.
5. Сколько кубов с ребром 2см необходимо для построения прямоугольного паралле-лепипеда с измерениями 12см,10см,6см? |
Критерии оценивания | |
«5» | 21-22 баллов |
«4» | 15-20 баллов |
«3» | 11-14 баллов |
Распределение
заданий по содержанию и уровню сложности .
Содержание | Воспроизведение знаний | Применение знаний | Интеграция | % |
Процент. | №1, №2 | №3 |
| 60% |
Объём куба. |
|
| №5 | 20% |
Построение диаграммы |
| №4 |
| 20% |
Итого |
40% |
40% |
20% |
100% |
Критерий
оценивания по проверяемым элементам.
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
1 | Запись числа в виде процента | Запись числа в виде процента | 4 | 4
|
2 | Нахождение % от числа | Правила перевода Выполнение действий с десятичными дробями | 1 2 |
3 |
3 | Нахождение числа по его % | Правила перевода Нахождение %, соответствующего данному числу Выполнение действий с десятичными дробями | 1 2
2 | 5
|
4 | Задание с графическим содержанием | Решение задания Изображения круговой диаграммы | 2 3
| 5
|
5 | Определение объёма фигур | Выбор способа решения задачи Знание формул объемов Решение задачи | 2 1 2 | 5 |
Итоговая контрольная работа по математике за курс 5 класса
Цель: проверка реализации ГОСО за курс 5 класса:
-умение выполнять действия с обыкновенными и десятичными дробями;
-умение решать задачу на проценты;
-умение решать уравнения;
-знание понятия развернутого угла, умение строить угол с помощью транспортира;
-знание
формулы объема прямоугольного параллелепипеда и его применение к решению задач.
Текст работы:
1 вариант | 2 вариант |
№ 1. Вычислите: | |
∙ + 6 : 1 — 6,7
| ∙ — 3 : 7 + 8,4
|
№ 2. Решите задачу: | |
За один день ученик прочитал 36 страниц книги, что составляет 12% всех страниц книги. Сколько всего страниц в книге?
| В классе 18 девочек, что составляет 60% всех учеников класса. Сколько всего учеников в классе? |
№3. Решите уравнение: | |
(0,95х – 1,82): 1,7 = 3,4
| (0,85х – 1,72): 1,3 = 2,6 |
№ 4. | |
1. Луч ВК делит развернутый угол АВС на два угла так, что градусная мера угла АВК в 3,5 раза больше градусной меры угла СВК. Чему равны градусные меры углов АВК и СВК. Постройте данные углы.
| 4. Луч ВК делит развернутый угол АВС на два угла так, что градусная мера угла АВК в 6,2 раза меньше градусной меры угла СВК. Чему равны градусные меры углов АВК и СВК. Постройте данные углы. |
№ 5. Решите задачу: | |
5. Даны два прямоугольных параллелепипеда. Длина одного параллелепипеда в 4 раза больше длины другого, ширина – в 6 раз больше ширины другого, высота – в 8 раз меньше высоты другого. Объем какого из параллелепипедов больше? Во сколько раз?
| 5. |
|
|
Критерии оценивания | |
«5» | 24-25 баллов |
«4» | 18-23 балла |
«3» | 10-17 баллов |
«2» | менее 10 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % соотношение |
Дробные числа и действия над ними |
№1 |
|
|
20% |
Процент | №2 |
|
|
20% |
Уравнения |
|
№3 |
|
20% |
Угол |
| №4 |
| 20% |
Объем тела |
|
| №5 | 20% |
Итого | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполненное задание |
1
| Решение примера на порядок действий | 1) Знание порядка действий | 1 балл | 5 баллов |
2)Умение выполнять умножение и деление обыкновенных дробей | 2 балла | |||
3)Умение выполнять сложение и вычитание дробей | 2 балла | |||
2 | Решение задачи на проценты | 1)Краткая запись задачи | 1 балл | 5 баллов |
2)Знание способа решения задачи | 1 балл | |||
3) Вычислительная техника | 3 балла | |||
3 | Решение уравнения | 1)Знание связи между компонентами уравнения | 2 балла | 5 баллов |
2)Вычислительная техника | 3 балла | |||
4 | Решение задачи на построение углов | 1) Знание понятия развернутого угла | 1 балл | 5 баллов |
2)Составление уравнения по задаче | 1 балл | |||
3) Решение уравнения 4) Построение углов | 1 балл 2 балла | |||
5 | Решение задачи на вычисление объема прямоу-гольного парал-лелепипеда | 1) Знание формулы объема параллелепипеда | 1 балл | 5 баллов |
2) Решение задачи | 2 балла | |||
3) Анализ результатов | 2 балла |
Урок математики 5 класс «Сложение и вычитание дробей с одинаковыми знаменателями.
 Решение уравнений» | Учебно-методический материал по математике (5 класс):
Решение уравнений» | Учебно-методический материал по математике (5 класс):Опубликовано 29.01.2021 — 13:22 — Зангирова Ксения Николаевна
видео урока математики в 5 класса. Тема «Сложение и вычитание дробей с одинаковыми знаменателями. Решение уравнений». Урок разработан в рамках участия в конкурсе «Учитель года 2021».
Материалы в архиве:
1. Видео урока по ссылке
https://dnevnikru-my.sharepoint.com/:v:/g/personal…
2. Технологическая карта урока математики
3. Раздаточный материал
4. Презентация к уроку
Скачать:
Реклама
Подтяните оценки и знания с репетитором Учи.ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Записаться >
Предварительный просмотр:
Технологическая карта урока
Класс 5Д
Тема: Сложение и вычитание дробей с одинаковыми знаменателями. Решение уравнений
Решение уравнений
Цель: формирование навыков сложения и вычитания дробей с одинаковыми знаменателями; способствовать развитию математической грамотности; оперативной памяти, произвольного внимания, наглядно-действенного мышления; воспитывать культуру поведения при фронтальной, индивидуальной и групповой работе.
Универсальные учебные действия: личностные – способность к самооценке на основе критерия успешности учебной деятельности; регулятивные – умения определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке, работать коллективно по составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки, планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение; коммуникативные – умения оформлять свои мысли в устной форме; слушать и понимать речь других, совместно договариваться о правилах поведения и общения и следовать им; познавательные – умение ориентироваться в своей системе знаний.
Планируемый образовательный результат: знать правила сложения и вычитания дробей с одинаковыми знаменателями, уметь безошибочно выполнять сложение и вычитание дробей с одинаковыми знаменателями, уметь решать уравнения (на основе зависимости компонентов).
Основные понятия: сложение и вычитание дробей с одинаковыми знаменателями, уравнения.
Ресурсы: презентация, раздаточный материал
Организация пространства: фронтальная работа, индивидуальная работа, работа в парах.
этап | Деятельность учителя/ задания урока | Деятельность обучающихся | УУД |
Организационный (1мин) | Добрый день. Проверьте свою готовность к уроку. Присаживайтесь. Откройте тетради, запишите дату и «классная работа» Перед Вами «Карта урока». В ходе урока Вы будете решать задания, в графу «Отметка о выполнении» поставить «+», если задание выполнено полностью верно; «-» — если задание выполнено не верно. | Приветствуют учителя. Открывают тетради, записывают дату и тему урока | |
Мотивационный. Актуализация знаний (5 мин) | Вспомните, какую тему мы с Вами изучаем. Как сложить (вычесть) с одинаковыми знаменателями? Чтобы узнать тему урока, я предлагаю Вам отгадать кроссворд, по вертикали выделено кодовое слово сегодняшнего урока. (задаются вопросы кроссворда) Сформулируйте тему и цель урока. Вспомним правила решения уравнений. Соотнесите определение с определяемым понятием, используя стрелки. | Называют тему, которую изучают. Говорят правила. Отгадывают кроссворд, называют кодовое слово. Формулируют тему и цель урока. Выполняют задание на соотнесение. | познавательные – умение ориентироваться в своей системе знаний |
Решение задач 1з – 2 мин 2 з – 5 мин 3з – 3 мин Физминутка – 1 мин 4з – 4 мин 5з – 5 мин 6з – 10 мин | 1 задание. Найди ошибку. На экране представлено решение уравнения. Найдите ошибку и объясните почему. 2 задание. Решите уравнение, выбрав одно из предложенных. (Проверка решения) В каких заданиях мы можем еще встретить уравнение? Давайте вспомним алгоритм решения задачи с помощью уравнения. 3 задание. Собрать алгоритм. Расставьте в верной последовательности алгоритм решения задачи на уравнение. Физминутка 4 задание. Составить уравнение по краткой записи. Работа в парах над составлением уравнения. (Каждому ряду дана своя схема) 5 задание. Заполни пропуски в решении задачи с помощью уравнения 6 задание. | Выполняют предложенные задания. | личностные – способность к самооценке на основе критерия успешности учебной деятельности; регулятивные – умения определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке, работать коллективно по составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки, планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение; коммуникативные – умения оформлять свои мысли в устной форме; слушать и понимать речь других, совместно договариваться о правилах поведения и общения и следовать им; познавательные – умение ориентироваться в своей системе знаний. |
Рефлексия. | При подведении итогов урока заполните таблицу «Знаю – хочу узнать», поставив «+» напротив предложения в соответствующую колонку Сколько знаков «+» Вы поставили в колонку «знаю», «хочу узнать» Блиц-опрос Подведем итог тому, что сегодня повторяли на уроке:
Расшифруй слово | Заполняют таблицу, отвечают на вопросы учителя. | личностные – способность к самооценке на основе критерия успешности учебной деятельности; регулятивные – оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки |
Домашнее задание (1 мин) | Выполните дз, осуществив выбор
| Записывают дз |
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
Урок математики 5 класс
Слайд 2
Карта урока
Слайд 3
1 2 3 4 5 6 7
Слайд 4
у м е н ь ш а е м о е д р о б ь з н а м е н а т е л ь в ы ч и т а н и е р а з н о с т ь с л о ж е н и е н ч и с л и т е л ь е
Слайд 5
Сложение и вычитание дробей с одинаковыми знаменателями. Решение уравнений
Слайд 6
Определение Определяемое понятие Чтобы найти ___________, надо из суммы вычесть известное слагаемое Уменьшаемое Чтобы найти __________, надо к разности прибавить вычитаемое Уравнение Равенство, содержащее неизвестное Слагаемое Чтобы найти ______, надо из уменьшаемого вычесть разность Корень уравнение Значение неизвестного, при подстановке которого в уравнение получаем верное числовое равенство. Вычитаемое
Вычитаемое
Слайд 7
Найди ошибку
Слайд 8
Решите уравнение (одно на выбор)
Слайд 9
Проверка Ответ: Ответ:
Слайд 10
Проверка Ответ:
Слайд 11
Составьте алгоритм Прочитать задачу Составить уравнение Истолковать результат в соответствии с условием задачи. Составить краткую запись по условию задачи. Определить, что необходимо взять за x . Решить уравнение. Записать ответ.
Слайд 12
Составьте алгоритм Прочитать задачу Составить краткую запись по условию задачи. Определить, что необходимо взять за x . Составить уравнение Решить уравнение. Истолковать результат в соответствии с условием задачи. Записать ответ.
Слайд 13
Составьте уравнение по условию задачи
Слайд 15
Заполни пропуски На родительском собрании класса родителями было решено пойти в поход на г. Азов. Решили сходить в субботу. Выйти от школы в 9 часов утра. В поход собрались 9 мальчиков и 8 девочек класса. За первые 30 минут прошли всего пути, за следующие 30 минут еще некоторую часть путь. Оказалось, что за час было пройдено всего пути. Какая часть пути была пройдена за вторые 30 минут? Первые 30 мин — Вторые 30 мин — ?
Оказалось, что за час было пройдено всего пути. Какая часть пути была пройдена за вторые 30 минут? Первые 30 мин — Вторые 30 мин — ?
Слайд 16
Пусть x – часть пути, которую школьники прошли за вторые 30 минут. Тогда всего они прошли По условию задачи известно, что за час они прошли пути. Составим уравнение пути прошли школьники за вторые 30 минут. Ответ: пути прошли школьники за вторые 30 минут.
Слайд 17
Решите задачу, составив уравнение Осенью мы с классом посетили природный парк в Нижнесергинском районе «Оленьи ручьи». Весь путь до парка составил 140 км, на весь путь потратили 2 часа 20 минут. За первый час мы проехали всего пути. За 1 час 20 минут – оставшийся путь. Какую часть пути мы проехали за 1 час 20 минут? Сколько километров составляет вторая часть пути?
Слайд 19
«Знаю – хочу узнать» Знаю Хочу узнать Сложение дробей с одинаковыми знаменателями Вычитание дробей с одинаковыми знаменателями Нахождение неизвестного слагаемого Дробную черту можно заменить знаком «деление» Нахождение неизвестного уменьшаемого Выделение целой части из неправильной дроби Нахождение неизвестного вычитаемого Представление смешанного числа в неправильную дробь Сравнение обыкновенных дробей с одинаковыми числителями Сравнение обыкновенных дробей с одинаковыми знаменателями
Слайд 20
М О Л Ц Д Ы М О Л Ц Д Ы
Слайд 21
Домашнее задание Решите задачу из Яндекс. Учебника Решите уравнения по ссылке в интерактивной тетради Skysmart : https:// edu.skysmart.ru/student/tiguvikito Составьте задачу, которую можно решить уравнением и запишите ее решение.
Учебника Решите уравнения по ссылке в интерактивной тетради Skysmart : https:// edu.skysmart.ru/student/tiguvikito Составьте задачу, которую можно решить уравнением и запишите ее решение.
Предварительный просмотр:
Задания для урока
Кроссворд
1 | ||||||||||||||
2 | ||||||||||||||
3 | ||||||||||||||
4 | ||||||||||||||
5 | ||||||||||||||
6 | ||||||||||||||
7 | ||||||||||||||
у | м | е | н | ь | ш | а | е | м | о | е | ||||
д | р | о | б | ь | ||||||||||
з | н | а | м | е | н | а | т | е | л | ь | ||||
в | ы | ч | и | т | а | н | и | е | ||||||
р | а | з | н | о | с | т | ь | |||||||
с | л | о | ж | е | н | и | е | |||||||
н | ||||||||||||||
ч | и | с | л | и | т | е | л | ь | ||||||
е |
Вопросы:
- Как называются компонент действия, из которого вычитают?
- Запись вида называется…
- Число, которое показывает, на сколько частей разделили целое.

- С помощью какого арифметического действия можно найти, на сколько одно число больше другого?
- Результат вычитания.
- Результатом какого арифметического действия является значение суммы.
- Число, которое показывает, сколько равных частей от целого взяли.
Соотнесите определение и определяемое понятие
Определение | Определяемое понятие |
Чтобы найти ___________, надо из суммы вычесть известное слагаемое | Уменьшаемое |
Чтобы найти __________, надо к разности прибавить вычитаемое | Уравнение |
Равенство, содержащее неизвестное | Слагаемое |
Чтобы найти ______, надо из уменьшаемого вычесть разность | Корень уравнение |
Значение неизвестного, при подстановке которого в уравнение получаем верное числовое равенство. | Вычитаемое |
1 задание. Найди ошибку
2 задание. Решите уравнение (выбор)
3 задание. Собрать алгоритм
- Прочитать задачу
- Составить уравнение
- Истолковать результат в соответствии с условием задачи.
- Составить краткую запись по условию задачи.
- Определить, что необходимо взять за x.
- Решить уравнение.
- Записать ответ.
(1,4,5,2,6,3,7)
4 задание. Составьте уравнение по условию задачи
5 задание. Заполни пропуски.
На родительском собрании класса родителями было решено пойти в поход на г. Азов. Решили сходить в субботу. Выйти от школы в 9 часов утра. В поход собрались 9 мальчиков и 8 девочек класса. За первые 30 минут прошли всего пути, за следующие 30 минут еще некоторую часть путь. Оказалось, что за час было пройдено всего пути. Какая часть пути была пройдена за вторые 30 минут?
Первые 30 мин —
Вторые 30 мин — ?
Пусть x – часть пути, которую школьники прошли за вторые 30 минут.
Тогда всего они прошли
По условию задачи известно, что за час они прошли пути. Составим уравнение
пути прошли школьники за вторые 30 минут.
Ответ: пути прошли школьники за вторые 30 минут.
6 задание. Решите задачу, составив уравнение.
Осенью мы с классом посетили природный парк в Нижнесергинсокм районе «Оленьи ручьи». Весь путь до парка составил 140 км, на весь путь потратили 2 часа 20 минут. За первый час мы проехали всего пути. За 1 час 20 минут – оставшийся путь. Какую часть пути мы проехали за 1 час 20 минут? Сколько километров составляет вторая часть пути?
Рефлексия.
Знаю | Хочу узнать | |
Сложение дробей с одинаковыми знаменателями | ||
Вычитание дробей с одинаковыми знаменателями | ||
Нахождение неизвестного слагаемого | ||
Дробную черту можно заменить знаком «деление» | ||
Нахождение неизвестного уменьшаемого | ||
Выделение целой части из неправильной дроби | ||
Нахождение неизвестного вычитаемого | ||
Представление смешанного числа в неправильную дробь | ||
Сравнение обыкновенных дробей с одинаковыми числителями | ||
Сравнение обыкновенных дробей с одинаковыми знаменателями |
По теме: методические разработки, презентации и конспекты
Урок по математике «Сложение и вычитание дробей с одинаковыми знаменателями»
Цель урока: научить складывать и вычитать дроби с одинаковыми знаменателями. ..
..
Конспект урока математики «Сложение и вычитание дробей с одинаковыми знаменателями», 7 класс
Конспект урока математики в 7 классе коррекционной школы VIII вида по теме «Сложение и вычитание дробей с одинаковыми знаменателями»….
Заготовка для интерактивной доски к уроку в 5 классе по теме: «Сложение и вычитание дробей с одинаковыми знаменателями. Решение задач»
Данная заготовка предназначена для использования на уроке интерактивной доски TRUMPH BOARD. Исользуется на этапе повторения, устного счета, самопроверке,физкультминутке. Также содержит ребус, со…
Технологическая карта урока по математике «Сложение и вычитание дробей с одинаковыми знаменателями» 5 класс
Технологическая карта урока…
Урок математики Сложение и вычитане дробей с одинаковыми знаменателями 5 класс
Урок математики…
Урок математики в 5 классе Тема урока: Сложение и вычитание дробей с одинаковыми знаменателями.
Урок математики в 5 классе Тема урока: Сложение и вычитание дробей с одинаковыми знаменателями. …
…
Математика. 5 класс. Тема: «Сложение и вычитание дробей с одинаковыми знаменателями». Выражения дробей. Презентация. К учебнику Н. Виленкина.
Презентация для интерактивной доски для 5 класса на тему Сложения и Вычитания дробей. Сделано с помощью программы OpenOffice….
Поделиться:
Решение уравнений с дробями — Математика и Английский
Математика 6 класс уравнения с дробями и иксом
Порой кажется, что на уроках по математике чем дальше, тем сложнее. Но на самом деле все темы, как кирпичики: если разобрался с дробями и уравнениями — решать дробные уравнения будет легко. Об этом и расскажем. Поехали!
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде A/b, где A — числитель дроби, B — знаменатель. Есть два формата записи:
Есть два формата записи:
- обыкновенный вид — ½ или a/b, десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное. Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
Что поможет в решении:
- если А не равно нулю, то у уравнения единственный корень: х = −b : а; если А равно нулю, а B не равно нулю — у уравнения нет корней; если А и B равны нулю, то корень уравнения — любое число.
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют Дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как Область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: Произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка; умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение; делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую. Избавимся от знаменателя. Умножим каждый член уравнения на х.
Умножим каждый член уравнения на х.
Пример 2. Найти корень уравнения
Область допустимых значений: х ≠ −2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2) Избавимся от знаменателя. Умножим каждый член уравнения на х.
Пример 3. Решить дробное уравнение:
Пример 2. Найти корень уравнения
Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую. Избавимся от знаменателя. Умножим каждый член уравнения на х.
Такие уравнения еще называют дробно-рациональными.
Skysmart. ru
01.03.2019 19:42:17
2019-03-01 19:42:17
Источники:
Https://skysmart. ru/articles/mathematic/reshenie-uravnenij-s-drobyami
Уравнения с дробями | Математика » /> » /> .keyword { color: red; }
Математика 6 класс уравнения с дробями и иксом
Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами.
Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами.
Сначала на примере одного линейного уравнения с дробями рассмотрим оба способа решения.
1 способ: Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Приводим к общему знаменателю дроби в каждой части уравнения:
Это — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:
При делении чисел с разными знаками получаем отрицательное число. По правилу деления дробей :
После сокращения имеем:
(В данном случае ответ можно записать и в виде десятичной дроби: х=-0,8).
Обе части уравнения умножим почленно на наименьший общий знаменатель всех входящих в него дробей, в данном случае он равен 24:
При умножении на знаменатель дроби сокращаются, в знаменателе остается единица, которую не пишем. От линейного уравнения с дробями перешли к линейному уравнению с целыми числами:
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части уравнения делим на число, стоящее перед иксом:
Как видите, второй способ существенно упрощает решение линейного уравнения с дробями.
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей. Здесь он равен 60:
Вместо линейного уравнения с дробями получили линейное уравнение с целыми числами. Неизвестные переносим в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Сокращаем дробь на 3:
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей:
В результате линейное уравнение с дробями заменили на линейное уравнение с целыми числами:
Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Это простейшее линейное уравнение.
Www. for6cl. uznateshe. ru
05.03.2018 3:08:10
2018-03-05 03:08:10
Источники:
Http://www. for6cl. uznateshe. ru/uravneniya-s-drobyami/
Тесты по теме Решение уравнений онлайн | Online Test Pad » /> » /> .keyword { color: red; }
Математика 6 класс уравнения с дробями и иксом
Тест по теме: Решение уравнений — МАТЕМАТИКА 6 КЛАСС Для того чтобы выполнить данный тест, вам необходимо ознакомиться с учебным материалом, который представлен здесь, либо открыть учебник на стр. 239-241 и прочитать параграф 41.
239-241 и прочитать параграф 41.
Простейшие тригонометрические уравнения
Тест включает в себя следующие вопросы: 1) нахождение значений аркфункций 2) решение уравнений вида sinx=a 3) решение уравнений вида cosx=a 4) решение уравнений вида tg x=a В тесте 77 вопросов, из которых в случайном порядке для решения выбирается 20.
Уравнения. Математика 5 класс.
Тест предназначен для контроля знаний по теме «Решение уравнений» в 5 классе
Решение уравнений и решение задач с помощью уравнений
Контрольный тест по математике 6 класс по теме «Решение уравнений и задач с помощью уравнений» (Мерзляк и др)
Решение задач на составление уравнения.
Тест для обучающихся 6-7 классов. Предназначен для проверки знаний, умений, навыков по теме «Решение задач на составление уравнения».
Теорема Виета
Тема «Теема Виета». Тест предназначен для первичной проверки усвоения материала по теме. Проверяет минимальный уровень. Состоит из пяти вопросов с выбором ответа. В последнем задании предполагается выбор нескольких вариантов ответа. Может быть использован на первом уроке по теме (уроке открытия нового знания) как самостоятельная работа.
Состоит из пяти вопросов с выбором ответа. В последнем задании предполагается выбор нескольких вариантов ответа. Может быть использован на первом уроке по теме (уроке открытия нового знания) как самостоятельная работа.
Решение уравнений и решение задач с помощью уравнений
Тест математика 6 класс по теме решение уравнений и задач с помощью уравнений
Вычислить без программ и калькулятора Часть 2
Тест предназначен для учеников 9-11 классов для проверки умения нестандартных вычислений. Тест требует следующих знаний и умений: 1) введение новой(-ых) переменной (-ых) 2) разложения многочлена на множители 3) свойств квадратичного трехчлена 4) нахождение целых корней многочлена Дан пример решения вначале каждого вопроса
Решение простейших тригонометрических уравнений
Решить простейшие тригонометрические уравнения, используя справочный материал
Самостоятельная работа по теме «Уравнения». 6 класс
Самостоятельная работа представляет собой тест и посвящена решению уравнений. На прохождение теста отводится 1 час 30 минут.
На прохождение теста отводится 1 час 30 минут.
Решение уравнений
Тест по математике для учащихся 7 классов по теме: Преобразования и решение уравнений с использованием тестовых заданий открытого типа (выбор из вариантов), и закрытого типа — ввода численных ответов.
Деление на десятичную дробь. Уравнения.
Тест предназначен для контроля знаний по теме «Деление десятичных дробей. Решение уравнений» в 5 классе. За каждое правильно выполненное задвание выставляется 1 балл. Количество попыток ограничено.
Линейное уравнение с двумя переменными
Тест по теме «Линейное уравнение с двумя переменными. Корни линейного уравнения с двумя переменными»
Решение линейных уравнений (со скобками)
В тест включены задания на решение линейных уравнений, в записи которых есть скобка. В тест случайным образом выбираются 5 уравнений из общей базы заданий. Сколько уравнений верно решите, такая и будет оценка. Время выполнения не ограничено.
Иррациональные уравнения-2
Тест предназначен для проверки, полученных знаний по теме «Иррациональные уравнения»
Алгебра 7 класс решите уравнение
Данный тест предназначен для контроля знаний по алгебре учащихся 7 классов по теме» УРАВНЕНИЕ»
Экзамен по математике 1 курс 2 семестр вариант 1 группа 511
Количество вопросов в тесте: 12. Количество вопросов в тесте: 12. Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Введите в поле ответа полученный результат и только после этого приступайте к выполнению следующего задания. В тесте 12 вопросов с кратким ответом. Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 38.02.01 Экономика и бухгалтерский учет по отраслям.
Итоговый тест по теме Таблица умножения и деления с числами 6-8
Закрепление знаний по таблице умножения и деления с числами 7-8
Подготовка к ВПР по математике 7 класс (задание №9 — решение уравнений)
Данный тест по теме «Решение линейных уравнений» в 7 классе, предназначен для отработки полученных знаний, подготовке к ВПР
Тест по теме: «Решение вычислительных задач на компьютере»
Тест содержит 10 обязательных вопросов теоретического характера и 1 практический вопрос, который является необязательным для выполнения, оценка за него выставляется дополнительная. Максимальное количество баллов -15 (100%) Оценка за тест выставляется системой автоматически, в соответствии со следующей таблицей: Процент выполнения задания Отметка 95% и более «5» 75% — 94% «4» 50% — 74% «3» Менее 50% «2»
Максимальное количество баллов -15 (100%) Оценка за тест выставляется системой автоматически, в соответствии со следующей таблицей: Процент выполнения задания Отметка 95% и более «5» 75% — 94% «4» 50% — 74% «3» Менее 50% «2»
Показательные уравнения
Тест по теме «Показательные уравнения». Проверяем навыки решения простейших показательных уравнений.
Решение уравнений в 7-9 классах
Тест предназначен для проверки знаний учащихся 7-9 классов по решению уравнений.
Решение уравнений 6 класс
Данный тест предназначен для закрепления материала по теме «Решение уравнений». Очень внимательно читайте задание и инструкцию к работе. Желаю удачи.
Решение уравнений
Тест по теме «Решение уравнений» предназначен для учащихся 6 класса
Контрольная работа «Действия с десятичными дробями» 5 класс
Контрольная работа «Действия с десятичными дробями» для 5 класса состоит из прмеров на все действи с десятичными дробями, уравнения, задач на действия с десятичными дробями.
Контрольная работа по теме «Решение уравнений» 6 или 7 класс
Данный тест предназначен для закрепления материала по теме «Решение уравнений». Очень внимательно читайте задание и инструкцию к работе. Желаю удачи.
Итоговая контрольная работа, 6 класс
В тесте проверяются темы » Уравнение. Свойства умножжения. Координатная плоскость»
Тест по теме «Решение уравнений»
Тест предназначен для проверки знаний по теме «Решение уранвений» на уроке математике в 6 классе
Экзамен по математике 1 курс 2 семестр вариант 2 группа 511
Количество вопросов в тесте: 12 Количество вопросов в тесте: 12. Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Введите в поле ответа полученный результат и только после этого приступайте к выполнению следующего задания. В тесте 12 вопросов с кратким ответом. Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 38. 02.01 Экономика и бухгалтерский учет по отраслям.
02.01 Экономика и бухгалтерский учет по отраслям.
Экзамен по математике 2 курс 4 семестр вариант 2 1121
Количество вопросов в тесте: 12. Количество вопросов в тесте: 12 Количество вопросов в тесте: 12. Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Введите в поле ответа полученный результат и только после этого приступайте к выполнению следующего задания. В тесте 12 вопросов с кратким ответом. Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 09.01.01 Наладчик аппаратного и программного обеспечения.
Экзамен по математике 2 курс 4 семестр вариант 1 группа 1121
Количество вопросов в тесте: 12 Количество вопросов в тесте: 12. Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Введите в поле ответа полученный результат и только после этого приступайте к выполнению следующего задания. В тесте 12 вопросов с кратким ответом. Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 09.01.01 Наладчик аппаратного и программного обеспечения.
Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 09.01.01 Наладчик аппаратного и программного обеспечения.
Экзамен по математике 1 курс 2 семестр вариант 1 группа 1211
Количество вопросов в тесте: 12. Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Введите в поле ответа полученный результат и только после этого приступайте к выполнению следующего задания. В тесте 12 вопросов с кратким ответом. Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 09.02.07 Информационные системы и программирование.
Экзамен по математике 1 курс 2 семестр вариант 2 группа 1211
Количество вопросов в тесте: 12. Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Введите в поле ответа полученный результат и только после этого приступайте к выполнению следующего задания. В тесте 12 вопросов с кратким ответом. Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 09.02.07 Информационные системы и программирование.
Тест предназначен для студентов среднеспециальных учебных заведений, обучающихся по специальности 09.02.07 Информационные системы и программирование.
Контрольный тест по математике 6 класс по теме «Решение уравнений и задач с помощью уравнений» (Мерзляк и др)
Тест для обучающихся 6-7 классов. Предназначен для проверки знаний, умений, навыков по теме «Решение задач на составление уравнения».
Тест предназначен для проверки знаний учащихся 7-9 классов по решению уравнений.
Onlinetestpad. com
25.05.2018 23:28:47
2018-05-25 23:28:47
Источники:
Https://onlinetestpad. com/ru/tests/solving-equations
Уравнения с десятичными дробями. Уравнения с десятичными дробями 5 класс.
- Альфашкола
- Статьи org/ListItem»>Уравнения с десятичными дробями
Давайте разберем как проще решать уравнения с десятичными дробями и покажем это на примере. Алгоритм решения десятичных уравнений не отличается от решения обычных уравнений, то есть надо найти неизвестное. Напомним правило, как решать уравнения:
Пример 1. Решите уравнение \(2,5+1,2x=1,7+1,6x\)
Решение: 1 способ
\(2,5+1,2x=1,7+1,6x\)
\(2,5-1,7=1,6x-1,2x\)
\(0,8=0,4x\)
\(x = 2\)
Решение: 2 способ
\(2,5+1,2x=1,7+1,6x\)
Домножим обе части уравнения на 10:
\(25+12x=17+16x\)
\(25-17=16x-12x\)
\(8=4x\)
\(x=2\)
Ответ: \(x=2\)
Пример 2. Решите уравнение \(2,5(6+2x)+4,2=1,2-5,5x\)
Решение:
\(2,5(6-2x)+4,2=1,2-8x\)
\(15-5x+4,2=1,2-8x\)
\(19,2-1,2=5x-8x\)
\(18=-3x\)
\(x =-6\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Юрий Викторович Седнев
Репетитор по математике
Стаж (лет)
Образование:
Российский химико-технологический университет (б.МХТИ) имени Д.И.Менделеева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-11 классов и биология 5-11 классы. Подготовка к ОГЭ, ЕГЭ. Преподаватель философии и экономики. Химия — самая интересная наука, связывает все естествознание, точные науки и физику с жизнью, биологией и медициной. Ее нужно знать и сдавать в разные вузы, особенно медицинские. Я участвовал и готовил участников олимпиад всех уровней, от местных до международных, занимаюсь интеграцией, развитием и связью образования и науки, «от школы до нобелевских». Автор электронных учебных материалов и пособий для поступающих по химии.
Подготовка к ОГЭ, ЕГЭ. Преподаватель философии и экономики. Химия — самая интересная наука, связывает все естествознание, точные науки и физику с жизнью, биологией и медициной. Ее нужно знать и сдавать в разные вузы, особенно медицинские. Я участвовал и готовил участников олимпиад всех уровней, от местных до международных, занимаюсь интеграцией, развитием и связью образования и науки, «от школы до нобелевских». Автор электронных учебных материалов и пособий для поступающих по химии.
Иван Владимирович Чикин
Репетитор по математике
Стаж (лет)
Образование:
Рязанский государственный университет имени С.А. Есенина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Более пяти лет успешно готовлю учеников к сдаче ОГЭ и ЕГЭ, кроме того могу помочь развить разговорные навыки, подтянуть школьную программу. Обучаю в основном по учебникам иностранных издательств, но беру лучшее от классической школы. Ученик это в первую очередь личность со своими интересами и стремлениями, так что всегда нахожу индивидуальный подход.
Обучаю в основном по учебникам иностранных издательств, но беру лучшее от классической школы. Ученик это в первую очередь личность со своими интересами и стремлениями, так что всегда нахожу индивидуальный подход.
Марине Альбертовна Симонян
Репетитор по математике
Стаж (лет)
Образование:
Ереванский госпединститут русского и иностранных языков им. В.Я.Брюсова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор русского языка и литературы 1-11 классов. Давно влюблена в русский язык! Считаю, что языки призваны развивать интеллект, а языковое мышление — первая ступень в развитии логического мышления. Имея богатый опыт преподавательской и репетиторской деятельности, смогу передать свои знания и помогу в решении учебных задач.
Давно влюблена в русский язык! Считаю, что языки призваны развивать интеллект, а языковое мышление — первая ступень в развитии логического мышления. Имея богатый опыт преподавательской и репетиторской деятельности, смогу передать свои знания и помогу в решении учебных задач.
Похожие статьи
- Трапеция, средняя линия трапеции
- Основные формулы производной
- Простейшие уравнения с модулем
- Сколько одно число составляет в процентах от другого?
- РУДН: Прикладная информатика (учебный план, проходной балл)
- Подготовка к контрольной работе по геометрии
- Как написать каноническое и параметрическое уравнение прямой, образованной пересечением плоскостей
- Месяц до каникул: как помочь ребенку продержаться?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Обыкновенные дроби, часть 3.
 5 класс
5 классПохожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Обыкновенные дроби
часть 35 класс
— Сложение дробей с одинаковыми
знаменателями.
— Вычитание дробей с одинаковыми
знаменателями.
— Решение уравнений.
— Решение задач.
Чтобы сложить дроби с
одинаковыми знаменателями, надо
сложить их числители, а знаменатель
оставить прежним.
3
3+1
1
=
+
=
8
8
8
3
3+5
5
=
+
=
8
8
8
4
8
8
=
8
1
Чтобы вычесть дроби с одинаковыми
знаменателями, надо из числителя
уменьшаемого вычесть числитель вычитаемого, а
знаменатель оставить прежним.

3
3-1
1
2
=
=
8
8
8
8
3
3
=
8
8
0
При решении уравнений
необходимо пользоваться правилами
решения уравнений, свойствами
сложения и вычитания.
Решение уравнений с
использованием правил.
Решение уравнений с
применением свойств.
51
32
;
+х =
85
85
32
51
х =
;
85 85
19
х =
.
85
19
Ответ:
85
Выражение в левой части уравнения
Подсказка 1
является суммой.
слагаемоеПодсказка
+ слагаемое
2 = сумма.
Чтобы найди неизвестное
слагаемое, Подсказка
надо из суммы
3 вычесть
известное слагаемое.
12
78
;
— у =
90
90
78 12
у =
;
90 90
66
у =
.
90
66
Ответ:
90
Выражение в левой части уравнения
Подсказка 1
является разностью.
уменьшаемое – вычитаемое =
Подсказка 2
разность
Чтобы найди неизвестное
вычитаемое,Подсказка
надо из уменьшаемого
3
вычесть разность.

8
11
а=
;
25
25
8
11
а =
+
;
25
25
19
а =
.
25
19
Ответ:
25
Выражение в левой части уравнения
Подсказка 1
является разностью.
уменьшаемое – вычитаемое =
Подсказка 2
разность
Чтобы найди неизвестное
уменьшаемое,
Подсказка
надо к3разности
прибавить вычитаемое.
7
3
+( х +
=
19
19
3
18
+х =
19
19
3
11
+х=
;
19
19
11 3
х=
;
19 19
8
х =
.
19
18
;
19
7
;
19
ИСПОЛЬЗОВАНИЕ ПРАВИЛ
РЕШЕНИЯ УРАВНЕНИЙ.
В левой части уравнения
Подсказка 1
выражение является суммой.
Неизвестное содержится в
Подсказка 2
слагаемом.
8
Ответ:
19
(
37 5
— ( +у =
44 44
5
37
+у =
44
44
5
20
+у=
;
44
44
20 5
у=
;
44 44
15
у =
.
44
17
;
44
17
;
44
ИСПОЛЬЗОВАНИЕ ПРАВИЛ
РЕШЕНИЯ УРАВНЕНИЙ.

В левой части уравнения
Подсказка 1
выражение является разностью.
Неизвестное содержится в
Подсказка 2
вычитаемом.
15
Ответ:
44
(
18 8
21
b+
=
;
73 73 73
В левой части уравнения
18 21 8
Подсказка 1
выражение является разностью.
b+
=
;
+
73 73 73
18 = 29
b+
;
Неизвестное содержится в
Подсказка 2
73 73
уменьшаемом.
29 18
b=
;
73 73
11
11
b =
Ответ:
.
73
73
ИСПОЛЬЗОВАНИЕ ПРАВИЛ
РЕШЕНИЯ УРАВНЕНИЙ.
7
3
+( х +
=
19
19
7
3
+
+х =
19 19
10
18
+х=
;
19
19
18 10
х=
;
19 19
8
х =
.
19
18
;
19
18
;
19
ПРИМЕНЕНИЕ СВОЙСТВ
СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В левой части уравнения можно
применить Подсказка
сочетательное
1 свойство
сложения .
Чтобы к числу прибавить сумму ,
можно к этому числу прибавить
Подсказка 2
сначала одно слагаемое, а потом
другое.

8
Ответ:
19
(
37 5
— ( +у =
44 44
37 5
-у =
44 44
32
17
— у=
;
44
44
32 17
у=
;
44 44
15
у =
.
44
17
;
44
17
;
44
ПРИМЕНЕНИЕ СВОЙСТВ
СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В левой части уравнения можно
применить
Подсказка
свойство вычитания
1
суммы из числа. .
Чтобы из числа вычесть сумму,
можно вычесть
Подсказка
сначала
2
одно
слагаемое, а потом другое.
15
Ответ:
44
(
18 8
b+
=
73 73
18 8
+b =
73 73
10
21
+ b=
;
73
73
21 10
b=
;
73 73
11
b =
.
73
21
;
73
21
;
73
ПРИМЕНЕНИЕ СВОЙСТВ
СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В левой части уравнения можно
применить
Подсказка
свойство вычитания
1
числа из суммы.
Чтобы вычесть число из суммы,
можно сначала вычесть это число
Подсказка 2
из одного слагаемого, а потом
прибавить другое.

11
Ответ:
73
15. Решение задач.
В первый день Саша прочитал 924
книги, а во второй день — 9 книги.
Сколько страниц прочитал Саша за два
дня, если в книге 144 страницы?
144 стр.
2
9
4
9
6
9
2
4
9
9
1) + = (книги) – прочитал Саша за 2 дня.
2) 144 : 9 ∙ 6 = 96 (стр.)
Ответ: За 2 дня Саша прочитал 96 страниц.
16. Решение задач.
5В первый день Маша прочитала 12
4
книги, а во второй день — 12 книги.
Сколько страниц в книге, если Маша за
два дня прочитала 36 страниц?
36 стр.
5
4
12
12
5 + 4 = 9 (книги) – прочитала Маша за 2 дня.
12 12 12
1)
2) 36 : 9 ∙ 12 = 48 (стр.)
Ответ: В книге 48 страниц.
English Русский Правила
5.1 Уравнения с дробями | Простые уравнения
5.1 Повторить решение простых уравнений
В прошлом году вы узнали, что алгебраическое уравнение представляет собой математическое предложение, содержащее
комбинации чисел, символов, переменных и математических операторов. Алгебраическое уравнение всегда имеет равенство
знак. Вы также узнали, что мы решаем уравнение, когда находим значение переменной, которая делает
уравнение истинно. Это называется раствором уравнения. Например, цифра 2
решение уравнения
.
Алгебраическое уравнение всегда имеет равенство
знак. Вы также узнали, что мы решаем уравнение, когда находим значение переменной, которая делает
уравнение истинно. Это называется раствором уравнения. Например, цифра 2
решение уравнения
.
алгебраическое уравнение Алгебраическое уравнение — это математическое предложение, содержащее комбинацию чисел, символов, переменных и математических операторов. Он всегда имеет знак равенства.
решить Когда мы решаем уравнение, мы находим значение переменной, которая делает уравнение верным.
решение Решением уравнения является значение переменной, которая делает уравнение верным.
В следующем рабочем примере показано, как решить простое уравнение.
Рабочий пример 5.1: Решение простой уравнение и проверка решения
Решите следующее уравнение и проверьте решение:
Шаг 1: Раскройте скобки по дистрибутивному закону.
\начать{выравнивать} 2(х+4)+х&=-2(х+1)+20 \\ 2х+8+х&=-2х-2+20 \\ 3x+8&=-2x+18 \end{выравнивание} Если по обе стороны от
уравнение, соберите их.
Если по обе стороны от
уравнение, соберите их.Шаг 2: Используйте аддитивные обратные уравнения, чтобы расположить уравнение так, чтобы все члены с переменными находились на слева, а все постоянные члены справа.
Не забудьте сделать то же самое с обеих сторон уравнения.
\начать{выравнивать} 2(х+4)+х&=-2(х+1)+20 \\ 2х+8+х&=-2х-2+20 \\ 3x+8&=-2x+18 \\ 3x+8{\color{red}{\;-\;8}}{\color{green}{\;+\;2x}} &=-2x{\color{green}{\;+\;2x }}+18 {\color{red}{\;-\;8}} \\ \end{выравнивание}Шаг 3: Упростите обе части уравнения.
\начать{выравнивать} 2(х+4)+х&=-2(х+1)+20 \\ 2х+8+х&=-2х-2+20 \\ 3x+8&=-2x+18 \\ 3x+8{\color{red}{\;-\;8}}{\color{green}{\;+\;2x}} &=-2x{\color{green}{\;+\;2x }}+18 {\color{red}{\;-\;8}} \\ 3x+2x &=18-8 \\ 5x &=10 \end{выравнивание}Шаг 4: Если у переменной есть коэффициент, примените мультипликативное значение, обратное коэффициенту.
\начать{выравнивать} 2(х+4)+х&=-2(х+1)+20 \\ 2х+8+х&=-2х-2+20 \\ 3x+8&=-2x+18 \\ 3x+8{\color{red}{\;-\;8}}{\color{green}{\;+\;2x}} &=-2x{\color{green}{\;+\;2x }}+18 {\color{red}{\;-\;8}} \\ 3x+2x &=18-8 \\ 5x &=10 \\ {\ color {оранжевый} {\ frac {1} {5} \ times}} \ frac {5x} {1} & = {\ color {orange} {\ frac {1} {5} \ times}} \ frac {10}{1} \\ \end{выравнивание} Запомни
сделать это с обеих сторон уравнения.
Запомни
сделать это с обеих сторон уравнения.Шаг 5: Упростите обе части уравнения.
\начать{выравнивать} 2(х+4)+х&=-2(х+1)+20 \\ 2х+8+х&=-2х-2+20 \\ 3x+8&=-2x+18 \\ 3x+8{\color{red}{\;-\;8}}{\color{green}{\;+\;2x}} &=-2x{\color{green}{\;+\;2x }}+18 {\color{red}{\;-\;8}} \\ 3x+2x &=18-8 \\ 5x &=10 \\ {\ color {оранжевый} {\ frac {1} {5} \ times}} \ frac {5x} {1} & = {\ color {orange} {\ frac {1} {5} \ times}} \ frac {10}{1} \\ \frac{5x}{5}&=\frac{10}{5} \\ \поэтому х&=2 \end{выравнивание}Шаг 6. Проверьте свое решение.
\начать{выравнивать} \text{LHS}&=2(x+4)+x \\ &=2(2+4)+2 \\ &=2(6)+2 \\ &=12+2\\ &=14 \end{выравнивание} Замените переменную в левой части (LHS) исходного .
уравнение с решением. Вычислите значение левой части.
Замените переменную в левой части (LHS) исходного .
уравнение с решением. Вычислите значение левой части.Шаг 7: Повторите шаг 6 для правой части (RHS) исходного уравнения .
\начать{выравнивать} \text{RHS}&=-2(x+1)+20 \\ &=-2(2+1)+20 \\ &=-2(3)+20 \\ &=-6+20\\ &=14 \end{выравнивание}Шаг 8: Сравните свои ответы на шагах 6 и 7. Если они совпадают, ваше решение верно. Если бы не ты где-то ошибся. Решите уравнение еще раз.
Решение верное.
Упражнение 5.1. Решите простые уравнения и проверьте решения
Решите каждое из следующих уравнений и проверьте решения.
\начать{выравнивать} 13+3&=2x-3+3 \новая строка 16&=2x\новая строка \frac{16}{2}&=\frac{2x}{2} \newline 8&=х\новая строка \поэтому х&=8 \end{выравнивание}
а также значит точно так же.

Проверка:
\начать{выравнивать} 13&=2(8)-3 \новая строка 13&=16-3 \новая строка 13&=13 \новая строка \поэтому \text{левый}&=\текст{правый} \end{выравнивание}\начать{выравнивать} 39&=21+7q-4q \новая строка 39&=21+3q \новая строка 39-21&=21-21+3q \новая строка 18&=3q \новая строка \frac{18}{3}&=\frac{3q}{3} \newline 6&=q \новая строка \поэтому q&=6 \end{выравнивание}
Проверка:
\начать{выравнивать} 39&=21+5(6)-4(6)+2(6) \новая строка 39&=21+30-24+12 \новая строка 39&=63-24 \новая строка 39&=39 \новая строка \поэтому \text{левый}&=\текст{правый} \end{выравнивание}\начать{выравнивать} 2(у+3)&=10 \\ 2у+6&=10\\ 2у+6-6&=10-6 \\ 2у&=4\\ \frac{2y}{2}&=\frac{4}{2} \\ \поэтому у&=2 \end{выравнивание}
Проверка:
\начать{выравнивать} 2(2+3)&=10 \\ 2(5)&=10 \\ 10&=10\\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}\начать{выравнивать} 2(у+1)&=6(у-1) \\ 2у+2&=6у-6\\ 2у+2-2-6у &= 6у-6у-6-2 \\ -4y&=-8\\ \frac{-4y}{-4}&=\frac{-8}{-4} \\ \поэтому у&=2 \end{выравнивание}
Проверка:
\начать{выравнивать} 2(у+1)&=6(у-1) \\ 2(2+1)&=6(2-1) \\ 2(3)&=6(1) \\ 6&=6 \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}\начать{выравнивать} 2(5а-3)-5(7а-3)&=2а \\ 10а-6-35а+15&=2а\\ -25а+9&= 2а \\ -25а+9-9-2а&=2а-2а-9\\ -27а&=-9\ \frac{-27a}{-27}&=\frac{-9}{-27} \\ \поэтому a&=\frac{1}{3} \end{выравнивание}
Проверка:
\начать{выравнивать} 2(5а-3)-5(7а-3)&=2а \\ 2(\frac{5}{1} \times \frac{1}{3}-3) — 5(\frac{7}{1} \times\frac{1}{3}-3)&=\ frac{2}{1}\times\frac{1}{3} \\ 2(\frac{5}{3}-\frac{9}{3})-5(\frac{7}{3}-\frac{9}{3})&=\frac{2}{3} }\\ \frac{2}{1}(\frac{-4}{3})-\frac{5}{1}(\frac{-2}{3})&=\frac{2}{3}\ \ \frac{-8}{3}+\frac{10}{3}&=\frac{2}{3}\\ \frac{2}{3}&=\frac{2}{3} \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}
5.
 2 Решение уравнений с дробями
2 Решение уравнений с дробямиВ прошлом году вы научились решать простые уравнения с дробями. В следующем рабочем примере показано, как решить уравнение с дробями, имеющими константы в качестве знаменателей.
Рабочий пример 5.2: Решение уравнения с дробями, в знаменателях которых есть константы
Решите следующее уравнение и проверьте решение:
Шаг 1: Найдите на ЖК-дисплее знаменатели.
ЖК-дисплей 3 и 6 равен 6.
Шаг 2: Умножьте все члены уравнения с ЖК-дисплеем из шага 1.
\начать{выравнивать} {\color{red}{\frac{6}{1}\times}} \frac{2x-1}{3}&=\frac{5x-1}{6}{\color{red}{\times \фракция{6}{1}}}\\ \end{выравнивание}Обратите внимание, что мы делаем одно и то же с обеих сторон уравнения.
Шаг 3: Для каждого члена уравнения найдите HCF знаменателя члена и LCD из шага 1.
 Разделите на HCF. 91}}{1}\\
2(2x-1)&=5x-1
\конец{выравнивание} \]
Разделите на HCF. 91}}{1}\\
2(2x-1)&=5x-1
\конец{выравнивание} \]Помните, что число или переменная остаются неизменными, если вы делите или умножаете их на 1, для пример а также .
Шаг 5: Решите уравнение.
\начать{выравнивать} 2(2x-1)&=5x-1 \\ 4x-2&=5x-1 \\ 4x-2+2-5x&=5x-5x-1+2 \\ -х&=1 \\ \frac{-x}{-1}&=\frac{1}{-1} \\ \поэтому х&=-1 \end{выравнивание}Шаг 6. Проверьте свое решение. Не забудьте подставить решение вместо переменной в оригинал уравнение.
\начать{выравнивать} \frac{2x-1}{3}&=\frac{5x-1}{6} \\ \frac{2(-1)-1}{3}&=\frac{5(-1)-1}{6} \\ \frac{-2-1}{3}&=\frac{-5-1}{6}\\ \frac{-3}{3}&=\frac{-6}{6} \\ -1&=-1 \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}
Упражнение 5.2. Решение уравнения с дробями, в знаменателе которых есть константы
Решите каждое из следующих уравнений и проверьте решения. 5}{1} \\
х-1&=5\\
х-1+1&=5+1 \\
\поэтому х&=6
\конец{выравнивание} \]
91}{1} \\
2(b-1)&=b+1\\
2b-2&=b+1 \\
2b-b-2+2&=b-b+1+2\\
\поэтому b&=3 \\
\конец{выравнивание} \]
5}{1} \\
х-1&=5\\
х-1+1&=5+1 \\
\поэтому х&=6
\конец{выравнивание} \]
91}{1} \\
2(b-1)&=b+1\\
2b-2&=b+1 \\
2b-b-2+2&=b-b+1+2\\
\поэтому b&=3 \\
\конец{выравнивание} \]
Проверка:
\начать{выравнивать} \frac{3-1}{2}&=\frac{3+1}{4} \\ \frac{2}{2}&=\frac{4}{4} \\ 1&=1 \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}В следующем рабочем примере показано, как решить уравнение с дробями, в состав которых входят переменные. знаменатели.
Рабочий пример 5.3: Решение уравнения с дробями, имеющими переменные знаменатели
Решите следующее уравнение и проверьте решение:
Шаг 1: Найдите на ЖК-дисплее знаменатели.
Найдите на ЖК-дисплее числа в знаменателях:
- Простые множители знаменателей:
- ЖК-дисплей:
Найти ЖК переменных в знаменателях:
- Единственная переменная:
Шаг 2: Умножьте все члены уравнения на ЖК-дисплей из шага 1.
\начать{выравнивать} {\ color {red} {\ frac {12x} {1} \ times}} \ frac {2x + 1} {3} + {\ color {red} {\ frac {12x} {1} \ times}} \ frac{5}{12x}&=\frac{3}{4x}{\color{red}{\times\frac{12x}{1}}} +\frac{2x}{3}{\color{red }{\times\frac{12x}{1}}}\\ \end{выравнивание}
Обратите внимание, что мы умножаем каждый член в обеих частях уравнения на ЖКД.
92-5\
4x&=4\\
\frac{4x}{4}&=\frac{4}{4} \\
\поэтому х&=1
\end{выравнивание}Шаг 6. Проверьте свое решение. Не забудьте заменить переменную решением в исходном . уравнение.
\начать{выравнивать} \frac{2(1)+1}{3}+\frac{5}{12(1)}&=\frac{3}{4(1)}+\frac{2(1)}{3} \\ \frac{3}{3}+\frac{5}{12}&=\frac{3}{4}+\frac{2}{3} \\ \frac{12}{12}+\frac{5}{12}&=\frac{9}{12}+\frac{8}{12}\\ \frac{17}{12}&=\frac{17}{12} \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание} 9{2а}}{1}\\ 8&=4а \\ \frac{8}{4}&=\frac{4a}{4}& \\ 2&=а \\ \поэтому а&=2 \end{выравнивание}Проверка:
\начать{выравнивать} \frac{8}{6(2)}&=\frac{2}{3} \\ \frac{8}{12}&=\frac{2}{3} \\ \frac{2}{3}&=\frac{2}{3} \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}\начать{выравнивать} \frac{2y}{1}\times\frac{3}{2}-\frac{2y}{1}\times\frac{4}{y}&=1\times\frac{2y}{1} \\ \frac{\cancel{2y}^y}{1}\times\frac{3}{\cancel 2^1}-\frac{\cancel{2y}^2}{1}\times\frac{4} {\ отменить у ^ 1} & = \ гидроразрыва {2y} {1} \\ 3г-8&=2г\\ 3у-2у-8+8&=2у-2у+8\\ \поэтому у&=8 \\ \end{выравнивание} 91}}+\frac{1}{5}&=\frac{1}{\frac{-5}{2}}\\ \frac{3}{1}\times \frac{1}{-5}+\frac{1}{5}&=\frac{1}{1}\times\frac{2}{-5} \ \ -\frac{3}{5}+\frac{1}{5}&=-\frac{2}{5} \\ -\frac{2}{5}&=-\frac{2}{5} \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}
Помните, что деление на дробь равносильно умножению на обратную величину дробная часть.
 3}{1} \\
7б+15&=б-3\
7б+15-15-б&=б-3-б-15\\
6б&=-18\
\frac{6b}{6}&=\frac{-18}{6} \\
\поэтому b&=-3
\конец{выравнивание} \]
3}{1} \\
7б+15&=б-3\
7б+15-15-б&=б-3-б-15\\
6б&=-18\
\frac{6b}{6}&=\frac{-18}{6} \\
\поэтому b&=-3
\конец{выравнивание} \]Проверка:
\начать{выравнивать} \frac{7}{15}+\frac{1}{-3}&=\frac{1}{15}-\frac{1}{5(-3)} \\ \frac{7}{15}-\frac{5}{15}&=\frac{1}{15}+\frac{1}{15}\\ \frac{2}{15}&=\frac{2}{15} \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}Помните, что вычитание числа равносильно добавлению аддитивной инверсии числа. Например .
\[ \начать{выравнивать} \frac{72x}{1}\times\frac{1}{4x}+\frac{72x}{1}\times\frac{5}{9х}{1} \\ 18+40х-36&=60+х\\ 18-18+40х-36+36-х&=60+х-х-18+36\\ 39х&=78\\ \frac{39x}{39}&=\frac{78}{39} \\ \поэтому х&=2 \конец{выравнивание} \]
Проверка:
\начать{выравнивать} \frac{1}{4(2)}+\frac{5}{9}-\frac{3}{6(2)}&=\frac{5}{6(2)}+\frac{1 {72} \\ \frac{1}{8}+\frac{5}{9}-\frac{3}{12}&=\frac{5}{12}+\frac{1}{72}\\ \frac{9}{72}+\frac{40}{72}-\frac{18}{72}&=\frac{30}{72}+\frac{1}{72}\\ \frac{31}{72}&=\frac{31}{72} \\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}
В главе 4 вы узнали, что многочлен — это алгебраическое выражение с двумя или более членами, одно из которых может быть
константа, а остальные члены состоят из коэффициентов при переменных, возведенных в положительные степени. Бином имеет два
термины, например
. В следующем рабочем примере показано, как решить уравнение с дробями.
которые имеют биномиальные знаменатели.
Бином имеет два
термины, например
. В следующем рабочем примере показано, как решить уравнение с дробями.
которые имеют биномиальные знаменатели.
Рабочий пример 5.4: Решение уравнения с дробями, имеющими биномиальные знаменатели
Решите следующее уравнение и проверьте решение:
Шаг 1: Найдите на ЖК-дисплее знаменатели.
Рассматривайте каждый знаменатель как коэффициент LCD. Следовательно, LCD двух знаменателей: .
Шаг 2: Умножьте все члены уравнения с ЖК-дисплеем из шага 1.
\начать{выравнивать} {\ color {red} {\ frac {(x-3) (2x + 1)} {1} \ times}} \ frac {1} {x-3} & = \ frac {3} {2x + 1} {\ цвет {красный} {\ раз \ гидроразрыва {(x-3) (2x + 1)} {1}}} \\ \end{выравнивание} 91}{1}}}\\ \конец{выравнивание}\]Шаг 4: Умножьте коэффициенты, оставшиеся в каждом члене.
 1 (а-1)} {1} \\
2(2а+1)&=1(а-1) \\
4а+2&=а-1\\
4а+2-2-а&=а-а-1-2 \\
3а&=-3 \\
\frac{3a}{3}&=\frac{-3}{3}\\
\поэтому а&=-1
\конец{выравнивание} \]
91}{1} \\
2(3b-1)&=1(3b+2) \\
6б-2&=3б+2\\
6б-2+2-3б&=3б-3б+2+2 \\
3b&=4 \\
\frac{3b}{3}&=\frac{4}{3}\\
\поэтому b&=\frac{4}{3}
\конец{выравнивание} \]
1 (а-1)} {1} \\
2(2а+1)&=1(а-1) \\
4а+2&=а-1\\
4а+2-2-а&=а-а-1-2 \\
3а&=-3 \\
\frac{3a}{3}&=\frac{-3}{3}\\
\поэтому а&=-1
\конец{выравнивание} \]
91}{1} \\
2(3b-1)&=1(3b+2) \\
6б-2&=3б+2\\
6б-2+2-3б&=3б-3б+2+2 \\
3b&=4 \\
\frac{3b}{3}&=\frac{4}{3}\\
\поэтому b&=\frac{4}{3}
\конец{выравнивание} \]Проверка:
\начать{выравнивать} \frac{2}{\frac{3}{1}\times\frac{4}{3}+2}&=\frac{1}{\frac{3}{1}\times\frac{4} {3}-1} \\ \frac{2}{4+2}&=\frac{1}{4-1}\\ \frac{2}{6}&=\frac{1}{3}\\ \frac{1}{3}&=\frac{1}{3}\\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание} 91(2г+1)}{1} \\ 2(у+3)&=3(2у+1) \\ 2у+6&=6у+3\\ 2у+6-6-6у&=6у-6у+3-6 \\ -4y&=-3 \\ \frac{-4y}{-4}&=\frac{-3}{-4}\\ \поэтому y&=\frac{3}{4} \конец{выравнивание} \]Проверка:
\начать{выравнивать} \ frac {\ frac {3} {4} + \ frac {3} {1}} {\ frac {2} {1} \ times \ frac {3} {4} + \ frac {1} {1}} &=1\разрыв{1}{2} \\ \ frac {\ frac {3} {4} + \ frac {12} {4}} {\ frac {6} {4} + \ frac {4} {4}} & = \ frac {3} {2} \\ \ гидроразрыва {15} {4}} {\ гидроразрыва {10} {4}} & = \ гидроразрыва {3} {2} \\ \frac{15}{4}\times\frac{4}{10}&=\frac{3}{2}\\ \frac{15}{10}&=\frac{3}{2}\\ \frac{3}{2}&=\frac{3}{2}\\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание} 91}&=0 \\ 3(х+3)-2(х-8)&=0 \\ 3x+9-2x+16&=0 \\ 3x+9-2x+16&=0 \\ х+25&=0 \\ х+25-25&=-25 \\ \поэтому х&=-25\\ \конец{выравнивание} \]Проверка:
\начать{выравнивать} \frac{3}{-25-8}-\frac{2}{-25+3}&=0 \\ \frac{3}{-33}-\frac{2}{-22}&=0\\ \frac{1}{-11}+\frac{1}{11}&=0\\ 0&=0\\ \поэтому \text{левый}&=\текст{правый} \end{выравнивание}
5.
 3 Использование уравнений для решения задач
3 Использование уравнений для решения задачУравнения чрезвычайно полезны при решении задач, которые описываются словами. В предыдущие годы вы узнали, что эти шаги могут быть использованы для решения проблемы, которая описана словами:
- Поймите проблему: Внимательно прочитайте вопрос несколько раз. Определите информацию, которую вы имеют. Убедитесь, что вы знаете, что спрашивают. Может поможет нарисовать картинку.
- Составьте план: Определите неизвестное(ые). Сделать одного неизвестным . Если неизвестных несколько, выразите их все через . Напишите уравнение, которое можно использовать для решения задачи.
- Выполнить план: Решить уравнение.
- Оглянитесь назад: Проверьте свои решения. Убедитесь, что вы даете ответы на все, что было спросил.
Рабочий пример 5.5: Решение задачи с помощью уравнение
Мать старше дочери на 30 лет.
Пять лет назад возраст дочери составлял одну седьмую часть возраст матери. Подсчитайте, сколько лет матери и ее дочери в настоящее время.
Шаг 1: Разберитесь в проблеме.
- Дано: Мать старше дочери на 30 лет
- Дано: Пять лет назад возраст дочери был возраста матери
- Вопрос: Настоящий возраст матери и дочери
Шаг 2: Разработайте план.
- Настоящий возраст дочери:
- Настоящий возраст матери:
- Возраст дочери пять лет назад:
91}{1} \\
7(х-5)&=х+25 \\
7х-35&=х+25\\
7х-х-35+35&=х-х+25+35 \\
6х&=60\\
\frac{6x}{6}&=\frac{60}{6} \\
\поэтому х&=10
\конец{выравнивание} \]
Следовательно:
- Настоящий возраст дочери: лет
- Настоящий возраст матери: лет
Шаг 4: Оглянитесь назад.
 5}{1} \\
5&=5 \\
\поэтому \text{левый}&=\текст{правый}
\конец{выравнивание} \]
5}{1} \\
5&=5 \\
\поэтому \text{левый}&=\текст{правый}
\конец{выравнивание} \]Дочери в настоящее время 10 лет, а матери в настоящее время 40 лет.
Упражнение 5.5. Использование уравнений для решения задач
Ваш класс собирается в автобусную поездку, и вы хотите купить еды и воды для поездки. В каком-то магазине, Пакеты арахиса стоят в пять раз дороже, чем пакетики воды. Если вы потратите \(₦\,250\) на пакетиках с водой и \(₦\,500\) на пачках арахиса можно купить 35 пакетиков воды и пачек вообще арахис. Определить стоимость пакетика воды и стоимость пакета арахиса. 91} &=\фракция{35x}{1} \\ 350&=35х\\ \frac{35x}{35}&=\frac{350}{35} \\ \поэтому х&=10 \конец{выравнивание} \]
Цена пакетика с водой .
Цена пакета арахиса составляет .Периметр квадрата на 21 единицу длиннее половины одной из его сторон.
 Вычислите длину его стороны.
Вычислите длину его стороны.Пусть длина стороны будет .
Тогда периметр равен . 91}{1}+\frac{21}{1}\times\frac{2}{1} \\ 8x&=x+42 \\ 8х-х&=х-х+42 \\ \frac{7x}{7}&=\frac{42}{7} \\ \поэтому х&=6 \конец{выравнивание} \]Длина стороны 6 единиц.
Ширина прямоугольника на одну единицу больше, чем одна треть его длины. Периметр прямоугольника 34 единицы. Определить длину и ширину прямоугольника.
Пусть длина будет . 91}&=\frac{32}{1}\times\frac{3}{1}\\ 6x+2x&=96 \\ 8х&=96\\ \frac{8x}{8}&=\frac{96}{8} \\ \поэтому х&=12 \конец{выравнивание} \]
Длина 12 шт.
Ширина 5 единиц.Если к числу прибавить 15, то одна треть ответа будет равна удвоению числа. Определить число.
Пусть число будет .
 1}&=\frac{2x\times 3}{1} \\
х+15&=6х\\
х-6х+15-15 &= 6х-6х-15 \\
-5x&=-15\\
\frac{-5x}{-5}&=\frac{-15}{-5} \\
\поэтому х&=3 \\
\конец{выравнивание} \]
1}&=\frac{2x\times 3}{1} \\
х+15&=6х\\
х-6х+15-15 &= 6х-6х-15 \\
-5x&=-15\\
\frac{-5x}{-5}&=\frac{-15}{-5} \\
\поэтому х&=3 \\
\конец{выравнивание} \]Число 3.
Восемнадцать бананов и двадцать семь тамариндов должны быть разделены между группой детей. Один ребенок в группа не хочет никаких бананов. Остальные дети получают одинаковое количество бананов. Два дополнительных дети присоединяются к группе, когда тамаринды делятся и все получают одинаковое количество тамариндов. количество бананов на ребенка равно количеству тамариндов на ребенка. Сколько детей было в оригинальная группа? 91}{1} \\ 18(х+2)&=27(х-1) \\ 18х+36 &= 27х-27\\ 18x-27x+36-36 &= 27x-27x-27-36 \\ -9x&=-63\\ \frac{-9x}{-9}&=\frac{-63}{-9} \\ \поэтому х&=7 \\ \конец{выравнивание} \]
В исходной группе было 7 детей.
5.4 Резюме
- Алгебраическое уравнение – это математическое предложение, содержащее комбинацию чисел, символов, переменных и
математические операторы.
 Он всегда имеет знак равенства.
Он всегда имеет знак равенства. - Решением уравнения является значение переменной, которая делает уравнение верным.
- Когда мы решаем уравнение, мы находим значение переменной, которая делает уравнение верным.
- Чтобы решить уравнения с дробями, мы можем следовать этому методу:
- Найдите на ЖК-дисплее знаменатели.
- Умножьте все члены уравнения на ЖКД знаменателей.
- Для каждого члена уравнения разделите на HCF знаменателей этого члена и LCD.
- Умножьте множители, оставшиеся в каждом члене.
- Решите уравнение.
- Проверьте решение.
- Мы можем выполнить следующие шаги, чтобы решить проблему, которая описана словами:
- Поймите проблему, внимательно прочитав ее.
- Составьте план, определив неизвестные и написав уравнение.
- Выполните план, решив уравнение.
- Оглянитесь назад, проверив свое решение.

Уравнения с дробями — Полный курс алгебры
Навыки
в
A L G E B R A
Содержание | Дом
24
Очистка фракций
2-й уровень
ЧТОБЫ РЕШИТЬ УРАВНЕНИЕ С Дробями, мы преобразуем его в уравнение без дробей, которое мы знаем, как решать. Техника называется очисткой фракций.
Пример 1. Решите для 90 559 x 90 560 :
| x 3 | + | x − 2 5 | = 6, |
Решение . Очистить дроби следующим образом:
Умножьте обе части уравнения — каждый член — на НОК знаменателей. Тогда каждый знаменатель будет равен разделить на его кратное. Тогда у нас получится уравнение без дробей.
НОК 3 и 5 равно 15. Поэтому умножьте обе части уравнения на 15.
| 15 · | x 3 | + | 15 · | x − 2 5 | = 15 · 6 |
Слева умножьте каждое слагаемое на 15. Теперь каждый знаменатель будет делиться на 15 — это и есть точка — и у нас получится следующее простое уравнение, «очищенное» от дробей:
| 5 х + 3( х — 2) | = | 90. |
| Легко решается следующим образом: | ||
| 5 x + 3 x − 6 | = | 90 |
| 8 x | = | 90 + 6 |
| x | = | 96 8 |
| = | 12. | |
Мы говорим «умножить» обе части уравнения, тем не менее мы пользуемся тем фактом, что порядок, в котором мы умножаем или делим, не имеет значения. (Урок 1.) Поэтому мы делим НОК сначала на каждый знаменатель и таким образом очищаем дроби.
Мы выбираем число , кратное каждого знаменателя, потому что тогда каждый знаменатель будет его делителем.
Пример 2. Очистить дроби и решить для x :
| x 2 | − | 5 x 6 | = | 1 9 |
Решение . НОК 2, 6 и 9 равно 18. (Урок 23 арифметики.) Умножьте обе части на 18 — и сократите.
9 x − 15 x = 2.
На самом деле не обязательно писать 18. Ученик должен просто посмотреть на и увидеть, что 2 будет входить в число 18 девять (9) раз. Таким образом, этот член становится равным 9 x .
Таким образом, этот член становится равным 9 x .
Далее, посмотрите на и убедитесь, что 6 превратится в 18 три (3) раза. Таким образом, этот член становится равным 3 90 585 · 90 586 -5 90 559 x 90 560 = -15 90 559 x 90 560 .
Наконец, посмотрите на , и вы увидите, что 9 превратится в 18 два (2) раза. Таким образом, этот член становится равным 2 · 1 = 2,
.Вот очищенное уравнение, за которым следует его решение:
| 9 x − 15 x | = | 2 | |
| −6 x | = | 2 | |
| x | = | 2 −6 | |
| x | = | — | 1 3 |
Пример 3. Решите для 90 559 x 90 560 :
Решите для 90 559 x 90 560 :
½(5 х — 2) = 2 х + 4,
Решение . Это уравнение с дробью. Очистить дроби, умножив обе части на 2:
| 5 х − 2 | = | 4 x + 8 |
| 5 x − 4 x | = | 8 + 2 |
| x | = | 10. |
В следующих задачах очистите дроби и решите для x :
Чтобы увидеть каждый ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
| Проблема 1. | x 2 | — | x 5 | = | 3 |
LCM
10. Вот очищенное уравнение и его решение: Вот очищенное уравнение и его решение: | |||||
| 5 x | − | 2 х | = | 30 | |
| 3 x | = | 30 | |||
| х | = | 10. | |||
При решении любого уравнения с дробями в следующей строке вы пишете —
5 x − 2 x = 30
— должно быть , а не дробей.
| Задача 2. | x 6 | = | 1 12 | + | x 8 |
LCM
24. Вот очищенное уравнение и его решение: Вот очищенное уравнение и его решение: | |||||
| 4 x | = | 2 + 3 х | |||
| 4 х − 3 х | = | 2 | |||
| х | = | 2 | |||
| Задача 3. | х − 2 5 | + | x 3 | = | x 2 |
| LCM 30. Вот очищенное уравнение и его решение: | |||||
| 6 (х — 2) + 10 х | = | 15 x | |||
| 6 х − 12 + 10 х | = | 15 x | |||
| 16 х − 15 х | = | 12 | |||
| х | = | 12. | |||
Задача 4. Дробь равна дроби.
| х − 1 4 | = | x 7 | |
| LCM 28. Вот очищенное уравнение и его решение: | |||
| 7( х — 1) | = | 4 x | |
| 7 х − 7 | = | 4 x | |
| 7 х − 4 х | = | 7 | |
| 3 x | = | 7 | |
| х | = | 7 3 | |
Мы видим, что когда одна дробь равна одной дроби, уравнение можно очистить путем «перемножения».
| Если | ||||
| а б | = | в г | , | |
| затем | ||||
| объявление | = | до н.э. . | ||
| Задача 5. | x − 3 3 | = | x − 5 2 |
| Вот очищенное уравнение и его решение: | |||
| 2( х — 3) | = | 3( х — 5) | |
| 2 х − 6 | = | 3 х − 15 | |
| 2 х − 3 х | = | − 15 + 6 | |
| − х | = | −9 | |
| х | = | 9 | |
Задача 6. | х — 3 х — 1 | = | x + 1 x + 2 | ||
| Вот очищенное уравнение и его решение: | |||||
| ( х — 3)( х + 2) | = | ( х — 1)( х + 1) | |||
| х ² − х − 6 | = | х ² − 1 | |||
| − х | = | −1 + 6 | |||
| − х | = | 5 | |||
| х | = | −5. | |||
| Задача 7. | 2 x − 3 9 | + | x + 1 2 | = | х − 4 |
| LCM 18. Вот очищенное уравнение и его решение: | |||||
| 4 х — 6 + 9 х + 9 | = | 18 х − 72 | |||
| 13 х + 3 | = | 18 х − 72 | |||
| 13 х − 18 х | = | − 72 − 3 | |||
| −5 90 559 x 90 560 | = | −75 | |||
| х | = | 15. | |||
| Задача 8. | 2 х | − | 3 8 x | = | 1 4 |
| LCM 8 х . Вот очищенное уравнение и его решение: | |||||
| 16 − 3 | = | 2 х | |||
| 2 x | = | 13 | |||
| х | = | 13 2 | |||
2-й уровень
Следующий урок: задачи со словами
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Игры дроби для пятиклассников онлайн
Часто задаваемые вопросы:Q1: Как мы можем умножать дроби?
Ответ: Чтобы умножить дроби, мы умножаем числители обеих дробей, чтобы получить новый числитель, и умножаем знаменатели обеих дробей, чтобы получить новый знаменатель. Затем мы можем упростить полученную дробь, если это возможно. Например, 4/5 х 2/3 = (4 х 2) / (5 х 3) = 8/15.
В2. Как складывать правильные дроби?
Ответ: Чтобы сложить правильные дроби, если знаменатели совпадают, сложите числители, сохраняя знаменатель одинаковым. Чтобы сложить дроби с разными знаменателями, нам сначала нужно преобразовать обе дроби в дроби с общим знаменателем, а затем сложить их так же, как мы складываем одинаковые дроби.
В3. Как вы учите детей складывать и вычитать дроби?
Ответ: Чтобы складывать или вычитать дроби с одинаковыми знаменателями, дети должны складывать или вычитать числители, сохраняя знаменатель одинаковым. Чтобы сложить или вычесть дроби с разными знаменателями, нам сначала нужно преобразовать обе дроби в дроби с общим знаменателем, а затем сложить или вычесть их так же, как мы делали это раньше в случае одинаковых знаменателей.
В4. Как упростить дроби в математике?
Ответ: Мы можем упростить дроби, разделив числитель и знаменатель на их наибольший общий делитель. Например, чтобы упростить 12/18, мы сначала находим наибольший общий делитель 12 и 18, который равен 6. Теперь разделим и числитель, и знаменатель на 6, чтобы получить упрощенную форму 12/18, которая равна 2/3.
В5: В каком классе изучают сложение и вычитание дробей?
Ответ: Складывать и вычитать дроби с одинаковыми знаменателями изучают в 4 классе. А складывать и вычитать дроби с разными знаменателями изучают в 5 классе, где сначала нужно обе дроби преобразовать в дроби с общим знаменателем, а затем сложить или вычитать их так же, как мы делаем с дробями с теми же знаменателями.
А складывать и вычитать дроби с разными знаменателями изучают в 5 классе, где сначала нужно обе дроби преобразовать в дроби с общим знаменателем, а затем сложить или вычитать их так же, как мы делаем с дробями с теми же знаменателями.
В6: Как вы решаете текстовые задачи на деление дробей?
Ответ: Первый шаг — понять задачу со словами, чтобы определить числа или дроби, которые необходимо разделить. Затем разделите полученные числа или дроби, чтобы получить ответ.
В7. Как умножить дробь на целое число?
Ответ: Чтобы умножить дробь на целое число, нужно умножить числитель дроби на целое число, а знаменатель оставить прежним. Это дает нам продукт, и мы можем упростить продукт, если это необходимо.
Дроби вводятся в 3 классе. Это сложная тема для детей этого возраста, поскольку они привыкли только к основным математическим понятиям, таким как счет. Поэтому рекомендуется использовать много математических игр, манипуляций и занятий. Если вы прямо объясните части дроби 3-класснику, это определенно вызовет путаницу. Вместо этого, в реальных жизненных ситуациях, таких как раздача пирожных друзьям или покупка половины/четверти фунта овощей или заправка топливного бака автомобиля на четверть/половину/полностью и т. д.
Если вы прямо объясните части дроби 3-класснику, это определенно вызовет путаницу. Вместо этого, в реальных жизненных ситуациях, таких как раздача пирожных друзьям или покупка половины/четверти фунта овощей или заправка топливного бака автомобиля на четверть/половину/полностью и т. д.
SplashLearn предлагает программу обучения, основанную на деятельности, для достижения четко определенных наборов навыков обучения. Такие действия, как определение дробей и моделирование дробей , дают детям прочную основу для изучения темы.
Математические игры для дробей:
В 5 классе дети переходят от основных понятий дроби к сложению, вычитанию, умножению и делению дробей. Использование математических игр — эффективный способ для относительно сложных тем, подобных этим. Некоторые из математических игр, обсуждаемых ниже, могут улучшить понимание математических операций над дробями.
Сложение с использованием дробных кругов: Количество игроков 2-4
Дробные круги, разрезанные на разные дроби, смешиваются между собой. Каждый ребенок случайным образом берет один дробный круг из лота по мере того, как подходит его/ее очередь. Тот, кто завершает все первым, выигрывает игру.
Каждый ребенок случайным образом берет один дробный круг из лота по мере того, как подходит его/ее очередь. Тот, кто завершает все первым, выигрывает игру.
Игра в кости с дробным сложением: Количество игроков 2–4
Каждый ребенок может бросить кубик со знакомыми дробями, такими как , , , на сторонах. Дроби, брошенные каждым ребенком, каждый раз складываются, и тот, кто первым достигает целого, выигрывает игру. Его можно сделать более интересным, добавив отрицательные дроби, чтобы дети также применяли свойства вычитания.
Построение дробных полос для умножения: Количество игроков 1
Имея квадратную сетку, скажем, размером 10 на 10, построение дробных полос для представления дробей, заданных путем выбора и перетаскивания нужных массивов, может быть учебным занятием. Далее детей нужно заставить построить дробь произведения аналогичным образом.
Математические приемы для обучения дробям
Дроби вводятся в 3 классе с использованием таких приемов, как дробные круги, дробные диаграммы и дробная стенка.
Полоски дробей: Визуальные модели, такие как полоски дробей, очень помогают в объяснении таких понятий, как сложение, вычитание, умножение и деление дробей.
Дополнение:
Вычитание:
Умножение:
Division:
Division:
. :
Дети уже в 4 классе знакомы со сложением и вычитанием дробей с одинаковыми знаменателями.
В 5 классе дети узнают, как складывать дроби с разными знаменателями.
Рассмотрим пример сложения дробей ½ и ¼.
Это может быть представлено полосами дробей, как показано на рисунке.
Поскольку знаменатели не совпадают, нельзя просто сложить числители, чтобы сложить две дроби.
Здесь первым шагом является оценка первой дроби, если бы целое было разделено на 4.
При делении целого на четыре равные части первая дробь будет иметь вид:
То есть заштрихованы две части из четырех. Это эквивалентно затенению одной части из двух.
Это эквивалентно затенению одной части из двух.
Таким образом, эквивалентно .
Итак, сложение можно представить как:
Алгебраически сложение можно выполнить как + .
Дети уже умеют находить равные дроби, умножая числитель и знаменатель на одно и то же число. Итак, первое правило сложения разных дробей — писать слагаемые с одинаковым знаменателем, используя равнозначные дроби. Тогда дроби подобны и могут быть сложены путем сложения числителей.
Например, добавьте .
Умножьте числитель и знаменатель первой дроби на 3, а знаменатель второй дроби — на 4. Итак, добавьте:
+ .
Вычитание дробей можно выполнять по тому же правилу.
Например, — .
Дети также используют понятие сложения и вычитания разных дробей в текстовых задачах.
Например, Зинат закончила свой проект с Тиной, а Тина сделала его. Вместе какая часть проекта завершена?
Чтобы найти готовую деталь, нужно сложить две дроби.
. Итак, проект завершен.
Дети также оценивают правильность результатов, сопоставляя размер дополнений.
Например, рассмотрим дроби и . Если сумма этих двух чисел будет записана как путем сложения числителей и знаменателей по отдельности, ребенок 5-го класса может указать, что она неверна, поскольку она меньше половины, тогда как одно из слагаемых равно половине.
Сложение и вычитание смешанных дробей:
Сложение смешанных дробей с разными знаменателями можно смоделировать с помощью дробной полосы, числовой прямой или дробной черты.
Рассмотрим дополнение .
Как складывать дроби в числовой строке, показанной ниже.
Алгебраически это можно сделать двумя способами. Целые части и дробные части и дробные части могут быть добавлены отдельно. То есть
Другой способ — переписать смешанное число в неправильную дробь. Затем сгенерируйте эквивалентные дроби так, чтобы слагаемые имели одинаковый знаменатель. Теперь сложите две одинаковые дроби.
Теперь сложите две одинаковые дроби.
Здесь смешанная дробь может быть записана как . Сложение можно выполнить, как показано ниже:
Добавление различных рабочих листов со смешанными дробями в SplashLearn имеет достаточно проблем, чтобы тщательно попрактиковаться в теме. Некоторые задачи требуют точного ответа, в то время как другие требуют, чтобы ребенок округлил ответ до ближайшей половины. Это также дает практику для концепции округления.
Следующая концепция заключается в вычитании смешанных дробей. Более простой способ — разделить целую и дробную части и вычесть.
Просто ребенку нужно быть особенно осторожным с вычитанием с перегруппировкой.
Например, ребенок может ошибиться в , если разделит целую и дробную части и вычитает.
Это можно сделать следующим образом:
Теперь вычтите.
=
Вычитание, в отличие от задач калькулятора смешанных дробей, в SplashLearn не просто просит детей вводить окончательные ответы, но готовит детей к каждому шагу вычислений, подобных приведенному выше. Также, как и в случае сложения, детей просят округлить сложные дроби до 0, 1 или ½.
Также, как и в случае сложения, детей просят округлить сложные дроби до 0, 1 или ½.
Словесные задачи играют роль моста между теорией и применением темы в математике. Решая словесные задачи на вычитание в отличие от смешанных чисел, дети закрепляют базовые знания и применяют их в реальных жизненных ситуациях.
Дробь в виде деления числителя на знаменатель:
Предположим, что 25 фунтов сахара поровну распределены между 6 людьми. Чтобы найти количество сахара, полученное каждым человеком, нужно 25 разделить на 6. То есть 25 ÷ 6 или . Таким образом, дробь — это еще один способ представления деления. Записывается как деление числителя на знаменатель.
Записав в виде смешанной дроби, каждый человек получит фунты сахара.
Умножение двух дробей:
Умножение всегда представляет собой повторяющееся сложение. То есть умножение дроби на 3 равносильно сложению дроби 3 раза. В 4 классе дроби дети научились умножать дробь на целое число с помощью наглядных моделей, а также методом прямого умножения.
Когда дробь умножается на целое число c, это, по сути, число a, сложенное вместе c раз и разделенное на число c. Представьте, что три бутерброда делят четверо детей. Таким образом, каждый получит по бутерброду. Обратите внимание, что продукт — это, по сути, часть бутерброда, которую получил каждый ребенок, умноженная на количество детей. Таким образом, это произведение в сумме дает общее количество бутербродов, то есть 3.
В 5 классе дети учатся умножать дроби с помощью дробных полосок изначально.
Позже они понимают, что при умножении дробей числители умножаются вместе, как и знаменатель.
То есть . Дети применяют это свойство для прямого умножения дробей.
То есть .
Умножение смешанных дробей:
Рассмотрим умножение двух дробей, хотя бы одна из которых является смешанной дробью. Сначала преобразуйте смешанную дробь в неправильную дробь. Затем умножьте числители и знаменатели отдельно.
Например, чтобы умножить и , сначала перепишите как неправильную дробь, следуя математическому порядку операций.
Теперь умножьте две дроби.
Неправильную дробь можно записать как смешанную дробь как .
Процедура умножения смешанных дробей аналогична.
Теперь уменьшите общие делители двух дробей, которые необходимо умножить.
SplashLearn предоставляет хорошо оформленный рабочий лист по теме умножения смешанных дробей. Там вы можете практиковать навыки и опыт вычислений.
Сложные задачи, такие как нахождение площади прямоугольного бассейна дробных размеров, дают практическое применение вычислений, изученных по теме. Кроме того, дети также решают задачи с более сложными дробями, такими как смешанные дроби, используя аналогичную технику.
Интерпретация умножения как масштабирования
Когда необходимо умножить две дроби, и если мы сравним размер одного из факторов с размером произведения, мы можем фактически предсказать размер произведения в зависимости от размера второго фактор.
Например, рассмотрим дроби и . Второй множитель больше 1. Таким образом, произведение будет числом, большим, чем первый множитель. То есть умножение на дробь, большую 1, расширит вторую дробь.
Второй множитель больше 1. Таким образом, произведение будет числом, большим, чем первый множитель. То есть умножение на дробь, большую 1, расширит вторую дробь.
Аналогично, рассмотрим произведение и . Второй фактор. Таким образом, умножение на сократит значение первого множителя . То есть умножение на дробь меньше 1 приведет к сжатию второй дроби.
SplashLearn предлагает широкий спектр практических задач по этой теме с оценкой возможных значений факторов, а также продукта.
Деление дробей на целые числа:
Рассмотрим задачу на деление, . Переведя это на слова, каков будет размер каждой части, если разделить на 4 равные части?
Это можно представить с помощью дробных полос, как показано на рисунке:
Алгебраически деление на число эквивалентно записи дроби с числом в качестве знаменателя и делимым в качестве числителя. То есть деление эквивалентно умножению на обратное.
Деление на 4 аналогично умножению на .
Рабочие листы для деления дробей на деление единичной дроби на целое число
Словесные задачи, связанные с темой, можно решить либо с помощью дробных полос, как указано выше, либо путем решения уравнений с дробями, которые представляют задачу.
Например, если торт в четверть фунта, то есть фунт, поровну распределен между 5 людьми, то найдите вес торта, который получит каждый человек.
Уравнение, представляющее проблему, .
Решение уравнения, .
То есть каждый человек получит фунтов торта.
Деление целого числа на дробную часть:
Теперь, как разделить целое число на дробную часть?
Яблоки нужно раздать детям по половинке яблока. Если яблок шесть, скольким детям можно их раздать?
Это можно перевести как сколько половинок в целом 6?
Используя символ деления, можно записать это как .
Алгебраически деление 6 на то же самое, что и умножение 6 на .
Дети могут практиковать визуальные модели, а также алгебраическое деление для деления целого числа на единичную дробь в
Дети применяют знания по теме для решения словесных задач, например, сколько одной четвертой может быть подается из 3-х пицц?
То же, что и
Класс 5 Учебный план
Ниже перечислены необходимые навыки со ссылками на ресурсы, которые помогут с этими навыками. Мы также поощряем множество упражнений и работу с книгами. Curriculum Home
Мы также поощряем множество упражнений и работу с книгами. Curriculum Home
Важно: это только руководство.
Обратитесь в местное управление образования, чтобы узнать их требования.
Класс 5 | Умножение
☐ Используйте различные стратегии для умножения трехзначных чисел на трехзначные. Примечание. Умножение на любое число, превышающее трехзначный множитель/множимое, должно выполняться с использованием технологии.
☐ Играть в Математика реакции
☐ Длинное умножение
☐ Длинные рабочие листы умножения
☐ Проверьте свое умножение — таблицы умножения от 2 до 15
☐ Понять, как умножать отрицательные числа
☐ Умножение минусов дает плюс
☐ Целые числа и целые числа
☐ Определение отрицательного значения
☐ Номер строки
☐ Развивайте беглость с фактами умножения до 12x
☐ Определение таблиц умножения
☐ Тренажер по математике — Умножение
☐ Рабочие листы по умножению
☐ Умножение — Таблицы умножения
☐ Советы и рекомендации по умножению
☐ Таблица умножения для печати
☐ Таблица умножения для печати — маленький размер
☐ Проверьте свои математические способности
☐ Проверьте свое умножение — таблицы умножения от 2 до 15
5 класс | Деление
☐ Используйте различные стратегии для деления трехзначных или четырехзначных чисел на однозначные или двузначные числа. Примечание: деление на любое число, большее двузначного делителя, должно выполняться с использованием технологии.
Примечание: деление на любое число, большее двузначного делителя, должно выполняться с использованием технологии.
☐ Рабочие листы отдела математики
☐ Исправьте уравнение
☐ Подразделение
☐ Легко проверить, можно ли разделить одно число на другое без остатка, используя правила делимости.
☐ Правила делимости
☐ Факторы и множители
5 класс | Числа
☐ Чтение и запись целых чисел до миллионов
☐ Поместите значение
☐ Определение целого числа
☐ Упражнение: Досчитай до миллиарда
☐ Признать, что некоторые числа делятся только на единицу и на себя (простые), а другие имеют несколько делителей (составные)
☐ Упражнение: Рисование звезд
☐ Таблица простых чисел и калькулятор
☐ Простые и составные числа
☐ Определение простого числа
☐ Определение составного номера
☐ Список простых чисел
☐ Вычислить кратные целого числа и наименьшее общее кратное двух чисел
☐ Наименьшее общее кратное
☐ Калькулятор наименьших множителей
☐ Наименее распространенное кратное определение
☐ Факторы и множители
☐ Множественное определение
☐ Определите факторы данного числа
☐ Все факторы числа
☐ Определение фактора
☐ Факторизация простых чисел
☐ Правила делимости
☐ Простые и составные числа
☐ Калькулятор простой факторизации
☐ Факторы и множители
☐ Найдите общие делители и наибольший общий делитель двух чисел
☐ Наибольший общий делитель
☐ Калькулятор наибольшего общего коэффициента
☐ Определение наибольшего общего делителя
☐ Определение общего фактора
☐ Факторы и множители
☐ Определение фактора
☐ Вычислить арифметическое выражение, используя порядок операций, включая умножение, деление, сложение, вычитание и круглые скобки
☐ Кронштейны
☐ Умные блоки
☐ Порядок действий — БОДМАС
☐ Порядок действий — PEMDAS
☐ Определение порядка операций
☐ Калькулятор порядка операций
☐ Сравните и упорядочите числа до миллионов
☐ Определение заказа
☐ Номера для заказа
☐ Заказ игры
☐ Округление чисел до сотых и до ближайших 10 000
☐ Округление чисел
☐ Определение округления
☐ Поместите значение
☐ Десятичные числа
☐ Понять структуру разряда в десятичной системе счисления: * 10 единиц = 1 десяток * 10 десятков = 1 сотня * 10 сотен = 1 тысяча * 10 тысяч = 1 десяток тысяч * 10 тысяч = 1 сотня тысяч * 10 сотен тысяч = 1 миллион
☐ Упражнение: Досчитай до миллиарда
☐ Поместите значение
☐ Значение разряда Определение
☐ Понимать разницу между множителем и кратным целому числу,
☐ Факторы и множители
5 класс | Десятичные числа
☐ Сравните десятичные числа, используя , или =
☐ Равно меньше и больше символов
☐ Заказ десятичных знаков
☐ Определение заказа
☐ Заказ игры
☐ Сравните десятичные числа от 0 до 1
☐ Сравните десятичные числа: от -1 до +1
☐ Десятичные числа
☐ Используйте различные стратегии для сложения, вычитания, умножения и деления десятичных долей до тысячных
☐ Сложение десятичных знаков
☐ Деление десятичных дробей
☐ Умножение десятичных дробей
☐ Анимация деления десятичных дробей
☐ Анимация умножения десятичных знаков
☐ Вычитание десятичных дробей
☐ Десятичные рабочие листы
☐ Чтение, запись и упорядочивание десятичных долей до тысячных
☐ Десятичные числа
☐ Заказ игры
☐ Заказ десятичных знаков
☐ Определение заказа
☐ Сравните десятичные числа от 0 до 1
☐ Сравните десятичные числа: от -1 до +1
☐ Равно меньше и больше символов
☐ Преобразование процентов в десятичные дроби
☐ Знакомство с процентами
☐ Определение процента
☐ Десятичные дроби и проценты
☐ Преобразование процентов в десятичные дроби
5 класс | Дроби
☐ Упростить дроби до меньших членов
☐ Упрощение дробей
☐ Рабочие листы дробей
☐ Эквивалентные дроби
☐ Наибольший общий делитель
☐ Дроби
☐ Строка номера дроби
☐ Определение эквивалентных дробей
☐ Преобразование неправильных дробей в смешанные числа, а смешанных чисел в неправильные дроби
☐ Неправильные дроби
☐ Смешанные фракции
☐ Рабочие листы дробей
☐ Определение неправильной дроби
☐ Определение смешанной фракции
☐ Используйте различные стратегии для сложения и вычитания дробей с одинаковыми знаменателями
☐ Добавление дробей
☐ Вычитание дробей
☐ Рабочие листы дробей
☐ Общий знаменатель
☐ Наименьший общий знаменатель
☐ Складывать и вычитать смешанные числа с одинаковыми знаменателями
☐ Добавление дробей
☐ Смешанные фракции
☐ Сложение и вычитание смешанных дробей
☐ Рабочие листы дробей
☐ Вычитание дробей
☐ Оцените суммы и разности дробей с одинаковыми знаменателями.
☐ Сравнение дробей
☐ Добавление дробей
☐ Вычитание дробей
☐ Создать эквивалентные дроби по заданной дроби
☐ Эквивалентные дроби
☐ Рабочие листы дробей
☐ Определение эквивалентных дробей
☐ Упрощение дробей
☐ Дроби
☐ Наибольший общий делитель
☐ Строка номера дроби
☐ Сравнивайте и упорядочивайте дроби, включая разные знаменатели (с использованием и без использования числовой прямой) Примечание. Часто используемые дроби, такие как те, которые могут быть указаны на линейке, мерном стакане и т. д.
☐ Сравните дроби
☐ Сравнение дробей
☐ Строка номера дроби
☐ Заказ игры
☐ Эквивалентные дроби
☐ Сравните доли единиц измерения
☐ Номер строки
☐ Сравните дроби, используя , или =
☐ Сравните доли единиц измерения
☐ Сравните дроби
☐ Сравнение дробей
☐ Равно меньше и больше символов
☐ Заказ игры
☐ Общий знаменатель
☐ Эквивалентные дроби
☐ Складывать, вычитать, умножать и делить дроби (включая смешанные дроби), знаменатели которых являются степенями десятичных дробей.
☐ Деление дробей
☐ Умножение дробей
☐ Рабочие листы десятичных дробей
☐ Обратная дробь
☐ Вычитание дробей
☐ Добавление дробей
☐ Разделить дробь на целое число
☐ Деление дробей на целые числа
☐ Умножить дробь на целое число
☐ Умножение дробей
☐ Выразите десятичные дроби в виде эквивалентной формы дробей со знаменателем в степени 10
☐ Десятичные числа
☐ Рабочие листы десятичных дробей
☐ Таблица дробей/десятичных чисел
☐ Десятичные дроби и проценты
☐ Калькулятор десятичной дроби
☐ Преобразование десятичных дробей в дроби
☐ Преобразование процентов в дроби
☐ Знакомство с процентами
☐ Преобразование процентов в дроби
☐ Десятичные дроби и проценты
☐ Определение процента
5 класс | Проценты
☐ Поймите, что процент означает часть 100
☐ Знакомство с процентами
☐ Определение процента
☐ Преобразование дробей или десятичных знаков в проценты
☐ Десятичные дроби и проценты
☐ Преобразование дробей в проценты
☐ Преобразовать десятичные дроби в проценты
5 класс | Соотношения
☐ Понимание концепции соотношения
☐ Соотношения
☐ Ratio — приготовить шоколадные чипсы
☐ Ratio — Рецепт шоколадных чипсов
☐ Определение коэффициента
☐ Экспресс-коэффициенты в различных формах
☐ Соотношения
☐ Ratio — приготовить шоколадные чипсы
☐ Ratio — Рецепт шоколадных чипсов
5 класс | Измерение
☐ Используйте линейку для измерения с точностью до сантиметра или миллиметра
☐ Определение линейки
☐ Метрическая длина
☐ Упражнение: Откройте для себя длины
☐ Деятельность: личные измерения
☐ Метрические измерения с Мэгги
☐ Определение личных ссылок для метрических единиц длины
☐ Метрическая длина
☐ Метрические измерения с Мэгги
☐ Метрическая система измерения
☐ Деятельность: личные измерения
☐ Определите общепринятые эквивалентные единицы длины (метрические)
☐ Конвертер единиц измерения
☐ Метрическая длина
☐ Метрические измерения с Мэгги
☐ Перевод длин в метрическую систему
☐ Конвертер единиц измерения
☐ Метрические измерения с Мэгги
☐ Метрическая длина
☐ Определить инструменты и методы, необходимые для измерения с соответствующим уровнем точности: длины и углы
☐ Точность и прецизионность
☐ Определение линейки
☐ Использование транспортира
☐ Упражнение: Откройте для себя длины
☐ Определение транспортира
☐ Измерьте и начертите углы с помощью транспортира
☐ Использование транспортира
☐ Определение транспортира
☐ Градусов
☐ Круговая диаграмма
☐ Упражнение: Как высоко?
☐ Понимание температуры
☐ Интерактивный термометр
☐ Определение температуры
☐ Определение термометра
☐ Определение
градусов по Фаренгейту☐ Определение Цельсия
☐ Знакомство со стандартными единицами измерения США
☐ Метрические измерения с Мэгги
☐ Понимание температурных шкал Цельсия и Фаренгейта, включая температуру замерзания и кипения воды по двум шкалам
☐ Интерактивный термометр
☐ Определение температуры
☐ Определение термометра
☐ Определение
градусов по Фаренгейту☐ Определение Цельсия
☐ Знакомство со стандартными единицами измерения США
☐ Метрические измерения с Мэгги
☐ Используйте линейку для измерения с точностью до дюйма, 1/2, 1/4 или 1/8 дюйма
☐ Деятельность: личные измерения
☐ Упражнение: Откройте для себя длины
☐ Определение линейки
☐ Стандартная длина США
☐ Знакомство со стандартными единицами измерения США
☐ Определение личных ссылок на стандартные единицы длины США
☐ Стандартная длина США
☐ Знакомство со стандартными единицами измерения США
☐ Деятельность: личные измерения
☐ Определите общепринятые эквивалентные единицы длины (США)
☐ Конвертер единиц измерения
☐ Стандартная длина США
☐ Знакомство со стандартными единицами измерения США
☐ Преобразование длин в системе США
☐ Преобразование длины
☐ Конвертер единиц измерения
☐ Знакомство со стандартными единицами измерения США
☐ Стандартная длина США
5 класс | Время
☐ Рассчитать прошедшее время в часах и минутах
☐ Секундомеры
☐ Сложение и вычитание времени
☐ Определение минуты
☐ Определение часа
☐ Полуночная головоломка
☐ Песочные часы 1 Пазл
☐ Песочные часы 2 Пазл
☐ Упражнение: Досчитай до миллиарда
☐ Преобразование времени в минутах и секундах в секунды или часов и минут в минуты
☐ Метрическая система измерения
5 класс | Геометрия (плоскость)
☐ Вычислите формулу периметра для заданных входных значений
☐ Определение периметра
☐ Периметр
☐ Вычислить периметр правильных и неправильных многоугольников
☐ Определение периметра
☐ Периметр
☐ Определение полигона
☐ Определение правильного многоугольника
☐ Полигоны
☐ Определение неправильного многоугольника
☐ Определите соответствующие части конгруэнтных треугольников
☐ Как определить, конгруэнтны ли треугольники
☐ Определение конгруэнтности
☐ Конгруэнтно
☐ Конгруэнтные треугольники
☐ Определите и нарисуйте линии симметрии основных геометрических фигур
☐ Геометрия — Отражение
☐ Художник по симметрии
☐ Симметрия отражения
☐ Определение симметрии
☐ Определение линейной симметрии
☐ Упражнение: Симметрия фигур
☐ Линии симметрии плоских фигур
☐ Нанесите точки на график для формирования основных геометрических фигур (идентифицируйте и классифицируйте)
☐ Маска пришельца из координат
☐ Диплодок, использующий координаты
☐ Точка
☐ Декартовы координаты
☐ Вычислить периметр основных геометрических фигур, начерченных на координатной плоскости (прямоугольники и фигуры, составленные из прямоугольников, стороны которых имеют целочисленные длины и параллельны осям)
☐ Периметр
☐ Прямоугольник
☐ Декартовы координаты
☐ Интерактивные декартовы координаты
☐ Определите пары подобных треугольников или других геометрических фигур
☐ Аналогичный
☐ Аналогичное определение
☐ Подобные треугольники
☐ Головоломка жонглера Сэма Лойда
☐ Определите отношение соответствующих сторон подобных треугольников
☐ Подобные треугольники
☐ Классифицировать четырехугольники по свойствам их углов и сторон
☐ Интерактивные четырехугольники
☐ Четырехугольники — Квадрат Прямоугольник Ромб Трапеция Параллелограмм
☐ Четырехугольник Определение
☐ Квадратное определение
☐ Определение прямоугольника
☐ Определение ромба
☐ Определение трапеции
☐ Определение параллелограмма
☐ Определение воздушного змея
☐ Знайте, что сумма внутренних углов четырехугольника равна 360 градусов
☐ Внутренние углы многоугольников
☐ Интерактивные четырехугольники
☐ Четырехугольники — Квадрат Прямоугольник Ромб Трапеция Параллелограмм
☐ Классифицировать треугольники по свойствам их углов и сторон
☐ Интерактивные треугольники
☐ Треугольники — Равнобедренные, равнобедренные и разносторонние
☐ Углы остро-тупые прямые и правые
☐ Знайте, что сумма внутренних углов треугольника равна 180 градусам
☐ Внутренние углы многоугольников
☐ Треугольники содержат 180 градусов
☐ Интерактивные треугольники
☐ Треугольники — Равнобедренные, равнобедренные и разносторонние
☐ Найдите недостающий угол, если даны два угла треугольника
☐ Внутренние углы многоугольников
☐ Треугольники содержат 180 градусов
☐ Интерактивные треугольники
☐ Треугольники — Равнобедренные, равнобедренные и разносторонние
☐ Определите пары конгруэнтных треугольников или других геометрических фигур
☐ Конгруэнтно
☐ Определение конгруэнтности
☐ Конгруэнтные треугольники
☐ Как определить, конгруэнтны ли треугольники
☐ Знайте, что прямой угол равен 90 градусов, прямой угол равен 180 градусам, а полный круг равен 360 градусам.
☐ Прямые углы
☐ Дополнительные уголки
☐ Градусов
☐ Прямые уголки
☐ Внешний уголок
☐ Внешние углы многоугольников
☐ Внутренний уголок
☐ Дополнительные углы
☐ Полный оборот
☐ Упражнение: Часы и углы
☐ Понимать, что подразумевается под порядком вращательной симметрии плоской формы, и знать, как найти его значение.
☐ Вращательная симметрия
☐ Точечная симметрия
☐ Упражнение: Составьте мандалу
☐ Симметрия — отражение и вращение
☐ Художник по симметрии
☐ Понимать, что понимают под правильными и неправильными многоугольниками; выпуклые и вогнутые многоугольники; и сложные многоугольники.
☐ Полигоны
☐ Интерактивные полигоны
☐ Определение правильного многоугольника
☐ Определение неправильного многоугольника
☐ Понять, что подразумевается под точечной симметрией
☐ Точечная симметрия
☐ Вращательная симметрия
☐ Художник по симметрии
☐ Понять, что подразумевается под вершиной угла и смежными углами
☐ Смежные углы
5 класс | Геометрия (тело)
☐ Понимание Платоновых тел
☐ Вращающийся додекаэдр
☐ Вращающийся икосаэдр
☐ Советы по построению платоновых тел
☐ Вращающийся октаэдр
☐ Вращающийся тетраэдр
☐ Платоновые тела
☐ Вращающийся куб
☐ Шаблон кубической модели
☐ Шаблон модели октаэдра
☐ Шаблон модели тетраэдра
☐ Шаблон модели додекаэдра
☐ Шаблон модели икосаэдра
☐ Многогранники
☐ Упражнение: Исследование твердых тел
☐ Постройте модели Платоновых тел из их сетей.
☐ Шаблон кубической модели
☐ Шаблон модели тетраэдра
☐ Шаблон модели октаэдра
☐ Шаблон модели додекаэдра
☐ Шаблон модели икосаэдра
☐ Шаблон кубической сетки
☐ Шаблон сетки тетраэдра
☐ Шаблон сетки октаэдра
☐ Шаблон сетки додекаэдра
☐ Шаблон сетки икосаэдра
☐ Вызов Пентамино
☐ Набор пентамино
☐ Платоновые тела
☐ Советы по построению платоновых тел
☐ Пирамиды
☐ Призмы с примерами
☐ Анимированные модели многогранников
☐ Понимание многогранников и классификация их как Платоновых тел, призм, пирамид и т. д.
☐ Многогранники
☐ Платоновые тела
☐ Призмы с примерами
☐ Пирамиды
5 класс | Алгебра
☐ Определите и используйте соответствующую терминологию при обращении к константам, переменным и алгебраическим выражениям
☐ Алгебра — Определения
☐ Определение константы
☐ Определение переменной
☐ Определение выражения
☐ Определение коэффициента
☐ Определение оператора
☐ Перевод простых словесных выражений в алгебраические выражения
☐ Введение в алгебру
☐ Введение в алгебру: умножение
☐ Определение проблемы
☐ Решение словесных вопросов
☐ Подставлять присваиваемые значения в переменные выражения и оценивать, используя порядок операций
☐ Введение в алгебру
☐ Введение в алгебру: умножение
☐ Замена
☐ Порядок действий — БОДМАС
☐ Порядок действий — PEMDAS
☐ Открытые предложения
☐ Калькулятор порядка операций
☐ Решите простые одношаговые уравнения, используя основные факты о целых числах
☐ Введение в алгебру
☐ Введение в алгебру: умножение
☐ Умные блоки
☐ Открытые предложения
☐ Решите и объясните простые одношаговые уравнения, используя обратные операции с целыми числами
☐ Обратный
☐ Обратный
☐ Введение в алгебру
☐ Введение в алгебру: умножение
☐ Открытые предложения
☐ Создание и объяснение закономерностей и алгебраических взаимосвязей (пример: 2,4,6,8. .. алгебраически равно 2n (удвоение))
.. алгебраически равно 2n (удвоение))
☐ Последовательности
☐ Сопоставление игрового шаблона — Числа
☐ Числовые последовательности — Квадратный куб и Фибоначчи
☐ Создавайте собственные шаблоны чисел
☐ Определение шаблона номера
☐ Создание алгебраических или геометрических узоров с использованием конкретных объектов или визуальных рисунков (например, вращение и затенение геометрических фигур)
☐ Сопоставление игрового шаблона — Числа
☐ Создавайте собственные шаблоны чисел
☐ Определение шаблона
☐ Выкройки
☐ Свободная игра фигур
☐ Сопоставление шаблонов игр — фигуры
☐ Определение числового шаблона
☐ Упражнение: Составьте мандалу
☐ Сопоставление шаблонов воспроизведения — Цвета
☐ Числовые последовательности — Квадратный куб и Фибоначчи
☐ Знайте разницу между закрытым предложением и открытым предложением.
☐ Открытые предложения
5 класс | Координаты
☐ Определите и нанесите точки в первом квадранте
☐ Маска пришельца из координат
☐ Интерактивные декартовы координаты
☐ Диплодок, использующий координаты
☐ Квадрант
☐ Определение точки
☐ Нажми на координату
☐ Точка
5 класс | Логика
☐ Используйте логические рассуждения для решения задач, требующих различных навыков
☐ Логические головоломки
☐ Добро пожаловать в математику
☐ Изучение математики
☐ Язык математики
☐ Определение проблемы
5 класс | Данные
☐ Сбор и запись данных из различных источников (например, газет, журналов, опросов, диаграмм и опросов)
☐ Что такое данные?
☐ Определение опроса
☐ Отображение данных в виде линейного графика для отображения увеличения или уменьшения во времени
☐ Графики данных
☐ Линейные графики
☐ Вычислите среднее значение для заданного набора данных и используйте его для описания набора данных
☐ Подлая машина
☐ Как рассчитать среднее значение
☐ Среднее определение
☐ Поиск центральной ценности
☐ Формулировать выводы и делать прогнозы по графикам
☐ Линейные графики
☐ Круговая диаграмма
☐ Пиктограммы
☐ Деятельность: Парковочные места
☐ Гистограммы
5 класс | Оценка
☐ Обоснованность оценки
☐ Оценка
☐ Визуальная оценка
☐ Определение оценки
☐ Советы и рекомендации по оценке
☐ Определение оценки
☐ Игры на оценку
☐ Оценка сумм, разностей, произведений и частных десятичных дробей
☐ Оценка
☐ Игры на оценку
☐ Определение оценки
☐ Определение оценки
☐ Советы и рекомендации по оценке
☐ Обоснуйте обоснованность ответов, используя оценку
☐ Оценка
☐ Советы и рекомендации по оценке
☐ Определение оценки
☐ Определение оценки
☐ Игры на оценку
☐ Округление чисел
5 класс | Вероятность
☐ Перечислите возможные результаты однособытийного эксперимента
☐ Вероятность
☐ Спиннер — человек, принимающий решения
☐ Упражнение: Эксперимент с кубиком
☐ Упражнение: Эксперимент с игральными костями
☐ Запишите результаты эксперимента, используя дроби/отношения
☐ Вероятность
☐ Соотношения
☐ Упражнение: Эксперимент с кубиком
☐ Упражнение: Эксперимент с игральными костями
☐ Создайте выборочное пространство и определите вероятность одного события, учитывая простой эксперимент (например, бросок числового куба)
☐ Игра в кости
☐ Вероятность
☐ Спиннер — человек, принимающий решения
☐ Упражнение: Эксперимент с кубиком
☐ Упражнение: Эксперимент с игральными костями
☐ Найдите вероятности в числовой строке вероятностей
☐ Линия вероятности
☐ Вероятность
Рабочие листы с одношаговыми уравнениями
Рабочие листы с одношаговыми уравнениями содержат эксклюзивные страницы для решения уравнений с дробными, целыми и десятичными числами. Выполняйте основные арифметические действия — сложение, вычитание, умножение и деление для решения уравнений. Упражнения по применению уравнений в реальной жизни доступны здесь для передачи практических знаний. Этот набор рабочих листов для печати специально разработан для учащихся 6-х, 7-х и 8-х классов. Включены бесплатные образцы рабочих листов.
Выполняйте основные арифметические действия — сложение, вычитание, умножение и деление для решения уравнений. Упражнения по применению уравнений в реальной жизни доступны здесь для передачи практических знаний. Этот набор рабочих листов для печати специально разработан для учащихся 6-х, 7-х и 8-х классов. Включены бесплатные образцы рабочих листов.
Выберите тип уравнения:
Одношаговый | Сложение и вычитание
Одношаговый | Умножение и деление
Одношаговое уравнение | Смешанные операции
Целые числа: смешанные операции | Уровень 1
Различные одношаговые уравнения, включающие все четыре основные операции, представлены в этих смешанных рабочих листах в формате PDF. Выполните соответствующую операцию и найдите неизвестную переменную.
Целые числа: смешанные операции | Уровень 2
Повышая вашу практику, коэффициенты отображаются в положительных и отрицательных целых числах. Сохраните переменную с одной стороны, возьмите коэффициент и константу с другой стороны и решите.
Сохраните переменную с одной стороны, возьмите коэффициент и константу с другой стороны и решите.
Фракции: смешанные операции | Уровень 1
Сложите, вычтите, умножьте и разделите, чтобы решить одношаговые уравнения дробей в этих рабочих листах уровня 1, которые используют правильные и неправильные дроби в качестве коэффициентов и констант.
Фракции: смешанные операции | Уровень 2
Умеренная практика ждет здесь учащихся 7-х и 8-х классов! Решите серию одношаговых уравнений, члены которых содержат дроби и смешанные числа.
Десятичные числа: смешанные операции
Члены одношаговых уравнений в этих таблицах являются либо десятичными, либо целыми числами. Здесь задействованы все четыре арифметических действия для решения задач.
Целые, дробные и десятичные числа
В этих распечатываемых рабочих листах коэффициент каждого одношагового уравнения может быть целым числом, дробью или десятичным числом. Полную практику можно дать детям, решая эти уравнения.
Рабочие листы задач с одношаговыми уравнениями
Используйте эту сборку одношаговых задач с уравнениями, включающими целые числа, десятичные дроби и дробные коэффициенты.
(15 рабочих листов)
Решите и проверьте решение
Решите каждое одношаговое уравнение, чтобы найти неизвестную переменную. Подставьте значение переменной в данное уравнение, чтобы проверить решение уравнения. Этот набор рабочих листов идеально подходит для учащихся 7 и 8 классов.
Одношаговые уравнения MCQ | Целые числа
В этих раздаточных материалах доступно множество вопросов с несколькими вариантами ответов. Решите указанные уравнения и выберите правильные целые числа из предложенных вариантов.
Решите указанные уравнения и выберите правильные целые числа из предложенных вариантов.
Одношаговые уравнения MCQ | Дроби
Решение уравнений, нахождение уравнения с заданным решением и оценка выражений с полученными значениями — это навыки, которые вы можете приобрести в этих рабочих листах MCQ в формате pdf с дробями.
Стоимость продукта
Эти рабочие листы для печати содержат основанное на деятельности упражнение для определения стоимости продуктов. Ценники объектов представлены в виде уравнения. Решите уравнения.
Перевод одношагового уравнения
Учащиеся 6 класса должны прочитать каждое словосочетание/предложение и перевести его в соответствующее одношаговое линейное уравнение.
Какой у меня номер?
Угадай мой номер! Эти забавные математические загадки помогают детям легко понимать и переводить предложения в уравнения. Попробуйте все эти интересные задачи.
Применение в геометрии: введите 1
Расширьте свои знания, решая эти одношаговые уравнения по геометрии. В рабочих листах PDF «Тип 1» найдите неизвестные стороны заданной формы, решив одношаговые уравнения.
Традиционные единицы США
Метрические единицы
Приложение по геометрии: Тип 2
Рабочие листы для печати «Тип 2» содержат задачи, основанные на приложениях по геометрии. Примените свойства фигур, чтобы найти неизвестные параметры.
Традиционные единицы США
Метрические единицы
Связанные рабочие листы
»Двухшаговое уравнение
»Многоэтапное уравнение
»Задачи со словами
»Упрощение алгебраических выражений
»Перевод фраз
Уравнения с дробями — GCSE Maths
Введение
Что такое уравнения с дробями?
Как решать уравнения с дробями
Рабочий лист уравнений с дробями
Распространенные заблуждения
Практика уравнений с дробями вопросы
Уравнения с дробями Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое уравнения с дробями?
Как решать уравнения с дробями
Рабочий лист уравнений с дробями
Распространенные заблуждения
Практика уравнений с дробями вопросы
Уравнения с дробями Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем об уравнениях с дробями, в том числе о решении уравнений с дробями, где неизвестным является знаменатель дроби.
Также есть рабочие листы уравнений с дробями, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое уравнения с дробями?
Уравнения с дробями включают решение уравнений, в которых неизвестная переменная является частью числителя и/или знаменателя дроби.
Чтобы решить уравнения с дробями, нам нужно выяснить, каково значение неизвестной переменной. Мы решаем уравнения, используя «метод балансировки», применяя обратную операцию к обеим частям уравнения.
обратная операция сложения равна вычитанию .
обратная операция вычитания равна сложению .
обратная операция умножения равна делению .
обратная операция деления есть умножение .
См. также: Решение уравнений и линейных уравнений
Что такое уравнения с дробями?
Как решать уравнения с дробями
Чтобы решать уравнения с дробями:
- Определите операции, которые применяются к неизвестной переменной.
- Примените обратные операции по одной к обеим частям уравнения.
- Запишите окончательный ответ, проверив его правильность.
Как решать уравнения с дробями
Рабочий лист уравнений с дробями
Получите бесплатный рабочий лист уравнений с дробями, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист уравнений с дробями
Получите бесплатный рабочий лист уравнений с дробями, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Уравнения с дробями примеры
Пример 1: уравнения с одной операцией
Решить:
\[\frac{x}{5}=4\]
- Определите операции, которые применяются к неизвестной переменной .
Неизвестная переменная x.
В левой части уравнения x делится на 5 (знаменатель дроби).
\[\frac{x}{5}\]
2 Примените обратные операции, по одной, к обеим частям уравнения .
Обратным к «делению на 5» является «умножение на 5».
Нам нужно умножить обе части уравнения на 5.
3 Запишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=20\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{20}{5}=20\div5=4\]
Пример 2: уравнения с одной операцией
Решить:
\[\frac{x}{3}=8\]
Определите операции, которые применяются к неизвестной переменной .
Неизвестная переменная x.
Глядя на левую часть уравнения, x делится на 3 (знаменатель дроби).
\[\frac{x}{3}\]
Примените обратные операции по одной к обеим частям уравнения .
Обратным к «делению на 3» является «умножение на 3».
Нам нужно умножить обе части уравнения на 3.
Напишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=24\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{24}{3}=24\div3=8 \]
Пример 3: уравнения с двумя операциями
Решить:
\[\frac{x+1}{2}=7\ ]
Определить операции , которые применяются к неизвестной переменной .
Неизвестная переменная x.
Глядя на левую часть уравнения, 1 прибавляется к x, а затем делится на 2 (знаменатель дроби).
\[\frac{x+1}{2}\]
Примените обратные операции по одной к обеим частям уравнения .
Нам нужно проделать обратные операции в обратном порядке.
Сначала нам нужно умножить обе части уравнения на 2.
Затем нам нужно вычесть 1 из обеих частей.
Запишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=13\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{13+1}{2}=\frac{14}{2}=14\div2=7\]
Пример 4: уравнения с двумя операциями
Решить:
\[\frac {x}{4}-2=3\]
Определить операции, применяемые к неизвестной переменной .
Неизвестная переменная x.
Глядя на левую часть уравнения, x делится на 4 (знаменатель дроби), а затем вычитается 2.
\[\frac{x}{4}-2\]
Примените обратные операции по одной к обеим частям уравнения .
Нам нужно проделать обратные операции в обратном порядке.
Сначала нам нужно добавить 2 к обеим частям уравнения.
Затем нам нужно умножить обе части уравнения на 4.
Запишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=20\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{20}{4}-2=20\div4 -2=5-2=3\]
Пример 5: уравнения с тремя операциями
Решить:
\[\frac{3x} {5}+1=7\]
Определить операции, применяемые к неизвестной переменной .
Неизвестная переменная x.
Глядя на левую часть уравнения, x умножается на 3, затем делится на 4 (знаменатель дроби) и затем прибавляется 1.
\[\frac{3x}{5}+1\]
Применить обратные операции по одной к обеим частям уравнения .
Нам нужно проделать обратные операции в обратном порядке.
Сначала нам нужно вычесть 1 из обеих частей уравнения.
Затем нам нужно умножить обе части уравнения на 5 и, наконец, разделить обе части на 3.
Запишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=10\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{3\times10}{5}+1=\frac{30}{5}+1=6+1=7\]
Пример 6: уравнения с тремя операциями
Решить:
\[\frac{2x-1}{7}=3\]
Определите операции, которые применяются к неизвестной переменной .
Неизвестная переменная x.
Глядя на левую часть уравнения, x умножается на 2, затем вычитается 1. Затем делим на 7 (знаменатель).
\[\frac{2x-1}{7}\]
Применить обратные операции по одной к обеим частям уравнения .
Нам нужно проделать обратные операции в обратном порядке.
Сначала нам нужно умножить обе части уравнения на 7.
Затем нам нужно добавить 1 к обеим частям и, наконец, разделить обе части на 2.
Запишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=11\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{2\times11 -1}{7}=\frac{22-1}{7}=\frac{21}{7}=3\]
Пример 7: уравнения с неизвестной в знаменателе
Решите:
\[\frac{24}{x}=6\]
Определите операции, которые применяются к неизвестной переменной .
Неизвестная переменная x.
Глядя на левую часть уравнения, x является знаменателем. 24 делится на х.
\[\frac{24}{x}\]
Примените обратные операции по одной к обеим частям уравнения .
Нам нужно умножить обе части уравнения на x.
Тогда мы можем разделить обе части на 6.
Запишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=4\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{24}{4}=24\div4=6\]
Пример 8: уравнения с неизвестным в знаменателе
Решить:
\[\frac{18}{x}-6 =3\]
Определить операции, которые применяются к неизвестной переменной .
Неизвестная переменная x.
Глядя на левую часть уравнения, x является знаменателем. 18 делится на x и затем вычитается 6.
\[\frac{18}{x}-6\]
Примените обратные операции, по одной, к обеим частям уравнения .
Сначала мы добавляем 6 к обеим частям уравнения.
Затем нам нужно умножить обе части уравнения на x.
Тогда мы можем разделить обе части на 9.
Запишите окончательный ответ, проверив его правильность .
Окончательный ответ:
\[x=2\]
Мы можем проверить ответ, подставив его обратно в исходное уравнение.
\[\frac{18}{2}-6=9-6=3\]
Общие заблуждения
- Типы чисел
. Неизвестное не обязательно должно быть целым числом (целыми числами), оно также может быть дробью или десятичным числом и может быть положительным или отрицательным.
- Сторона уравнения, на которой стоит неизвестная
Неизвестная переменная, представленная буквой, часто находится в левой части уравнений, однако это не обязательно. Это также может быть в правой части уравнения.
Это также может быть в правой части уравнения.
- Умножение обеих частей уравнения
При умножении каждой стороны уравнения числа распространенной ошибкой является забывание умножения каждого члена.
Напр.
Решите: \frac{x}{2}+3=9
Здесь мы не умножили +3 на 2, что привело к неправильному ответу:
Здесь мы правильно умножили каждое слагаемое на знаменатель:
- Наименьший общий знаменатель (LCD)
Часто путают решение уравнений с участием дробей и сложение и вычитание дробей. При сложении и вычитании нам нужно найти наименьший/наименьший общий знаменатель (иногда называемый наименьшим общим кратным или lcm), тогда как при решении уравнений с дробями нам нужно умножить обе части уравнения на знаменатель дроби.
Практика уравнений с дробями
Уравнения с дробями Вопросы GCSE
1. Решить \frac{x}{5}=3
(1 балл)
Показать ответ
x=15
для правильного ответа
(1)
2. Решение \ frac {x-3} {7} = 2
Решение \ frac {x-3} {7} = 2
(2 марок)
Показать Ответ
111. 3=14
за правильный первый шаг
(1)
x = 17
для правильного ответа
(1)
3. Решить \ frac {5a+6} {2} = 23
(3 марки)
Show Ответ
(3 марки)
.
5a+6 = 46
Для правильного первого шага
(1)
5a = 40
Для правильного второго шага
(1)
x = 8
Для правильного ответа
(1)
Контрольный список обучения
Вы теперь узнали, как:
- Решить уравнения, когда существуют фракции
- Фракции, где неизвестный — деноматор
Следующие уроки —
- Фактор
- 5555.
Все еще застрял?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.


 Вычислительные навыки
Вычислительные навыки Решите
задачу:
Решите
задачу: окружность.
окружность. Найдите
градусную меру угла DBE, если
Найдите
градусную меру угла DBE, если Реши задачу с помощью уравнения:
Реши задачу с помощью уравнения:

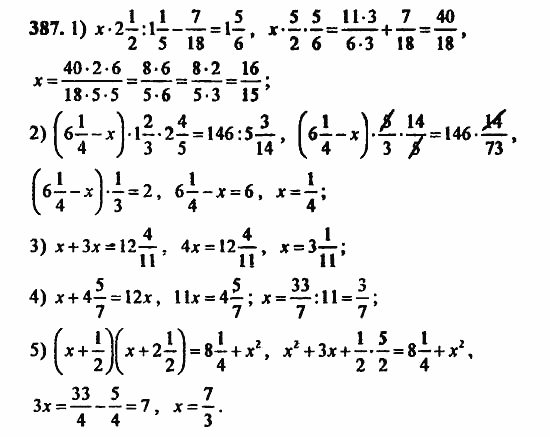

 Длина одного шага Арман и Серик идут рядом.
Длина
Длина одного шага Арман и Серик идут рядом.
Длина 
 Сравните дроби:
Сравните дроби: Какую часть выделенного земельного участка очистили ученики за
два дня?
Какую часть выделенного земельного участка очистили ученики за
два дня?


 Запишите в виде десятичных дробей
частное:
Запишите в виде десятичных дробей
частное: Решите уравнение
Решите уравнение Сколько стоит 1 кг
груш?
Сколько стоит 1 кг
груш?
 Вычислите:
Вычислите: «мода»
«мода» 40%
учеников класса умеют кататься на лыжах, остальные на коньках. Начертите
круговую диаграмму учеников, умеющих кататься на лыжах и на коньках.
40%
учеников класса умеют кататься на лыжах, остальные на коньках. Начертите
круговую диаграмму учеников, умеющих кататься на лыжах и на коньках. Решите задачу графически:
Решите задачу графически: Даны два
прямоугольных параллелепипеда. Длина одного параллелепипеда в 6 раз меньше
длины другого, ширина – в 9 раз больше ширины другого, высота – в 3 раза
меньше высоты другого. Объем какого из параллелепипедов больше? Во сколько
раз?
Даны два
прямоугольных параллелепипеда. Длина одного параллелепипеда в 6 раз меньше
длины другого, ширина – в 9 раз больше ширины другого, высота – в 3 раза
меньше высоты другого. Объем какого из параллелепипедов больше? Во сколько
раз? На уроке Вы будете не только решать задания, но и оценивать собственную деятельность. Отметка за урок будет выставлена с учетом заполнения данной карты.
На уроке Вы будете не только решать задания, но и оценивать собственную деятельность. Отметка за урок будет выставлена с учетом заполнения данной карты.
 Решить задачу, составив по условию задачи уравнение.
Решить задачу, составив по условию задачи уравнение. Подведение итогов (2 мин)
Подведение итогов (2 мин) Учебника
Учебника
