5 корней из 243: Mathway | Популярные задачи

2

Как решить 5 корней? – Обзоры Вики

Аналогично, как получить root 5? Как найти квадратный корень из 5?

1. √5 = √5.
2. √5 = 2.23.

Каково значение корня 5? Значение корня 5, уменьшенное до 5 знаков после запятой, равно √5 = 2.23606. У него есть место с большим списком иррациональных алгебраических чисел.

Во-вторых, что такое квадрат 5? Список идеальных квадратов

НОМЕР	ПЛОЩАДЬ	КВАДРАТНЫЙ КОРЕНЬ
5	25	2.236
6	36	2. 449
7	49	2.646
8	64	2.828

• 17 ноября 2021 г.

Является ли корень 5 иррациональным числом?

Это иррациональное алгебраическое число.

Как найти корень 5-й степени из 32? Пятый корень из 32 равен 2.

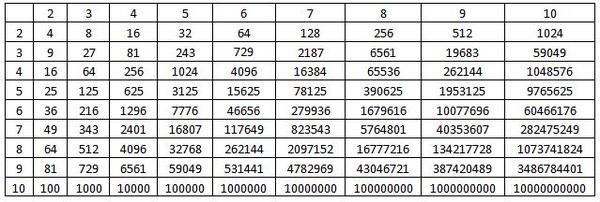
Каковы корни пятой степени числа 3125?

Пример 5-го корня чисел

5-й корень из 1 = 1	Корень пятый из 7,776 = 6
Корень пятый из 32 = 2	Корень пятый из 7,776 = 7
Корень пятый из 243 = 3	Корень пятый из 32,768 = 8
Корень пятый из 1,024 = 4	Корень пятый из 59,049 = 9
Корень пятый из 3,125 = 5	Корень пятый из 100,000 = 10

Июль 4, 2020

Чему равен куб корня 5? Кубы и кубические корни Список от 1 до 15

Число	Куб (а 3 )	Кубический корень ∛a
5	125	1. 710
6	216	1.817
7	343	1.913
8	512	2.000

Является ли корень 5 иррациональным числом?

√5 — это иррациональное число.

Как найти квадратный корень из 5 без калькулятора? Следовательно, значение корня 5 равно √5 = 2.2360… Вы можете найти значение квадратного корня из всех несовершенных квадратных чисел с помощью метода деления в длину.

Как написать 5 в квадрате?

Как вы видели ранее, 5² называется «пять в квадрате». «Пять в квадрате» означает умножь пять на себя. В математике мы называем умножение числа само на себя «возведением в квадрат» числа.

Что означает 8 в квадрате?

Возведение числа в квадрат означает процесс умножение числа с собой. Полученный результат называется квадратом заданного исходного числа.

Как 5 иррационально? Предположим, что √5 — рациональное число. Если √5 рационально, это означает, что его можно записать в виде a/b, где целые числа a и b не имеют общего делителя, отличного от 1, и b ≠ 0. Это означает, что 5 делит a². … Итак, делаем вывод, что √5 иррационально.

Как доказать корень 5? Пусть 5 — рациональное число.

1. тогда он должен быть в форме qp, где q=0 (p и q взаимно просты)
2. p2 делится на 5.
3. Итак, p делится на 5.
4. Итак, q делится на 5.
5. Таким образом, p и q имеют общий делитель 5.
6. Мы предположили, что p и q взаимно просты, но здесь они являются общим делителем 5.

5 рационально или иррационально?

Число 5 присутствует в действительных числах. Поэтому цифра 5 рациональное, целое, целое число и реальное число.

Как вы пишете 5-й корень на компьютере? нажмите клавишу Alt и введите 8730, используя цифровая клавиатура, чтобы сделать квадратный корень √ символ. Только в документах Microsoft Word введите 221B и нажмите клавиши Alt и X, чтобы сделать символ кубического корня ∛. (1/4) (лет)

3-8

9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 95-(243)=0

Пошаговое решение :

Шаг 1 :

Калькулятор корней многочленов :

1. 1    Найти корни (нули) :       F(x) = x представляет собой набор методов, направленных на нахождение значений x, для которых   F(x)=0    

Rational Roots Test является одним из вышеупомянутых инструментов. Он найдет только рациональные корни, то есть числа x, которые могут быть выражены как частное двух целых чисел

Теорема о рациональных корнях утверждает, что если многочлен равен нулю для рационального числа P/Q , то P является множителем замыкающей константы, а  Q является фактором ведущего коэффициента

В этом случае ведущий коэффициент равен 1 , а конечная константа – -243.

 Коэффициент(ы):

ведущего коэффициента:  1
 константы замыкания:  1 ,3 ,9 ,27 ,81 ,243

 Проверим ….

4 9 09003 9 P

1 0

90

	Q		P/Q		F(P/Q)		Divisor
	-1		1		-1. 00		-244.00
	-3		1		-3.00		-486.00
	-9		1		-9,00		-59292.00
	-27		1		-27.00		-14349150.00
	-81		1		-81.00		-34867844644.00
	-243		1		-243.00		-847288609686.00
	1		1		1. 00		-242.00
	3		1		3,00		0,00		x-3	4    990       1        9.00       58806.00           27       1        27.00       14348664.00           81       1        81,00       3486784158,00 243 1 243,00 847288609200,00

. многочлен можно разделить на q*x-p Обратите внимание, что q и p происходят из P/Q, приведенного к наименьшим членам

В нашем случае это означает, что
   x ⁵ -243 
можно разделить с X-3

Длинное отделение полинома:

1. 2 Полиномиальное длинное разделение
Разделитие: x ⁵ -243
(«Dividend»)
By: X-3 («Divisor»)
90900.00. 900900. 90

90......
.0005

Dividend

x 5

—

243

— divisor

* x 4

x 5

—

3x 4

Остаток

3x 4

—

243

— divisor

* 3x 3

3x 4

—

9x 3

Остаток

9x 3

—

243

— divisor

* 9x 2

9x 3

—

27x 2

Остаток

27x 2

—

243

— divisor

* 27x 1

27x 2

—

81x

Остаток

81x

—

243

— divisor

* 81x 0

81x

—

243

Остаток

0

Коэффициент: x ⁴ +3x ³ +9x ² +27x +81: 0 + ² +27x +81: 0

0

0

0

0

0

20

0

0

0

0

0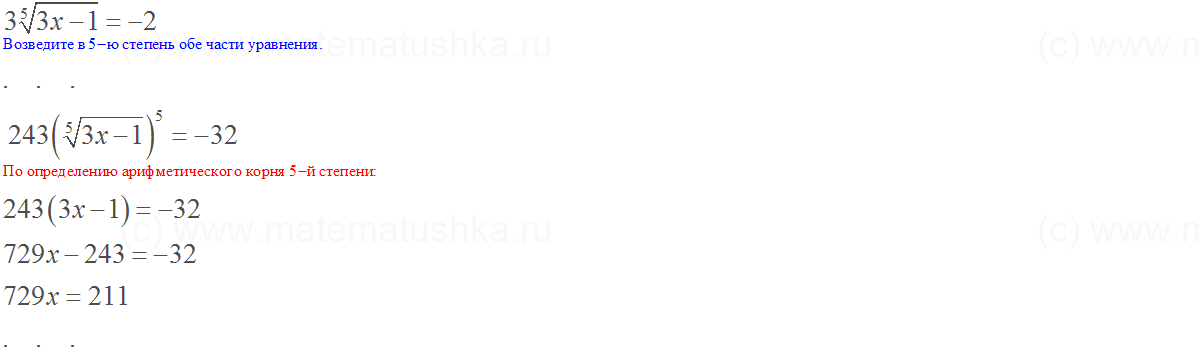

. (нули) числа:       F(x) = x ⁴ +3x ³ +9x ² +27x+81

     См. теорию на шаге 1.1
В этом случае ведущий коэффициент равен 1, а замыкающая константа 81.

 Коэффициент(ы):

из ведущего коэффициента: 1
Константа следа: 1, 3, 9, 27, 81

Тест …

	P	09390	P	09390	P	3990	P	390	P			P			. /Q		F(P/Q)		Divisor
	-1		1		-1.00		61.00
	-3		1		-3.00		81.00
	-9		1		-9. 00		4941,00
	-27		1		-27,00		478305.00
	-81		1		-81.00		41509341.00
	1		1		1,00		121,00
	3

4 0 5  4    1111111111313

	3.00		405.00
	9		1		9.00		9801.00
	27		1		27,00		597861,00			1 10004	81		1		81,00		44702361,00

POLYNOMIAL ROOTS. 4 + 3x ³ + 9x ² + 27x + 81) • (x — 3) = 0

Шаг 2 :

Теория – корни произведения:

 2.1    Произведение нескольких членов равно нулю.

 Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю.

 Теперь мы будем решать каждый термин = 0 отдельно

 Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении 

 Любое решение термина = 0 также решает произведение = 0.

Уравнения четвертой степени:

2.2     Решить   x ⁴ +3x ³ +9x ² +27x+81 = 0

другой обходной путь.

Метод поиска: вычислить значения полинома для всех целых точек между x=-20 и x=+20

Интервал, на котором происходит смена знака, не найден. Следовательно, аппроксимация пополам не может быть использована. Поскольку это многочлен четной степени, он может даже не иметь действительных (в отличие от мнимых) корней. уравнение : 
                      x = 3

Было найдено одно решение:

                   x = 3

Кубический корень из 243 — Как найти кубический корень из 243? [Решено]

 

 

Значение кубического корня из 243, округленное до 6 знаков после запятой, равно 6,240251. Это действительное решение уравнения x ³ = 243. Кубический корень из 243 выражается как ∛243 или 3 ∛9 в радикальной форме и как (243) ^⅓ или (243) ^0,33 в радикальной форме. показательная форма. Разложение числа 243 на простые множители равно 3 × 3 × 3 × 3 × 3, следовательно, кубический корень из 243 в его низшей радикальной форме выражается как 3 ∛9.

• Кубический корень из 243:
  6.240251469
• Кубический корень из 243 в экспоненциальной форме: (243) ^⅓
• Кубический корень из 243 в радикальной форме: ∛243 или 3 ∛9

1.	Что такое кубический корень из 243?
2.	Как вычислить кубический корень из 243?
3.	Является ли кубический корень из числа 243 иррациональным?
4.	Часто задаваемые вопросы о кубическом корне из 243

Что такое кубический корень из 243?

Кубический корень из 243 — это число, которое при трехкратном умножении само на себя дает произведение 243. Поскольку 243 можно выразить как 3 × 3 × 3 × 3 × 3. Следовательно, кубический корень из 243 = ∛(3 × 3 × 3 × 3 × 3) = 6,2403.

☛ Проверить: Калькулятор кубического корня

Как вычислить значение кубического корня из 243?

Кубический корень из 243 по методу Галлея

Его формула ∛a ≈ x ((x ³ + 2a)/(2x ³ + a))
где,
a = число, кубический корень которого вычисляется
x = целочисленное предположение его кубического корня.

Здесь а = 243
Предположим, что x равен 6
. [∵ 6 ³ = 216, а 216 — ближайший совершенный куб, меньший 243]
⇒ х = 6
Следовательно,
∛243 = 6 (6 ³ + 2 × 243)/(2 × 6 ³ + 243)) = 6,24
⇒ ∛243 ≈ 6,24
Таким образом, кубический корень из 243 приблизительно равен 6,24.

Является ли кубический корень из числа 243 иррациональным?

Да, потому что ∛243 = ∛(3 × 3 × 3 × 3 × 3) = 3 ∛9 и его нельзя выразить в виде p/q, где q ≠ 0. Следовательно, значение кубического корня из 243 — иррациональное число.

☛ Также проверьте:

• Кубический корень из 125
• Кубический корень из 3000
• Кубический корень из 432
• Кубический корень из 23
• Кубический корень из 192
• Кубический корень из 189
• Кубический корень из 19

 

Кубический корень из 243 решенных примеров

1. Пример 1: Дан объем куба 243 в ³ . Найдите длину стороны куба.

   Решение:

   Объем куба = 243 в ³ = a ³
   ⇒ а ³ = 243
   Укоренение куба с обеих сторон,
   ⇒ а = ∛243 в
   Поскольку кубический корень из 243 равен 6,24, длина стороны куба равна 6,24 дюйма.

2. Пример 2. Найдите действительный корень уравнения x ³ − 243 = 0.

   Решение:

   х ³ — 243 = 0 т.е. х ³

   = 243
   Решение для x дает нам
   x = ∛243, x = ∛243 × (-1 + √3i))/2 и x = ∛243 × (-1 — √3i))/2
   где я называется мнимой единицей и равен √-1.
   Игнорирование мнимых корней,
   х = ∛243
   Следовательно, действительный корень уравнения x ³ − 243 = 0 равен x = ∛243 = 6,2403.

3. Пример 3: Каково значение ∛243 ÷ ∛(-243)?

   Решение:

   Кубический корень из -243 равен минусу кубического корня из 243.
   ⇒ ∛-243 = -∛243

   Следовательно,
   ⇒ ∛243/∛(-243) = ∛243/(-∛243) = -1

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы посмотреть на мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Забронируйте бесплатный пробный урок

Часто задаваемые вопросы о кубическом корне из 243

Каково значение кубического корня из 243?

Мы можем выразить 243 как 3 × 3 × 3 × 3 × 3, то есть ∛243 = ∛(3 × 3 × 3 × 3 × 3) = 6,24025. Следовательно, значение кубического корня из 243 равно 6,24025.

Что такое куб кубического корня из 243?

Куб кубического корня из 243 есть само число 243, т. е. (∛243) ³ = (243 ^1/3 ) ³ = 243.

Почему значение кубического корня из 243 Иррациональный?

Значение кубического корня из 243 не может быть выражено в виде p/q, где q ≠ 0.