Разделите на простые множители числа 54,65,99,162,10000… -reshimne.ru
Новые вопросы
Ответы
54:2=27:3=9:3=3:3=1
65:5=13:13=1
99:3=33:3=11:11=1
162:2=81:3=27:3=9:3=3:3=1
10000:2=5000:2=2500:2=1250:2=625:5=125:5=25:5=5:5=1
Похожие вопросы
63:21=??? Как раписать…
Решите уравнение с пропорциями:
9:5=х:4
7 1/3:1 5/6=0,6х:0,75
54/3=0,9/4,7-4,2…
Выпешивсе табличные случаи деленияв которых делимое равно 24…
До обеда рабочий 21 деталь ,а после обеда Три раза больше насколько больше деталей он изготовит после обеда чем до обеда ?. ..
..
Помогите разделить в столбик
13.568:64
В СТОЛБИК…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
ПравоФранцузский язык
Немецкий язык
МХК
ОБЖ
Психология
ГДЗ(дүж) решения для учебника Математика Алдамуратова 5 класс 2017 OTVETKZ.
 COM
COMГлава I. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
1.1. Натуральные числа и нуль
134567891011121314151617
1.2. Координатный луч. Изображение натуральных чисел и числа нуль на координатном луче
18192021222324252627
1.3. Сравнение натуральных чисел. Двойное неравенство
282930313233343536373839
1.4. Сложение и вычитание натуральных чисел
4041424344454647484950
1.5. Умножение и деление натуральных чисел. Основное свойство частного
5152535455565758596061
1.6. Свойства арифметических действий
6263646566676869707172
1.7. Арифметические действия над натуральными числами
73747576777879
1.8. Числовые выражения. Буквенные выражения
8081828384858687888990
1.
 9. Упрощение выражений
9. Упрощение выражений919293949596979899100101102103
1.10. Уравнение
104105106107108109110111112113114115116117118119120
121
1.11. Формулы. Вычисление по формулам
122123124125126127128129130131132133134135136137138139140
1.12. Числовые последовательности
141142143144145146147148149150
Упражнения для повторения главы I
151152153154155156157158159160161162163164165166
2.1. Делители натурального числа. Кратные натурального числа
167168169170171172173174175176177178179180181182183184185186187188
Глава II. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
2.2. Простые числа. Составные числа
189190191192193194195196197198199200
2.3. Основные свойства делимости
201202203204205206207208209210211212213214
2.
 4. Признаки делимости натуральных чисел на 2, 5 и 10
4. Признаки делимости натуральных чисел на 2, 5 и 10215216217218219220221222223224225226227
2.5. Признаки делимости натуральных чисел на 3 и на 9
228229230231232233234235236237238239
2.6. Степень числа
240
241242243244245246247248249250251252253254255256257258259260261262
2.7. Разложение составных чисел на простые множители
263264265266267268269270271272273274275
2.8. Наибольший общий делитель. Взаимно простые числа.
276277278279280281282283284285286287288290291292293294295
2.9. Наименьшее общее кратное
296297298299300301302303304305306307308309310311312313314315
Упражнения для повторения главы II
316317318319320321322323324325326327
2.10. Движение по реке
328329330331332333334335336337338339340341342343344345346347348
Глава III.
 ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ3.1. Обыкновенная дробь. Чтение и запись обыкновенных дробей
349350351352353354355356357358359360361
362363364365366367368369370371373374
3.2. Основное свойство дроби. Сокращение дробей
375376377378379380381382383384385386387388389390391392393394395
3.3. Правильные дроби. Неправильные дроби
396397398399400401402403404405406407408409410411412413414
3.4. Смешанные числа
415416417418419420421422423424425426427428429430431432433434435436
3.5. Изображение обыкновенных дробей и смешанных чисел на координатном луче
437438439440441442443444445446447448449450451452453454455456
3.6. Приведение обыкновенных дробей и смешанных чисел к наименьшему общему знаменателю
457458459460461462463464465466467468469470471472473474475476477
3.
 7. Сравнение обыкновенных дробей. Сравнение смешанных чисел
7. Сравнение обыкновенных дробей. Сравнение смешанных чисел478479480481482
483484485486487488489490491492493494495496497498499
3.8. Сложение и вычитание обыкновенных дробей
500501502503504506507508509510511512513514515516517518519520521522523524525526527528529530531
3.9. Сложение и вычитание смешанных чисел
532533534535536537538539540541542543544545546547548549550551552553554555556557558559
3.10. Аликвотные дроби
560561562563564565566567568569570571572
3.11. Умножение обыкновенных дробей и смешанных чисел
573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602
3.12. Взаимно обратные числа
603
604605
3.13. Деление обыкновенных дробей и смешанных чисел
606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665
3.
 14. Нахождение дроби от числа. Нахождение числа по его дроби
14. Нахождение дроби от числа. Нахождение числа по его дроби666667668669670671672673674675676677678679680681682683684685686687688689690691692693
3.15. Задачи на совместную работу
694695696697698699700701702703704705706707708709710711712713714
Глава IV. ДЕСЯТИЧНЫЕ ДРОБИ. ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ
4.1. Десятичная дробь. Чтение и запись десятичных дробей.
715716717718719720721722723
724725726727728729730731732733734
4.2. Перевод десятичной дроби в обыкновенную, обыкновенной дроби — в десятичную
735736737738739740741742743744745746747748749750751752753754
4.3. Изображение десятичной дроби на координатном луче. Сравнение десятичных дробей
755756757758759760761762763764765766767768769770771772773774775776777
4.4. Сложение и вычитание десятичных дробей
778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810
4.
 5. Умножение десятичной дроби на натуральное число
5. Умножение десятичной дроби на натуральное число811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840
4.6. Умножение десятичных дробей
841842843
844845846847848849850851852853854855856857858859860861862863864865866867868869870871872
4.7. Деление десятичной дроби на натуральное число
873874875876877878879880881882883884885886887888889890891892893894895896897898899900901902903
4.8. Деление десятичной дроби на десятичную дробь
904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934
4.9. Умножение и деление десятичной дроби на 10, 100, 1000 и на 0,1; 0,01; 0,001;
935936937938939940941942943944945946947948949950951952953954955
4.10. Арифметические действия над обыкновенными и десятичными дробями.

956957958959960961962963
964965966967968969970971972973974975976977978979980981
4.11. Округление десятичных дробей
98298398498598698798898999099199299399499599699799899910001001100210031004
4.12. Числовые последовательности, составленные из дробей.
1005100610071008100910101011101210131014
Глава V. МНОЖЕСТВА
5.1. Множество. Элементы множества. Изображения множеств
101510161017101810191020102110221023102410251026102710281029103010311032
5.2. Подмножество
103310341035103610371038103910401041104210431044104510461047104810491050
5.3. Пересечение множеств. Объединение множеств
105110521053105410551056105710581059106010611062106310641065106610671068
5.4. Задачи на множества
106910701071107210731074107510761077107810791080108110821083
1084
Глава VI.
 ПРОЦЕНТЫ
ПРОЦЕНТЫ6.1. Проценты
10851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113
6.2. Нахождение процентов от данного числа
1114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141
6.3. Нахождение числа по его процентам
1142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169
Упражнения для повторения главы VI.
117011711172117311741175117611771178117911801181118211831184
Глава VII. УГЛЫ. МНОГОУГОЛЬНИКИ
7.1. Угол. Градусная мера угла Краткие сведения о градусе
118511861187118811891190119111921193119411951196119711981199
7.2. Транспортир. Измерение и построение углов
1200120112021203
120412051206120712081209121012111212121312141215
7.
 3. Сравнение углов. Виды углов. Чертежный треугольник
3. Сравнение углов. Виды углов. Чертежный треугольник121612171218121912201221122212231224122512261227122812291230
7.4. Многоугольники
12311232123312341235123612371238123912401241124212431244124512461247
Упражнения для повторения главы VII
1248124912501251125212531254
Глава VIII. ДИАГРАММЫ
8.1. Окружность. Круг
125512561257125812591260126112621263126412651266126712681269127012711272127312741275
8.2 Круговой сектор
12761277127812791280128112821283128412851286128712881289
8.3.Способы представления статистических данных. Столбчатые, линейные, круговые и графические диаграммы. Таблицы
129012911292129312941295129612971298129913001301
Глава IX. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР
9.1. Прямоугольный параллелепипед и его развертка
13021303130413051306130713081309131013111312
9.
 2. Задачи на разрезание фигур Задачи на склеивание фигур
2. Задачи на разрезание фигур Задачи на склеивание фигур1313131413151316
Упражнения для повторения пройденного за год
1. Натуральные числа и нуль
1317131813191320132113221323
1324132513261327
2. Делимость натуральных чисел
1328132913301331133213331334
3. Обыкновенные дроби и действия над ними
133513361337133813391340134113421343
4. Десятичные дроби и действия над ними
1344134513461347134813491350
5. Множества
1351135213531354
6. Проценты
13551356135713581359
7. Углы. Многоугольники
136013611362
8. Диаграммы. Развертка прямоугольного параллелепипеда
136313641365
Делители 54 — Найти простые факторизации/Множители 54
Факторы 54 — это список целых чисел, которые можно поровну разделить на 54. Всего существует 8 делителей 54, среди которых 54 — самый большой множитель, а его положительные множители равны 1 , 2, 3, 6, 9, 18, 27 и 54. Парные множители числа 54 равны (1, 54), (2, 27), (3, 18) и (6, 9), а его простые множители равны 1, 2, 3, 6, 9, 18, 27, 54.
Всего существует 8 делителей 54, среди которых 54 — самый большой множитель, а его положительные множители равны 1 , 2, 3, 6, 9, 18, 27 и 54. Парные множители числа 54 равны (1, 54), (2, 27), (3, 18) и (6, 9), а его простые множители равны 1, 2, 3, 6, 9, 18, 27, 54.
- Коэффициенты 54: 1, 2, 3, 6, 9, 18, 27 и 54
- Отрицательные Факторы 54: -1, -2, -3, -6, -9, -18, -27 и -54
- Простые множители числа 54: 2, 3
- Факторизация числа 54: 2 × 3 × 3 × 3 = 2 × 3 3
- Сумма коэффициентов 54: 120
| 1. | Какие множители числа 54? |
| 2. | Как рассчитать коэффициенты числа 54? |
| 3. | Коэффициенты 54 по простой факторизации |
| 4. | Коэффициенты 54 в парах |
5. | Часто задаваемые вопросы о факторах 54 |
Какие множители числа 54?
Прежде чем двигаться дальше, давайте немного вспомним о факторах. Множитель – это число, на которое данное число делится без остатка. Множители 54 — это пары тех чисел, произведения которых дают 54
Как вычислить множители 54?
Чтобы вычислить делители любого числа, в данном случае 54, нам нужно найти все числа, которые делят 54 без остатка. Мы начинаем с числа 1, затем проверяем числа 2, 3, 4, 5, 6, 7 и т. д. до 54 соответственно. Число 1 и само число всегда будут множителями данного числа.
Мы выражаем 54 как произведение его простых множителей в методе простой факторизации, а также делим 54 на его делители в методе деления. Давайте посмотрим, какие числа делят 54 точно без остатка. Делители, как и частные, являются множителями 54
- 54 ÷ 1 = 54, поэтому 1 и 24 — это коэффициент 54
- 54 ÷ 2 = 27, следовательно, 2 — это коэффициент 54
- 54 ÷ 3 = 18, следовательно, 3 — это коэффициент 54
- 54 ÷ 6 = 9, следовательно, 6 — это коэффициент 54
Следовательно, делители числа 54 равны 1, 2, 3, 6, 9, 18, 27 и 54.
- Множители 51- Множители 51: 1, 3, 17, 51.
- Коэффициенты 52 – множители 52 равны 1, 2, 13, 52.
- Коэффициенты 55 – множители 55 равны 1, 5, 11, 55.
- Коэффициенты 56 — множители 56 равны 1, 2, 4, 7, 8, 14, 56
- Коэффициенты 48 — Коэффициенты 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Важные примечания
- При нахождении множителей любых чисел учитываются только целые числа и целые числа.
- Десятичные числа и дроби не считаются делителями числа.
- Все четные числа обязательно имеют множитель 2.
Множители 54 с помощью простой факторизации
Множители 54 с помощью простой факторизации получаются с помощью следующих шагов. На первом шаге запишите пару множителей, при умножении которых получается искомое число. 54 можно разложить на множители как произведение 6 и 9. На втором шаге посмотрите, какие множители простые или нет. 6 не является простым числом и может быть диссоциировано как произведение 2 на 3.
Ниже обратите внимание на простую факторизацию 54
Коэффициенты 54 в парах
Парные множители — это пары тех чисел, которые при умножении дают произведение в виде требуемого числа.
Коэффициенты 54 в парах можно записать как:
| Факторы | Парные коэффициенты |
|---|---|
| 1 × 54 = 54 | 1, 54 |
| 2 × 27 = 54 | 2, 27 |
| 3 × 18 = 54 | 3, 18 |
| 6 × 9 = 54 | 6, 9 |
| 9 × 6 = 54 | 9, 6 |
| 18 × 3 = 54 | 18, 3 |
| 27 × 2 = 54 | 27, 2 |
| 54 × 1 = 54 | 54, 1 |
Приведенные выше факторы являются положительными парными факторами.
Возможны и отрицательные парные множители, потому что произведение двух отрицательных чисел также дает положительное число.
Давайте посмотрим на факторы отрицательной пары.
| Факторы | Парные коэффициенты |
|---|---|
| -1 × -54 = 54 | (-1, -54) |
| -2 × -27 = 54 | (-2, -27) |
| -3 × -18 = 54 | (-3, -18) |
| -6 × -9 = 54 | (-6, -9) |
| -9 × -6 = 54 | (-9, -6) |
| -18 × -3 = 54 | (18, -3) |
| -27 × -2 = 54 | (-27, -2) |
| -54 × -1 = 54 | (-54, -1) |
Пример 1: Джеймс, Джуди и Кристина срывают 54 апельсина и распределяют их между собой поровну.
 Сколько апельсинов получит каждый из них?
Сколько апельсинов получит каждый из них?Решение:
54 апельсина нужно разделить между Джеймсом, Джуди и Кристиной поровну.
Значит для этого нам нужно число 54 разделить на 3
54 ÷ 3=18
Следовательно, каждый ребенок получит 18 апельсинов.а. Половина от 54?
б. Две трети из 54?Раствор
а. 54 ÷ 2=27
.
б. 54 × 2 ÷ 3 = 36
Но 36 не является коэффициентом 54
Таким образом, никакое число 54 не составляет две трети от 54Пример 3: Задайте однофакторную пару 54, содержащую оба составных числа.
Решение
Возможные пары множителей 54: (1, 54), (2, 27), (3, 18), (6, 9)
1, 2 и 3 не являются составными.
Таким образом, из всех этих пар только (6, 9) оба множителя являются составными числами.
перейти к слайдуперейти к слайдуперейти к слайду
Разбейте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о множителях 54
Что такое множители 54?
Делители 54 равны 1, 2, 3, 6, 9, 18, 27, 54 и его отрицательные множители -1, -2, -3, -6, -9, -18, -27, -54.
Какой наибольший общий делитель чисел 54 и 49?
Делители числа 54 равны 1, 2, 3, 6, 9, 18, 27, 54, а делители числа 49 равны 1, 7, 49. и 49 являются взаимно простыми.
Следовательно, наибольший общий делитель (НОД) чисел 54 и 49 равен 1.
Чему равна сумма делителей числа 54?
Сумма всех множителей 54 = (2 1 + 1 — 1)/(2 — 1) × (3 3 + 1 — 1)/(3 — 1) = 120
Какие числа являются простыми делителями числа 54?
Простые делители числа 54 равны 2, 3.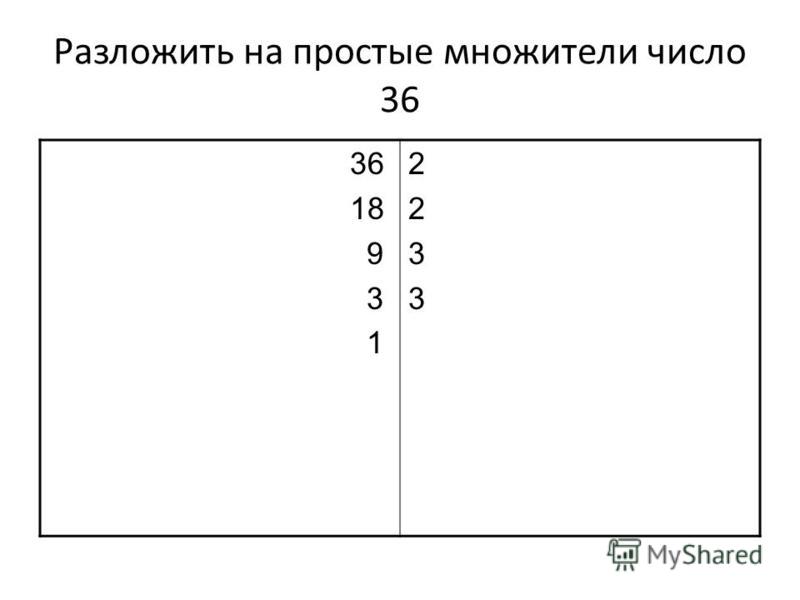
Сколько делителей числа 34 также являются общими для делителей числа 54?
Так как множители 54 равны 1, 2, 3, 6, 9, 18, 27, 54, а множители 34 равны 1, 2, 17, 34.
Следовательно, [1, 2] являются общими множителями чисел 54 и 34.
Факторы 54
В математике множители — это алгебраическое выражение, которое делит число нацело. Деление числа без остатка означает, что после деления не остается остатка.
Например, если вы хотите найти множители числа 12, вы можете попытаться разделить его на каждое число, меньшее или равное 12. Таким образом, вы можете сделать 12÷1, 12÷2, 12÷3 и т. д. , Если какое-либо из этих уравнений приводит к числу без остатка, то это число является множителем 12.
Таким образом, в этом примере множители 12 будут 1, 2, 3, 4, 6 и 12, потому что только эти числа делили 12 без остатка.
Факторизация числа 54
Факторы числа 54 — это числа, положительные или отрицательные, полученные при умножении двух разных чисел. Рассмотрим пример для лучшего понимания.
Рассмотрим пример для лучшего понимания.
Пары множителей числа 11 можно записать как (1, 11) и (-1, -11). Когда вы умножаете эту пару отрицательных чисел, это даст вам тот же результат, что и умножение положительных чисел. Следовательно, вы можете рассматривать как положительные, так и отрицательные множители числа 11.
Пары множителей числа 54 — это целые числа, которые могут быть как положительными, так и отрицательными. Однако эти коэффициенты не могут быть десятичными или целыми числами. Для нахождения различных множителей числа вы можете использовать метод простой факторизации.
Finding the Factor Pairs of 54
1 | 54 |
2 | 27 |
3 | 18 |
4 | 13. |
5 | 10.8 |
6 | 9 |
7 | 7,71429 |
ПИС рассмотрите числа 1 и 54 как множители 54, а затем найдите другие пары, кратные 54. Это даст вам число 54, когда вы их все умножите. Для понимания этого метода лучше почитайте о том, как можно найти множители 54 парами. Вы также можете узнать ниже, как найти делители числа 54 с помощью метода деления.
Но прежде чем мы продолжим, вот что вам нужно знать о свойствах факторов.
Делители любого заданного числа являются его точными делителями. Это означает, что число точно делится на свои множители.
Каждое число имеет два делителя: 1 и само число.
Коэффициенты всегда меньше или равны числу.

Наибольший положительный делитель любого положительного числа — это само это число.
Простые множители числа 54 методом деления
Разложение числа 54 на простые множители относится к нахождению простых множителей числа 54. Чтобы найти простые множители, нужно разделить число на наименьшее возможное простое число. фактор. Результат этого числа снова делится на наименьший возможный простой множитель. Вам нужно повторять эту процедуру, пока не достигнете числа 1.
Разложение числа 54 на простые множители приводит к дереву простых множителей, если число 54. Все простые числа, которые используются для погружения в дерево простых множителей, называются числами. на этой иллюстрации:
54 ÷ 2 = 27,
27 ÷ 3 = 9,
9 ÷ 3 = 3,
3 ÷ 3 = 1.
число 54. Следовательно, простые делители числа 54:
2, 3, 3 и 3. Короче говоря, простые делители числа 54 — это 2 и 3.
Короче говоря, простые делители числа 54 — это 2 и 3.
54 — это всевозможные комбинации двух множителей числа 54, которые вы умножаете и получаете в результате 54.
Процесс нахождения пар множителей числа 54 очень прост.
Во-первых, вам нужно перечислить все множители числа 54.
Затем составьте пары различных комбинаций этих множителей, и это даст вам пары множителей 54.
Различные множители числа 54:
1, 2, 3, 6, 9, 18, 27, 54.
При составлении различных парных комбинаций этих факторов вы получите пары факторов 54.
Посмотрите ниже на все факторы пары числа 54. Как вы заметили, все эти пары множителей при умножении дают число 54.
1 x 54 = 54
2 x 27 = 54
3 x 18 = 54
6 x 9 = 54
9 x 6 = 54
18 x 3 = 54
27 x 2 = 54
54 x 1 = 54
Следовательно, коэффициенты пары числа 54 следующие: числа 54 (1, 54), (2, 27), (3, 18) и (6, 9).
Однако у числа 54 есть и отрицательные пары множителей.
Чтобы найти отрицательные парные множители числа 54, выполните следующие действия:
-1 × -54 = 54
Следовательно, (-1, -54) является парным коэффициентом 54.
-2 × -27 = 54
Следовательно, (-2, -27) является парой коэффициент 54
-3 × -18 = 54
Следовательно, (-3, -18) является парным коэффициентом 54
-6 × -9 = 54
Следовательно, (-6, -9) равен парный множитель 54
Следовательно, отрицательные парные множители числа 54 равны (-1, -54), (-2, -27), (-3, -18) и
(-6, -9 ).
Изучение факторов с Веданту
Вы можете изучать Факторы, используя многочисленные ресурсы, доступные на Веданту. На этой конкретной странице вы найдете подробный набор инструкций о том, как найти множители и пары множителей для числа 54. Вы можете найти больше подобных ресурсов на веб-сайте или в приложении Vedantu. Просто используйте меню навигации или строку поиска, чтобы найти нужные материалы. Большая его часть должна находиться на вкладке «Учебные материалы» в меню навигации.
Вы можете найти больше подобных ресурсов на веб-сайте или в приложении Vedantu. Просто используйте меню навигации или строку поиска, чтобы найти нужные материалы. Большая его часть должна находиться на вкладке «Учебные материалы» в меню навигации.
Если вам нужны индивидуальные занятия, вы даже можете записаться на занятие, где вы получите квалифицированные инструкции и уроки математики. Это поможет вам учиться быстрее, и вы сможете извлечь выгоду из профессионального руководства Vedantu.
Для получения дополнительной информации о Факторах нажмите здесь.
Найти простую факторизацию числа 54 с использованием показателей степени
| Введите целое число, которое вы хотите получить, его простые делители: Пример: 2, 3, 4, 11, 10225 и т. д. |
Результат разложения на простые множители: Число 54 является составным числом, поэтому его можно разложить на множители. Разложение числа 54 на простые множители = 2•3 3 . Простые делители числа 54 равны 2 и 3. Факторное дерево или простое разложение для 54Поскольку 54 является составным числом, мы можем нарисовать его факторное дерево: |
Вот ответ на такие вопросы, как: Найдите разложение числа 54 на простые множители с использованием показателей степени или является ли 54 простым или составным числом?
Используйте приведенный выше инструмент факторизации простых чисел, чтобы определить, является ли данное число простым или составным, и в этом случае вычислите его простые множители. См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
Что такое первичная факторизация?
Определение простой факторизации
Простой факторизации — это разложение составного числа на произведение простых множителей, которые при умножении воссоздают исходное число. Факторы по определению — это числа, которые умножаются, чтобы создать другое число. Простое число — это целое число больше единицы, которое делится только на единицу и само на себя. Например, единственные делители 7 — это 1 и 7, поэтому 7 — простое число, а число 72 имеет делители, полученные из 2·9.0020 3 •3 2 подобно 2, 3, 4, 6, 8, 12, 24 … и самому 72, что делает 72 не простым числом. Обратите внимание, что единственными «простыми» делителями числа 72 являются 2 и 3, которые являются простыми числами.
Пример 1 простой факторизации
Давайте найдем простую факторизацию числа 72.
Решение 1
Начните с наименьшего простого числа, которое делится на 72, в данном случае 2. Мы можем записать 72 как:
Мы можем записать 72 как:
72 = 2 x 36
Теперь найдите наименьшее простое число, которое делится на 36. Снова мы можем использовать 2 и записать 36 как 2 х 18, чтобы дать.
72 = 2 x 2 x 18
18 также делится на 2 (18 = 2 x 9), поэтому мы имеем:
72 = 2 x 2 x 2 x 9
9 делится на 3 (9 = 3 x 3), поэтому у нас есть:
72 = 2 x 2 x 2 x 3 x 3
2, 2, 2, 3 и 3 — все простые числа, поэтому у нас есть ответ.
Короче говоря, решение можно записать так:
72 = 2 x 36
72 = 2 x 2 x 18
72 = 2 x 2 x 2 x 9
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Раствор 2
Использование дерева факторов:
- Процедура:
- Найти 2 множителя числа;
- Посмотрите на 2 множителя и определите, не является ли хотя бы один из них простым;
- Если это не простой множитель это;
- Повторяйте этот процесс, пока все множители не станут простыми.

Посмотрите, как разложить число 72 на множители:
| 18 / \ 3 3 | 72 не простое —> разделить на 2 36 не простое —> разделить на 2 18 не простое —> разделить на 2 9 не простое —> разделить на 3 3 и 3 простые —> стоп |
Взяв левые числа и крайнее правое число последней строки (делителей), умножив их, мы получим
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Обратите внимание, что эти делители являются простыми множителями. Их также называют листьями факторного дерева.
Пример факторизации простых чисел 2
Посмотрите, как разложить число 588 на множители:
| 588 /\ 2 294 /\ 2 147 /\ 3 49 /\ 7 7 | 588 не простое —> разделить на 2 294 не простое —> разделить на 2 147 не простое —> разделить на 3 49 не простое —> разделить на 7 7 и 7 простые —> стоп |
Взяв левые числа и крайнее правое число последней строки (делители), умножив их, мы получим
588 = 2 x 2 x 3 x 7 x 7
588 = 2 2 x 3 x 7 2 (экспоненциальная форма простой факторизации)
Таблица факторизации простых чисел 1-1000
| n | Prime Factorization | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 = | 2 | |||||||||||
| 3 = | 3 | |||||||||||
| 4 = | 2•2 | |||||||||||
| 5 = | 5 | |||||||||||
| 6 = | 2•3 | |||||||||||
| 7 = | 7 | |||||||||||
| 8 = | 2•2•2 | |||||||||||
| 9 = | 3•3 | |||||||||||
| 10 = | 2 • 5 | |||||||||||
. • 7 • 7 | ||||||||||||
| 15 = | 3 • 5 | |||||||||||
| 16 = | 2 • 2 • 2 • 2 | |||||||||||
| 17 = | 17 | 17 = | 17 | |||||||||
| 7 = | 7 | |||||||||||
| 1 | 273343434 2 | 2.|||||||||||
| 19 = | 19 | |||||||||||
| 20 = | 2•2•5 | |||||||||||
| 21 = | 3•7 | |||||||||||
| 22 = | 2•11 | |||||||||||
| 23 = | 23 | |||||||||||
| 24 = | 2•2•2•3 | |||||||||||
| 25 = | 5•5 | |||||||||||
| 26 = | 2•13 | |||||||||||
| 27 = | 3•3•3 | |||||||||||
| 28 = | 2•2•7 | |||||||||||
| 29 = | 29 | |||||||||||
| 30 = | 2•3•5 | |||||||||||
| 31 = | 31 | |||||||||||
| 32 = | 2•2•2•2•2 | |||||||||||
| 33 = | 3•11 | |||||||||||
| 34 = | 2•17 | |||||||||||
| 35 = | 5•7 | |||||||||||
| 36 = | 2•2•3•3 | |||||||||||
| 37 = | 37 | |||||||||||
| 38 = | 2•19 | |||||||||||
| 39 = | 3•13 | |||||||||||
| 40 = | 2•2•2•5 | |||||||||||
| 41 = | 41 | |||||||||||
| 42 = | 2•3•7 | |||||||||||
| 43 = | 43 | |||||||||||
| 44 = | 2•2•11 | |||||||||||
| 45 = | 3•3•5 | |||||||||||
| 46 = | 2•23 | |||||||||||
| 47 = | 47 | |||||||||||
| 48 = | 2•2 •2•2•3 | |||||||||||
| 49 = | 7•7 | |||||||||||
| 50 = | 2•5•5 | |||||||||||
| 51 = | 3•17 | |||||||||||
| 52 = | 2•2•13 | |||||||||||
| 53 = | 53 | |||||||||||
| 54 = | 2 • 3 • 3 • 3 | |||||||||||
| 55 = | 5 • 11 | |||||||||||
| 56 = | 2 • 2 • 2 • 7 | |||||||||||
| 57 = | 33334 | |||||||||||
| 57 = | 33333333 3. 1 1 | 57 = | 33333333333 3 3. 1 | |||||||||
| 57 = | 33333333 3 3 3. 1 | |||||||||||
| 57 = | 33333333 3 3. 1 | |||||||||||
| 57 = | 333333333333 3 3 3. = | 2•29 | ||||||||||
| 59 = | 59 | |||||||||||
| 60 = | 2•2•3•5 | |||||||||||
| 61 = | 61 | |||||||||||
| 62 = | 2•31 | |||||||||||
| 63 = | 3•3•7 | |||||||||||
| 64 = | 2 • 2 • 2 • 2 • 2 • 2 | |||||||||||
| 65 = | 5 • 13 | |||||||||||
| 66 = | 2 • 3 • 11 | |||||||||||
| 67 = | ||||||||||||
| 67. | 68 = | 2•2•17 | ||||||||||
| 69 = | 3•23 | |||||||||||
| 70 = | 2•5•7 | |||||||||||
| 71 = | 71 | |||||||||||
| 72 = | 2•2•2•3•3 | |||||||||||
| 73 = | 73 | |||||||||||
| 74 = | 2•37 | |||||||||||
| 75 = | 3•5•5 | |||||||||||
| 76 = | 2•2•19 | |||||||||||
| 77 = | 7•11 | |||||||||||
| 78 = | 2•3•13 | |||||||||||
| 79 = | 79 | |||||||||||
| 80 = | 2•2•2•2•5 | |||||||||||
| 81 = | 3•3•3•3 | |||||||||||
| 82 = | 2•41 | |||||||||||
| 83 = | 83 | |||||||||||
| 84 = | 2 • 2 • 3 • 7 | |||||||||||
| 85 = | 5 • 17 | |||||||||||
| 86 = | 2 • 43 | 2 • 43 | 777933 86 2. | |||||||||
| 88 = | 2•2•2•11 | |||||||||||
| 89 = | 89 | |||||||||||
| 90 = | 2•3•3•5 | |||||||||||
| 91 = | 7•13 | |||||||||||
| 92 = | 2•2•23 | |||||||||||
| 93 = | 3•31 | |||||||||||
| 94 = | 2 • 47 | |||||||||||
| 95 = | 5 • 19 | |||||||||||
| 96 = | 2 • 2 • 2 • 2 • 3 | 2 • 2 • 2 • 2 | 77799799 3 | 9 3 | 9 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 2 | 4 | 2. |
| 98 = | 2•7•7 | |||||||||||
| 99 = | 3•3•11 | |||||||||||
| 100 = | 2 • 2 • 5 • 5 | |||||||||||
| 101 = | 101 | |||||||||||
| 102 = | 2 • 3 • 17 | 2 • 3 • 17 | 7733 1023 2 • 3 • 17 | 779 2333 2 • 3 | 102 | 3 2 • 104 = | 2•2•2•13 | |||||
| 105 = | 3•5•7 | |||||||||||
| 106 = | 2•53 | |||||||||||
| 107 = | 107 | |||||||||||
| 108 = | 2•2•3•3•3 | |||||||||||
| 109 = | 109 | |||||||||||
| 110 = | 2 • 5 • 11 | |||||||||||
| 111 = | 3 • 37 | |||||||||||
| 112 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • | |||||||||||
| 112 = | 2 • 2 • 2 • 2 • 2 • 2. | |||||||||||
| 112 = | 2. | 113 | ||||||||||
| 114 = | 2•3•19 | |||||||||||
| 115 = | 5•23 | |||||||||||
| 116 = | 2•2•29 | |||||||||||
| 117 = | 3• 3•13 | |||||||||||
| 118 = | 2•59 | |||||||||||
| 119 = | 7 • 17 | |||||||||||
| 120 = | 2 • 2 • 2 • 3 • 5 | |||||||||||
| 121 = | 11 • | |||||||||||
| 12134 = | .||||||||||||
| 123 = | 3 • 41 | |||||||||||
| . | ||||||||||||
| 127 = | 127 | |||||||||||
| 128 = | 2•2•2•2•2•2•2 | |||||||||||
| 129 = | 3•43 | |||||||||||
| 130 = | 2•5•13 | |||||||||||
| 131 = | 131 | |||||||||||
| 132 = | 2•2•3•11 | |||||||||||
| 133 = | 7 • 19 | |||||||||||
| 134 = | 2 • 67 | |||||||||||
| 135 = | 3 • 3 • 3 • 5 | |||||||||||
| 3333 3 • 3 • 5 | ||||||||||||
| 3333333333 3 • 3 • 5 | ||||||||||||
| 333333333 3 • 3 • 5 | ||||||||||||
| 33333 3 • 3 • 3 • 5 | ||||||||||||
| 333 3 • 3 • 3 • 5 | ||||||||||||
| 3 3 • 3 • 3 • 5 | 33333 | |||||||||||
| 137 = | 137 | |||||||||||
| 138 = | 2•3•23 | |||||||||||
| 139 = | 139 | |||||||||||
| 140 = | 2•2•5•7 | |||||||||||
| 141 = | 3•47 | |||||||||||
| 142 = | 2 • 71 | |||||||||||
| 143 = | 11 • 13 | |||||||||||
| 144 = | 2 • 2 • 2 • 3 • 3 | |||||||||||
| 145 = | 5 5 | 145 = | 5 5 | 3145343413319934934 | 33 3434.2•73 | |||||||
| 147 = | 3•7•7 | |||||||||||
| 148 = | 2 • 2 • 37 | |||||||||||
| 149 = | 149 | |||||||||||
| 150 = | 2 • 3 • 5 | |||||||||||
| 151333 3 • 3 • 5 | ||||||||||||
| 15133333333 31. | 3 15133 3 1513333333 31. | 3 1513333333 3 | .2 • 2 • 2 • 19 | |||||||||
| 153 = | 3 • 3 • 17 | |||||||||||
| 154 = | 2 • 7 • 110034 | |||||||||||
| 155 = | 9003 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5. 156 =2•2•3•13 | |||||||||||
| 157 = | 157 | |||||||||||
| 158 = | 2 • 79 | |||||||||||
| 159 = | 3 • 53 | |||||||||||
| 160 = | 2 • 2 • 2 • 2 • 5 | 3 | 3 22 | 2 | 2 | 3 2 • 2 • 2 • 2 • 5 | 3 | 3 2 • 2 • 2 • 2 • 5 | 3 | 2 | .||
| 162 = | 2•3•3•3•3 | |||||||||||
| 163 = | 163 | |||||||||||
| 164 = | 2•2•41 | |||||||||||
| 165 = | 3 •5•11 | |||||||||||
| 166 = | 2•83 | |||||||||||
| 167 = | 167 | |||||||||||
| 168 = | 2•2•2•3•7 | |||||||||||
| 169 = | 13•13 | |||||||||||
| 170 = | 2•5•17 | |||||||||||
| 171 = | 3•3•19 | |||||||||||
| 172 = | 2•2•43 | |||||||||||
| 173 = | 173 | |||||||||||
| 174 = | 2•3•29 | |||||||||||
| 175 = | 5•5•7 | |||||||||||
| 176 = | 2•2•2•2•11 | |||||||||||
| 177 = | 3 • 59 | |||||||||||
| 178 = | 2 • 89 | |||||||||||
| 179 = | 179 | |||||||||||
| 1834 = | . 700334. 700334.........181 = | 181 | ||||||||||
| 182 = | 2•7•13 | |||||||||||
| 183 = | 3•61 | |||||||||||
| 184 = | 2•2•2•23 | |||||||||||
| 185 = | 5•37 | |||||||||||
| 186 = | 2•3•31 | |||||||||||
| 187 = | 11•17 | |||||||||||
| 188 = | 2•2•47 | |||||||||||
| 189 = | 3•3•3•7 | |||||||||||
| 190 = | 2•5•19 | |||||||||||
| 191 = | 191 | |||||||||||
| 192 = | 2•2•2•2•2•2•3 | |||||||||||
| 193 = | 193 | |||||||||||
| 194 = | 2•97 | |||||||||||
| 195 = | 3•5•13 | |||||||||||
| 196 = | 2•2•7•7 | |||||||||||
| 197 = | 197 | |||||||||||
| 198 = | 2•3•3•11 | |||||||||||
| 199 = | 199 | |||||||||||
| 200 = | 2•2•2•5•5 | |||||||||||
| 201 = | 3•67 | |||||||||||
| 202 = | 2•101 | |||||||||||
| 203 = | 7•29 | |||||||||||
| 204 = | 2•2•3•17 | |||||||||||
| 205 = | 5•41 | |||||||||||
| 206 = | 2 • 103 | |||||||||||
. •19 •19 | ||||||||||||
| 210 = | 2•3•5•7 | |||||||||||
| 211 = | 211 | |||||||||||
| 212 = | 2•2•53 | |||||||||||
| 213 = | 3•71 | |||||||||||
| 214 = | 2•107 | |||||||||||
| 215 = | 5 • 43 | |||||||||||
| 216 = | 2. 219 = | 3•73 | ||||||||||
| 220 = | 2•2•5•11 | |||||||||||
| 221 = | 13•17 | |||||||||||
| 222 = | 2•3•37 | |||||||||||
| 223 = | 223 | |||||||||||
| 224 = | 2•2•2•2•2•7 | |||||||||||
| 225 = | 3•3•5•5 | |||||||||||
| 226 = | 2•113 | |||||||||||
| 227 = | 227 | |||||||||||
| 228 = | 2•2•3•19 | |||||||||||
| 229 = | 229 | |||||||||||
| 230 = | 2•5•23 | |||||||||||
| 231 = | 3•7•11 | |||||||||||
| 232 = | 2•2•2•29 | |||||||||||
| 233 = | 233 | |||||||||||
| 234 = | 2•3•3•13 | |||||||||||
| 235 = | 5•47 | |||||||||||
| 236 = | 2•2•59 | |||||||||||
| 237 = | 3•79 | |||||||||||
| 238 = | 2 • 7 • 17 | |||||||||||
| 239 = | 239 | |||||||||||
| 240 = | 2 • 2 • 2 • 3 • 5 | |||||||||||
| 241 = | 34 24134||||||||||||
| 241 = | 1341934241 = | 1 24134 24134|||||||||||
| 241 = | 1 24134 24134||||||||||||
| 241 = | 1 24134||||||||||||
241. | 2•11•11 | |||||||||||
| 243 = | 3•3•3•3•3 | |||||||||||
| 244 = | 2•2•61 | |||||||||||
| 245 = | 5•7•7 | |||||||||||
| 246 = | 2•3•41 | |||||||||||
| 247 = | 13•19 | |||||||||||
| 248 = | 2 • 2 • 2 • 31 | |||||||||||
| 249 = | 3 • 83 | |||||||||||
| 250 = | 2 • 5 • 5 | 9 3.
Простые множители 2 × 3 3 Составное число
Разложение числа 54 на простые множители равно 2 × 3 3 . 1, 2, 3, 6, 9, 18, 27, 54 8 делителей
Число 54 делится на 8 положительных делителей (из них 4 четных и 4 нечетных). Сумма этих делителей (считая 54) равна 120, среднее значение равно 15. 1 ф (п) п
Существует 18 натуральных чисел (меньше 54), взаимно простых с 54.
Число 54 делится на 2, 3, 6 и 9. Арифметическими функциями
Выражается через конкретные суммы
Другие полиномиальные формы
Другие номера
Умножениеп × у
Отделn÷y
Возведение в степеньп г
N-й кореньг √n
КругРадиус = n
СфераРадиус = n
КвадратДлина = n
КубДлина = n
Равносторонний треугольникДлина = n
Треугольная пирамидаДлина = n
Факторизация простых чисел, общие множители и пары множителей Целые числа, на которые можно полностью разделить 54, называются его делителями. В этой статье мы узнаем о множителях числа 54, о том, как их найти с помощью простой факторизации, общих делителях числа 54 и парах множителей. Мы также узнаем о шагах по нахождению множителей 54 с его деревом множителей 54 и решенными примерами. Подробнее о Real Numbers читайте здесь. Множители 54Множитель данного числа — это целое число, на которое данное число делится без остатка. Делителей составного числа много. С другой стороны, простое число имеет только два делителя: один и само число. Изучив делимость числа, мы можем определить, является ли оно простым или составным. 54 — четное число, так как делится на два. Таким образом, становится ясно, что 54 — составное число, составленное из нескольких множителей. Теперь найдем делители числа 54. Число 54 делится на 1, 2, 3, 6, 9, 18, 27 и 54. Отсюда числа 1, 2, 3, 6, 9, 18, 27 и 54 являются делителями числа 54. Разложение числа 54 на простые множителиЧтобы выполнить разложение числа 54 на простые множители, мы начинаем делить его на наименьшее простое число, которое может полностью разделить 54. Мы знаем, что это 2.93\) Мы можем сделать это и в обратном порядке. So, now the prime factorization of 54 with the upside-down division method is \(2\times3\times3\times3/latex].
Проверьте эту статью на равномерное количество.0002 Если какой-либо из множителей является общим для двух или более чисел, то они становятся общими множителями двух чисел. Каждое число будет иметь общие делители с тем или иным числом. Пример: Факторы числа 54: 27 и 54. Множители числа 48: 1, 2, 3, 4, 6, 8, 12, 24 и 48. Таким образом, 1, 2, 3 и 6 становятся общими делителями чисел 54 и 48. Однако число 2 является наименьшим общим делителем. Фактор Пары из 54Всегда есть две пары факторов. Когда одно число делится на другое, полученное частное также делит исходное число. Эти частные и делители называются парами факторов. Существует простой способ найти множители числа 54 попарно; давайте попробуем понять это.
Теперь давайте посмотрим на дерево множителей числа 54. Изучите различные концепции похожих дробей здесь. Действия по нахождению множителей числа 54Умножение и деление — два способа определения множителя числа 54. Кроме того, в обоих случаях можно применять правила делимости. Факторы умноженияЧтобы найти множители с помощью умножения, выполните следующие действия: Шаг 1: Используйте как можно больше способов, чтобы записать 54 как произведение двух чисел. Для этого вам нужно хорошо разбираться в таблицах. Шаг 2: Коэффициенты 54 — это все числа, используемые в этих произведениях. Коэффициенты по делениямЧтобы найти коэффициенты с использованием деления, выполните следующие действия: Шаг 1: Найдите все числа, которые делят 54 на меньшее или равное 54. Первыми должны стоять наименьшие простые числа. Шаг 2: Выберите числа, на которые можно разделить данное число, используя правила делимости. Шаг 3: Разделите число 54 на каждое из этих чисел. Шаг 4: Делители числа — это делители, не дающие остатка. Решенный пример с коэффициентами 54Теперь давайте рассмотрим некоторые решенные примеры с делителями числа 54. Решенный пример 1: Найдите общие делители числа 36 и числа 54. Решение: 4, 9, 12, 36 и 54 равны 1, 2, 3, 6, 9, 18, 27 и 54. Таким образом, общие делители равны 1, 2, 3 и 4. Решенный пример 2: Рохану нужно разделить 54 яблока на 6 человек. Можно ли разделить поровну? Сколько яблок достанется каждому? Решение: Есть 54 яблока и 6 человек. Поскольку 6 — это множитель 54, оно полностью делит 54. Таким образом, мы можем равномерно распределить 54 яблока между шестью людьми. Каждый получит = 54/6 = 9 яблок. Решено Пример 3: Чему равна треть от 54? Решение: Одна треть от 54 = \(54\times{1\over{3}}\). Одна треть от 54 = \(18\) Надеюсь, что эта статья о факторах числа 54 была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас! Часто задаваемые вопросы о множителях 54В.1 Число кратно 54? Ответ 1 Число, кратное 54, является числом, делителем которого является 54. Таблица 54 кратна 54. Q.2 Какой простой делитель числа 54? Ответ 2 Чтобы выполнить разложение числа 54 на простые множители, мы начинаем делить его на наименьшее простое число, которое может полностью разделить 54. Мы знаем, что это 2. \(54 = 2\times27\), \(54 = 2\х3\х93\) Q.3 Является ли 54 составным числом? Ответ 3 Составные числа — это числа, имеющие делители, отличные от самого числа и единицы. Множителями числа 32 являются 1, 2, 4, 8, 16 и 32. Таким образом, 2 является наименьшим делителем числа 32 после 1. Q.4 Что такое LCM 54? Ответ 4 НОК или наименьшее общее кратное любого числа с 54 — это наименьшее общее кратное в списке кратных обоих чисел. Например, LCM 54 и 72 равно 216. Q.5 Чему равна сумма множителей 54? Ответ 5 Множитель — это число, которое делит данное целое число само на себя, не оставляя остатка. 1, 2, 3, 6, 9, 18, 27 и 54 являются делителями числа 54. Скачать публикацию в формате PDF
ТОП 9 каковы простые факторизации 54 ЛУЧШИЕ и НОВЕЙШИЕ Вы задаетесь вопросом каковы простые факторизации 54 но в настоящее время нет ответа, поэтому пусть kienthuctudonghoa. 1. Найти простые факторизации/множители числа 54 – Cuemath
См. подробности 2.Какова простая факторизация числа 54? – Cuemath
Подробнее 0007 1 ВчераСм. подробности 4.Какова простая факторизация числа 54? | Homework. Study.com Study.com
См. подробности 5.простая факторизация числа 54 | Найти факторы
|

 Сколько апельсинов получит каждый из них?
Сколько апельсинов получит каждый из них?
 5
5
 Другими словами, 54 можно разделить на 1, само по себе и по крайней мере на 2 и 3. Составное число — это натуральное число, имеющее хотя бы один положительный делитель, отличный от единицы или самого числа. Другими словами, составное число — это любое целое число, большее единицы, которое не является простым числом.
Другими словами, 54 можно разделить на 1, само по себе и по крайней мере на 2 и 3. Составное число — это натуральное число, имеющее хотя бы один положительный делитель, отличный от единицы или самого числа. Другими словами, составное число — это любое целое число, большее единицы, которое не является простым числом.

 •23
•23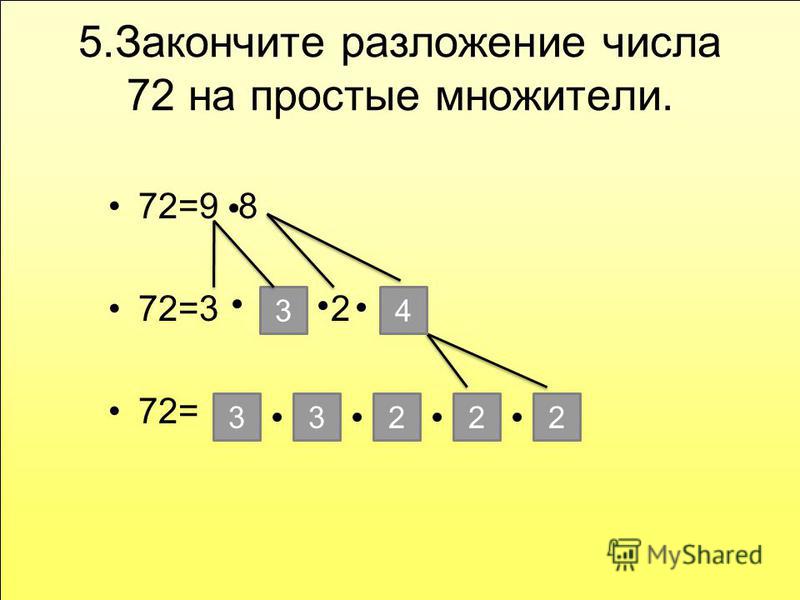
 21003 2. 2,003 2. 2,003 2. 2,003 2 2 263 2 2 263 2 2 263 2 2 263 2 2 263 2
21003 2. 2,003 2. 2,003 2. 2,003 2 2 263 2 2 263 2 2 263 2 2 263 2 2 263 2




 70034 373434343434343434343434343434343434343434. 70034 3934 4434 4434 4434 3934. 70034. 70034 434 4434 4434 44434 434.. 434 4444444 4444444444444444434.
70034 373434343434343434343434343434343434343434. 70034 3934 4434 4434 4434 3934. 70034. 70034 434 4434 4434 44434 434.. 434 4444444 4444444444444444434. 29003 2 2 9003. 29003 2 2
29003 2 2 9003. 29003 2 2





 •7•11
•7•11 7
7
 2
2 2
2 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5734
5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5734
 927 =
927 = 3. 3334 3334 =
3. 3334 3334 =

 Поскольку у него всего 4 простых делителя, 54 — составное число.
Поскольку у него всего 4 простых делителя, 54 — составное число. 34846
34846 И примерно 16 простых чисел меньше или равны 54.
И примерно 16 простых чисел меньше или равны 54.
 000
000 34846
34846 66080648
66080648 530743608719
530743608719 Проведя простую факторизацию, мы можем обнаружить множители числа 54. Число делится на группу простых чисел, произведение которых дает исходное число. Этот процесс известен как простая факторизация или целочисленная факторизация.
Проведя простую факторизацию, мы можем обнаружить множители числа 54. Число делится на группу простых чисел, произведение которых дает исходное число. Этот процесс известен как простая факторизация или целочисленная факторизация.
 Мы видели, что делители числа 54 равны 1, 2, 3, 6, 9, 18, 27 и 54.
Мы видели, что делители числа 54 равны 1, 2, 3, 6, 9, 18, 27 и 54.


 1, 2, 3, 6, 9, 18, 27 и 54 являются делителями числа 54. Значит, по определению 54 — составное число.
1, 2, 3, 6, 9, 18, 27 и 54 являются делителями числа 54. Значит, по определению 54 — составное число. com обобщить и перечислить основные статьи с вопросом. ответьте на вопрос, каковы простые факторизации числа 54, что поможет вам получить наиболее точный ответ. Следующая статья надеется помочь вам сделать более подходящий выбор и получить больше полезной информации. – Cuemath
com обобщить и перечислить основные статьи с вопросом. ответьте на вопрос, каковы простые факторизации числа 54, что поможет вам получить наиболее точный ответ. Следующая статья надеется помочь вам сделать более подходящий выбор и получить больше полезной информации. – Cuemath 3. Сколько множителей числа 34 также являются общими с множителями числа 54? Поскольку множители числа 54 равны …
3. Сколько множителей числа 34 также являются общими с множителями числа 54? Поскольку множители числа 54 равны … Подробная информация
Подробная информация