Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов . Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.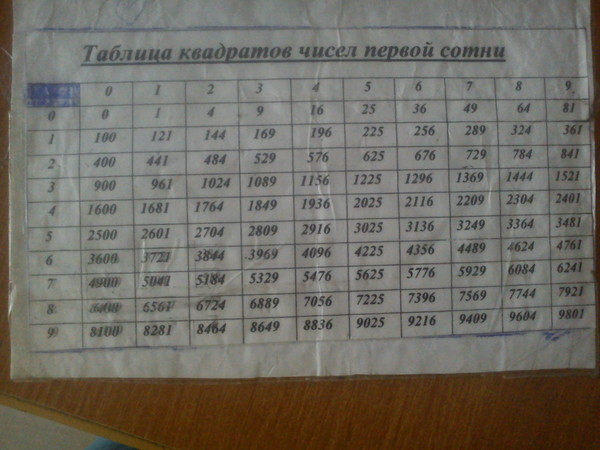 Free xml sitemap generator Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица корней от 1 до 20. Квадратный корень
В данной статье мы с вами разберем такое понятие как квадратный корень, какие бывают виды корней , а так же рассмотрим таблицу корней и то как ей пользоваться.
Итак, что же такое квадратный корень. Для того чтобы это понять воспользуемся примерами из школьного курса и рассмотрим простое уравнение, типа: х2 = 4. Что бы его решить нужно понять какое число нужно возводить в квадрат для получения 4. Это не так уж и сложно так как таблица умножения подсказывает нам что это 2 либо -2. с целью упрощения математического решения и ввели понятие квадратного корня с присвоением ему специального символа?.
Квадратным корнем положительного числа а, будет только положительное число квадрат от которого равняется а.
Как вы думаете почему а может быть только положительное число. Опять обратимся к примеру и найдем корень для?(-9). И это будет 32 = 9, но не — 9, а если возьмем -3. Проверим (-3)2 = 9. Опять не получается и все это из-за того что не существует таких чисел, которые в квадрате давали бы число со знаком минус.
Проверим (-3)2 = 9. Опять не получается и все это из-за того что не существует таких чисел, которые в квадрате давали бы число со знаком минус.
Можно заметить что квадратный корень в решении, может быть только положительным числом, но почему тогда в первом уравнении упоминалось как 2 так и -2? Объясняю, есть квадратные уравнения и арифметические квадратные корни от числа и это разные вещи. Например х2=4 не тоже самое что х=?4.
Да, в этом легко запутаться, но когда нужно только извлечь корень от какого либо числа, то в ответе получим исключительно положительный ответ.
Для удобства и быстроты нахождения решений, существует , которая содержит в себе уже готовые извлеченные корни. Пользуйтесь!
Верхняя строка содержит единицы, а левый столбец десятки. К примеру вам необходимо узнать квадратный корень числа 54. Ищем десятки с левой стороны (это будет цифра 5), а единицы с верху (это будет цифра 4). При пересечении этих значений и находится нужный нам ответ который равен 6,7082.
Также есть таблица квадратов, не путайте с таблицей корней . Выглядит она так:
Она удобно если вам нужно сразу получить значение двухзначного числа в квадрате. К примеру, нужно возвести 89 в квадрат. Находим 8 слева, 9 сверху, на пересечении значение квадрата — 7921.
Чем больше вы будите работать с корнями, тем реже будите пользоваться данной таблицей. Так как все значения со временем запоминаются. Это как таблица умножения, которой мы пользуемся только для изучения и запоминания.
С корнями возможно производить только три действия и это:
Умножать,
— делить,
-возводить в степень.
Свойства и Примеры объединены и показаны в таблице.
Когда срочно нужна курсовая работа, а времени на её написание практически нет. Стоит обратиться за помощью, которая находиться на сайте http://zakazat-kursovuyu.ru/index.php/zakaz-kursovoj . Ценой и качеством Вы будите приятно удивленны.
Извлечение квадратного корня по таблицам. В § 93 на примере извлечения квадратного корня из числа 20 мы показали, как можно вычислить приближённо с необходимой степенью точности. Однако, даже для того чтобы найти искомый корень с точностью до 0,01, пришлось проделать много вычислений. Чтобы облегчить вычислительную работу, составлены специальные таблицы квадратных корней, в которых даны приближённые значения квадратных корней из чисел.
В § 93 на примере извлечения квадратного корня из числа 20 мы показали, как можно вычислить приближённо с необходимой степенью точности. Однако, даже для того чтобы найти искомый корень с точностью до 0,01, пришлось проделать много вычислений. Чтобы облегчить вычислительную работу, составлены специальные таблицы квадратных корней, в которых даны приближённые значения квадратных корней из чисел.
В таблицах В. М. Брадиса даны квадратные корни с точностью до 0,001 чисел от 1 до 10 с промежутком в 0,01 и чисел от 10 до 100 с промежутком в 0,1. Устройство и употребление таблицы такое же, как и таблицы квадратов.
Поясним на примерах, как следует пользоваться таблицами квадратных корней.
В первом столбце находим число 6,7 и рядом с ним во втором столбце квадратный корень из него: 2,588 (по округлении получим 2,6).
В первом столбце находим число 27; в этом же ряду в столбце под номером 6 находим: (по округлении получим: 5,25).
По предыдущему находим: . В столбце «поправок» за № 4 находим число
3, которое прибавляем к последней цифре числа 7,503. Получаем: .
Получаем: .
Подкоренное число можно записать так:
(или по округлении 20,7).
Чтобы получить подкоренное число 427, мы должны в числе 4,27, которое содержится в таблице, передвинуть запятую на два знака вправо, тогда в результате 2,066, взятом из таблицы, придётся перенести запятую в ту же сторону на один знак.
Находим Тогда Это нетрудно объяснить. Число 28,68, корень из которого находится по таблице, в 100 раз больше подкоренного числа.
Значит, правильный результат будет в 10 раз меньше результата, найденного из таблицы.
Поясним подробнее эту запись. Сначала находим затем к последнему знаку прибавляем поправку, равную 1, тогда
Увеличив результат в 100 раз, получим:
7) Вычислить значение выражения при
Решение. Находим по таблицам:
(третьи цифры оставлены как запасные).
Умножаем:
Складываем:
Примечание. Если два числа состоят из одних и тех же значащих цифр, то отсюда ещё не следует, что квадратные корни из этих чисел также состоят из одних и тех же значащих цифр.
Поясним это такими примерами:
Извлечение квадратного корня на счётной линейке. Так как извлечение квадратного корня есть действие, обратное возведению чисел в квадрат, то для вычисления квадратного корня пользуемся теми же шкалами, что и при возведении в квадрат, то есть шкалой квадратов А и основной шкалой
Но действие извлечения квадратного корня производится в порядке, обратном действию возведения в квадрат. При возведении в квадрат мы основание отмечали визиром на шкале и результат читали на шкале А. Здесь же, наоборот, значение подкоренного числа отмечаем визирной чертой на шкале квадратов А и против визирной черты на основной шкале читаем значение корня. На чертеже 39 находим;
Если надо найти то визирную черту ставим против 40 в правой половине шкалы квадратов и читаем ответ на основной шкале; 6,32.
Извлечение квадратного корня из любых чисел можно свести к одному из двух рассмотренных случаев.
В качестве примеров возьмём те числа, из которых мы на страницах 216-217 извлекали квадратный корень по таблицам:
Теперь сформулируем правило извлечения квадратного корня:
1) Подкоренное число представляем в виде однозначного или двузначного числа, умножив (или разделив) его на чётную степень десяти.
2) Если подкоренное число представлено в виде однозначного числа, его устанавливают визиром на левой половине квадратной шкалы А; если же оно представлено двузначным числом, то — на правой половине квадратной шкалы.
3) Результат отсчитывается по визиру на основной шкале.
Существует другое правило, позволяющее определить, в какой половине шкалы квадратов следует установить подкоренное число при извлечении квадратного корня.
Подкоренное число разбивают на грани, по две цифры в каждой грани, влево от запятой, если число больше 1, и вправо от запятой, если число меньше 1.
Если первая слева грань (не считая граней, состоящих из одних нулей) содержит одну значащую цифру, то число устанавливается в левой половине шкалы квадратов, если же в этой грана две цифры, то — в правой половине.
Например: .
Пользуясь этим способом, легко установить значность числа и положение запятой, так как каждая грань подкоренного числа, стоящая слева от запятой, даёт у корня один знак до запятой, а каждая чисто нулевая грань справа от запятой (если подкоренное число меньше единицы) даёт у корня один нуль после запятой.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Арифметический квадратный корень в математике с примерами решения и образцами выполнения
Оглавление:
Определение:
Арифметическим квадратным корнем из положительного числа а называется такое положительное число х, квадрат которого равен а.
Например, арифметическим квадратным корнем из 49 будет число 7, так как . Квадратный корень из единицы равен единице.
Арифметический квадратный корень из числа а обозначается символом
Примеры:
По определению из равенства следует, что
Извлечение квадратного корня является действием, обратным возведению в квадрат.
Квадратный корень из 0 равен 0.
В дальнейшем (см. гл. XXXIV) рассматриваются квадратные и другие корни в более расширенном (алгебраическом) смысле.
Извлечение арифметического квадратного корня из многозначных натуральных чисел, представляющих собой точные квадратыПрежде всего обратим внимание на следующую таблицу:
и т.д.
Из этой таблицы можно сделать следующее заключение.
Если натуральное число, представляющее точный квадрат, выражается с помощью одной или двух цифр, то квадратный корень из него будет выражаться одной цифрой.
Например:
Если число выражается с помощью трех или четырех цифр, то квадратный корень из него будет число двузначное.
Например:
Если число выражается с помощью пяти или шести цифр, то квадратный корень из него будет число трехзначное и т. д.
Например:
Вывод правила извлечения квадратного корня из натурального числа, представляющего точный квадрат
Предполагая, что число 7569 есть точный квадрат, мы можем утверждать, что будет числом двузначным. Обозначим число десятков этого двузначного числа буквой х, а число единиц—буквой у. Тогда
По определению корня получим
Целых сотен содержится в левой части 75, а в правой либо , либо больше. Поэтому
Значит, есть точный квадрат, содержащийся в числе 75. Но таких квадратов есть несколько, а именно: 64, 49, 36 и т. д. Докажем, что за надо брать наибольший из этих квадратов.
В самом деле, если бы мы взяли за , например, 49, то искомый корень содержал бы 7 десятков и несколько единиц и, будучи возведен в квадрат, дал бы число, меньшее 6400, т. е. меньшее точного квадрата, заключающегося в числе 7569.
е. меньшее точного квадрата, заключающегося в числе 7569.
Таким образом, число десятков искомого корня равно квадратному корню из наибольшего точного квадрата, заключающегося в числе сотен данного числа 7569.
Итак, х = 8. Теперь равенство
примет вид:
или
В левой части 116 десятков, а в правой либо 16у, либо больше, чем 16у. Поэтому
или
или
Значит, у равен или 7, или 6, или 5 и т. д.
Чтобы узнать настоящее значение у, придется последовательно испытать каждое из этих возможных значений, начиная с наибольшей цифры 7. В данном примере это испытание показывает, что надо взять у = 7. Действительно, выражение при у = 7 оказывается в точности равным числу 1169.
Если бы значение выражения при у = 7 оказалось больше, чем 1169, то следовало бы испытывать цифру 6 и т. д.
д.
Итак,
Правило. Чтобы извлечь квадратный корень из многозначного целого числа, разбивают его справа налево на грани по две цифры в каждой. В последней грани может оказаться либо одна, либо две цифры.
Чтобы найти первую цифру корня, извлекают квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани. Чтобы найти вторую цифру корня, из первой грани вычитают квадрат первой цифры корня и к остатку приписывают следующую грань. После этого число десятков получившегося остатка делят на удвоенную первую цифру корня; полученное целое кисло подвергают испытанию.
Следующие цифры корня находят по такому же приему.
Пример:
Найти
1-й шаг. Число, стоящее под знаком корня, разбиваем на грани по две цифры справа налево:
2-й шаг. Извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой грани слева.
3-й шаг.
(Число 159 назовем первым остатком
4-й шаг.
Число 16 есть удвоенная найденная цифра 8)
5-й шаг. Делим число десятков первого остатка на 16. Получаем в целой части нуль. Эту цифру нуль приписываем к числу 16 и умножаем 160 на нуль. Найденную цифру нуль записываем также справа рядом с цифрой 8.
(Число 15 938 назовем вторым остатком).
6-й шаг. Делим число десятков второго остатка на 160, т.е. на удвоенное найденное уже число 80. Получаем в целой части цифру 9. Эту цифру 9 записываем справа рядом с цифрами 8 и 0.
7-й шаг.
Пример:
Пример:
Извлечение квадратного корня с точностью до 1 из многозначных чисел, не являющихся точными квадратамиЭту операцию поясним на примерах.
Пример:
Очевидно, что а . Поэтому число 19 есть приближенное значение с точностью до 1 с недостатком, а 20 — с избытком. Очевидно, что
Очевидно, что
Пример:
Число 224 есть приближенное значение с точностью до 1 с недостатком, а 245 — с избытком, так как
Извлечение квадратного корня из целых чисел с произвольно заданной точностьюЭту операцию поясним опять же на примерах.
1) Найти приближенное значение с точностью до
Найдем сначала с точностью до 1.
Легко понять, что значение с точностью до будет с недостатком , а с избытком
2) Найти приближенное значение с точностью до .
Найдем сначала с точностью до единицы:
Значение с точностью до будет с недостатком , а с избытком .
При извлечении квадратного корня с точностью до вычисления можно располагать так:
Здесь каждый раз мы приписывали к остатку два нуля. Иначе говоря, мы предварительно представляли в форме
где после запятой поставлено четное число нулей.
Если в десятичной дроби после запятой имеется нечетное число десятичных знаков, то следует приписать еще один десятичный знак, равный нулю, и лишь после этого разбивать подкоренное число на грани.
Примеры:
16,03 есть приближенное значение о недостатком о точностью до 0,01.
16,04 будет приближенным значением с избытком с той же точностью.
Пользуясь правилами извлечения квадратного корня, можно установить, например, что
Теорема о квадратном корне из двух
Теорема:
Среди целых и дробных чисел не существует такого числа, которое равнялось бы точно .
Эту теорему можно сформулировать и так: среди целых и дробных чисел нет такого числа, квадрат которого равнялся бы точно двум.
Доказательство:
Сначала докажем, что среди целых чисел не существует такого числа, квадрат которого равен 2. Квадрат единицы есть единица; квадрат двух — четыре; квадраты последующих целых чисел будут числами, еще большими, чем четыре. Поэтому нет такого целого числа, квадрат которого был бы равен 2:
Теперь докажем, что среди дробей также нет такой дроби, квадрат которой был бы равен 2.
Предположим противное тому, что требуется доказать, т. е. предположим, что существует дробное число , квадрат которого равен 2. Мы можем считать дробь несократимой, так как в виде несократимой дроби можно представить всякое дробное число.
Итак, допустим, что
где р и q — целые взаимно простые* числа. Но тогда из равенства (А) получим, что . Из последнего равенства следует, что р есть четное число. (Если бы р было нечетным, то было бы также нечетным, а потому равенство не могло иметь места.) Но всякое четное число можно представить в виде произведения, в котором один множитель равен двум, а другой — целому числу. Поэтому где —целое. Подставляя в равенство вместо р выражение получим , или Отсюда следует, что и q есть четное число.
Итак, оказалось, что числа р и q оба четные, что противоречит несократимости дроби .
Таким образом, предположение, что существует дробное число, квадрат которого равен 2, привело нас к противоречию. Следовательно, такой дроби не существует, что и требовалось доказать.
Замечание:
Аналогично можно доказать, что среди целых и дробных чисел не существует и таких, квадраты которых были бы равны, например 3; 5; 6; 7; 8; 10; 11; 12; 13; 14; 15; 17;…
Ниже мы убедимся в существовании прямолинейных отрезков, отношение длин которых также не выражается ни целым, ни дробным числом, подобно тому как не выражается целым, или дробным числом, например, .
Несоизмеримые отрезки
Общей мерой двух отрезков называется такой отрезок, который укладывается в каждом из данных точно целое число раз.
Например, если отрезок MN (рис. 61) укладывается точно в отрезке АВ р раз, а в отрезке CD q раз, где р и q — целые числа, то отрезок MN будет общей мерой отрезков АВ и CD.
Если два отрезка имеют общую меру, то ах отношение выражается отношением целых чисел.
В предыдущем примере
Обратное утверждение тоже справедливо, а именно:
если отношение двух отрезков равно отношению целых чисел, то эти отрезки имеют общую меру.
Пусть, например,
Тогда часть отрезка CD будет их общей мерой.
На первый взгляд может показаться, что любые два отрезка имеют ту или иную общую меру. Однако в действительности это не так. Ниже, в следующем параграфе, мы докажем существование отрезков, не имеющих общей меры.
Отрезки, имеющие общую меру, называются соизмеримыми.
Отрезки же, не имеющие общей меры, называются несоизмеримыми.
Теорема о существовании несоизмеримых отрезков
Теорема:
Диагональ и сторона квадрата несоизмеримы.
Доказательство. Допустим противное, т. е. допустим, что диагональ и сторона квадрата соизмеримы. Тогда будет существовать некоторая общая мера этих отрезков.
е. допустим, что диагональ и сторона квадрата соизмеримы. Тогда будет существовать некоторая общая мера этих отрезков.
Пусть эта общая мера укладывается на диагонали АС квадрата ABCD р раз, а на стороне АВ q раз. Если эту общую меру принять за единицу длины, то длины диагонали и стороны квадрата выразятся просто целыми числами р и q , а построенные на них квадраты (рис. 62) будут иметь площади, соответственно равные и (квадратных единиц).
На этом рисунке фигура ABCD есть квадрат, построенный на стороне АВ, а квадрат ACEF есть квадрат, построенный на диагонали АС.
Но, как видно из рисунка 62, квадрат ACEF, построенный на диагонали, вдвое больше данного квадрата ABCD (по площади), ибо состоит из четырех таких треугольников, каких данный квадрат содержит два.
Следовательно,
Но, как мы видели раньше (см. стр. 244), это невозможно. Значит, диагональ и сторона квадрата несоизмеримы.
Таким образом, мы доказали существование таких отрезков, точное отношение которых не выражается ни целым, ни дробным числом, т. е. доказали существование несоизмеримых отрезков.
О длине отрезка, несоизмеримого с отрезком, принятым за единицу длины
Пусть отрезки АВ и CD (рис. 63) несоизмеримы.
Примем длину отрезка CD за единицу длины. Тогда по доказанному в предыдущем параграфе длину АВ нельзя выразить никаким ни целым, ни дробным числом, если мы хотим, чтобы это выражение было бы абсолютно точным.
Теперь покажем процесс, с помощью которого можно находить длину АВ приближенно.
Первый шаг. На отрезке А В откладываем последовательно от точки А отрезок CD (рис. 64).
Пусть оказалось, что отрезок CD уложился на АВ раз, где целое число (на рис. 64 = 3), и образовался остаток MB (разумеется меньший, чем CD). Такой остаток обязательно будет, так как в противном случае отрезки АВ и CD были бы соизмеримыми.
Второй шаг. На отрезке MB отложим последовательно часть CD от точки М. Пусть часть CD уложилась на отрезке MB раз ( — целое число) и образовался остаток (на рис. 64 = 7). Разумеется, остаток будет меньше CD.
На отрезке MB отложим последовательно часть CD от точки М. Пусть часть CD уложилась на отрезке MB раз ( — целое число) и образовался остаток (на рис. 64 = 7). Разумеется, остаток будет меньше CD.
Остаток опять же обязательно будет получаться в силу несоизмеримости отрезков АВ и CD.
Третий шаг. На новом остатке станем откладывать отрезка CD. Получим целое число и новый остаток.
(Точка на рис. 74 не указана.)
Этот процесс мы продолжаем дальше, делая четвёртый, пятый и дальнейшие шаги.
В силу несоизмеримости отрезков АВ и CD этот процесс теоретически никогда пе закончится и развернет перед нами бесконечный символ
состоящий из бесконечного множества цифр, поставленных рядом друг с другом, который можно записать и так:
Обрывая наш измерительный процесс, скажем, на пятом шаге, мы получим десятичную дробь
которая будет выражать длину АВ приближенно с недостатком с точностью до .
Десятичная дробь
будет выражать длину АВ приближенно с избытком с точностью до .
Обратим внимание на два факта, которые мы установили в этой главе.
1. Не существует ни целого, ни дробного числа, квадрат которого оказался бы равным точно двум.
2.Не существует ни целого, ни дробного числа, которое выражало бы точно длину отрезка, несоизмеримого с единицей длины.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Исследовательская работа на тему: «Извлечение квадратных корней из больших чисел без калькулятора»
МУНИЦИПАЛЬНОЕ ОБРАЗОВАНИЕ
Ханты-Мансийского автономного округа – Югры
ГОРОДСКОЙ ОКРУГ ГОРОД ПЫТЬ-ЯХ
Муниципальное автономное общеобразовательное учреждение
«Комплекс средняя общеобразовательная школа – детский сад»
(МАОУ «КСОШ – ДС»)
Исследовательская работа
на тему:
«Извлечение квадратных корней из больших чисел
без калькулятора»
Выполнили:
Ученица 8 «б» класса Бублик Татьяна
Ученик 8 «б» класса Анемподистов Андрей
Научный руководитель:
Учитель математики Калиновская Елена Владимировна
Пыть-Ях
2019
Содержание
I. Введение…………………………………………………………………………3
Введение…………………………………………………………………………3
II. Основная часть…………………………… …………………………………….4
2.1.Метод Древнего Вавилона……………………………………………….4
2.2. Канадский метод………………………………………………………….5
2.3Вычисление корня столбиком…………………………………… ………5
2.4.Отбрасывания квадрата………………………..……………………………..6
2.5.Арифметический метод…………………………………………………..7
2.6. Извлечение квадратного корня из чисел, оканчивающихся на 25……8
Результаты исследования…………………………………..…………………….9
Заключение……………………………….………………………………….…..10
Литература………………….…………………………………………………….11
Приложения ……………………………………………………………………..12
«Зри в корень»
К. Прудков
I. Введение
В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учебе, в быту, в профессиональной деятельности. Кроме того, быстрый счет — настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения.
Такие навыки помогут человеку в учебе, в быту, в профессиональной деятельности. Кроме того, быстрый счет — настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения.
Актуальность выбранной темы состоит в том, что извлечь квадратный корень без калькулятора — это очень сложная задача. Но так как на уроках математики не разрешается пользоваться калькулятором, а таблица квадратов не всегда под рукой, да и на экзамене на ОГЭ таблица квадратов дается только для двузначных чисел, как же быть, если подкоренное выражение восьмизначное число?
Таким образом, выделяем проблему: отсутствие в учебниках различных способов извлечения квадратных корней лишает возможности применения учащимися быстрых способов извлечения квадратного корня.
Цель: изучить способы вычисления арифметических корней без калькулятора и показать рациональное применение на практике.
Задачи:
1. Изучить (соцопрос) умение учащихся извлекать квадратные корни без калькулятора;
2. Ознакомиться с литературой по данной теме, используя Интернет-ресурсы;
Ознакомиться с литературой по данной теме, используя Интернет-ресурсы;
3. Рассмотреть способы вычисления арифметического корня;
4. Познакомить с этими способами одноклассников.
II. Основная часть.
В ходе данного исследования были выявлены следующие методы извлечения квадратного корня
- Метод Древнего Вавилона
- Канадский метод
- Вычисление корня столбиком
- Отбрасывания квадрата
- Арифметический метод
- Извлечение квадратного корня из чисел, оканчивающихся на 25
2.1. Метод Древнего Вавилона
Около 4000 лет назад вавилонские ученые уже составляли таблицы квадратов чисел и квадратных корней из чисел. Они умели находить приблизительное значение квадратного корня из любого целого числа.
Использовали древние вавилоняне следующий метод нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а2+b , где а2 ближайший к числу х точный квадрат натурального числа а, и пользовались формулой
≈
Извлечем с помощью формулы корень квадратный, например, из числа 46
== 6+
Результат извлечения корня из 46 с помощью калькулятора 6,7823299. .. Как видим, метод вавилонян дает хорошее приближение к точному значению корня.
.. Как видим, метод вавилонян дает хорошее приближение к точному значению корня.
Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх знаков после запятой. Вот их формула:
Где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.
Например:
Результат извлечения корня из 2215 с помощью калькулятора 47,063786… Очевидно, что метод дает хорошее приближение к точному значению корня,
а также несложен и удобен.
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня.
Алгоритм извлечения квадратного корня столбиком
- Чтобы извлечь квадратный корень из данного целого числа, разбивают его справа налево на грани, по две цифры в каждой, кроме первой (крайней левой), в которой может быть и одна цифра.

- Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
- Для нахождения второй цифры, из первой грани вычитают квадрат первой цифры корня, к остатку сносят вторую грань и число десятков получившегося числа делят на удвоенную первую цифру корня; полученное целое число снова подвергают испытанию.
- Испытание проводится так: за вертикальной чертой (слева от остатка) пишут удвоенное, ранее найденное число корня, и к нему с правой стороны приписывают испытуемую цифру; получившееся после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, больше остатка, то испытуемая цифра не годится и надо испытать следующую меньшую цифру.
- Следующие цифры корня находят с помощью того же приёма.
- Если после снесения грани число десятков получившегося числа окажется меньше делителя, т.е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.
Например:
1
2 4 119
4 96
288 2304
8 2304
0
Разбиваем данное число справа налево по две цифры. У нас получилось три группы чисел (2’19’04), первое из которых однозначное число 1. Первая цифра искомого числа должна быть наибольшей, квадрат которой не превышает 2. Это цифра 1, так как 12 = 1
У нас получилось три группы чисел (2’19’04), первое из которых однозначное число 1. Первая цифра искомого числа должна быть наибольшей, квадрат которой не превышает 2. Это цифра 1, так как 12 = 1
Метод трудоемкий, а также требует логики и хороших вычислительных навыков.
2.4. Отбрасывание квадрата
Здесь необходимо уточнить, что этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа.
1. Извлечение корней до числа = 5625
Например: = = 31 + 25 = 56.
Число 3136 представим в виде суммы, выделив из этого числа квадрат 36, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (31) прибавляем всегда 25. Получим ответ 56.
2.Извлечение корней больше числа = 5625
Например: = = 78 + = 78 + 11 = 89
Число 7921 представим в виде суммы 7800 и выделенного квадрата 121. Затем к числу сотен прибавить квадратный корень из 121.(11) Получим ответ 89.
Этот способ достаточно интересен и в какой — то мере оригинален, но достаточно сложен в запоминании из–за двойственности алгоритма и применим только для четырёхзначных чисел точных корней, но мы проработали множество примеров и убедились в его правильности. Кроме всего этот способ доступен тем, кто уже запомнил наизусть квадраты чисел от 11 до 29, ведь без их знания он будет бесполезен.
2.5. Арифметический метод
Для квадратов чисел верны следующие равенства:
1 = 12
1 + 3 = 22
1 + 3 + 5 =32
1 + 3 + 5 + 7 = 42 и так далее.
Поэтому, чтобы знать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю. Подсчитав количество выполненных действий, определяем целую часть квадратного корня. Это и будет ответом
Например: чтобы извлечь произведём действия:
144-1=143
143-3=140
140-5=135
135-7=128
128-9=119
119-11=108
108-13=95
95-15=80
80-17=63
63-19=44
44-21=23
23-23=0
Общее количество вычитаний — 12, поэтому = 12.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть.
2.6. Извлечение квадратного корня из чисел, оканчивающихся на 25
Можно легко вычислить квадратный корень из чисел, оканчивающихся на 25, в тех случаях, когда ответ — целое число.
Для этого ту часть числа, которая стоит под корнем перед 25, надо представить как произведение двух последовательных чисел: a·(a+1). Тогда искомый квадратный корень равен a5. На практике этим способом можно без труда вычислить квадратный корень из трехзначных и четырехзначных чисел, оканчивающихся на 25. Рассмотрим этот способ на примерах.
Пример: , ,
Перед 25 стоит число 6. Его надо представить как произведение двух последовательных чисел: 6=2·3, то есть a=2. Значит,
= 25
75
= 135
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
В ходе работы по данной теме проведено исследование «Выявление способов извлечения квадратных корней, которыми владеют одноклассники и используют в решении». Основными методами исследования были: анкетирование (Приложение 5),анализ учебников по алгебре за курс 8 класса (Приложение 4) сбор информации, статистическая обработка и анализ полученных результатов.
Основными методами исследования были: анкетирование (Приложение 5),анализ учебников по алгебре за курс 8 класса (Приложение 4) сбор информации, статистическая обработка и анализ полученных результатов.
Обработка анкетных данных (Приложение 1,2,3) учащихся 8 классов позволила сделать следующий вывод: школьники, при извлечении квадратных корней, чаще всего пользуются калькулятором и таблицей квадратов двузначных чисел. Другими способами извлечения корней мало кто пользуется.
ЗАКЛЮЧЕНИЕ
Вычисление квадратного корня из многозначного числа и по сей день является трудной задачей, но мы нашли на неё ответ. В ходе данного проекта, мы проанализировали учебники, провели соцопрос и занялись исследованием по данной теме. Выявили, что проблема, которую мы выбрали, оказалась актуальной, как и было предположено. Хочется отметить, что каждый из выше перечисленных способов индивидуален, и любой сможет выбрать тот, который подходит именно ему. В заключение проекта хотелось бы отметить, что ученики, которым впоследствии представили эти методы вынесения многозначного арифметического корня (Приложение 6), сейчас активно используют хотя бы один из них в повседневной жизни.
Литература и сайты Интернета:
- Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.
- http://festival.1september.ru
- http://www.murderousmaths.co.uk/books/sqroot.htm
- http://www.life123.com/question/Square-Root-without-a-Calculator
- http://www.megabotan.ru/pages/
- http://ru.wikipedia.ord/wiki/teorema/
- https://ru.wikihow.com/%D0%B8%D0%B7%D0%B2%D0%BB%D0%B5%D1%87%D1%8C-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D1%8B%D0%B9-%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D1%8C-%D0%B1%D0%B5%D0%B7-%D0%BA%D0%B0%D0%BB%D1%8C%D0%BA%D1%83%D0%BB%D1%8F%D1%82%D0%BE%D1%80%D0%B0
- https://yourtutor.info/%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D1%8B%D0%B9-%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D1%8C-%D0%B1%D0%B5%D0%B7-%D0%BA%D0%B0%D0%BB%D1%8C%D0%BA%D1%83%D0%BB%D1%8F%D1%82%D0%BE%D1%80%D0%B0
Приложение 1
Приложение 2
Приложение 3
Учебник | Автор | Пункт | Способы извлечения из корня |
Алгебра 8 | Г. С.Б. Суворова Е.А. Бунимович | 2.1 Задача о нахождении стороны квадрата. 2.2 Иррациональные числа. | С помощью таблицы квадратов двухзначных чисел. Разложение на множители. |
Алгебра 8 | Ю.Н. Макарычев Н.Г. Миндюк | 12. Квадратный корень. 14. Нахождение приближенных значений квадратного уравнения. 16. Квадратный корень из произведения дроби. | С помощью таблицы квадратов. С помощью калькулятора. Разложение на множители |
Алгебра 8 | А.Г Мордкович |
| С помощью калькулятора Таблица квадратов Разложение на простые множители |
Приложение 4
Анализ учебных пособий по алгебре 8 класса
Приложение 5
Анкета
- Оказывались ли вы в такой ситуации, когда нужно извлечь корень из многозначных чисел, не имея под рукой ни таблицы, ни калькулятора?
- Да
- Нет
- Умеете ли вы извлекать квадратный корень без таблиц и калькуляторов?
- Да
- Нет
- Испытываю затруднение
- Укажите известные вам способы извлечения квадратных корней из многозначных чисел:
- С помощью таблицы
- С помощью калькулятора
Укажите свой способ извлечения корня:
_______________________________________________________
Спасибо за участие!
Приложение 6
Конспект урока по алгебре в 8 классе «Квадратный корень из произведения и дроби»
Муниципальное бюджетное общеобразовательное учреждение
«Головчинская средняя общеобразовательная школа с углубленным изучением отдельных предметов»
Грайворонского района Белгородской области
Конспект урока по алгебре
в 8 классе
«Квадратный корень из произведения и дроби»
подготовила
учитель математики
Иванченко Любовь Ивановна
с. Головчино
Головчино
2013
Тип урока: урок формирования умений и навыков
Цели:
способствовать выработке навыков и умений нахождения квадратного корня из произведения и дроби; нахождения значения произведения и частного арифметических квадратных корней;
способствовать развитию наблюдательности, математического мышления, умения анализировать и делать выводы;
побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Оборудование:
Ход урока
Организационный момент
Учитель:
Сегодня у нас не совсем обычный урок, к нам пришли гости. Посмотрите на наших гостей, улыбнитесь им, посмотрите друг на друга и тоже улыбнитесь, ведь от улыбки станет всем теплей, поднимется настроение. Ребята, я вас попрошу поставить на полях своих тетрадей ту оценку, которую вы хотели бы получить за урок.
Ребята, я вас попрошу поставить на полях своих тетрадей ту оценку, которую вы хотели бы получить за урок.
Предлагаю вам выполнить письменную работу «Математический словарь»
Запишите математические термины:
Арифметический корень.
Подкоренное выражение.
Извлечение корня.
Радикал.
Рациональное число.
Иррациональное число.
Квадратный корень из произведения.
Квадратный корень из дроби.
Взаимопроверка. Как вы считаете, какая тема объединяет эти математические термины?
( Квадратные корни.) А какую тему мы изучали на прошлом уроке? (Квадратный корень из произведения и дроби.)
Постановка целей урока.
Для того чтобы урок прошел успешно, необходимо повторить теорию.
II. Устная работа
1. Учитель: Ребята, опираясь на «Математический словарь», составьте и задайте вопросы по теме своим одноклассникам.
Сформулируйте определение арифметического квадратного корня.
Выпишите обозначение квадратного корня из числа а.
Назовите подкоренное выражение.
При каких значениях а выражение имеет смысл?
Продолжите запись: ()2 = …
Продолжите запись:= …
Сформулируйте теорему о квадратном корне из произведения.
Продолжите запись: = …
Сформулируйте теорему о квадратном корне из дроби.
Учитель задает учащимся те вопросы, которые не прозвучали в ходе опроса.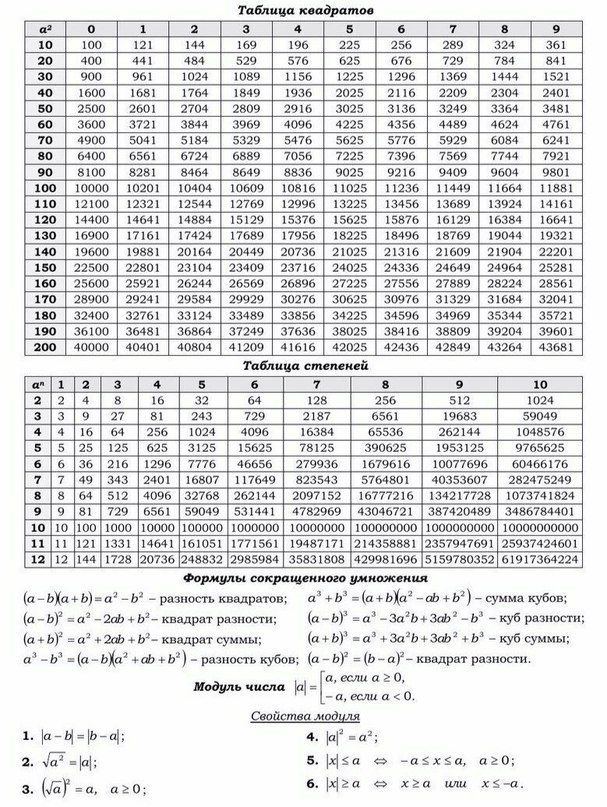
2. Вычислите:
а) ; б) ; в) ; г) ;
д) ; е)
Даются подробные объяснения.
3. Сравните: и .
III. Работа на доске и в тетрадях со всеми учащимися
1. Учитель: А как вы нашли произведение и частное корней?
Ученик: Поменяв в тождествах и местами их левые и правые части, получим: и .
Вопрос. В каком случае пользуются этими тождествами? (При умножении и делении квадратных корней).
2. Разобрать решение примеров 4 и 5 на с. 86 учебника.
3. Решить № 385 (а, б, в, ж) на доске и в тетрадях.
4. Решить № 386 самостоятельно с последующей проверкой. Один ученик решает самостоятельно у доски, остальные учащиеся решают в тетрадях. Если возникают затруднения, можно обратиться за помощью к соседу по парте или к учителю. Затем проверяется решение.
Затем проверяется решение.
IV. Задания по выбору.
1. Используя свойства квадратного корня, найдите с помощью таблицы квадратов, значение выражения:
; ; ; ; ; ; ; .
Самопроверка.
Ответы: 15; 18; 22; 270; 1,1; 4,1; 0,36; 70.
2. Тестовая работа.
1) Вычислите .
1) 3,75 2) 1,4 3) 1,25 4) 1,5
2) Решите уравнение 0,5у 2 = 8.
1) 2; -2 2) 2 3) 4; -4 4) 4
3) Найдите значение у, при котором
1) 2,5 2) 3) 4) 2,5; -2,5
4)Применив свойства арифметического квадратного корня, вычислите .
1) 5; -5 2) 25 3) 5 4) 25; — 25
5) Вычислите без помощи калькулятора.
1) 2) 3) 4)
6) Даны числа: Сколько среди них рациональных?
1) 1 2) 2 3) 3 4) 4
Ответы. 1. 4
1. 4
2. 3
3. 3
4. 3
5. 2
6. 3
Самопроверка. Работа над ошибками. Итог.
V. Творческое задание «Смотри, не ошибись!»
Определить неизвестный множитель:
Взаимопроверка.
VI. Задание «Проверь, не пользуясь калькулятором»
VII. Резервное задание для обеспечения занятости и развития наиболее подготовленных учащихся.
VIII. Домашнее задание: по выбору п.16, № 387(1 стр.), 383 или составить задание для учащихся по данной теме. Для желающих № 381.
IX. Подведение итогов.
Выставление оценок самими учащимися.
Учитель:
1. Поднимите, пожалуйста, руки те, кто достиг своих поставленных целей.
Поднимите руки те, кто получил оценку выше той, которую поставил себе на полях в начале урока.
А теперь поднимите руки те, кто не достиг тех результатов, которые намечал в начале урока.
Что еще нужно подучить, над чем нужно поработать?
Список использованной литературы
Макарычев Ю.Н. Алгебра: учебник для 8 класса общеобразовательных учреждений/ Ю.Н. Макарычев, К.И. Нешков, Н.Г. Миндюк, С.Б. Суворова; под ред. С.А. Теляковского. – М.: Просвещение, 2008.
Конте А.С. Алгебра: математические диктанты. 7-9 классы. – Волгоград: Учитель, 2007.
Терехова Т.
 В. и др. Сборник тестовых заданий для тематического и итогового контроля. Алгебра 8 класс.- М: «Интеллект-Центр», 2006.
В. и др. Сборник тестовых заданий для тематического и итогового контроля. Алгебра 8 класс.- М: «Интеллект-Центр», 2006.
Как вычисляется корень из числа. Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней
В математике вопрос о том, как извлекать корень, считается относительно несложным. Если возвести в квадрат числа из натурального ряда: 1, 2, 3, 4, 5 …n, то у нас получится следующий ряд квадратов: 1, 4, 9, 16 …n 2 . Ряд квадратов является бесконечным, и если внимательно посмотреть на него, то вы увидите, что в нем нет очень многих целых чисел. Почему это так, объясним немного позже.
Корень из числа: правила вычисления и примеры
Итак, мы возвели число 2 в квадрат, то есть умножили его само на себя и получили 4. А как извлечь корень из числа 4? Сразу скажем, что корни могут быть квадратными, кубическими и какой угодно степени до бесконечности.
Степень корня – всегда натуральное число, то есть нельзя решить такое уравнение: корень в степени 3,6 из n.
Квадратный корень
Вернемся к вопросу о том, как извлечь корень квадратный из 4. Так как возводили мы число 2 именно в квадрат, то и корень будем извлекать квадратный. Для того чтобы правильно извлечь корень из 4, нужно просто правильно подобрать число, которое при возведении в квадрат дало бы число 4. И это, конечно же, 2. Посмотрите на пример:
- 2 2 =4
- Корень из 4 = 2
Этот пример довольно простой. Попробуем извлечь корень квадратный из 64. Какое число при умножении самого на себя дает 64? Очевидно, что это 8.
- 8 2 =64
- Корень из 64=8
Кубический корень
Как выше было сказано, корни бывают не только квадратными, на примере попробуем более понятно объяснить, как извлечь кубический корень или корень третьей степени. Принцип извлечения кубического корня тот же самый, что и у квадратного, разница лишь в том, что искомое число изначально было умножено само на себя не единожды, а дважды. То есть, допустим, мы взяли следующий пример:
- 3x3x3=27
- Естественно, кубическим корнем из числа 27 будет тройка:
- Корень 3 из 27 = 3
Допустим, необходимо найти кубический корень из 64. Для решения этого уравнения достаточно найти такое число, которое при возведении в третью степень дало бы 64.
Для решения этого уравнения достаточно найти такое число, которое при возведении в третью степень дало бы 64.
- 4 3 =64
- Корень 3 из 64 = 4
Извлечь корень из числа на калькуляторе
Конечно, лучше всего учиться извлекать квадратные, кубические и корни другой степени на практике, путем решения многих примеров и запоминания таблицы квадратов и кубов небольших чисел. В будущем это очень облегчит и сократит время решения уравнений. Хотя, нужно отметить, что порой требуется извлечь корень из такого большого числа, что подобрать правильное число, возведенное в квадрат, будет стоить очень больших трудов, если вообще это возможно. На помощь в извлечении квадратного корня придет обычный калькулятор. Как на калькуляторе извлечь корень? Очень просто введите число, из которого хотите найти результат. Теперь внимательно посмотрите на кнопки калькулятора. Даже на самом простом из них найдется клавиша со значком корня. Нажав на нее, вы немедленно получите готовый результат.
Не из каждого числа можно извлечь целый корень, рассмотрим следующий пример:
Корень из 1859 = 43,116122…
Вы можете параллельно попробовать решить этот пример на калькуляторе. Как видите, полученное число не является целым, более того, набор цифр после запятой является не конечным. Более точный результат могут дать специальные инженерные калькуляторы, на дисплее же обычных полный результат просто не умещается. А если вы продолжите начатый ранее ряд квадратов, то не найдете в нем числа 1859 именно потому, что число, которое возвели в квадрат для его получения, не является целым.
Если вам необходимо извлечь корень третьей степени на простом калькуляторе, то необходимо нажать дважды на кнопку со знаком корня. Для примера возьмем использованное выше число 1859 и извлечем из него кубический корень:
Корень 3 из 1859 = 6,5662867…
То есть, если число 6,5662867… возвести в третью степень, то мы получим приблизительно 1859. Таким образом, извлекать корни из чисел не сложно, достаточно лишь запомнить выше приведенные алгоритмы.
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень . Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней .
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.

Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
…
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа .
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 20 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу.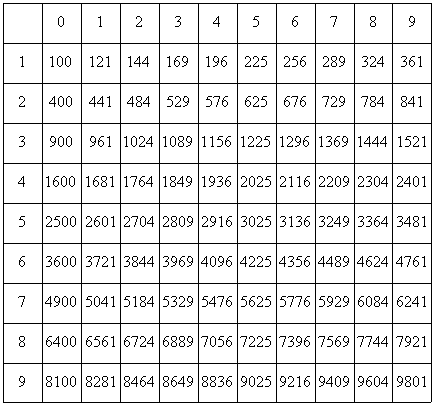 Значит, это и есть корень.
Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
900 30 2
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 50 2
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 60 2
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня.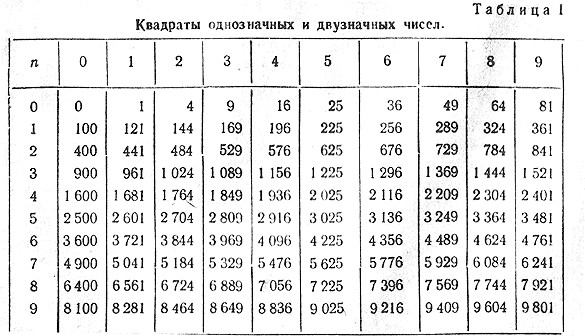 Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6.
 Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6.
Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ.
 Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n.
 Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
Напишите найденное n сверху справа, а квадрат n запишите снизу справа.- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329.
 Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.

- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Понимание процесса
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8.
 То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8.
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?
Таблица квадратов целых чисел от 0
до 99
включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0
до 99
. Для примера выберем строку 8
десятков и столбец 3
единицы, этим мы зафиксировали число 83
. Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0
до 99
. На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
Для примера выберем строку 8
десятков и столбец 3
единицы, этим мы зафиксировали число 83
. Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0
до 99
. На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n
-ой степени из числа a
, при этом число a
содержится в таблице n
-ых степеней.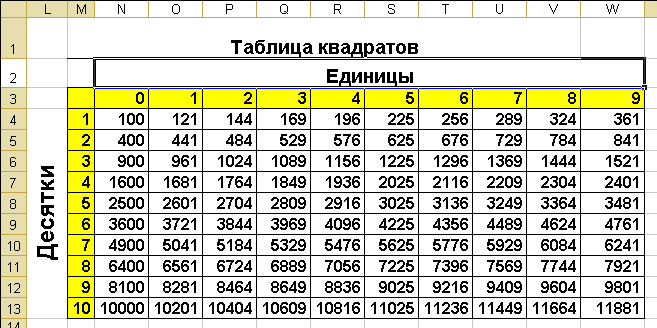 По этой таблице находим число b
такое, что a=b n
. Тогда , следовательно, число b
будет искомым корнем n
-ой степени.
По этой таблице находим число b
такое, что a=b n
. Тогда , следовательно, число b
будет искомым корнем n
-ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Поясним этот момент.
Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2
, откуда понятно, что квадратный корень из 144
равен 12
.
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2
. Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7
не кратна трем. Следовательно, кубический корень из числа 285 768
не извлекается нацело.
Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7
не кратна трем. Следовательно, кубический корень из числа 285 768
не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169 .
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Приведем краткую запись решения: .
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n
числа 0, 10, 100, …
до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n
на предыдущем этапе, укажет соответствующий старший разряд.
Для этого последовательно возводятся в степень n
числа 0, 10, 100, …
до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n
на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9
. При этом параллельно вычисляются n
-ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9
.
При этом параллельно вычисляются n
-ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9
.
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
На кружке показала, как в столбик можно извлекать квадратные корни. Вычислить корень можно с произвольной точностью, найти сколько угодно цифр в его десятичной записи, даже если он получается иррациональным. Алгоритм запомнился, а вопросы остались. Непонятно было, откуда взялся метод и почему он дает верный результат. В книжках этого не было, а может, просто не в тех книжках искала. В итоге, как и многое из того, что на сегодняшний день знаю и умею, вывела сама.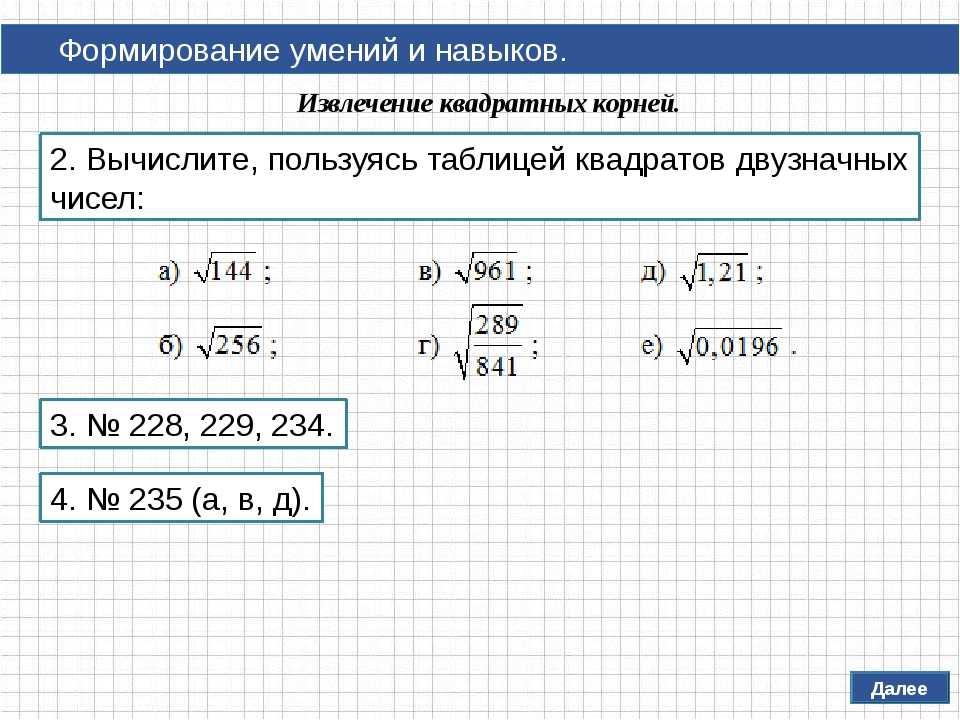 Делюсь своим знанием здесь. Кстати сказать, до сих пор не знаю, где приведено обоснование алгоритма)))
Делюсь своим знанием здесь. Кстати сказать, до сих пор не знаю, где приведено обоснование алгоритма)))
Итак, сначала на примере рассказываю, “как работает система”, а потом объясняю, почему она на самом деле работает.
Возьмем число (число взято “с потолка”, только что в голову пришло).
1. Разбиваем его цифры на пары: те, что стоят слева от десятичной запятой, группируем по две справа налево, а те, что правее – по две слева направо. Получаем .
2. Извлекаем квадратный корень из первой группы цифр слева — в нашем случае это (ясно, что точно корень может не извлекаться, берем число, квадрат которого максимально близок к нашему числу, образованному первой группой цифр, но не превосходит его). В нашем случае это будет число . Записываем в ответ — это старшая цифра корня.
3. Возводим число, которое стоит уже в ответе — это — в квадрат и вычитаем из первой слева группы цифр — из числа . В нашем случае остается .
4. Приписываем справа следующую группу из двух цифр: . Число , которое уже стоит в ответе, умножаем на , получаем .
Число , которое уже стоит в ответе, умножаем на , получаем .
5. Теперь следите внимательно. Нам нужно к числу справа приписать одну цифру , и число умножить на , то есть на ту же самую приписанную цифру. Результат должен быть как можно ближе к , но опять-таки не больше этого числа. В нашем случае это будет цифра , ее записываем в ответ рядом с , справа. Это следующая цифра в десятичной записи нашего квадратного корня.
6. Из вычитаем произведение , получаем .
7. Далее повторяем знакомые операции: приписываем к справа следующую группу цифр , умножаем на , к полученному числу > приписываем справа одну цифру, такую, чтобы при умножении на нее получилось число, меньшее , но наиболее близкое к нему –– это цифра –– следующая цифра в десятичной записи корня.
Вычисления запишутся следующим образом:
А теперь обещанное объяснение. Алгоритм основан на формуле
Комментариев: 50
2 Антон:
Слишком сумбурно и запутано.
 Разложите всё по пунктам и пронумеруйте их. Плюс: объясните откуда в каждом действии мы подставляем нужные значения. Никогда раньше не вычислял корень в столбик – разобрался с трудом.
Разложите всё по пунктам и пронумеруйте их. Плюс: объясните откуда в каждом действии мы подставляем нужные значения. Никогда раньше не вычислял корень в столбик – разобрался с трудом.5 Юлия:
6 :
Юлия, 23 на данный момент записано справа, это две первые (слева) уже полученные цифры корня, стоящие в ответе. Умножаем на 2 согласно алгоритму. Повторяем действия, описанные в пункте 4.
7 zzz:
ошибка в “6. Из 167 вычитаем произведение 43 * 3 = 123 (129 нада), получаем 38.”
непонятно как после запятой получилось 08…9 Федотов Александр:
А ещё в докалькуляторную эпоху нас в школе учили не только квадратный, но и кубический корень в столбик извлекать, но это более нудная и кропотливая работа. Проще было таблицами Брадиса воспользоваться или логарифмической линейкой, которую мы уже в старших классах изучали.
10 :
Александр, Вы правы, можно извлекать в столбик и корни больших степеней.
 Я собираюсь написать как раз о том, как находить кубический корень.
Я собираюсь написать как раз о том, как находить кубический корень.12 Сергей Валентинович:
Уважаемая Елизавета Александровна! Мной в конце 70-х разработана схема автоматического (т.е. не подбором) вычисления квадр. корня на арифмометре “Феликс”. Если заинтересуетесь, могу выслать описание.
14 Vlad aus Engelsstadt:
(((Извлечение квадратного корня в столбик)))
Алгоритм упрощается, если использовать 2-ную систему счисления, которую изучают в информатике, но полезно и в математике. А.Н. Колмогоров в популярных лекциях для школьников приводил этот алгоритм. Его статью можно найти в “Чебышёвском сборнике” (Математический журнал, ищите ссылку на него в интернете)
К случаю сказать:
Г.Лейбниц в свое время носился с идеей о переходе от 10-ной системы счисления к двоичной из-за ее простоты и доступности для начинающих (младших школьников). Но устоявшиеся традиции ломать это все равно что лбом ломать крепостные ворота: можно, но бесполезно. Вот и получается как по наиболее цитируемому в былые времена бородатому философу: традиции всех мертвых поколений подавляют сознание живых.
Вот и получается как по наиболее цитируемому в былые времена бородатому философу: традиции всех мертвых поколений подавляют сознание живых.До следующих встреч.
15 Vlad aus Engelsstadt:
))Сергей Валентинович, да, мне интересно…((
Бьюсь об заклад, что это вариация под “Феликс” Вавилонского метода извлечения коня квадратного методом последовательных приближений. Этот алгоритм был перекрыт методом Ньютона (метод касательных)
Интересно, не ошибся ли я в прогнозе?
18 :
2Vlad aus Engelsstadt
Да, алгоритм в двоичной системе должен быть проще, это довольно очевидно.
О методе Ньютона. Может, оно и так, но все равно интересно
20 Кирилл:
Спасибо большое. А алгоритма так и нету, неизвестно откуда он взялся, но результат правильный получается. СПАСИБО БОЛЬШОЕ! Долго искал это)
21 Александр:
А каким образом пойдёт извлечение корня из числа, где вторая слева-направо группа весьма мала? к примеру, любимое всеми число 4 398 046 511 104 .
 после первого вычитания не получается продолжить всё по алгоритму. Объясните пожалуйста.
после первого вычитания не получается продолжить всё по алгоритму. Объясните пожалуйста.22 Алексей:
Да, знаю этот способ. Я, помню, вычитал его в книге “Алгебра” какого-то старого издания. Тогда еще по аналогии сам вывел, как так же в столбик извлекать кубический корень. Но там уже сложнее: каждая цифра определяется уже не в одно (как для квадратного), а в два вычитания, да еще там каждый раз надо перемножать длинные числа.
23 Артем:
В примере извлечения квадратного корня в столбик из 56789,321 имеются опечатки. Группа цифр 32 приписана дважды к числам 145 и 243, в числе 2388025 вторую 8 необходимо заменить на 3. Тогда последнее вычитание следует записать так: 2431000 – 2383025 = 47975.
Дополнительно, при делении остатка на увеличенное в два раза значение ответа (без учета запятой), получим добавочное количество значащих цифр (47975/(2*238305) = 0.100658819…), которые следует дописать к ответу (√56789,321 = 238,305… = 238,305100659).
24 Сергей:
По всей видимости алгоритм пришел из книги Исаака Ньютона “Всеобщая арифметика или книга о арифметических синтезе и анализе”. Вот выдержка из неё:
ОБ ИЗВЛЕЧЕНИИ КОРНЕЙ
Чтобы извлечь из числа квадратный корень, прежде всего следует поставить над его цифрами через одну, начиная с единиц, точки. Затем следует в частном или в корне написать цифру, квадрат которой равен или ближайший по недостатку к цифрам или цифре, предшествующим первой точке. После вычитания этого квадрата остальные цифры корня будут последовательно найдены посредством деления остатка на удвоенную величину уже извлеченной части корня и вычитания всякий раз из остатка квадрата последней найденной цифры и ее удесятеренного произведения на названный делитель.
25 Сергей:
Поправьте ещё название книги “Всеобщая арифметика или книга оБ арифметических синтезе и анализе”
26 Александр:
Спасибо за интересный материал. Но мне этот метод представляется несколько более сложным, чем нужно, например, школьнику.
 Я применяю более просто метод, основанный на разложении квадратичной функции с помощью первых двух производных. Формула его такая:
Я применяю более просто метод, основанный на разложении квадратичной функции с помощью первых двух производных. Формула его такая:
sqrt(x)= A1+A2-A3, где
А1 – целое число, квадрат которого ближе всего к х;
А2 – дробь, в числителе х-А1, в знаменателе 2*А1.
Для большинства чисел, встречающихся в школьном курсе, этого достаточно, чтобы получить результат с точностью до сотых.
Если нужен более точный результат, берем
А3 – дробь, в числителе А2 в квадрате, в знаменателе 2*А1+1.
Конечно, для применения нужна таблица квадратов целых чисел, но это в школе не проблема. Запомнить эту формулу достаточно просто.
Меня, правда, смущает, что А3 я получил опытным путем в результате экспериментов с электронной таблицей и не вполне понимаю, почему этот член имеет такой вид. Может, подскажете?27 Александр:
Да, я тоже рассматривал эти соображения, но дьявол кроется в деталях. Вы пишете:
“поскольку a2 и b отличаются уже довольно мало”. Вопрос именно стоит, насколько мало.
Эта формула хорошо работает на числах второго десятка и гораздо хуже (не до сотых, только до десятых) на числах первого десятка. Почему так происходит уже трудно понять без привлечения производных.28 Александр:
Я уточню, в чем я вижу преимущество предложенной мной формулы. Она не требует не вполне естественного разбиения чисел на пары цифр, которое, как показывает опыт, часто выполняется с ошибками. Смысл ее очевиден, а для человека, знакомого с анализом, тривиален. Хорошо работает на числах от 100 до 1000, наиболее часто встречающихся в школе.
29 Александр:
Кстати, я немного покопался и нашел точное выражение для А3 в моей формуле:
А3= А22 /2(A1+A2)30 vasil stryzhak:
В наше время, повсеместного использования вычислительной техники, вопрос извлечения квадратного коня из числа с практической точки зрения не стоит. Но для любителей математики, несомненно, представляют интерес различные варианты решения данной задачи.
 В школьной программе способ данного вычисления без привлечения дополнительных средств должен иметь место наравне с умножением и делением в столбик. Алгоритм вычисления должен быть не только запоминаемым, но и понятным. Классический метод, предоставленный в данном материале для обсуждения с раскрытием сущности, в полной мере соответствует вышеназванным критериям.
В школьной программе способ данного вычисления без привлечения дополнительных средств должен иметь место наравне с умножением и делением в столбик. Алгоритм вычисления должен быть не только запоминаемым, но и понятным. Классический метод, предоставленный в данном материале для обсуждения с раскрытием сущности, в полной мере соответствует вышеназванным критериям.
Существенным недостатком предлагаемого Александром способа является использование таблицы квадратов целых чисел. Каким большинством чисел встречающихся в школьном курсе она ограничена автор умалчивает. Что касается формулы, то в целом она мне импонирует в виду относительно высокой точностью вычисления.31 Александр:
для 30 vasil stryzhak
Я ни о чем не умолчал. Таблица квадратов предполагается до 1000. В мое время в школе ее просто заучивали наизусть и она была во всех учебниках математики. Я в явном виде назвал этот интервал.
Что до вычислительной техники, то она не применяется, в основном, на уроках математики, если только не идет специально тема применения калькулятора. Калькуляторы сейчас встроены в устройства, запрещенные к применению на ЕГЭ.
Калькуляторы сейчас встроены в устройства, запрещенные к применению на ЕГЭ.32 vasil stryzhak:
Александр, спасибо за разъяснение!Я считал,что для предлагаемого метода теоретически необходимо помнить или пользоваться таблицей квадратов всех двузначных чисел.Тогда для подкоренных чисел не входящих в интервал от 100 до 10000 можно использовать прием их увеличения или уменьшения на необходимое количество порядков переносом запятой.
33 vasil stryzhak:
39 АЛЕКСАНДР:
МОЯ ПЕРВАЯ ПРОГРАММА НА ЯЗЫКЕ “ЯМБ” НА СОВЕТСКОЙ МАШИНЕ “ИСКРА 555″ БЫЛА НАПИСАНА ДЛЯ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА ПО АЛГОРИТМУ ИЗВЛЕЧЕНИЯ В СТОЛБИК! а сейчас забыл как извлекать в ручную!
Квадратный корень от 1 до 20
Квадратный корень от 1 до 20 — это список квадратных корней из всех чисел от 1 до 20. Квадратный корень может иметь как положительные, так и отрицательные значения. Положительные значения квадратных корней от 1 до 20 находятся в диапазоне от 1 до 4,47214.
В квадратных корнях от 1 до 20 числа 1, 4, 9 и 16 являются полными квадратами, а остальные числа являются неполными квадратами, т.е. их квадратный корень будет иррациональным. Квадратный корень от 1 до 20 в радикальной форме выражается как √x, а в экспоненциальной форме он выражается как (x) ½ .
Квадратные корни от 1 до 20:
- В подкоренной форме: √x
- В экспоненциальной форме: (x) ½
- Наибольший квадратный корень: √20 = 4,4721
Где x — любое число от 1 до 20.
| 1. | Квадратный корень от 1 до 20 |
| 2. | Квадратный корень от 1 до 20 PDF |
| 3. | Как вычислить квадратный корень от 1 до 20? |
| 4. | Часто задаваемые вопросы |
Квадратный корень от 1 до 20 Таблица
Квадратный корень от 1 до 20
Изучение квадратного корня от 1 до 20 поможет вам быстро упростить длинные уравнения, занимающие много времени. Значение квадратных корней от 1 до 20 до 3 знаков после запятой указано в таблице ниже.
Значение квадратных корней от 1 до 20 до 3 знаков после запятой указано в таблице ниже.
Квадратный корень от 1 до 20 с округлением до 3 знаков после запятой | |
√1 = 1 | √2 = 1,414 |
√3 = 1,732 | √4 = 2 |
√5 = 2,236 | √6 = 2,449 |
√7 = 2,646 | √8 = 2,828 |
√9 = 3 | √10 = 3,162 |
√11 = 3,317 | √12 = 3,464 |
√13 = 3,606 | √14 = 3,742 |
√15 = 3,873 | √16 = 4 |
√17 = 4,123 | √18 = 4,243 |
√19 = 4,359 | √20 = 4,472 |
Ученикам рекомендуется тщательно запомнить эти значения квадратного корня от 1 до 20 для более быстрого выполнения математических вычислений. Нажмите на кнопку загрузки, чтобы сохранить копию в формате PDF.
Нажмите на кнопку загрузки, чтобы сохранить копию в формате PDF.
Квадратный корень от 1 до 20 для идеальных квадратов
В таблице ниже показаны значения квадратных корней от 1 до 20 для идеальных квадратов.
√1 = 1 | √4 = 2 |
√9 = 3 | √16 = 4 |
Квадратный корень от 1 до 20 для неидеальных квадратов
В таблице ниже показаны значения квадратного корня от 1 до 20 для неидеальных квадратов.
√2 = 1,414 | √3 = 1,732 |
√5 = 2,236 | √6 = 2,449 |
√7 = 2,646 | √8 = 2,828 |
√10 = 3,162 | √11 = 3,317 |
√12 = 3,464 | √13 = 3,606 |
√14 = 3,742 | √15 = 3,873 |
√17 = 4,123 | √18 = 4,243 |
√19 = 4,359 | √20 = 4,472 |
☛ Проверка: Калькулятор квадратного корня
Как вычислить квадратный корень от 1 до 20?
Метод 1: простая факторизация
Пример: значение √4
- Простая факторизация числа 4 равна 2 × 2
- Парные простые множители: 2
Следовательно, значение √4 = 2
Метод 2: метод длинного деления
Квадратные корни чисел от 1 до 20
Решенные примеры на квадратный корень от 1 до 20
Пример 1: Квадратный металлический лист имеет площадь 11 кв.
 дюймов. Найдите длину стороны металлического листа.
дюймов. Найдите длину стороны металлического листа.Решение:
Пусть a будет длиной стороны металлического листа
Площадь квадратного металлического листа = 11 в 2 = a 2
т. е. a 2 = 11
a = √11 = 3,317 дюйма
Следовательно, длина стороны металлического листа составляет 3,317 дюйма.
Пример 2: Если круглая столешница имеет площадь 15π кв. дюймов. Найдите радиус столешницы в дюймах?
Решение:
Площадь круглой столешницы = 15π в 2 = πr 2
т. е. 15 = r 2 . Следовательно, радиус = √15
Используя значения от 1 до 20 таблицы квадратного корня, радиус столешницы = √15 дюймов = 3,873 дюйма
Пример 3: Найдите значение 9√15 + 6√13
Решение:
9√15 + 6√13 = 9 × (3,873) + 6 × (3,606) [значение √15 = 3,873 и √13 = 3,606]
Следовательно, 9√15 + 6√13 = 34,857 + 21,636 = 56,493
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы по квадратному корню от 1 до 20
Каково значение квадратного корня от 1 до 20?
Значение квадратного корня от 1 до 20 представляет собой число (x 1/2 ), умноженное само на себя дает исходное число. Он может иметь как отрицательные, так и положительные значения. В диапазоне от 1 до 20 квадратные корни из 1, 4, 9 и 16 являются целыми числами (рациональными), а квадратные корни из 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14 , 15, 17, 18, 19 и 20 — десятичные числа, которые не являются ни конечными, ни повторяющимися (иррациональными).
Если взять квадратные корни от 1 до 20, сколько из них будут иррациональными?
Числа 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19 и 20 — неполные квадраты. Следовательно, их квадратный корень будет иррациональным числом (не может быть выражено в виде p/q, где q ≠ 0).
Какие существуют методы вычисления квадратных корней от 1 до 20?
Для вычисления значения квадратного корня от 1 до 20 обычно используются два метода. Для полных квадратов (1, 4, 9, и 16), мы можем использовать метод простой факторизации и для несовершенных квадратов (2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19 и 20 ) можно использовать метод длинного деления.
Какие значения квадратных корней от 1 до 20 находятся между 2 и 3 включительно?
Значения квадратных корней от 1 до 20 между 2 и 3 составляют √4 (2), √5 (2,236), √6 (2,449), √7 (2,646), √8 (2,828) и √9 (3 ).
Каково значение 21 плюс 2 квадратного корня из 16?
Значение √16 равно 4. Таким образом, 21 + 2 × √16 = 21 + 2 × 4 = 29. Следовательно, значение 21 плюс 2 квадратного корня из 16 равно 29.
Сколько чисел в квадратных корнях от 1 до 20 являются рациональными?
Числа 1, 4, 9 и 16 являются полными квадратами, поэтому их квадратные корни будут целыми числами, т.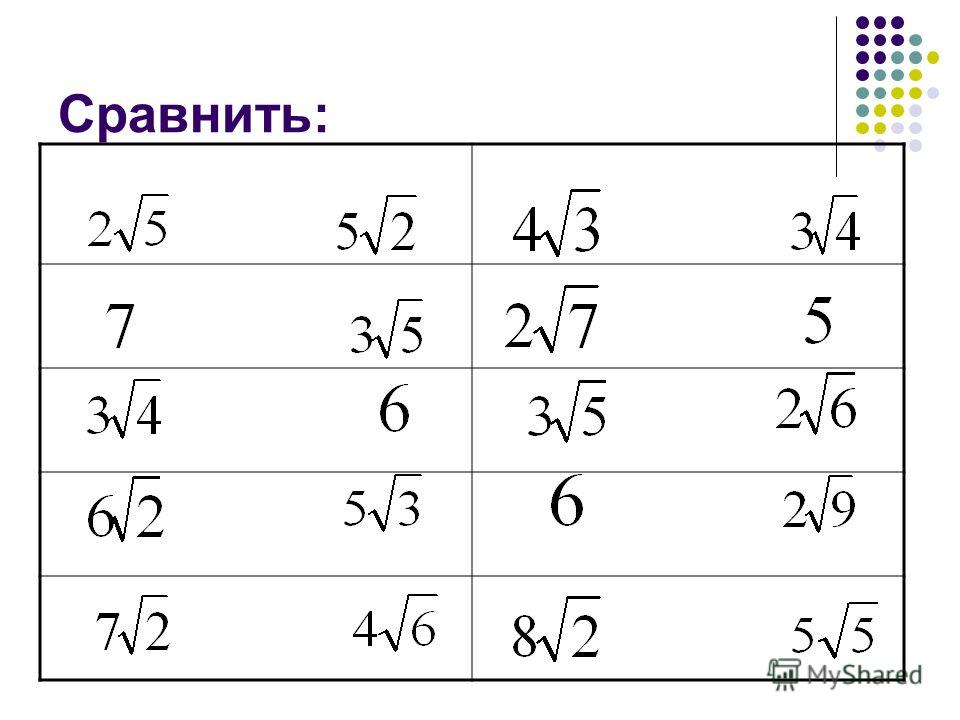 е. могут быть выражены в виде p/q, где q ≠ 0. Следовательно, квадратный корень из чисел 1, 4 , 9 и 16 — рациональные числа.
е. могут быть выражены в виде p/q, где q ≠ 0. Следовательно, квадратный корень из чисел 1, 4 , 9 и 16 — рациональные числа.
Таблица квадратных корней
Ищете ли вы список полных квадратных корней или полную таблицу квадратных корней от 1 до 100, таблица квадратных корней на этой странице поможет вам найти радикалы! Существуют как цветные, так и черно-белые версии диаграмм в формате PDF для печати.
Таблица извлечения квадратного корня
Прекрасно оформленные таблицы на этой странице готовы к отправке прямо на ваш принтер с высоким разрешением и станут прекрасным дополнением к базовым папкам по геометрии и алгебре вашего ученика.
Красочная диаграмма с идеальными квадратами от 1 до 15 не только имеет визуальное представление площади квадрата, связанной с каждым вычислением корня, но также показывает названия частей выражения квадратного корня (подкоренный знак, подкоренное число и корень). и краткое описание того, как конкретная задача умножения квадратов связана с уравнением квадратного корня.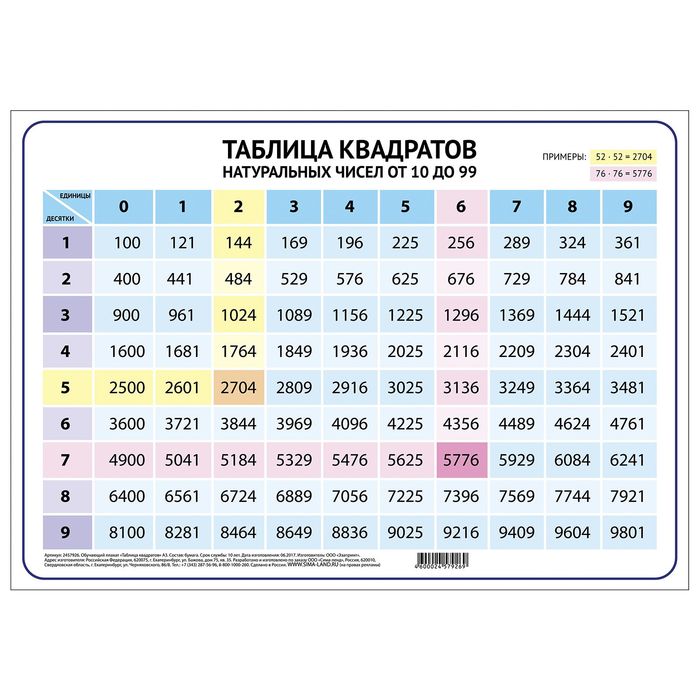
Что такое квадратные корни?
Хороший способ объяснить учащимся квадратный корень — это описать его как обратную операцию умножения числа на самого себя. Студенты часто знакомы с функциями, которые дополняют друг друга (например, сложение и вычитание). Использование этой схемы для описания нахождения корней как специального решения задачи на умножение в обратном порядке — отличный умственный ярлык для объяснения не только квадратных корней, но и различных корней счисления как Что ж.
Квадратный корень из некоторого числа (а) — это другое число (б), которое при умножении само на себя дает (а). В общем случае это означает bxb=a, демонстрируя, что (b) является квадратным корнем из (a) или, в конкретном примере, 3×3=9., демонстрируя, что 3 является квадратным корнем из 9.
Хотя мы обычно изучаем квадратные корни в контексте целых чисел, мы также можем находить квадратные корни чисел, которые не являются целыми числами. Например, квадратный корень из 10 — это десятичное число, близкое к 3,16227 (это можно проверить, умножив это число на само себя на калькуляторе, и вы получите значение, очень близкое к 10).
Так что же делает
идеальным Квадратный корень?Если умножить натуральное число само на себя, получится полный квадрат. Произведение этого умножения будет целым числом, а квадратный корень из этого значения будет исходным числом, которое также было целым числом. Эти целые целые корни известны как совершенные квадратные корни.
Итак, как вы, наверное, догадались, несовершенный квадрат будет иметь квадратный корень, который не является целым числом (у него есть десятичная или дробная часть), как квадратный корень из 10, который мы вычислили выше. На самом деле все эти корни будут иррациональными числами с десятичными значениями, которые продолжаются вечно. Из-за этого несовершенные квадратные корни округляются до некоторой степени десятичной точности для практических приложений. Это действительно интересная математическая тема, в которую вы можете погрузиться, если хотите узнать больше.
Как вычисляются квадратные корни?
Поскольку квадратные корни для большинства чисел иррациональны, метод их точного вычисления несколько громоздкий. Процедура вычисления квадратных корней произвольных чисел заключается в том, чтобы начать с оценки, а затем постепенно уточнять ее, пока вы не получите значение с достаточной точностью для ваших нужд. Вы можете найти более подробную информацию о том, как вычисляются квадратные корни, в Википедии, и эти методы, по сути, являются тем, что делает ваш карманный калькулятор, когда вы нажимаете клавишу квадратного корня.
Процедура вычисления квадратных корней произвольных чисел заключается в том, чтобы начать с оценки, а затем постепенно уточнять ее, пока вы не получите значение с достаточной точностью для ваших нужд. Вы можете найти более подробную информацию о том, как вычисляются квадратные корни, в Википедии, и эти методы, по сути, являются тем, что делает ваш карманный калькулятор, когда вы нажимаете клавишу квадратного корня.
Корни в таблице квадратных корней 1-100 на этой странице округлены до четырех знаков после запятой для корней несовершенных квадратов.
Что такое корни высшего порядка?
Квадратные корни — это только начало!
Кубический корень похож на квадратный корень, но значение корня умножается само на себя три раза, чтобы получить значение «куб». Так, например, 2x2x2=8 подразумевает, что кубический корень из 8 равен 2.
Вы можете найти корни более высокого порядка, помимо квадратов и кубов, но только у этих двух есть специальные имена. Например, корень четвертой степени из 16 равен 2, поскольку 2x2x2x2 (всего умножить 4 двойки) равно 16. Вы заметите, что это также 2, возведенное в 4-ю степень (показатель степени), и вы увидите очень четкую обратную зависимость. между корнями n-й степени и применением показателей к числу.
Вы заметите, что это также 2, возведенное в 4-ю степень (показатель степени), и вы увидите очень четкую обратную зависимость. между корнями n-й степени и применением показателей к числу.
Что такое главный корень числа?
Если ваши дети столкнулись с отрицательными числами, они уже знают, что два отрицательных числа, умноженные вместе, дают положительный результат. Из-за этого на самом деле есть два квадратных корня из положительного числа… Один положительный, а другой отрицательный. Например, -2x-2=4, поэтому квадратный корень из 4 может быть равен 2 или -2. Мы отличаем положительный корень от отрицательного корня, называя его главным корнем числа.
А что насчет корней отрицательных чисел?
Если квадратный корень может быть действительным числом (целым, если это корень из полного квадрата, или десятичной дробью, если это корень из неполного квадрата), мы знаем, что получим положительный результат, умножив это число сам по себе. Невозможно получить отрицательный квадратный результат, умножив одно и то же число на само себя, потому что вы умножаете либо положительное на положительное, либо отрицательное на отрицательное. .. И то, и другое всегда дает положительный результат.
.. И то, и другое всегда дает положительный результат.
Способ, которым мы получаем квадратные корни из отрицательных чисел, состоит в том, чтобы ввести совершенно новый тип чисел, и, конечно, поскольку мы называем наборы целых и десятичных чисел действительными числами , мы можем ловко изобрести новый набор мнимых чисел , чтобы сделать что-то совершенно другое.
Мнимые числа вводят единичное мнимое число i , которое явно представляет собой квадратный корень из -1. Введя эту мнимую единицу, можно вычислить квадратный корень из отрицательного числа как значение с мнимым результатом. Например, квадратный корень из -4 становится 2i.
Что такое постоянная Пифагора?
Постоянная Пифагора — это квадратный корень из 2. Поскольку 2 не является полным квадратом, его квадратный корень — иррациональное число. Это число появляется во многих геометрических операциях, но на самом деле это просто квадратный корень.
На приведенной выше диаграмме квадратного корня вы можете видеть, что значение квадратного корня из 2 приблизительно равно 1,4142, и эту константу полезно запомнить.
Рабочие листы показателей Рабочие листы умножения (квадраты и кубы) Рабочие листы деления (квадраты и кубы)
История рабочего листа
Список квадратных корней для первых 1000 чисел
- Дом
- Таблицы
- Квадратные корни
| № | Квадратные корни | ||
|---|---|---|---|
| 1 | 1 | ||
| 2 | 1.4142135623731 | ||
| 3 | 1.7320508075689 | ||
| 4 | 2 | ||
| 5 | 2. 23606798 23606798 | ||
| 6 | 2.44 | 427832 | |
| 7 | 2,6457513110646 | ||
| 8 | 2,8284271247462 | ||
| 9 | 3 | ||
| 10 | 3.1622776601684 | ||
| 11 | 3.31662474 | ||
| 12 | 3,4641016151378 | ||
| 13 | 3.605551275464 | ||
| 14 | 3,7416573867739 | ||
| 15 | 3,87262074 | ||
| 16 | 4 | ||
| 17 | 4. 1231056256177 1231056256177 | ||
| 18 | 4.2426406871193 | ||
| 19 | 4.358898 | ||
| 20 | 4.472135 | ||
| 21 | 4,5825756 | 8 | |
| 22 | 4.675 | ||
| 23 | 4,7 | 5233127 | |
| 24 | 4.89897 | 664 | |
| 25 | 5 | ||
| 26 | 5.09135928 | ||
| 27 | 5.1 | 4227066||
| 28 | 5. 2 2 | 6221292||
| 29 | 5.3851648071345 | ||
| 30 | 5.4772255750517 | ||
| 31 | 5.56776436283 | ||
| 32 | 5,65685424 | ||
| 33 | 5,744562646538 | ||
| 34 | 5.8309518 | ||
| 35 | 5. | 996 | |
| 36 | 6 | ||
| 37 | 6.0827625302982 | ||
| 38 | 6.164414002969 | ||
| 39 | 6. 24493984 24493984 | ||
| 40 | 6.3245553203368 | ||
| 41 | 6.4031242374328 | ||
| 42 | 6.48074069 | ||
| 43 | 6.557438524302 | ||
| 44 | 6.63324 | 108 | |
| 45 | 6.708203 | ||
| 46 | 6.782329 53 | ||
| 47 | 6.855654600401 | ||
| 48 | 6. | 32302755||
| 49 | 7 | ||
| 50 | 7. 0710678118655 0710678118655 | ||
| 51 | 7.1414284285429 | ||
| 52 | 7.211102550928 | ||
| 53 | 7.28010988 | ||
| 54 | 7.34846 | ||
| 55 | 7.41610957 | ||
| 56 | 7.4833147735479 | ||
| 57 | 7,54352707 | ||
| 58 | 7,6157731058639 | ||
| 59 | 7,6811457478686 | ||
| 60 | 7,7459666 | 8||
| 61 | 7. 81024067 81024067 | ||
| 62 | 7.8740078740118 | ||
| 63 | 7, | 3 | 38 |
| 64 | 8 | ||
| 65 | 8.0622577482985 | ||
| 66 | 8.124038404636 | ||
| 67 | 8.1853527718725 | ||
| 68 | 8.2462112512353 | ||
| 69 | 8.3066238629181 | ||
| 70 | 8.3666002653408 | ||
| 71 | 8.42614764 | ||
| 72 | 8. 4852813742386 4852813742386 | ||
| 73 | 8.5440037453175 | ||
| 74 | 8.6023252670426 | ||
| 75 | 8.6602540378444 | ||
| 76 | 8.7177 0813 | ||
| 77 | 8.774 | 73921||
| 78 | 8.8317608663278 | ||
| 79 | 8.8881 | 3156 | |
| 80 | 8. | 1 | |
| 81 | 9 | ||
| 82 | 9.0553851381374 | ||
| 83 | 9. 11043357 11043357 | ||
| 84 | 9.1651513899117 | ||
| 85 | 9.21 | 572929||
| 86 | 9.2736184 | 7 | |
| 87 | 9.32737888 | ||
| 88 | 9.38083151 | ||
| 89 | 9.43320566 | ||
| 90 | 9.486832 51 | ||
| 91 | 9.5393 | ||
| 92 | 9,5 | 0466254 | |
| 93 | 9,643650760993 | ||
| 94 | 9,6 | 7148327 | |
| 95 | 9,7467 | 809||
| 96 | 9. 797 797 | 11327 | |
| 97 | 9,8488578017961 | ||
| 98 | 9,899494 | 17 | |
| 99 | 9, | 43710662 | |
| 100 | 10 | ||
| 101 | 10.04 21121 | ||
| 102 | 10.099504 | 2||
| 103 | 10.1488 | 092 | |
| 104 | 10.19803 | 86 | |
| 105 | 10.246 | 596||
| 106 | 10.2 | 140987||
| 107 | 10. 344080432789 344080432789 | ||
| 108 | 10.3 | 845413||
| 109 | 10.440306508911 | ||
| 110 | 10.488088481702 | ||
| 111 | 10,535653752853 | ||
| 112 | 10,583005244258 | ||
| 113 | 10.630145812735 | ||
| 114 | 10.677078252031 | ||
| 115 | 10.7238052 | ||
| 116 | 10.77032 | ||
| 117 | 10,816653826392 | ||
| 118 | 10. 8627804912 8627804912 | ||
| 119 | 10. | 2114636 | |
| 120 | 10. | ||
| 121 | 11 | ||
| 122 | 11.045361017187 | ||
| 123 | 11.0 | 506409||
| 124 | 11.13552872566 | ||
| 125 | 11.1803399 | ||
| 126 | 11.2240322 | ||
| 127 | 11.26 | ||
| 128 | 11.313708498985 | ||
| 129 | 11. 3578166 3578166 | ||
| 130 | 11.401754250991 | ||
| 131 | 11.44552314226 | ||
| 132 | 11.48 | ||
| 133 | 11,5325625 | ||
| 134 | 11.575836 | ||
| 135 | 11.618 | 8622 | |
| 136 | 11,6619691 | ||
| 137 | 11.704699 | ||
| 138 | 11.747340124471 | ||
| 139 | 11.7822552 | ||
| 140 | 11.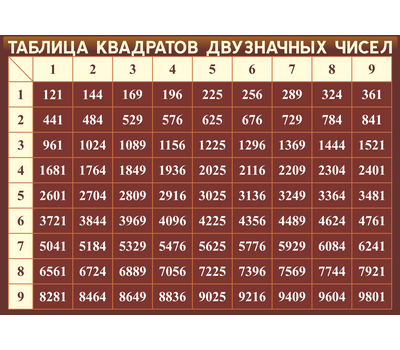 83215 83215 | ||
| 141 | 11.874342087038 | ||
| 142 | 11. | 5287813 | |
| 143 | 11. | 0743101||
| 144 | 12 | ||
| 145 | 12.0415 | 792||
| 146 | 12.0830455 | ||
| 147 | 12.124355652982 | ||
| 148 | 12.165525060596 | ||
| 149 | 12.206555615734 | ||
| 150 | 12.247448713916 | ||
| 151 | 12. 288205727445 288205727445 | ||
| 152 | 12.328828005938 | ||
| 153 | 12.36 | 76853||
| 154 | 12.40 45991 | ||
| 155 | 12.44989 | ||
| 156 | 12.4899 | 797||
| 157 | 12.529 | 6142||
| 158 | 12.56 89977 | ||
| 159 | 12.60 | 12918||
| 160 | 12.64 | 40674||
| 161 | 12.68857754045 | ||
| 162 | 12. 727 727 | ||
| 163 | 12.767145334804 | ||
| 164 | 12.806248474866 | ||
| 165 | 12,845232578665 | ||
| 166 | 12.8840725 | ||
| 167 | 12. | ||
| 168 | 12. | ||
| 169 | 13 | ||
| 170 | 13.038404810405 | ||
| 171 | 13.0766 622 | ||
| 172 | 13.114877048604 | ||
| 173 | 13. 152 152 | 7966 | |
| 174 | 13.190 | 8273 | |
| 175 | 13.228756555323 | ||
| 176 | 13.26649 | 22||
| 177 | 13.30413469565 | ||
| 178 | 13.341664064126 | ||
| 179 | 13.37 | 6026 | |
| 180 | 13.416407864999 | ||
| 181 | 13.453624047074 | ||
| 182 | 13.4 | 563232 | |
| 183 | 13,52774 | ||
| 184 | 13,5646591 | ||
| 185 | 13. 601470508735 601470508735 | ||
| 186 | 13.6381816 | ||
| 187 | 13,6747 | 177 | |
| 188 | 13.71130 | ||
| 189 | 13.747727084868 | ||
| 190 | 13.78404875209 | ||
| 191 | 13.820274 | 5||
| 192 | 13.856406460551 | ||
| 193 | 13.8 | ||
| 194 | 13. | 8277184||
| 195 | 13, | ||
| 196 | 14 | ||
| 197 | 14. 035668847618 035668847618 | ||
| 198 | 14.07124727947 | ||
| 199 | 14.106735 6 | ||
| 200 | 14.142135623731 | ||
| 201 | 14.177446878758 | ||
| 202 | 14.212670403552 | ||
| 203 | 14.247806848775 | ||
| 204 | 14.282856857086 | ||
| 205 | 14.317821063276 | ||
| 206 | 14.3527000 | ||
| 207 | 14.3874 | ||
| 208 | 14. 422205101856 422205101856 | ||
| 209 | 14.4568322 | ||
| 210 | 14.4 | 746189||
| 211 | 14,5258334 | ||
| 212 | 14.5602161 | ||
| 213 | 14.5 | 519326 | |
| 214 | 14.628738838328 | ||
| 215 | 14.6628782 | ||
| 216 | 14.696 | 6699 | |
| 217 | 14.730 | 2656||
| 218 | 14.764823060233 | ||
| 219 | 14,7 586949 | ||
| 220 | 14. 8323191 8323191 | ||
| 221 | 14.866068747319 | ||
| 222 | 14.8925751 | ||
| 223 | 14. | 4523068||
| 224 | 14, | ||
| 225 | 15 | ||
| 226 | 15.0332 | 373||
| 227 | 15.06651 | 19 | |
| 228 | 15.09 70541 | ||
| 229 | 15.132745 | 2||
| 230 | 15. 165750888103 165750888103 | ||
| 231 | 15.1 153571 | ||
| 232 | 15.231546211728 | ||
| 233 | 15.264337522474 | ||
| 234 | 15.2540778 | ||
| 235 | 15.3216756 | ||
| 236 | 15.3622 | 737 | |
| 237 | 15.3 | ||
| 238 | 15.427248620542 | ||
| 239 | 15.45 | 3374||
| 240 | 15.4 | 38483 | |
| 241 | 15,52417469626 | ||
| 242 | 15,55634 | 04 | |
| 243 | 15. 58845726812 58845726812 | ||
| 244 | 15.62049 | 13||
| 245 | 15,652475842499 | ||
| 246 | 15.684387141358 | ||
| 247 | 15.716233645502 | ||
| 248 | 15.748015748024 | ||
| 249 | 15.77 38059 | ||
| 250 | 15.811388300842 | ||
| 251 | 15.84297 | 55 | |
| 252 | 15.874507866388 | ||
| 253 | 15. | ||
| 254 | 15. | 7450509 | |
| 255 | 15, | 71||
| 256 | 16 | ||
| 257 | 16.03121 | 81||
| 258 | 16.062378404209 | ||
| 259 | 16.0 | 1 | |
| 260 | 16.1245154 | ||
| 261 | 16.1554 | 404 | |
| 262 | 16.186414056239 | ||
| 263 | 16.217274740227 | ||
| 264 | 16. 248076809272 248076809272 | ||
| 265 | 16.2788205961 | ||
| 266 | 16.30 | 303||
| 267 | 16.340134638368 | ||
| 268 | 16.370705543745 | ||
| 269 | 16.40121 | 57||
| 270 | 16.431676725155 | ||
| 271 | 16.462077633154 | ||
| 272 | 16.4 | ||
| 273 | 16,522711641858 | ||
| 274 | 16.552 | 7247 | |
| 275 | 16. 583123 583123 | 7 | |
| 276 | 16.613247725836 | ||
| 277 | 16.6433163 | ||
| 278 | 16.673332000533 | ||
| 279 | 16.7032 | ||
| 280 | 16.733200530682 | ||
| 281 | 16.76305461424 | ||
| 282 | 16.7 | 623747 | |
| 283 | 16.822603841261 | ||
| 284 | 16.85229 | ||
| 285 | 16.881 | 6134 | |
| 286 | 16. | 4525288 | |
| 287 | 16. | ||
| 288 | 16.2748477 | ||
| 289 | 17 | ||
| 290 | 17.02 | 65926 | |
| 291 | 17.058722109232 | ||
| 292 | 17.0880074 | ||
| 293 | 17.117242768624 | ||
| 294 | 17.146428199482 | ||
| 295 | 17.175564037318 | ||
| 296 | 17.204650534085 | ||
| 297 | 17. 233687 233687 | 4 | |
| 298 | 17.262676501632 | ||
| 299 | 17.2 | 465791||
| 300 | 17.320508075689 | ||
| 301 | 17.34 | 72897 | |
| 302 | 17.3781471 | ||
| 303 | 17.4068 | 529 | |
| 304 | 17.4355 | 163||
| 305 | 17.46424 | ||
| 306 | 17.4 | 684536 | |
| 307 | 17.521415467935 | ||
| 308 | 17,549 | ||
| 309 | 17,5783 | 247 | |
| 310 | 17. 606816861659 606816861659 | ||
| 311 | 17.6351 | 548||
| 312 | 17,663521732656 | ||
| 313 | 17.6 | 012954||
| 314 | 17.720045146669 | ||
| 315 | 17.74823 | 99||
| 316 | 17.776388834631 | ||
| 317 | 17.8044 | ||
| 318 | 17.832554500127 | ||
| 319 | 17.860571099492 | ||
| 320 | 17.888543819998 | ||
| 321 | 17. | ||
| 322 | 17, | 8444926 | |
| 323 | 17.0755611 | ||
| 324 | 18 | ||
| 325 | 18.02775637732 | ||
| 326 | 18.055470085268 | ||
| 327 | 18.083141320025 | ||
| 328 | 18.110770276275 | ||
| 329 | 18.138357147217 | ||
| 330 | 18.1654585 | ||
| 331 | 18.1 | ||
| 332 | 18. 220867158289 220867158289 | ||
| 333 | 18.2482875 | ||
| 334 | 18.275666882497 | ||
| 335 | 18.303005217723 | ||
| 336 | 18.330302779823 | ||
| 337 | 18.3575586 | ||
| 338 | 18.38477631085 | ||
| 339 | 18.411 | 9522 | |
| 340 | 18.43 | 14586 | |
| 341 | 18.466185312619 | ||
| 342 | 18.4 | 008907||
| 343 | 18. 52025 52025 | ||
| 344 | 18.5472369 | ||
| 345 | 18.574175621007 | ||
| 346 | 18.601075237738 | ||
| 347 | 18.627 | 0197 | |
| 348 | 18.654758106178 | ||
| 349 | 18.6815416 | ||
| 350 | 18.708286 | ||
| 351 | 18.7349 | 195 | |
| 352 | 18.761663039294 | ||
| 353 | 18.7882 | ||
| 354 | 18. 814887722227 814887722227 | ||
| 355 | 18.841443681417 | ||
| 356 | 18.867 | ||
| 357 | 18.8 | ||
| 358 | 18. | 7||
| 359 | 18. | 5321496 | |
| 360 | 18.5 | ||
| 361 | 19 | ||
| 362 | 19.026244 | ||
| 363 | 19.052558883258 | ||
| 364 | 19.078784028339 | ||
| 365 | 19.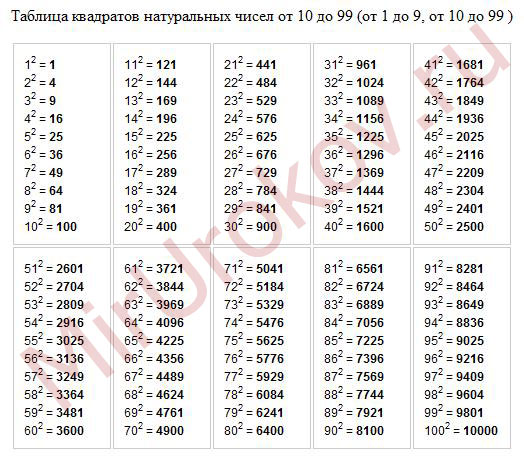 104 1044543 | ||
| 366 | 19.131126469709 | ||
| 367 | 19.157244060668 | ||
| 368 | 19.1833260 | ||
| 369 | 19.20 | 12299 | |
| 370 | 19.235384061671 | ||
| 371 | 19.261360284258 | ||
| 372 | 19.287301521986 | ||
| 373 | 19.313207 | ||
| 374 | 19.33 | ||
| 375 | 19.364 | 1037 | |
| 376 | 19. 3 3 | 429665 | |
| 377 | 19.416487838948 | ||
| 378 | 19.4422220 | ||
| 379 | 19.467 | 3932 | |
| 380 | 19.4 | 689618||
| 381 | 19.51 | ||
| 382 | 19.544820285692 | ||
| 383 | 19.5703857 | ||
| 384 | 19.595 | 2265||
| 385 | 19.621416870349 | ||
| 386 | 19.646882704388 | ||
| 387 | 19. 672315572906 672315572906 | ||
| 388 | 19.6603592 | ||
| 389 | 19.723082 | ||
| 390 | 19.748417658131 | ||
| 391 | 19.773719 | ||
| 392 | 19.79898 23 | ||
| 393 | 19.824227601599 | ||
| 394 | 19.84 | 41279||
| 395 | 19.874606 | 2 | |
| 396 | 19.89 42132 | ||
| 397 | 19. | 8845171 | |
| 398 | 19. 949 949 | 326||
| 399 | 19. 4355438 | ||
| 400 | 20 | ||
| 401 | 20.0249843 | ||
| 402 | 20.049 | ||
| 403 | 20.074859899885 | ||
| 404 | 20.09 42242 | ||
| 405 | 20.1246117 | ||
| 406 | 20.14 | 7961||
| 407 | 20.174241001832 | ||
| 408 | 20.19 76724 | ||
| 409 | 20. 223748416157 223748416157 | ||
| 410 | 20.248456731317 | ||
| 411 | 20.273134 | 3 | |
| 412 | 20.2130184 | ||
| 413 | 20.322401432902 | ||
| 414 | 20.346989 | 6 | |
| 415 | 20.371548787463 | ||
| 416 | 20.3 | 054371||
| 417 | 20.420577856662 | ||
| 418 | 20.445048300261 | ||
| 419 | 20.46 | ||
| 420 | 20. 4931919 4931919 | ||
| 421 | 20,518284528683 | ||
| 422 | 20,542638584174 | ||
| 423 | 20.566 | 1203||
| 424 | 20.5 | 281974||
| 425 | 20.615528128088 | ||
| 426 | 20.63 4055 | ||
| 427 | 20.663 9772 | ||
| 428 | 20.688160865577 | ||
| 429 | 20.712315177208 | ||
| 430 | 20. 736441353328 736441353328 | ||
| 431 | 20.7605394 | ||
| 432 | 20.7846096 | ||
| 433 | 20.808652046685 | ||
| 434 | 20.832666656 | ||
| 435 | 20,856653614614 | ||
| 436 | 20.880613017821 | ||
| 437 | 20.4 | 7||
| 438 | 20, | 56||
| 439 | 20, | 6839757||
| 440 | 20,6 | ||
| 441 | 21 | ||
| 442 | 21. 0237 0237 | 629 | |
| 443 | 21.047565179849 | ||
| 444 | 21.071307505705 | ||
| 445 | 21.0 | 109729 | |
| 446 | 21.118712081943 | ||
| 447 | 21.142374511866 | ||
| 448 | 21.166010488517 | ||
| 449 | 21.18 | ||
| 450 | 21.213203435596 | ||
| 451 | 21.236760581595 | ||
| 452 | 21.2602 | 469 | |
| 453 | 21. 2837793 2837793 | ||
| 454 | 21.307275752663 | ||
| 455 | 21.33072 | 02 | |
| 456 | 21.354156504063 | ||
| 457 | 21.377558326432 | ||
| 458 | 21.400 | 9033 | |
| 459 | 21.424285285629 | ||
| 460 | 21.447610589527 | ||
| 461 | 21.470 | 3584 | |
| 462 | 21.4 | ||
| 463 | 21.51743479135 | ||
| 464 | 21. 54065 54065 | 38 | |
| 465 | 21.563858652848 | ||
| 466 | 21.587033144923 | ||
| 467 | 21.610182784974 | ||
| 468 | 21.633307652784 | ||
| 469 | 21.656407827708 | ||
| 470 | 21.67 | ||
| 471 | 21.702534414211 | ||
| 472 | 21.7255609824 | ||
| 473 | 21.748563170932 | ||
| 474 | 21.771541057077 | ||
| 475 | 21. 7 7 | 717703||
| 476 | 21.817424229271 | ||
| 477 | 21.84032 42 | ||
| 478 | 21.863211109075 | ||
| 479 | 21.886068628239 | ||
| 480 | 21.908 | ||
| 481 | 21. | ||
| 482 | 21. | 84001 | |
| 483 | 21. 0 6 | ||
| 484 | 22 | ||
| 485 | 22.022715545545 | ||
| 486 | 22. 045407685049 045407685049 | ||
| 487 | 22.0680764 | ||
| 488 | 22.0 | 034375||
| 489 | 22.113344387496 | ||
| 490 | 22.135 | 1179||
| 491 | 22.15851 6 | ||
| 492 | 22.181073012819 | ||
| 493 | 22.203603311175 | ||
| 494 | 22.226110770893 | ||
| 495 | 22.2485 | 287 | |
| 496 | 22.27105745132 | ||
| 497 | 22. 2 2 | ||
| 498 | 22.315 | ||
| 499 | 22.3383079 | ||
| 500 | 22.3606798 | ||
| 501 | 22.38302 | 99 | |
| 502 | 22.405356502408 | ||
| 503 | 22.4276614 | ||
| 504 | 22.449 | ||
| 505 | 22.472205054244 | ||
| 506 | 22.4 | ||
| 507 | 22,5166604 | ||
| 508 | 22,538855339169 | ||
| 509 | 22,561028345357 | ||
| 510 | 22. 58317 58317 | ||
| 511 | 22.60530 | 15 | |
| 512 | 22.62741699797 | ||
| 513 | 22.64 | 05812 | |
| 514 | 22.6715680 | ||
| 515 | 22.6 | 43582 | |
| 516 | 22.715633383201 | ||
| 517 | 22.737634001804 | ||
| 518 | 22.75 | 53482 | |
| 519 | 22.781571499789 | ||
| 520 | 22.803508501983 | ||
| 521 | 22. 825424421027 825424421027 | ||
| 522 | 22.84731 | 92 | |
| 523 | 22.86 | 52059||
| 524 | 22.8 | 284519||
| 525 | 22. | ||
| 526 | 22, | ||
| 527 | 22, | 0566498||
| 528 | 22.0586152 | ||
| 529 | 23 | ||
| 530 | 23.021728866443 | ||
| 531 | 23.043437243606 | ||
| 532 | 23. 065125189342 065125189342 | ||
| 533 | 23.0867 | 23 | |
| 534 | 23.108440016583 | ||
| 535 | 23.130067012441 | ||
| 536 | 23.15167380558 | ||
| 537 | 23.173260452513 | ||
| 538 | 23.1 | ||
| 539 | 23.216373532488 | ||
| 540 | 23.2377245 | ||
| 541 | 23.25 | ||
| 542 | 23.2808 | ||
| 543 | 23. 3023603 3023603 | ||
| 544 | 23.323807579381 | ||
| 545 | 23.345235059858 | ||
| 546 | 23.3666428 | ||
| 547 | 23.388031127053 | ||
| 548 | 23.40 | 21439||
| 549 | 23.430742 | ||
| 550 | 23.452078799117 | ||
| 551 | 23.47338 | 11||
| 552 | 23.4 | 248941||
| 553 | 23.515 | 261 | |
| 554 | 23. 53720459188 53720459188 | ||
| 555 | 23.5584379 | ||
| 556 | 23.57 | 45103||
| 557 | 23.600847442412 | ||
| 558 | 23.622023622035 | ||
| 559 | 23.643180835074 | ||
| 560 | 23.66431 | ||
| 561 | 23.685438564654 | ||
| 562 | 23.70653 | ||
| 563 | 23.727621035409 | ||
| 564 | 23.748684174076 | ||
| 565 | 23. 7648009 7648009 | ||
| 566 | 23.7 | ||
| 567 | 23.811761799581 | ||
| 568 | 23.832750575626 | ||
| 569 | 23.853720883753 | ||
| 570 | 23.874672772627 | ||
| 571 | 23.8 | 2||
| 572 | 23. | 1486203||
| 573 | 23. | ||
| 574 | 23. | ||
| 575 | 23.97 | ||
| 576 | 24 | ||
| 577 | 24.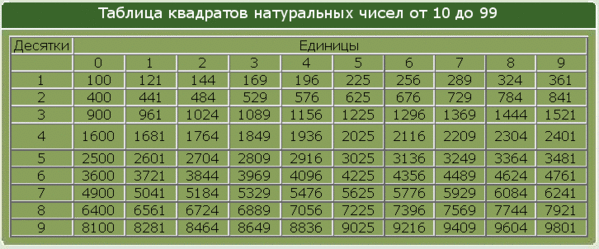 0208242 0208242 | ||
| 578 | 24.041630560343 | ||
| 579 | 24.062418831032 | ||
| 580 | 24.08318 | ||
| 581 | 24.103 | 6388||
| 582 | 24.12467616363 | ||
| 583 | 24.1453 | 299 | |
| 584 | 24.1660 | ||
| 585 | 24.186773244896 | ||
| 586 | 24.20743687382 | ||
| 587 | 24.228082879171 | ||
| 588 | 24. 248711305964 248711305964 | ||
| 589 | 24.26 | 99023 | |
| 590 | 24.289 | 2982||
| 591 | 24.3104 | 286||
| 592 | 24.331050121193 | ||
| 593 | 24.3515 | ||
| 594 | 24.372115213908 | ||
| 595 | 24.3 | 835301 | |
| 596 | 24.413111231467 | ||
| 597 | 24.433583445741 | ||
| 598 | 24.454038521275 | ||
| 599 | 24. 474476501041 474476501041 | ||
| 600 | 24.4 | 427832 | |
| 601 | 24.515301344263 | ||
| 602 | 24.5356882 | ||
| 603 | 24.556058315617 | ||
| 604 | 24.576411454889 | ||
| 605 | 24.5752498 | ||
| 606 | 24.617067250182 | ||
| 607 | 24.637369 | ||
| 608 | 24.657656011876 | ||
| 609 | 24.677 | ||
| 610 | 24. 6070457 6070457 | ||
| 611 | 24.718414188617 | ||
| 612 | 24.738633753706 | ||
| 613 | 24.75883680628 | ||
| 614 | 24.7786728 | ||
| 615 | 24.79 | ||
| 616 | 24.81 | ||
| 617 | 24.83 | ||
| 618 | 24.85 | ||
| 619 | 24.8709249 | ||
| 620 | 24.89979 | ||
| 621 | 24. | 1588754 | |
| 622 | 24.939 | ||
| 623 | 24. | 7||
| 624 | 24.9799 | 594 | |
| 625 | 25 | ||
| 626 | 25.0199 | 394||
| 627 | 25.0391098 | ||
| 628 | 25.059 | ||
| 629 | 25.07 07969 | ||
| 630 | 25.09 | ||
| 631 | 25.11 74161 | ||
| 632 | 25.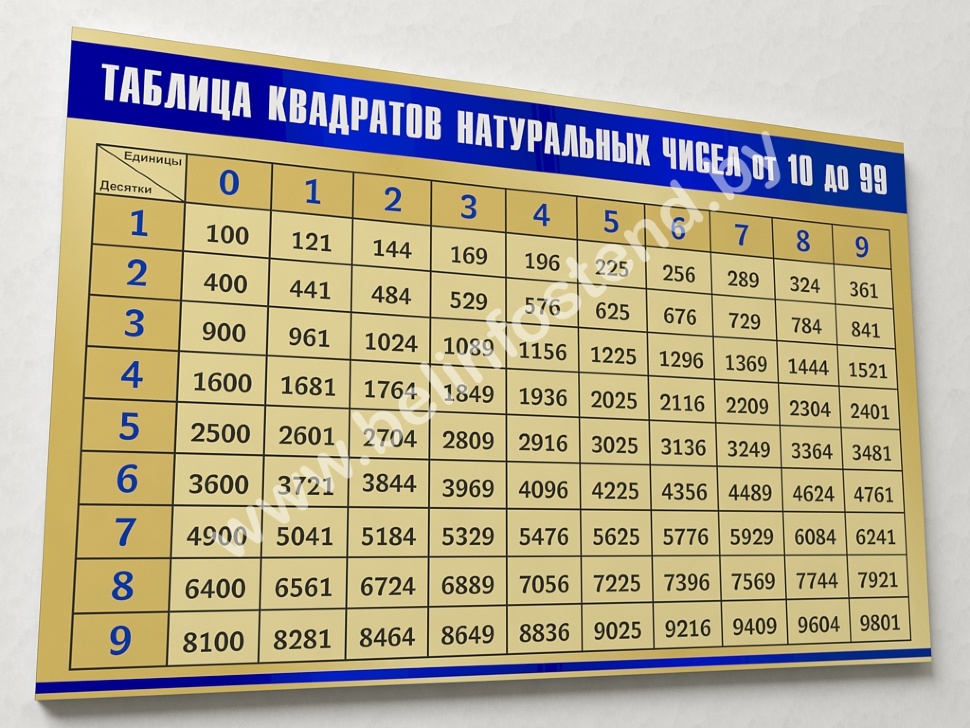 13 13 | 79953 | |
| 633 | 25.1594 | 818||
| 634 | 25.17 | 24028||
| 635 | 25.19 | 36708 | |
| 636 | 25.21 25837 | ||
| 637 | 25.238858 | ||
| 638 | 25.25866188063 | ||
| 639 | 25.27844 | ||
| 640 | 25.2281347 | ||
| 641 | 25.317 2344 | ||
| 642 | 25. 337718 337718 | ||
| 643 | 25.357444666212 | ||
| 644 | 25.377155080899 | ||
| 645 | 25.31 | ||
| 646 | 25.416530054278 | ||
| 647 | 25.4361 | ||
| 648 | 25.455844122716 | ||
| 649 | 25.475478405714 | ||
| 650 | 25.4 | ||
| 651 | 25.514701644346 | ||
| 652 | 25,5342 | ||
| 653 | 25,553864678361 | ||
| 654 | 25. 573423705089 573423705089 | ||
| 655 | 25.5 | ||
| 656 | 25.612496 | 1 | |
| 657 | 25.632011235953 | ||
| 658 | 25.651510676761 | ||
| 659 | 25.6709 | 987 | |
| 660 | 25.6 15733 | ||
| 661 | 25.709 | ||
| 662 | 25.72 | 60537||
| 663 | 25.748786379167 | ||
| 664 | 25.7681 45 | ||
| 665 | 25. 787593 787593 | 5 | |
| 666 | 25.8061128 | ||
| 667 | 25.82634314029 | ||
| 668 | 25.8456 | 64||
| 669 | 25.865034312755 | ||
| 670 | 25.88435821109 | ||
| 671 | 25. 76 | ||
| 672 | 25. | ||
| 673 | 25. | 3542146||
| 674 | 25. | 94||
| 675 | 25.2113533 | ||
| 676 | 26 | ||
| 677 | 26.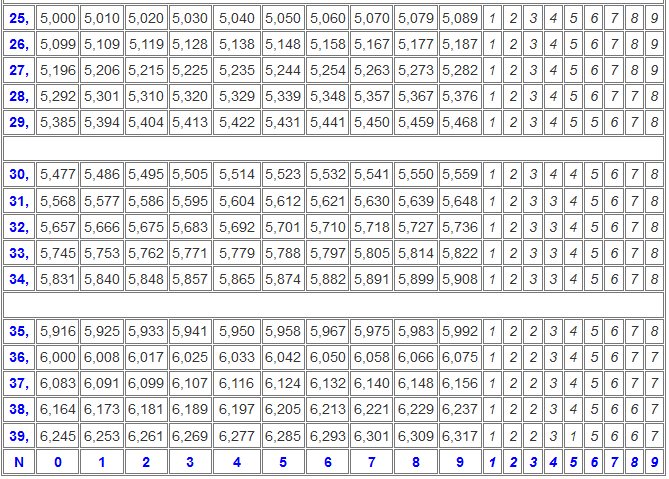 01 01 | ||
| 678 | 26.038433132583 | ||
| 679 | 26.057628441591 | ||
| 680 | 26.07680 | ||
| 681 | 26.0 | 7014||
| 682 | 26.1151201 | ||
| 683 | 26.1342686 | ||
| 684 | 26.1533 | 244 | |
| 685 | 26.172504656605 | ||
| 686 | 26.1 | 707418 | |
| 687 | 26.210684844162 | ||
| 688 | 26. 22 22 | ||
| 689 | 26.24880 | 13||
| 690 | 26.267851073127 | ||
| 691 | 26.28687885619 | ||
| 692 | 26.3058 | 932 | |
| 693 | 26.3248 | 176||
| 694 | 26.3438739 | ||
| 695 | 26.362852652928 | ||
| 696 | 26.381811 | ||
| 697 | 26.400757564888 | ||
| 698 | 26.41968 | 46||
| 699 | 26. 438608132805 438608132805 | ||
| 700 | 26.457513110646 | ||
| 701 | 26.476404589747 | ||
| 702 | 26.4 | 598984||
| 703 | 26.514147167126 | ||
| 704 | 26.5329843 | ||
| 705 | 26.5518360 | ||
| 706 | 26.570660511173 | ||
| 707 | 26.58 | 00617||
| 708 | 26.60826 | ||
| 709 | 26.627053 | ||
| 710 | 26. 645825188948 645825188948 | ||
| 711 | 26.664583251947 | ||
| 712 | 26.683328128253 | ||
| 713 | 26.70205 37 | ||
| 714 | 26.720778431775 | ||
| 715 | 26.739483 | 2||
| 716 | 26.758176320519 | ||
| 717 | 26.776855677992 | ||
| 718 | 26.7 | 013949||
| 719 | 26.814175355584 | ||
| 720 | 26.832815729997 | ||
| 721 | 26. 851443164195 851443164195 | ||
| 722 | 26.870057685089 | ||
| 723 | 26.88865 | 98||
| 724 | 26. | ||
| 725 | 26. | 4035673||
| 726 | 26. | ||
| 727 | 26.962 | 5426||
| 728 | 26. 5126464 | ||
| 729 | 27 | ||
| 730 | 27.018512172213 | ||
| 731 | 27.037011669192 | ||
| 732 | 27. 0554 0554937 | ||
| 733 | 27.0731362 | ||
| 734 | 27.0 | ||
| 735 | 27.110883423452 | ||
| 736 | 27.12 | 32501 | |
| 737 | 27.147743 | 6 | |
| 738 | 27.166155414412 | ||
| 739 | 27.184554438136 | ||
| 740 | 27.202 | ||
| 741 | 27.221315177632 | ||
| 742 | 27.239676 | 2 | |
| 743 | 27. 258026340878 258026340878 | ||
| 744 | 27.2763633 | ||
| 745 | 27.2 | 127912||
| 746 | 27.313000567495 | ||
| 747 | 27.331300737433 | ||
| 748 | 27.34 | 62355||
| 749 | 27.367864366808 | ||
| 750 | 27.386127875258 | ||
| 751 | 27.40437 | 89||
| 752 | 27.422618401604 | ||
| 753 | 27.440845468024 | ||
| 754 | 27. 45 45 | ||
| 755 | 27.477263328068 | ||
| 756 | 27.4 | 169735||
| 757 | 27.5136325 | ||
| 758 | 27.5317997 | ||
| 759 | 27.549 | 7912||
| 760 | 27.568018 | ||
| 761 | 27,586228448267 | ||
| 762 | 27.604347483685 | ||
| 763 | 27.622454633866 | ||
| 764 | 27.640549 | ||
| 765 | 27. 658633371879 658633371879 | ||
| 766 | 27.676705006196 | ||
| 767 | 27.6 | 848252||
| 768 | 27.712812 | ||
| 769 | 27.73084 | 24 | |
| 770 | 27.748873851023 | ||
| 771 | 27.76688675383 | ||
| 772 | 27.7848879789 | ||
| 773 | 27.802877548916 | ||
| 774 | 27.820855486487 | ||
| 775 | 27.83882181415 | ||
| 776 | 27. 856776554368 856776554368 | ||
| 777 | 27.87471 33 | ||
| 778 | 27.8 | 361963 | |
| 779 | 27. | 1473906 | |
| 780 | 27. | ||
| 781 | 27. | 7224964 | |
| 782 | 27, | 29 | |
| 783 | 27. 7159266 | ||
| 784 | 28 | ||
| 785 | 28.017851452244 | ||
| 786 | 28.0356 | 752 | |
| 787 | 28. 053520278211 053520278211 | ||
| 788 | 28.0713376 | ||
| 789 | 28.08 | ||
| 790 | 28.106 | 511||
| 791 | 28.12472222085 | ||
| 792 | 28.1424 | ||
| 793 | 28.160255680657 | ||
| 794 | 28.178005607211 | ||
| 795 | 28.1 | 359743||
| 796 | 28.213471 | 2 | |
| 797 | 28.231188426986 | ||
| 798 | 28. 2488 2488 | ||
| 799 | 28.266588050205 | ||
| 800 | 28.284271247462 | ||
| 801 | 28.301 | 617 | |
| 802 | 28.31 | ||
| 803 | 28.33725463061 | ||
| 804 | 28.3548 | 516 | |
| 805 | 28.372521 | ||
| 806 | 28.3133157 | ||
| 807 | 28.407745422684 | ||
| 808 | 28.425340807104 | ||
| 809 | 28. 442 442 | ||
| 810 | 28.460498 | 5 | |
| 811 | 28.478061731796 | ||
| 812 | 28.4 | ||
| 813 | 28.513154858767 | ||
| 814 | 28.530685235374 | ||
| 815 | 28.54820484724 | ||
| 816 | 28.565713714171 | ||
| 817 | 28.583211855913 | ||
| 818 | 28.60069 | 5 | |
| 819 | 28.618176042508 | ||
| 820 | 28. 635642126553 635642126553 | ||
| 821 | 28.6530 789 | ||
| 822 | 28.670542373663 | ||
| 823 | 28.687 5562 | ||
| 824 | 28.705400188815 | ||
| 825 | 28.72281323269 | ||
| 826 | 28.7402157264 | ||
| 827 | 28.757607689097 | ||
| 828 | 28.77498 | 76||
| 829 | 28.7 | 0||
| 830 | 28. 8081776 8081776 | ||
| 831 | 28.827070610799 | ||
| 832 | 28.844410203712 | ||
| 833 | 28.86173 | 24 | |
| 834 | 28.87 | 56387 | |
| 835 | 28.8 | 5536||
| 836 | 28. | ||
| 837 | 28. | 2282979 | |
| 838 | 28. | ||
| 839 | 28. | ||
| 840 | 28. 34 | ||
| 841 | 29 | ||
| 842 | 29. 017236257094 017236257094 | ||
| 843 | 29.034462281916 | ||
| 844 | 29.0516780 | ||
| 845 | 29.068883707497 | ||
| 846 | 29.08607 | ||
| 847 | 29.10326442171 | ||
| 848 | 29.12043 | ||
| 849 | 29.137604568667 | ||
| 850 | 29.15475 | 27||
| 851 | 29.171163 | ||
| 852 | 29.1890353 | ||
| 853 | 29. 20616373302 20616373302 | ||
| 854 | 29.2232783 | ||
| 855 | 29.240383034427 | ||
| 856 | 29.257477676656 | ||
| 857 | 29.274562336609 | ||
| 858 | 29.2 | 031754 | |
| 859 | 29.308701779506 | ||
| 860 | 29.32575659723 | ||
| 861 | 29.342801502242 | ||
| 862 | 29.35 11806 | ||
| 863 | 29.376861643137 | ||
| 864 | 29. 3 3 | 8 | |
| 865 | 29.410882339705 | ||
| 866 | 29.427877 | 4||
| 867 | 29.444863728671 | ||
| 868 | 29.46183 12 | ||
| 869 | 29.478805 | 7||
| 870 | 29.4 | 407505||
| 871 | 29.51270 | 47 | |
| 872 | 29.52 | 20467 | |
| 873 | 29.546573405388 | ||
| 874 | 29.5634 | 189||
| 875 | 29. 580398 580398 | 8 | |
| 876 | 29.5972 897 | ||
| 877 | 29.614185789922 | ||
| 878 | 29.631064780058 | ||
| 879 | 29.647 | 0747||
| 880 | 29.6647 | 383||
| 881 | 29.681644159312 | ||
| 882 | 29.6 809835 | ||
| 883 | 29.715315 | 7||
| 884 | 29.7321374 | ||
| 885 | 29.748 | 1287||
| 886 | 29. 765752132274 765752132274 | ||
| 887 | 29.782545223671 | ||
| 888 | 29.79 | 51503||
| 889 | 29.816103031751 | ||
| 890 | 29.832867780353 | ||
| 891 | 29.84 | ||
| 892 | 29.8663636 | ||
| 893 | 29.8831055 | ||
| 894 | 29.89 75452 | ||
| 895 | 29. | 0603303 | |
| 896 | 29. | 92 | |
| 897 | 29. | ||
| 898 | 29, 8127543 | ||
| 899 | 29.870113 | ||
| 900 | 30 | ||
| 901 | 30.016662039607 | ||
| 902 | 30.033314835362 | ||
| 903 | 30.049 | 2633||
| 904 | 30.0665 | 746||
| 905 | 30.083217 | 3||
| 906 | 30.0986585 | ||
| 907 | 30. 1164406 1164406 | ||
| 908 | 30.133038346639 | ||
| 909 | 30.14 | ||
| 910 | 30.166206257997 | ||
| 911 | 30.182776545573 | ||
| 912 | 30.19 | 41083 | |
| 913 | 30.21588 76 | ||
| 914 | 30.232432 | 2||
| 915 | 30.248966 | 8||
| 916 | 30.265491 | 3||
| 917 | 30.282007859453 | ||
| 918 | 30. 2 2815086 | ||
| 919 | 30.315012782448 | ||
| 920 | 30.331501776206 | ||
| 921 | 30.3470987 | ||
| 922 | 30.364452 | 8 | |
| 923 | 30.380 | 1927||
| 924 | 30.3 307141 | ||
| 925 | 30.413812651491 | ||
| 926 | 30.430248109406 | ||
| 927 | 30.4466746 | ||
| 928 | 30.4630 | 456 | |
| 929 | 30. 47 47 | ||
| 930 | 30.495 | ||
| 931 | 30.5122 | 785||
| 932 | 30.528675044947 | ||
| 933 | 30.5450486 | ||
| 934 | 30,561413579872 | ||
| 935 | 30.57776 41 | ||
| 936 | 30.5 | 081557 | |
| 937 | 30.610455730028 | ||
| 938 | 30,626785662227 | ||
| 939 | 30.6431068 | ||
| 940 | 30. 65 65 | 33512||
| 941 | 30.675723300356 | ||
| 942 | 30.6 | 506446||
| 943 | 30.708305065568 | ||
| 944 | 30.7245829 | ||
| 945 | 30.7408522 | ||
| 946 | 30.7571129 | ||
| 947 | 30,773365106858 | ||
| 948 | 30.78 | 36681||
| 949 | 30.805843601499 | ||
| 950 | 30.822070014845 | ||
| 951 | 30. 8382878 8382878 | ||
| 952 | 30.8544 083 | ||
| 953 | 30.8706866 | ||
| 954 | 30.8868961 | ||
| 955 | 30.4280725 | ||
| 956 | 30. | ||
| 957 | 30, | 65 | |
| 958 | 30. | ||
| 959 | 30, 5134404 | ||
| 960 | 30,6769659 | ||
| 961 | 31 | ||
| 962 | 31. 016124838542 016124838542 | ||
| 963 | 31.0322412 | ||
| 964 | 31.04834 | 2 | |
| 965 | 31.06444 | 18||
| 966 | 31.08054053584 | ||
| 967 | 31.0610932 | ||
| 968 | 31.1126208 | ||
| 969 | 31.128764832547 | ||
| 970 | 31.144823004795 | ||
| 971 | 31.160872 | ||
| 972 | 31.176 | 624 | |
| 973 | 31. 1 1 | 4 | |
| 974 | 31.2088654 | ||
| 975 | 31.2249899 | ||
| 976 | 31.2409627 | ||
| 977 | 31.25699 | 76 | |
| 978 | 31.2729 | 224||
| 979 | 31.2889756 | ||
| 980 | 31.304 | 4997||
| 981 | 31.320 | 6732||
| 982 | 31.33687 | ||
| 983 | 31.352830813182 | ||
| 984 | 31. 368774282716 368774282716 | ||
| 985 | 31.38470 | 5 | |
| 986 | 31.400636 | ||
| 987 | 31.41655614481 | ||
| 988 | 31.4324672 | ||
| 989 | 31.448370387033 | ||
| 990 | 31.464265445105 | ||
| 991 | 31.480152477394 | ||
| 992 | 31.4 | 4 | |
| 993 | 31.511 | 3177 | |
| 994 | 31.527765540869 | ||
| 995 | 31.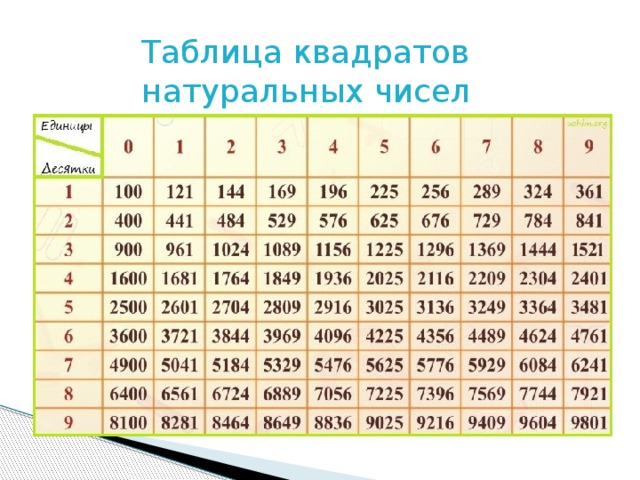 5436205 5436205 | ||
| 996 | 31.55 | 76119||
| 997 | 31.575306807694 | ||
| 998 | 31.5 | ||
| 999 | 31.606 | 8558 | |
| 1000 | 31.622776601684 |
В математике квадратным корнем из числа а называется такое число у, что у 2 = а; другими словами, число y, квадрат которого (результат умножения числа на себя, или y × y) равен a. Например, 4 и -4 являются квадратными корнями из 16, потому что 4 2 = (-4) 2 = 16,
Используя таблицу квадратных корней, найдите квадратные корни следующих 3509…
Перейти к
- Квадраты и квадратные корни.
 Упражнение 3.1.
Упражнение 3.1. - Квадраты и квадратные корни. Упражнение 3.2.
- Квадраты и квадратные корни. Упражнение 3.3.
- Квадраты и квадратные корни. Упражнение 3.4.
- Квадраты и квадратные корни. Упражнение 3.5.
- Квадраты и квадратные корни. Упражнение 3.6.
- Квадраты и квадратные корни.
 Упражнение 3.7.
Упражнение 3.7. - Квадраты и квадратные корни. Упражнение 3.8.
- Квадраты и квадратные корни. Упражнение 3.9.
- Рациональное число
- Полномочия
- Квадраты и квадратные корни
- Куб и кубические корни
- Игра с числами
- Алгебраические выражения и тождества
- Факторизация
- Отдел алгебраических выражений
- Линейное уравнение с одной переменной
- Прямые и обратные варианты
- Время и работа
- Процент
- Скидка на убыток и налог на добавленную стоимость
- Сложные проценты
- Понимание многоугольников фигур
- Понимание фигур Четырехугольники
- Понимание фигур Специальные типы четырехугольников
- Практическая геометрия
- Визуализация фигур
- Площадь трапеции и многоугольника
- Объем Площадь Прямоугольный Куб
- Площадь поверхности и объем правого кругового цилиндра
- Классификация и табулирование данных
- Классификация и табулирование данных Графическое представление данных в виде гистограмм
- Графическое представление данных в виде круговых диаграмм или круговых диаграмм
- Вероятность обработки данных
- Введение в графики
Главная >
РД Шарма Решения
Класс 8
Математика
>
Глава 3. Квадраты и квадратные корни
>
Квадраты и квадратные корни. Упражнение 3.9.
>
Вопрос 8
Квадраты и квадратные корни
>
Квадраты и квадратные корни. Упражнение 3.9.
>
Вопрос 8
Вопрос 8 Квадраты и квадратные корни Упражнение 3.9
Используя таблицу квадратных корней, найдите квадратные корни из следующего:
3509
Ответ:
Из известной нам таблицы квадратных корней,
Квадратный корень из 3509это:
√3509 = 59,2368
∴ Квадратный корень из 3509 равен 59,235
Стенограмма видео
[Музыка] помогите вам с этим, дорогой студент, я amita sun Задача, которая выглядит следующим образом: используя таблицу квадратного корня, найдите квадратный корень следующего числа, которое равно 3, пять, ноль, девять, поэтому, когда нам нужно найти квадратный корень числа, используя таблицу квадратного корня, мы начинаем с факторизации числа, которое вы правильно используя метод простой факторизации, поэтому мы должны найти множители простых множителей данного числа, поэтому давайте обнаружим, что out или, скорее, мы должны выразить число через его простые множители, поэтому простые множители 2 3 5 и 7 равны не [Музыка] данные числа не делятся ни на один из этих простых множителей 2 3 5 или 7 поэтому давайте попробуем 11 я думаю 11 произведений 11 3s это 33 11 единицы это 11 остаток от 9дает нам одну девятку еще один раз можно использовать одиннадцать, так что одиннадцать двоек — это двадцать два, остаток от девяти дает нам двадцать девять, и, как вы знаете, двадцать девять — это простое число, поэтому двадцать девять единиц — это двадцать девять, поэтому мы сделали факторизацию данного числа Теперь позвольте мне выразить это как произведение тех же самых факторов, так что 3509 равно 11 в квадрате, умноженному на 29. Теперь, если мне нужен квадратный корень из 3509, мне также нужно поставить знак квадратного корня справа от меня, так что правильно сторона стороны теперь я разделю, так что это станет квадратным корнем из 11 в квадрате, умноженным на квадратный корень из 29теперь квадратный корень из 11 в квадрате не что иное, как 11, а квадратный корень из 29, как вы можете видеть, находится в правой части левой части экрана. Я скопировал его из таблицы квадратных корней, поэтому квадратный корень из 29 равен 5,385. Итак, позвольте мне подставить это значение здесь, и я поставлю его как 11, умноженное на пять целых три восемь пять, поэтому давайте сделаем умножение пять целых три восемь пять, умноженное на одиннадцать, равно одиннадцати пятерок 55 11 8 из 11 8 равно 88 плюс 5 равно 93 3 переноса 9 11 3 — это 33, а 9 — это 42 2 переноса 4 одиннадцать пятерок — это 55, а 4 — это 59Итак, наш ответ 59,235, так что это квадратный корень из заданного числа 59,235 — это наш ответ, я надеюсь, вы поняли это объяснение, пожалуйста, оставьте комментарий в разделе комментариев и регулярно посещайте наш канал для получения дополнительных домашних заданий, которые вы также можете подписаться на канал спасибо
Теперь, если мне нужен квадратный корень из 3509, мне также нужно поставить знак квадратного корня справа от меня, так что правильно сторона стороны теперь я разделю, так что это станет квадратным корнем из 11 в квадрате, умноженным на квадратный корень из 29теперь квадратный корень из 11 в квадрате не что иное, как 11, а квадратный корень из 29, как вы можете видеть, находится в правой части левой части экрана. Я скопировал его из таблицы квадратных корней, поэтому квадратный корень из 29 равен 5,385. Итак, позвольте мне подставить это значение здесь, и я поставлю его как 11, умноженное на пять целых три восемь пять, поэтому давайте сделаем умножение пять целых три восемь пять, умноженное на одиннадцать, равно одиннадцати пятерок 55 11 8 из 11 8 равно 88 плюс 5 равно 93 3 переноса 9 11 3 — это 33, а 9 — это 42 2 переноса 4 одиннадцать пятерок — это 55, а 4 — это 59Итак, наш ответ 59,235, так что это квадратный корень из заданного числа 59,235 — это наш ответ, я надеюсь, вы поняли это объяснение, пожалуйста, оставьте комментарий в разделе комментариев и регулярно посещайте наш канал для получения дополнительных домашних заданий, которые вы также можете подписаться на канал спасибо
Похожие вопросы
Используя таблицу квадратных корней, найдите квадратные корни из следующего: 7
Используя таблицу квадратных корней, найдите квадратные корни из следующих чисел: 15
Используя таблицу квадратных корней, найдите квадратные корни следующего:74
Используя таблицу квадратных корней, найдите квадратные корни следующего:82
Используя таблицу квадратных корней, найдите квадратные корни следующего:198
Используя таблицу квадратных корней, найдите квадратные корни следующего: 540
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Квадраты и квадратные корни Упражнение 3. 1
1
Квадраты и квадратные корни Упражнение 3.2
Квадраты и квадратные корни Упражнение 3.3
Упражнения для квадратов и квадратных корней.
Рациональные числа
Степени
Квадраты и квадратные корни
Куб и кубические корни
Игра с числами
Алгебраические выражения и тождества
Факторизация
Отдел алгебраических выражений
Линейное уравнение в одной переменной
Прямые и обратные вариации
Время и работа
Процент
СКРЕДЕНИЯ ПОЛУЧЕНИЯ ПОЛУЧЕНИЯ
COMPOUNT CONTER
Понимание SHAPES
Compound Compound
Понимание Shapes. Понимание фигур Четырехугольники
Понимание фигур Специальные типы четырехугольников
Практическая геометрия
Визуализация фигур
Площадь трапеции и многоугольника
Объемная площадь поверхности прямоугольного куба
Площадь поверхности и объем прямого кругового цилиндра
Классификация и табулирование данных
Классификация и табулирование данных Графическое представление данных в виде гистограмм
Графическое представление данных В виде круговых диаграмм или круговых диаграмм
Вероятность обработки данных
Знакомство с диаграммами
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Квадратный корень
Основная информация
вторая мощность.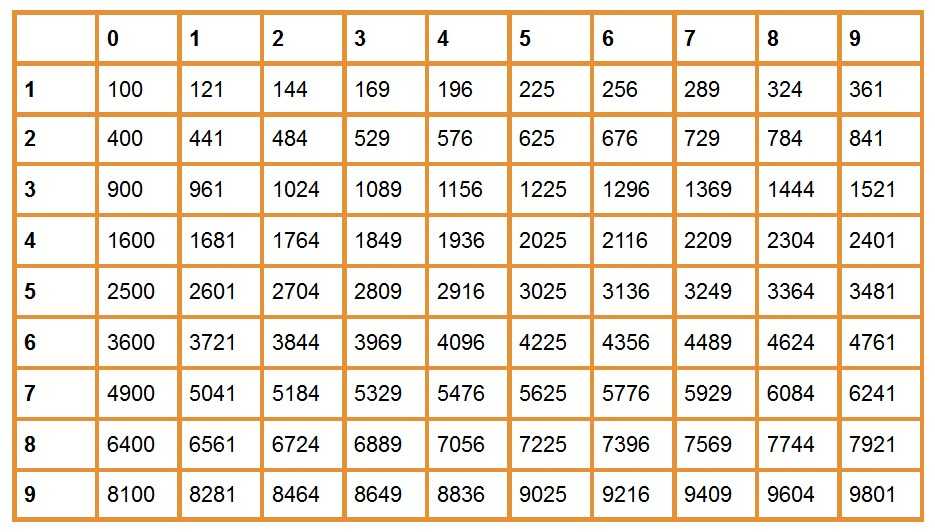
Найдите площадь квадрата со стороной 3 см
S = 3 2 = 9 см 2
. Теперь решим обратную задачу. А именно, зная площадь квадрата, найдем длину его стороны. Для этого воспользуемся таким инструментом как корень . Корнем может быть квадрат, куб или n-я степень .
Теперь нас интересует квадратный корень. Он также известен как корень второй степени .
Чтобы найти длину стороны нашего квадрата, нам нужно найти число, вторая степень которого равна 9. Это число 3. Это число корень .
Введем новый символ для работы с корнями.
Корневой символ выглядит как
. Это потому, что корень слова используется в математике как радикал . А слово радикал происходит от латинского radix (что означает корень). Первая буква слова по основанию — это r, которая позже была преобразована в корневой символ .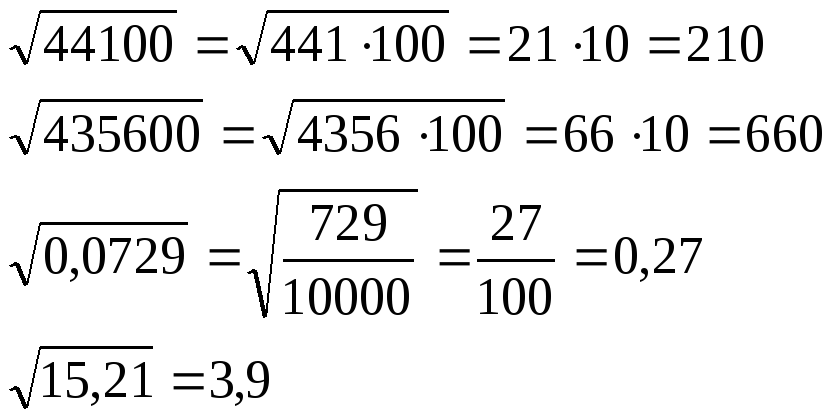
Под корнем находится подкорневое выражение. В нашем случае подкорневым выражением является число 9 (площадь квадрата).
Нас интересовал квадратный корень (он же корень второй степени), поэтому мы поставили цифру 2 слева над корнем. Это число называется индексом корня (или степенью корня)
Получили выражение, которое читается так: «квадратный корень из 9. С этого момента возникает новая задача найти сам корень.
Если число 3 возвести во вторую степень, то получится число 9. Следовательно, ответом является число 3:
Итак, квадрат площадью 9 см 2 имеет сторону, длина которой 3 см. Вышеприведенное действие называется извлечением квадратного корня .
Нетрудно догадаться, что квадратный корень из 9тоже отрицательное число -3. Его показатель степени во второй степени также дает число 9
. Оказывается, выражение
имеет два значения: 3 и -3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ только один, а именно 3.
Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ только один, а именно 3.
В общем случае квадратный корень имеет два противоположных значения: положительное и отрицательное.
Например, извлеките квадратный корень из числа 4
Это выражение имеет два значения: 2 и -2, потому что, если вы возведете эти числа во вторую степень, вы получите тот же результат 4
Следовательно, ответ на выражение вида
записывается с плюсом и минусом. Плюс и минус означают, что квадратный корень имеет два противоположных значения.
Запишите ответ на выражение
с плюсом и минусом:
Определения
Определим квадратный корень.
Квадратный корень из a равен a числу b , вторая степень которого равна и .
То есть число b должно быть таким, чтобы выполнялось равенство b 2 = a . Число b (он же корень) обозначается радикалом
Число b (он же корень) обозначается радикалом
таким образом, что . На практике левая и правая части меняются местами и мы видим обычное выражение
Например, квадратный корень из числа 16 равен числу 4, потому что число 4 во второй степени равно 16
4 2 = 16
Корень 4 можно обозначить радикалом
так что .
Также квадратный корень из 16 равен -4, так как -4 во второй степени равно 16
(−4) 2 = 16
Если при решении задачи интересует только положительное значение, то root называется не просто квадратным корнем, а арифметическим квадратным корнем .
Арифметический квадратный корень из a есть неотрицательное число b (b ≥ 0), при котором выполняется равенство b 2 = a .
В нашем примере квадратные корни числа 16 — это корни 4 и -4, но только корень из 4 является арифметическим.
В разговорном языке можно использовать аббревиатуру. Например, полное выражение
читается как « — квадратный корень из шестнадцати », а сокращенная версия — « — корень из шестнадцати ».
Термины корень и квадрат не следует путать. Квадрат — это число, которое является результатом возведения любого числа во вторую степень. Например, числа 25, 36, 49являются квадратами, потому что они являются результатом возведения чисел 5, 6 и 7 во вторую степень соответственно.
Корни 5, 6 и 7. Это те числа, которые во второй степени равны 25, 36 и 49 соответственно.
Чаще всего в квадратных корнях показатель степени корня вообще не указывается. Например, вместо записи
вы можете использовать обозначение . Если вы найдете корень без показателя степени в учебнике по математике, вы должны знать, что это квадратный корень.
Квадратный корень из единицы равен единице. То есть верно следующее равенство:
То есть верно следующее равенство:
Это потому, что единица во второй степени равна единице:
1 2 = 1
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:
Квадратный корень из нуля равен нулю. То есть равенство
верно, потому что 0 2 = 0.
Выражение вида
не имеет смысла. Например, выражение не имеет смысла, поскольку вторая степень любого числа является положительным числом. Невозможно найти число, у которого вторая степень равна -4.
Если выражение вида
возвести во вторую степень, то есть написать , то это выражение будет равно подкоренному выражению a
Например, выражение
равно 4
Это потому, что выражение
равно 2. Но это значение сразу возводится во вторую степень, и результат равен 4.
Но это значение сразу возводится во вторую степень, и результат равен 4.
Другие примеры:
Корень квадрата числа равен модулю этого числа:
Например, корень из числа 5, возведенный во вторую степень, равен модулю числа 5
Если отрицательное число возвести во вторую степень, ответ снова будет положительным. Например, корень из -5, возведенный во вторую степень, равен модулю -5. А модуль -5 равен 5
Действительно, если, не используя правило
, вычислить выражение обычным способом — сначала возведя число -5 во вторую степень, затем извлекая результат, мы получим ответ 5
Правило
не следует путать с правилом . Правило верно для любого a, а правило верно, если выражение имеет смысл.
В некоторых учебниках корневой знак может стоять без верхней строки. Это выглядит так:
Примеры: √4, √9, √16.
Меньшее число соответствует меньшему корню, большее число соответствует большему корню.
Например, рассмотрим числа 49и 64. Число 49 меньше числа 64.
49 < 64
Если извлечь из этих чисел квадратные корни, то числу 49 соответствует меньший корень, а числу 64 — больший корень. Действительно, √49 = 7, а √64 = 8,
√49 < √64
Отсюда:
7 < 8
Примеры извлечения квадратного корня
Давайте рассмотрим несколько простых примеров извлечения квадратного корня.
Пример 1. Извлеките квадратный корень из √36
Этот квадратный корень равен числу, квадрат которого равен 36. Это число 6, потому что 6 2 = 36.
√36 = 6
Пример 2. Извлеките квадратный корень из √49
Этот квадратный корень равен числу, квадрат которого равен 49. Это число 7, потому что 7 2 = 49.
√49 = 7
В таких простых примерах достаточно знать таблицу умножения. Например, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
Например, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
7 × 7 = 49
, но 7 × 7 равен 7 2
7 2 = 49
Следовательно, √49 = 7.
Пример 3. Извлеките квадратный корень √1003
.
Этот квадратный корень равен числу, квадрат которого равен 100. Это число 10, потому что 10 2 = 100
√100 = 10
Число 100 — это последнее число, корень которого можно извлечь с помощью умножения стол. Для чисел больше 100 квадратные корни можно найти с помощью таблицы квадратов.
Пример 4. Извлеките квадратный корень из √256
Этот квадратный корень представляет собой число, квадрат которого равен 256. Чтобы найти это число, воспользуйтесь таблицей квадратов.
Найдите в таблице квадратов число 256 и, двигаясь от него влево и вверх, определите цифры, из которых состоит число, квадрат которого равен 256
Мы видим, что это число равно 16. Значит, √256 = 16.
Значит, √256 = 16.
Пример 5. Найдите значение выражения 2√16
В этом примере число 2 умножается на выражение с корнем. Сначала вычислите корень √16, затем умножьте его на число 2. 4.
Значение переменной x равно 16, потому что
. Итак, корень уравнения равен 16.
Примечание. Корень уравнения не следует путать с квадратным корнем. Корень уравнения — это значение переменной, при котором уравнение преобразуется в допустимое числовое равенство. А квадратный корень — это число, вторая степень которого равна выражению под корнем .
Подобные примеры решаются с использованием определения квадратного корня. Давайте сделаем то же самое.
Из определения мы знаем, что квадратный корень из
равен числу b, при котором выполняется равенство b 2 = a.
Применим равенство b 2 = a к нашему примеру
. Переменная b это число 4, а переменная a это выражение под корнем , а именно переменная х
Переменная b это число 4, а переменная a это выражение под корнем , а именно переменная х
В выражении 4 2 = х вычисляем левую часть, получаем 16 = х. Поменяем местами левую и правую части, и получим x = 16. В результате найдем значение переменной x.
Пример 7. Решить уравнение
Перенесем -8 вправо, поменяв знак:
Возведем правую часть во вторую степень и приравняем к переменной х
900 правая часть, получаем 64 = x. Поменяем местами левую и правую части, получим x = 64. Итак, корень уравнения
— это 64.
Пример 8. Решите уравнение
Давайте воспользуемся определением квадратного корня:
Переменная b — это число 7, а переменная b — подкоренное выражение 3 + a 9. Возведем число 7 во вторую степень и приравняем его к 3 + 5х
В выражении 7 2 = 3 + 5х вычислим левую часть и получим 49 = 3 + 5х. Это обычное линейное уравнение. Решите это:
Это обычное линейное уравнение. Решите это:
Корень уравнения
равен . Проверим это, подставив в исходное уравнение:
Пример 9. Найдите значение выражения
В этом выражении число 2 умножается на квадратный корень из числа 49.
Сначала извлеките квадратный корень и умножьте его на число 2
Приблизительное значение квадратного корня
Не каждый квадратный корень можно извлечь. Вы можете извлечь квадратный корень, только если сможете найти число, вторая степень которого равна подкорневому выражению.
Например, вы можете извлечь квадратный корень из
, потому что вы можете найти число, вторая степень которого равна квадратному выражению подкореня. Это число 8, потому что 8 2 = 64. То есть
И из
нельзя извлечь квадратный корень, потому что невозможно найти число, вторая степень которого равна 3. В данном случае это сказал, что квадратный корень из числа 3 не может быть извлечен.
В данном случае это сказал, что квадратный корень из числа 3 не может быть извлечен.
Но можно извлечь квадратный корень из числа 3 из приближение . Приблизительно извлечь квадратный корень означает найти значение, которое во второй степени будет как можно ближе к подкорневому выражению.
Аппроксимированное значение ищется с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и т.д.
Найдите значение корня
приблизительно с точностью до десятых. Фраза «с точностью до десятых» указывает на то, что приблизительное значение корня будет представлять собой десятичную дробь с одной цифрой после запятой.
Сначала найдем ближайшее меньшее число, корень которого можно извлечь. Это число 1. Корень этого числа равен самому числу:
√1 = 1
Аналогичным образом найдите ближайшее большее число, корень которого можно извлечь. Это число 4. Корень этого числа равен 2
√4 = 2
√1 меньше √4
√1 < √4
И √3 больше √1, но меньше √4 . Запишем это в виде двойного неравенства:
Запишем это в виде двойного неравенства:
√1 < √3 < √4
Точные значения корней √1 и √4 известны. Это числа 1 и 2
1 < √3 < 2
Тогда очевидно, что значение корня √3 будет десятичным, так как между числами 1 и 2 нет целых чисел.
Чтобы найти приблизительное значение квадратного корня из √3, мы проверим десятичные дроби между 1 и 2, возведя их в квадрат. Мы будем делать это до тех пор, пока не получим значение, максимально близкое к 3. Давайте проверим, например, дробь 1,1
1,1 2 = 1,21
Результат равен 1,21, что не очень близко к 3. Таким образом, 1,1 не подходит в качестве приближения для квадратного корня из √3, потому что оно мало.
Проверим тогда дробь 1,8
1,8 2 = 3,24
Получится 3,24, что близко к подкорневому выражению, но превышает его на 0,24. Таким образом, 1,8 не подходит в качестве приближения к корню √3, потому что оно велико.
Тогда проверим дробь 1,7
1,7 2 = 2,89
Получится 2,89, что уже близко к примерному подкорневому выражению. Таким образом, 1,7 — это приблизительное значение квадратного корня из √3. Напомним, что знак аппроксимации имеет вид ≈
Таким образом, 1,7 — это приблизительное значение квадратного корня из √3. Напомним, что знак аппроксимации имеет вид ≈
√3 ≈ 1,7
Значение 1,6 проверять не нужно, потому что результат равен 2,56, что на три дальше, чем значение 2,89. А значение 1,8, как было показано ранее, уже велико.
В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение может быть получено еще более точно. Для этого его нужно найти с точностью до сотых.
, чтобы найти значение в пределах сотых, проверьте десятичные десятички между 1,7 и 1,8
1,7 <√3 <1,8
Давайте проверьте фракцию 1,74
1,74 2 = 3,0276
Результат 3,0276, что является близко к подкорневому выражению, но превышает его на 0,0276. Таким образом, значение 1,74 велико для корня √3.
Проверим дробь 1,73
1,73 2 = 2,9929
В результате получится 2,9929, что близко к подкоренному выражению √3. Таким образом, 1,73 будет приближением к квадратному корню из √3 с точностью до сотых.
Процесс нахождения приблизительного значения квадратного корня продолжается бесконечно. Таким образом, корень √3 можно найти с точностью до тысячных, десятитысячных и т. д.:
√3 = 1,732 (с точностью до тысячных)
√3 = 1,7320 (с точностью до десятитысячных)
√ 3 = 1,73205 (оценивается с точностью до сотен тысячных).
Еще один квадратный корень можно извлечь из целых чисел. Аппроксимированное значение квадратного корня √3 в целых числах равно единице:
√3 ≈ 1
Значение 2 было бы слишком большим, поскольку возведение этого числа во вторую степень дает число 4, которое больше, чем подкорневое выражение. Нас интересуют значения, которые при возведении во вторую степень равны подкоренному выражению или максимально близки к нему, но не превышают его.
В зависимости от поставленной задачи допускается найти значение, вторая степень которого больше квадратного корня. Это значение называется приблизительным значением квадратного корня с избытком. Поговорим об этом подробнее.
Поговорим об этом подробнее.
Приближенное значение квадратного корня с недостатком и избытком
Иногда может возникнуть задача, требующая найти приближенное значение корня с недостатком или избытком.
В предыдущей теме мы нашли примерное значение корня √3 с точностью до десятых с дефицитом. Дефицит понимается в том смысле, что нам не хватило еще каких-то частей до значения 3. Таким образом, найдя приблизительное значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, потому что, если вы возведете это число во вторую степень, вы получите результат 2,89.. Этому результату не хватает еще 0,11, чтобы получить число 3. То есть 2,89 + 0,11 = 3.
Избыточные значения — это приближения, которые при возведении во вторую степень дают результат, превышающий подкорневое выражение. Например, вычислив в качестве приближения корень √3, мы проверили значение 1,8. Это значение является аппроксимацией корня √3 с точностью до десятых, поскольку возведение 1,8 во второй степени дает 3,24. Этот результат превышает выражение подкорня на 0,24. То есть 3,24 — 3 = 0,24.
Этот результат превышает выражение подкорня на 0,24. То есть 3,24 — 3 = 0,24.
Приблизительное значение квадратного корня √3 из целых чисел также было найдено с недостатком:
√3 ≈ 1
Это потому, что когда вы возводите единицу в квадрат, вы получаете единицу. То есть цифра 3 все-таки два коротких.
Аппроксимированное значение квадратного корня √3 также можно найти с точностью до ближайшего целого числа с превышением. Тогда этот корень аппроксимируется как 2
√3 ≈ 2
Это потому, что если вы возведете 2 в квадрат, вы получите 4. Число 4 больше выражения подкореня 3 на единицу. При приближении квадратного корня с избытком желательно указать, что корень извлекается с избытком:
√3 ≈ 2 (с избытком)
Потому что приближение чаще ищут с недостатком, чем с избытком.
Дополнительно следует отметить, что в некоторых учебниках фразы «с точностью до целого», «с точностью до десятой», «с точностью до сотой» заменены на «с точностью до 1», «с точностью до 0,1».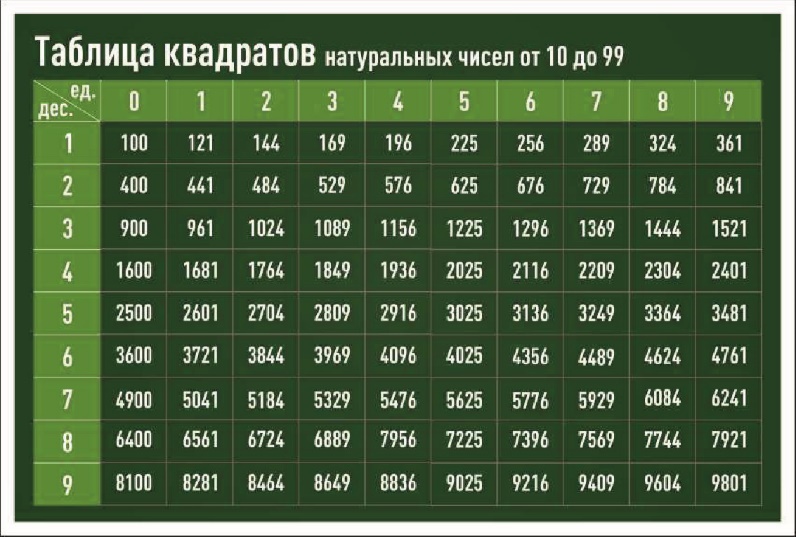 «, «с точностью до 0,01» соответственно.
«, «с точностью до 0,01» соответственно.
Например, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это означает, что корень нужно извлечь примерно с точностью до сотых:
√5 ≈ 2,23
Пример 2. Извлечение квадратного корня от 51 до ближайшего 1
√51 ≈ 7
Пример 3. Извлечение квадратного корня из 51 до ближнего 0,1
. Пример 4. Извлечь квадратный корень из 51 с точностью до 0,01 ; 100], то квадратный корень из этого начального числа будет принадлежать интервалу [1; 10]. Например, пусть начальное число равно 64. Это число принадлежит интервалу [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать интервалу [1; 10]. Теперь вспомните таблицу умножения. Какое умножение двух одинаковых множителей дает 64? Ясно, что умножение 8 × 8 равно 8 2 = 64. Таким образом, квадратный корень из 64 равен 8.
0002 Число 49 принадлежит интервалу [1; 100]. Таким образом, квадратный корень принадлежит интервалу [1; 10]. Этот корень равен числу 7, потому что 7 2 = 49
√49 = 7
Пример 2. Извлеките квадратный корень из числа 1
Число 1 принадлежит интервалу [1; 100]. Таким образом, квадратный корень принадлежит интервалу [1; 10]. Этот корень равен 1, потому что 1 2 = 1
√1 = 1
Пример 3. Извлеките квадратный корень из 100
Число 100 принадлежит интервалу [1; 100]. Таким образом, квадратный корень принадлежит интервалу [1; 10]. Квадратный корень равен 10, так как 10 2 = 100
√100 = 10
Ясно, что интервал [1; 100] также содержит числа, из которых нельзя извлечь квадратные корни. Для таких чисел корень надо извлечь примерно. Однако приближенный корень также будет лежать в интервале [1; 10].
Например, извлеките квадратный корень из числа 37. Не существует целого числа, вторая степень которого равна 37. Следовательно, извлечение квадратного корня должно быть приближенным. Извлеките его с точностью до сотых:
Не существует целого числа, вторая степень которого равна 37. Следовательно, извлечение квадратного корня должно быть приближенным. Извлеките его с точностью до сотых:
√37 ≈ 6,08
Чтобы было проще, можно найти ближайшее меньшее число, из которого извлекается корень. В данном примере это было число 36. Квадратный корень из него равен 6. Затем, начиная с числа 6, мы можем найти приблизительное значение корня √37, сверяя различные десятичные дроби, целая часть которых равна 6.
Квадраты числа от 1 до 10 надо знать наизусть. Ниже приведены эти квадраты:
1 2 = 1
2 2 = 4
3 2 = 9
4 2 = 16
5 2 = 25
6 2 = 36
7 2 = 49
8 2 = 64
9 0007 2
7 2 = 64
2 = 81
29 2 = 64
2
7 2 = 64
2 2 = 64
9 2
2 = 64
9 2
2 = 64
9 0007 2
2 = 100
И наоборот, надо знать значения квадратных корней из этих квадратов:
второй степени, то в полученном числе будет в два раза больше нулей.
Например, 6 2 = 36. Прибавьте один ноль к числу 6, чтобы получить 60. Возведите 60 во вторую степень, чтобы получить 3600.
60 2 = 3600
6 и возведя его во вторую степень, вы получите число с четырьмя нулями. То есть в два раза больше нулей:
600 2 = 360000
Тогда можно сделать следующий вывод:
Если исходное число содержит квадрат и четное количество нулей, можно извлечь квадратный корень из это число. Для этого извлеките квадратный корень из известного нам квадрата и затем запишите половину количества нулей от исходного числа.
Например, извлекаем квадратный корень из числа 900. Видим, что это число имеет знакомый нам квадрат 9. Извлекаем из него квадратный корень, и получаем 3
Теперь из исходного числа выпишем половину количество нулей. Исходное число 900 содержит два нуля. Половина этого количества нулей составляет один ноль. Запишите его в ответе после цифры 3
Пример 2. Извлеките квадратный корень из
Извлеките квадратный корень из
Здесь мы снова имеем знакомый квадрат 9и четное количество нулей. Извлеките корень из 9 и запишите половину количества нулей. Исходное число содержит четыре нуля. Половина этого количества нулей составляет два нуля:
Пример 3. Извлеките квадратный корень из 36000000
Здесь у нас есть знакомый квадрат 36 и четное количество нулей. Извлеките корень из числа 36 и запишите половину количества нулей. Исходное число имеет шесть нулей. Половина — это три нуля:
Пример 4. Извлечение квадратного корня из 2500
Здесь у нас есть знакомый квадрат 25 и четное количество нулей. Извлеките корень из числа 25 и запишите половину количества нулей. Исходное число имеет два нуля. Половина равна одному нулю:
Если число подкореня увеличить (или уменьшить) на 100, 10000, то корень увеличится (или уменьшится) соответственно в 10, 100 раз.
Например,
. Если мы увеличим номер подкореня в 100 раз, квадратный корень увеличится в 10 раз:
Если мы увеличим номер подкореня в 100 раз, квадратный корень увеличится в 10 раз:
Обратно, если в равенстве
уменьшить число подкореня в 100 раз, то квадратный корень уменьшится в 10 раз:
Пример 2. Увеличьте число подкореня в равенстве
на 10000, тогда квадратный корень из 70 увеличится в 100 раз.
Пример 3. Уменьшите номер подкорня
в 100 раз, тогда квадратный корень из 70 уменьшится в 10 раз.
Этот шаблон позволяет извлечь квадратный корень из десятичной дроби, если рассматриваемая дробь содержит две цифры после точки, и эти две цифры образуют знакомый нам квадрат. В таких случаях умножьте данное десятичное число на 100. Затем извлеките квадратный корень из полученного числа и уменьшите подкоренное число в сто раз.
Например, извлеките квадратный корень из числа 0,25.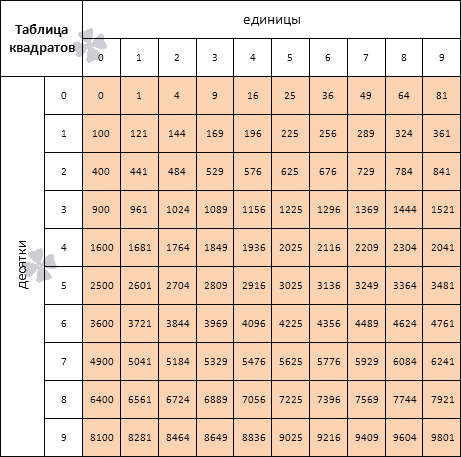 Это десятичное число имеет две цифры после точки, и эти две цифры образуют знакомый квадрат 25.
Это десятичное число имеет две цифры после точки, и эти две цифры образуют знакомый квадрат 25.
Умножьте десятичное число 0,25 на 100, чтобы получить 25. И квадратный корень из 25 извлечь легко:
Но изначально нам нужно было извлекаем корень из 0,25, а не из 25. Чтобы исправить ситуацию, возвращаем нашу десятичную дробь. Если мы уменьшим число подкореня в 100 раз, то получим 0,25 под корнем и ответ уменьшится в 10 раз:
Обычно в таких случаях достаточно уметь двигать точку. Потому что сдвиг точки числа вправо на две цифры аналогичен умножению этого числа на 100.
В предыдущем примере можно было сдвинуть точку вправо на две цифры в подчиненном числе 0,25, но в результирующем ответе , вы можете переместить его влево на одну цифру .
Например, извлеките корень из числа 0,81. Мысленно сдвигаем точку вправо на две цифры, получаем 81. Теперь извлекаем квадратный корень из 81 и получаем 9. В ответе 9 сдвинем точку влево на одну цифру, получим 0,9. Итак,
Итак,
.
Это правило работает и в ситуации, когда за точкой следуют четыре цифры, и эти цифры образуют знакомый нам квадрат.
Например, десятичное число 0,1225 содержит четыре цифры после точки. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.
Тогда мы можем извлечь квадратный корень из 0,1225. Умножьте это десятичное число на 10000, чтобы получить 1225. Квадратный корень из 1225 можно извлечь с помощью таблицы квадратов:
Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, уменьшим число подкореня в равенстве
в 10000 раз. В итоге десятичная дробь 0,1225 формируется под корнем, а правая часть уменьшается в 100 раз
Тот же шаблон будет работать для извлечения корней из дробей типа 12,25. Если цифры, составляющие десятичную дробь, образуют знакомый нам квадрат с четным числом цифр после запятой, мы можем извлечь корень из десятичной дроби.
Умножьте десятичное число 12,25 на 100, чтобы получить 1225. Извлеките корень из 1225
Теперь в равенстве
уменьшите число подкореня в 100 раз. В результате число под корнем равно 12,25, и, соответственно, ответ уменьшается в 10 раз.
Если исходное число принадлежит интервалу [100; 10000], то квадратный корень из этого начального числа будет принадлежать интервалу [10; 100].
В этом случае применяется таблица квадратов:
Например, пусть начальное число 576. Это число принадлежит интервалу [100; 10000]. Сразу заключаем, что квадратный корень из 576 принадлежит диапазону [10; 100]. Теперь откройте таблицу квадратов и посмотрите, какое число во второй степени равно 576
Мы видим, что это число равно 24. Итак,
.
Пример 2. Извлеките квадратный корень из 432.
Число 432 принадлежит интервалу [100; 10000]. Поэтому квадратный корень следует искать в интервале [10; 100]. Откройте таблицу квадратов и посмотрите, какое число во второй степени равно 432. Мы находим, что числа 432 нет в таблице квадратов. В этом случае квадратный корень надо искать приближенно.
Поэтому квадратный корень следует искать в интервале [10; 100]. Откройте таблицу квадратов и посмотрите, какое число во второй степени равно 432. Мы находим, что числа 432 нет в таблице квадратов. В этом случае квадратный корень надо искать приближенно.
Извлеките квадратный корень из 432 с точностью до десятых.
В таблице квадратов ближайшим числом к 432 является 400. Квадратный корень из него равен 20. Начиная с числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.
Проверим, например, число 20,8. Для этого возведем в квадрат:
20,8 2 = 432,64
Получится 432,64, что больше исходного числа 432 на 0,64. Мы видим, что значение 20,8 велико для корня √432. Проверим тогда значение 20,7
20,7 2 = 428,49
В качестве корня подойдет значение 20,7, так как при возведении этого числа в квадрат получается число 428,49, что меньше исходного числа 432, но близко к нему. Итак, √432 ≈ 20,7
Не нужно запоминать интервалы, чтобы узнать, в каких границах находится корень. Можно воспользоваться методом нахождения ближайших квадратов с четным числом нулей в конце.
Можно воспользоваться методом нахождения ближайших квадратов с четным числом нулей в конце.
Например, извлеките корень из числа 4225. Мы знаем ближайший наименьший квадрат 3600 и ближайший больший квадрат 4900
3600 < 4225 < 4900
Извлеките квадратные корни из чисел 3600 и 4900. числа 60 и 70 соответственно:
Тогда видно, что квадратный корень из 4225 находится между 60 и 70. Его можно найти даже методом поиска. Корни 60 и 70 исключаются сразу, так как они являются корнями чисел 3600 и 4900. Тогда можно проверить, например, корень 64. Возвести его в квадрат (или умножить это число само на себя)
Корня 64 нет хороший. Проверим корень 65
Получается 4225. Значит 65 это корень из 4225.
Идентичные преобразования с квадратными корнями
С квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.
Квадратный корень произведения
Квадратный корень произведения является выражением формы
, где a и b некоторые числа.
Например, выражение
представляет собой квадратный корень из произведения 4 и 9.
Чтобы извлечь такой квадратный корень, вы должны отдельно извлечь квадратные корни из множителей 4 и 9, представляя выражение
как произведение корней . Если мы вычислим эти корни по отдельности, мы получим произведение 2 × 3, что равно 6.
Конечно, можно избежать подобных манипуляций и сначала вычислить подкорневое выражение 4 × 9, равное 36. Затем извлечь квадратный корень из 36
Но при извлечении квадратных корней из больших чисел, это правило может быть очень полезным.
Предположим, вы хотите извлечь квадратный корень из 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12
Но представим, что таблицы квадратов под рукой нет. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составляют числа, из которых извлекаются квадратные корни.
В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составляют числа, из которых извлекаются квадратные корни.
Итак, разложим число 144 на простые множители:
Получилось следующее разложение:
Разложение содержит четыре двойки и две тройки. Все числа в расширении перемножаются. Это позволяет представить произведения одинаковых множителей в виде степени с показателем 2.
Тогда четыре двойки можно заменить на запись 2 2 × 2 2 , а две тройки заменить на 3 2
В результате получим следующее разложение:
Теперь можно извлечь квадратный корень из разложения 144
Применить правило извлечения квадратного корня из произведения:
Ранее было сказано, что если подкоренное выражение возвести в второй степени, то этот квадратный корень равен модулю подкорневого выражения.
Тогда вы получите произведение 2 × 2 × 3, равное 12
Простые множители представлены в виде степени для удобства и краткости. Допускается также записывать их под корень как есть, чтобы потом их умножение давало новые множители.
Допускается также записывать их под корень как есть, чтобы потом их умножение давало новые множители.
Таким образом, разложив 144 на простые множители, мы получим разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под корнем как оно есть:
затем перемножить некоторые из множителей так что извлекаются квадратные корни. В этом случае можно умножить две двойки дважды и две тройки один раз:
Затем примените правило извлечения квадратного корня из произведения и получите окончательный ответ:
Вы можете использовать правило извлечения квадратного корня для извлечения квадратного корня из произведения и других больших чисел. Сюда входят числа, которых нет в квадратной таблице.
Например, извлеките квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.
Итак, разложим число 13456 на простые множители:
В разложении четыре двойки и два числа 29. Двойки представлены дважды как 2 2 . А два числа 29 представлены как 29 2 . В результате получаем следующее разложение 13456
Двойки представлены дважды как 2 2 . А два числа 29 представлены как 29 2 . В результате получаем следующее разложение 13456
Теперь извлечем квадратный корень из разложения 13456
Итак, если a ≥ 0 и b ≥ 0, то
. То есть корень произведения неотрицательных множителей равен произведению корней этих множителей.
Докажем равенство
. Для этого воспользуемся определением квадратного корня.
По определению квадратный корень из а есть число b , при котором выполняется равенство b 2 = .
В нашем случае нужно убедиться, что правая часть равенства
при возведении во вторую степень даст подкорневое выражение левой части, то есть выражение аб .
Итак, запишем правую часть равенства
и возведем во вторую степень:
Теперь воспользуемся правилом возведения произведения в степень. Согласно этому правилу каждый множитель данного произведения должен быть возведен в указанную степень:
Согласно этому правилу каждый множитель данного произведения должен быть возведен в указанную степень:
Ранее было сказано, что если выражение вида
возвести во вторую степень, мы получим подкоренное выражение . Применим это правило. Тогда получаем аб . Это подкорневое выражение квадратного корня из
Это означает, что равенство
верно, потому что при возведении правой части во вторую степень получается подкорневое выражение левой части.
Правило извлечения квадратного корня из произведения также работает, если под корнем более двух множителей. То есть справедливо следующее уравнение:
, когда a ≥ 0 и b ≥ 0, c ≥ 0.
Пример 1. Найдите значение квадратного корня
Запишите корень
как произведение корней, извлеките их, а затем найдите значение произведения:
Пример 2. Найдите значение квадратного корня
Найдите значение квадратного корня
Представим число 250 как произведение 25 и 10. Сделаем это под корнем: множители 10 и 10 под корнем. Умножьте их, и вы получите 100
Тогда применим правило извлечения квадратного корня из произведения и получим окончательный ответ:
Пример 3. Найдем значение квадратного корня власть к власти. Представим мощность 11 4 в виде (11 2 ) 2 .
Теперь воспользуемся правилом извлечения квадратного корня из квадрата числа:
В нашем случае квадратный корень (11 2 ) 2 будет 11 2 . Проще говоря, внешний показатель степени 2 исчезнет, а внутренний показатель останется:
Затем возведем число 11 во вторую степень и получим окончательный ответ:
Этот пример также можно решить с помощью правило извлечения квадратного корня из произведения. Для этого запишите подкорневое выражение 11 4 как произведение 11 2 × 11 2 . Затем извлеките квадратный корень из этого произведения:
Затем извлеките квадратный корень из этого произведения:
Пример 4. Найдите значение квадратного корня
Перепишем степень 3 4 в виде (3 2 ) 2 2 в виде 6
, а степень 7 5 3 ) 2Далее используем правило извлечения квадратного корня из произведения:
Далее используем правило извлечения квадратного корня из квадрата числа:
Вычислите произведение результирующих мощностей и получите окончательный ответ:
Множители под корнем могут быть десятичными. Например, извлеките квадратный корень из произведения
. Запишите корень из
как произведение корней, извлеките их, затем найдите значение полученного произведения:
Пример 6. Найти значение квадратного корня0011 умножить на число n , а второй множитель равен разделить на это число n , тогда произведение не изменит .
Например, произведение 8 × 4 равно 32
8 × 4 = 32
Умножьте множитель 8, скажем, на число 2, и разделите множитель 4 на то же число 2. Тогда вы получить произведение 16 × 2, что также равно 32.
(8 × 2) × (4 : 2) = 32
Это свойство полезно при решении некоторых задач извлечения квадратного корня. Множители подкорневого выражения можно умножать и делить так, чтобы из них извлекались корни.
Например, извлеките квадратный корень из произведения
. Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то нельзя извлечь корни √1,6 и √90, потому что они неизвлекаемые.
Анализируя подкорневое выражение 1,6 × 90, мы видим, что если первый множитель 1,6 умножить на 10, а второй множитель 90 разделить на 10, то произведение равно 16 × 9. Из такого произведения квадратный корень можно извлечь, используя правило извлечения квадратного корня из произведения.
Запишем полное решение этого примера:
Процесс умножения и деления можно выполнять в уме. Вы также можете пропустить подробные обозначения извлечения квадратного корня из каждого частного. Тогда решение становится короче:
Пример 9. Найдите значение квадратного корня
Умножьте первый множитель на 10 и разделите второй на 10. Тогда под корнем образуется произведение 36 × 0,04, из которого извлекается квадратный корень:
Если поменять местами левую и правую части равенства
, получится равенство . Это преобразование позволяет упростить вычисление некоторых корней.
Например, узнать значение выражения
.
Из чисел 10 и 40 нельзя извлечь квадратные корни. Воспользуемся правилом
, то есть заменим выражение из двух корней выражением с одним корнем, при котором будет произведение чисел 10 и 40
Теперь найдем значение произведения под корнем:
И извлечем квадратный корень из числа 400. Оно равно 20
Оно равно 20
Множители под корнем можно разложить на множители, сгруппировать, представить в виде степени и умножить для получения новых множителей, из которых извлекаются корни.
Например, найдите значение выражения
.
Воспользуемся правилом
Множитель 32 равен 2 5 . Представим этот множитель в виде 2 × 2 4
Умножьте множители 2 и 2, чтобы получить 4. И давайте представим множитель 2 4 в виде степени с индексом 2
3 Теперь воспользуемся правилом и вычислить окончательный ответ: Пример 12. Найдите значение выражения
Воспользуемся правилом0003
Теперь под корнем четыре двойки и две семерки. Четыре двойки можно записать как 2 2 × 2 2 , а две семерки как 7 2
Теперь воспользуемся правилом
и вычислим окончательный ответ:
Квадратный корень из дроби
Квадратный корень из
— это дробь, числитель которой представляет собой квадратный корень из из , а знаменатель — квадратный корень из б .
Например, квадратный корень из дроби
— это дробь, числитель которой равен квадратному корню из 4, а знаменатель — квадратному корню из 9.
Вычислите квадратные корни в числителе и знаменателе:
Таким образом, квадратный корень дроби
равен .
Докажем, что равенство
верно.
Возведем правую часть во вторую степень. Если результат составляет дробь от
, это означает, что равенство истинно:
Пример 1. Извлеките квадратный корень из
Используйте правило извлечения квадратного корня из дроби:
Преобразуйте из 2. Извлеките квадратный корень из
-корень выражения в неправильную дробь, затем используем правило извлечения квадратного корня из дроби: Пример 3. Извлеките квадратный корень из
Извлеките квадратный корень из
Квадратный корень из 0,09 равен 0,3. Но можно извлечь этот корень, используя правило извлечения квадратного корня из дроби.
Представим подкорневое выражение в виде дроби. 0,09 это девять сотых:
Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:
Пример 4. Найти значение выражения
Извлечь корни из 0,59 , затем сложите результаты:
Можно также воспользоваться правилом извлечения квадратного корня из дроби:
В данном примере первый способ был проще и удобнее.
Пример 5. Найти значение выражения
Сначала вычислить квадратный корень, затем умножить его на 10. Вычесть результат из 4.
Пример 6. Найти выражение
Сначала найдите значение квадратного корня из
. Это 0,6, так как 0,6 2 = 0,36.
Теперь вычислим полученное выражение. Согласно порядку операций, мы должны сначала выполнить умножение, затем сложение:
Вынесение множителя из-под корня
В некоторых задачах может быть полезно вынести множитель из-под знака корня.
Возьмем квадратный корень из произведения
. Согласно правилу извлечения квадратного корня из произведения, вы должны извлечь квадратный корень из каждого множителя произведения:
В нашем примере квадратный корень извлекается только из множителя 4. Мы извлекаем его и оставляем выражение
без изменений:
Это число , вынесенное из-под корневого знака .
На практике подкорневое выражение чаще всего необходимо разложить на множители.
Пример 2. Вынести множитель из-под знака корня в выражении
Разложить подкоренное выражение на множители 9и 2.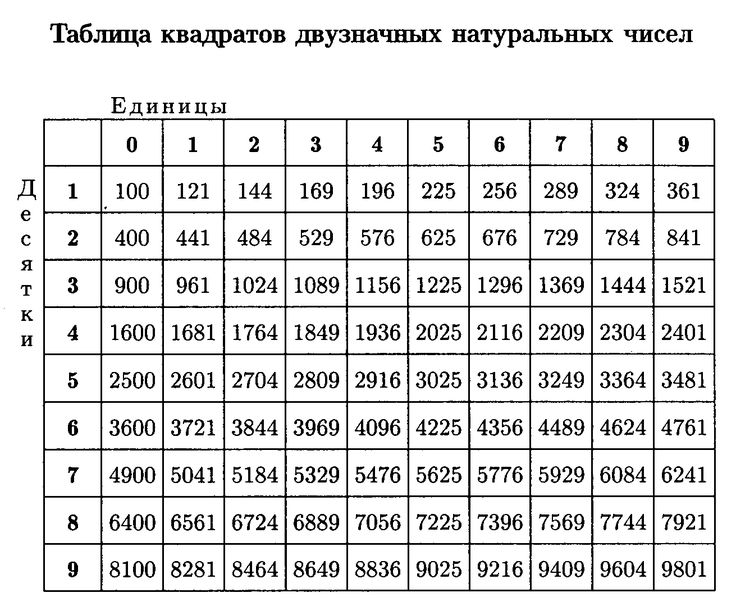 Тогда получаем:
Тогда получаем:
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Можно извлечь только корень фактора 9. Оставить множитель 2 под корнем:
Пример 3. Вынести множитель из-под знака корня в выражении
Разложить подкоренное выражение на множители 121 и 3. Тогда получим:
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Можно извлечь только корень множителя 121. Оставьте выражение √3 под корнем:
Пример 4. Вынести множитель из-под знака корня в выражении
Использовать правило извлечения квадратного корня из произведения:
Квадратный корень извлекается только из числа 121. Извлеките его, а выражение √15 оставьте без изменений:
Получается, что множитель 11 вынесен из-под знака корня. Удаляемый множитель принято писать перед выражением с корнем. Поменяйте местами выражения √15 и 11:
Пример 5. Вынести множитель из-под знака корня в выражении
Вынести множитель из-под знака корня в выражении
Разложить подкоренное выражение на множители 4 и 3
Использовать правило извлечения квадратного корня произведения:
Извлечем корень из числа 4 и оставим выражение √3 без изменений:
Пример 6. Упростим выражение
Представим второе слагаемое
как . А третье слагаемое можно представить в виде
Теперь в выражениях
и , вынесем множитель из-под корня:
Во втором слагаемом
умножьте числа -4 и 4. Перепишем остаток слагаемого без изменений:
Обратите внимание, что квадратный корень из √3 является общим множителем в результирующем выражении. Выносим за скобки:
Вычисляем содержимое скобок, получаем -1
Если множитель равен -1, записывается только минус.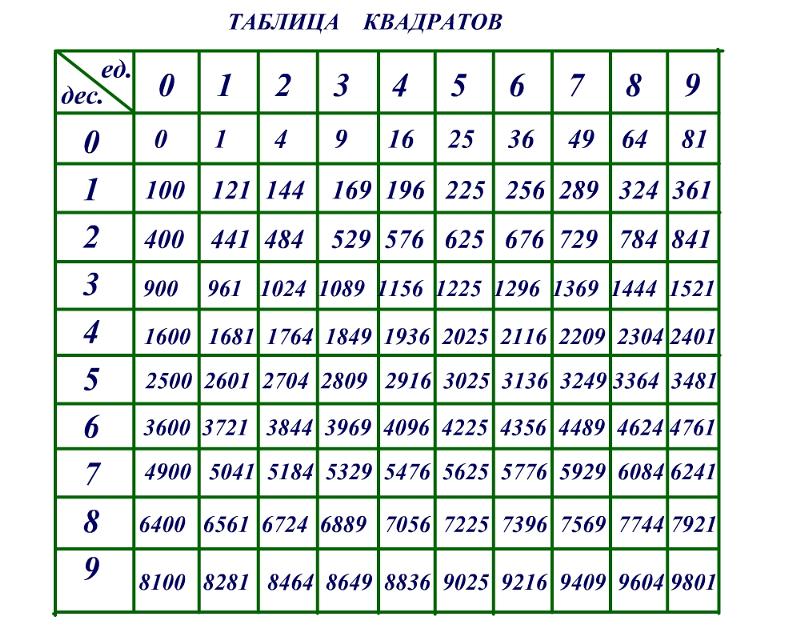 Один опущен. Тогда окончательный ответ будет -√3
Один опущен. Тогда окончательный ответ будет -√3
. Поставьте множитель под знаком корня
. Рассмотрим следующее выражение:
В этом выражении число 5 умножается на квадратный корень из числа 9. Найти значение этого выражения.
Сначала извлеките квадратный корень, затем умножьте его на число 5.
Квадратный корень из 9равно 3. Умножаем его на число 5. Тогда получаем 15
Число 5 в данном случае было множителем. Поставим этот множитель под знаком корня. Но сделать это нужно так, чтобы значение исходного выражения не изменилось в результате наших действий. Проще говоря, поставив под знаком корня множитель 5, результирующее выражение все равно должно быть 15.
Значение выражения не изменится, если число 5 возвести во вторую степень и только потом поставить под корень :
Итак, если дано выражение
и вы хотите поставить множитель a под знаком корня, то вы должны возвести множитель а во вторую степень и положить его под корень:
Пример 1.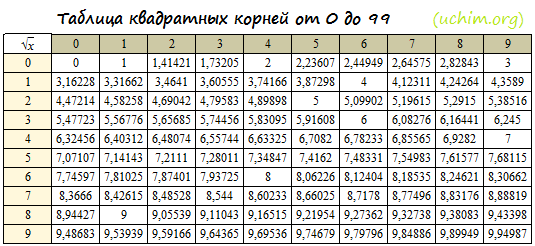 Поставьте множитель под знаком корня выражения
Поставьте множитель под знаком корня выражения
Возведите число 7 во вторую степень и поставьте под знаком корня:
Пример 2. Поставьте множитель под знаком корня выражения 9Пример 3. признак корня. Ранее было сказано, что выражение вида
не имеет смысла.
Однако, если перед знаком корня стоит отрицательный множитель, то минус можно оставить за знаком корня, а само число поставить под знаком корня.
Пример 4. Под знаком корня выражения ставится множитель
В этом примере под знаком корня ставится только 3. Минус остается за знаком корня:
Пример 5. Возведение в степень в следующем выражении:
Используйте формулу квадрата суммы двух выражений:
( 9002 ) 2 = а 2 + 2 аб + b 2
Переменная a в данном случае равна √3, а переменная b равна √2:
Теперь нужно упростить полученное выражение.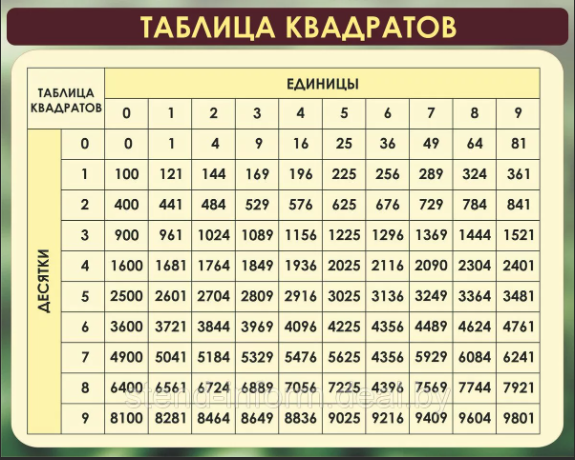
Для выражений
и будем применять правило . Ранее мы говорили, что если выражение вида возвести во вторую степень, то это выражение равно подкорневому выражению а.
А в выражении
для коэффициентов и применяем правило . То есть заменить произведение корней одним общим корнем:
Приведем подобные термины. В этом случае мы можем сложить термы 3 и 2. И в терме
вычислить произведение, которое находится под корнем:
Задачи для самостоятельного решения
Задача 1. Найти значение квадратного корня:
Решение:
Показать Решение
Задача 2. Найти значение квадратного корня: 90 0002 Решение: 9 0 0 0 0 3: 9 0 0 0 0 3
Показать решение
Задача 3. Найти значение квадратного корня:
Решение:
Показать решение
Задача 4. Найти значение выражения:
Решение:
Показать решение
Задача 5.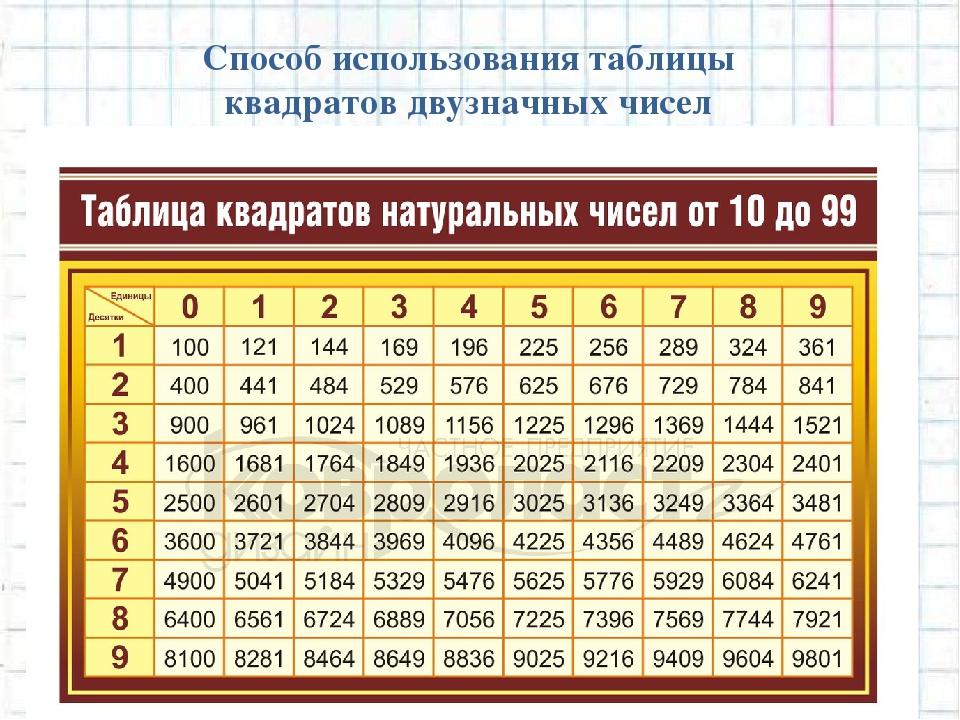 Найти значение квадратного корня:
Найти значение квадратного корня:
Решение:
2 Показать 3
2 Решение2
Задача 6. Найдите значение квадратного корня:
Решение:
Показать решение
Задача 7. Найдите значение квадратного корня:
Решение:
Показать решение
Задача 8. Найдите значения следующие выражения:
Solution:
Show Solution
Task 9. Extract the square root of the number 4624
Solution:
Show Solution
Task 10. Extract the square root of the number 11025
Solution:
Показать решение
Задача 11. Найти значение квадратного корня:
Решение:
Показать решение
Задача 12. Найти значение квадратного корня:
Решение:
Показать решение
Задача 13. Найти значение квадратного корня:
Решение:
Показать решение
Задача 14. Найти значение квадратного корня:
Решение:
Показать решение
2 Задача 14. Найти значение квадратного корня:
Найти значение квадратного корня: Решение: Найдите значение квадратного корня:
Решение:
Показать решение
Задача 16. Найдите значение выражения:
Решение:
Показать решение
Задача 17. Найдите значение выражения:
Решение:
Показать решение
Задача 18. Найти значение выражения:
Решение:
Показать решение
Задача 19. Найти значение выражения:
Показать решение:
Показать решение:
Задача 20. Найдите значение выражения:
Решение:
Показать решение
Задача 21. Найдите значение выражения:
Решение:
Показать решение
Задача 22. Найдите значение выражения:
Решение:
Показать решение
Задача 23. Найти значение выражения:
Решение:
Показать решение
Задача 24. Найти значение выражения:
Показать решение:
Показать решение:
Решение:
Показать решение Задача 25. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Задача 26. Найдите значение выражения:
Решение:
Показать решение
Задача 27. Найдите значение выражения:
Решение:
Показать решение
Задача 28. Найти значение выражения:
Решение:
Показать решение
Задача 29. Найти значение выражения:
Показать решение:
Показать решение:
Решение:
Показать решение Задача 30. Найдите значение выражения:
Решение:
Показать решение
Задача 31. Найдите значение выражения:
Решение:
Показать решение
Задача 32. Найдите значение выражения:
Решение:
Показать решение
Задача 33. Найти значение выражения:
Решение:
Показать решение
Задача 34. Вынести множитель из-под корня знак:
Решение:
3 Показать . Решение
Задача 35. Вынести множитель из-под корня:
Решение:
Показать решение
Задача 36. Вынести множитель из-под корня:
Вынести множитель из-под корня:
Решение:
Показать решение
Задача 37. Вынести множитель из-под корня:
Решение:
Показать решение
Задача 38. Вынести множитель из-под корня:
Решение:
Показать решение
Задача 39 Вынести множитель из-под корня:
Решение:
Показать решение
Задача 40. Вынести множитель из-под корня:
Решение:
Показать решение
Задача 41. Вынести множитель из-под знака корня:
Решение:
Показать решение
Задача 42. Вынести множитель из-под корня:
Решение:
Показать решение
Задача 43. Вынести множитель из-под корня:
Решение:
Показать решение
Задача 44. Вынести множитель из-под корня в следующих выражениях:
Решение:
Показать решение
Задача 45. Подставить множитель под знаком корня:
Решение:
Показать Решение
Задача 46. Подставить множитель под корень знак:
Подставить множитель под корень знак:
Решение:
Показать Решение
Задача 47. Подставить множитель 90 Решение 90: под корень 900: знак 90: 0: под 900
Показать решение
Задача 48. Подставить множитель под знак корня:
Решение:
Показать решение
Задача 49. Подставить множитель под знак корня:
Решение:
Показать решение
Задача 50. Поставить множитель под знаком корня в следующих выражениях:
Решение:
Показать решение
Задача 51. Упростить выражение:
Показать решение:
2
Задача 52. Упростить выражение:
Решение:
Показать решение
Задача 53. Упростить выражение:
Решение:
Показать решение
Задача 54. Упростить выражение:
Решение:
Показать решение
Задача 55. Упростить выражение:
Решение:
Показать решение
Задача 56. Упростить выражение:
Упростить выражение:
Решение:
Показать решение
Задача 57. Упростить выражение выражения :
Решение:
Показать решение
Задача 58. Упростить выражение:
Решение:
Показать решение
Задача 59. Упростить выражение:
Решение:
Показать решение
Задача 60. Упростить выражение:
Решение:
Показать решение
Квадратные корни и логарифмы без калькулятора (Часть 3) – Mean Green Math
John Quintanilla История, Предварительное исчисление 5 Минут
Я в середине серии постов об элементарной операции вычисления квадратного корня. Это такая элементарная операция, потому что почти у каждого калькулятора есть кнопка, и сегодня студенты привыкли быстро получать ответ, не задумываясь над тем, (1) что означает ответ или (2) какую магию калькулятор использует для нахождения квадратных корней. . Мне нравится показывать моим будущим учителям средней школы краткую историю по этой теме… отчасти для того, чтобы углубить их знания о том, что они, вероятно, считают простой концепцией, но также и для того, чтобы дать им небольшую оценку старшим.
. Мне нравится показывать моим будущим учителям средней школы краткую историю по этой теме… отчасти для того, чтобы углубить их знания о том, что они, вероятно, считают простой концепцией, но также и для того, чтобы дать им небольшую оценку старшим.
Сегодняшняя тема — использование таблиц журналов. Я предполагаю, что многие читатели либо забыли, как пользоваться таблицами журналов, либо их даже не учили, как их использовать. После демонстрации того, как логарифмические таблицы использовались в прошлом, я закончу некоторыми мыслями об их эффективности для обучения студентов логарифмам в первый раз.
Это будет довольно длинный пост о таблицах журналов. В следующем посте я расскажу, как можно использовать таблицы журналов для вычисления квадратных корней.
Для начала снова вернемся во времена до появления карманных калькуляторов… скажем, 1912.
До появления карманных калькуляторов у большинства профессиональных ученых и инженеров были математические таблицы для хранения значений логарифмов, тригонометрических функций и т. п. Следующие изображения взяты из одной из моих ценных вещей: College Mathematics, Kaj L. Nielsen (Barnes & Noble, New York, 1958). Какой-то святой дал мне эту книгу в детстве в конце 1970-х; поверьте мне, он был сильно изношен к тому времени, когда я поступил в колледж.
п. Следующие изображения взяты из одной из моих ценных вещей: College Mathematics, Kaj L. Nielsen (Barnes & Noble, New York, 1958). Какой-то святой дал мне эту книгу в детстве в конце 1970-х; поверьте мне, он был сильно изношен к тому времени, когда я поступил в колледж.
С появлением дешевых карманных калькуляторов математические таблицы ушли в прошлое. Единственное место, где какие-либо общепринятые математические таблицы появляются в современном использовании, — это учебники по статистике, в которых указаны площади и критические значения нормального распределения, распределения Стьюдента и тому подобного.
Тем не менее, математические таблицы не пережиток далекого прошлого. Когда я изучал логарифмы и тригонометрические функции в школе в начале 1980-х — одно поколение назад — я отчетливо помню, что в моем школьном учебнике были эти таблицы в конце книги.
И я твердо убежден, что в качестве упражнения по истории таблицы журналов все еще можно использовать сегодня, чтобы углубить навыки учащихся в логарифмах. В этом посте и в части 4 этой серии я обсуждаю, как можно использовать логарифмическую таблицу для вычисления логарифмов и (используя язык прошлых поколений) антилогарифмов без калькулятора. В части 5 я выскажу свое мнение о педагогической пользе логарифмических таблиц, даже несмотря на то, что сегодня логарифмы проще вычислять с помощью научных калькуляторов. В части 6 я вернусь к квадратным корням, а именно к тому, как можно использовать логарифмические таблицы для нахождения квадратных корней.
В этом посте и в части 4 этой серии я обсуждаю, как можно использовать логарифмическую таблицу для вычисления логарифмов и (используя язык прошлых поколений) антилогарифмов без калькулятора. В части 5 я выскажу свое мнение о педагогической пользе логарифмических таблиц, даже несмотря на то, что сегодня логарифмы проще вычислять с помощью научных калькуляторов. В части 6 я вернусь к квадратным корням, а именно к тому, как можно использовать логарифмические таблицы для нахождения квадратных корней.
Как пользоваться таблицей, Часть 1. Как вы читаете эту таблицу? Крайний левый столбец показывает цифру единиц и цифру десятых, а верхний ряд показывает цифру сотых. Так, например, нижняя строка показывает десять различных логарифмов по основанию 10:
Таким образом, вместо того, чтобы вводить числа в калькулятор, для нахождения этих логарифмов использовалась таблица. Вы заметите, что эти значения с точностью до четырех знаков после запятой совпадают со значениями, найденными на современном калькуляторе.
Как пользоваться таблицей, Часть 2. Что, если мы пытаемся возвести логарифм числа между и, которое имеет более двух знаков после запятой, например ? Из таблицы мы знаем, что значение должно лежать между
и
Таким образом, для оценки мы будем использовать линейную интерполяцию. Это причудливый способ сказать: «Найдите линию, соединяющую и , и найдите точку на линии с координатой . График $y = \log_{10} x$, конечно, не является прямой линией, но мы надеемся, что эта линейная интерполяция будет достаточно близка к правильному ответу.
Нахождение этой линии представляет собой простое упражнение в форме точки-наклона линии:
Помня, что эта логарифмическая таблица верна только до четырех значащих цифр, мы оцениваем .
Немного потренировавшись, можно относительно легко выполнять приведенные выше расчеты. Кроме того, во многих таблицах журналов прошлого был столбец под названием «пропорциональные части», который по существу заменял шаг линейной интерполяции, что значительно ускоряло использование таблицы.
Опять же, это соответствует результату современного калькулятора с точностью до четырех знаков после запятой:
Как пользоваться таблицей, Часть 3 . До сих пор мы обсуждали логарифмы чисел между и и антилогарифмы чисел между и . Давайте теперь рассмотрим, что произойдет, если мы выберем число за пределами этих интервалов.
Чтобы найти , мы видим, что
Интуитивно мы знаем, что ответ должен лежать между и , поэтому ответ должен быть . Значение является необходимым.
Затем мы находим линейной интерполяцией. Из таблицы мы видим, что
и
Используя линейную интерполяцию, мы находим
Помня, что эта логарифмическая таблица верна только до четырех значащих цифр, мы оцениваем , так что .
Опять же, это соответствует результату современного калькулятора до четырех знаков после запятой (в данном случае пяти значащих цифр):
Как пользоваться таблицей, Часть 4 . Теперь рассмотрим, что произойдет, если мы выберем положительное число меньше . Чтобы найти , заметим, что
Теперь рассмотрим, что произойдет, если мы выберем положительное число меньше . Чтобы найти , заметим, что
Мы уже нашли линейной интерполяцией. Таким образом, мы заключаем, что . Опять же, это соответствует результату современного калькулятора с точностью до четырех знаков после запятой (в данном случае пяти значащих цифр):
Итак, вот как вычислять логарифмы без калькулятора: мы полагаемся на чью-то тяжелую работу, чтобы вычислить эти числа. логарифмы (которые поколение назад можно было найти в конце каждого учебника по математическому анализу), и мы умело используем законы логарифмов и линейной интерполяции.
Таблицы журнала, конечно, подвержены ошибкам округления. (Если на то пошло, то же самое можно сказать и о карманных калькуляторах, но округление происходит так глубоко в десятичном представлении — 12-й или 13-й цифре, — что учащиеся почти никогда не замечают ошибку округления и, таким образом, могут выработать досадную привычку думать, что результат калькулятора всегда точно правильный. )
)
Для двухстраничной таблицы, найденной в школьном учебнике, результаты обычно были точными до четырех значащих цифр. Профессиональные инженеры и ученые, однако, нуждались в большей точности, и поэтому у них было целых книг таблиц. Для таблицы с 5 степенями точности потребуется около 20 печатных страниц, а для таблицы с 6 степенями точности потребуется около 200 печатных страниц. В самом деле, если вы обратитесь к старым и пыльным книгам любой приличной университетской библиотеки, вы сможете найти эти старые книги с математическими таблицами.
Другими словами, именно так был построен Бруклинский мост в эпоху, когда еще не было карманных калькуляторов.
В этот момент вы можете спросить: «Хорошо, мне не нужно использовать калькулятор, чтобы использовать таблицу журнала. Но вернемся на шаг. Как значения в таблице журнала были рассчитаны без калькулятора?» Это вполне резонный вопрос, но этот пост и так становится достаточно длинным. Возможно, я затрону этот вопрос в следующем посте.
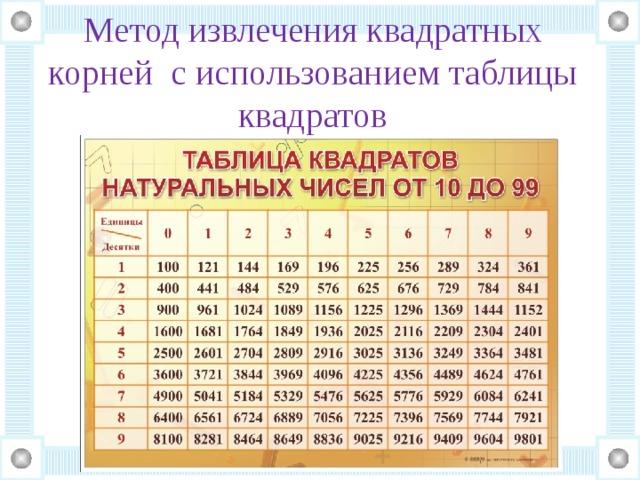 Найдите значение выражения:
Найдите значение выражения: Вынести множитель из-под корня:
Вынести множитель из-под корня: Подставить множитель под корень знак:
Подставить множитель под корень знак: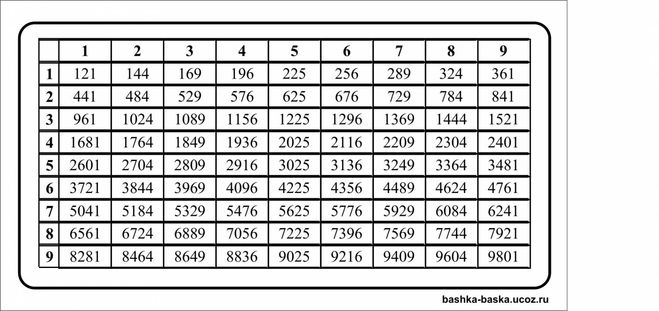 Упростить выражение:
Упростить выражение: . Мне нравится показывать моим будущим учителям средней школы краткую историю по этой теме… отчасти для того, чтобы углубить их знания о том, что они, вероятно, считают простой концепцией, но также и для того, чтобы дать им небольшую оценку старшим.
. Мне нравится показывать моим будущим учителям средней школы краткую историю по этой теме… отчасти для того, чтобы углубить их знания о том, что они, вероятно, считают простой концепцией, но также и для того, чтобы дать им небольшую оценку старшим.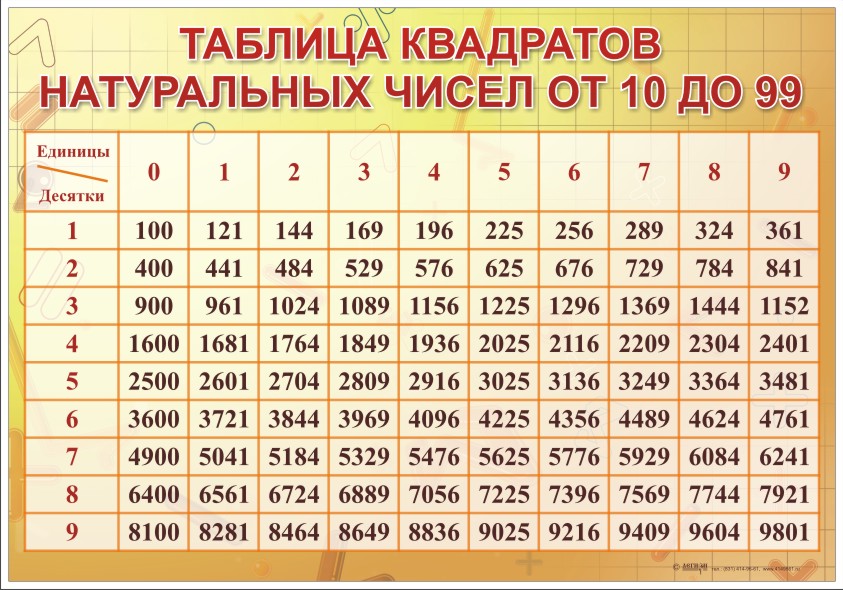 п. Следующие изображения взяты из одной из моих ценных вещей: College Mathematics, Kaj L. Nielsen (Barnes & Noble, New York, 1958). Какой-то святой дал мне эту книгу в детстве в конце 1970-х; поверьте мне, он был сильно изношен к тому времени, когда я поступил в колледж.
п. Следующие изображения взяты из одной из моих ценных вещей: College Mathematics, Kaj L. Nielsen (Barnes & Noble, New York, 1958). Какой-то святой дал мне эту книгу в детстве в конце 1970-х; поверьте мне, он был сильно изношен к тому времени, когда я поступил в колледж. В этом посте и в части 4 этой серии я обсуждаю, как можно использовать логарифмическую таблицу для вычисления логарифмов и (используя язык прошлых поколений) антилогарифмов без калькулятора. В части 5 я выскажу свое мнение о педагогической пользе логарифмических таблиц, даже несмотря на то, что сегодня логарифмы проще вычислять с помощью научных калькуляторов. В части 6 я вернусь к квадратным корням, а именно к тому, как можно использовать логарифмические таблицы для нахождения квадратных корней.
В этом посте и в части 4 этой серии я обсуждаю, как можно использовать логарифмическую таблицу для вычисления логарифмов и (используя язык прошлых поколений) антилогарифмов без калькулятора. В части 5 я выскажу свое мнение о педагогической пользе логарифмических таблиц, даже несмотря на то, что сегодня логарифмы проще вычислять с помощью научных калькуляторов. В части 6 я вернусь к квадратным корням, а именно к тому, как можно использовать логарифмические таблицы для нахождения квадратных корней.

 Теперь рассмотрим, что произойдет, если мы выберем положительное число меньше . Чтобы найти , заметим, что
Теперь рассмотрим, что произойдет, если мы выберем положительное число меньше . Чтобы найти , заметим, что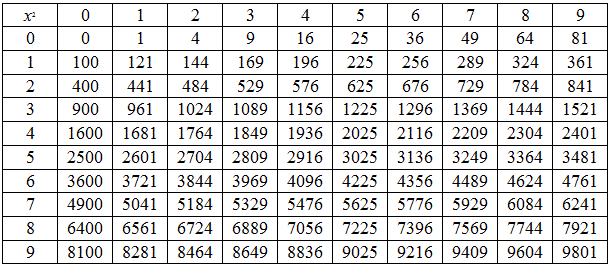 )
)

 …) + Таблицы Брадиса / / Таблица квадратов — таблица квадратных корней натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ). Таблица квадратных корней. Квадраты чисел. Корни чисел.
…) + Таблицы Брадиса / / Таблица квадратов — таблица квадратных корней натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ). Таблица квадратных корней. Квадраты чисел. Корни чисел. Введите свой запрос:
Введите свой запрос:


 Р. Дорофеев
Р. Дорофеев В. и др. Сборник тестовых заданий для тематического и итогового контроля. Алгебра 8 класс.- М: «Интеллект-Центр», 2006.
В. и др. Сборник тестовых заданий для тематического и итогового контроля. Алгебра 8 класс.- М: «Интеллект-Центр», 2006.
 Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Проверка на калькуляторе дает нам ответ 5,92 — мы были правы. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70». Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
Напишите найденное n сверху справа, а квадрат n запишите снизу справа. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
 То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8 Разложите всё по пунктам и пронумеруйте их. Плюс: объясните откуда в каждом действии мы подставляем нужные значения. Никогда раньше не вычислял корень в столбик – разобрался с трудом.
Разложите всё по пунктам и пронумеруйте их. Плюс: объясните откуда в каждом действии мы подставляем нужные значения. Никогда раньше не вычислял корень в столбик – разобрался с трудом. Я собираюсь написать как раз о том, как находить кубический корень.
Я собираюсь написать как раз о том, как находить кубический корень. Вот и получается как по наиболее цитируемому в былые времена бородатому философу: традиции всех мертвых поколений подавляют сознание живых.
Вот и получается как по наиболее цитируемому в былые времена бородатому философу: традиции всех мертвых поколений подавляют сознание живых. после первого вычитания не получается продолжить всё по алгоритму. Объясните пожалуйста.
после первого вычитания не получается продолжить всё по алгоритму. Объясните пожалуйста.
 Я применяю более просто метод, основанный на разложении квадратичной функции с помощью первых двух производных. Формула его такая:
Я применяю более просто метод, основанный на разложении квадратичной функции с помощью первых двух производных. Формула его такая:
 В школьной программе способ данного вычисления без привлечения дополнительных средств должен иметь место наравне с умножением и делением в столбик. Алгоритм вычисления должен быть не только запоминаемым, но и понятным. Классический метод, предоставленный в данном материале для обсуждения с раскрытием сущности, в полной мере соответствует вышеназванным критериям.
В школьной программе способ данного вычисления без привлечения дополнительных средств должен иметь место наравне с умножением и делением в столбик. Алгоритм вычисления должен быть не только запоминаемым, но и понятным. Классический метод, предоставленный в данном материале для обсуждения с раскрытием сущности, в полной мере соответствует вышеназванным критериям. Калькуляторы сейчас встроены в устройства, запрещенные к применению на ЕГЭ.
Калькуляторы сейчас встроены в устройства, запрещенные к применению на ЕГЭ. дюймов. Найдите длину стороны металлического листа.
дюймов. Найдите длину стороны металлического листа. Упражнение 3.1.
Упражнение 3.1. Упражнение 3.7.
Упражнение 3.7. Найти значение квадратного корня:
Найти значение квадратного корня: