Меню сайта Форма входа ИНФОРМАЦИЯ На данный момент в школе учатся 1300 детей На данный момент свободные мест в школе нет количество 1-х классов — 5, 10-х классов — 1 (с профильными группами: социально-экономический и социально-педагогический) Вакансии на данный момент: | Билет №1 1.Десятичная запись дробных чисел. Примеры. 2.Понятие множества. Примеры. 3. Задание: тип№2 стр.8 Билет №2 Билет №3 Билет №4 2.Графики. 3.Задание: тип 36 стр. 20 Билет №5 Билет№6 Билет №7 Билет №8 Билет №9 Билет №10 Билет №11 Билет №12 Билет №13 Билет №14 Билет №15 Билет №16 Билет №17 Билет №18 Билет №19 Билет №20 Билет №21 Билет №22 1.Пропорциональное деление Билет №23 Билет №24 Билет №25 3.Задание: тип 4, стр.154 | Block title внимание полезные ссылки Минпросвещения РФ Министерство науки и высшего образования РФ Федеральный портал «Российское образование» Единое окно доступа к образовательным ресурсам Единая коллекция цифровых образовательных ресурсов Федеральный центр информационно образовательных ресурсов Сайт Управления образования г-к Анапа портал Президентской библиотеки Присоединяйтесь к официальной группе Вконтакте официальная группа ЕГЭ Вконтакте Календарь
Архив записей Сайт обновлен | ||||||||||||||||||||||||||||||||||||||||||||
01Математика — 6 класс.
 Математика — Деление натуральных чисел на трехзначные числа
Математика — Деление натуральных чисел на трехзначные числа- Решение
- Видеорешение
1. Умножим \(\displaystyle 351\) на \(\displaystyle 1{\small:}\)
\(\displaystyle 351=351 \cdot {\bf 1}{\small.}\)
| \(\displaystyle 4\) | \(\displaystyle 6\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | |
| \(\displaystyle –\) | ||||||||
| \(\displaystyle \bf 3\) | \(\displaystyle \bf 5\) | \(\displaystyle \bf 1\) | \(\displaystyle \bf 1\) | \(\displaystyle 3\) | \(\displaystyle 2\) | |||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | |||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | |||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle 0\) |
2. Вычитаем:
Вычитаем:
\(\displaystyle 463-351={\bf 112}{\small.}\)
| \(\displaystyle 4\) | \(\displaystyle 6\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | |
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle 2\) | |||
| \(\displaystyle \bf 1\) | \(\displaystyle \bf 1\) | \(\displaystyle \bf 2\) | \(\displaystyle {\small?}\) | |||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | |||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle 0\) |
Сносим десятки числа \(\displaystyle 463{\bf 3}2\) (это цифра \(\displaystyle 3{\small:}\))
| \(\displaystyle 4\) | \(\displaystyle 6\) | \(\displaystyle 3\) | \(\displaystyle \bf 3\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | |
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle 2\) | |||
| \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle \bf 3\) | |||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | |||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle 0\) |
3. Умножаем \(\displaystyle 351\) на \(\displaystyle 3{\small:}\)
Умножаем \(\displaystyle 351\) на \(\displaystyle 3{\small:}\)
\(\displaystyle 1053=351 \cdot {\bf 3}{\small.}\)
| \(\displaystyle 4\) | \(\displaystyle 6\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | |
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle \bf 3\) | \(\displaystyle 2\) | |||
| \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | |||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle \bf 1\) | \(\displaystyle \bf 0\) | \(\displaystyle \bf 5\) | \(\displaystyle \bf 3\) | |||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle 0\) |
4. Вычитаем:
Вычитаем:
\(\displaystyle 1123-1053={\bf 70}{\small.}\)
| \(\displaystyle 4\) | \(\displaystyle 6\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | |
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle 2\) | |||
| \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | |||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 1\) | \(\displaystyle 0\) | \(\displaystyle 5\) | \(\displaystyle 3\) | |||||
| \(\displaystyle \bf 7\) | \(\displaystyle \bf 0\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle 0\) |
Сносим единицы числа \(\displaystyle 4633{\bf 2}\) (это цифра \(\displaystyle 2{\small:}\))
| \(\displaystyle 4\) | \(\displaystyle 6\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle \bf 2\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | |
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle 2\) | |||
| \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | |||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 1\) | \(\displaystyle 0\) | \(\displaystyle 5\) | \(\displaystyle 3\) | |||||
| \(\displaystyle 7\) | \(\displaystyle 0\) | \(\displaystyle \bf 2\) | ||||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | \(\displaystyle {\small?}\) | ||||||
| \(\displaystyle 0\) |
5. Умножаем \(\displaystyle 351\) на \(\displaystyle 2{\small:}\)
Умножаем \(\displaystyle 351\) на \(\displaystyle 2{\small:}\)
\(\displaystyle 702=351 \cdot {\bf 2}.\)
| \(\displaystyle 4\) | \(\displaystyle 6\) | \(\displaystyle 3\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | |
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 3\) | \(\displaystyle 5\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 3\) | \(\displaystyle \bf 2\) | |||
| \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | |||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle 1\) | \(\displaystyle 0\) | \(\displaystyle 5\) | \(\displaystyle 3\) | |||||
| \(\displaystyle 7\) | \(\displaystyle 0\) | \(\displaystyle 2\) | ||||||
| \(\displaystyle –\) | ||||||||
| \(\displaystyle \bf 7\) | \(\displaystyle \bf 0\) | \(\displaystyle \bf 2\) | ||||||
| \(\displaystyle 0\) |
Таким образом, мы восстановили весь процесс деления в столбик.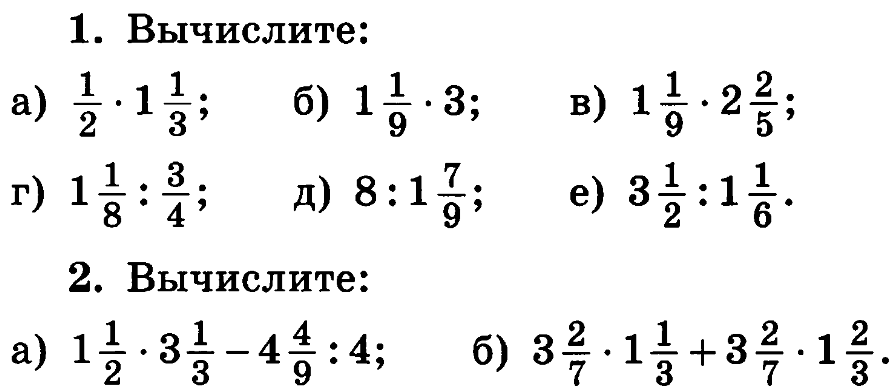
Разделение многозначных десятичных знаков — Common Core: Математика для 6-го класса
All Common Core: Математические ресурсы для 6-го класса
6 Диагностических тестов 186 практических тестов Вопрос дня Карточки Learn by Concept
Common Core: помощь по математике для 6-го класса » Система счисления » Свободное сложение, вычитание, умножение и деление многозначных десятичных чисел: CCSS.Math.Content.6.NS.B.3 » Деление многозначных десятичных чисел
Решите:
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая запятую вправо:
Если мы переместим десятичную запятую на одну позицию в делителе, мы также должны переместить десятичную запятую на одну позицию в делимом:
Новая задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 76 может войти в 197
76 может войти в 197 два раза, поэтому мы пишем 2 над 7 в делимом:
Затем мы умножаем 2 на 76 и записываем это произведение под 197 и вычитаем:
Теперь мы уменьшаем 6 из делимого, чтобы получить 45 в 456.
Подумайте: сколько раз можно 76 перейти в 456?
76 может войти в 465 шесть раз, поэтому мы пишем 6 над 6 в делимом:
Затем мы умножаем 6 на 76 и записываем это произведение под 456 и вычитаем:
У нас остается без остатка и конечное частное 2,6
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
Задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем делить как обычно:
Подумайте: сколько раз 12 может войти в 8
12 не может войти в 8, поэтому мы пишем 0 над 8 в делимом:
Так как 12 не может входим в число 8, объединяем разряд единиц и разряд десятых и думаем, сколько раз 12 может входить в число 85. Число разделено на десятичную дробь, но ради умножения мы думаем о нем как о 85.
Подумайте: сколько раз 12 может войти в 85
12 может войти в 85 семь раз, поэтому мы пишем 7 над 5 в делимом:
Затем мы умножаем 12 на 7 и записываем это произведение под 85 и вычитаем:
Теперь мы уменьшаем 8 из делимого, чтобы превратить 1 в 18.
Подумайте: сколько раз можно 12 перейти в 18?
12 может войти в 18 один раз, поэтому мы пишем 1 над 8 в делимом:
Затем мы умножаем 12 на 1 и записываем это произведение под 18 и вычитаем:
Теперь у нас осталось с 6 в нашем делимом, и мы не можем умножить 12 на что-либо, чтобы получить 6. Мы присоединяем или добавляем ноль к нашему делимому, который мы можем перенести рядом с 6, и теперь это будет 60. Мы не изменили значение нашего делимое, мы добавили ноль, чтобы число делилось на 12.
Подумайте: сколько раз 12 может перейти в 60?
12 может войти в 60 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 12 и 5 и записываем это произведение под 60 и вычитаем:
У нас остается без остатка и окончательное частное 0,715
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
Задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем делить, как обычно:
Подумайте: сколько раз 9 может войти в 8
9 не может войти в 8, поэтому мы пишем 0 над 8 в делимом:
Поскольку 9 не может входим в число 8, объединяем разряд единиц и разряд десятых и думаем, сколько раз 9 может входить в число 87. Число разделено на десятичную дробь, но ради умножения мы думаем о нем как о 87.
Подумайте: сколько число 9 может входить в число 87
9 может входить в число 87 девять раз, поэтому мы пишем 9над 7 в делимом:
Затем мы умножаем 9 на 9 и записываем это произведение под 87 и вычитаем:
Теперь мы уменьшаем 3 из делимого, чтобы превратить 6 в 63.
Подумайте: сколько раз 9 может быть 63?
9 может войти в 63 семь раз, поэтому мы пишем 7 над 3 в делимом:
Затем мы умножаем 9 и 7 и записываем это произведение под 63 и вычитаем:
У нас не осталось остатка и окончательное частное 0,97
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
95
5 Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая запятую вправо:
Если мы переместим десятичную запятую на одну позицию в делителе, мы также должны переместить десятичную запятую на одну позицию в делимом:
Новая задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 18 может войти в 45
18 может войти в 45 два раза, поэтому мы пишем 2 вместо 5 в делимом:
Затем мы умножаем 2 на 18 и записываем это произведение под 45 и вычитаем:
Теперь 18 нельзя умножить на целое число, чтобы получить 9, поэтому приложите или добавьте ноль к делимому, чтобы получить число, которое делится на 18. Мы не меняем значение делимого, добавляя ноль. Перенесите этот 0 рядом с 9, чтобы получить 90.
Подумайте: сколько раз 18 может превратиться в 90?
18 может войти в 90 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 5 и 18 и пишем это произведение под 90 и вычитаем:
У нас не осталось остатка и окончательное частное 2,5
Сообщить об ошибке
Решить:
5
5 Возможные ответы: Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая десятичный разряд вправо:
Мы делаем это, перемещая десятичный разряд вправо:
Если мы переместим десятичную дробь на один разряд в делителе, мы также должны переместить десятичную дробь на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом: уже поставили запятую в наш ответ. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем делить как обычно:
Подумайте: сколько раз 52 может войти в 1
52 не может войти в 1, поэтому мы пишем 0 над 1 в делимом:
Мы не использовали 1 в разряде сотен, поэтому теперь мы подставляем 0 в разряд десятков и пытаемся разделить его на 52
Подумайте: сколько раз 52 может входить в число 10
52 не может входить в 10, поэтому мы пишем 0 над 0 в делимом:
Мы не использовали 10, поэтому теперь мы подставляем 1 из разряда единиц и пытаемся разделить его на 52
Подумайте: сколько раз 52 может войти в 101
52 может войти в 101 один раз, поэтому мы пишем 1 над 1 в делимом:
Затем мы умножаем 52 на 1 и записываем это произведение под 101 и вычтите:
Теперь мы уменьшим 4 из делимого, чтобы превратить 49 в 494. напишите 9 над 4 в делимом:
напишите 9 над 4 в делимом:
Затем мы умножаем 52 на 9 и пишем это произведение под 494 и вычитаем:
Теперь 52 нельзя умножить на целое число, чтобы получить 26, поэтому приложение или добавьте ноль к делимому, чтобы получить число делится на 52. Мы не меняем значение делимого, добавляя ноль. Сократите этот 0 рядом с 26, чтобы получить 260.
Подумайте: сколько раз 52 может перейти в 260?
52 может войти в 260 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 52 на 5 и записываем это произведение под 260 и вычитаем:
У нас не остается остатка, и окончательное частное равно 1,95
Сообщить об ошибке
5 Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая десятичный разряд вправо:
Мы делаем это, перемещая десятичный разряд вправо:
Если мы переместим десятичную дробь на один разряд в делителе, мы также должны переместить десятичную дробь на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом: уже поставили запятую в наш ответ. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 2 может войти в 4
2 может войти в 4 два раза, поэтому мы пишем 2 над 4 в делимом:
Далее, мы умножаем 2 на 2 и пишем это произведение под 4 и вычитаем:
Теперь мы уменьшаем 0 из делимого, чтобы превратить 0 в 00.
Подумайте: сколько раз 2 может перейти в 0
2 может перейти в 0 ноль раз, поэтому мы пишем 0 над 0 в делимом:
Затем мы умножаем 2 на 0 и пишем это произведение под 0 и вычитаем:
Теперь мы уменьшаем 9 из делимого, чтобы сделать 0 в 9.
2 может превратиться в 9 четыре раза, поэтому мы пишем 4 вместо 9 в делимом:
Затем мы умножаем 2 и 4 и пишем это произведение под 9 и вычитаем:
Теперь 2 нельзя умножить на целое число, чтобы получить a 1, поэтому добавьте ноль к делимому, чтобы получить число, делящееся на 2. Мы не меняем значение делимого, добавляя ноль. Поместите этот 0 рядом с 1, чтобы получить 10.
Подумайте: сколько раз 2 может быть 10?
2 может войти в 10 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 2 и 5 и записываем это произведение под 10 и вычитаем:
У нас остается без остатка и конечное частное 204,5
Сообщить об ошибке
Какое число в задаче является делимым?
Возможные ответы:
Ни один из вариантов ответа не является правильным.
Правильный ответ:
Объяснение:
Делимое — это то, что вы делите или делите в задаче на деление. Это сумма, которую вы хотите разделить. В этой задаче дивиденд. В задаче на деление первым указывается делимое.
Это сумма, которую вы хотите разделить. В этой задаче дивиденд. В задаче на деление первым указывается делимое.
Сообщить об ошибке
Какая модель правильно представлена в блоке сотен?
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.
Вам нужно заштриховать прямоугольник площадью 0,24. Итак, заштрихуйте 24 квадратика, в десятичной модели.
Существует множество прямоугольников площадью 0,24. Вам нужно заштриховать тот, который имеет длину 0,6.
Отсутствует коэффициент 0,4, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,4 на 0,6 равна 0,24. Следовательно, 0,24 ÷ 0,6 = 0,4
Сообщить об ошибке
Решите задачу, используя предоставленную модель области.
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.
Вам нужно заштриховать прямоугольник площадью 0,12. Итак, заштрихуйте 12 маленьких квадратов в десятичной модели.
Существует множество прямоугольников площадью 0,12. Вам нужно заштриховать тот, который имеет длину 0,3.
Отсутствует коэффициент 0,4, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,4 на 0,3 равна 0,12. Следовательно, 0,12 ÷ 0,3 = 0,4
Сообщить об ошибке
Какая модель правильно представляет блок сотен?
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.
Вам нужно заштриховать прямоугольник площадью 0,25. Итак, заштрихуйте 25 квадратиков, в десятичной модели.
Существует множество прямоугольников площадью 0,25. Вам нужно заштриховать тот, который имеет длину 0,5.
Отсутствует коэффициент 0,5, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,5 на 0,5 равна 0,25. Следовательно, 0,25 ÷ 0,5 = 0,5
Сообщить об ошибке
Уведомление об авторских правах
All Common Core: Математические ресурсы для 6-го класса
6 Диагностических тестов
186 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Long Division Worksheets
Share to PinterestPinterestShare to FacebookFacebookShare to PocketPocketShare to TwitterTwitterShare to EmailEmailShare to FlipboardFlipboard Worksheets
Printables
PuzzlesT-shirts
Math Worksheets
Go Free Ad 900!
Основные математические рабочие листы
Рабочие листы с дробями
Словесные задачи
Алгебра
Другие рабочие листы
Измерения и преобразования
Образцы и головоломки
Раскраска по номерам
Праздники и сезоны
Раннее обучение
Печатные формы
Калькуляторы
Рабочие листы по математике по классам на беглости студента с основными фактами деления.
 Эти длинные рабочие листы деления помогут постепенно обрести уверенность, когда вы будете готовы!
Эти длинные рабочие листы деления помогут постепенно обрести уверенность, когда вы будете готовы!
Длинное деление — особая веха, потому что оно требует использования нескольких шагов, алгоритма, который включает в себя не только основные математические факты сложения, вычитания и умножения, но также потому, что требует определенной интуиции и решения проблем. Даже многозначное умножение довольно механическое по сравнению с навыками, необходимыми для решения задачи на длинное деление вручную.
Эти длинные рабочие листы для деления содержат задачи разного уровня сложности, которые облегчают процесс. Особенно, если вы вводите длинное деление в 3-м классе, вы обнаружите, что диапазон сложностей в таблицах является нежным введением в этот часто устрашающий математический предмет! Рабочие листы на длинное деление без остатка
24 Рабочие листы на длинное деление Рабочие листы на длинное деление, не производящие частные с остатком. Когда вы впервые изучаете длинные шаги деления, эти рабочие листы являются отправной точкой.
Рабочие листы на длинное деление без остатка
Рабочие листы на длинное деление с остатком
36 Рабочие листы на длинное деление Эти рабочие листы на длинное деление имеют частные с остатком. Каждый рабочий лист содержит подробные развернутые ответы, которые шаг за шагом показывают, как выполнять деление в длинное число.
Рабочие листы длинного деления с остатками
Рабочие листы длинного деления Monster
40 Рабочие листы длинного деления Рабочие листы с самыми длинными в мире задачами на деление! Потренируйтесь с ними, и вы избавитесь от страха перед монстром длинного дивизиона!
Рабочие листы на длинное деление Monster
Деление на десять множителей
16 Рабочие листы на длинное деление Рабочие листы на длинное деление с задачами на десятичные множители с остатком и без него. Работа над этими задачами может привести к несколько иным навыкам, например, к отбрасыванию нулей для решения задач, что немного отличается от шагов для традиционного деления в полные числа, но все же укрепляет те же концепции.
Работа над этими задачами может привести к несколько иным навыкам, например, к отбрасыванию нулей для решения задач, что немного отличается от шагов для традиционного деления в полные числа, но все же укрепляет те же концепции.
Деление на десять множителей
Деление на множители 25
16 Рабочие листы с длинным делением Эти рабочие листы с длинным делением сосредоточены на множителях 25. Существует две группы рабочих листов, включая наборы с остатками и наборы без остатка .
Деление на множители 25
Рабочие листы на длинное деление с многозначными делителями
24 Рабочие листы на длинное деление Рабочие листы на длинное деление с многозначными делителями, множествами с остатками и множествами без остатка. Эти рабочие листы начинаются с простых задач, которые помогают освоить многозначные делители и укрепить уверенность, прежде чем переходить к более сложным задачам на деление в длину.
Рабочие листы на длинное деление с многозначными делителями
Рабочие листы на длинное деление с десятичными дробями
28 Рабочие листы на длинное деление Практические рабочие листы на деление с дробными значениями, выраженными в виде десятичных дробей, включая рабочие листы на длинное деление с сотыми обучение делению денежных сумм).
Рабочие листы длинного деления с десятичными дробями
Рабочие листы длинного деления
Обучение делению в большую сторону является важной вехой в обучении математике. Длинное деление, как и более длинное умножение, требует нескольких шагов для вычисления ответа. Тем не менее, длинное деление является одной из первых процедур, где для поиска правильного ответа могут потребоваться некоторые подходы по следам и ошибкам или эксперименты. Часто определение правильного следующего шага в задаче на деление в длину, особенно в задаче на деление на несколько цифр, может потребовать «обоснованного предположения» для определения следующей цифры частного. Проверка этого предположения на шаге умножения алгоритма деления в длину имеет решающее значение, поскольку гарантирует, что результат на этом этапе задачи меньше фактического делителя. Многим учащимся сложно справиться с этими более сложными процедурами, и из-за этого длинное деление кажется более сложной задачей, чем должно быть. Добавьте длинное деление с остатками или длинное деление с десятичными знаками, и пейзаж действительно станет минным полем разочарования.
Проверка этого предположения на шаге умножения алгоритма деления в длину имеет решающее значение, поскольку гарантирует, что результат на этом этапе задачи меньше фактического делителя. Многим учащимся сложно справиться с этими более сложными процедурами, и из-за этого длинное деление кажется более сложной задачей, чем должно быть. Добавьте длинное деление с остатками или длинное деление с десятичными знаками, и пейзаж действительно станет минным полем разочарования.
Рабочие листы на деление на длинное деление в этом разделе сайта предназначены для постепенного ознакомления с различными темами, чтобы навыки деления на длинное формировались постепенно, а области сложности можно было укреплять, не опасаясь проблем с делением на длинное. Изучение того, как делать длинное деление, включает в себя множество шагов, включая умножение и вычитание, а также базовое понимание фактов деления. Пока учащиеся хорошо овладевают предшествующими математическими операциями, длинное деление может быть возможностью продемонстрировать результаты своей тяжелой работы на предыдущих этапах своего математического путешествия.
 Мы делаем это, перемещая десятичный разряд вправо:
Мы делаем это, перемещая десятичный разряд вправо:  напишите 9 над 4 в делимом:
напишите 9 над 4 в делимом: Мы делаем это, перемещая десятичный разряд вправо:
Мы делаем это, перемещая десятичный разряд вправо: 
 Это сумма, которую вы хотите разделить. В этой задаче дивиденд. В задаче на деление первым указывается делимое.
Это сумма, которую вы хотите разделить. В этой задаче дивиденд. В задаче на деление первым указывается делимое.


 Работа над этими задачами может привести к несколько иным навыкам, например, к отбрасыванию нулей для решения задач, что немного отличается от шагов для традиционного деления в полные числа, но все же укрепляет те же концепции.
Работа над этими задачами может привести к несколько иным навыкам, например, к отбрасыванию нулей для решения задач, что немного отличается от шагов для традиционного деления в полные числа, но все же укрепляет те же концепции.
 Проверка этого предположения на шаге умножения алгоритма деления в длину имеет решающее значение, поскольку гарантирует, что результат на этом этапе задачи меньше фактического делителя. Многим учащимся сложно справиться с этими более сложными процедурами, и из-за этого длинное деление кажется более сложной задачей, чем должно быть. Добавьте длинное деление с остатками или длинное деление с десятичными знаками, и пейзаж действительно станет минным полем разочарования.
Проверка этого предположения на шаге умножения алгоритма деления в длину имеет решающее значение, поскольку гарантирует, что результат на этом этапе задачи меньше фактического делителя. Многим учащимся сложно справиться с этими более сложными процедурами, и из-за этого длинное деление кажется более сложной задачей, чем должно быть. Добавьте длинное деление с остатками или длинное деление с десятичными знаками, и пейзаж действительно станет минным полем разочарования.


 Совместные действия над обыкновенными и десятичными дробями
Совместные действия над обыкновенными и десятичными дробями Задание: тип 96, стр.188
Задание: тип 96, стр.188 Эти длинные рабочие листы деления помогут постепенно обрести уверенность, когда вы будете готовы!
Эти длинные рабочие листы деления помогут постепенно обрести уверенность, когда вы будете готовы!