| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0.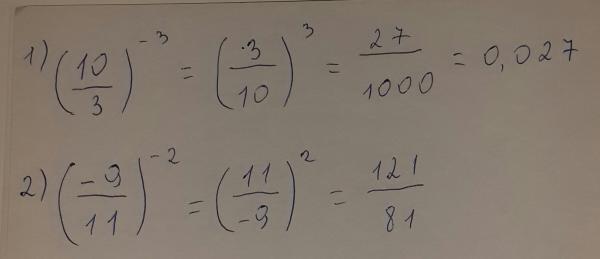 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Научная нотация MCAT без вычислений
Ниже приведена расшифровка моего обучающего видео MCAT Math video 4 — Научная нотация для сложения, вычитания, умножения и деления.
(Нажмите здесь, чтобы посмотреть на YouTube)
[Начать расшифровку]
Лия здесь с Leah5sci.com/MCAT, и в этом видео я покажу вам, как использовать научную нотацию в вопросах в стиле MCAT без калькулятора, когда это приходит к сложению, вычитанию, умножению и делению.
Когда дело доходит до сложения и вычитания степеней, если вы имеете дело с одной и той же степенью, все, что вам нужно сделать, это сложить и вычесть коэффициент и сохранить степень. Например, вам дано 4,7 × 10¯³ + 2,3 × 10¯³ . Оба числа в вопросе умножены на 10 минус 3, поэтому все, что нам нужно сделать, это добавить 4,7 и 2,3.
Давайте начнем с коэффициента, 4 и 2 равно 6, точка 7 и точка 3 равна 1 дает нам в сумме 7,0×10¯³. Десять минус 3 не изменилось, и все, что я сделал, это добавил два числа.
Когда силы разные, но они достаточно близки, вы хотите превратить их в одну и ту же силу, а затем относиться к ней одинаково. Давайте не будем усложнять, скажем, у меня есть 5×10¯³ + 6×10¯⁴. Я не могу просто сложить 5 и 6, потому что имею дело с разными способностями.
Давайте не будем усложнять, скажем, у меня есть 5×10¯³ + 6×10¯⁴. Я не могу просто сложить 5 и 6, потому что имею дело с разными способностями.
Итак, что я хочу сделать, это превратить первое число в степень отрицательного числа 4 или второе число в степень отрицательного числа 3. В предыдущем видео я показал вам трюк для умножения и деления на коэффициент 10, просто перемещая десятичная. Вы можете найти это видео вместе со всей моей серией MCAT Math без калькулятора на моем веб-сайте leah5sci.com/MCATMATH.
Научное обозначение — это просто еще один способ представления степеней 10, и если я буду относиться к нему таким образом, трюк с перемещением десятичных знаков все еще применим. Если у меня есть число вроде 10¯³, то способ сделать это число равным 10¯⁴ состоит в том, чтобы разделить его на 10. Теперь запомните трюк, который я вам показал: если у меня есть пример, и я умножаю 10 на 10, я не t изменить идентичность примера.
Итак, если я возьму 10¯³ и разделю на 10, я получу 10¯⁴. Я должен обосновать это, умножив это число (5) на 10. 5×10 равно 50. Замена 5×10¯³ на 50×10¯⁴ дает точно такое же значение. Теперь, когда у меня есть 50×10¯⁴, я могу добавить это к 6×10¯⁴, потому что они имеют одинаковую мощность. 50 + 6 равно 56, и мы по-прежнему сохраняем 10¯⁴.
Теперь в типичной научной нотации вам нужно только одно число, за которым сразу следует десятичная дробь. Поэтому я должен сделать это, умножив десять на десять снова, или просто подумать об этом, как когда я уменьшаю число, то есть я перемещаю десятичный разряд на 1 пробел влево, я увеличиваю значение своего показателя степени. Таким образом, 56 разделить на 10 равно 5,6, 10¯⁴ умножить на 10 равно 10¯³. Другими словами, я снова использую этот трюк, умножив 10 на 10, и быстро получил ответ. Итак, окончательный ответ на этот вопрос — 5,6×10¯³.
Умножение показателей степени может отображаться в вашем MCAT следующим образом:
Найдите концентрацию NO3-, когда 6,8×10¯⁷ молей NANO₃ добавляют к 5,1×10¯³ л h30.
Поиск молярностей по теме, которая будет обсуждаться в серии «Химия» на leah5sci.com/MCATChemistry, а пока давайте сосредоточимся на математике. Мы хотим найти молярность, которая равна моль/л (M=моль/л). О числах, о которых не может быть и речи, мы имеем следующее уравнение:
M=моль/л = 6,8×10¯⁷ / 5,1×10¯³ моль/л
Это сбивает с толку многих учеников, потому что они усложняют задачу. Итак, давайте поговорим о правилах, а затем давайте решим проблему. Когда дело доходит до умножения, все, что вы делаете, это умножаете число, а затем ДОБАВЛЯЕТЕ степени.
(2×10⁴)(4×10²)=8×10⁶ -> В этом случае у нас есть 2×4, что равно 8. Для показателей степени 10⁴ и 10² мы добавляем 4 и 2, что равно 6, что дает нам ответ 8 ×10⁶.
Для деления вы делите числа, а затем вычитаете степени. В этом случае имеем:
3 x 10⁶ ÷ 6 x 10³ , мы установим это следующим образом: 3 разделить на 6, это 3/6, мы можем упростить это до 1/3, что равно 0,33, это дробь, которую вы должны знать. Если вы еще этого не знаете, скачайте мое руководство по математике MCAT на моем веб-сайте https://leah5sci.com/MCATMath.
Если вы еще этого не знаете, скачайте мое руководство по математике MCAT на моем веб-сайте https://leah5sci.com/MCATMath.
Затем мы вычитаем показатели степени, у нас есть 10⁶ и 10³, 6 минус 3 равно 3, что дает мне ответ 0,5 x 10³. Теперь это неправильная научная нотация, поэтому мы фактически переместим десятичную 1 пробел вправо, умножив на 10, и уменьшим показатель степени на 1 число, которое по существу делится на 10, другими словами, мы умножаем и делим на 10, давая мне фактический ответ 0,5 × 10² или просто 500.
Вернемся к нашему вопросу. Для такого вопроса MCAT не ищет точное значение, вместо этого они ищут что-то достаточно близкое, и вы обычно видите ответы, которые имеют силу повсюду.
Итак, мы ищем приблизительное число, но правильную мощность. Степень в этом случае равна 10¯⁷, деленной на 10¯³, поэтому у нас есть 7 минус отрицательное 3. Отрицательное 7 минус отрицательное 3, Минус Отрицательное сокращается, так что это действительно Отрицательное 7 плюс 3 (-7 + 3), что дает мне новый показатель степени из 10¯⁴.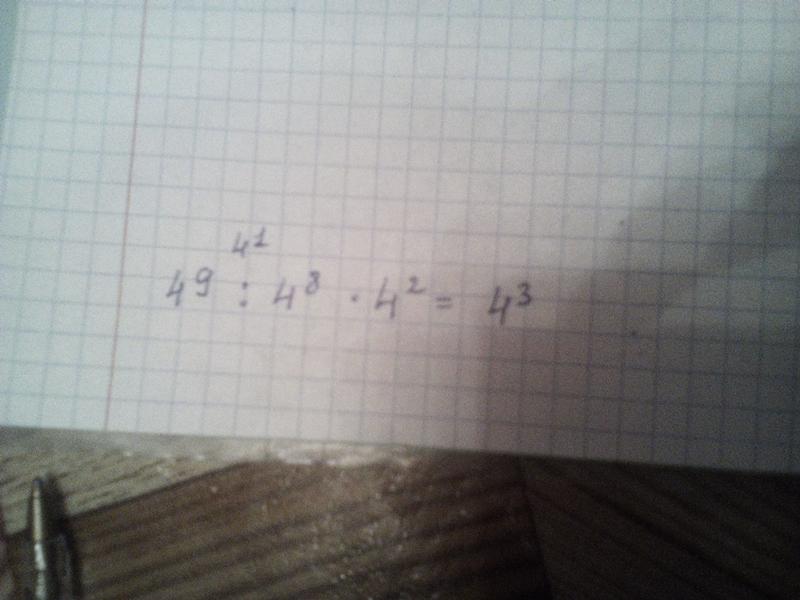
Сами числа 6,8 приблизительно равны 7, 5,1 приблизительно равны 5, поэтому мы имеем 7/5 x 10¯⁴. Это неподходящий ответ, и в следующем видео я разберу дроби и отношения более подробно, а пока посмотрите на это так; 7/5 на самом деле 5/5 + 2/5 5/5 равно 1, поэтому у нас есть 1 и 2/5 x 10¯⁴. Два на пять (2/5) — это дробь, которую вы должны распознать, потому что один на пять (1/5) — это целых два (0,2), поэтому два на пять (2/5) — это четыре (0,4).
Это дает нам окончательный ответ 1,4 x 10¯⁴. Введя начальные числа в калькулятор, я получил 1,33 x 10¯⁴, что на MCAT достаточно близко.
Не забудьте присоединиться ко мне в следующем видео, где я покажу вам, как решать квадраты и квадратные корни, когда дело доходит до MCAT.
Вы застряли на определенной теме MCAT? Я предлагаю частное онлайн-обучение, где я фокусируюсь на ваших потребностях, чтобы укрепить ваши индивидуальные слабости. Подробную информацию о репетиторстве можно найти по ссылке ниже или на моем веб-сайте leah5sci.com/MCATTutor.
Подробную информацию о репетиторстве можно найти по ссылке ниже или на моем веб-сайте leah5sci.com/MCATTutor.
Вас ошеломил огромный объем информации, необходимой для MCAT? Вы обеспокоены тем, что отсутствие надлежащего учебного плана и низкий балл MCAT помешают вам поступить в медицинскую школу?
Моя новая электронная книга Стратегия экзамена MCAT — это 6-недельное руководство по преодолению MCAT поможет вам сформулировать конкретный учебный план, помогая вам понять, где вы находитесь сейчас, определить свои цели и выяснить, что нужно для их достижения. и это ваше БЕСПЛАТНО, если вы подпишитесь на мою рассылку по электронной почте на MCATExamStrategy.com.
Подписавшись на мою рассылку по электронной почте, вы также будете первыми, кто узнает, когда у меня появятся новые видео, шпаргалка по учебному пособию MCAT, советы и многое другое! Ссылка снова MCATExamStrategy. com.
com.
[Конец транскрипции]
Посмотреть видео MCAT Math 4 — Научная нотация для сложения, вычитания, умножения и деления.
Произведение трех и более чисел. Степени отрицательных чисел.
ДОМ: Математика — Геометрия
Произведение трех и более чисел. Как вы узнали из арифметики, если нужно умножить три или более чисел, это не имеет значения. в каком порядке числа умножаются. То есть, чтобы умножить 2 X 3 X 4, мы могли бы сначала перемножить первые два числа, а затем умножить результат на третье число, как:
Мы могли бы сначала перемножить два последних числа, а затем умножить результат на первое число, например:
Мы могли бы сначала перемножить первое и третье числа, а затем умножить результат на второе число, как:
Когда некоторые из чисел положительные, а некоторые отрицательные, мы можем следовать тому же методу, который использовался выше.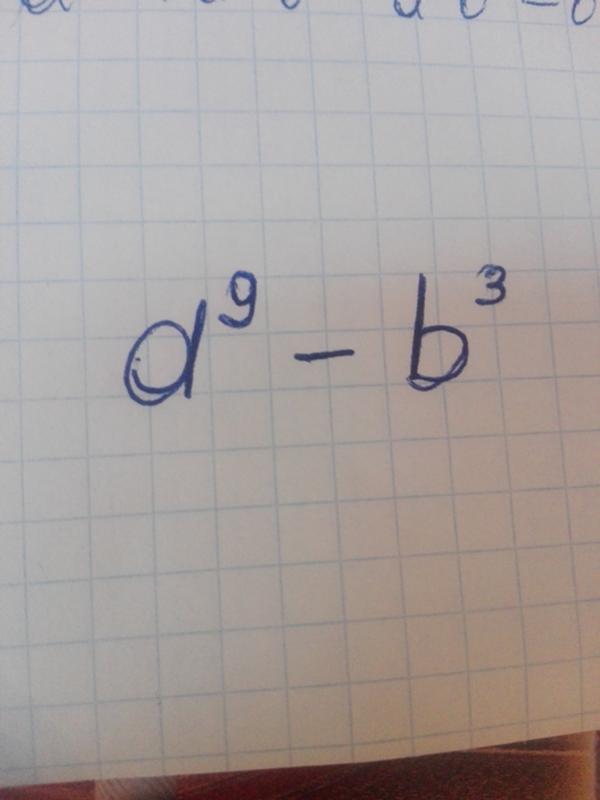
Поскольку произведение двух отрицательных чисел положительно, всякий раз, когда в произведении есть четное число (два, четыре, шесть и т. д.) отрицательных множителей, произведение положительно; всякий раз, когда в произведении имеется нечетное число (один, три, пять и т. д.) отрицательных факторов, произведение является отрицательным.
ПРИМЕРЫ: Нахождение произведения трех или более чисел
1. Найдите продукт:
Раствор. Так как этот член содержит нечетное число (три) отрицательных множителей, произведение будет отрицательным.
Перемножив четыре множителя вместе и пометив произведение минусом, мы имеем:
2. Упростить:
Раствор. Поскольку этот член содержит четыре (четное число) отрицательных факторов, ответ будет положительным.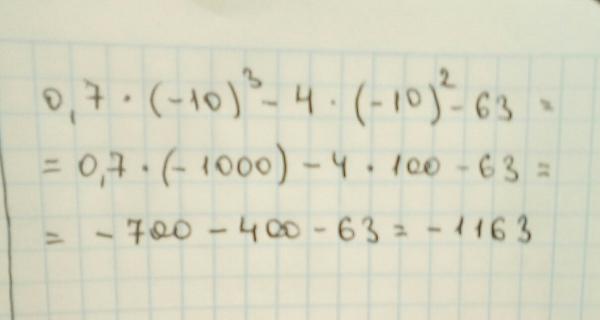 Следовательно, мы можем приступить к упрощению термина, убрав общие множители в числителе и знаменателе; то есть мы можем разделить 20 в числителе и 35 в знаменателе на общий делитель 5, и мы можем разделить 18 в числителе и 66 в знаменателе на общий делитель 6. Эта работа обычно изображается как следует:
Следовательно, мы можем приступить к упрощению термина, убрав общие множители в числителе и знаменателе; то есть мы можем разделить 20 в числителе и 35 в знаменателе на общий делитель 5, и мы можем разделить 18 в числителе и 66 в знаменателе на общий делитель 6. Эта работа обычно изображается как следует:
Умножение коэффициентов в числителе и в знаменатель = 144/77
3. Умножьте: (4a 2 b 3 c 3 )(-3a 2 b 3 c 2 ).
УПРАЖНЕНИЯ: Умножение и деление чисел со знаком
Упростите каждое из следующих действий:
Ответы :
Степени отрицательных чисел. Ранее мы узнали, что 3 означает
а . а . а, и что 3 4 означает 3 .3 . 3 . 3. Аналогично, (-a) 3 означает
.(-а)(-а)(-а) и (-3) 4 означает (-3)(-3)(-3)(-3). Таким образом, если отрицательное число возвести в четную степень, оно содержит четное число отрицательных множителей; следовательно, его значение будет положительным. Если отрицательное число возвести в нечетную степень, оно содержит нечетное количество отрицательных множителей; следовательно, его значение будет отрицательным.
Ранее мы узнали, что 3 означает
а . а . а, и что 3 4 означает 3 .3 . 3 . 3. Аналогично, (-a) 3 означает
.(-а)(-а)(-а) и (-3) 4 означает (-3)(-3)(-3)(-3). Таким образом, если отрицательное число возвести в четную степень, оно содержит четное число отрицательных множителей; следовательно, его значение будет положительным. Если отрицательное число возвести в нечетную степень, оно содержит нечетное количество отрицательных множителей; следовательно, его значение будет отрицательным.
В этот момент мы должны заметить разницу между -a 2 и (-a) 2 . Обозначение -a 2 означает -1a 2 , а -1 не возводится во вторую степень. Следовательно, -a 2 = 1a 2 , а (-a) 2 означает (-a)(-a) и равно a 2 . Точно так же -2 4 означает -1(2) 4 , что равно -16, а (-2) 4 равно 16.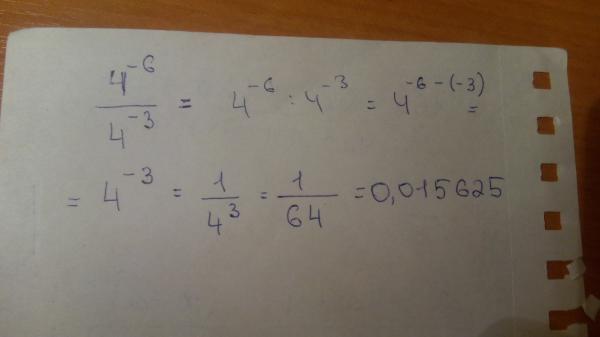
ИЛЛЮСТРАТИВНЫЕ ПРИМЕРЫ: Оценка степеней отрицательных чисел
1. Найдите значение (-3) 5 .
Решение. Поскольку отрицательное число -3 возведено в нечетную степень, его значение будет отрицательным; следовательно
(-3) 5 = -243
2. Найдите значение -2(-4) 3 .
Раствор. Поскольку отрицательное число -4 возведено в нечетную степень, его значение будет отрицательным; следовательно
-2(-4) 3 = -2(-64)
= 128
УСТНЫЕ УПРАЖНЕНИЯ: Нахождение значений степеней отрицательных чисел
Укажите значение каждого из следующих:
Ответы: 1. 9. 2. 16. 3. -125. 4. -2. 5. -27. 6. -5. 7. -3. 8. 1. 9. 256. 10. -1. 11. -32. 12. 25. 13. -64 14. 625. 15. -3125. 16. 6. 17. -1. 18. -8. 19. -4. 20. 4. 21. 1 22. -1024. 23. -243. 24. 81. 25. -1.
9. 2. 16. 3. -125. 4. -2. 5. -27. 6. -5. 7. -3. 8. 1. 9. 256. 10. -1. 11. -32. 12. 25. 13. -64 14. 625. 15. -3125. 16. 6. 17. -1. 18. -8. 19. -4. 20. 4. 21. 1 22. -1024. 23. -243. 24. 81. 25. -1.
Вычисление алгебраических выражений. На других страницах мы оценивали алгебраические выражения, когда нам давали числовые значения букв. В этих задачах значения букв были положительными. Теперь мы будем оценивать выражения, когда значения букв являются числами со знаком; то есть, когда значения букв положительные или отрицательные.
ИЛЛЮСТРАТИВНЫЕ ПРИМЕРЫ: Вычисление алгебраических выражений
УСТНЫЕ УПРАЖНЕНИЯ: Вычисление алгебраических выражений
1. Если x = -2, каково значение 3x?
2. Если a = -5, каково значение -2a?
3. Если y = -1, каково значение -y?
4. Если b = -3, каково значение 9+б?
6. Если b = -3, каково значение 9 -b ?
6. Если x = -5, каково значение 9 -2x?
7. Если y = -6, каково значение 2y + 12 ?
8. Если x = -4, каково значение 3x -7?
Если x = -4, каково значение 3x -7?
9. Если a =-2, каково значение a 2 ?
10. Если b = -3, каково значение -2b 2 ?
11. Если x = -3, каково значение 4 + x 2 ?12. Если y = -2, каково значение 6 -y 2 ?
Ответы : 1. -6. 2. 10. 3. 1. 4. 6. 5. 12. 6. 19. 7. 0. 8. — 19.030 9. 4. 10. -18. 11. 13. 12. 2.
УПРАЖНЕНИЯ: Вычисление алгебраических выражений
Если a = -2, b = 3, x = -1 и y = -3 , найдите значение каждого из следующих выражений:
Ответы : 1.
Ответы : 7. -32. 8. -1. 9. 5. 10. 7. 11. 10. 12. -8. 13. 13. 14. 5 15. 16.
Найдите числовое значение каждого из следующих:
Ответы : 16. (а) -8; (б) 8; (в) 8; (г) 24. 17. (а) 9; (б) -27; (в) -9;
(г)
-405. 18. (а)-64; (б) 256; (в) -48; (г) 512. 19. (а)-4; (Би 2;
(с)
-4; (г) 16. 20. (а)-75; (б) 90; (с) 675; (г) 135.
УПРАЖНЕНИЯ ПО ОБЗОРУ ГЛАВЫ
Ответы: 1. -3. 2. -18. 3. 6. 4. -5а 2 . 5. -6xy 2 . 6. 3x 2 . 7. 20. 8. -3г. 9. -6а 3 б 3 . 10. 18. 11. -8. 12. 0. 13. -7. 14. 12. 15. -24. 16. 12. 17. -50. 18. 8. 19. 24а 2 б 2 . 20. 4ax-12ay-2xy.
2а(3х-4у)-х(2а+3у)-(4ау-ху)
Ответы: 21.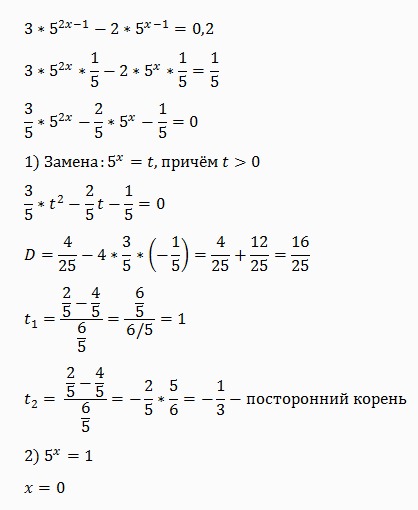 2. 22. (3x -y) -(2a -b). 23. 36a 3 b 2 e 3 . 24. 2(а + б). 25. х -(а + б). 26. -300. 27. 3x 2 -10x -3. 28. -4. 29. -9. 30. -15.
2. 22. (3x -y) -(2a -b). 23. 36a 3 b 2 e 3 . 24. 2(а + б). 25. х -(а + б). 26. -300. 27. 3x 2 -10x -3. 28. -4. 29. -9. 30. -15.
КУМУЛЯТИВНЫЙ ОБЗОР УПРАЖНЕНИЙ
1. В выражении 7x чему равен коэффициент при x?
2. Выразите алгебраически «четыре меньше, чем удвоенное число х».
3. Найдите значение 3xy, когда x = 2 и y = -4.
4. Умножить x 2 на x 3
5. Если 3x = 18, найдите значение x.
6.
Разделите 6xy на 3x.
7. Решите для x: 5x -7 = 13,
8. Дважды определенное число при увеличении на 11 равно 23. Найдите число.
9. Вычтите 45 из 27.
10. Если x = -2, найдите значение 2x + 5.
11. Найдите значение: (2)(-5)(-3).
12. Найдите частное: -12/-3
13. Каково значение (-3) 3 ?
14. Упростите, собрав подобные члены: 3y -5y -2y + y.
15. Разделите -10 на -¼.
16. В выражении 7x2y чему равен показатель x? показатель у?
17. Найдите значение выражения 3x 2 + 4x + 7, когда x = -2.
18.
