| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Python | Арифметические операции с числами
Последнее обновление: 23.
01.2022
Python поддерживает все распространенные арифметические операции:
+
Сложение двух чисел:
print(6 + 2) # 8
—
Вычитание двух чисел:
print(6 - 2) # 4
*
Умножение двух чисел:
print(6 * 2) # 12
/
Деление двух чисел:
print(6 / 2) # 3.0
//
Целочисленное деление двух чисел:
print(7 / 2) # 3.5 print(7 // 2) # 3
Данная операция возвращает целочисленный результат деления, отбрасывая дробную часть
**
Возведение в степень:
print(6 ** 2) # Возводим число 6 в степень 2. Результат - 36
%
Получение остатка от деления:
print(7 % 2) # Получение остатка от деления числа 7 на 2.
Результат - 1
В данном случае ближайшее число к 7, которое делится на 2 без остатка, это 6. Поэтому остаток от деления равен 7 — 6 = 1
Результат - 1
При последовательном использовании нескольких арифметических операций их выполнение производится в соответствии с их приоритетом. В начале выполняются операции с большим приоритетом. Приоритеты операций в порядке убывания приведены в следующей таблице.
Операции | Направление |
** | Справо налево |
* / // % | Слева направо |
+ — | Слева направо |
Пусть у нас выполняется следующее выражение:
number = 3 + 4 * 5 ** 2 + 7 print(number) # 110
Здесь начале выполняется возведение в степень (5 ** 2) как операция с большим приоритетом, далее результат умножается на 4 (25 * 4), затем происходит сложение
(3 + 100) и далее опять идет сложение (103 + 7).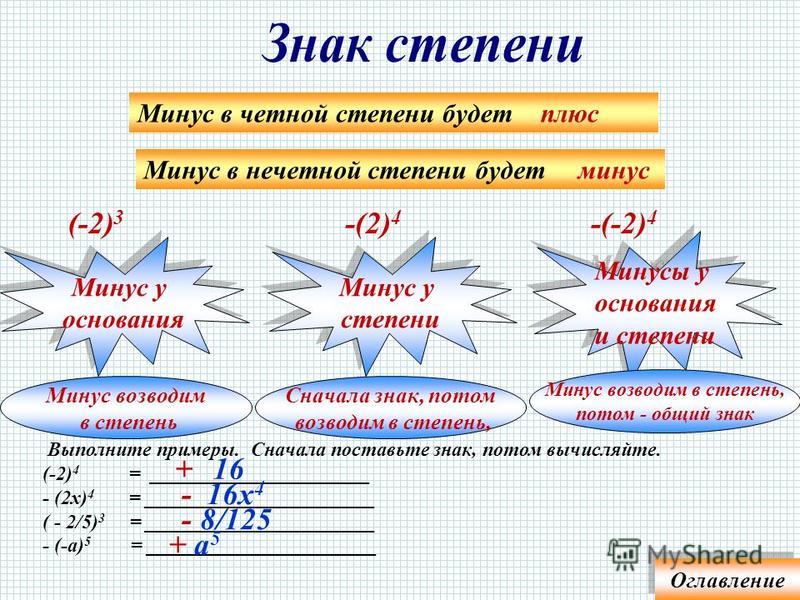
Чтобы переопределить порядок операций, можно использовать скобки:
number = (3 + 4) * (5 ** 2 + 7) print(number) # 224
Следует отметить, что в арифметических операциях могут принимать участие как целые, так и дробные числа. Если в одной операции участвует целое число (int) и число с плавающей точкой (float), то целое число приводится к типу float.
Арифметические операции с присвоением
Ряд специальных операций позволяют использовать присвоить результат операции первому операнду:
+=
Присвоение результата сложения
-=
Присвоение результата вычитания
*=
Присвоение результата умножения
/=
Присвоение результата от деления
//=
Присвоение результата целочисленного деления
**=
Присвоение степени числа
%=
Присвоение остатка от деления
Примеры операций:
number = 10 number += 5 print(number) # 15 number -= 3 print(number) # 12 number *= 4 print(number) # 48
Округление и функция round
При операциях с числами типа float надо учитывать, что результат операций с ними может быть не совсем точным.
Например:
first_number = 2.0001 second_number = 5 third_number = first_number / second_number print(third_number) # 0.40002000000000004
В данном случае мы ожидаем получить число 0.40002, однако в конце через ряд нулей появляется еще какая-то четверка. Или еще одно выражение:
print(2.0001 + 0.1) # 2.1001000000000003
В случае выше для округления результата мы можем использовать встроенную функцию round():
first_number = 2.0001 second_number = 0.1 third_number = first_number + second_number print(round(third_number)) # 2
В функцию round() передается число, которое надо округлить. Если в функцию передается одно число, как в примере выше, то оно округляется до целого.
Функция round() также может принимать второе число, которое указывает, сколько знаков после запятой должно содержать получаемое число:
first_number = 2.0001 second_number = 0.
1
third_number = first_number + second_number
print(round(third_number, 4)) # 2.1001
В данном случае число third_number округляется до 4 знаков после запятой.
Если в функцию передается только одно значение — только округляемое число, оно округляется то ближайшего целого
Примеры округлений:
# округление до целого числа print(round(2.49)) # 2 - округление до ближайшего целого 2 print(round(2.51)) # 3
Однако если округляемая часть равна одинаково удалена от двух целых чисел, то округление идет к ближайшему четному:
print(round(2.5)) # 2 - ближайшее четное print(round(3.5)) # 4 - ближайшее четное
Округление производится до ближайшего кратного 10 в степени минус округляемая часть:
# округление до двух знаков после запятой print(round(2.554, 2)) # 2.55 print(round(2.5551, 2)) # 2.56 print(round(2.554999, 2)) # 2.55 print(round(2.
499, 2)) # 2.5
Однако следует учитывать, что функция round() не идеальный инструмент. Например, выше при округление до целых чисел применяется правило, согласно которому,
если округляемая часть одинаково удалена от двух значений, то округление производится до ближайшего четного значения. В Python в связи с тем, что
десятичная часть числа не может быть точно представлена в виде числа float, то это может приводить к некоторым не совсем ожидаемым результатам. Например:
# округление до двух знаков после запятой print(round(2.545, 2)) # 2.54 print(round(2.555, 2)) # 2.56 - округление до четного print(round(2.565, 2)) # 2.56 print(round(2.575, 2)) # 2.58 print(round(2.655, 2)) # 2.65 - округление не до четного print(round(2.665, 2)) # 2.67 print(round(2.675, 2)) # 2.67
Подобно о проблеме можно почитать к документации.
НазадСодержаниеВперед
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс | 0046 | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 9 | знак умножения | умножение | 2 /3 × 5/6 |
| : | знак деления | деление | 1/2 : 3 |
| 4 деления 4 деления 6 | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|
Наиболее распространенные мнемоники для запоминания этого порядка операций: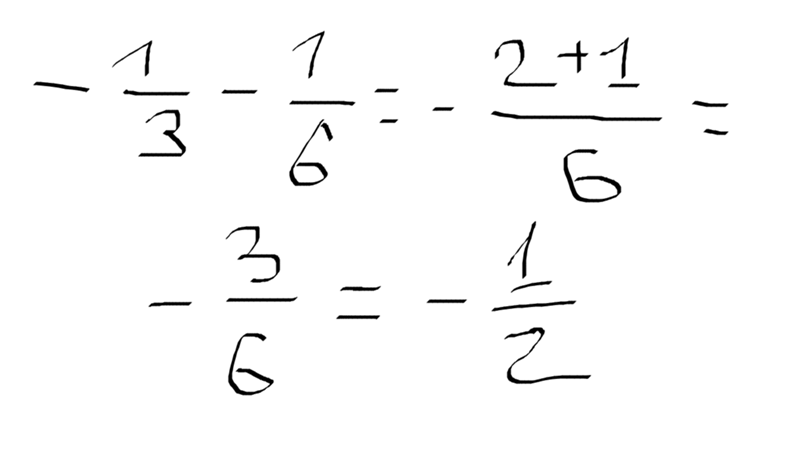 
Какая часть носков Макса коричневого или черного цвета?