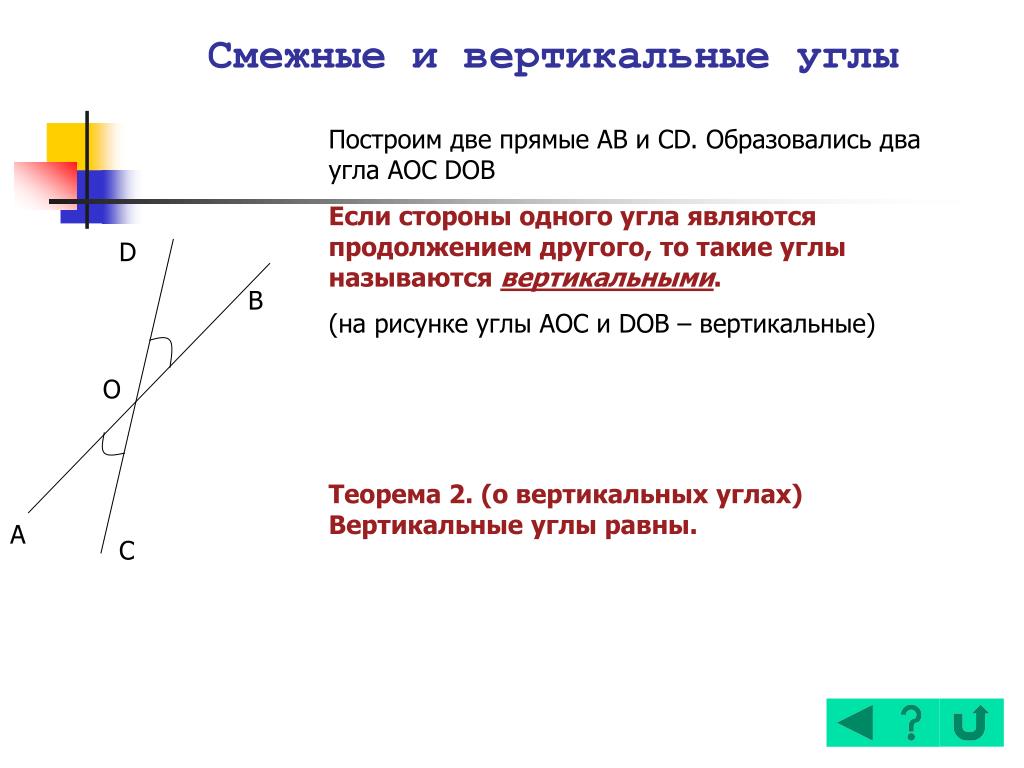
Так как $\angle \alpha \neq \angle \beta$, то и разности, стоящие в правых частях последних равенств также не равны, причем при равенстве уменьшаемого та разность меньше, где вычитаемое больше, следовательно $\angle \alpha_{1} < \angle \beta_{1}$.
Что и требовалось доказать.
Свойства (тригонометрические соотношения)
- Синусы смежных углов равны. Их косинусы и тангенсы равны по величине, но имеют противоположные знаки (за исключением неопределённых значений).
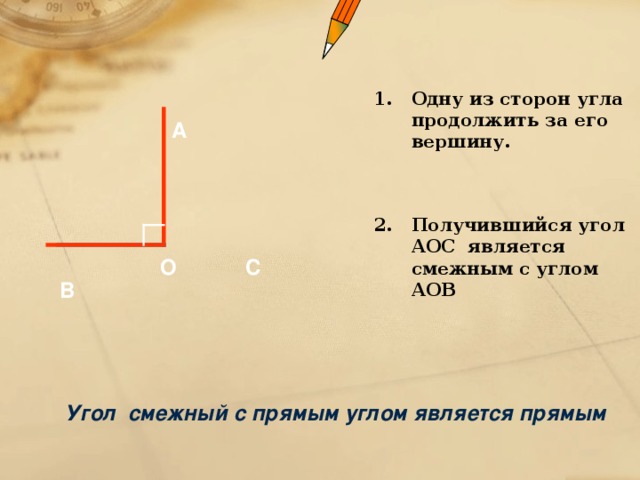
- Чтобы построить угол, смежный данному, надо одну из сторон рассматриваемого угла продлить за вершину (рис. 3).
Читать дальше: что такое острый угол.
Определение смежных. Смежные и вертикальные углы
Как найти смежный угол?
Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе.
Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.
Определение и свойства смежных углов
Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.
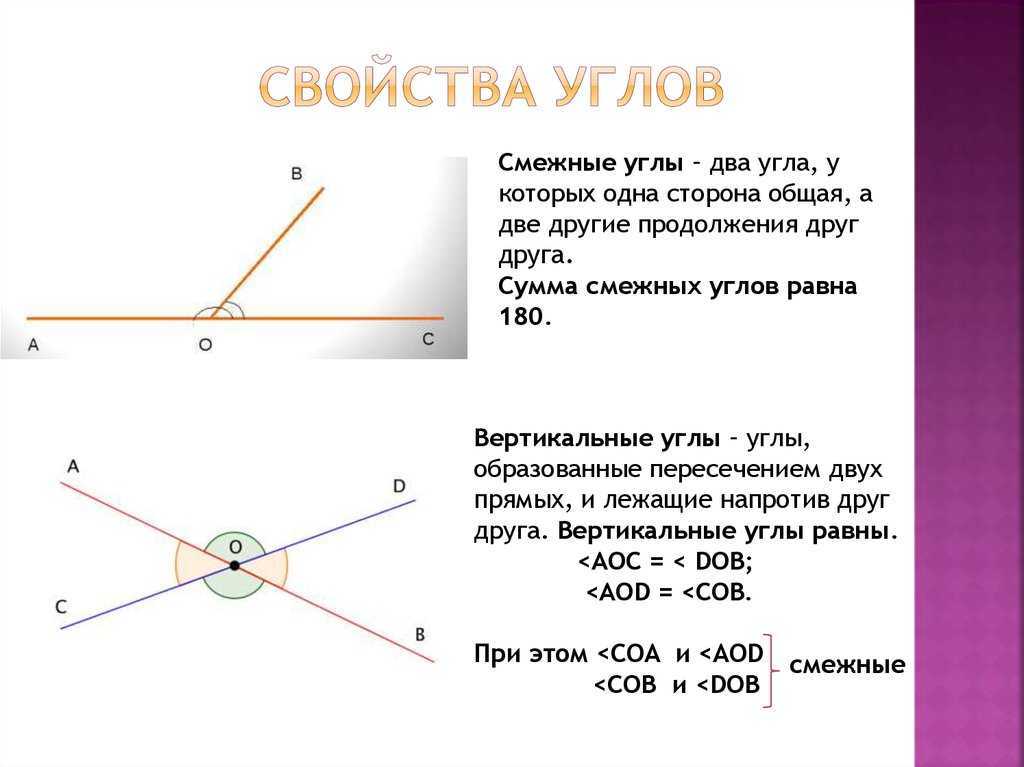
К основным свойствам смежных углов относят
- Смежные углы имеют общую вершину и одну сторону;
- Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
- Синусы смежных углов всегда равны;
- Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.
Как найти смежные углы
Обычно даются три вариации задач на нахождение величины смежных углов
- Дана величина основного угла;
- Дано соотношение основного и смежного угла;
- Дана величина вертикального угла.
Каждый вариант задачи имеет свое решение. Рассмотрим их.
Дана величина основного угла
Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.
Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Дано соотношение основного и смежного угла
В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла.
В этом случае решение будет выглядеть, как уравнение пропорции:
- Обозначаем долю пропорции основного угла, как переменную «Y».
- Долю относящуюся к смежному углу обозначаем, как переменную «Х».
- Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
- Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
- Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
- Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.
Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.
Дана величина вертикального угла
Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.
Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.
Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Также вы можете прочесть наши полезные статьи и .
Что такое смежный угол
Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°.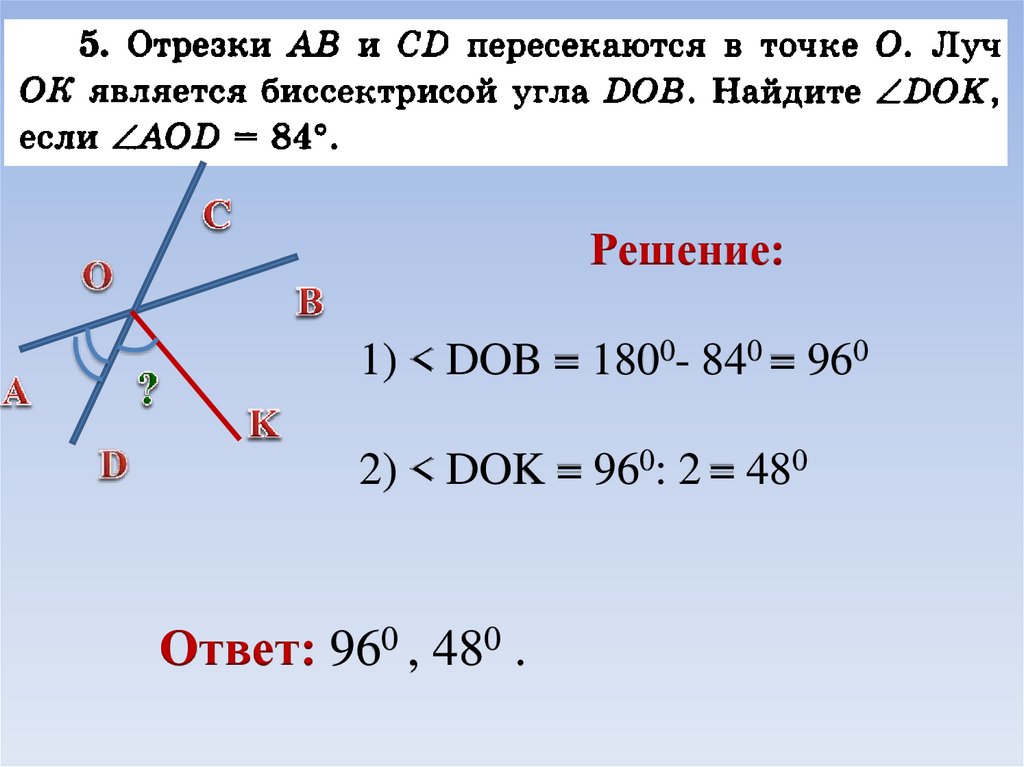
Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
рис. 2
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
рис. 3
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см.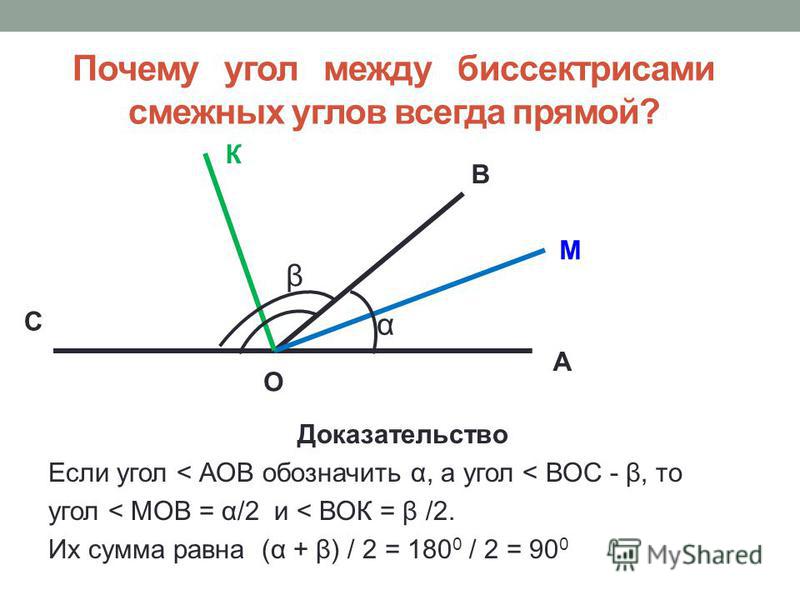
рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
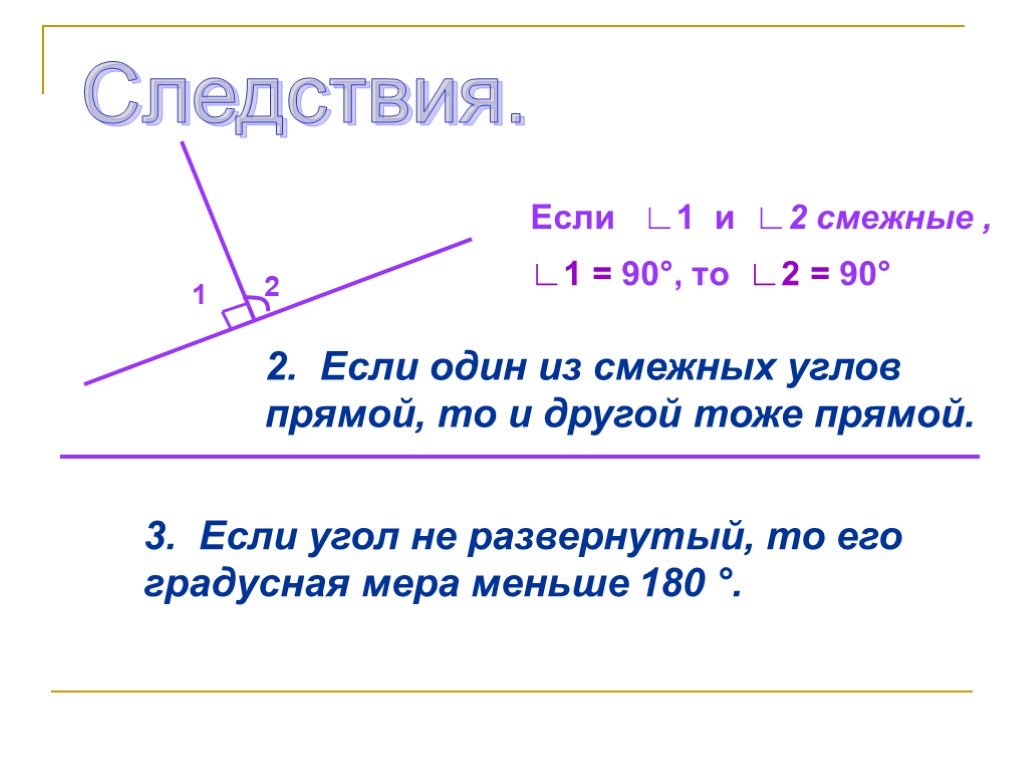
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые.
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол — это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.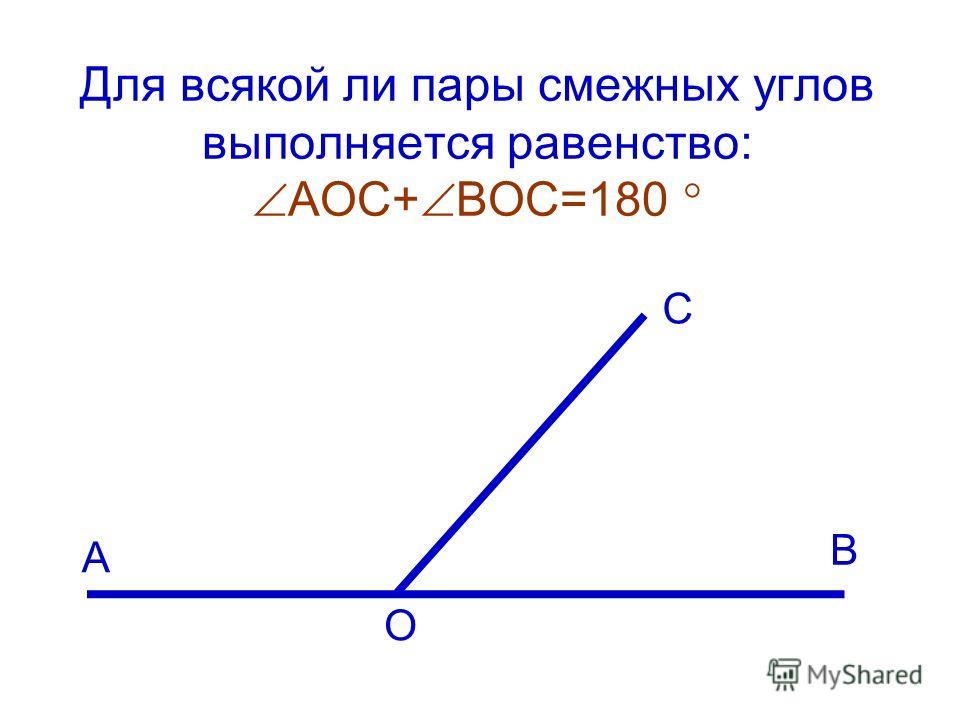
рис. 4
Связь математики с музыкой
«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Задание 1.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Задание 2.
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Задание 3.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.
Математический диктант на повторение ранее выученного материала
1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла.
Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно.
Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Вопросы:
- Что такое угол?
- Какие бывают типы углов?
- Какая особенность смежных углов?
Два угла размещнные на одной прямой и имеющие одну вершину называются смежными.
Иначе — если сумма двух углов на одной прямой равна 180 градусам и одна сторона у них общая, то это смежные углы.
1 смежный угол + 1 смежный угол = 180 градусов.
Смежные углы -это два угла, у которых одна сторона общая, а две другие стороны в целом образуют прямую линию.
Сумма двух смежных углов всегда равна 180 градусам. К примеру, если один угол 60 градусов, то второй обязательно будет равен 120 градусам (180-60).
Углы АОС и ВОС являются смежными углами, потому что соблюдается все условия характеристики смежных углов:
1.
ОС -общая сторона двух углов
2.АО -сторона угла АОС, ОВ -сторона угла ВОС. Вместе эти стороны образуют прямую линию АОВ.
3.Угла два и сумма их равна 180 градусов.
Вспоминая школьный курс геометрии, про смежные углы мы можем сказать следующее:
у смежных углов — одна сторона общая, а другие две стороны принадлежат одной прямой, то есть находятся на одной прямой. Если по рисунку, то углы СОВ и ВОА — это смежные углы, сумма которых всегда равна 180 , так как они разделяют развернутый угол, а развернутый угол всегда равен 180 .
Смежные углы понятие легкое в геометрии. Смежные углы, угол плюс угол дают 180 градусов в общей сумме.
Два смежных угла — это будет один развернутый угол.
Есть еще несколько свойств. Со смежными углами задачи решать и теоремы доказывать легко.
Смежные углы образуются при проведении луча из произвольной точки прямой. Тогда эта произвольная точка оказывается вершиной угла, луч — общей стороной смежных углов, а прямая от которой проведен луч — двумя оставшимися сторонами смежных углов.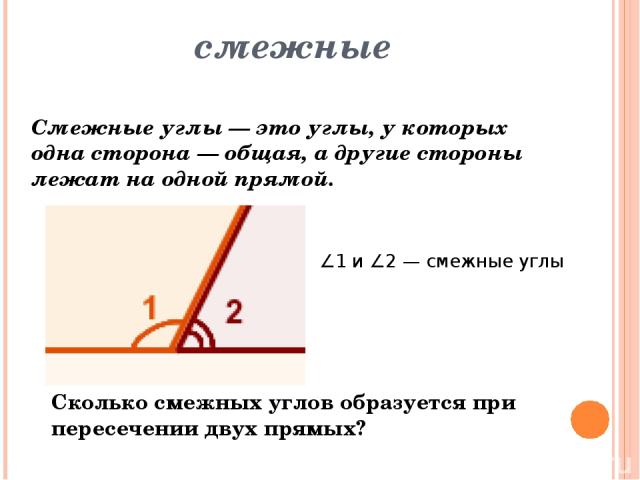
Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.
Итак, что же такое смежный угол? Определение:
Смежными называются два угла с общей вершиной и одной общей стороной, причем две другие стороны этих углов лежат на одной прямой.
И небольшой видео урок, где толково показано про смежные углы, вертикальные углы, плюс про перпендикулярные прямые, которые являются частным случаем смежных и вертикальных углов
Смежные углы — это углы, у которых одна сторона общая, а вторая является одной линией.
Смежные углы — это углы, зависящие друг от друга. То есть если общую строну слегка повернуть, то один угол уменьшится на сколько-то градусов и автоматически второй угол увеличится на столько же градусов.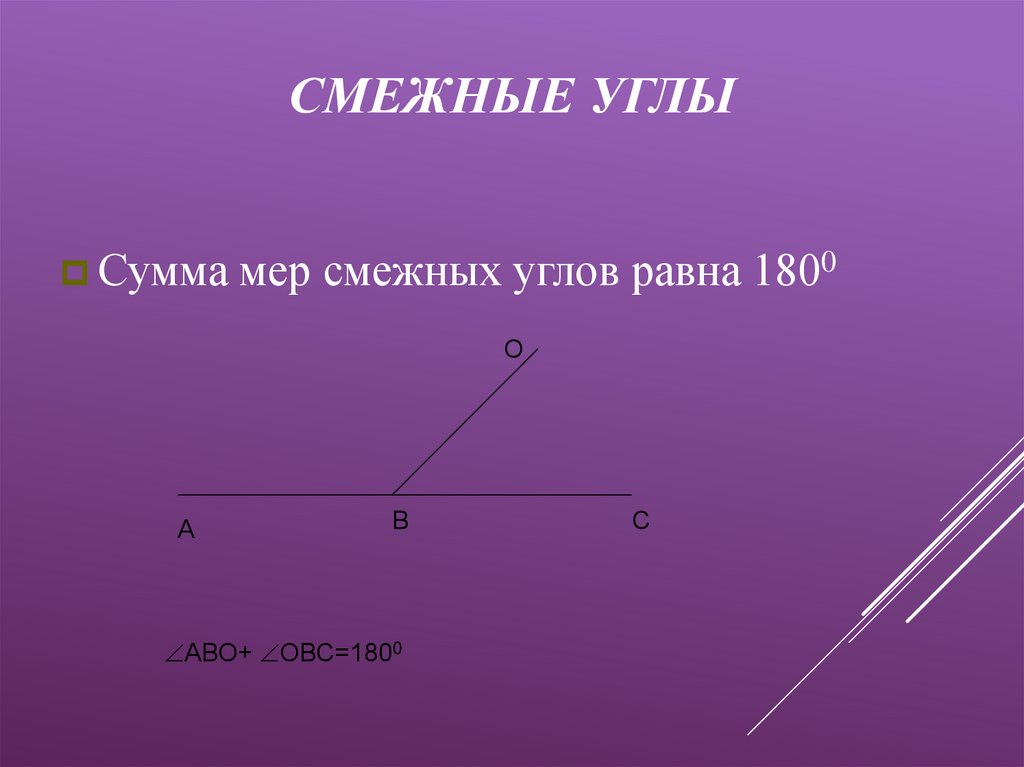
Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.
Общая же сумма смежных углов всегда равна 180 градусов.
Из курса геометрии, (насколько я помню за 6 класс) смежными называются два угла, у которых одна сторона общая, а другие стороны являются дополнительными лучами, сумма смежных углов равна 180. Каждый из двух смежных углов, дополняет другой до развернутого угла. Пример смежных углов:
Смежные углы это два угла с общей вершиной, одна из сторон которых общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные).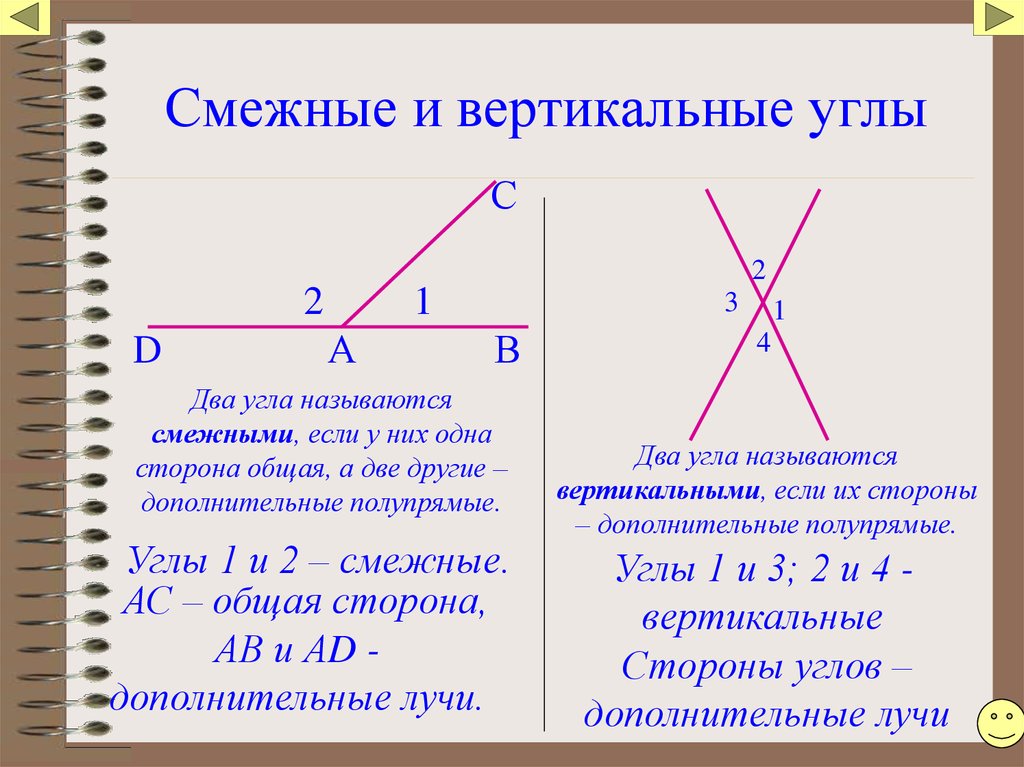
В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано.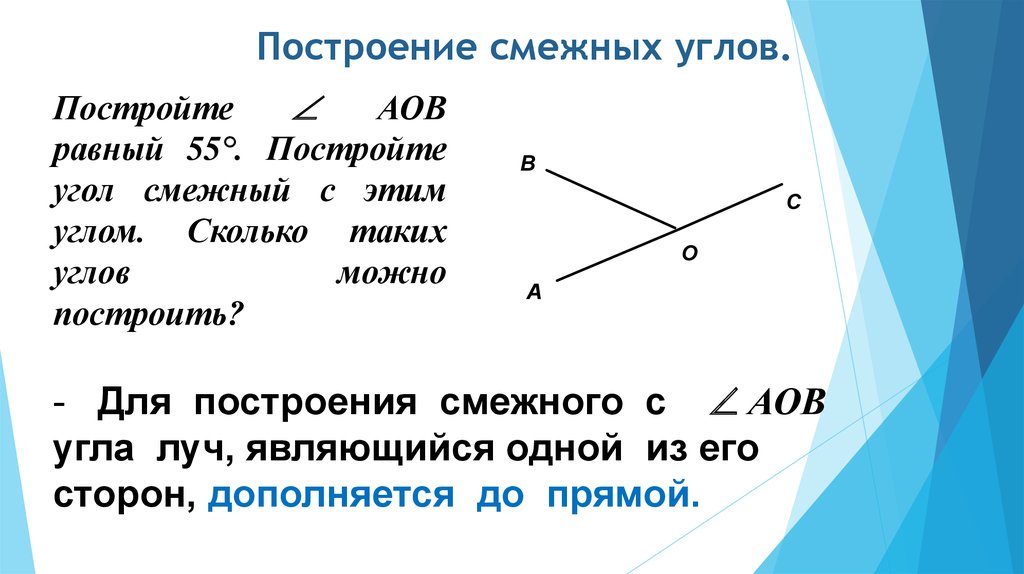
Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.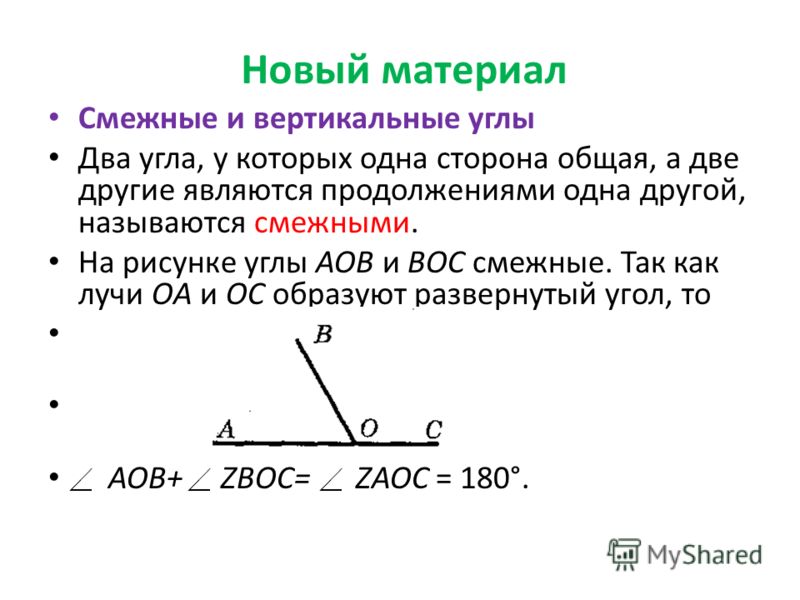
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d.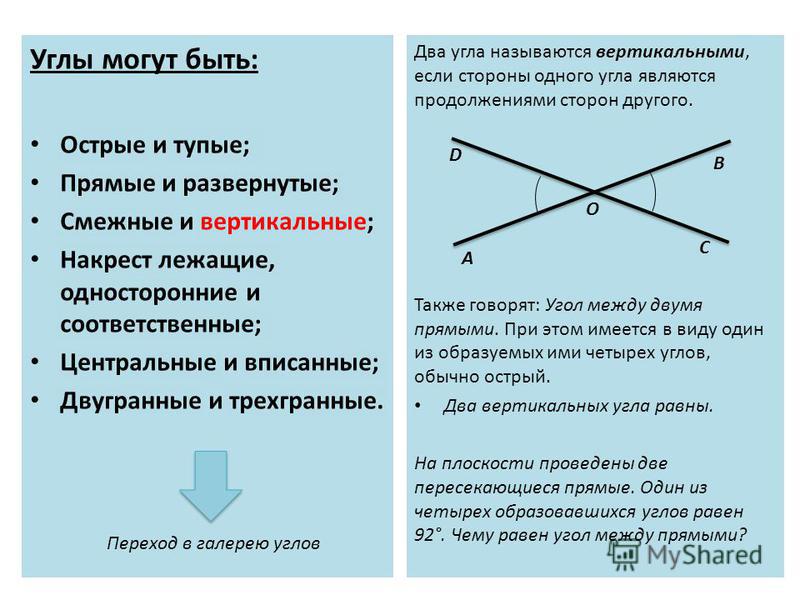
Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис.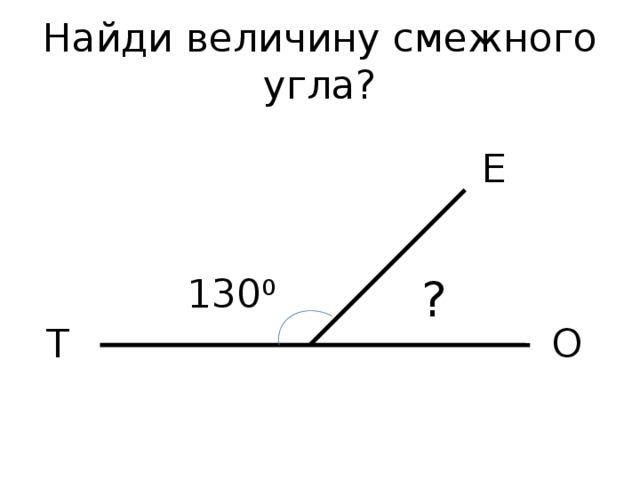
34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 .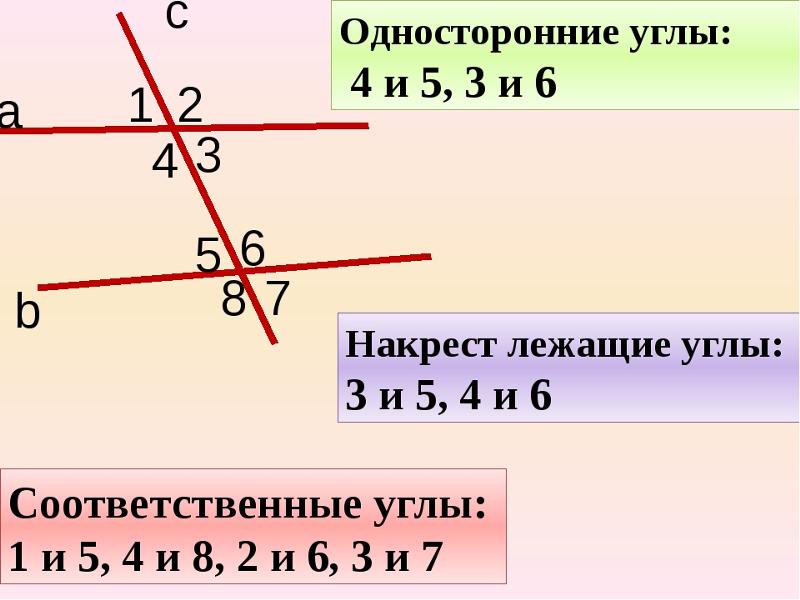
Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.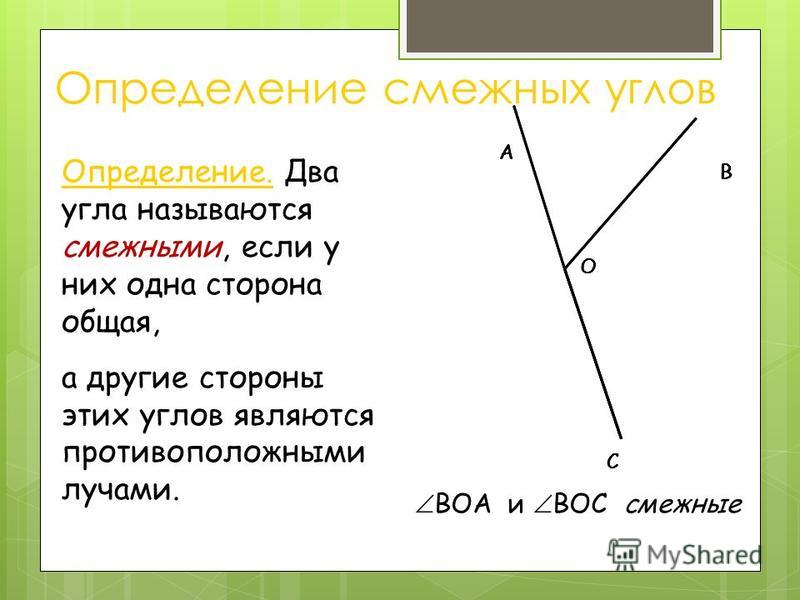
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
Нахождение стороны прямоугольного треугольника
Найдите сторону, зная другую сторону и угол
Мы можем найти неизвестную сторону в прямоугольном треугольнике, если знаем:
- одной длины и
- один угол (кроме прямого угла).
Пример: Глубина до морского дна
Корабль стоит на якоре на морском дне.
Мы знаем:
- длину кабеля (30 м) и
- угол, который кабель образует с морским дном
Итак, мы должны найти глубину!
Но как?
Ответ: использовать синус, косинус или тангенс!
Но какой?
Какой из синус, косинус или тангенс использовать?
Чтобы узнать какие, сначала даем имен сторонам:
- Смежный примыкает (рядом) к углу,
- Противоположный противоположный угол,
- и самая длинная сторона Гипотенуза .
Теперь, для сторона, которую мы уже знаем , и сторона , которую мы пытаемся найти , мы используем первые буквы их имен и фразу «SOHCAHTOA», чтобы решить, какая функция:
СОХ… | S ine: sin(θ) = O pposite / H ypotenuse | |
…КАХ… | C осин: cos(θ) = A djacent / H ypotenuse | |
…ТОА | T угол: tan(θ) = O pposite / A djacent |
Вот так:
Пример: глубина морского дна (продолжение)
Найдите названий двух сторон, над которыми мы работаем:
- сторона, которую мы знаем, это гипотен использовать
- сторона, которую мы хотим найти, равна , противоположной углу (проверьте сами, что «d» находится напротив угла 39°)
Теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», которая дает нам « SOH cahtoa», которая говорит нам, что нам нужно использовать Sine :
S ine: sin(θ) = O pposite / H ypotenuse
Теперь подставим известные нам значения:
sin(39°) = d / 30
9000 4 И решить это уравнение! Но как вычислить sin(39°) .
.. ?
Используйте свой калькулятор. |
sin(39°) = 0,6293…
Теперь у нас есть:
0,6293… = d / 30
Теперь немного перегруппируем и решим:
900 04 Начать с: 0,6293 … = d / 30Поменять местами стороны:d / 30 = 0,6293…
Умножить обе стороны на 30:d = 0,6293… x 30
Рассчитать:d = 18,88 с точностью до 2 знаков после запятой
Глубина заложения анкерного кольца под отверстием составляет 18,88 м
Шаг за шагом
Вот четыре шага, которые необходимо выполнить:
- Шаг 1 Найдите названия двух сторон, которые мы используем, одну, которую мы пытаемся найти, и другую, которую мы уже знаем, из противоположной, смежной и гипотенузы.
- Шаг 2 Используйте SOHCATOA, чтобы решить, какой из синус, косинус или Тангенс для использования в этом вопросе.
- Шаг 3 Для синуса запишите Противоположность/Гипотенуза, для Косинуса запишите Смежность/Гипотенуза или для Тангенса запишите Противоположность/Смежность. Одним из значений является неизвестная длина.
- Шаг 4 Решите, используя свой калькулятор и свои навыки в алгебре.
Примеры
Давайте рассмотрим еще несколько примеров:
Пример: найти высоту самолета.
Мы знаем, что расстояние до самолета равно 1000
А угол равен 60°
Какова высота самолета?
Осторожно! Угол 60° находится вверху, поэтому сторона «h» равна Смежному углу!
- Шаг 1 Мы используем две стороны: A djacent (h) и H ypotenuse (1000).
- Шаг 2 SOH CAH TOA говорит нам использовать C озин.
- Шаг 4 Решить:
Начните с: cos 60° = h/1000
Перестановка: h/1000 = cos 60°
Рассчитать cos 60°: h/ 1000 = 0,5
Умножить обе части к 10:00: ч = 0,5 х 1000
ч = 500
Высота самолета = 500 метров
Шаг 1 Джацент (7).
- Шаг 2 SOHCAH TOA говорит нам использовать агент T .
- Шаг 4 Решить:
Начните с:tan 53° = y/7
Swap:y/7 = tan 53°
Умножить обе части на 7:y = 7 tan 53°
Вычислить:y = 7 x 1,32704…
y = 9,29 до 2 знаков после запятой 90 005
Боковой у = 9,29
Пример: Радиомачта
Имеется мачта высотой 70 метров.
Трос идет к вершине мачты под углом 68°.
Какой длины провод?
- Шаг 1 Мы используем две стороны: O pposite (70) и H ypotenuse (w).
- Шаг 2 SOH CAHTOA говорит нам использовать S ine.
- Шаг 3 Запишите:
sin 68° = 70/ш
- Шаг 4 Решить:
Неизвестная длина стоит внизу (в знаменателе) дроби!
Таким образом, нам нужно использовать несколько иной подход при решении:
Начните с:sin 68° = 70/w
Умножьте обе стороны на w:w × (sin 68°) = 70
Разделите обе стороны на «sin 68°»:w = 70 / (sin 68°)
Рассчитать: w = 70 / 0,9271.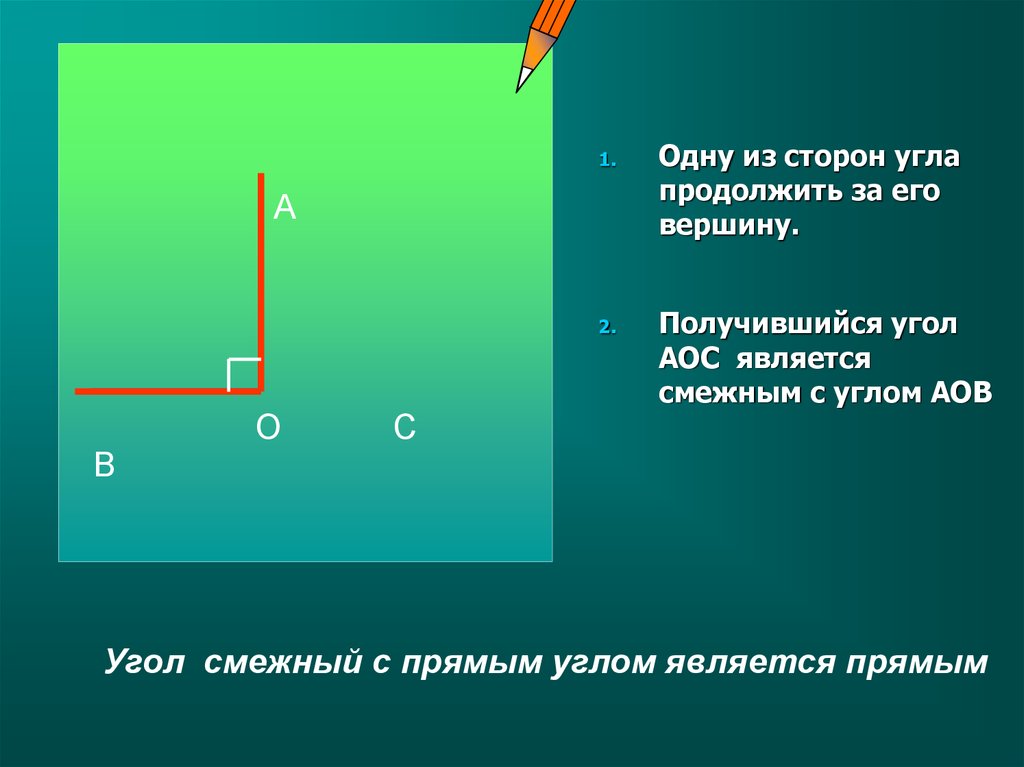
..
w = 75,5 м с точностью до 1 знака после запятой
Длина провода = 75,5 м
258, 1504, 1505, 1506, 1507, 2346, 2347, 2348, 3935, 248
смежных углов — определение, значение, свойства, примеры
LearnPracticeDownload
Смежные углы — это углы, имеющие общее плечо (сторону) и общую вершину, но не пересекающиеся. Угол образуется, когда два луча встречаются в общей конечной точке, а смежные углы — это те углы, которые всегда располагаются рядом друг с другом. Когда сумма двух смежных углов равна 180°, они называются линейной парой углов. Давайте узнаем больше о смежных углах и посмотрим на некоторые примеры смежных углов на этой странице.
| 1. | Что такое смежные углы? |
| 2. | Свойства смежных углов |
| 3. | Примеры смежных углов |
4. | Часто задаваемые вопросы о смежных углах |
Что такое смежные углы?
Два угла называются смежными углами , если они имеют общую вершину, общую сторону и не пересекаются. Обратите внимание на следующий рисунок, чтобы понять, как выглядят смежные углы. Углы 1 и 2 смежные, так как имеют общую сторону BD и общую вершину B.
Смежные углы Определение
Смежные углы — это углы, которые всегда расположены рядом друг с другом таким образом, что они имеют общую вершину и общую сторону, но не перекрывают друг друга.
Примеры смежных углов
Мы можем видеть множество реальных примеров смежных углов.
Смежные углы в реальной жизни
- Самый распространенный реальный пример смежных углов можно увидеть в двух кусках пиццы, расположенных рядом друг с другом.
- Еще один распространенный пример можно увидеть в часах, которые показывают часовую, минутную и секундную стрелки, которые образуют смежные углы, когда все 3 находятся далеко друг от друга.
- Мы можем найти 3 смежных угла в руле автомобиля.
Свойства смежных углов
Приведенные ниже свойства смежных углов помогают нам легко их идентифицировать.
- Смежные углы всегда имеют общее плечо.
- У них общая вершина.
- Они не пересекаются.
- У них есть необычная рука по обеим сторонам общей руки.
- Два смежных угла могут быть дополнительными или дополнительными на основе суммы мер отдельных углов.
Как найти смежные углы?
Смежные углы легко идентифицировать с помощью двух основных свойств — смежные углы всегда имеют общую сторону и общую вершину. Если любые два угла удовлетворяют только одному из этих свойств, они не будут считаться смежными углами. Необходимо, чтобы углы выполняли оба свойства. Например, если любые два угла имеют общую вершину, но между ними есть угол, это означает, что они не имеют общей стороны. Следовательно, они не могут быть смежными углами.
Обратите внимание на следующий рисунок, чтобы определить смежные углы.
Важные примечания
Вот список нескольких важных примечаний, относящихся к соседним углам.
- Если два угла смежные, то их сумма равна углу, образованному двумя не общими плечами и одним общим плечом.
- Если луч стоит на прямой, то сумма образующихся смежных углов равна 180°.
- Если сумма двух смежных углов равна 180°, то они называются парой линейных углов. Все линейные пары являются дополнительными, поскольку сумма дополнительных углов составляет 180°. Однако не обязательно, чтобы все дополнительные углы были линейными парами. Чтобы образовать линейную пару, линии должны пересекаться друг с другом и образовывать смежные углы.
- Если сумма двух смежных углов равна 180°, то необщие стороны образуют прямую.
☛Статьи по теме
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о смежных углах и связанных с ними темах.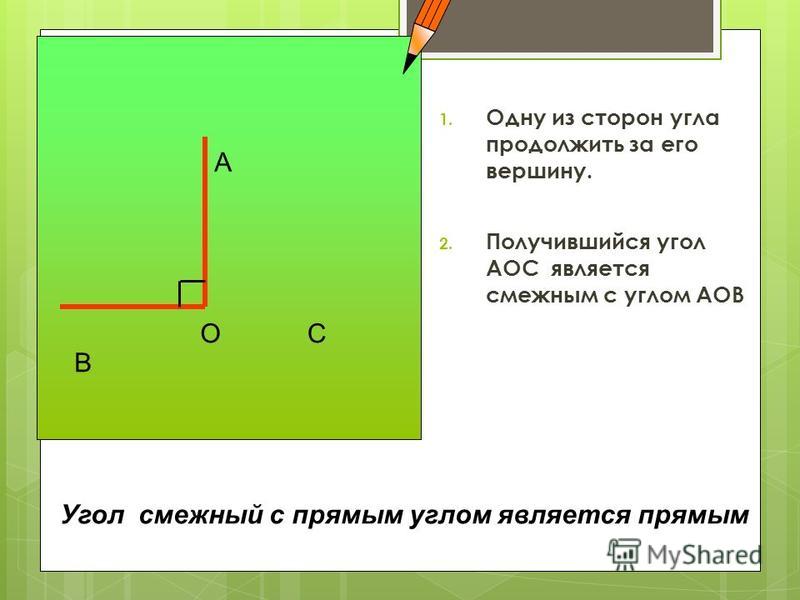
- Пары уголков
- Дополнительные уголки
- Измерение углов
- Прямой угол
- Типы углов
Смежные углы Примеры
Пример 1: Перечислите 5 пар смежных углов на следующем рисунке.
Решение: Ниже приведены пять пар смежных углов.
∠AOE, ∠EOC
∠EOC, ∠COB
∠COB, ∠BOD
∠BOD, ∠AOD
∠AOD, ∠АОЕ
Пример 2: Смежны ли углы, отмеченные цифрами 1 и 2 на следующих рисунках? Обоснуйте свои ответы.
Решение: Ясно, что ∠1, ∠2 имеют общую вершину O и общий луч OB. Следовательно, ∠1, ∠2 — смежные углы.
Пример 3: Укажите истинное или ложное значение относительно свойств смежных углов.
а.) Смежные углы всегда являются дополнительными.
б.) Смежные углы всегда имеют общую вершину и общее плечо.
c.) Если два смежных угла на прямой относятся как 2 : 3, то градусная мера этих углов равна 72° и 108°
Решение:
а) Ложные смежные углы не всегда могут быть дополнительными. Если любые два смежных угла образуют вместе прямую, то они образуют дополнительные смежные углы.
б.) Правда, смежные углы всегда имеют общую вершину и общее плечо.
в) Если два смежных угла на прямой относятся как 2 : 3, то градусная мера этих углов равна 72° и 108°
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по смежным углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о смежных углах
Что такое смежные углы в геометрии?
Два угла называются смежными углами , если они имеют следующие характеристики:
- Имеют общую вершину.
- Они имеют общую сторону или луч.
- Они не пересекаются.
Могут ли 2 смежных угла быть дополнительными?
Да, смежные углы могут быть дополнительными, если их сумма составляет 180°. Смежные углы можно определить как два угла, которые имеют общую вершину и общую сторону. Любые два смежных угла могут быть дополнительными углами или дополнительными углами в зависимости от суммы измерения углов.
Могут ли вертикальные углы быть смежными?
Нет, вертикальные углы никогда не могут быть смежными. Смежные углы — это два угла рядом друг с другом, в то время как вертикальные углы противоположны друг другу.
Приведите несколько примеров смежных углов в повседневной жизни.
Смежные углы часто встречаются в нашей повседневной жизни. Например, в руле автомобиля, трех стрелках часов, двух кусочках пиццы, которые лежат рядом друг с другом в коробке из-под пиццы, и так далее.
Могут ли 2 смежных угла перекрываться?
Нет, смежные углы никогда не могут находиться один над другим, или, другими словами, углы не могут перекрываться.
Углы, расположенные рядом друг с другом в одной вершине и имеющие общую сторону, являются смежными углами.
Что дают в сумме смежные углы?
Сумма двух смежных углов может быть либо дополняющей, либо дополняющей в зависимости от их величин. Если два смежных угла положить рядом друг с другом на прямой линии, они дадут в сумме 180°, потому что это будут смежные дополнительные углы. Если смежные углы не образуют линейных пар, то их сумма не будет равна 180°.
В чем разница между смежными углами и парой линейных углов?
Смежные углы могут образовывать или не образовывать вместе прямую линию. Им просто нужно выполнить то свойство, что они имеют общую вершину и общую сторону. Однако линейная пара углов всегда образует прямую линию, и, следовательно, их сумма всегда равна 180°.
Как определить смежные углы?
Смежные углы легко идентифицировать с помощью двух основных свойств:
- Смежные углы всегда имеют общую сторону.
- Смежные углы всегда имеют общую вершину.
