Онлайн дробный калькулятор с целыми числами и десятичными дробями: Онлайн калькулятор для преобразования десятичных дробей в обыкновенные дроби

Содержание

Онлайн калькулятор дробей

В математике для обозначения части целого или целого и его части используется понятие дроби. По форме записи выделяют обыкновенные дроби и десятичные.

Обыкновенные дроби

Обыкновенная дробь – это форма записи рационального числа в виде \(\frac{m}{n}\), где m – натуральное число, n – рациональное. Здесь m является числителем, а n – знаменателем. Известно, что любое натуральное число можно представить в виде дроби, то есть как частное от деления одного натурального числа на другое.

Примеры таких дробей: \(\frac{7}{10}\), \(\frac{187}{3}\), \(\frac{2}{2}\)

В свою очередь, обыкновенные дроби можно разделить на правильные и неправильные. В правильных дробях числитель меньше знаменателя, а также все выражение меньше 1: \(\frac{5}{8}\), \(\frac{3}{10}\), \(\frac{145}{146}\)

Неправильная дробь больше или равна 1, а ее числитель больше знаменателя или равен ему: \(\frac{13}{12}\), \(\frac{147}{4}\), \(\frac{11}{11}\)

Также любую неправильную дробь можно представить в виде суммы целой и дробной частей, при этом дробная часть либо правильная дробь, либо равна 0. Такое представление называют смешанным числом. Чтобы получить его, нужно выполнить следующий алгоритм:

Разделим числитель дроби на ее знаменатель и получим остаток, если он есть.
Полученное частное – это целая часть смешанного числа, остаток – это числитель дробной части, а знаменатель дробной части совпадает со знаменателем неправильной дроби.

Пусть дана дробь \(\frac{35}{4}\). Разделив числитель на знаменатель, получим: \(35=8\cdot4+3\). Здесь 8 — целая часть смешанного числа, 3 — числитель дробной части, а 4 — ее знаменатель. Получим: \(8\frac{3}{4}\)

Основное свойство обыкновенных дробей

Основное свойство дроби заключается в том, что при домножении числителя и знаменателя на одно и то же число получается равная первоначальной дробь.

\[\frac{3}{7}=\frac{3\cdot4}{4\cdot4}=\frac{12}{16}\]

Как следствие, можно сокращать дроби, то есть делить числитель и знаменатель на общий делитель с получением новой дроби, имеющей такое же значение, как и первоначальная.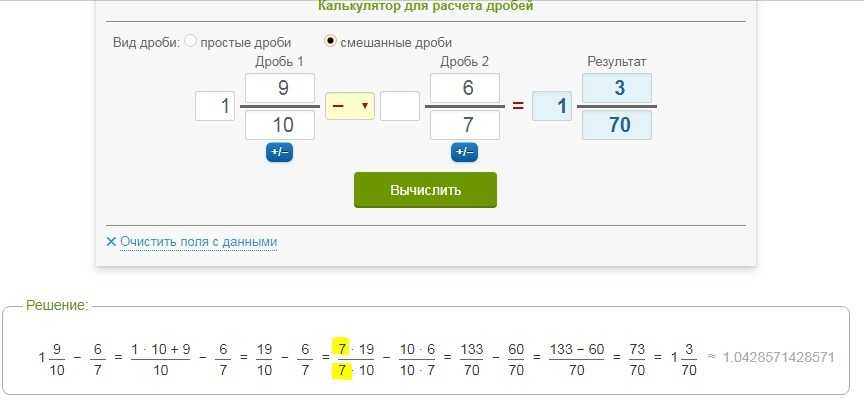 n}\), где p –целое, n – натуральное.

\[0,5,~3,14\dots,~0,124(33)\]

Здесь целая часть – это числа до запятой, дробная – числа после запятой.

Известно, что любую обыкновенную дробь, являющуюся в свою очередь рациональным числом, можно преобразовать в десятичную:

\[\frac{37}{4}=\frac{37\cdot25}{4\cdot25}=9,25\]

Десятичные дроби делятся на:

Конечные, то есть имеющие конечное число знаков после запятой. Существует теорема, утверждающая, что действительное число можно представить в виде конечной десятичной дроби тогда и только тогда, когда его можно представить как несократимую обыкновенную дробь, знаменатель может иметь в своем разложении на простые числа только 2 и 5: \(9,25,~0,12567,~35,1\)

Бесконечные десятичные дроби имеют бесконечное число знаков после запятой. Например, число \(pi=3,14159\dots\).
Периодические десятичные дроби относятся к бесконечным, но они среди знаков после запятой имеют последовательность цифр, повторяющуюся с определенного знака:\(9,28(5),~0,55(67),~35,(1)\). Здесь период – это повторяющаяся группа цифр (или одна повторяющаяся цифра).

Действия с дробями

Определены действия сложения, вычитания, умножения и деления дробей. Также на множестве действительных и рациональных чисел существует отношение порядка, поэтому дроби можно сравнивать между собой.

Сравнение дробей

Известно, что если обыкновенные дроби имеют одинаковые знаменатели, большая дробь та, у которой больший числитель.

\[\frac{7}{6}>\frac{1}{6}\]

Если же у дробей различные знаменатели, то сначала они приводятся к общему знаменателю, а затем точно так же сравниваются по числителям.

\[\frac{3}{7}

В десятичных дробях сначала сравниваются целые части – дробь, имеющая большую целую часть, больше.

\[8,24

Если же целые части равные, то идет аналогичное сравнение по знакам после запятой.

\[17,6794>17,67\]

Сложение дробей

Для обыкновенных дробей с одинаковыми знаменателями сложение выполняется по следующему правилу:

\[\frac{a}{n}+\frac{b}{n}=\frac{a+b}{n}\]

Например:

\[\frac{1}{13}+\frac{10}{13}=\frac{1+10}{13}=\frac{11}{13}\]

Кроме того:

\[\frac{a}{b}+0=0+\frac{a}{b}=\frac{a}{b}\]

Дроби с разными знаменателями сначала приводят к общему знаменателю, а затем складывают:

\[\frac{a}{b}+\frac{c}{d}=\frac{a\cdot d+c\cdot b}{bd}\]

К примеру:

\[\frac{6}{7}+\frac{1}{2}=\frac{6\cdot2+1\cdot7}{7\cdot2}=\frac{19}{14}=1\frac{5}{14}\]

При сложении смешанных чисел сначала складываются их целые части, а затем дробные по правилам сложения дробей.

\[1\frac{3}{5}+2\frac{1}{5}=3\frac{4}{5}\]

При действии с десятичными дробями в начале складываются целые части, а потом поразрядно дробные, начиная с младшего разряда.

\[245,319+12,24=257,559\]

Так как дроби – это всего лишь представления действительных и рациональных чисел, на них распространяются свойства ассоциативности и коммутативности.

Умножение дробей

При умножении обыкновенных дробей в числитель полученной дроби записывается произведение числителей множителей, а в знаменатель – произведение знаменателей. То есть:

\[\frac{a}{b}\cdot\frac{c}{d}=\frac{ac}{bd}\]

Например:

\[\frac{4}{27}\cdot\frac{9}{16}=\frac{4\cdot9}{27\cdot16}=\frac{1}{12}\]

Кроме того:

\[\frac{a}{b}\cdot n=n\cdot\frac{a}{b}=\frac{a\cdot n}{b}\]

В частности:

\[\frac{a}{b}\cdot0=0\cdot\frac{a}{b}=0\]

Если перемножаются смешанные числа, то сначала они переводятся в неправильные дроби, а затем действует первое правило:

\[5\frac{2}{7}\cdot6\frac{1}{8}=\frac{37}{7}\cdot\frac{49}{8}=\frac{37\cdot49}{7\cdot8}=\frac{259}{8}=32\frac{3}{8}\]

При умножении десятичных дробей выполняют данное действие, не обращая внимания на наличие запятых, а затем в полученном числе ставят запятую, отделяя ей столько чисел справа, сколько имеется знаков после запятой в обоих множителях вместе.

\[3,4\cdot18,2=61,88\]

Также выполняются свойства коммутативности, ассоциативности.

Деление дробей

При делении одной обыкновенной дроби на другую вводится понятие взаимно обратных дробей, то есть дробей, дающих в произведении 1.

Для проведения действия деления необходимо делимое домножить на дробь, взаимно обратную делителю, по правилу умножения.

\[\frac{a}{b}:\frac{c}{d}=\frac{a}{b}\cdot\frac{d}{c}=\frac{ad}{bc}\]

Например:

\[\frac{3}{8}:\frac{9}{16}=\frac{3}{8}\cdot\frac{16}{9}=\frac{3\cdot16}{8\cdot9}=\frac{2}{3}\]

Кроме того:

\[\frac{a}{b}:n=\frac{a}{b\cdot n}\]

При делении двух смешанных чисел они сначала приводятся к виду неправильной дроби, а затем только делятся одно на другое.

\[3\frac{2}{3}:1\frac{1}{6}=\frac{11}{3}:\frac{7}{6}=\frac{11}{3}\cdot\frac{6}{7}=\frac{22}{7}=3\frac{1}{7}\]

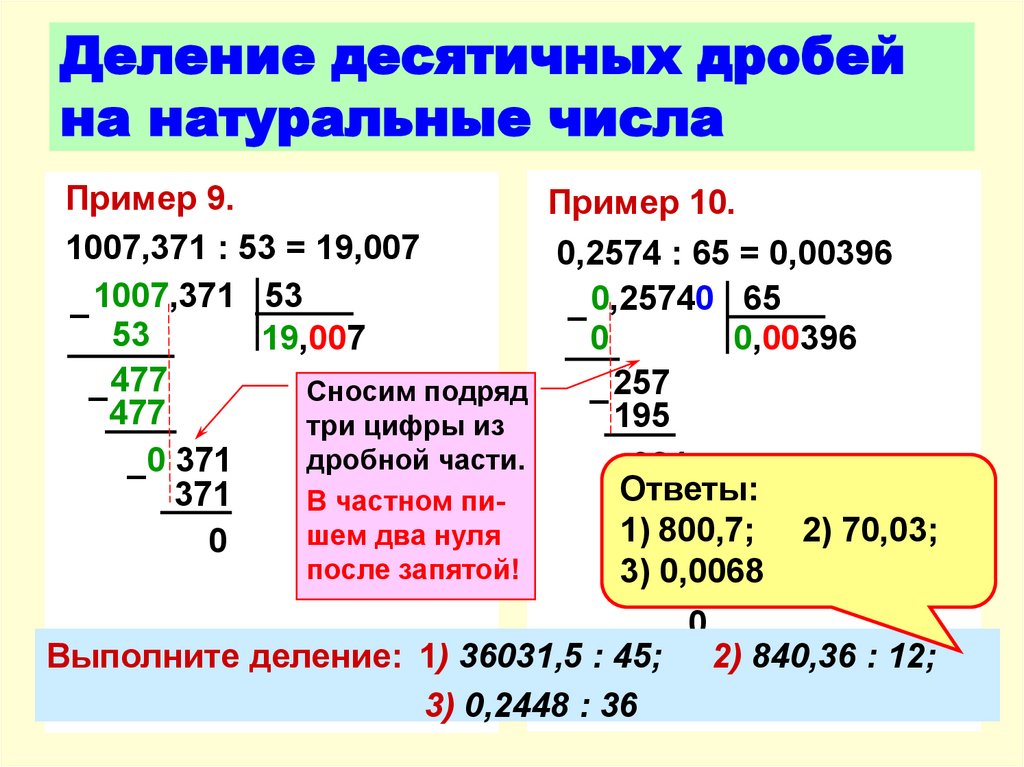
Если нужно разделить десятичную дробь на число, то действуют аналогично делению двух целых чисел, а запятая ставится сразу после того, как целая часть была разделена на число.

\[22,1:13=1,7\]

При делении одной десятичной дроби на другую необходимо действовать следующим образом: в делимом и делителе переносят запятую вправо на столько знаков, сколько их в делителе после запятой. Затем выполняется обычное деление десятичной дроби на число.

\[36,4:0,065=36400:65=560\]

Быстро выполнить действия над дробями можно с помощью онлайн калькулятора дробей. Наш бесплатный калькулятор позволит сложить дроби любого вида, перемножить, разделить за считанные секунды. Все, что вам необходимо сделать — это просто ввести данные обыкновенные, десятичные или смешанные дроби в калькуляторе. Информацию про наш сервис можно посмотреть здесь. А если у вас остались вопросы, то вы можете задать их в нашей группе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Калькулятор Смешанных Чисел — Mathcracker.Com

Решатели Алгебра

Инструкции: Используйте этот калькулятор для вычисления смешанных дробей. Укажите смешанную дробь в поле ниже.

Смешанная дробь, которую вы хотите преобразовать (Например: 2 3/2)

Как использовать этот калькулятор смешанных чисел

Калькулятор смешанных дробей поможет вам вычислить любое алгебраическое выражение со смешанными числами и дробями, которые вы предоставите. Например, вы можете ввести смешанное число ‘2 3/4’, и калькулятор преобразует его в обычную дробь и уменьшит ее.

После того, как вы ввели смешанное число/ дробное выражение, вам нужно нажать «Вычислить», и все шаги будут показаны для вас.

Что такое смешанная дробь

A смешанная фракция это просто целое число, которое идет вместе с дробью. Формат такой: сначала идет целое число, затем пробел, а затем дробь. Например, следующая дробь является смешанной:

\[2\,\,\frac{2}{3}\]

В данном случае целое число — «2», а дробь — «2/3». Наличие этих двух элементов вместе в данном случае означает, что мы их складываем. Таким образом, когда мы пишем смешанная дробь, мы имеем в виду следующее:

\[2\,\,\frac{2}{3} = 2 + \frac{2}{3}\]

Как вычислить смешанные числа

Основная идея заключается в простом сокращении смешанного числа до суммы дробей. То есть необходимо разделить целую и дробную части смешанного числа и оперировать ими как обычными дробями.

Каковы этапы вычисления смешанных чисел

Шаг 1: Четко определите, какое смешанное число мы хотим проанализировать
Шаг 2: Извлечение целой части и дробной части смешанного числа
Шаг 3: Преобразуйте целую часть в дробь, а затем просто оперируйте ими как дробями

Зачем иметь дело со смешанными дробями?

Использование смешанных дробей (также известных как смешанные числа) — это своего рода унаследованная нотация. На самом деле она не имеет заметного значения и не играет никакой важной роли. Но знать, как ими оперировать, полезно, поскольку они время от времени появляются в формулах.

Пример: вычисление смешанного числа

Запишите в виде дроби: \(1\,\,\frac{1}{3}\).

Решение:

Нам нужно упростить следующую заданную смешанную дробь: \(\displaystyle 1 \,\, \frac{ 1}{ 3}\).

Получается следующий расчет:

\( \displaystyle 1 \,\, \frac{ 1}{ 3}\)

This is the given mixed fraction

\( = \,\,\)

\(\displaystyle 1\,\,\frac{ 1}{ 3}\)

By definition, the mixed fraction can be written this way

\( = \,\,\)

\(\displaystyle 1+\frac1{ 3}\)

Using \(3\) as the common denominator

\( = \,\,\)

\(\displaystyle \frac{ 1 \times 3 + 1}{ 3}\)

This is a regular fraction obtained after expanding the denominator

\( = \,\,\)

\(\displaystyle \frac{ 4}{ 3}\)

чем завершается расчет.

Пример: еще одно вычисление смешанных дробей

Вычислите следующее смешанное число \(3 + 2\,\,\frac{2}{3}\).

Решение:

Сначала нужно упростить следующую заданную смешанную дробь: \(\displaystyle 2 \,\, \frac{ 2}{ 3}\).

Получается следующий расчет:

\( \displaystyle 2 \,\, \frac{ 2}{ 3}\)

This is the given mixed fraction

\( = \,\,\)

\(\displaystyle 2\,\,\frac{ 2}{ 3}\)

By definition, the mixed fraction can be written this way

\( = \,\,\)

\(\displaystyle 2+\frac2{ 3}\)

Using \(3\) as the common denominator

\( = \,\,\)

\(\displaystyle \frac{ 2 \times 3 + 2}{ 3}\)

This is a regular fraction obtained after expanding the denominator

\( = \,\,\)

\(\displaystyle \frac{ 8}{ 3}\)

Теперь нам нужно вычислить и упростить следующее выражение: \(\displaystyle 3+\frac{8}{3}\).

Получается следующий расчет:

\( \displaystyle 3+\frac{8}{3}\)

Amplifying in order to get the common denominator 3

\( = \,\,\)

\(\displaystyle 3\cdot\frac{3}{3}+\frac{8}{3}\)

Finding a common denominator: 3

\( = \,\,\)

\(\displaystyle \frac{3\cdot 3+8}{3}\)

Expanding each term: \(3 \times 3+8 = 9+8\)

\( = \,\,\)

\(\displaystyle \frac{9+8}{3}\)

Adding up the terms in the numerator

\( = \,\,\)

\(\displaystyle \frac{17}{3}\)

чем завершается расчет.

Другие дробные вычисления

Смешанные числа реже используются в математических обозначениях, поскольку более практичным является их выражение в виде обычных дробей. В определенной степени преобразование дробей в смешанные числа почти аналогично перевод из дробной в десятичную систему , поскольку вы определяете целую часть и десятичную часть.

Смешанные дроби по сути соответствуют дробному исчислению, в котором «пустое место» между целым числом и дробью можно заменить знаком «+», так что получается простое сложение дробей.

Онлайн-калькулятор дробей поддерживает сложение, умножение, вычитание и деление дробей.

Калькуляторы можно использовать для сложения, вычитания, умножения или деления дробей. Кроме того, существуют также инструменты, которые можно использовать для упрощения дробей или преобразования десятичных чисел в дроби и наоборот.

Калькулятор правильных/неправильных дробей
Этот калькулятор может выполнять сложение, вычитание, умножение или деление правильных и неправильных дробей. Ввод, указанный в любом из полей, может быть как положительным, так и отрицательным числом.

Калькулятор смешанных чисел
Этот калькулятор можно использовать для сложения, вычитания, умножения или деления смешанных дробей. Ввод, указанный в любом из полей, может быть как положительным, так и отрицательным числом.

Калькулятор упрощения дробей
Этот инструмент можно использовать для упрощения смешанных дробей. Здесь ввод, предоставленный в поле целого числа, может быть как положительным, так и отрицательным.

Калькулятор десятичных дробей
Этот калькулятор преобразует десятичные числа в дроби. Введенные здесь данные могут быть как положительными, так и отрицательными числами.

Калькулятор дробей в десятичные числа
Этот калькулятор преобразует дроби в десятичные числа. Ввод, указанный в любом из полей, может быть как положительным, так и отрицательным числом.

Калькулятор дробей больших чисел
Этот калькулятор можно использовать для вычислений дробей с очень большими целыми числами.

Что такое дроби?
Дроби используются для представления некоторой части целого. Дроби обычно имеют формат a/b. Здесь число до косой черты называется числителем, а число после косой черты называется знаменателем. Знаменатель представляет собой целое, а числитель представляет количество равных частей целого.

Например: Предположим, все это представляет собой лоток с 12 яйцами. Когда лоток полон, его можно представить дробью 12/12. Теперь, если вы достанете из лотка 5 яиц, то вынутая часть будет представлена дробью 5/12. Принимая во внимание, что часть, оставшаяся в лотке, будет представлена дробью 7/12.

В общем, есть три типа дробей, которые упомянуты ниже:

Правильные дроби: В этом виде дроби значение числителя ниже значения знаменателя. Дроби, такие как 3/7, 2/9и т. д. можно назвать правильными дробями.
Неправильные дроби: Для этих дробей значение числителя больше или равно знаменателю. Например, 9/5, 12/12, 267/23 и т. д. — все это неправильные дроби.
Смешанные дроби: Эти дроби представляют собой другой способ представления неправильных дробей. Их также можно назвать упрощенной версией неправильных дробей. Например, неправильную дробь 19/4 можно представить как смешанную дробь 4 ¾.

Дроби могут быть как положительными, так и отрицательными числами. Знаменатель дроби не может быть равен нулю (0).

Что такое калькулятор дробей?
Приведенные выше калькуляторы дробей представляют собой цифровые инструменты, которые можно использовать для выполнения математических расчетов с использованием дробей. Эти калькуляторы можно использовать для сложения, вычитания, умножения или деления правильных, неправильных или смешанных дробей. Существуют также инструменты, которые можно использовать для упрощения смешанных дробей или преобразования десятичных чисел в дроби и наоборот.

Как работают эти калькуляторы дробей?
Будучи онлайн-инструментами, вышеуказанные калькуляторы дробей могут быть легко доступны с таких устройств, как смартфон или ноутбук с подключением к Интернету. Ниже приводится краткое описание того, как работает каждый из этих калькуляторов:

Калькулятор правильных и неправильных дробей
Этот калькулятор может выполнять вычисления с использованием правильных и неправильных дробей. В этом калькуляторе есть два раздела, где можно ввести нужные дроби. В каждом из этих разделов есть отдельное поле для ввода числителя и знаменателя дроби. Ввод, указанный в любом из этих полей, может быть как положительным, так и отрицательным. Между обоими разделами есть поле с раскрывающимся меню, в котором перечислены все математические функции, которые можно применять между обеими дробями. В этом меню пользователи могут выбрать сложение (+), вычитание (-), умножение (x) или деление (/). Введите необходимые данные и нажмите кнопку «Рассчитать», чтобы просмотреть результат.

Отображение вывода: Страница результатов этого калькулятора дает вывод в виде дроби, а также в десятичном виде. Шаги, задействованные в расчете, отображаются прямо под результатом. Кроме того, под ним есть кнопка «+ Показать дальнейшее объяснение», которую можно щелкнуть, чтобы просмотреть объяснение шагов, связанных с расчетом.