Как построить и прочитать график функции: Построение графика функции y = f(x + l) + m — урок. Алгебра, 8 класс.

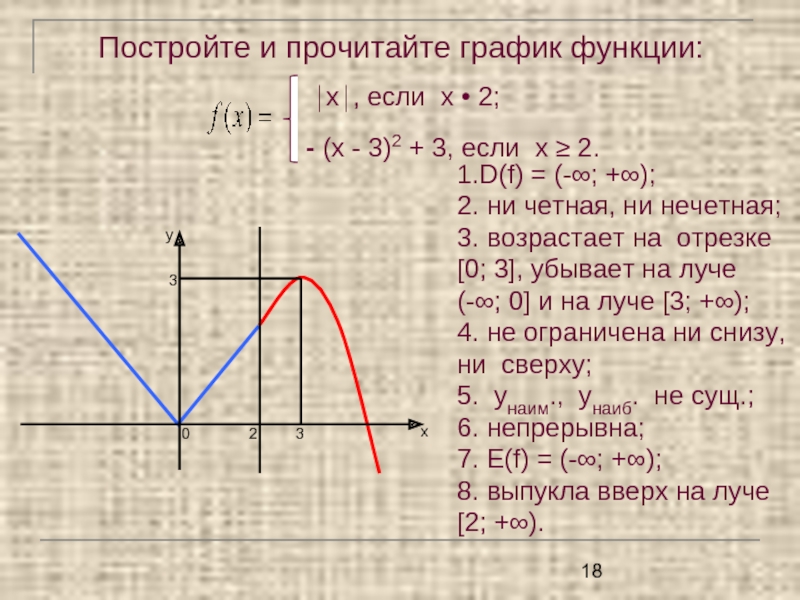
«Чтение свойств функции по графику функции»

Конденко Любовь Николаевна

Учитель высшей квалификационной категории

Средней школы № 1 г. Елабуга

ТЕМА: «ЧТЕНИЕ СВОЙСТВ ФУНКЦИИ ПО ГРАФИКУ ФУНКЦИИ»

“График – это говорящая линия,

которая может о многом рассказать”

М.Б. Балк

Цели:

• Образовательные

Продолжить формирование у учащихся понятия, что функция- математическая модель, позволяющая описывать изучать разнообразные зависимости между реальными величинами.

Обобщить и систематизировать систему функциональных понятий (функция, значение функции, график, аргумент, область определения и область значений функции, возрастание, убывание, монотонность, сохранение знака). Формирование свободного чтения графиков, формирование умений отражать свойства функций на графике.

• Развивающие

Развитие всех познавательных процессов, в частности функционального стиля мышления. Развитие графической культуры.

• Воспитательные

Вырабатывать внимание, самостоятельность при работе на уроке. Воспитывать гордость за учёных, инженеров, конструкторов, создавших теорию графиков, применивших теорию к практической деятельности .Осуществлять профессиональную ориентацию учащихся.

1.Актуализация знаний

 

2. Формирование умений , навыков.

Функция – одно из основных математических общенаучных понятий, зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает различные законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении у = х² геодезист или геометр увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы у сопротивления воздуха или воды от скорости х движения. Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации. В школьном курсе изучается немало функций.

Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их предметы взаимосвязаны. Они еще не умели считать , но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя не будет голодать; чем сильнее натянуть тетиву лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее в пещере.

Оно сыграло и поныне играет большую роль в познании реального мира .Идея функциональной зависимости присутствует уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами.

Функция является одним из основных понятий математики, в частности математического анализа, так как математические модели реальных ситуаций, изучаемые на протяжении всего курса алгебра, напрямую связаны с функциями.

В технике и физике часто пользуются именно графическим способом задания функции. Более того , по- мере развития математики все активнее проникает графический метод в самые различные области жизни человека. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике.

 

Задание № 1.

 

Само слово «функция» (от латинского functio — совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673 году в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати он его ввел с1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа». В восемнадцатом веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».

Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во «Введении в анализ бесконечного»): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего восемнадцатого века.

Как видно из представленных определений, само понятие функции фактически отождествлялось с аналитическим выражением. Новые шаги в развитии естествознания и математики вызвали и дальнейшее обобщение понятия функции.

 

Графиком функции — называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции.

График функции у =f(x)) строиться по точкам; чем больше точек вида (х;f(Х)) мы возьмем, тем более точное представление о графике получим. Если этих точек взять достаточно много, то и представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает нам, что график нужно изобразить в виде сплошной линии.

Находясь на выставке картин, мы рассматриваем произведения искусств и обращаем внимание на то, сумел ли художник предать глубину, завершенность образного содержания.

Картина является итогом длительных наблюдений и размышлений художника над жизнью. График функции это своего рода «портрет» функции. Чтобы научиться видеть и создавать такие картины необходимо знать основные математические функции и их свойства.

Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения.

По графику можно прочитать многие свойства функции, можно решать неравенства и уравнения.

 

Читая ,график функции мы можем делать выводы об :

• Области определения

• Области значений

• Нулях функции

• Знакопостоянстве

• Монотонности

• Четности

• Периодичности

• Экстремумах

• Ограниченности

• Непрерывности

Выполним задание:

 

 

Множество всех значений независимой переменной, которые она может принимать называют областью определения функции.

Если известен график функции, то область ее определения найти нетрудно. Для этого достаточно спроецировать график на ось абсцисс. То числовое множество, геометрическая модель которого получится на оси абсцисс в результате указанного проецирования, и будет представлять собой область определения функции.

Ответ: (-9;9]

Выполним задание:

 

 

Множество всех значений зависимой переменной называют областью значений функции.

Если известен график функции, то область значений найти сравнительно нетрудно. Для этого достаточно спроецировать график на ось ординат. То числовое множество, геометрическая модель которого получится на оси ординат в результате указанного проецирования, и будет представлять собой область значений функции.

Ответ: [-4;6).

Выполним задание:

 

 

Функция у равное f(х) достигает на промежутке Х своего наибольшего значения, если существует такая точка х

0 Î Х, что для всех х Î Х выполняется неравенство f(x) ≤ f(x₀).

Из рисунка видим, что при х =-3, f(-3)=3 и это значение больше других значений функции.

Ответ: 3.

 

 

 

На практике удобнее пользоваться следующей формулировкой: функция возрастает, если большему значению аргумента соответствует большее значение функции. Или используя геометрическое истолкование понятий возрастания: двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в гору.

Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Или используя геометрическое истолкование понятий убывания: двигаясь по графику убывающей функции слева направо, мы как бы спускаемся в горы.

Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.

Выполним задание:

Найти промежутки монотонности функции у=f (x), заданной графиком.

Для определения промежутков монотонности будем использовать геометрическое истолкование : двигаясь по графику убывающей функции слева направо, мы как бы спускаемся в горы ,а двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в гору.

 

Функция возрастает на промежутках [-5;-2) и на (-2; 1]

Функция у=f(x ) убывает на промежутках (-9;- 5] и на [1; 9].

На слайде 13 представлено задание из единого государственного экзамена: На каком из следующих рисунков изображен график функции, возрастающей на промежутке [-1;2].

 

Функцию y=f(x) называют периодической с периодом Т, Т≠0, если для любого х из области определения функции выполняются равенства f(x-T) = f(x)= =f(x+T).

Число Т, удовлетворяющее указанному условию, называется периодом функции y= f (x).

Если функция у=f(x) имеет период Т, то для построения графика функции нужно сначала построить часть графика на любом промежутке длины Т, а затем сдвинуть эту часть по оси Ох вправо и влево на Т, 2Т, 3Т и так далее.

Обычно стараются, если это возможно, выделить наименьший положительный период, его и называют основным периодом.

Задание 1.

Функция у =f (x), имеющая период Т = 4 задана графиком на промежутке [-1; 3].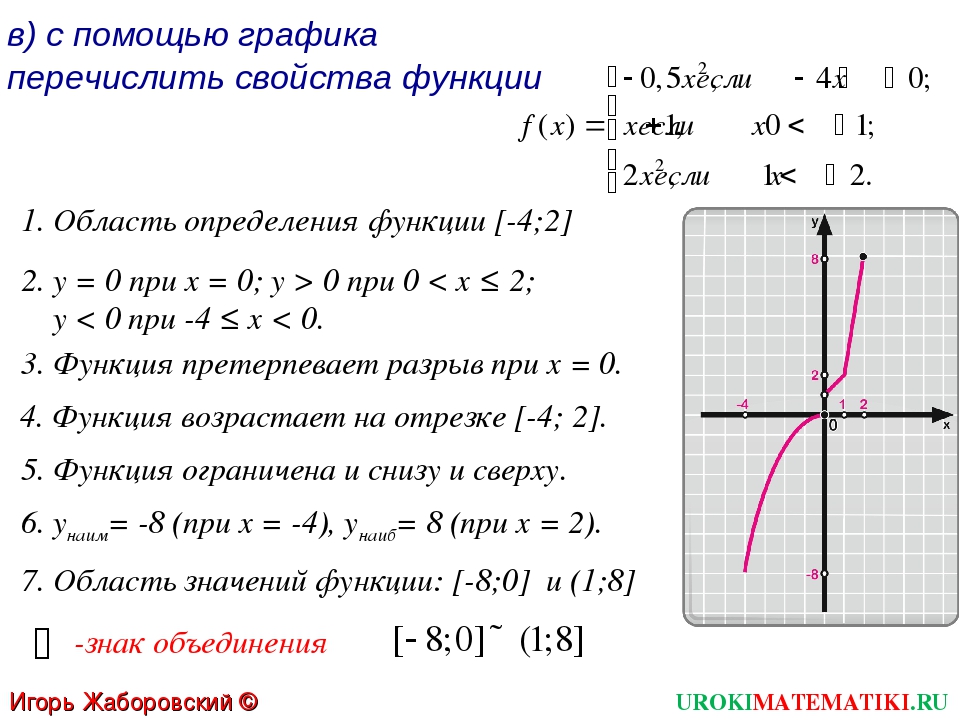 Найдите значение этой функции при х = 10.

Задание2.

Функция у=f(x) определена на всей числовой прямой и является периодической с периодом 4. На рисунке изображен график этой функции при -3≤х≤1. Найдите значение выражения f(-6)∙f(-3)∙f(13).

Выполнить эти задания можно двумя способами.

1 способ:

Используя определение периодической функции достраиваем график функции с учетом периода вдоль оси абсцисс. Затем по графику находим значение функции для указанных значений аргументов.

2 способ:

Используя равенство f(x-T)= f(x)= f(x+T).

Решение можно посмотреть в презентации на слайдах 15, 16.

Определение четной и нечетной функции.

Функция y= f(x) называется четной, если область ее определения симметрична относительно нуля и для любого значения х, из области определения верно равенство f(-х)=f(x). График четной функции симметричен относительно оси ординат.

На слайде приведены примеры четных функций и примеры симметрии относительно прямой.

Функция y=f(x) называется нечетной, если ее область определения симметрична относительно нуля и для любого значения х из области определения верно равенство f(-х)=-f(x).

График нечетной функции симметричен относительно начала координат.

На слайде приведен пример симметрии относительно точки и на следующем слайде примеры графиков нечетных функций, изучаемых в школьном курсе алгебры. На графиках показана симметрия точек графика относительно начала координат. (Слайды 17-19).

На 20 слайде предложено задание:

Укажите график четной функции. (Решение можно посмотреть на слайде 20).

Определение промежутков знакопостоянства.

Решите неравенство f(x)≥0, если на рисунке изображен график функции у=f(x).

Решите неравенство f(x)≤0, если на рисунке изображен график функции у=f(x).

 

Другими словами нужно найти промежутки знакопостоянства функции у равное f(x).Функция принимает значение, равное нулю в тех точках, в которых график функции пересекает ось абсцисс. Функция принимает отрицательные значения на множестве тех значений аргумента, которым соответствуют части графика, расположенные ниже оси абсцисс, то есть f(x) меньше или равно нулю. Функция принимает положительные значения на множестве тех значений аргумента, которым соответствуют части графика, расположенные выше оси абсцисс, те есть f(x) больше или равно нуля.

f(x) ≥0 на промежутках хÎ (-9;-7,2]U(-1,8;5,8]

f(x)≤0 на промежутках хÎ [7,2;-1,8)U[5,8;9,2].

«Как построить график функции F(x)+m»

Дата публикации: 09 апреля 2017.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой. 2-4, -1<x≤2. \end {cases}$

Чтение: Графики линейных функций (часть I) | Конечная математика |

Модуль 2: Линейные функции в бизнесе

 

Когда мы работаем с новой функцией, полезно знать как можно больше о функции: ее графике, где функция равна нулю, и любых других особенностях поведения функции. Мы начнем это исследование линейных функций с рассмотрения графиков.

При построении графика линейной функции существует три основных способа ее построения:

1. Нанесение точек (не менее 2) и проведение линии через точки
2. Используя начальное значение (выводится, когда x = 0) и скорость изменения (наклон)
3. Использование преобразований функции тождества f ( x ) = x

Пример 1

График

f(x)=5−23x\displaystyle{f{{({x})}}}={5}-\frac{{2}}{{3}}{x}f(x)= 5−32​x

путем построения точек

В общем, мы оцениваем функцию на двух или более входных данных, чтобы найти по крайней мере две точки на графике. Обычно лучше всего выбирать входные значения, которые будут «хорошо работать» в уравнении. В этом уравнении числа, кратные 3, будут хорошо работать из-за 

23\displaystyle\frac{{2}}{{3}}32​

в уравнении и, конечно же, используя x = 0, чтобы получить точку пересечения по вертикали. Вычисление f(x) при x = 0, 3 и 6:

f(0)=5−23(0)=5\displaystyle{f{{({0})}}}={5 }-\frac{{2}}{{3}}{({0})}={5}f(0)=5−32​(0)=5

f(3)=5−23( 3)=3\displaystyle{f{{({3})}}}={5}-\frac{{2}}{{3}}{({3})}={3}f(3) =5−32​(3)=3

f(6)=5−23(6)=1\displaystyle{f{{({6})}}}={5}-\frac{{2} }{{3}}{({6})}={1}f(6)=5−32​(6)=1

Эти оценки говорят нам о том, что точки (0,5), (3,3) и (6,1) лежат на графике линии. Нанеся эти точки и проведя через них линию, мы получим график

. При использовании начального значения и скорости изменения на графике необходимо учитывать графическую интерпретацию этих значений. Помните, что начальное значение функции является выходом, когда вход равен нулю, поэтому в уравнении f ( x ) = b + m x график включает точку (0, б ). На графике это вертикальная точка пересечения — точка пересечения графика с вертикальной осью.

Для скорости изменения полезно вспомнить, что мы рассчитали это значение как text{Change of Input}}}m=Change of InputChange of Output​

На графике линии это говорит нам о том, что если мы разделим разность по вертикали или рост выходных данных функции на разность по горизонтали или запустим , входов, мы получим скорость изменения, также называемую наклоном линии.

м = изменение выходных данных изменение входных данных = riserun \ displaystyle {m} = \ frac {{\ text {изменение выходных данных}}} {{\ text {изменение входных данных}}} = \ frac {{\ text {rise }}}{{\text{run}}}m=Change of InputChange of Output​=runrise​

Обратите внимание, что это отношение одинаково независимо от того, какие две точки мы используем

Графическая интерпретация линейного уравнения

Графически в уравнении f ( x ) = b + m x

b — это точка пересечения по вертикали графика, которая говорит нам, что мы можем начать наш график с точки (0, b )

м. до следующей точки

Как только у нас будет хотя бы 2 точки, мы можем расширить график линии влево и вправо.

Пример 2

График

f(x)=5−23x\displaystyle{f{{({x})}}}={5}-\frac{{2}}{{3}}{x}f(x)= 5−32​x

с использованием пересечения по вертикали и наклона.

Вертикальное пересечение функции равно (0, 5), что дает нам точку на графике линии.

Наклон 

−23\displaystyle-\frac{{2}}{{3}}−32​

. Это говорит нам о том, что на каждые 3 единицы график «бежит» по горизонтали, по вертикали «подъем» уменьшается на 2 единицы. При построении графика мы можем использовать это, сначала нанеся на график точку пересечения по вертикали, а затем используя наклон, чтобы найти вторую точку. От начального значения (0, 5) наклон говорит нам, что если мы сдвинемся вправо на 3, мы сдвинемся вниз на 2, переместив нас в точку (3, 3). Мы можем продолжить это снова, чтобы найти третью точку в (6, 1). Наконец, продлите линию влево и вправо, содержащую эти точки.

Попробуйте сейчас 1

Учтите, что наклон

−23\displaystyle-\frac{{2}}{{3}}−32​

, найдите на графике другую точку с отрицательным значением x .

Другим вариантом построения графика является использование преобразований функции тождества f ( x ) = x . В уравнении f ( x ) = м x м действуют как вертикальное растяжение функции тождества. Когда м отрицательный, также имеется вертикальное отражение графика. Глядя на некоторые примеры:

В f ( x ) = m x + b , b действует как сдвиг по вертикали, перемещая график вверх и вниз, не влияя на наклон линии. Некоторые примеры:

Использование вертикального растяжения или сжатия вместе с вертикальным сдвигом — еще один способ взглянуть на определение различных типов линейных функций. Хотя это может быть не самый простой способ построения графика функции такого типа, убедитесь, что вы практикуете каждый метод.

Пример 3

График

f(x)=−3+12x\displaystyle{f{{({x})}}}=-{3}+\frac{{1}}{{2}}{x}f(x )=−3+21​x

с использованием преобразований.

Уравнение представляет собой график функции идентичности, сжатый по вертикали на ½ и сдвинутый по вертикали вниз на 3.

Обратите внимание, как это хорошо сравнивается с другим методом, где точка пересечения по вертикали находится в точке (0, –3), и чтобы добраться до другой точки, мы поднимаемся (поднимаемся по вертикали) на 1 единицу и бежим (идем по горизонтали) на 2 единицы, чтобы добраться до следующая точка (2, –2) и следующая (4, –1). В этих трех точках (0, –3), (2, –2) и (4, –1) выходные значения изменяются на +1, а 9Значения 0016 x изменяются на +2, что соответствует уклону м = 1/2.

Пример 4

Сопоставьте каждое уравнение с одной из линий на графике ниже

f(x)=2x+3\displaystyle{f{{({x})}}}={2}{x}+{3}f(x )=2x+3

g(x)=2x−3\displaystyle{g{{({x})}}}={2}{x}-{3}g(x)=2x−3

h(x)=-2x+3\displaystyle{h}{({x})}=-{2}{x}+{3}h(x)=-2x+3

j(x)=12x +3\displaystyle{j}{({x})}=\frac{{1}}{{2}}{x}+{3}j(x)=21​x+3

Только на одном графике точка пересечения по вертикали равна –3, поэтому мы можем сразу сопоставить этот график с 9. 0016 г(х) . Из трех графиков с точкой пересечения по вертикали в точке 3 только один имеет отрицательный наклон, поэтому мы можем сопоставить эту линию с h(x) . Из двух других более крутая линия будет иметь больший наклон, поэтому мы можем сопоставить этот график с уравнением f(x) , а более плоская линия с уравнением j(x) .

В дополнение к пониманию основного поведения линейной функции (увеличение или уменьшение, распознавание наклона и вертикального пересечения) часто бывает полезно знать горизонтальное пересечение функции, где она пересекает горизонтальную ось.

Поиск горизонтального пересечения

точка пересечения функции по горизонтали — это место, где график пересекает горизонтальную ось. Если у функции есть точка пересечения по горизонтали, ее всегда можно найти, решив f(x) = 0.

Пример 5

Найдите горизонтальное пересечение

f(x)=−3+12x\displaystyle{f{{({x})}}}=-{3}+\frac{{1}}{{2}}{x }f(x)=−3+21​x

Установка функции равной нулю, чтобы определить, какие входные данные поместят нас на горизонтальную ось,

0=-3+12x\displaystyle{0}=-{3}+\frac{{1}}{{2}}{x}0=-3+21​x

3=12x\displaystyle{ 3}=\frac{{1}}{{2}}{x}3=21​x

x=6\displaystyle{x}={6}x=6

График пересекает горизонтальную ось в точке ( 6,0)

Есть два особых случая линий: горизонтальная линия и вертикальная линия.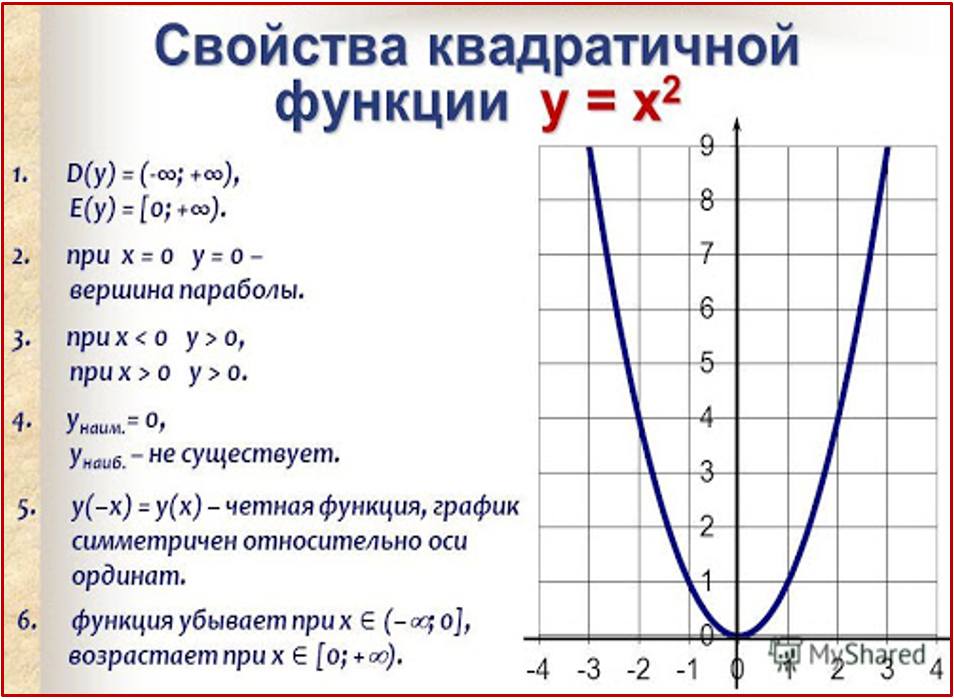 На горизонтальной линии, подобной изображенной справа, обратите внимание, что между любыми двумя точками изменение результатов равно 0. В уравнении наклона числитель будет равен 0, в результате чего наклон будет равен 0. Использование наклона 0 в , уравнение упрощается до .

Обратите внимание, что горизонтальная линия имеет точку пересечения по вертикали, но не имеет точки пересечения по горизонтали (если только это не линия

f(x)=0\displaystyle{f{{({x})}}}={0}f(x) =0

).

В случае вертикальной линии обратите внимание, что между любыми двумя точками изменение входных данных равно нулю. В уравнении наклона знаменатель будет равен нулю, и вы можете вспомнить, что мы не можем делить на ноль; наклон вертикальной линии не определен. Вы также можете заметить, что вертикальная линия не является функцией. Чтобы написать уравнение вертикальной линии, мы просто пишем input=value, например.

Обратите внимание, что вертикальная линия имеет точку пересечения по горизонтали, но не имеет точки пересечения по вертикали (если только это не линия x = 0).

Горизонтальные и вертикальные линии

Горизонтальные линии имеют уравнения вида

Вертикальные линии имеют уравнения вида x = a

Пример 6

Напишите уравнение для горизонтальной линии, изображенной выше.

Эта линия будет иметь уравнение  f ( x ) = 2

Пример 7

Напишите уравнение для вертикальной линии, показанной выше.

Эта линия будет иметь уравнение  x = 2

Попробуйте сейчас 2

Опишите функцию f ( x ) = 6 – 3 x в терминах преобразований единичной функции и найдите ее точку пересечения по горизонтали.

• Методы построения графиков линейных функций
• Другое название склона = подъем/спуск
• Горизонтальные пересечения (а,0)
• Горизонтальные линии
• Вертикальные линии

Попробуйте сейчас Ответы

1. (–3,7) можно найти, начав с точки пересечения по вертикали, поднявшись на 2 единицы и 3 в отрицательном горизонтальном направлении. Вы могли бы также ответить (–6, 9) или (–9, 11) и т. д.
2. Вертикально растянуто в 3 раза, Вертикально отражено (перевернуто по оси x ), Вертикально сдвинуто вверх на 6 единиц. 6 – 3 х = 0, когда х = 2

Лицензии и атрибуты

Содержимое по лицензии CC, совместное использование ранее

• Глава 2: Функции. Авторы : Дэвид Липпман и Мелони Расмуссен. Расположен по адресу : http://www.opentextbookstore.com/precalc/1.4/Chapter%202.doc. Лицензия : CC BY: Attribution

Предыдущая

Следующая

Рисование графиков математических функций с помощью Math Assistant в OneNote

Одна запись

Делать заметки

Делать заметки

Рисование графиков математических функций с помощью Math Assistant в OneNote

OneNote для Интернета OneNote для Windows 10 Math Assistant Дополнительно. .. Меньше

Создавайте графики рукописных или напечатанных уравнений с помощью Math Assistant в OneNote. Вы даже можете манипулировать переменными, чтобы увидеть визуальный эффект изменений, превращая Math Assistant в мощного тренера по математике.

Примечание. Эта функция доступна только в OneNote для Интернета или OneNote для Windows 10. У вас должна быть действующая подписка на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена ​​последняя версия Office.

1. Откройте настольное приложение OneNote или войдите в Office.com и выберите OneNote .

   Совет: Если вы не видите OneNote сразу, откройте Средство запуска приложений  , чтобы найти его.

2. org/ListItem»>

   Откройте существующий блокнот или создайте новый блокнот.

3. Выберите вкладку Draw и напишите или введите свое уравнение.

4. Используйте инструмент Lasso Select  , чтобы нарисовать круг вокруг уравнения.

5. Выберите  Math  , чтобы открыть панель Math Assistant.

6. В раскрывающемся меню Выберите действие В раскрывающемся меню Математика выберите График в 2D или График с обеих сторон в 2D .

Чтобы настроить график, созданный Math Assistant, выполните любое из следующих действий, если оно доступно:

Примечание.   Если вы используете OneNote на устройстве с сенсорным экраном, график можно настроить пальцами. Используйте один палец для перемещения графика. Сведите два пальца, чтобы изменить уровень увеличения. В OneNote для Интернета вы можете использовать стрелки по бокам графика, чтобы изменить его положение.

• Выберите или коснитесь значка с двойной стрелкой  Сброс  , чтобы восстановить исходное состояние графика.

• Когда график будет выглядеть так, как вы хотите, выберите или коснитесь  Вставить на страницу  , чтобы поместить его в виде снимка экрана на текущую страницу.

Примечание: Чтобы изменить способ отображения графика (градусы, радианы, граданы), выберите или коснитесь  Настройки  , когда открыта панель математических вычислений.

Дополнительные функции построения графиков

В зависимости от типа графика могут быть доступны следующие функции:

• Чтение значений x-y:   Наведите указатель мыши на точку на линии графика, чтобы увидеть значения x и y в OneNote для Windows 10. В OneNote для Интернета — линию, чтобы просмотреть значения.

• Управление параметрами:   Если у вас есть уравнение с параметрами, такими как ax+b, используйте знаки + и — под графиком, чтобы изменить значения a и b.

• Основные функции графика:  Математический помощник вычисляет интересную информацию о графике, такую ​​как нули, точки пересечения, минимумы, максимумы и многое другое. Используйте флажки, чтобы выбрать, какие функции вы хотите отобразить на графике.

Узнать больше

Создавайте математические уравнения с помощью рукописного ввода или текста с помощью помощника по математике в OneNote.

Решайте математические уравнения с помощью Math Assistant в OneNote

Типы задач, поддерживаемые Math Assistant

Создайте тренировочную математическую викторину

Типы задач, которые можно отображать в 2D-графике

При использовании Math Assistant в OneNote вы заметите, что раскрывающийся список Выберите действие под уравнением изменяется в зависимости от выбранного вами уравнения. Следующие типы задач можно изобразить в 2D с помощью Math Assistant.

Примечание. Эта функция доступна только при наличии подписки на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена ​​последняя версия Office.

Выражения (с переменной)
Полиномиальные массивы
Уравнения	Вы можете График в 2D  или График с обеих сторон в 2D при работе с уравнениями. Выберите График в 2D , чтобы увидеть решение уравнения.   Выберите График обеих сторон в 2D , чтобы просмотреть график двух функций по разные стороны от знака равенства.
Системы уравнений
Полярные координаты	Чтобы построить график функции в полярных координатах, r необходимо выразить как функцию тета.
Неравенства	При работе с неравенствами можно  Построить двухмерный график  или  Построить двумерный график с обеих сторон . No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт