625 в корень 4 степени: 625 в 4 степени

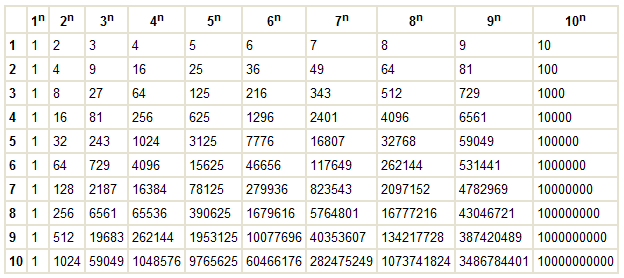
Таблица степеней натуральных чисел

Если калькулятора нет под рукой, то воспользуйтесь данной таблицей. Основания степени лежат первой колонке и указаны синим цветом, показатели степени — в заголовках столбцов и указаны красным цветом.

Например, чтобы вычислить четыре в шестой степени, нужно найти строку с числом 4 и на пересечении со столбцом 6 получить результат: 4⁶  = 4096.

Столбец 2, таким образом — это таблица квадратов натуральных чисел, а столбец 3 — таблица кубов натуральных чисел.

Столбцы — показатель степени (красный) Строки — основание степени (синий)	2	3	4	5	6	7	8	9	10
2	4	8	16	32	64	128	256	512	1 024
3	9	27	81	243	729	2 187	6 561	19 683	59 049
4	16	64	256	45  = 1 024	46  = 4 096	16 384	65 536	262 144	1 048 576
5	25	125	625	3 125	15 625	78 125	390 625	1 953 125	9 765 625
6	36	216	1 296	7 776	46 656	279 936	1 679 616	10 077 696	60 466 176
7	49	343	2 401	16 807	117 649	823 543	5 764 801	40 353 607	282 475 249
8	64	512	4 096	32 768	262 144	2 097 152	16 777 216	134 217 728	1 073 741 824
9	81	729	6 561	59 049	531 441	4 782 969	43 046 721	387 420 489	3 486 784 401
10	100	1 000	10 000	100 000	1 000 000	10 000 000	100 000 000	1 000 000 000	10 000 000 000
11	121	1 331	14 641	161 051	1 771 561	19 487 171	214 358 881	2 357 947 691	25 937 424 601
12	144	1 728	20 736	248 832	2 985 984	35 831 808	429 981 696	5 159 780 352	61 917 364 224
13	169	2 197	28 561	371 293	4 826 809	62 748 517	815 730 721	10 604 499 373	137 858 491 849
14	196	2 744	38 416	537 824	7 529 536	105 413 504	1 475 789 056	20 661 046 784	289 254 654 976
15	225	3 375	50 625	759 375	11 390 625	170 859 375	2 562 890 625	38 443 359 375	576 650 390 625
16	256	4 096	65 536	1 048 576	16 777 216	268 435 456	4 294 967 296	68 719 476 736	1 099 511 627 776
17	289	4 913	83 521	1 419 857	24 137 569	410 338 673	6 975 757 441	118 587 876 497	2 015 993 900 449
18	324	5 832	104 976	1 889 568	34 012 224	612 220 032	11 019 960 576	198 359 290 368	3 570 467 226 624
19	361	6 859	130 321	2 476 099	47 045 881	893 871 739	16 983 563 041	322 687 697 779	6 131 066 257 801
20	400	8 000	160 000	3 200 000	64 000 000	1 280 000 000	25 600 000 000	512 000 000 000	10 240 000 000 000
21	441	9 261	194 481	4 084 101	85 766 121	1 801 088 541	37 822 859 361	794 280 046 581	16 679 880 978 201
22	484	10 648	234 256	5 153 632	113 379 904	2 494 357 888	54 875 873 536	1 207 269 217 792	26 559 922 791 424
23	529	12 167	279 841	6 436 343	148 035 889	3 404 825 447	78 310 985 281	1 801 152 661 463	41 426 511 213 649
24	576	13 824	331 776	7 962 624	191 102 976	4 586 471 424	110 075 314 176	2 641 807 540 224	63 403 380 965 376
25	625	15 625	390 625	9 765 625	244 140 625	6 103 515 625	152 587 890 625	3 814 697 265 625	95 367 431 640 625

См. также: Использование степеней двойки в информатике для хранения чисел — таблица степеней двойки и чисел которые можно записать указанным числом бит.

2080.1947  

 Свойства квадратного корня. Властивості квадратного кореня | Описание курса | Показательная функция. Показова функція 

   

Интегрированный урок по алгебре и информатике, 11-й класс

• Морозова Татьяна Николаевна

Разделы: Математика, Информатика

Класс: 11

---

Тема урока: «Корень n-ной степени и его свойства. Нахождение корня n-ной степени с помощью электронной таблицы Excel.»

Цели урока: ввести понятие корня n-ой степени; познакомить учащихся с решением уравнений вида хⁿ=a^{; рассмотреть примеры вычисления корней n-ой степени; ввести формулу Ньютона для приближенного вычисления корней р-ой степени; формирование навыков и умений нахождения корня р-ой степени с помощью компьютера.}

Ход урока.

1. Слово учителя.

• Здравствуйте, ребята. Сегодня на уроке мы познакомимся со следующими понятиями: корень n-ой степени, арифметический корень n-ой степени из числа, с решениями уравнений вида хⁿ=a, научимся находить целые корни и с помощью формулы Ньютона приближенные значения корня р-ой степени. Сейчас учащиеся 8 класса, изучающие тему “Квадратные корни”, познакомят вас с историей возникновения квадратного корня, термина “радикал”, т.е. корень, и напомнят определение квадратного корня.
• С давних пор, наряду с отысканием площади квадрата по известной длине его стороны, приходилось решать и обратную задачу: “Какой должна быть сторона квадрата, чтобы его площадь равнялась а ?”. Такую задачу умели решать еще четыре тысячи лет назад вавилонские ученые. Они составили таблицы квадратов чисел и квадратных корней из чисел. Вавилоняне использовали метод приближенного извлечения квадратных корней , который состоял в следующем: “Пусть а – некоторое число (имеется в виду натуральное число), не являющееся полным квадратом. Представим а в виде суммы b²+c, где с – достаточно мало по сравнению с b². Тогда, например, если а=112, то квадратный корень из а равен 10,6. Проверка: 10,6² =112,36.
• Указанный метод извлечения квадратного корня подробно описан древнегреческим ученым Героном Александрийским. В эпоху Возрождения европейские математики обозначали корень латинским словом Radix (корень), а затем сокращенно буквой R (отсюда произошел термин “радикал”, которым принято называть знак корня). Некоторые немецкие математики XV века для обозначения квадратного корня пользовались точкой. Эту точку ставили перед числом, из которого нужно извлечь корень. Позднее вместо точки стали ставить ромбик, а в последствии знак V и над выражением, из которого извлекается корень, проводили черту. Затем знак V и черту стали соединять.
• Квадратным корнем из числа а называется число, квадрат которого равен а.
• Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
• Аналогично определим корень n-ой степени. Корнем n-ой степени из числа а называется такое число, n-ая степень которого равна а.
• Примеры:

Корень третьей степени из числа 27 равен 3, т.к. 3³=27.

Корень шестой степени из числа 64 равен 2 и (-2), т.к. 2⁶=64 и (-2)⁶=64.

Согласно данному определению, корень n-ой степени из числа а – это решение уравнения хⁿ=а. Число корней данного уравнения зависит от n и а.

Рассмотрим функцию f(x)=xⁿ. Эта функция при любом n возрастает на промежутке от нуля до бесконечности и принимает все значения из этого промежутка.

По теореме о корне уравнение xⁿ=a для любого а из промежутка от нуля до бесконечности имеет неотрицательный корень, и притом только один. Его называют арифметическим корнем n-ой степени .

Арифметическим корнем n-ой степени из числа а называют неотрицательное число, n-ая степень которого равна а.

Арифметический корень третьей степени из числа 8 равен 2, т.к. 2³=8

Арифметический корень четвертой степени из дроби 81/16 равен 3/2.

При четных n функция f(x)=xⁿ четна, отсюда следует, что:

1. если а>0, то уравнение имеет корни;
2. если а=0, то х=0;
3. если а<0, то уравнение действительных корней не имеет.

Пример: решить уравнение х⁴=81. Отсюда х=3 или х= -3.

При нечетных n функция f(x)=xⁿ возрастает на всей числовой прямой и , отсюда, уравнение имеет при любых а один корень.

Пример: решить уравнение х⁵= -32. Отсюда х= -2.

Устно решить следующие задачи:

1. Проверьте справедливость равенств:

А) корень четвертой степени из 16 равен 2.

Б) корень седьмой степени из числа ( — 1 ) равен –1.

В) корень девятой степени из 0 равен 0.

Г) корень третьей степени из числа ( — 343) равен -7.

2. Вычислите:

А) корень третьей степени из числа –27

Б) корень четвертой степени из числа 81.

В) корень пятой степени из числа –32.

Г) корень пятой степени из дроби 1/32.

Д) корень четвертой степени из дроби 81/625.

3. Решите уравнение:

А) х⁶=5;

Б) х⁵=3;

В) х³+4=0.

• Вы уже заметили, что часто в решении уравнений появляются корни – иррациональные числа. Их значения можно найти приближенно, используя формулу Ньютона:

У_n+1=1/Р[(Р-1)У_n+Х/У_n^p-1].

(Далее класс делится на 2 группы: одна группа работает на компьютере, используя обучающую карточку, другая группа работает по индивидуальным карточкам по алгебре за партами.)

Карточка для работы на компьютере (используют электронную таблицу Excel).

Используя формулу Ньютона, вычислите х с точностью EPS=0.000001 для Х=277234 и Р=7 при начальном приближении У₀=5.

Выполните следующие шаги:

1. Создайте заголовок задания. Запишите формулу Ньютона. Расположите строки в центре и выберите подходящий для них шрифт.
2. Запишите в ячейку А5 текст “Х=”, в ячейку В5 значение 277234. Выровняйте содержимое А5 по правому краю, содержимое В5 – по левому. Таким же образом запишите в ячейку С5 – “Р=”, D5 – 7, Е5 – “EPS=”, F5 – 0.000001, G5 – “У₀=”, Н5-5.
3. Создайте шапку таблицы, записав в ячейки D7 и Е7 “№ шага” и “У” соответственно.
4. Запишите в ячейку D8 значение 0. Скопируйте в ячейку Е8 содержимое ячейки Н5. Запишите в следующую строку столбца D номер очередного шага и в следующую строку столба Е – формулу Ньютона.
5. Повторите пункт 4, скопировав формулу Ньютона из предыдущей строки. Повторяйте эти действия каждый раз в таблицу по одной строке.
6. Создайте рамку таблицы.
7. Занесите в ячейку D16 текст “результат”, а в ячейку Е16 – результат с заданной точностью – до 6 значащих цифр.

Карточки по алгебре ( 3-х уровневые).

Вариант 1.

1. Решите уравнения

а) х⁴=10; б) х¹⁰-15=0; в) х⁷+128=0

2. Решите неравенства:

а) х⁴<3; б) х¹¹>7

3. Найдите значение числового выражения:

а) корень девятой степени из -1;

б) корень пятой степени из 0;

в) корень четвертой степени из дроби 81/256.

Вариант 2.

1. Решите уравнения

а) 16х⁴ -1=0; б) 0,01х³+10=0; в) 0,02х⁶-1,28=0

2. Решите неравенства:

а) х³<5; б) х¹⁰>10

3. Найдите значение числового выражения:

а) корень четвертой степени из выражения 16•625;

б) корень пятой степени из выражения 32•243;

в) корень четвертой степени из дроби 128/8.

Вариант 3.

1. Решите уравнения

а) 125х³=1; б) 0,001х¹⁰-1,5=0; в)0,04 х⁷+128=0

1. Решите неравенства:

а) 2х⁴<12; б) 5х¹¹>35

2. Найдите значение числового выражения:

а) корень четвертой степени из выражения 48•27;

б) корень пятой степени из выражения 160•625;

в) корень шестой степени из дроби 128/2.

Итог урока, задание на дом.

13.01.2004

Резорбция апикального корня после ортодонтического лечения — ретроспективное исследование

. 2007 авг; 29 (4): 408-12.

дои: 10. 1093/ejo/cjm016. Epub 2007 13 июля.

Сату Ападжалахти ¹ , Яакко Сакари Пелтола

принадлежность

• ¹ Кафедра стоматологической радиологии, Институт стоматологии, Хельсинкский университет, Финляндия. [email protected]

• PMID: 17631606
• DOI: 10.1093/эджо/cjm016

Сату Ападжалахти и др. Евро J Ортод. 2007 авг.

. 2007 авг; 29 (4): 408-12.

дои: 10. 1093/эджо/cjm016. Epub 2007 13 июля.

Авторы

Сату Ападжалахти ¹ , Яакко Сакари Пелтола

принадлежность

• ¹ Кафедра стоматологической радиологии, Институт стоматологии, Хельсинкский университет, Финляндия. [email protected]

• PMID: 17631606
• DOI: 10.1093/эджо/cjm016

Абстрактный

Цель исследования состояла в том, чтобы сравнить частоту и тяжесть резорбции апикального корня у пациентов, леченных различными ортодонтическими аппаратами, и оценить влияние продолжительности лечения на степень резорбции апикального корня. Еще одной целью было проанализировать степень резорбции апикального корня в различных группах зубов у пациентов с резорбцией корня. Выборка состояла из 625 пациентов (269мужчин, 356 женщин) в возрасте 8-16 лет на начало лечения. Наиболее часто использовались активные съемные пластины и несъемные аппараты. После исключения рентгенограмм плохого качества окончательная выборка включала 601 пациента (348 женщин, 253 мужчины). Резорбцию корней всех групп зубов, кроме третьих моляров, оценивали по панорамным рентгенограммам до и после лечения. Корреляцию резорбции корня с методом и продолжительностью лечения изучали с помощью полиномиального логистического регрессионного анализа. Из групп зубов резцы верхней челюсти чаще всего демонстрировали резорбцию апикального корня, за ними следуют резцы нижней челюсти. Резорбция корня достоверно коррелировала с лечением несъемной аппаратурой (P < 0,001). Кроме того, было установлено, что продолжительность лечения несъемными аппаратами значительно (P < 0,01) влияет на степень резорбции корня. Средняя продолжительность лечения у пациентов без резорбции корня составила 1,5 года, а у пациентов с выраженной резорбцией — 2,3 года. Наиболее выраженная резорбция наблюдалась на резцах и премолярах верхней челюсти. Сделан вывод, что при длительном лечении несъемной аппаратурой возрастает риск выраженной резорбции. Пациентам с длительным лечением рекомендуется 6-месячное рентгенологическое наблюдение.

Похожие статьи

• Наружная резорбция корня с помощью самолигирующей системы Damon — ретроспективное исследование.

  Хандем Р.Х., Янсон Г., Матиас М., де Фрейтас К.М., де Лима Д.В., Гариб Д.Г., де Фрейтас М.Р. Хандем Р.Х. и соавт. Прог Ортод. 2016 дек;17(1):20. doi: 10.1186/s40510-016-0133-1. Epub 2016 1 июля. Прог Ортод. 2016. PMID: 27365168 Бесплатная статья ЧВК.

• Рентгенологический анализ наружной апикальной резорбции корней верхних резцов во время активного ортодонтического лечения.

  Мохандесан Х., Раванмер Х., Валеи Н. Мохандесан Х. и др. Евро J Ортод. 29 апреля 2007 г. (2): 134–139. дои: 10.1093/ejo/cjl090. Epub 2007, 17 января. Евро J Ортод. 2007. PMID: 17229789

• Факторы, связанные с резорбцией апикального корня верхних резцов у ортодонтических пациентов.

  Нигул К., Джагомаги Т. Нигул К. и др. Стоматология. 2006;8(3):76-9. Стоматология. 2006. PMID: 17191062

• Факторы риска резорбции корней после ортодонтического лечения.

  Лопатене К., Думбравайте А. Лопатене К. и соавт. Стоматология. 2008;10(3):89-95. Стоматология. 2008. PMID: 1

42 Обзор.

• Апикальная резорбция корня связана с комплексным ортодонтическим лечением, но явно не зависит от предшествующих характеристик зуба или ортодонтических методов.

  Захровски Дж., Йеске А. Захровски Дж. и соавт. J Am Dent Assoc. 2011 Январь; 142 (1): 66-8. doi: 10.14219/jada.archive.2011.0030. J Am Dent Assoc. 2011. PMID: 21193769 Обзор.

Посмотреть все похожие статьи

Цитируется

• Оценка режима тракции лабиально ретинированных клыков с помощью прозрачных элайнеров и . стационарное устройство: сравнительное исследование, основанное на трехмерном анализе методом конечных элементов.

  Ся Ц., Хе Ю., Цзя Л., Ван С., Ван В., Ван С., Сонг Дж., Фань Ю. Ся Кью и др. Фронт Биоэнг Биотехнолог. 2022 5 октября; 10:1004223. doi: 10.3389/fbioe.2022.1004223. Электронная коллекция 2022. Фронт Биоэнг Биотехнолог. 2022. PMID: 36277381 Бесплатная статья ЧВК.

• Динамика, эффективность и побочные эффекты интрузии полной дуги верхней челюсти с использованием временных фиксирующих устройств (мини-винты): анализ методом конечных элементов.

  Мажари М., Ханехмасджеди М., Мажари М., Аташкар Н., Рахшан В. Мажари М. и соавт. Биомед Рез Инт. 2022 7 октября; 2022:6706392. дои: 10.1155/2022/6706392. Электронная коллекция 2022. Биомед Рез Инт. 2022. PMID: 36254137 Бесплатная статья ЧВК.

• Изменение длины корня во время ортодонтического лечения верхних резцов с предшествующей травмой зубов: продольное контролируемое исследование.

  Смейерс Ф., Фивез С., Ван Горп Г., Виллемс Г., Деклерк Д., Беньони Г., Вердонк А., Фьювс С., Каденас де Льяно-Перула М. Смейерс Ф. и соавт. Clin Oral Investig. 2022 г., 18 августа. doi: 10.1007/s00784-022-04679-4. Онлайн перед печатью. Clin Oral Investig. 2022. PMID: 35982348

• Влияние ортодонтических усилий на длину корня несформированных вторых премоляров нижней челюсти: рандомизированное клиническое исследование с разделенным ртом.

  Далайе К., Бади М., Бехназ М., Кавусинежад С. Далай К. и др. Стоматологический пресс J Orthod. 2021 25 октября; 26 (5): e2119355. doi: 10.1590/2177-6709.26.5.e2119355.весло. Электронная коллекция 2021. Стоматологический пресс J Orthod. 2021. PMID: 35640080 Бесплатная статья ЧВК. Клиническое испытание.

• Резорбция зубов. Часть 2: Клиническая классификация.

  Эббот П.В., Лин С. Эббот П.В. и соавт. Дент Трауматол. 2022 авг; 38 (4): 267-285. дои: 10.1111/изд.12762. Epub 2022 23 мая. Дент Трауматол. 2022. PMID: 35605161 Бесплатная статья ЧВК. Обзор.

Просмотреть все статьи «Цитируется по»

термины MeSH

[Решено] Какова цифра единицы в {(6374)1793 × (625)317&

Вариант 1: 0

Бесплатно

CT: Общий интеллект и мышление (набор для практики)

1,4 миллиона пользователей

10 вопросов

20 баллов

8 минут

Дано:

{(6374) ¹⁷⁹³  × (625) ³¹⁷  × (341) ⁴⁹¹ }

Использованное понятие:

Цикличность единицы измерения

91930

Х

Х ¹

Х ²

Х ³

Х ⁴

1

1

1

1

1

2

2

4

8

6

3

3

9

7

1

4

4

6

4

6

5

5

5

5

5

6

6

6

6

6

7

7

9

3

1

8

8

4

2

6

9

9

1

9

1

Расчет:

Единая цифра 6374 ¹⁷⁹³

4 ¹ = 4

Единой цифры 625 ³¹⁷

Unit Digit of 5

Unit Digit of 5 9000 3

UnitiT of 5

. 341) ⁴⁹¹

Единица измерения всегда равна 1

Единица измерения = 4 × 5 × 1 = 0

∴ Единица измерения будет равна 0.

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления SSC CGL

Последнее обновление: 28 октября 2022 г.

Предварительный экзамен SSC CGL 2022 Дата выхода на официальный сайт SSC 31 октября 2022 года!  Предварительный экзамен будет проводиться с 1 по 13 декабря 2022 года. Ранее была активирована ссылка на статус результатов SSC CGL для Tier II 2021 Marks Status Link. Кандидаты могут проверить свои оценки, посетив официальный сайт. SSC CGL 2022 продолжается, и кандидаты подали заявки на него до 13 октября 2022 года. Уведомление SSC CGL 2022 было отправлено 17 сентября 2022 года. Право на получение SSC CGL — это степень бакалавра в соответствующей дисциплине. В этом году SSC полностью изменил шаблон экзамена, и для того же кандидаты должны ссылаться на новый шаблон экзамена SSC ​​CGL.

No related posts.