Площадь треугольника. Формулы
Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c – стороны треугольника,
R– радиус описанной окружности,
r – радиус вписанной окружности,
h[b],h[a],h[c] – высоты , проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma – углы возле вершин.
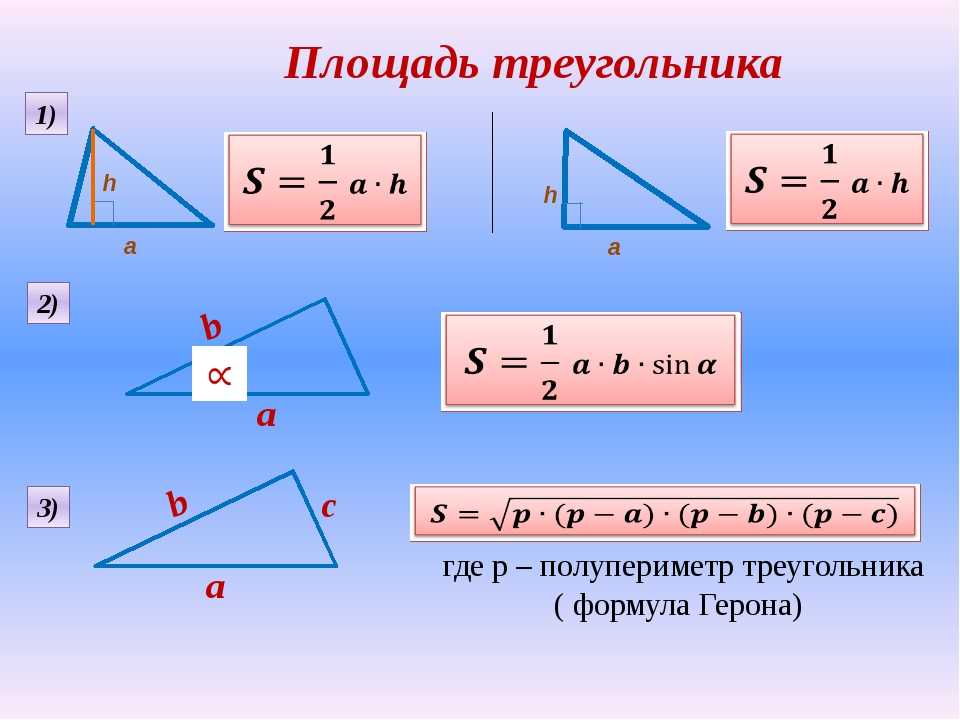
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
На языке формул это определение можно записать так
Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
то с первой формулы площади следуют однотипные вторые
Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
5. Формула площади через сторону и котангенс прилегающих углов следующая
Формула площади через сторону и котангенс прилегающих углов следующая
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.
7. Формула Герона применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
а затем определяют площадь по формуле
или
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9. Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
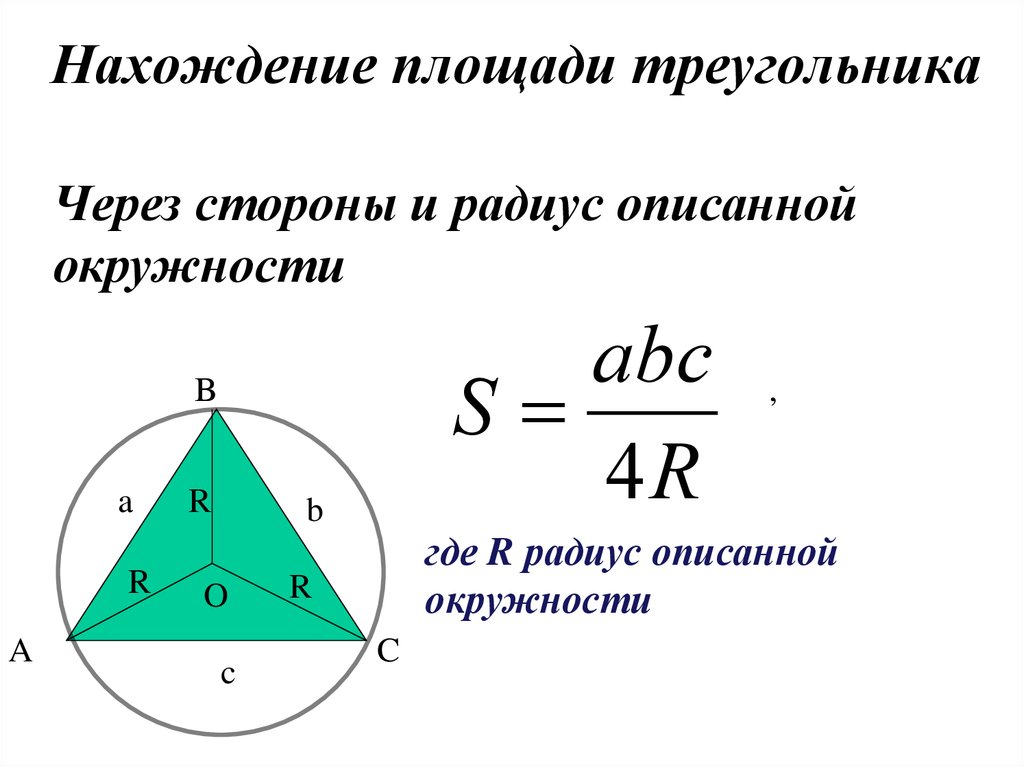
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
Ну и напоследок — частные случаи :
Площадь прямоугольного треугольника с катетами a и b равна половине их произведения
Формула площади равностороннего ( правильного ) треугольника=
= одной четвертой произведения квадрату стороны на корень из тройки.
Пример. Стороны треугольника равны 3, 5, 6 см. Найти площадь треугольника.
Решение: Применим формулу Герона, для этого сначала найдем полупериметр
Подставляем в формулу площади
Ответ:Площадь треугольника равна 7.48 сантиметров квадратных.
————————————
Скачать все приведенные формулы площади треугольника Вы можете по следующей ссылке. Распечатывайте их и используйте в обучении.
{jd_file file==19}
Если материал был полезен Вам — поделитесь ссылкой с друзьями.
Посмотреть материалы:
- Прямоугольный треугольник. Задачи
- Периметр и площадь прямоугольника
- Квадрат. Формулы
- Периметр и площадь параллелограмма
- Формулы площади трапеции
- Ромб. Площадь, периметр
{jcomments on}
Площадь треугольника
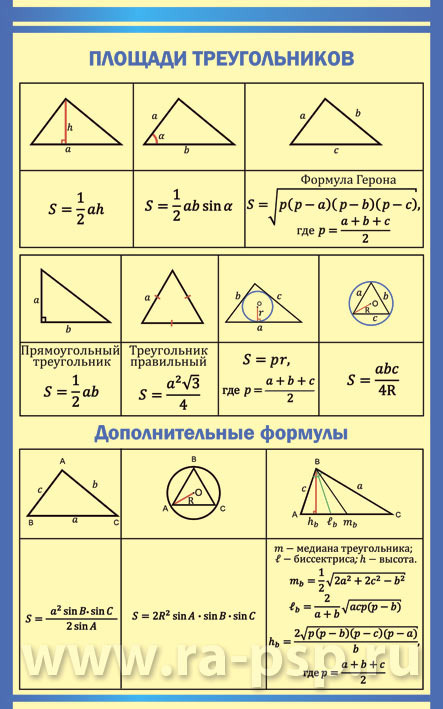
Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.
Примечание. Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:
- «Формулы площади равнобедренного треугольника»
- «Формулы площади прямоугольного треугольника»
- «Формулы площади равностороннего треугольника»
Формулы площади треугольника
Пояснения к формулам:
a, b, c — длины сторон треугольника, площадь которого мы хотим найти
r — радиус вписанной в треугольник окружности
R — радиус описанной вокруг треугольника окружности
h — высота треугольника, опущенная на сторону
p — полупериметр треугольника, 1/2 суммы его сторон (периметра)
α — угол, противолежащий стороне a треугольника
β — угол, противолежащий стороне b треугольника
γ — угол, противолежащий стороне c треугольника
ha, hb, hc — высота треугольника, опущенная на сторону a, b, c
Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.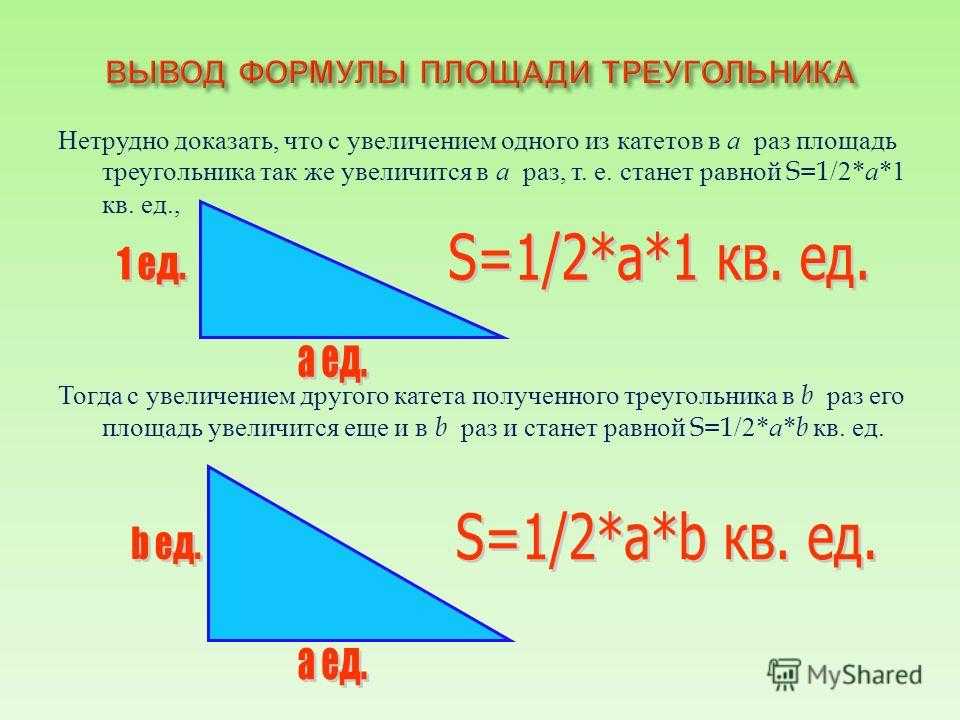
- Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2 ) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
- Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
- Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
- Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
- Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
- Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
- Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов.
 (Формула 8)
(Формула 8) - Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
- Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
- Формула 11 позволяет вычислить площадь треугольника по координатам его вершин, которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений
См. также площадь равнобедренного треугольника.
Примечание. Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √
В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √
Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.
Решение.
Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ
Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60
В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два.
Он будет равен корню из трех на два.
S = 15 √3 / 2
Ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)
Найти площадь равностороннего треугольника со стороной 3см.
Решение.
Площадь треугольника можно найти по формуле Герона:
S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
Поскольку a = b = c формула площади равностороннего треугольника примет вид:
S = √3 / 4 * a2
S = √3 / 4 * 32
S = 9 √3 / 4
Ответ: 9 √3 / 4.
Задача. Изменение площади при изменении длины сторон
Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?
Решение.
Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.
Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.
Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:
S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
(см. первую строку рисунка внизу)
Длины сторон произвольного треугольника заданы переменными a, b, c.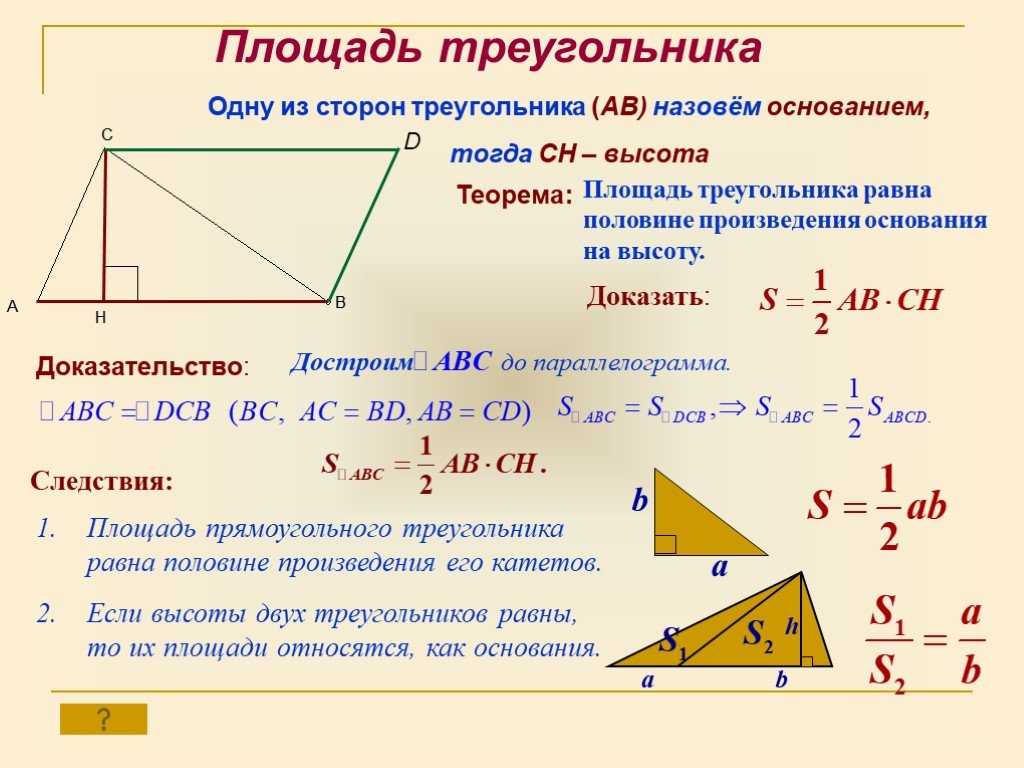
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:
S2 = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c) )
(см. вторую строку на рисунке внизу)
Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда
S2 = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — на третьей строке рисунка
S2 = 1/4 sqrt( 256 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — четвертая строка
Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S2 = 16 * 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
(см. пятую строку рисунка внизу)
Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.
S2 / S = 16
(см. внизу подробнее запись в виде дроби и ее сокращения — в последней строке)
На рисунке логика вычисления решения, описанного выше, приведена уже в виде формул (одна за другой)
Ответ: Площадь треугольника увеличится в 16 раз
10380.6235
Сумма углов треугольника | Описание курса | Медиана треугольникаКалькулятор треугольника
Укажите, что вы знаете о треугольнике:
Треугольник:
Калькулятор решает треугольник, заданный тремя его свойствами. Каждый треугольник имеет шесть основных характеристик: три стороны a, b, c и три угла (α, β, γ). Классическая задача тригонометрии состоит в том, чтобы указать три из этих шести характеристик и найти остальные три.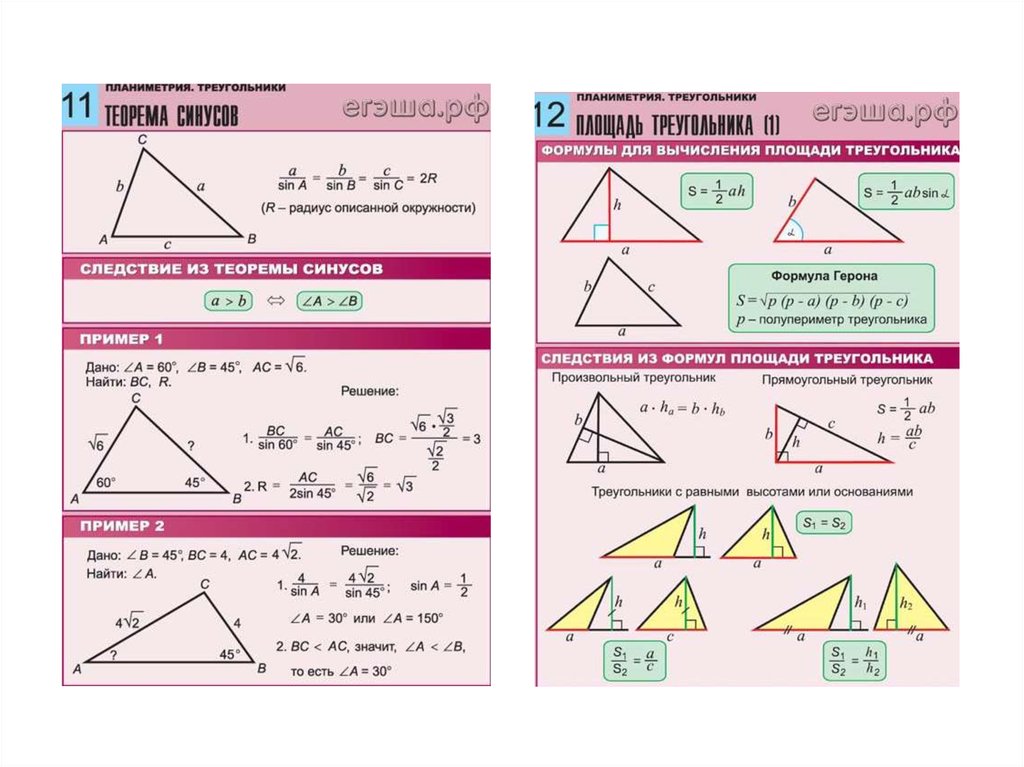 Конечно, наш калькулятор решает треугольники из комбинаций основных и производных свойств, таких как площадь, периметр, высота, медиана и т. д.
Обычно по длине трех сторон (SSS), сторона-угол-сторона или угол-сторона-угол.
Конечно, наш калькулятор решает треугольники из комбинаций основных и производных свойств, таких как площадь, периметр, высота, медиана и т. д.
Обычно по длине трех сторон (SSS), сторона-угол-сторона или угол-сторона-угол.
Как этот калькулятор треугольников решает треугольник?
Расчет общего треугольника состоит из двух фаз:
- Экспертная фаза различна для разных задач. Калькулятор пытается по введенным данным вычислить размеры трех сторон треугольника. Он постепенно применяет базу знаний к введенным данным, которая представлена, в частности, отношениями между отдельными параметрами треугольника.
Они последовательно применяются и комбинируются, и вычисляются параметры треугольника. Калькулятор повторяется до тех пор, пока треугольник не вычислит все три стороны.
Например, соответствующая высота вычисляется из заданной площади треугольника и соответствующей стороны. По известным высоте и углу можно рассчитать прилегающую сторону и т. д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона.
д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона. - Второй этап — вычисление свойств треугольника по имеющимся длинам его трех сторон.
Примеры ввода треугольника:
a=3 b=4 c=5 … расчет треугольника по трем сторонам a,b,c.
B=45 c=10 a=9 … треугольник вычисляется по двум сторонам a,c и углу B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 … как ввести прямоугольный треугольник.
a=3 β=25 γ=45 … расчет треугольника, если известны сторона и два угла.
a=3 β=25 T=12 … расчет треугольника, если известны сторона, угол и площадь треугольника.
T=2.5 c=2 b=4 … найти сторону a, если известны стороны b, c и площадь треугольника T.
ma=1 b=2.5 c=2 … вычисление треугольника, если мы знаем одну медиану и любые две стороны.
ma=1 mb=2.5 mc=2 … расчет треугольника по трем медианам.
ha=220, hb=165 hc=132 . .. треугольник вычисляется по трем высотам.
.. треугольник вычисляется по трем высотам.
a=7 β=40 mc=5 … расчет треугольника по одной стороне, одному углу и одной медиане.
a:b:c=2:3:4 T=2.5 … треугольник, где известно отношение сторон и его площадь.
A:B:C=1:4:5 a=2 … расчет треугольника, если известно отношение внутренних углов к одной стороне.
Что означают символы?a, b, c... стороны BC, AC, AB
A, B, C или α, β, γ... внутренние углы
ha, hb, hc... высоты
ma, mb, mc. .. медианы
T ... площадь
p ... периметр
s ... полупериметр
Треугольники в текстовых задачах:
- Равнобедренный 2
Равнобедренный треугольный каркас имеет длину 72 метра по сторонам и 18 метров на его базе. Найдите периметр рамки. - Вычислить
Рассчитайте площадь треугольника ABE AB = 38 мм и высоту E = 42 мм Ps: попробуйте выполнить быстрый расчет - Пересечение 64854
Нарисуйте любой треугольник. Сделайте оси двух его сторон. Их пересечение представляет собой точку S. (а) Измерьте расстояние точки S от всех трех вершин (б) Проведите ось третьей стороны.
Их пересечение представляет собой точку S. (а) Измерьте расстояние точки S от всех трех вершин (б) Проведите ось третьей стороны. - Высота прямого RT
Прямоугольный треугольник ABC имеет гипотенузу c длиной 9 см и часть гипотенузы cb = 3 см. Какова высота этого прямоугольного треугольника? - Диагональ
Может ли это быть диагональный ромб в два раза длиннее его стороны? - Euclid2
Прямоугольный треугольник ABC с прямым углом при вершине C имеет сторону a=29 и высоту v=17. Вычислите периметр треугольника. - Вектор 7
Даны вектор OA(12,16) и вектор OB(4,1). Найдите вектор AB и вектор |A|. - Вычислить
Вычислить длину стороны равностороннего треугольника площадью 50 см². - Законы
Из какого закона непосредственно следует справедливость теоремы Пифагора в прямоугольном треугольнике? … - Трапеция — RR
Найдите площадь прямоугольной трапеции ABCD с прямым углом при вершине A; a = 3 дм b = 5 дм c = 6 дм d = 4 дм - Стороны 3
Стороны равностороннего треугольника равны 9,4 см, с точностью до ближайшего десятичного знака. Найдите верхнюю границу стороны этого треугольника.
Найдите верхнюю границу стороны этого треугольника. - Треугольник 3
Треугольник имеет основание 5 5/6 футов и высоту 7 2/5 футов. Найдите площадь треугольника в виде смешанного числа. - Викторина
Две стороны равнобедренного треугольника равны 7 км и 39 км. Какой длины третья сторона? - Площадь RT 2
Вычислите площадь прямоугольного треугольника, катеты которого равны 5,8 см и 5,8 см. - Найдите
Найдите третий внутренний угол треугольника ABC, где: α = 48°, γ = 65°.
другие задачи на треугольник »
Посмотрите также сборник математических задач и вопросов нашего друга:
- треугольник
- прямоугольный треугольник
- Формула Герона
- Закон синусов
- Закон косинусов
- Теорема Пифагора
- Неравенство треугольника
- Подобие треугольников
- Теорема о прямоугольных треугольниках о высоте
- 901 .
Калькулятор площади треугольника
Автор: Ханна Памула, кандидат наук
Отзыв от Богны Шик и Адены Бенн
Последнее обновление: 15 сентября 2022 г.
Содержание:
- Формула площади треугольника
- Как найти площадь треугольника?
- Площадь равностороннего треугольника
- Хотите узнать больше?
Этот калькулятор площади треугольника может помочь в определении площади треугольника. В базовой формуле площади треугольника должны быть заданы основание и высота, но что, если у нас их нет? Как вычислить площадь треугольника, у которого только 3 стороны? Калькулятор площади треугольника здесь для вас. Попробуй! Если вы все еще не знаете, как найти площадь треугольника, посмотрите описание ниже.
Формула площади треугольника
Треугольник — одна из основных геометрических фигур. Самая известная и самая простая формула, которую почти все помнят со школы:
-
площадь = 0,5 * b * h, гдеb— длина основания треугольника, аh— это высота/высота треугольника.
Однако иногда трудно найти высоту треугольника. В этом случае можно использовать многие другие уравнения, в зависимости от того, что вы знаете о треугольнике:
Три стороны (SSS)
Если известны длины всех сторон, используйте формулу Герона:
площадь = 0,25 * √( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
Две стороны и угол между ними (SAS)
Вы можете легко вычислить площадь треугольника с помощью тригонометрии:
площадь = 0,5 * a * b * sin(γ)
Два угла и сторона между ними (ASA)
Существуют различные версии формул площади треугольника — для ее получения можно использовать, например, тригонометрию или закон синусов:
площадь = a² * sin(β) * sin(γ) / (2 * sin(β + γ))
Если вы ищете другие формулы или калькуляторы, связанные с треугольниками, посмотрите этот калькулятор прямоугольного треугольника, калькулятор теоремы Пифагора и калькулятор закона косинусов.

Как найти площадь треугольника?
Предположим, что мы знаем две стороны и угол между ними:
- Введите длину первой стороны . В нашем примере он может быть равен 9 дюймам .
- Введите вторую сторону треугольника . Давайте выберем 5 дюймов.
- Определить угол между двумя известными сторонами . Например, 30 градусов.
- Посмотрите, как наш калькулятор площади треугольника выполняет все расчеты за вас! Площадь для нашего случая равна 11,25 дюйма².
Площадь равностороннего треугольника
Чтобы вычислить площадь равностороннего треугольника, вам нужно знать только сторону:
площадь = a² * √3 / 4Хотя мы не делали отдельный калькулятор для площади равностороннего треугольника вы можете быстро рассчитать ее в этом калькуляторе площади треугольника. Просто используйте подраздел для площади треугольника с 3 сторонами — как вы знаете, каждая сторона имеет одинаковую длину в равностороннем треугольнике.


 (Формула 8)
(Формула 8)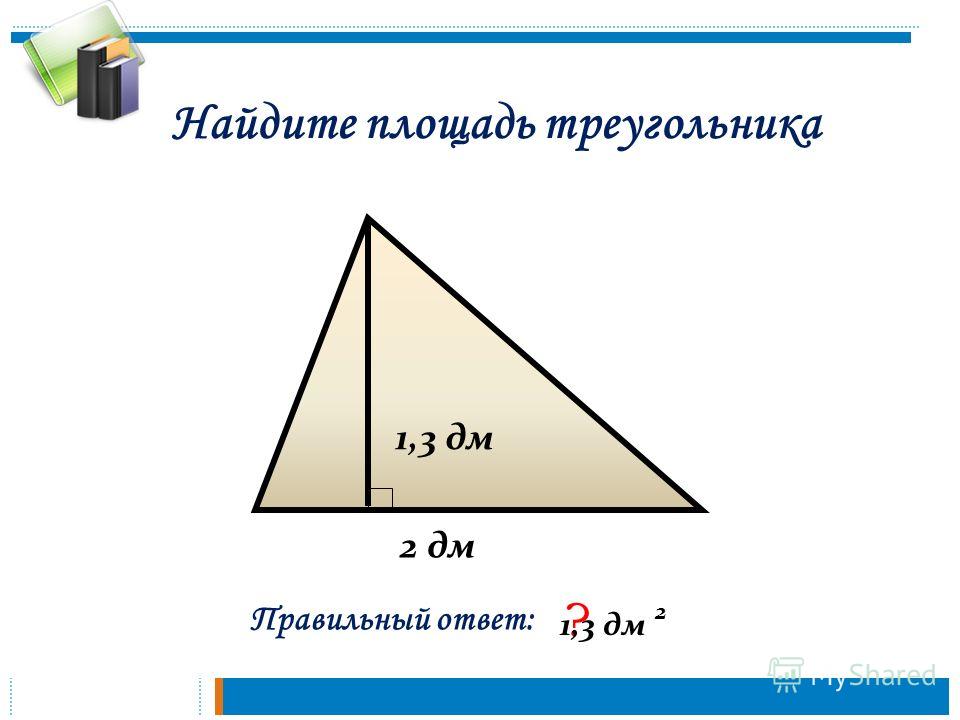 д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона.
д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона. Их пересечение представляет собой точку S. (а) Измерьте расстояние точки S от всех трех вершин (б) Проведите ось третьей стороны.
Их пересечение представляет собой точку S. (а) Измерьте расстояние точки S от всех трех вершин (б) Проведите ось третьей стороны. Найдите верхнюю границу стороны этого треугольника.
Найдите верхнюю границу стороны этого треугольника.