8 делить на 40: 8 разделить на 40 сколько будет? ответ:0,2

Mathway | Популярные задачи

1	Оценить с использованием заданного значения	квадратный корень из 50
2	Оценить с использованием заданного значения	квадратный корень из 45
3	Вычислить	5+5
4	Вычислить	7*7
5	Разложить на простые множители	24
6	Преобразовать в смешанную дробь	52/6
7	Преобразовать в смешанную дробь	93/8
8	Преобразовать в смешанную дробь	34/5
9	График	y=x+1
10	Оценить с использованием заданного значения	квадратный корень из 128
11	Найти площадь поверхности	сфера (3)	
12	Вычислить	54-6÷2+6
13	График	y=-2x
14	Вычислить	8*8
15	Преобразовать в десятичную форму	5/9
16	Оценить с использованием заданного значения	квадратный корень из 180
17	График	y=2
18	Преобразовать в смешанную дробь	7/8
19	Вычислить	9*9
20	Risolvere per C	C=5/9*(F-32)
21	Упростить	1/3+1 1/12
22	График	y=x+4
23	График	y=-3
24	График	x+y=3
25	График	x=5
26	Вычислить	6*6
27	Вычислить	2*2
28	Вычислить	4*4
29	Вычислить	1/2+(2/3)÷(3/4)-(4/5*5/6)
30	Вычислить	1/3+13/12
31	Вычислить	5*5
32	Risolvere per d	2d=5v(o)-vr
33	Преобразовать в смешанную дробь	3/7
34	График	y=-2
35	Определить наклон	y=6
36	Перевести в процентное соотношение	9
37	График	y=2x+2
38	График	y=2x-4
39	График	x=-3
40	Решить, используя свойство квадратного корня	x^2+5x+6=0
41	Преобразовать в смешанную дробь	1/6
42	Преобразовать в десятичную форму	9%
43	Risolvere per n	12n-24=14n+28
44	Вычислить	16*4
45	Упростить	кубический корень из 125
46	Преобразовать в упрощенную дробь	43%
47	График	x=1
48	График	y=6
49	График	y=-7
50	График	y=4x+2
51	Определить наклон	y=7
52	График	y=3x+4
53	График	y=x+5
54	График	3x+2y=6
55	Решить, используя свойство квадратного корня	x^2-5x+6=0
56	Решить, используя свойство квадратного корня	x^2-6x+5=0
57	Решить, используя свойство квадратного корня	x^2-9=0
58	Оценить с использованием заданного значения	квадратный корень из 192
59	Оценить с использованием заданного значения	квадратный корень из 25/36
60	Разложить на простые множители	14
61	Преобразовать в смешанную дробь	7/10
62	Risolvere per a	(-5a)/2=75
63	Упростить	x
64	Вычислить	6*4
65	Вычислить	6+6
66	Вычислить	-3-5
67	Вычислить	-2-2
68	Упростить	квадратный корень из 1
69	Упростить	квадратный корень из 4
70	Найти обратную величину	1/3
71	Преобразовать в смешанную дробь	11/20
72	Преобразовать в смешанную дробь	7/9
73	Найти НОК	11 , 13 , 5 , 15 , 14	, , , ,
74	Решить, используя свойство квадратного корня	x^2-3x-10=0
75	Решить, используя свойство квадратного корня	x^2+2x-8=0
76	График	3x+4y=12
77	График	3x-2y=6
78	График	y=-x-2
79	График	y=3x+7
80	Определить, является ли полиномом	2x+2
81	График	y=2x-6
82	График	y=2x-7
83	График	y=2x-2
84	График	y=-2x+1
85	График	y=-3x+4
86	График	y=-3x+2
87	График	y=x-4
88	Вычислить	(4/3)÷(7/2)
89	График	2x-3y=6
90	График	x+2y=4
91	График	x=7
92	График	x-y=5
93	Решить, используя свойство квадратного корня	x^2+3x-10=0
94	Решить, используя свойство квадратного корня	x^2-2x-3=0
95	Найти площадь поверхности	конус (12)(9)	
96	Преобразовать в смешанную дробь	3/10
97	Преобразовать в смешанную дробь	7/20
98	Преобразовать в смешанную дробь	2/8
99	Risolvere per w	V=lwh
100	Упростить	6/(5m)+3/(7m^2)

Деление в столбик | Наука делать уроки

Самое главное правило, с которого мы начинаем изучать деление в столбик:

Пример: 792 разделить на 2

Начнём деление с сотен

1 Образуем первое неполное делимое:  7 сотен — первое неполное делимое.

Значит, в записи частного будет 3 цифры.

• Узнаем, сколько сотен будет в частном: разделим 7 на 2, получим 3.
• Узнаем, сколько сотен  разделили: умножим 3 на 2, получим 6.
• Узнаем, сколько сотен не разделили: вычтем 6 из 7, получим 1.

Проверим цифру сотен частного: сравним остаток 1 с делителем 2; сотен осталось меньше, чем 2, значит, цифру сотен частного нашли правильно.

2 Образуем второе неполное делимое: 1 сотня да ещё 9 десятков, всего 19 десятков.

• Узнаем, сколько десятков будет в частном: разделим 19 на 2, получим 9.
• Узнаем, сколько десятков разделили: умножим 9 на 2, получим 18.
• Узнаем, сколько десятков не разделили: вычтем 18 из 19, получим 1.

Проверим цифру десятков частного: сравним остаток 1 с делителем 2. Десятков осталось меньше, чем 2, значит, цифру десятков частного нашли правильно.

3 Образуем третье неполное делимое: 1 десяток и 2 единицы, всего 12 единиц.

• Узнаем, сколько единиц будет в частном: разделим 12 на 2, получим 6.
• Узнаем, сколько единиц разделили: умножим 6 на 2,  получим 12.
• Узнаем, сколько единиц не разделили: вычтем 12 из 12, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 2, значит, цифру единиц частного нашли верно.

Читаем ответ:  792 разделить на 2 получится 396

Образец записи

(Кликните по картинке)

Компоненты действия деления

(Кликните по картинке)

На верх

Ваша Помощница

— умная и нужная
шпаргалка

Кликните, чтобы скачать и затем распечатать

Образец рассуждения

во время записи
деления в столбик

 

 

Внимательно просмотрите и примените в своих действиях!

Какие ошибки при делении

можно сделать и
как их избежать

[Видео]

Внимательно просмотрите,

чтобы не совершать ошибок!

На верх

Правила для других случаев деления

• Правило 1
• Правило 2
• Правило 3
• Правило 4
• Правило 5
• Правило 6
• Правило 7
• Правило 8
• Правило 9
• Правило 10
• План деления

Деление на однозначное число, когда первое неполное делимое — это двузначное число

Пример: 192 разделить на 4

 

Начнём деление с сотен. 1 сотня не делится на 4. Значит будем делить десятки. 19 десятков можно разделить  на 4.

1 Образуем первое неполное делимое:  19 десятков — первое неполное делимое.

Значит, в записи частного будет 2 цифры.

• Узнаем, сколько десятков будет в частном: разделим 19 на 4, получим 4.
• Узнаем, сколько десятков разделили: умножим 4 на 4, получим 16.
• Узнаем, сколько десятков не разделили: вычтем 19 из 16, получим 3.

Проверим цифру десятков частного: сравним остаток 3 с делителем 4. Десятков осталось меньше, чем 4, значит, цифру десятков частного нашли правильно.

2 Образуем второе неполное делимое: 3 десятка и 2 единицы, всего 32 единицы.

• Узнаем, сколько единиц будет в частном: разделим 32 на 4, получим 8.
• Узнаем, сколько единиц разделили: умножим 8 на 4,  получим 32.
• Узнаем, сколько единиц не разделили: вычтем 32 из 32, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 4, значит, цифру единиц частного нашли верно.

Читаем ответ:  192 разделить на 4 получится 48 

Деление на однозначное число, когда в записи частного есть цифра 0

Пример: 612 разделить на 2

 

Начнём деление с сотен.

1 Образуем первое неполное делимое:  6 сотен — первое неполное делимое.

Значит, в записи частного будет 3 цифры.

• Узнаем, сколько сотен будет в частном: разделим 6 на 2, получим 3.
• Узнаем, сколько сотен  разделили: умножим 3 на 2, получим 6.
• Узнаем, сколько сотен не разделили: вычтем 6 из 6, получим 0.

Проверим цифру сотен частного: сравним остаток 0 с делителем 2; сотен осталось меньше, чем 2, значит, цифру сотен частного нашли правильно.

2 Образуем второе неполное делимое: 0 сотен да ещё 1 десяток, всего 1 десяток.

• Узнаем, сколько десятков будет в частном: разделим 1 на 2, получим 0.
• Узнаем, сколько десятков разделили: умножим 0 на 2, получим 0.
• Узнаем, сколько десятков не разделили: вычтем 0 из 1, получим 1.

Проверим цифру десятков частного: сравним остаток 1 с делителем 2. Десятков осталось меньше, чем 2, значит, цифру десятков частного нашли правильно.

3 Образуем третье неполное делимое: 1 десяток и 2 единицы, всего 12 единиц.

• Узнаем, сколько единиц будет в частном: разделим 12 на 2, получим 6.
• Узнаем, сколько единиц разделили: умножим 6 на 2,  получим 12.
• Узнаем, сколько единиц не разделили: вычтем 12 из 12, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 6, значит, цифру единиц частного нашли верно.

Читаем ответ:  612 разделить на 2 получится 306

Деление на двузначное число

Пример: 828 разделить на 36

 

Начнём деление с сотен. 8 сотен не делится на 36.  Значит, будем делить десятки. 82 десятка можно разделить  на 36.

1 Образуем первое неполное делимое:  82 десятка — первое неполное делимое.

Значит, в записи частного будет 2 цифры.

• Узнаем, сколько десятков будет в частном: разделим 82 на 36, получим 2.
• Узнаем, сколько десятков разделили: умножим 2 на 36, получим 72.
• Узнаем, сколько десятков не разделили: вычтем 72 из 82, получим 10.

Проверим цифру десятков частного: сравним остаток 10 с делителем 36. Десятков осталось меньше, чем 36, значит, цифру десятков частного нашли правильно.

2 Образуем третье неполное делимое: 10 десятков и 2 единицы, всего 102 единицы.

• Узнаем, сколько единиц будет в частном: разделим 102 на 36, получим 3.
• Узнаем, сколько единиц разделили: умножим 3 на 36,  получим 102.
• Узнаем, сколько единиц не разделили: вычтем 102 из 102, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 36, значит, цифру единиц частного нашли верно.

Читаю ответ:  828 разделить на 36 получится 23

Часто пробная цифра частного не подходит и её нужно изменять.

Пример: 168 разделить на 28

 

Начнём деление с сотен.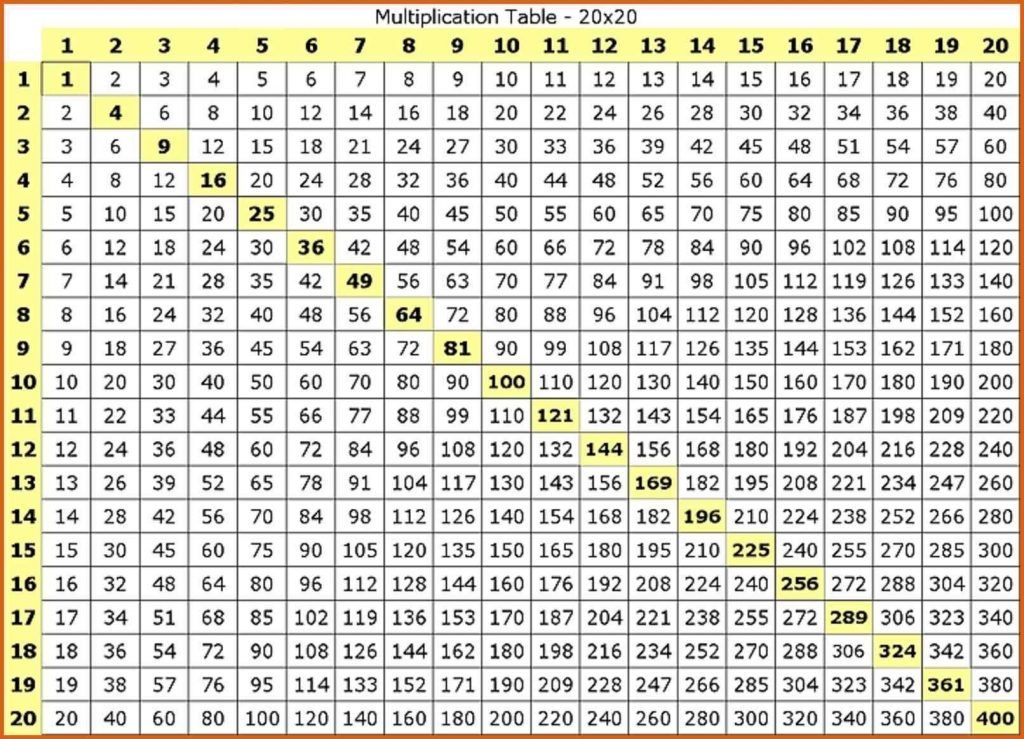

1 сотня не делится на 28.  Значит, будем делить десятки. 16 десятков нельзя  разделить  на 28. Делим единицы. 168 можно разделить на 28.

1 Образуем первое неполное делимое:  168 единиц — первое неполное делимое.

Значит, в записи частного будет 1 цифра.

Чтобы было легче подобрать цифру частного будем делить   16  на 2, получится 8. Цифра 8 не окончательная, а пробная, потому что требовалось разделить  168 на 28, а мы разделили на 20. Эту цифру надо проверить: умножим 8 на 28, получится 224. Число 224 – это больше, чем делимое, значит 8 нам не подходит и надо взять цифру меньше. Пробуем цифру 7. Умножим 7 на 28, получится 196. Число 196 тоже больше, чем делимое. Пробуем число 6. Умножим 6 на 28, получится 168. Число 6 нам подходит.

• Узнаем, сколько единиц разделили: умножим 6 на 28,  получим 168.
• Узнаем, сколько единиц не разделили: вычтем 168 из 168, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 28, значит, цифру единиц частного нашли верно.

Читаем ответ:  168 разделить на 28 получится 6

 

Деление на двузначное число, когда первое неполное делимое — трёхзначное число

Пример: 488 разделить на 61

 

Начнём деление с сотен. 4 сотни нельзя разделить на 61. Будем делить десятки. 48 десятков нельзя разделить на 61. Будем делить единицы. 488 единиц можно разделить на 61.

1 Образуем первое неполное делимое:  488 единиц — первое неполное делимое.

Значит, в записи частного будет 1 цифра.

Чтобы было легче подобрать цифру частного будем делить не на 61, а на 60.

• Узнаем, сколько единиц будет в частном: разделим 488 на 60. Для этого разделим 48 на 6,  получим 8. Цифра 8 не окончательная, а пробная, потому что требовалось разделить  488 на 61, а мы разделили на 60. Эту цифру надо проверить: умножим 61 на 8, получится 488.
• Узнаем, сколько единиц разделили: умножим 8 на 61,  получим 488.
• Узнаем, сколько единиц не разделили: вычтем 488 из 488, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 61, значит, цифру единиц частного нашли верно.

Читаю ответ:  488 разделить на 61 получится 8

Часто пробная цифра частного не подходит и её нужно изменять.

Пример: 651 разделить на 93

 

Начнём деление с сотен. 6 сотен нельзя разделить на 93. Будем делить десятки. 65 десятков нельзя разделить на 93. Будем делить единицы. 651 единицу можно разделить на 93.

1 Образуем первое неполное делимое:  651 единиц — первое неполное делимое.

Значит, в записи частного будет 1 цифра.

Чтобы было легче подобрать цифру частного будем делить не на 93, а на 90.

• Узнаем, сколько единиц будет в частном: разделим 651 на 90. Для этого разделим 65 на 9,  получим 8. Цифра 8 не окончательная, а пробная, потому что требовалось разделить  651 на 93, а мы разделили на 90. Эту цифру надо проверить: умножим 93 на 8, получится 744. Мы получили число 744, которое больше, чем наше делимое. Значит, цифру единиц частного подобрали неверно. Возьмём цифру единиц частного на 1 меньше не 8, а 7. Проверим. Для этого 7 умножим на 93. Получится 651. Число 7 нам подходит.
• Узнаем, сколько единиц разделили: умножим 7 на 93,  получим 651.
• Узнаем, сколько единиц не разделили: вычтем 651 из 651, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 93, значит, цифру единиц частного нашли верно.

Читаем ответ:  651 разделить на 93 получится 7

Деление на числа, оканчивающиеся нулями

Пример: 480 разделить на 60

 

Начнём деление с сотен. 4 сотни не делятся на 60. Будем делить десятки. 48 не делится на 60. Делим единицы. 480 единиц на 60 разделить можно.

1 Образуем первое неполное делимое:  480 единиц — первое неполное делимое.

Значит, в записи частного будет 1 цифра.

• Узнаем, сколько единиц будет в частном: разделим 480 разделим на 10 и полученное частное  48 разделим на 6, получим 8.
• Узнаем, сколько единиц разделили: умножим 8 на 60,  получим 480.
• Узнаем, сколько единиц не разделили: вычтем 480 из 480, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 60, значит, цифру единиц частного нашли верно.

Читаю ответ:  480 разделить на 60 получится 8 

Деление на трёхзначное число

Пример: 856 разделить на 214

 

Начнём деление с сотен.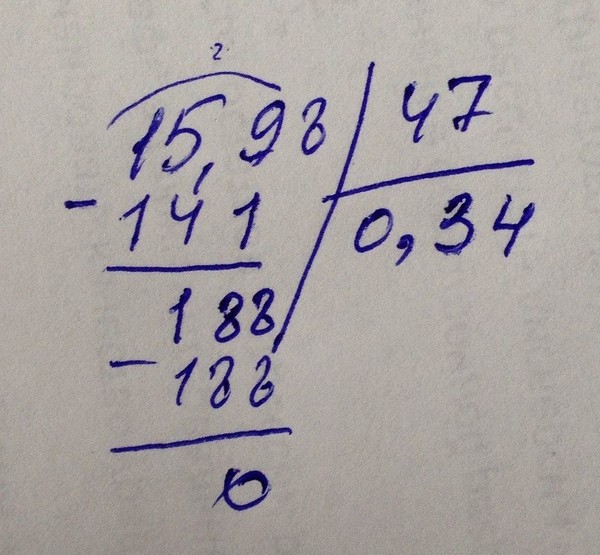 8 сотен не делятся на 214. Будем делить десятки. 85 не делится на 214. Делим единицы. 856 единиц на 214 разделить можно.

1 Образуем первое неполное делимое:  856 единиц — первое неполное делимое.

Значит, в записи частного будет 1 цифра.

Чтобы подобрать цифру частного будем делить не на 214, а на 200. Для этого разделим 8 на 2, получим 4. Проверим цифру 4. Умножим  214 на 4, получится 856.

• Узнаем, сколько единиц разделили: умножим 4 на 214,  получим 856.
• Узнаем, сколько единиц не разделили: вычтем 856 из 856, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 856, значит, цифру единиц частного нашли верно.

Читаем ответ:  856 разделить на 214 получится 4 

Деление  с остатком

Пример: 152 разделить на 40

 

Начнём деление с сотен. 1 сотня не делится на 40. Будем делить десятки. 15 десятков не делится на 40. Делим единицы. 152 единицы на 40 разделить можно.

1 Образуем первое неполное делимое:  152 единицы — первое неполное делимое.

Значит, в записи частного будет 1 цифра.

Узнаем, сколько единиц будет в частном: разделим  152 на 10 и полученное частное 15 разделим на 4, получится 3.

• Узнаем, сколько единиц разделили: умножим 40 на 3,  получим 120.
• Узнаем, сколько единиц не разделили: вычтем 120 из 152, получим 32.

32 – это остаток.

Проверим цифру единиц частного: сравним остаток 32 с делителем 40. Единиц осталось меньше, чем 40 , значит, цифру единиц частного нашли верно.

Читаем ответ:  152 разделить на 40 получится 3 и  остаток 32

Деление  четырехзначного  числа  на  двузначное.

Пример: 5130 разделить на 90

 

Начнём деление с тысяч. 5 тысяч нельзя разделить на 90. Будем делить сотни. 51 сотню  нельзя разделить на 90. Будем делить десятки. 513 десятков  можно разделить на 91.

1 Образуем первое неполное делимое:  513 десятков — первое неполное делимое.

Значит, в записи частного будет 2 цифры.

• Узнаем, сколько десятков будет в частном: разделим 513 на 10 и полученное частное 51 разделим на 9, получим 5.
• Узнаем, сколько десятков разделили: умножим 90 на 5, получим 450.
• Узнаем, сколько десятков не разделили: вычтем 450 из 513, получим 63.

Проверим цифру десятков частного: сравним остаток 63 с делителем 90. Десятков осталось меньше, чем 90, значит, цифру десятков частного нашли правильно.

2 Образуем второе неполное делимое: 63 десятка – это 630 единиц.

• Узнаем, сколько единиц будет в частном: разделим 630 на 10 и полученное частное 63 разделим на 9, получим 7.
• Узнаем, сколько единиц разделили: умножим 7 на 90,  получим 630.
• Узнаем, сколько единиц не разделили: вычтем 630 из 630, получим 0.

Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 630, значит, цифру единиц частного нашли верно.

Читаем ответ:  5130 разделить на 90 получится 57

Объясни, как выполнено деление, по плану:

 

• Назови первое неполное делимое;
• Расскажи, как нашли первую цифру частного;
• Расскажи, как проверили эту цифру частного;
• Назови второе неполное делимое;
• Расскажи, как нашли вторую цифру частного;
• Расскажи, как проверили эту цифру частного;

Проверь результат, выполнив умножение.

ПДД РФ, 9. Расположение транспортных средств на проезжей части \ КонсультантПлюс

• Главная
• Документы
• 9. Расположение транспортных средств на проезжей части

Подготовлена редакция документа с изменениями, не вступившими в силу

Постановление Правительства РФ от 23. 10.1993 N 1090 (ред. от 31.12.2020) «О Правилах дорожного движения» (вместе с «Основными положениями по допуску транспортных средств к эксплуатации и обязанности должностных лиц по обеспечению безопасности…

ПДД РФ, 9. Расположение транспортных средств на проезжей части

9.1. Количество полос движения для безрельсовых транспортных средств определяется разметкой и (или) знаками 5.15.1, 5.15.2, 5.15.7, 5.15.8, а если их нет, то самими водителями с учетом ширины проезжей части, габаритов транспортных средств и необходимых интервалов между ними. При этом стороной, предназначенной для встречного движения на дорогах с двусторонним движением без разделительной полосы, считается половина ширины проезжей части, расположенная слева, не считая местных уширений проезжей части (переходно-скоростные полосы, дополнительные полосы на подъем, заездные карманы мест остановок маршрутных транспортных средств).

(в ред. Постановлений Правительства РФ от 14.12.2005 N 767, от 10. 05.2010 N 316)

(см. текст в предыдущей редакции)

9.1(1). На любых дорогах с двусторонним движением запрещается движение по полосе, предназначенной для встречного движения, если она отделена трамвайными путями, разделительной полосой, разметкой 1.1, 1.3 или разметкой 1.11, прерывистая линия которой расположена слева.

(п. 9.1(1) введен Постановлением Правительства РФ от 28.06.2017 N 761)

9.2. На дорогах с двусторонним движением, имеющих четыре или более полосы, запрещается выезжать для обгона или объезда на полосу, предназначенную для встречного движения. На таких дорогах повороты налево или развороты могут выполняться на перекрестках и в других местах, где это не запрещено Правилами, знаками и (или) разметкой.

(п. 9.2 в ред. Постановления Правительства РФ от 10.05.2010 N 316)

(см. текст в предыдущей редакции)

9.3. На дорогах с двусторонним движением, имеющих три полосы, обозначенные разметкой (за исключением разметки 1.9), из которых средняя используется для движения в обоих направлениях, разрешается выезжать на эту полосу только для обгона, объезда, поворота налево или разворота. Выезжать на крайнюю левую полосу, предназначенную для встречного движения, запрещается.

9.4. Вне населенных пунктов, а также в населенных пунктах на дорогах, обозначенных знаком 5.1 или 5.3 или где разрешено движение со скоростью более 80 км/ч, водители транспортных средств должны вести их по возможности ближе к правому краю проезжей части. Запрещается занимать левые полосы движения при свободных правых.

(в ред. Постановления Правительства РФ от 14.12.2005 N 767)

(см. текст в предыдущей редакции)

В населенных пунктах с учетом требований настоящего пункта и пунктов 9.5, 16.1 и 24.2 Правил водители транспортных средств могут использовать наиболее удобную для них полосу движения. При интенсивном движении, когда все полосы движения заняты, менять полосу разрешается только для поворота налево или направо, разворота, остановки или объезда препятствия.

(в ред. Постановления Правительства РФ от 24.01.2001 N 67)

(см. текст в предыдущей редакции)

Однако на любых дорогах, имеющих для движения в данном направлении три полосы и более, занимать крайнюю левую полосу разрешается только при интенсивном движении, когда заняты другие полосы, а также для поворота налево или разворота, а грузовым автомобилям с разрешенной максимальной массой более 2,5 т — только для поворота налево или разворота. Выезд на левую полосу дорог с односторонним движением для остановки и стоянки осуществляется в соответствии с пунктом 12.1 Правил.

(в ред. Постановлений Правительства РФ от 25.09.2003 N 595, от 10.05.2010 N 316)

(см. текст в предыдущей редакции)

Абзац исключен. — Постановление Правительства РФ от 10.05.2010 N 316.

(см. текст в предыдущей редакции)

9.5. Транспортные средства, скорость движения которых не должна превышать 40 км/ч или которые по техническим причинам не могут развивать такую скорость, должны двигаться по крайней правой полосе, кроме случаев объезда, обгона или перестроения перед поворотом налево разворотом или остановкой в разрешенных случаях на левой стороне дороги.

(в ред. Постановления Правительства РФ от 24.01.2001 N 67)

(см. текст в предыдущей редакции)

9.6. Разрешается движение по трамвайным путям попутного направления, расположенным слева на одном уровне с проезжей частью, когда заняты все полосы данного направления, а также при объезде, повороте налево или развороте с учетом пункта 8. 5 Правил. При этом не должно создаваться помех трамваю. Выезжать на трамвайные пути встречного направления запрещается. Если перед перекрестком установлены дорожные знаки 5.15.1 или 5.15.2, движение по трамвайным путям через перекресток запрещается.

(в ред. Постановлений Правительства РФ от 24.01.2001 N 67, от 14.12.2005 N 767, от 28.03.2012 N 254)

(см. текст в предыдущей редакции)

9.7. Если проезжая часть разделена на полосы линиями разметки, движение транспортных средств должно осуществляться строго по обозначенным полосам. Наезжать на прерывистые линии разметки разрешается лишь при перестроении.

9.8. При повороте на дорогу с реверсивным движением водитель должен вести транспортное средство таким образом, чтобы при выезде с пересечения проезжих частей транспортное средство заняло крайнюю правую полосу. Перестроение разрешается только после того, как водитель убедится, что движение в данном направлении разрешается и по другим полосам.

9.9. Запрещается движение транспортных средств по разделительным полосам и обочинам, тротуарам и пешеходным дорожкам (за исключением случаев, предусмотренных пунктами 12. 1, 24.2 — 24.4, 24.7, 25.2 Правил), а также движение механических транспортных средств (кроме мопедов) по полосам для велосипедистов. Запрещается движение механических транспортных средств по велосипедным и велопешеходным дорожкам. Допускается движение машин дорожно-эксплуатационных и коммунальных служб, а также подъезд по кратчайшему пути транспортных средств, подвозящих грузы к торговым и другим предприятиям и объектам, расположенным непосредственно у обочин, тротуаров или пешеходных дорожек, при отсутствии других возможностей подъезда. При этом должна быть обеспечена безопасность движения.

(в ред. Постановлений Правительства РФ от 14.12.2005 N 767, от 22.03.2014 N 221)

(см. текст в предыдущей редакции)

9.10. Водитель должен соблюдать такую дистанцию до движущегося впереди транспортного средства, которая позволила бы избежать столкновения, а также необходимый боковой интервал, обеспечивающий безопасность движения.

9.11. Вне населенных пунктов на дорогах с двусторонним движением, имеющих две полосы, водитель транспортного средства, для которого установлено ограничение скорости, а также водитель транспортного средства (состава транспортных средств) длиной более 7 м должен поддерживать между своим и движущимся впереди транспортным средством такую дистанцию, чтобы обгоняющие его транспортные средства могли без помех перестроиться на ранее занимаемую ими полосу. Это требование не действует при движении по участкам дорог, на которых запрещается обгон, а также при интенсивном движении и движении в организованной транспортной колонне.

(п. 9.11 в ред. Постановления Правительства РФ от 24.01.2001 N 67)

(см. текст в предыдущей редакции)

9.12. На дорогах с двусторонним движением при отсутствии разделительной полосы островки безопасности, тумбы и элементы дорожных сооружений (опоры мостов, путепроводов и тому подобное), находящиеся на середине проезжей части, водитель должен объезжать справа, если знаки и разметка не предписывают иное.

(п. 9.12 введен Постановлением Правительства РФ от 25.09.2003 N 595)

ПДД РФ, 8. Начало движения, маневрирование ПДД РФ, 10. Скорость движения

Сколько 40 разделить на 8 с использованием длинного деления?

Запутались в длинном делении? К концу этой статьи вы сможете разделить 40 на 8, используя деление в длинную сторону, и сможете применить ту же технику к любой другой задаче на деление в длинную сторону! Давайте взглянем.

Хотите быстро научиться или показать учащимся, как решить деление 40 на 8, используя деление в длинную сторону? Включи это очень быстрое и веселое видео прямо сейчас!

Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что представляет собой каждая часть деления:

• Первое число, 40, называется делимым.
• Второе число 8 называется делителем.

Здесь мы разберем каждый шаг процесса длинного деления на 40, разделенного на 8, и объясним каждый из них, чтобы вы точно поняли, что происходит.

40 разделить на 8 пошаговое руководство

Шаг 1

Первый шаг — поставить задачу деления с делителем слева и делимым справа, как показано ниже:

Шаг 2

Мы можем выяснить, что делитель (8) входит в первую цифру делимого (4), 0 раз. Теперь мы это знаем, мы можем положить 0 вверху:

Шаг 3

Если мы умножим делитель на результат на предыдущем шаге (8 x 0 = 0), мы теперь можем добавить этот ответ под делимым:

Шаг 4

Далее из второй цифры делимого (4 — 0 = 4) вычтем результат предыдущего шага и запишем этот ответ ниже:

		0
8		4	0
	—	0
		4

Step 5

Move the second digit of the dividend (0) down like so:

		0
8		4	0
	—	0
		4	0

Шаг

. Divisor (8). Дозушное (8). Дозушное время (8). Дозушное время (8). Дозушное время (8). Дозушное (8). Дозушное время (8). Дозушное (8). Дозушное время (8). Дозушное время (8). we can put 5 on top:

		0	5
8		4	0
	—	0
		4	0

Шаг 7

Если мы умножим делитель на результат предыдущего шага (8 x 5 = 40), то теперь мы можем добавить этот ответ под делимым:

			5
8		4	0
	—	0
		4	0
		4	0

Шаг 8

Далее вычтем результат предыдущего шага из третьей цифры делимого (40 — 40 = 0) и запишем этот ответ ниже:

2 Итак, что получится, если разделить число 4 на 4?

Если вы дочитали до этого урока, молодец! Больше не осталось цифр, чтобы двигаться вниз от делимого, а это значит, что мы решили задачу деления в длинную сторону.

Ваш ответ — это верхнее число, а любой остаток будет нижним числом. Таким образом, для 40, разделенных на 8, окончательное решение:

5

Остаток 0

Дополнительные расчеты для вас

Теперь вы изучили метод деления 40 на 8, вот несколько других способов, которыми вы можете выполнить расчет:

• С помощью калькулятора, если вы набрали 40 разделить на 8, вы получите 5.
• Вы также можете представить 40/8 в виде смешанной дроби: 5 0/8
• Если вы посмотрите на смешанную дробь 5 0/8, вы увидите, что числитель совпадает с остатком (0), знаменатель — это наш первоначальный делитель (8), а целое число — это наш окончательный ответ (5 ).

Калькулятор деления на длинное деление

Введите еще одну задачу на деление на длинное деление

Следующая задача на деление на длинное деление

Хотите еще больше деления на длинное деление, но не хотите вводить два числа в калькулятор выше? Без проблем. Вот следующая задача, которую вам нужно решить:

Сколько будет 40, разделенное на 9 с помощью деления в длинное число?

Случайные задачи на длинное деление

Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите задачи на длинное деление, а? Ниже приведена куча случайно сгенерированных вычислений для вашего долгого деления удовольствия:

Чему равно 525, разделенное на 742 с использованием длинного деления?

Чему равно 94, разделенное на 861 в длинное деление?

Чему равно 670, разделенное на 819 с использованием длинного деления?

Чему равно 265, разделенное на 729 в ​​длинное деление?

Чему равно 374, разделенное на 826 в длинное деление?

Чему равно 871, разделенное на 997 в длинное деление?

Чему равно 768, разделенное на 779 в длинное деление?

Чему равно 725, разделенное на 943 с использованием длинного деления?

Сколько будет 865 разделить на 991 с использованием длинного деления?

Сколько 82 разделить на 788 в длинное деление?

Чему равно 215, разделенное на 742 с использованием длинного деления?

Чему равно 900, разделенное на 924 с использованием длинного деления?

Чему равно 548, разделенное на 806 с использованием длинного деления?

Чему равно 894, разделенное на 954 в длинное деление?

Чему равно 454, разделенное на 632 с использованием длинного деления?

Чему равно 80, разделенное на 285 с использованием длинного деления?

Чему равно 25, разделенное на 169 с помощью деления в длинное число?

Чему равно 589, разделенное на 636 с использованием длинного деления?

Чему равно 392, разделенное на 426 с использованием длинного деления?

Чему равно 813, разделенное на 841 в длинное деление?

Чему равно 304, разделенное на 830 с использованием длинного деления?

Чему равно 957, разделенное на 962 в длинное деление?

Чему равно 71, разделенное на 431 в длинное деление?

Чему равно 525, разделенное на 800 с использованием длинного деления?

Чему равно 874, разделенное на 913 в длинное деление?

Сколько будет 78 разделить на 961 с использованием длинного деления?

Чему равно 392, разделенное на 442 в длинное деление?

Сколько 111 разделить на 577 в длинное деление?

Чему равно 689, разделенное на 855 в длинное деление?

Чему равно 61, разделенное на 703 с использованием длинного деления?

Чему равно 517, разделенное на 877 в длинное деление?

Чему равно 958, разделенное на 994 в длинное деление?

Чему равно 225, разделенное на 896 в длинном делении?

Сколько 530 разделить на 830 в длинное деление?

Чему равно 719, разделенное на 734 с использованием длинного деления?

Чему равно 757, разделенное на 822 с использованием длинного деления?

Чему равно 227, разделенное на 351 в длинном делении?

Чему равно 346, разделенное на 779 с использованием длинного деления?

Чему равно 850, разделенное на 877 в длинное деление?

Чему равно 635, разделенное на 931 с использованием длинного деления?

Чему равно 393, разделенное на 882 в длинное деление?

Чему равно 383, разделенное на 588 в длинное деление?

Сколько будет 800 разделить на 943 с использованием длинного деления?

Чему равно 996, разделенное на 999 в длинное деление?

Чему равно 681, разделенное на 689 в длинное деление?

Чему равно 494, разделенное на 984 в длинное деление?

Чему равно 279, разделенное на 948 в длинном делении?

Чему равно 138, разделенное на 657 в длинное деление?

Чему равно 466, разделенное на 639 с использованием длинного деления?

Чему равно 225, разделенное на 928 в длинное деление?

Чему равно 283, разделенное на 404 в длинном делении?

Чему равно 460, разделенное на 514 с использованием длинного деления?

Чему равно 724, разделенное на 777 с использованием длинного деления?

Чему равно 628, разделенное на 772 в длинное деление?

Чему равно 37, разделенное на 839 в длинное деление?

Чему равно 649, разделенное на 701 с использованием длинного деления?

Сколько 910 разделить на 918 в длинное деление?

Чему равно 127, разделенное на 693 в длинное деление?

Чему равно 569, разделенное на 688 в длинное деление?

Чему равно 22, разделенное на 404 с использованием длинного деления?

Чему равно 523, разделенное на 739 с использованием длинного деления?

Чему равно 633, разделенное на 996 в длинное деление?

Чему равно 124, разделенное на 250 в прямом делении?

Чему равно 347, разделенное на 687 в длинное деление?

Чему равно 599, разделенное на 791 в длинное деление?

Чему равно 73, разделенное на 203 с использованием длинного деления?

Чему равно 190, разделенное на 771 с использованием длинного деления?

Сколько будет 364, разделенное на 621 с использованием длинного деления?

Чему равно 631, разделенное на 866 в длинное деление?

Что такое 811, разделенное на 947 с использованием длинного деления?

Чему равно 549, разделенное на 668 в длинное деление?

Чему равно 718, разделенное на 883 в длинное деление?

Чему равно 624, разделенное на 721 с использованием длинного деления?

Сколько 813 разделить на 838 в длинное деление?

Сколько 116 разделить на 436 в длинное деление?

Чему равно 319, разделенное на 826 в длинное деление?

Чему равно 678, разделенное на 887 в длинное деление?

Чему равно 527, разделенное на 776 с использованием длинного деления?

Чему равно 851, разделенное на 967 с помощью деления в большую сторону?

Чему равно 459, разделенное на 898 в длинное деление?

Чему равно 784, разделенное на 1000 с использованием длинного деления?

Чему равно 681, разделенное на 772 в длинное деление?

Чему равно 295, разделенное на 780 в длинном делении?

Чему равно 128, разделенное на 240 в прямом делении?

Сколько 84 разделить на 87 в длинное деление?

Чему равно 230, разделенное на 658 с помощью деления в большую сторону?

Что такое 196 разделить на 887 с использованием длинного деления?

Чему равно 497, разделенное на 809 с использованием длинного деления?

Чему равно 969, разделенное на 977 в длинное деление?

Чему равно 390, разделенное на 601 с использованием длинного деления?

Чему равно 735, разделенное на 896 с использованием длинного деления?

Чему равно 973, разделенное на 998 в длинное деление?

Чему равно 96, разделенное на 878 в длинное деление?

Сколько 114 разделить на 117 в длинное деление?

Сколько 269 разделить на 447 с помощью деления в большую сторону?

Чему равно 206, разделенное на 841 с использованием длинного деления?

Чему равно 98, разделенное на 419 в длинное деление?

Чему равно 625, разделенное на 871 с использованием длинного деления?

Чему равно 949, разделенное на 966 в длинное деление?

Чему равно 732, разделенное на 928 с использованием длинного деления?

Сколько 972 разделить на 998 в длинное деление?

Список плей-офф футбольной недели 2022 года 9: 40 лучших в дивизионах из 11 игроков и 24 лучших в дивизионах из 8 игроков

• Футбол

Список плей-офф футбольной недели 9 2022 года: 40 лучших в дивизионах из 11 игроков и 24 лучших в дивизионах из 8 игроков

Джефф Киммерли
Старший редактор MHSAA. com

19 октября 2022 г.

Вот список футбольных школ Атлетической ассоциации средних школ Мичигана, в котором указаны их рекорды побед и поражений и средние показатели плей-офф за восьмую неделю сезона.

Школы в этом списке разделены по дивизионам и упорядочены по среднему баллу плей-офф. Лучшие 32 команды по среднему показателю плей-офф в каждом дивизионе с 11 игроками и 16 лучших команд по среднему показателю плей-офф в каждом дивизионе с 8 игроками получат право участвовать в плей-офф MHSAA Football, который начнется 28 октября. Дивизионы были определены до начала сезона, и приведенные ниже списки включают не только команды, которые в настоящее время потенциально могут пройти квалификацию, но и следующие восемь команд в каждом дивизионе. (Неустойки, подтвержденные на этой неделе, уже добавлены и отражены в отчетах о победах и поражениях и очках плей-офф ниже.)

Чтобы просмотреть список всех футбольных школ плей-офф, подробную информацию об очках плей-офф отдельных школ и сообщить об ошибках, посетите страницу Football Сводка очков плей-офф .

Объявление квалификационных игр и жеребьевки первого раунда плей-офф с 11 и 8 игроками состоится в 18:00. Воскресенье, 23 октября, на «Selection Sunday Show» на Bally Sports Detroit и на его веб-сайте. Отборочные матчи плей-офф и пары будут опубликованы на веб-сайте MHSAA после воскресного шоу Selection.

ДИВИЗИЯ НА 11 ИГРОКОВ 1

1. Бельвиль, 8-0, 79,875
2. Макомб Дакота, 8-0, 79,643
3. Брайтон, 8-0, 79,500

, 8-0, Рокфорд, 8-0 79.500
5. Каледония, 8-0, 78.875
6. Вест Блумфилд, 7-1, 75.875
7. Кларкстон, 6-2, 75.750
8. Лапир, 7-1, 74.000
9. Дэвисон, 7-1 , 73.375
10. Рочестер Адамс, 7-1, 72.875
11. Клинтон Тауншип Чиппева Вэлли, 6-2, 71.500
12. Ромео, 6-2, 70.000
13. Нортвилл, 7-1, 69.875
14. Grandville, 6-2, 68.375
15. Ютика Эйзенхауэр, 6-2, 66.750
16. Southfield Arts & Technology, 6-2, 65.625
17. Saline, 6-2, 64.125
18. Детройт Католический Центр , 6-2, 63.504
19. Дирборн, 6-2, 61.750
20. Нови, 5-3, 61.500
21. Трой, 6-2, 61.250
22. Холт, 5-3, 59.714
23. Энн Арбор Гурон, 5-3, 59,667
24. Ист-Кентвуд, 5-3, 58,018
25. Хартленд, 5-3, 57,750
26. Гранд-Ледж, 6-2, 56,714
27. Браунстаун Вудхейвен, 6-2, 55,804
28. Гранд Блан, 4-4, 52.125
29. Детройт Касс Тек, 5-3, 51.679
30. Озеро Орион, 4-4, 50.500
31. Рочестер Хиллз Стони Крик, 4-4, 49.625
32. Ливония Стивенсон, 4-4, 49.000
33. Нью-Балтимор Анкор-Бей, 3-5, 48.125
34. Рочестер, 4-4, 46.125
35. Холланд Вест Оттава, 3-5, 45.000
36. Хауэлл, 3- 5, 43.500
37. Уэстленд Джон Гленн, 3-5, 43.000
38. Монро, 3-5, 42.750
39. Трой Атенс, 4-4, 42.625
40. Дженисон, 2-6, 41.375

ДИВИЗИЯ НА 11 ИГРОКОВ 2

1. Декстер, 8-0, 80.042
2. Бирмингем Сихолм, 7-1, 71.250
3. Ливония Франклин, 7-1, 70.750
4. Сентрал-Рапидс 8-0, 69,500
5. Маскегон Мона Шорс, 7-1, 67,125
6. Мидленд, 7-1, 66,750
7. Темперанс Бедфорд, 7-2, 65,528
8. Уоррен Де Ла Саль Коллегиэйт, 7-1 , 65,375
9. Розвилл, 6-2, 64,875
10. Батл-Крик Сентрал, 7-1, 64,107
11. Уотерфорд Мотт, 6-2, 63,625
12. Байрон Центр, 6-2, 63,500
13. Port Huron Northern, 7-1, 60.500
14. Farmington, 6-2, 60.000
15. Saginaw Heritage, 6-2, 59.500
16. Grosse Pointe South, 5-3, 58.875
16. South Lyon Восток, 6-2, 58.875
18. Южный Лион, 6-2, 58.607
19. Ист-Лансинг, 6-2, 57.964
20. Порт-Гурон, 6-2, 55.500
21. Шварц-Крик, 6-2, 55.250
21. Traverse City Central, 4-4, 55.250
23. Muskegon Reeths-Puffer, 5-3, 52.000
24. Dearborn Heights Crestwood, 6-2, 51.500
25. Harrison Township L’Anse Creuse, 4- 4, 50.500
26. Portage Northern, 5-3, 50.357
27. St Clair Shores Lakeview, 5-3, 50.125
28. White Lake Lakeland, 4-4, 49.875
29. Warren Cousino, 5-3, 48.250
29. Уоррен Мотт, 4-4, 48.250
31. Милфорд, 4-4, 47.875
32. Бирмингем Гроувс, 5-3, 47.750
33. Ипсиланти Линкольн, 3-5, 44.625
34. Portage Central, 3-5, 44.607
35. Ferndale, 4-4, 44.375
36. North Farmington, 2-6, 43.750
37. Bay City Western, 4-4, 43.000
38. Detroit UD Jesuit, 4-4, 42.286
39. Харпер Вудс, 3–5, 41,375
40. Мидленд Доу, 3–5, 39,375

ОТДЕЛЕНИЕ НА 11 ИГРОКОВ 3

7-1, 67,625
3. Трентон, 7-1, 66,750
4. Мейсон, 8-0, 65,500
5. Гибралтар Карлсон, 7-1, 64,250
6. Сент-Джозеф, 7-1, 63,232
7 Гросс-Пойнт-Норт, 8-0, 62,875
8. Зеланд-Уэст, 7-1, 62,625
9. Маскегон, 6-2, 61,250
10. Фентон, 6-2, 58,875
11. Линден, 5-3, 56,125
12. Детройт Мартин Лютер Кинг, 5-2, 54.238
13. Саутгейт Андерсон, 5-3, 53.750
14. ДеВитт, 5-3, 52.000
15. Ривер Руж, 5-2, 51.917
16. Хаслетт, 6–2, 51,125
16. Лоуэлл, 5–3, 51,125
18. Кадиллак, 5–3, 50,375
19. Оберн-Хиллз, Эйвондейл, 5–3, 49,875
20. Куперсвилль, 5–3, 49,250 20,25 Блумфилд Хиллз Брат Райс, 3-4, 48.000
22. Джексон, 4-4, 46.625
23. Аллен Парк, 4-4, 46.607
24. Ист-Гранд-Рапидс, 3-5, 45.875
25. Парма Вестерн, 5 -3, 45,661
26. Холли, 4-4, 45.500
27. Сидар-Спрингс, 4-4, 44.607
28. Детройт Генри Форд, 5-3, 44.399
29. Детройт Ренессанс, 4-4, 44.274
30. Сент-Клер Шорс Лейк-Шор, 4-4, 43.125
31. Лансинг Уэверли, 4-4, 43.089
32. Гейлорд, 5-3, 43.000
33. Спарта, 5-3, 42.625
34. Нью-Бостон Гурон, 5-3 , 42.250
35. Стерджис, 5-3, 41.750
36. Стивенсвилл Лейкшор, 3-5, 40.857
37. Sault Ste. Мари, 5-3, 39,625
38. Гранд-Рапидс Нортвью, 3-5, 35,250
39. Восточная Зеландия, 2–6, 34.875
40. Озеро Ричленд Галл, 3–5, 34.500

ДИВИЗИОН НА 11 ИГРОКОВ 4

1. Уайтхолл, 9–0, 64.097 2 Гранд-Рапидс , 8-0, 62. 250
3. Текумсе, 8-0, 62.125
4. Гудрич, 7-1, 60.750
5. Редфорд Юнион, 8-0, 60.375
6. Ривервью, 8-0, 59.875
7. Гастингс, 7-1, 58.819
8. Эдвардсбург, 7-1, 58.625
9. Норт Бранч, 7-1, 53.917
10. Шарлотта, 7-1, 52.875
11. Челси, 5-3, 51.458
12. Фриланд, 7-1, 50.250
13. Дирборн Дивайн Чайлд, 6-2, 50.125
14. Хадсонвилл Юнити Кристиан, 5-3, 50.069
15. Фрутпорт, 6-2, 49.750
16. Мэдисон Хайтс Ламфер , 6-2, 49,125
17. Ада Форест Хиллз Истерн, 6-2, 48,375
18. Кросвелл-Лексингтон, 6-2, 46,375
19. Лудингтон, 6-2, 46,194
20. Ортонвилл Брэндон, 5-3 , 45.750
21. Three Rivers, 5-3, 45.625
22. Garden City, 5-3, 45.250
23. Vicksburg, 4-4, 44.875
24. Carleton Airport, 6-2, 44.500
25. Livonia Clarenceville, 5-3, 43.750
26. Orchard Lake St. Mary’s, 3-5, 43.625
27. Marysville, 5-3, 42.768
28. Big Rapids, 6-2, 41.000
28. Paw Пау, 4-4, 41.000
30. Гранд-Рапидс Кристиан, 3-5, 40. 750
31. Найлз, 4-4, 40.375
32. Адриан, 4-4, 39.875
32. Вэйланд, 4-4, 39.875
34. Лейк Фентон, 3-5, 38.625
35. Маршалл, 4-4, 38.000
36. Детройт Ист Инглиш, 4-4, 36.667
37. Лансинг Секстон, 4-4, 36.339
38. Центральная линия, 5 -3, 35,768
39. Allendale, 3-5, 35.000
40. Fremont, 4-4, 34.569

11-PLAYER DIVISION 5

1. Frankenmuth, 8-0, Central, Grand Rapids 1.0523 1, 59.875
3. Корунья, 7-1, 59.500
4. Марин Сити, 7-1, 57.125
5. Маскегон Окридж, 7-1, 56.194
6. Портленд, 7-1, 55.750
7. Армада, 7-1, 55.625
8. Белдинг, 7-1, 53.875
9. Кингсфорд, 6-2, 51.083
10. Уильямстон, 6-2, 49.500
11. Глэдвин, 8-0, 48.500
12. Детройт Кантри День, 5-2, 46.679
13. Берриен-Спрингс, 6-1, 45.732
14. Romulus Summit Academy North, 6-2, 45.250
15. Флэт-Рок, 5-3, 45.125
16. Кингсли, 6-2, 45.000
17. Ховард-Сити Tri County, 7-1, 42.875
18. Dundee, 6-2, 42.750
18. Saginaw Swan Valley, 5-3, 42.750
20. St. Clair Shores South Lake, 6-2, 42.500
21. Olivet, 6-2, 41.750
22. Pontiac Notre Dame Prep, 5-3, 41.000
23. Хопкинс, 5-3, 40.875
24. Флинт Хамади, 7-1, 40.839
25. Ogemaw Heights, 6-2, 40.125
26. Детройт Денби, 5-3, 39.988
27. Шеперд, 6-2, 39.250
28. Католическая школа Каламазу Хакетт, 4-4, 38.524
29. Эссексвилл Гарбер, 5-3, 38.250
Юго-Восточный , 5-3, 36.696
31. Йель, 4-4, 36.375
32. Лейк-Одесса Лейквуд, 6-2, 36.125
33. Берч-Ран, 4-4, 35.125
34. Гавань Бентон, 4-4, 34.732
35. Гросс-Иль, 4–4, 34,250
36. Ричмонд, 3–5, 34,125
37. Флинт Пауэрс Католик, 3–5, 33,161
38. Уитмор-Лейк, 6–2, 31,625
39. Midland Bullock Creek, 4–4, 31.429
40. Macomb Lutheran North, 3–5, 30.875

ОТДЕЛЕНИЕ НА 11 ИГРОКОВ 6

1. Grand Rapids West Qatar, 7–1, 61.750
6 2. Almont -2, 52,167
3. Гладстон, 6-2, 51,125
4. Экорс, 8-0, 50,738
5. Мэдисон Хайтс Бишоп Фоли, 8-0, 48,750
6. Константин, 7-1, 48,125
6. Дюран, 8-0, 48.125
8. Рид Сити, 7-1, 48.000
9. Клинтон, 8-0, 47.750
10. Негони, 8-0, 47.139
11. Университет Уоррена Мичиган, 7-1, 46.536
12. Бьюкенен, 7-1, 45.054
13. Стэндиш-Стерлинг, 7-0, 44.946
14. Миллингтон, 7-1, 44.804
15. Бойн Сити, 8-0, 44.750
16. Подготовка к колледжу Detroit Voyageur , 6-2, 41.000
17. Овидий-Элси, 6-2, 40.000
18. Кент Сити, 6-2, 37.250
19. Клэр, 5-3, 36.875
20. Манисти, 5-3, 35.819
21. Католический центр Маскегон, 6-2, 35.500
22. Уотервлит, 5-3, 35.232
23. Меномини, 4-4, 34.792
24. Детройт Северо-Западный, 5-3, 34.292
25. Элк-Рапидс, 6- 2, 34.250
26. Калумет, 5-3, 34.014
27. Монтегю, 3-5, 33.944
28. Хоутон, 5-3, 33.764
29. Санфорд Меридиан, 5-3, 33.250
30. Лансинг Католик, 3-5 , 33.000
31. Лейнсбург, 6-2, 32.500
32. Дирборн Хайтс Робишо, 3-5, 30.500
33. Детройт Першинг, 4-4, 30.321
4-4, 30.143
36. Лютеранский Вестленд, 5-3, 29.750
36. Стокбридж, 5-3, 29.750
38. Ремус Чиппева Хиллз, 3-5, 29.375
39. Ида, 3-5, 28.500
40. Хиллсдейл, 3-5, 28.482

ДИВИЗИОН НА 11 ИГРОКОВ 7

1. Траверс-Сити Сент-Фрэнсис, 8-0, 53.250
2. Детройт Сентрал, 8-0, 51.213, 3.905 Хадсон 8-0, 47.750
4. Джексон Люмен Кристи, 5-3, 47.000
5. Итака, 7-1, 39.804
6. Норт Маскегон, 7-1, 39.500
7. Лоутон, 6-2, 39.232
8 Наполеон, 8-0, 38.750
9. Шарлевуа, 7-1, 38.500
10. Элктон-Пиджен-Бей Порт Лейкер, 8-0, 38.125
11. Юнион-Сити, 7-1, 36.750
12. Нью-Лотроп , 6-2, 36,625
13. Скулкрафт, 6-3, 35.716
14. Монро Сент-Мэри Католический центр, 3-5, 34.375
15. Плохой топор, 6-3, 34.083
16. Университет Гросс-Пойнт-Вудс Лиггетт, 6-2, 34.000
17. Певамо-Вестфалия, 5-3, 33,375
18. Делтон Келлог, 4-4, 32,792
19. Гомер, 6-2, 32,625
20. Монтроуз, 5-3, 32,250
21. Равенна, 5- 3, 31.625
22. Манчестер, 5-3, 31.500
23. Касс Сити, 5-3, 30.375
24. Грасс-Лейк, 5-3, 30.250
25. Бензи Сентрал, 3-5, 28.071
26. Лейк Городская, 5-3, 27.500
27. Бат, 5-3, 27.321
28. Найлс Брендивайн, 4-4, 27.107
29. Эри Мейсон, 5-3, 26.500
30. Л’Анс, 4-4, 26.264
31. Бертон Бендл, 4-4, 26.161
32. Джонсвилл, 4-4, 25.125
33. Перри, 3-5, 23.875
34. Лесли, 2-6, 23.125
35. Бивертон, 2-6, 23.000
36. Детройт Лойола , 1-7, 22.661
37. Ганновер-Хортон, 2-6, 20.875
38. Сандаски, 2-6, 20.667
39. Гейлсбург-Аугуста, 2-5, 20.577
40. Харрисон, 2-6, 20.125

ОТДЕЛ НА 11 ИГРОКОВ 8

1. Айрон Маунтин, 7-1, 44.764
2. Оттава Лейк Уайтфорд, 8-0, 44.250
3. Убли, 8-0, 40.000
4. Бил Сити, 8-0, 38.625
5. Морской пехотинец City Cardinal Mooney, 7-1, 38. 250
6. Saginaw Michigan Lutheran Seminary, 7-1, 37.875
7. Harbour Beach, 7-1, 35.875
8. Fowler, 7-1, 35.375
9. Riverview Gabriel Richard, 5-3, 35.125
10. Эварт, 7-1, 34.375
11. Рединг, 6-2, 33.625
12. Сент-Игнас, 6-2, 33.375
13. Маунт Клеменс, 7-1, 32.613
14. Франкфурт, 7-1, 32.250
15. Сентервиль, 6-2, 31.970
16. Барк Ривер-Харрис, 6-2, 31.125
17. Сагино Нувель, 5-3, 30.964
18. Карсон Сити- Кристалл, 7-1, 30.250
19. Кларкстон Эверест Коллегиат, 5-3, 29.214
20. Декейтер, 5-3, 29.036
20. Белый Голубь, 5-3, 29.036
22. Ишпэминг, 4-4, 28.847
23. Белое облако, 6-2, 28,750
24. Флинт Бичер, 4-3, 28,536
25. Академия бизнеса и технологий Мелвиндейла, 6-2, 28,488
26. Детройтская академия лидерства, 3-5, 28,167
27. Эддисон, 4-4, 25.875
27. МакБейн, 4-4, 25.875
29. Марлетт, 4-4, 25.750
30. Восточный Джордан, 4-4, 25.250
31. Детройт Сообщество, 4-4 , 24. 292
32. Петербург Саммерфилд, 4-4, 24.125
33. Вассар, 4-4, 23.917
34. Стерлинг Хайтс Паркуэй Кристиан, 3-5, 23.250
35. Дансвилл, 3-5, 20.250
35. Рочестер Hills Lutheran Northwest, 3-5, 20.250
37. Unionville-Sebewaing, 2-6, 20.167
38. Manton, 3-5, 19.625
39. Burton Bentley, 3-5, 19.286
40. Мейпл-Сити-Глен-Лейк, 3-5, 18.875

ОТДЕЛЕНИЕ НА 8 ИГРОКОВ 1

1. Мунисинг, 8-0, 37.375
2. Мартин, 7-1, 37.250
, 8-Меррилл 3. 0, 36.250
3. Роджерс Сити, 8-0, 36.250
5. Кингстон, 8-0, 34.375
6. Браун Сити, 7-1, 33.875
7. Ньюберри, 7-1, 32.804
8. Оберн-Хиллз Окленд Кристиан, 7-1, 31.625
9. Норвегия, 6-2, 31.083
10. Адриан Ленави Кристиан, 6-2, 30.750
11. Брекенридж, 6-2, 30.375
11. Гоблз, 6-2, 30.375
13. Теконша, 7-1, 29.643
14. Редьярд, 5-3, 28.161
15. Фултон, 6-2, 28.125
16. Индиан Ривер Инланд Лейкс, 5-3, 28.054
3, 27.625
18. Пикфорд, 5-3, 27.411
19. Месик, 5-3, 26.607
20. Марцелл, 5-3, 26.500
21. Бриттон Дирфилд, 5-3, 26.232
22. Центральный католик , 5-3, 25.857
23. Батл-Крик Сент-Филип, 4-4, 25.518
24. Саттонс-Бей, 3-5, 24.804

8-ИГРОВЫЙ ДИВИЗИОН 2

8-0 36,625
2. Марион, 8-0, 34.857
3. Климакс-Скоттс, 7-1, 34.250
4. Пауэрс Норт Централ, 8-0, 33.958
5. Пек, 7-1, 32.375
6. О Грес- Симс, 7-1, 31.625
6. Моррис, 7-1, 31.625
8. Лесопарк Кристал Фолс, 7-1, 30.458
9. Мендон, 6-2, 30.000
10. Позен, 7-1, 29.875
11. Гейлорд-Сент-Мэри, 6-2, 28.929
12. Центральное озеро, 6-2, 28.500
13. Озеро Линден-Хаббелл, 5-3, 25.708
14. Сидарвилль, 5-3, 25.536
15. Камден-Фронтиер, 4-4, 25.250
16. Стефенсон, 5-3, 24.958
17. Кинд Норт Гурон, 5-3, 24.625
18. Бэй Сити Олл Сэйнтс, 4-4, 23.000
19. Афины, 4-4, 22.625
20. Питтсфорд, 4-4, 22.250
21. Вайоминг Tri-unity Christian, 4-4, 21. 875
22. Mio, 3-5, 21.750
23. Atlanta, 3-5, 21.375
24. New Haven Merrit Academy, 4-4, 21.125

MHSAA является частной , некоммерческая корпорация добровольного членства более чем 1500 государственных и частных старших классов средних школ и неполных средних / средних школ, которая существует для разработки общих правил допуска к занятиям спортом и соревнований. Никакие государственные средства или доллары налогов не поддерживают MHSAA, которая была первой такой ассоциацией на национальном уровне, которая не принимала членские взносы или вступительные взносы на турниры от школ. Школы-члены, которые обеспечивают соблюдение этих правил, могут участвовать в турнирах MHSAA, которые ежегодно собирают более 1,3 миллиона зрителей.

-0-

Метки: Список очков плей-офф

• Футбол

ЧЕМПИОНЫ ГОСУДАРСТВА! Мичиган: 9-я неделя дополнительных очков

21 октября 2022 г.

На этой неделе на ЧЕМПИОНАТАХ ГОСУДАРСТВА! Дополнительный момент: Лорн Плант, Сидней Кариел и Девин Гарднер подводят итоги примечательных игр 8-й недели, а также анонсируют основные игры 9-й недели.0523 7:06 — Декстер против Салина, итоги
8:53 — Вудхейвен против Саутгейта, Андерсон, итоги
9:57 — Cass Tech #17 в рейтинге
14:17 — Mona Shores #20 в рейтинге
17:17 — Mr. Футбольная награда
19:35 — Промо-акция Detroit Athletic Club Athlete of the Year
20:50 — DMC Gamechangers
22:24 — Награда Anvil
26:59 — Дэвисон в Lapeer превью 
28:28 — Rockford в Каледонии превью
29: 50 — Бельвиль в Брайтоне — превью игры недели

Метки: Чемпионы штата! Спортивная сеть

• Загрузи больше

Сколько будет 8 разделить на 4 в виде дроби?

Домашнее задание. Помощь.

• задачи на дроби
• задачи на слова
• деление

вопрос 11 января 2013 г. в Word ответы на задачи по анонимно

Ваш ответ

2 ответа

8/4=2

ДА, 2 — это фракшун (вырожденный)

ответил 11 января 2013 г. по аноним

я не знаю. я тупой

ответил 29 апреля по Джейсон Тернер

Похожие вопросы

1 ответ

8 разделить на 3 1/2

спросил 11 ноября 2015 г. в Pre-алгебра ответы по Кейли Робертс | 1.4k просмотров

• задачи на дроби
• деление

1 ответ

сколько будет 756 миллионов разделить на 4500

спросил 4 декабря 2013 г. в Word ответы на задачи по анонимный | 394 просмотра

• деление
• словесные задачи

1 ответ

Сколько 1 галлон разделить на 3?

спросил 14 мая 2013 г. в исчислении ответы по анонимный | 908 просмотров

• деление
• словесные задачи

1 ответ

что является пробелом разделить на 7 равно 40 разделить на 8

вопрос 10 января 2015 г. в других математических темах по анонимный | 1,4 тыс. просмотров

• деление

2 ответа

34 разделить на 8

спросил 7 мая 2014 г. по алгебре 1 ответы по анонимный | 578 просмотров

• деление
• математика
• деление

1 ответ

что такое 3,04 доллара разделить на 8 человек ?

спросил 19 июня 2013 г. в исчислении ответы по анонимный | 509 просмотров

• деление
• длинное деление

1 ответ

сколько 8+y разделить на 2

спросил 16 июня 2013 г. по алгебре 1 ответы по анонимный | 283 просмотра

• деление дробей
• задачи по алгебре
• деление
• решение уравнений

1 ответ

чему равно 1 1/4 разделить на 5/8?

спросил 6 мая 2013 г. в Word ответы на задачи по анонимный | 553 просмотра

• отдел

1 ответ

2 1/8 разделить на 1 1/3 = показать работу

вопрос 1 мая 2013 по алгебре 1 ответы по анонимный | 530 просмотров

• деление

1 ответ

работа на 8 разделить на 180

спросил 4 декабря 2012 г. в Word ответы на задачи по анонимный | 568 просмотров

• деление

1 ответ

как разделить 240 разделить на 40 в длинном делении

спросил 7 мая 2013 г. в Word ответы на задачи по анонимный | 854 просмотров

• длинное деление
• задачи по алгебре
• деление
• и решение уравнений

1 ответ

что такое 9,3 миллиарда долларов разделить на 4,2 миллиона долларов в долларах0003

спросил 22 марта 2013 г. в Word ответы на задачи по анонимный | 857 просмотров

• словесная задача
• деление

1 ответ

Покажите мне произведение для 4216 разделить на 6. .. Калькулятор говорит 702r6… Когда я делаю это на бумаге, я получаю 702r2

	0	5
8		4	0
	—	0
		4	0
	—	4	0
			0
2 спросили2 26 февраля 2013 г. в Pre-алгебра ответы по анонимный | 541 просмотров деление 1 ответ Сколько будет 82 разделить на 23 в длинном делении? спросил 13 октября 2012 г. в ответах по статистике по анонимный | 566 просмотров деление 2 ответа 17,5 разделить на 3 в виде дроби спросил 26 декабря 2014 г. в задачах на дроби по Элайджа | 2,7 тыс. просмотров задачи на дроби 1 ответ сколько будет 1 1/3 стакана разделить на 2 в виде дроби? спросил 22 сентября 2013 г. в других математических темах по анонимный | 2,4 тыс. просмотров #dividing_mixed_numbers_with_whole_numbers задачи на дроби деление дробей 1 ответ 5/17 разделить на 7/12 в виде дроби вопрос 18 марта 2013 г. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт