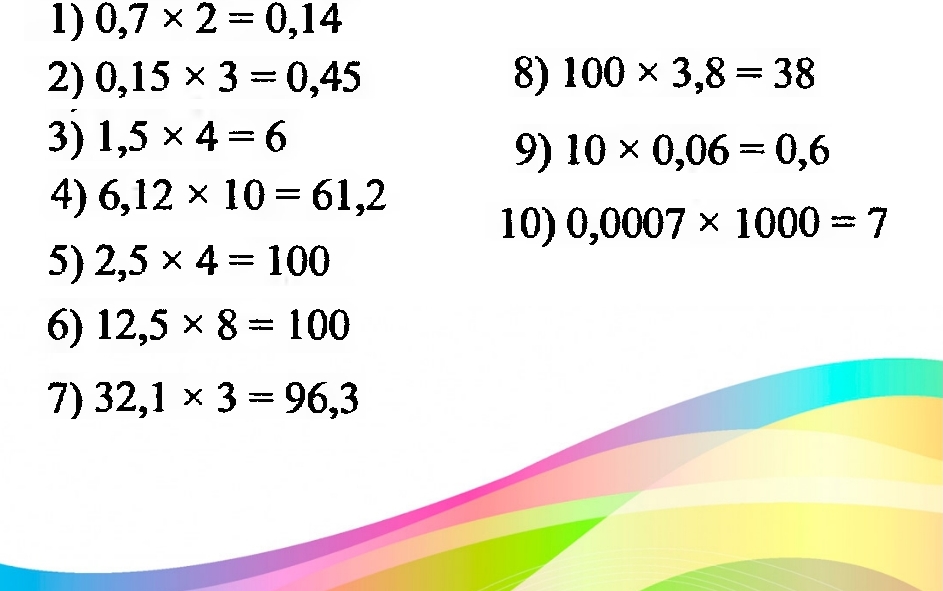Приёмы быстрого счёта без калькулятора
1. Быстрый счёт без калькулятора. Приемы быстрого счета.
Научиться быстро считать не так уж сложно, ахорошему математику просто необходимо владеть
основными приемами быстрого счета.
Рассмотрим некоторые способы быстрого
устного счета, которые
рассчитаны на ум
«обычного» человека и не требуют уникальных
способностей.
РАЗЛИЧНЫЕ СПОСОБЫ
СЛОЖЕНИЯ И ВЫЧИТАНИЯ
СЛОЖЕНИЕ
Основное правило для выполнения сложения в уме
звучит так:
Чтобы прибавить к числу 9, прибавьте к нему 10 и
отнимите 1; чтобы прибавить 8, прибавьте 10 и отнимите
2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т.д.
Например, 56+8=56+10-2=64;
65+9=65+10 -1=74.
СЛОЖЕНИЕ В УМЕ ДВУЗНАЧНЫХ ЧИСЕЛ
Если цифра единиц в
прибавляемом числе
больше5, то число необходимо округлить в сторону
увеличения, а затем вычесть ошибку округления из
полученной суммы.
Если же цифра единиц меньше, то прибавляем
сначала десятки, а потом единицы.
Например, 34+48=34+50 – 2 = 82;
27+31=27+30+1 =58.
СЛОЖЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ
Складываем слева на право, то есть сначала
сотни, потом десятки, а затем единицы.
Например, 359+523= 300+500+50+20+9+3=
=800 +70 +12 = 882;
456+298=400+200+50+90+6+8=600+140+14=754.
ВЫЧИТАНИЕ
Чтобы вычесть два числа в уме, нужно округлить
вычитаемое, а затем подкорректируйте полученный
ответ.
Например, 56 – 9 = 56 – 10 + 1 = 47;
436 – 87 = 436 — 100 + 13 = 349.
Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете
пользоваться этим простым правилом:
Отнимите от 9 все цифры, кроме последней. А последнюю
цифру отнимите от 10:
Например, 1000 — 648
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352
РАЗЛИЧНЫЕ СПОСОБЫ
УМНОЖЕНИЯ И ДЕЛЕНИЯ
Умножение и деление на 4.
Чтобы умножить число на 4, его дважды удваивают.
Например, 527 · 4 = (527 · 2) · 2 = 1054 · 2 = 2108.
Чтобы число разделить на 4 , его дважды делят на 2.
Например, 2648 : 4 = (2648 : 2) : 2 = 1324 : 2 = 662.
Умножение и деление на 5.
Чтобы умножить число на 5, нужно его умножить
на 10 и разделить на 2.
Например, 348 · 5= (348 · 10) : 2 = 3480 : 2 = 1740.
Чтобы число разделить на 5, нужно умножить его
на 0,2, то есть в удвоенном исходном числе отделить
запятой последнюю цифру.
Например, 51 : 5 = 51 · 0,2 = 10,2.
Умножение на число, оканчивающееся на 5.
Чтобы четное двузначное число умножить на число,
оканчивающееся на 5, следует применить правило: если один из
сомножителей увеличить в несколько раз, а другой – уменьшить
во столько же раз, произведение не изменится.
Например,
44 · 5 = (44 : 2) · 5 · 2 = 22 · 10 = 220;
26 · 35 = (26 : 2) · 35 · 2 = 13 · 70 = 910;
36 · 45 = (36 : 2) · 45 · 2 = 18 · 90 = 1625;
18 · 65 = (18 : 2) · 65 · 2 = 9 · 130 = 1170;
12 · 75 = (12 : 2) · 75 · 2 = 6 · 150 = 900;
14 · 85 = (14 : 2) · 85 · 2 = 7 · 170 = 1190;
12 · 95 = (12 : 2) · 95 · 2 = 6 · 190 = 1140.
При умножении на 65, 75, 85, 95 числа следует брать
небольшие, в пределах второго десятка. В противном случае
вычисления усложнятся.
Умножение на 25.
Чтобы умножить число на 25, нужно его умножить
на 100/4, то есть умножить на 100 и разделить на 4.
Например, 348 · 25 = (348 · 100) : 4 = (34800 : 2) : 2 =
17400 : 2 = 8700.
Умножение на 1,5.
Чтобы умножить число на 1,5 нужно к исходному
числу прибавить его половину.
Например, 228 · 1,5 = 228 + 114 = 342.
14. Умножение на 9
Чтобы умножить любое число от 1 до 9 на 9, посмотритена руки.
Загните палец, который соответствует умножаемому числу
(например 9×3 – загните третий палец), посчитайте пальцы до
загнутого пальца (в случае 9×3 – это 2), затем посчитайте после
загнутого пальца (в нашем случае – 7). Ответ: 27.
Умножение на 9.
Чтобы умножить число на 9, к
приписывают 0 и отнимают исходное число.
Например, 847 · 9 = 8470 – 847 = 7623.
нему
Умножение многозначных чисел на 9.
1. Число десятков увеличим на 1 и вычтем из множимого.
2. К результату приписываем дополнение цифры единиц
множимого до 10.
Например, 576 · 9
1. 576 – (57+1)=518
2. 10 — 6 =4
Ответ: 5184
379 · 9
1. 379 – (37 + 1) =341
2.10 — 9 = 1
Ответ: 3411
Умножение на 99
1. Из числа вычитаем число его сотен, увеличенное на 1.
2. Находим дополнение числа, образованного двумя последними
цифрами до 100.
3. Приписываем дополнение к предшествующему результату.
Пример:
27 · 99
134 · 99
27 – 1 = 26 (сотен – 0+1)
134 – 2 = 132 (сотня – 1 + 1)
100 — 27 = 73
100 – 34 = 66
27 · 99 = 2673
134 · 99 = 13266
Умножение на 11.
1 способ. Чтобы число умножить на 11, к нему приписывают 0 и
прибавляют исходное число.
Например, 243 · 11 = 2430 + 243 = 2673.
2 способ. Если хочешь умножить число на 11, то поступай так:
запиши число, которое нужно умножить на 11, а между цифрами
исходного числа вставь сумму этих цифр.
Если сумма получается двузначное число, то 1 прибавляем
к первой цифре исходного числа.
Например, 45 · 11 = 4 (4+5)7= 967.
Умножение на 12.
Чтобы
умножить число на 12: нужно удваивать
поочередно каждую цифру и прибавлять к ней поочередно ее
«соседа».
Например, 63247 · 12
Необходимо записывать цифры множимого через
интервал и каждую цифру результата писать точно под
цифрой числа 63247, из которой она образовалась.
63247 · 12 дважды 7 будет = 14, переносим 1
4
63247 · 12 дважды 4 + 7 + 1 = 16, переносим 1
64
63247 · 12 дважды 2 + 4 + 1 = 9
964
Следующие шаги аналогичны.
Окончательный ответ : 63247 · 12= 758964.
Умножение на 22, 33, …, 99.
Чтобы двузначное число умножить на 22, 33, …, 99, надо
этот множитель представить в виде произведения однозначного
числа на 11, то есть 44 = 4 · 11; 55 = 5 · 11.
Затем произведение первых чисел умножить на 11:
Например, 24 · 22 = 24 · 2 · 11 = 48 · 11 = 528
23 · 66 =23 · 6 · 11=138 · 11=1518
Умножение трехзначного числа на 101.
Чтобы умножить трехзначное на 101,
увеличиваем
первый множитель на число его сотен и приписываем к нему
справа две последние цифры первого множителя.
Например, 125 · 101 = 126(125+1)25 =12625
Этот прием дети легко усваивают при записи вычисления
в столбик.
х125
101
+ 125
125
12625
Возведение в квадрат числа, оканчивающегося цифрой 5.
Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 65),
умножают число его десятков (6) на число десятков, увеличенное на 1 (на 6+1 = 7), и
к полученному числу приписывают 25
(6 · 7)25 = 4225
Например: 952 =(9 · 10)25= 9025; 1252 = (12 · 13)25=15625
Возведение в квадрат числа, близкого к 50.
Если хочешь возвести в квадрат число, близкое к 50, но большее 50, то
поступай так:
1) вычти из этого числа 25;
2) припиши к результату двумя цифрами квадрат избытка данного числа над 50.
Примеры:
1) 582 = 3364. Объяснение: 58 – 25 = 33, 58-50=8, 82 = 64, 582 = 3364.
2) 672 = 4489. Объяснение: 67 – 25 = 42, 67 – 50 = 17, 172 =289, 672 = 4200 + 289 =
= 4489.
Если хочешь возвести в квадрат число, близкое к 50, но меньшее 50, то
поступай так:
1) вычти из этого числа 25;
2) припиши к результату двумя цифрами квадрат недостатка данного числа до 50.
Примеры:
1) 482 = 2304. Объяснение: 48 – 25 = 23, 50 – 48 =2, 22 = 4, 482 = 2304.
2) 372 = 1369. Объяснение: 37 – 25 = 12,= 13, 132 =169, 372 = 1200 + 169 = 1369.
Умножение на 37.
Чтобы умножить число на 37, надо это число разделить на
3 и умножить на 111.
Например: 24 · 37 = (24 : 3) · 37 · 3 = 8 · 111 = 888;
27 · 37 = (27 : 3) · 111 = 999.
Деление на 37.
Чтобы число разделить на 37, надо это число разделить на
111 и умножить на 3.
Например: 999 : 37 = 999 :111 · 3 = 27;
888 : 37 = 888 :111 · 3 = 24.
Чтобы научиться устно умножать и делить на 37, надо
хорошо знать таблицу умножения на три и признак делимости
на три.
Умножение двух рядом стоящих чисел
При умножении двух рядом стоящих чисел надо
сначала перемножить цифры десятков, затем цифру
десятков умножить на сумму цифр единиц и, наконец,
надо перемножить цифры единиц.
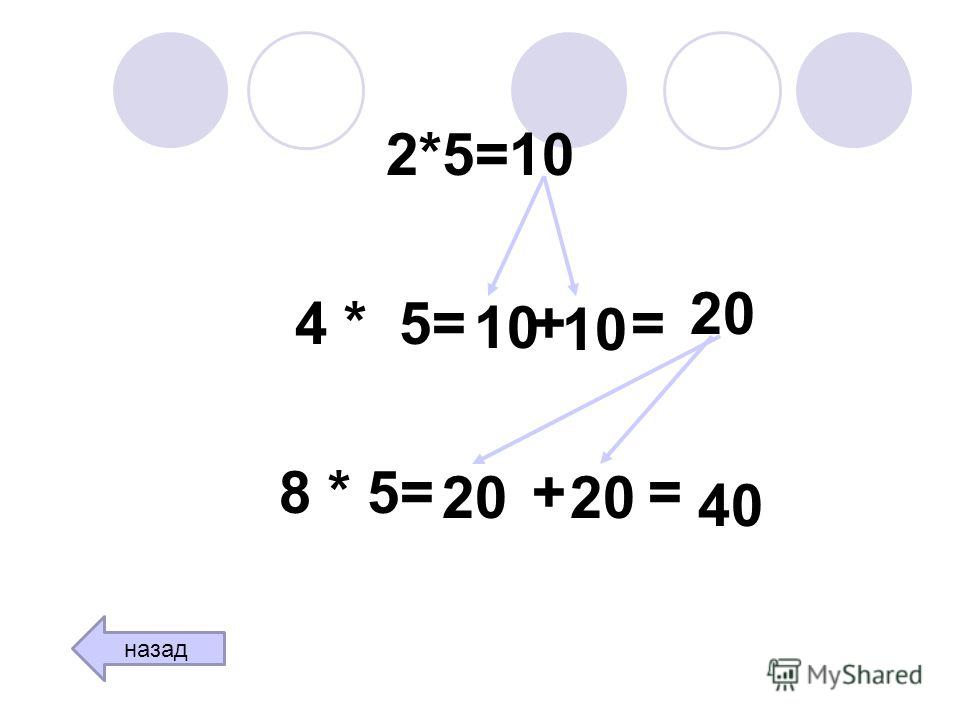Получим ответ.Например: 12 ×13
Шаг1. 1 × 1 = 1
Шаг 2. 1 × (2+3) = 5
Шаг 3. 2 × 3 = 6
Ответ: 156
Умножение пары чисел, у которых цифры десятков одинаковые, а сумма
цифр единиц составляет 10
Пример:
24 × 26 = (24 – 4) × (26 + 4) + 4 × 6 = 20 × 30 + 24 = 624.
Числа 24 и 26 округляем до десятков, чтобы получить число сотен, и к числу
сотен прибавляем произведение единиц.
18 × 12 = 2 × 1 сот. + 8 × 2 = 200 + 16 = 216;
23 × 27 = 2 × 3 × 100 + 3 × 7 = 621;
34 × 36 = 3 × 4 сот. + 4 × 6 = 1224;
71 × 79 = 7 × 8 сот. + 1 × 9 = 5609;
82 × 88 = 8 × 9 сот. + 2 × 8 = 7216.
Можно решать устно и более сложные примеры:
108 × 102 = 10 × 11 сот. + 8 × 2 = 11016;
204 × 206 = 20 × 21 сот. +4 × 6 = 42024;
802 × 808 = 80 × 81 сот. +2 × 8 = 648016.
Проверка:
× 802
808
6416
6416__
648016
Умножение чисел, оканчивающихся на 1.
При умножении чисел, оканчивающихся на 1, надо сначала перемножить
цифры десятков и правее полученного произведения записать под этим числом
сумму цифр десятков, а затем перемножить 1 на 1 и записать еще правее.
Сложив столбиком, получим ответ.
1) 81 × 31 = ?
8 × 3 = 24
8 + 3 = 11
1×1=
1
2511
81 × 31 = 2511
2) 21 × 31 = ?
2×3=6
2 +3 = 5
1×1= 1
651
21 × 31 = 651
3) 91 × 71 = ?
9 × 7 = 63
9 + 7 = 16
1×1= 1
6461
91 × 71 = 6461
Умножение двузначных чисел, у которых сумма цифр
десятков равна 10, а цифры единиц одинаковые.
Правило. При умножении двузначных чисел. у которых
сумма цифр десятков равна 10, а цифры единиц одинаковые,
надо перемножить цифры десятков. и прибавить цифру единиц,
получим число сотен и к числу сотен прибавим произведение
единиц.
Примеры:
72 × 32 = (7 × 3 + 2)сот. + 2 × 2 = 2304;
64 × 44 = (6 × 4 + 4) × 100 + 4 × 4 = 2816;
53 × 53 = (5 × 5 +3) × 100 + 3 × 3 = 2809;
18 × 98 = (1 × 9 + 8) × 100 + 8 × 8 = 1764;
24 × 84 = (2 × 8 + 4) ×100+ 4 × 4 = 2016;
63 × 43 = (6 × 4 +3) × 100 +3 × 3 = 2709;
35 × 75 = (3 × 7 + 5) × 100 +5 × 5 = 2625.
Заключение.
Как мы видим, быстрый счет это уже не тайна за
семью печатями, а научно разработанная система. Раз
есть система, значит ее можно изучать, ей можно
следовать, ею можно овладеть.
Все рассмотренные нами методы устного счёта
говорят о многолетнем интересе ученых и простых
людей к игре с цифрами.
Используя некоторые из этих методов на уроках
или дома, можно развить скорость вычислений,
привить интерес к математике, добиться успехов в
изучении всех школьных предметов.
«Как перевести метры в сотки?» — Яндекс Кью
ПопулярноеСообщества
ГеометрияЗнатоки+3
Анонимный вопрос
·
278,9 K
ОтветитьУточнитьАлександра Федоровская
Маркетинг
3,7 K
Маркетолог, преподаватель, а также молодая мама.
· 27 нояб 2018
Одна сотка представляет собой квадрат 10 на 10 метров, следовательно, она равна 100 квадратными метрам.
Что бы узнать, сколько будет земельный участок в сотках, вам нужно вычислить его площадь, т.е. умножить длину на ширину, а далее разделить на 100.
203,2 K
Метрополитен
23 августа 2020
Подробности можно было не говорить
Комментировать ответ…Комментировать…
Межа
57
кадастровое бюро МЕЖА · 14 февр 2021 · megageo.ru
Отвечает
Олег Межа
Если квадратные метры в сотки, то легко:
100 кв.м. = 1 сотка
100 соток = 1 гектар
1 гектар = 10000 кв.м.
Если линейные, то умножит длину на ширину, применимо к фигурам, где углы в 90 градусов.
Пример:
10 м на 15 м = 150 кв.
м. = 1.5 сотки
35 м на 20 м = 700 кв.м. = 7 соток
8 м на 12 м = 96 кв.м. = 0.96 сотки
Если требуется уточнить площадь земельного… Читать далее
18,9 K
Комментировать ответ…Комментировать…
Olya A.
200
Красота без ума, милочка, это не дар, а наказание природы. · 16 нояб 2018
Очень просто! Допустим длина = 20 метров, а ширина = 25 метров. Получаем площадь: 20*25 = 500 квадратных метров. Одна сотка = 100 квадратных метров, значит 500 кв.м. = 5 соток.
76,4 K
Надежда Шатина
10 января 2020
Все верно
Комментировать ответ…Комментировать…
Рассчитать.рф — Калькуляторы онлайн!
177
Широкий список онлайн-калькуляторов для проведения самых разных вычислений · 31 окт 2020 · рассчитать.
рф
Отвечает
Александр Дубасов
Одна сотка равняется 100 квадратным метрам. Соответственно, чтобы перевести значение площади из квадратных метров в сотки, его нужно разделить на сто. Онлайн калькулятор: https://рассчитать.рф/перевести-квадратные-метры-в-сотки/
Онлайн-калькуляторы на все случаи жизни!
Перейти на рассчитать.рф16,8 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
8 раз (8x) Генератор таблиц таблицы умножения
Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Приведенный выше ресурс умножения и деления соответствует (полностью или частично) стандарту 3OA07, взятому из Общего базового стандарта по математике (см. выдержку ниже). Различные ресурсы, перечисленные ниже, соответствуют одному стандарту.
Свободно умножайте и делите в пределах 100, используя такие стратегии, как отношение между умножением и делением (например, зная, что 8 x 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
Упражнение
Карточки
- Соответствующие карточки умножения (таблица 3x) (различные представления умножения)
- Соответствующие карточки умножения (таблица 4x) (различные представления умножения)
- Соответствующие карточки умножения (таблица 5х) (различные представления умножения)
- Соответствующие карточки умножения (таблица 6х) (различные представления умножения)
- Соответствующие карточки умножения (таблица 7х) (различные представления умножения)
- Соответствующие карточки умножения (таблица 8x) (различные представления умножения)
Таблица
Таблицы умножения
- Произведения до 100 : 4 на странице (карманный формат)
- Настраиваемая таблица умножения (установите строки и столбцы)
- Таблица умножения (в масштабе)
- Произведения до 100, например от 1 x 1 до 10 x 10
- Продукты до 144 напр.
1 x 1 до 12 x 12
1 x 1 до 12 x 12Таблицы умножения
- Таблицы умножения (от x1 до x12) (цветные)
- A Колесо умножения (выберите таблицу от 1 до 10 – включает возможность перемешивания)
Пример/1 9001 000
Flashcard
- Деление на 2, 3, 4, ?, 11, 12 варианты до 144 карт
- Делимое до 45 напр. 45 ÷ 5
- Дивиденды до 81 напр. 81 ÷ 9
- Продукты до 45 напр. 6 x 4
- Продукты до 81 напр. 8 x 7
- 1 раз (1x) до 12 раз (12x) столов Выбор таблицы из выпадающего списка – 144 возможных карты
- Деление – Делители до 5
- Деление – Делители до 9
- Деление – Делители до 12
- Карточки: таблицы умножения от двух до двенадцати, например. до 12 х 12
- Умножение – умножение до 5
- Умножение – умножение до 9
- Умножение – умножение до 12
Карточки
- Треугольники фактов для печати (умножение и деление) – 7 страниц, 901 большой размер, 901 факт. Треугольники (умножение и деление)
Треугольники (умножение и деление)Игра
Игры с ответами
- Магниты: таблицы от 2x до 10x
- Какой символ оператора отсутствует? например 5 ? 4 = 9, 20 ? 5 = 4
Игра на совпадение
- Игра «Удвоение числа» (1 из 2)
- Игра «Удвоение числа» (2 из 2)
- Умножение до 25 (например, 5 x 5)
- Умножение до 45 (например, .45) x 9)
- Умножение до 81 (например, 9 x 9)
- Таблицы от 2x до 9x
Целевая игра
- Только столы 2x, 5x и 10x 9 – необязательные ограничения по времени)
Number line
- Blank: 10 Intervals & Hops – for practice with times tables and other patterns
Puzzle
Crossword
- Multiplication Crossword (to x10)
- Multiplication Crossword (to x12)
Ящики умножения
- Ящики умножения (таблицы от 2x до 7x)
- Ящики умножения (таблицы от 7x до 12x)
Квадраты умножения
- Квадраты умножения (Fiddly)
- Multiplication Squares (Tricky)
Number Jumbles
- Multiplication Jumbles (Fiddly)
- Multiplication Jumbles (Tricky)
- Multiplication Jumbles (Trickier)
Table
- Printable division tables & flash cards
Таблицы деления
- Деление от 1 до 6 напр. 6 таблиц/стр.
- Деление от 7 до 12 напр. 6 таблиц/стр.
- Деление от 1 до 12 напр. 12 таблиц/ стр.
6 таблиц/стр.Таблицы умножения
- 1 таблица умножения (1x)
- 1x до 6x напр. 6 таблиц/стр.
- от 1x до 12x напр. 12 таблиц/стр.
- 2-кратная таблица (2x)
- 3-кратная таблица (3x)
- 4-кратная таблица (4x)
- 5-кратная таблица (5x)
- 6-кратная таблица (6x)
- 7-кратная таблица ( 7x)
- Таблица умножения на 9 (9x)
Рабочий лист
- Удваивает до 10 напр. 2 x 1 до 2 x 10
- Удваивается до 50 напр. 4 х 9= 36, поэтому 8 x 9 = 72
- 2x таблица, например. от 1 x 2 до 10 x 2
- 3x стол напр. от 1 x 3 до 10 x 3
- 4x стол напр. от 1 x 4 до 10 x 4
- 5x стол напр. от 1 x 5 до 10 x 5
- 6x стол напр. от 1 x 6 до 10 x 6
- 7x стол напр. от 1 x 7 до 10 x 7
- 8x стол напр. от 1 x 8 до 10 x 8
- 9x стол напр. от 1 x 9 до 10 x 9
- 10x стол напр. От 1 x 10 до 10 x 10
- Таблицы 2x и 4x
- Таблицы 3x и 6x
- Умножение на 2–9: Смешанный (1 из 4)
- Умножение от 2 до 9: Смешанный (2 из 4)
от 1 x 9 до 10 x 9Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 .
Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | minus sign | subtraction | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций . BEDMAS — скобки, экспоненты, деление, умножение, сложение, вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
|
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
