Квадратные и биквадратные уравнения. Биквадратное уравнение, решение биквадратных уравнений
Перед тем, как решать биквадратные уравнения, необходимо разобраться, что собой являет данное выражение. Итак, это уравнение четвертой степени, которое можно записать в таком виде: «(ах 4) + (bx 2) + с = 0 ». Его общий вид можно записать в виде «ах ». Чтобы решить уравнение подобного рода, необходимо применить метод под названием «подстановка неизвестных». Согласно ему, выражение «х 2 » необходимо заменить другой переменной. После такой подстановки получается простое квадратное уравнение, решение которого в дальнейшем не составляет особого труда.
Необходимо:
— чистый лист бумаги;
— пишущая ручка;
— элементарные математические навыки.
Инструкция:
- Итак, необходимо изначально записать выражение на листке бумаги. Первый этап его решения состоит в простой процедуре замены выражения «х 2 » на простую переменную (например «к »).
 После того, как Вы это сделали, у Вас должно получиться новое уравнение: «(ак 2) – (bк) + с = 0 ».
После того, как Вы это сделали, у Вас должно получиться новое уравнение: «(ак 2) – (bк) + с = 0 ». - Далее, чтобы правильно решить биквадратное уравнение, нужно вначале найти корни для «
- В ходе расчета дискриминанта мы можем узнать, имеет ли решение наше биквадратное уравнение, ведь если в итоге данное значение получится со знаком минус, то оно просто-напросто может не иметь решения в дальнейшем. В случае же если дискриминант будет равняться нулю, тогда у нас будет одно единственное решение, определенное такой формулой: «к = — (b / 2 * а) ». Ну и в случае, если наш дискриминант окажется больше нуля, тогда у нас получится два решения.
 Для нахождения двух решений необходимо будет взять квадратный корень от « D » (то есть с дискриминанта). Полученное значение нужно будет записать в виде переменной «QD ».
Для нахождения двух решений необходимо будет взять квадратный корень от « D » (то есть с дискриминанта). Полученное значение нужно будет записать в виде переменной «QD ». - Следующий шаг – непосредственное решение квадратного уравнения , которое у Вас получилось. Для этого Вам необходимо будет подставить в формулу уже известные значения. Для одного из решений: «к1 = (-b + QD) / 2 * а », а для другого: «к2 = (-b — QD) / 2 * а ».
- И, наконец, завершающий этап – нахождение корней биквадратного уравнения . Для этого необходимо будет взять квадратный корень из полученных до этого решений обычного квадратного уравнения. Если же дискриминант был равен нулю, и у нас было только одно решение, тогда в этом случае корней получится два (с отрицательным и с положительным значением квадратного корня). Соответственно, если дискриминант был больше нуля, то наше биквадратное уравнение будет иметь целых четыре корня.
Впервые квадратные уравнения сумели решить математики древнего Египта.
Общее правило решения квадратных уравнений, преобразованных в вид х 2 + bх = с , было описано немецким математиком М. Штифелем. Он и сформулировал в 1544 году общее правило решения квадратных уравнений, приведенных к единому каноническому виду
х 2 + bх + с = 0 при всевозможных вариациях знаков и коэффициентов b и с.
Франсуа Виет вывел формулы квадратного уравнения в общем виде, однако он работал только с положительными числами.
Тарталья, Кардано, Бомбелли – итальянские ученые, которые среди первых в XVI веке учитывают кроме положительных еще и отрицательные корни.
Выводом формулы решения квадратных уравнений общего вида занимался Виет. Одно свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал).
После трудов нидерландского математика Альберта Жирара, а также Декарта и Ньютона, методы решения квадратных уравнений приняли современный вид.
Квадратные уравнения
1. Вспомним уже знакомые способы решения и исследования квадратных уравнений:
- выделение полного квадрата;
- по формуле корней для квадратного уравнения;
- по теореме Виета;
- на основании свойств квадратичной функции.
В процессе решения уравнений необходимо следить за множеством допустимых значений неизвестного, т.к. оно может изменяться. В случае его расширения следует проверять найденное решение, не является ли оно посторонним
для данного уравнения. В случае, если произошло сужение, необходимо убедиться, не являются ли потерянные значения неизвестных решениями данного уравнения. Процесс нахождения выпавших решений не всегда легко выполним, поэтому желательно избегать сужение множества допустимых значений неизвестных уравнения.
В случае, если произошло сужение, необходимо убедиться, не являются ли потерянные значения неизвестных решениями данного уравнения. Процесс нахождения выпавших решений не всегда легко выполним, поэтому желательно избегать сужение множества допустимых значений неизвестных уравнения.
2. Типичные ошибки при решении уравнений.
По правилам можно преобразовывать исходное уравнение в равносильное ему, при этом, вы знаете, что: обе части уравнения можно делить или умножать на одно и то же, отличное от нуля, число.
1) Если уравнение имеет вид f(х) · g(х) = p(х) · g(х), то деление обеих частей на одинаковый множитель g(x), как правило, недопустимо. Данное действие может привести к потере корней: могут быть потеряны корни уравнения g(х) = 0, если ни существуют.
Пример 1.
Решить уравнение 2(х – 3) = (х – 3)(х + 5).
Решение.
Здесь нельзя сокращать на множитель (х – 3).
2(х – 3) – (х – 3)(х + 5) = 0, вынесем общую скобку:
(х – 3)(-х – 3) = 0, теперь
х – 3 = 0 или -х – 3 = 0;
х = 3 или х = -3.
Ответ: -3; 3.
2) Уравнение вида f(х) / g(х) = 0 можно заменить системой:
{f(x) = 0,
{g(x) ≠ 0.
Она равносильна исходному уравнению.
Или можно решить уравнение f(x) = 0, а уже затем исключить найденных корней те, которые обращают в нуль знаменатель g(x).
Встречаются дробно-рациональные уравнения, которые сводятся к квадратным уравнениям.
Пример 2.
Решить уравнение: (х + 3) / (х – 3) + (х – 3) / (х + 3) = 10/3 + 36/(х – 3)(х + 3).
Решение.
Умножив обе части уравнения на общий знаменатель и заменив исходное уравнение целым, получим равносильную систему:
{3(х + 3) 2 + 3(х – 3) 2 = 10(х – 3)(х + 3) + 3 · 36;
{(х – 3)(х +3) ≠ 0.
В результате получим два корня: х = 3 или х = -3, но х ≠ 3 и х ≠ -3.
Ответ: уравнение корней не имеет.
Пример 3.
Решить уравнение: (х + 5)(х 2 + 4х — 5)/(х + 5)(х + 2) = 0.
Решение.
Часто ограничиваются таким решением:
(х 2 + 4х – 5) / (х + 2) = 0.
{х = -5, х = 1,
{х ≠ -2.
Ответ: -5; 1.
Правильный ответ: 1.
Пример 4.
При выполнении распространенных заданий на исследование квадратного уравнения следующего вида: «Не вычисляя действительных корней х 1 и х 2 уравнения 2х 2 + 3х + 2 = 0, найти значение х 1 2 + х 2 2 » банальная невнимательность приводит к грубой ошибке.
Действительно, по теореме Виета,
х 1 2 + х 2 2 = (х 1 + х 2) 2 – х 1 х 2 = (-3/2) 2 – 2 · 1 = 1/4.
Однако, теоремой можно было воспользоваться при существовании действительных корней. В данном примере D
Ответ: значение х 1 2 + х 2 2 не существует.
Пример 5.
Вычислить отрицательный коэффициент b и корни уравнения х 2 + bх – 1 = 0, если с увеличением каждого из этих корней на единицу они становятся корнями уравнения х 2 – b 2 х – b = 0.
Решение.
Пусть х 1 и х 2 – корни уравнения х 2 + bх – 1 = 0. Тогда по т. Виета
х 1 + х 2 = -b и х 1 х 2 = -1 (*). С другой стороны, по условию
(х 1 + 1) + (х 2 + 1) = b 2 и (х 1 + 1)(х 2 + 1) = -b.
Перепишем:
х 1 + х 2 = b 2 – 2 и (х 1 + 1)(х 2 + 1) = -b.
Теперь, учитывая условия (*), получим b 2 – 2 = -b, следовательно,
b 1 = -2, b 2 = 1. По условию подходит b 1 = -2.
Значит, исходное уравнение имеет вид х 2 – 2х – 1 = 0, корнями являются числа х 1,2 = 1 ± √2.
Ответ: b 1 = -2, х 1,2 = 1 ± √2.
Уравнения, приводимые к квадратным. Биквадратные уравнения
Уравнения вида ах 4 + bх 2 + c = 0, где а ≠ 0 , называются биквадратными уравнениями с одной переменной.
Для решения биквадратного уравнения нужно сделать подстановку х 2 = t, найти корни t 1 и t 2 квадратного уравнения аt 2 + bt + c = 0 и решить уравнения х 2 = t 1 и х 2 = t 2 . Они имеют решения лишь в случае, когда t 1,2 ≥ 0.
Пример 1.
Решить уравнение х 4 + 5х 2 – 36 = 0.
Решение.
Подстановка: х 2 = t.
t 2 + 5t – 36 = 0. По т. Виета t 1 = -9 и t 2 = 4.
х 2 = -9 или х 2 = 4.
Ответ: В первом уравнении корней нет, из второго: х = ±2.
Пример 2.
Решить уравнение (2х – 1) 4 – 25(2х – 1) 2 + 144 = 0.
Решение.
Подстановка: (2х – 1) 2 = t.
t 2 – 25t + 144 = 0. По т. Виета t 1 = 9 и t 2 = 16.
(2х – 1) 2 = 9 или (2х – 1) 2 = 16.
2х – 1 = ±3 или 2х – 1 = ±4.
Из первого уравнения два корня: х = 2 и х = -1, из второго тоже: х = 2,5 и х = -1,5.
Ответ: -1,5; -1; 2; 2,5.
Таким образом, процесс решения любых уравнений состоит в последовательной замене данного уравнения другим, равносильным ему и более простым уравнением.
Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog. сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Инструкция
Способ подстановкиВыразите одну переменную и подставте ее в другое уравнение. Выражать можно любую переменную по вашему усмотрению. Например, выразите «у из второго уравнения:
х-у=2 => у=х-2Затем подставьте все в первое уравнение:
2х+(х-2)=10Перенесите все без «х в правую часть и подсчитайте:
2х+х=10+2
3х=12 Далее, чтобы «х, разделите обе части уравнения на 3:
х=4.Итак, вы нашли «х. Найдите «у. Для этого подставьте «х в то уравнение, из которого вы выразили «у:
у=х-2=4-2=2
у=2.
Сделайте проверку. Для этого подставьте получившиеся значения в уравнения:
2*4+2=10
4-2=2
Неизвестные найдены верно!
Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.
Так как в «у со знаком «+ , а во втором «- , то вы можете выполнить операцию сложения, т.е. левую часть складываем с левой, а правую с правой:
2х+у+(х-у)=10+2Преобразуйте:
2х+у+х-у=10+2
3х=12
х=4Подставьте «х в любое уравнение и найдите «у:
2*4+у=10
8+у=10
у=10-8
у=2По 1-ому способу можете , что найдены верно.
Если нет четко выраженных переменных, то необходимо немного преобразовать уравнения.
В первом уравнении имеем «2х, а во втором просто «х. Для того, чтобы при сложении или «х сократился, второе уравнение умножьте на 2:
х-у=2
2х-2у=4Затем вычтите из первого уравнения второе:
2х+у-(2х-2у)=10-4Заметим, если перед скобкой стоит минус, то после раскрытия поменяйте на противоположные:
2х+у-2х+2у=6
3у=6
у=2«х найдите, выразив из любого уравнения, т.е.
х=4
Видео по теме
Уравнение , в общем виде записанное ах+bу+с=0, называется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит бесконечное множество решений, поэтому в задачах оно всегда чем-либо дополняется – еще одним уравнением или ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя переменными следует разными способами.
Вам понадобится
- — линейное уравнение с двумя переменными;
- — второе уравнение или дополнительные условия.

Инструкция
Если дана система из двух линейных уравнений, решайте ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными поменьше и выразите одну из переменных, например, х. Затем подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные – в правую. Найдите у и подставьте в любое из первоначальных уравнений, найдите х.
Решить систему из двух уравнений можно и другим способом. Умножьте одно из уравнений на число, чтобы коэффициент перед одной из переменных, например, перед х, был одинаков в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть аналогично и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте найденное значение у в любое из первоначальных равенств. Найдите х.
Третий способ решения системы двух линейных уравнений – графический. Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.
Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.
Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.
Источники:
- как решить уравнение с одной переменной
Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.
В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.
Вам понадобится
- — система из трех уравнений с тремя неизвестными.
Инструкция
Если два из трех системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными . Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.
Некоторые системы уравнений можно вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из на или переменную так, чтобы сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.
Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.
Найдите матрицу А в степени (-1) предварительно отыскав , обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.
Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.
Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.
Источники:
- решений уравнений с тремя неизвестными
Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше. Решать системы можно несколькими методами.
Инструкция
Самый распространенный метод решения системы уравнений — это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.
Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.
Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2. 2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.
2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.
Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений . Если решение было одно, то будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.
Видео по теме
Одним из классических способов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований переводится в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.
Инструкция
Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z — после Y и так далее. В правой части каждого уравнения неизвестных быть не должно. {2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]
{2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]
Мы получили снова четыре корня:
Вот так решаются все биквадратные уравнения. Конечно, это не самый быстрый способ, зато он самый надежный. Попробуйте самостоятельно прорешать такие же примеры, как и в этом видео. В ответе значения иксов нужно записывать через точку с запятой — вот так, как я записывал. На этом урок закончен. Удачи!
Всем еще со школы известно такое понятие, как уравнения. Уравнение — это равенство, содержащее одну или несколько переменных. Зная то, что одна из частей данного равенства равна другой, можно вычленять отдельные части уравнения, перенося те или иные его составляющие за знак равенства по четко оговоренным правилам. Можно упростить уравнение до необходимого логического завершения в виде х=n, где n — это любое число.
С начальной школы все дети проходят курс изучения различной сложности. Позже в программе появляются более сложные линейные уравнения — квадратные, затем идут кубические уравнения. Каждый последующий вид уравнений имеет новые методики решения, становится труднее в изучении и повторении.
Каждый последующий вид уравнений имеет новые методики решения, становится труднее в изучении и повторении.
Однако после этого возникает вопрос о решении такого вида уравнений, как биквадратные уравнения. Данный вид, несмотря на кажущуюся сложность, решается достаточно просто: главное — уметь привести такие уравнения в должный вид. Их решение изучается за один-два урока вместе с практическими заданиями, если у учащихся имеются базовые знания о решении квадратных уравнений.
Что необходимо знать человеку, столкнувшемуся с этим типом уравнений? Для начала то, что они включают в себя только четные степени переменной «икс»: четвертая и, соответственно, вторая. Чтобы биквадратное уравнение было решаемо, необходимо привести его к виду Как это сделать? Достаточно просто! Нужно всего лишь заменить «икс» в квадрате на «игрек». Тогда устрашающий для многих школьников «икс» в четвертой степени превратится в «игрек» в квадрате, а уравнение примет вид обычного квадратного.
Далее оно решается как обычное квадратное уравнение: раскладывается на множители, после чего находится значение таинственного «игрека». Чтобы решить биквадратное уравнение до конца, нужно найти из числа «игрек» — это и будет искомая величина «икс», после нахождения значений которого можно будет поздравить себя с успешным завершением расчетов.
Чтобы решить биквадратное уравнение до конца, нужно найти из числа «игрек» — это и будет искомая величина «икс», после нахождения значений которого можно будет поздравить себя с успешным завершением расчетов.
Что же следует помнить, решая уравнения данного вида? Первое и самое главное: игрек не может быть отрицательным числом! Само условие, что игрек — это квадрат числа икс, исключает подобный вариант решения. Поэтому если при первичном решении биквадратного уравнения одно из значений «игрек» получается у вас положительным, а второе — отрицательным, необходимо взять только его положительный вариант, иначе биквадратное уравнение будет решено неверно. Лучше сразу ввести правило, что переменная «игрек» больше либо равна нулю.
Второй немаловажный нюанс: число «икс», являясь квадратным корнем числа «игрек», может быть как положительным, так и отрицательным. Допустим, если «игрек» равен четырем, то биквадратное уравнение будет иметь два решения: два и минус два. Это происходит по той причине, что отрицательное число, возведенное в четную степень, равно числу того же модуля, но отличного знака, возведенному в ту же степень. Поэтому всегда стоит помнить об этом немаловажном моменте, иначе можно попросту потерять один или несколько ответов уравнения. Лучше всего сразу писать, что «икс» равен плюс-минус квадратному корню от «игрек».
Поэтому всегда стоит помнить об этом немаловажном моменте, иначе можно попросту потерять один или несколько ответов уравнения. Лучше всего сразу писать, что «икс» равен плюс-минус квадратному корню от «игрек».
В общем и целом, решение биквадратных уравнений — это достаточно просто и не требует больших временных затрат. На изучение этой темы в школьной программе хватает двух академических часов — не считая, конечно, повторений и контрольных работ. Биквадратные уравнения стандартного вида решаются очень легко, если соблюдать перечисленные выше правила. Их решение не составит для вас никакого труда, потому что оно подробно расписано в учебниках математики. Удачной вам учебы и успехов в решении любых, не только математических, задач!
Презентация для дистанционного урока в программе ZOOM в 8 -го класса по теме «Биквадратные уравнения»
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи▪Презентации
Материал опубликовала
#8 класс #Алгебра #Учебно-методические материалы #Презентация #Все учителя #Школьное образование
Алгебра 8 класс «Рациональные уравнения. Биквадратные уравнения»
Рациональные уравнения в свою очередь бывают разные. Сегодня мы познакомимся с одним из рациональных уравнений
Решить уравнение: 1) х²=9 2) х²=3 3) х²= -25 4) х²= 5) х²- 49=0 Устный счет
Цели урока:
Дать определение биквадратного уравнения, научиться решать биквадратные уравнения, исследовать корни биквадратного уравнения.
Определение. Уравнение вида ах⁴+bх²+с=0, где а, b и с –данные числа и а≠0, а х — неизвестное, называют биквадратным уравнением.
х⁴-4х²+3=0 Пример1: Чтобы решить биквадратное уравнение, вводят новое неизвестное при помощи равенства х2 = y
Пример 2: 2х⁴-3х²+5=0 Ответ:
Пример 3: 9х⁴-6х²+1=0
Пример 4: х⁴+10х²+25=0
Решить уравнение Имеет один корень Ответ: Решить уравнение Решение: Ответ: -1; 0; 1. Пример 5: Пример 6:
Пример 7:
Алгоритм решения биквадратного уравнения: Введем в уравнение новую переменную путем обозначения какого- то выражения из этого уравнения; Вместо этого выражения подставляем новую переменную и получим квадратное уравнение относительно новой переменной;
3) Решаем полученное квадратное уравнение;
3) Решаем полученное квадратное уравнение;
4) Способом подстановки находим значение исходной переменной;
5) С помощью проверки определяем корни данного уравнения.
Работа в парах. № Уравнение Знак дискриминанта Корни нового уравнения Знаки корней нового уравнения Корни исходящего уравнения Кол-во решений биквадратного уравнения 1 х4-10х2+9=0 2 2х4 –х2-1=0 3 х4+5х2+4=0 4 2х4+5х2+4=0 5 х4-8х2+16=0 6 х4+8х2+16=0
Из рассмотренных примеров видно, что биквадратное уравнение может иметь четыре, три, два, один действи-тельный корень, но может и не иметь корней.
Работа с учебником. Выполняем у доски и на месте №297-297(а).
Задание на дом. п. 5.2.прочитать, №294 (письменно ответить на вопросы), решить уравнения по ссылке https://edu.skysmart.ru/student/semihipale, задание рассчитано на 50 минут выполнить до 12.01
Итог урока. Какие же уравнения называются биквадратными? Алгоритм решения биквадратного уравнения? От чего зависит число решений биквадратного уравнения?
12. Связь между корнями и коэффициентами любого полиномиального уравнения
содержание > квадратное уравнение > 12. Связь между корнями и коэффициентами любого полиномиального уравнения.
|
Получение нового представления золотого сечения путем решения биквадратного уравнения
Журнал прикладной математики и физики Том 02 № 13 (2014 г. ),
Код статьи:52434,3 стр.
),
Код статьи:52434,3 стр.
10.4236/jamp.2014.213134
Получение нового представления золотого сечения путем решения биквадратного уравнения
Леонардо Мондаини 1,2
1 Отделение онкологии, Университет Альберты, Эдмонтон, Канада
2 Grupo de Física Teórica e Experimental, Департамент Ciências Naturais, Федеральный университет штата Рио-де-Жанейро, Рио-де-Жанейро Жанейро, Бразилия
Электронная почта: [email protected],
mondaini@unirio. br
br
Авторское право © 2014 г. автора и Scientific Research Publishing Inc.
Эта работа находится под лицензией Creative Commons Attribution International License. (CC BY).
http://creativecommons.org/licenses/by/4.0/
Поступила в редакцию 31 октября 2014 г.; пересмотрено 29 ноября 2014 г.; принято 9 декабря 2014 г.
РЕЗЮМЕ
В настоящей работе мы покажем, как различные способы решения биквадратных уравнений могут
приводят нас к различным представлениям ее решений. Частное уравнение, которое
имеет золотое сечение, и его обратное значение в качестве решения показано в качестве примера.
Ключевые слова:
Золотое сечение, алгебраические уравнения, рекреационная математика, история математики
1. Введение
Изучением алгебраических уравнений занимались самые яркие математические умы во всем мире.
много веков. Среди основных результатов исследований в этой
площадь, получение формулы решения общих квадратных уравнений
что вместе с формулой решения общих кубических уравнений достигло
Никколо Фонтана (Тарталья) 1 , привело к созданию комплексных чисел,
поскольку применение этих формул привело к «загадочной» вещи: квадрату
корень отрицательного числа. Решение общих уравнений четвертой степени Людовико
Феррари (ученик Кардано) завершает эту картину, как только она была установлена.
что решение в радикалах для общих уравнений степени, равной или большей
больше 5 не может быть достигнуто (результат, впервые доказанный вундеркиндами Нильсом
Абель и Эварист Галуа). В настоящей работе, которую можно отнести к
области развлекательной математики и призван стимулировать интерес читателей
с доуниверситетским математическим образованием, чтобы вдохновить их на дальнейшее
изучения предмета, мы сосредоточимся на интересном аспекте, связанном с конкретным
уравнение четвертой степени, а именно биквадратное.
Решение общих уравнений четвертой степени Людовико
Феррари (ученик Кардано) завершает эту картину, как только она была установлена.
что решение в радикалах для общих уравнений степени, равной или большей
больше 5 не может быть достигнуто (результат, впервые доказанный вундеркиндами Нильсом
Абель и Эварист Галуа). В настоящей работе, которую можно отнести к
области развлекательной математики и призван стимулировать интерес читателей
с доуниверситетским математическим образованием, чтобы вдохновить их на дальнейшее
изучения предмета, мы сосредоточимся на интересном аспекте, связанном с конкретным
уравнение четвертой степени, а именно биквадратное.
Остальная часть этой работы организована следующим образом. Частное уравнение, имеющее
золотое сечение и его обратное соотношение как решения представлены в разделе 2. В разделах
3 и 4, мы решаем это уравнение, используя два разных алгоритма. Наконец, в разделе
5, мы представляем наши заключительные замечания.
Частное уравнение, имеющее
золотое сечение и его обратное соотношение как решения представлены в разделе 2. В разделах
3 и 4, мы решаем это уравнение, используя два разных алгоритма. Наконец, в разделе
5, мы представляем наши заключительные замечания.
2. Интересное уравнение
Начнем с рассмотрения следующего характеристического уравнения [2] [3]
(1)
куда это симметричная действительная матрица, определяемая
(2)
и
является соответствующим
единичная матрица. Обратите внимание, что мы можем переписать уравнение (1) следующим образом:
Обратите внимание, что мы можем переписать уравнение (1) следующим образом:
(3)
или
(4)
Это простое биквадратное уравнение обладает интересной особенностью. Форма его решения выражаются, зависит, по-видимому, от алгоритма ее решения. Даже больше интересен тот факт, что один из этих алгоритмов дает числа и (а также их соответствующие симметричные решения) как решения, которые являются наиболее известным представлением этого вездесущего математического явления, а именно, золотое сечение [4] и его обратное значение. Это известное число появляется исторически как решение квадратного уравнения
(5)
которая связана с геометрической задачей деления заданного отрезка
в то, что называется золотым сечением, которое знаменитый астроном Иоганнес
Кеплер назвал «одной из двух жемчужин геометрии» (вторая — пифагорейская
теорема). В переводе на математический язык золотое сечение означает, что отрезок
разрезается в точке
так, чтобы весь сегмент был в том же отношении к большей части
в качестве
находится в другой части,.
это
В переводе на математический язык золотое сечение означает, что отрезок
разрезается в точке
так, чтобы весь сегмент был в том же отношении к большей части
в качестве
находится в другой части,.
это
(6)
Это, в свою очередь, приводит к квадратному уравнению
уже упоминалось, положительный корень которого есть.
Обратите внимание, что когда,
Значение
является обратной величиной золотого сечения, т. е. 0,6180339.887… В следующих разделах мы применим два разных алгоритма по порядку.
решить уравнение (4).
е. 0,6180339.887… В следующих разделах мы применим два разных алгоритма по порядку.
решить уравнение (4).
3. Первый алгоритм
Во-первых, мы решим уравнение (4), используя алгоритм, очень похожий на тот, первоначально использовался Людовико Феррари в его решении уравнений четвертой степени. (полиномиальные уравнения четвертой степени) 2 [5] . Чтобы сделать это, начнем с того, что заметим, что уравнение (4) также можно переписать следующим образом:
(7)
или
(8)
Левая часть этого уравнения, полный квадрат, может быть тривиально упрощена как
. (9)
откуда следует, что
(10)
или
(11)
При решении вышеприведенных уравнений с помощью известной квадратичной формулы находим что решения уравнения с даны
(12)
тогда как для уравнения с (которое идентично уравнению (5) с) у нас есть следующие решения
(13)
Таким образом, полный набор решений исходного биквадратного уравнения задается к
(14)
где мы еще раз напоминаем читателю, что
является обычным представлением для золотого сечения, и
является его обратным.
4. Второй алгоритм
Второй алгоритм следует обычному методу решения биквадратных уравнений. В таком методе мы начинаем с рассмотрения следующей замены переменных
, (15)
что позволяет привести уравнение (4) к виду
(16)
Непосредственное применение квадратичной формулы дает решения
(17)
С, тогда мы имеем следующий набор решений для исходного уравнения 3
(18)
5. Заключительные замечания
Мы видели, что явно различные решения получаются при решении уравнения (4) по формуле
два разных алгоритма.
Однако мы можем легко убедиться, что они идентичны. Просто вычислите квадрат и проверьте это! Затем мы получили новое представление для золотого сечения, а именно
(19)
Благодарности
Эта работа была частично поддержана CNPq.
Ссылки
- Boyer, C.B. и Merzbach, U.C. (1991) История математики. 2-е издание, Джон Wiley & Sons, Inc., Нью-Йорк.
- Вайсштейн, Э. У. Характеристическое уравнение. MathWorld―A Веб-ресурс Wolfram. http://mathworld.wolfram.com/CharacteristicEquation.html
- Липшуц, С. и
Липсон, М.
 (2013) Линейная алгебра — схемы Шаума. 5-е издание, Макгроу-Хилл
Компании, Inc., Нью-Йорк.
(2013) Линейная алгебра — схемы Шаума. 5-е издание, Макгроу-Хилл
Компании, Inc., Нью-Йорк. - Ливио, М. (2002) Золотое сечение: История Фи, Самое удивительное число в мире. Бродвейские книги, Нью-Йорк.
- Кардано, Г. (1993) Ars Magna или Правила алгебры. Dover Publications, Минеола.
ПРИМЕЧАНИЯ
1 Обычно формула решения общего кубического уравнения имеет вид приписывается Джироламо Кардано и, таким образом, получает его имя. Более подробный описание о споре за приоритет этого решения можно найти в [1] .
2 Целью алгоритма Феррари для решения общей квартики является
имеют полные квадраты в обеих частях уравнения.

 После того, как Вы это сделали, у Вас должно получиться новое уравнение: «(ак 2) – (bк) + с = 0 ».
После того, как Вы это сделали, у Вас должно получиться новое уравнение: «(ак 2) – (bк) + с = 0 ».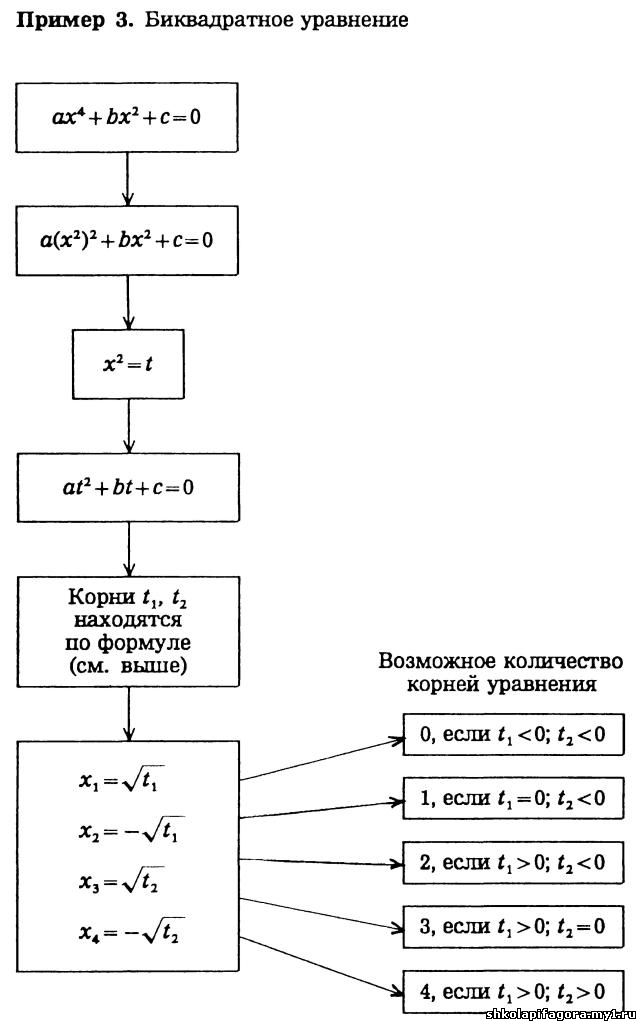 Для нахождения двух решений необходимо будет взять квадратный корень от « D » (то есть с дискриминанта). Полученное значение нужно будет записать в виде переменной «QD ».
Для нахождения двух решений необходимо будет взять квадратный корень от « D » (то есть с дискриминанта). Полученное значение нужно будет записать в виде переменной «QD ».
 РФ
РФ x нет +a 1 x n-1 +a 2 x n-2 +…+a n-1 x + a n =0, тогда
x нет +a 1 x n-1 +a 2 x n-2 +…+a n-1 x + a n =0, тогда .. = ∑α i α j = (-1 ) 2 a 2/ a 0
.. = ∑α i α j = (-1 ) 2 a 2/ a 0  x n
x n  (2013) Линейная алгебра — схемы Шаума. 5-е издание, Макгроу-Хилл
Компании, Inc., Нью-Йорк.
(2013) Линейная алгебра — схемы Шаума. 5-е издание, Макгроу-Хилл
Компании, Inc., Нью-Йорк.