Определение арифметического корня натуральной степени. Арифметический квадратный корень и его свойства
Площадь квадратного участка земли равна 81 дм². Найти его сторону. Предположим, что длина стороны квадрата равна х дециметрам. Тогда площадь участка равна х ² квадратным дециметрам. Так как по условию эта площадь равна 81 дм², то х ² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Заметим, что один из квадратных корней х = 9 является положительным числом. Его называют арифметическим квадратным корнем из числа 81 и обозначают √81, таким образом √81 = 9.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен
Например, числа 6 и — 6 являются квадратными корнями из числа 36. При этом число 6 является арифметическим квадратным корнем из 36, так как 6 — неотрицательное число и 6² = 36. Число — 6 не является арифметическим корнем.
Арифметический квадратный корень из числа а обозначается так: √а.
Знак называется знаком арифметического квадратного корня; а — называется подкоренным выражением. Выражение √а читается так: арифметический квадратный корень из числа а. Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а «.
Действие нахождения квадратного корня из числа называют извлечением квадратного корня. Это действие является обратным к возведению в квадрат.
Возводить в квадрат можно любые числа, но извлекать квадратные корни можно не из любого числа.
Выражение √а имеет смысл только при а ≥ 0. Определение квадратного корня можно кратко записать так: √а ≥ 0, (√а )² = а . Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
Квадратный корень из дроби
Вычислим . Заметим, что √25 = 5, √36 = 6, и проверим выполняется ли равенство .
Так как и , то равенство верно. Итак, .
Теорема: Если а ≥ 0 и b > 0, то т. е. корень из дроби равен корню из числителя, деленному на корень из знаменателя.
Так как √а ≥0 и √b > 0, то .
По свойству возведения дроби в степень и определению квадратного корня теорема доказана. Рассмотрим несколько примеров.
Вычислить , по доказанной теореме .
Второй пример: Доказать, что , если а ≤ 0, b .
Еще примерчик: Вычислить .
.
Преобразование квадратных корней
Вынесение множителя из-под знака корня. Пусть дано выражение . Если а ≥ 0 и b ≥ 0, то по теореме о корне из произведения можно записать:
Такое преобразование называется вынесение множителя из под знака корня. Рассмотрим пример;
Вычислить при х = 2. Непосредственная подстановка х = 2 в подкоренное выражение приводит к сложным вычислениям. Эти вычисления можно упростить, если вначале вынести из-под знака корня множители: . Подставив теперь х = 2, получим:.
Итак, при вынесении множителя из-под знака корня представляют подкоренное выражение в виде произведения, в котором один или несколько множителей являются квадратами неотрицательных чисел. Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а ≥ 0 и b ≥ 0. если же а
Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а ≥ 0 и b ≥ 0. если же а
Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)
Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)
Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.
Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:
Корни бывают чётной степени (наш любимый $\sqrt{a}$, а также всякие $\sqrt{a}$ и даже $\sqrt{a}$) и нечётной степени (всякие $\sqrt{a}$, $\sqrt{a}$ и т.
{2}}=1$.
Кубические корни тоже часто встречаются — не надо их бояться:
\[\begin{align} & \sqrt{27}=3; \\ & \sqrt{-64}=-4; \\ & \sqrt{343}=7. \\ \end{align}\]
Ну, и парочка «экзотических примеров»:
\[\begin{align} & \sqrt{81}=3; \\ & \sqrt{-32}=-2. \\ \end{align}\]
Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!
А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.
Зачем вообще нужны корни?
Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?
Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа.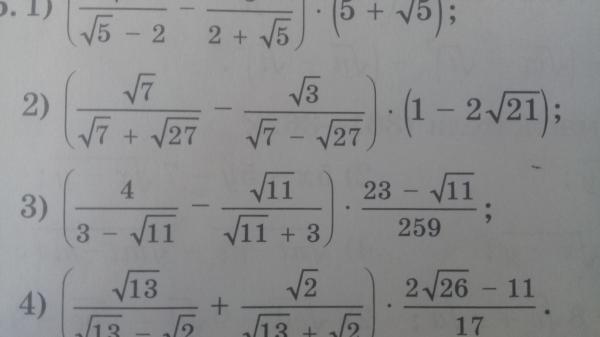 Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:
Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:
\[\begin{align} & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end{align}\]
Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:
Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:
Это же очень удобно! Все вычисления сокращаются в разы, и можно не тратить кучу листов пергамента блокнотиков на запись какого-нибудь 5 183 . Такую запись назвали степенью числа, у неё нашли кучу свойств, но счастье оказалось недолгим.
После грандиозной пьянки, которую организовали как раз по поводу «открытия» степеней, какой-то особо упоротый математик вдруг спросил: «А что, если нам известна степень числа, но неизвестно само число?» Вот, действительно, если нам известно, что некое число $b$, допустим, в 5-й степени даёт 243, то как нам догадаться, чему равно само число $b$?
Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. {n}}=a\]
{n}}=a\]
Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.
Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:
\[\sqrt{2}=1,414213562…\]
Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:
\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]
Или вот ещё пример:
\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]
Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).
Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.
Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.
Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.
\[\begin{align} & \sqrt{2+\sqrt{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt{\sqrt{-32}}=\sqrt{-2}\approx -1,2599… \\ \end{align}\]
Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. {2}}$:
{2}}$:
График квадратичной функции даёт два корня: положительный и отрицательный
Попробуем с помощью этого графика посчитать $\sqrt{4}$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:${{x}_{1}}=2$ и ${{x}_{2}}=-2$. Это вполне логично, поскольку
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y , т. {3}}$:
{3}}$:
Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Из этого графика можно сделать два вывода:
- Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
- Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
- Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
- А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок. {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.
Впрочем, все эти проблемы актуальны лишь для чётных показателей.
Вынесение минуса из-под знака корня
Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:
\[\sqrt{-a}=-\sqrt{a}\]
Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:
\[\begin{align} & \sqrt{-8}=-\sqrt{8}=-2; \\ & \sqrt{-27}\cdot \sqrt{-32}=-\sqrt{27}\cdot \left(-\sqrt{32} \right)= \\ & =\sqrt{27}\cdot \sqrt{32}= \\ & =3\cdot 2=6. \end{align}\]
\end{align}\]
Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.
И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них. {n}}=a$.
{n}}=a$.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
Область поиска арифметического корня — неотрицательные числа
Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. {2}}}=\sqrt{4} \gt 0. \\ \end{align}$
{2}}}=\sqrt{4} \gt 0. \\ \end{align}$
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Алгебраический корень: для тех, кто хочет знать больше
Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному. {n}}=a \right. \right\}\]
{n}}=a \right. \right\}\]
Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:
- Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
- Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
- Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.
Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.
Пример. Вычислите выражения:
\[\overline{\sqrt{4}};\quad \overline{\sqrt{-27}};\quad \overline{\sqrt{-16}}.
\]
Решение. С первым выражением всё просто:
\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
\[\overline{\sqrt{-27}}=\left\{ -3 \right\}\]
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
\[\overline{\sqrt{-16}}=\varnothing \]
Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.
Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt{-16}$, и многие другие странные вещи.
Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
Корнем степени n из действительного числа a , где n — натуральное число, называется такое действительное число x , n -ая степень которого равна a .
Корень степени n из числа a обозначается символом . Согласно этому определению .
Нахождение корня n -ой степени из числа a называется извлечением корня. Число а называется подкоренным числом (выражением), n — показателем корня. При нечетном n существует корень n -ой степени для любого действительного числа a . При четном n существует корень n -ой степени только для неотрицательного числаa . Чтобы устранить двузначность корня n -ой степени из числа a , вводится понятие арифметического корня n -ой степени из числа a .
Понятие арифметического корня степени N
Если и n — натуральное число, большее 1 , то существует, и только одно, неотрицательное число х , такое, что выполняется равенство .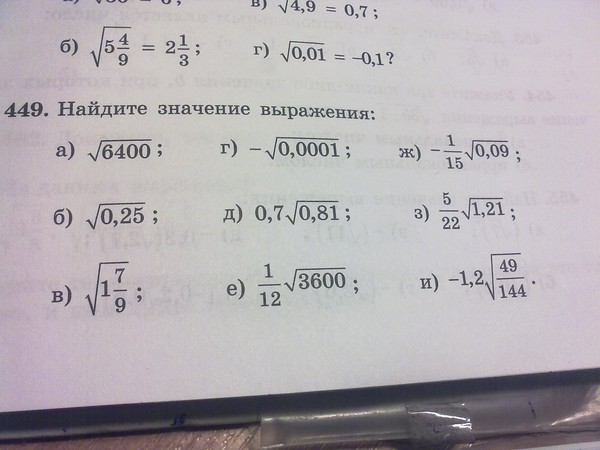 Это число х называется арифметическим корнем n -й степени из неотрицательного числа а и обозначается . Число а называется подкоренным числом, n — показателем корня.
Это число х называется арифметическим корнем n -й степени из неотрицательного числа а и обозначается . Число а называется подкоренным числом, n — показателем корня.
Итак, согласно определению запись , где , означает, во-первых, что и, во-вторых, что , т.е. .
Понятие степени с рациональным показателем
Степень с натуральным показателем: пусть а — действительное число, а n — натуральное число, большее единицы, n -й степенью числа а называют произведение n множителей, каждый из которых равен а , т.е. . Число а — основание степени, n — показатель степени. Степень с нулевым показателем: полагают по определению, если , то . Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если и n — натуральное число, то . Степень с дробным показателем: полагают по определению, если и n — натуральное число, m — целое число, то .
Операции с корнями.
Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и одновременно возвести в n-ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в n раз и одновременно извлечь корень n-ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной величине отрицательного показателя:
Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной величине отрицательного показателя:
Теперь формула a m: a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a -3 .
Если мы хотим, чтобы формула a m: a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n–ой степени из m-ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
Случай 1.
Где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т. n = a*b.
n = a*b.
Что и требовалось доказать. Значит свойство верно. Эти свойства очень часто придется использовать при упрощении выражений содержащих арифметические корни.
Раздел 2 теоретические основы стоматологии детского возраста и избранные вопросы смежных дисциплин
001. Пульпа формируется
а) из мезенхимы зубного мешочка
б) из мезенхимы зубного сосочка
в) из эпителиальной ткани, образующей внутренний слой эмалевого органа
г) из эпителиальной ткани, образующей наружный слой эмалевого органа
д) из передней половины эпителиальной пластинки
002. Дентин формируется
а) из мезенхимы зубного мешочка
б) из мезенхимы зубного сосочка
в) из эпителиальной ткани, образующей внутренний слой эмалевого органа
г) из эпителиальной ткани, образующей наружный слой эмалевого органа
д) из передней половины эпителиальной пластинки
003. Цемент корня зуба формируется
Цемент корня зуба формируется
а) из мезенхимы зубного мешочка
б) из мезенхимы зубного сосочка
в) из эпителиальной ткани, образующей верхний слой эмалевого органа
г) из передней половины эпителиальной пластинки
д) из эпителиального влагалища
004. Периодонт формируется
а) из мезенхимы зубного мешочка
б) из мезенхимы зубного сосочка
в) из эпителиальной ткани, образующей наружный слой эмалевого органа
г) из эпителиальной ткани, образующей внутренний слой эмалевого органа
д) из передней половины эпителиальной пластинки
005. Эмаль зуба формируется
а) из мезенхимы зубного мешочка
б) из мезенхимы зубного сосочка
в) из эпителиальных клеток, образующих внутренний слой эмалевого органа
г) из эпителиальной ткани, образующей наружный слой эмалевого органа
006. Насмитова оболочка формируется
Насмитова оболочка формируется
а) из мезенхимы зубного мешочка
б) из мезенхимы зубного сосочка
в) из эпителиальной ткани, образующей внутренний слой эмалевого органа
г) из эпителиальной ткани, образующей наружный слой эмалевого органа
007. Минерализация 51,61,71,81 зубов начинается
а) на 2-3 месяце утробной жизни
б) на 4-5 месяце утробной жизни
в) на 6-7 месяце утробной жизни
г) на 7-8 месяце утробной жизни
д) на 8-9 месяце утробной жизни
008. Минерализация 52,62,72,82 зубов начинается
а) на 3-4 месяце утробной жизни
б) на 4-4.5 месяце утробной жизни
в) на 5-6 месяце утробной жизни
г) на 6-7 месяце утробной жизни
д) на 8-9 месяце утробной жизни
009. Минерализация 53,63,73,83; 55,65,75,85 зубов начинается
Минерализация 53,63,73,83; 55,65,75,85 зубов начинается
а) на 3-м месяце утробной жизни
б) на 5-м месяце утобной жизни
в) на 6-м месяце утробной жизни
г) на 7-м месяце утробной жизни
д) на 8-м месяце утробной жизни
010. Минерализация 54,64,74,84 зубов начинается
а) на 3-м месяце утробной жизни
б) на 5-м месяце утробной жизни
в) на 6-м месяце утробной жизни
г) на 7-м месяце утробной жизни
д) на 8-м месяце утробной жизни
011. Зубы 51,61,71,81 прорезываются
а) на 4-5 месяце жизни ребенка
б) на 5-6 месяце жизни ребенка
в) на 6-8 месяце жизни ребенка
г) на 9-10 месяце жизни ребенка
д) на 11-12 месяце жизни ребенка
012. Зубы 52,62,72,82 прорезываются
Зубы 52,62,72,82 прорезываются
а) на 2-5 месяце жизни ребенка
б) на 6-12 месяце жизни ребенка
в) на 7-8 месяце жизни ребенка
г) на 12-17 месяце жизни ребенка
д) на 17-20 месяце жизни ребенка
013. Зубы 53,63,73,83 прорезываются
а) на 8-10 месяце жизни ребенка
б) на 10-12 месяце жизни ребенка
в) на 12-15 месяце жизни ребенка
г) на 16-20 месяце жизни ребенка
д) на 17-19 месяце жизни ребенка
014. Зубы 54,64,74,84 прорезываются
а) на 9-12 месяце жизни ребенка
б) на 12-16 месяце жизни ребенка
в) на 17-20 месяце жизни ребенка
г) на 10-15 месяце жизни ребенка
д) на 11-13 месяце жизни ребенка
015. Зубы 55,65,75,85 прорезываются
Зубы 55,65,75,85 прорезываются
а) на 9-10 месяце жизни ребенка
б) на 10-12 месяце жизни ребенка
в) на 12-18 месяце жизни ребенка
г) на 18-20 месяце жизни ребенка
д) на 20-30 месяце жизни ребенка
016. Формирование корней 51,61,71,81 зубов заканчивается
а) в возрасте ребенка 1.5 года
б) в возрасте ребенка 2-2.5 года
в) в возрасте ребенка 3 года
г) в возрасте ребенка 4 года
д) в возрасте ребенка 5 лет
017. Формирование корней 52,62,72,82 зубов заканчивается
а) в возрасте ребенка 2 года
б) в возрасте ребенка 3 года
в) в возрасте ребенка 4 года
г) в возрасте ребенка 5 лет
д) в возрасте ребенка 6 лет
018. Формирование корней 53,63,73,83 зубов заканчивается
Формирование корней 53,63,73,83 зубов заканчивается
а) в возрасте ребенка 2-3 года
б) в возрасте ребенка 3-3.5 года
в) в возрасте ребенка 3-4 лет
г) в возрасте ребенка 4-5 лет
д) в возрасте ребенка 5-5,5 лет
019. Формирование корней 54,64,74,84 зубов заканчивается
а) в возрасте ребенка 2-3 года
б) в возрасте ребенка 3-4 года
в) в возрасте ребенка 4-5 лет
г) в возрасте ребенка 5-6 лет
д) в возрасте ребенка 6-7 лет
020. Формирование корней 55,65,75,85 зубов заканчивается
а) в возрасте ребенка 3 года
б) в возрасте ребенка 4 года
в) в возрасте ребенка 5 лет
г) в возрасте ребенка 6 лет
д) в возрасте ребенка 7 лет
021. Cроки максимального рассасывания корней 51,61,71,81 зубов
Cроки максимального рассасывания корней 51,61,71,81 зубов
а) в возрасте ребенка 3-3.5 года
б) в возрасте ребенка 4-4.5 года
в) в возрасте ребенка 5-5.5 лет
г) в возрасте ребенка 5.5-6.5 лет
д) в возрасте ребенка 6.5-7 лет
022. Cроки максимального рассасывания корней 52,62,72,82 зубов
а) в возрасте ребенка 3-4 лет
б) в возрасте ребенка 4-5 лет
в) в возрасте ребенка 5-6 лет
г) в возрасте ребенка 5.5-7 лет
д) в возрасте ребенка 8 лет
023. Cроки минимального рассасывания корней 53,63,73,83 зубов
а) в возрасте ребенка 5-6 лет
б) в возрасте ребенка 6-7 лет
в) в возрасте ребенка 8.5-9 лет
г) в возрасте ребенка 10-11 лет
д) в возрасте ребенка 11-12 лет
024. Cроки максимального рассасывания корней 54,64,74,84 зубов
Cроки максимального рассасывания корней 54,64,74,84 зубов
а) в возрасте ребенка 7 лет
б) в возрасте ребенка 8 лет
в) в возрасте ребенка 9 лет
г) в возрасте ребенка 10 лет
д) в возрасте ребенка 11 лет
025. Cроки максимального рассасывания корней 55,65,75,85 зубов
а) в возрасте ребенка 6-7 лет
б) в возрасте ребенка 8-8.5 лет
в) в возрасте ребенка 9-9.5 лет
г) в возрасте ребенка 9-10 лет
д) в возрасте ребенка 10-11 лет
026. Какой тип резорбции корней молочных зубов является физиологическим?
а) I — равномерная резорбция всех корней
б) II — резорбция с преобладанием процесса в области одного корня
в) III — резобрция с преобладанием процесса в области бифуркации корней
г) резорбция корней в результате хронического воспаления тканей периодонта
д) I, II, III типы резорбции корней
027. Какой вид резорбции корней молочных зубов при хроническом воспалении периодонтита?
Какой вид резорбции корней молочных зубов при хроническом воспалении периодонтита?
а) равномерная резорбция всех корней
б) резорбция с преобладанием в области одного корня
в) резорбция с преобладанием процесса в области биофуркации
г) патологический вид резорбции
д) физиологический вид резорбции
028. Укажите сроки закладки зачатков постоянных зубов
а) на 1-м месяце утробной жизни
б) на 5-6 месяце утробной жизни
в) на 5-6 месяце жизни ребенка
г) на 2-м году жизни ребенка
д) на 4-5 году жизни ребенка
029. Минерализация 16,26,36,46 зубов начинается
а) на 5-м месяце утробной жизни
б) на 3-4-м месяце жизни ребенка
в) в конце антенатального периода
г) в возрасте ребенка 1-1. 5 года
5 года
д) в возрасте 2-2.5 лет
030. Минерализация 11,21,31,41 зубов начинается
а) на 8-м месяце утробной жизни
б) при рождении ребенка
в) на 5-м месяце жизни ребенка
г) на 1-м году жизни ребенка
д) на 2-м году жизни ребенка
031. Минерализация 15,25,35,45 зубов начинается
а) на 6-м месяце утробной жизни
б) на 1-м году жизни ребенка
в) на 2-2.5 году жизни ребенка
г) в возрасте ребенка 3 лет
д) в возрасте ребенка 4 года
032. Минерализация 17,27,37,47 зубов начинается
а) на 7-м месяце утробной жизни
б) в возрасте ребенка 1-1.5 года
в) в возрасте ребенка 1. 5-2.5 года
5-2.5 года
г) в возрасте ребенка 2.5-3 года
д) в возрасте ребенка 3-4 года
033. Зубы 11,21,31,41 прорезываются
а) в возрасте ребенка 5-6 лет
б) в возрасте ребенка 6-7 лет
в) в возрасте ребенка 6-8 лет
г) в возрасте ребенка 8 лет
д) в возрасте ребенка 9 лет
034. Зубы 12,22,32,42 прорезываются
а) в возрасте ребенка 5-6 лет
б) в возрасте ребенка 5-7 лет
в) в возрасте ребенка 6-8 лет
г) в возрасте ребенка 8 лет
д) в возрасте ребенка 9 лет
035. Зубы 13,23,33,43 прорезываются
а) в возрасте ребенка 5-7 лет
б) в возрасте ребенка 7-9 лет
в) в возрасте ребенка 7-11 лет
г) в возрасте ребенка 8-12 лет
д) в возрасте ребенка 9-10 лет
036. Зубы 14,15,24,25,34,35,44,45 прорезываются
Зубы 14,15,24,25,34,35,44,45 прорезываются
а) в возрасте ребенка 5-7 лет
б) в возрасте ребенка 7-11 лет
в) в возрасте ребенка 8-10 лет
г) в возрасте ребенка 8-12 лет
д) в возрасте ребенка 9-13 лет
037. Зубы 16,26,36,46 прорезываются
а) в возрасте ребенка 5-7 лет
б) в возрасте ребенка 7-9 лет
в) в возрасте ребенка 7-11 лет
г) в возрасте ребенка 8-10 лет
д) в возрасте ребенка 8-12 лет
038. Зубы 17,27,37,47 прорезываются
а) в возрасте ребенка 7-9 лет
б) в возрасте ребенка 8-11 лет
в) в возрасте ребенка 9-13 лет
г) в возрасте ребенка 10-12 лет
д) в возрасте ребенка 11-14 лет
039. Формирование корней 11,21,31,41 зубов заканчивается
Формирование корней 11,21,31,41 зубов заканчивается
а) в возрасте 8-9 лет
б) в возрасте 9-10 лет
в) в возрасте 10-12 лет
г) в возрасте 10-13 лет
д) в возрасте 11-12 лет
040. Формирование коней 12,22,32,42 зубов заканчивается
а) в возрасте ребенка 8-10 лет
б) в возрасте ребенка 9-10 лет
в) в возрасте ребенка 10-11 лет
г) в возрасте ребенка 11-12 лет
д) в возрасте ребенка 12-13 лет
041. Формирование корней 13,23,33,43 зубов заканчивается
а) в возрасте ребенка 9-10 лет
б) в возрасте ребенка 10-12 лет
в) в возрасте ребенка 12-14 лет
г) в возрасте ребенка 13-15 лет
д) в возрасте ребенка 15-16 лет
042. Формирование корней 14,24,34,44 зубов заканчивается
Формирование корней 14,24,34,44 зубов заканчивается
а) в возрасте ребенка 9-10 лет
б) в возрасте ребенка 10-11 лет
в) в возрасте ребенка 11-12 лет
г) в возрасте ребенка 12 лет
д) в возрасте ребенка 13-14 лет
043. Формирование корней 15,25,35,45 зубов заканчивается
а) в возрасте ребенка 9-10 лет
б) в возрасте ребенка 10-11 лет
в) в возрасте ребенка 11-12 лет
г) в возрасте ребенка 12-13 лет
д) в возрасте ребенка 14 лет
044. Формирование корней 16,26,36,46 зубов заканчивается
а) в возрасте ребенка 9-10 лет
б) в возрасте ребенка 10-11 лет
в) в возрасте ребенка 12 лет
г) в возрасте ребенка 13 лет
д) в возрасте ребенка 14 лет
045. Формирование корней 17,27,37,47 зубов заканчивается
Формирование корней 17,27,37,47 зубов заканчивается
а) в возрасте ребенка 9 лет
б) в возрасте ребенка 10 лет
в) в возрасте ребенка 13 лет
г) в возрасте ребенка 14 лет
д) в возрасте ребенка 15 лет
046. Чтобы снизить комплекс негативных реакций организма ребенка на лечение у стоматолога необходимо выполнить следующие мероприятия
а) во время манипуляции должны присутствовать родители
б) консультация невропатолога
в) мобилизация волевых усилий ребенка для повышения уровня мотивации к лечению
г) установление психологического контакта с ребенком
д) выбирается индивидуально
047. Для снятия психоэмоционального напряжения ребенка в условиях поликлиники чаще используются
а) снотворные
б) транквилизаторы диазепамового ряда
в) наркотические препараты
г) обезболивающие
д) не применяются
048. При удалении временного зуба в стадии значительной резорбции корней дает достаточную анестезию
При удалении временного зуба в стадии значительной резорбции корней дает достаточную анестезию
а) проводниковое обезболивание
б) аппликационное обезболивание
в) ингаляционный наркоз
г) инфильтрационное обезболивание
д) внутрикостное обезболивание
049. Укажите наиболее частое показание к применению местного инъекционного обезболивания в детской терапевтической стоматологии
а) неосложненный кариес
б) кюретаж зубодесневых карманов
в) хронический периодонтит
г) хронический пульпит
д) острая травма зуба с повреждением пульпы
050. Раствор адреналина в обезболивающий раствор детям до 3 лет
а) не добавляют
б) добавляют 2 капли раствора адреналина на 5 мл обезболивающего раствора
в) добавляют 2 капли раствора адреналина на 10 мл обезболивающего раствора
г) добавляют 1 каплю раствора адреналина на 5 мл раствора анестетика
д) добавляют 1 каплю р-ра адреналина на 10 мл анестетика
051. Укажите оптимальное нахождение конца инъекционной иглы при проведении проводниковой анестезии у нижнечелюстного отверстия у детей?
Укажите оптимальное нахождение конца инъекционной иглы при проведении проводниковой анестезии у нижнечелюстного отверстия у детей?
а) обязательно продвигать конец инъекционной иглы в нижнечелюстное отверстие
б) требуется точность проведения конца иглы к устью отверстия
в) можно ввести обезболивающий раствор в окружающие отверстие ткани
г) можно ввести обезболивающий раствор на 2 см кпереди от нижнечелюстного отверстия
д) этот метод обезболивания не применяется
052. Тактика по отношению к проведению туберальной анестезии при удалении временных жевательных зубов
а) обязательно проводить
б) не требуется
в) туберальную анестезию сочетать с местно-инфильтрационной
г) является методом выбора
д) не имеет значительных преимуществ перед местно-инфильтрационной
053. Лучшим анестетиком для периостотомии при гнойном воспалительном процессе является
Лучшим анестетиком для периостотомии при гнойном воспалительном процессе является
а) тримекаин 1%
б) новокаин 2% с добавлением адреналина
в) новокаин 2% без добавления адреналина
г) лидокаин 2% с добавлением адреналина
д) новокаин 1% с добавлением адреналина
054. Максимальная доза (допустимая) новокаина 2% для ребенка 5 лет
а) 1 мл
б) 2 мл
в) 5 мл
г) 10 мл
д) 20 мл
055. Преимущества тримекаина перед новокаином
а) более сильный анестетик
б) седативный эффект
в) менее выражены аллергические свойства
г) быстрее наступает эффект
д) все перечисленное
056. На возможность возникновения обморока у пациента не влияет
На возможность возникновения обморока у пациента не влияет
а) ребенок пришел натощак
б) долгое ожидание в очереди
в) неспокойное поведение других пациентов
г) суровость врача
д) не назван
057. При лечении обморока главным является
а) введение супрастина
б) введение средств, стимулирующих сердечную деятельность
в) горизонтальное положение больного
г) горизонтальное положение больного и рефлекторная стимуляция дыхания и кровообращения
д) не назван
058. С дефектом техники мандибулярной анестезии можно связать
а) неврит лицевого нерва
б) альвеолит в зоне удаленного зуба
в) воспалительную контрактуру крыловидных мышц
г) гематому в области ментального отверстия
д) ни один из перечисленных
059. Методикой проведения внутрикостной анестезии является
Методикой проведения внутрикостной анестезии является
а) обезболивающий раствор вводится только путем электрофореза
б) в основание десневого сосочка
в) перфорируя кость в периапикальной области
г) у детей не используется
д) место введения раствора в кость не имеет значения
060. Более рациональными способами обезболивания при вскрытии абсцессов и флегмон челюстно-лицевой области у детей являются
а) проводниковая местная анестезия
б) местно-инфильтрационное обезболивание с премедикацией
в) интубационный наркоз
г) масочный ингаляционный наркоз
д) аппликационная анестезия с премедикацией
061. Противопоказанием к использованию наркоза для санации полости рта в поликлинике может явиться
а) возраст до 3-х лет
б) наличие острого респираторного заболевания
в) аллергия к местным анестетикам
г) ребенок имеет болезнь Дауна
д) не названо
062. Укажите наиболее эффективный метод обезболивания при витальной экстирпации пульпы 43,42,41,31,32,33
Укажите наиболее эффективный метод обезболивания при витальной экстирпации пульпы 43,42,41,31,32,33
а) инфильтрационная анестезия
б) аппликационная анестезия
в) проводниковая анестезия
г) проводниково-инфильтрационная анестезия
д) ни одна из названных
063. Укажите наиболее частое показание к применению местного инъекционного обезболивания в детской терапевтической стоматологии
а) неосложненный кариес
б) лечение пульпитов
в) при острых и обострившихся хронических периодонтитах
г) при снятии зубных отложений
д) кюретаж зубодесневых карманов
064. Показанием к применению аппликационного обезболивания в терапевтической стоматологии не может быть
а) обработка патологических зубодесневых карманов
б) препарирование твердых тканей постоянных зубов
в) лечение заболеваний слизистой оболочки полости рта
г) обезболивание места вкола инъекционной иглы
д) при повреждении слизистой оболочки полости рта
065. Укажите профилактику аллергических осложнений местного инъекционного обезболивания
Укажите профилактику аллергических осложнений местного инъекционного обезболивания
а) правильное приготовление и хранение местных анестетиков
б) проведение цветной пробы по Лукомскому
в) взаимодействие в работе медперсонала
г) точное соблюдение методики проведения местной инъекционной анестезии
д) тщательное выяснение аллергического анализа
066. Положительными свойствами лидокаина являются
а) вызывать быстро наступающую глубокую и продолжительную анестезию
б) не вызывать существенных изменений пульса, артериального давления, дыхания
в) совместимости с сульфаниламидами, наркотическими веществами, антибиотиками
г) малотоксичность
д) все перечисленное
067. Укажите наиболее рациональный метод обезболивания для удаления 36 по поводу хронического периодонтита
а) электрообезболивание
б) общее обезболивание
в) аппликационное обезболивание
г) проводниковое обезболивание
д) акупунктура
068. При удалении моляров верхней челюсти у детей наболее целесообразна
При удалении моляров верхней челюсти у детей наболее целесообразна
а) проводниковая анестезия
б) инфильтрационная анестезия при помощи шприца
в) общее обезболивание
г) аппликационная анестезия
д) акупунктура
069. Рост челюстных корней у детей происходит
а) равномерно по годам
б) наиболее активно: в 1-3 года, 6-8 лет, 13-15 лет
в) наиболее активно: 3-5 лет, 10-12 лет
г) наиболее активно до года
д) наиболее активно после 15 лет
070. У новорожденных зачатки зубов на верхней челюсти находятся
а) в десневом валике
б) в альвеолярном отростке
в) прилежат к дну глазницы
г) резцы уже прорезались
д) отсутствуют
071. Для челюстных костей детского возраста характерны следующие анатомические особенности
Для челюстных костей детского возраста характерны следующие анатомические особенности
а) губчатое вещество преобладает над компактным, слабо минерализовано, богато васкуляризовано
б) компактный слой преобладает над губчатым, хорошо минерализован, слабо васкуляризован
в) компактный слой преобладает над губчатым, слабо васкуляризован и минерализован
г) преобладает губчатое вещество, хорошо минерализовано
д) компактное и губчатое вещества представлены поровну
072. Срастание костей неба происходит
а) на первом году жизни
б) в первом триместре беременности
в) во втором триместре беременности
г) в третьем триместре беременности
д) не срастается никогда
073. У детей одонтогенные воспалительные процессы чаще встречаются
а) после 10 лет
б) в 1-3 года
в) в 6-8 лет
г) в 3-5 лет
д) в 10-12 лет
074. Временные зубы у детей имеют
Временные зубы у детей имеют
а) большую пульповую камеру, широкие каналы
б) большую пульповую камеру, узкие каналы
в) маленькую пульповую камеру, широкие каналы и большое верхушечное отверстие
г) пульповая камера не сформирована
д) маленькая пульповая камера, узкие каналы и узкое верхушечное отверстие
075. Становление дезинтоксикационной функции печени и почек происходит
а) к 1 году
б) к 3-4 годам
в) к 6-8 годам
г) к 10 годам
д) после 15 лет
076. Иммунологическая реактивность у новорожденного
а) у доношенных высокая, у недоношенных низкая
б) у доношенных низкая, у недоношенных высокая
в) как у доношенных, так и у недоношенных высокая
г) как у доношенных, так и у недоношенных низкая
д) у новорожденных иммунологической реактивности нет
077. Барьерная способность лимфатической системы у детей завершается
Барьерная способность лимфатической системы у детей завершается
а) к периоду новорожденности
б) формируется к году
в) заканчивается формирование после 15 лет
г) формируется к 7 годам
д) формируется к 10 годам
078. Экспозиция диатермокоагуляции пульпы при методе витальной экстирпации
а) 3-4 сек
б) 6-7 сек
в) 60 сек
г) 20 сек
д) 1 мин 20 сек
079. Целесообразным физиотерапевтическим методом при обострении после пломбирования канала при наличии отека, гиперемии является
а) гидротерапия
б) микроволны
в) УВЧ
г) электрофорез новокаина
д) излучение гелий-неонового лазера
080. При кариесе наиболее целесообразен
При кариесе наиболее целесообразен
а) электрофорез
б) общее ультрафиолетовое облучение
в) КУФО
г) микроволны
д) дарсенваль
081. При лечении так называемого остаточного или корневого пульпита в зубе с плохопроходимыми корневыми каналами лучше применять
а) диатермокоагуляцию
б) внутриканальное УВЧ
в) электрофорез иода (10% настойка)
г) электрофорез трипсина
д) флуктуоризацию
082. УВЧ-терапия показана при следующих заболеваниях
а) при кариесе
б) при хроническом периодонтите
в) при пороке зубов
г) при острой форме периодонтита
д) при хроническом пульпите
083. Лекарственные вещества вводятся
Лекарственные вещества вводятся
а) с положительного полюса
б) с полюса, имеющего одинаковый заряд с ионом лекарственного вещества
в) с полюса, имеющего заряд, противоположный иону лекарственного вещества
г) с отрицательного полюса
д) с любого полюса
084. Электрофорез — это
а) применение с лечебной целью электротока
б) применение с лечебной целью электротока высокой частоты
в) введение лекарственных веществ в ткани посредством тока
г) введение лекарственных веществ в ткани посредством светового излучения
д) введение лекарственных веществ с помощью ультразвукового аппарата
085. Гидрофильная прокладка должна
а) предохранять кожу от ожога
б) способствовать равномерному распределению тока
в) уменьшать сопротивление ткани постоянному току
г) уменьшать нагревание ткани
д) уменьшать раздражающее действие переменного тока
086. Гальванизация в стоматологии — это
Гальванизация в стоматологии — это
а) применение с лечебной целью постоянного электрического тока высокого напряжения
б) применение с лечебной целью переменного электрического тока высокого напряжения
в) применение с лечебной целью постоянного электрического тока низкого напряжения и небольшой силы
г) применение света с лечебной целью
д) применение с лечебной целью импульсного тока низкого напряжения и частоты
087. Физиологическое действие постоянного тока на живые ткани обусловлено
а) перемещением ионов, нарушением ионной конъюктуры тканей
б) нагреванием тканей вследствие образования значительного количества топлива
в) раздражающим действием тока
г) воздействием постоянного тока на лимфатические и кровеносные сосуды
д) воздействием на нервные рецепторы
088. Физическими факторами, применяемыми для профилактики кариеса, являются
Физическими факторами, применяемыми для профилактики кариеса, являются
а) импульсный ток низкого напряжения и частоты
б) криотерапия и гипотерапия
в) переменные электрические токи и электромагнитные поля
г) электрофорез и светолечение
д) парафино-, озокерито- и грязелечение
3-8Квадратный корень из 81 — Как найти квадратный корень из 81?
LearnPracticeDownload
81 — это число в форме полного квадрата и четвертая степень числа 3, т. е. ( 3 4 ). В этом уроке мы вычислим квадратный корень из 81 методом многократного вычитания и решим несколько интересных задач.
е. ( 3 4 ). В этом уроке мы вычислим квадратный корень из 81 методом многократного вычитания и решим несколько интересных задач.
- Квадратный корень из 81 : √81 = 9
- Квадрат 81: 81² = 6 561
| 1. | Что такое квадратный корень из 81? |
| 2. | Является ли квадратный корень из 81 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 81? |
| 4. | Важные примечания по квадратному корню из 81 |
| 5. | Сложные вопросы |
| 6. | Часто задаваемые вопросы о квадратном корне из 81 |
Что такое квадратный корень из 81?
- Квадратный корень числа — это число, которое при умножении на себя дает исходное число как произведение.
 Нахождение квадратного корня числа является обратным действием возведения числа в квадрат.
Нахождение квадратного корня числа является обратным действием возведения числа в квадрат. - 81 = а × а = а 2
- Таким образом, a = √81= √(9 × 9)
- 9 × 9 = 81 или -9 × -9 = 81. Следовательно, √81 = ± 9
- Это показывает, что 81 — полный квадрат.
Является ли квадратный корень из 81 рациональным или иррациональным?
- Рациональное число определяется как число, которое может быть выражено в виде частного или деления двух целых чисел, т. е. p/q, где q не равно 0.
- 9 и -9 могут быть выражены как 9/1 и -9/1
- Оба числа могут быть представлены в виде рационального числа.
- Следовательно, квадратный корень из 81 является рациональным числом.
Как найти квадратный корень из 81?
Квадратный корень из 81 можно вычислить с помощью различных методов, таких как разложение на простые множители или метод повторного вычитания.
Квадратный корень из 81 методом многократного вычитания
Начните с 81 и продолжайте вычитать последовательные нечетные числа, пока не получите ноль. Общее число, которое мы вычитаем, представляет собой квадратный корень из 81.
Общее число, которое мы вычитаем, представляет собой квадратный корень из 81.
- 81 — 1 = 80
- 80 — 3 = 77
- 77 — 5 = 72
- 72 — 7 = 65
- 65 — 9 = 56
- 56 -11 = 45
- 45 -13 = 32
- 32 -15 = 17
- 17 — 17 = 0
Таким образом, начиная с 81, мы вычли 9 раз, чтобы получить 0. Таким образом, квадратный корень из 81 равен 9.
Квадратный корень из 81 методом простой факторизации главные факторы.
Исследуйте Квадратные корни с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 16
- Квадратный корень из 169
- Квадратный корень из 25
- Квадратный корень из 125
- Квадратный корень из 100
Важные примечания
- Квадратный корень из 81 выражается как √81 в радикальной форме и как 81 ½ в экспоненциальной форме.

- Квадратный корень из 81 означает второй корень из 81 = +9 или -9
- Квадратный корень только из полных квадратов можно легко вычислить с помощью метода простой факторизации или метода повторного вычитания. 81 — идеальный квадрат.
Сложные вопросы
- Майк использует лестницу длиной 15 футов и начинает красить стену. Ножка лестницы 9в футах. Если высота стены от земли 12 футов, то на каком расстоянии от земли находится основание лестницы?
Пример 1: Сэм решил посадить в своем саду 81 розу таким образом, чтобы в каждом ряду было столько растений, сколько рядов. Найдите количество рядов и количество растений в каждом ряду.
Решение:
Количество рядов × количество растений розы = 81 растение розы
Учитывая, что количество рядов = количество растений = n
п × п = 81 91 103 п 2 = 81
n = ± 9
Ряды и растения нумеруются только положительно.
Следовательно, у Сэма может быть 9 рядов по 9 роз в каждом.Пример 2: Данио находит квадратное цифровое изображение на веб-сайте. Изображение содержало 810 000 пикселей. Какова высота изображения в пикселях?
Решение:
Пиксели, занимаемые изображением = площадь квадратного изображения = 810 000 пикселей.
Длина или высота изображения = сторона квадрата
сторона × сторона = 810000
сторона = √ 810000
= (81 × 10000) ½
= (9 2 × 100 2 ) ½
= (9 × 100) = 900 пикселей 90 907
перейти к слайдуперейти к слайду
Хотите создать прочную основу для изучения математики?
Выйдите за рамки заучивания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 81
Чему равен квадратный корень из 81?
Квадратный корень из 81 равен +9 или -9.
Почему квадратный корень из 81 меньше 9?
81 = — 9 х -9. Таким образом, квадратный корень из 81 может быть отрицательным 9.
Является ли 81 иррациональным числом?
Нет, 81 — рациональное число. Его можно выразить рациональным числом как 81/1
Между какими двумя числами лежит квадратный корень из 81?
Квадратный корень из 81 лежит между 8 и 10.
Какими методами можно найти квадратный корень из 81?
Мы можем найти квадратный корень из 81, используя метод факторизации простых чисел или метод повторного вычитания.
Рабочие листы по математике и визуальная программа
81 квадратный корень? | √81
| Пожалуйста, введите реальный номер: |
| Результат квадратного корня: |
Вот ответ на такие вопросы, как: 81 квадратный корень? | √81 или чему равен квадратный корень из 81?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа. См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
Вавилонский метод, также известный как метод Героя
См. ниже пошаговое вычисление квадратного корня из 81 с помощью вавилонского метода , также известный как Метод Героя .
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это число х, такое что х 2 = а, другими словами, число х, квадрат которого равен а. Например, 9 — это квадратный корень из 81, потому что 9 2 = 9•9 = 81, -9 — это квадратный корень из 81, потому что (-9) 2 = (-9)•(-9) = 81.
Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до ближайшей тысячной.
| нет | нет 2 | √ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.000 | |||||||
| 2 | 4 | 1. 414 414 | |||||||
| 3 | 9 | 1.732 | |||||||
| 4 | 16 | 2.000 | |||||||
| 5 | 25 | 2.236 | |||||||
| 6 | 36 | 2.449 | |||||||
| 7 | 49 | 2.646 | |||||||
| 8 | 64 | 2.828 | |||||||
| 9 | 81 | 3.000 | |||||||
| 10 | 100 | 3.162 | |||||||
| 11 | 121 | 3.317 | |||||||
| 12 | 144 | 3,464 | |||||||
| 13 | 169 | 3,606 | |||||||
| 14 | 1969 | 3,742 | |||||||
| 196 | 3,742 | ||||||||
| 0004 15 | 225 | 3.873 | |||||||
| 16 | 256 | 4.000 | |||||||
| 17 | 289 | 4.123 | |||||||
| 18 | 324 | 4.243 | |||||||
| 19 | 361 | 4. 359 359 | |||||||
| 20 | 400 | 4.472 | |||||||
| 21 | 441 | 4.583 | |||||||
| 22 | 484 | 4.699 3 | 22 | 484 | 4.6990 | ||||
| 23 | 529 | 4.796 | |||||||
| 24 | 576 | 4.899 | |||||||
| 25 | 625 | 5.000 | .
| 7.071 |
| нет | нет 2 | √ | |
|---|---|---|---|
| 51 | 2,601 | 7.141 | |
| 52 | 2,704 | 7.211 | |
| 53 | 2,809 | 7.280 | |
| 54 | 2,916 | 7.348 | |
| 55 | 3,025 | 7,416 | |
| 56 | 3,136 | 7,483 | |
| 57 | 3,249 | 7.550 | |
| 58 | 3,364 | 7. 616 616 | |
| 59 | 3,481 | 7.681 | |
| 60 | 3,600 | 7.746 | |
| 61 | 3,721 | 7,810 | |
| 62 | 3 844 | 7,874 | |
| 63 | 3 969 | 7,937 | |
| 64 | 4 000 4.9376 | 8.000 | |
| 65 | 4,225 | 8.062 | |
| 66 | 4,356 | 8.124 | |
| 67 | 4,489 | 8.185 | |
| 68 | 4,624 | 8.246 | |
| 69 | 4 761 | 8.307 | |
| 70 | 4 900 | 8,367 | |
| 5 041 | 8.426 | 0011 | |
| 72 | 5,184 | 8.485 | |
| 73 | 5,329 | 8.544 | |
| 74 | 5,476 | 8. 602 602 | |
| 75 | 5,625 | 8.660 |
| нет | нет 2 | √ |
|---|---|---|
| 76 | 5 776 | 8,718 |
| 77 | 5 929 | 8,775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6 724 | 9.055 |
| 83 | 6 889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 9.165 | ||
| 9.165 | 0005 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9. |

 {2}}=1$.
{2}}=1$. \]
\]
 Нахождение квадратного корня числа является обратным действием возведения числа в квадрат.
Нахождение квадратного корня числа является обратным действием возведения числа в квадрат.

 657
657 633
633